Throughout this section are presented the results obtained when applying the methodology proposed by the authors to the case study presented in the previous section. There are three sub-sections. The first one presents the results for the selected Scenario. Since there is a limitation space, the authors choose to show the full and detailed study for one scenario where k = 3. The second sub-section present the aggregated results for the remaining k scenarios studied. In the third sub-section is presented the sensitivity analysis study concerning the influence of dynamic tariffs on the remuneration of DR.
5.1. Selected Scenario: k = 3
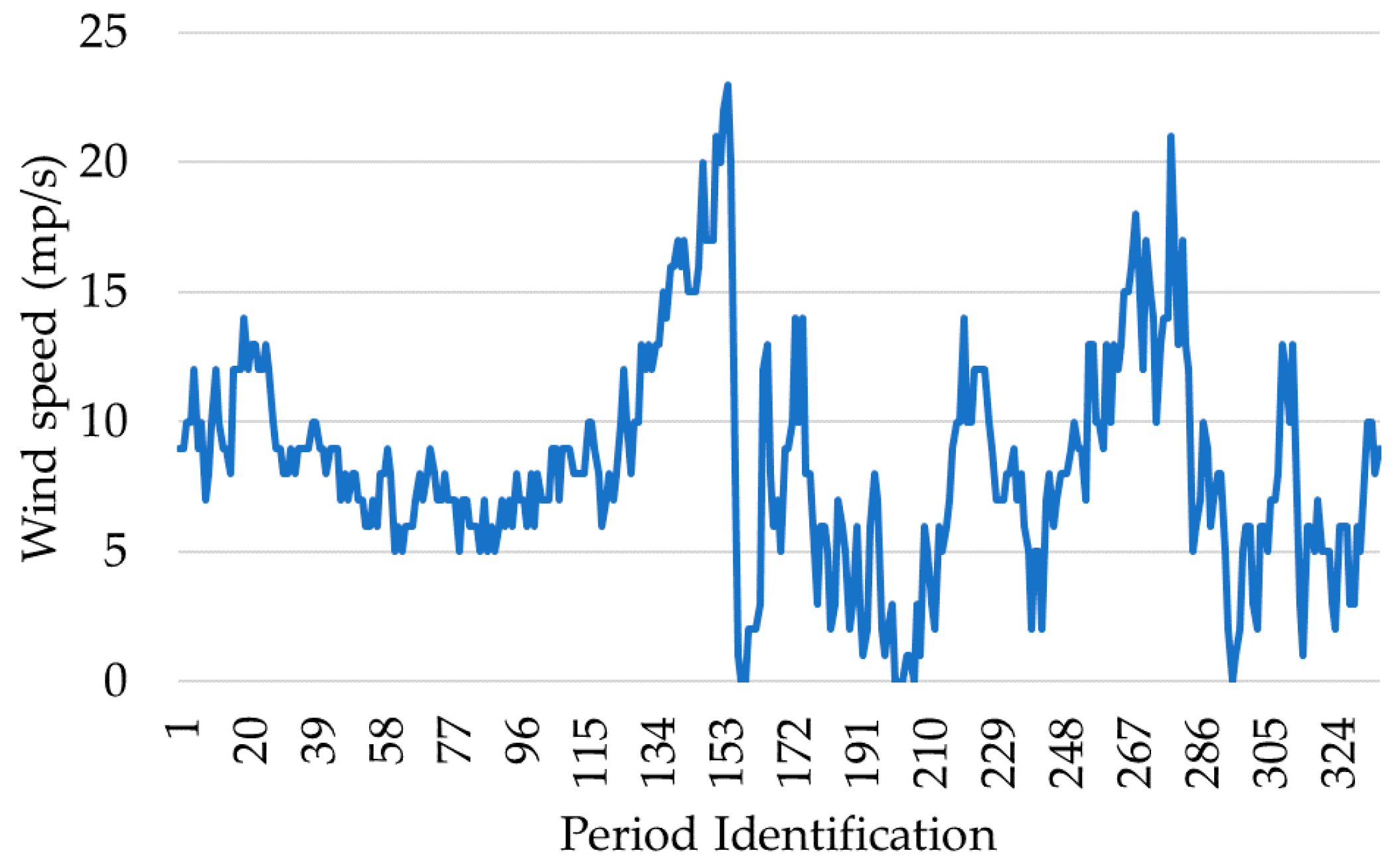
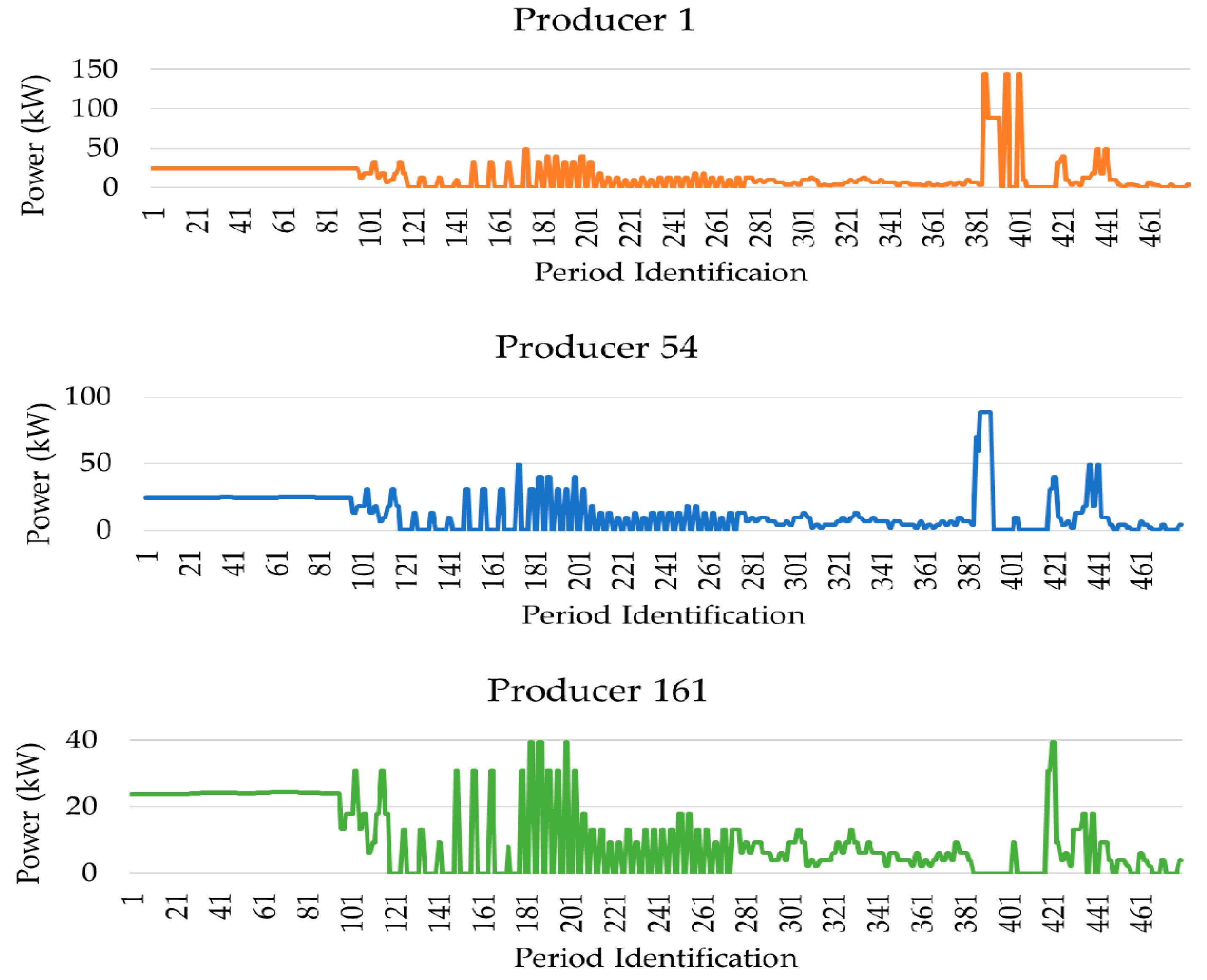
Although the main focus is on the consumers’ results regarding DR programs, the results of the optimization for wind generation, when k = 3, are presented. The results from one wind producer for each group found through k-means are presented in
Figure 7.
As can be seen, there are many periods in which the result for these three wind producers reaches a value of 0, however, when comparing with
Figure 2, there was wind in these periods. This is the effect of cut-in and cut-out wind speeds.
Since the second phase of the proposed methodology is the focus of this work, one of the k values was selected, k = 3. The aggregation phase is done using the clustering method k-means through software R and considering separate clusters, i.e., each resource is grouped by type—DR and DG. Consumers of IDR programs will be the focus of this study being the only resources considered in the aggregation presented in this section. As mentioned and due to the high number of consumers in the database studied,
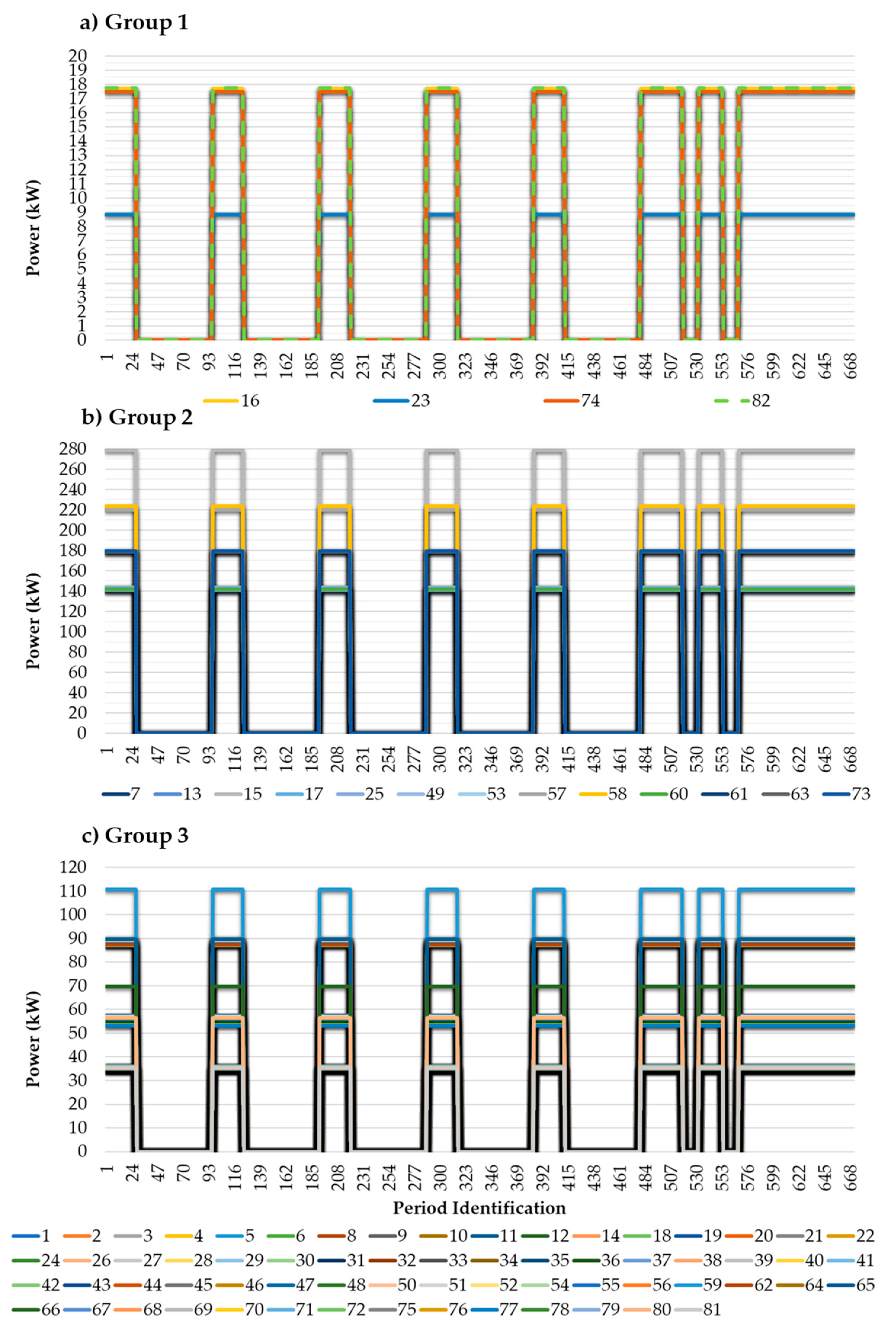
Figure 8 shows the results of the optimization only for Medium Commerce consumers belonging to IDR.
The figures are divided by the groups that were formed by the chosen aggregation method, k-means, for the 82 elements of Medium Commerce. The x-axis represents the periods studied, with each being assigned an identification. The database is divided into 15-min periods. To form a full week, period 1 represents the hour 00 and minute 00 of the day January 2, 2018 and the last period represents hour 23 and minute 15 of day January 8, 2018.
Figure 8a presents the results for Group 1 consisting of four elements. Through the analysis of the graph, we can see these elements are the ones that obtained a lower reduction during the week, not reaching the 20 kW in any of the studied periods. Group 2, shown in
Figure 8b, consisted of 13 elements, obtained reductions between 140 and 280 kW. In relation to Group 3,
Figure 8c shows the results and since this group holds most of the elements, about 65. This group contains elements that managed to reduce, although they are lower values to Group 2, between approximately 35 and 110 kW. In all the figures, there are periods in which reduction was not possible, and it is also emphasized that, when there was reduction, it is maximum and equal in all periods for each consumer.
The k-means function also gives the centroid value for each group. The centroid values allow us to estimate the average value of reduced power, making it easier to assign a new resource to a given group.
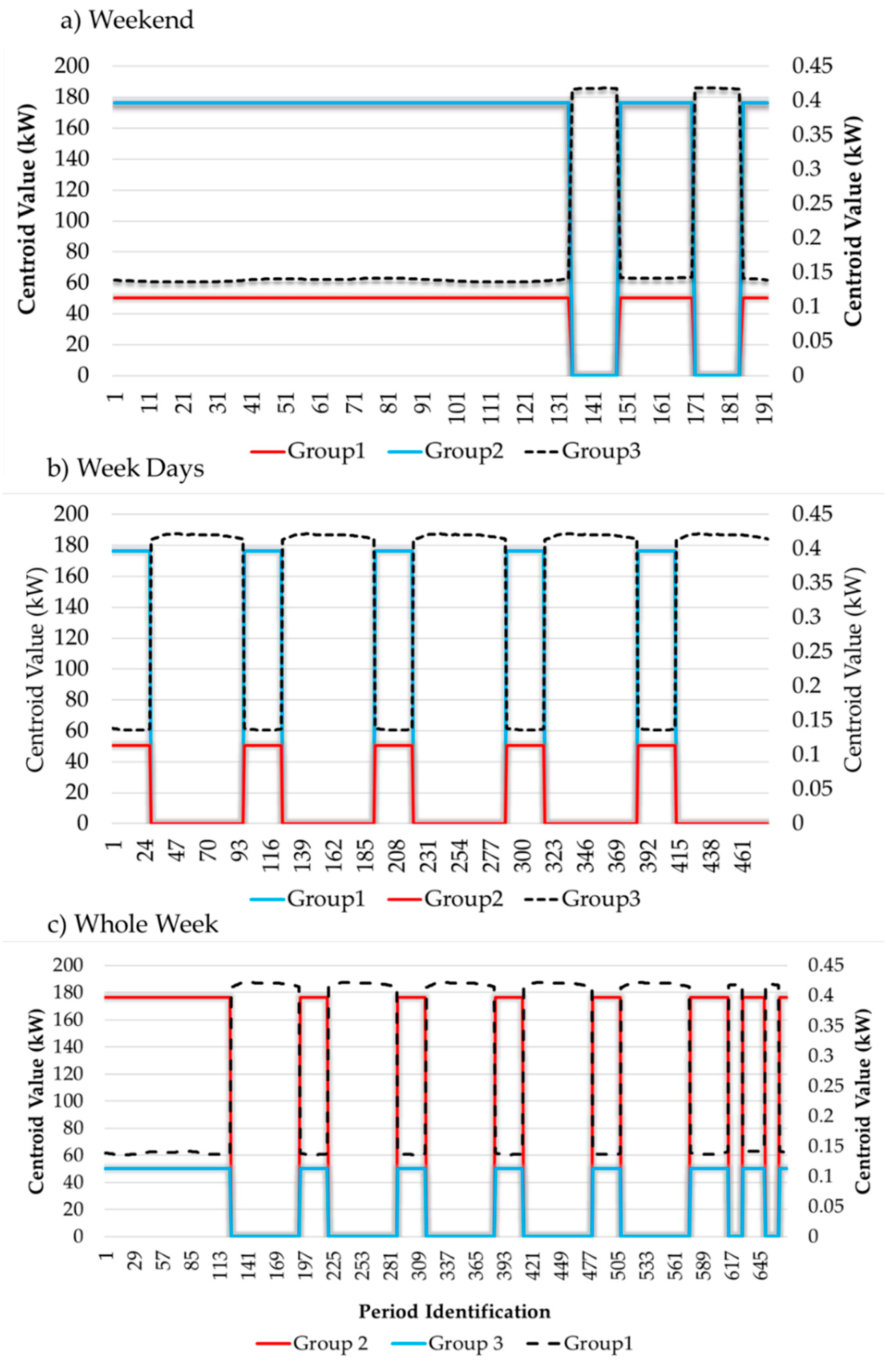
Figure 9 presents this value for different aggregations studied in the proposed methodology—WW, WD and W—and always for k = 3. Due to the difference in scale of some curves, there are two y-axes to be able to see those that are in the dashed line.
Although the notation of the assigned group is different, it is possible to perceive a tendency to create groups with a similar level of centroids. In other words, there is a group of consumers, where in certain periods, it achieves high reductions up to 175kW; another with medium reductions around 50 kW and the remainder with values that do not reach ~1 kW. This information allows the aggregator to allocate new resources faster to existing groups, bypassing this step and moving to pay.
Table 3 shows the tariffs for each group and the result of the total remuneration of the different scenarios studied in the proposed methodology, for the k selected in this section.
Through the initial price of each resource, the definition of the tariff was made finding the maximum price of each group, and all elements will be paid at the highest tariff. In this way, most of the resources will benefit, since most of these will see the price of remuneration rise. The first part of
Table 3 shows the final remuneration rate of each group. The total final remuneration value was calculated by the product of the contribution of each IDR consumer and the respective group rate. That is, only the resources that were scheduled, are remunerated. When comparing the remunerations, the case of separately aggregating the WD and W would be more important for the aggregator. The resources are paid at high rates and even then, it will be possible to save in relation to WW aggregation
5.2. Other Scenarios: k = 4 to k = 6
In this subsection the results for the aggregation of consumers of IDR programs and their respective remuneration by groups will be presented. The aggregation was done once again using the capabilities of the k-means clustering method and through software R. Throughout this subsection three different k, k = 4 to k = 6 are analyzed. For each of these, three different scenarios were studied, as expected in the proposed methodology: WW, WD and W.
Table 4 shows the summary of results for the application of the selected clustering method for the three scenarios studied and for k = 4 to k = 6. This table shows the element numbers for each group. Analyzing WW, in k = 4 Group 1 gathers the largest number of elements, where 51% belong to SC and 48% to DM. Still in this group are the totality of LC and ID elements. Group 2 consists only in MC elements, containing 65 of the 85 elements belonging to the database. Group 3 is constituted by DM and SC in its majority, with only 4 MC elements. Group 4 contains the remaining MC elements. Turning to k = 5, Groups 1, 2 and 5 contain only MC elements; Group 3 is the group that aggregates more elements and contains the same elements as Group 1 of k = 4; Group 4 consists in 67% DM, 33% SC and a small percentage of MC. Finally, in k = 6, Groups 1, 5 and 6 with only MC elements; Group 2 is divided in DM and SC element; Group 3 has 99.71% DM elements and 0.29% MC; Group 4 contains all elements of the LC and ID database and still 76% of the DM and 79% of the SC.
Regarding to WD, in k = 4, Groups 1,3 and 4 consist of MC elements in their entirety; Group 2 aggregates the remaining types of consumers and only 4 MC elements. In k = 5, group 1 aggregates the total LC and ID and still a large part of elements of DM and SC, this time there is no MC in this group that contains most of the elements; the MC elements are grouped into Groups 2,3 and 5; Group 4 consists of DM in 69.84%, SC in 30.02% and MC in 0.13%. Finally, at k = 6, the elements of MC form the Groups 1,3 and 4; Group 2 consists of 90.63% DM elements, the remainder are SC and MC; group 5, unlike the previous one, is constituted mostly by SC and the remaining elements are DM; the last group, contains the elements of LC, ID, DM and SC.
For the case of W, in k = 4, Group 1 consists mostly of DM elements and 4 MC consumers; Group 2 contains 9828 elements of SC, 8782 of DM and the entire LC and ID elements from database; Group 3 and Group 4 aggregate only MC elements. At k = 5, Groups 1 and 2 comprehend only MC elements; Group 3 contains the totality of SC, LC and ID also counting with some elements of DM; Group 4 contained of elements of DM only; Group 5 contains 1369 elements of DM and 4 elements of MC. Finally, at k = 6, Groups 1, 2 and 3 have elements of MC only; Group 4 contains 99.71% DM and 0.29% MC; Group 5 is comprised in its entirety by DM and Group 6 contains all the elements of SC, LC and ID and 4363 elements of DM.
In this way it is concluded that the elements of MC are quite different from each other and from the other types, being a constant the formation of groups with only these elements. Consumers of DM and SM are similar, forming, for the most part, groups with each other. Regarding LC and ID, in all cases, they belonged to the same group.
The selected clustering method, in addition to assigning the group to each element of the database, outputs the centroid of each group. Due to space constraints, it was not possible to display all values for all periods.
Table 5 shows the maximum and minimum values of each group for the periods of each case.
Starting with WW, in k = 4 there are two groups that not exceed 2 kW, group 3 and 4; Group 1 reaches 176.30 kW and Group 2 reaches 50.36 kW. In k = 5, some groups remain the same in relation to the previous k, namely Group 1, group 3 and 4; Group 2 this time reaches 39.81 kW and Group 5 reaches 88.80 kW. For k = 6, the groups with the lowest value are 2, 4 and 6; the remainder are in the range of 40.38 kW and 205.54 kW.
Then the case of WD, at k = 4, the group with the lowest value does not reach 1 kW, while Groups 1, 3 and 4 reach 106.67 kW, 205.55 kW and 40.39 kW, respectively. At k = 5, there are more groups around 1 kW, these being 1,2 and 3; for Groups 5 and 6, the values are higher around 50 kW and 175 kW, respectively. Finally, k = 6, Groups 2,4 and 5 find their maxima between 40 and 205 kW approximately, while the others remain with their values close to 1 kW.
Finally, in W, k = 4 formed two groups that are around 1 kW and the rest have their maximums at 50.36 kW and 176.30 kW. In k = 5, the groups with smaller values remain as k = 4; Group 3 has a maximum of 88.80 kW, Group 4 reaches 176.30 kW and Group 5 drops to 39.81 kW. For k = 6, Group 1 does not reach 0.5 kW, Group 2 is around 180 kW, Group 3 has a maximum of 39.81 kW, Group 4 is around 1 kW, Group 5 was close to reaching 89 kW and Group 6 has a minimum value of 0.28 kW and a maximum value of 0.29 kW.
Thus, it is concluded that there are three main bands: consumers with small reductions (~1 kW), consumers with medium reductions (~39 kW and 107 kW) and consumers with high reductions (above 107 kW). The analysis of the
Table 5 is useful in case the VPP wants to introduce new resources or consumers to the already aggregated ones. Through the knowledge of these three types of bands and in the case of existing historical data, VPP can perceive in which group these are inserted without having to go through all the phases again.
The remuneration of the members of the groups is made taking into account the tariffs in
Table 6. The tariffs presented were created taking into account the value of the initial tariff of each of the elements. The authors considered that the remuneration tariff of each group would be the maximum value of each group. Thus, all elements would benefit.
As presented, the values are higher than the case if the resources were remunerated with the initial tariff. Still, it can be advantageous for the aggregator since with the implemented tariff, the actual response from one of the resources associated with this entity is more reliable, as the resources with same characteristics will be in the same group and paid at highest price, with the proposed methodology. In this way, for WW, the lowest pay price was found through k = 6, with 1,145,528.00 m.u. If we compare this value with the sum of WD and W for k = 6, we realize that this value is higher, concluding that with a greater amount of information it will be possible to find groups that are better suited to the situation. Regarding WD, the highest value was obtained in k = 4, almost reaching 900 000,00 m.u. For the W, this is the only one that the possibility of remuneration through aggregation groups, gets a lower value than the individual, in k = 6, with 228,161.48 m.u.
The higher tariff is 0.2253 m.u./kWh, found in both WW and WD. Regarding W, since that cost was not available, the higher one, and mostly used, is 0.1986 m.u./kWh. The results of remuneration for each group and for the totals are shown in
Table 7.
In
Table 7, although the remuneration proposed in the methodology is higher than the total in the individual remuneration case (in most cases), this difference will be important to keep resources motivated to participate in the management of the network operation. With this, VPP will be able to reduce the uncertainty associated with the participation of these resources and even attract more resources for aggregation. To prove this, another study was carried out.
For the lowest value of remuneration found in the three k clusters studied in this section (k = 6), we intend to compare this remuneration method with other methods. Thus,
Table 8 shows the definition of the methods tested and
Table 9 the results obtained by method for each of the study scenarios. The results of the first phase of the methodology—optimization were considered for this study. Thus, null values also considered as consumers who have not reduced their consumption, will not be considered for the application of this methods.
Method 1 proposes that each consumer should be remunerated individually. Thus, according to what has reduced in a given period, each of the consumers receives according to the tariff applied in that same period. Method 2 applies the average for the tariffs of each type of consumer. For example, for all consumers DM is calculated the average tariff and then applied to all equally. Method 3 uses the remuneration formula presented in [
15] and [
28] and is done individually. Method 4 is presented in the methodology proposed in this paper.
By analyzing
Table 9, it’s easy to realize that Method 3 is the one that generates the lowest total remuneration, in all cases. However, compared with the other methods, it is considered that if consumers are remunerated in this way, they may not be motivated to participate with the VPP. The remaining methods have closer results. In W, the highest value is presented by Method 2 and in the remaining, WD and WW, Method 4. It is difficult to guarantee the reduction by each consumer since it is voluntary for DR programs, however it is anticipated that the greater the incentive is, the higher is the participation. In this way, according with the limits imposed for VPP to manage the market and still remunerate each consumer fairly, Method 4 becomes the more successful. However, in order to discuss even further the relevance of the proposed methodology, another comparison was performed: taking into account that the resources are paid according their availability, in other words, the provided demand reduction, in the case of the consumers.
Table 10 presents the value of remuneration with this non-discriminatory approach for the three scenarios.
Comparing the values from
Table 10 with the previous
Table 9, has been proven that the proposed methodology can provide lower remuneration costs for the aggregator and still reward fairly every consumer for their participation.
5.3. Influence of the variations in the dynamic tariffs
Another test was carried out to analyze the influence of the formation of the tariff on the final remuneration. In this way, tests were performed for the three different time frames. The formation of the tariff for this specific case was made through two tariffs: the fixed tariff and an indexed tariff. The indexed tariff is the real-time energy price for the week selected for the previous study case (January 2, 2018 to January 8, 2018).
Table 11 shows the average values for each day of the study week. It is emphasized that this study was done only for DR consumers associated with VPP.
The objective will be to understand the influence that this new tariff will have on the final remuneration results. To assessment this method, several tests were performed varying the weight of each of the variables that form this new tariff.
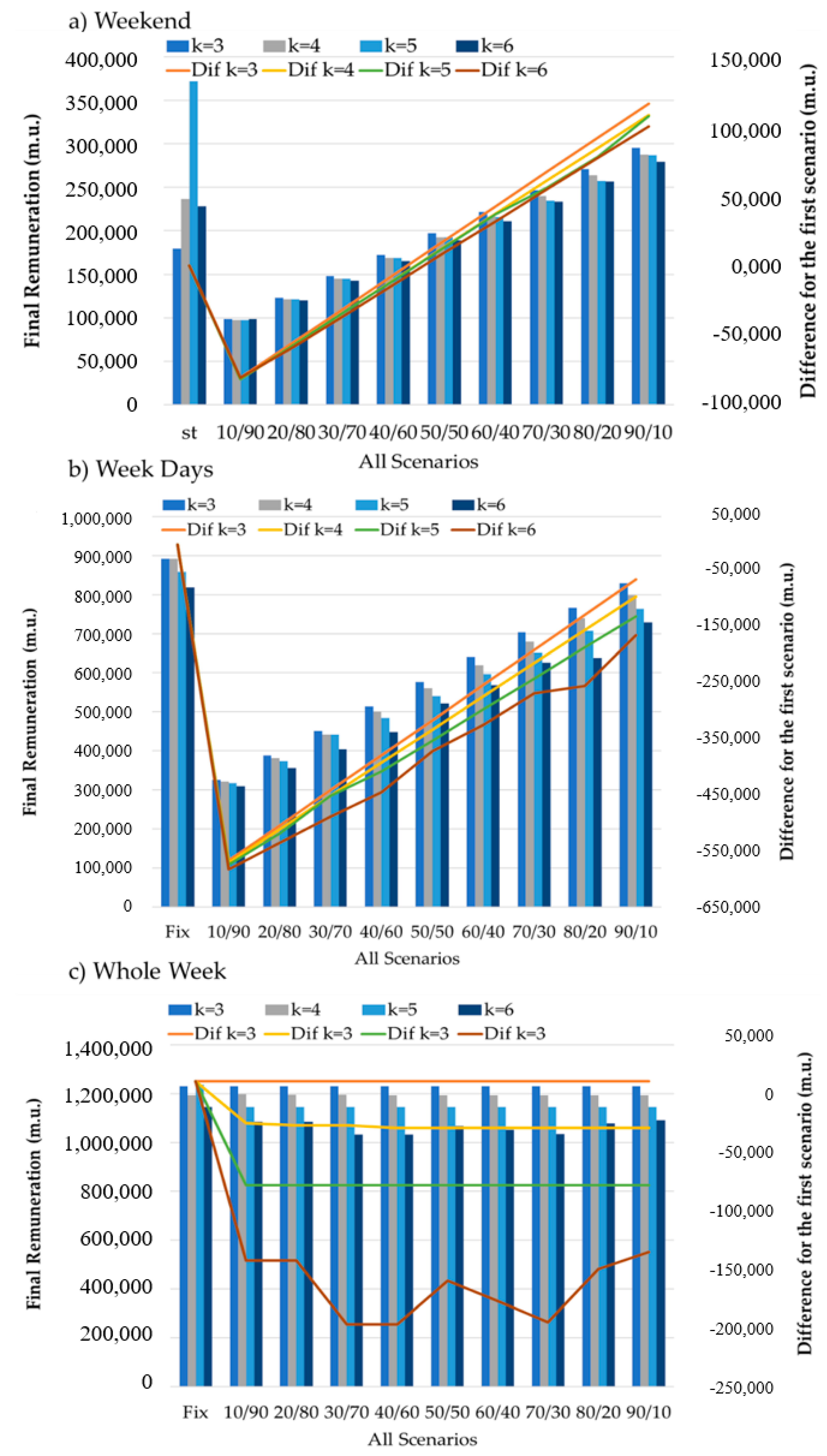
Figure 10 shows the results. Fix is considered to be the study for fixed tariff only; in the following cases, the first value represents the percentage of fixed tariff present in this situation and the second value the percentage of tariff indexed in the same situation. This figure also presents a line for each k studied. This line represents the final remuneration difference between the case study with the initial tariff and the remaining ones. With this, it will be possible to understand the effect of the indexed tariff on the final remuneration.
Starting from W, it is noticeable that in the case where the tariff is fixed, the highest value was found in k = 5, not reaching this value in any other case. It is also noted that the value of the difference ceases to be negative from the 50/50 case. The highest positive difference value reached in this study was 81,469.71 m.u. in k = 5 in the 10/90 case. This would be expected, since the weight of the indexed tariff is higher and this was the case that reached the highest value of remuneration, as already mentioned.
Turning to WD, in the initial case, only fixed tariff, the remuneration value formed by k = 3 and k = 4 are very similar, these being the highest values verified. Here, the difference did not reach a positive importance, being –582,548.17 m.u. the lowest value reached. The difference of values is practically linear in all cases except for k = 6 that varies a lot regarding the others.
Concerning WW, and contrary to the other studies, the final remuneration values obtained were not very different from the initial case. The most notorious differences are found in k = 6 but although do not reach the –200,000.00 m.u. value for any case study. The value of k = 3 is equal, maintaining the difference null; in k = 4 it reaches –38,309.32 m.u.; in k = 5 the value is the same for all situations, keeping a difference of –85,213.07 m.u.
Thus, it can be concluded that, by studying the weekend and the week separately, there is an influence of the notable indexed tariff on all clusters formed. In the case of the study of the whole week, the influence of this new tariff only begins to be noticed in values greater than k.
Therefore, for VPP, it is more beneficial to consider the indexed tariff in the formation of the remuneration tariff. In this study and for most cases, the higher the percentage of the indexed tariff in the formation, the lower the final remuneration was. It should be noted, however, that the value of this indexed tariff is much lower than the fixed tariff, justifying the values obtained.
When comparing with the case of the resources being remunerated individually, for W and WD it is more beneficial to opt for this new form of remuneration because the values can be twice inferior. In relation to WW, this new approach does not compensate for 96,913.33 m.u.
Regarding the selection of k, which corresponds to the number of DR programs or remuneration tariffs to be implemented and offered by the VPP to the aggregated consumers and producers, it should be decided taking into consideration the provided results. In fact, it is not intended in the proposed methodology to provide a decision on the ideal k; it is rather intended to provide the VPP the means to make that decision since in different operation scenarios, despite the costs and remunerations resulting from the application of the proposed methodology, it can be only possible to implement a certain number of tariffs or programs according to the technical and regulatory limitations.