1. Introduction
Nowadays, the largest part of the world energy consumption is covered by fossil fuels. However, fossil fuels contribute to greenhouse gas emissions causing environmental issues such as global warming and climate change. Stocks of fossil fuels are also finite and they are decreasing gradually. To meet human activity needs while fighting global warming, it is important to decrease the part of fossil fuels by using alternative energy sources like renewable energies. Among these, deep geothermal energy does not depend on weather conditions (unlike solar energy for example) and then has the advantage of being able to be exploited continuously. According to the geothermal well conditions, this geothermal energy can be converted for electricity generation or can be used directly as a heat source. A combination of these two applications is feasible and it improves energy efficiency, which is generally low using only electricity production (about 15% with the use of an Organic Rankine Cycle (ORC) for geothermal application [
1]). This introduces the notion of Combined Heat and Power (CHP) production [
2].
In this energy context, a consortium of ten partners, led by “FONROCHE Géothermie”, is working on the FONGEOSEC project, part of the “Investments for the future” program funded by the French state and managed by the French Agency for Environment and Energy (ADEME). The aim of this project is to design and create an innovative demonstrator of a high-energy geothermal power plant. The geothermal energy will be used to produce electricity and heat. The cycle chosen to produce electricity is an ORC due to its well-known technology and since the nature of the geothermal fluid allows its use. The geothermal fluid also generates heat to supply a District Heating Network (DHN) which is a convenient solution for the heating of buildings, domestic hot water, or industrial applications, for example. A DHN improves energy efficiency compared with individual heat production since it allows great interaction between the different uses which can be cascaded and also the introduction of other renewable energies and industrial waste heat recovery.
Energy and exergy analysis can be used to determine the performance of energy systems. The first one only considers the quantity of energy by application of the first law of thermodynamics. Exergy uses also the second law of thermodynamics and considers irreversibility involved in the system. Exergy represents the quantity and the quality of energy [
3]. Comparing energy and exergy analysis for a cogeneration-based district energy system, Rosen et al. [
2] have shown that exergy approach provides more useful information than energy analysis and enables to localize accurately inefficient processes. Therefore, for power plants, including geothermal plants, exergy analysis is commonly used to determine the plant performance. Ganjehsarabi et al. [
4] carried out an exergy analysis of Dora II geothermal plant based in Turkey. In this plant, cooling towers and turbines were identified as the less performant equipment and responsible for the main part of the exergy destruction (respectively 15% and 12% of total exergy entering the plant), while preheaters were the most performant equipment. The re-injection of the geothermal fluid represented the main exergy losses with 32% of the total exergy input. In this study, the influence of inlet temperature and pressure on exergy performance of turbines was also investigated. A pressure increase led to a negligible performance deterioration, whereas a temperature increase led to a significant performance improvement. Sadreddini et al. [
5] performed sensitivity analyses of different parameters on the performance of a Combined Cooling, Heating, and Power plant. The studied parameters were the pinch temperature of heat exchangers, inlet and outlet pressures of the gas turbine, the ORC turbine, the air cavern, and the ejector present in the plant. Since some parameters exhibited reverse influences on exergy performance of the plant, an optimum operating point could be defined. Thereby, the authors presented and highlighted the interest of numerical optimization, which enabled, in their case, a 16.86% decrease in the exergy destruction.
Several studies deal with optimization of an ORC using exergy losses or exergy efficiency, also known as the second law efficiency, as the objective function. Irreversibilities have to be minimized, whereas the exergy efficiency, defined by Equation (1), has to be maximized.
Depending on choice of
and
, different definitions for exergy efficiency can be obtained [
3]. In the following literature, authors may not have used the same definition.
In these ORC optimization studies, two aims result in these optimizations:
The determination of the best working fluid: Dai et al. [
6] investigated the ORC performance for low-grade (418.15 K) waste heat recovery. ORC systems with 10 different working fluids were optimized by means of a genetic algorithm. Some parameters are fixed in the same way for the different optimizations (temperature of the condenser, pinch in the evaporator, mass flow rate). Then, turbine inlet temperature and pressure were optimized for each system in order to maximize the exergy efficiency. Isobutane and R-236ea presented the best performance. Roy et al. [
7] studied the second law efficiency for three fluids for a similar temperature and more important mass flow of the waste heat source. R-123 had the best results. Second law efficiency was also studied by Heberle et al. [
8] for geothermal CHP generation. The parallel and the series connections between the ORC and the heat generation was studied for four fluids in a range of 353–453 K. The most efficient configuration was found to be the series connection using isopentane. For parallel connection, R-227ea gave the best results. Some studies also deal with mixtures as working fluid. Hence, Le et al. [
9] studied different mixtures of R-245fa and n-pentane and they obtained that it was the pure n-pentane which exhibited the best performance regarding the maximization of exergetic efficiency. It should be pointed out that in these studies, only thermodynamic considerations have been discussed. Other criteria such as stability, safety, compatibility with material, cost, etc., are not considered.
The determination of the best configuration: This approach is often coupled with the previous one. For a 453.15 K geothermal source, Yari [
10] studied four cycle configurations (simple ORC, ORC with Internal Heat Exchanger (IHE), regenerative ORC, and regenerative ORC with IHE) for three fluids regarding exergy destruction, exergy and energy efficiencies. For exergetic optimization, simple ORC and ORC with IHE presented the same result, which was the best, while regenerative ORC with IHE was better from the energy point of view. Astolfi et al. [
11] studied 54 fluids for simple ORC and ORC with IHE. The geothermal source temperature ranged from 393.15 to 453.15 K and superheating of vapor phase was considered. Results confirmed that superheating was non-profitable regarding the second law efficiency and that when the reinjection temperature was limited to 343.15 K, it was worth using an IHE, while simple ORC was preferable when no temperature limit was set. Maraver et al. [
12] drew the same conclusion using exergy efficiency optimization for a higher source temperature (573.15 K). However, in their study, for a 443.15 K source the simple ORC had better performance with and without reinjection temperature limit, which is in contradiction with Astolfi et al.’s studies. Then, it appears that the use of the IHE cannot be generalized since its interest depends on the studied case.
For DHN studies, although economic and environmental aspects are widely studied, Rezaie and Rosen [
13] confirmed that exergy analysis was a useful tool and provided important information about system performances. Gong and Werner [
14] used exergy analysis to compare the four generations of DHN. The use of liquid water instead of steam, from first generation to second generation, and the decrease of the network temperature level up to the fourth generation unsurprisingly led to lower exergy factor (Carnot factor). It can still be reduced in the future using renewables and heat recovery. They also pointed out that currently two thirds of the exergy content in heat supply input are lost in the heat distribution chain and that development of fourth generation DHN should reduce this loss. Sanaei and Nakata [
15] optimized the design of a DHN by maximizing exergy efficiency for an existing district. They studied different cases depending on preliminary choice of energy system to recover the heat needed for the DHN. They highlighted that, in some cases, energy efficiencies were very close but these cases could be distinguished by the exergy efficiency. This suggest that exergy is more reliable to evaluate energetic performance of the system.
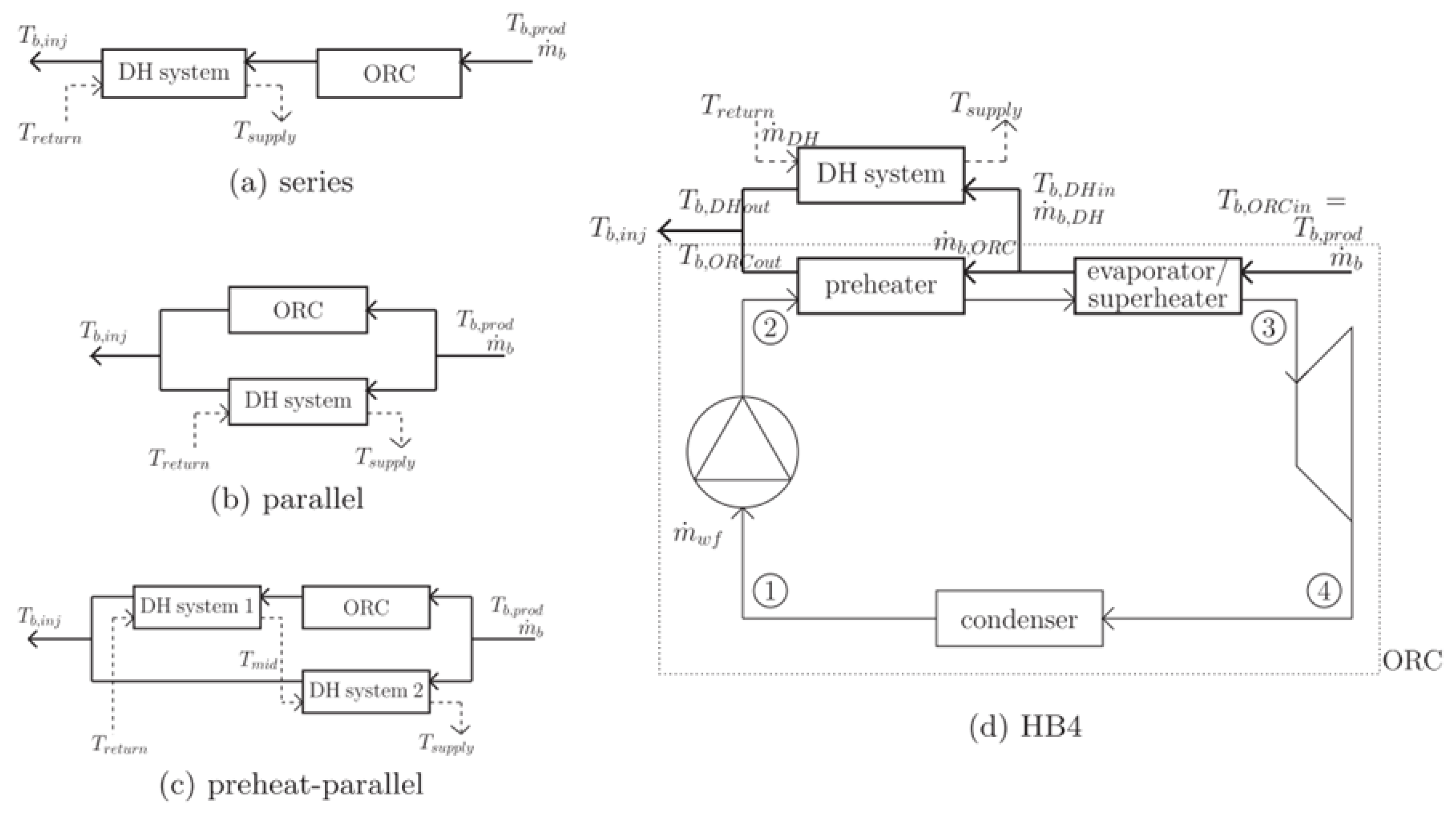
Van Erdeweghe et al. studied the optimal configuration (connection between ORC and DHN) of a geothermal plant. At first, only series and parallel configurations were studied [
16]. Next, two other configurations are added: the preheat-parallel and a hybrid (named HB4) configurations [
17]. All these configurations are presented in
Figure 1. In the HB4 configuration, the evaporation step of the ORC is separated in two parts: an evaporator and a preheater. The geothermal flow rate is split after the evaporator: part of the flow is used in the preheater and part of the flow is used to satisfy the heat demand of the DH system. Hence, the temperature at which the geothermal fluid delivers heat to the DH system is higher compared to the series CHP and lower compared to the parallel CHP. The net power produced was maximized for the four configurations in different conditions (heat demand, supply, and return temperatures for DHN and temperature and mass flow rate of the geothermal source). At the optimal solution, the exergy efficiency was then calculated and configurations were compared. In most cases, the HB4 configuration presented higher efficiency. In case of high-temperature DHN, parallel configuration could exhibit a better performance for low heat demands and low value of geothermal production temperature. However, the exergy efficiency was not optimized and no exergy losses were considered in DHN, which was only represented by heat demand and temperatures. Therefore, the DHN topology was not taken into account. Moreover, among literature on CHP system optimization, simultaneous optimization of the power generation and the heat distribution in CHP plant are not widespread, as specified by Marty et al. [
18], who pointed out this need and performed such an optimization.
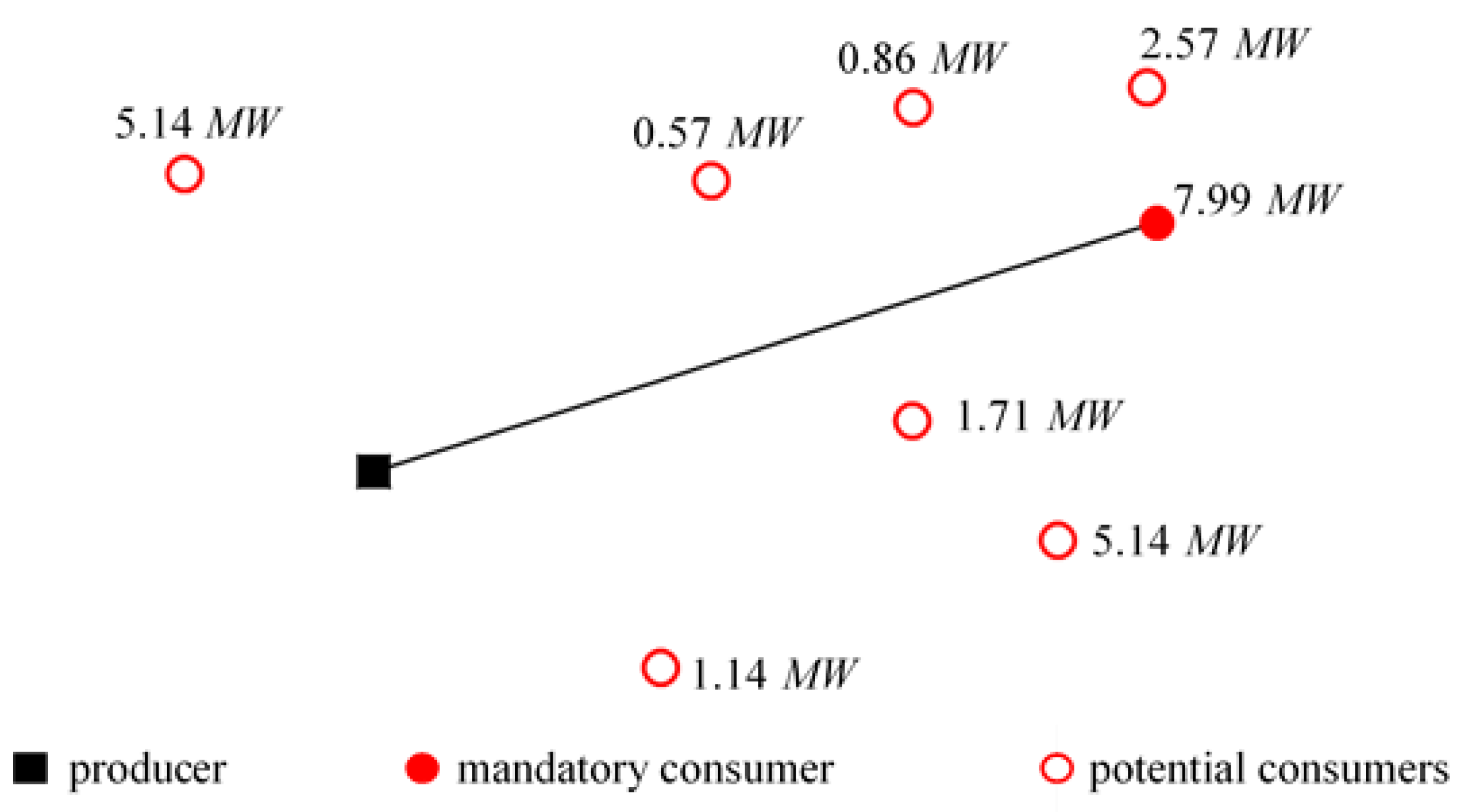
In the present study and the previous one [
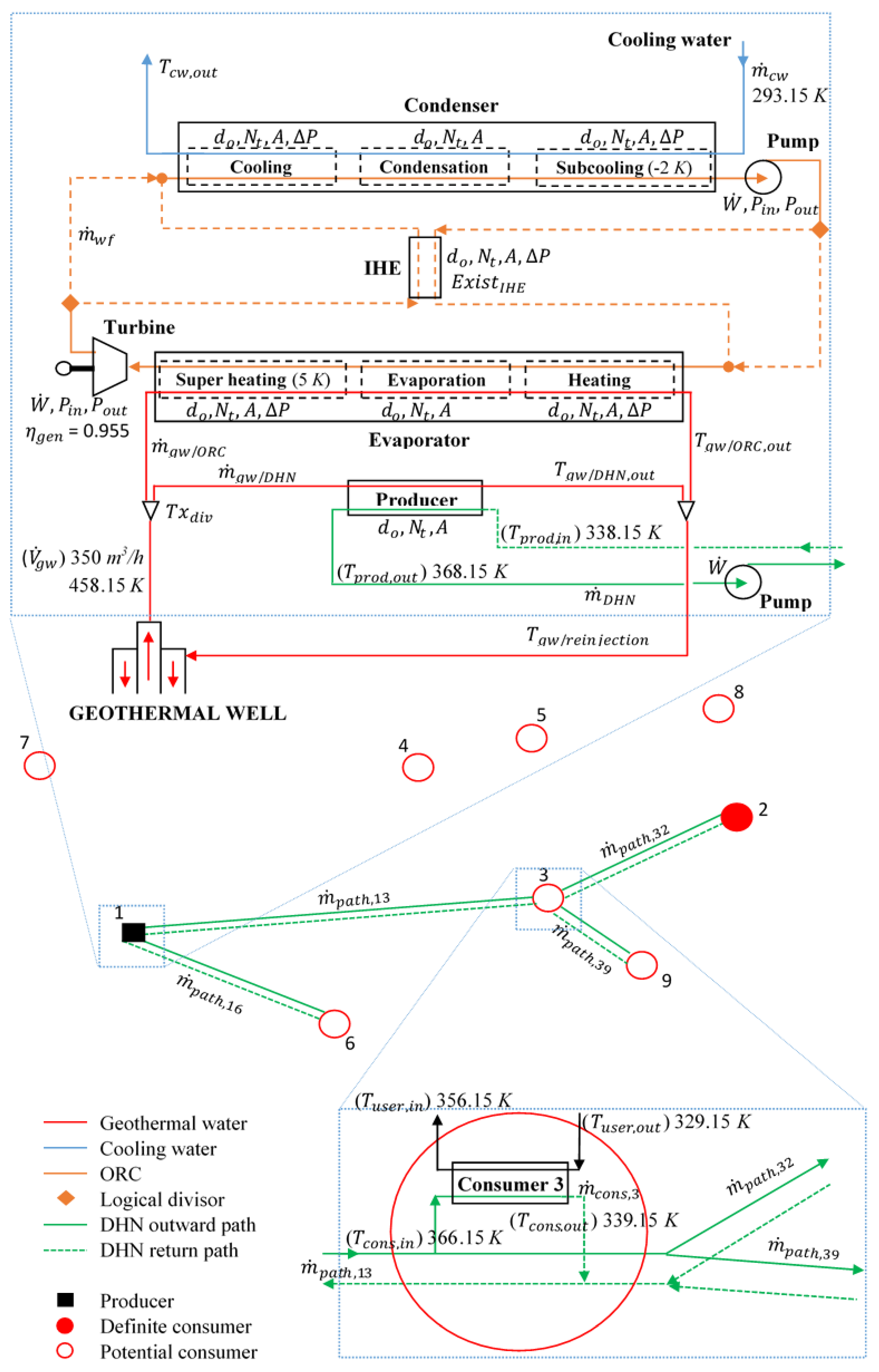
18], what is original is that the ORC and the DHN topology are simultaneously optimized. A DHN and an ORC system are both supplied in parallel by a geothermal well. The working fluid chosen based on preliminary studies performed by partners, is the R 245fa refrigerant. Only this fluid is considered in the present study. Nevertheless, other fluids will be tested in future studies. The question of the existence of an IHE in the ORC is also considered. Concerning the DHN, the producer is located but its heat production available for the DHN has to be determined based on the consumers’ heat demands. Only one consumer, named definite consumer, is known to be connected to the DHN. Other consumers, named potential consumers, are also considered but their connections to the DHN are not imposed and have to be determined by the optimization. Finally, optimal distribution of the geothermal source for electricity production and for heat production is determined.
The other originality of the present paper is that the studied objective function is now the total exergy loss (including exergy destruction) to be minimizing, whereas the previous paper optimized the annual profit. The optimization problem is first reminded with main assumptions, optimization variables and equations. The exergetic model is then detailed. Exergy analysis is performed for the two optimal solutions (economic and exergetic objective functions), and results are finally compared.
3. Results and Discussions
In this paper, three cases were studied. First, the exergy analysis of the solution of
maximization is performed (study denoted
). Secondly, the exergy analysis of the solution of
minimization with fixed DHN configuration of the solution of the previous study is performed (study denoted
*). Thirdly, the exergy analysis of the solution of
minimization without constraint on the topology is performed (study denoted
). Detail of exergy losses and destruction appearing in the system and exergetic efficiencies are presented in
Table 4 for each studied case. First, it can be noted that none of the optimal design included the IHE.
Finally, a sensitive analysis (impact of temperature and mass flow rate of geothermal source) was performed considering minimization.
3.1. Exergy Analysis for Solution
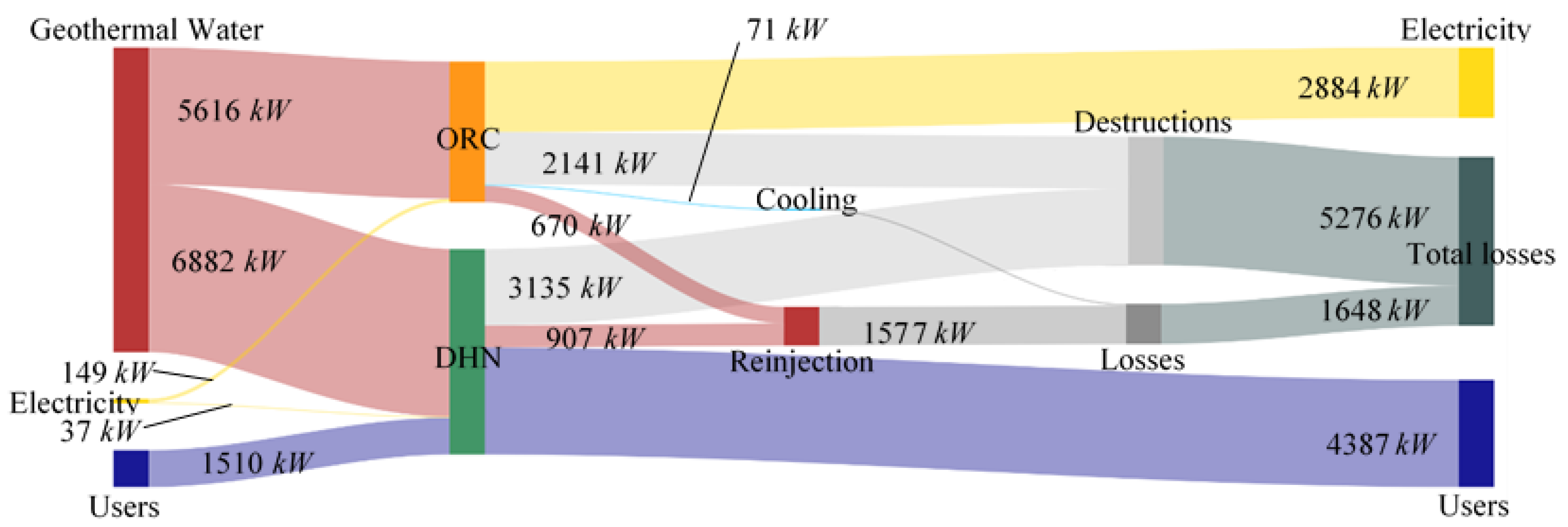
At the solution, the exergy flow diagram and the optimal DHN topology obtained in case of
is presented respectively in
Figure 4 and
Figure 5. The detail of exergy destructions and losses can be completed with the value presented in
Table 4.
We can see in
Figure 4 that destructions represent the main part of total exergy losses (76.2%). Exergy losses induced by the reinjection is widely more important than losses induced by the warming of the cooling water. The main destruction of the system results from the DHN and more specifically from the producer heat exchanger: the exergy destruction in this exchanger represents 70.6% of destructions occurring in the DHN and 32.0% of total exergy losses. In the ORC, evaporator and turbine are responsible for the more exergy destruction (respectively 45.9% and 31.9% of destructions occurring in the ORC and 14.2% and 9.9% of total exergy losses). Nevertheless, the condenser is the less efficient component in the ORC and more generally in the plant. The optimal solution does not involve the IHE in the ORC.
The ORC induces less destruction and losses than the DHN whose exergetic efficiency is slightly lower than the one of the ORC (41.8% against 48.7%).
3.2. Exergy Analysis for * Solution
In this optimization, the DHN configuration is fixed at the configuration of the solution of the previous optimization, which is represented in
Figure 5. Since temperature in DHN and heat required are also fixed, the entire DHN is fixed at the previous solution. Only the size of the producer heat exchanger, the geothermal fluid mass flow rate (
) and the geothermal outlet temperature (
) are optimization variables. Then, for this fixed configuration, for a given required heat, a decrease of the temperature of the geothermal source at the outlet of the producer heat exchanger,
, will lead to a decrease of the mass flow rate,
, and thus an increase of the mass flow rate toward the ORC. This induces an increase of electricity produced and then sold. Moreover, a lower temperature
leads to lower losses appearing in reinjection. Then, the two optimizations with the two objective functions (
and
*) converge toward the same solution regarding the DHN as reported in
Table 5 (which also includes the results for
. These results are discussed later). The value of
obtained is the lowest as possible, limited by the pinch temperature in the producer.
Regarding the ORC, both objectives converge toward a different . This temperature is slightly lower in case of *. Therefore, the losses appearing in reinjection decrease and the heat exchange in evaporator increases. The working fluid mass flow rate, temperatures and pressures are also slightly modified. The destroyed exergy is then increased for the evaporator and the turbine and decreased for the condenser and the pump. Finally, the total losses in the ORC and then in plant is slightly decreased (−0.35% and −0.15% respectively).
3.3. Exergy Analysis for Solution
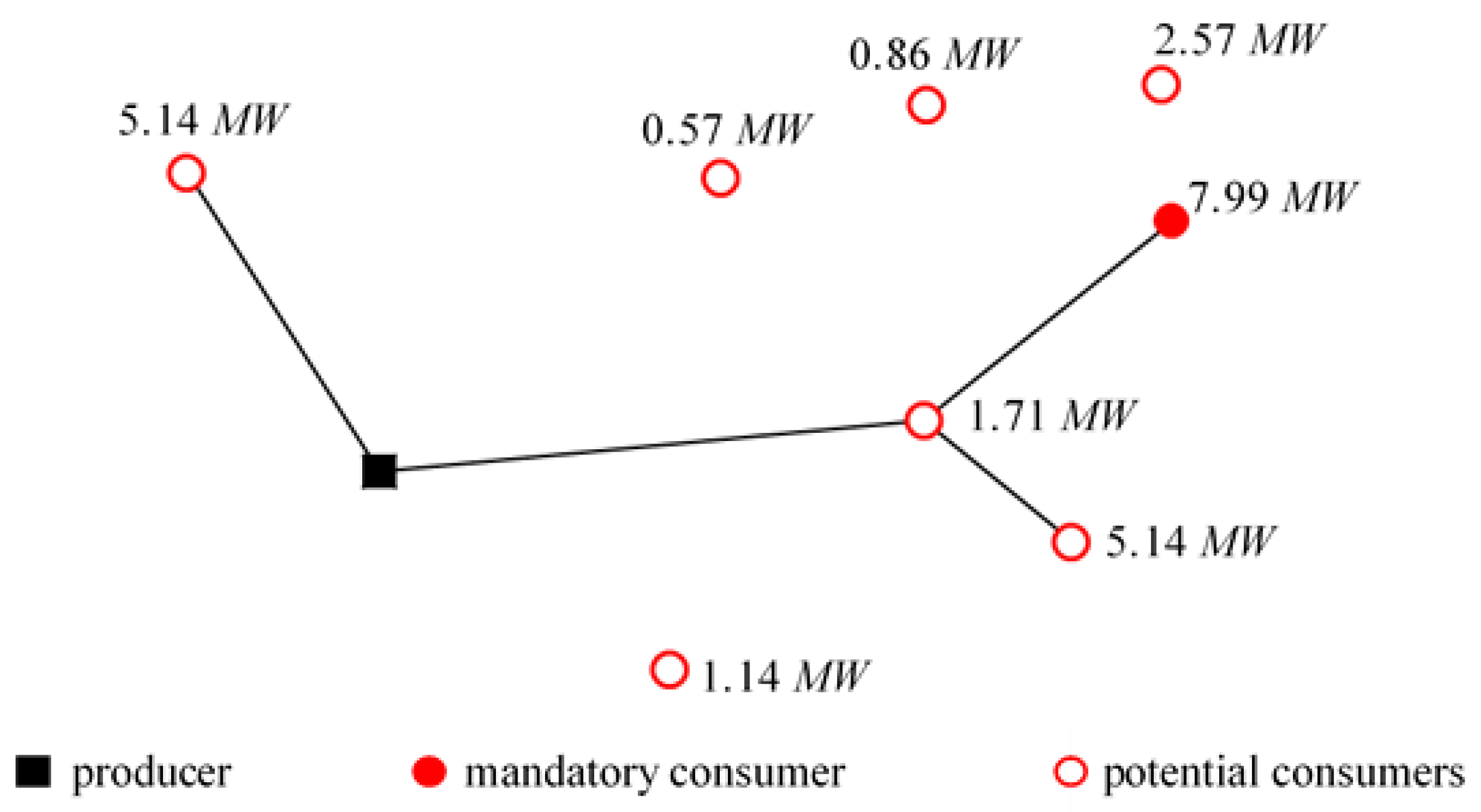
Compared to the previous solution, since the degree of freedom is increased and thus the research field is larger (the DHN configuration is not imposed), a better result is obtained as expected (
Table 4). The obtained exergy flow diagram and the optimal DHN topology in case of
are presented respectively in
Figure 6 and
Figure 7.
The optimal solution is obtained for the smallest as possible DHN (only the definite consumer is connected to the network). Regarding previous results ( and * optimizations), the ORC has better efficiency than the DHN. In this solution, this is still true even if ORC efficiency is deteriorated in present case. This could lead to thinking that it is always more interesting, from an exergy point of view, to privilege the ORC as long as ORC exergetic efficiency is the highest. This point is discussed in the next section.
Since DHN temperatures are fixed in the model and optimisations converge toward the same value of
(
Table 5), exergetic efficiencies for the DHN and its components (pump, producer and consumers heat exchangers) remain unchanged regardless the studied case.
Table 6 summarized the value of
and
for the three different studied cases. Regarding exergy losses, the
case enables to decrease the
value to 207 kW but induces also a decrease to 394 k€/year of
(compared to
). A multi-objective approach could enable to find a better compromise to decrease
without a too important decrease of
(not presented in this paper).
Because geothermal water conditions (flow rate and temperature) can be different than the used conditions, a sensitivity analysis on these two conditions was carried out and is presented in the next section.
3.4. Sensitivity Analysis for
Evolutions of
,
,
, and
with volumetric flow rate and with the temperature of the inlet geothermal water (respectively
and
) are considered using the
formulation. Each of those parameters are decreased individually. These evolutions are presented in
Figure 8 and
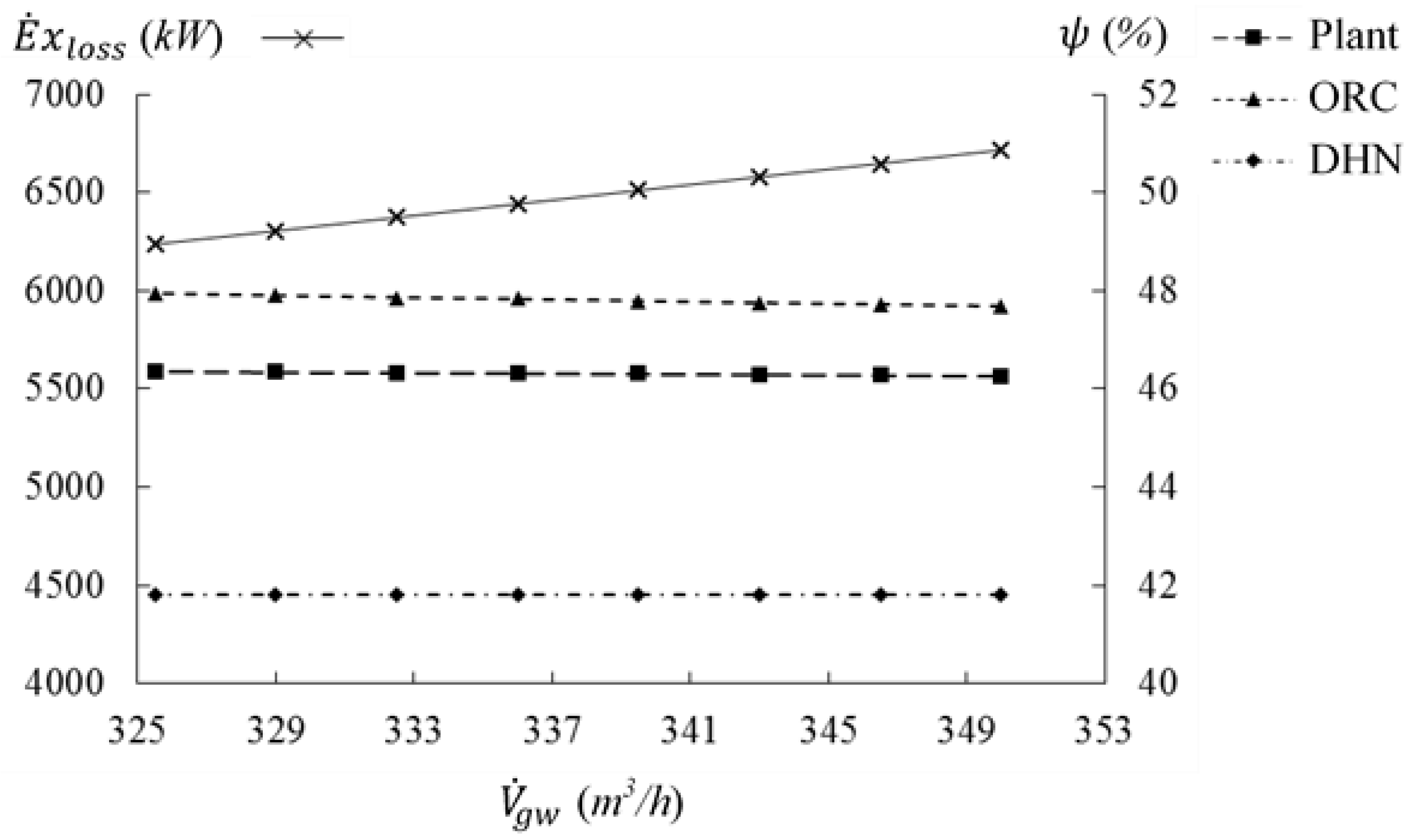
Figure 9 for the variation of the volumetric flow rate and the variation of the temperature, respectively.
Regarding volumetric flow rate decreasing, the optimal configuration of the DHN remains unchanged (see
Figure 7). The flow rate toward the DHN is not modified and efficiency of the DHN is therefore quite similar (
Figure 8). The flow rate toward the ORC is necessarily decreased since it is the difference between decreasing geothermal flow rate and constant flow rate toward the DHN. However, the ORC conditions (temperatures and pressures) are nearly the same, then efficiencies of ORC and the plant are slightly increased. A decrease by 7% of volumetric flow rate (transition from 350 m
3/h to 325.5 m
3/h) leads to a decrease in total exergy losses (−7.15%).
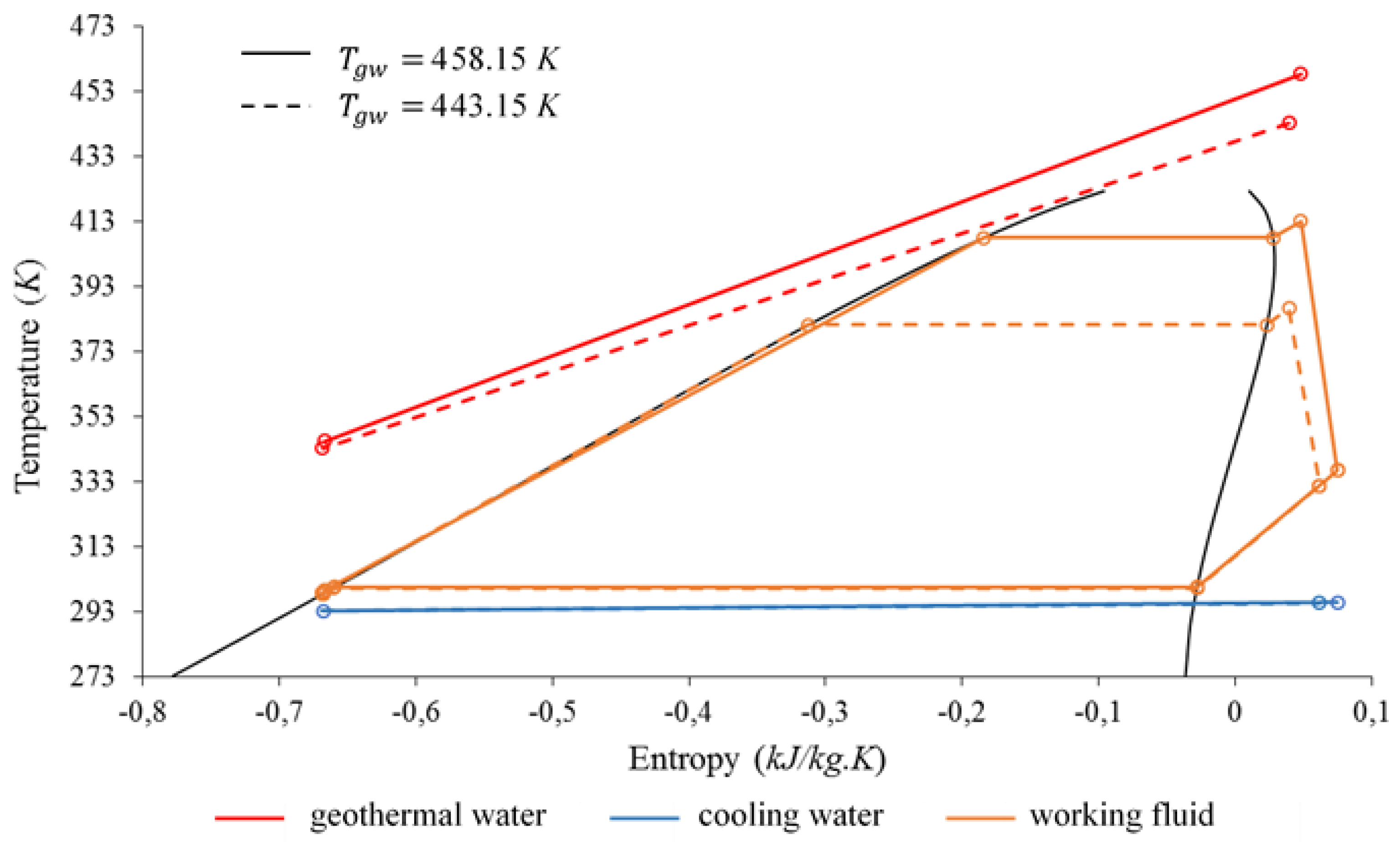
Unlike previous observation on volumetric flow rate decreasing, the decrease of temperature of the geothermal water involves a significant modification of the ORC conditions (easily represented in
T-s diagram in
Figure 10 already presented in Marty et al. [
18]).
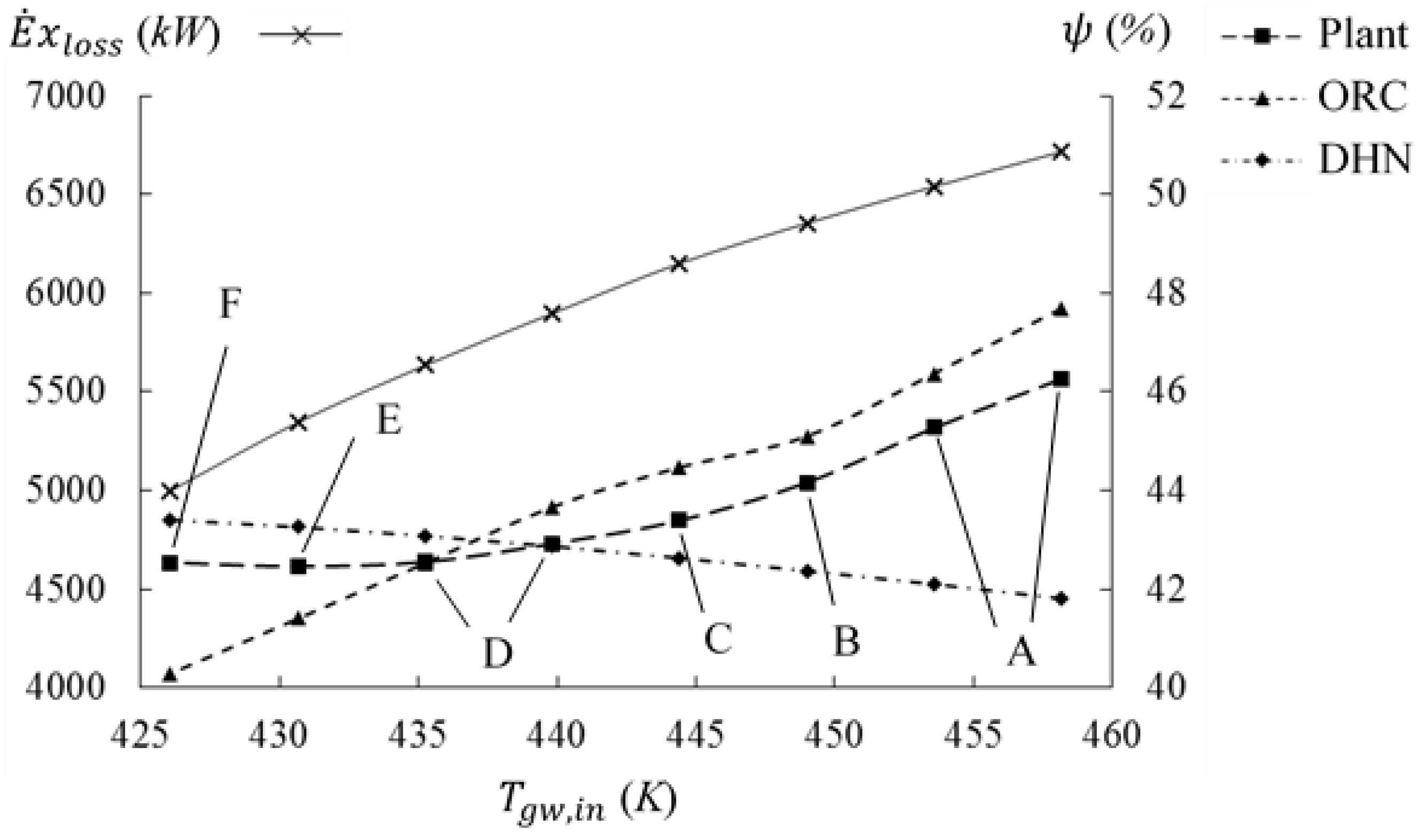
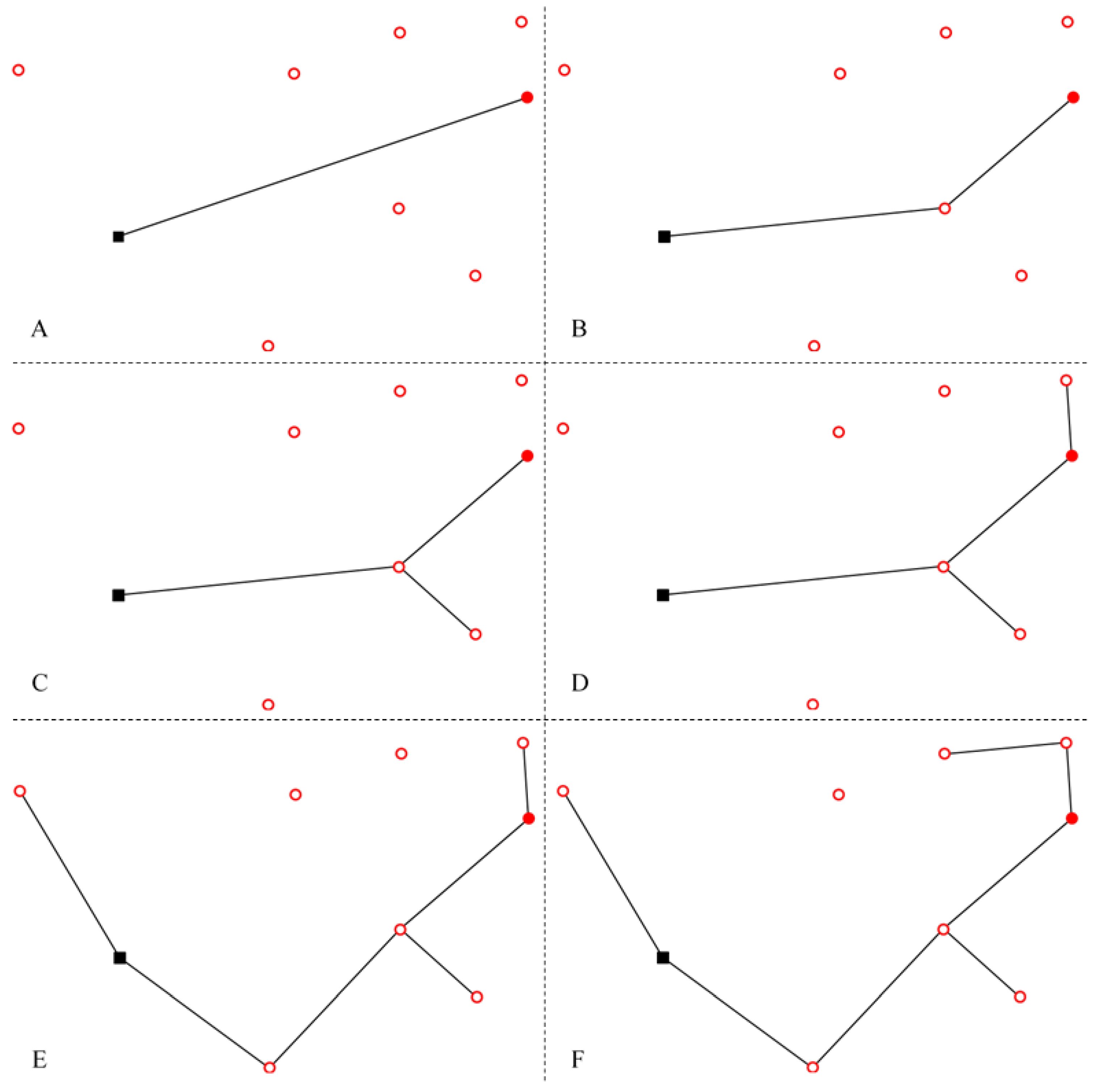
Figure 9 leads to the conclusion that the lower the temperature, the lower the exergy efficiency of the ORC. Therefore, the flow entering the ORC becomes less important and the flow towards the DHN is more and more privileged. In the
Figure 9, eight optimization results are presented. These eight results lead to six different DHN configurations denoted from A to F. The corresponding different DHN configurations are presented in
Figure 11, which clearly shows that the DHN is increasingly longer as the temperature decreases. In the initial condition (
= 458.15 K),
is equal to 22% (22% of geothermal water is used for the DHN). It is equal to 92% for
= 426.09 K. A temperature decrease by 7% (transition from 458.15 K to 426.09 K) leads to a significant decrease in total exergy losses (−24.90%).
In the previous section, obtaining the possible smallest DHN has led to thinking that this DHN configuration is better as long as the ORC exergetic efficiency is better than that of DHN. The follow-up of the DHN configuration with the geothermal water temperature (especially between about 440 K and 455 K) shows it is not true since B, C, and D configurations (
Figure 11) are obtained in this condition. Comparison of exergetic efficiency does not permit concluding about DHN configuration even in case of exergy losses minimization.
4. Conclusions
In this paper, an optimization exergy model is presented and applied to a geothermal Combined Heat and Power plant. Setting-up optimization enables to determine simultaneously: (1) the sizing of the Organic Rankine Cycle, (2) the best distribution between electricity and heat production, and (3) the topology of the District Heating Network. In order to solve efficiently the resulting MINLP problem, a solving strategy is used and it has been presented in a previous paper with results of the economic optimization [
18]. In the present work, exergetic optimization, using the total exergy losses as objective function is performed.
An exergy analysis is carried out for both optimizations (economic and exergetic). Results show different optimal DHN configurations, the part of the geothermal source toward ORC is then also modified. However, in any cases, evaporator and turbine present the higher exergy destruction in ORC. Although the condenser presents half the exergy destruction of the evaporator, its exergy efficiency is the lowest in the plant. The authors also point out that the minimization of exergy losses tends to lead to a decrease of the DHN size. A sensitivity analysis shows that exergy losses decrease with the decreased of geothermal flow rate and geothermal temperature. The decrease of flow rate does not have significant change on operating points on ORC and DHN configuration. This is not true anymore for the decrease of temperature where operating points on ORC are significantly modified. ORC efficiency drops and the DHN is progressively favoured by the optimization even if ORC efficiency is higher than the DHN one. This reinforces the need to use a simultaneous approach as presented in this work and the previous one [
18]. The IHE is never chosen regardless of the studied geothermal conditions. Since DHN temperatures are fixed, DHN and its components efficiencies stay unchanged whatever the studied case. It will be interesting to compare future results (free temperatures) with present results (fixed temperatures) to conclude about influences of this hypothesis. Finally, compared to
, the minimization of
induces a significant decrease of
value. This shows the interest of a future multi-objective study. Indeed, multi-objective optimization can be understood as an efficient way to deal with conflicting objectives simultaneously. There exists a possibly infinite number of solutions among which a trade-off can be chosen to satisfy the preferences of the human decision maker. In the studied case (i.e., the geothermal plant), one can choose to favour economics or exergy savings. In fact, in the past decade, economic optimization was most often favoured regardless of exergy wastes. However, nowadays, to account for the global warming, mentalities and uses have to change. Taking into account exergy efficiency when making a decision will become common. With a multi-objective optimization tool, it will be up to the decision maker to know how far he wants to take it into account. Moreover, the cost of exergy wastes will probably increase, which leads to reducing the gap between the two conflicting objectives.