Impedance Estimation with an Enhanced Particle Swarm Optimization for Low-Voltage Distribution Networks
Abstract
:1. Introduction
- (i)
- Time synchronized voltage, current, and power measurements in low-voltage networks cannot be obtained simultaneously at different points. The methods referenced above (except [17]) assume that the measurement data are exactly synchronized or ignore phasor differences among measurement equipment such as smart meters.
- (ii)
- Generalization of the network model [12] assumes a topology that may be applicable to almost all low voltage distribution networks, but operational data such as the secondary voltage at pole transformers are not always available. On the other hand, in [17], the model topology is limited so it does not require accurate measurement of pole transformer secondary voltages. As network models become more general, information required for impedance estimation becomes more demanding.
- (iii)
- Convergence of optimization approaches may fail. In [16], the network impedances are obtained from simultaneous equations, but in the case study, it is shown that optimization by linear programming (LP) sometimes does not converge when there are network topology errors or even power theft. A weighted least squares (WLS) state estimator approach was adopted in [13] but WLS is only effective when the measurement data is exactly synchronized. Conventional WLS cannot be utilized for non-synchronized datasets.
- solves the problem (ii) above by implementing a modified general model that considers the distance from pole transformer to secondary consuming node, making impedance estimation more practical.
- solves the problem (iii) above by improving the accuracy of estimation with an enhanced PSO algorithm having an adaptive inertia weighting method.
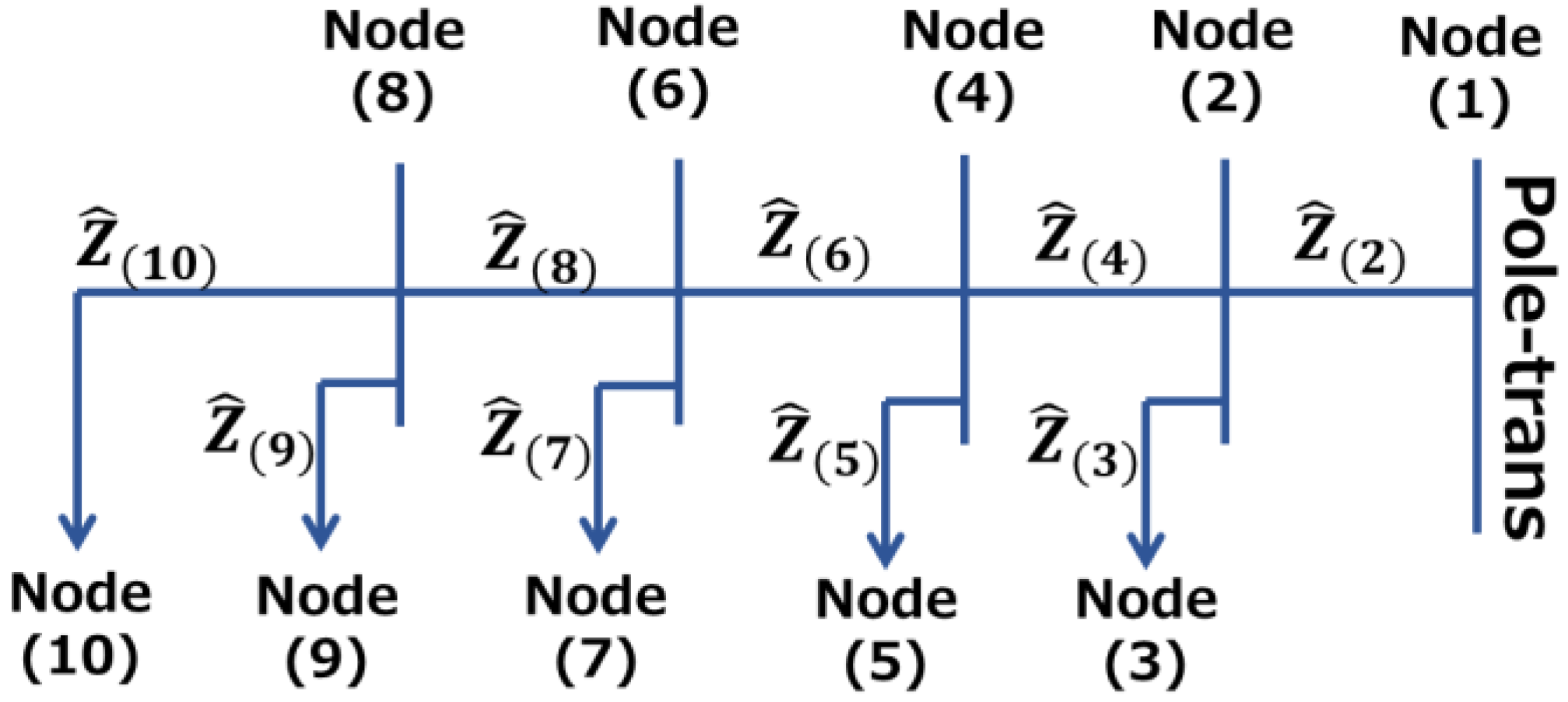
2. Simulation Model
- The topology and order of all nodes are already known.
- Every T-node where a consumer connects has a device, such as a smart meter, to measure the current, voltage, and power factor.
- Each device indicates how much active and reactive power it consumes at any point in time, but cannot be exactly time synchronized across multiple consumers. Thus, information about phase differences between users cannot be shared.
- Each device can measure and share only the rms values of voltage and current. The information measured by each device is shared among all consumers to enable impedance estimation.
- A device that measures current, voltage, and active and reactive power, including phase information, does not exist on Node(1).
- The pole transformer properties are unknown, so the transformer’s secondary voltage is unknown, but is stable. Here “stable” implies that the voltage magnitude remains constant so that all devices can measure the voltage synchronously. Normally, one second would be enough of a window for this measurement since we are collecting only the rms voltage without its phase.
3. The Enhanced PSO
- (1)
- Coefficients and can be combined as b while maintaining the reliability of the model to obtain optimal solutions.
- (2)
- The coefficients and are major contributors to an optimal solution. The other coefficients and are fixed arbitrarily to enable the model to generalize.
4. Case Study
- (1)
- Power consumption is measured at each consuming node in time intervals as shown in Table 1. In this simulation, six consumption patterns (load patterns) are given. In a real situation, the number of the load patterns will be as many as needed because the consumption pattern will innately vary over time and the measuring devices continuously take data.
- (2)
- (3)
- Impedance is estimated without regard to phase differences of voltage and current between nodes since it is considered unknown. The impedances are estimated by recursively solving (13).
- (1)
- The cost function in (11) reacts strongly when the error e is larger than 0.01.
- (2)
- The adaptive inertia weight in (16) improves the PSO algorithm accuracy.
5. Conclusions
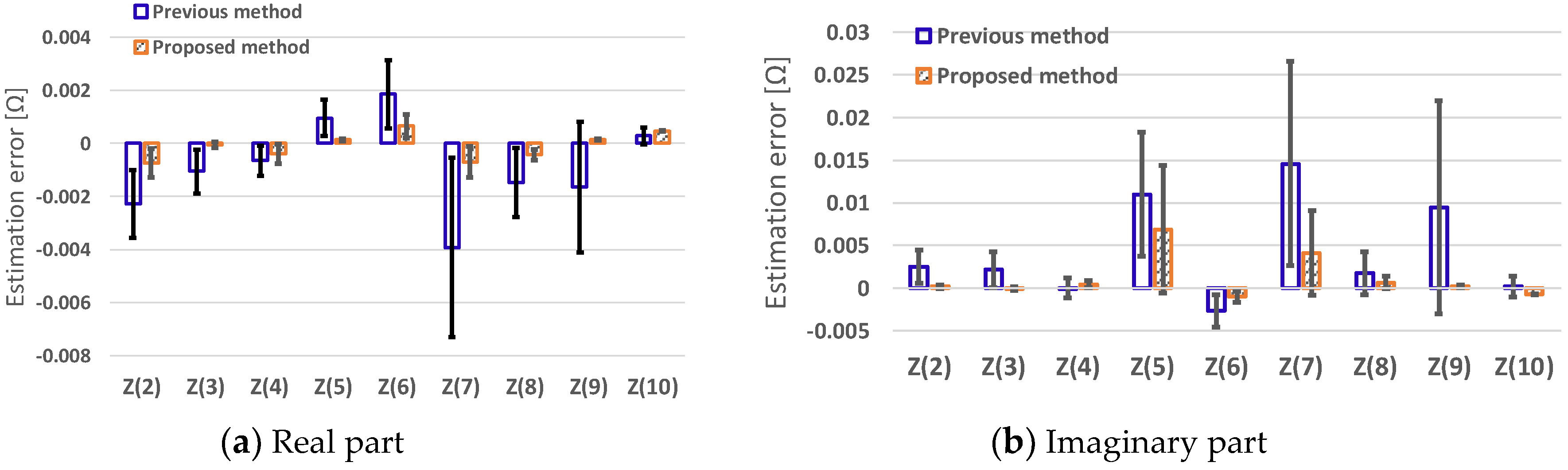
- The proposed method estimates an extended part of the low-voltage distribution feeder, , with reasonable error. The average error rate of the real part was 1.4% and that of the imaginary part was 0.8%.
- The proposed method estimates impedance as well as or better than the previous method in terms of estimation average and confidence intervals of the estimation.
- The proposed method still has a huge error rate on the imaginary part of and even though the accuracy is improved over the previous method. The appropriate load patterns are needed to obtain better accuracy on and .
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| n | real number, 2 ≤ n |
| i | an index of nodes, 1 ≤ i ≤ n |
| node voltage at Node(2i) | |
| line current injected to Node(2i) from Node(2i − 2) | |
| injected apparent power to Node(2i) | |
| impedance between Node(2i) and Node(2i − 2) |
References
- Liu, E.; Bebic, J. Distribution system voltage performance analysis for high-penetration photovoltaics distribution system voltage performance analysis for high-penetration photovoltaics. In Proceedings of the 2008 IEEE Energy 2030 Conference, Atlanta, GA, USA, 17–18 November 2008. [Google Scholar]
- Kordkheili, R.A.; Bak-Jensen, B.; R-Pillai, J.; Mahat, P. Determining maximum photovoltaic penetration in a distribution grid considering grid operation limits. In Proceedings of the 2014 IEEE PES General Meeting Conference Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
- Masters, C.L. Voltage rise: The big issue when connecting embedded generation to long 11 kV overhead lines. Power Eng. J. 2002, 16, 5–12. [Google Scholar] [CrossRef]
- Kabiri, R.; Holmes, D.G.; McGrath, B.P.; Meegahapola, L.G. LV grid voltage regulation using transformer electronic tap changing, with pv inverter reactive power injection. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 1182–1192. [Google Scholar] [CrossRef]
- Salih, S.N.; Chen, P. On coordinated control of OLTC and reactive power compensation for voltage regulation in distribution systems with wind power. IEEE Trans. Power Syst. 2015, 31, 4026–4035. [Google Scholar] [CrossRef]
- Vovos, P.N.; Kiprakis, A.E.; Wallace, A.R.; Harrison, G.P. Centralized and distributed voltage control: Impact on distributed generation penetration. IEEE Trans. Power Syst. 2007, 22, 476–483. [Google Scholar] [CrossRef]
- Demirok, E.; González, P.C.; Frederiksen, K.H.B.; Sera, D.; Rodriguez, P.; Teodorescu, R. Local reactive power control methods for overvoltage prevention of distributed solar inverters in low-voltage grids. IEEE J. Photovolt. 2011, 1, 174–182. [Google Scholar] [CrossRef]
- Dall’Anese, E.; Dhople, S.V.; Giannakis, G.B. Optimal dispatch of photovoltaic inverters in residential distribution systems. IEEE Trans. Sust. Energy 2014, 5, 487–497. [Google Scholar] [CrossRef]
- Dall’Anese, E.; Dhople, S.V.; Giannakis, G.B. Decentralized optimal dispatch of photovoltaic inverters in residential distribution systems. IEEE Trans. Sust. Energy 2014, 29, 957–967. [Google Scholar] [CrossRef]
- Elkhatib, M.E.; El-Shatshat, R.; Salama, M.M.A. Novel coordinated voltage control for smart distribution networks with DG. IEEE Trans. Smart Grid 2011, 2, 598–605. [Google Scholar] [CrossRef]
- Marra, F.; Yang, G.Y.; Traeholt, C.; Larsen, E.; Ostergaard, J.; Blazic, B.; Deprez, W. EV charging facilities and their application in LV feeders with photovoltaics. IEEE Trans. Smart Grid 2013, 4, 1533–1540. [Google Scholar] [CrossRef]
- Peppanen, J.; Reno, M.J.; Broderick, R.J.; Grijalva, S. Distribution system model calibration with big data from AMI and PV inverters. IEEE Trans. Smart Grid 2016, 7, 2497–2506. [Google Scholar] [CrossRef]
- Castillo, M.R.M.; London, J.B.A.; Bretas, N.G. Network branch parameter validation based on a decoupled state/parameter estimator and historical data. In Proceedings of the 2009 IEEE Bucharest, Bucharest, Romania, 28 June–2 July 2009. [Google Scholar]
- Castillo, M.R.M.; London, J.B.A.; Bretas, N.G. An approach to power system branch parameter estimation. In Proceedings of the 2008 IEEE Electric Power Energy Conference, Vancouver, BC, Canada, 6–7 October 2008. [Google Scholar]
- Wu, Z.; Zora, L.T.; Phadke, A.G. Simultaneous transmission line parameter and PMU measurement calibration. In Proceedings of the IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
- Berrisford, A.J. A tale of two transformers: An algorithm for estimating distribution secondary electric parameters using smart meter data. In Proceedings of the 26th IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Regina, SK, Canada, 5–8 May 2013. [Google Scholar]
- Han, S.; Kodaira, D.; Han, S.; Kwon, B.; Hasegawa, Y.; Aki, H. An automated impedance estimation method in low-voltage distribution network for coordinated voltage regulation. IEEE Trans. Smart Grid 2016, 7, 1012–1020. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 6 August 2002. [Google Scholar]
- Han, S.; Kodaira, D.; Han, S.; Baek, J. Practical impedance estimation in low-voltage distribution network. IFAC-PapersOnLine 2015, 48, 312–315. [Google Scholar] [CrossRef]
- Trelea, I.C. The particle swarm optimization algorithm: Convergence analysis and parameter selection. Inf. Process. Lett. 2003, 85, 317–325. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y. Comparing inertia weights and constriction factors in particle swarm optimization. In Proceedings of the 2000 Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000. [Google Scholar]
- Črepinšek, M.; Liu, S.-H.; Mernik, M. Exploration and exploitation in evolutionary algorithms. ACM Comput. Surv. 2013, 45, 1–33. [Google Scholar] [CrossRef]
- Eberhart, R.C. Fuzzy adaptive particle swarm optimization. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001. [Google Scholar]
- Taherkhani, M.; Safabakhsh, R. A novel stability-based adaptive inertia weight for particle swarm optimization. Appl. Soft Comput. 2016, 38, 281–295. [Google Scholar] [CrossRef]
- Nickabadi, A.; Ebadzadeh, M.M.; Safabakhsh, R. A novel particle swarm optimization algorithm with adaptive inertia weight. Appl. Soft Comput. J. 2011, 11, 3658–3670. [Google Scholar] [CrossRef]
- Yang, X.; Yuan, J.; Yuan, J.; Mao, H. A modified particle swarm optimizer with dynamic adaptation. Appl. Math. Comput. 2007, 189, 1205–1213. [Google Scholar] [CrossRef]
- Arumugam, M.S.; Rao, M.V.C. On the improved performances of the particle swarm optimization algorithms with adaptive parameters, cross-over operators and root mean square (RMS) variants for computing optimal control of a class of hybrid systems. Appl. Soft Comput. J. 2008, 8, 324–336. [Google Scholar] [CrossRef]


| Load Pattern | S(3) [KVA] | S(5) [KVA] | S(7) [KVA] | S(9) [KVA] | S(10) [KVA] |
|---|---|---|---|---|---|
| #1 | 2.00 + 0.15i | 2.00 + 0.10i | 2.50 + 0.30i | 2.00 + 1.00i | 0.50 + 0.30i |
| #2 | 1.00 + 0.40i | 3.00 + 0.50i | 1.00 + 0.20i | 2.70 + 1.50i | 0.50 + 0.30i |
| #3 | 0.80 + 0.30i | 1.50 + 0.20i | 0.70 + 0.10i | 1.20 + 0.30i | 0.40 + 0.20i |
| #4 | 0.30 + 0.15i | 1.30 + 0.20i | 1.10 + 0.30i | 3.10 + 0.30i | 0.35 + 0.20i |
| #5 | 1.25 + 0.13i | 0.55 + 0.26i | 1.34 + 0.45i | 2.30 + 1.30i | 0.35 + 0.20i |
| #6 | 1.00 + 0.15i | 1.10 + 0.20i | 0.30 + 0.05i | 3.50 + 2.10i | 0.60 + 0.35i |
| Impedance | Actual [Ω] | Average of Estimates by Previous Method [Ω] | Average of Estimates by Proposed Method [Ω] | |||
|---|---|---|---|---|---|---|
| Re | Im | Re | Im | Re | Im | |
| 0.0512 | 0.0267 | 0.0489 (4.5%) | 0.0292 (9.5%) | 0.0504 (1.4%) | 0.0269 (0.8%) | |
| 0.0436 | 0.0020 | 0.0425 (2.4%) | 0.0042 (105.5%) | 0.0435 (0.1%) | 0.0020 (1.3%) | |
| 0.0512 | 0.0267 | 0.0505 (1.3%) | 0.0266 (0.0%) | 0.0508 (0.8%) | 0.0271 (1.8%) | |
| 0.0436 | 0.0020 | 0.0445 (2.2%) | 0.0131 (536.0%) | 0.0437 (0.3%) | 0.0089 (336.2%) | |
| 0.0512 | 0.0267 | 0.0530 (3.6%) | 0.0240 (9.9%) | 0.0518 (1.3%) | 0.0257 (3.7%) | |
| 0.0436 | 0.0020 | 0.0396 (9.0%) | 0.0166 (710.0%) | 0.0429 (1.6%) | 0.0061 (199.0%) | |
| 0.0512 | 0.0267 | 0.0497 (2.9%) | 0.0284 (6.7%) | 0.0507 (0.8%) | 0.0273 (2.5%) | |
| 0.0436 | 0.0020 | 0.0419 (3.8%) | 0.0115 (461.2%) | 0.0437 (0.3%) | 0.0023 (12.2%) | |
| 0.0948 | 0.0287 | 0.0950 (0.3%) | 0.0289 (0.7%) | 0.0952 (0.5%) | 0.0280 (2.4%) | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kodaira, D.; Park, J.; Kim, S.Y.; Han, S.; Han, S. Impedance Estimation with an Enhanced Particle Swarm Optimization for Low-Voltage Distribution Networks. Energies 2019, 12, 1167. https://doi.org/10.3390/en12061167
Kodaira D, Park J, Kim SY, Han S, Han S. Impedance Estimation with an Enhanced Particle Swarm Optimization for Low-Voltage Distribution Networks. Energies. 2019; 12(6):1167. https://doi.org/10.3390/en12061167
Chicago/Turabian StyleKodaira, Daisuke, Jingyeong Park, Sung Yeol Kim, Soohee Han, and Sekyung Han. 2019. "Impedance Estimation with an Enhanced Particle Swarm Optimization for Low-Voltage Distribution Networks" Energies 12, no. 6: 1167. https://doi.org/10.3390/en12061167
APA StyleKodaira, D., Park, J., Kim, S. Y., Han, S., & Han, S. (2019). Impedance Estimation with an Enhanced Particle Swarm Optimization for Low-Voltage Distribution Networks. Energies, 12(6), 1167. https://doi.org/10.3390/en12061167







