Distributed Reconciliation in Day-Ahead Wind Power Forecasting
Abstract
:1. Introduction
2. Hierarchical Time-Series and Forecast Reconciliation
2.1. The Forecast Reconciliation Problem
2.2. An Overview of the State of the Art
2.3. Generalized Least Squares Reconciliation
2.4. Trace Minimization Reconciliation
2.4.1. Ordinary Least Squares (OLS) Reconciliation
2.4.2. Weighted Least Squares (WLS) Reconciliation
2.4.3. Hierarchical Least Squares (HLS) Reconciliation
2.4.4. Minimum Trace (MinT) Reconciliation and Shrinkage Estimator
3. Proposed Distributed Reconciliation Methods
3.1. Game Theoretical Optimal (GTOP) Reconciliation
3.2. Constrained GTOP Solved by ADMM
| Algorithm 1 constrained GTOP Algorithm |
| 1: Require: base forecasts ; ; 2: aggregated consistency ; boundary constraint 3: Input: 4: Output: reconciled forecasts 5: while stopping criteria do 6: 7: 8: 9: 10: end while 11: , |
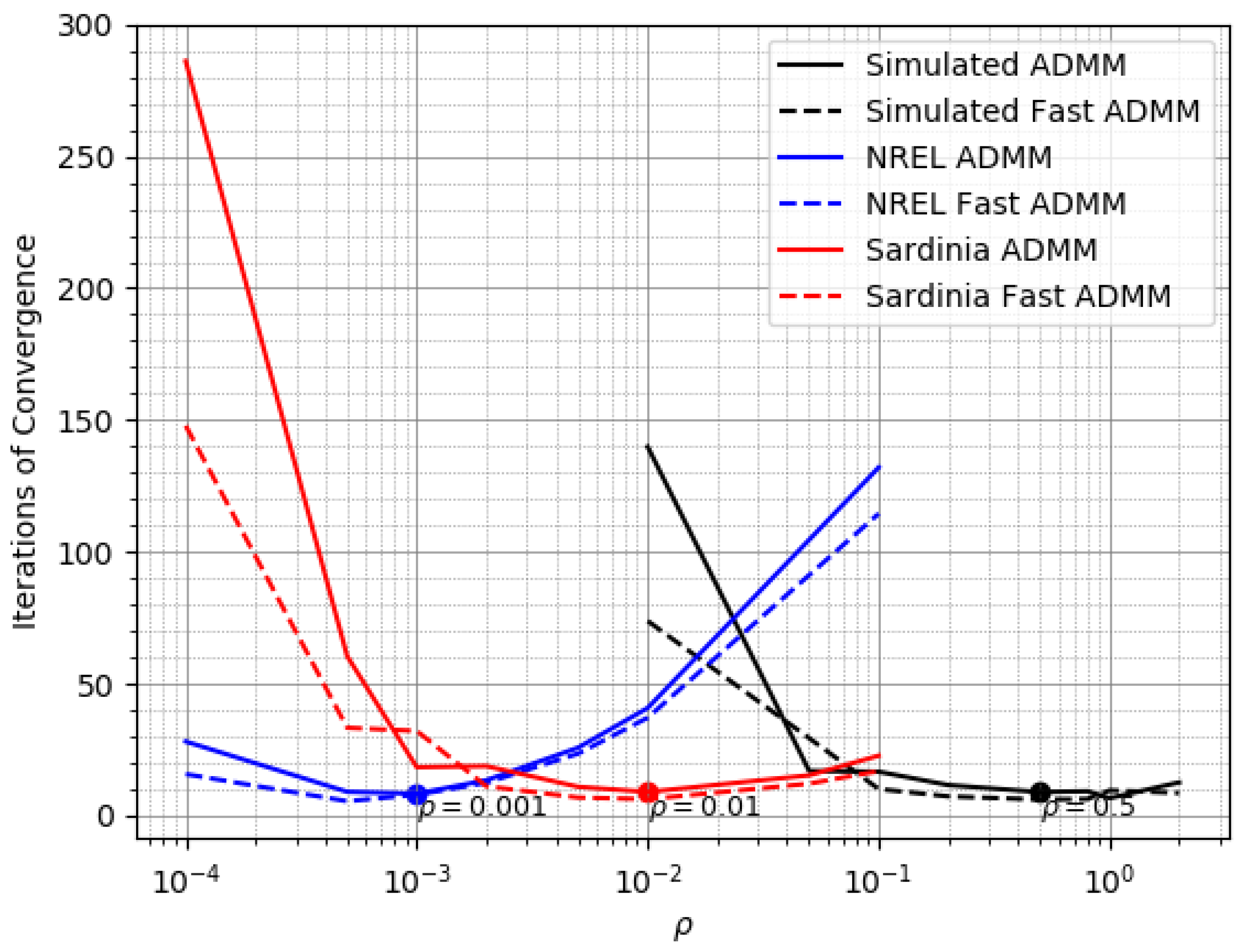
3.3. Online Estimate of Individual Variance
3.4. Boundary Constraint
4. Application and Case-Studies
4.1. Framework and Verification
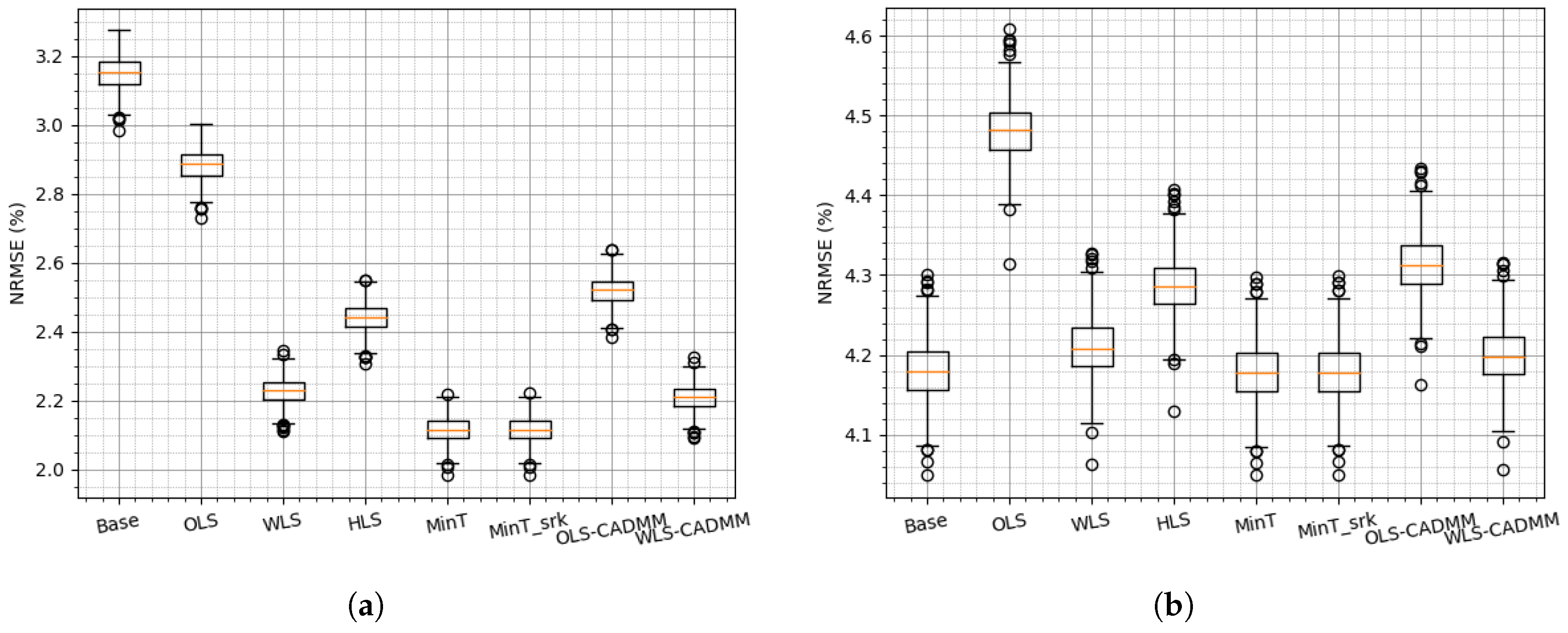
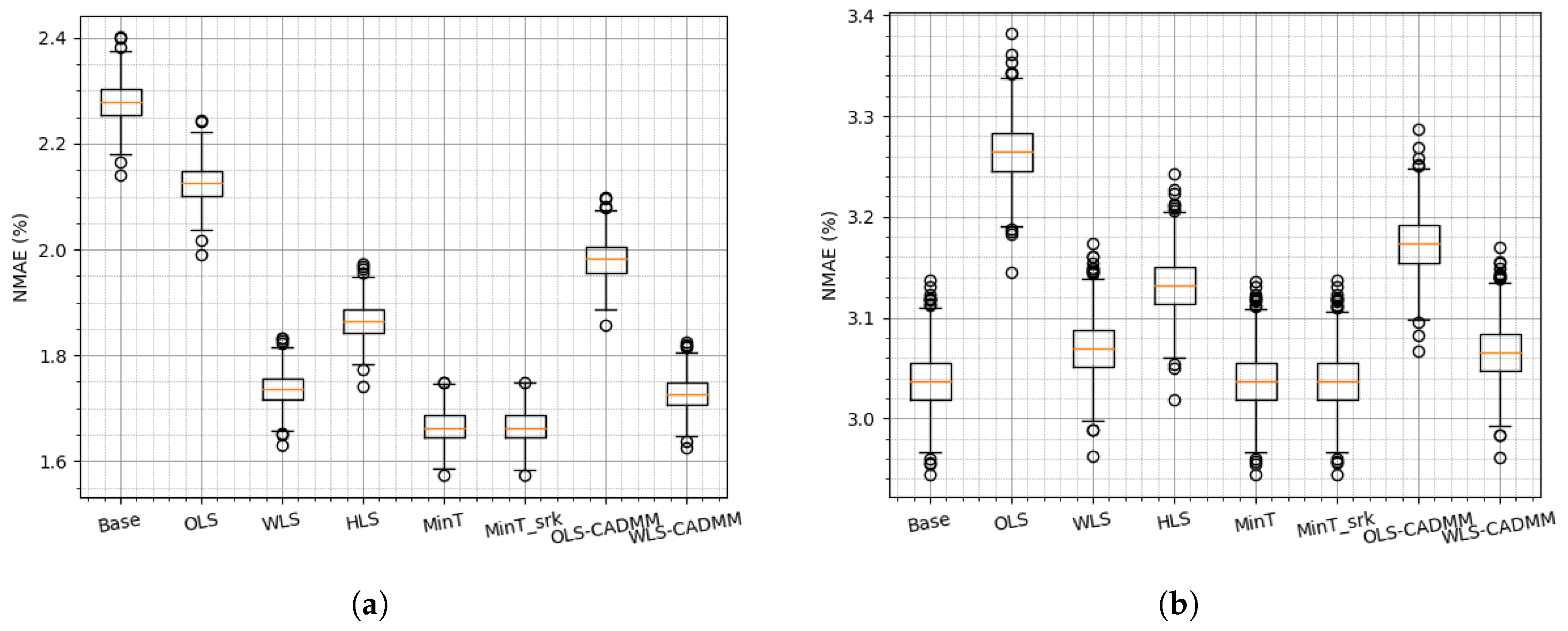
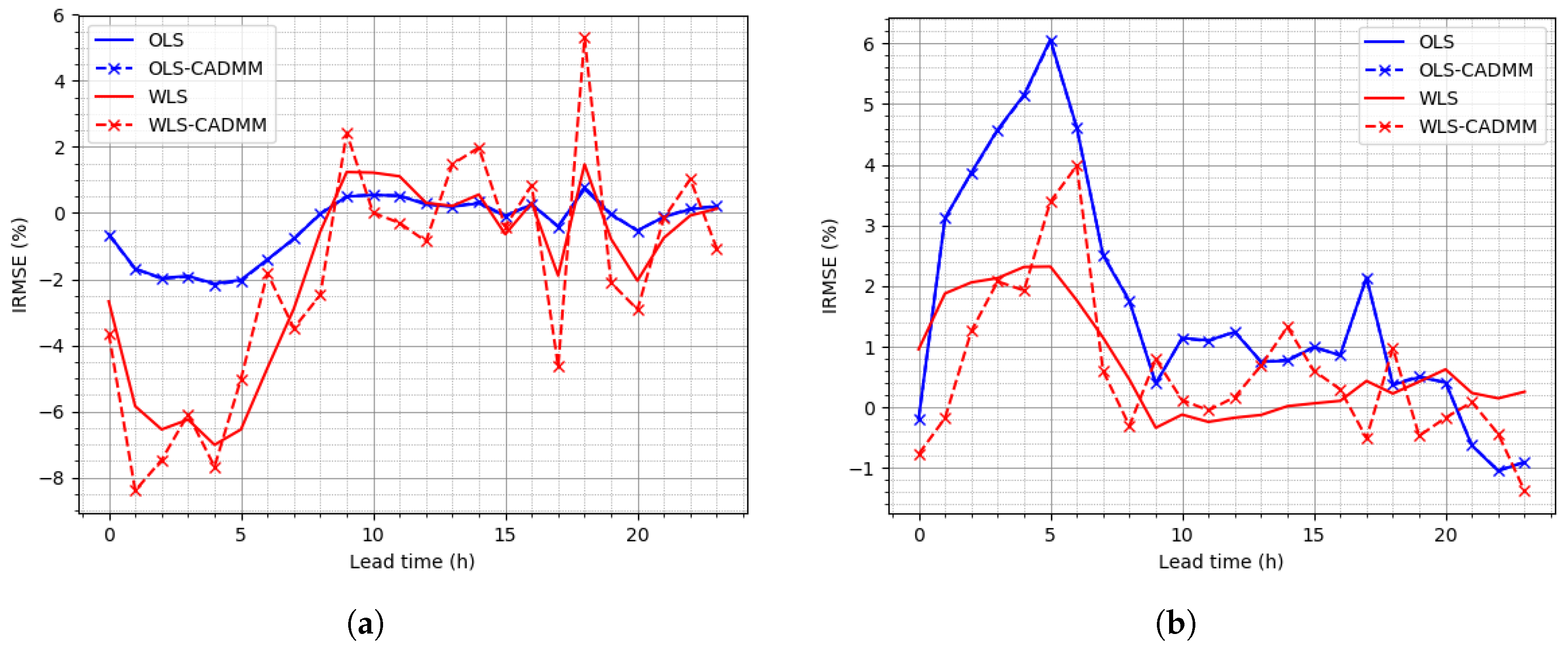
4.2. Reconciliation on the Simulated Dataset
4.3. Reconciliation on the NREL Dataset
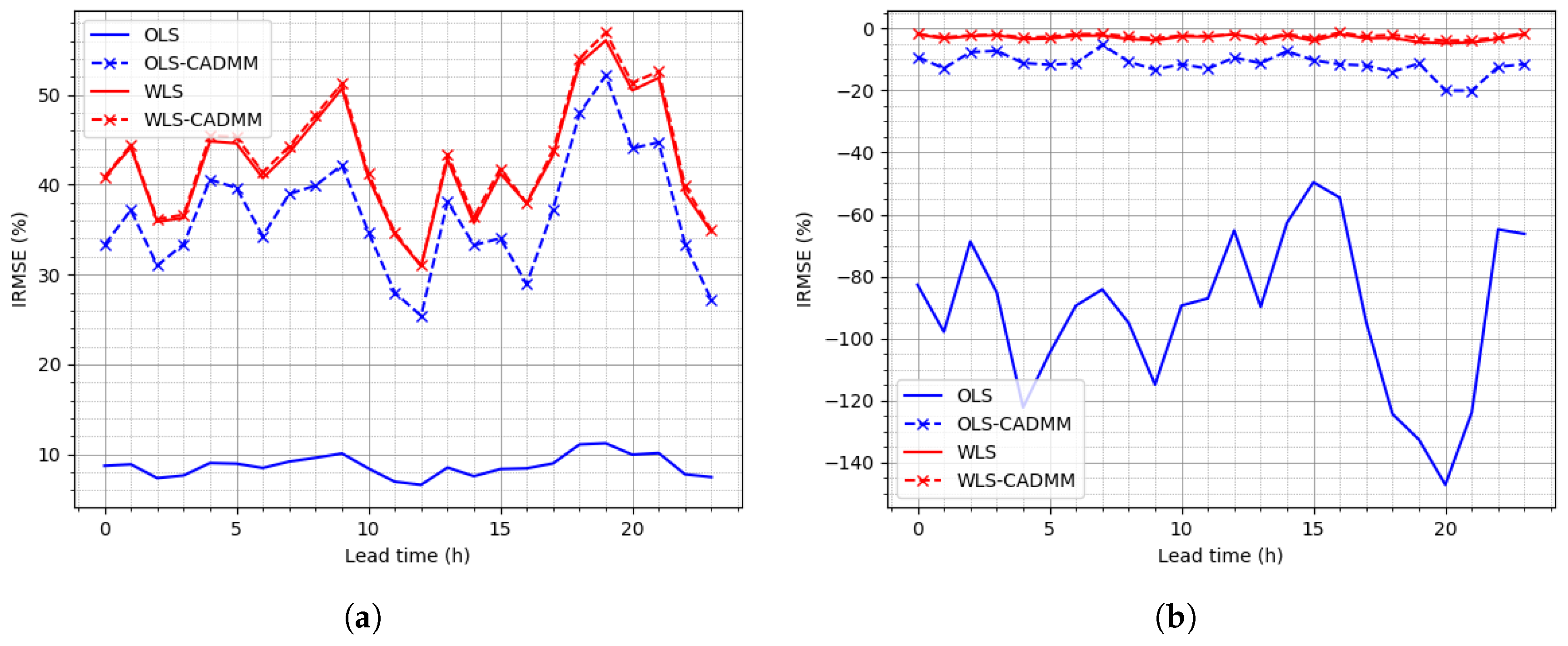
4.4. Reconciliation on the Sardinia Dataset
5. Conclusions and Perspectives
Author Contributions
Funding
Conflicts of Interest
Appendix A. Radial Basis Function Based Support Vector Regression
References
- Fliedner, G. Hierarchical forecasting: Issues and use guidelines. Ind. Manag. Data Syst. 2001, 101, 5–12. [Google Scholar] [CrossRef]
- Christoph, W. Essays in Hierarchical Time Series Forecasting and Forecast Combination. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2018. [Google Scholar]
- Lobo, M.G.; Sanchez, I. Regional wind power forecasting based on smoothing techniques, with application to the spanish peninsular system. IEEE Trans. Power Syst. 2012, 27, 1990–1997. [Google Scholar] [CrossRef]
- Fabbri, A.; Roman, T.G.S.; Abbad, J.R.; Quezada, V.H.M. Assessment of the cost associated with wind generation prediction errors in a liberalized electricity market. IEEE Trans. Power Syst. 2005, 20, 1440–1446. [Google Scholar] [CrossRef]
- Lu, Z.; Ye, X.; Qiao, Y.; Min, Y. Initial exploration of wind farm cluster hierarchical coordinated dispatch based on virtual power generator concept. CSEE J. Power Energy Syst. 2015, 1, 62–67. [Google Scholar] [CrossRef]
- Meng, K.; Zhang, W.; Li, Y.; Dong, Z.Y.; Xu, Z.; Wong, K.P.; Zheng, Y. Hierarchical SCOPF considering wind energy integration through multiterminal VSC-HVDC grids. IEEE Trans. Power Syst. 2017, 32, 4211–4221. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, J. Least Squares-based optimal reconciliation method for hierarchical forecasts of wind power generation. IEEE Trans. Power Syst. 2018, 1. [Google Scholar] [CrossRef]
- Yang, D.; Quan, H.; Disfani, V.R.; Liu, L. Reconciling solar forecasts: Geographical hierarchy. Sol. Energy 2017, 146, 276–286. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Lee, A.J.; Wang, E. Fast computation of reconciled forecasts for hierarchical and grouped time series. Comput. Data Anal. 2016, 97, 16–32. [Google Scholar] [CrossRef]
- Athanasopoulos, G.; Hyndman, R.J.; Kourentzes, N.; Petropoulos, F. Forecasting with temporal hierarchies. Eur. J. Oper. Res. 2017, 262, 60–74. [Google Scholar] [CrossRef]
- van Erven, T.; Cugliari, J. Game-theoretically optimal reconciliation of contemporaneous hierarchical time series forecasts. In Modeling and Stochastic Learning for Forecasting in High Dimensions; Springer International Publishing: Cham, Switzerland, 2015; pp. 297–317. [Google Scholar]
- Lei, M.; Shiyan, L.; Chuanwen, J.; Hongling, L.; Yan, Z. A review on the forecasting of wind speed and generated power. Renew. Sustain. Energy Rev. 2009, 13, 915–920. [Google Scholar] [CrossRef]
- Giebel, G.; Brownsword, R.; Kariniotakis, G.; Denhard, M.; Draxl, C. The State-Of-The-Art in Short-Term Prediction of Wind Power: A Literature Overview, 2nd ed.; ANEMOS.plus: Paris, France, 2011. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Fan, S. Global Energy Forecasting Competition 2012. Int. J. Forecast. 2014, 30, 357–363. [Google Scholar] [CrossRef]
- Siebert, N. Development of Methods for Regional Wind Power Forecasting. Ph.D. Thesis, École Nationale Supérieure des Mines de Paris, Paris, France, 2008. [Google Scholar]
- Yan, J.; Zhang, H.; Liu, Y.; Han, S.; Li, L.; Lu, Z. Forecasting the high penetration of wind power on multiple scales using multi-to-multi mapping. IEEE Trans. Power Syst. 2018, 33, 3276–3284. [Google Scholar] [CrossRef]
- Hyndman, R.; Athanasopoulos, G. Optimally reconciling forecasts in a hierarchy. Foresight 2014, 2014, 42–48. [Google Scholar]
- Hyndman, R.J.; Ahmed, R.A.; Athanasopoulos, G.; Shang, H.L. Optimal combination forecasts for hierarchical time series. Comput. Stat. Data Anal. 2011, 55, 2579–2589. [Google Scholar] [CrossRef]
- Wickramasuriya, S.L.; Athanasopoulos, G.; Hyndman, R.J. Optimal forecast reconciliation for hierarchical and grouped time series through trace minimization. J. Am. Stat. Assoc. 2018, 1–16. [Google Scholar] [CrossRef]
- Jooyoung, J.; Anastasios, P.; Fotios, P. Reconciliation of probabilistic forecasts with an application to wind power. arXiv, 2018; arXiv:1808.02635. [Google Scholar]
- Yang, D.; Quan, H.; Disfani, V.R.; Rodríguez-Gallegos, C.D. Reconciling solar forecasts: Temporal hierarchy. Sol. Energy 2017, 158, 332–346. [Google Scholar] [CrossRef]
- Campbell, S.; Meyer, C. Generalized Inverses of Linear Transformations; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2009. [Google Scholar] [CrossRef]
- Schäfer, J.; Strimmer, K. A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics. Stat. Appl. Genet. Mol. Biol. 2005, 4, 32. [Google Scholar] [CrossRef] [PubMed]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Goldstein, T.; O’Donoghue, B.; Setzer, S.; Baraniuk, R. Fast alternating direction optimization methods. SIAM J. Imaging Sci. 2014, 7, 1588–1623. [Google Scholar] [CrossRef]
- Harris, R.I.; Cook, N.J. The parent wind speed distribution: Why Weibull? J. Wind Eng. Ind. Aerodyn. 2014, 131, 72–87. [Google Scholar] [CrossRef]
- Lydia, M.; Kumar, S.S.; Selvakumar, A.I.; Kumar, G.E.P. A comprehensive review on wind turbine power curve modeling techniques. Renew. Sustain. Energy Rev. 2014, 30, 452–460. [Google Scholar] [CrossRef]
- Jowder, F.A. Wind power analysis and site matching of wind turbine generators in Kingdom of Bahrain. Appl. Energy 2009, 86, 538–545. [Google Scholar] [CrossRef]
- Draxl, C.; Clifton, A.; Hodge, B.M.; McCaa, J. The Wind Integration National Dataset (WIND) Toolkit. Appl. Energy 2015, 151, 355–366. [Google Scholar] [CrossRef]
- Pennock, K. Updated Eastern Interconnect Wind Power Output and Forecasts for ERGIS: July 2012. Available online: https://www.nrel.gov/docs/fy13osti/56616.pdf (accessed on 1 October 2012).
- Zheng, L.; Hu, W.; Min, Y. Raw wind data preprocessing: A data-mining approach. IEEE Trans. Sustain. Energy 2015, 6, 11–19. [Google Scholar] [CrossRef]
- Kramer, O.; Gieseke, F. Short-term wind energy forecasting using Support Vector Regression. In Proceedings of the 6th International Conference SOCO—2011 Soft Computing Models in Industrial and Environmental Applications, Salamanca, Spain, 6–8 April 2011; Corchado, E., Snášel, V., Sedano, J., Hassanien, A.E., Calvo, J.L., Ślȩzak, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 271–280. [Google Scholar]
- Zeng, J.; Qiao, W. Support vector machine-based short-term wind power forecasting. In Proceedings of the 2011 IEEE/PES Power Systems Conference and Exposition, Phoenix, AZ, USA, 20–23 March 2011; pp. 1–8. [Google Scholar] [CrossRef]

| Estimator | Covariance Matrix | Matrix Property |
|---|---|---|
| OLS | Identity matrix | diagonal matrix |
| WLS | diagonal matrix | |
| HLS | full matrix | |
| MinT | full matrix | |
| MinT_srk | full matrix |
| Dataset | Wind Speeds | Power Output |
|---|---|---|
| Simulated dataset | Randomly generated | Simulated |
| NREL dataset | Provided | Simulated |
| Sardinia dataset | Provided | Measured |
| Parameters | Interval |
|---|---|
| the cut-in speed m/s | [3, 4] |
| the rated speed m/s | [12, 15] |
| the cut-out speed m/s | [24, 25] |
| Weibull shape factor C | [1.6, 2] |
| Weibull scale factor | [6, 8] |
| wind farm capacity MW | [20, 30] |
| Node 1 | Node 2 | Node 3 | Node 4 | Node 5 | Node 6 | Bottom Level | Node AGG | |
|---|---|---|---|---|---|---|---|---|
| Base | 7.76 | 6.62 | 6.96 | 6.88 | 6.75 | 7.44 | 7.07 | 10.90 |
| OLS | 16.69 | 17.68 | 17.35 | 8.88 | 9.92 | 8.90 | 13.24 | 9.95 |
| WLS | 7.73 | 6.63 | 6.96 | 7.23 | 6.92 | 8.18 | 7.28 | 6.28 |
| OLS-CADMM | 8.34 | 7.25 | 7.56 | 7.74 | 7.67 | 8.43 | 7.83 | 6.91 |
| WLS-CADMM | 7.73 | 6.63 | 6.96 | 7.19 | 6.92 | 8.02 | 7.24 | 6.23 |
| Node 1 | Node 2 | Node 3 | Node 4 | Node 5 | Node 6 | Bottom Level | Node AGG | |
|---|---|---|---|---|---|---|---|---|
| Base | 5.34 | 4.62 | 4.82 | 4.90 | 4.79 | 5.18 | 4.94 | 6.65 |
| OLS | 9.73 | 9.48 | 9.53 | 6.11 | 6.55 | 6.06 | 7.91 | 6.25 |
| WLS | 5.34 | 4.64 | 4.83 | 5.18 | 4.91 | 5.68 | 5.09 | 4.49 |
| OLS-CADMM | 6.16 | 5.36 | 5.55 | 5.54 | 5.51 | 5.83 | 5.66 | 4.96 |
| WLS-CADMM | 5.34 | 4.64 | 4.83 | 5.14 | 4.91 | 5.57 | 5.07 | 4.45 |
| Base | OLS | WLS | OLS-CADMM | WLS-CADMM |
|---|---|---|---|---|
| 4.34 | 13.13 | 3.68 | 4.29 | 3.63 |
| Node 1 | Node 2 | Node 3 | Node 4 | Bottom Level | Node AGG | |
|---|---|---|---|---|---|---|
| Base | 11.68 | 9.15 | 12.29 | 12.40 | 11.38 | 7.56 |
| OLS | 11.54 | 8.93 | 11.96 | 12.12 | 11.14 | 7.61 |
| WLS | 11.55 | 9.05 | 12.21 | 12.29 | 11.28 | 7.76 |
| OLS-CADMM | 11.54 | 8.93 | 11.96 | 12.12 | 11.14 | 7.61 |
| WLS-CADMM | 11.60 | 9.07 | 12.15 | 12.28 | 11.27 | 7.76 |
| Node 1 | Node 2 | Node 3 | Node 4 | Bottom Level | Node AGG | |
|---|---|---|---|---|---|---|
| Base | 7.11 | 4.90 | 7.69 | 7.71 | 6.85 | 4.94 |
| OLS | 7.09 | 4.85 | 7.67 | 7.65 | 6.81 | 4.95 |
| WLS | 7.09 | 4.86 | 7.67 | 7.68 | 6.82 | 4.98 |
| OLS-CADMM | 7.09 | 4.85 | 7.67 | 7.65 | 6.81 | 4.95 |
| WLS-CADMM | 7.14 | 5.12 | 8.02 | 7.90 | 7.04 | 5.08 |
| Base | OLS | WLS | OLS-CADMM | WLS-CADMM |
|---|---|---|---|---|
| 5.82 | 5.61 | 5.75 | 5.61 | 5.75 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, L.; Pinson, P. Distributed Reconciliation in Day-Ahead Wind Power Forecasting. Energies 2019, 12, 1112. https://doi.org/10.3390/en12061112
Bai L, Pinson P. Distributed Reconciliation in Day-Ahead Wind Power Forecasting. Energies. 2019; 12(6):1112. https://doi.org/10.3390/en12061112
Chicago/Turabian StyleBai, Li, and Pierre Pinson. 2019. "Distributed Reconciliation in Day-Ahead Wind Power Forecasting" Energies 12, no. 6: 1112. https://doi.org/10.3390/en12061112
APA StyleBai, L., & Pinson, P. (2019). Distributed Reconciliation in Day-Ahead Wind Power Forecasting. Energies, 12(6), 1112. https://doi.org/10.3390/en12061112




