Abstract
Natural gas is often described as the cleanest fossil fuel. The consumption of natural gas is increasing rapidly. Accurate prediction of natural gas spot prices would significantly benefit energy management, economic development, and environmental conservation. In this study, the least squares regression boosting (LSBoost) algorithm was used for forecasting natural gas spot prices. LSBoost can fit regression ensembles well by minimizing the mean squared error. Henry Hub natural gas spot prices were investigated, and a wide range of time series from January 2001 to December 2017 was selected. The LSBoost method is adopted to analyze data series at daily, weekly and monthly. An empirical study verified that the proposed prediction model has a high degree of fitting. Compared with some existing approaches such as linear regression, linear support vector machine (SVM), quadratic SVM, and cubic SVM, the proposed LSBoost-based model showed better performance such as a higher R-square and lower mean absolute error, mean square error, and root-mean-square error.
1. Introduction
As a low carbon and eco-efficient energy resource, natural gas has become an energy option to mitigate the environmental impacts of traditional fossil fuels for human beings. Natural gas is one of the most important energy resources in the world, and it fulfils more than one-fifth of energy demand worldwide [1]. Nowadays, natural gas is extensively used for residences, commerce, transportation, electric power, and industrial production. Natural gas price forecasting is increasingly playing an essential role for stakeholder groups highly sensitive to price fluctuation [2]. The forecast has widespread applications in all walks of life. Accurate natural gas price forecasting of one, three, five, or more months into the future is extremely significant in energy management, economic development, and environmental conservation.
Most of the international natural gas trade requires pipelines or ships for transport, because of the regional division of natural gas production and consumption. Some natural gas price systems with obvious regional characteristics have been formed around the world on account of geographical restrictions and freight rates. There are four representative prices including Henry Hub price in the United States, Average Import Cost Insurance and Freight (CIF) price in Germany, National Balancing Point (NBP) natural gas price in the United Kingdom, and Liquefied Natural Gas (LNG) price in Japan. From the perspective of pricing mechanism, North America and Britain carry out market pricing through the interplay of supply and demand gas-on-gas competition (GOG). Continental Europe adopts oil price escalation (OPE), which is linked with crude oil. Japan uses LNG pricing mechanism linked to Japan Crude Cocktail (JCC) and some regions (e.g., Russia and central Asia) still adopt monopoly pricing [3]. These pricing systems are strongly associated with natural gas trade around the world. Natural gas prices fluctuate dramatically and we take the Henry Hub natural gas spot price in the United States as an example to explain. There are several sharp price fluctuations (e.g., October to December 2005 and April to July 2008) from 2001–2009. The change of natural gas prices is basically stable except for some small fluctuations within a narrow range since 2009. The determinants of natural gas price are complex and diversified, since the natural gas market is completely deregulated and market-driven. The price suffers from various factors and parameters, e.g., other energy prices, exploration activity, and supply-demand relation. Thus, it is a challenging task to accurately forecast natural gas price.
So far, many methods have been proposed for natural gas price forecasting. By reviewing the existing work, these methods can be divided into two categories: structural models and data-driven methods. MacAvoy (2000) predicted a long-term negative trend of wellhead gas price obtained by the simulation of a partial equilibrium model of the American industry [4]. Buchananan et al. (2001) obtained the direction of monthly natural gas spot price movements from the viewpoint of trader positions [5]. Woo et al. (2006) established a relationship by utilizing a partial adjustment regression model to assess the trend of natural gas price in California [6]. With the development of artificial intelligence technology (AI) and its powerful performance, the focus has gradually shifted from econometrics and AI technology. Nguyen et al. (2010) studied the prices of monthly natural gas forward products using wavelet transform and adaptive models and obtained the lowest normalized mean square error (NMSE) (the value is 0.15384) using the adaptive generalized autoregressive conditional heteroskedasticity (GARCH) with multicomponent forecast [7]. Azadeh et al. (2012) developed a hybrid neuro-fuzzy method consisting of artificial neural network (ANN), fuzzy linear regression (FLR), and conventional regression (CR) to estimate natural gas prices of domestic and industrial sectors in Iran [8].
Most publications focus on short-term load forecasting (STLF). For instance, Zheng et al. (2017) used a hybrid algorithm to construct an STLF model [9], Kuo et al. (2018) introduced a high precision artificial neural networks model [10], and Merkel et al. (2018) proposed deep neural network regression for short-term natural gas load forecasting [11]. In recent years, there are some works with respect to short-term price forecasting in the natural gas spot market. Abrishami (2011) analyzed gas price forecasting with a hybrid intelligent framework consisting of group method of data handling (GMDH) neural networks and rule-based exert system (RES) [12]. Compared with GMDH neural networks and multilayer feed-forward neural networks, the hybrid intelligent framework afforded better forecasting results using daily Henry Hub spot price from 2006–2010. However, some results obtained from the hybrid intelligent forecasting method are unconvincing, because they cannot be reproduced. Busse et al. (2012) studied the daily spot natural gas price in the German NetConnect market using a dynamic forecasting method and a nonlinear autoregressive exogenous model (NARX) neural network, because the used NARX method with only five factors (temperature, exchange rate, and the settlements of three major gas hubs) is slightly better than the naive NARX method [13].
The study reported by Salehnia (2013) is one of the few studies that really forecasts the spot price in the natural gas market [14]. Using Gamma test analysis, several nonlinear models including local linear regression (LLR), dynamic local linear regression (DLLR), and ANN models have been utilized to test spot prices (daily, weekly, and monthly) for Henry Hub from 1997–2012. They verified that the ANN models have a higher accuracy in predicting the natural gas spot prices than LLR and DLLR, whereas the ANN models are not good at forecasting market price shocks. Ceperic et al. (2017) presented a strategic seasonality-adjusted, support vector machine (SVM)-based model and some improvements to the forecasting method based on SVM [15]. They used feature selection algorithms to generate model inputs. They investigated short-term Henry Hub spot natural gas prices using classical time series models such as naive, autoregression (AR), and autoregressive integrated moving average (ARIMA) and machine learning neural network and support vector regression (NN and SVR). They found that the gains are not necessarily apparent even though machine learning exhibits some improvements based on traditional time-series methods. According to this brief literature overview, it can be found that these methods [12,13,14,15] often showed better performance than traditional time-series methods in predicting natural gas prices.
For the above works on short-term price forecasting for natural gas spot markets, they consider small time periods, in general, no more than five years. In fact, it is easy to facilitate a short-term prediction while attaining an accurate forecasting result. However, fore-and-aft connection and influence in a long time period still exist and thus it is essential to investigate a long time period forecast. So far, few works exist in long time period price forecasting for natural gas spot markets. To this end, we consider such a prediction of natural gas spot price from 2001–2017 based on a boosting method. As a general method, boosting can improve the performance of any learning algorithm [16,17]. Boosting method is one of the popular ensemble learning methods used in machine learning [18]. The advantage of the boosting method lies in combining a series of weak classifiers to generate a very important “committee,” and it can provide increasing significance to bad classification with iteration [19,20]. Such a simple trick provides dramatic improvements in the classification performance.
In this study, the least squares regression boosting (LSBoost) method [21,22], one of the most popular boosting methods, was used to address the regression problem of natural gas price forecasting. LSBoost uses the least squares as the loss criteria and thus can fit regression ensembles well to minimize the mean-squared error [23]. According to the best of our knowledge, this is the first time the LSBoost method was applied in natural gas price forecasting. The original schema of the application is proposed. By studying the benefits of machine learning based on LSBoost prediction, the literature on gas price prediction was added. Moreover, it is shown that compared with the existing methods, LSBoost can significantly improve the prediction accuracy of natural gas price.
The rest of the paper proceeds as follows. The next section introduces three types of machine learning tools involved in this paper. Section 3 shows data preparation and description, model validation technique, and forecasting performance evaluation criteria. Section 4 states empirical and comparative research. Section 5 concludes this work.
2. Preliminaries
In this study, three types of machine learning tools including linear regression, SVM, and boosting algorithms were used.
2.1. Linear Regression
Linear regression is a very common predictive analysis method. The basic idea is to utilize linear predictor functions to model the relationships between response and explanatory variables. The parameters used in the model are also calculated from the training data. For linear regression model fitting, the least square function is often used. Linear regression ranks as one of the most popular methods applied to various disciplines such as finance [24], economics [25], environmental science [26], and machine learning [27]. For example, electricity consumption forecasting in Italy using linear regression models was reported [28].
2.2. SVM
SVM is a supervised learning method and often used in regression analysis [29]. SVM finally resorts to the linear regression technique. However, SVM first maps the input space into a high-dimensional feature space. The increase in space dimension leads to a higher computational complexity and even dimension disaster. To solve this problem, the kernel function is used for mapping [30]. One kernel function means one SVM model. For example, linear kernel function: and polynomial kernel function: , where and represent two variables in the input space. Setting, and correspond to the kernel functions of quadratic SVM and cubic SVM, respectively. SVM has vast applications in the field of energy analysis and price forecasting. For example, a crude oil price forecasting scheme based on SVM is reported [31].
2.3. Boosting
Boosting is a supervised learning algorithm that can reduce bias and variance [32]. Boosting converts a weak learner into a strong learner. A weak learner is only slightly correlated with the true classification, whereas a strong learner is arbitrarily well-correlated with the true classification [33]. Boosting can promote the model predictions for any given learning algorithm, because the principle of boosting is to train weak learners sequentially and each learner tries to correct its predecessor. Boosting provides good accuracy levels for many problems and thus one of the most prominent regression and classification techniques.
The concept of gradient boosting proposed by Friedman extends the boosting to regression by introducing the gradient boosting machine (GBM) method [34,35]. Gradient boosting builds a prediction model in the form of an ensemble of weak prediction models and in a stage-wise manner [36]. Decision trees typically act as weak learners. The generalization is achieved by optimizing an arbitrary differentiable loss function. Gradient boosting sequentially adds predictors to an ensemble, and each one corrects its predecessor. It fits the new predictor to the residual errors. The generic gradient boosting method is shown in Algorithm 1, where and represent the explanatory variable and response variable, respectively. More details are reported in the literature [37,38].
| Algorithm 1. The gradient boosting algorithm. |
| Input: A training set , a loss function , number of iterations |
| Initialize, |
| For to do: |
| , |
| End for |
| Output: The final regression function . |
There are plenty of boosting algorithms [39], such as AdaBoost, LogitBoost, GentleBoost RobustBoost, LPBoost, TotalBoost, and RUSBoost. However, only LSBoost designed for regression while others algorithms are usually used for classification. LSBoost is one of the gradient boosting methods that uses the least squares as the loss criteria [23]. Each step is to endow a new learner with a difference between the observed response and aggregated prediction of all the learners grown previously. Moreover, boosting can directly identify important features and evaluate predictor importance (PI), since LSBoost only chooses a single feature at each round to approximate the alignment accuracy residual. More details about PI evaluation are given in Appendix A. LSBoost has become one of the most prominent regression techniques and can provide an acceptable accuracy level for prediction problems. The algorithm is briefly described in Algorithm 2, where and represent the explanatory variable and response variable, respectively. More details are reported in the literature [23,38].
| Algorithm 2. The LSBoost algorithm. |
| Input: A training set , a loss function , number of iterations . |
| Initialize, |
| For to do: |
| , |
| End for |
| Output: The final regression function . |
3. Datasets and Models
Prior to model construction, we make a few research preparation works, which are comprised of data preparation and description, model validation technique, and forecasting performance evaluation criteria.
3.1. Data Preparation and Description
Until now, Henry Hub is not only the largest pricing point, but also the foundation for traded natural gas future contracts and other derivatives. Therefore, the historical price data of Henry Hub were selected as the observations data, and the period is from January 2001 to December 2017. This study aimed to predict the natural gas spot prices by experimentally investigating the natural gas spot price series at different frequencies, e.g., daily, weekly, and monthly. After data preprocessing, the data series of natural gas spot price includes 4260 observations of daily data, 886 observations of weekly data, and 204 observations of monthly data. In addition, there are only 4260 observations of daily data since natural gas is only traded on weekdays and some data are missing.
Figure 1 shows the daily, weekly, and monthly price trends in this period, respectively. As shown in Figure 1, some fluctuations exist. Especially, the 537th observation in Figure 1a shows the highest value 18.48 that occurred on 25 February 2003. Note that, for such several fluctuations, it is difficult to make a precise prediction. In addition, Table 1 shows the descriptive statistical features of natural gas spot price series for daily, weekly, and monthly trends.
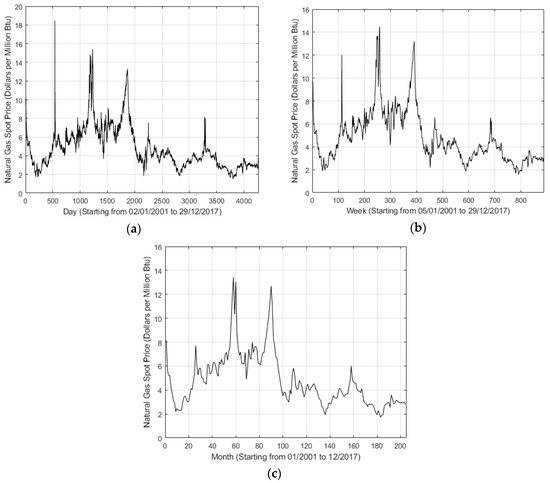
Figure 1.
Henry Hub natural gas spot price series data of different timescales. (a) Daily, (b) Weekly, (c) Monthly.

Table 1.
Summary of descriptive statistics of natural gas spot price series for different timescales.
Based on Ceperic et al.’s work [15] and Natural Gas Summary [40], explanatory variables were obtained from the following sources: Heating Oil Prices (HO), WTI oil Prices (WTI), Baker Hughes US Natural Gas Rotary Rig Count (NGRRC), Total US Natural Gas Marketed Production (NGMP), Total US Natural Gas Consumption (NGC), Total US Natural Gas Underground Storage Capacity (NGUSC), and Total US Natural Gas Imports (NGI). The response variable is the natural gas spot price. The explanatory variables are almost associated with natural gas prices. Moreover, they demonstrate various driving factors of natural gas price to some extent. All the data collected in this study were obtained from the Energy Information Administration (EIA) website [40].
3.2. Model Validation Techniques
Cross-validation (CV) was used to estimate the prediction accuracy to avoid overfitting [41]. The CV is achieved by dividing the dataset into folds and estimating the accuracy on each fold with other folds as training data. As a result, the CV can obtain effective information from limited data as much as possible. The CV partitions a dataset into a training sample and validation (testing) sample. K-fold CV is a common form of CV; it randomly splits the training dataset into k subsamples of almost equal size. In this study, 10-fold CV was used, because k = 10 is widely used in practice.
3.3. Forecasting Performance Evaluation Criteria
To evaluate the forecasting performance, four statistical methods were used for measuring the forecasting errors. The methods include the following: R-square (R2) measures the goodness-of-fit for the entire regression [42]. The R2 value ranges from 0–1. The closer the value is to 1, the better the goodness-of-fit of the regression line to the observed value and vice versa [43,44]:
where is the actual value at the time , is the prediction value at the time , and is the number of observed data.
The mean absolute error (MAE) is a quantity to measure how close the forecasts or predictions are to the final outcomes. MAE can be expressed as follows [45,46]:
Mean square error (MSE) calculates the square of differences between the observed and predicted values, penalizing the highest gaps [47,48].
Root-mean-square error (RMSE) can well quantify large forecast errors owing to high sensitivity. Consequently, RMSE can be applied to scenarios that can tolerate smaller errors while enhancing the effect of larger errors. More details are provided in the literature [47,49,50]:
In these three criteria MAE, MSE, and RMSE, the smaller values indicate the better forecasting performance of the model, because they reveal the deviation between actual and predicted values.
4. Empirical Analysis
In this section, empirical and comparative studies were carried out on natural gas spot price forecasting. Our model is based on the LSBoost algorithm and Henry Hub natural gas spot prices. The daily, weekly, and monthly data were used to investigate the Henry Hub natural gas spot prices from January 2001 to December 2017.
4.1. An Empirical Study of Natural Gas Price Series
Table 2 shows the forecasting performance of LSBoost for different timescales. Table 2 shows that the R-square values for daily, weekly, and monthly predictions are 0.91, 0.90, and 0.78, respectively, indicating that the proposed prediction model has a high degree of fitting. The RMSE values for daily, weekly, and monthly predictions are 0.6615, 0.7153, and 1.0567, respectively. From the trend of RMSE values from daily to monthly, it can be deduced that the forecast performance is related to the amount of data, i.e., the more particular and plentiful the data information, the more accurate the forecast results. Furthermore, with respect to MAE and MSE, consistent deductions were obtained. In addition, all the findings of MAE, MSE, and RMSE verify small deviations between the actual and estimated values, and thus the fitting is extremely excellent.

Table 2.
Forecasting performance evaluation for different timescales.
For a visual understanding of forecasting effect, a relationship between time and the natural gas spot price is shown in Figure 2, where x-axis and y-axis represent the timescale and natural gas spot price, respectively. During the data preparation, some data preprocessing operations were performed. For example, if the natural gas spot price on a certain day is missing, then it is deleted. Thus, x-axis was allowed to represent the record number rather than the direct daily, weekly, and monthly timescales. In Figure 2, the blue points represent the actual prices, whereas the yellow points correspond to the predicted values. Figure 2 shows that the yellow points basically fall over the blue points, indicating that the prediction condition well reflects the tendency of the actual status. Moreover, notably, a similar conclusion can be obtained that the weekly and monthly cases are worse than the daily cases due to the decrease in data information.
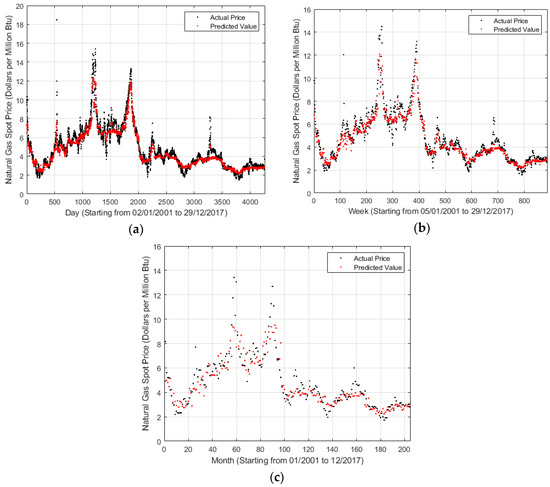
Figure 2.
LSBoost outputs for different timescales. (a) Daily; (b) Weekly; (c) Monthly.
Some fluctuations were not still predicted well, such as around September to December 2005 and April to July 2008. This can be attributed to many factors. For example, the price of natural gas skyrocketing on September to December 2005 is caused by a high price and rising demand in the U.S. market, a dispute between Russia and Ukraine over natural gas prices, etc. After that, the benchmark price of American natural gas first increased and then started falling, and finally gradually stabilized. On one hand, it is closely related to the supply and demand situation of the domestic natural gas market in the United States. In the case of a relatively stable market consumption, accelerated development of unconventional natural gas resources drives the rapid growth of natural gas reserves and output, thus increasing the output significantly faster than the consumption. On the other hand, the natural gas market in the United States is mature. Natural gas price is strongly related to the international oil price, and the fluctuation in international oil price has directly affected the change in natural gas price since 2008. The financial crisis had a major impact on the global natural gas market since the second half of 2008. The consumption of natural gas in the world’s major natural gas markets has declined, and the gas price has dropped sharply. Henry Hub natural gas price dropped from 12.69 dollars per million btu in June 2008 to 5.82 dollars per million btu in December.
Figure 3 shows the distribution status of actual and predicted values for natural gas spot prices, where x-axis and y-axis represent the actual and predicted values, respectively. Figure 3 shows that when the price varies from 2–8, most of the blue points are close to or even hit the straight line. This indicates an excellent prediction provided that the price is no more than 8 or so. However, in the case of price larger than 8, it does not have a good prediction due to some extra factors. For example, in February 2003, the factors such as supply–demand imbalance, systematical and policy reason, and weather variations make the price quickly increase, reaching 18.48 dollars per million btu.
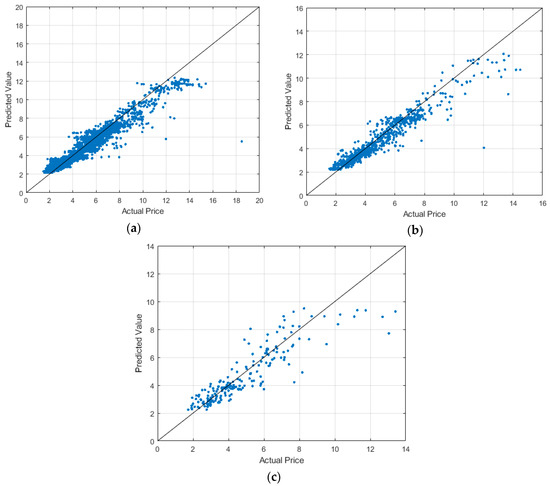
Figure 3.
Predicted values versus actual values in different timescales (a) Daily; (b) Weekly; (c) Monthly.
Table 3 shows the importance degree of seven explanatory variables for natural gas spot price prediction. As shown in Table 3, the importance rank of variables in daily data from low to high is WTI, NGI, NGC, NGRRC, HO, NGUSC, and NGMP. The rank in weekly data is NGI, WTI, NGC, NGRRC, HO, NGUSC, and NGMP, whereas the rank in monthly data is NGC, NGI, WTI, HO, NGRRC, NGUSC, and NGMP. The day rank is almost the same as the week rank, but both have a large difference with the month rank. As a whole, NGI is a weaker factor. In the day rank, the effect of WTI is the weakest, whereas in the month rank, NGC is weaker than NGI. In summary, NGMP is the most significant factor, probably because the price easily suffers from the supply–demand relationship.

Table 3.
The importance degree of seven explanatory variables.
4.2. Comparisons of Existing Predictive Methods
To highlight the performance of the proposed model, comparisons were made with some existing classical prediction methods such as linear regression, linear SVM, quadratic SVM, and cubic SVM. The comparison results in different timescales are shown in Table 4, Table 5 and Table 6. The results show that LSBoost can achieve the highest R-square and lowest MAE, MSE, and RMSE among all the methods. SVM is frequently used in energy prediction and also natural gas price forecasting [15]; however, the effect is worse than the LSBoost method. One important reason is that LSBoost can recognize important variables and only selects one variable to approximate the precision residue each round. As shown in Table 4, Table 5 and Table 6, linear SVM has the lowest R-square and highest MAE, MSE, and RMSE. Linear regression is popular in prediction analysis but still has a great performance gap with the proposed model.

Table 4.
Comparison of existing methods for the daily forecast.

Table 5.
Comparison of existing methods for the weekly forecast.

Table 6.
Comparison of existing methods for the monthly forecast.
In addition, obviously, linear prediction methods including linear regression and linear SVM showed worse performance in forecasting natural gas prices than the other three models. As reported by Malliarisa, the nonlinear methods were best for crude oil, heating oil, gasoline, and natural gas forecasting, even though both linear and nonlinear techniques are used in forecasting interrelated energy product prices [51]. The proposed model fills in a blank space of LSBoost for applications in natural gas spot price forecasting.
5. Conclusions
The goal of this study was to introduce a new machine learning approach LSBoost for natural gas price forecasting. Using seven variables including HO, WTI, NGRRC, NGMP, NGC, NGUSC, and NGI, Henry Hub natural gas spot prices starting from January 2001 to December 2017 were investigated. The LSBoost algorithm shows superiority in natural gas price prediction, because it achieved the highest R-square and lowest MAE, MSE, and RMSE compared with the existing methods such as linear regression, linear SVM, quadratic SVM, and cubic SVM. Our experiments on the datasets demonstrate that LSBoost model is superior and promising. In the future, we consider possible improvements in the proposed model based on the LSBoost method in terms of predicting performance, and we will try to extend the method and analysis presented in this study to forecast other fuel prices, such as crude oil.
Author Contributions
Conceptualization, M.S. and Z.Z.; methodology, Z.Z. and Y.Z.; software, M.S. and Y.Z.; validation, M.S. and, Z.Z. and Y.Z.; formal analysis, D.Z.; investigation, M.S.; resources, M.S. and D.Z.; data curation, M.S. and Y.Z.; writing—original draft preparation, M.S.; writing—review and editing, Z.Z. and, Y.Z. and D.Z.; visualization, M.S. and, Y.Z. and D.Z.; supervision, Z.Z.; project administration, Z.Z. and D.Z.; funding acquisition, D.Z.
Funding
This research received no external funding.
Acknowledgments
This work was supported by the China Natural Science Funding No. 71673134 and Six Talents Peak Project of Jiangsu Province (No. JY-036).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
LSboost [35] is an ensemble method based on many regression trees as weak learners . It assigns different weight to each tree in order to minimize the MSE between the target value and the predicted value . The model initially uses the median of all actual values () and combines the weighted regress trees to reduce the MSE for each as:
where is the weight for the nth tree, is the number of trees, and with is the learning rate.
Since each tree splits points on selected feature/predictor at each level, the predictor importance (PI) can be measured based on how often a predictor is used in constructing the tree. Normally, the more a predictor is used with these trees, the higher its importance. The actual PI is measured based on the amount of improved prediction performance (MSE change) when splitting data points on that predictor.
References
- International Energy Agency (IEA). Key World Energy Statistics. 2018. Available online: https://webstore.iea.org/key-world-energy-statistics-2018 (accessed on 8 March 2019).
- Nick, S.; Thoenes, S. What drives natural gas prices?—A structural VAR approach. Energy Econ. 2014, 45, 517–527. [Google Scholar] [CrossRef]
- The International Gas Union (IGU). Wholesale Gas Price Survey. 2018. Available online: https://www.igu.org/publication/301683/31 (accessed on 8 March 2019).
- MacAvoy, P.W.; Moshkin, N.V. The new long-term trend in the price of natural gas. Resour. Energy Econ. 2000, 22, 315–338. [Google Scholar] [CrossRef]
- Buchanan, W.K.; Hodges, P.; Theis, J. Which way the natural gas price: An attempt to predict the direction of natural gas spot price movements using trader positions. Energy Econ. 2001, 23, 279–293. [Google Scholar] [CrossRef]
- Woo, C.K.; Olson, A.; Horowitz, I. Market efficiency, cross hedging and price forecasts: California’s natural-gas markets. Energy 2006, 31, 1290–1304. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Nabney, I.T. Short-term electricity demand and gas price forecasts using wavelet transforms and adaptive models. Energy 2010, 35, 3674–3685. [Google Scholar] [CrossRef]
- Azadeh, A.; Sheikhalishahi, M.; Shahmiri, S. A hybrid neuro-fuzzy approach for improvement of natural gas price forecasting in vague and noisy environments: domestic and industrial sectors. In Proceedings of the International Conference on Trends in Industrial and Mechanical Engineering (ICTIME’2012), Dubai, UAE, 24–25 March 2012; pp. 123–127. [Google Scholar]
- Zheng, H.; Yuan, J.; Chen, L. Short-term load forecasting using EMD-LSTM neural networks with a Xgboost algorithm for feature importance evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef]
- Kuo, P.H.; Huang, C.J. A high precision artificial neural networks model for short-term energy load forecasting. Energies 2018, 11, 213. [Google Scholar] [CrossRef]
- Merkel, G.; Povinelli, R.; Brown, R. Short-term load forecasting of natural gas with deep neural network regression. Energies 2018, 11, 2008. [Google Scholar] [CrossRef]
- Abrishami, H.; Varahrami, V. Different methods for gas price forecasting. Cuadernos Econ. 2011, 34, 137–144. [Google Scholar] [CrossRef][Green Version]
- Busse, S.; Helmholz, P.; Weinmann, M. Forecasting day ahead spot price movements of natural gas—An analysis of potential influence factors on basis of a NARX neural network. In Proceedings of the Tagungsband der Multikonferenz Wirtschaftsinformatik (MKWI), Braunschweig, Germany, 29 February–2 March 2012; pp. 1–3. [Google Scholar]
- Salehnia, N.; Falahi, M.A.; Seifi, A.; Adeli, M.H.M. Forecasting natural gas spot prices with nonlinear modeling using gamma test analysis. J. Natl. Gas Sci. Eng. 2013, 14, 238–249. [Google Scholar] [CrossRef]
- Čeperić, E.; Žiković, S.; Čeperić, V. Short-term forecasting of natural gas prices using machine learning and feature selection algorithms. Energy 2017, 140, 893–900. [Google Scholar]
- Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. In Proceedings of the Thirteenth International Conference on International Conference on Machine Learning (ICML), Bari, Italy, 3–6 July 1996; pp. 148–156. [Google Scholar]
- Schapire, R.E. The Boosting Approach to Machine Learning: An Overview. Nonlinear Estimation and Classification; Springer: New York, NY, USA, 2003; pp. 149–171. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2007; pp. 1–738. [Google Scholar]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef]
- Freund, Y. Boosting a weak learning algorithm by majority. Inf. Comput. 1995, 121, 256–285. [Google Scholar] [CrossRef]
- Mendes-Moreira, J.; Soares, C.; Jorge, A.M.; Sousa, J.F.D. Ensemble approaches for regression: A survey. ACM Comput. Surveys 2012, 45, 10. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning, Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2009; pp. 1–745. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. The capital asset pricing model: Theory and evidence. J. Econ. Perspect. 2004, 18, 25–46. [Google Scholar] [CrossRef]
- Ehrenberg, R.G.; Smith, R.S. Modern Labor Economics: Theory and Public Policy, 13th ed.; Routledge: New York, NY, USA, 2018. [Google Scholar]
- DeFries, R.S.; Rudel, T.; Uriarte, M.; Hansen, M. Deforestation driven by urban population growth and agricultural trade in the twenty-first century. Nat. Geosci. 2010, 3, 178–181. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques, 4th ed.; Morgan Kaufmann: Cambridge, UK, 2016. [Google Scholar]
- Bianco, V.; Manca, O.; Nardini, S. Electricity consumption forecasting in Italy using linear regression models. Energy 2009, 34, 1413–1421. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Statist. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Xie, W.; Yu, L.; Xu, S.Y.; Wang, S.Y. A new method for crude oil price forecasting based on support vector machines. In Proceedings of the International Conference on Computational Science (ICCS), Reading, UK, 28–31 May 2006; pp. 444–451. [Google Scholar]
- Freund, Y.; Schapire, R.; Abe, N. A short introduction to boosting. J. Jpn. Soc. Artif. Intell. 1999, 14, 771–780. [Google Scholar]
- Kearns, M.; Valiant, L. Cryptographic limitations on learning Boolean formulae and finite automata. J. ACM 1994, 41, 67–95. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting (with discussion and a rejoinder by the authors). Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Mason, L.; Baxter, J.; Bartlett, P.L.; Frean, M.R. Boosting algorithms as gradient descent. In Proceedings of the 12th International Conference on Neural Information Processing Systems (NIPS), 29 November–4 December 1999; pp. 512–518. [Google Scholar]
- Moonam, H.M.; Qin, X.; Zhang, J. Utilizing data mining techniques to predict expected freeway travel time from experienced travel time. Math. Comput. Simul. 2019, 155, 154–167. [Google Scholar] [CrossRef]
- Reddy, L.V.; Yogitha, K.; Bandhavi, K.; Vinay, G.S.; Kumar, G.D. A Modern Approach Student Performance Prediction using Multi-Agent Data Mining Technique. i-Manag. J. Softw. Eng. 2015, 10, 14–20. [Google Scholar] [CrossRef]
- EIA. Available online: https://www.eia.gov/ (accessed on 8 March 2019).
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th international joint conference on artificial intelligence (IJCAI), Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1145. [Google Scholar]
- Cameron, A.C.; Windmeijer, F.A. An r-squared measure of goodness of fit for some common nonlinear regression models. J. Econ. 1997, 77, 329–342. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Simpson, T.W. Comparative studies of metamodelling techniques under multiple modelling criteria. Struct. Multidiscipl. Optim. 2001, 23, 1–13. [Google Scholar] [CrossRef]
- Touzani, S.; Granderson, J.; Fernandes, S. Gradient boosting machine for modeling the energy consumption of commercial buildings. Energy Build. 2018, 158, 1533–1543. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Malliaris, M.; Malliaris, S. Forecasting inter-related energy product prices. Eur. J. Financ. 2008, 14, 453–468. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).