Photon-Mediated Thermoelectric and Heat Currents through a Resonant Quantum Wire-Cavity System
Abstract
1. Introduction
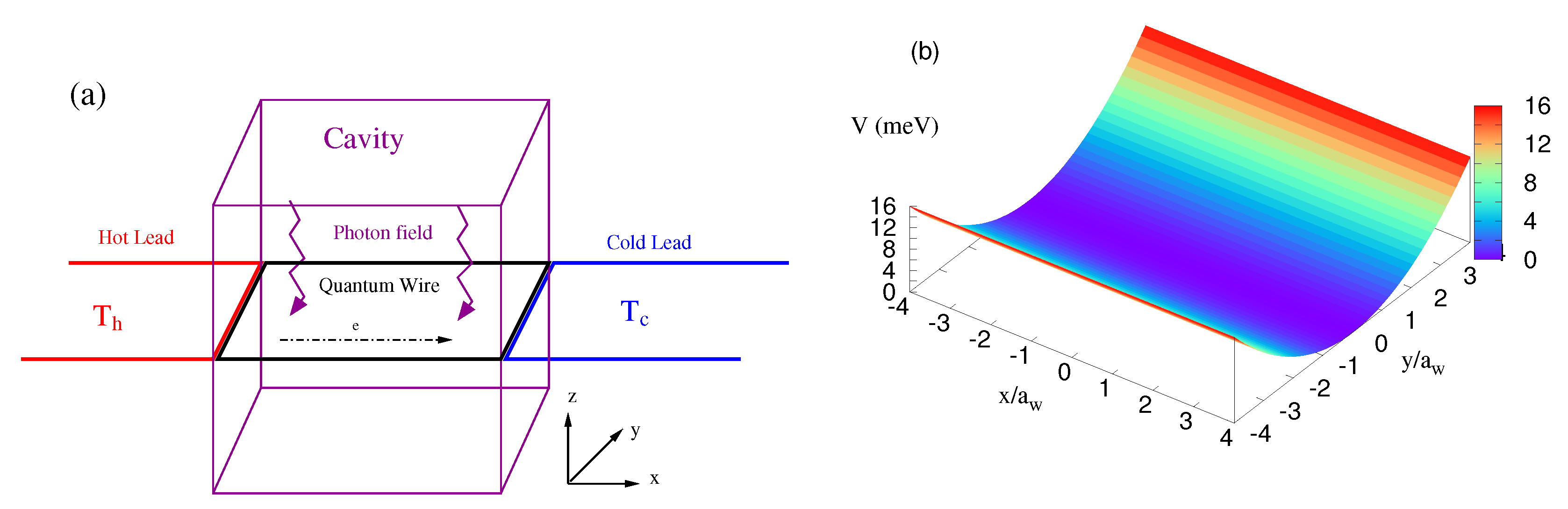
2. Model
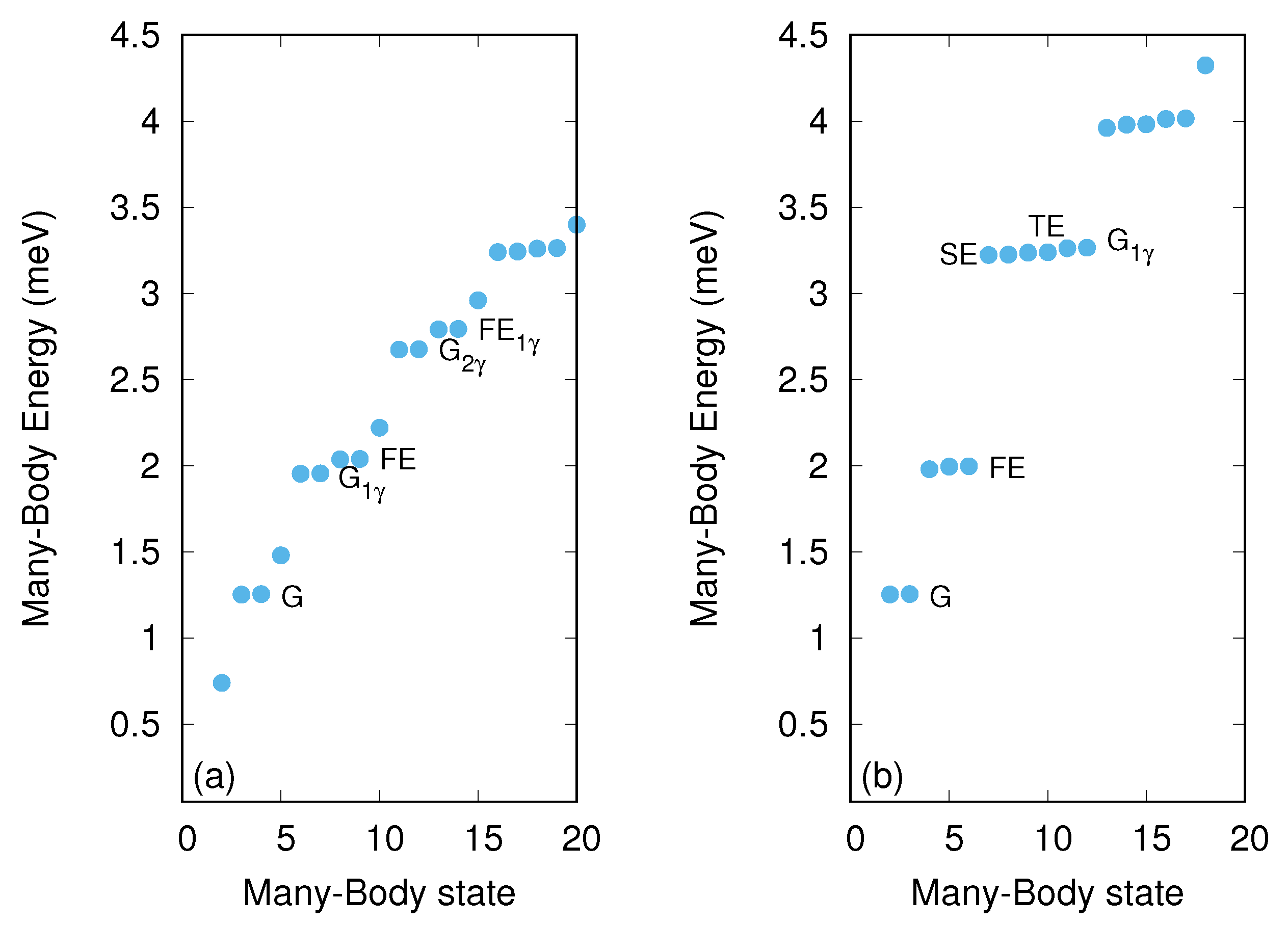
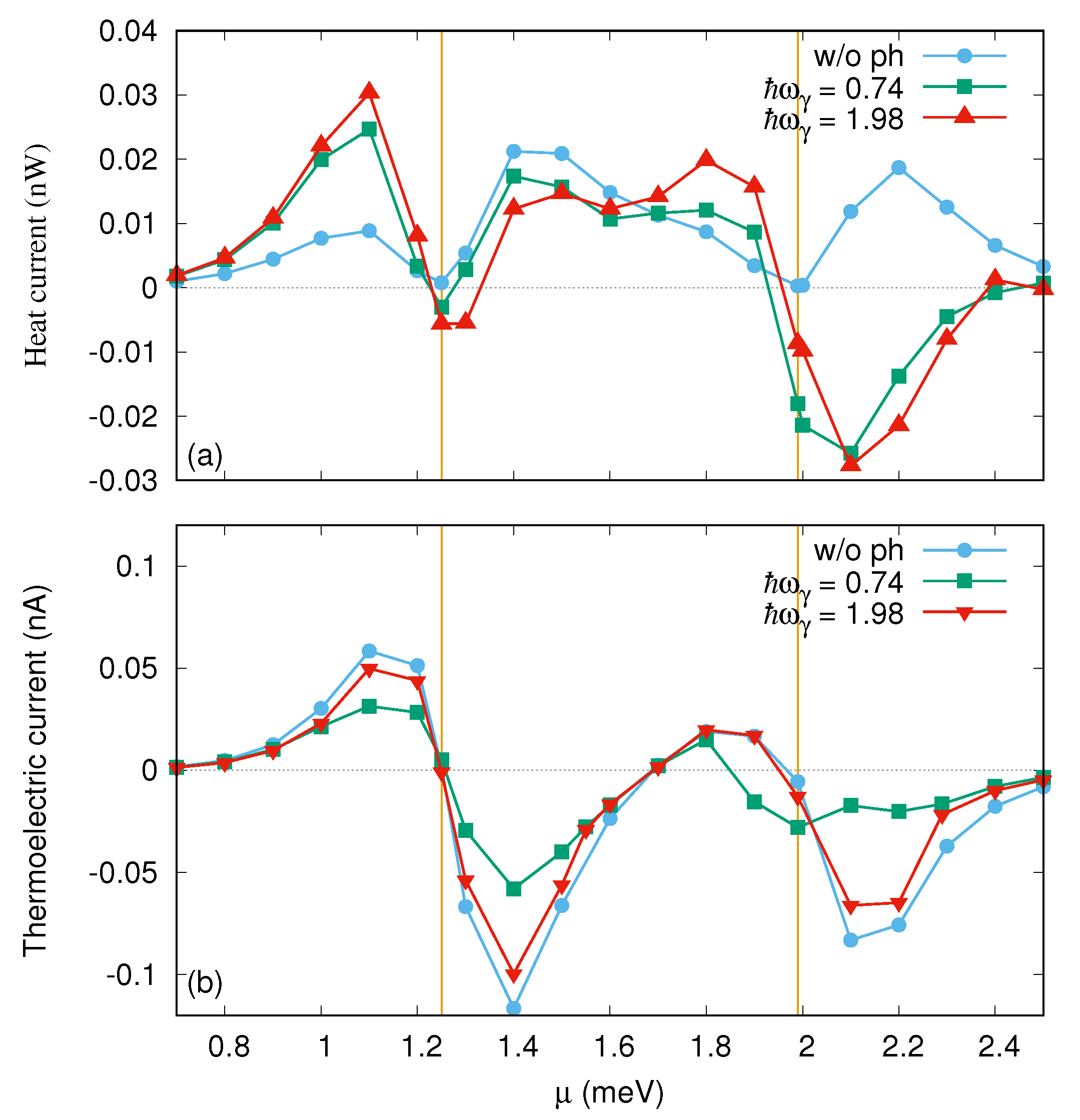
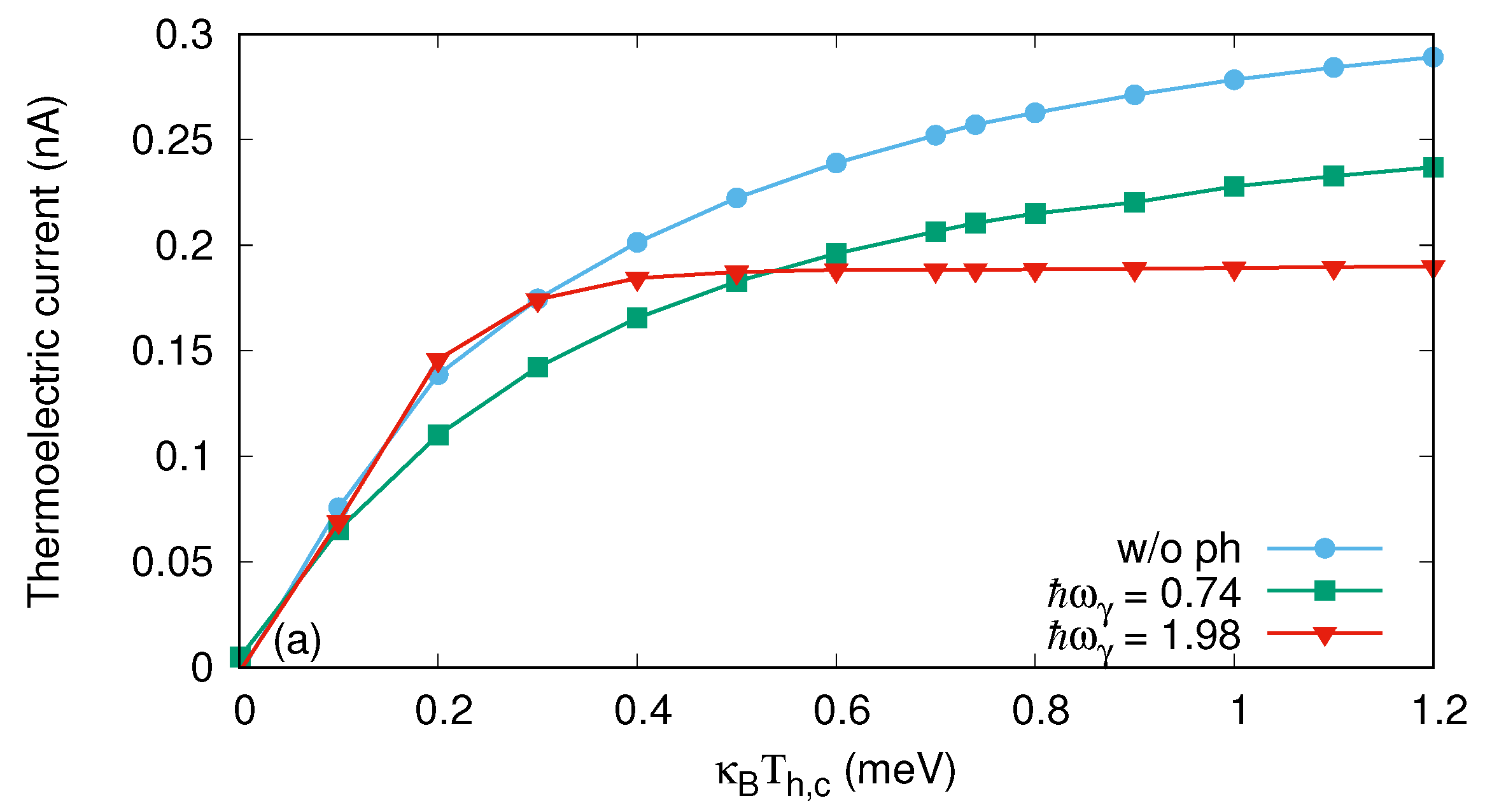
3. Results
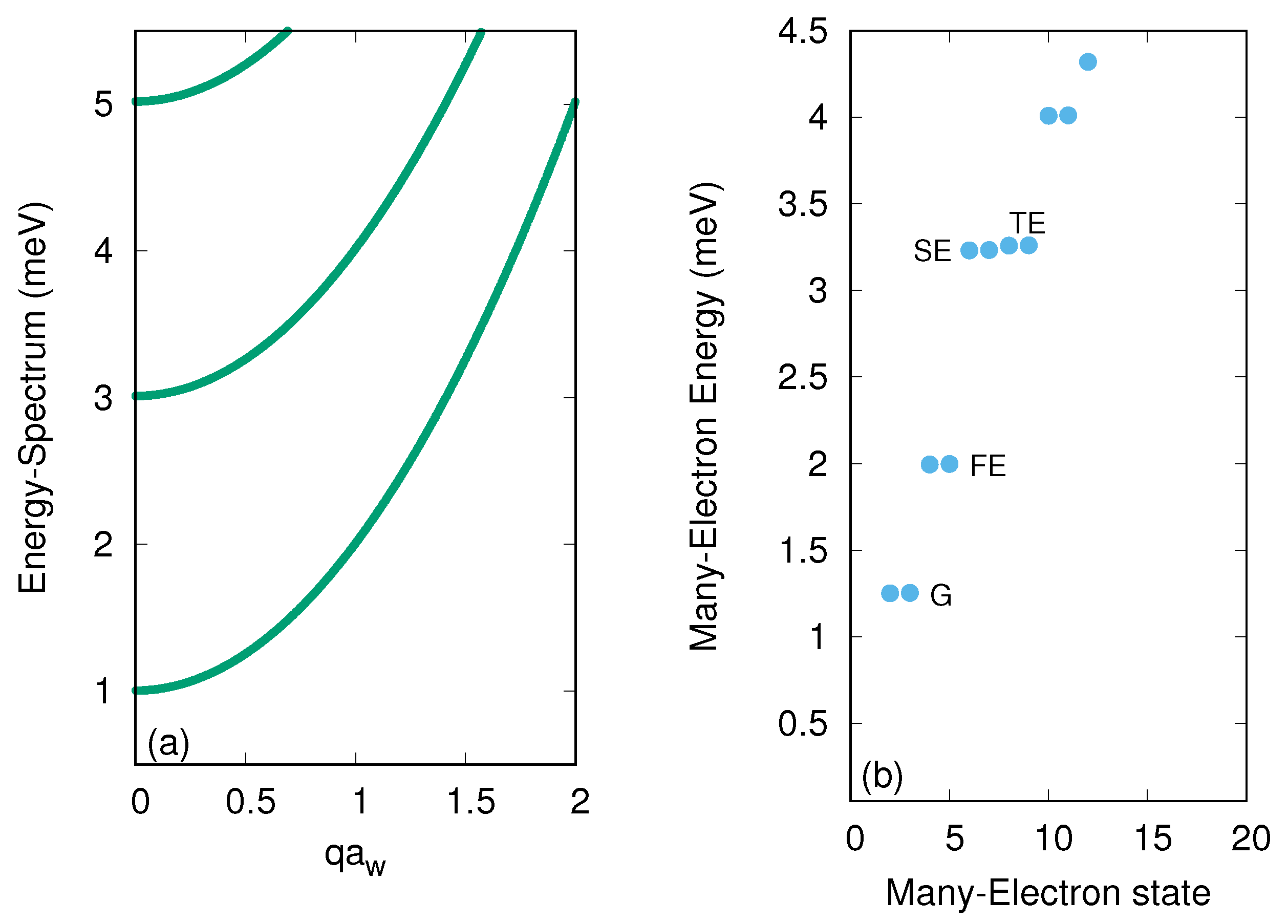
3.1. The Quantum Wire without Photon Field
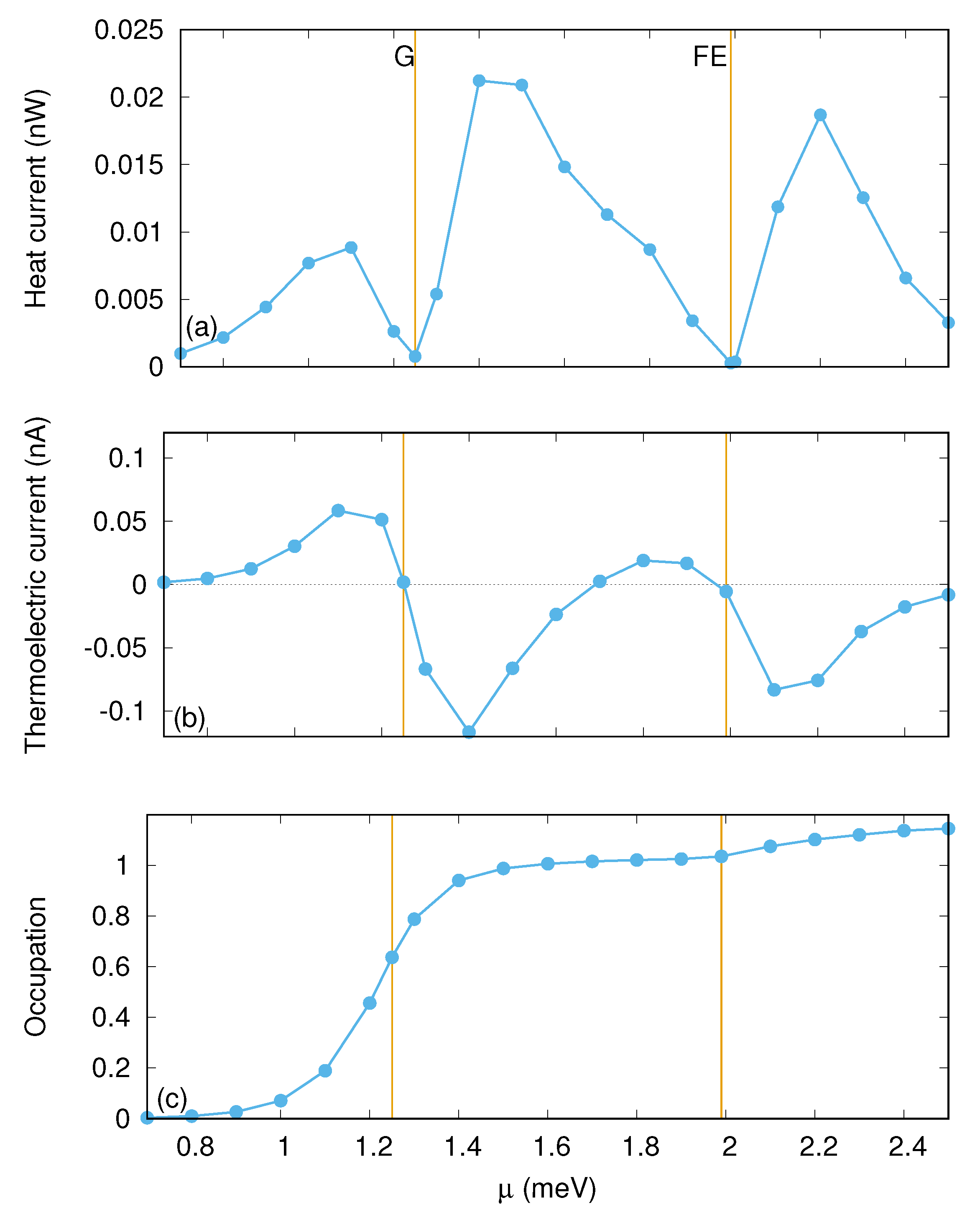
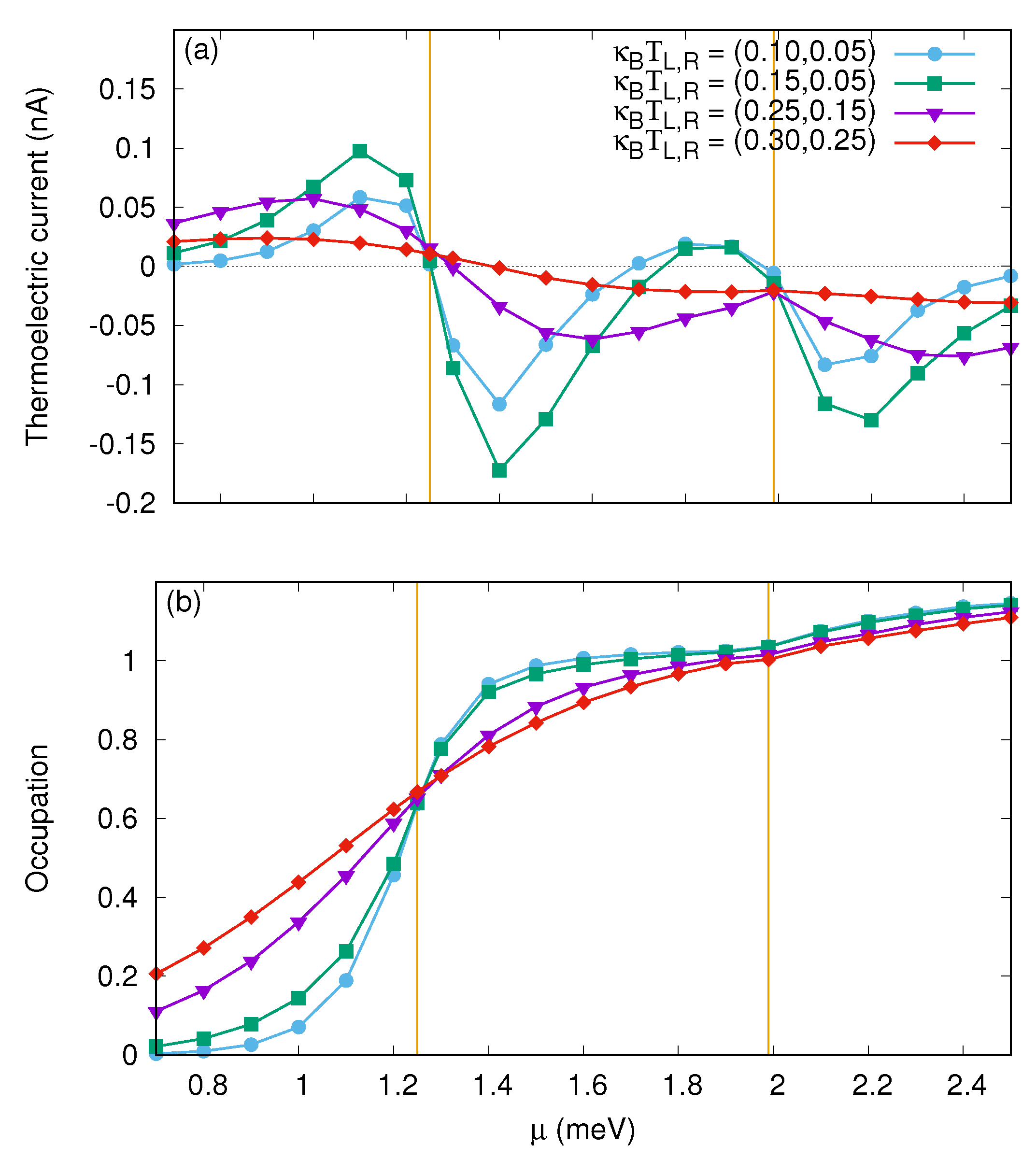
3.2. The Quantum Wire with Photon Field
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ZT | Figure of merit |
| G | Ground-state energy |
| One-photon replica of the ground-state | |
| Two-photon replica of the ground-state | |
| FE | First-excited state energy |
| One-photon replica of the first-excited state energy | |
| SE | Second-excited state energy |
| TE | Third-excited state energy |
References
- Yoon, H.S.; Lee, J.Y.; Kim, H.S.; Kim, M.S.; Kim, E.S.; Shin, Y.J.; Chu, W.S.; Ahn, S.H. A comparison of energy consumption in bulk forming, subtractive, and additive processes: Review and case study. Int. J. Precis. Eng. Manuf. Green Technol. 2014, 1, 261–279. [Google Scholar] [CrossRef]
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Canovas-Carrasco, S.; Garcia-Sanchez, A.J.; Garcia-Haro, J. A nanoscale communication network scheme and energy model for a human hand scenario. Nano Commun. Netw. 2018, 15, 17–27. [Google Scholar] [CrossRef]
- Aricò, A.S.; Bruce, P.; Scrosati, B.; Tarascon, J.M.; van Schalkwijk, W. Nanostructured materials for advanced energy conversion and storage devices. Nat. Mater. 2005, 4, 366–377. [Google Scholar] [CrossRef] [PubMed]
- Pop, E. Energy dissipation and transport in nanoscale devices. Nano Res. 2010, 3, 147–169. [Google Scholar] [CrossRef]
- Ren, J.; Zhu, J.X.; Gubernatis, J.E.; Wang, C.; Li, B. Thermoelectric transport with electron-phonon coupling and electron-electron interaction in molecular junctions. Phys. Rev. B 2012, 85, 155443. [Google Scholar] [CrossRef]
- Talbo, V.; Saint-Martin, J.; Retailleau, S.; Dollfus, P. Non-linear effects and thermoelectric efficiency of quantum dot-based single-electron transistors. Sci. Rep. 2017, 7, 14783. [Google Scholar] [CrossRef]
- Snyder, G.J.; Snyder, A.H. Figure of merit ZT of a thermoelectric device defined from materials properties. Energy Environ. Sci. 2017, 10, 2280–2283. [Google Scholar] [CrossRef]
- Szczech, J.R.; Higgins, J.M.; Jin, S. Enhancement of the thermoelectric properties in nanoscale and nanostructured materials. J. Mater. Chem. 2011, 21, 4037–4055. [Google Scholar] [CrossRef]
- Majumdar, A. Thermoelectricity in Semiconductor Nanostructures. Science 2004, 303, 777–778. [Google Scholar] [CrossRef]
- Heremans, J.P.; Dresselhaus, M.S.; Bell, L.E.; Morelli, D.T. When thermoelectrics reached the nanoscale. Nat. Nanotechnol. 2013, 8, 471–473. [Google Scholar] [CrossRef] [PubMed]
- Alam, H.; Ramakrishna, S. A review on the enhancement of figure of merit from bulk to nano-thermoelectric materials. Nano Energy 2013, 2, 190–212. [Google Scholar] [CrossRef]
- Harman, T.C.; Taylor, P.J.; Spears, D.L.; Walsh, M.P. Thermoelectric quantum-dot superlattices with high ZT. J. Electron. Mater. 2000, 29, L1–L2. [Google Scholar] [CrossRef]
- Sothmann, B.; Sánchez, R.; Jordan, A.N. Thermoelectric energy harvesting with quantum dots. Nanotechnology 2015, 26, 032001. [Google Scholar] [CrossRef] [PubMed]
- Trocha, P.; Barnaś, J. Large enhancement of thermoelectric effects in a double quantum dot system due to interference and Coulomb correlation phenomena. Phys. Rev. B 2012, 85, 085408. [Google Scholar] [CrossRef]
- Wierzbicki, M.; Swirkowicz, R. Influence of interference effects on thermoelectric properties of double quantum dots. Phys. Rev. B 2011, 84, 075410. [Google Scholar] [CrossRef]
- Wang, Q.; Xie, H.; Nie, Y.H.; Ren, W. Enhancement of thermoelectric efficiency in triple quantum dots by the Dicke effect. Phys. Rev. B 2013, 87, 075102. [Google Scholar] [CrossRef]
- Hicks, L.D.; Dresselhaus, M.S. Effect of quantum-well structures on the thermoelectric figure of merit. Phys. Rev. B 1993, 47, 12727–12731. [Google Scholar] [CrossRef]
- Liu, J.; Sun, Q.F.; Xie, X.C. Enhancement of the thermoelectric figure of merit in a quantum dot due to the Coulomb blockade effect. Phys. Rev. B 2010, 81, 245323. [Google Scholar] [CrossRef]
- Kolenda, S.; Wolf, M.J.; Beckmann, D. Observation of Thermoelectric Currents in High-Field Superconductor-Ferromagnet Tunnel Junctions. Phys. Rev. Lett. 2016, 116, 097001. [Google Scholar] [CrossRef]
- Bathen, M.E.; Linder, J. Spin Seebeck effect and thermoelectric phenomena in superconducting hybrids with magnetic textures or spin-orbit coupling. Sci. Rep. 2017, 7, 41409. [Google Scholar] [CrossRef] [PubMed]
- Karwacki, L.; Barnaś, J. Thermoelectric properties of a quantum dot coupled to magnetic leads by Rashba spin-orbit interaction. Phys. Rev. B 2018, 98, 075413. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Arnold, T.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Photon-induced tunability of the thermospin current in a Rashba ring. J. Phys. Condens. Matter 2018, 30, 145303. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Spin-dependent heat and thermoelectric currents in a Rashba ring coupled to a photon cavity. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 95, 102–107. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Effects of photon field on heat transport through a quantum wire attached to leads. Phys. Lett. A 2018, 382, 199–204. [Google Scholar] [CrossRef]
- Abdullah, N.R. Optical control of spin-dependent thermal transport in a quantum ring. Phys. Lett. A 2018, 382, 1432–1436. [Google Scholar] [CrossRef]
- Ojanen, T.; Jauho, A.P. Mesoscopic Photon Heat Transistor. Phys. Rev. Lett. 2008, 100, 155902. [Google Scholar] [CrossRef]
- Joulain, K.; Drevillon, J.; Ezzahri, Y.; Ordonez-Miranda, J. Quantum Thermal Transistor. Phys. Rev. Lett. 2016, 116, 200601. [Google Scholar] [CrossRef] [PubMed]
- Meschke, M.; Guichard, W.; Pekola, J.P. Single-mode heat conduction by photons. Nature 2006, 444, 187–190. [Google Scholar] [CrossRef] [PubMed]
- Chi, F.; Dubi, Y. Microwave-mediated heat transport in a quantum dot attached to leads. J. Phys. Condens. Matter 2012, 24, 145301. [Google Scholar] [CrossRef]
- Abdullah, N.R. Magnetically and Photonically Tunable Double Waveguide Inverter. IEEE J. Quantum Electron. 2016, 52, 1–6. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Fatah, A.H.; Fatah, J.M.A. Effects of magnetic field on photon-induced quantum transport in a single dot-cavity system. Chin. Phys. B 2016, 25, 114206. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Coherent transient transport of interacting electrons through a quantum waveguide switch. J. Phys. Condens. Matter 2015, 27, 015301. [Google Scholar] [CrossRef] [PubMed]
- Gudmundsson, V.; Jonsson, T.H.; Bernodusson, M.L.; Abdullah, N.R.; Sitek, A.; Goan, H.S.; Tang, C.S.; Manolescu, A. Regimes of radiative and nonradiative transitions in transport through an electronic system in a photon cavity reaching a steady state. Annalen der Physik 2017, 529, 1600177. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Delocalization of electrons by cavity photons in transport through a quantum dot molecule. Physica E 2014, 64, 254–262. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Optical switching of electron transport in a waveguide-QED system. Phys. E Low-Dimens. Syst. Nanostruct. 2016, 84, 280–284. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Competition of static magnetic and dynamic photon forces in electronic transport through a quantum dot. J. Phys. Condens. Matter 2016, 28, 375301. [Google Scholar] [CrossRef]
- Tagani, M.B.; Soleimani, H.R. Photon–phonon -assisted thermoelectric effects in the molecular devices. Phys. E Low-Dimens. Syst. Nanostruct. 2013, 48, 36–41. [Google Scholar] [CrossRef]
- Golsanamlou, Z.; Vishkayi, S.I.; Tagani, M.B.; Soleimani, H.R. Thermoelectric properties of metal/molecule/metal junction for different lengths of polythiophene. Chem. Phys. Lett. 2014, 594, 51–57. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Cavity-Photon Controlled Thermoelectric Transport through a Quantum Wire. ACS Photonics 2016, 3, 249–254. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdullah, N.R.; Marif, R.B.; Rashid, H.O. Photon-Mediated Thermoelectric and Heat Currents through a Resonant Quantum Wire-Cavity System. Energies 2019, 12, 1082. https://doi.org/10.3390/en12061082
Abdullah NR, Marif RB, Rashid HO. Photon-Mediated Thermoelectric and Heat Currents through a Resonant Quantum Wire-Cavity System. Energies. 2019; 12(6):1082. https://doi.org/10.3390/en12061082
Chicago/Turabian StyleAbdullah, Nzar Rauf, Rawezh Bakr Marif, and Hunar Omar Rashid. 2019. "Photon-Mediated Thermoelectric and Heat Currents through a Resonant Quantum Wire-Cavity System" Energies 12, no. 6: 1082. https://doi.org/10.3390/en12061082
APA StyleAbdullah, N. R., Marif, R. B., & Rashid, H. O. (2019). Photon-Mediated Thermoelectric and Heat Currents through a Resonant Quantum Wire-Cavity System. Energies, 12(6), 1082. https://doi.org/10.3390/en12061082




