Generalised Regression Hypothesis Induction for Energy Consumption Forecasting
Abstract
1. Introduction
2. Related Work
2.1. Symbolic Regression
2.2. Multi-Objective Optimisation Paradigm
3. Methods
3.1. Straight Line Programs for Time Series Prediction
3.2. Single-Objective Problem Formulation
3.3. Multi-Objective Problem Formulation
3.4. Algorithm Description
- Crossover operator. Two parents and are used in both single- and multi-objective approaches in order to generate two new children and . The operator starts out selecting a random rule from . After that, an ordered set of rules R is calculated as the set of rules that can be reached from the selected rule . Then, a random rule from is selected, where is the number of rules included in R. The offspring is created as a copy of the parent and the rules in R are copied into and renamed from to . Finally, the offspring is generated with the same procedure, but exchanging the roles of both parents and . An example of this operator is shown in Figure 1, where rule was selected randomly from parent . After that, the ruleset U is created as the set of rules that can be reached from . In this case, , and is renamed as . Then, a random position is selected in , and the offspring is created as a copy of with the replacement of rules in R, starting from .
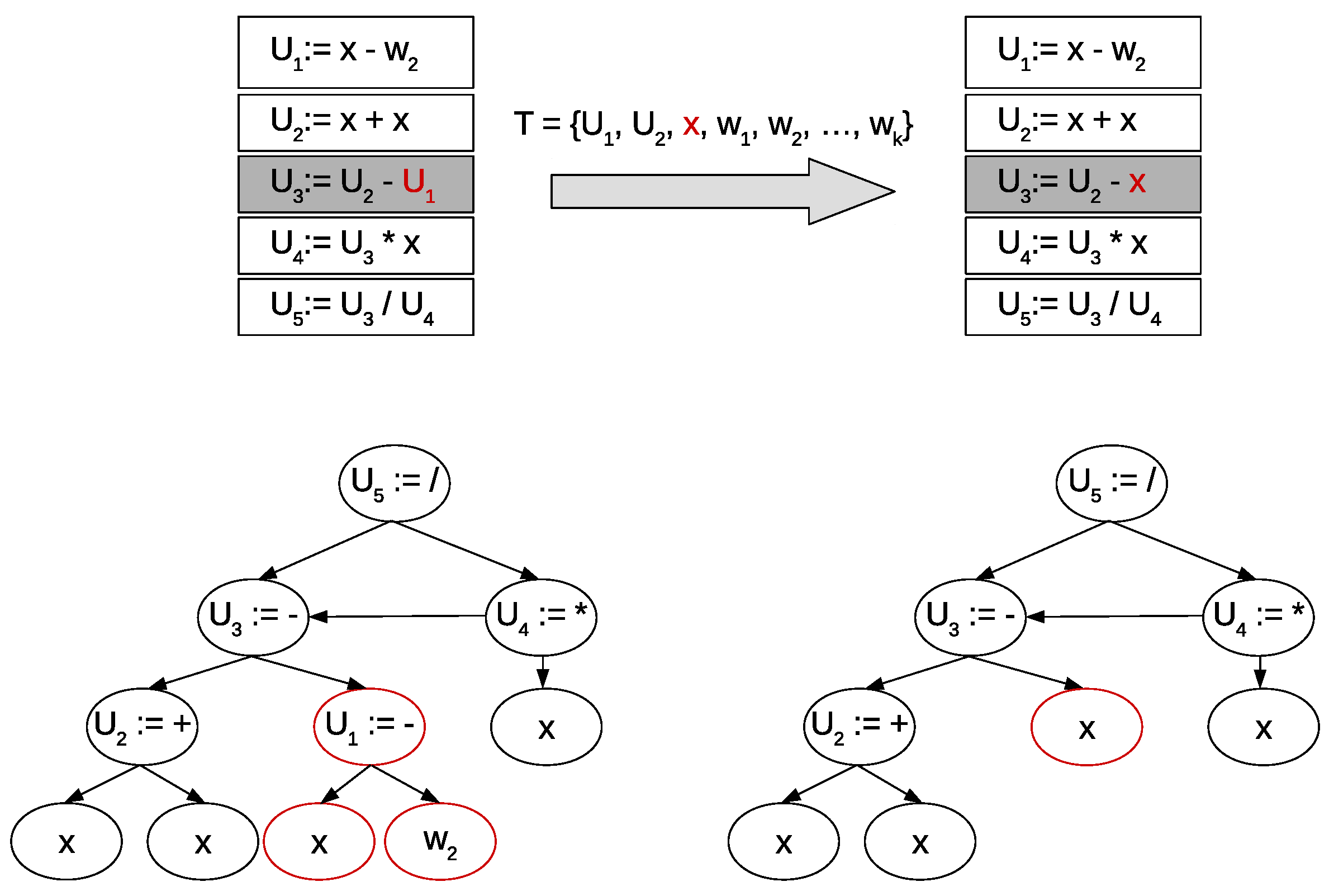
- Mutation operator. Given a SLP table of an individual of the population, a random element of the consequent of a random rule is exchanged for another random symbol. If the selected element is an operator, it is exchanged by another valid operator and if the selected element is an operand, it is exchanged by a terminal symbol or a reference to other rule, as shown in Figure 2. On the other hand, if the mutation operator exchanges a binary operator by an unary operator, the second operand of the rule is left to the value ∅. Nevertheless, if the operator mutes an unary operator to a binary operator, then the second operand is randomly selected from the set of valid operands of the production rule (independent variables, parameters or references to other rules of the SLP table).
4. Experimentation
- A first study attempted to empirically validate whether the described problem can be solved with the proposed formulations. Thus, we built different scenarios with synthetic data, with the aim of validating the performance of each approach under a controlled experimental environment that eases the analysis of performance of the approaches. To that end, Section 4.1 describes a set of benchmark algebraic expressions to be used in the experiments, and the results obtained with each approach. This section ends with a discussion of the results obtained.
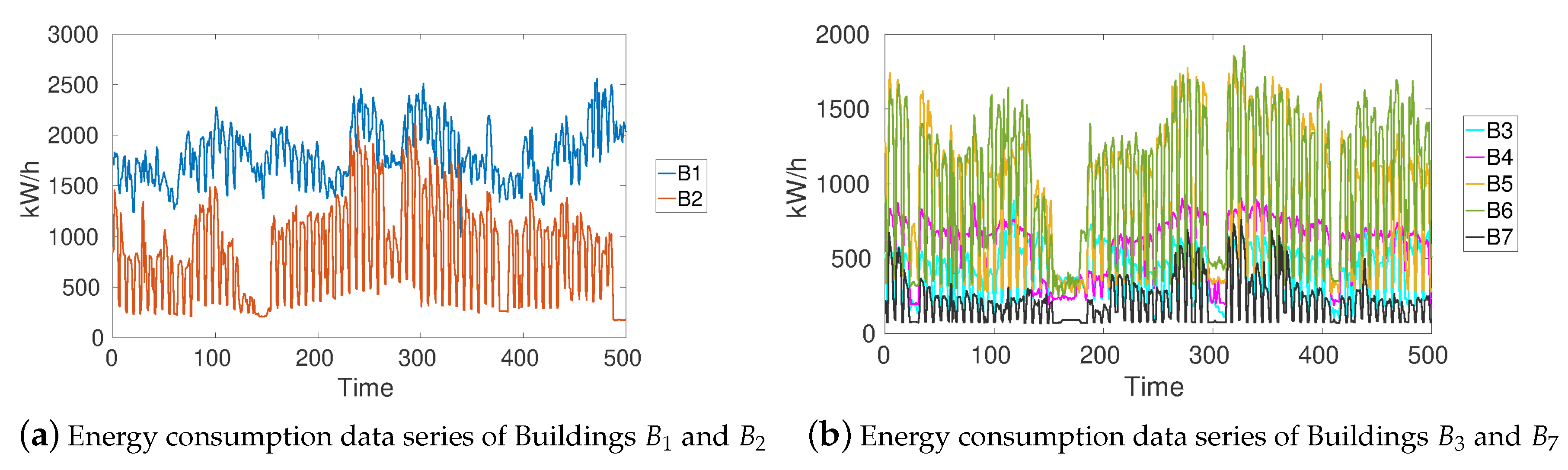
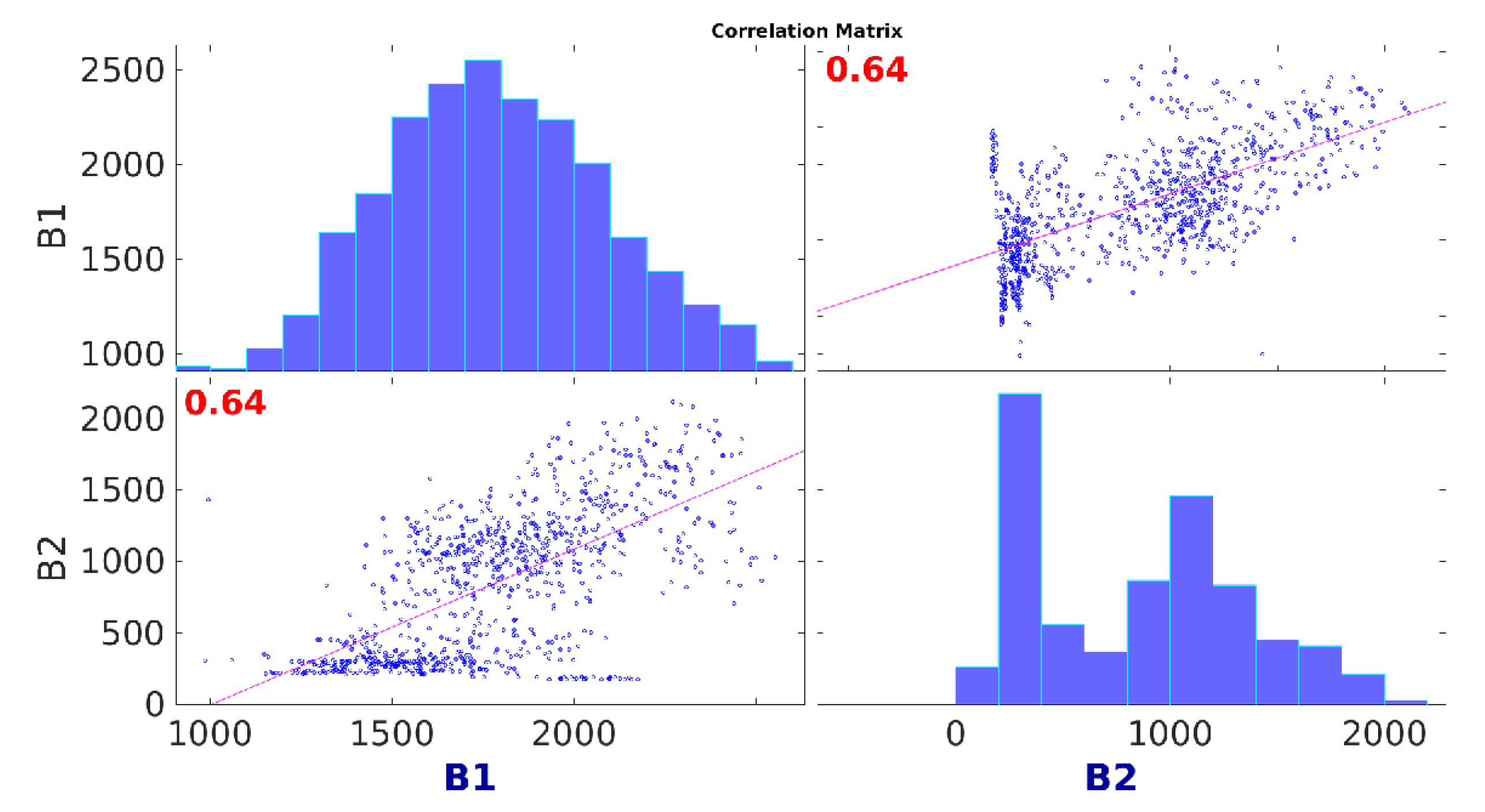
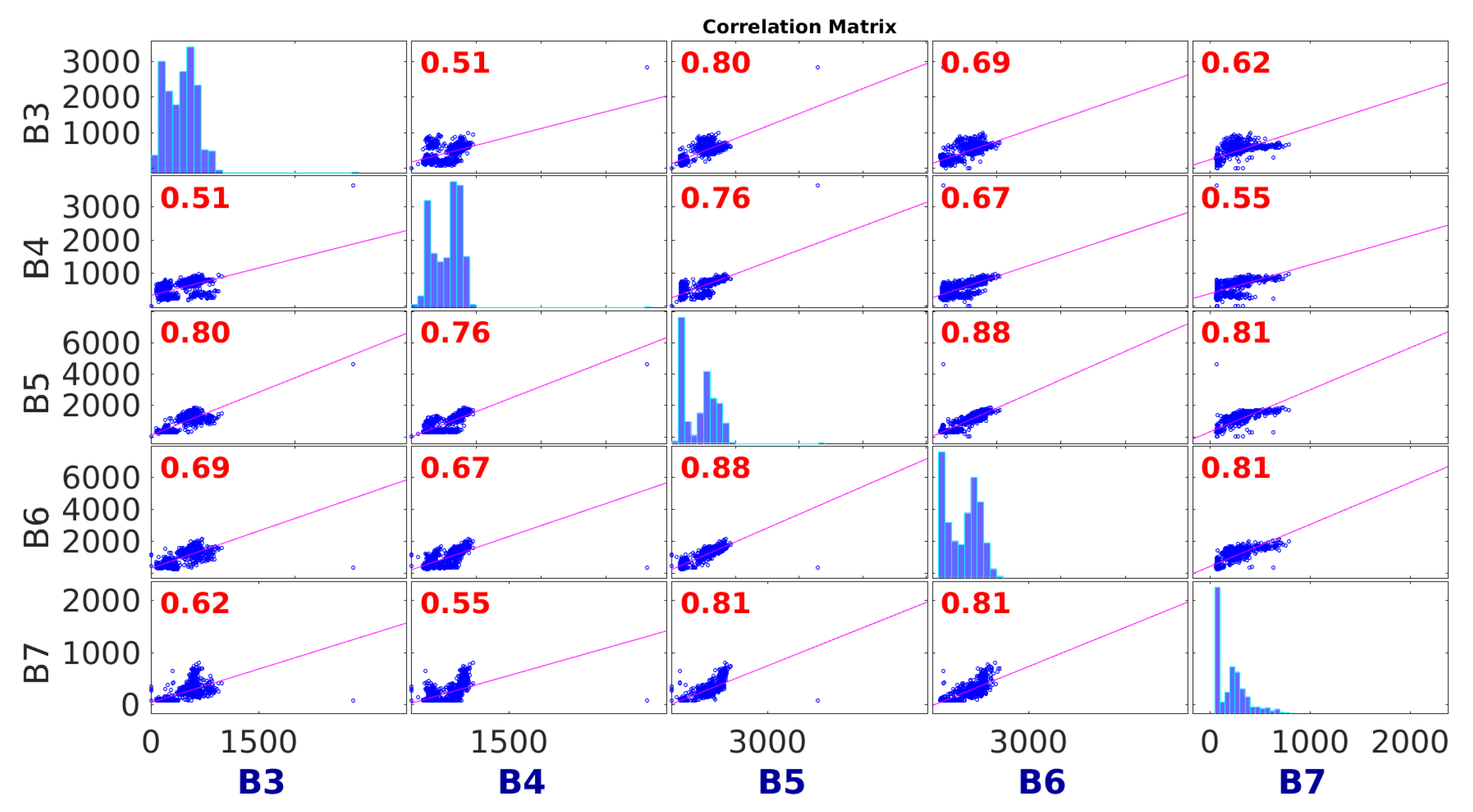
- In the second experiment (Section 4.2), we tackled a real problem about energy consumption prediction. In it, we were provided with the energy consumption time series of a set of buildings for which we assumed there is a medium or high correlation and the goal was to find a single parameterised algebraic expression that can explain the global/common behaviour of all related energy consumption data series.
4.1. Experimentation with Synthetic Data
4.1.1. Data Acquisition
4.1.2. Experimental Settings
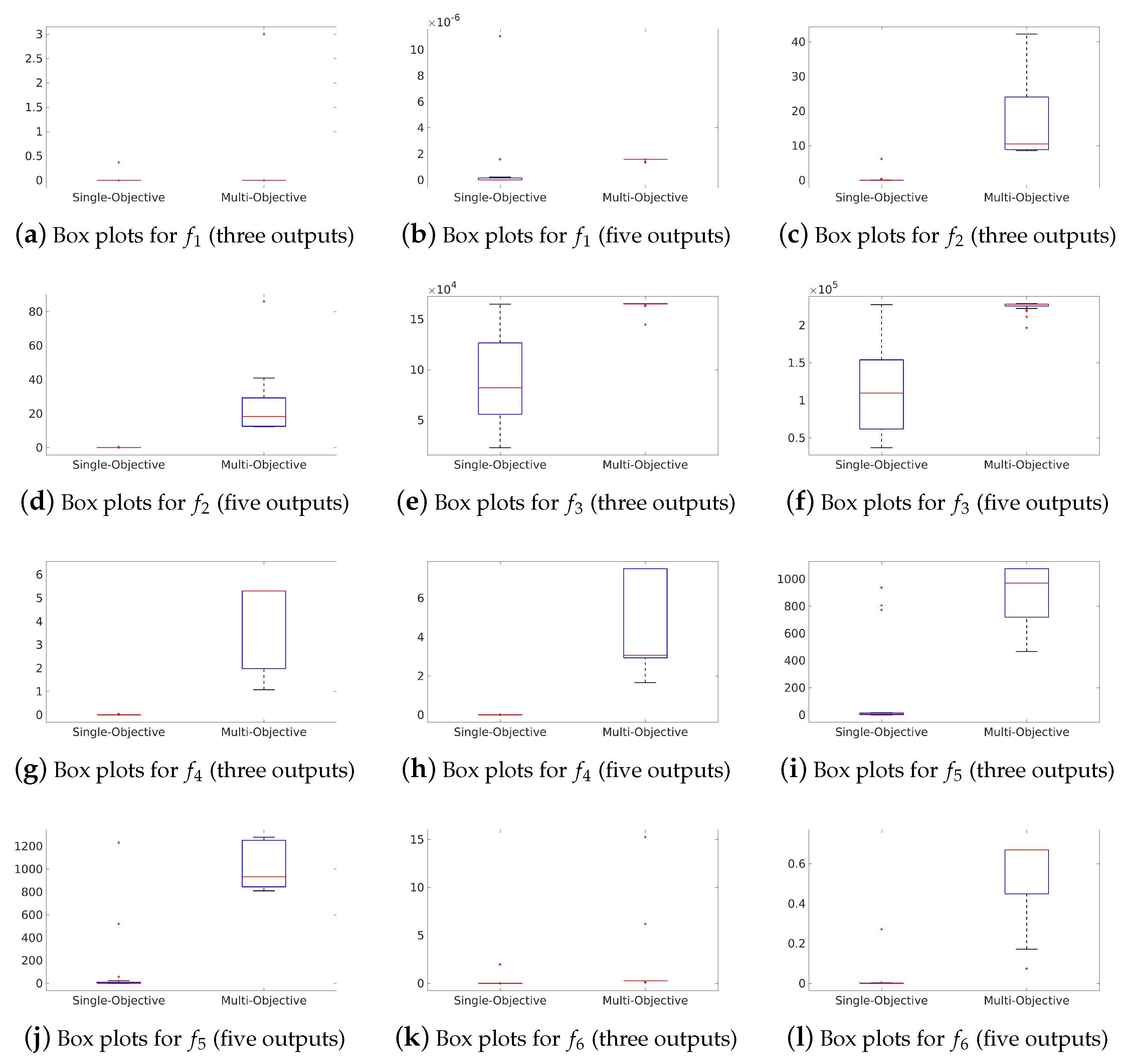
4.1.3. Results and Discussion
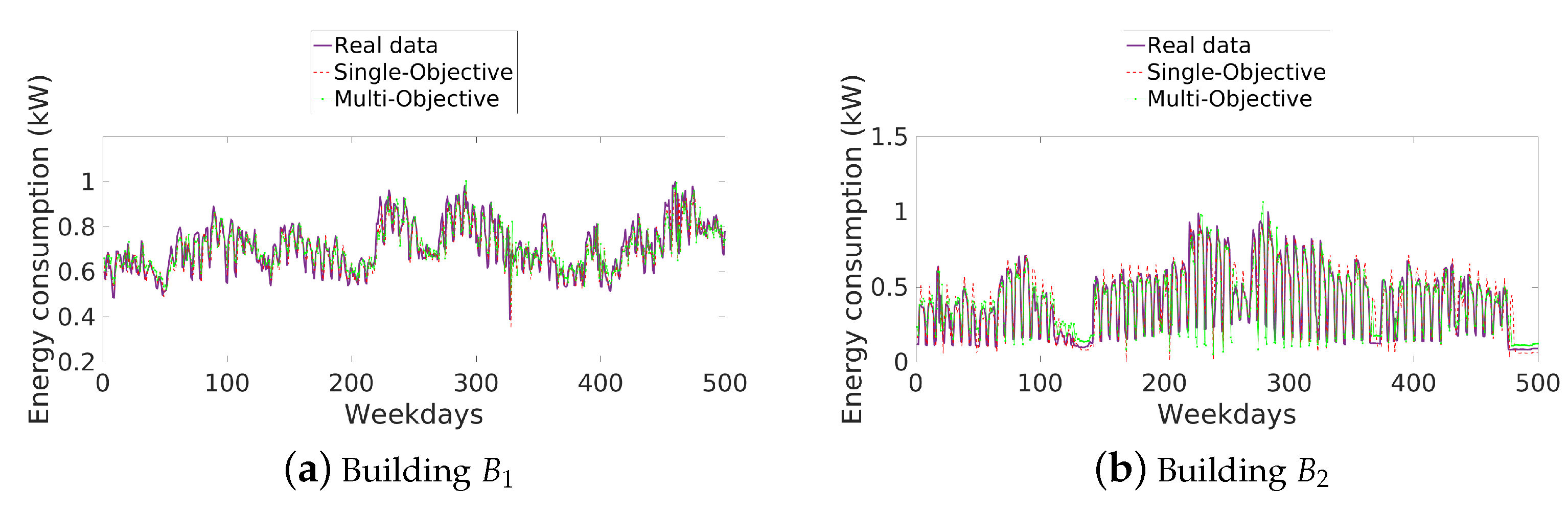
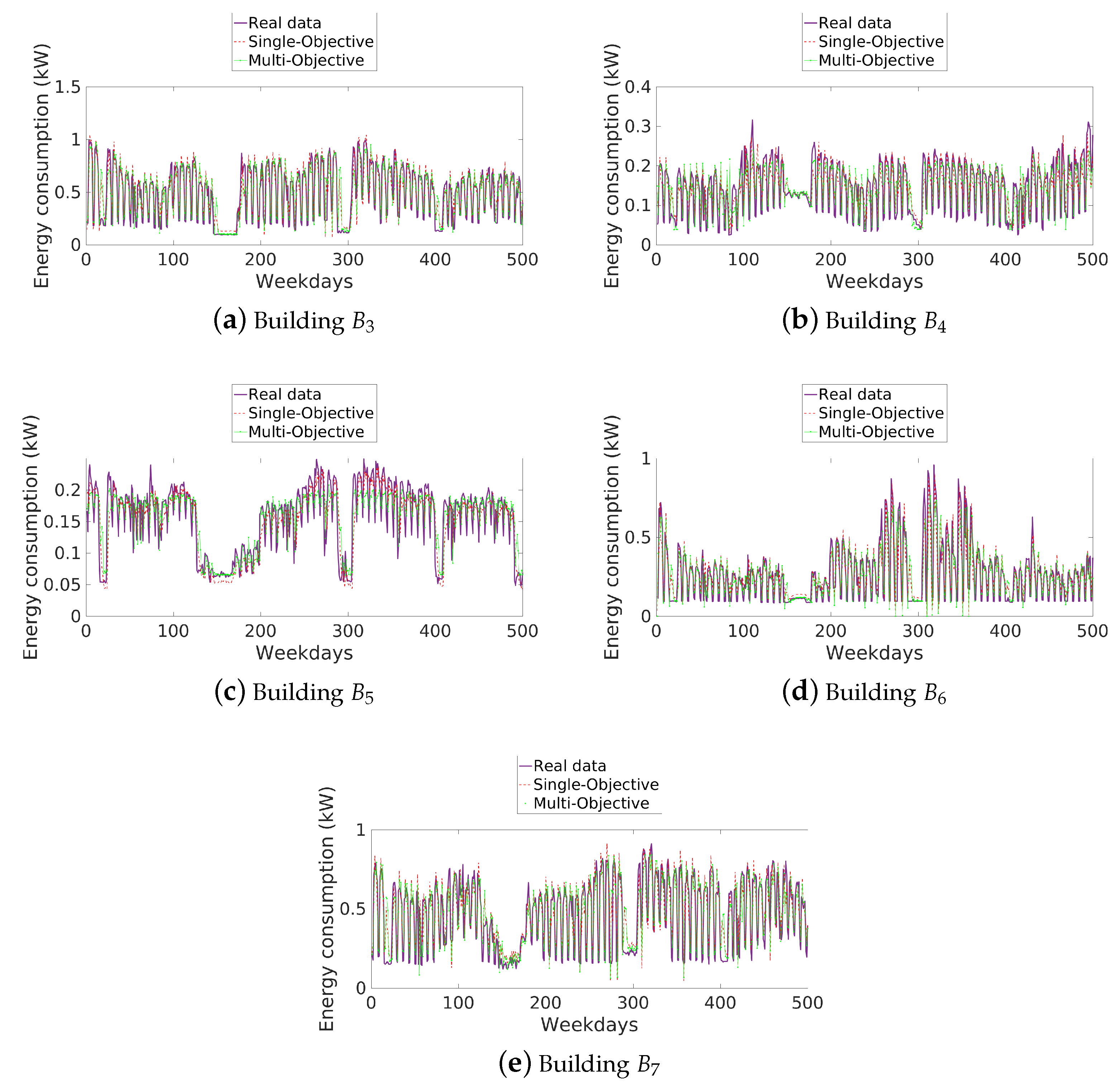
4.2. Experimentation with Real Data
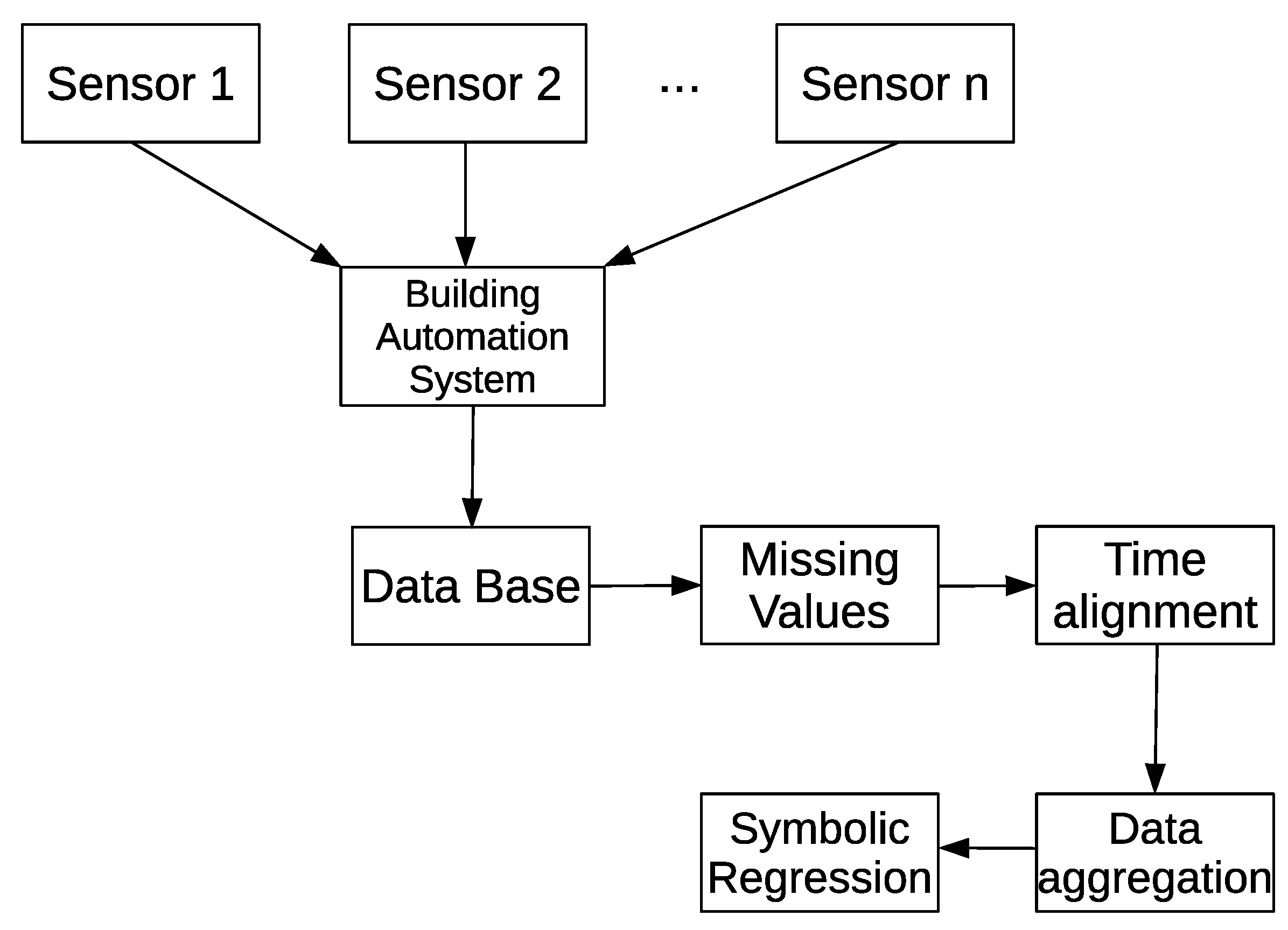
4.2.1. Data Acquisition
4.2.2. Experimental Settings
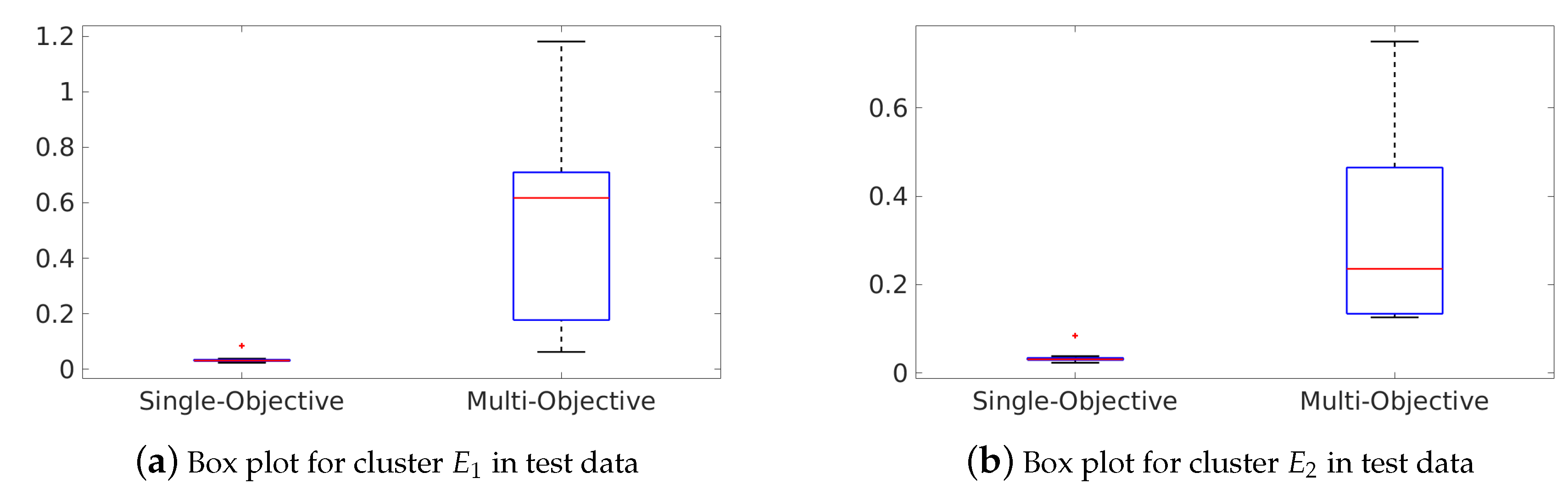
4.2.3. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Santamouris, M. Innovating to zero the building sector in Europe: Minimising the energy consumption, eradication of the energy poverty and mitigating the local climate change. Sol. Energy 2016, 128, 61–94. [Google Scholar] [CrossRef]
- Berardi, U. A cross-country comparison of the building energy consumptions and their trends. Resour. Conserv. Recycl. 2017, 123, 230–241. [Google Scholar] [CrossRef]
- Höller, J.; Tsiatsis, V.; Mulligan, C.; Karnouskos, S.; Avesand, S.; Boyle, D. Chapter 13—Commercial Building Automation. In From Machine-To-Machine to the Internet of Things; Academic Press: Cambridge, MA, USA, 2014; pp. 269–279. [Google Scholar]
- Molina-Solana, M.; Ruiz, M.M.R.D.; Gómez-Romero, J.; Martin-Bautista, M. Data Science for Building Energy Management: A review. Renew. Sustain. Energy Rev. 2017, 70, 598–609. [Google Scholar] [CrossRef]
- Chou, J.S.; Telaga, A.S. Real-time detection of anomalous power consumption. Renew. Sustain. Energy Rev. 2014, 33, 400–411. [Google Scholar] [CrossRef]
- Cui, W.; Wang, H. A New Anomaly Detection System for School Electricity Consumption Data. Information 2017, 8, 151. [Google Scholar] [CrossRef]
- Lü, X.; Lu, T.; Kibert, C.J.; Viljanen, M. Modeling and forecasting energy consumption for heterogeneous buildings using a physical–statistical approach. Appl. Energy 2015, 144, 261–275. [Google Scholar] [CrossRef]
- Gourlis, G.; Kovacic, I. Building Information Modelling for analysis of energy efficient industrial buildings—A case study. Renew. Sustain. Energy Rev. 2017, 68, 953–963. [Google Scholar] [CrossRef]
- Guan, J.; Nord, N.; Chen, S. Energy planning of university campus building complex: Energy usage and coincidental analysis of individual buildings with a case study. Energy Build. 2016, 124, 99–111. [Google Scholar] [CrossRef]
- Gomez, J.A.; Anjos, M.F. Power capacity profile estimation for building heating and cooling in demand-side management. Appl. Energy 2017, 191, 492–501. [Google Scholar] [CrossRef]
- Capozzoli, A.; Piscitelli, M.S.; Brandi, S. Mining typical load profiles in buildings to support energy management in the smart city context. Energy Procedia 2017, 134, 865–874. [Google Scholar] [CrossRef]
- Zhao, J.; Lasternas, B.; Lam, K.P.; Yun, R.; Loftness, V. Occupant behavior and schedule modeling for building energy simulation through office appliance power consumption data mining. Energy Build. 2014, 82, 341–355. [Google Scholar] [CrossRef]
- Balaji, B.; Xu, J.; Nwokafor, A.; Gupta, R.; Agarwal, Y. Sentinel: Occupancy Based HVAC Actuation Using Existing WiFi Infrastructure Within Commercial Buildings. In Proceedings of the 11th ACM Conference on Embedded Networked Sensor Systems, Roma, Italy, 11–15 November 2013; pp. 17:1–17:4. [Google Scholar]
- Amber, K.P.; Aslam, M.W.; Mahmood, A.; Kousar, A.; Younis, M.Y.; Akbar, B.; Chaudhary, G.Q.; Hussain, S.K. Energy Consumption Forecasting for University Sector Buildings. Energies 2017, 10, 1579. [Google Scholar] [CrossRef]
- Shabani, A.; Zavalani, O. Hourly Prediction of Building Energy Consumption: An Incremental ANN Approach. Eur. J. Eng. Res. Sci. 2017, 2, 27. [Google Scholar] [CrossRef]
- Neto, A.H.; Fiorelli, F.A.S. Comparison between detailed model simulation and artificial neural network for forecasting building energy consumption. Energy Build. 2008, 40, 2169–2176. [Google Scholar] [CrossRef]
- Biswas, M.R.; Robinson, M.D.; Fumo, N. Prediction of residential building energy consumption: A neural network approach. Energy 2016, 117, 84–92. [Google Scholar] [CrossRef]
- Jain, R.K.; Smith, K.M.; Culligan, P.J.; Taylor, J.E. Forecasting energy consumption of multi-family residential buildings using support vector regression: Investigating the impact of temporal and spatial monitoring granularity on performance accuracy. Appl. Energy 2014, 123, 168–178. [Google Scholar] [CrossRef]
- Deb, C.; Zhang, F.; Yang, J.; Lee, S.E.; Shah, K.W. A review on time series forecasting techniques for building energy consumption. Renew. Sustain. Energy Rev. 2017, 74, 902–924. [Google Scholar] [CrossRef]
- Yasmeen, F.; Sharif, M. Forecasting electricity consumption for Pakistan. Int. J. Emergy Technol. Adv. Eng. 2014, 4, 496–503. [Google Scholar]
- Baca Ruiz, L.G.; Cuéllar, M.P.; Calvo-Flores, M.D.; Jiménez, M.C.P. An Application of Non-Linear Autoregressive Neural Networks to Predict Energy Consumption in Public Buildings. Energies 2016, 9, 684. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F.; Fung, A.S.; Raahemifar, K. Artificial neural network (ANN) based model predictive control (MPC) and optimization of HVAC systems: A state of the art review and case study of a residential HVAC system. Energy Build. 2017, 141, 96–113. [Google Scholar] [CrossRef]
- Jovanovic, R.Z.; Sretenovic, A.A.; Zivkovic, B.D. Ensemble of various neural networks for prediction of heating energy consumption. Energy Build. 2015, 94, 189–199. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Mourshed, M.; Rezgui, Y. Trees vs Neurons: Comparison between random forest and ANN for high-resolution prediction of building energy consumption. Energy Build. 2017, 147, 77–89. [Google Scholar] [CrossRef]
- Wang, Z.; Srinivasan, R.S. A review of artificial intelligence based building energy use prediction: Contrasting the capabilities of single and ensemble prediction models. Renew. Sustain. Energy Rev. 2017, 75, 796–808. [Google Scholar] [CrossRef]
- Yildiz, B.; Bilbao, J.; Sproul, A. A review and analysis of regression and machine learning models on commercial building electricity load forecasting. Renew. Sustain. Energy Rev. 2017, 73, 1104–1122. [Google Scholar] [CrossRef]
- Braun, M.; Altan, H.; Beck, S. Using regression analysis to predict the future energy consumption of a supermarket in the UK. Appl. Energy 2014, 130, 305–313. [Google Scholar] [CrossRef]
- McKay, B.; Willis, M.J.; Barton, G.W. Using a tree structured genetic algorithm to perform symbolic regression. In Proceedings of the First International Conference on Genetic Algorithms in Engineering Systems: Innovations and Applications, Sheffield, UK, 12–14 September 1995; pp. 487–492. [Google Scholar]
- Willis, M.; Hiden, H.; Marenbach, P.; McKay, B.; Montague, G. Genetic programming: An introduction and survey of applications. In Proceedings of the Second International Conference On Genetic Algorithms in Engineering Systems: Innovations And Applications, Glasgow, UK, 2–4 September 1997; pp. 314–319. [Google Scholar]
- Langdon, W.B. Genetic Programming—Computers Using “Natural Selection” to Generate Programs. In Genetic Programming and Data Structures: Genetic Programming + Data Structures = Automatic Programming! Springer: Boston, MA, USA, 1998; pp. 9–42. [Google Scholar]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Rueda Delgado, R.; Baca Ruíz, L.G.; Pegalajar Cuéllar, M.; Delgado Calvo-Flores, M.; Pegalajar Jiménez, M.D.C. A Comparison Between NARX Neural Networks and Symbolic Regression: An Application for Energy Consumption Forecasting. In Information Processing and Management of Uncertainty in Knowledge-Based Systems. Applications; Springer: Cham, Switzerland, 2018; pp. 16–27. [Google Scholar]
- Yang, G.; Li, W.; Wang, J.; Zhang, D. A comparative study on the influential factors of China’s provincial energy intensity. Energy Policy 2016, 88, 74–85. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Abraham, A.; Nath, B. A Linear Genetic Programming Approach for Modelling Electricity Demand Prediction in Victoria. In Hybrid Information Systems; Abraham, A., Köppen, M., Eds.; Physica-Verlag HD: Heidelberg, Germany, 2002; pp. 379–393. [Google Scholar]
- Behera, R.; Pati, B.B.; Panigrahi, B.P.; Misra, S. An Application of Genetic Programming for Power System Planning and Operation. Int. J. Control Syst. Instrum. 2012, 3, 15–20. [Google Scholar]
- Hassan, G.N.A. Multiobjective Genetic Programming for Financial Portfolio Management in Dynamic Environments. Ph.D. Thesis, University College London, London, UK, 2010. [Google Scholar]
- Marler, R.T.; Arora, J.S. The weighted sum method for multi-objective optimization: New insights. Struct. Multidiscip. Optim. 2010, 41, 853–862. [Google Scholar] [CrossRef]
- Jakob, W.; Gorges-Schleuter, M.; Blume, C. Application of Genetic Algorithms to Task Planning and Learning. In Proceedings of the Parallel Problem Solving from Nature 2, PPSN-II, Brussels, Belgium, 28–30 September 1992; pp. 293–302. [Google Scholar]
- Marler, R.; Arora, J. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Schaffer, J.D. Multiple Objective Optimization with Vector Evaluated Genetic Algorithms. In Proceedings of the 1st International Conference on Genetic Algorithms, Pittsburgh, PA, USA, 19–23 July 1985; pp. 93–100. [Google Scholar]
- Keerativuttiumrong, N.; Chaiyaratana, N.; Varavithya, V. Multiobjective Co-operative Co-evolutionary Genetic Algorithm. Parallel Probl. Solving Nat.-PPSN VII 2002, 2439, 288–297. [Google Scholar]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength pareto evolutionary algorithm for multiobjective optimization. In Evolutionary Methods for Design Optimization and Control with Applications to Industrial Problems; International Center for Numerical Methods in Engineering: Athens, Greece, 2001; pp. 95–100. [Google Scholar]
- Knowles, J.; Corne, D. The Pareto archived evolution strategy: A new baseline algorithm for Pareto multiobjective optimisation. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 1, pp. 98–105. [Google Scholar]
- Srinivas, N.; Deb, K. Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Yang, M.D.; Lin, M.D.; Lin, Y.H.; Tsai, K.T. Multiobjective optimization design of green building envelope material using a non-dominated sorting genetic algorithm. Appl. Therm. Eng. 2017, 111, 1255–1264. [Google Scholar] [CrossRef]
- Wu, R.; Mavromatidis, G.; Orehounig, K.; Carmeliet, J. Multiobjective optimisation of energy systems and building envelope retrofit in a residential community. Appl. Energy 2017, 190, 634–649. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; Stasio, C.D.; Mauro, G.M.; Vanoli, G.P. CASA, cost-optimal analysis by multi-objective optimisation and artificial neural networks: A new framework for the robust assessment of cost-optimal energy retrofit, feasible for any building. Energy Build. 2017, 146, 200–219. [Google Scholar] [CrossRef]
- Hamdy, M.; Hasan, A.; Siren, K. Applying a multi-objective optimization approach for Design of low-emission cost-effective dwellings. Build. Environ. 2011, 46, 109–123. [Google Scholar] [CrossRef]
- Alonso, C.L.; Puente, J.; Montana, J.L. Straight Line Programs: A New Linear Genetic Programming Approach. In Proceedings of the 2008 20th IEEE International Conference on Tools with Artificial Intelligence, Dayton, OH, USA, 3–5 November 2008; Volume 2, pp. 517–524. [Google Scholar]
- Nicolau, M.; Agapitos, A.; O’Neill, M.; Brabazon, A. Guidelines for defining benchmark problems in Genetic Programming. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 1152–1159. [Google Scholar]
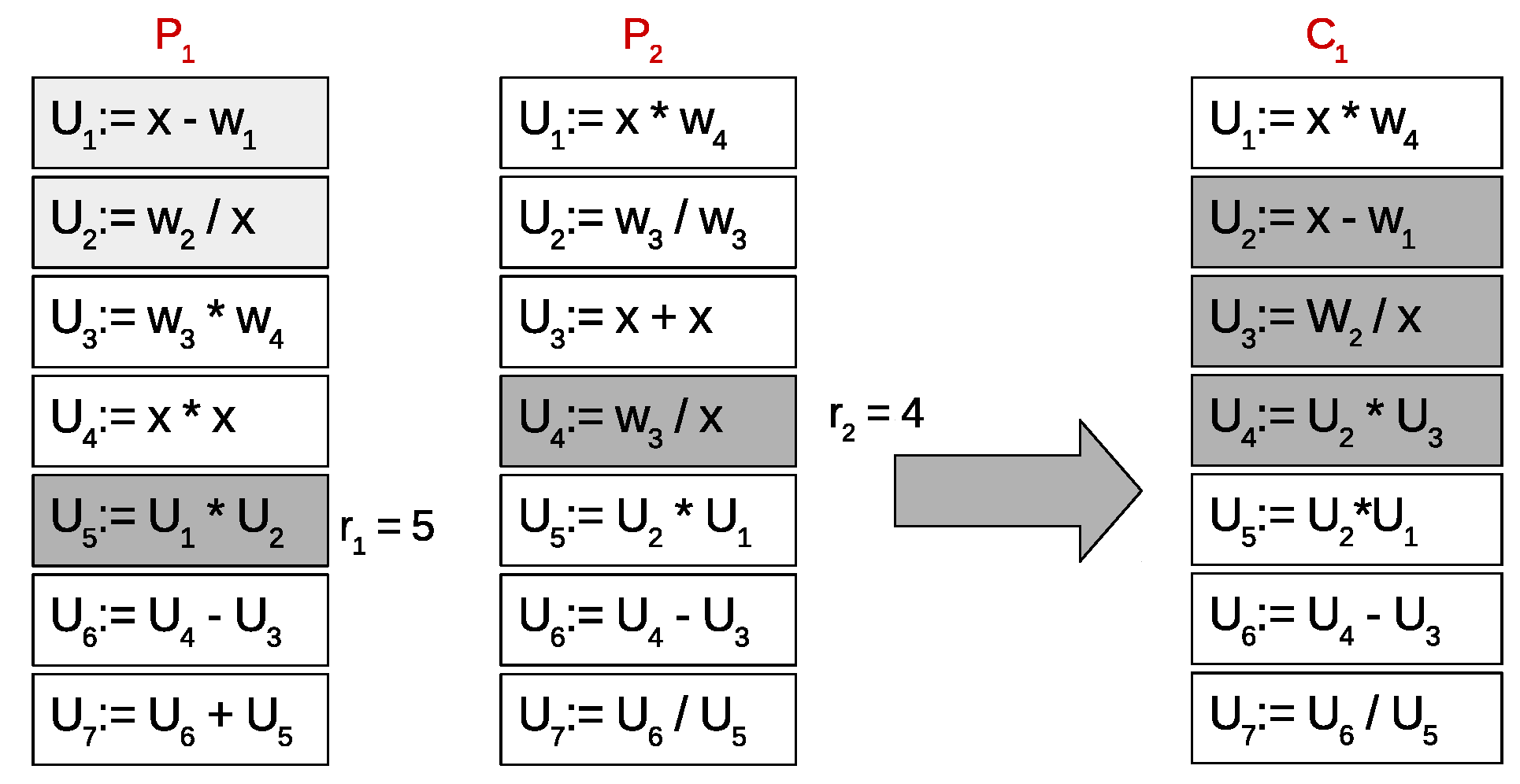
| Items | 3 Datasets | 5 Datasets | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TRAIN | ||||||||||||
| Single objective | ||||||||||||
| Median | ||||||||||||
| Best | ||||||||||||
| Worst | ||||||||||||
| Time (s.) | ||||||||||||
| Size | ||||||||||||
| Parameters | ||||||||||||
| Multi objective | ||||||||||||
| Median | ||||||||||||
| Best | ||||||||||||
| Worst | ||||||||||||
| Time (s.) | ||||||||||||
| Size | 12 | |||||||||||
| Parameters | 3 | |||||||||||
| TEST | ||||||||||||
| Single-Objective | ||||||||||||
| Median | ||||||||||||
| Best | ||||||||||||
| Worst | ||||||||||||
| Multi-Objective | ||||||||||||
| Median | ||||||||||||
| Best | ||||||||||||
| Worst | 3 | |||||||||||
| Train | Test | |||
|---|---|---|---|---|
| 3 Datasets | 5 Datasets | 3 Datasets | 5 Datasets | |
| (x) | (+) | (+) | (+) | |
| (x) | (+) | (+) | (+) | |
| (-) | (x) | (+) | (+) | |
| (x) | (x) | (+) | (+) | |
| (x) | (+) | (+) | (+) | |
| (-) | (x) | (+) | (+) | |
| Train | Test | |||
|---|---|---|---|---|
| Single-Objective | ||||
| Median | ||||
| Best | ||||
| Worst | ||||
| Time | - | - | ||
| Size | 10.83 | 11.56 | - | - |
| Parameters | 2.43 | 3 | - | - |
| Multi-Objective | ||||
| Median | ||||
| Best | ||||
| Worst | ||||
| Time | - | - | ||
| Size | 11.03 | 4.73 | - | - |
| Parameters | 2.9 | 1.46 | - | - |
| KW Test | (-) | (x) | (+) | (+) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rueda, R.; Cuéllar, M.P.; Molina-Solana, M.; Guo, Y.; Pegalajar, M.C. Generalised Regression Hypothesis Induction for Energy Consumption Forecasting. Energies 2019, 12, 1069. https://doi.org/10.3390/en12061069
Rueda R, Cuéllar MP, Molina-Solana M, Guo Y, Pegalajar MC. Generalised Regression Hypothesis Induction for Energy Consumption Forecasting. Energies. 2019; 12(6):1069. https://doi.org/10.3390/en12061069
Chicago/Turabian StyleRueda, R., M. P. Cuéllar, M. Molina-Solana, Y. Guo, and M. C. Pegalajar. 2019. "Generalised Regression Hypothesis Induction for Energy Consumption Forecasting" Energies 12, no. 6: 1069. https://doi.org/10.3390/en12061069
APA StyleRueda, R., Cuéllar, M. P., Molina-Solana, M., Guo, Y., & Pegalajar, M. C. (2019). Generalised Regression Hypothesis Induction for Energy Consumption Forecasting. Energies, 12(6), 1069. https://doi.org/10.3390/en12061069






