Measurement Uncertainty Propagation through Basic Photovoltaic Cell Models
Abstract
1. Introduction
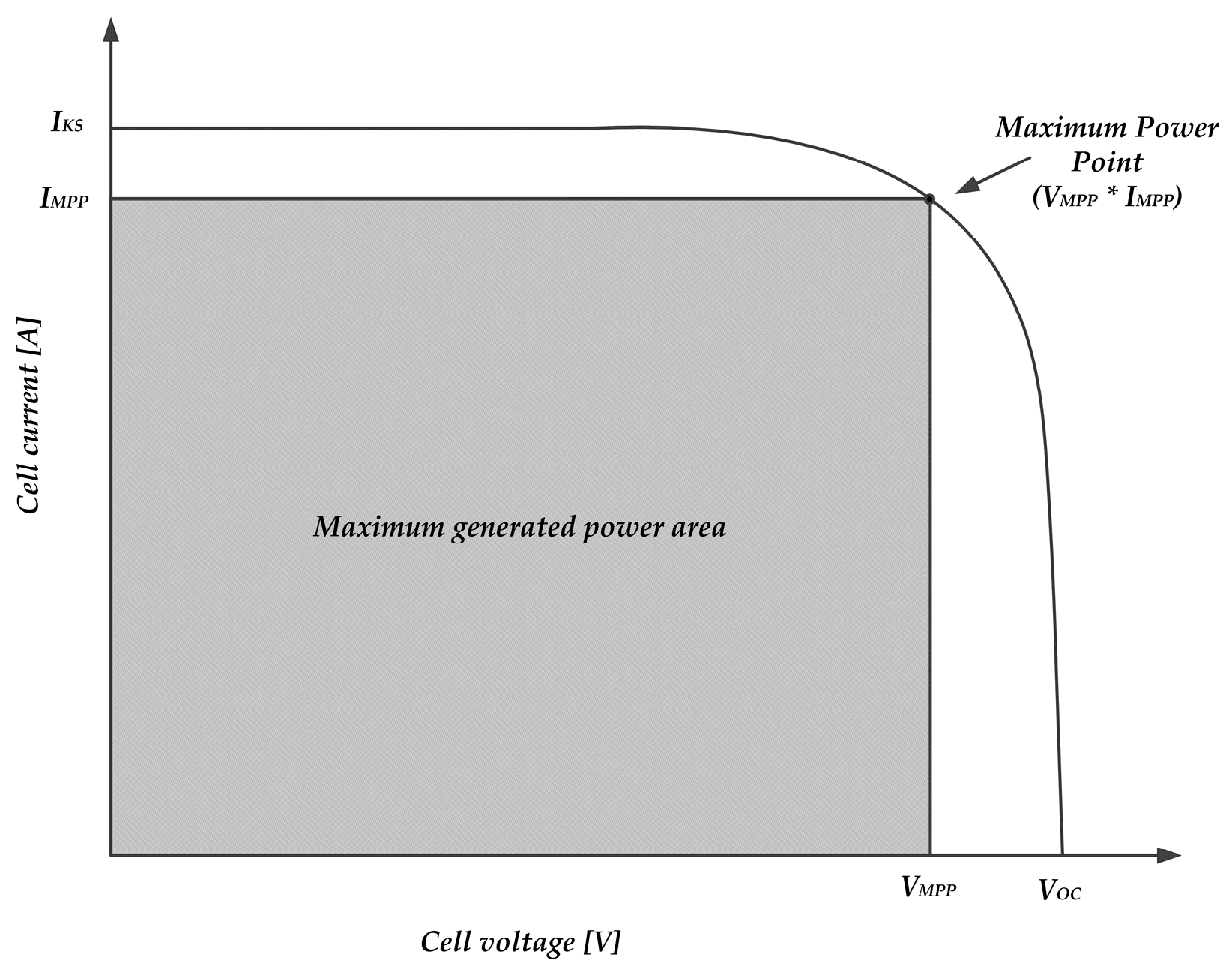
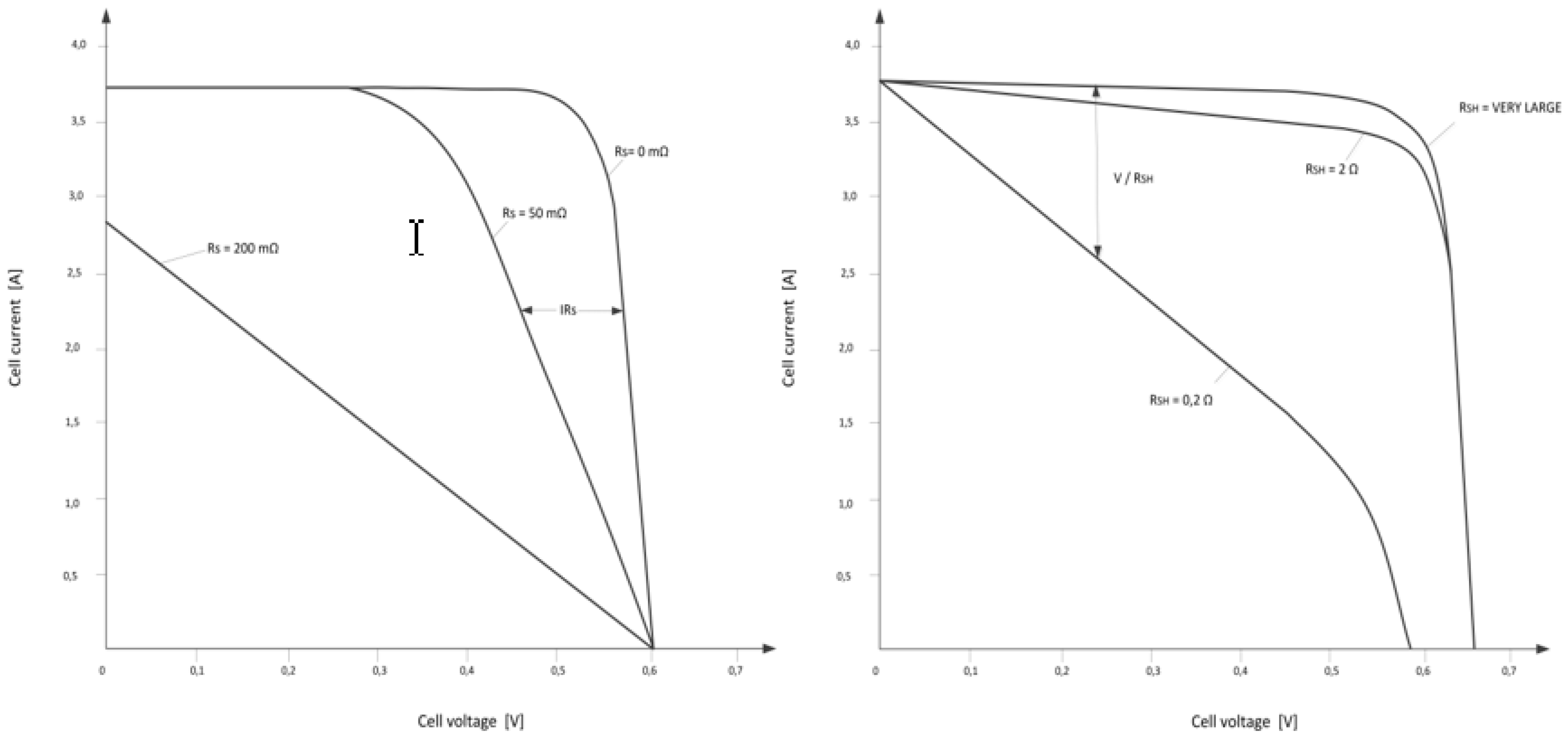
2. The Fill Factor of the Photovoltaic Cell—State of the Art
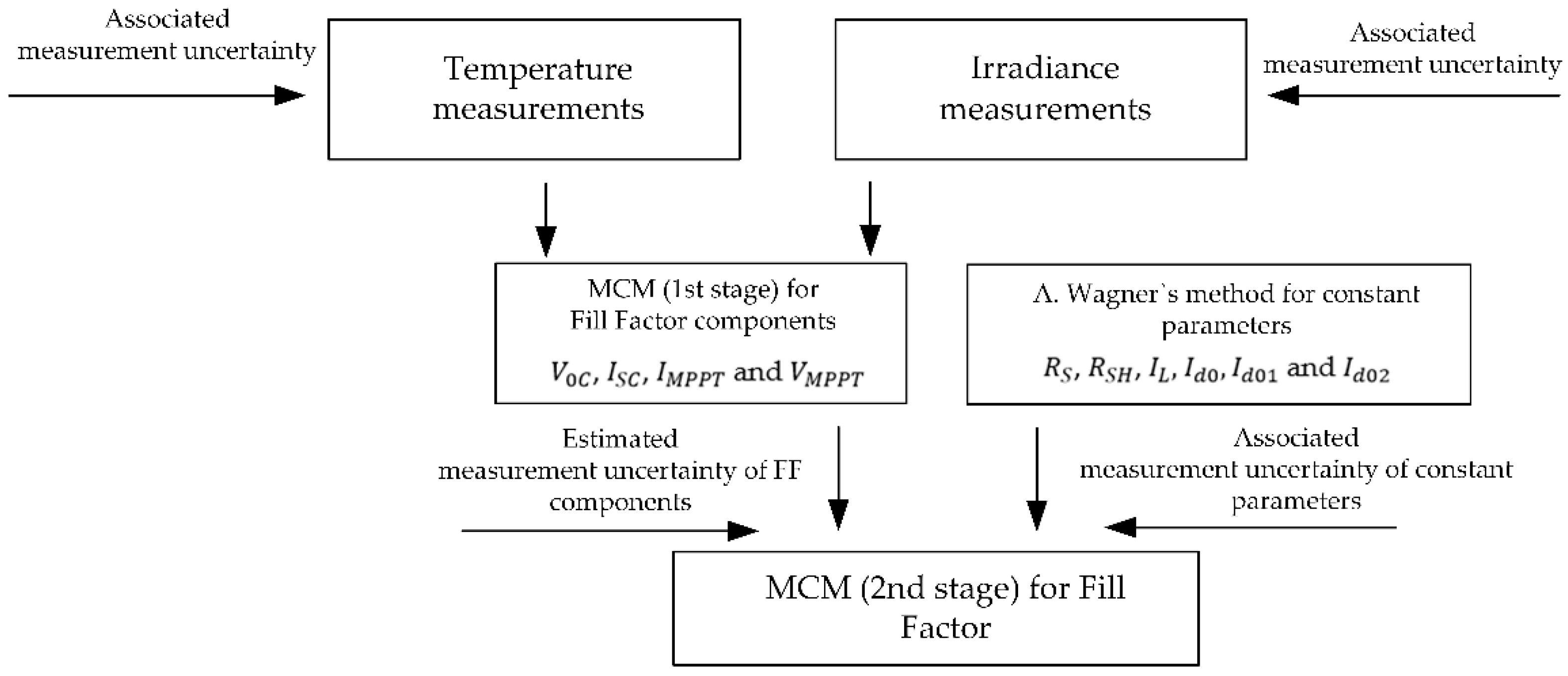
3. Fill Factor Components Calculation Procedure
4. Practical Results of the Uncertainty Calculation Procedure
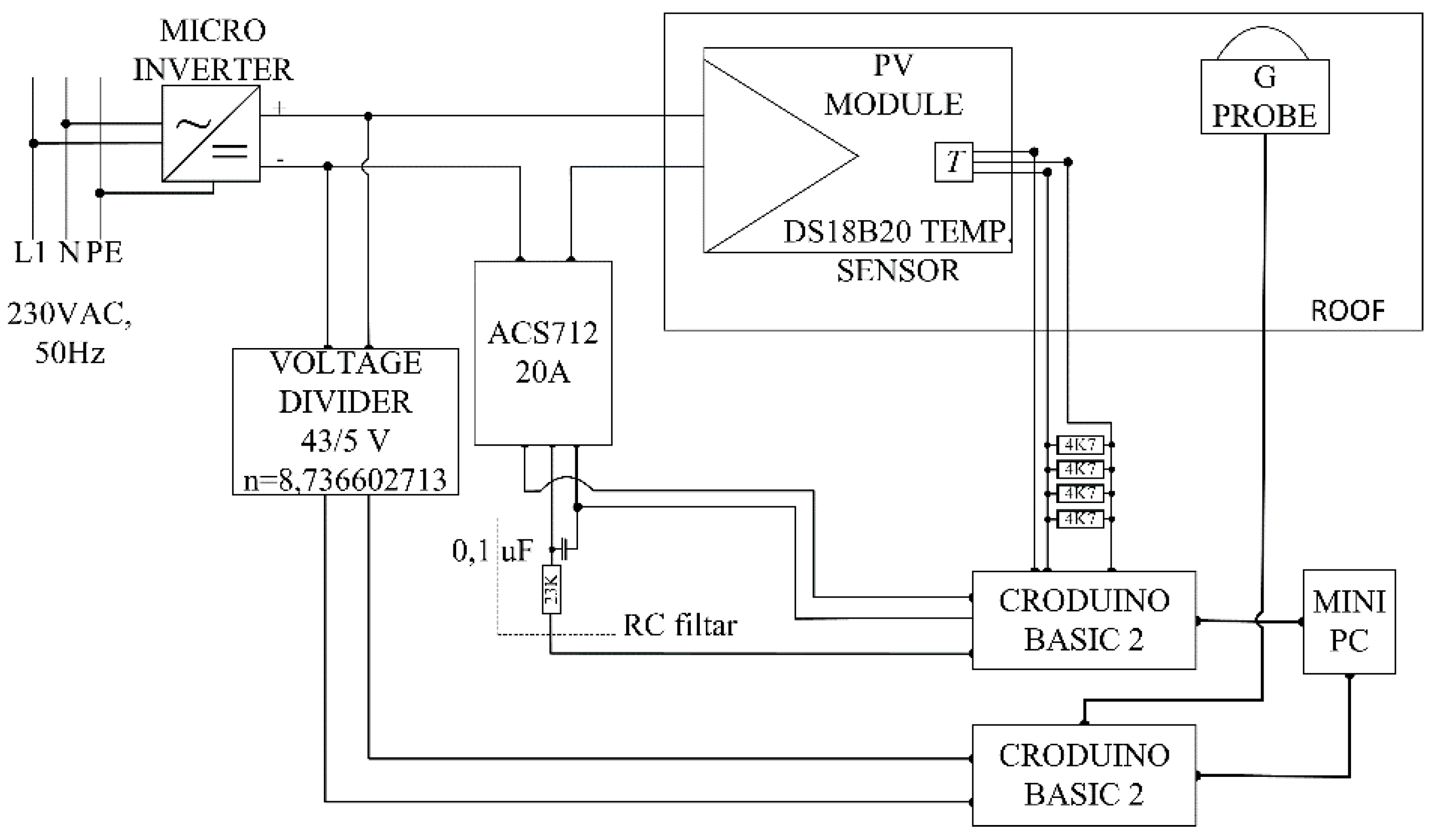
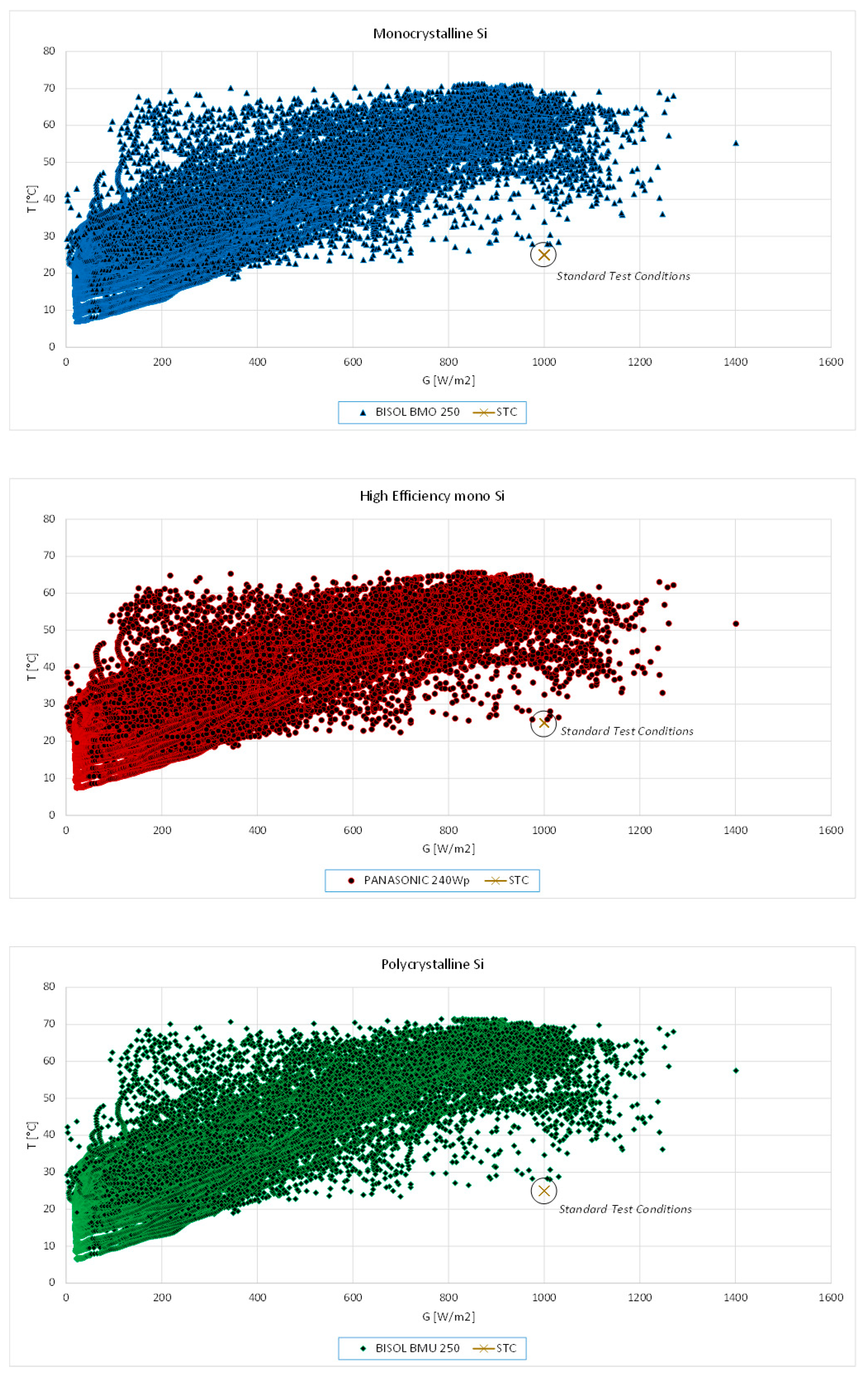
4.1. Site Information
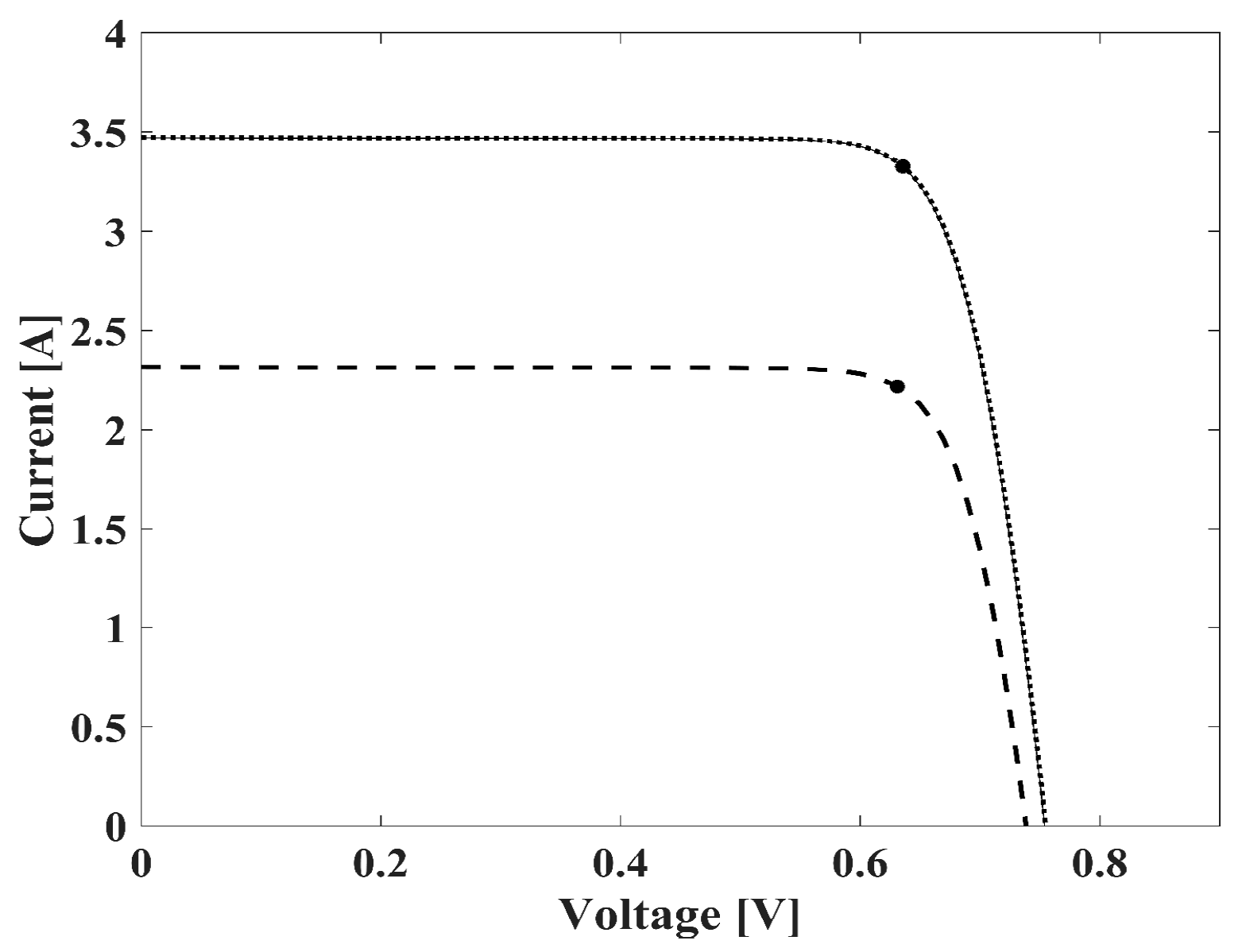
4.2. Measurement System Definition and Measurement Results
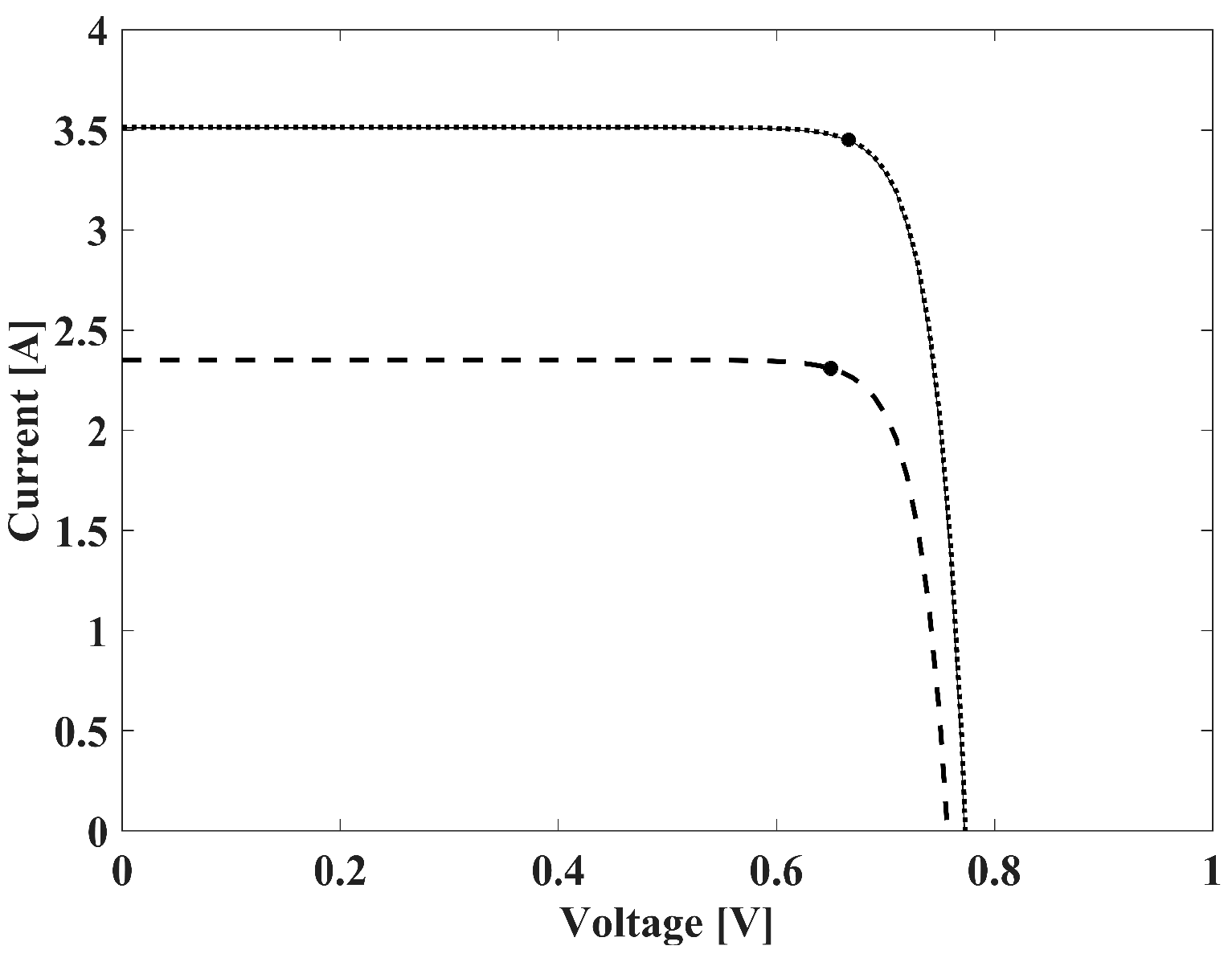
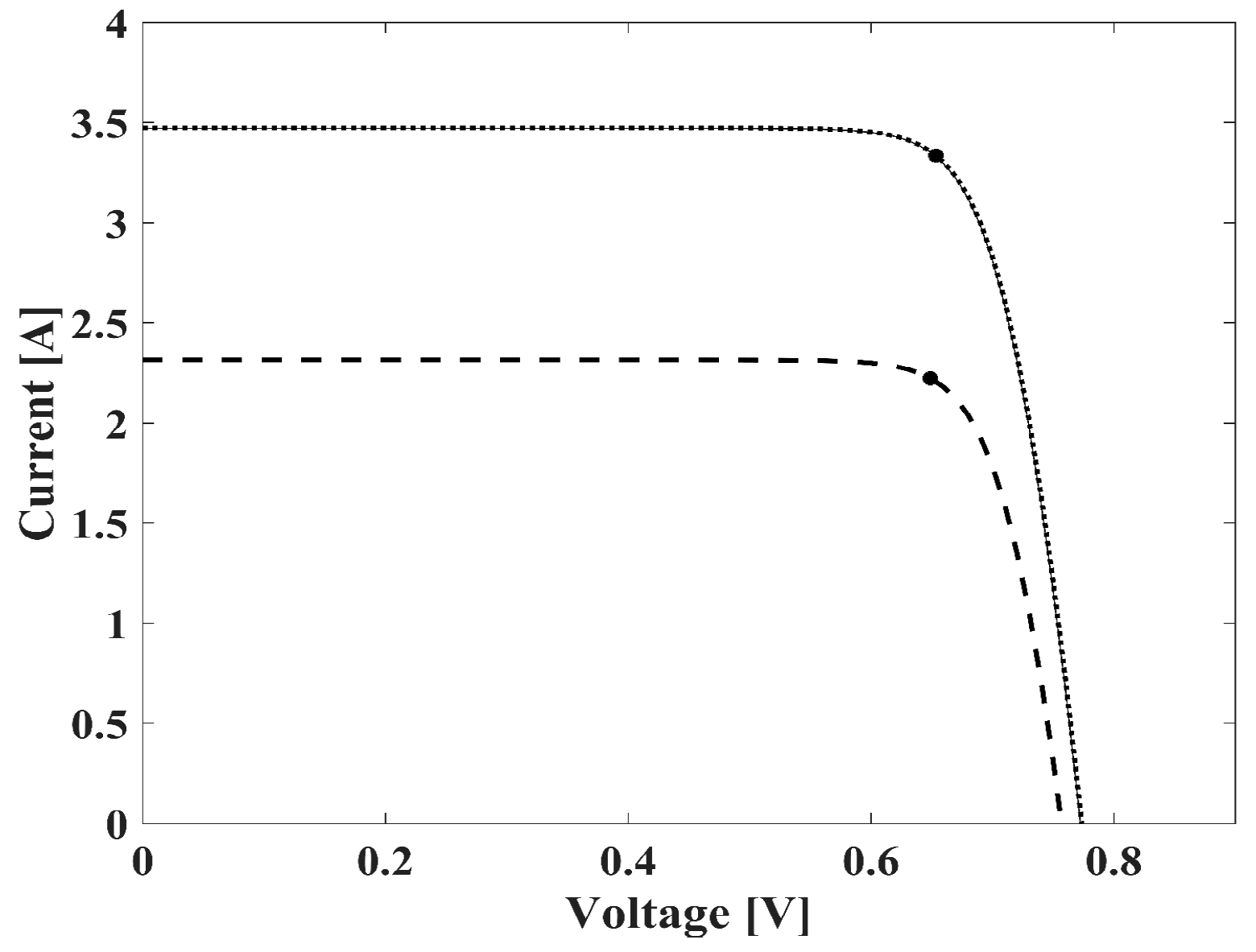
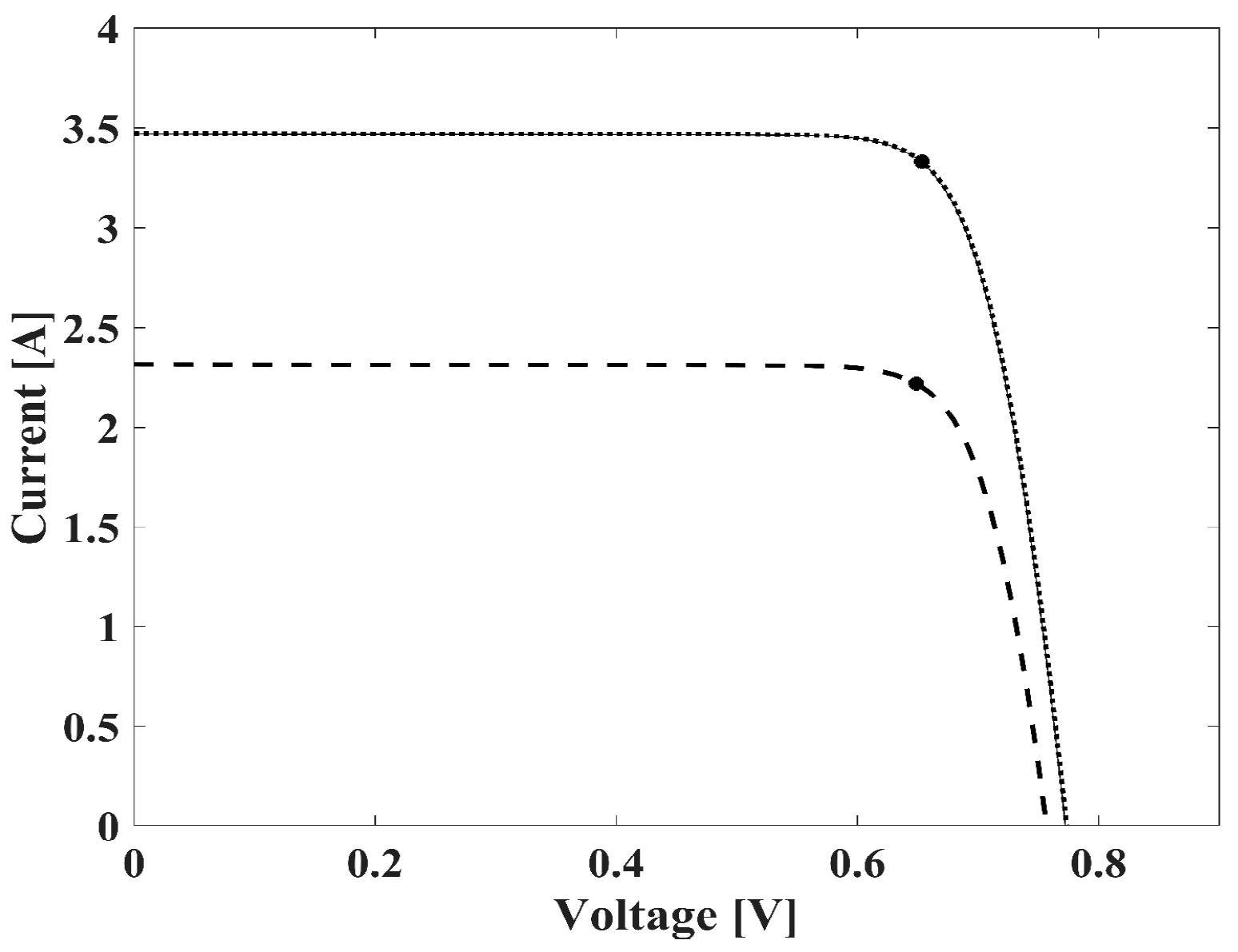
4.3. Calculation Results for One-Diode Model without Resistance
4.4. Calculation Results for One-Diode Model with One Resistance
4.5. Calculation Results for One-Diode Model with Two Resistances
4.6. Calculation Results for Two-Diode Model with Two Resistances
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Output current [A] | |
| Output voltage [V] | |
| Photo-generated current [A] | |
| Diode current [A] | |
| Shunt resistance [Ω] | |
| Series resistance [Ω] | |
| Short-circuit current [A] | |
| Open circuit voltage [V] | |
| Global irradiance [W/m2] | |
| Irradiance at STC conditions [W/m2] | |
| Temperature coefficient for short-circuit current [A/K] | |
| Cell temperature [K] | |
| Cell temperature at STC conditions [K] | |
| Diode reverse saturation currents [A] | |
| Electron charge [C] | |
| Boltzmann’s constant [J/K] | |
| Diode ideality factor | |
| Thermal voltage [K] | |
| Diode voltage [V] | |
| Maximum power point [W] | |
| Current at maximum power point [A] | |
| Voltage at maximum power point [V] | |
| Standard Test Condition |
References
- Ferrero, A.; Salicone, S. Uncertainty: Only one mathematical approach to its evaluation and expression? IEEE Trans. Instrum. Meas. 2012, 61, 2167–2178. [Google Scholar] [CrossRef]
- Bich, W. From Errors to Probability Density Functions. Evolution of the Concept of Measurement Uncertainty. IEEE Trans. Instrum. Meas. 2012, 61, 2153–2159. [Google Scholar] [CrossRef]
- Sapozhnikova, K.; Chunovkina, A.; Taymanov, R. “Measurement” and related concepts. Their interpretation in the VIM. Measurement 2013, 50, 390–396. [Google Scholar] [CrossRef]
- Vilbaste, M.; Slavin, G.; Saks, O.; Pihl, V.; Leito, I. Can coverage factor 2 be interpreted as an equivalent to 95% coverage level in uncertainty estimation? Two case studies. Measurement 2010, 43, 392–399. [Google Scholar] [CrossRef]
- Cox, M.G.; Siebert, B.R.L. The use of a Monte Carlo method for evaluating uncertainty and expanded uncertainty. Metrologia 2006, 43, S178–S188. [Google Scholar] [CrossRef]
- JCGM 100:2008. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; 2008; Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf (accessed on 12 June 2018).
- Rodríguez-Gonzálvez, P.; González-Aguilera, D.; Hernández-López, D.; González-Jorge, H. Accuracy assessment of airborne laser scanner dataset by means of parametric and non-parametric statistical methods. IET Sci. Meas. Technol. 2015, 9, 505–513. [Google Scholar] [CrossRef]
- Azpurua, M.; Tremola, C.; Paez, E. Comparison of the GUM and Monte Carlo methods for the uncertainty estimation in electromagnetic compatibility testing. Prog. Electromagn. Res. 2011, 34, 125–144. [Google Scholar] [CrossRef]
- Bertrand-Krajewski, J.-L.; Ribeiro, A.S.; Almeida, M.D.C. Evaluation of Uncertainties in Measurements; 2011; Available online: http://www.prepared-fp7.eu/viewer/file.aspx?FileInfoID=441 (accessed on 12 June 2018).
- JCGM 101:2008. Evaluation of Measurement Data—Supplement 1 to the “Guide to the Expression of Uncertainty in Measurement”—Propagation of Distributions Using a Monte Carlo Method; 2008; Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_101_2008_E.pdf (accessed on 12 June 2018).
- Hack, P.D.S.; Caten, C. Ten Measurement Uncertainty: Literature Review and Research trends. IEEE Trans. Instrum. Meas. 2012, 61, 2116–2124. [Google Scholar] [CrossRef]
- Giordani, A.; Mari, L. Measurement, models, and uncertainty. IEEE Trans. Instrum. Meas. 2012, 61, 2144–2152. [Google Scholar] [CrossRef]
- Willink, R. On using the Monte Carlo method to calculate uncertainty intervals. Metrologia 2006, 43, L39–L42. [Google Scholar] [CrossRef]
- Dobrić, G.; Žarković, M.; Šošić, D. Fuzzy-based Monte Carlo simulation for harmonic load flow in distribution networks. IET Gener. Transm. Distrib. 2015, 9, 267–275. [Google Scholar]
- Harris, P.M.; Cox, M.G. On a Monte Carlo method for measurement uncertainty evaluation and its implementation. Metrologia 2014, 51, S176–S182. [Google Scholar] [CrossRef]
- Tolić, I.; Miličević, K.; Tokić, A. Measurement Uncertainty of Transmission Line Resistance Calculation Using GUM and AMC Method. IET Sci. Meas. Technol. 2017, 11, 339–345. [Google Scholar] [CrossRef]
- Tolić, I.; Miličević, K.; Mujović, S. Cross-Border Transmission Line Losses Calculation Using Adaptive Monte Carlo Method. IET Sci. Meas. Technol. 2017, 11, 400–405. [Google Scholar] [CrossRef]
- Tolić, I.; Miličević, K.; Šuvak, N.; Biondić, I. Non-linear Least Squares and Maximum Likelihood Estimation of Probability Density Function of Cross-Border Transmission Losses. IEEE Trans. Power Syst. 2018, 33, 2230–2238. [Google Scholar] [CrossRef]
- Kosyachenko, L.A. Solar Cells—Silicon Wafer-Based Technologies; Kosyachenko, L.A., Ed.; InTech: London, UK, 2011; ISBN 978-953-307-747-5. [Google Scholar]
- Liu, H. Power Rating Uncertainty Analysis of Electrical Performance of Photovoltaic Modules. In Proceedings of the IEEE PES ISGT ASIA, Tianjin, China, 21–24 May 2012; pp. 1–4. [Google Scholar]
- Xiang, J.; Wei, W.; Cai, H. Modelling, analysis and control design of a two-stage photovoltaic generation system. IET Renew. Power Gener. 2016, 10, 1195–1203. [Google Scholar]
- Singh, B.; Jain, C.; Verma, A.K.; Shahani, D.T. Adaptive noise cancellation based harmonic elimination in grid integrated photovoltaic system. IET Renew. Power Gener. 2016, 10, 1096–1104. [Google Scholar]
- Elgendy, M.A.; Atkinson, D.J.; Zahawi, B. Experimental investigation of the incremental conductance maximum power point tracking algorithm at high perturbation rates. IET Renew. Power Gener. 2016, 10, 133–139. [Google Scholar] [CrossRef]
- Hua, C.; Fang, Y.; Chen, W. Hybrid maximum power point tracking method with variable step size for photovoltaic systems. IET Renew. Power Gener. 2016, 10, 127–132. [Google Scholar] [CrossRef]
- Antonio, L.; Hegedus, S. Handbook of Photovoltaic Science and Engineering, 2nd ed.; Wiley: Chichester, West Sussex, UK, 2003; ISBN 0471491969. [Google Scholar]
- Greulich, J.; Glatthaar, M.; Rein, S. Fill factor analysis of solar cells’ current-voltage curves. Prog. Photovolt. Res. Appl. 2010, 18, 511–515. [Google Scholar] [CrossRef]
- Quintana, M.A.; King, D.L.; McMahon, T.J.; Osterwald, C.R. Commonly observed degradation in field-aged photovoltaic modules. In Proceedings of the Conference Record of the Twenty-Ninth IEEE Photovoltaic Specialists Conference, New Orleans, LA, USA, 19–24 May 2002; pp. 1436–1439. [Google Scholar]
- King, D.L.; Quintana, M.A.; Kratochvil, J.A.; Ellibee, D.E.; Hansen, B.R. Photovoltaic Module Performance and Durability Following Long-term Field Exposure. Prog. Photovolt. Res. Appl. 2000, 8, 241–256. [Google Scholar] [CrossRef]
- Khanna, A.; Mueller, T.; Stangl, R.A.; Hoex, B.; Basu, P.K.; Aberle, A.G. A fill factor loss analysis method for silicon wafer solar cells. IEEE J. Photovolt. 2013, 3, 1170–1177. [Google Scholar] [CrossRef]
- PV Resources. Available online: http://www.pvresources.com/en/introduction/introduction.php (accessed on 12 June 2018).
- Aparicio, M.P.; Pelegrí-sebastiá, J.; Sogorb, T.; Llario, V. Modeling of Photovoltaic Cell Using Free Software Application for Training and Design Circuit in Photovoltaic Solar Energy. New Dev. Renew. Energy 2013, 121–139. [Google Scholar]
- Bendel, C.; Wagner, A. Photovoltaic measurement relevant to the energy yield. In Proceedings of the 3rd World Conference on Photovoltaic Energy Conversion, Osaka, Japan, 11–18 May 2003; p. 4. [Google Scholar]
- Abdulkadir, M.; Samosir, A.S.; Yatim, A.H.M. Modeling and Simulation of a Solar Photovoltaic System, Its Dynamics and Transient Characteristics in LABVIEW. Int. J. Power Electron. Drive Syst. 2013, 3, 185–192. [Google Scholar] [CrossRef]
- Kolsi, S.; Samet, H.; Amar, M. Ben Design Analysis of DC-DC Converters Connected to a Photovoltaic Generator and Controlled by MPPT for Optimal Energy Transfer throughout a Clear Day. J. Power Energy Eng. 2014, 02, 27–34. [Google Scholar] [CrossRef]
- De Brito, M.A.G.; Galotto, L.; Sampaio, L.P.; De Azevedo Melo, G.; Canesin, C.A. Evaluation of the main MPPT techniques for photovoltaic applications. IEEE Trans. Ind. Electron. 2013, 60, 1156–1167. [Google Scholar] [CrossRef]
- Attivissimo, F.; Di Nisio, A.; Savino, M.; Spadavecchia, M. Uncertainty analysis in photovoltaic cell parameter estimation. IEEE Trans. Instrum. Meas. 2012, 61, 1334–1342. [Google Scholar] [CrossRef]
- Alsayid, B. Modeling and Simulation of Photovoltaic Cell/Module/Array with Two-Diode Model. Int. J. Comput. Technol. Electron. Eng. (IJCTEE) 2012, 1, 6–11. [Google Scholar]
- Batzelis, E.I. Simple PV Performance Equations Theoretically Well Founded on the Single-Diode Model. IEEE J. Photovolt. 2017, 7, 1400–1409. [Google Scholar] [CrossRef]
- Shongwe, S.; Hanif, M. Comparative Analysis of Different Single-Diode PV Modeling Methods. IEEE J. Photovolt. 2015, 5, 938–946. [Google Scholar] [CrossRef]
- Fares, M.A.; Atik, L.; Bachir, G.; Aillerie, M. Photovoltaic panels characterization and experimental testing. Energy Procedia 2017, 119, 945–952. [Google Scholar] [CrossRef]
- Sera, D. Series resistance monitoring for photovoltaic modules in the vicinity of MPP. In Proceedings of the 25th European Photovoltaic Solar Energy Conference, Valencia, Spain, 6–10 September 2010; pp. 4506–4510. [Google Scholar]
- REGPHOSYS—Photovoltaic Systems as Actuators of Regional Development. Available online: http://www.regphosys.eu/ (accessed on 14 June 2018).
- Renewable Energy Lab Osijek. Available online: http://reslab.ferit.hr/ (accessed on 15 June 2018).
- Chin, V.J.; Salam, Z.; Ishaque, K. An accurate modelling of the two-diode model of PV module using a hybrid solution based on differential evolution. Energy Convers. Manag. 2016, 124, 42–50. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Taheri, H. Simple, fast and accurate two-diode model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2011, 95, 586–594. [Google Scholar] [CrossRef]
- Wagner, A. Peak-power and internal series resistance measurement under natural ambient conditions. In Proceedings of the Third ISES-Europe Solar Congress, Copenhagen, Denmark, 19–22 June 2000. [Google Scholar]

| Name | Model | Expression |
|---|---|---|
| One-diode model without resistance | 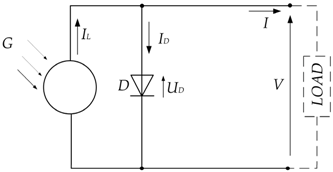 | |
| One-diode model with one resistance | 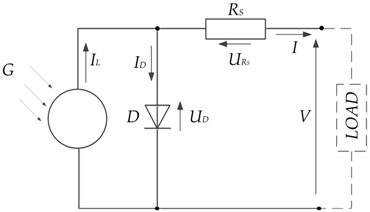 | |
| One-diode model with two resistances | 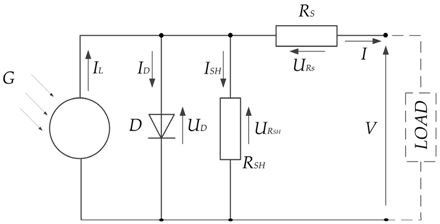 | |
| One-diode model with two resistances | 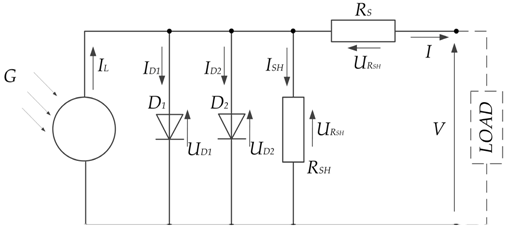 |
| Parameter | Nature of the Contribution | Probability Distribution | Value |
|---|---|---|---|
| T | Systematic | Rectangular | ±0.5 °C |
| G | Systematic | Rectangular | ±2.62% |
| I | Systematic | Rectangular | ±1.5% |
| U | Systematic | Rectangular | ±1% |
| Systematic | Rectangular | ±1.5% | |
| Systematic | Rectangular | ±1.5% |
| Module Technologies | RS [Ω] | RSH [Ω] | Id0 [A] | Id01 [A] | Id02 [A] |
|---|---|---|---|---|---|
| Monocrystalline | 0.01784 | 379.863 | 3.0318 × 10−7 | 6.607 × 10−8 | 5.3917 × 10−4 |
| High-efficiency monocrystalline | 0.006887 | 1412.587 | 7.7591 × 10−10 | 1.5653 × 10−10 | 2.6169 × 10−5 |
| Polycrystalline | 0.01113 | 343.891 | 6.06137 × 10−7 | 2.15999 × 10−7 | 7.9486 × 10−4 |
| All Modules | Monocrystalline | High-Efficiency Monocrystalline | Polycrystalline |
|---|---|---|---|
| Global irradiance G [W/m2] | 389.96 | 389.96 | 389.96 |
| Temperature T [°C] | 37.23 | 35.30 | 37.61 |
| One-Diode Model without Resistance | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Monocrystalline | High-Efficiency Monocrystalline | Polycrystalline | ||||||||||
| Parameter | Mean | Measurement Uncertainty | Low Limit | High Limit | Mean | Measurement Uncertainty | Low Limit | High Limit | Mean | Measurement Uncertainty | Low Limit | High Limit |
| 4.8640 | 0.0729 | 4.7447 | 4.9826 | 3.2452 | 0.0483 | 3.1648 | 3.3231 | 4.8649 | 0.0727 | 4.7485 | 4.9868 | |
| 0.4552 | 0.0006 | 0.454 | 0.4564 | 0.4212 | 0.0006 | 0.4201 | 0.4224 | 0.6201 | 0.0007 | 0.6187 | 0.6214 | |
| 0.3709 | 0.0008 | 0.3693 | 0.3724 | 0.3388 | 0.0008 | 0.3373 | 0.3404 | 0.5268 | 0.0009 | 0.5251 | 0.5286 | |
| 4.7027 | 0.0725 | 4.5827 | 4.8220 | 3.1444 | 0.0484 | 3.0652 | 3.2251 | 4.7569 | 0.0730 | 4.6375 | 4.8767 | |
| One-Diode Model with One Resistance | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Monocrystalline | High-Efficiency Monocrystalline | Polycrystalline | ||||||||||
| PARAMETER | Mean | Measurement Uncertainty | Low Limit | High Limit | Mean | Measurement Uncertainty | Low Limit | High Limit | Mean | Measurement Uncertainty | Low Limit | High Limit |
| 4.8630 | 0.0731 | 4.7434 | 4.9792 | 3.2441 | 0.0476 | 3.1697 | 3.3270 | 4.8616 | 0.0716 | 4.7403 | 4.9742 | |
| 0.4552 | 0.0006 | 0.4540 | 0.4564 | 0.4212 | 0.0006 | 0.4200 | 0.4224 | 0.6201 | 0.0007 | 0.6186 | 0.6215 | |
| 0.3069 | 0.0010 | 0.3052 | 0.3091 | 0.3305 | 0.0004 | 0.3297 | 0.3313 | 0.4882 | 0.0008 | 0.4867 | 0.4896 | |
| 4.4647 | 0.0662 | 4.3598 | 4.5748 | 3.0015 | 0.0452 | 2.9241 | 3.0705 | 4.6081 | 0.0697 | 4.4925 | 4.7177 | |
| One-Diode Model with Two Resistances | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Monocrystalline | High-Efficiency Monocrystalline | Polycrystalline | ||||||||||
| Parameter | Mean | Measurement Uncertainty | Low Limit | High Limit | Mean | Measurement Uncertainty | Low Limit | High Limit | Mean | Measurement Uncertainty | Low Limit | High Limit |
| 4.8641 | 0.0723 | 4.7477 | 4.9811 | 3.2450 | 0.0483 | 3.1704 | 3.3265 | 4.8626 | 0.0736 | 4.7490 | 4.9886 | |
| 0.4551 | 0.0006 | 0.4540 | 0.4564 | 0.4212 | 0.0006 | 0.4201 | 0.4224 | 0.6201 | 0.0007 | 0.6188 | 0.6215 | |
| 0.3069 | 0.0010 | 0.3052 | 0.3089 | 0.3305 | 0.0004 | 0.3296 | 0.3313 | 0.4882 | 0.0008 | 0.4869 | 0.4898 | |
| 4.4635 | 0.0652 | 4.3614 | 4.5765 | 3.0002 | 0.0453 | 2.9288 | 3.0744 | 4.6038 | 0.0673 | 4.4905 | 4.7131 | |
| Two-Diode Model with Two Resistances | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Monocrystalline | High-Efficiency Monocrystalline | Polycrystalline | ||||||||||
| Parameter | Mean | Measurement Uncertainty | Low Limit | High Limit | Mean | Measurement Uncertainty | Low Limit | High Limit | Mean | Measurement Uncertainty | Low Limit | High Limit |
| 4.8615 | 0.0717 | 4.7488 | 4.9864 | 3.2460 | 0.0481 | 3.1637 | 3.3220 | 4.8641 | 0.0737 | 4.7444 | 4.9809 | |
| 0.4709 | 0.0008 | 0.4694 | 0.4724 | 0.4243 | 0.0007 | 0.4229 | 0.4257 | 0.6670 | 0.0011 | 0.6648 | 0.6689 | |
| 0.3078 | 0.0008 | 0.3063 | 0.3094 | 0.3165 | 0.0006 | 0.3155 | 0.3177 | 0.4920 | 0.0008 | 0.4905 | 0.4934 | |
| 4.1920 | 0.0617 | 4.0944 | 4.2999 | 2.8143 | 0.0424 | 2.7447 | 2.8826 | 4.3753 | 0.0649 | 4.2682 | 4.4823 | |
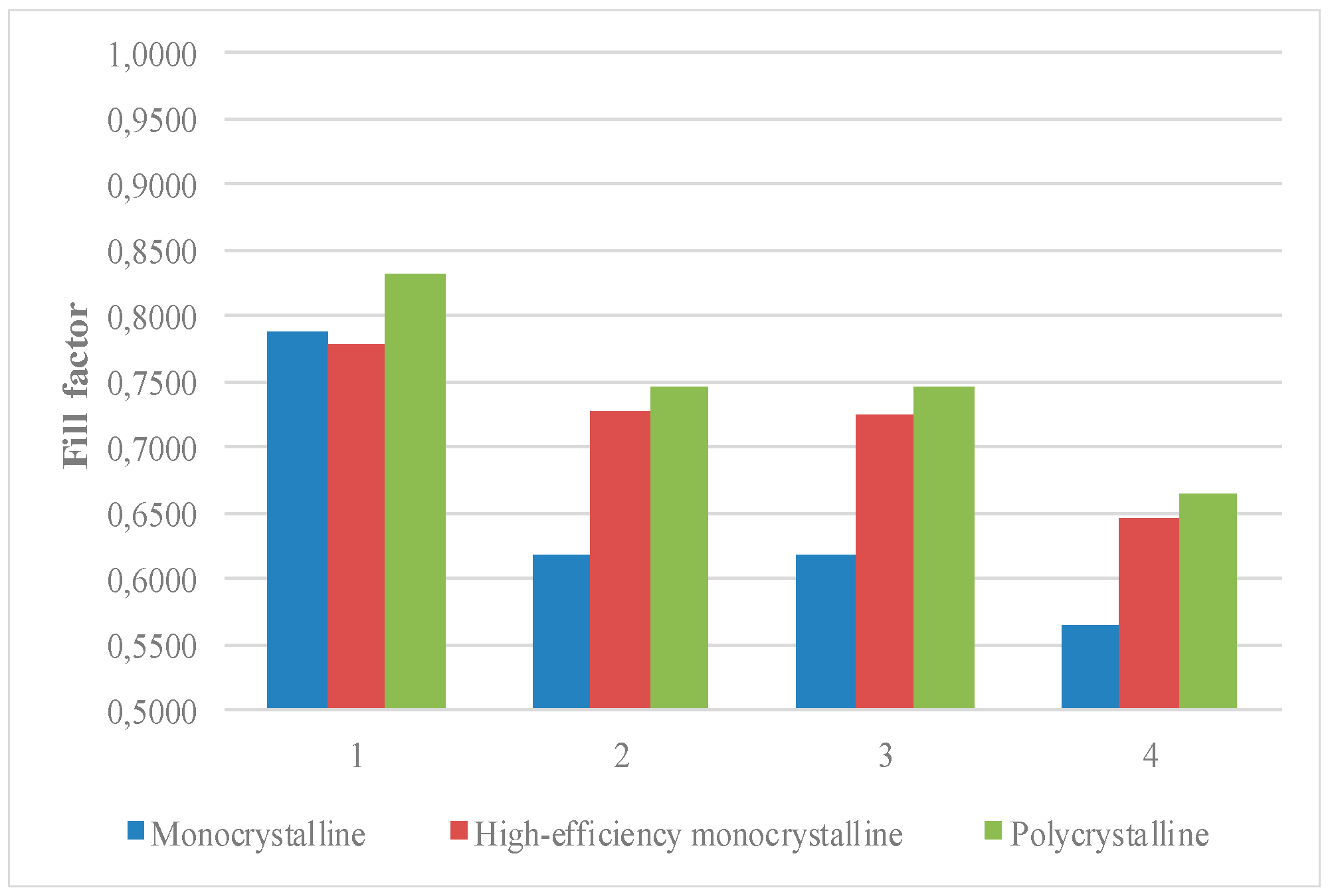
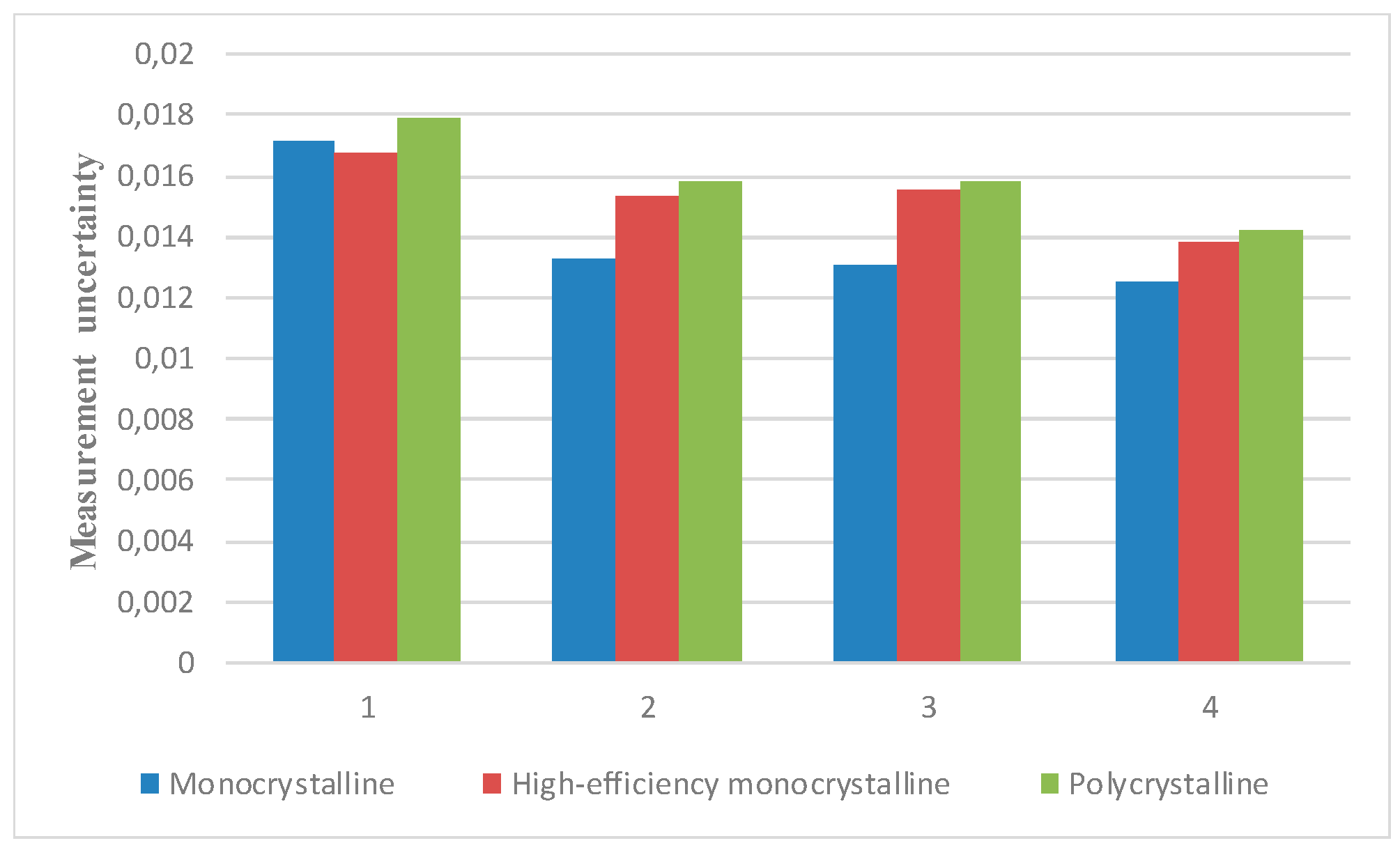
| Fill Factor | ||||||
|---|---|---|---|---|---|---|
| Monocrystalline | High-Efficiency Monocrystalline | Polycrystalline | ||||
| Mean | Measurement Uncertainty | Mean | Measurement Uncertainty | Mean | Measurement Uncertainty | |
| One diode model without resistance | 0.7880 | 0.0171 | 0.7795 | 0.0168 | 0.8309 | 0.0179 |
| One diode model with one resistance | 0.6191 | 0.0133 | 0.7262 | 0.0153 | 0.7464 | 0.0158 |
| One diode model with two resistances | 0.6190 | 0.0131 | 0.7256 | 0.0155 | 0.7456 | 0.0158 |
| Two diode model with two resistances | 0.5638 | 0.0125 | 0.6469 | 0.0138 | 0.6637 | 0.0142 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tolić, I.; Primorac, M.; Miličević, K. Measurement Uncertainty Propagation through Basic Photovoltaic Cell Models. Energies 2019, 12, 1029. https://doi.org/10.3390/en12061029
Tolić I, Primorac M, Miličević K. Measurement Uncertainty Propagation through Basic Photovoltaic Cell Models. Energies. 2019; 12(6):1029. https://doi.org/10.3390/en12061029
Chicago/Turabian StyleTolić, Ivan, Mario Primorac, and Kruno Miličević. 2019. "Measurement Uncertainty Propagation through Basic Photovoltaic Cell Models" Energies 12, no. 6: 1029. https://doi.org/10.3390/en12061029
APA StyleTolić, I., Primorac, M., & Miličević, K. (2019). Measurement Uncertainty Propagation through Basic Photovoltaic Cell Models. Energies, 12(6), 1029. https://doi.org/10.3390/en12061029





