1. Introduction
Soot particles are fine carbonaceous particulates that are formulated through multiple physical binning and chemical reaction processes of intermediate combustion products. They are invariably incepted and evolved in the flame region, and subsequently dispersed in the smoke layer. The soot formation mechanisms begin with the soot nuclei inception from precursor species and it follows by the formation of lager fractal object via particle-particle collision events, including coalescence and aggregation, as well as via surface growth reaction of the soot particulates. It ends with the breakage of the clusters into fragments that are eventually consumed via oxidation processes [
1,
2]. Soot particulates can be carcinogenic and they endanger our lives through toxication, suffocation, or causing permanent damage to our respiratory systems, such as trachea, blood vessels, and lungs [
3]. As a strong emitter and absorber of radiative heat, soot particulates significantly affect the global heat transfer process, both in the inflame and surrounding regions [
2,
4]. This is especially hazardous in compartment fire scenarios, where the inhalation of the toxic compounds, including flame generated gas mixture and soot particulates, combined its ability to obscure visibility through a combination of absorption and light scattering, can significantly interfere with the evacuation process [
5]. The recent development of bio-based fire retardants material could significantly reduce the generation of fire and smoke [
6,
7], however, there are still a considerable amount of other combustible materials, such as wood and plastic consumables, which could potentially pose a threat to building fire safety. Hence, the evolution of soot particles is of great interest to both research and industrial communities. Is useful in the design of fire protection engineering systems, such as smoke extraction, smoke curtain, pressurised zone, and sprinkler systems. Accordingly, this work aims to investigate the formation and destruction processes of soot particulates in a non-premixed buoyant flame that is commonly encountered in compartment or wildland fires.
Flame generated soot particles have been commonly studied via experimental approaches. For instance, soot particulates can be locally collected using thermophoresis sampling technique, and then be visualized with transmission electron microscope (TEM) imaging [
8]. Soot morphological information, e.g., projected area, radius of gyration, fractal dimension of the aggregates, primary particle size etc., can be collectively characterised. The second type of diagnostic approach is the optical based non-intrusive measuring technique, e.g., laser-induced incandescence (LII), elastic light scattering (ELS), small-angle neutron scattering (SANS), and small-angle X-ray scattering (SAXS), which provides insight into a wide variety of soot related properties, including size, structure, and composition of particulates [
9,
10,
11,
12]. However, spatial resolution of the measurement and the potential perturbation of the very combustion process under investigation when intrusive approaches are used limited the experimental approaches. Most of the optical and laser-based diagnostics are dependent on optical properties of the materials, which are very difficult characterise. Numerical modelling of soot particles using the population balance approach (PBA), on the other hand, can deliver informative data that are not assessable by experimental measurements alone, such as displaying the full spectrum of particle size and number density distribution for any location and time. Therefore, the use of numerical approaches can provide more theoretical insight that can significantly enhance our understanding of the soot formation mechanisms and the dispersion of soot particles for the research communities.
Numerical simulation of soot involves the appropriate description of the evolution of the fine hydrocarbon particulates as a result of incomplete combustion, which were subsequently immersed or recirculated back into the flammable gas mixture. This phenomenon could be resolved on various scales depending on the aim and focus of the investigation. For example, one conventional method that is commonly used in bushfire or compartment fire modelling is the macroscale level approach, in which only the hydrodynamics behaviours of the phase are resolved, and no more than a soot particle concentration (i.e., mass/volume fraction) term is resolved. However, such macroscale models were initially designed to assess industrial-scale fires and are usually limited to only simulate smoke movement, flow velocities, and temperatures changes due to soot radiation. Furthermore, the deviation of the predicted quantities is often beyond 20% when comparing with experimental measurements due to the lack of detail description of the actual physical and chemical processes that are involved [
13]. The microscale Eulerian–Lagrangian approach, on the other hand, tracks the motion of discrete elements by considering the interaction of discrete particles within the computational domain. It provides more fundamental insights into the detailed description of the soot species evolution, thus enabling the deliver simulation with improved prediction accuracy [
14]. Nevertheless, it is limited to microscopic level due to its immense requirement for small mesh sizes and it is not practical for medium-to large-scale fire modelling for the enormous computational cost. In practical engineering applications, most of the soot models used at present in commercial computational fluid dynamic (CFD) packages resolve the issue from an intermediate level, i.e., mesoscale, which focus on the local structural development and are aimed to investigate the evolvement of cluster groups e.g., droplets, bubbles, and particles [
15,
16,
17,
18,
19]. The mesoscale model categorised all sooting processes into the consideration of critical mechanisms and it limits its scope to predict key soot-related properties with reasonable accuracy, whilst notably reducing the computational effort required [
20,
21,
22]. The Direct Quadrature Method of Moments (DQMOM) soot model presented in this paper, therefore, is targeting to resolve soot evolution on a mesoscale level by taking into account all necessary soot processes that are involved the formation pathway, namely particle inception, aggregations, coagulation, surface growth, and oxidation.
One of the major drawbacks of common mesoscale soot models is the difficulty in quantifying case dependent properties. In practice modelling, such properties are often represented by an empirical value or are approximated by empirical formulations. This assumption or simplification, if not carefully justified, can generate large numerical errors. In fire modelling, the particulate size of soot species is one of the properties that has been oversimplified by most current mesoscale models. It is generally agreed that the soot particulate size can vary between a broad range, depending on various aspects, such as parent fuel composition, burner configuration, ambient condition, etc. The two-equations based semi-empirical model, e.g., Moss–Brookes soot model used in Fluent, however, considers a uniform soot particle size distribution (PSD) that is set based on a predefined empirical data, i.e., 35 nm [
20]. The population balance based Standard Method of Moments (SMM) soot model evaluates particle size distribution with the use of a presumed log-normal function that is based on experimental data collected under certain flaming conditions [
23]. The quadrature method of moment (QMOM) is an attractive alternative, which effectively resolves the enclosure by adopting a moment construction and inversion algorithm. This mathematical approach closed the population balance equation with limited computational burden and it proved to be numerically stable in most of its applications. Nevertheless, it is formulated based on a presumed particle size distribution method that is similar to the concept of SMM. The abovementioned numerical soot models could not directly evaluate the distribution of particle size that varies according to the combustion conditions, which could potentially lead to inaccuracies in determining the other soot properties that are particle size dependent.
The Direct Quadrature Method of Moments (DQMOM) that was developed by Marchisio and Fox [
24] directly solves the nodes and weights of the quadrature approximation of the number density function for an internal coordinate, e.g., particle sizes. This novel approach enables the prediction of the real-time and spatial size distribution and, hence, further improves the accuracy of soot mass fraction predictions. Previous numerical studies that implemented the DQMOM approach in soot modelling have showcased its competency to provide promising results with moderate computational burden [
25,
26,
27,
28]. However, those studies are mainly focused on the investigation of inertia-driven highly turbulent flame with relatively high fuel/oxidiser injection rate, for example, with 50 ms
−1 fuel injection rate. A DQMOM-based soot model targeting low-speed buoyancy-driven diffusion flame, which corresponds better to natural fire occurrences in open configuration, e.g., bushfire and compartment fire, has not been formulated and tested. Moreover, it has been reported that DQMOM algorithm can be numerically unstable and difficult to implement, i.e., generating unrealizable (negative) weights and nodes, if the system is not cautiously designed. Alternative approaches that were proposed by Mueller et al. and Chittipotula et al. [
28,
29] could potentially resolve the numerical issue. However, the alternative approaches often require solving additional sub-modules that are integrated to the framework or correction algorithms, which could significantly increase the computational cost or need the cumbersome coupling of the CFD code with an external mathematical package. This challenge could become more predominant when the investigated case has relatively small spatial-diffusion terms [
29], like the flame of the interest in this work. Therefore, it is critical to systematically investigate the effect of all modelling aspects to ensure the numerical robustness and simulation accuracy.
The information about soot particle size distribution could also aid the design of fire protection systems in practical engineering. Among previous works on smoke control systems [
30], it is discovered that the smoke detection system is mainly categorised into three types: (i) ionisation smoke alarms, (ii) light obscuration photoelectric alarms, and (iii) light scattering photoelectric alarms. When the soot particles reach a particular size, it will trigger the alarms by either (i) providing a voltage signal for ionisation alarms, (ii) blocking the light signals to the receiver for obscuration type photoelectric alarms, or (iii) changing the light scattering for scattering type photoelectric alarms. Nevertheless, the current drawbacks of the use of numerical models to predict the detection of smoke particulates are lacking in consideration of the particle size distribution. In essence, the alarms in numerical codes such as FDS is trigger by either gas temperature or smoke volume fraction, which often lead to inaccurate response time. With the application of the DQMOM approach, providing an enhanced understanding of soot formation and destruction processes, especially for the particle size distribution, will contribute to the prediction of fire protection systems.
In light of the above gaps in knowledge, this work will present, for the very first time, a detailed parametric study on the effects of key modelling aspects of an in-house soot model that is built based upon the DQMOM algorithm that enables the real-time tracking of the evolution of PSD. The proposed soot model is fully coupled with a gas-phase combustion model incorporating detailed chemistry, and it is specifically formulated for a for a low-speed buoyant diffusion flame configuration with optimised parameters. The results of the present model are validated against measurements from a self-constructed experiment in the Combustion Laboratory, School of Mechanical and Manufacturing Engineering, the University of New South Wales. Comprehensive assessments will be performed on a collection of key parameters within the DQMOM framework towards the performance of soot modelling for turbulent diffusion flames, and the objectives can be summarised, as follows:
- (i)
comparison of three nucleation laws, including Moss, Leung, and Fairweather, and discuss their effectiveness in predicting the changes in particle size due to the particle generations;
- (ii)
study of two different oxidation law including modified NSC and Said to investigate the appropriate soot particle reduction or disruption mechanisms for DQMOM;
- (iii)
investigating the influences of fractal dimensions towards the aggregation and surface growth mechanisms, as well as the effect on particle size distribution;
- (iv)
study the effect of diffusion coefficient for soot quantities and number density towards the dispersion of soot particles within the computational field; and,
- (v)
provide a deeper understanding of the soot formation process, in particular, within the flaming/soot nucleating region.
2. Mathematical Model
Numerical simulations have been carried out using an in-house population balance approach (PBA) DQMOM code coupled with Fluent solver (i.e., version 19.1). This computational fluid dynamics model incorporates sub-modelling components, including soot formation, turbulence, combustion, and radiation heat exchange to describe the fire phenomena. To take into account the highly irregular nature of the combustion process, several assumptions are made, including (i) the low Mach number flow equations are considered, (ii) the thermal-physical properties are constant, (iii) the ratio between mass and thermal diffusivity (Lewis number) is unity, (iv) no external body force and heat source are applied towards the flow, and (vi) non-adiabatic non-premixed combustion of the energy equation is adopted.
2.1. Governing Equations
The fully coupled, non-linear, and interactive physical and chemical processes that are involved in the turbulent reacting gas mixture caused by the pulsating diffusion flame is modelled using computational fluid dynamics techniques. With the application of the Favre averaging approach, the following governing equations, i.e., the continuity, Navier–Stokes, and scalar transport equations are utilised in this simulation study are given as:
where
and
are the mean density and pressure,
and
is the kinematic and turbulent viscosity,
and
are the Favre-averaged and fluctuation value of the mean fluid velocity,
and
are the mean and fluctuation value of the
th scalar,
and
are molecular and turbulent diffusivity, and
is the Favre-averaged chemical reaction source term.
2.2. Turbulence and Combustion Modelling
Literature works have suggested that the standard
-
model is usually suitable for modelling non-premixed diffusion and non-swirling flames, like the one under investigation in this work [
25,
26,
27,
28]. The chemical reaction source term in the transport equations of the involved reacting scalars is determined by the strained laminar flamelet approach, in which the combustion chemistry is a pre-assumed probability density function (pre-PDF) of the mixture fraction (
) and the scalar dissipation (
). In essence, the mixture fraction governs the amount of the fuel mixture in each control volume element in the simulation domain. The scalar dissipation is a term that is introduced to describe the strain and extinction of the flame, in which the magnitude of this quantity depicts the departure of the combustion process away from its chemical equilibrium [
31]. It should be noted that, in the present work, the GRI-MECH 3.0 detailed chemical reaction mechanisms, which includes 325 reaction steps and 53 chemical species [
32], was implemented to formulate the flamelet library for the strained laminar flamelet model, with ethylene (C
2H
4) being selected as the parental fuel. Such an approach of resolving turbulence-chemistry interaction has been demonstrated in previous studies to provide a reasonable result with moderate computational burden [
18,
33].
Figure 1 presents the post-processed flamelet profile results for major and minor species, respectively, at near-equilibrium and near-extinction scalar dissipation rates, being generated for 20 different scalar dissipation rates that range from 10
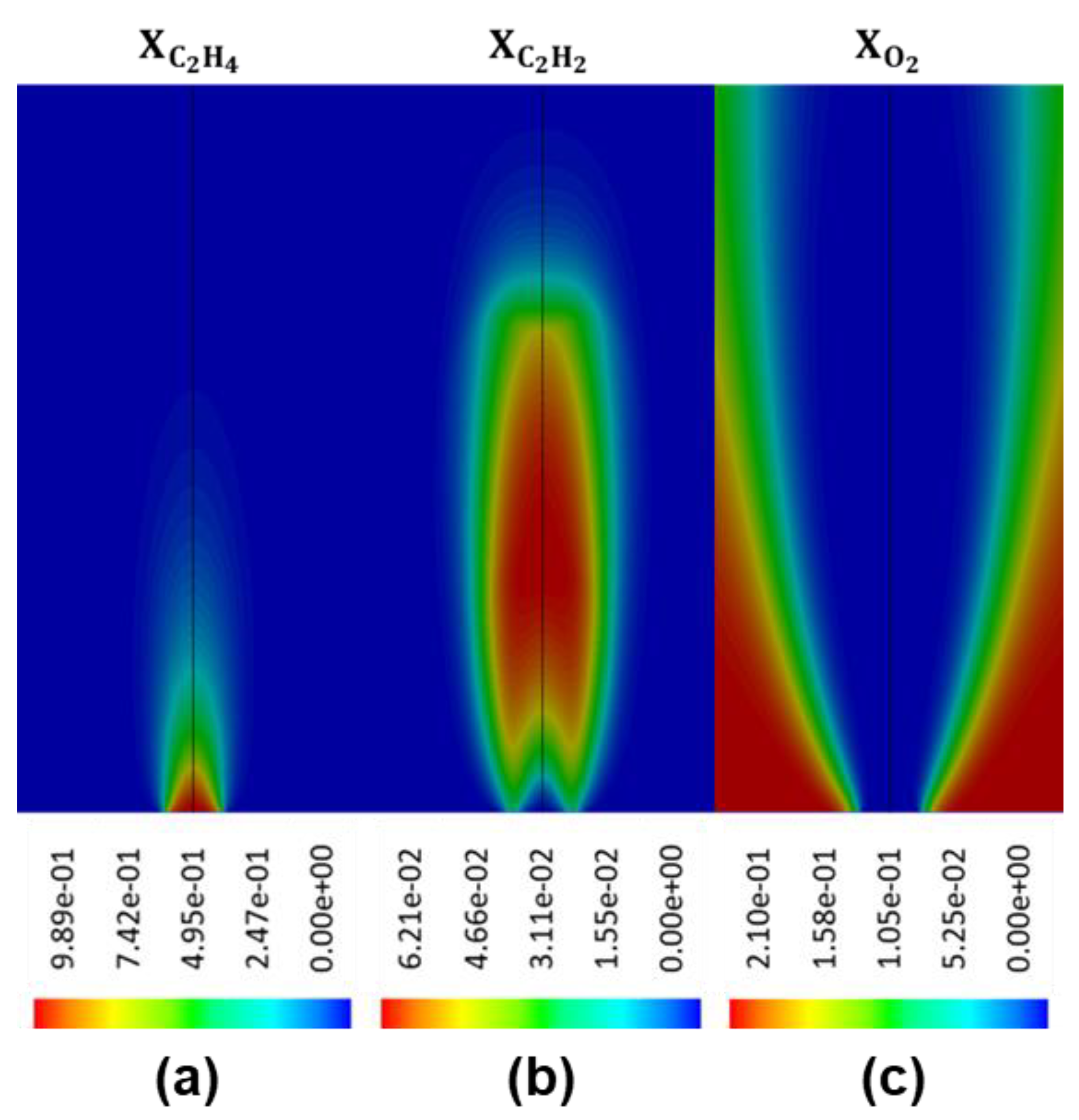
−6 to 180. As can be seen, the key significant combustion products are oxygen, carbon monoxide, carbon dioxide, water vapour, hydrogen, and acetylene, while minor species include hydrocarbon compounds, oxygen, and hydrogen molecules.
2.3. Direct Quadrature Method of Moments (DQMOM) Model
The DQMOM model is written in numerical code and then adapted into the CFD framework. It fully resolves the evolution of the soot particulates in turbulent flames and its size distribution to give a better representation of the soot formation and disruption mechanisms by the DQMOM model. The population balance equation for the Favre-averaged number density
is firstly described, similar to the transport equation for moments, as:
where
is the Favre-averaged number density function (NDF) of the internal coordinate vector
and
is the source terms taken into the consideration of all chemical and physical mechanisms that are involved in soot evolution.
The main idea behind this methodology is to resolve the closure by introducing a quadrature approximation to evaluate the development of the moments of NDF. For a length-based system with mono-variable
, the NDF can be expressed as:
where
and
are the weight and abscissas of node
of the quadrature approximation,
is the number of node points defined in the distribution of the internal coordinate, and
indicates the Dirac delta function. Various soot-related properties can be subsequently derived from the
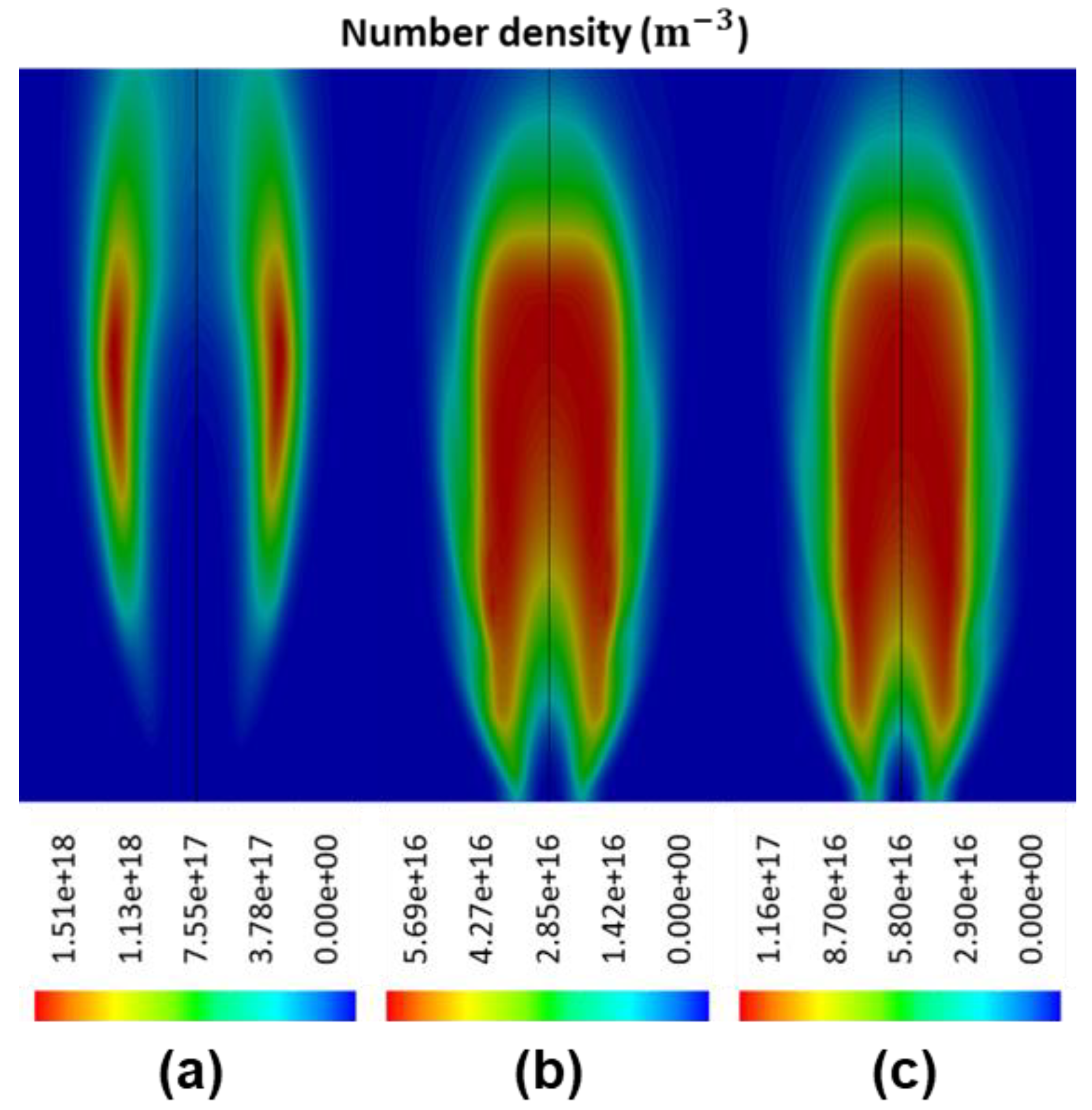
th moment of NDF. For example, with a length-based NDF, the particle number density, mean particle size, and volume fraction corresponding to the zeroth (
), first (
), and third moment (
), and can be resolved as:
Meanwhile, the weight and abscissas are solved through the DQMOM transport equations:
where
is defined as the
th weighted abscissa, and
and
are the source terms for weight and weighted abscissa, respectively. For a numerical system with
, the source terms of
and
can be determined via solving the following rank four linear system of the first four moments:
where
is a correction term of diffusion in real space expressed as:
and
is the integrated source term of the
th moments as:
In this particular soot modelling application, the integrated source term is evaluated as a summation of several contributions that account for critical physical and chemical mechanisms that are involved in soot evolution, e.g., nucleation, coagulation, surface growth, and oxidation. Each contribution can be expressed as a function of weight, weighted abscissas and the reaction rate of the mechanism. The formulation of the individual terms in the integrated source term is further described in detail in the following section.
2.4. Soot Formation Kinetics
In practical soot modelling, the following mechanisms are often defined as the key sooting process that is involved in the soot formation pathway, namely nucleation, aggregation, surface growth, and oxidation. Therefore, those mechanisms are considered in the formulation of the integrated source term, .
2.4.1. Nucleation
The in-flame soot formation commences with the inception process that solid-phase soot nuclei formed from the basic structural units (BSUs) consist of fuel fragments as a result of pyrolysis of the parent fuel [
34]. The nucleation is, so far, the most complicated and least-understood process in soot formation. A generally accepted description of the phenomena is that the BSUs would polymerise and grow in size to formulate liquid-like polycyclic aromatic hydrocarbons (PAHs) precursor species with no internal structure, and subsequently transformed into solid-phase soot nuclei [
2,
35,
36,
37,
38,
39], under certain flaming condition.
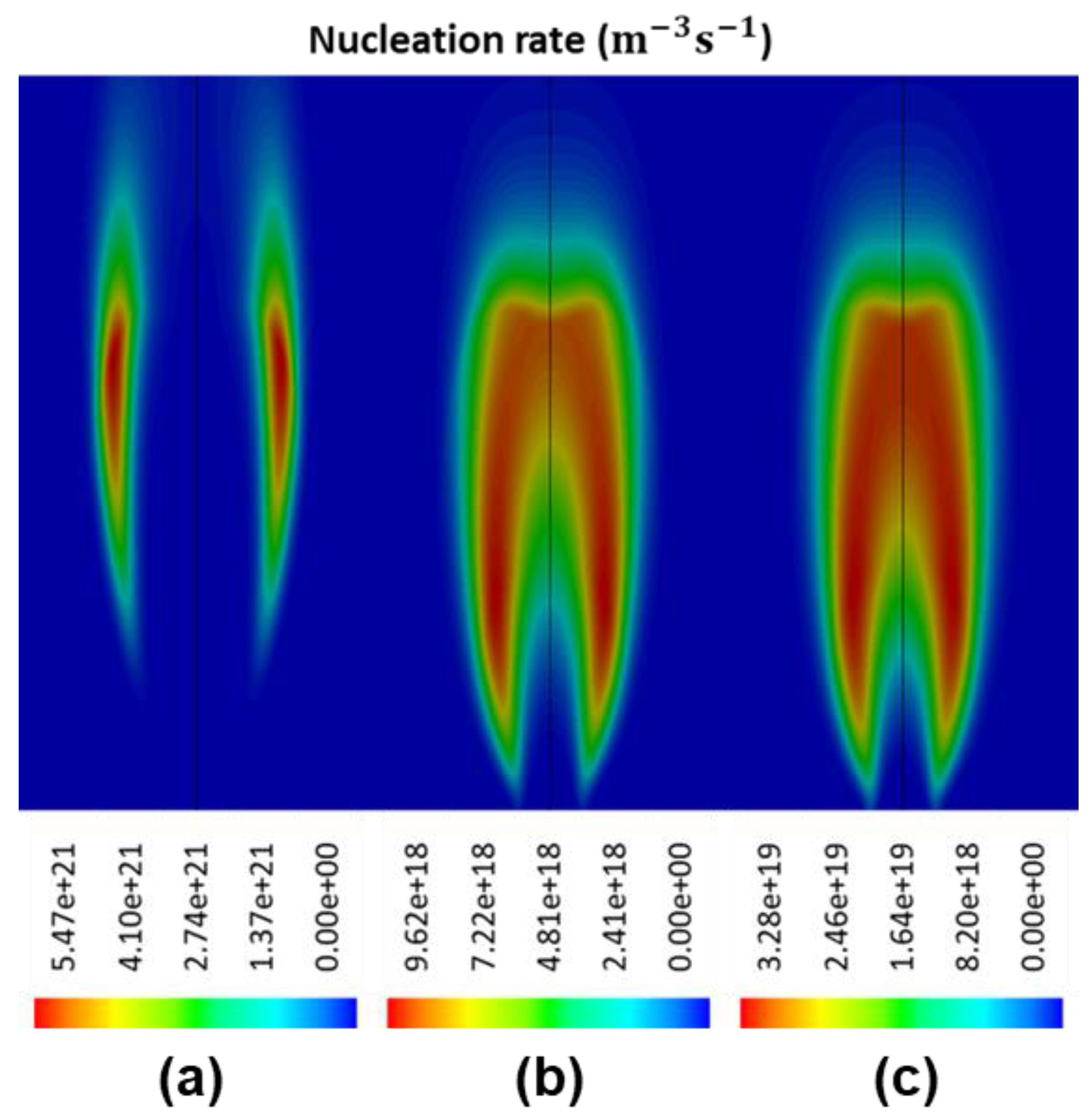
Numerically, the rate of nucleation is often expressed as a function of the concentration of acetylene, the main BSUs of hydrocarbon flame [
40]. The following nucleation kinetics, while employing Moss [
20], Leung [
40], and Fairweather [
27] approach to yield the reaction rates, refer to Equations (15)–(17), respectively, are considered in this study:
where
and
are local mixture density and the soot density (
),
is the Avogadro number,
is the gas constant,
is the local temperature of the mixture, and
and
are mole concentration and mole fraction of acetylene, respectively. The
term is defined as the minimum number of carbon atoms in the soot nucleus, which is proportional to the pre-defined nucleus size. As suggested in the literature, the value of
is defined as 700 in the Leung approach representing soot nucleus with size of about 2.4 nm, and
in the Fairweather approach corresponding to soot nucleus with size of about 18 nm [
27,
40].
The source term of
th moments due to particle inception can subsequently be evaluated as:
where
is the size of nuclei that is set based on the definition of
value.
2.4.2. Aggregation
As nascent soot particulates proceed to flow downstream, they evolve to form larger soot cluster with fractal structure, due to particle-particle collision that has insufficient time to complete particle merging (i.e., coalescence), and such a mechanism is referred to as aggregation [
1]. The rate of aggregation or collision efficiency of two soot particulates with collision radius R
c1 and R
c2 can be expressed with a single expression that interpolates the coagulation process between free molecular, continuum, as well as the transition regimes, as [
41]:
where
With
the Boltzmann constant,
the Knudsen number defined as the ratio between the molecular mean free path of gas mixture molecules and mean particle radius,
the soot particle mass, and
the collision radius. It is worth noting that, rather than adopting the diameter of soot particles, the collision radius
is a characteristic value that resembles the radius of gyration, and it is used to represent the characteristic dimension used to determine collision efficiency. The collision radius
is evaluated based on [
26]:
where
and
are diameter and volume of a representative soot primary particle,
is the volume of the soot aggregate, and
is the fractal dimension, a morphological property that describes the compactness of a fractal object such as soot particulates.
The source term of
th moments due to aggregation can subsequently be formulated as:
2.4.3. Molecular Growth
The mass and size of soot particulates can be increased via chemical and physical surface reactions and processes, for example, the hydrogen abstraction carbon addition based surface growth reaction and the condensation of precursor species onto the particle surfaces. Additionally, they could be decreased as the soot is consumed by the oxidation reactions with
molecules and
radicals attacking soot clusters as they enter the soot-oxidation zone [
2].
In practical soot modelling, as an alternative to the abovementioned complex surface reactions, a simplified reaction model, based on the use of BSUs, i.e., acetylene, to link the gas-phase chemistry to the continuous size change [
42], is used to formulate the reaction rate of surface growth
, as:
where
is the collision radius, the subscript “
” indicates the primary particle, thus the collision radius of a monomer will be equivalent to its radius, and
is the soot molecular weight (12 g·mol
−1). It should be noted that the term
is referred to as the soot surface area coefficient that is dependent on the size, as well as the fractal property of the soot aggregates [
26,
40].
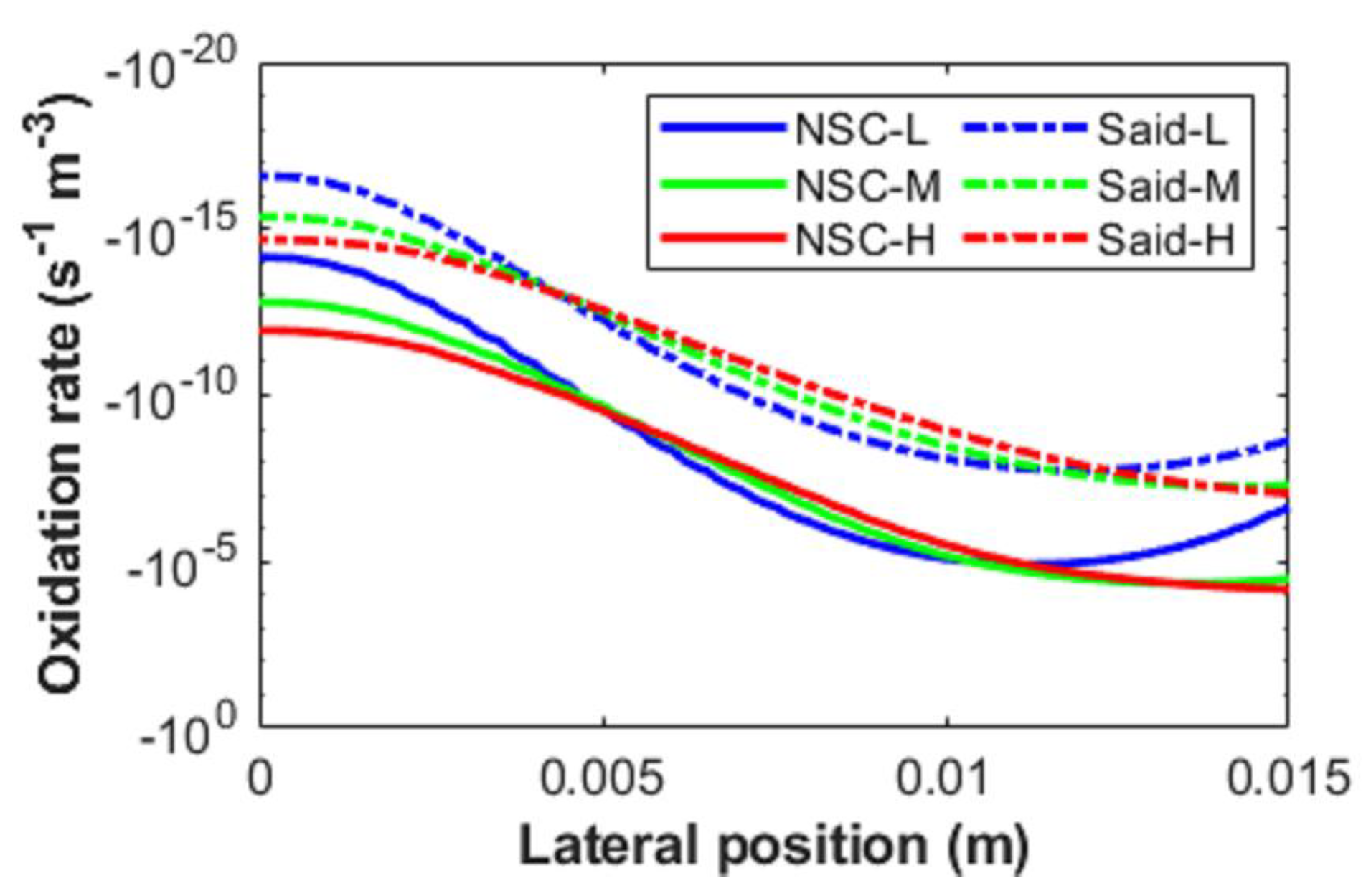
The oxidation process could also be simulated based on the concentration of reacting species and ambient conditions. Two oxidation approaches that have been widely accepted in a commercial package and research code, namely the Said approach [
43] and modified NSC approach [
20,
27], have been investigated in this work. The reaction rate determined based on the two approaches can be expressed as:
and
where
and
are the mass and mole fraction of oxygen and
and
are rate constants adopted from semi-empirical investigation [
20,
40]. Herein, a temperature dependent correction factor
, introduced by Liu et al., which tuned to best match the experimental observation of soot formation in smoking flame [
40,
44,
45], is defined as:
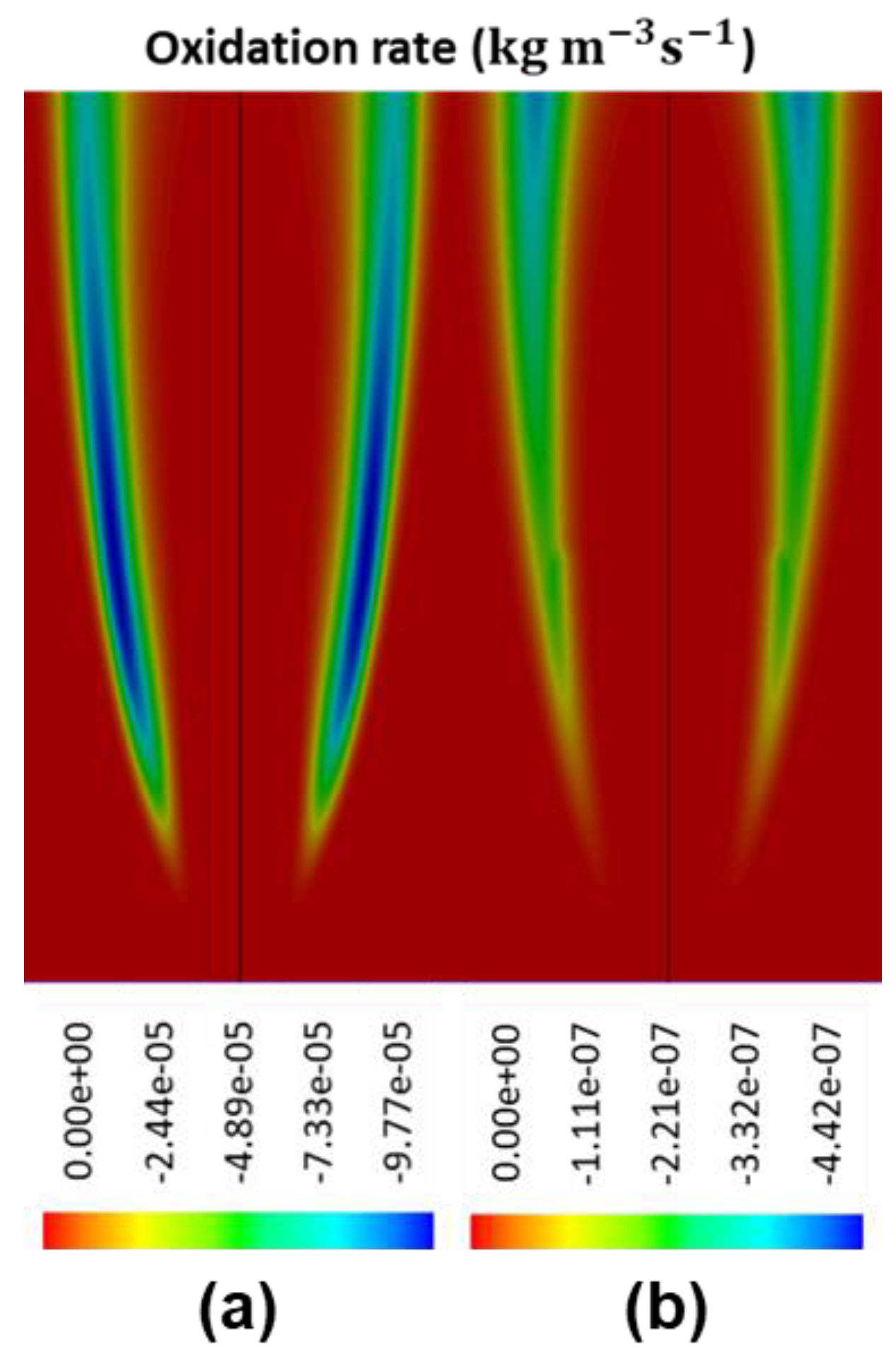
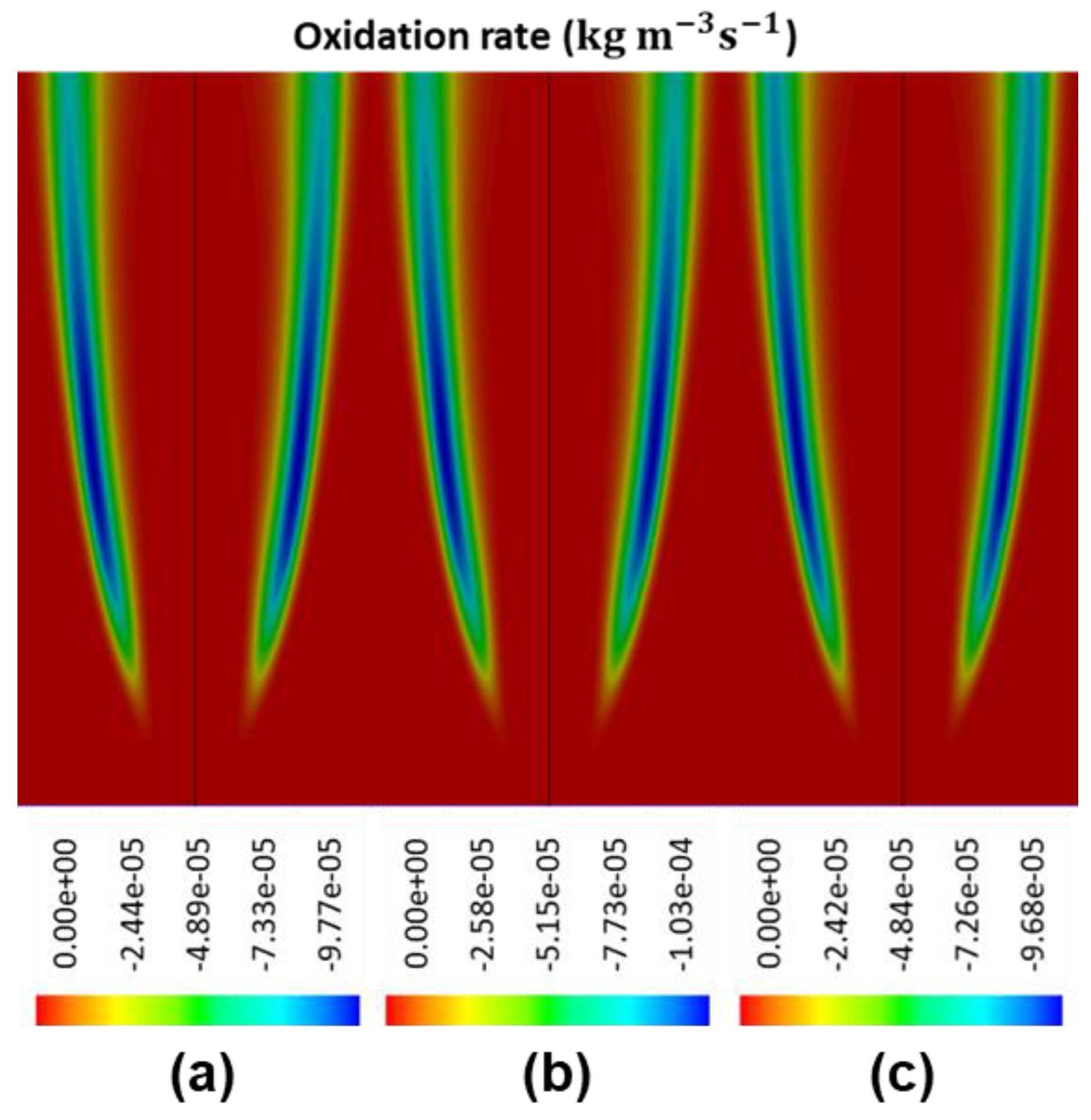
It should be noted that Liu’s correction factor becomes negligible as the local temperature is below and it approaches unity when the temperature increases to . Therefore, the correction factor also serves as a cut-off function that limits the oxidation reaction to regions with relatively high temperature.
The source terms of
th moments, due to the combined effects of surface growth and oxidation, applying the quadrature approximation, are:
2.5. Numerical and Case Configurations
The geometry of the model that is used in the current study replicates a laboratory scaled co-flow diffusion flame generated from an in-house built co-flow slot burner with a centre slot for fuel injection and two side slots for oxidiser supply. Both ethylene and air are injected at
, normal to the burner front through the fuel and oxidiser slots, respectively, and the combustion occurs at atmospheric pressure. It should be noted that, the injection rate of fuel applied in this work is significantly lower than the
that is used in other numerical studies adopting the DQMOM algorithm [
25,
26,
28]. A computational domain symmetrical with respect to burner centreline, with dimensions of
and
, is defined and applied with a non-uniform mesh of about
elements. Higher mesh resolution is applied at regions near the axis and close to burner front where both the flow development and intense chemical reaction are expected to take place. The dimension of the domain is set based on the observation of flame shape and the mesh configuration has been verified to ensure that the yield simulation result is independent of grid resolution.
One of the potential challenges of the DQMOM approach is that the system could be ill-conditioned when the weight and abscissas of the defined internal coordinate become null, i.e., raised when considering the regions with no soot particles or particulates with infinitely small particle size, which leads to a singular or near-singular condition when solving the linear system (Equations (9)–(12)). This ill-conditioned system could result in either the linear system being unable solve or solved with large numerical error. The issue can be resolved by seeding the domain with particles that have a size distribution that is predefined based upon the PD algorithm that was proposed by Gordon et al. [
46]. For mono-variate case with
, the pre-defined particle size
can be set as
and
and then applied to regions where the weights are null or abscissas are not defined.
The DQMOM coefficient matrix could also become near singular when the values of any pair of abscissas are equal, or getting too close to each other, resulting in numerical instability and yielding significant numerical error. To tackle the issue, a small perturbation was introduced to the abscissas to ensure non-distinct values of
in the DQMOM coefficient matrix, as suggested by Marchisio and Fox [
24].
Soot radiative heat transfer is taken into consideration by introducing an additional source term into the energy transport equation, which is defined as:
where
is the Stefan–Boltzmann constant,
is the ambient reference temperature that is defined as
, and the
is the absorption coefficient expressed as:
where
is the soot volume fraction, as evaluated from the third moment of the NDF.
2.6. Sensitivity Analysis
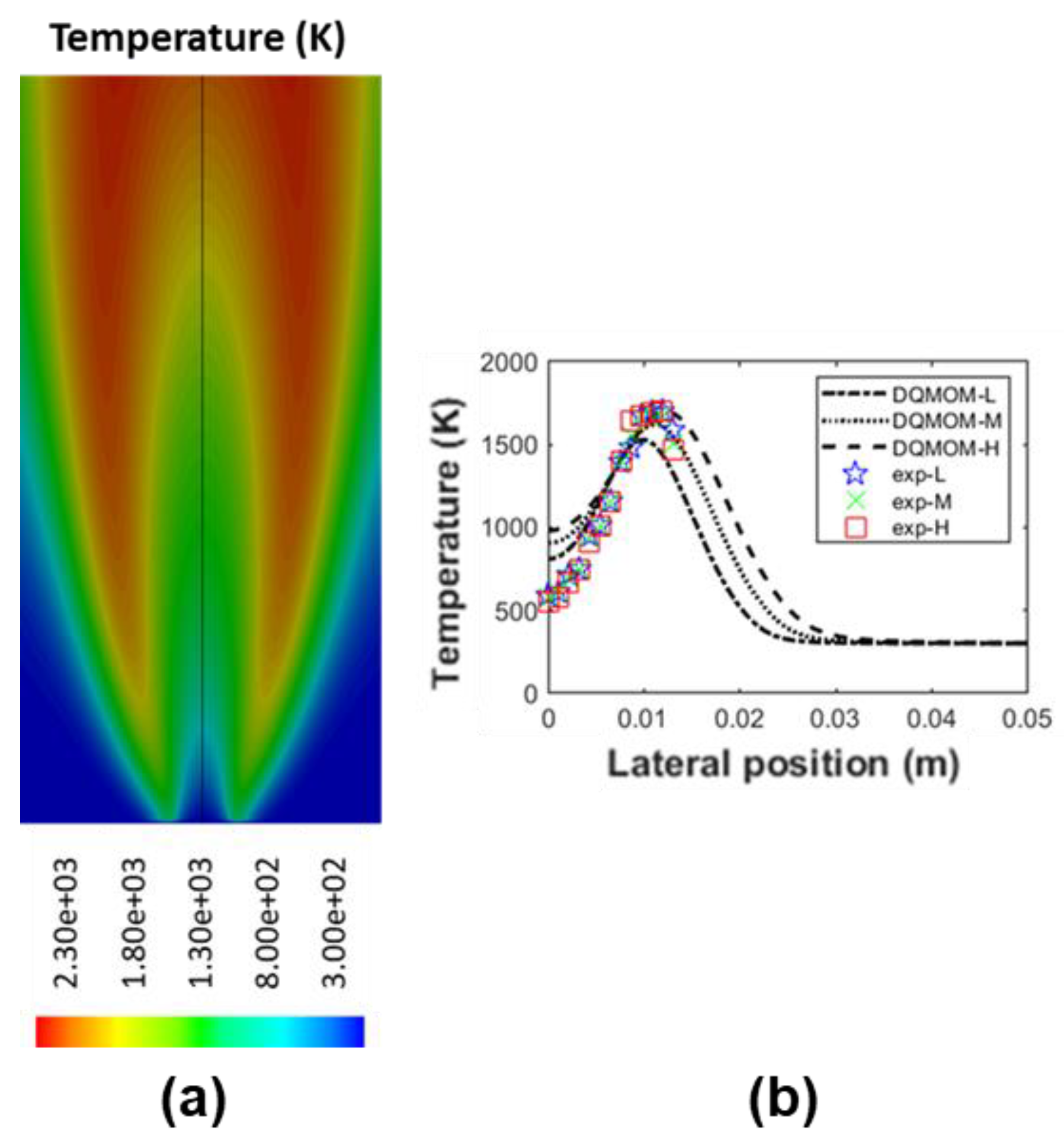
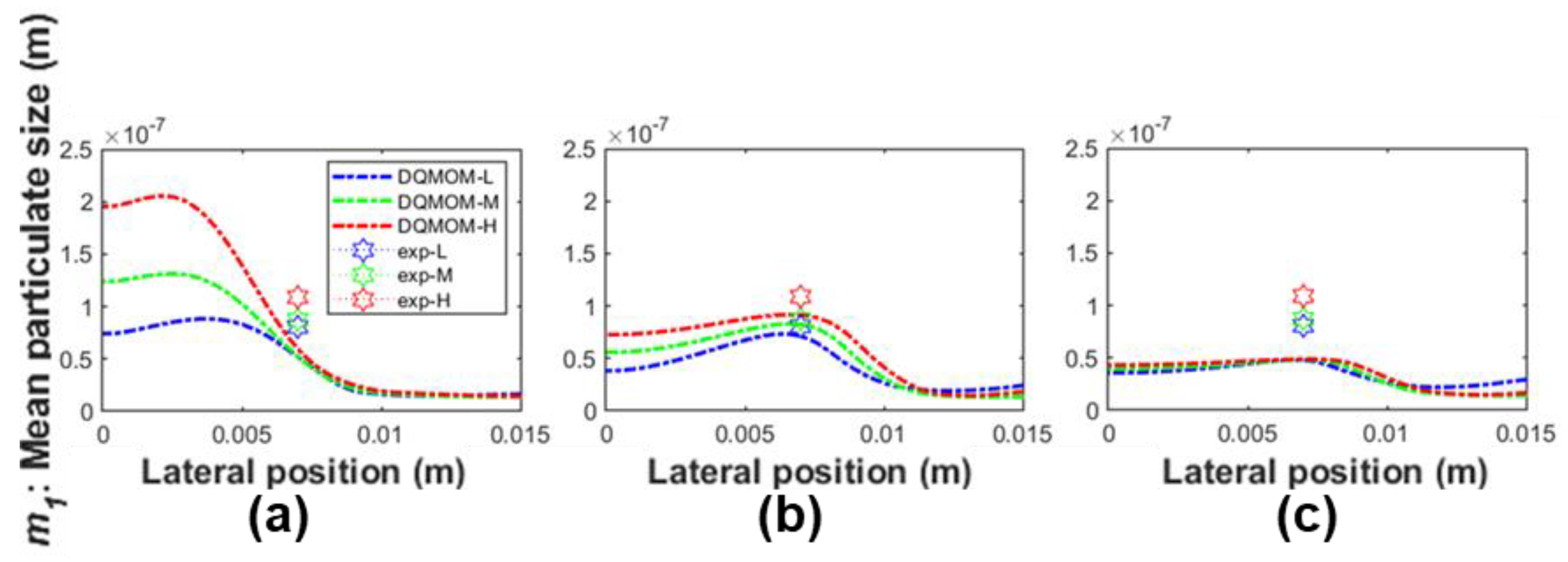
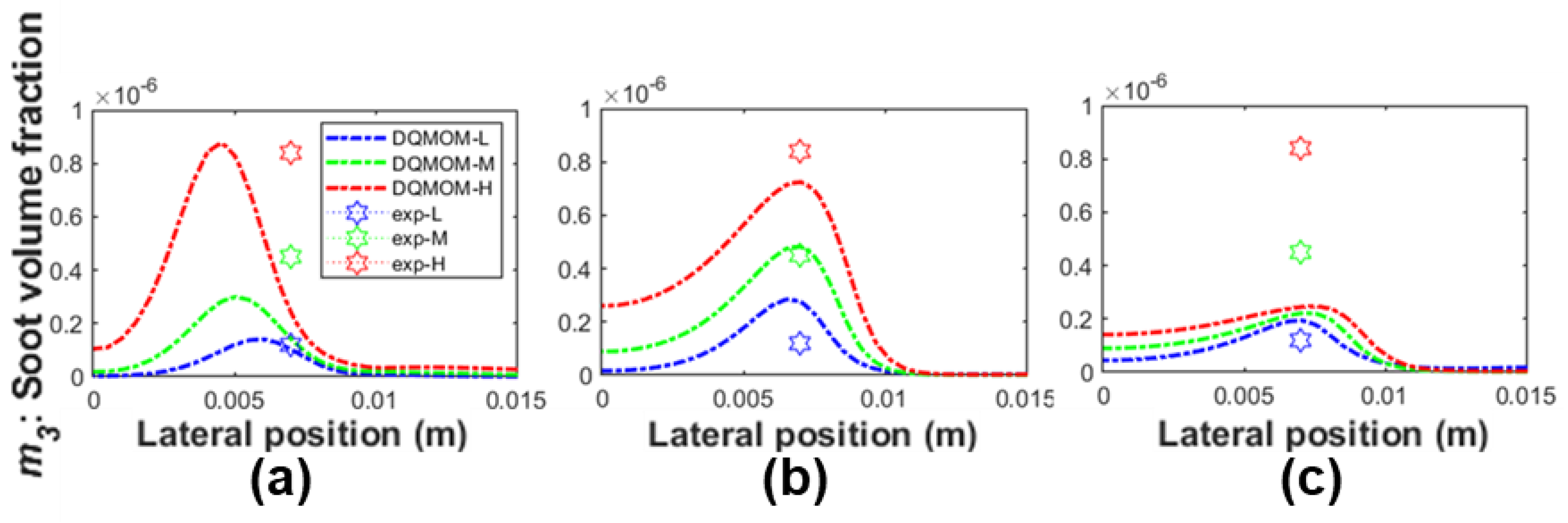
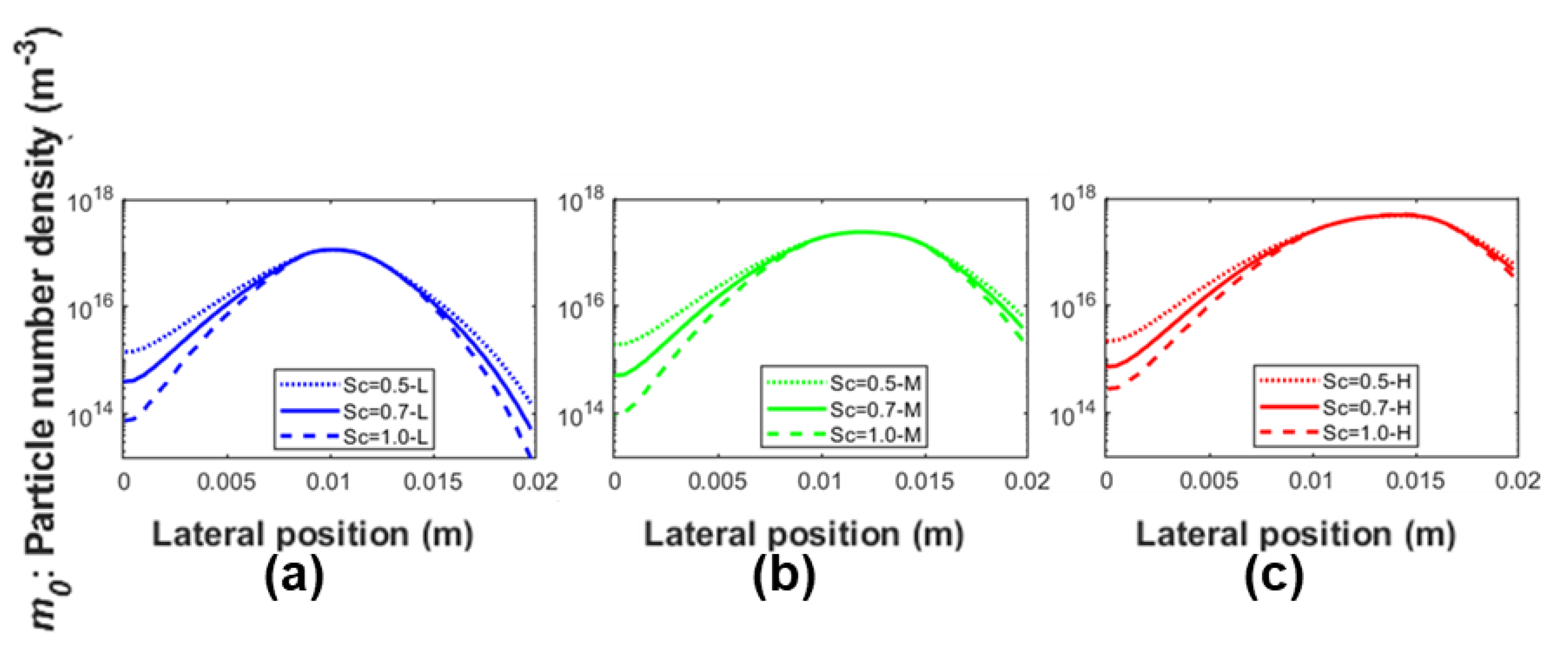
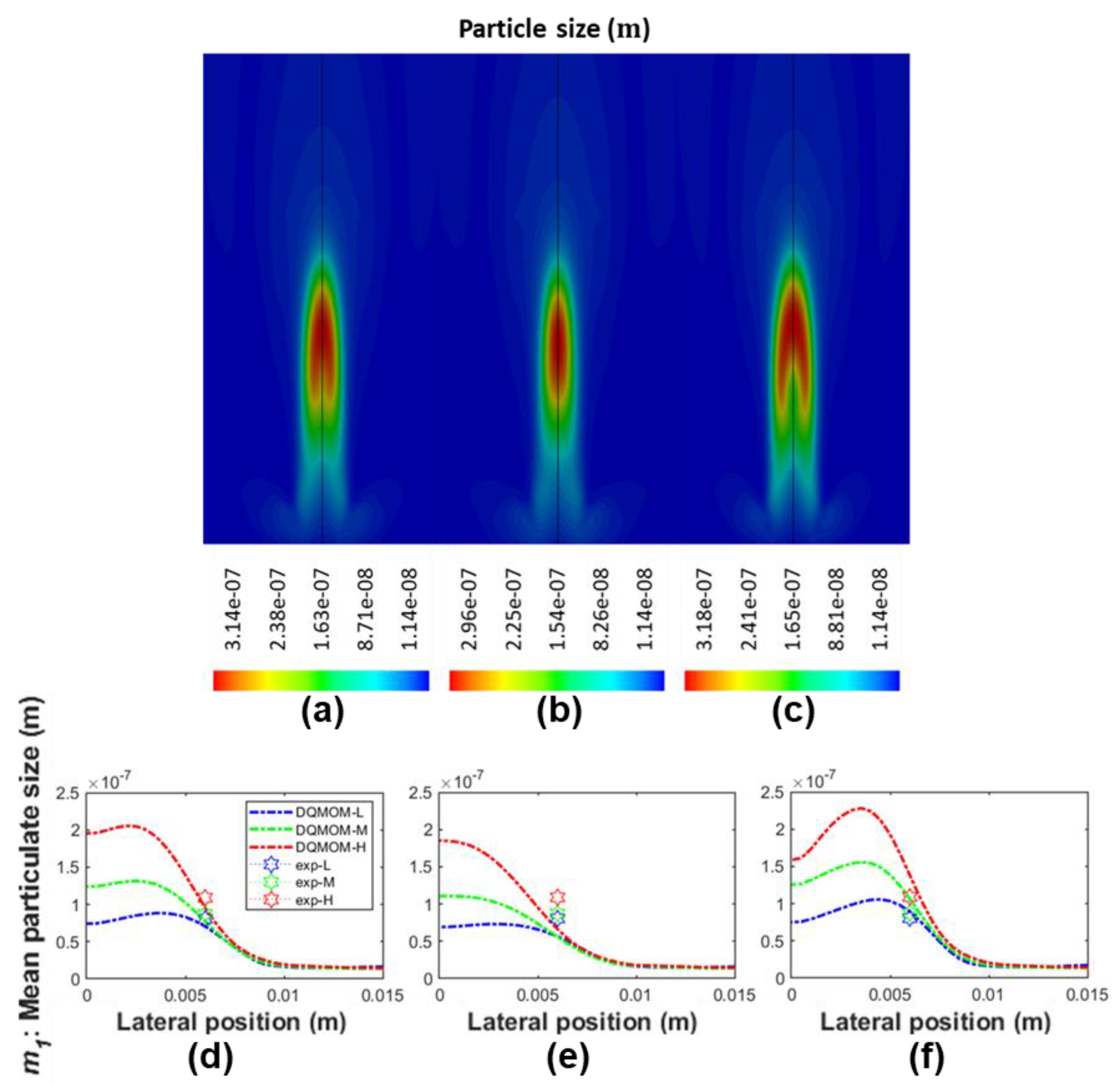
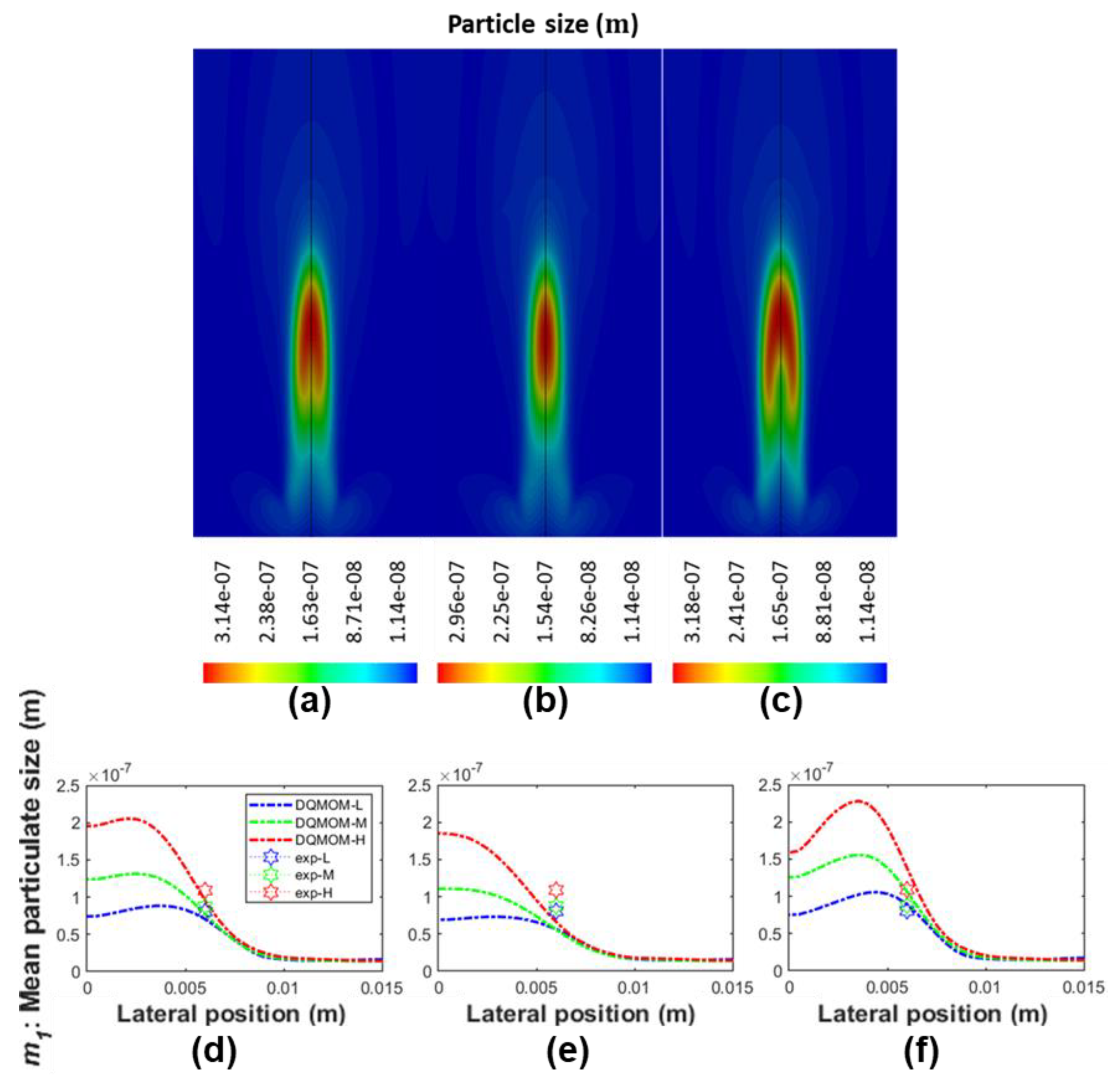
A comprehensive assessment is carried out to investigate the effect of the key components and submodules that are integrated within the framework on both the simulation result as well as the numerical stability of the system. The components and submodules of interest in this work are defined as: nucleation law, oxidation law, value of fractal dimension, and diffusivity. Nucleation and oxidation are fundamental soot mechanisms through the soot evolution. Fractal dimension is directly correlated to the evaluation of rate of soot mechanisms involving surface reactions. Diffusivity governs the spatial transportation and distribution of the soot species.
A summary of all simulation cases under investigation is tabulated in
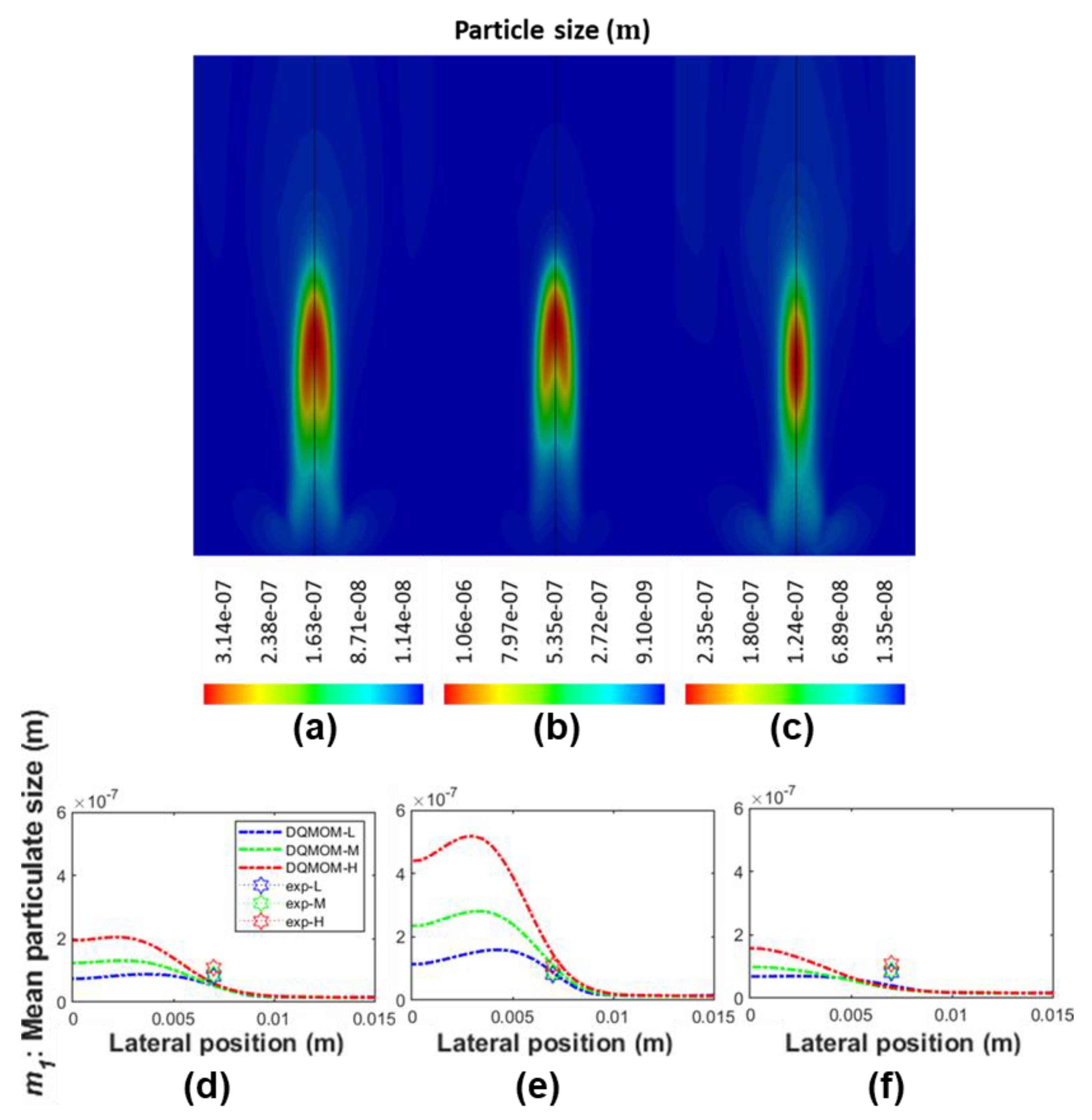
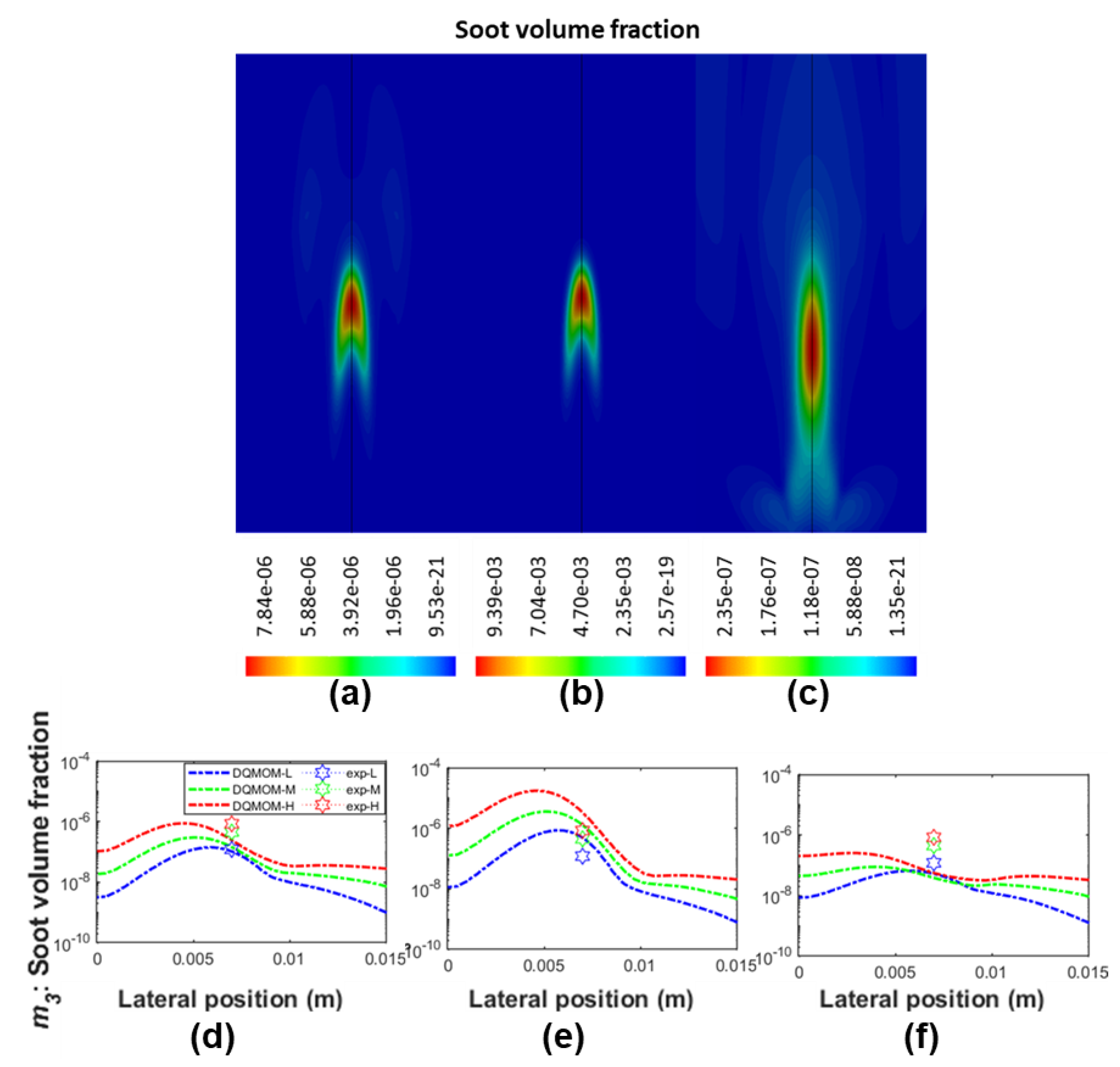
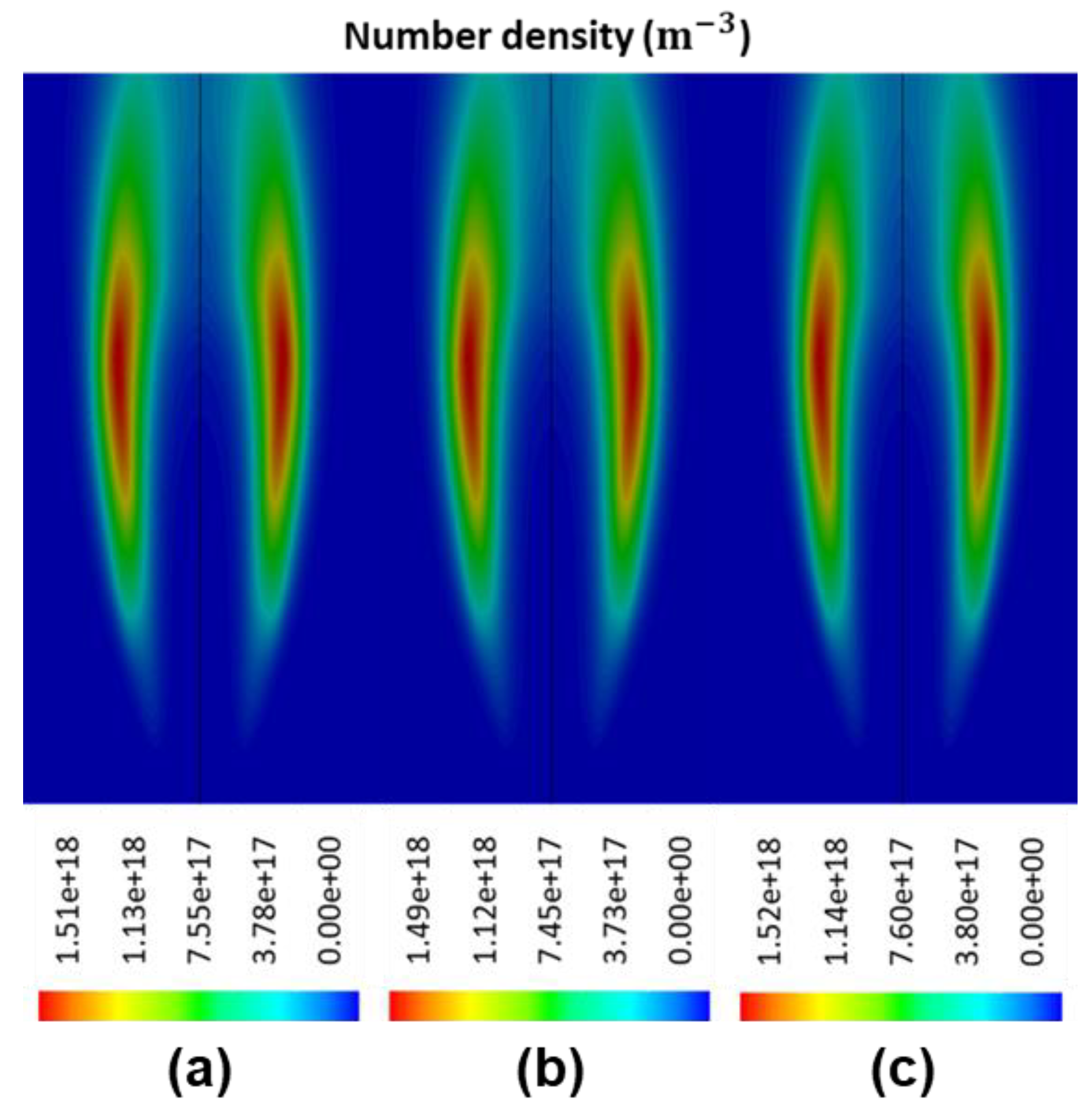
Table 1. Please note that, the simulation result generated from the baseline case (Case A) is compared with that evaluated from other cases (Case B to Case H), which have only one change in the modelling aspect made based on Case A, as well as the experimental data obtained from an in-house measurement. As mentioned earlier, the experiment measures the flame temperature and examines the soot particles using thermophoresis soot sampling and TEM imaging, at three selective height above burner (HAB). The selected HABs represent different typical stages of soot evolution within the flame, namely soot inception region (
HAB), soot growth region (
HAB), and soot mature region (
HAB), and they are referred to as ‘exp_L’, ‘exp_M’, and ‘exp_H’ in the following sections, respectively. Morphological information of the soot sample, such as size of primary particles, projected area, radius of gyration, and fractal dimension of the agglomerates, as well as soot volume fraction, are subsequently derived via either direct characterisation of the TEM images or an automatic image processing algorithm. Details of the experimental setup and post image processing are provided in our previous work [
47,
48,
49].
4. Conclusions
In this article, a fire field model that is associated with an in-house Direct Quadrature Method of Moments (DQMOM) code was specifically developed for buoyancy-driven low-speed turbulent diffusion flames. The DQMOM model embraced all major mechanisms for soot particle evolution/disruption, including nucleation, surface growth, and oxidation and coagulation. Furthermore, it was fully coupled with detailed chemistry gas-phase combustion model, which allows for predictions of intermediate chemical species to enhance the real-time tracking of the particle size distribution. The proposed model was not only capable of providing additional information for the soot particle distribution in the computational field, but it also yielded other important secondary properties, i.e., particle number density and local volume fraction with good accuracy and effective computational cost.
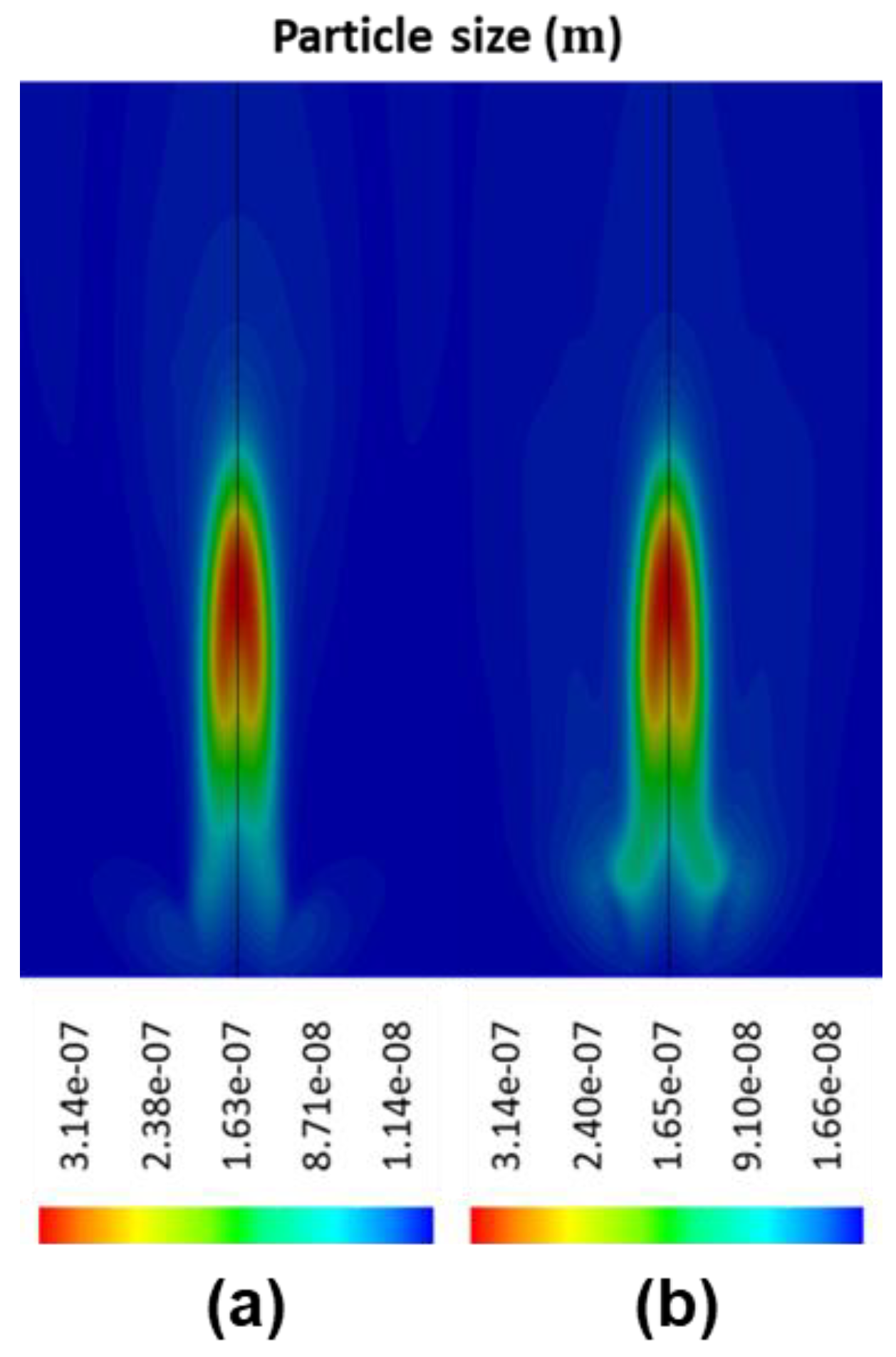
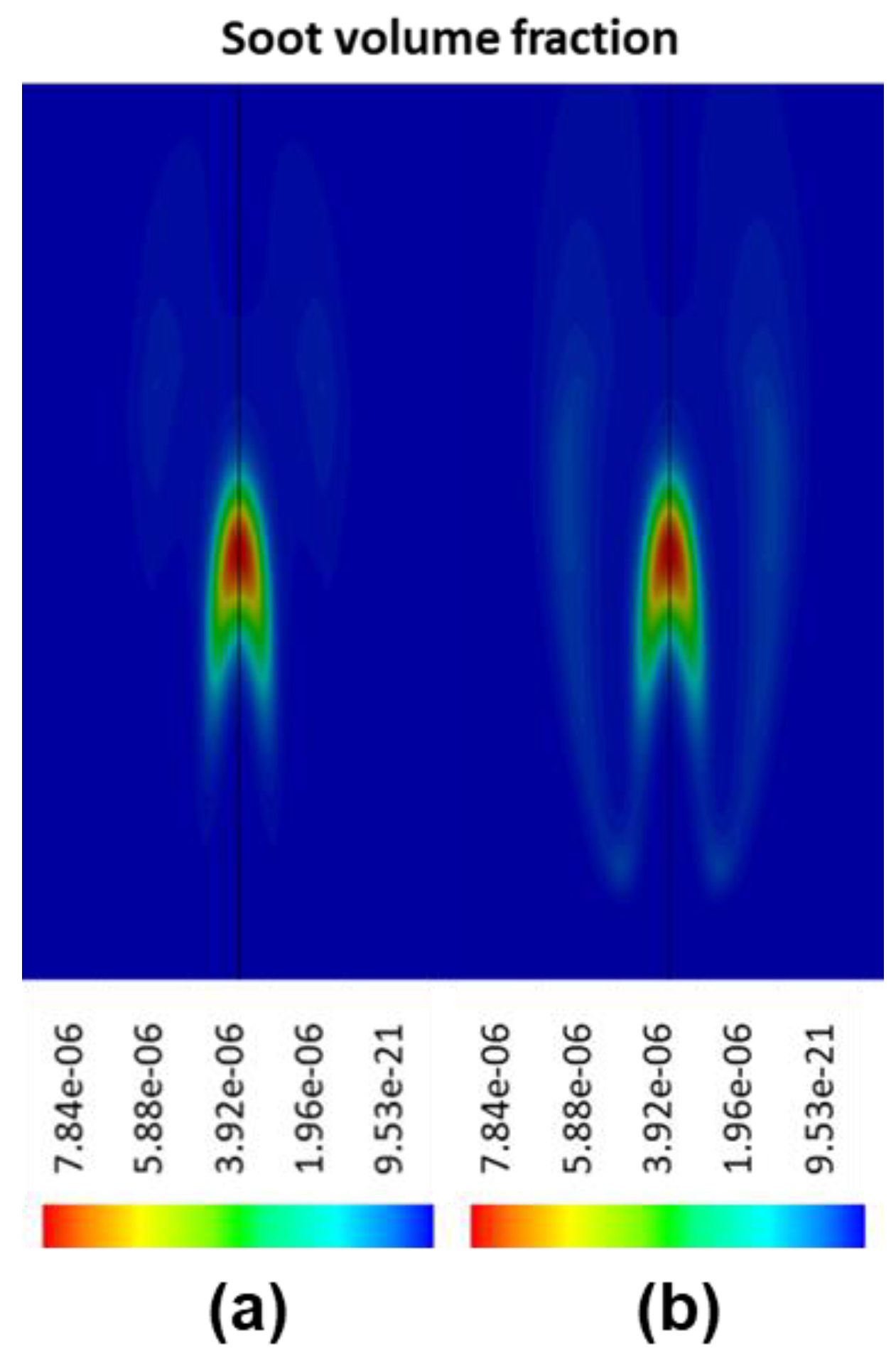
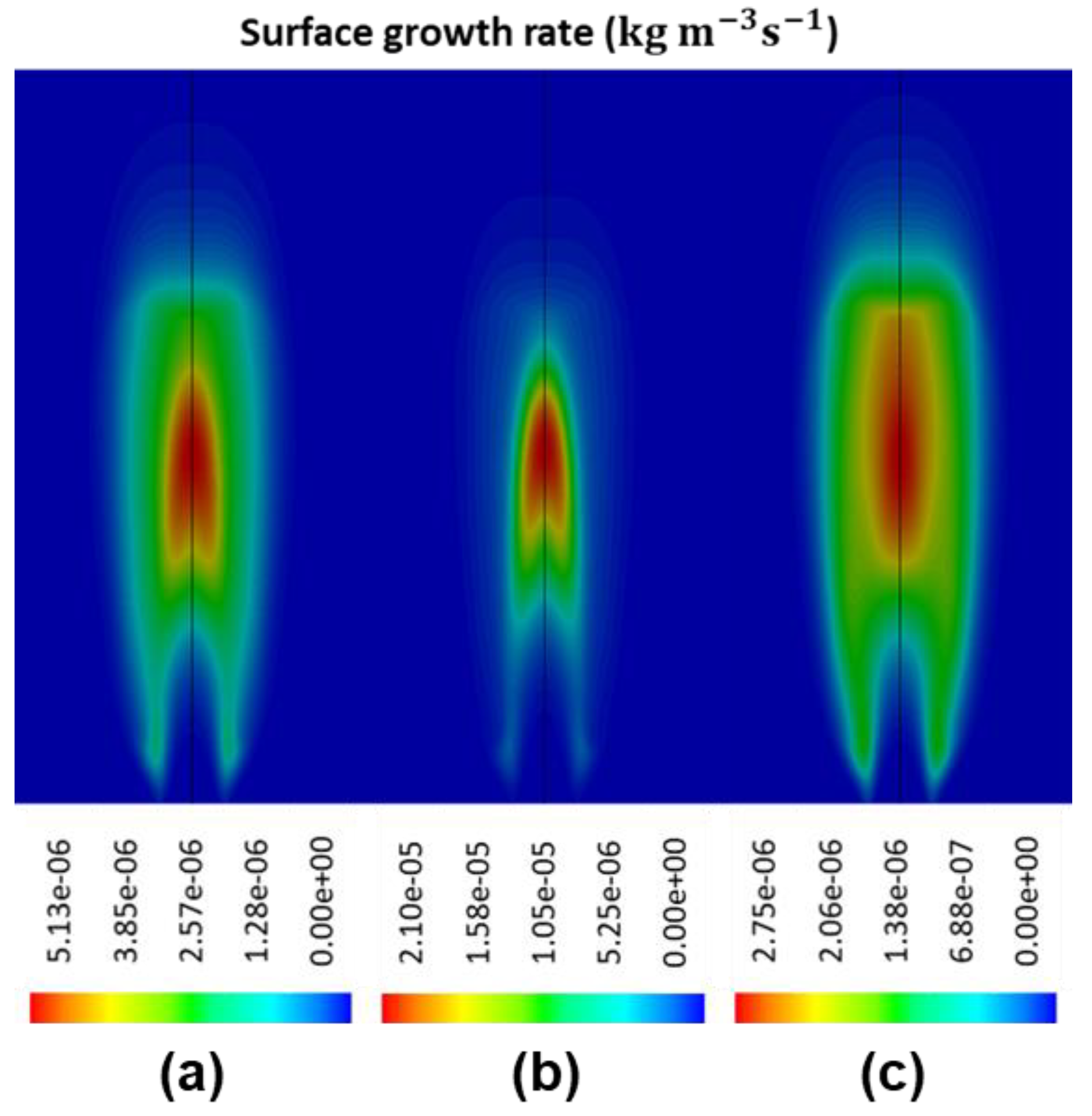
Using the proposed framework, a collection of soot nucleation and oxidation kinetics were numerically investigated and then compared against a self-conducted experiment while using ethylene/air burner with soot diagnostics imaging measurements. When compared with the Leung law and Fairweather law, it was found that the Moss nucleation law provided more accurate prediction of nucleation rate and the subsequent particle number density distribution. The Moss law was capable of limiting the soot inception to high flame temperature region. With regards to oxidation kinetics, the modified NSC law demonstrated better results when compared to the Said law. The modified NSC law constrained the oxidation rate at the surrounding region with the highest concentration of soot particulates, while the Said law under-predicted the oxidation rate at low-intermediate flame heights. In addition, the fractal dimension and Schmidt number were also examined in this study, and it was discovered that the value set of 2.0 and 0.9 yields the best result when compared with the experimental data.
In summary, combining the advantage of the improved DQMOM approach with the detailed chemistry combustion model, the proposed in-house CFD model significantly enhanced the temperature field, intermediate chemical species, and soot yield predictions, as well as providing a more comprehensive physical description of the evolution and disruption processes for soot particles. This enabled a better understanding of the nucleating region for soot particles and it agreed well against the experimental measurements. The high-fidelity prediction of soot particles will be a major advancement that is applicable to the design of fire protection engineering systems, including smoke extraction, curtains, and alarms.