Transient Response Estimation of an Offshore Wind Turbine Support System
Abstract
1. Introduction
2. Materials and Methods
2.1. Preliminaries
2.1.1. Wave Spectrum
2.1.2. Wave Loads
2.1.3. Discrete Fourier Transform
2.1.4. FD Dynamical Analysis Method
2.2. Wind Turbine Loadings
2.2.1. Offshore Wind Turbine Model with Initial Conditions
2.2.2. Calculation of External force in the Frequency Domain without Using DFT
2.2.3. Response Estimation of Support Structures with Nonzero Initial Conditions
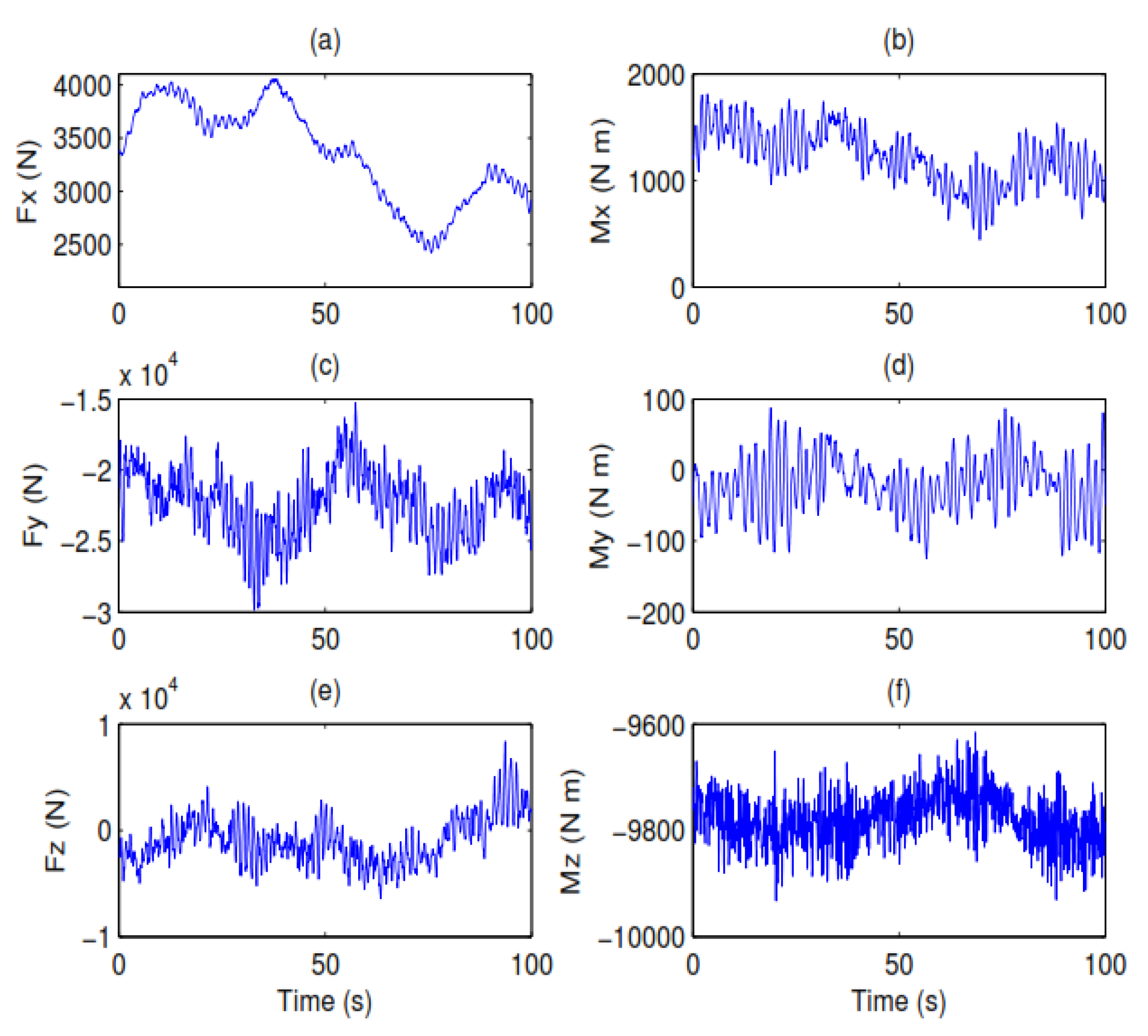
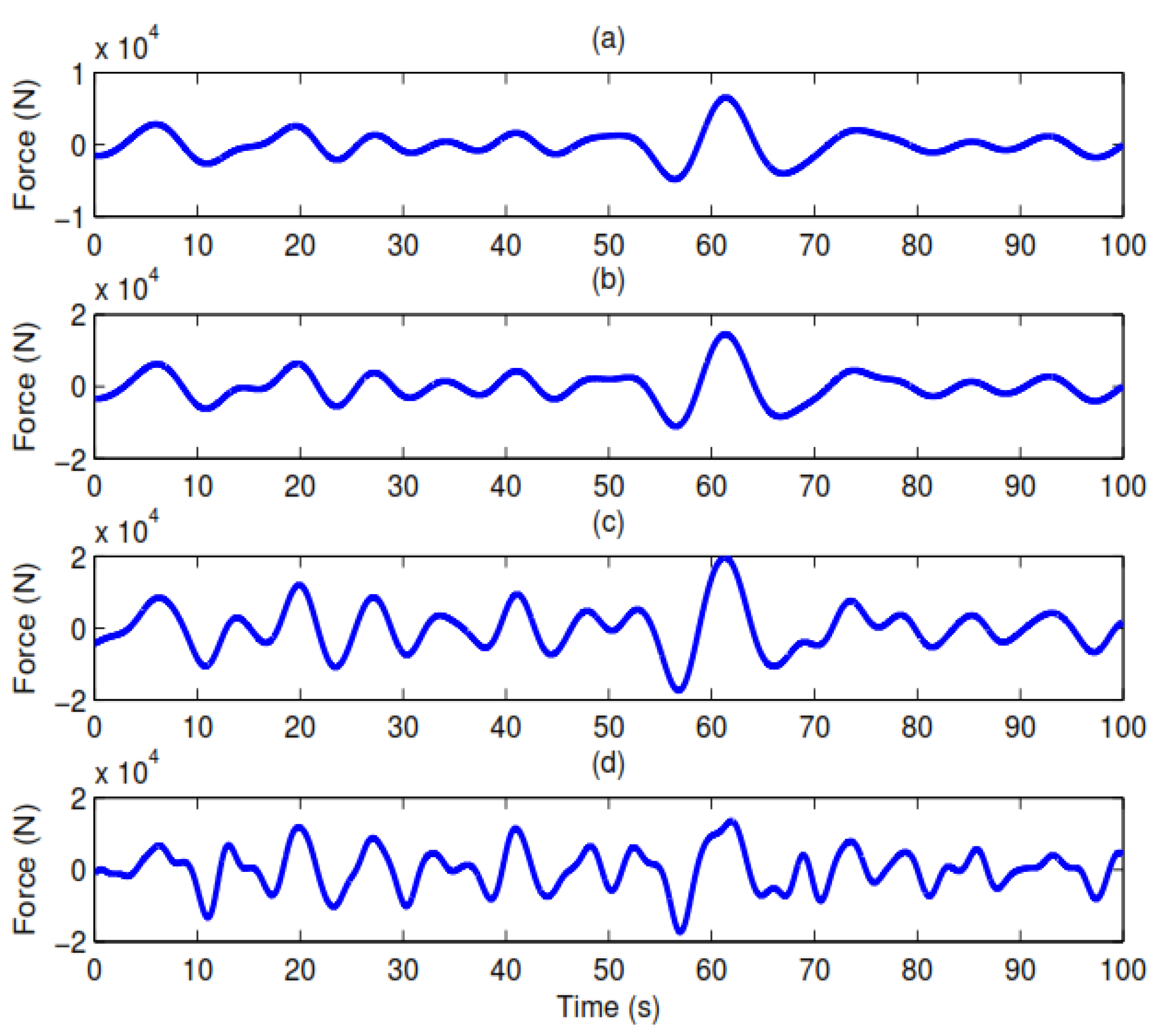
3. Results and Discussion
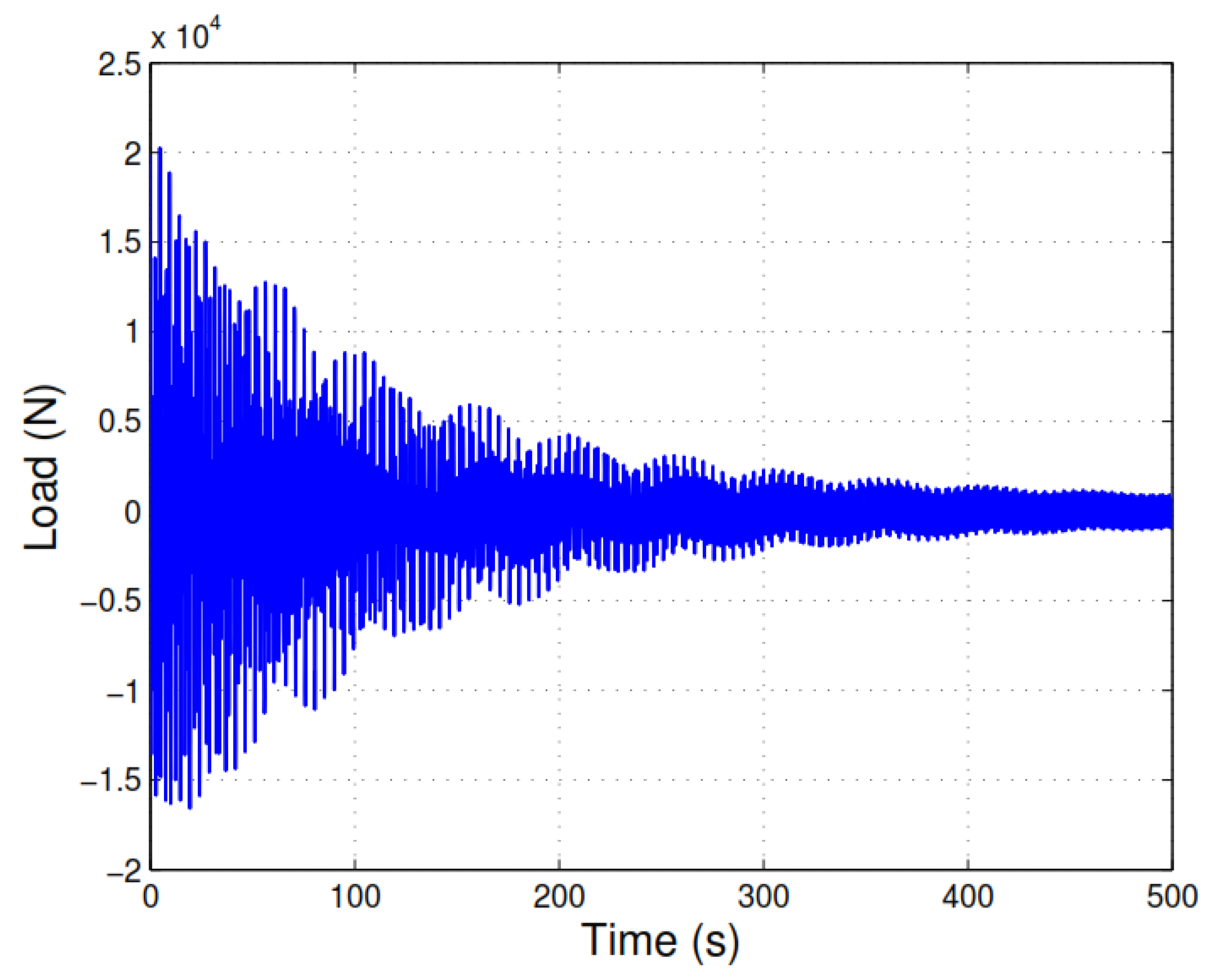
3.1. A Monopile-Supported Wind Turbine with Nonzero Initial Conditions
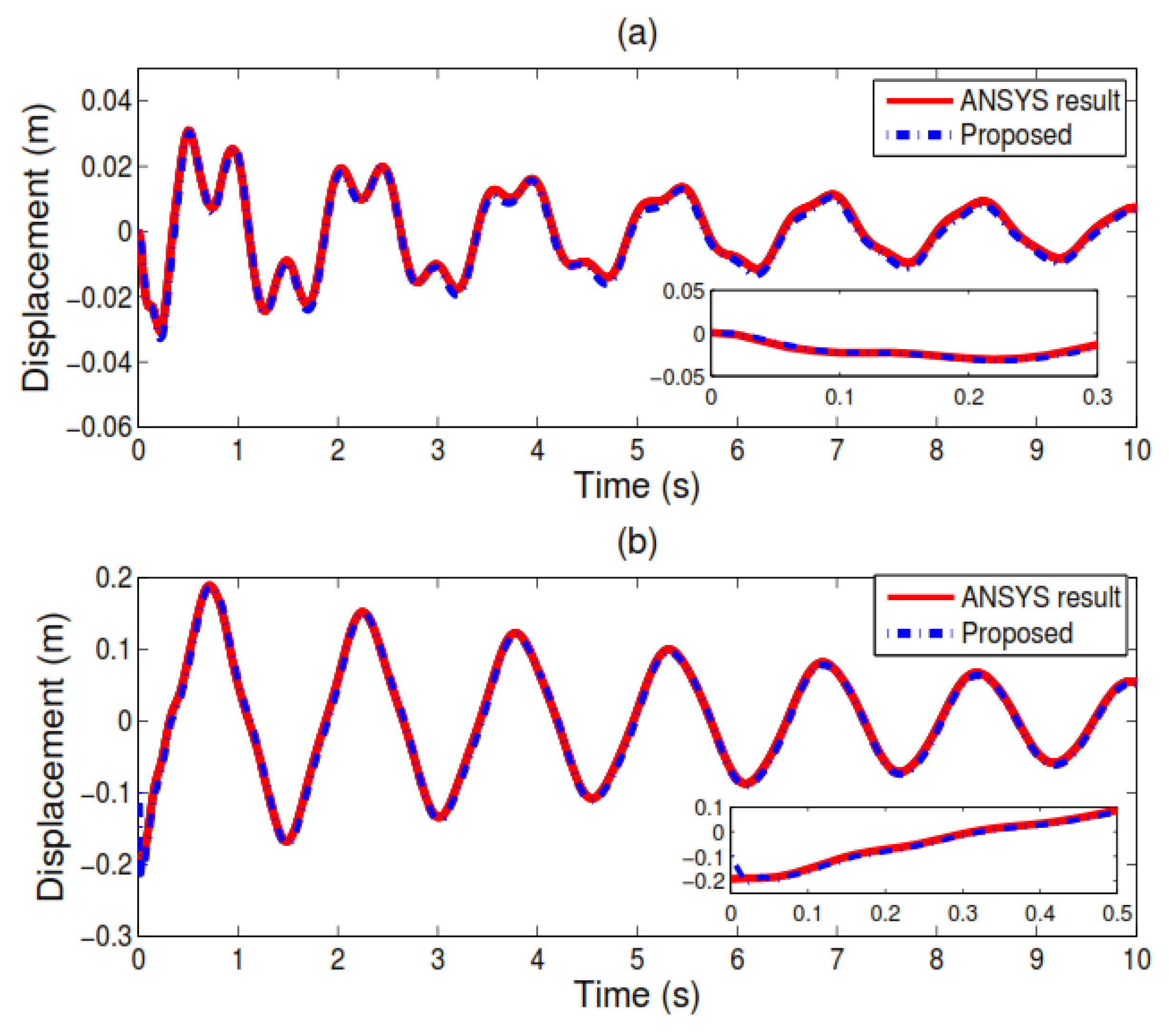
3.1.1. Response Estimation of the Structure with Zero Initial Conditions
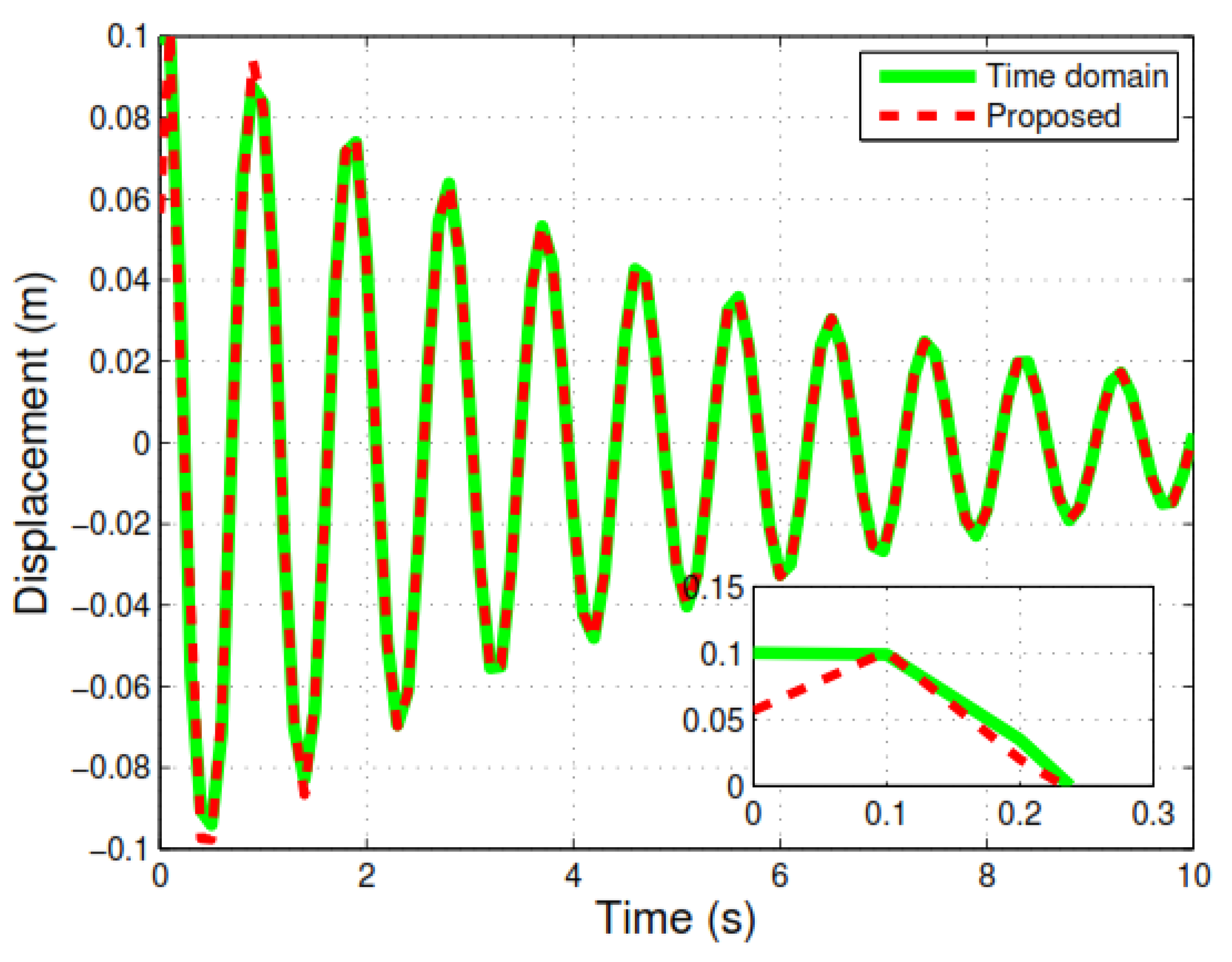
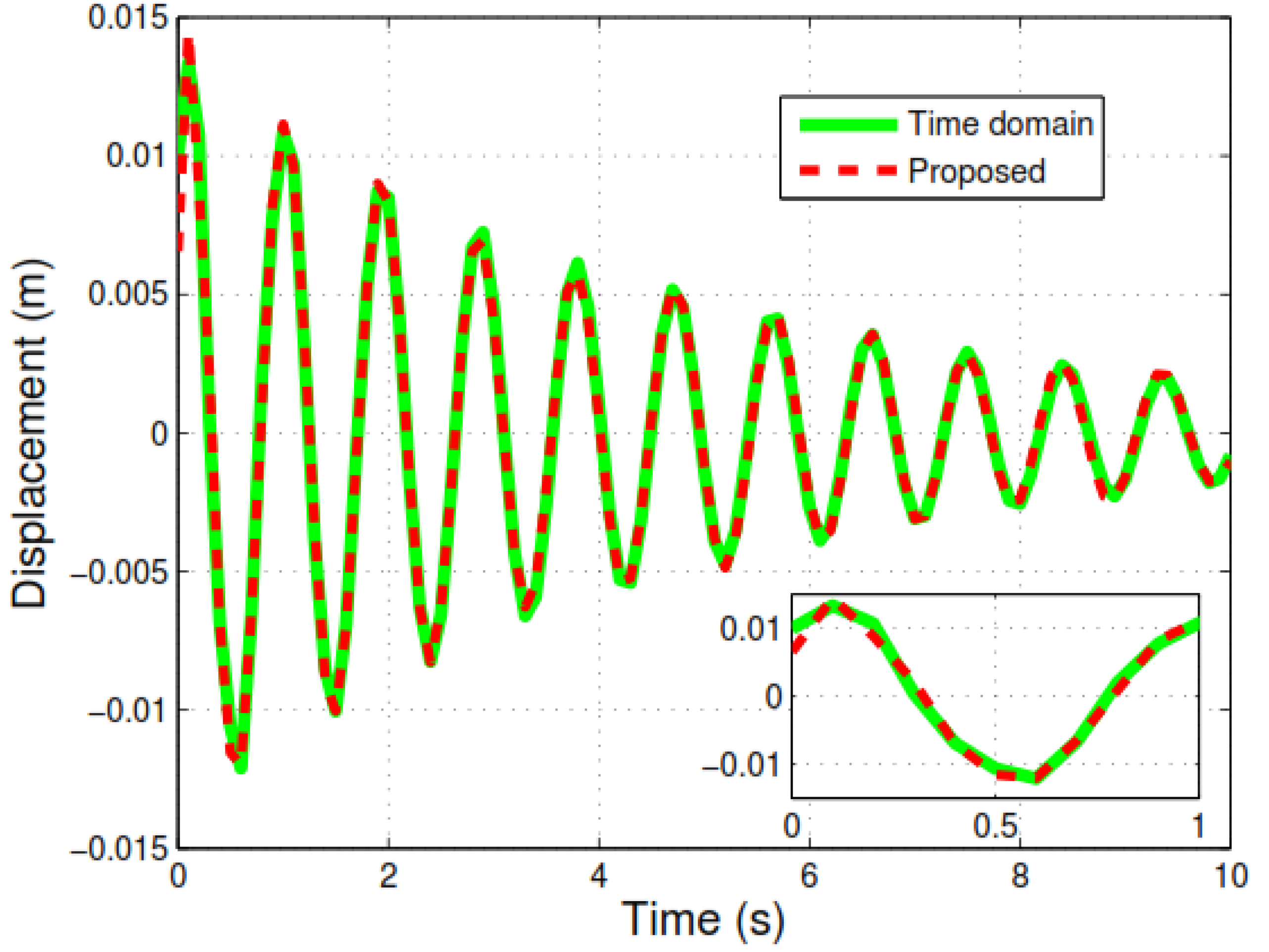
3.1.2. Free Response Estimation of the System
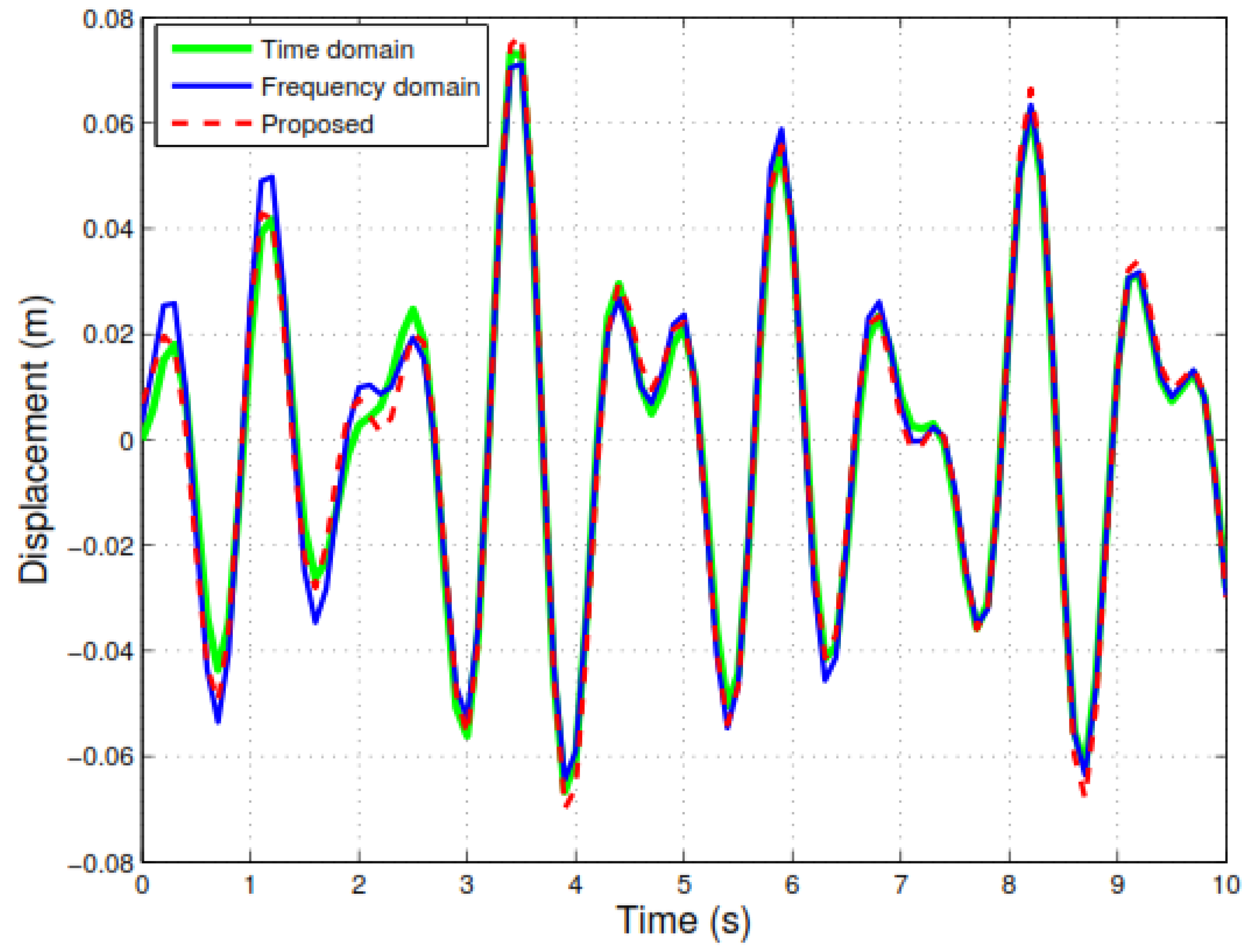
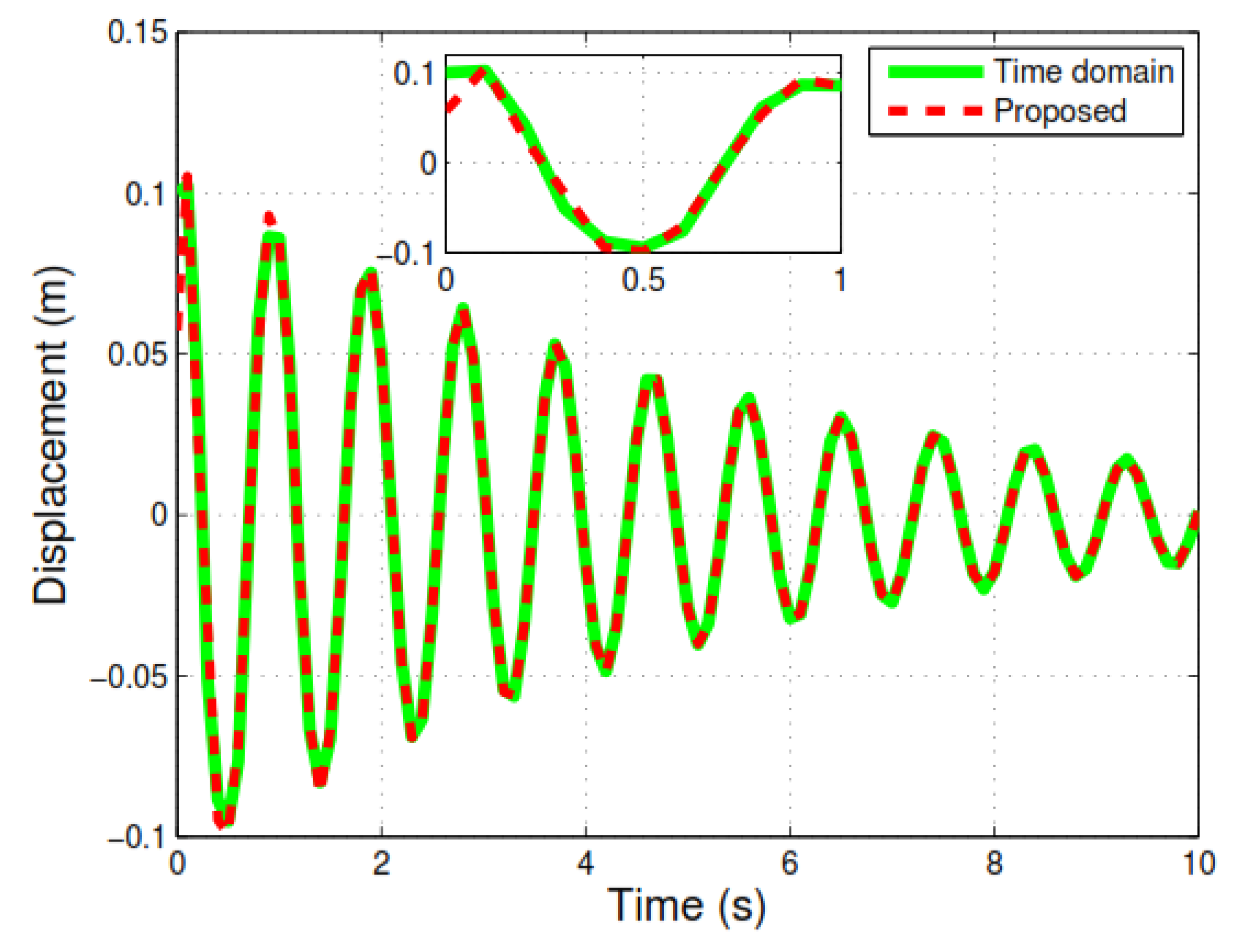
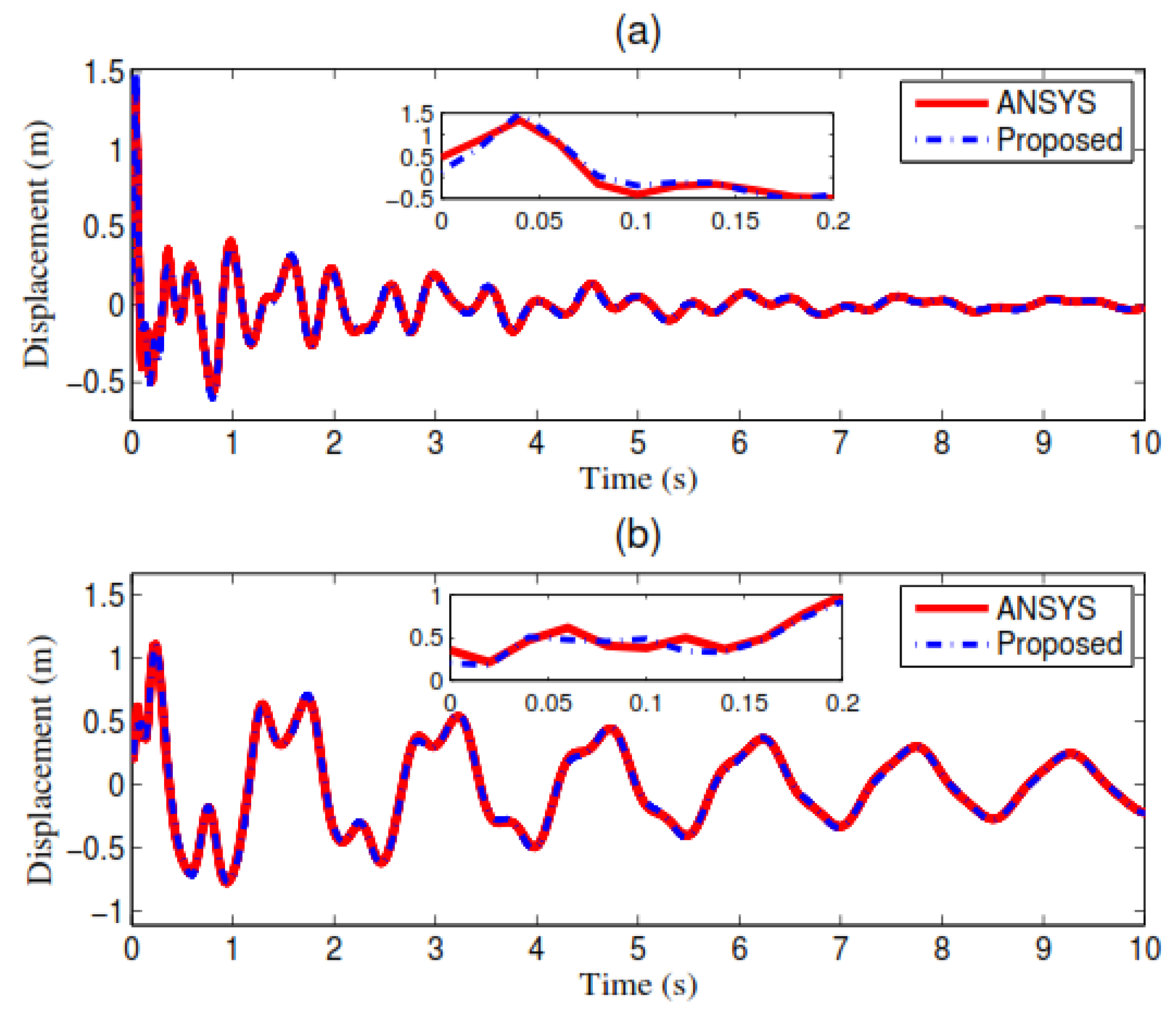
3.1.3. Response Estimation of the Structure with Nonzero Initial Conditions
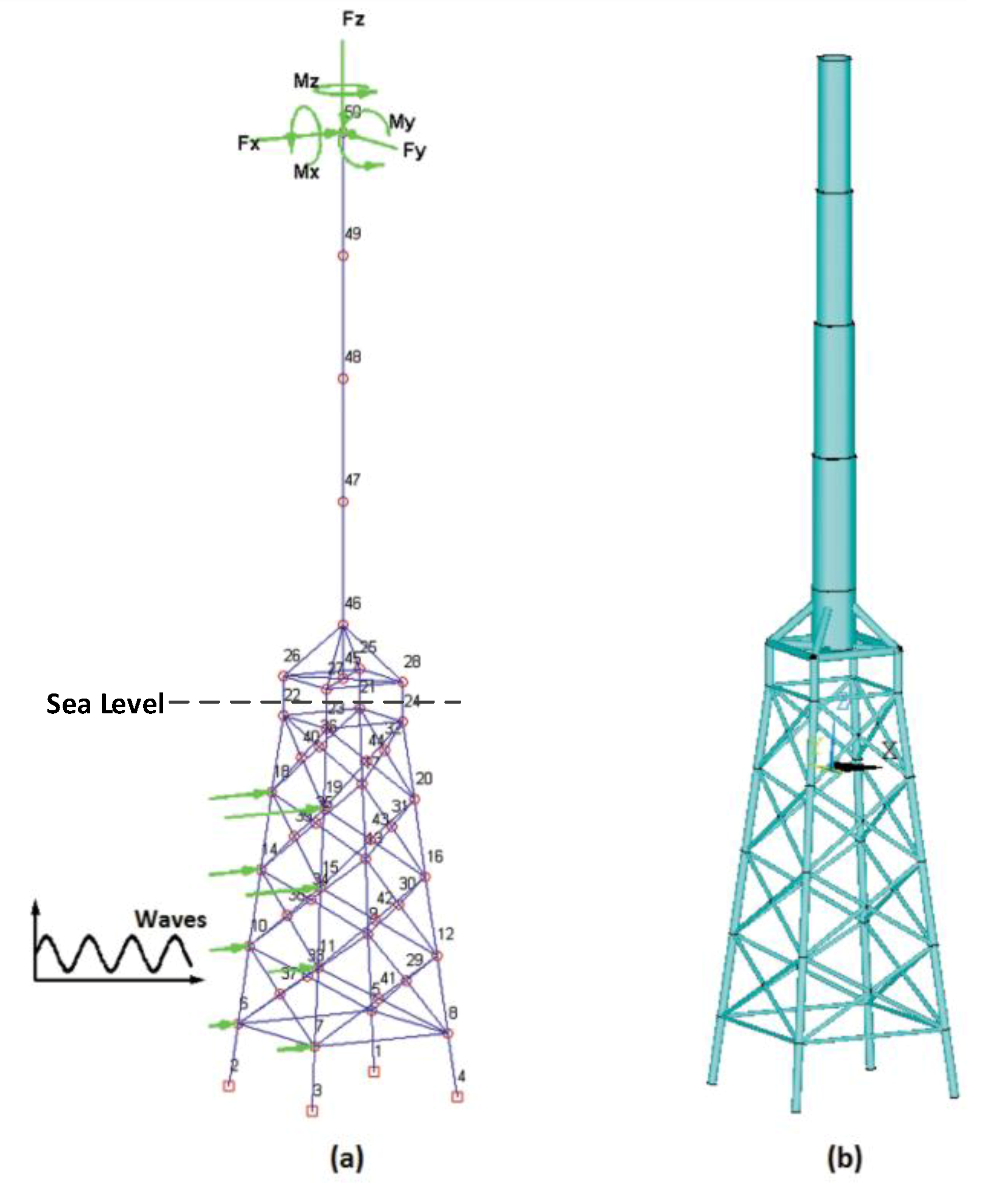
3.2. A Jacket Support Offshore Wind Turbine
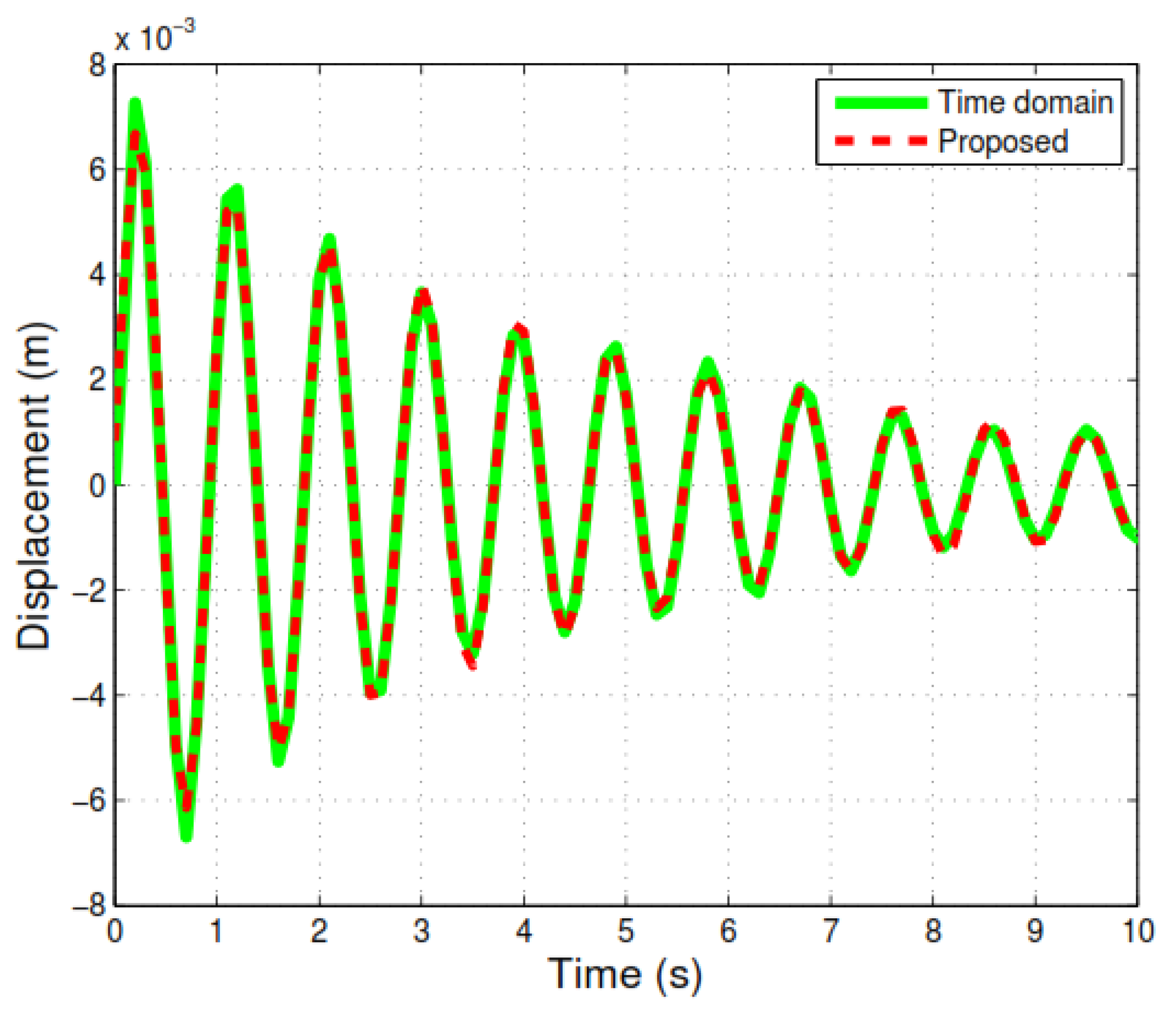
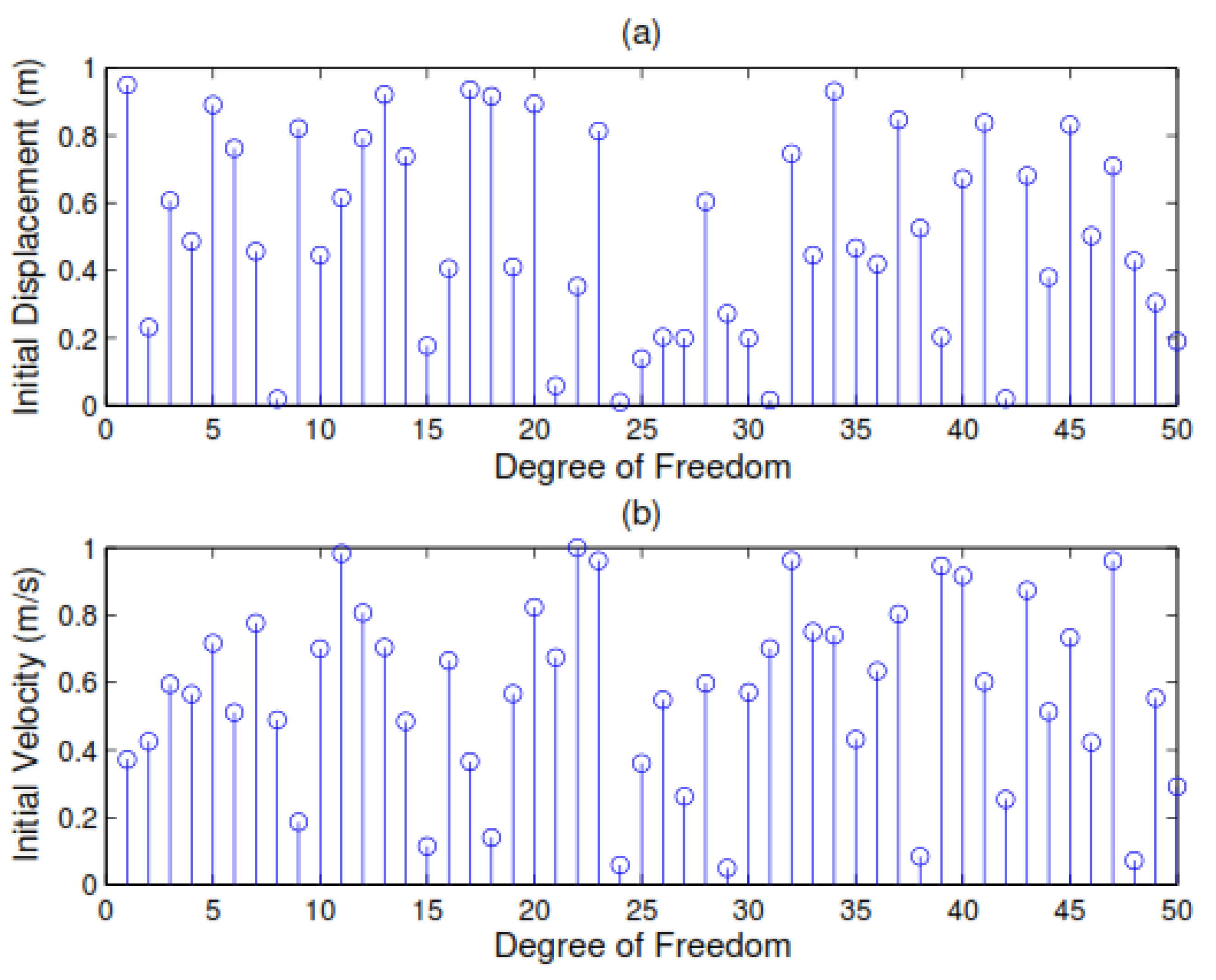
3.2.1. Response Estimation of the Structure with Partial Nonzero Initial Condition
3.2.2. Response Estimation of the Structure with Universal Nonzero Initial Conditions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Arany, L.; Bhattacharya, S.; Machdonald, J.H.G.; Hogan John, S. Closed form solution of Eigen frequency of monopile supported offshore wind turbines in deeper waters incorporating stiffness of substructure and SSI. Soil Dynam. Earthq. Eng. 2016, 83, 18–32. [Google Scholar] [CrossRef]
- Pérez-Collazo, C.; Greaves, D.; Lglesias, G. A review of combined wave and offshore wind energy. Renew. Sustain. Energy Rev. 2015, 42, 141–153. [Google Scholar] [CrossRef]
- Piersol, A.G.; Harris, C.M. Harri’s Shock and Vibration Handbook, 5th ed.; McGraw-Hill, Inc.: New York, NY, USA, 2017. [Google Scholar]
- Perez, T. Ship Motion Control: Course Keeping and Roll Reduction Using Rudder and Fins; Springer: London, UK, 2005. [Google Scholar]
- Hegseth, M.J.; Bachynski, E.E. A semi-analytical frequency domain model for efficient design evaluation of spar floating wind turbines. Mar. Struct. 2019, 64, 186–210. [Google Scholar] [CrossRef]
- Liu, F.S.; Lu, H.C.; Ji, C.Y. A general frequency-domain dynamic analysis algorithm for offshore structures with asymmetric matrices. Ocean Eng. 2016, 125, 272–284. [Google Scholar] [CrossRef]
- Liu, F.S.; Lu, H.C.; Li, H.J. Dynamic analysis of offshore structures with non-zero initial conditions in the frequency domain. J. Sound Vib. 2016, 366, 309–324. [Google Scholar] [CrossRef]
- Muk, C.O.; Bachynski, E.E.; Økland, O.D. Dynamic Responses of Jacket-Type Offshore Wind Turbines Using Decoupled and Coupled Models. J. Offshore Mech. Arctic Eng. 2017, 139, 041901. [Google Scholar]
- Seidel, M.; Ostermann, F.; Curvers, A.; Kuhn, M.; Kaufer, D.; Boker, C. Validation of offshore load simulations using measurement data from the DOWNVInD project. In Proceedings of the European Offshore Wind Conference, Stockholm, Sweden, 14–16 September 2009. [Google Scholar]
- Jia, J. An efficient nonlinear dynamic approach for calculating wave induced fatigue damage of offshore structures and its industrial applications for lifetime extension. Appl. Ocean Res. 2008, 30, 189–198. [Google Scholar] [CrossRef]
- Chen, I.W.; Wong BL Lin, Y.H. Design and analysis of jacket substructures for offshore wind turbines. Energies 2016, 9, 264. [Google Scholar] [CrossRef]
- Dong, W.B.; Moan, T.; Gao, Z. Long-term fatigue analysis of multi-planar tubular joints for jacket-type offshore wind turbine in time domain. Eng. Struct. 2011, 33, 2002–2014. [Google Scholar] [CrossRef]
- Anders, E.Z. Understanding FFT Second Edition Extensivel Y Revised Applications; Citrus Press: Titusville, FL, USA, 2004. [Google Scholar]
- Newman, J. Marine Hydrodynamics; MIT Press: Cambridge, MA, USA, 1977. [Google Scholar]
- Faltinsen, O. Hydrodynamic of High-Speed Marine Vehicles; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Liu, F.S.; Li, H.J.; Wang, W.Y.; Liang, B.C. Initial-condition consideration by transferring and loading reconstruction for the dynamic analysis of linear structures in the frequency domain. J. Sound Vib. 2015, 336, 164–178. [Google Scholar] [CrossRef]
- Support Structures for Wind Turbines; Offshore Standard, DNVGL- ST-0126; DNVGL: Akershus, Noway, 2018.
- Environmental Conditions and Environmental Loads; Recommended Practice, DNV-RP-C205; DNVGL: Akershus, Noway, 2007.
- Kim, J.H.; Kim, Y.H. A predictor-corrector method for structural nonlinear analysis. Comput. Methods Appl. Mech. Eng. 2001, 191, 959–974. [Google Scholar] [CrossRef]
- Erwin, K. Advanced Engineering Mathematics, 8th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1999. [Google Scholar]
- Golub, G.H. Matrix Computations, 3rd ed.; Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Shi, W.; Park, H.; Han, J.; Na, S.; Kim, C.W. A study on the effect of different modeling parameters on the dynamic response of a jacket-type offshore wind turbine in the Korean Southwest Sea. Renew. Energy 2013, 58, 50–59. [Google Scholar] [CrossRef]
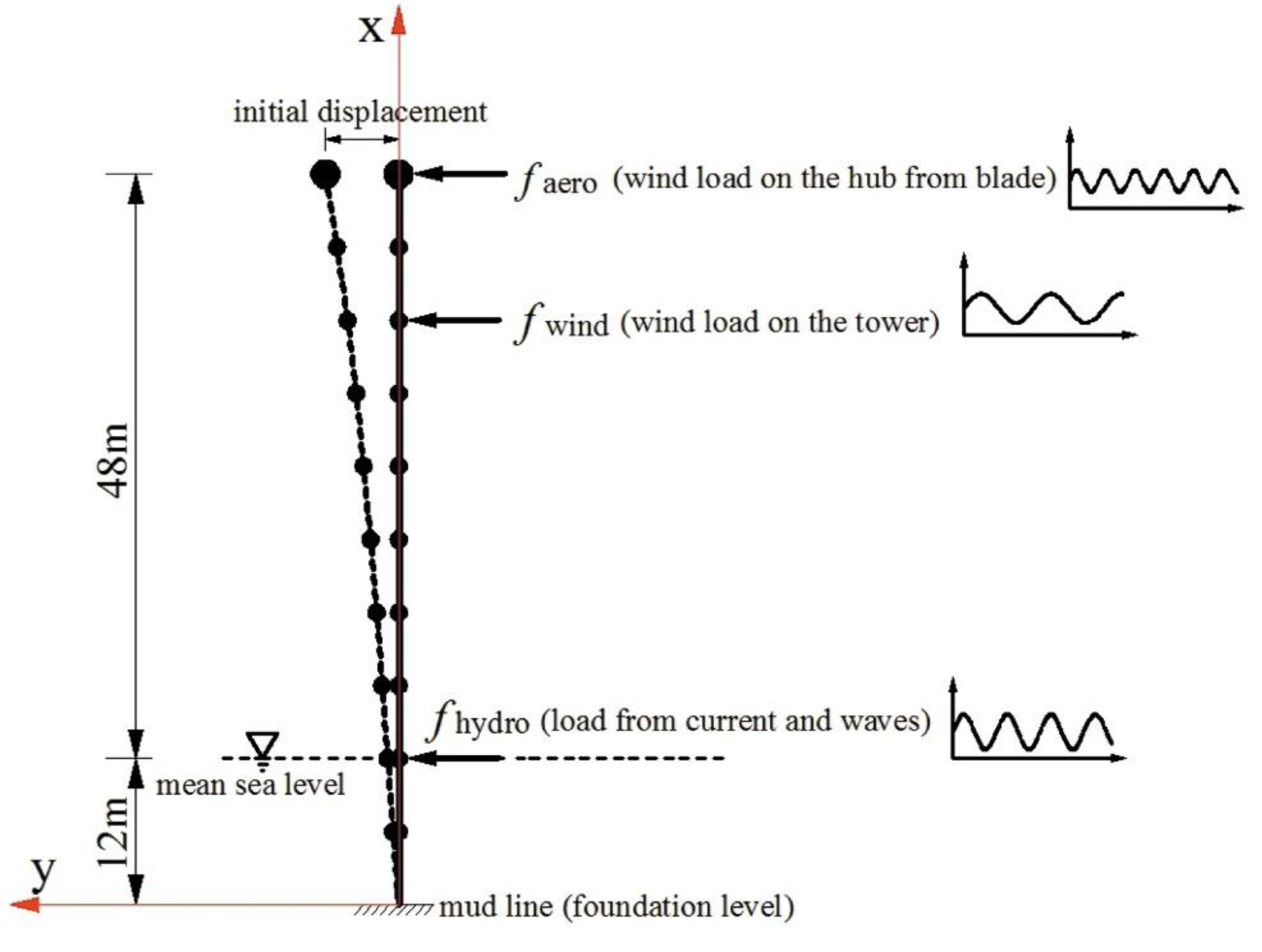
| n | fn(Hz) | ζn | Bn(m) | θn(rad) |
|---|---|---|---|---|
| 1 | 0.64 | −0.003 | 40 | −π/8 |
| 2 | 0.85 | −0.01 | 100 | −π/8 |
| 3 | 1.26 | −0.01 | 80 | π/6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Li, X.; Tian, Z.; Zhang, J.; Wang, B. Transient Response Estimation of an Offshore Wind Turbine Support System. Energies 2019, 12, 891. https://doi.org/10.3390/en12050891
Liu F, Li X, Tian Z, Zhang J, Wang B. Transient Response Estimation of an Offshore Wind Turbine Support System. Energies. 2019; 12(5):891. https://doi.org/10.3390/en12050891
Chicago/Turabian StyleLiu, Fushun, Xingguo Li, Zhe Tian, Jianhua Zhang, and Bin Wang. 2019. "Transient Response Estimation of an Offshore Wind Turbine Support System" Energies 12, no. 5: 891. https://doi.org/10.3390/en12050891
APA StyleLiu, F., Li, X., Tian, Z., Zhang, J., & Wang, B. (2019). Transient Response Estimation of an Offshore Wind Turbine Support System. Energies, 12(5), 891. https://doi.org/10.3390/en12050891






