1. Introduction
Cogeneration or combined heat and power (CHP) systems are defined as energy generation units that simultaneously produce electric (or mechanical) energy and useful heat from a single fuel source [
1]. The role of cogeneration in the process of reducing primary energy consumption, CO
2 emissions, and energy costs is widely acknowledged [
2]. This is mainly due to the higher energy efficiency achievable by CHP systems compared to the separate generation of electricity and heat. Moreover, cogeneration systems are considered a viable solution to promote the development of microgrids with distributed renewable energy [
3].
Nevertheless, the energy, environmental, and economic performances of CHP systems are highly dependent on their sizing and operational strategy. Indeed, undersizing and oversizing of cogeneration plants are frequent and may compromise the energy saving potential of those systems [
4]. For this reason, several methods have been proposed in recent years to identify the integrated optimal sizing and management of CHP plants. A non-exhaustive list of selected examples is as follows. Gimelli et al. [
5] presented a multi-objective optimization approach, based on a genetic algorithm, for the optimal design of modular cogeneration systems based on reciprocating gas engines. A sensitivity analysis was performed to evaluate the robustness of the optimal solution with respect to energetic, legislative, and market scenarios. Similarly, Beihong and Weiding [
6] proposed a mixed integer non-linear programming (MINLP) formulation to determine the capacity of a gas turbine cogeneration plant that minimizes the annual total cost, thus proving the importance of optimization methods in the design and operation of CHP systems. On the same topic, Aviso and Tan [
7] applied a different optimization tool, namely the fuzzy P-graph approach, for the optimal design of cogeneration and trigeneration systems. This approach allows the consideration of soft constraints on user demand and fuel availability. Likewise, Urbanucci and Testi [
8] proposed a probabilistic methodology for the optimal sizing of CHP units under uncertainty in energy demands, based on a Monte Carlo risk analysis. Moreover, the thermoeconomic approach was also applied to cogeneration systems, as in [
9], where Yokoyama et al. optimized both the exergy efficiency and the annual cost of a CHP gas turbine.
Even though the above-mentioned works are significant examples of optimization methodologies for cogeneration units, none of them consider a storage device in the energy system. Nevertheless, integrating thermal energy storages (TESs) into CHP systems can lead to higher operational flexibility and better overall performance. Indeed, as shown in [
10] by Fang and Lahdelma, the decoupling of heat and electric demands by storing the exceeding CHP thermal production allows maximization of the operation of cogeneration systems, thus reducing the load share covered by back-up units. During the years, several approaches for the optimization of cogeneration systems with storage devices have been proposed. For example, Kuang et al. [
11] applied a dynamic programming technique to define the most economical operation schedule of trigeneration systems. Elsido et al. [
12] proposed a MINLP formulation for a district heating network, combining evolutionary algorithms with mathematical programming. The optimal design and operation for both economic and environmental objectives of a CHP system with a thermal storage tank was investigated by Fuentes-Cortés et al. [
13], by exploiting commercial MINLP solvers.
The introduction of energy storage units makes the optimization of CHP systems significantly more complicated. In the absence of TES, the operation optimization problem can be considered “static”, since each timestep is independent of the others. Under this condition, it can be proven that the overall optimum corresponds to the sum of the optimums of every single timestep [
14]. Consequently, the optimal solution can be traced back to the solution of several optimization problems, one for each timestep, which, compared to the overall problem, are characterized by a lower dimensionality and, hence, by a lower computational cost. On the other hand, when a storage device is considered within the system, the problem becomes “dynamic”, because of the dependency between the optimization variables of adjacent timesteps. This results in a higher dimensionality—thus, a higher computational cost—of the optimization problem, which calls for the adoption of decomposition strategies, like the so-called rolling-horizon approach. Rolling-horizon techniques have been proven to effectively tackle the high dimensionality of optimization problems, by decomposing the problem in shorter periods, without affecting the quality of the results [
15].
The general problem of the integrated optimal sizing and operation of cogeneration systems usually results in a non-linear problem. Among the available optimization techniques, the state-of-the-art approach to solve this problem consists in linearizing the original problem to obtain a mixed integer linear programming (MILP) problem [
12]. This is mainly due to the guarantee of the global optimality of the solution and to the effectiveness of the available commercial MILP solvers. Nonetheless, when dealing with the optimal design problem, with the size of each component an optimization variable, strong assumptions have to be made to retain the linearity of the model: The efficiency of the units must be kept constant, the variation of the unitary cost of the components in relation to their size must be neglected, and the temperature of the storage cannot be directly tracked [
14]. To tackle those issues, a decomposition approach based on a two-level optimization algorithm is adopted in this work. At the upper level, the optimal design problem (i.e., the selection of CHP and storage capacities) is solved by means of a metaheuristic method, while at the lower level, the operational strategy is optimized by means of an MILP method. The design and operation problems must be solved simultaneously since they are intrinsically linked.
As already mentioned, the decomposition approach allows tracking of the average temperature of the storage in each timestep, and a better estimate of the thermal losses can be performed by considering also the impact of the storage geometrical characteristics. Indeed, in simpler models, the storage is seen as a simplified thermal battery, and its losses are assumed proportional to the energy content of the storage with a constant heat-loss coefficient, thus providing a poor physical representation of the system, as shown in [
15,
16]. In this paper, on the basis of the model proposed by Steen et al. [
16], a new formulation of the optimization problem is developed, capable of considering the impact of geometrical characteristics, the tank’s insulation properties, and the ambient conditions in the evaluation of TES heat losses. As well as including all the above-mentioned features, the main innovation of the proposed approach is the possibility of simulating and optimizing the operation of the storage when the temperature of the TES is below the operation threshold temperature. Furthermore, since the thermal storage makes the operation optimization problem “dynamic” and, consequently, computationally very expensive, a rolling-horizon approach is proposed.
To summarize, the main purpose and novelty of this study is to develop a comprehensive methodology for the integrated optimal sizing and operation of cogeneration systems with thermal energy storage. To the best of the authors’ knowledge, such a comprehensive approach is still missing. In view of this, the present paper aims to propose a thorough methodology with the following key characteristics:
A decomposition approach was adopted. At the upper level, the optimal design problem is solved by means of a genetic algorithm, while at the lower level, a MILP formulation is adopted to identify the optimal operation;
A novel MILP formulation for the TES was developed to obtain a better assessment of its optimal operation;
A rolling-horizon technique was implemented to reduce the computational time of the optimization problem.
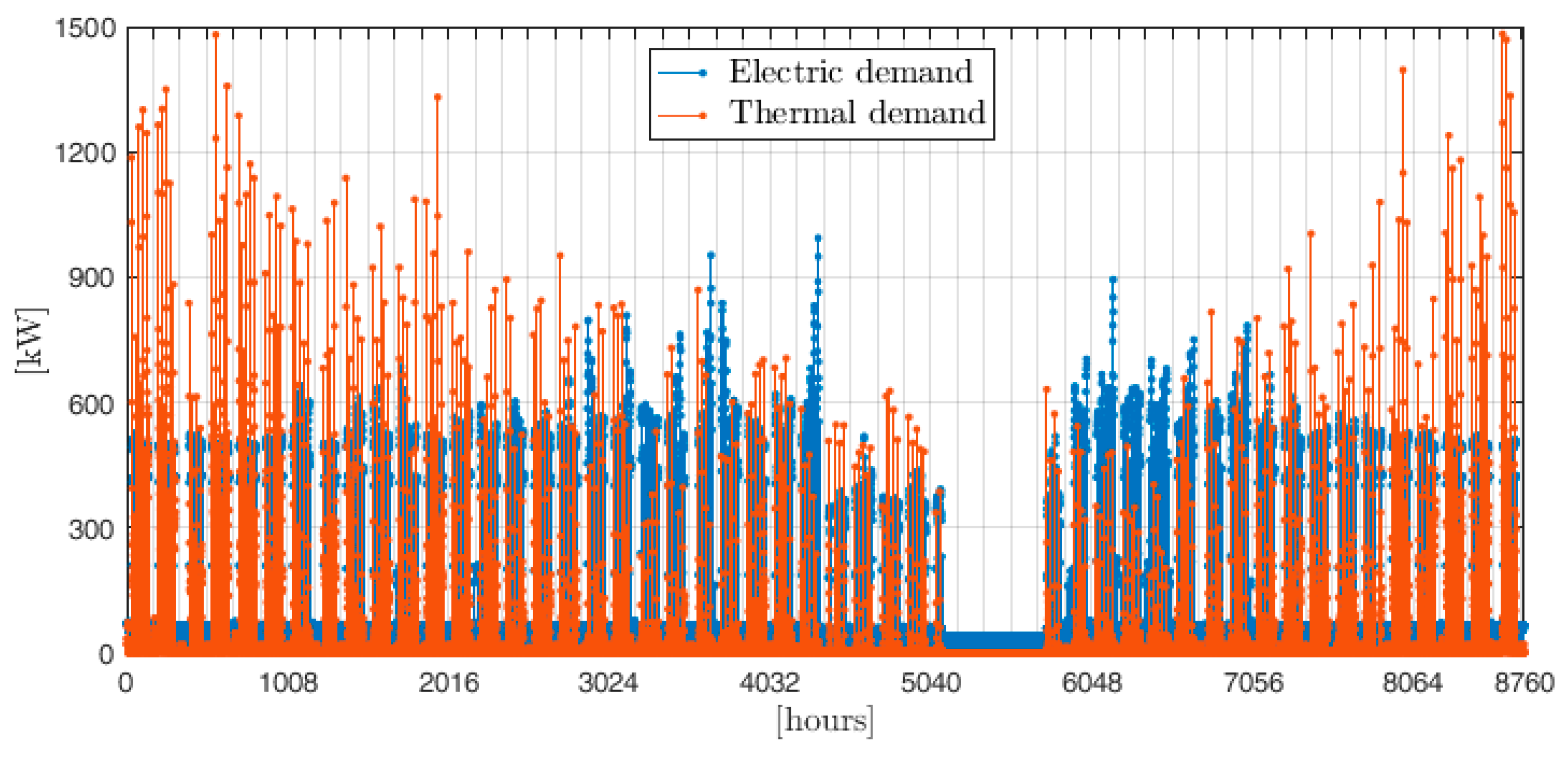
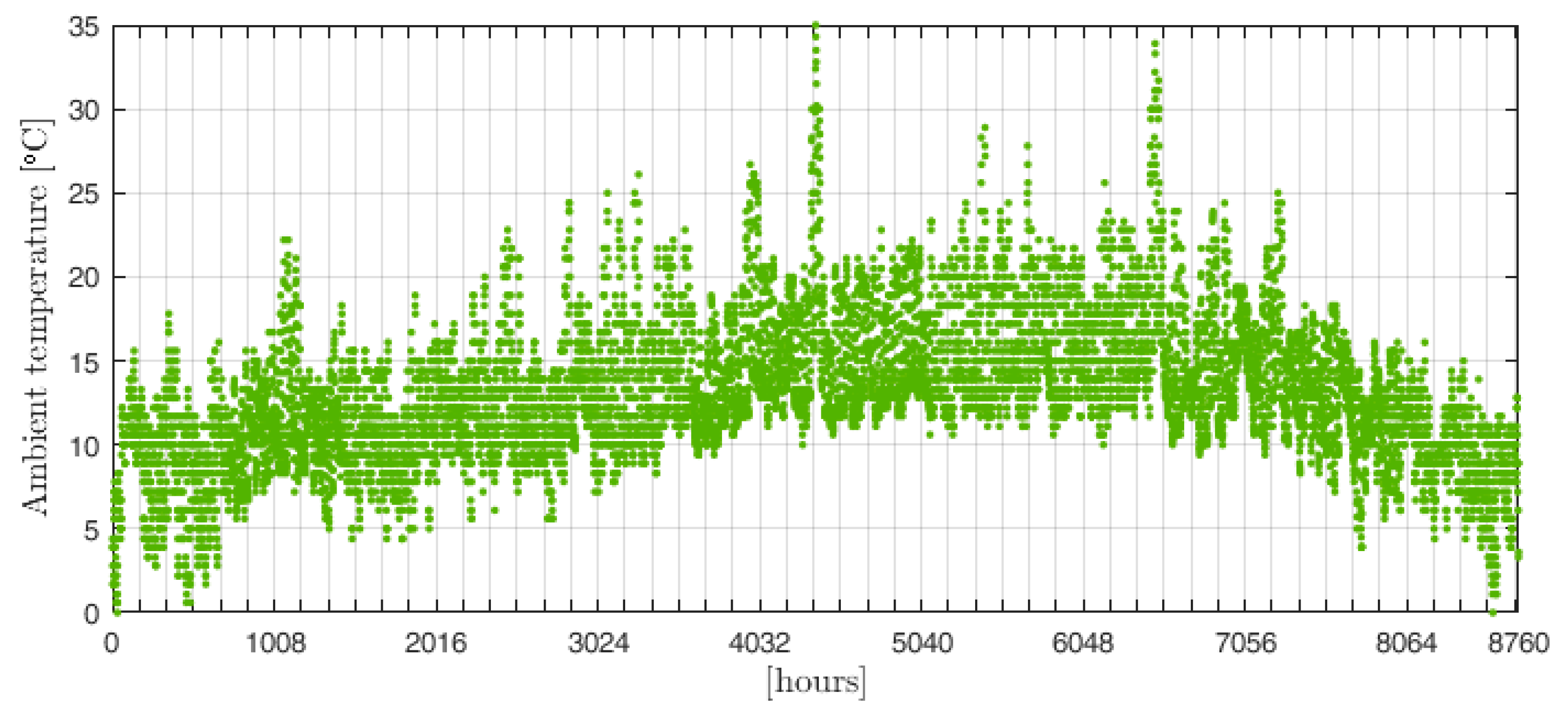
Finally, the proposed methodology was tested in a case study. To this end, hourly electric and thermal demands of a reference building (a secondary school located in San Francisco, California) were considered, and the optimal integrated sizing and operation of a cogeneration system with thermal energy storage were identified.
The rest of the paper is structured as follows. In
Section 2, the methodological framework is described: The energy system, the TES modeling, the optimization problem, and algorithm are presented in detail.
Section 3 presents the case study, while an in depth-analysis of the results follows in
Section 4. The last section contains concluding remarks.
2. Methodology
2.1. The Energy System
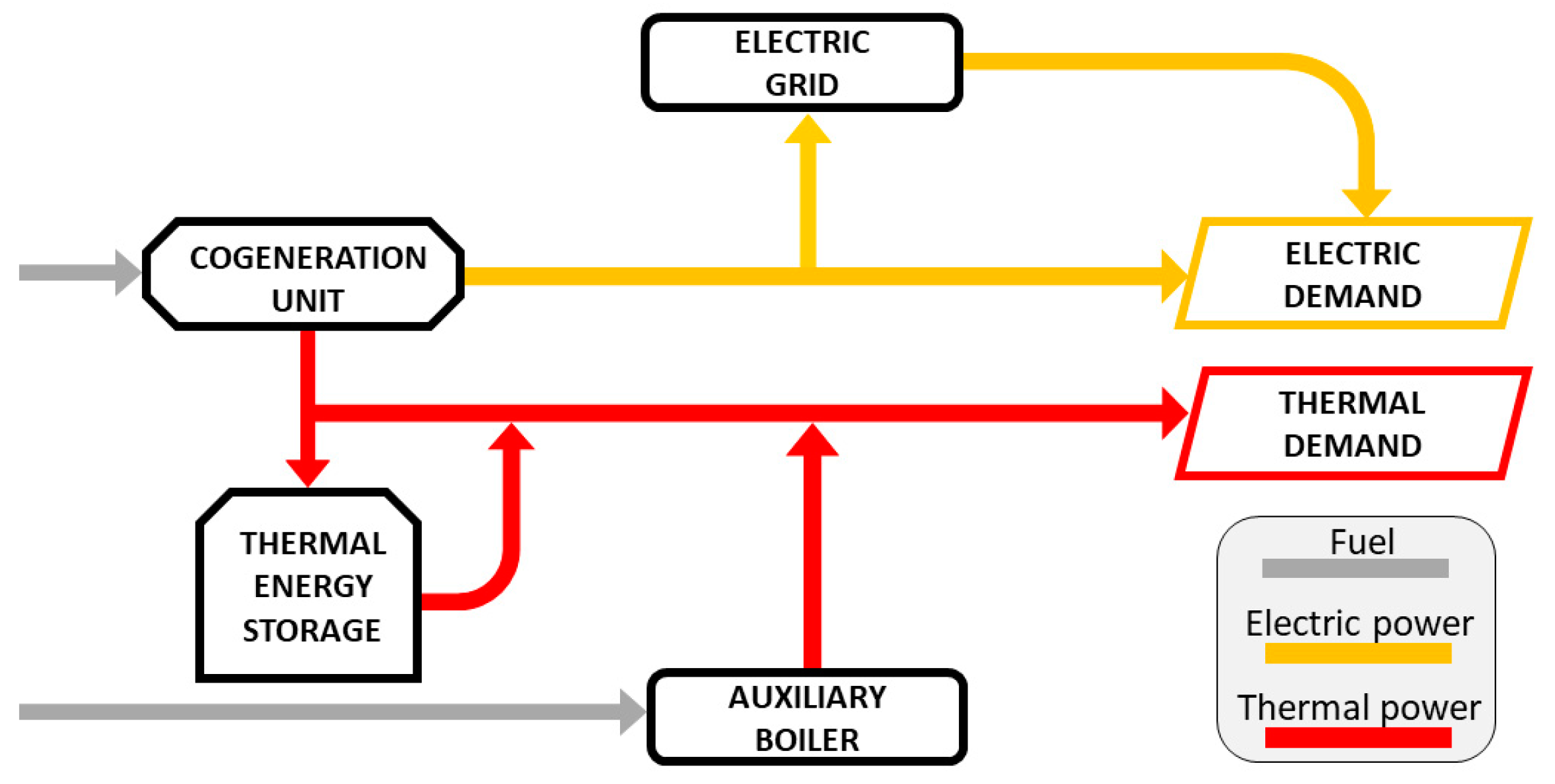
The energy system under consideration is schematically shown in
Figure 1. It comprises a cogeneration unit (e.g., an internal combustion engine), a thermal energy storage, and an auxiliary boiler. Moreover, the exchange of electricity with the regional grid is allowed (both selling and buying). Thus, the thermal demand can be met partly by the CHP heat production and partly by the boiler, while the electric demand can be covered partly by the CHP electric production and partly by the electric grid. The TES can be used to store the thermal energy recovered from the cogeneration unit and, subsequently, to cover the thermal demand.
An hourly timestep was adopted for the simulation of the system, as a compromise between the computational burden and temporal resolution of the scheduling problem. With this timestep length, the behavior of the machines based on the hourly energy flows can be considered, thus averaging the transient performances, which occur on shorter time scales. Indeed, among the considered generators, the internal combustion engine is the one with the longest dynamic response, with start-up times of around 2 minutes for the electric output and less than 15 minutes for the thermal output [
17].
2.2. Thermal Energy Storage Modeling
A cylindrical water tank is considered as the sensible-heat TES device. At each
i-
th timestep, an equivalent TES temperature (
) is defined on the basis of the stored energy (
), so that the following relationship holds:
with
as the water density,
, the storage volume,
, the specific heat of water, and
, the ambient temperature. In this way, the zero state of charge is the one corresponding to an equivalent TES temperature equal to the ambient temperature. The dynamic of the stored energy varies according to the following energy balance:
with
as the storage losses, whose formulation is discussed in detail below, and
and
as the energy delivered to and from the storage, respectively.
With the useful energy only a fraction of the whole TES energy content, due to the minimum temperature level that is useful to satisfy the thermal demand (
), the energy stored is considered as the sum of two terms: The useful available energy (
) and the residual energy (
):
where:
This distinction is also useful to highlight differences between the models available in the current literature to evaluate thermal-storage losses. In simpler models, the storage is seen as a simplified thermal battery, and its losses are accounted for only on the basis of the useful storage energy content by means of a constant heat-loss coefficient [
16]:
with:
Nevertheless, Equation (6), by considering only the contribution of the useful energy (“dynamic” losses) and neglecting that related to the residual energy (“static” losses), leads to an underestimation of the losses. Indeed, it has been shown by Omu et al. [
18] that considering static heat losses improves the accuracy of thermal-storage modeling, compared to a simplified thermal-battery model. To this end, different formulations that also consider the residual energy in the computation of the losses have been proposed [
13]. The latter reads:
The use of these models leads to an additional issue when the coupled problem of sizing and operation is considered in the MILP formulation. Indeed, as it can be seen from Equations (6) and (7), the heat losses depend on the amount of stored energy, as well as on the capacity and characteristics of the TES, such as the volume of the tank and the overall heat transfer coefficient. Consequently, by considering a constant overall heat-loss coefficient, the impact of these optimization parameters—specifically of the volume of the tank—on the storage losses is neglected, thus affecting the solution of the optimization problem. To overcome this issue, in the present work, the decomposition of the optimization problem at the design level and operation level was adopted, as described in the next section. By doing so, the effect of the volume of the tank on the heat-loss coefficient can be exactly considered. Thus, a model capable of considering both the energy and the sizing parameters in the storage heat-losses formulation is developed as follows.
From Equation (7), it can be seen that once the overall heat-transfer coefficient is identified, the value of the heat-loss coefficient can be expressed as a function of the surface of the storage tank, which in turn is a function of the storage volume. To this end, once the aspect ratio (λ) of the tank is defined, the relation between the surface and the volume of the storage tank can be formulated as follows:
and the heat-loss coefficient can be finally expressed as a function of the volume of the storage tank:
In this way, the approach of the fixed thermal efficiency of the storage, commonly found in the literature, can be overcome, and the thermal losses of the TES can be expressed as a function of the thermophysical and geometrical properties of the storage tank and medium, and the temperatures of the ambient surroundings and the storage itself.
Finally, the energy balance of the TES reads:
and the following linear constraints must be considered:
In Equations (16) and (17), is a binary variable, equal to 1 if the storage temperature in the i-th timestep is above its operational threshold, and, therefore, energy can be taken from the storage; otherwise, if the temperature of the storage is lower than , is equal to 0 and no useful energy can be taken from the TES. The introduction of this binary variable allows a more accurate simulation and optimization of the operation of the storage. Indeed, in traditional MILP formulations, the temperature of the storage cannot drop below its operation threshold, which is unrealistic and limits the operation optimization.
Moreover, Equations (15) and (16) define the maximum amounts of energy that can be charged and discharged in a single timestep, respectively. If external plate heat exchangers are considered for both the charging and discharging the storage, those quantities coincide with the capacity of the heat exchangers themselves. Therefore, and can be considered as design variables and are subject to optimization, once the investment cost of the plate heat exchangers is considered separately from that of the water storage tank.
2.3. Optimization Problem and Algorithm
The objective function to be minimized is the equivalent annual cost (
) of the system, which is calculated over the period of one year and composed of the annualized investment cost for the technologies,
, and the total annual operating cost,
:
where
is the capacity of the
j-th component to be installed (expressed in kW for the CHP, the boiler, and the plate heat exchangers, and in m
3 for the TES),
and
are the correlation parameters of the equipment cost as a function of the capacity, and
is the capital-recovery factor [
19]:
The total annual operating cost comprises the cost for purchasing electricity and natural gas and the revenue from selling electricity to the grid:
The optimization variables can be distinguished into two main groups: Sizing variables (, , , , ) and operation variables (, , , , , ).
Demand constraints must be satisfied in each
i-th timestep:
In addition to the energy balance and constraints for the TES (Equations (12)–(17)) shown in
Section 2.1), the following constraints and equations must be considered too:
where
is the load factor of the cogeneration unit, defined as
, and
is a binary variable equal to 1 when the CHP is on and equal to 0 when it is off. Equations (30) and (31) linearize the relationship between the electric and thermal efficiencies of the cogeneration unit with respect to its load factor, respectively.
Finally, the overall problem consists in the minimization of the equivalent annual cost:
which results in a mixed integer non-linear optimization problem, because of the non-linear variations of the unitary cost of the components in relation to their capacity, the part-load effects on CHP efficiencies, and the thermal energy storage model (the dependency of
and
on
).
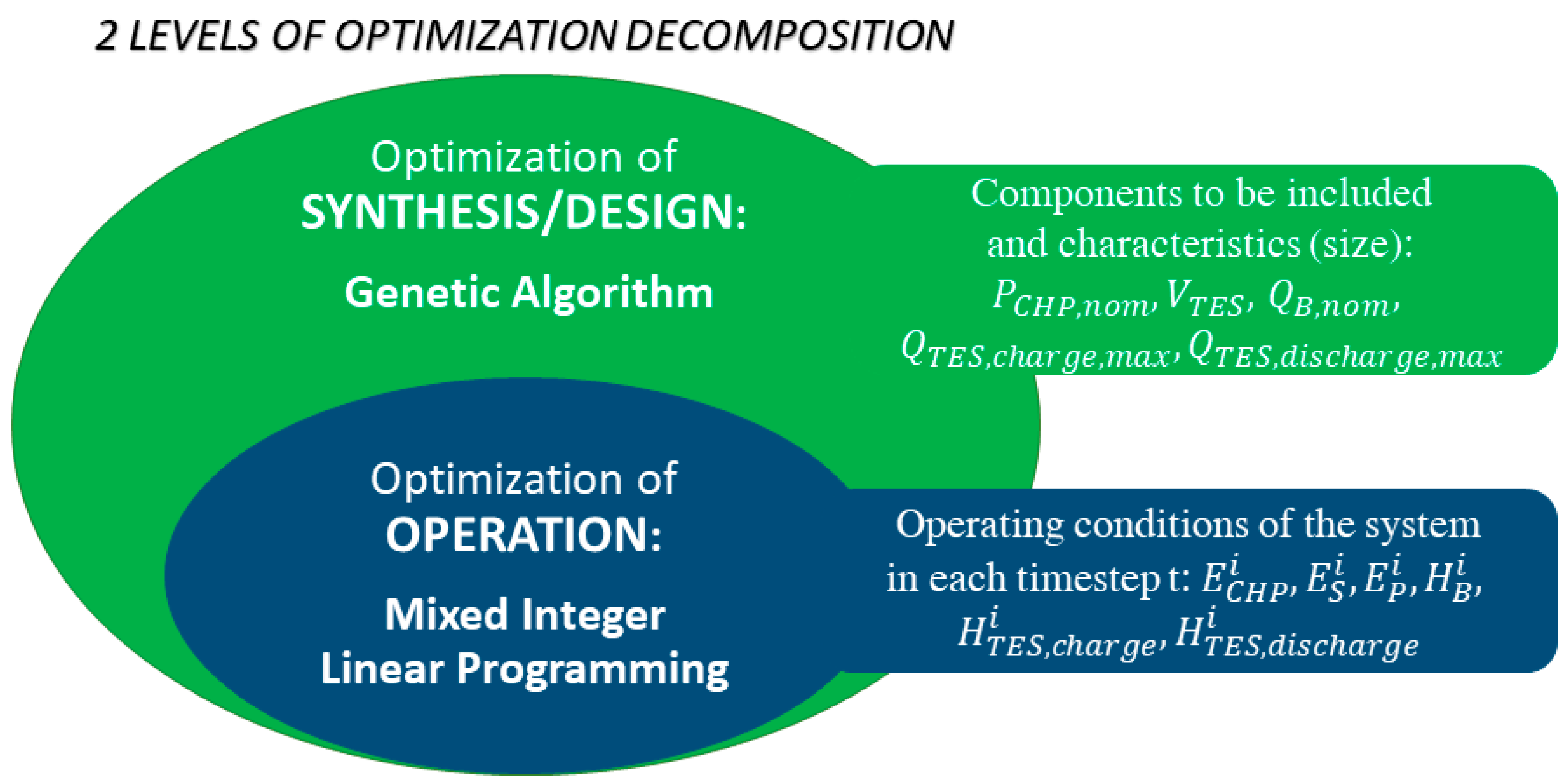
To this aim, the overall problem was decomposed into two levels and the optimization variables distinguished into two categories, as schematically summarized in
Figure 2. At the upper level, the synthesis/design problem, which identifies the components that should be included in the energy system and their capacities, is addressed by a genetic algorithm (GA). At the lower level, the optimal operation problem is solved by means of an MILP technique. The two problems are nested in each other and therefore they must be solved simultaneously. For each individual solution (components size) produced by the GA, the optimal annual operation cost is identified by the MILP solver, and, thus, the total EAC is calculated. This procedure is repeated for each individual of each generation produced by the GA, until the stopping criteria is met.
As already mentioned, this decomposition allows the benefits of the MILP formulation to be reaped, while overcoming its main drawbacks. Indeed, the part-load behavior of the CHP unit is considered, the variation of the unitary cost of the components in relation to their size is not neglected, and the effect of the storage volume on its heat-loss coefficient is taken into account.
The optimization was performed by using scripts written in the MATLAB environment. The commercial solver, CPLEX [
20], for the MILP optimization and the MATLAB Genetic Algorithm Solver [
21] were used. The settings and parameters adopted for the optimization algorithms are shown in
Table 1.
2.4. Rolling-Horizon Approach for the Decomposition of the Operation Problem
As stated above, the introduction of the storage in the energy system makes the operation optimization problem “dynamic”, because of the dependency between the optimization variables of adjacent timesteps. Therefore, once the sizes of the components are fixed, the problem of the minimization of the operational costs should be solved simultaneously for the whole optimization period (e.g., one year with an hourly resolution). This results in a very large number of variables and constraints, thus making the problem very challenging from the computational point of view [
14]. To tackle this issue, the rolling-horizon procedure can be adopted, which consists in dividing the investigated period into smaller periods and optimizing each subproblem in sequence [
22,
23].
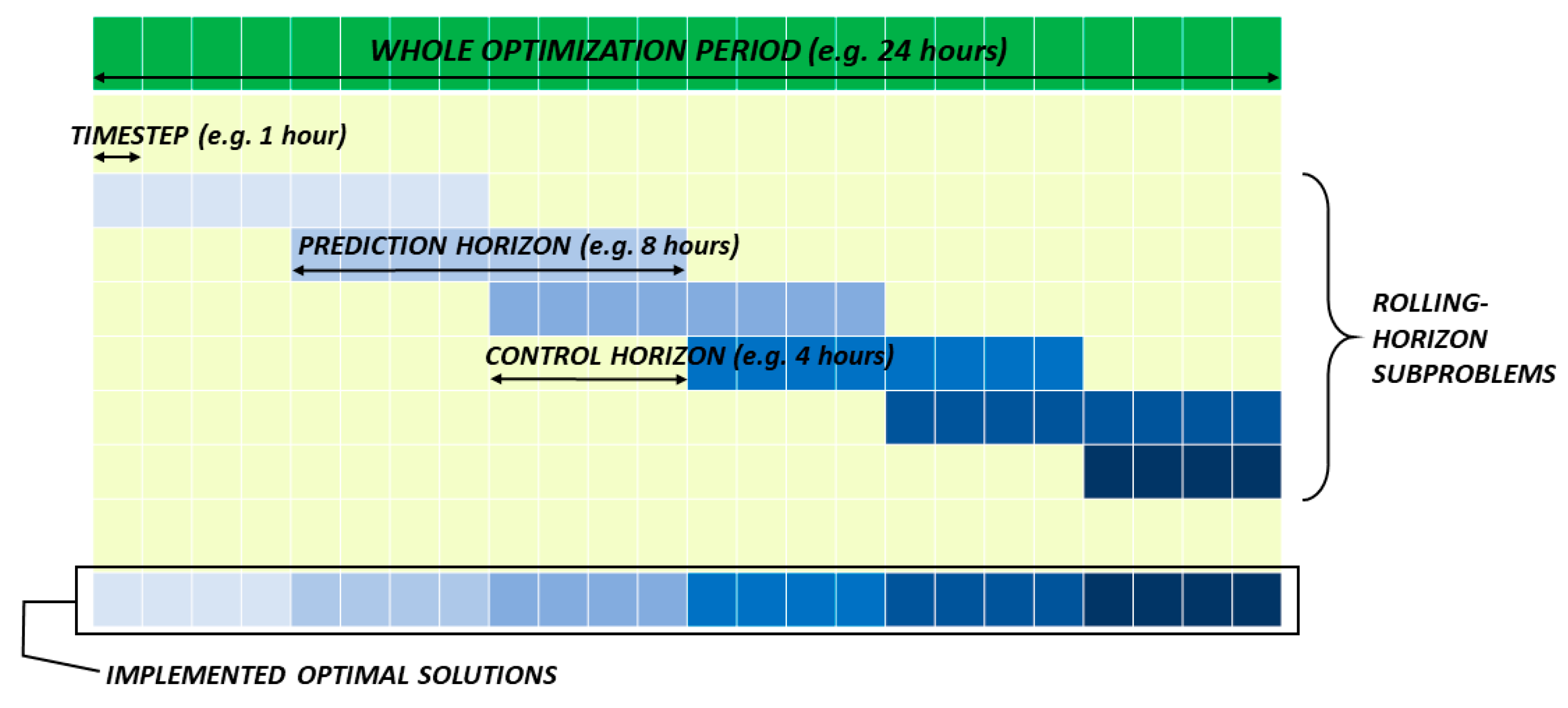
The rolling-horizon approach is schematically represented in
Figure 3. The length of each sub-period of optimization is called “prediction horizon”. Once the solution for a certain sub-period is found, it can be implemented for one or a few timesteps (the total duration of which is called the “control horizon”). Then, the problem is solved for the following sub-period, and so on, until the problem is solved for the whole optimization period.
Therefore, the original operation problem is divided in
subproblems, which optimize the operation in
consecutive timesteps:
where
goes from
to
,
is the length of the control horizon, and
is the length of the prediction horizon (both measured in the number of timesteps). All the other constraints and relationships considered for the whole operation optimization problem must still be considered and remain the same.
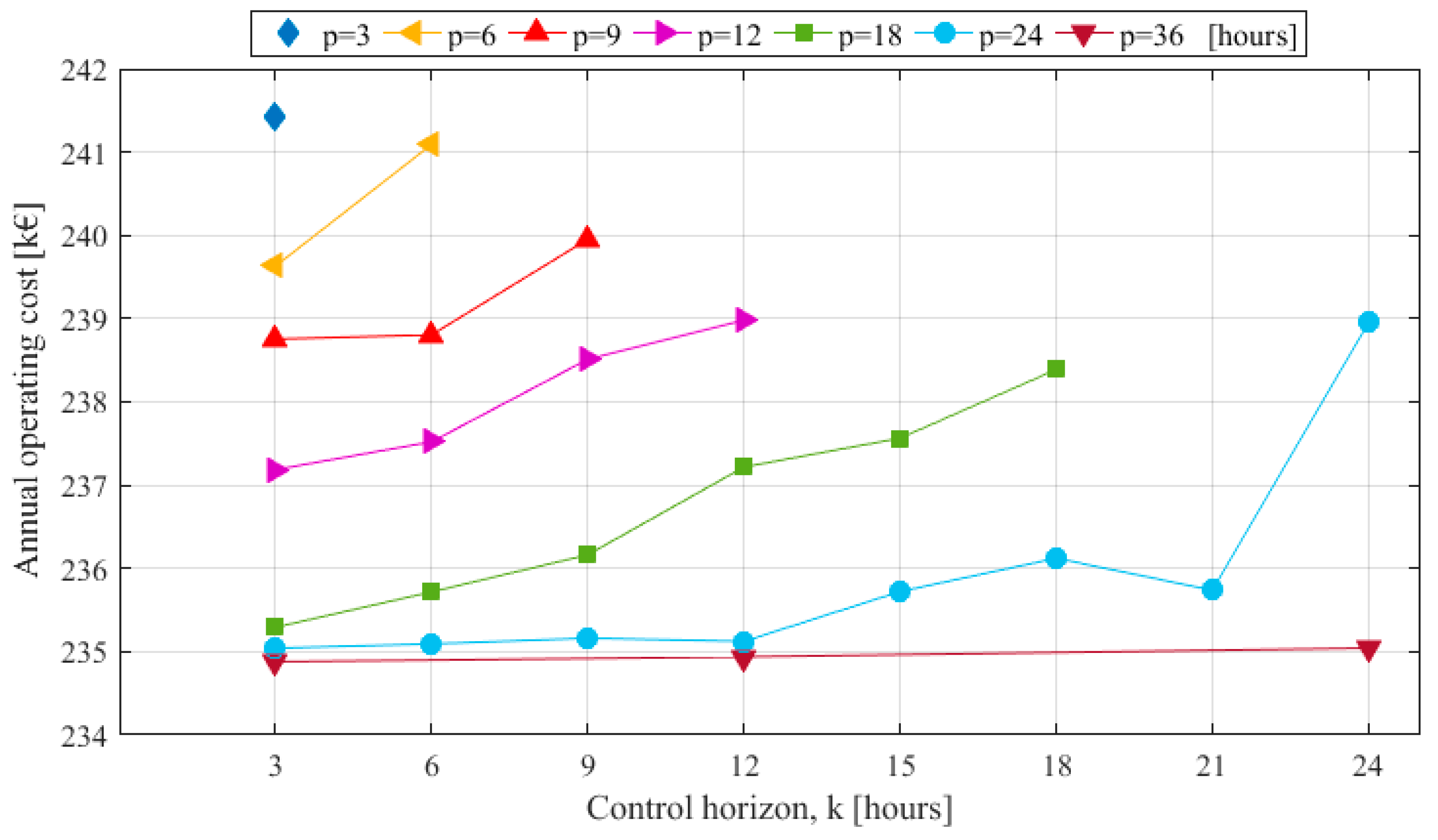
Two parameters must be set in the rolling-horizon decomposition of the operation problem: The length of the prediction and control horizons. As the former increases and the latter decreases, the overall solution becomes more and more accurate, until it coincides with the exact solution (i.e., the solution of the whole optimization period considered at once). On the other hand, as the prediction horizon becomes shorter and the control horizon gets longer, the computational time decreases. Therefore, a compromise must be achieved between these two conflicting objectives.
Moreover, as the size of the thermal energy storage increases, the minimum length of the rolling-horizon so that the solution is not different from the whole-period-at-once solution increases too [
24]. On the contrary, when no storage is included in the system, the problem becomes “static” and each timestep can be solved separately [
25].
5. Conclusions
A comprehensive methodology for the optimal design of cogeneration systems with integrated thermal energy storage was proposed in this paper. The integrated optimization problem of the sizing of the equipment and operational strategy was decomposed into two levels to take into account the part-load behavior of the cogeneration unit, variation of the unitary cost of the components in relation to their size, and the effect of the storage volume on its thermal losses. The optimal operation problem was formulated so as to exploit mixed integer linear programming solvers, while the optimal sizing was tackled by means of a genetic algorithm.
A novel mixed integer linear formulation for the thermal energy storage was proposed. Both “static” and “dynamic” heat losses were considered, and the heat-loss coefficient was defined as a function of the geometrical and thermophysical properties of the storage. The introduction of a binary variable allowed a more comprehensive simulation of the operation of the storage. Furthermore, a rolling-horizon procedure was presented to reduce the computational time of the optimization problem, while preserving the quality of the results.
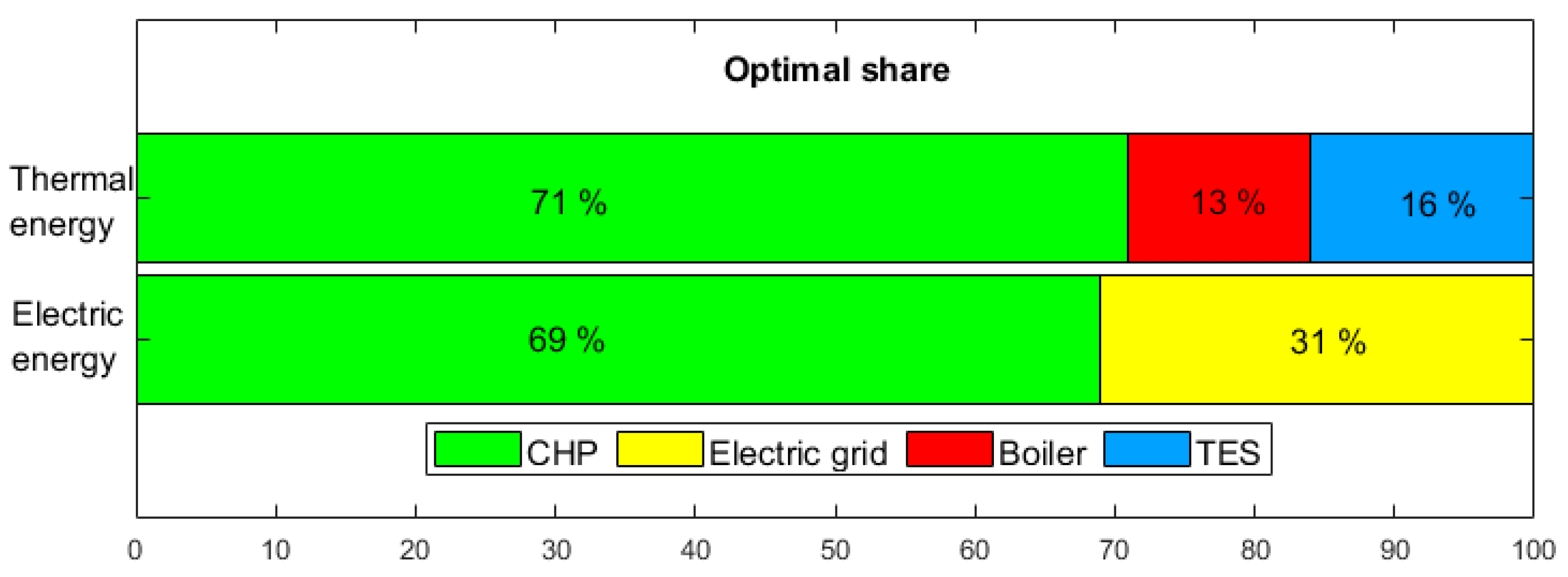
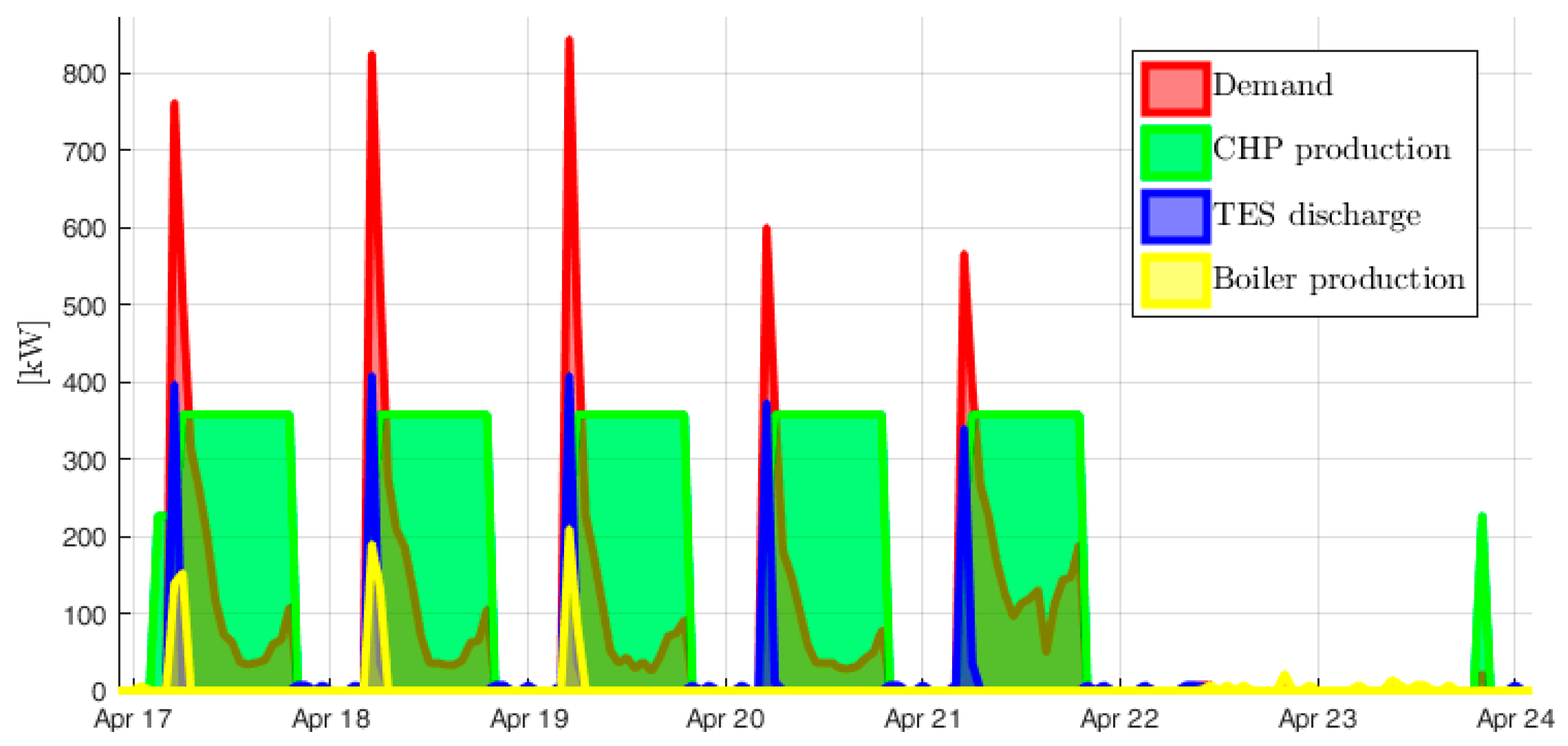
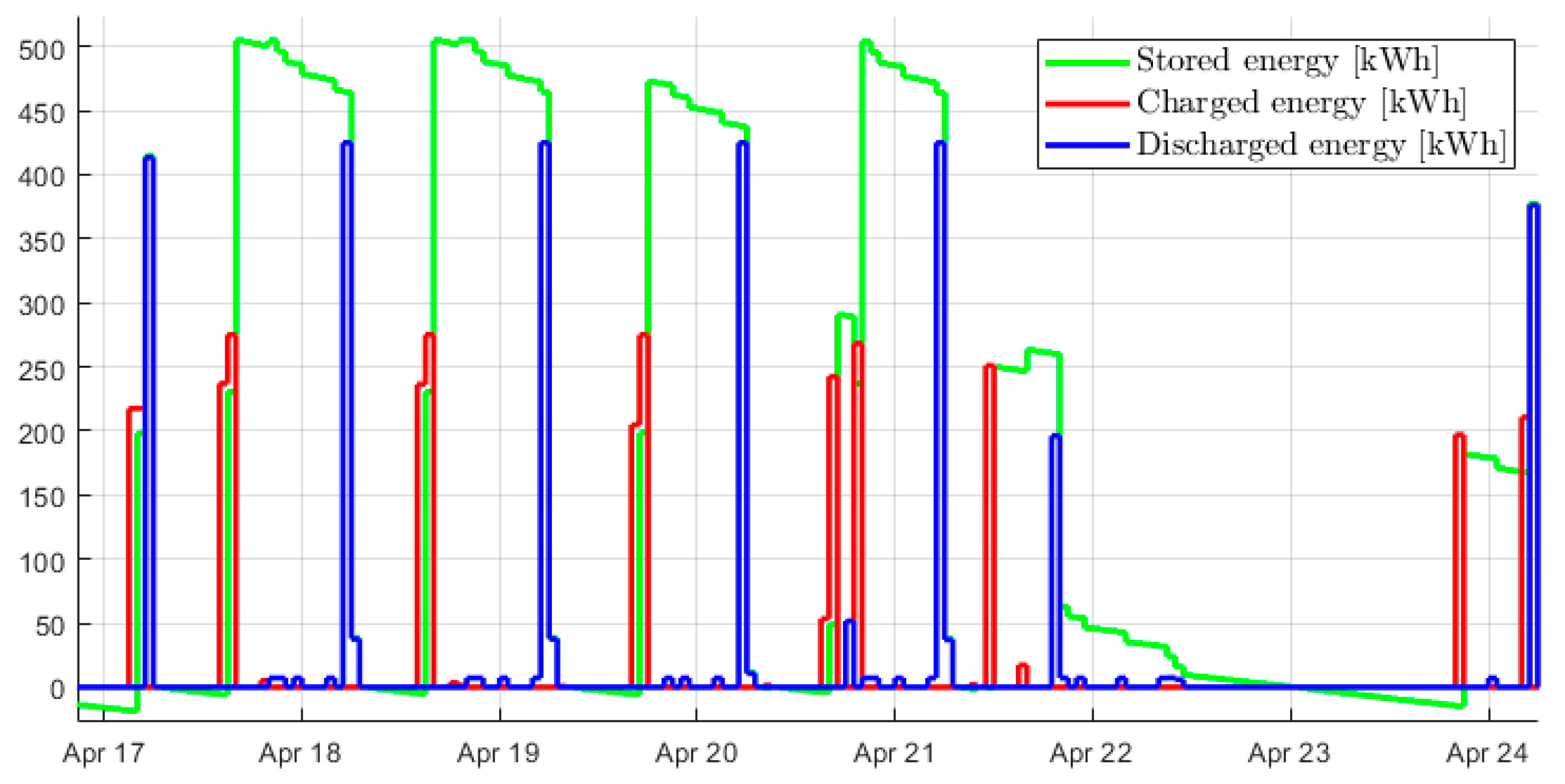
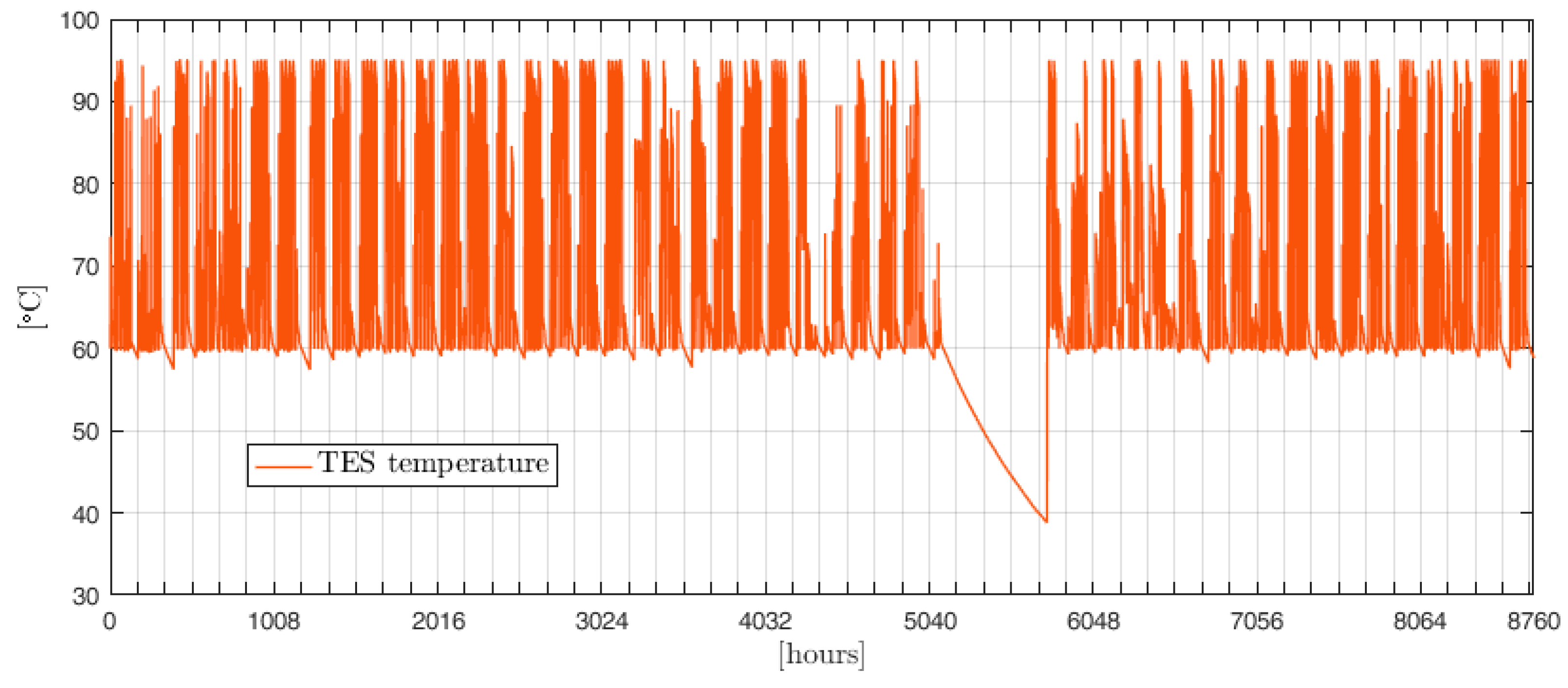
The methodology was tested in a case study, namely a secondary school located in San Francisco, California. The optimal size and operation of the cogeneration system with thermal energy storage were identified. Results from the optimization were presented and discussed. A parametric analysis led to the identification of the optimal values of the rolling-horizon parameters: 24 h for the prediction horizon and 12 h for the control horizon were chosen as a compromise between the accuracy of the results and the computational time. In the case study, the cogeneration unit directly covers around 70% of both the electric and thermal annual demand, while 16% of the latter is met by the storage.
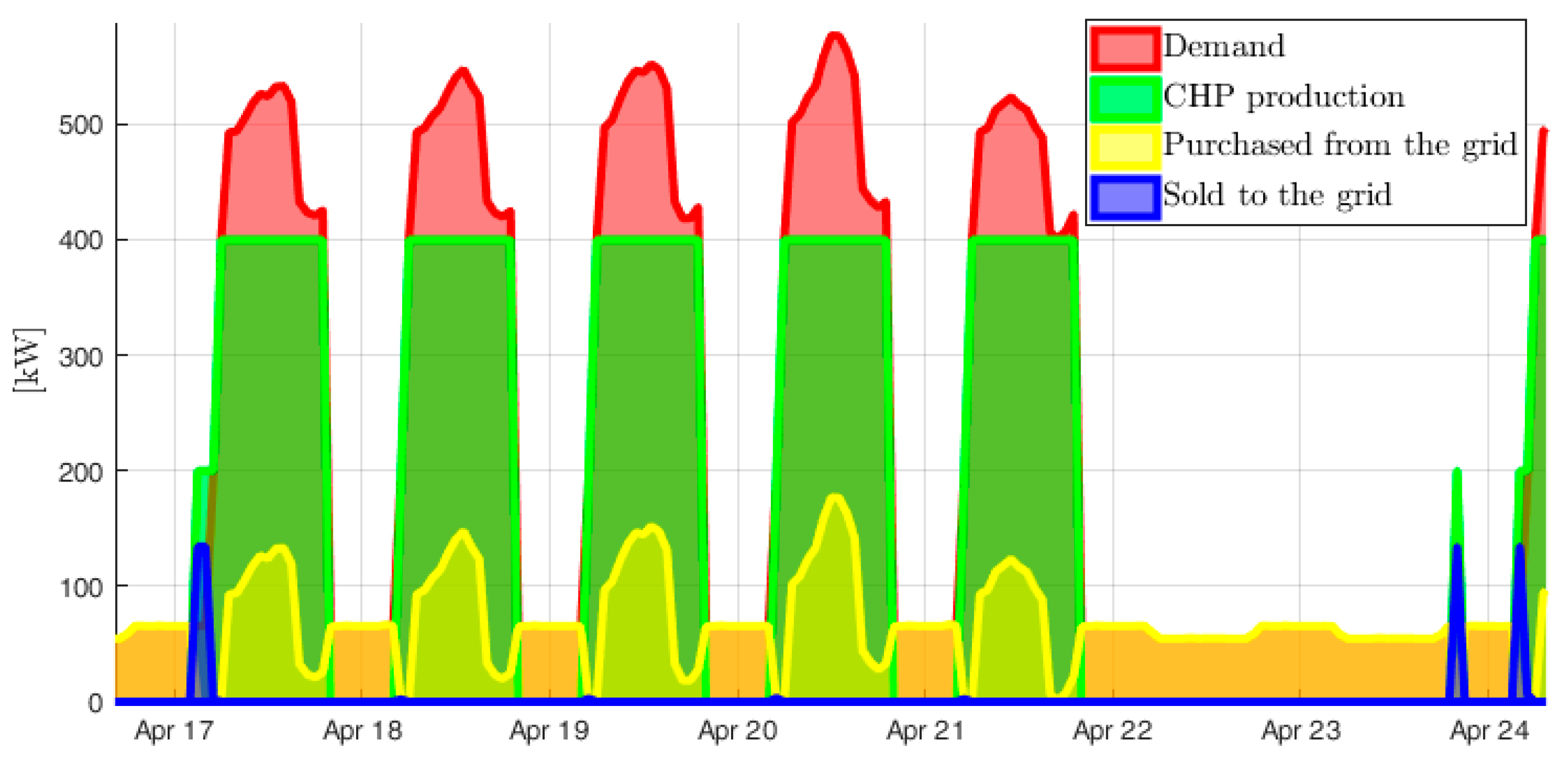
Moreover, the results showed how the proposed formulation allows control strategies for the thermal energy storage to be exploited that cannot be taken into account with conventional simplified formulations. Indeed, instead of keeping the state of charge of the storage always above its minimum operational threshold, the controller allows it to drop below its threshold value. This behavior is particularly marked during extended periods of low or nil demand, as in August, when the school is closed and the temperature of the storage drops significantly below its operational threshold.
Future research may focus on: More complex multi-energy systems (modular cogeneration, heat pumps, renewable energy technologies), the effect of uncertainties on the optimal design, and multi-objective optimization with further criteria (environmental, energetic, exergetic indicators).