Data Science for Vibration Heteroscedasticity and Predictive Maintenance of Rotary Bearings
Abstract
1. Introduction
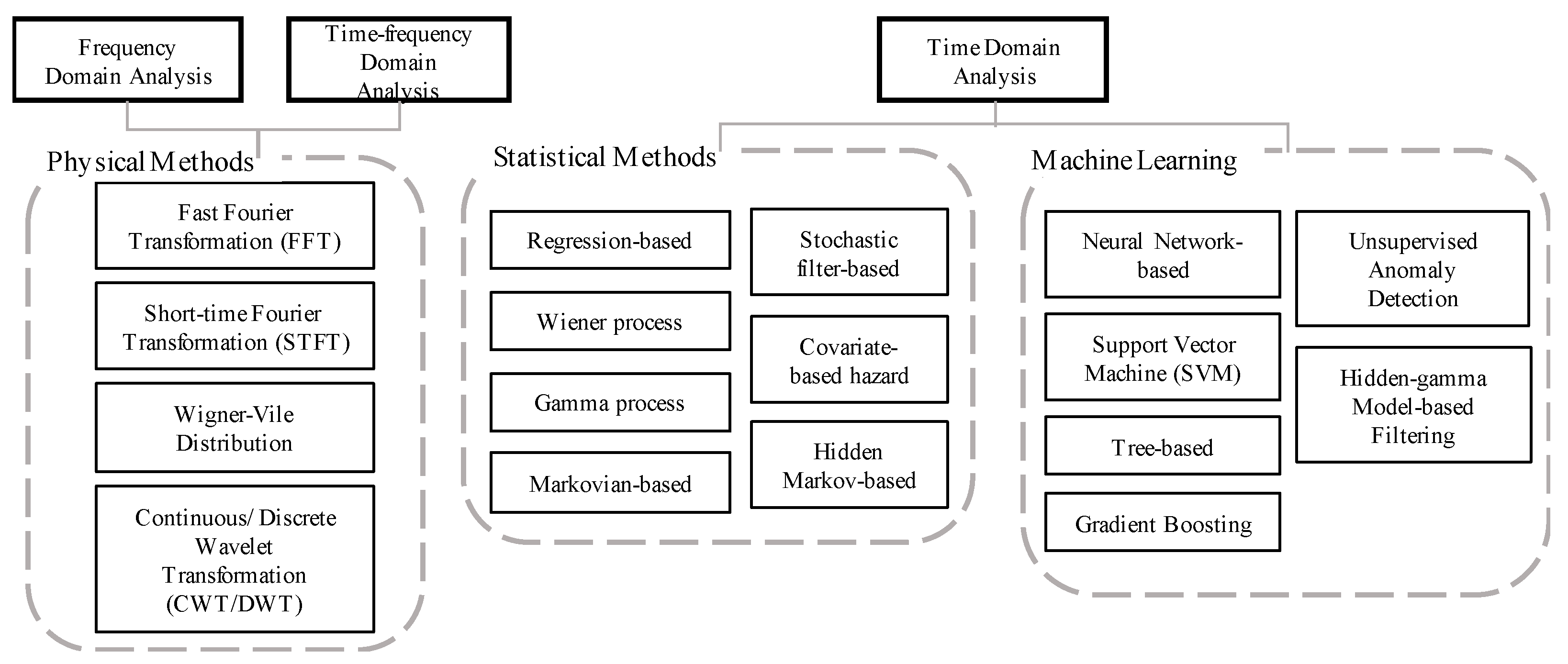
2. Fundamental Methods and Techniques
2.1. Sliding Window with Rolling and Tumbling Aggregates
- (1)
- Window size: a vector or list regarded as offsets compared to the current time.
- (2)
- Step size: moved by the step size of the number of data points rather than every point.
- (3)
- Selected statistic in the window: statistics such as mean, maximum, minimum, etc. can be calculated in the window.
2.2. Stepwise Regression
2.3. Ordinary Least Squares (OLS) and Heteroscedasticity
2.3.1. Weighted Least Squares (WLS)
2.3.2. Feasible Generalized Least Squares (FGLS)
2.4. Partial Least Squares (PLS) Regression
2.5. Support Vector Regression (SVR)
3. Data Science
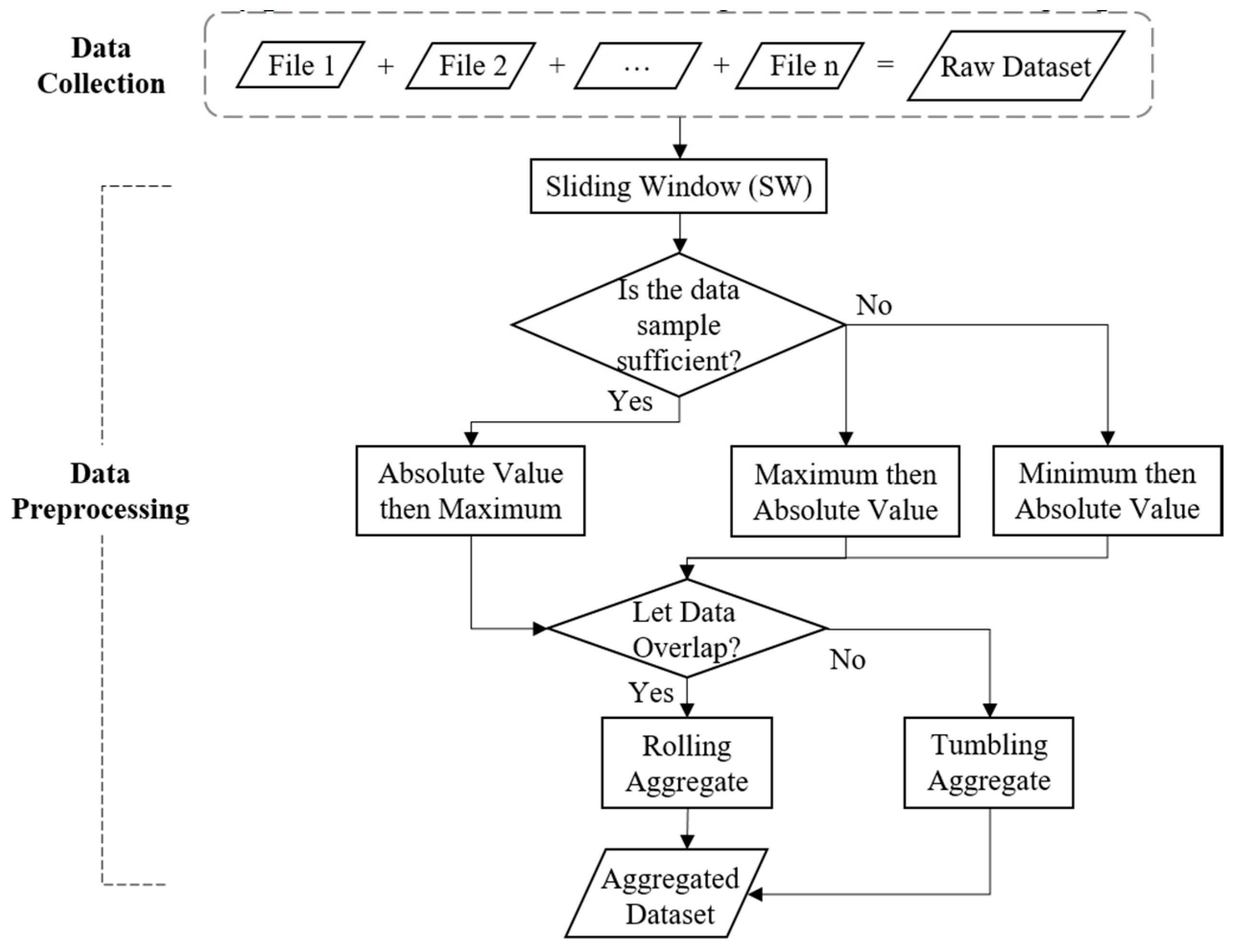
3.1. Experimental Platform and Data Collection
Experimental Platform and Data Collection
|
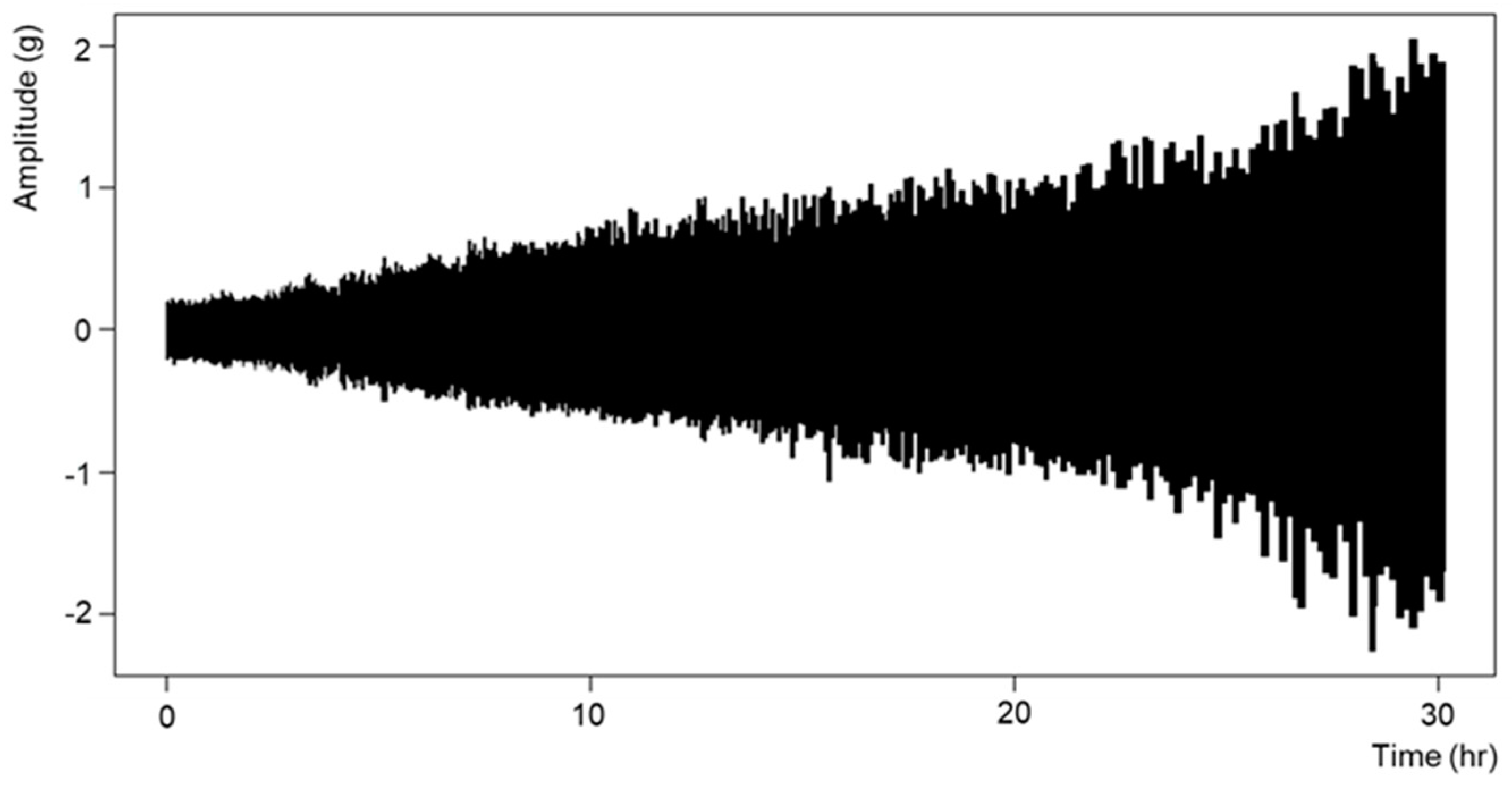
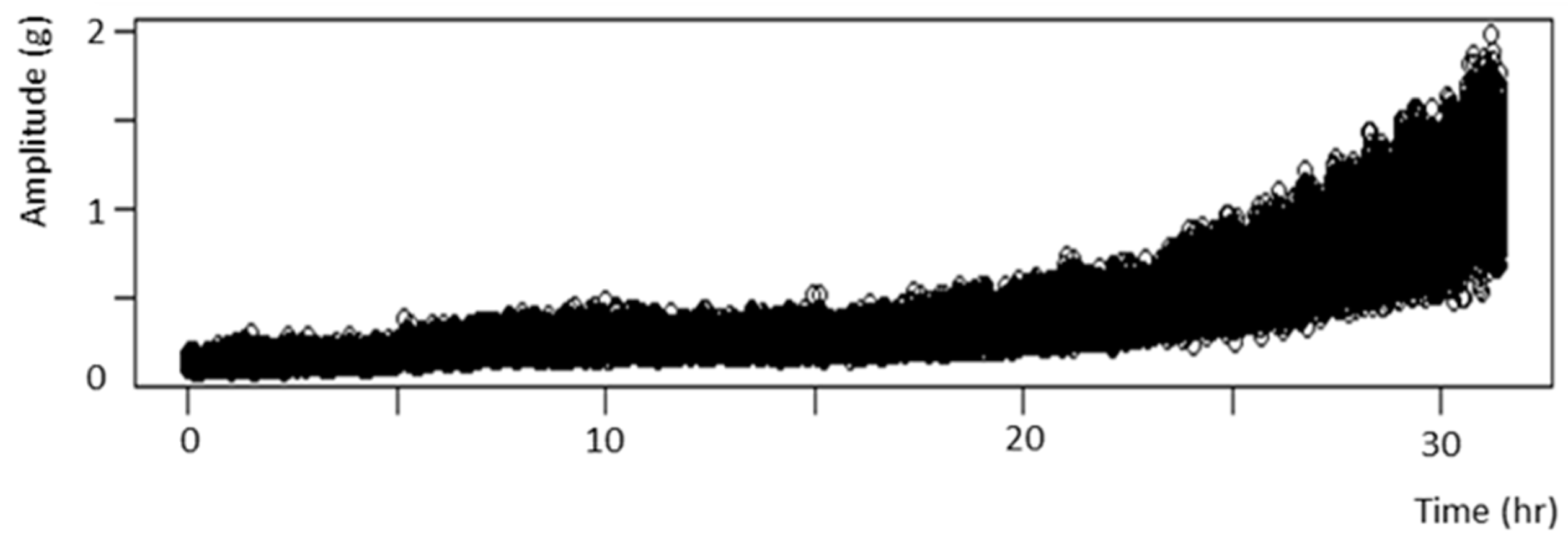
3.2. Data Preprocessing
Data Preprocessing
|
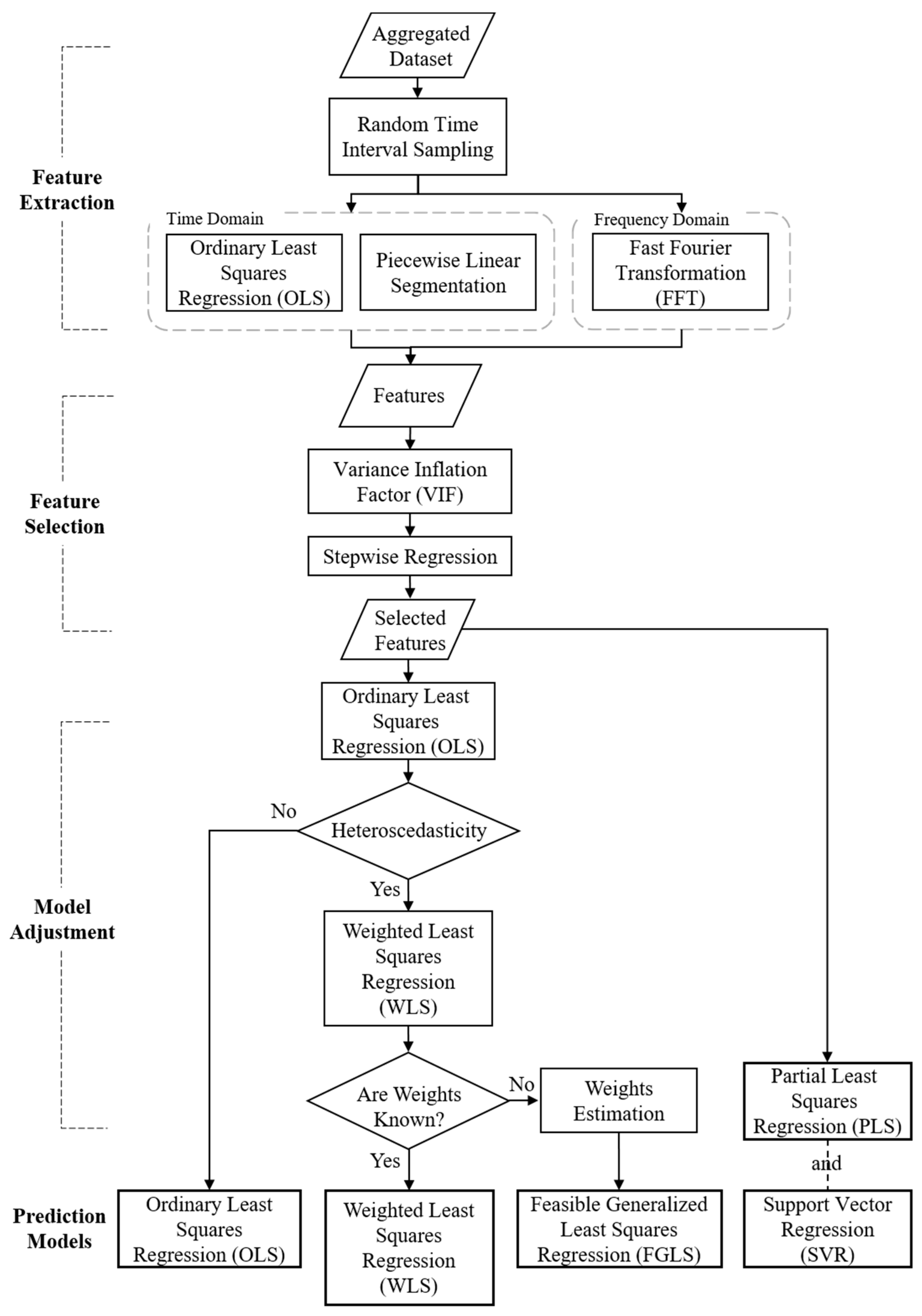
3.3. Feature Extraction
3.3.1. Time-series Dimension
- (1).
- mean squared error (MSE) =
- (2).
- slope = coefficient of time variable in OLS
- (3).
- intercept = coefficient in OLS
- (4).
- skewness =
- (5).
- kurtosis =
- (6).
- max = in the random interval
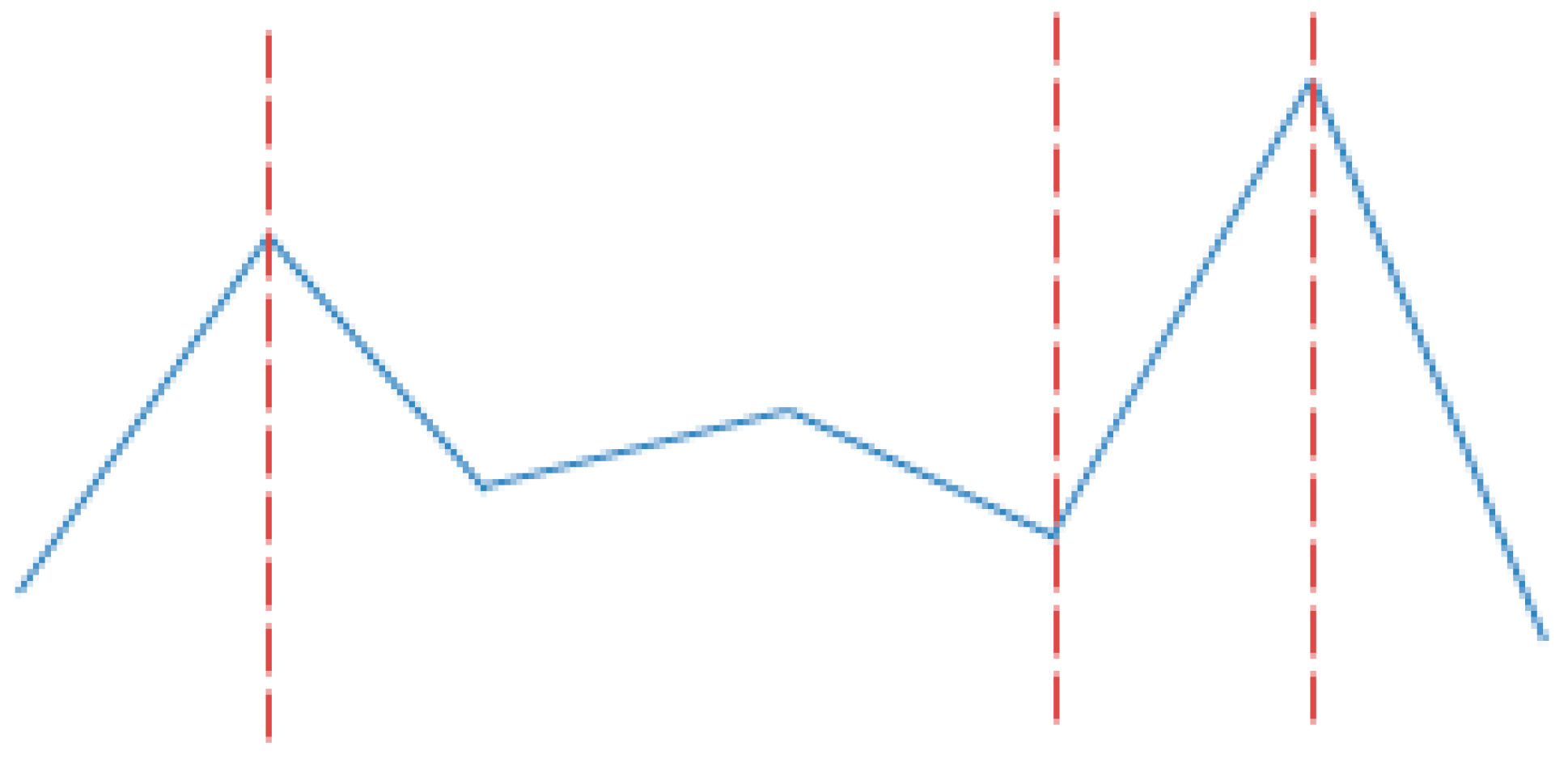
3.3.2. Change-point Dimension
- (7).
- standard deviation () =
- (8).
- first point = the time index when the first change-point occurs
- (9).
- skewness =
- (10).
- kurtosis =
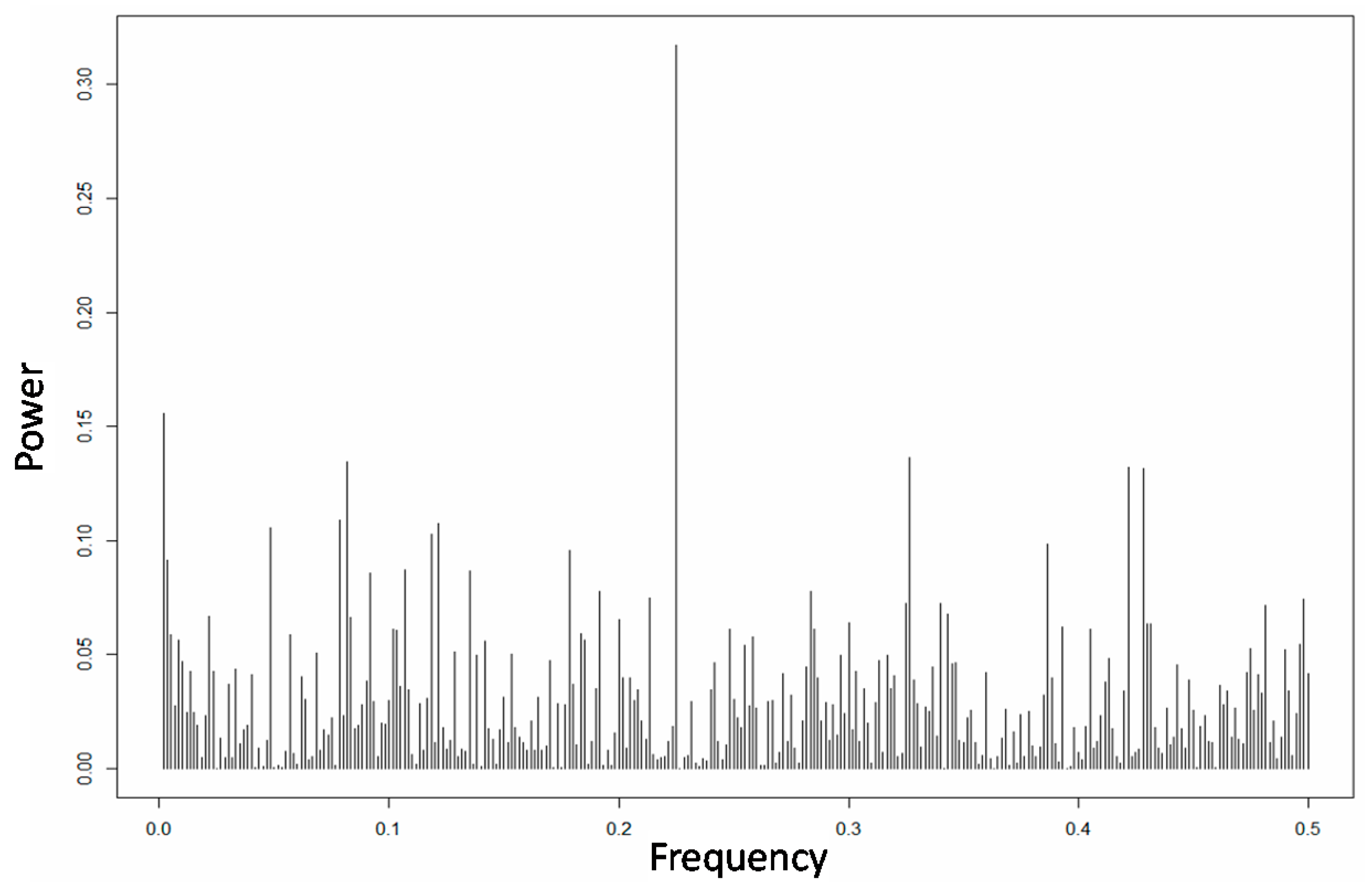
3.3.3. Frequency Domain
Feature Extraction
|
3.4. Feature Selection
3.5. Model Adjustment and Prediction
Model Adjustment and Prediction
|
4. Empirical Study and Experiments
4.1. Data collection and data preprocessing
- The sensors recorded the data at 25,600 data-points per second.
- Redundant information was removed and the data files were compiled into one large data table.
4.2. Feature Extraction
4.3. Feature Selection
4.4. Model Adjustment and Prediction
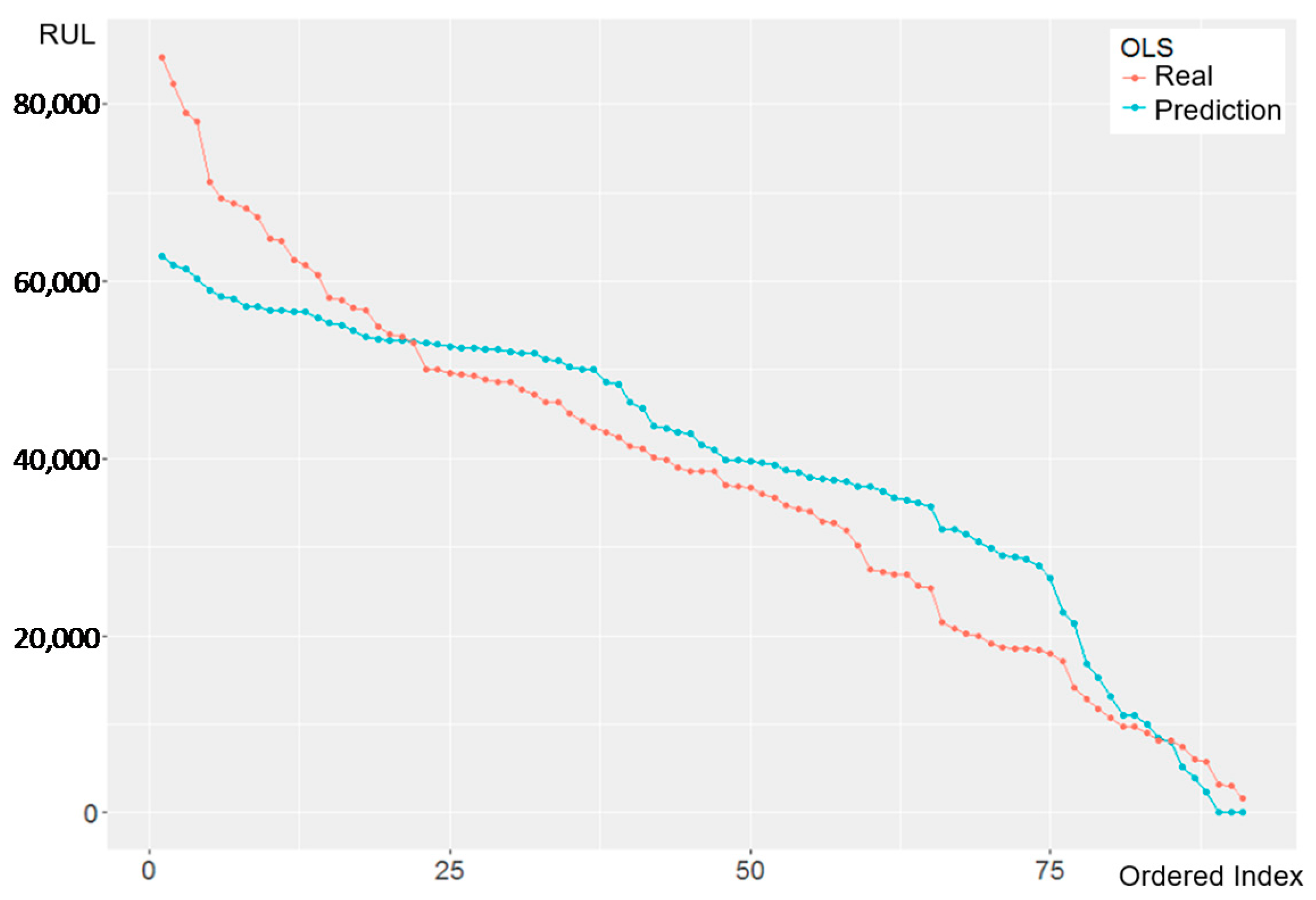
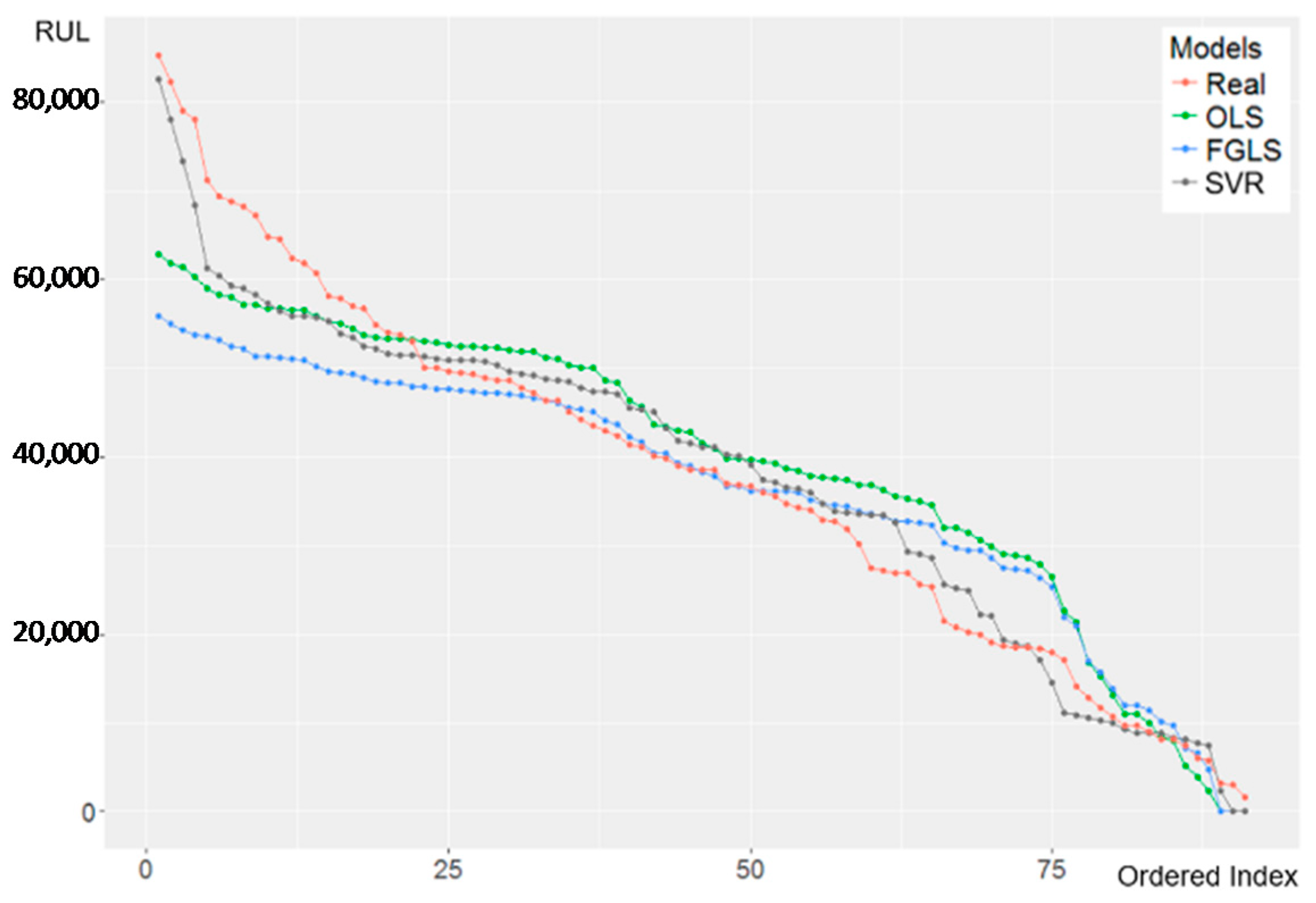
4.5. Prediction Result and Comparison
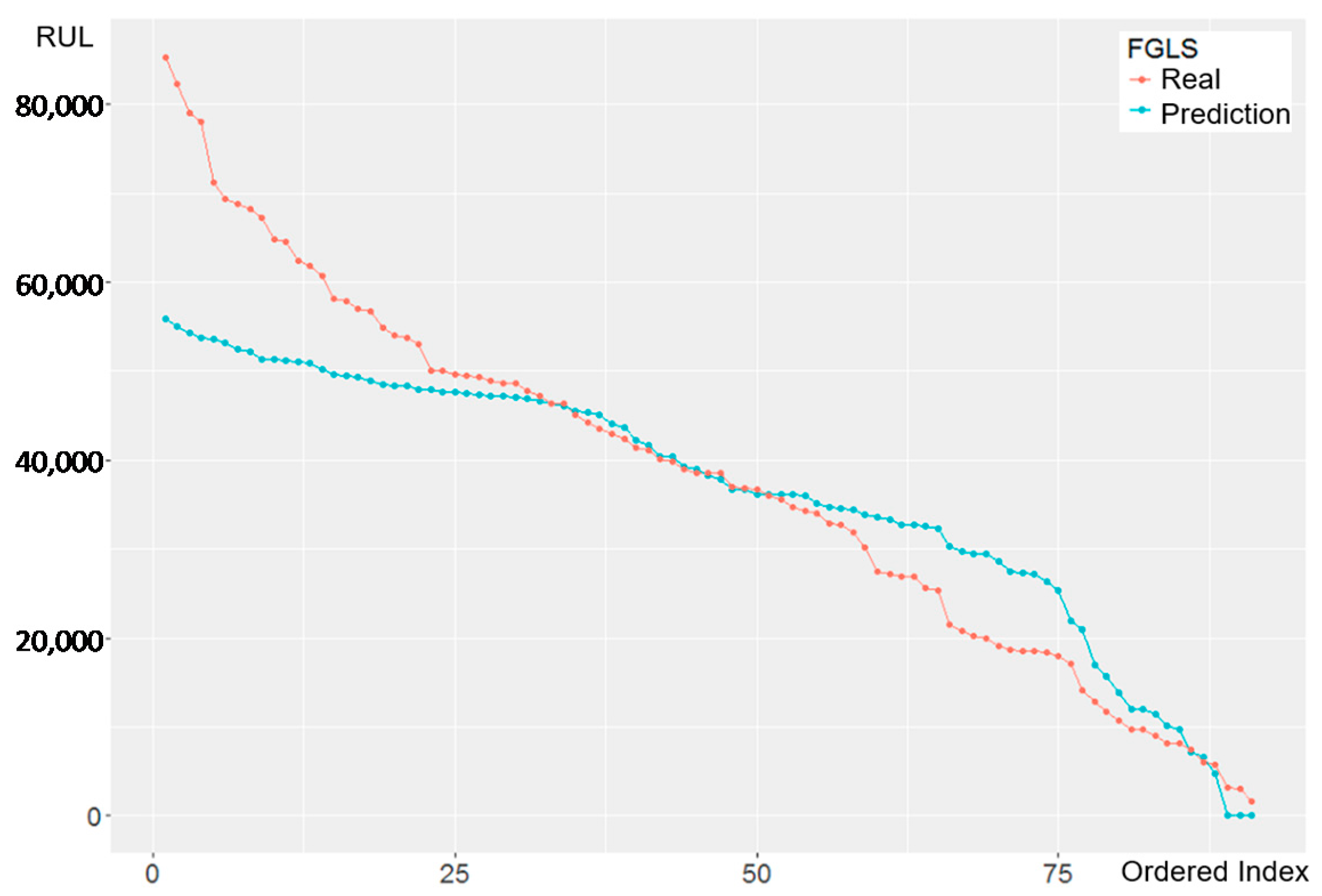
4.5.1. OLS & FGLS
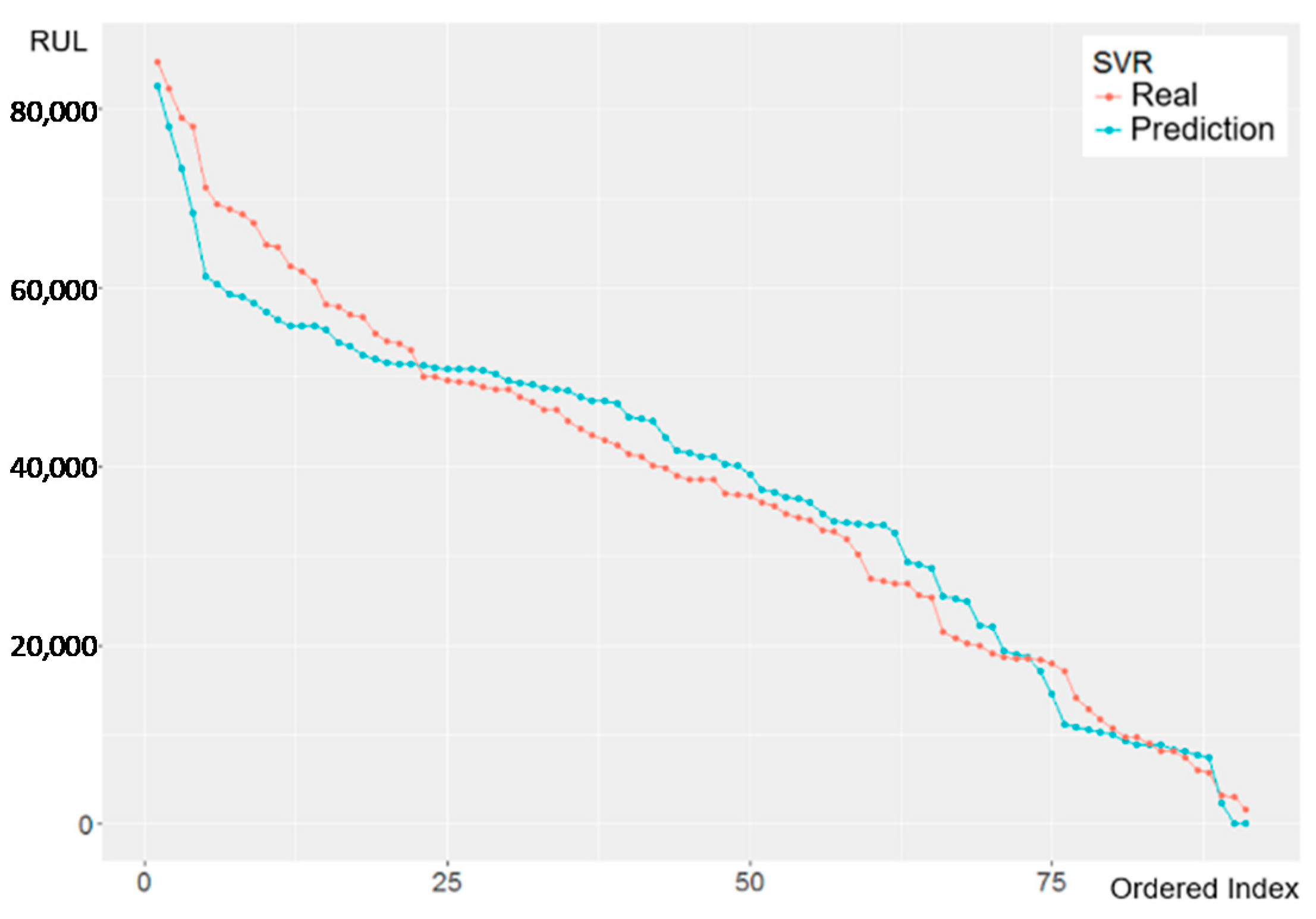
4.5.2. PLS & SVR
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- U.S. Congress. Industrial Energy Use; OTA-E-198; U.S. Congress, Office of Technology Assessment: Washington, DC, USA, June 1983.
- Thomson, W.T.; Fenger, M. Current signature analysis to detect induction motor faults. IEEE Ind. Appl. Mag. 2001, 7, 26–34. [Google Scholar] [CrossRef]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Jardine, A.K.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Lee, C.Y.; Tsai, T.L. Data science framework for variable selection, metrology prediction, and process control in TFT-LCD manufacturing. Robot. Comput. Integr. Manuf. 2019, 55, 76–87. [Google Scholar] [CrossRef]
- Susto, G.A.; Schirru, A.; Pampuri, S.; McLoone, S.; Beghi, A. Machine learning for predictive maintenance: A multiple classifier approach. IEEE Trans. Ind. Inform. 2015, 11, 812–820. [Google Scholar] [CrossRef]
- Si, X.S.; Wang, W.; Hu, C.H.; Zhou, D.H. Remaining useful life estimation–a review on the statistical data driven approaches. Eur. J. Oper. Res. 2011, 213, 1–14. [Google Scholar] [CrossRef]
- Yang, H.; Mathew, J.; Ma, L. Vibration Feature Extraction Techniques for Fault Diagnosis of Rotating Machinery: A Literature Survey. In Proceedings of the Asia-Pacific Vibration Conference, Gold Coast, Australia, 12–14 November 2003. [Google Scholar]
- Susto, G.A.; Schirru, A.; Pampuri, S.; Beghi, A.; De Nicolao, G. A hidden-Gamma model-based filtering and prediction approach for monotonic health factors in manufacturing. Control Eng. Pract. 2018, 74, 84–94. [Google Scholar] [CrossRef]
- Graß, A.; Beecks, C.; Soto, J.A.C. Unsupervised Anomaly Detection in Production Lines. In Machine Learning for Cyber Physical Systems. Technologien für die intelligente Automation (Technologies for Intelligent Automation); Beyerer, J., Kühnert, C., Niggemann, O., Eds.; Springer: Berlin/Heidelberg, Germnay, 2019; Volume 9. [Google Scholar]
- Heng, A.; Zhang, S.; Tan, A.C.; Mathew, J. Rotating machinery prognostics: State of the art, challenges and opportunities. Mech. Syst. Signal Process. 2009, 23, 724–739. [Google Scholar] [CrossRef]
- Keogh, E.; Chakrabarti, K.; Pazzani, M.; Mehrotra, S. Dimensionality reduction for fast similarity search in large time series databases. Knowl. Inf. Syst. 2001, 3, 263–286. [Google Scholar] [CrossRef]
- Fu, T.C. A review on time series data mining. Eng. Appl. Artif. Intell. 2011, 24, 164–181. [Google Scholar] [CrossRef]
- Bastiaans, M. On the sliding-window representation in digital signal processing. IEEE Trans. Acoust. Speechand Signal Process. 1985, 33, 868–873. [Google Scholar] [CrossRef]
- Malanda, A.; Rodriguez-Carreno, I.; Navallas, J.; Rodriguez-Falces, J.; Porta, S.; Gila, L. Sliding window averaging for the extraction of representative waveforms from motor unit action potential trains. Biomed. Signal Process. Control 2016, 27, 32–43. [Google Scholar] [CrossRef]
- Hocking, R.R. The analysis and selection of variables in linear regression. Biometrics 1976, 32, 1–49. [Google Scholar] [CrossRef]
- Lee, C.Y.; Chen, B.S. Mutually-exclusive-and-collectively-exhaustive feature selection scheme. Appl. Soft Comput. 2018, 68, 961–971. [Google Scholar] [CrossRef]
- Strutz, T. Data Fitting and Uncertainty: A Practical Introduction to Weighted Least Squares and Beyond; Vieweg and Teubner; Available online: https://www.springer.com/kr/book/9783658114558 (accessed on 27 February 2019).
- Tenenhaus, M.; Vinzi, V.E.; Chatelin, Y.M.; Lauro, C. PLS path modeling. Comput. Stat. Data Anal. 2005, 48, 159–205. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.J.; Vapnik, V. Support vector regression machines. In Advances in Neural Information Processing Systems; Available online: http://papers.nips.cc/paper/1238-support-vector-regression-machines.pdf (accessed on 27 February 2019).
- O’brien, R.M. A caution regarding rules of thumb for variance inflation factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
| Provider | Company | Remarks |
|---|---|---|
| Experiment | Electrical discharge fatigue destruction experiment | |
| Date | From #1 to #223 (with different hardware and software): 2016.7.25~2018.1.20 From #204 to #221 (with the same settings): 2017.11.26~2018.1.20 | |
| Target | Vibration signal data (amplitude) | |
| Settings | hydraulic oil: 15 mL revolution: 1800 rpm, 30 Hz (mechanical frequency) inverter: 60 Hz (electrical frequency) discharge switch: 6 A self-coupling switch: 16.8 V | |
| Program | Labview program (QMH structure) | |
| Collection frequency | 20 s every 10 min | |
| Stop time | Amplitude > Threshold | |
| Sample Size | three experiments (204, 205, and 206) with the same setting criteria | |
| Time & Revolution & Data point |
| 1 s = 30 rev = 25,600 points, 1/30 s = 1 rev = 853 points |
| Aggregation (turns 853 points into 1 point by SW) |
| 25,600 points ÷ 853 = 30 points/s, 1 point = 1/30 s |
| Return to real time |
| Steps in data preprocessing |
|
| Notes |
|
| Method/ Dimensions | Time-Series Dimension | Change-Point Dimension | Frequency Dimension |
|---|---|---|---|
| Method | OLS | Piecewise linear segmentation | FFT |
| Features | (1) Mse.ts (2) Slope.ts (3) Intercept.ts (4) Skewness.ts (5) Kurtosis.ts (6) Max.ts | (7) Sd.cp (8) First-point.cp (9) Skewness.cp (10) Kurtosis.cp | (11) Ampl1.f (12) Ampl1-freq.f (13) Ampl2.f (14) Ampl2-freq.f (15) Ampl-mean.f (16) Ampl-var.f (17) Ampl-skewness.f (18) Ampl-kurtosis.f |
| VIF Test | Stepwise Regression | ||
|---|---|---|---|
| Features | VIF | Features | State |
| Mse.ts | >10 | ||
| Slope.ts | Slope.ts | out | |
| Intercept.ts | >10 | ||
| Skewness.ts | Skewness.ts | out | |
| Kurtosis.ts | Kurtosis.ts | in | |
| Max.ts | Max.ts | in | |
| Sd.cp | Sd.cp | out | |
| First-point.cp | >10 | ||
| Skewness.cp | Skewness.cp | out | |
| Kurtosis.cp | Kurtosis.cp | out | |
| Ampl1.f | >10 | ||
| Ampl1-freq.f | Ampl1-freq.f | in | |
| Ampl2.f | Ampl2.f | in | |
| Ampl2-freq.f | Ampl2-freq.f | in | |
| Ampl-mean.f | >10 | ||
| Ampl-var.f | Ampl-var.f | out | |
| Ampl-skewness.f | Ampl-skewness.f | out | |
| Ampl-kurtosis.f | >10 | ||
| Coefficient | ||||
|---|---|---|---|---|
| Features | Estimate | Std. Error | t-Value | p-Value |
| (intercept) | 82213.7 | 1142.3 | 71.97 | <2 × 10−16 |
| Max.ts | −46856.5 | 1143.3 | −40.98 | <2 × 10−16 |
| Kurtosis.ts | 2552.9 | 250.1 | 10.21 | <2 × 10−16 |
| Ampl1-freq.f | −15082.7 | 3564.1 | −4.23 | 2.56 × 10−5 |
| Ampl2.f | 3327.4 | 827.9 | 4.02 | 6.34 × 10−5 |
| Ampl2-freq.f | −12951.2 | 2940.9 | −4.40 | 1.19 × 10−5 |
| OLS | Estimate | Std. Error | t-Value | p-Value |
|---|---|---|---|---|
| (Intercept) | 82196.5 | 1143.7 | 71.87 | <2 × 10−16 |
| Max.ts | −46850.2 | 1144.7 | −40.93 | <2 × 10−16 |
| Kurtosis.ts | 2545.5 | 250.4 | 10.17 | <2 × 10−16 |
| Ampl1-freq.f | −14999.1 | 3568.3 | −4.20 | 2.89 × 10−5 |
| Ampl2.f | 3426.3 | 827.1 | 4.14 | 3.76 × 10−5 |
| Ampl2-freq.f | −12801.0 | 2943.4 | −4.35 | 1.53 × 10−5 |
| FGLS | Estimate | Std. Error | t-Value | p-Value |
|---|---|---|---|---|
| (Intercept) | 73313.9 | 1091.7 | 67.16 | <2 × 10−16 |
| Max.ts | −40658.3 | 944.4 | −43.05 | <2 × 10−16 |
| Kurtosis.ts | 2277.4 | 153.7 | 14.82 | <2 × 10−16 |
| Ampl1-freq.f | −12084.4 | 2906.8 | −4.16 | 3.53 × 10−5 |
| Ampl2.f | 1929.8 | 567.1 | 3.40 | 0.0007 |
| k-Fold | k = 1 | k = 2 | … | k = 10 | Avg. | Std. | |
|---|---|---|---|---|---|---|---|
| Training dataset | R2 | 0.765 | 0.769 | … | 0.764 | 0.767 | 0.003 |
| RMSE | 11259 | 11114 | … | 11206 | 11115.86 | 71.61 | |
| Testing dataset | R2 | 0.733 | 0.775 | … | 0.711 | 0.691 | 0.053 |
| RMSE | 10785 | 11081 | … | 10555 | 11428.34 | 657.92 |
| k-Fold | k = 1 | k = 2 | … | k = 10 | Avg. | Std. | |
|---|---|---|---|---|---|---|---|
| Training dataset | R2 | 0.617 | 0.625 | … | 0.594 | 0.617 | 0.013 |
| RMSE | 12435 | 12364 | … | 12677 | 12211.61 | 121.58 | |
| Testing dataset | R2 | 0.574 | 0.627 | … | 0.563 | 0.566 | 0.033 |
| RMSE | 12919 | 12361 | … | 12880 | 12620.84 | 956.21 |
| k-Fold | k = 1 | k = 2 | … | k = 10 | Avg. | Std. | |
|---|---|---|---|---|---|---|---|
| Training dataset | R2 | 0.831 | 0.839 | … | 0.842 | 0.829 | 0.01 |
| RMSE | 9223 | 9041 | … | 9015 | 9066.63 | 90.54 | |
| Testing dataset | R2 | 0.907 | 0.834 | … | 0.915 | 0.824 | 0.055 |
| RMSE | 9090 | 10219 | … | 8165 | 9772.45 | 927 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-Y.; Huang, T.-S.; Liu, M.-K.; Lan, C.-Y. Data Science for Vibration Heteroscedasticity and Predictive Maintenance of Rotary Bearings. Energies 2019, 12, 801. https://doi.org/10.3390/en12050801
Lee C-Y, Huang T-S, Liu M-K, Lan C-Y. Data Science for Vibration Heteroscedasticity and Predictive Maintenance of Rotary Bearings. Energies. 2019; 12(5):801. https://doi.org/10.3390/en12050801
Chicago/Turabian StyleLee, Chia-Yen, Ting-Syun Huang, Meng-Kun Liu, and Chen-Yang Lan. 2019. "Data Science for Vibration Heteroscedasticity and Predictive Maintenance of Rotary Bearings" Energies 12, no. 5: 801. https://doi.org/10.3390/en12050801
APA StyleLee, C.-Y., Huang, T.-S., Liu, M.-K., & Lan, C.-Y. (2019). Data Science for Vibration Heteroscedasticity and Predictive Maintenance of Rotary Bearings. Energies, 12(5), 801. https://doi.org/10.3390/en12050801





