Harmonic Distortion Prediction Model of a Grid-Tie Photovoltaic Inverter Using an Artificial Neural Network
Abstract
:1. Introduction
2. Materials and Methods
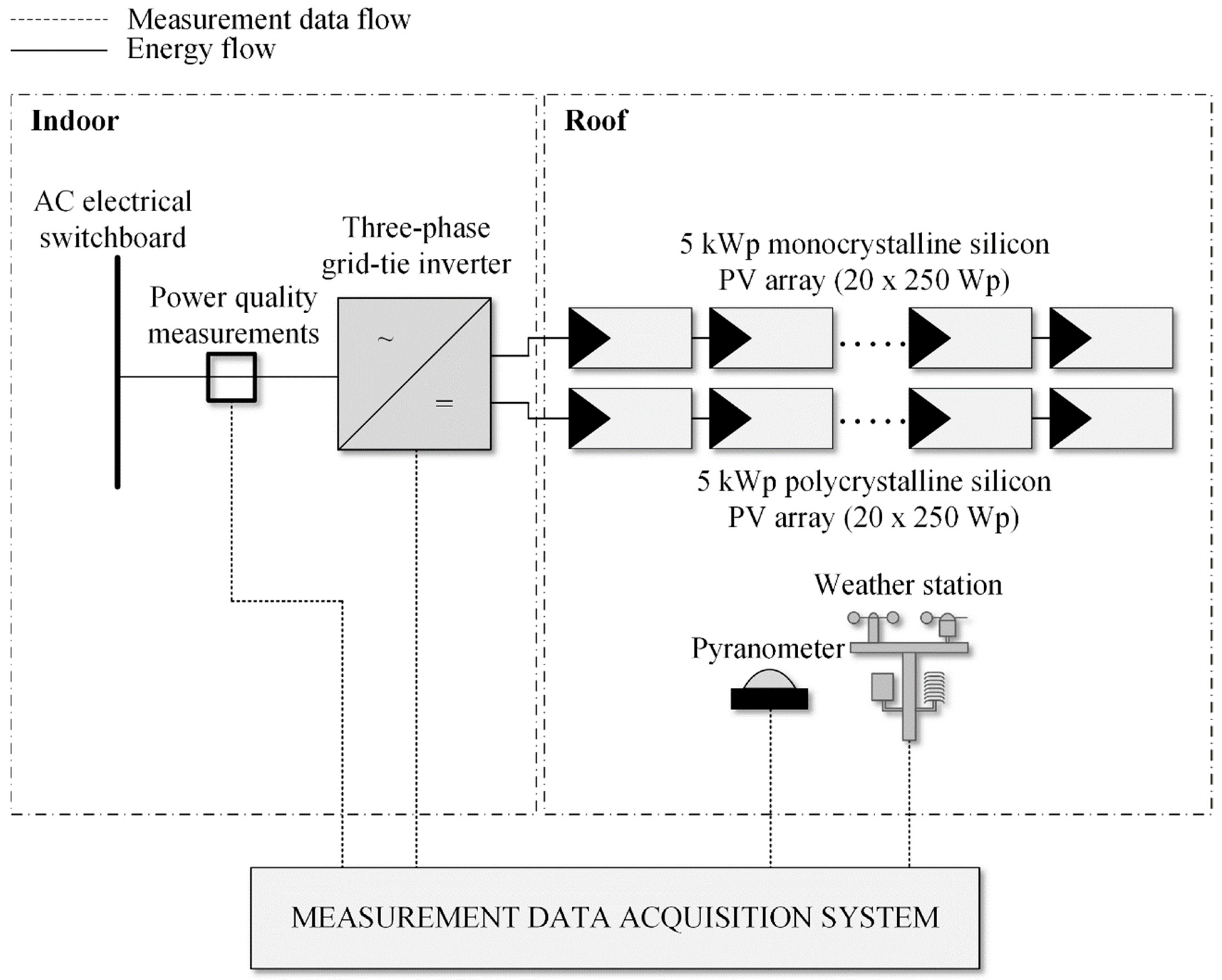
2.1. Description of the Site
2.2. Measurement Procedure
3. Analysis of the Measured Data
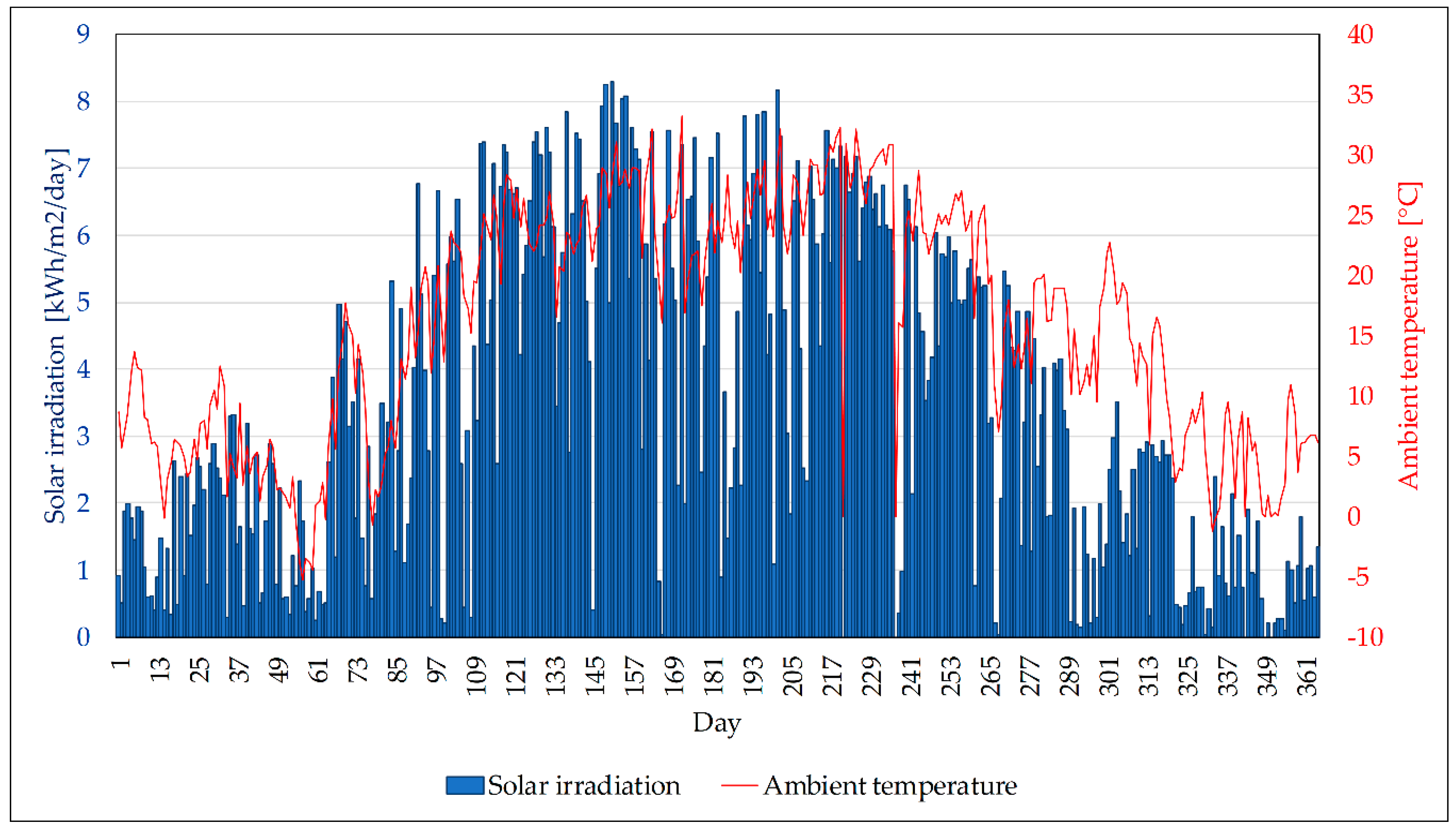
3.1. Meteorological Data
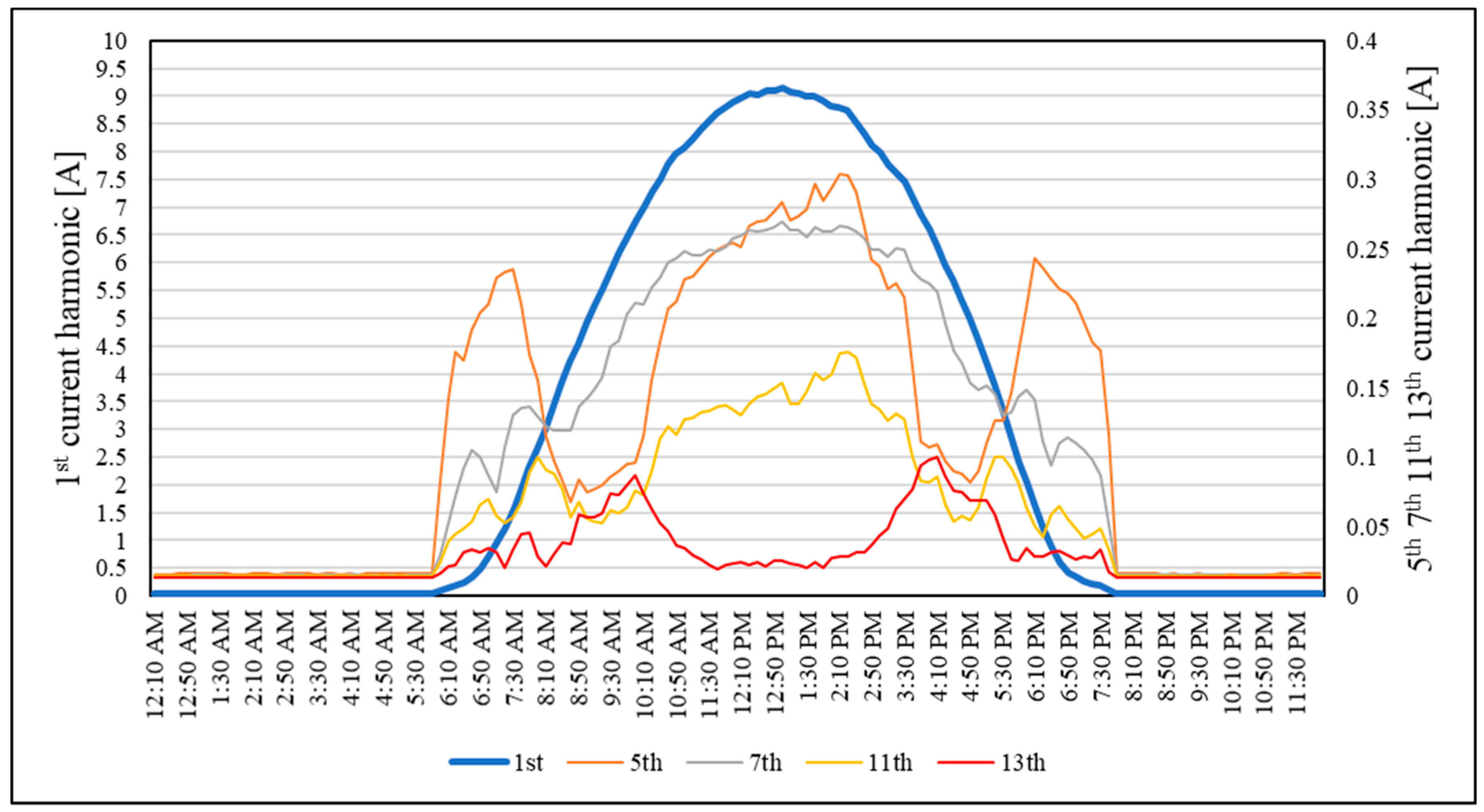
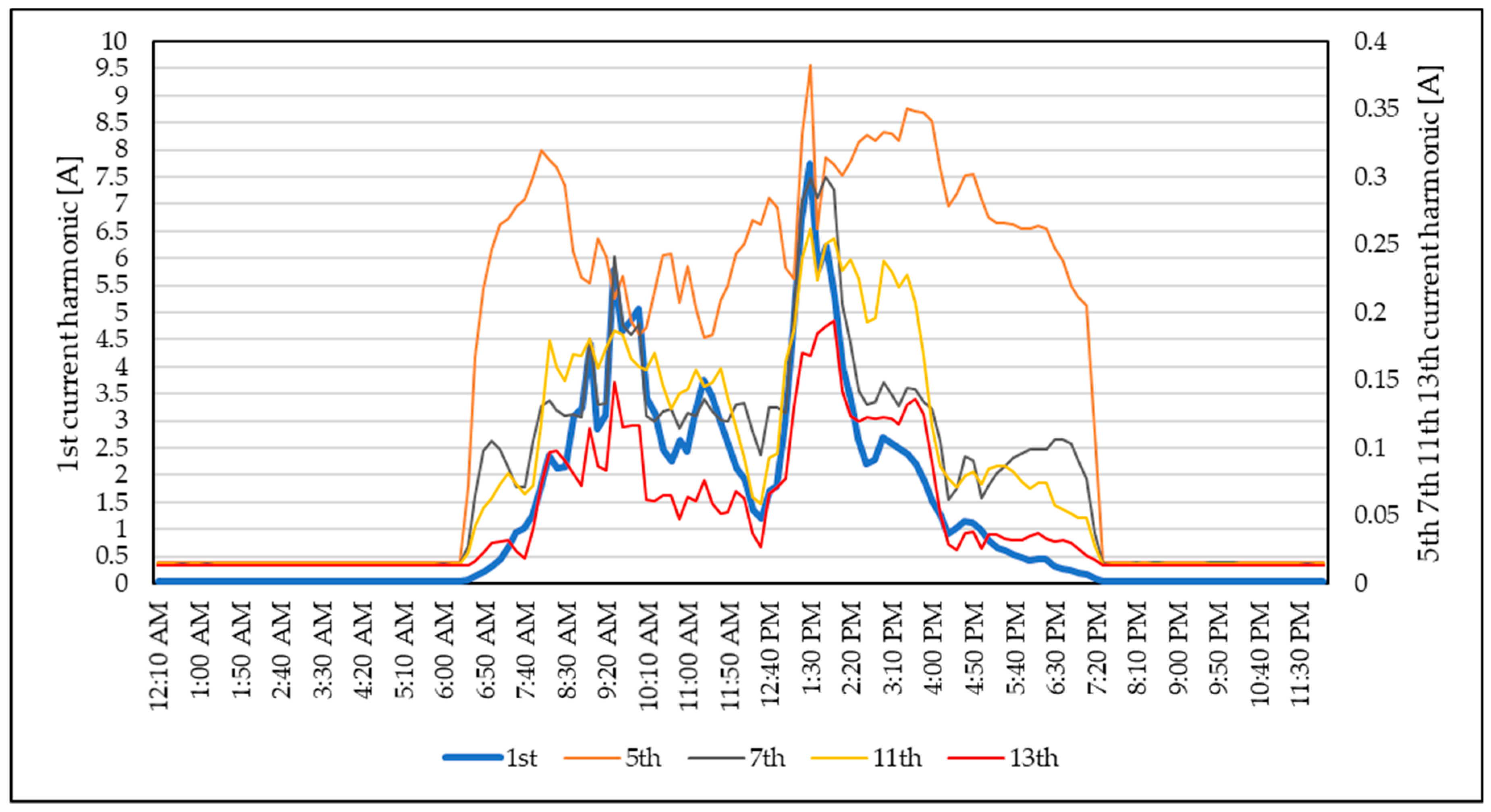
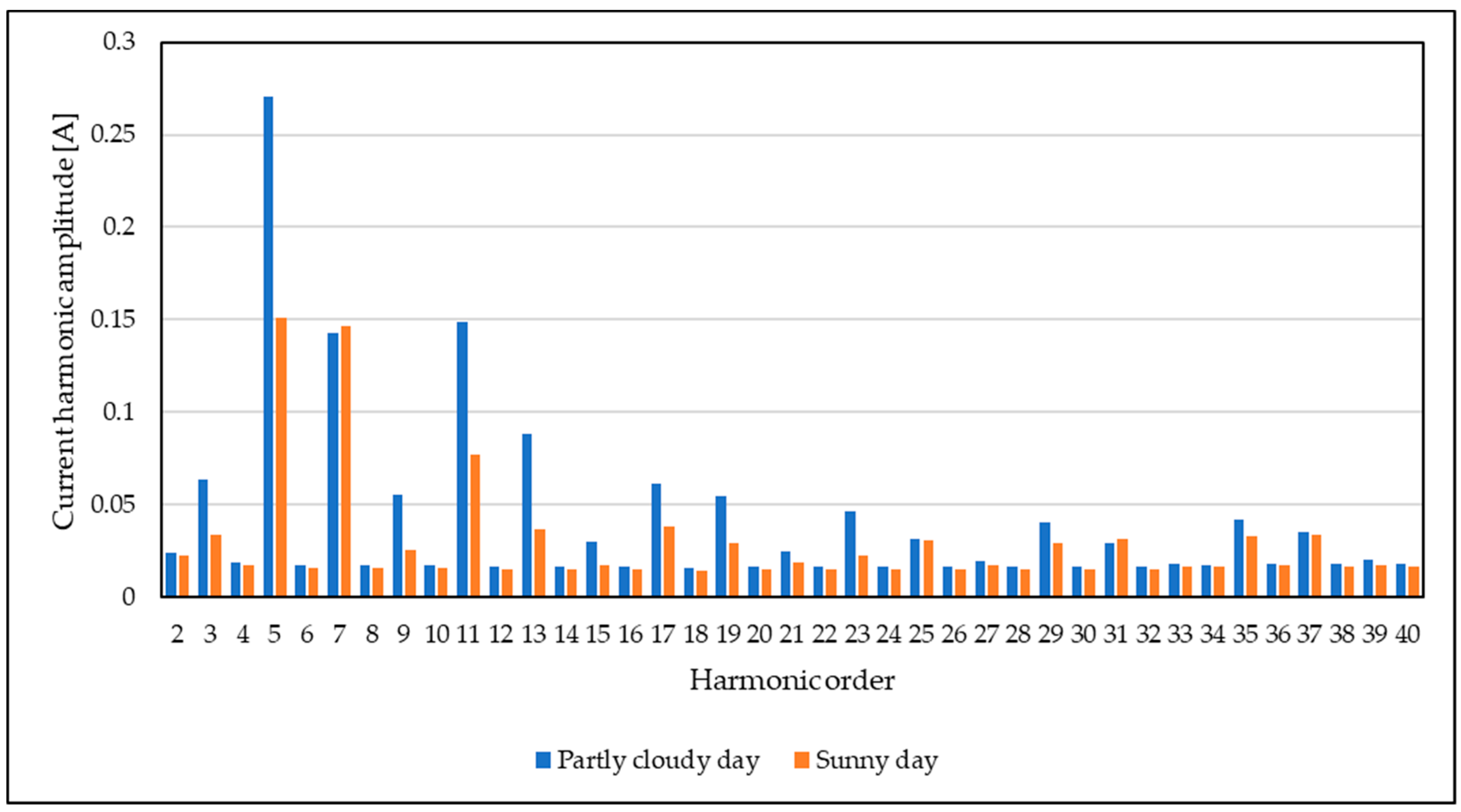
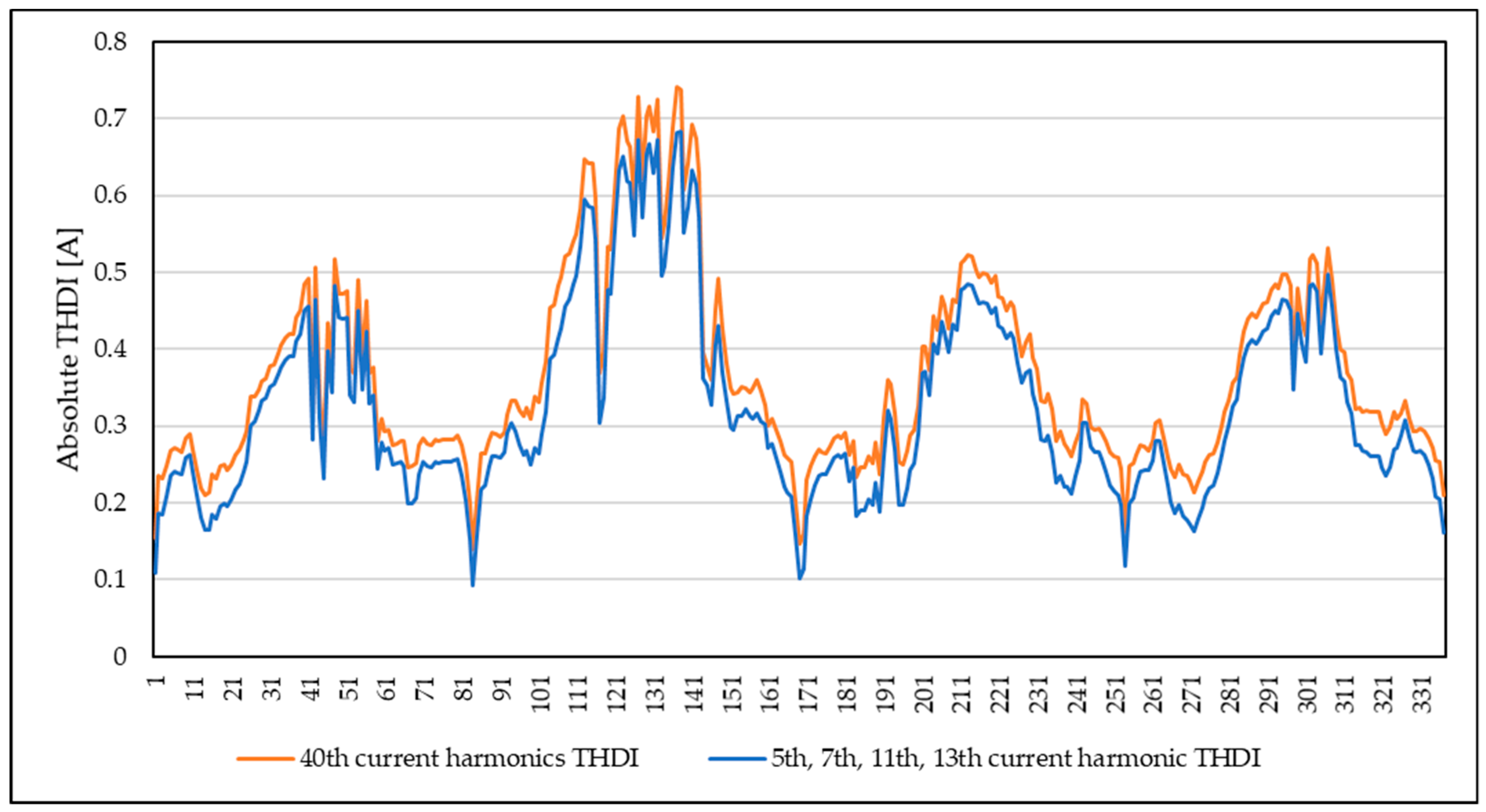
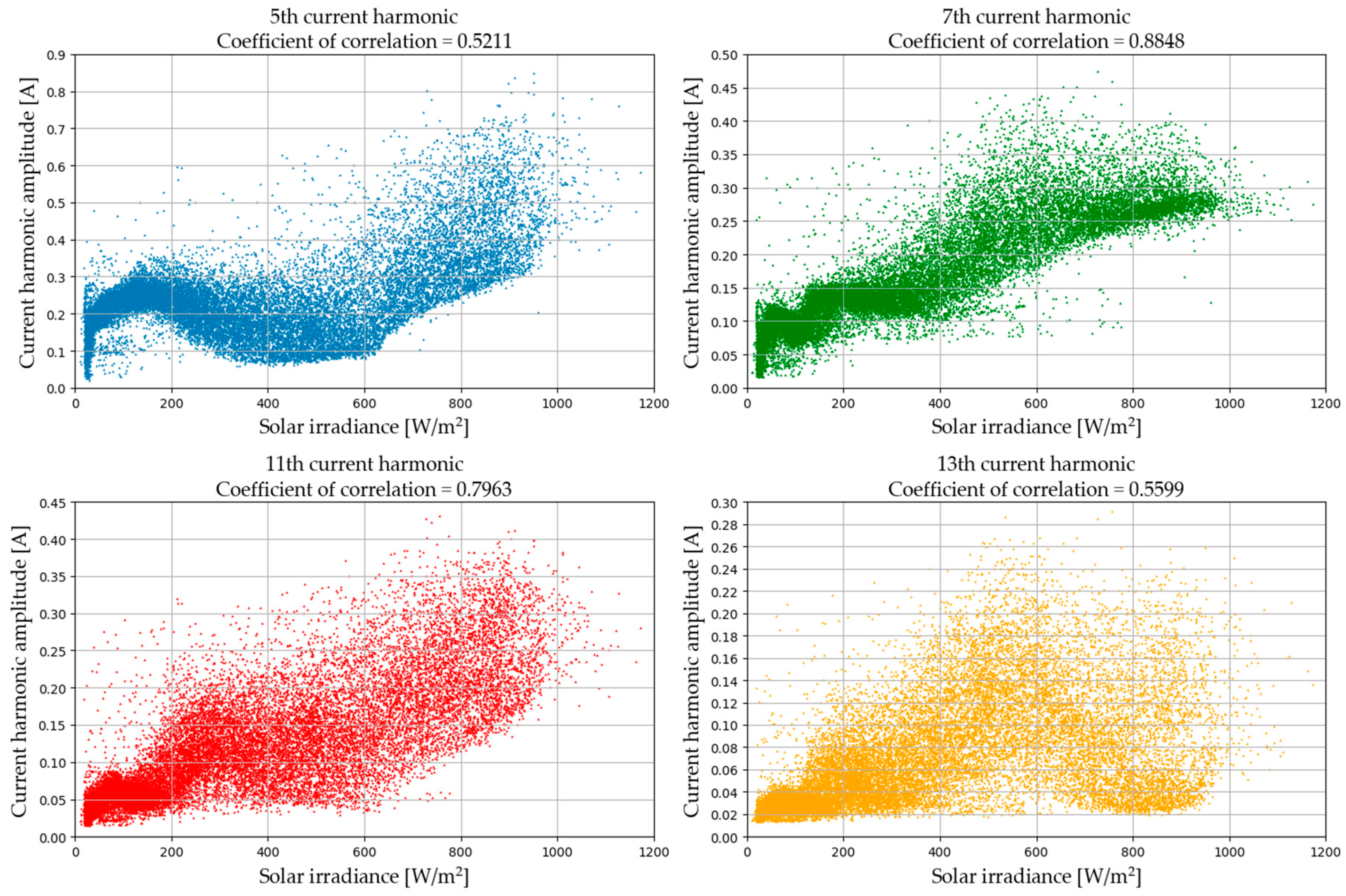
3.2. Power Quality Measurement Analysis
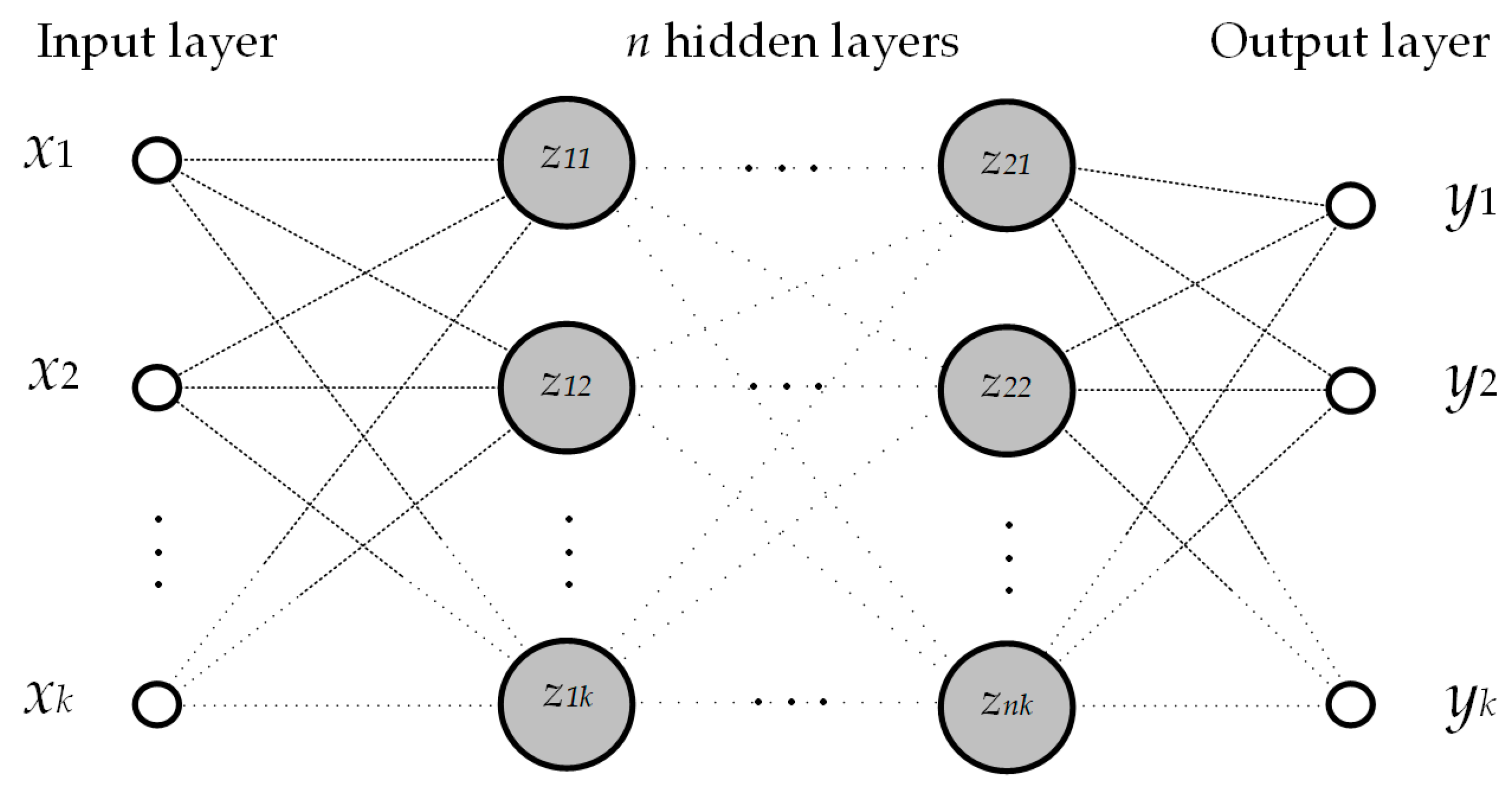
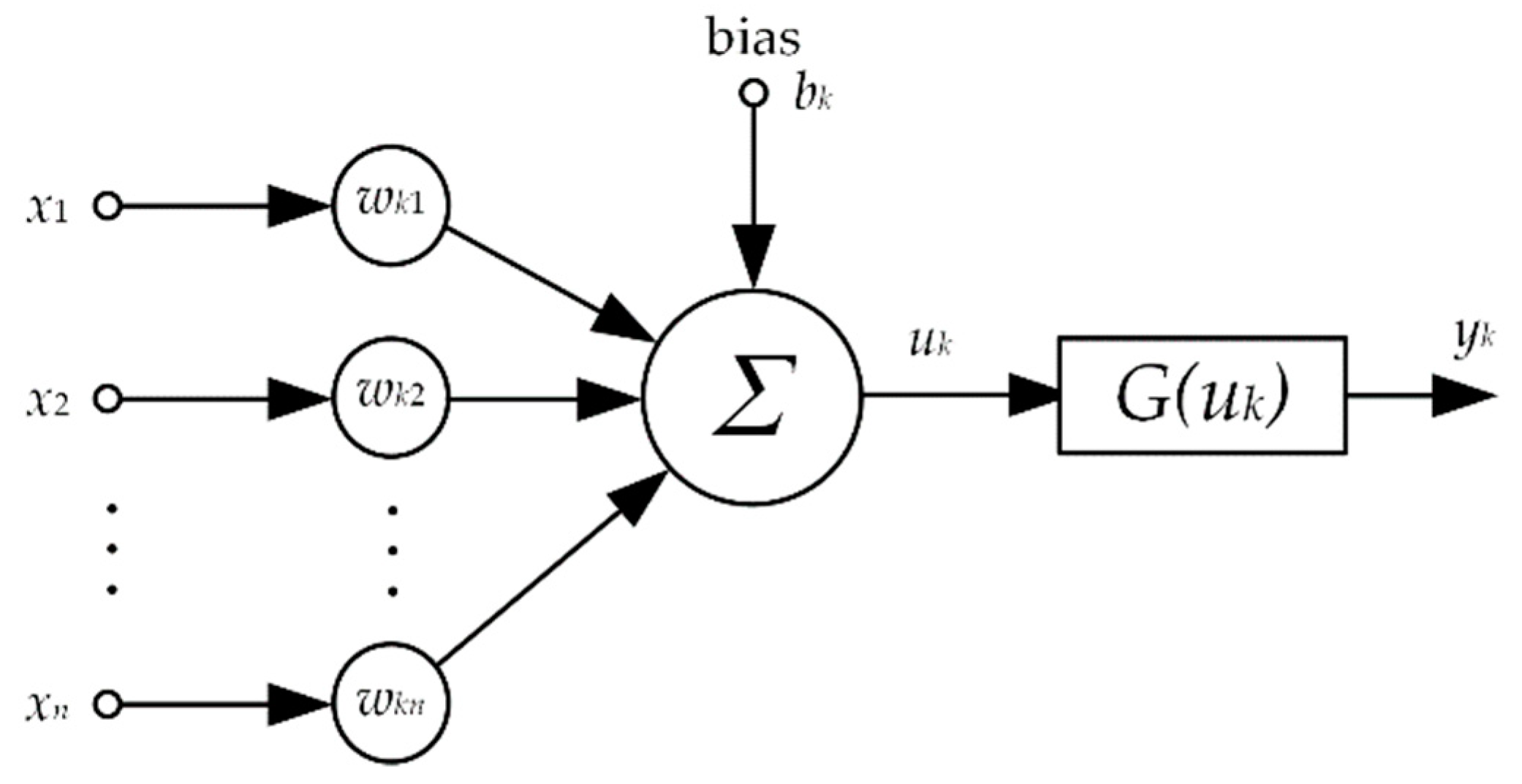
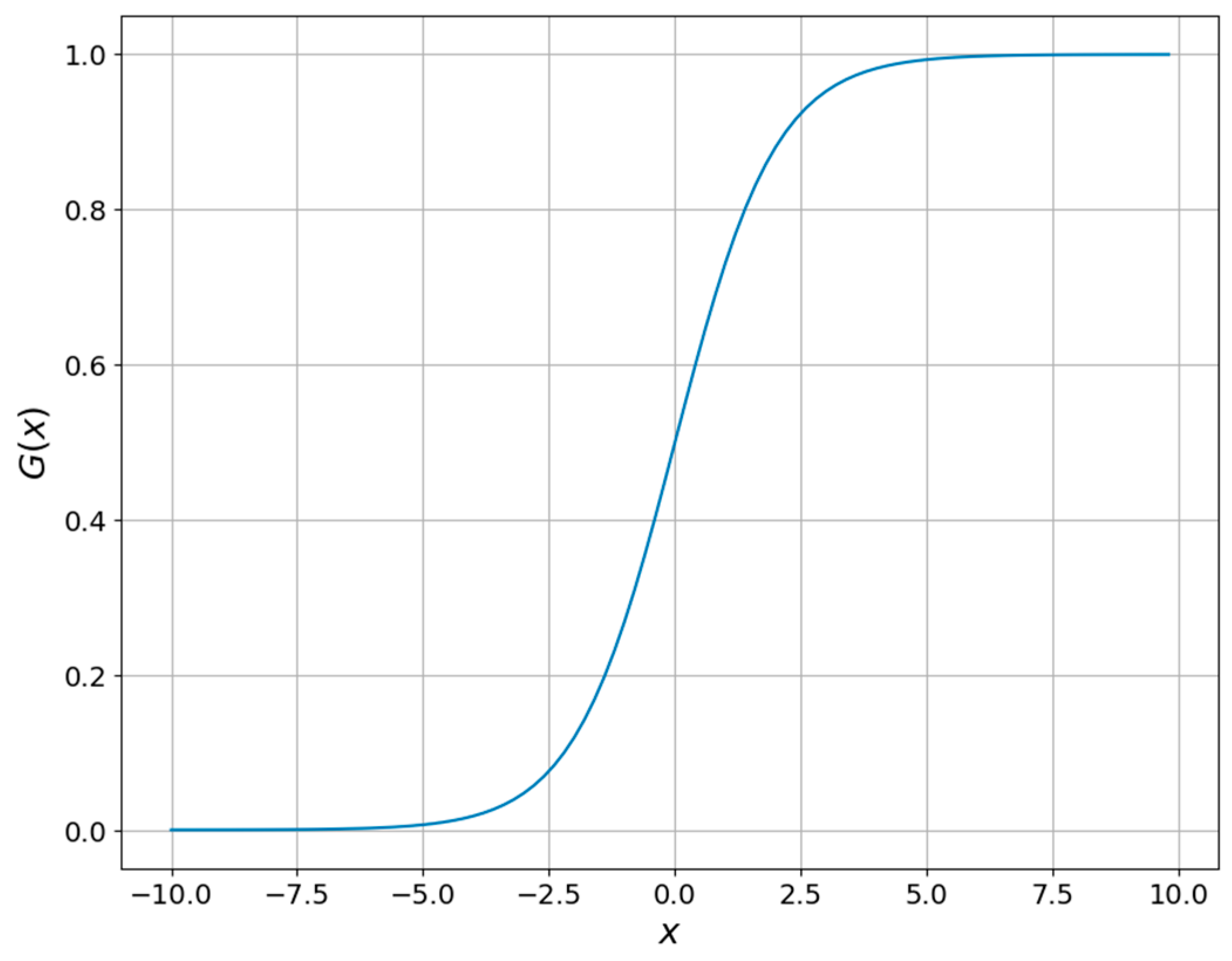
4. Current Harmonics Forecasting with ANN
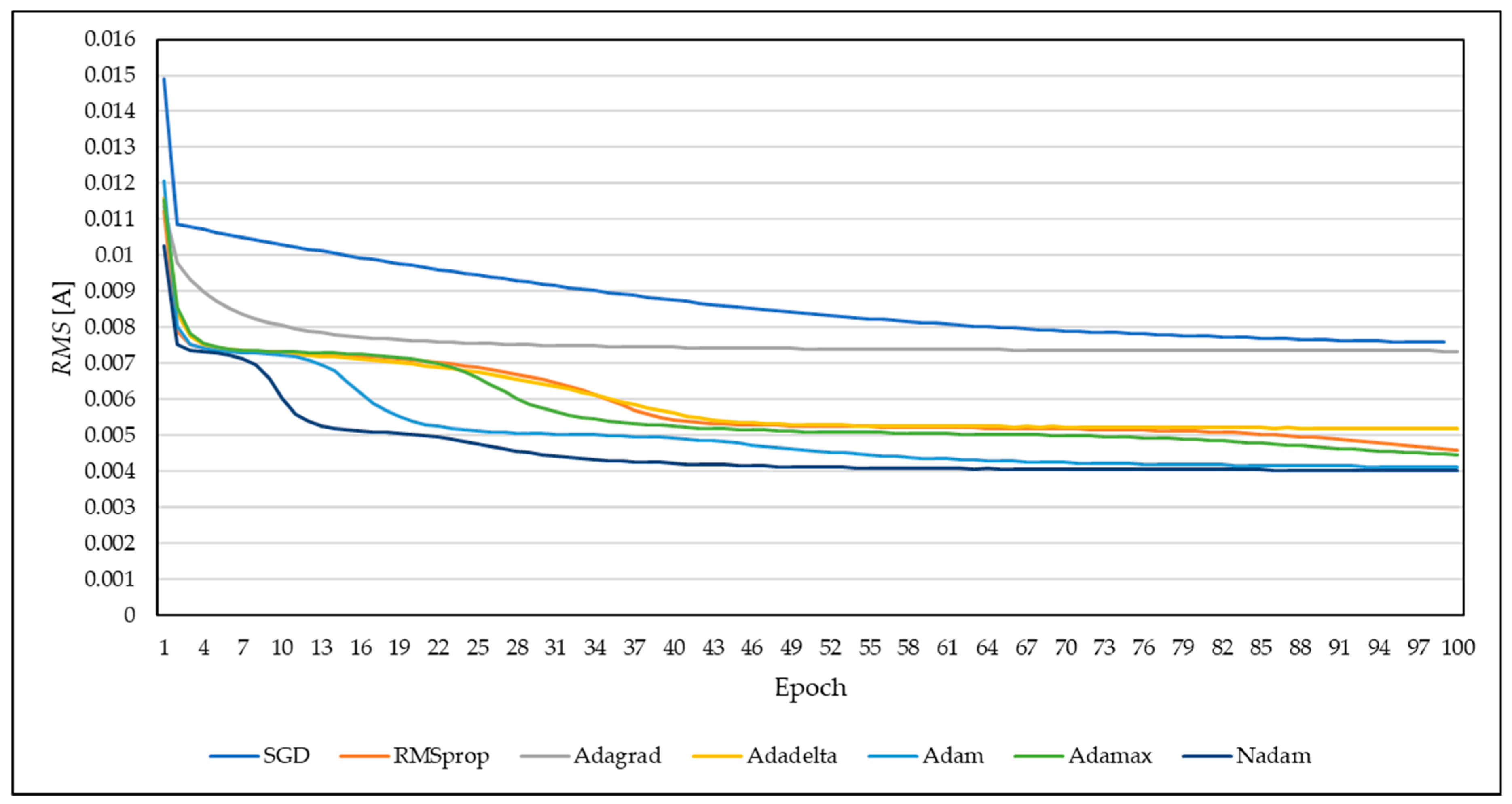
4.1. ANN Model Evaluation
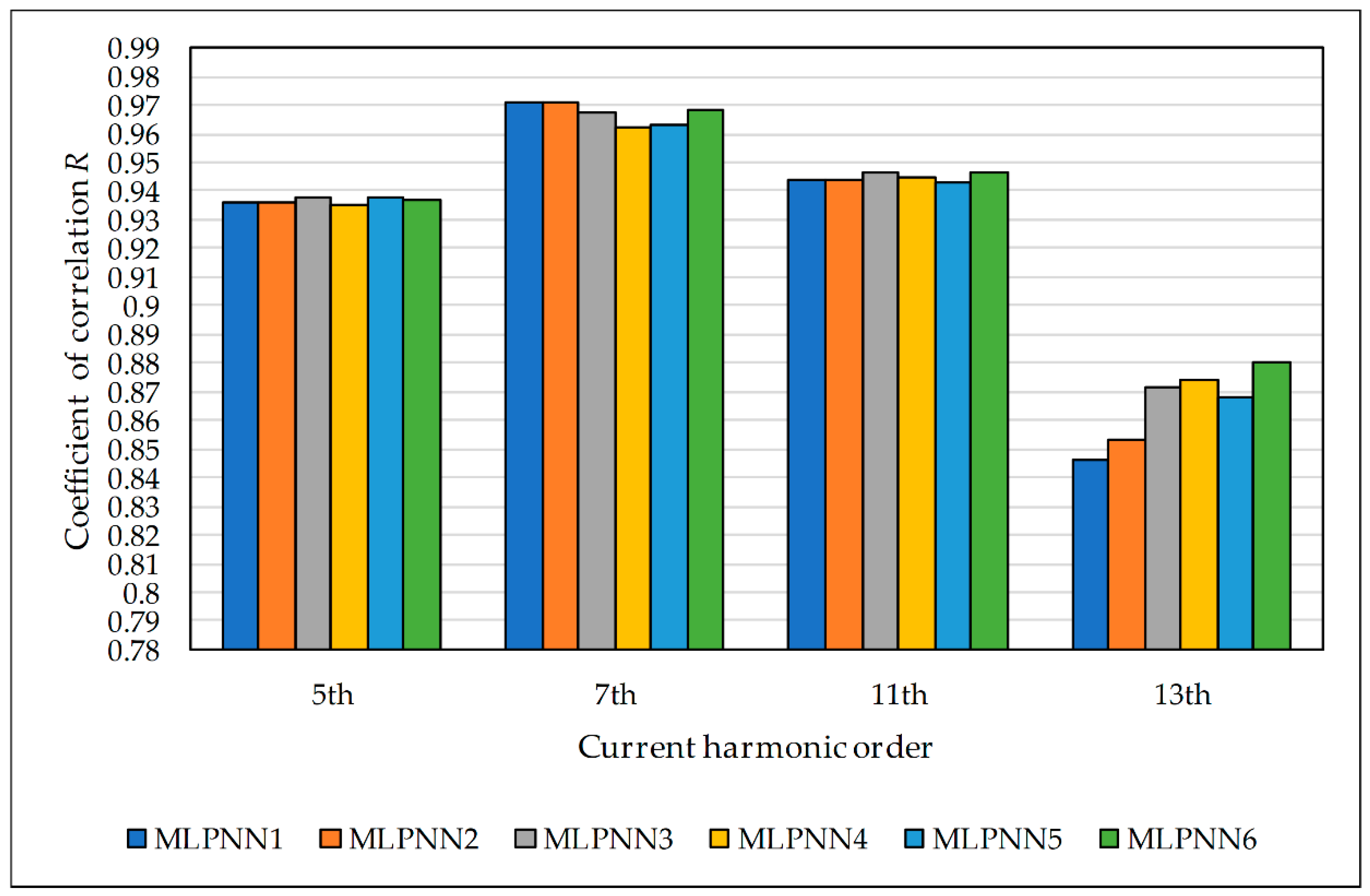
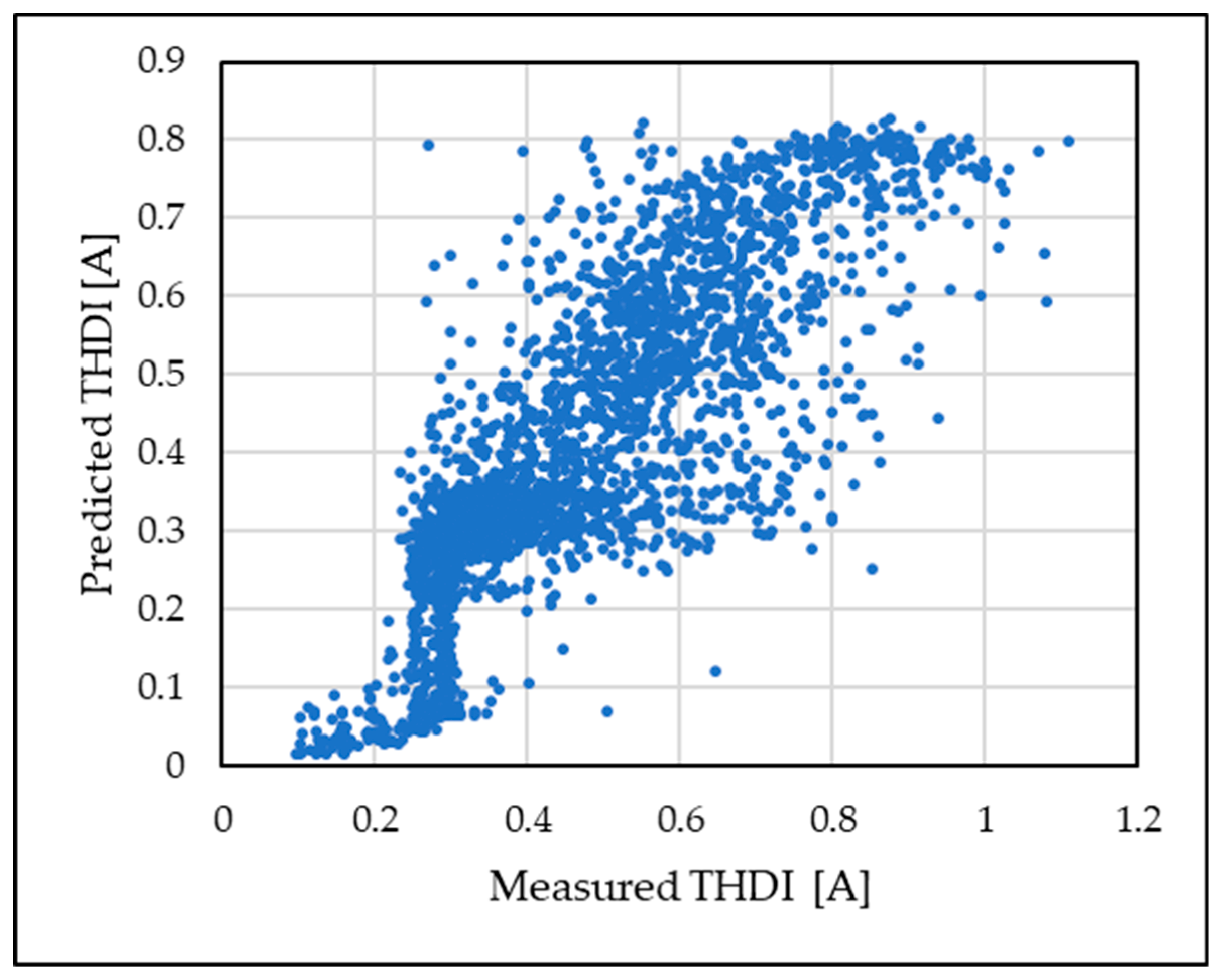
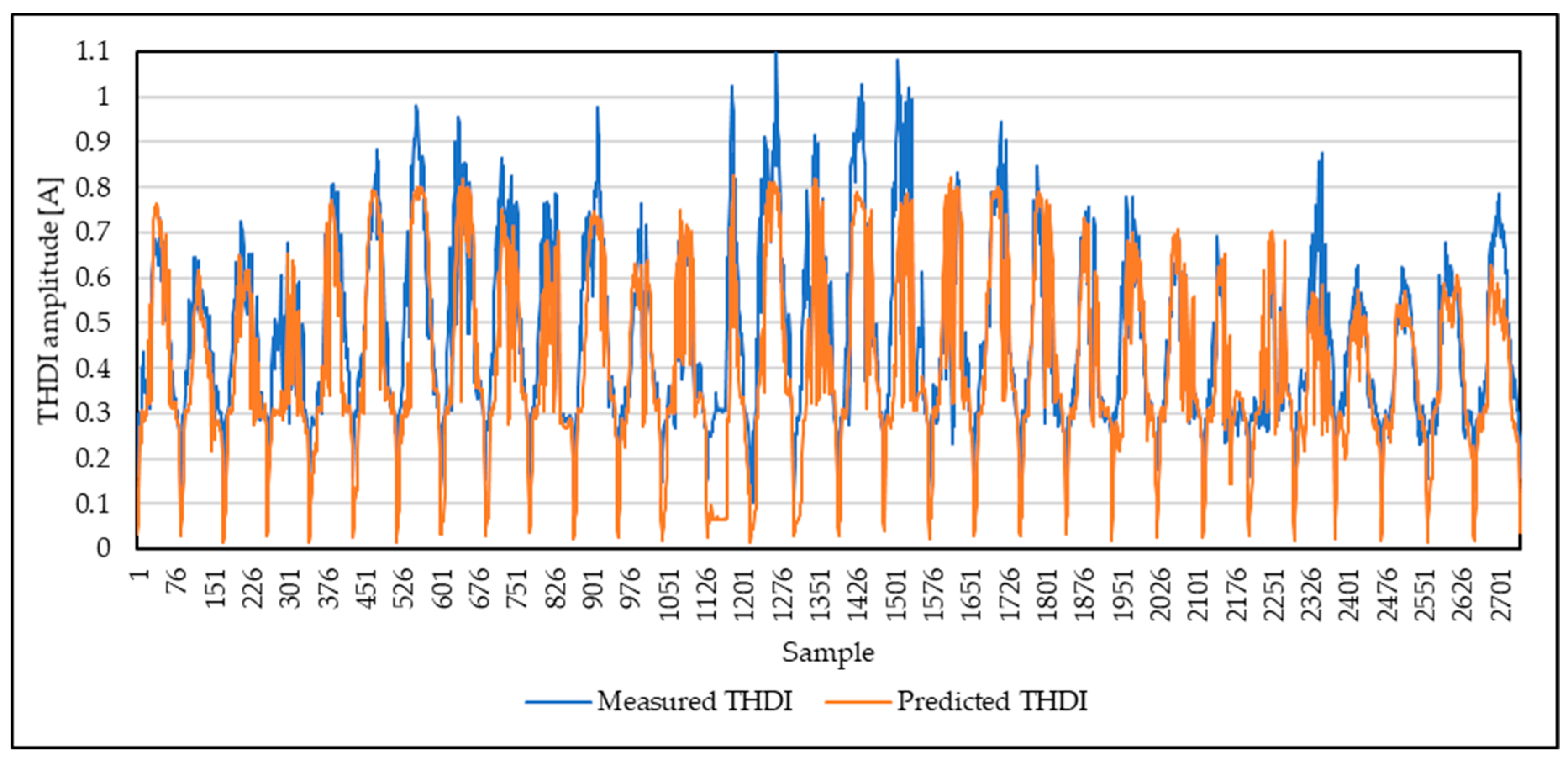
4.2. Simulations, Results, and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- REN21. Renewables 2018 Global Status Report; REN21 Secretariat: Paris, France, 2018; ISBN 9783981891133. [Google Scholar]
- Aiello, M.; Cataliotti, A.; Favuzza, S.; Graditi, G. Theoretical and Experimental Comparison of Total Harmonic Distortion Factors for the Evaluation of Harmonic and Interharmonic Pollution of Grid-Connected Photovoltaic Systems. IEEE Trans. Power Deliv. 2006, 21, 1390–1397. [Google Scholar] [CrossRef]
- Grady, W.M.; Santoso, S. Understanding Power System Hannonics. IEEE Power Eng. Rev. 2001, 21, 8–11. [Google Scholar] [CrossRef]
- Fekete, K.; Klaic, Z.; Majdandzic, L. Expansion of the residential photovoltaic systems and its harmonic impact on the distribution grid. Renew. Energy 2012, 43, 140–148. [Google Scholar] [CrossRef]
- Molina-García, A.; Honrubia-Escribano, A.; García-Sánchez, T.; Gómez-Lázaro, E.; Muljadi, E. Power quality surveys of photovoltaic power plants: Characterisation and analysis of grid-code requirements. IET Renew. Power Gener. 2015, 9, 466–473. [Google Scholar]
- Saini, M.K.; Kapoor, R. Classification of power quality events—A review. Int. J. Electr. Power Energy Syst. 2012, 43, 11–19. [Google Scholar] [CrossRef]
- Khokhar, S.; Mohd Zin, A.A.B.; Mokhtar, A.S.B.; Pesaran, M. A comprehensive overview on signal processing and artificial intelligence techniques applications in classification of power quality disturbances. Renew. Sustain. Energy Rev. 2015, 51, 1650–1663. [Google Scholar] [CrossRef]
- Pereira, H.A.; Freijedo, F.D.; Silva, M.M.; Mendes, V.F.; Teodorescu, R. Harmonic current prediction by impedance modeling of grid-tied inverters: A 1.4 MW PV plant case study. Int. J. Electr. Power Energy Syst. 2017, 93, 30–38. [Google Scholar] [CrossRef]
- McBee, K.D.; Simoes, M.G. Evaluating the Long-Term Impact of a Continuously Increasing Harmonic Demand on Feeder-Level Voltage Distortion. IEEE Trans. Ind. Appl. 2014, 50, 2142–2149. [Google Scholar] [CrossRef]
- Kow, K.W.; Wong, Y.W.; Rajkumar, R.K.; Rajkumar, R.K. A review on performance of artificial intelligence and conventional method in mitigating PV grid-tied related power quality events. Renew. Sustain. Energy Rev. 2016, 56, 334–346. [Google Scholar] [CrossRef]
- Merabet, L.; Saad, S.; Abdeslam, D.O.; Omeiri, A. A comparative study of harmonic currents extraction by simulation and implementation. Int. J. Electr. Power Energy Syst. 2013, 53, 507–514. [Google Scholar] [CrossRef]
- Cao, B.; Chang, L.; Shao, R. A simple approach to current THD prediction for small-scale grid-connected inverters. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 3348–3352. [Google Scholar]
- Rodway, J.; Musilek, P.; Misak, S.; Prokop, L. Prediction of PV power quality: Total harmonic distortion of current. In Proceedings of the 2013 IEEE Electrical Power & Energy Conference, Halifax, NS, Canada, 21–23 August 2013; pp. 1–4. [Google Scholar]
- Dumnic, B.; Popadic, B.; Milicevic, D.; Katic, V.; Corba, Z. Control of grid connected converter with improved power quality characteristic. In Proceedings of the PCIM Europe 2015, International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 19–20 May 2015; pp. 1–8. [Google Scholar]
- De La Rosa, F. Harmonics and Power Systems; Electric Power Engineering Series; CRC Press: Boca Raton, FL, USA, 2006; Volume 13, ISBN 978-0-8493-3016-2. [Google Scholar]
- Meteorological and Hydrological Institute of Croatia Climate in Croatia. Available online: http://klima.hr/klima.php?id=k1#pog1 (accessed on 30 January 2018).
- KACO New Energy GmbH. Operating Instructions Powador 12.0 TL3-20.0 TL3; KACO New Energy GmbH: Neckarsulm, Germany, 2016. [Google Scholar]
- Faculty of Electrical Engineering Computer Science and Information Technology Osijek Laboratory for Renewable Energy Sources. Available online: http://reslab.ferit.hr/ (accessed on 13 October 2018).
- IEC. IEC 61000-4-30 Electromagnetic Compatibility—Testing and Measurement Techniques—Power Quality Measurement Methods; International Electrotechnical Commission: Geneva, Switzerland, 2003. [Google Scholar]
- Haykin, S. Neural Networks A Comprehensive Foundation, 2nd ed.; Pearson: Hoboken, NJ, USA, 1999. [Google Scholar]
- Zhu, S.; Heddam, S.; Nyarko, E.K.; Hadzima-Nyarko, M.; Piccolroaz, S.; Wu, S. Modeling daily water temperature for rivers: Comparison between adaptive neuro-fuzzy inference systems and artificial neural networks models. Environ. Sci. Pollut. Res. 2019, 26, 402–420. [Google Scholar] [CrossRef] [PubMed]
- Dozat, T. Incorporating Nesterov Momentum into Adam. In Proceedings of the ICLR 2016 Workshop, San Juan, PR, USA, 2–4 May 2016; pp. 1–4. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- François Chollet Keras: The Python Deep Learning Library. Available online: https://keras.io/ (accessed on 25 January 2019).
- Google Brain Team TensorFlow. Available online: https://www.tensorflow.org/ (accessed on 24 January 2019).


| Manufacturer | Kaco |
|---|---|
| Model | Powador 12.0 TL3 |
| Circuit design | 6-pulse transformerless IGBT 1 |
| DC side | |
| Parameter | Value |
| Maximum PV generator input power (kW) | 12 |
| Maximum power point voltage range (V) | 280–800 |
| Starting voltage (V) | 250 |
| Maximum open-circuit voltage (V) | 1000 |
| Number of string inputs | 2 |
| Maximum short-circuit current (A) | 22.4 |
| AC side | |
| Rated power (kW) | 10 |
| Rated current (A) | 14.5 |
| Grid voltage (V) | 400/230 |
| Distortion factor (THDI) (%) | 2.22 |
| Maximum efficiency (%) | 98 |
| European efficiency (%) | 97.5 |
| Parameter | Solar Irradiance | Ambient Temperature |
|---|---|---|
| Mean value | 175.17 W/m2 | 14.65 °C |
| Minimum value | 7.26 W/m2 | −11.21 °C |
| Maximum value | 1172.03 W/m2 | 37.16 °C |
| Standard deviation | 248.91 W/m2 | 9.76 °C |
| Coefficient of variation | 1.42 | 0.67 |
| Parameter | 5th Current Harmonic (A) | 7th Current Harmonic (A) | 11th Current Harmonic (A) | 13th Current Harmonic (A) |
|---|---|---|---|---|
| Mean value | 0.0147 | 0.0142 | 0.0137 | 0.0130 |
| Maximum value | 0.8489 | 0.4733 | 0.4310 | 0.2915 |
| Minimum value | 0.1354 | 0.0961 | 0.0752 | 0.0437 |
| Standard deviation | 0.1278 | 0.0911 | 0.0662 | 0.0402 |
| Coefficient of variation | 1.0596 | 1.0550 | 1.1374 | 1.0869 |
| Model Name | Input Parameters | Architecture |
|---|---|---|
| MLPNN 1 | G | 1-11-4 |
| MLPNN 2 | G, Tamb | 2-11-4 |
| MLPNN 3 | G, Tamb, t | 3-11-4 |
| MLPNN 4 | G | 1-11-5-4 |
| MLPNN 5 | G, Tamb | 2-11-5-4 |
| MLPNN 6 | G, Tamb, t | 3-11-5-4 |
| Model Version | Current Harmonic | Validation | |||
|---|---|---|---|---|---|
| R | d | RMSE (A) | MAE (A) | ||
| MLPNN 1 (1-11-4) | 5th | 0.9356 | 0.9555 | 0.0693 | 0.0455 |
| 7th | 0.971 | 0.9804 | 0.032 | 0.0221 | |
| 11th | 0.9437 | 0.9598 | 0.0376 | 0.0252 | |
| 13th | 0.8459 | 0.8426 | 0.0374 | 0.021 | |
| MLPNN 2 (1-11-5-4) | 5th | 0.9358 | 0.9563 | 0.0687 | 0.0454 |
| 7th | 0.9706 | 0.9798 | 0.0323 | 0.022 | |
| 11th | 0.9437 | 0.9599 | 0.0375 | 0.0245 | |
| 13th | 0.8534 | 0.8567 | 0.0363 | 0.0216 | |
| Model Version | Current Harmonic | Validation | |||
|---|---|---|---|---|---|
| R | d | RMSE (A) | MAE (A) | ||
| MLPNN 3 (1-11-4) | 5th | 0.9381 | 0.9662 | 0.0658 | 0.0438 |
| 7th | 0.9676 | 0.9804 | 0.0324 | 0.0224 | |
| 11th | 0.9465 | 0.972 | 0.0336 | 0.0217 | |
| 13th | 0.8712 | 0.9124 | 0.0309 | 0.0185 | |
| MLPNN 4 (1-11-5-4) | 5th | 0.9354 | 0.9647 | 0.0673 | 0.0436 |
| 7th | 0.9626 | 0.9771 | 0.0343 | 0.0222 | |
| 11th | 0.945 | 0.9702 | 0.0345 | 0.0235 | |
| 13th | 0.8743 | 0.9225 | 0.03 | 0.0193 | |
| Model Version | Current Harmonic | Validation | |||
|---|---|---|---|---|---|
| R | d | RMSE (A) | MAE (A) | ||
| MLPNN 5 (1-11-4) | 5th | 0.9376 | 0.9664 | 0.066 | 0.045 |
| 7th | 0.9634 | 0.9801 | 0.033 | 0.0222 | |
| 11th | 0.9429 | 0.9694 | 0.0362 | 0.024 | |
| 13th | 0.8678 | 0.926 | 0.0299 | 0.0183 | |
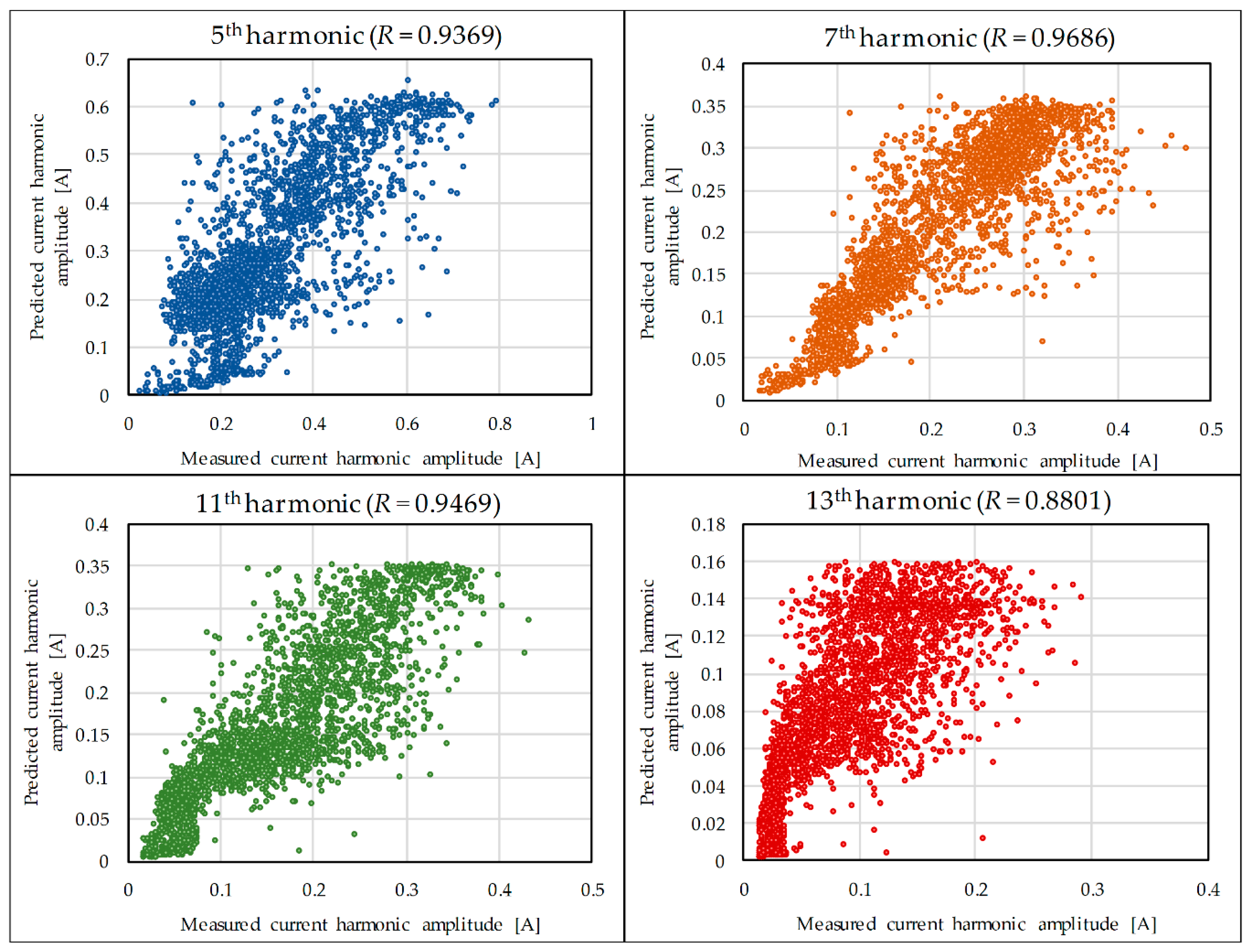
| MLPNN 6 (1-11-5-4) | 5th | 0.9369 | 0.9666 | 0.0651 | 0.0428 |
| 7th | 0.9686 | 0.9834 | 0.0306 | 0.0201 | |
| 11th | 0.9469 | 0.9722 | 0.034 | 0.0229 | |
| 13th | 0.8801 | 0.9253 | 0.0293 | 0.0191 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Žnidarec, M.; Klaić, Z.; Šljivac, D.; Dumnić, B. Harmonic Distortion Prediction Model of a Grid-Tie Photovoltaic Inverter Using an Artificial Neural Network. Energies 2019, 12, 790. https://doi.org/10.3390/en12050790
Žnidarec M, Klaić Z, Šljivac D, Dumnić B. Harmonic Distortion Prediction Model of a Grid-Tie Photovoltaic Inverter Using an Artificial Neural Network. Energies. 2019; 12(5):790. https://doi.org/10.3390/en12050790
Chicago/Turabian StyleŽnidarec, Matej, Zvonimir Klaić, Damir Šljivac, and Boris Dumnić. 2019. "Harmonic Distortion Prediction Model of a Grid-Tie Photovoltaic Inverter Using an Artificial Neural Network" Energies 12, no. 5: 790. https://doi.org/10.3390/en12050790
APA StyleŽnidarec, M., Klaić, Z., Šljivac, D., & Dumnić, B. (2019). Harmonic Distortion Prediction Model of a Grid-Tie Photovoltaic Inverter Using an Artificial Neural Network. Energies, 12(5), 790. https://doi.org/10.3390/en12050790







