Accurate and Fast Generation of Irregular Short Crested Waves by Using Periodic Boundaries in a Mild-Slope Wave Model
Abstract
:1. Introduction
2. Numerical Methodology
2.1. The Mild-Slope Wave Propagation Model, MILDwave
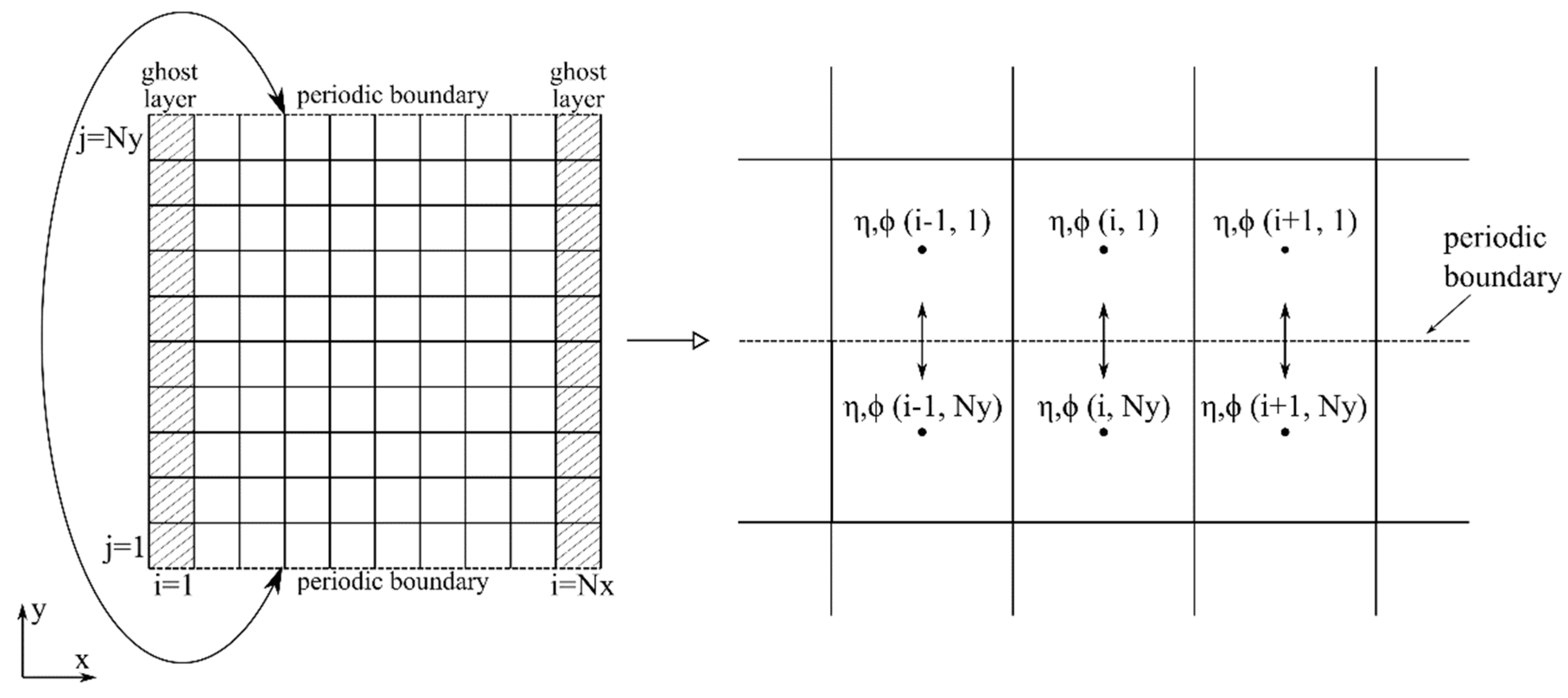
2.2. Periodic Boundaries
3. Results by the Model, MILDwave
3.1. Generation of Regular Waves
3.2. Generation of Irregular Long Crested Waves
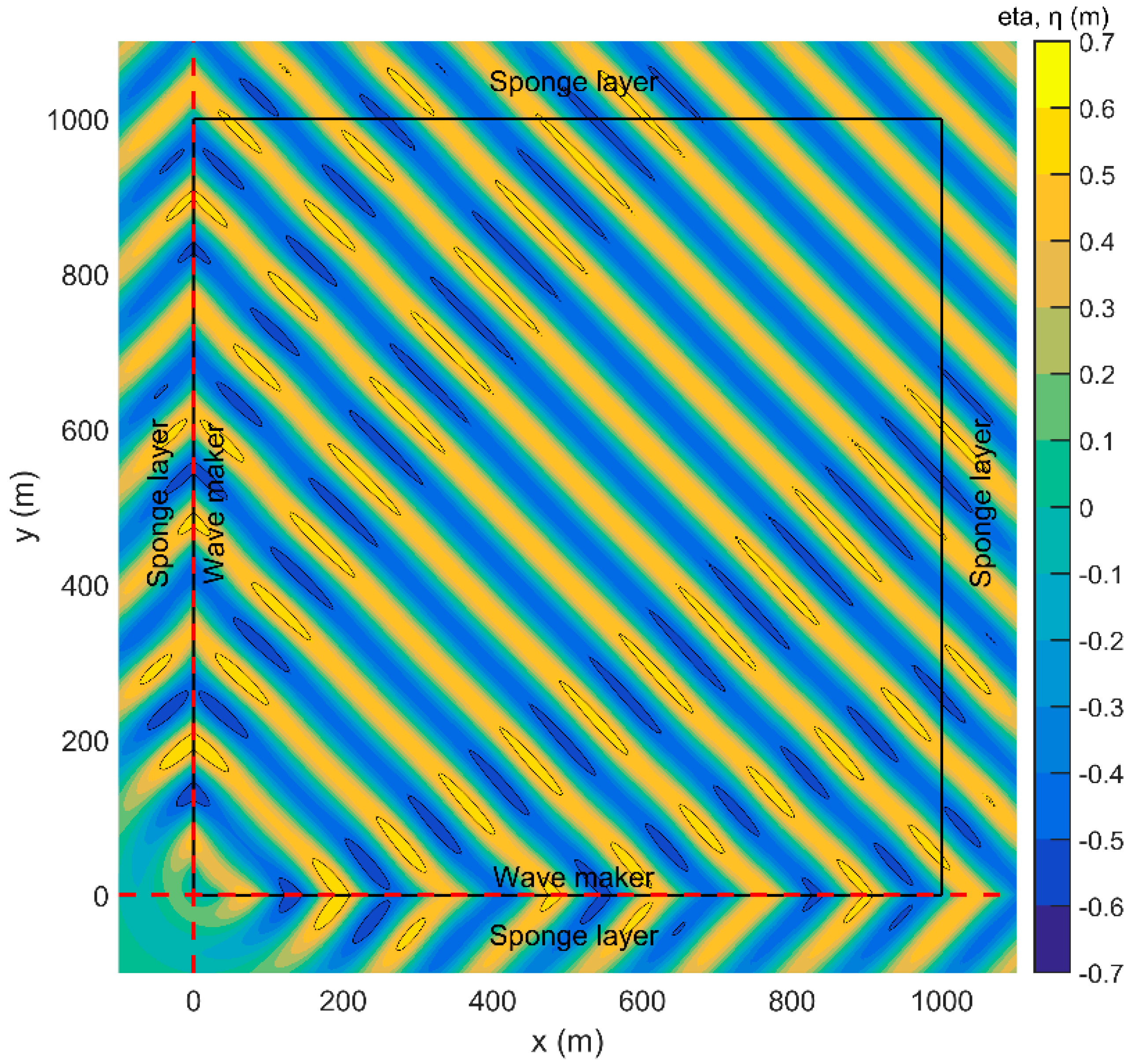
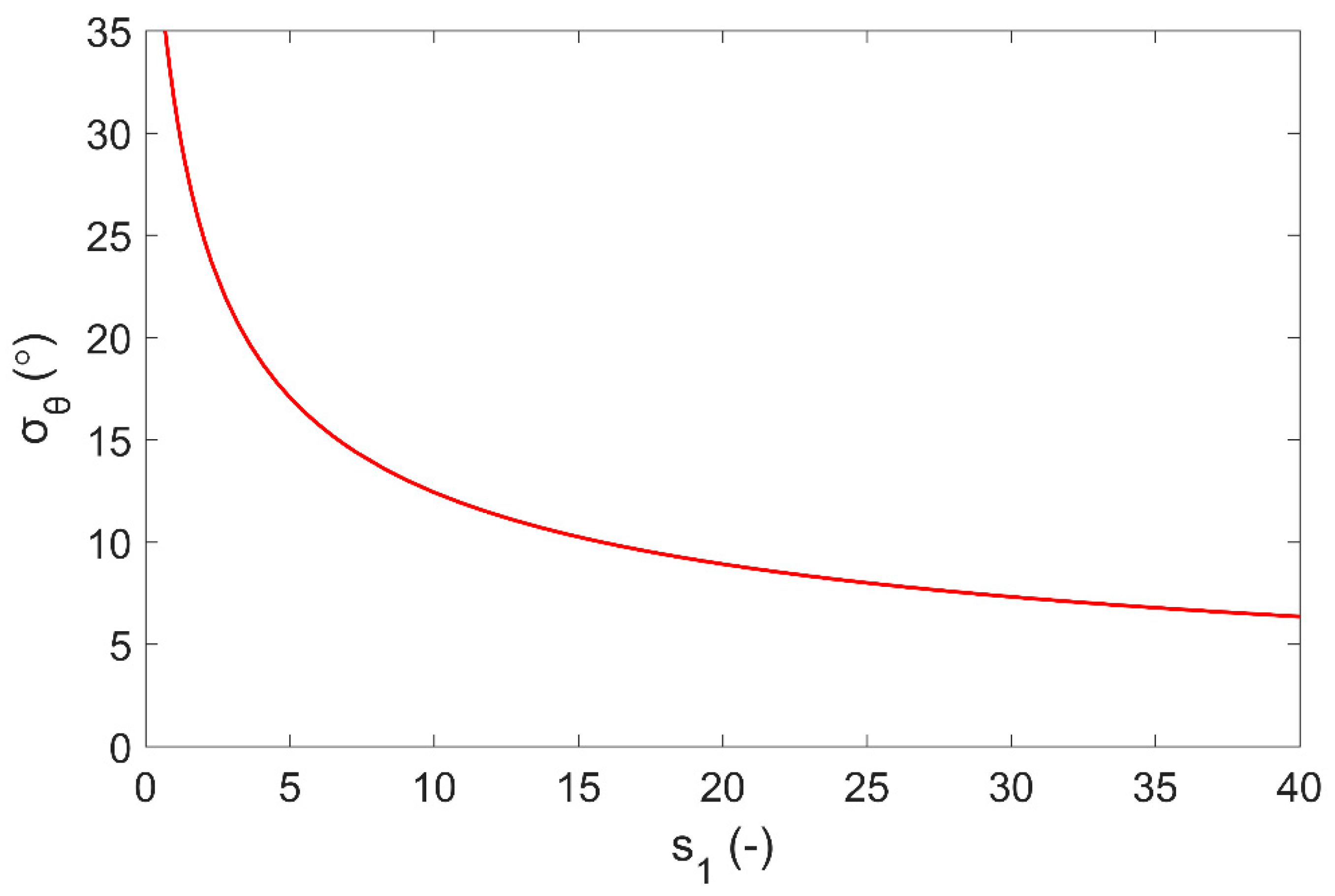
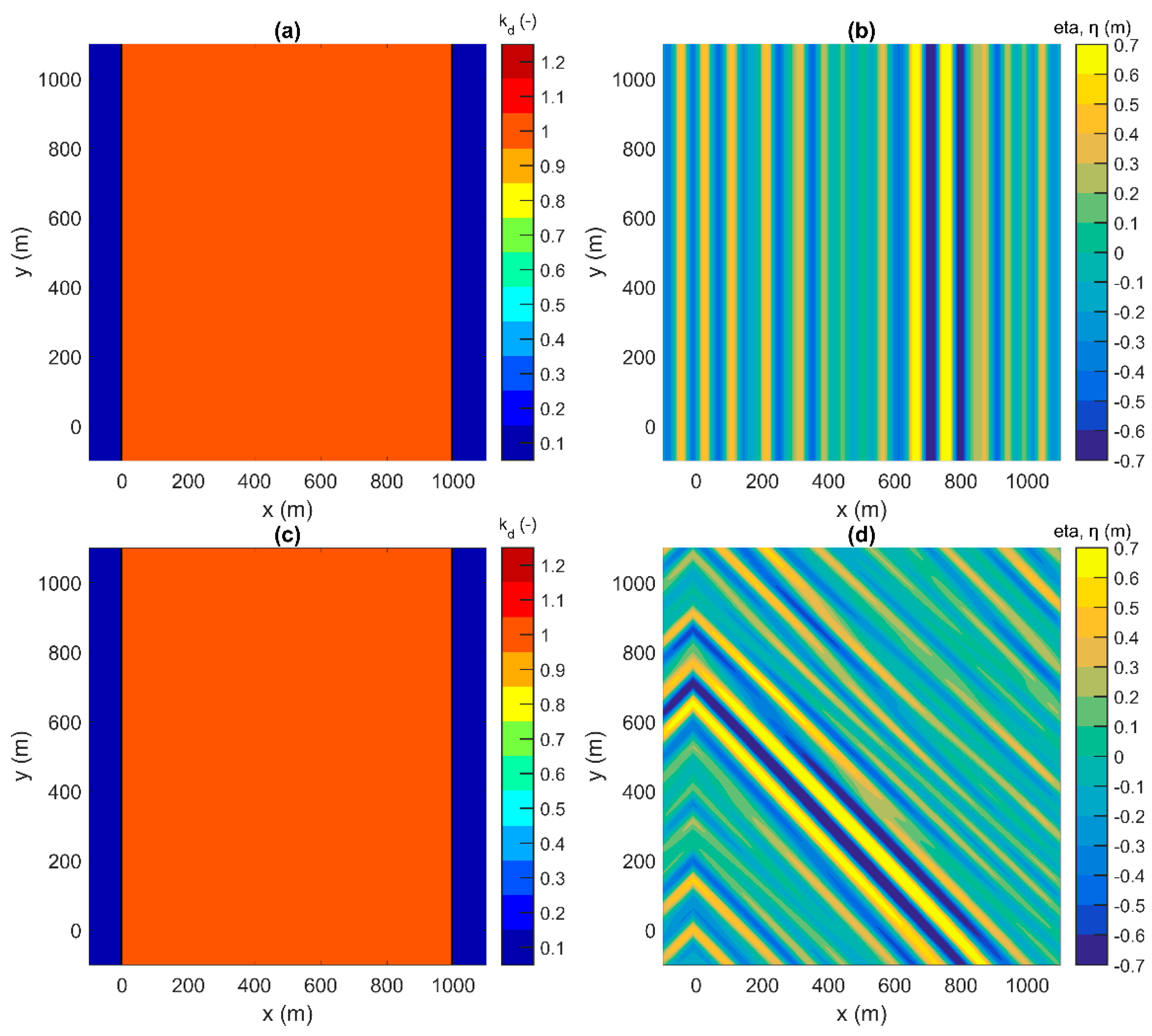
3.3. Generation of Irregular Short Crested Waves
4. Numerical Validation Using the Vincent and Briggs Shoal Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Berkhoff, J.C.W. Computation of combined refraction-diffraction. In Proceedings of the Thirteenth Conference on Coastal Engineering, Vancouver, BC, Canada, 10–14 July 1972; pp. 471–490. [Google Scholar] [CrossRef]
- Radder, A.C. On the parabolic equation method for water-wave propagation. J. Fluid Mech. 1979, 95, 159–176. [Google Scholar] [CrossRef]
- Copeland, G.J.M. A practical alternative to the “mild-slope” wave equation. Coast. Eng. 1985, 9, 125–149. [Google Scholar] [CrossRef]
- Radder, A.C.; Dingemans, M.W. Canonical equations for almost periodic, weakly nonlinear gravity waves. Wave Motion 1985, 7, 473–485. [Google Scholar] [CrossRef]
- Booij, N. A note on the accuracy of the mild-slope equation. Coast. Eng. 1983, 7, 191–203. [Google Scholar] [CrossRef]
- Suh, K.D.; Lee, C.; Park, W.S. Time-dependent equations for wave propagation on rapidly varying topography. Coast. Eng. 1997, 32, 91–117. [Google Scholar] [CrossRef]
- Larsen, J.; Dancy, H. Open boundaries in short wave simulations--A new approach. Coast. Eng. 1983, 7, 285–297. [Google Scholar] [CrossRef]
- Peregrine, D.H. Long waves on a beach. J. Fluid Mech. 1967, 27, 815–827. [Google Scholar] [CrossRef]
- Lee, C.; Suh, K.D. Internal generation of waves for time-dependent mild-slope equations. Coast. Eng. 1998, 34, 35–57. [Google Scholar] [CrossRef]
- Lee, C.; Yoon, S.B. Internal generation of waves on an arc in a rectangular grid system. Coast. Eng. 2007, 54, 357–368. [Google Scholar] [CrossRef]
- Kim, G.; Lee, C. Internal generation of waves on an arced band. Ocean Eng. 2013, 67, 77–88. [Google Scholar] [CrossRef]
- Lin, X.; Yu, X. A finite difference method for effective treatment of mild-slope wave equation subject to non-reflecting boundary conditions. Appl. Ocean Res. 2015, 53, 179–189. [Google Scholar] [CrossRef]
- Troch, P. MILDwave—A Numerical Model for Propagation and Transformation of Linear Water Waves; Internal Report; Department of Civil Engineering, Ghent University: Zwijnaarde, Belgium, 1998. [Google Scholar]
- Miles, M.D. A Note on Directional Random Wave Synthesis by the Single Summation Method. In Proceedings of the 23rd IAHR Congress, Ottawa, Canada, 21–25 August 1989; pp. 243–250. [Google Scholar]
- Sand, S.E.; Mynett, A.E. Directional Wave Generation and Analysis. In Proceedings of the IAHR Seminar on Wave Analysis and Generation in Laboratory Basins, Lausanne, Switzerland, 1–4 September 1987; pp. 363–376. [Google Scholar]
- Troch, P.; Stratigaki, V. Chapter 10—Phase-Resolving Wave Propagation Array Models. In Numerical Modelling of Wave Energy Converters; Folley, M., Ed.; Academic Press: Cambridge, MA, USA, 2016; pp. 191–216. [Google Scholar]
- Stratigaki, V.; Vanneste, D.; Troch, P.; Gysens, S.; Willems, M. NUMERICAL MODELING OF WAVE PENETRATION IN OSTEND HARBOUR. Coast. Eng. Proc. 2011, 1, 42. [Google Scholar] [CrossRef]
- Beels, C.; Troch, P.; De Backer, G.; Vantorre, M.; De Rouck, J. Numerical implementation and sensitivity analysis of a wave energy converter in a time-dependent mild-slope equation model. Coast. Eng. 2010, 57, 471–492. [Google Scholar] [CrossRef]
- Balitsky, P.; Verao Fernandez, G.; Stratigaki, V.; Troch, P. Assessment of the Power Output of a Two-Array Clustered WEC Farm Using a BEM Solver Coupling and a Wave-Propagation Model. Energies 2018, 11, 2907. [Google Scholar] [CrossRef]
- Verao Fernandez, G.; Balitsky, P.; Stratigaki, V.; Troch, P. Coupling Methodology for Studying the Far Field Effects of Wave Energy Converter Arrays over a Varying Bathymetry. Energies 2018, 11, 2899. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.; Smit, P. SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coast. Eng. 2011, 58, 992–1012. [Google Scholar] [CrossRef]
- Shi, F.; Kirby, J.T.; Harris, J.C.; Geiman, J.D.; Grilli, S.T. A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation. Ocean Model. 2012, 43–44, 36–51. [Google Scholar] [CrossRef]
- Brorsen, M.; Helm-Petersen, J. On the Reflection of Short-Crested Waves in Numerical Models. Int. Conf. Coast. Eng. 1998, 394–407. [Google Scholar] [CrossRef]
- Mitsuyasu, H.; Tasai, F.; Suhara, T.; Mizuno, S.; Ohkusu, M.; Honda, T.; Rikiishi, K. Observations of the Directional Spectrum of Ocean WavesUsing a Cloverleaf Buoy. J. Phys. Oceanogr. 1975, 5, 750–760. [Google Scholar] [CrossRef]
- Frigaard, P.; Helm-Petersen, J.; Klopman, G.; Stansberg, C.T.; Benoit, M.; Briggs, M.J.; Miles, M.; Santas, J.; Schäffer, H.A.; Hawkes, P.J. IAHR List of Sea Parameteres: an update for multidirectional waves. In Proceedings of the IAHR Seminar Multidirectional Waves and their Interaction with Structures, 27th IAHR Congress, San Francisco, CA, USA, 10–15 August 1997. [Google Scholar]
- Kuik, A.J.; van Vledder, G.P.; Holthuijsen, L.H. A Method for the Routine Analysis of Pitch-and-Roll Buoy Wave Data. J. Phys. Oceanogr. 1988, 18, 1020–1034. [Google Scholar] [CrossRef]
- Johnson, D.; Pattiaratchi, C. Boussinesq modelling of transient rip currents. Coast. Eng. 2006, 53, 419–439. [Google Scholar] [CrossRef]
- Dimakopoulos, A.S.; Dimas, A.A. Large-wave simulation of three-dimensional, cross-shore and oblique, spilling breaking on constant slope beach. Coast. Eng. 2011, 58, 790–801. [Google Scholar] [CrossRef]
- Borgman, L.E.; Panicker, N.N. Design Study for a Suggested Wave Gauge Array off Point Mugu; Technical Report 1–14; Hydraulic Engineering Laboratory, University of California at Berkeley: Berkeley, CA, USA, 1970. [Google Scholar]
- Vincent, C.L.; Briggs, M.J. Refraction—Diffraction of Irregular Waves over a Mound. J. Waterw. Port Coastal Ocean Eng. 1989, 115, 269–284. [Google Scholar] [CrossRef]
- Berkhoff, J.C.W.; Booy, N.; Radder, A.C. Verification of Numerical Wave Propagation Models for Simple Harmonic Linear Water Waves. Coast. Eng. 1982, 6, 255–279. [Google Scholar] [CrossRef]
- Bouws, E.; Günther, H.; Rosenthal, W.; Vincent, C.L. Similarity of the wind wave spectrum in finite depth water: 1. Spectral form. J. Geophys. Res. 1985, 90, 975. [Google Scholar] [CrossRef]



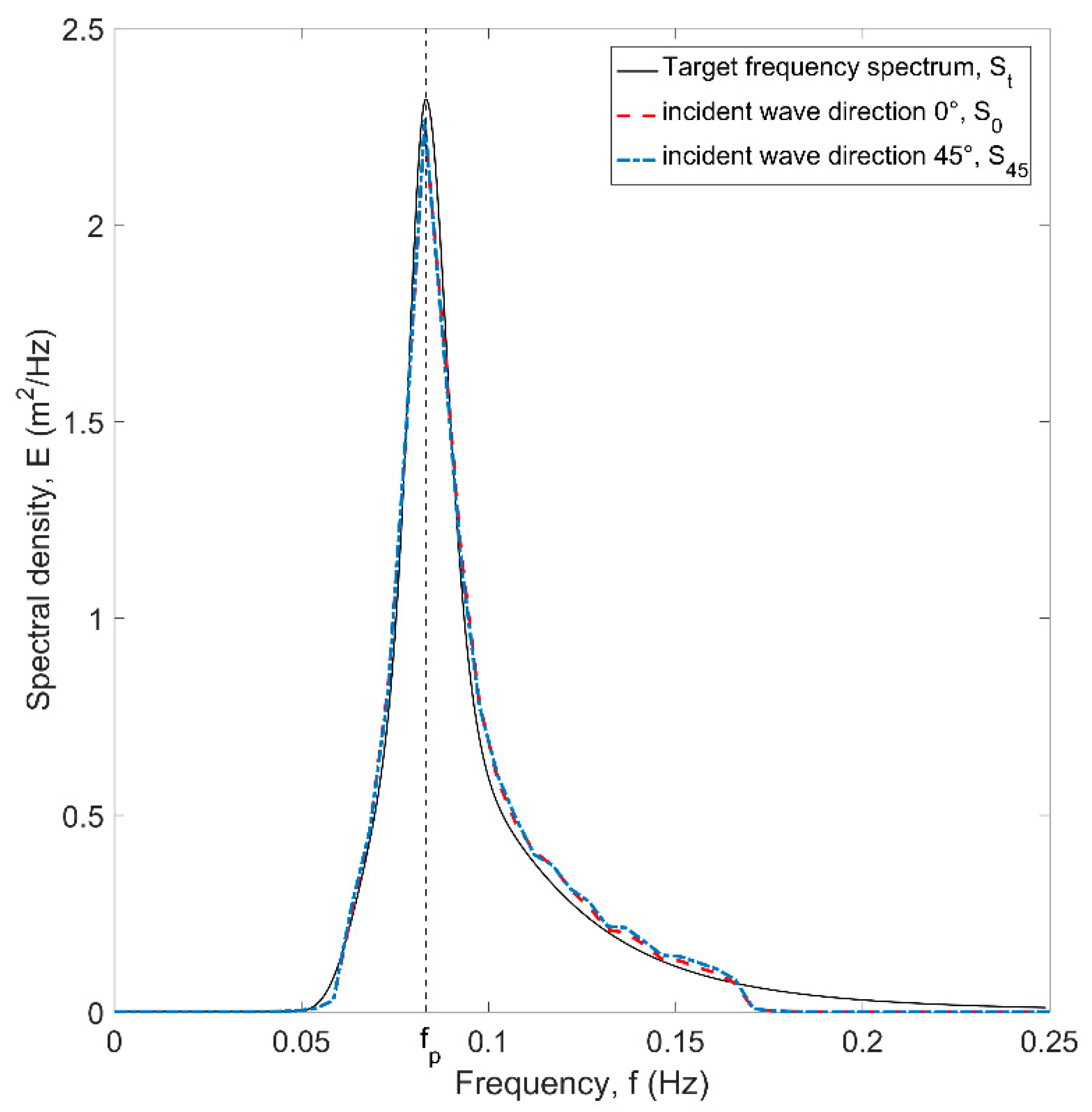
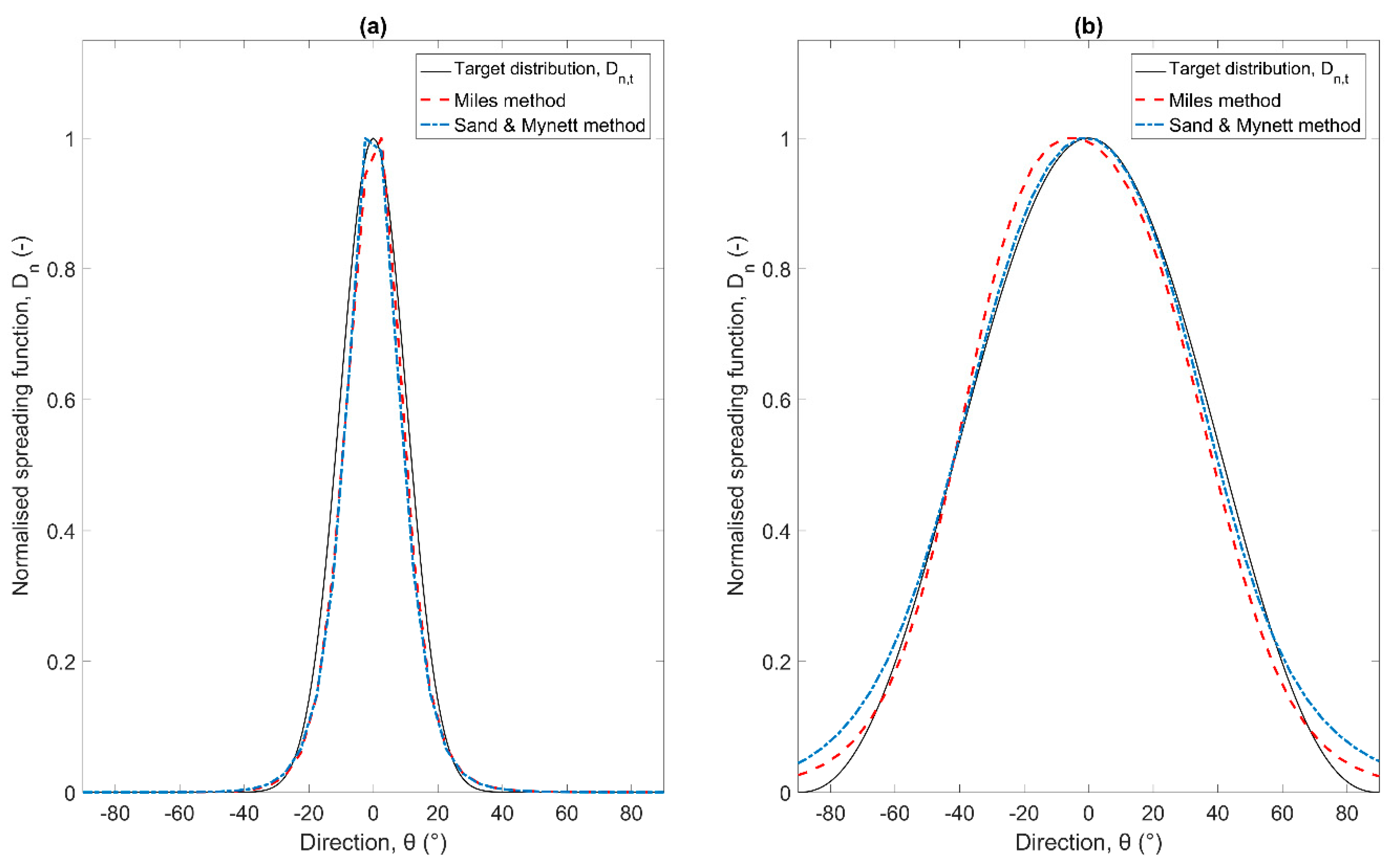
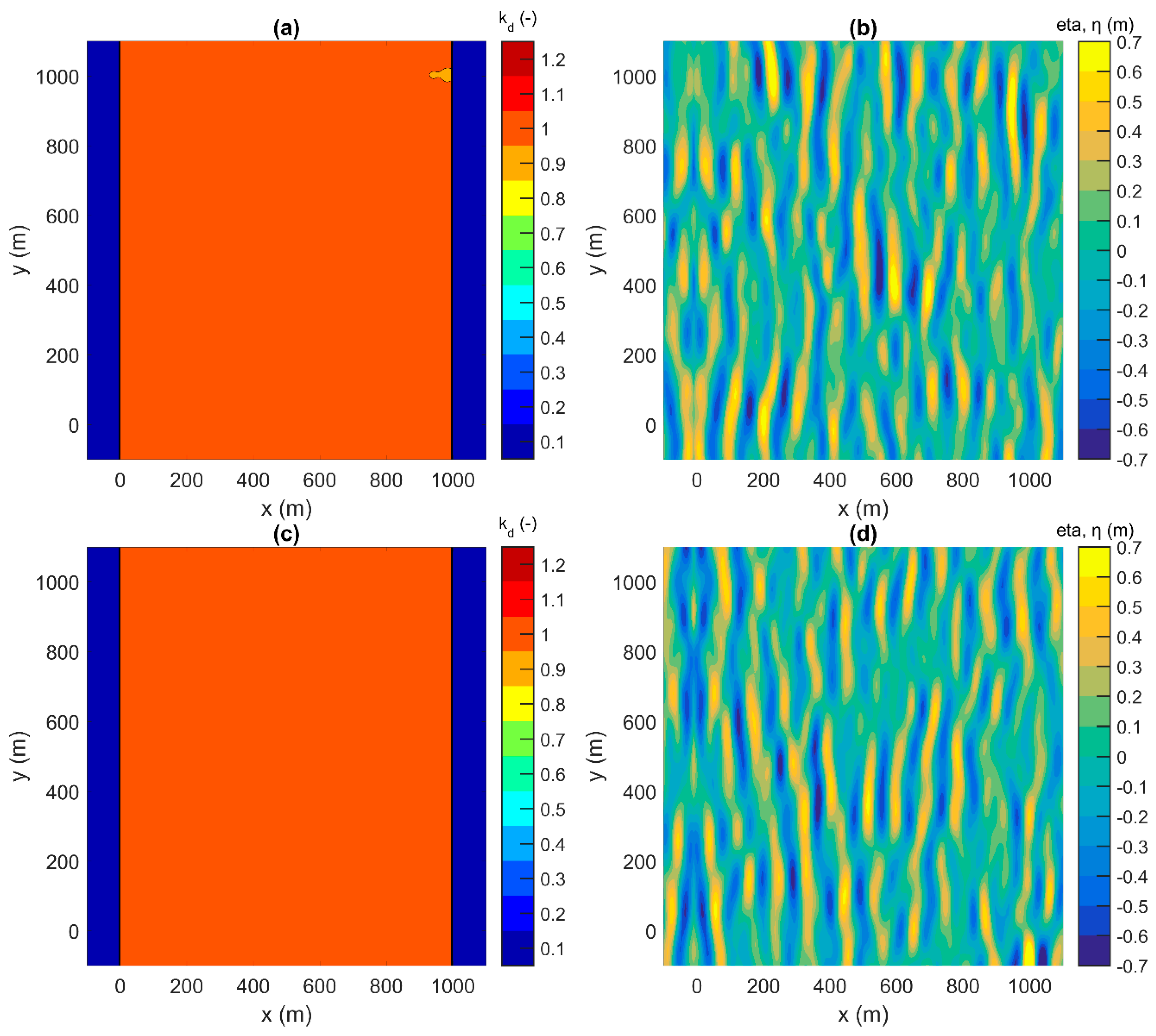




| Test Case ID | Phillips Constant, α (-) | Peak Enhancement Factor, γ (-) | Spreading Standard Deviation, σθ (°) | ||
|---|---|---|---|---|---|
| U3 | 1.3 | 2.54 | 0.00155 | 2 | 0 |
| N3 | 1.3 | 2.54 | 0.00155 | 2 | 10 |
| B3 | 1.3 | 2.54 | 0.00155 | 2 | 30 |
| U4 | 1.3 | 2.54 | 0.00047 | 20 | 0 |
| N4 | 1.3 | 2.54 | 0.00047 | 20 | 10 |
| B4 | 1.3 | 2.54 | 0.00047 | 20 | 30 |
| Test Case ID | U3 | N3 | B3 | U4 | N4 | B4 |
|---|---|---|---|---|---|---|
| RMSE | 0.141 | 0.048 | 0.068 | 0.068 | 0.102 | 0.070 |
| Skill | 0.869 | 0.955 | 0.936 | 0.940 | 0.905 | 0.924 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasarmidis, P.; Stratigaki, V.; Troch, P. Accurate and Fast Generation of Irregular Short Crested Waves by Using Periodic Boundaries in a Mild-Slope Wave Model. Energies 2019, 12, 785. https://doi.org/10.3390/en12050785
Vasarmidis P, Stratigaki V, Troch P. Accurate and Fast Generation of Irregular Short Crested Waves by Using Periodic Boundaries in a Mild-Slope Wave Model. Energies. 2019; 12(5):785. https://doi.org/10.3390/en12050785
Chicago/Turabian StyleVasarmidis, Panagiotis, Vasiliki Stratigaki, and Peter Troch. 2019. "Accurate and Fast Generation of Irregular Short Crested Waves by Using Periodic Boundaries in a Mild-Slope Wave Model" Energies 12, no. 5: 785. https://doi.org/10.3390/en12050785
APA StyleVasarmidis, P., Stratigaki, V., & Troch, P. (2019). Accurate and Fast Generation of Irregular Short Crested Waves by Using Periodic Boundaries in a Mild-Slope Wave Model. Energies, 12(5), 785. https://doi.org/10.3390/en12050785







