Abstract
Non-linear loads in circuits cause the appearance of harmonic disturbances both in voltage and current. In order to minimize the effects of these disturbances and, therefore, to control the flow of electricity between the source and the load, passive or active filters are often used. Nevertheless, determining the type of filter and the characteristics of their elements is not a trivial task. In fact, the development of algorithms for calculating the parameters of filters is still an open question. This paper analyzes the use of genetic algorithms to maximize the power factor compensation in non-sinusoidal circuits using passive filters, while concepts of geometric algebra theory are used to represent the flow of power in the circuits. According to the results obtained in different case studies, it can be concluded that the genetic algorithm obtains high quality solutions that could be generalized to similar problems of any dimension.
1. Introduction
The introduction of distributed generation and microgrids in power networks allow an efficient energy management and integration with renewable energy sources [1]. However, these grids include an increasing number of power electronic devices and non-linear electronic loads, such as power inverters, cycloconverters, speed drives, batteries, household appliances, among others. These non-linear loads increase the harmonic disturbances both in voltage and current, causing detrimental effects to the supply system and user equipment [2]. In consequence, these grids are seriously affected by events that degrade the power quality [3], and provoke excessive heating, protection faults, and inefficiencies in the transmission of energy [4], hence it becomes a critical task to determine precisely the electrical energy balances on the microgrid.
Different authors have presented models and theories in the past [5,6,7], but while all of them coincide in the study of the sinusoidal case, there is some controversy in the analysis of non-sinusoidal systems with a high harmonic content, such as modern microgrids. In particular, well-known theories, such as those proposed by Budeanu [8] and Fryze [9], have been questioned by different authors after demonstrating inconsistency and errors [10,11,12]. Therefore, it is important to investigate how to improve the compensation of the power factor in non-sinusoidal systems in the presence of harmonics. Some investigations have highlighted that algorithms for calculating the parameters of filters have rarely been discussed [13], although in recent years some authors have applied computational optimization methods, including meta-heuristic approaches, for optimizing filter parameters in circuits having harmonic distortion [2,14,15,16]. More specifically, genetic algorithms have been successfully applied in [17,18,19].
In this paper, an evolutionary algorithm is used to optimize the type and characteristics of passive filters for power factor compensation. The rest of the paper is organized as follows: Section 2 introduces some basic ideas about geometric algebra and its application to power systems. Section 3 describes the problem at hand and the genetic algorithm used as solution method. Section 4 presents the empirical study, while the main conclusions obtained are detailed in Section 5.
2. Geometric Algebra and Power Systems
Traditionally, electrical engineers have been taught to solve sinusoidal electrical circuits using complex number algebra, exactly as Steinmetz theory [20] introduced in the 19th century. It stated that differential equations in time domain can be transformed into algebra equations in complex domain. Under these assumptions, the apparent power can be expressed as:
where P is the active power, Q is the reactive power, and j is unit imaginary number.
The limitations of the algebra of complex numbers and the impossibility to apply the principle of conservation of energy to the apparent power quantity [21] have caused some researchers to propose alternative circuit analysis techniques, including those based on geometric algebra [22].
2.1. Basic Definitions of Geometric Algebra
Geometric algebra has its origins in the work of Clifford and Grassman in the 19th century and is considered as a unified language for mathematics and physics. It is based on the notion of an invertible product of vectors that captures the geometric relationship between two vectors, i.e., their relative magnitudes and the angle between them [23]. Some investigations have defined the properties of geometric algebra [24,25] applied to physics and engineering. Traditional concepts such as vector, spinor, complex numbers, or quaternions are naturally explained as members of subspaces in geometric algebra. It can be easily extended in any number of dimensions, this being one of its main strengths. Because these are geometrical objects, they all have direction, sense, and magnitude. The basics of GA properties are based on well established definitions around vectors. For example, a vector (a segment with direction and sense) can be multiplied by a vector in different ways, so the result has different meanings. In (2), the inner product is defined and the result is a scalar.
In (3) a new product is defined, the wedge product. The main difference with its cousin the outer product (see Figure 1) is that the result is neither a scalar nor a vector, but a new quantity called bivector.
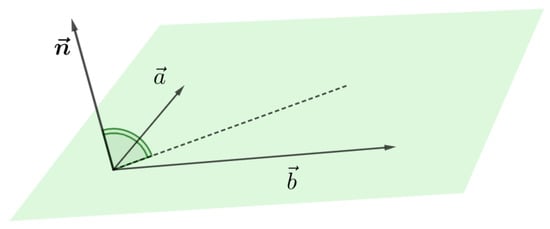
Figure 1.
Outer product of vectors and . The result is a vector , perpendicular to the plane formed by and .
A bivector is known to have direction, sense and magnitude in the same way a vector has. It defines an area enclosed by the parallelogram formed by both vectors (see Figure 2). This product complies with the anti-commutative property, i.e., . A bivector is a key concept in geometrical algebra and cannot be found in linear algebra or vector calculus. The outer product of two vectors produces a new entity in a plane that can be operated like vectors, i.e., addition, product, or even inverse. Like vectors, a bivector can be written as the linear combination of a base of bivectors.
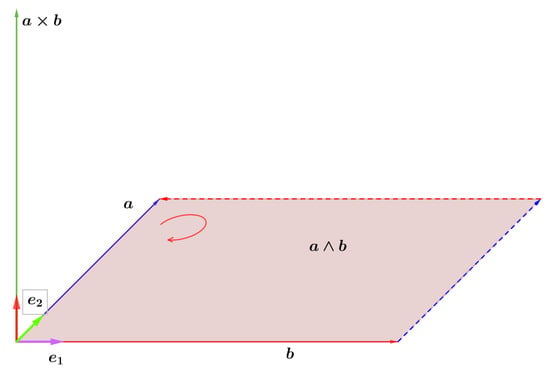
Figure 2.
Representation of a bivector .
Finally, the third product between vectors is defined in (4) as the geometric product and can be described as one of the major contributions in geometric algebra. Not only can vectors be multiplied geometrically, but bivectors and other entities, in general, can be used.
The result is a linear combination of the inner product and the wedge product. Equation (4) can be expanded to further find out new insights.
where is the scalar part and is the bivector part.
2.2. Application of Geometric Algebra to Power Systems
Recently, several researches have proven that geometric algebra or Clifford algebra is a powerful and flexible tool for representing the flow of energy or power in electrical systems [22,26]. Some authors have motivated the use of power theory based on geometric algebra as Physics’ unifying language, such that electrical magnitudes can be interpreted as Clifford multivectors [27]. More specifically, Clifford algebra is a valid mathematical tool to address the multicomponent nature of power in non-sinusoidal contexts [28,29,30] and has been used for analysis of harmonics [31].
The concept of non-active, reactive, or distorted power acquires a meaning that is more in line with its mathematical significance, making it possible to better understand energy balances and to verify the principle of energy conservation. Nevertheless, some authors have highlighted that the verification of the energy conservation law is only possible in sinusoidal situations [32]. To overcome these drawbacks, these authors proposed a new circuit analysis approach using geometric algebra to develop the most general proof of energy conservation in industrial building loads, with capability of calculating the voltage, current, and net apparent power in electrical systems in non-sinusoidal situations.
Different authors have proposed definitions to represent non-active power for distorted currents and voltages in electrical systems, although no single representation has been universally accepted. For example, in [33] a non-active power multivector from the most advanced multivectorial power theory based on the geometric algebra with the aim of analyzing the compensation of disturbing loads is presented, including the harmonic load compensation, identification, and metering between other applications. Other researches have shown that geometric algebra can be applied to analyze the apparent power defined in a poly-phase system having transmission lines with frequency-dependency under non-sinusoidal conditions [34].
Geometric Apparent Power
As several authors have shown, the use of apparent power loses its meaning under non-sinusoidal conditions, involving erroneous calculation of energy flows between the load and source. In contrast, [35] proposes the use of a new term called net apparent power or geometric apparent power . This concept is the result of the geometric product of voltage and current in domain (6).
which results in a scalar and a bivector when the voltage and current are sinusoids
It can be easily shown from (1) and (7) that
so is the active power derived from the scalar part and is the reactive power derived from the bivector part of the net apparent power multivector.
For the non-sinusoidal case, i.e., when harmonics are present in the voltage and/or current, the apparent power loses its validity and only can reflect the exact flow of energy in the circuit. Consider a general voltage waveform
that we can transfer to the geometric domain using [35]
where represents the product of n vectors and the subscripts c and s denote cosine and sine, respectively. Using (10), any waveform can be translated to the geometric domain , so the final result for the voltage is
In (11), the transformation given in [35] has been used and is reproduced here to make this paper more readable. [35] also demonstrates that the admittance of typical passive load is , so the harmonic current associated to h-th voltage harmonic is
and the total current
where is the in-phase current where is the quadrature current. The geometric apparent power is then
where is the in-phase geometric apparent power, is the degraded power (summation of cross-frequency products between voltage and current) and is the quadrature geometric apparent power.
Based on Equations (8) and (14), the power factor in domain can be defined as
in contrast to the clasical approach where is used. As demonstrated by [21], and are different concepts for non-sinusoidal scenarios, but reduces to the same in the sinudoidal case. Other power theories like Czarnecki’s based their power factor definition on the concept of apparent power , so it leads to different power factor results in non-sinusoidal situations.
3. Problem Description and Solution Strategy
This section describes the proposed problem in this research and details the characteristics of the genetic algorithm used to solve it.
3.1. Problem Description
Power systems operating under harmonic distortion must be optimized to reduce power losses and improve power quality [36,37]. Whether the system is linear or non-linear, it is necessary to provide reactances in parallel with the load in order to reduce these harmonics. The typical design of compensators is based on the knowledge of the susceptances of the system to different frequencies [38], something that is not easy to achieve when you have highly distorted systems. The main objective of non active power compensation is to minimize the source root mean square (RMS) current [5]. However, it is not a trivial task since it involves to determine which type of filter and characteristics of their components is more suitable for compensation purposes in a given circuit. For example, a capacitor with an optimal value connected in parallel to the load is an easy solution but this does not produce the absolute minimum of the distortion power [39], while other alternatives could improve it.
Some studies have highlighted that algorithms for calculating the parameters of filters has not been studied in detail [13], although some authors have implemented optimization algorithms for optimizing the configuration of the filters in circuits having harmonic distortion. For example, in [15] it was proposed a genetic algorithm to minimize current total harmonic distortion using LC passive harmonic filters. Other recent studies have applied swarm intelligence methods to comparatively evaluate single-tuned, double-tuned, triple-tuned, damped-double tuned, and C-type filters in order to improve the loading capability of a set of transformers under non-sinusoidal conditions [16]. In addition to the use of passive filters, some studies proposed algorithms for estimating the optimal parameters of active and hybrid filters. For example, in [2] it was proposed the use of direct neural intelligent techniques to improve performance of a shunt active filters. In other recent studies, it has been proposed the use of differential evolution (DE) algorithms to optimize the parameters of hybrid filters (combining active and passive filters) in order to minimize harmonic pollution [14]. The problem to be solved involves the determination of the most suitable type of passive filter and its parameters to minimize the source RMS current in order to get the optimal value .
3.2. Solution Approach
Genetic algorithms are optimization methods based on principles of natural selection and genetics [40]. Figure 3 shows the flowchart describing the operation of the genetic algorithm. It consists of a set (population) of solutions, each of which is called individual or phenotype, that evolve to reach solutions of high quality in terms of a fitness function. As an initialization step, a genetic algorithm randomly generates a set of solutions to a problem (a population of genomes). As Figure 4 shows, each individual is represented by a string of real numbers. Specifically, the data structure of each individual consists of three possible values for inductors L (Henry) and three possible values for capacitors C (Farad). All or some of these values will be considered in the optimization process depending on the filter choosed, which will be specified in the FT field (filter type), as described below. The actual values that can be assigned to inductors and capacitors are preset between two limits (upper and lower), so that the search space of the evolutionary algorithm is limited within reasonable margins. After calculating the fitness values for all solutions in a current population, the individuals for mating pool are selected using the operator of reproduction according to a given fitness function defined for the problem to be solved. In our problem the fitness function is
where is the source current calculated according to geometric algebra operations. These selection strategies aim to introduce a certain degree of elitism in the population. These solutions evolve by applying mutation and crossover operators that modify the genotype of the individuals. Offspring solutions substitute some old solutions of the population, and the new generation of individuals repeats the evolution process until a termination criterion is fulfilled (e.g., a maximum number of generations has been reached).
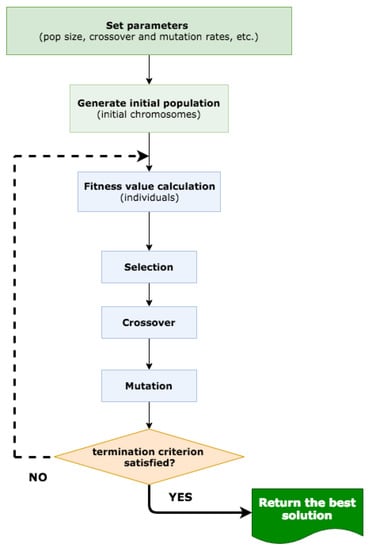
Figure 3.
Flowchart of the genetic algorithm.
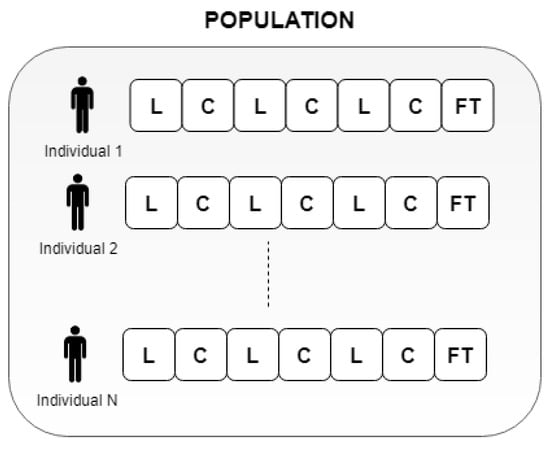
Figure 4.
Chromosome representation for the population. Note that the genes are real values for L, C, and integer for FT (Filter Type).
In this paper we have adapted a genetic algorithm solver for mixed-integer or continuous-variable optimization, constrained or unconstrained, included in the MATLAB Global Optimization Toolbox [41]. This toolbox allows to solve smooth or non-smooth optimization problems with constraints using different mutation and crossover operators. The original source code has been adapted to deal with the problem at hand. It also has been adapted to take into account the particularities of the proposed problem through GA. More specifically, an opensource implementation of GA “Clifford multivector toolbox” has been used, available at https://sourceforge.net/projects/clifford-multivector-toolbox/. A preliminary sensitivity analysis has been performed to determine the parameters of the algorithm, such that the values used in our study are: Population size: 100 individuals; crossover rate: 0.8; mutation rate: 0.2; selection criteria: roulette wheel selection; termination criteria: 50 iterations.
4. Empirical Study
This section presents the results obtained by the genetic algorithm in three different case studies.
4.1. Case Studies
- Czarnecki’s case study [39]: this example consists of simple circuit with a harmonic polluted ideal voltage source of normalized frequency rad/swith an active power W. Figure 5a shows the circuit load, while Figure 5b shows the solution found by Czarnecki with H, H, F, and F, who compensates the reactive power of the harmonic components by the 1-port X of a precalculated admitance. The method proposed by Czarnecki was able to compensate the source RMS current to 3.10 A from the initial 12.24 A [39].
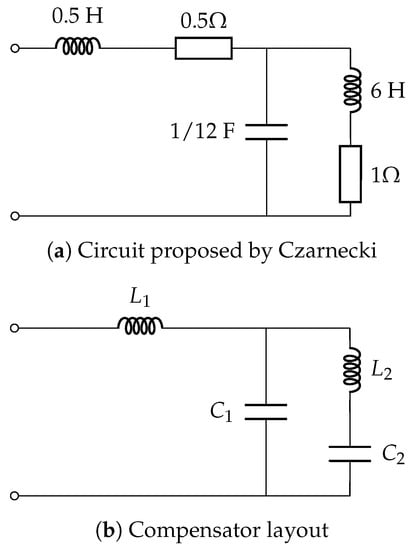 Figure 5. Load and compensator used by Czarnecki in [39].Using (10), the voltage in domain can be expressed as
Figure 5. Load and compensator used by Czarnecki in [39].Using (10), the voltage in domain can be expressed as - Castro-Nuñez and Castro-Puche’s case study [26]: this example (already studied by Czarnecki) consists of a circuit with a highly distorted voltage source with fundamental plus 2 harmonics and a linear load, being the voltagewhich translates towhere the uncompensated current is 44.72 A. Figure 6a shows the circuit with the distorted voltage source and the linear load, while Figure 6b displays the compensator for this linear load. The compensator design by Castro-Nuñez reduced the source RMS current to 20.10 A [22].
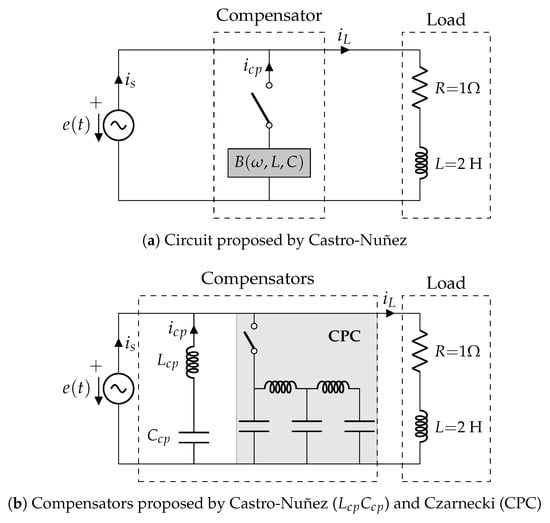 Figure 6. Circuit with distorted voltage source and a linear load used by Castro-Nuñez and Castro-Puche [22].
Figure 6. Circuit with distorted voltage source and a linear load used by Castro-Nuñez and Castro-Puche [22]. - Castilla’s case study [33]: this example consists of a circuit with a distorted voltage source with three harmonics given by:which translates towith an uncompensated RMS current of I = 4.21 A. Although the structure of this compensator was not described in the paper published by Castilla [33], this author indicated that it reduced the source RMS current to 3.21 A.
4.2. Filter Optimization
The genetic algorithm has been adapted to manage different types of filters widely used in the literature for compensating purposes and mitigation of current harmonics. Based on Equation (12), the admittance for a general load and harmonic h, is equal to
If we connect a pure reactive impedance in parallel with the load for current compensation, its admittance will be
For example, if we choose a simple LC series compensator, we have
So we need to make equal for every harmonic h to fully compensate the quadrature term. For the opmital case, the total current is reduced to since is equal to 0 after applying Kirchhoff laws.
Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 show the configurations used based on very well-known type of filters:
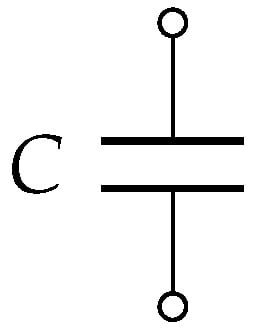
Figure 7.
C-type filter.
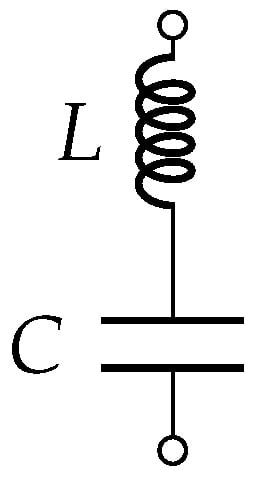
Figure 8.
Series LC-type filter.
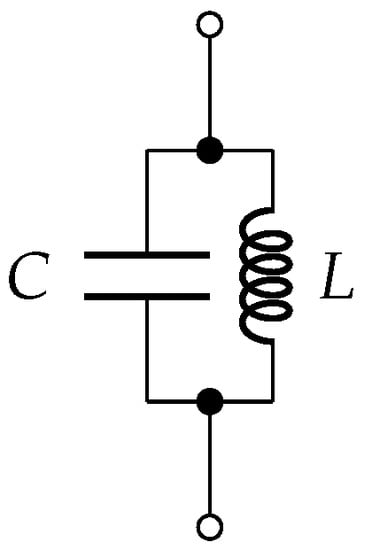
Figure 9.
Parallel LC-type filter.
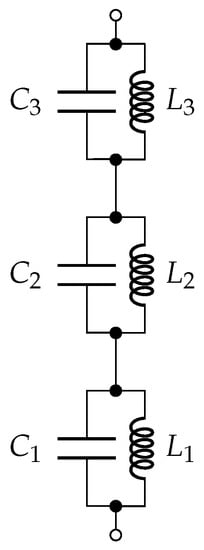
Figure 10.
Triple tune filter.
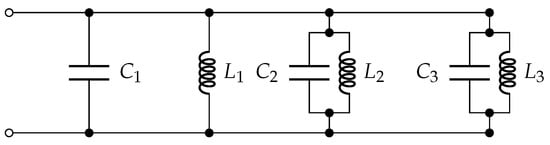
Figure 11.
Foster’s filter.
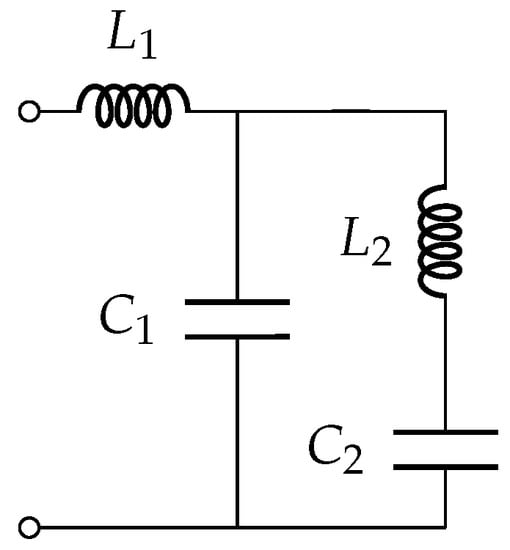
Figure 12.
Czarnecki’s 4-elements filter.
- C-type filter: it is is mainly used for suppressing the low order of harmonics [13].
- Series LC-type filter: this filter is also considered to reduce line current harmonics [42].
- Parallel LC-type filter: it provides low impedance shunt branches to the load’s harmonic current, which allows to reduce the harmonic current flowing into the line [42].
- Triple tuned filter: this type of filter is electrically equivalent to three parallel tuned filters connected in series [43].
- Foster’s filter: this filter combines in parallel single L-type and C-type filters and also parallel LC-type filters.
- Czarnecki’s 4-elements filter: it is a filter that combines two L and two C elements using a series/parallel configuration [39].
4.3. Simulation Results
Table 1, Table 2 and Table 3 show the results obtained by the genetic algorithm in the three case studies described above, being the RMS current through the supply source the objective to be minimized. The best, mean, and standard deviation of 10 independent runs are provided.

Table 1.
Compensated root mean square (RMS) current () obtained by the genetic algorithm in Czarnecki’s case study [39].

Table 2.
Compensated RMS current () obtained by the genetic algorithm in Castro-Nuñez and Castro-Puche’s case study [22].

Table 3.
Compensated RMS current () obtained by the genetic algorithm in Castilla’s case study [33].
As it can be seen in Table 1, in the case study proposed by Czarnecki [39], the filters “Triple tune”, “Foster”, and “Czarnecki 4” obtain high quality results, while “C-type”, “Series LC”, and “Parallel LC” filters are far from the optimal solution. Some similar conclusions are obtained when analyzing the date from Table 2, corresponding to the circuit proposed by Castro-Nuñez and Castro-Puche [22]. It is important to point out that better results are obtained in the case of Castro-Nuñez with the same choice of compensator (20.02 A vs. 20.10 A), although Castro-Nuñez does not specify the criterion for choosing the values of the L and C components, apart from discretionary choosing an LC series type compensator. Finally, the analysis of the results provided in Table 3 regarding to the filter proposed by Castilla [33], indicate that “Triple tune”, “Foster”, “Czarnecki”, and the series LC-type filter obtain high quality solutions. In summary, the genetic algorithm is able not only to equal but also to slightly improve the results obtained in these three case studies, which demonstrates that evolutionary approaches can be used to compensate the source current in different circuits using a variety of filters.
Table 4 shows the optimal values achieved for the 3 cases of study and the 6 proposed filters. The optimal current is also included for readability purposes.

Table 4.
Optimal values for L, C achieved by the genetic algorithm for the 3 cases of study and the 6 proposed filters.
Table 5 shows a summary comparison for each of the problems solved showing current values without compensation , the optimum current that a passive filtering can achieve , provided by each author , and the optimum current obtained by applying the technique used in this work . The value of the power factor for each of the above situations is also indicated plus the power factor without compensation using GA, . It should be noted that the power factor may differ between what is calculated by complex numbers and what is calculated by geometric algebra due to the different nature of the apparent power and the geometric apparent power . For the first case, the power factor is calculated as while for the second case it is . For example, for the Czarnecki case study, the apparent power without compensating is worth 1417 VA while compensated is worth 358.8 VA. However, using geometric algebra the power is worth 1842 VA and compensated is worth 359.25 VA. It should be noted that the final result of the compensation is quite similar since the proposed example is of low complexity as it only has 3 harmonics and low order. If we take into account the case of Castro-Nuñez or Castilla, the power of the proposed method is verified since with only 2 elements (LC filter series) or 3 elements, an almost optimal compensated current is obtained, unlike the original proposal of the author where the filter involved has many more elements and, therefore, much less economic. It should also be noted that the methodology proposed by Castro-Núñez indicates the path to follow when it comes to compensate for the correct power terms, , which is not possible to cancel with the traditional power theory because it does not account for those terms arising from crossed products between voltage and currents.

Table 5.
Comparison table for currents and power factor.
5. Conclusions
In recent years, different authors have shown that geometric algebra, also known as Clifford algebra, can be applied to analyze electric circuits. Having in mind that different studies have shown that geometric algebra is more appropriate than the algebra of complex numbers for the analysis of circuits with non-sinusoidal sources and linear loads, this investigation is an important contribution in estimating the type of filter and its parameters to optimize the quadrature current in electrical circuits. This leads to the compensation of new power terms like quadrature apparent power not included in the commonly accepted definition of electrical power standards. The traditional compensation of reactive power is exceeded by the compensation of cross products between current and voltage that have not been previously taken into account. The proposed approach is based on the use of a genetic algorithm, which is able to optimize the parameters of different types of passive filters. In particular, six widely used filters (single-tuned, double-tuned, triple-tuned, damped-double tuned, and C-type) were compared by regarding their contribution on the loading capability improvement of the transformers under non-sinusoidal conditions.
The results obtained in three test circuits found in the literature show that the application of genetic algorithms based on geometric algebra representations are powerful methods that are able to equal or even improve the results previously obtained by other authors using analytical methods. These results open the door to investigate the use of computational optimization methods for compensating the reactive power in complex circuits. As future work, it is planned to extend the analysis to larger circuits using these and other type of filters. Furthermore, multi-objective optimization methods will be considered to simultaneously optimize the reactive power compensation and to minimize the economic cost of the filters.
Author Contributions
Conceptualization, F.G.M. and R.B.; Methodology, R.B.; Software, A.A. and F.M.A.-C.; Validation, A.A., R.B. and F.M.A.-C.; Formal Analysis, F.G.M.; Investigation, F.G.M. and A.A.; Resources, F.M.A.-C.; Data Curation, R.B.; Writing—Original Draft Preparation, R.B., F.G.M. and F.M.A.-C.; Writing—Review & Editing, F.G.M., A.A., F.M.A.-C. and R.B.; Visualization, F.G.M.; Supervision, F.G.M.; Project Administration, F.G.M. and A.A.
Funding
This research received no external funding.
Acknowledgments
The authors want to acknowledge the CEIA3 campus for the support on this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. General Concepts
Given an ortho-normal base with for a vector space , it is possible to define a new space called geometrical algebra . This new space is characterized by bases not only composed of , but also of external products between these vectors. For example, in the case of a 3D Euclidean space, there is an ortho-normal base where . Applying the concept of Grassmann product or exterior product, you get
which is a new entity, different from a scalar or a vector because
squares to so we can conclude that we are facing a new element, which is called a bivector. In the same way, the external product of more than 3 vectors is called trivector, and in general, the product of k vectors is called k-vector. In this way, algebra can be developed with the base
Generally speaking, the elements of a geometric algebra are called multivectors () and can be expressed as a linear combination of the different bases
where each is an element of grade k, representing scalars (grade 0), vectors (grade 1), bivectors (grade 2), or in general k-vectors (grade k).
Appendix B. Geometric Operations
The geometric product is the cornerstone of geometric algebra and is indebted to the contributions of Grassman and Clifford. It is defined as the sum of the scalar product and the external product, and for the case of 2 vectors and
for the base vectors and with , we get bivectors
base vectors anticommute for because
On the other hand, unlike vectors which square to 1, bivectors square to −1
Finally, we detail some important operations that are used extensively in multivector operations. One of these properties is the reversion or which consists of
The norm of a multivector () is always a scalar and can be obtained
References
- Fang, X.; Misra, S.; Xue, G.; Yang, D. Smart grid—The new and improved power grid: A survey. IEEE Commun. Surv. Tutor. 2012, 14, 944–980. [Google Scholar] [CrossRef]
- Merabet, L.; Saad, S.; Abdeslam, D.O.; Merckle, J. Direct neural method for harmonic currents estimation using adaptive linear element. Electr. Power Syst. Res. 2017, 152, 61–70. [Google Scholar] [CrossRef]
- Bollen, M.H.; Das, R.; Djokic, S.; Ciufo, P.; Meyer, J.; Rönnberg, S.K.; Zavodam, F. Power quality concerns in implementing smart distribution-grid applications. IEEE Trans. Smart Grid 2017, 8, 391–399. [Google Scholar] [CrossRef]
- Bouzid, A.M.; Guerrero, J.M.; Cheriti, A.; Bouhamida, M.; Sicard, P.; Benghanem, M. A survey on control of electric power distributed generation systems for microgrid applications. Renew. Sustain. Energy Rev. 2015, 44, 751–766. [Google Scholar] [CrossRef]
- Czarnecki, L.S.; Pearce, S.E. Compensation objectives and currents’ physical components-based generation of reference signals for shunt switching compensator control. IET Power Electron. 2009, 2, 33–41. [Google Scholar] [CrossRef]
- Willems, J.L. Budeanu’s reactive power and related concepts revisited. IEEE Trans. Instrum. Meas. 2011, 60, 1182–1186. [Google Scholar] [CrossRef]
- De Léon, F.; Cohen, J. AC power theory from Poynting theorem: Accurate identification of instantaneous power components in nonlinear-switched circuits. IEEE Trans. Power Deliv. 2010, 25, 2104–2112. [Google Scholar] [CrossRef]
- Budeanu, C. Puissances Reactives Et Fictives; Number 2; Impr. Cultura Nationala: Bouchares, Romania, 1927. [Google Scholar]
- Staudt, V. Fryze-Buchholz-Depenbrock: A time-domain power theory. In Proceedings of the 2008 International School on Nonsinusoidal Currents and Compensation (ISNCC 2008), Lagow, Poland, 10–13 June 2008; pp. 1–12. [Google Scholar]
- Czarnecki, L.S. What is wrong with the Budeanu concept of reactive and distortion power and why it should be abandoned. IEEE Trans. Instrum. Meas. 1987, 1001, 834–837. [Google Scholar] [CrossRef]
- Czarnecki, L. Budeanu and Fryze: Two frameworks for interpreting power properties of circuits with nonsinusoidal voltages and currents. Electr. Eng. 1997, 80, 359–367. [Google Scholar] [CrossRef]
- Czarnecki, L.S. Currents’ physical components (CPC) concept: A fundamental of power theory. In Proceedings of the 2008 International School on Nonsinusoidal Currents and Compensation (ISNCC 2008), Lagow, Poland, 10–13 June 2008; pp. 1–11. [Google Scholar]
- Xiao, Y.; Zhao, J.; Mao, S. Theory for the design of C-type filter. In Proceedings of the 2004 11th International Conference on Harmonics and Quality of Power, Lake Placid, NY, USA, 12–15 September 2004; pp. 11–15. [Google Scholar]
- Biswas, P.P.; Suganthan, P.N.; Amaratunga, G.A. Minimizing harmonic distortion in power system with optimal design of hybrid active power filter using differential evolution. Appl. Soft Comput. 2017, 61, 486–496. [Google Scholar] [CrossRef]
- Li, W.; Man, Y.; Li, G. Optimal parameter design of input filters for general purpose inverter based on genetic algorithm. Appl. Math. Comput. 2008, 205, 697–705. [Google Scholar] [CrossRef]
- Karadeniz, A.; Balci, M.E. Comparative evaluation of common passive filter types regarding maximization of transformer’s loading capability under non-sinusoidal conditions. Electr. Power Syst. Res. 2018, 158, 324–334. [Google Scholar] [CrossRef]
- Chen, Y.M. Passive filter design using genetic algorithms. IEEE Trans. Ind. Electr. 2003, 50, 202–207. [Google Scholar] [CrossRef]
- Klempka, R. Passive power filter design using genetic algorithm. Praz. Elektrotech. 2013, 5, 294–301. [Google Scholar]
- Lachichi, A.; Junyent-Ferre, A.; Green, T. filter design optimization for LV modular multilevel converters in hybrid ac/dc microgrids application. In Proceedings of the 2018 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Algiers, Algeria, 28–31 October 2018; pp. 1–5. [Google Scholar]
- Steinmetz, C.P. Theory and Calculation of Alternating Current Phenomena; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1916; Volume 4. [Google Scholar]
- Castro-Núñez, M.; Londoño-Monsalve, D.; Castro-Puche, R. M, the conservative power quantity based on the flow of energy. J. Eng. 2016, 2016, 269–276. [Google Scholar] [CrossRef]
- Castro-Nunez, M.; Castro-Puche, R. The IEEE Standard 1459, the CPC power theory, and geometric algebra in circuits with nonsinusoidal sources and linear loads. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 2980–2990. [Google Scholar] [CrossRef]
- Sangston, K.J. Geometry of complex data. IEEE Aerosp. Electr. Syst. Mag. 2016, 31, 32–69. [Google Scholar] [CrossRef]
- Hestenes, D.; Sobcyk, G. Clifford Algebra to Geometric Calculus: A Unified Language for Mathematics and Physics (Fundamental Theories of Physics); Kluwer Academic Publishers: Aarhus, Denmark, 1987. [Google Scholar]
- Chappell, J.M.; Drake, S.P.; Seidel, C.L.; Gunn, L.J.; Iqbal, A.; Allison, A.; Abbott, D. Geometric algebra for electrical and electronic engineers. Proc. IEEE 2014, 102, 1340–1363. [Google Scholar] [CrossRef]
- Castro-Nunez, M.; Castro-Puche, R. Advantages of geometric algebra over complex numbers in the analysis of networks with nonsinusoidal sources and linear loads. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 2056–2064. [Google Scholar] [CrossRef]
- Petroianu, A.I. A geometric algebra reformulation and interpretation of Steinmetz’s symbolic method and his power expression in alternating current electrical circuits. Electr. Eng. 2015, 97, 175–180. [Google Scholar] [CrossRef]
- Menti, A.; Zacharias, T.; Milias-Argitis, J. Geometric algebra: A powerful tool for representing power under nonsinusoidal conditions. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 601–609. [Google Scholar] [CrossRef]
- Castilla, M.; Bravo, J.C.; Ordonez, M. Geometric algebra: A multivectorial proof of Tellegen’s theorem in multiterminal networks. IET Circuits Devices Syst. 2008, 2, 383–390. [Google Scholar] [CrossRef]
- Castilla, M.; Bravo, J.C.; Ordonez, M.; Montaño, J.C. Clifford theory: A geometrical interpretation of multivectorial apparent power. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 3358–3367. [Google Scholar] [CrossRef]
- Gilbert, J.E.; Gilbert, J.; Murray, M. Clifford Algebras and Dirac Operators in Harmonic Analysis; Cambridge University Press: Cmabridge, UK, 1991; Volume 26. [Google Scholar]
- Bravo, J.C.; Castilla, M.V. Energy conservation law in industrial architecture: An approach through geometric algebra. Symmetry 2016, 8, 92. [Google Scholar] [CrossRef]
- Castilla, M.V. Control of disturbing loads in residential and commercial buildings via geometric algebra. Sci. World J. 2013, 2013. [Google Scholar] [CrossRef]
- Jeon, S.J. Representation of apparent power of non-sinusoidal multi-line power system using geometric algebra. Trans. Korean Inst. Electr. Eng. 2009, 58, 2064–2070. [Google Scholar]
- Castro-Núñez, M.; Castro-Puche, R.; Nowicki, E. The use of geometric algebra in circuit analysis and its impact on the definition of power. In Proceedings of the 2010 International School on Nonsinusoidal Currents and Compensation (ISNCC), Lagow, Poland, 15–18 June 2010; pp. 89–95. [Google Scholar]
- Henderson, R.D.; Rose, P.J. Harmonics: The effects on power quality and transformers. IEEE Trans. Ind. Appl. 1994, 30, 528–532. [Google Scholar] [CrossRef]
- De La Rosa, F. Harmonics and Power Systems; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- El-Saadany, E.; Zeineldin, H. An optimum reactance one-port compensator for harmonic mitigation. Electr. Power Qual. Util. J. 2005, 11, 77–82. [Google Scholar]
- Czarnecki, L.S. Minimisation of distortion power of nonsinusoidal sources applied to linear loads. In IEE Proceedings C-Generation, Transmission and Distribution; IET Digital Library: Hertfordshire, UK, 1981; Volume 128, pp. 208–210. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; The MIT Press: Cambridge, MA, USA; London, UK, 1975. [Google Scholar]
- Mathworks. Genetic algorithm solver. In MATLAB Global Optimization Toolbox; The MathWorks, Inc.: Natick, MA, USA, 2018. [Google Scholar]
- Peng, F.Z.; Su, G.J.; Farquharson, G. A series LC filter for harmonic compensation of AC drives. In Proceedings of the 30th Annual IEEE Power Electronics Specialists Conference (PESC 99), Charleston, SC, USA, 1 July 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 1, pp. 213–218. [Google Scholar]
- Bartzsch, C.; Huang, H.; Roessel, R.; Sadek, K. Triple tuned harmonic filters-design principle and operating experience. In Proceedings of the International Conference on Power System Technology (PowerCon 2002), Kunming, China, 13–17 October 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 1, pp. 542–546. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).