Simulation of Thermal Behaviour of a Lithium Titanate Oxide Battery
Abstract
1. Introduction
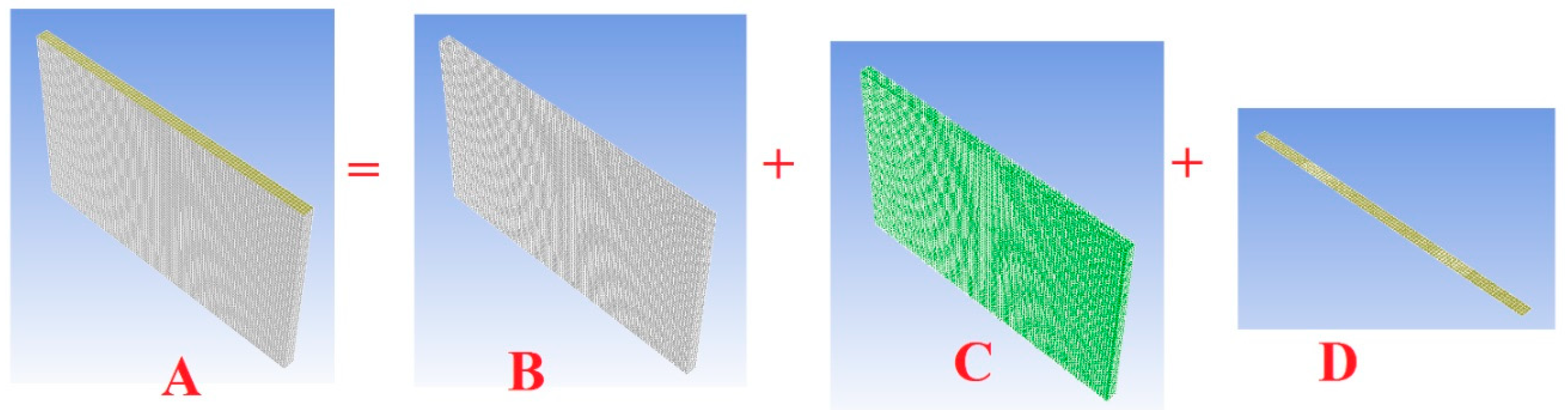
2. The Battery Modelling
- (1)
- Positive current tab meshing structure;
- (2)
- Interior part of positive current tab;
- (3)
- Positive current tab;
- (4)
- Skin of positive current tab;
- (5)
- Contact region of positive current tab.
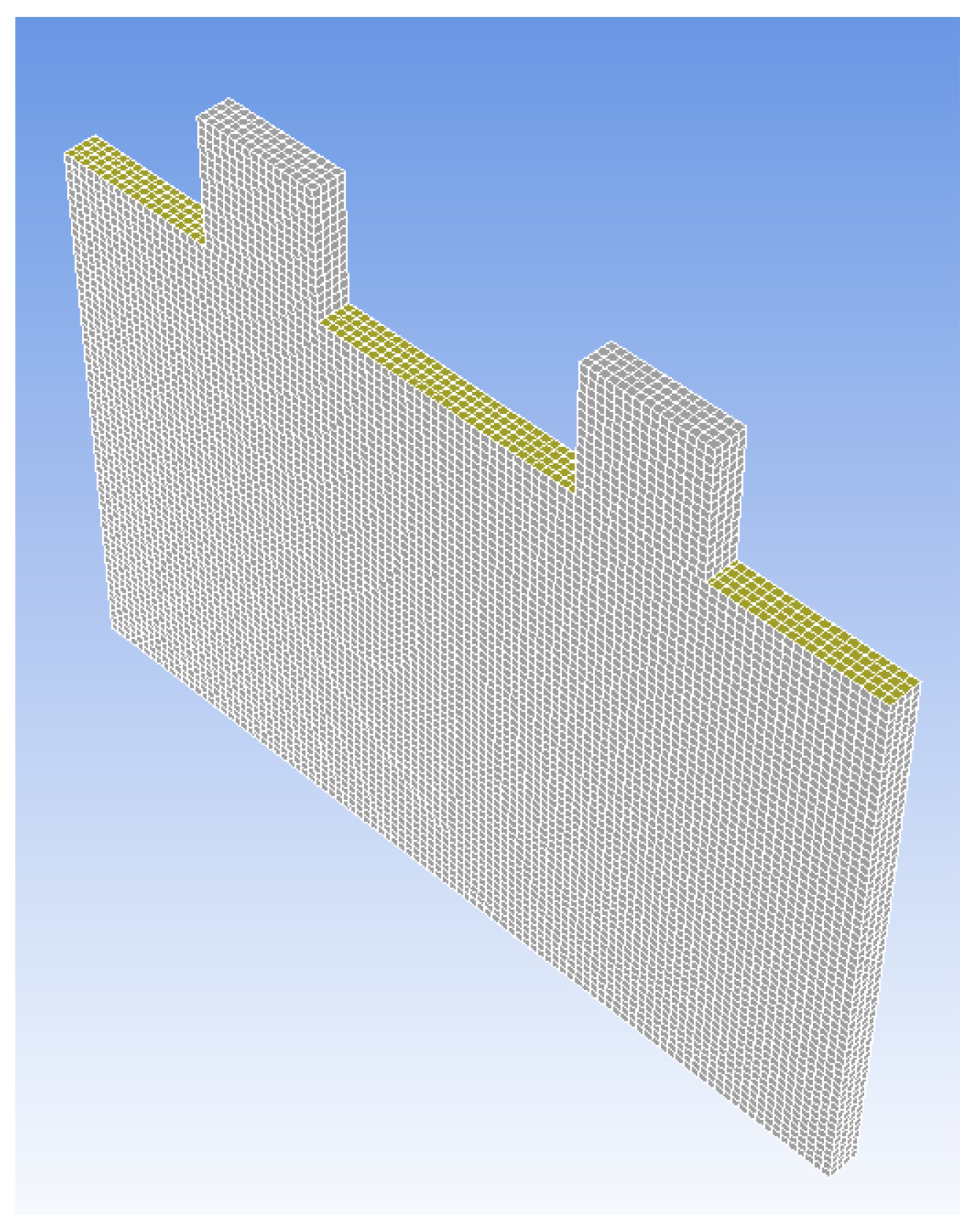
- (A)
- Meshing of battery cell stacked construction;
- (B)
- Skin of active volume;
- (C)
- Active volume;
- (D)
- Contact region of active volume.
3. Identification of Model Parameters
3.1. Determination of Thermal Parameters
- : Specific heat capacity
- : Volumetric heat generation
- : Physical mass
- : Thermal conduction in direction i
- : Temperature
- : Stefan–Boltzmann constant
- : Emissivity of the battery cell surface
- : Ambient temperature
- : Convective heat transfer
- : Battery surface temperature
- : Kinematics viscosity of the fluid
- : Coefficient of volume expansion
- : Gravitational acceleration
- : Characteristic length of the geometry
- : Heat flux
- : Temperature gradient
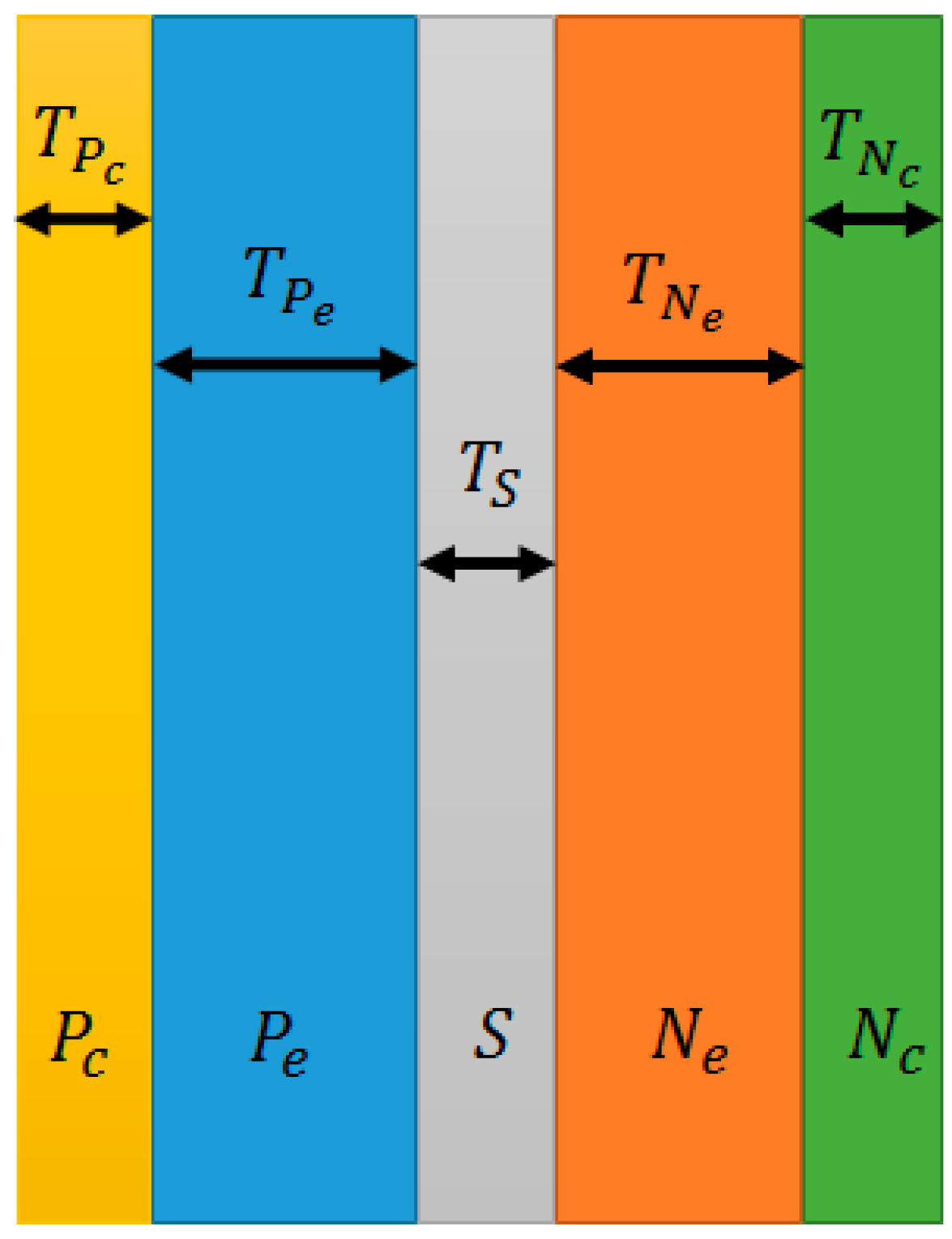
- : Thickness
- : Thermal diffusivity
- : Thickness of negative current collector
- : Thickness of negative electrode
- : Thickness of separator
- : Thickness of positive electrode
- : Thickness of positive current collector
- : Thermal conductivity of positive current collector
- : Thermal conductivity of positive electrode
- : Thermal conductivity of separator
- : Thermal conductivity of negative electrode
- : Thermal conductivity of negative current collector
- : Density of positive current collector
- : Density of positive electrode
- : Density of separator
- : Density of negative electrode
- : Density of negative current collector
- : Heat capacity of positive current collector
- : Heat capacity of positive electrode
- : Heat capacity of separator
- : Heat capacity of negative electrode
- : Heat capacity of negative current collector
- : Electric conductivity of positive current collector
- : Electric conductivity of positive electrode
- : Electric conductivity of negative current collector
- : Electric conductivity of negative electrode
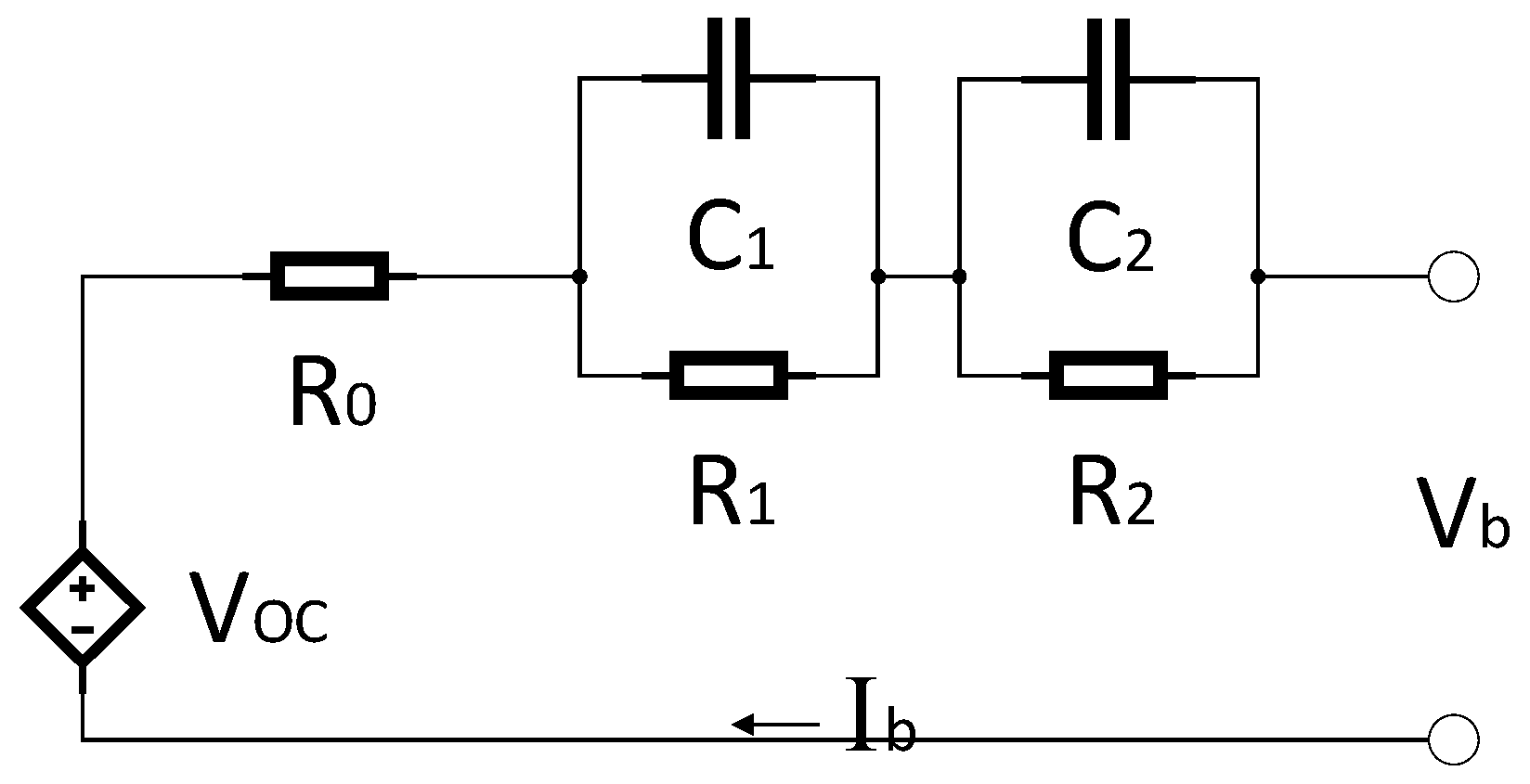
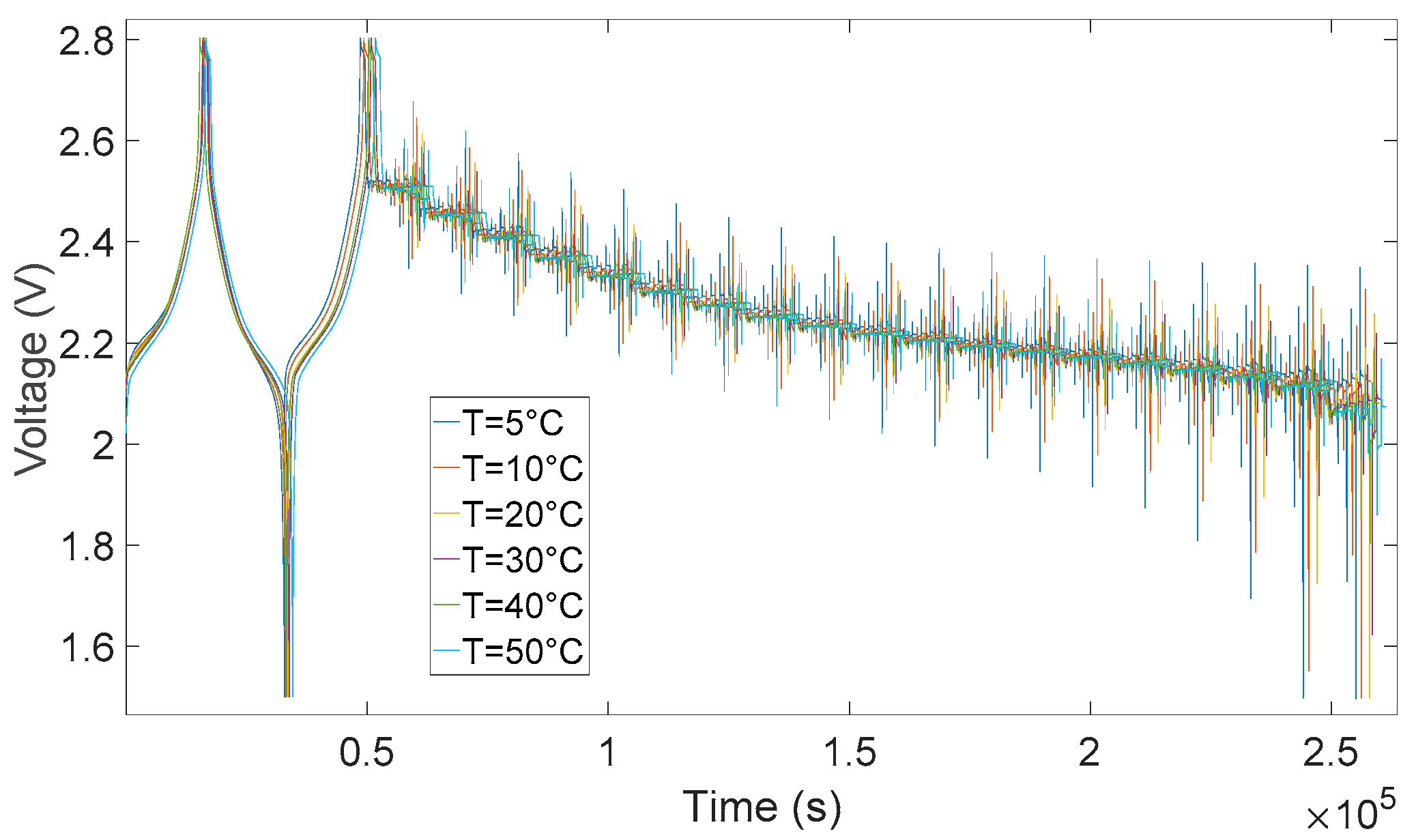
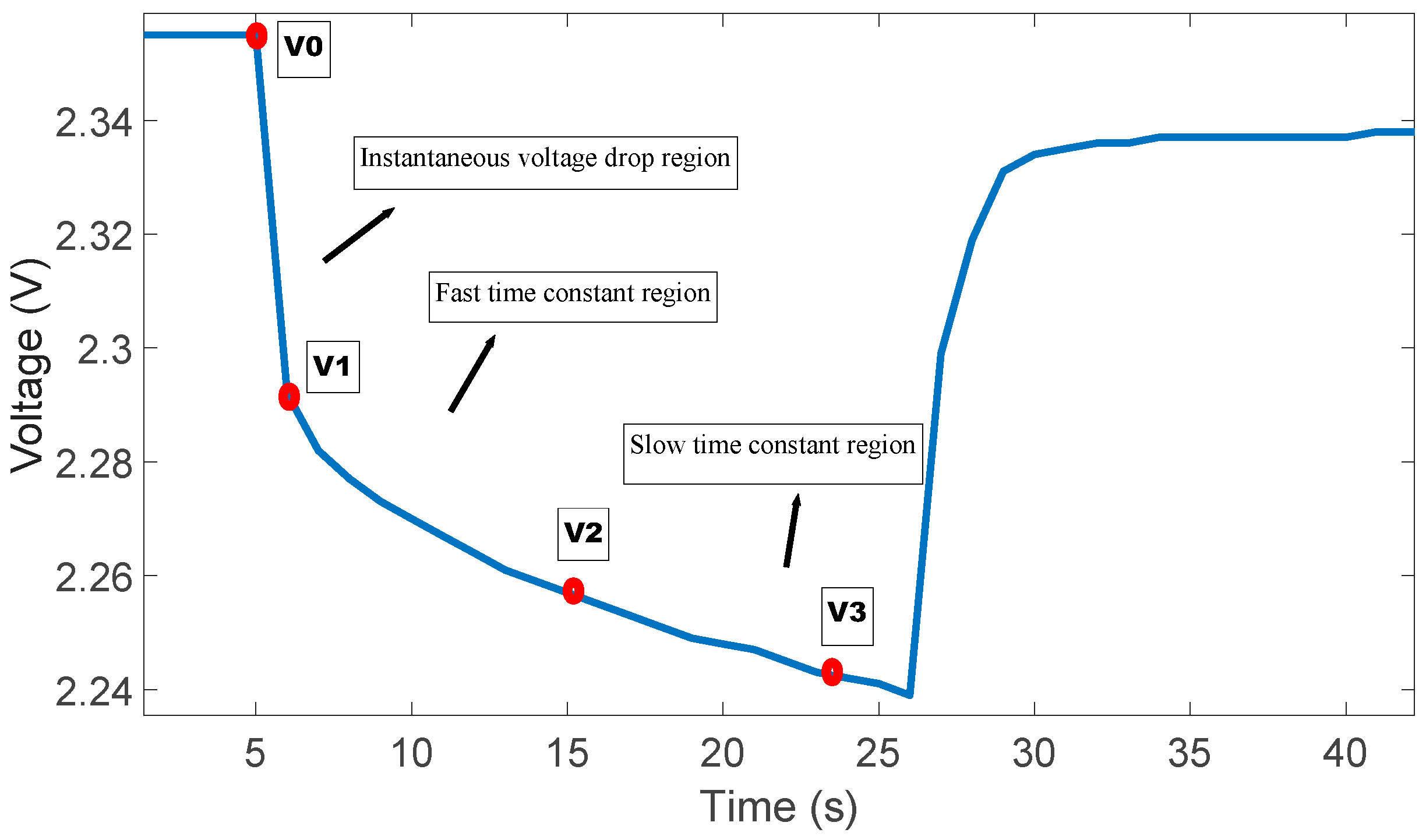
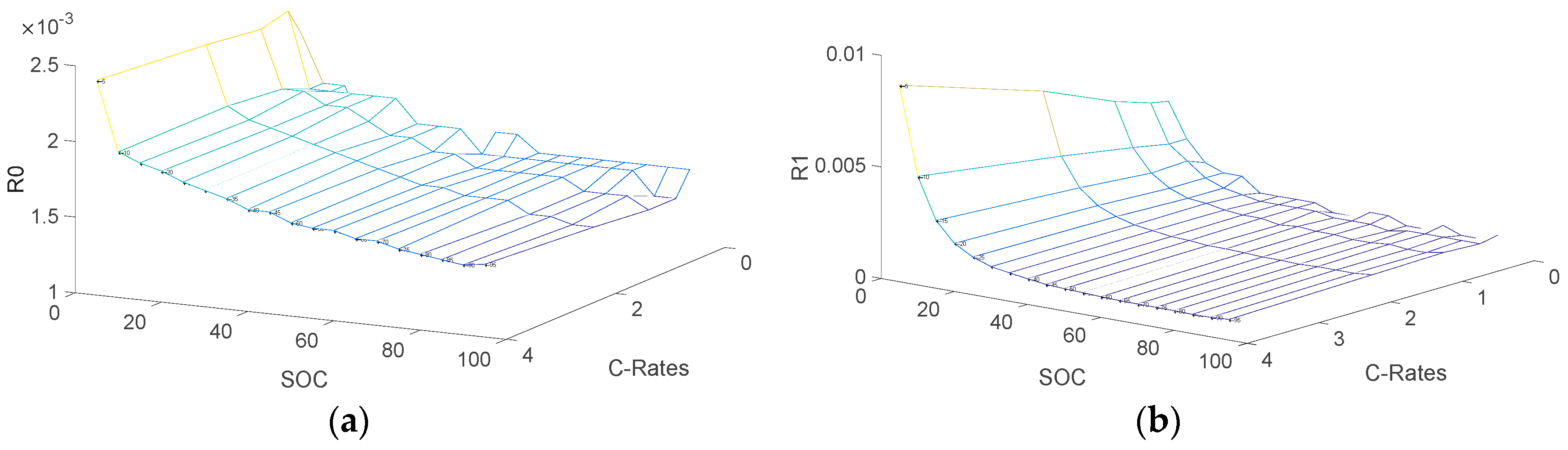
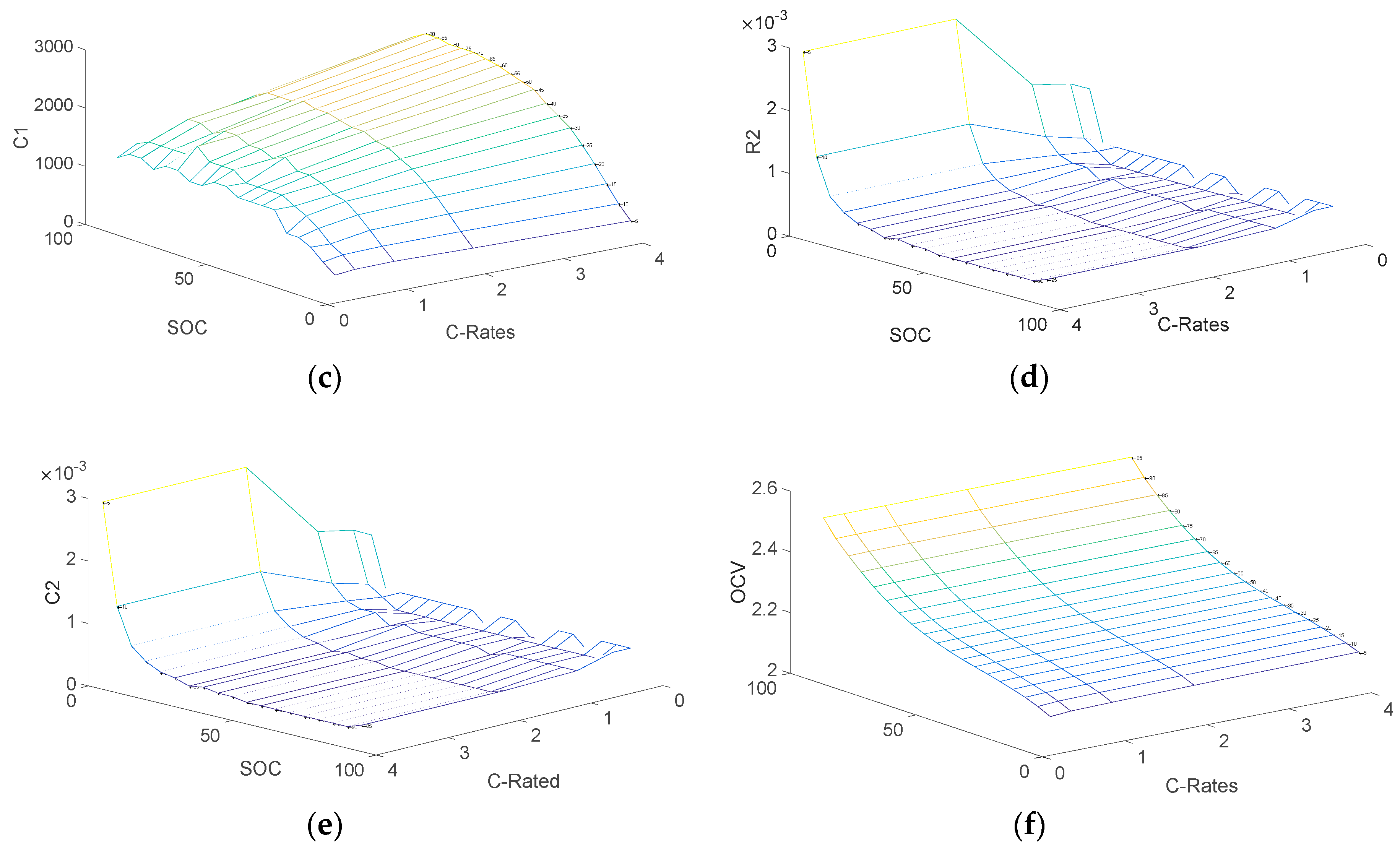
3.2. Determination of Electrical Parameters
- V0: Battery voltage before the discharge current pulse is applied.
- R0: Ohmic resistance
- I: Amplitude of the current pulse.
- V1: Battery voltage one seconds (t1) after the discharge current is applied.
- R1, C1: Resistance and capacitance of the first RC network
- V2: Battery voltage ten seconds (t2) after the discharge current is applied.
- V3: Battery voltage eighteen seconds (t3) after the discharge current is applied.
- R2, C2: Resistance and capacitance of the second RC network
4. Modelling Method
- : Volumetric transfer
- : Heat capacity
- : Heat generation
- : Thermal conductivity
- : Effective electric conductivities
- : Phase potential
- : Temperature
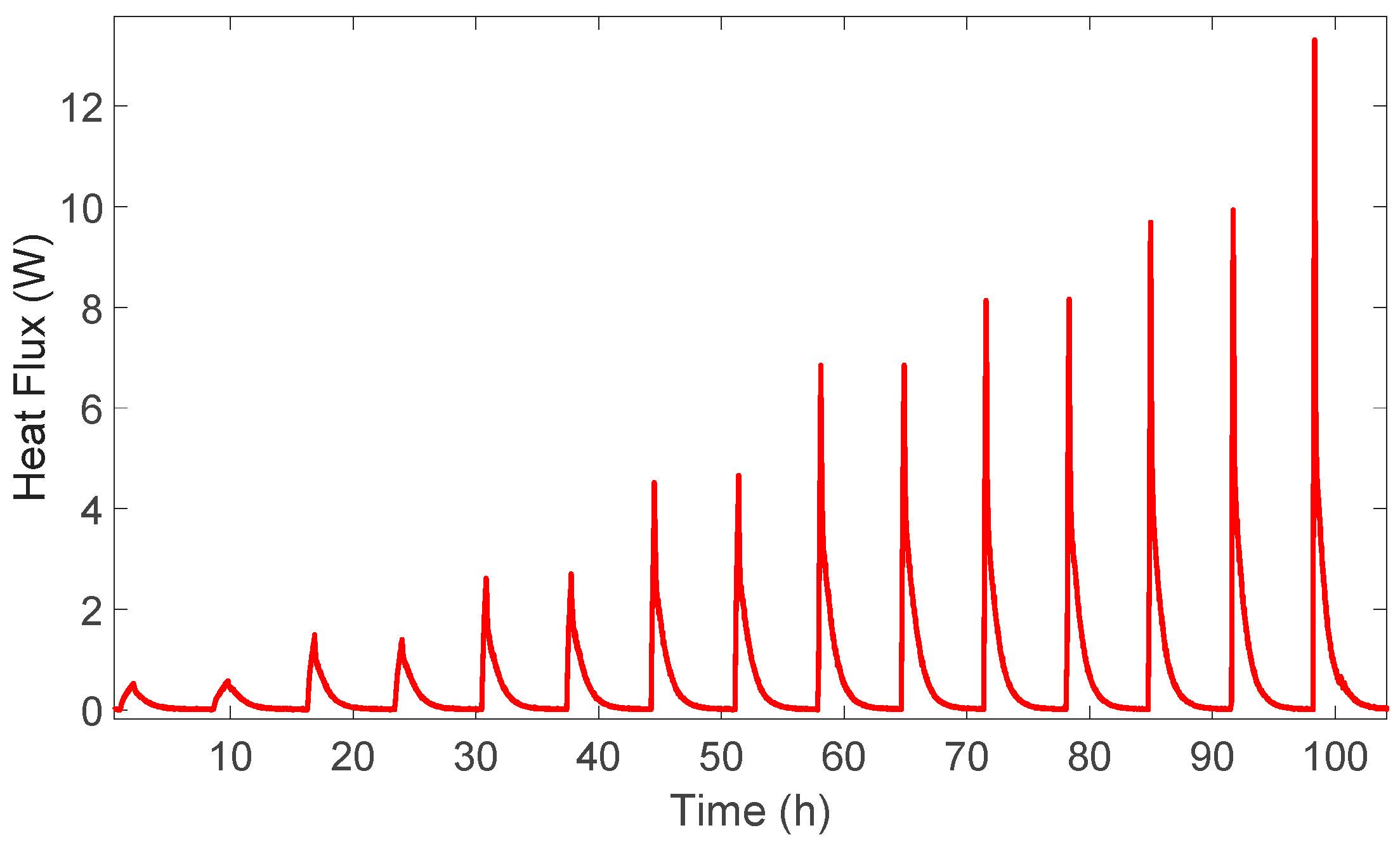
5. Measurement of Heat Generation Rates
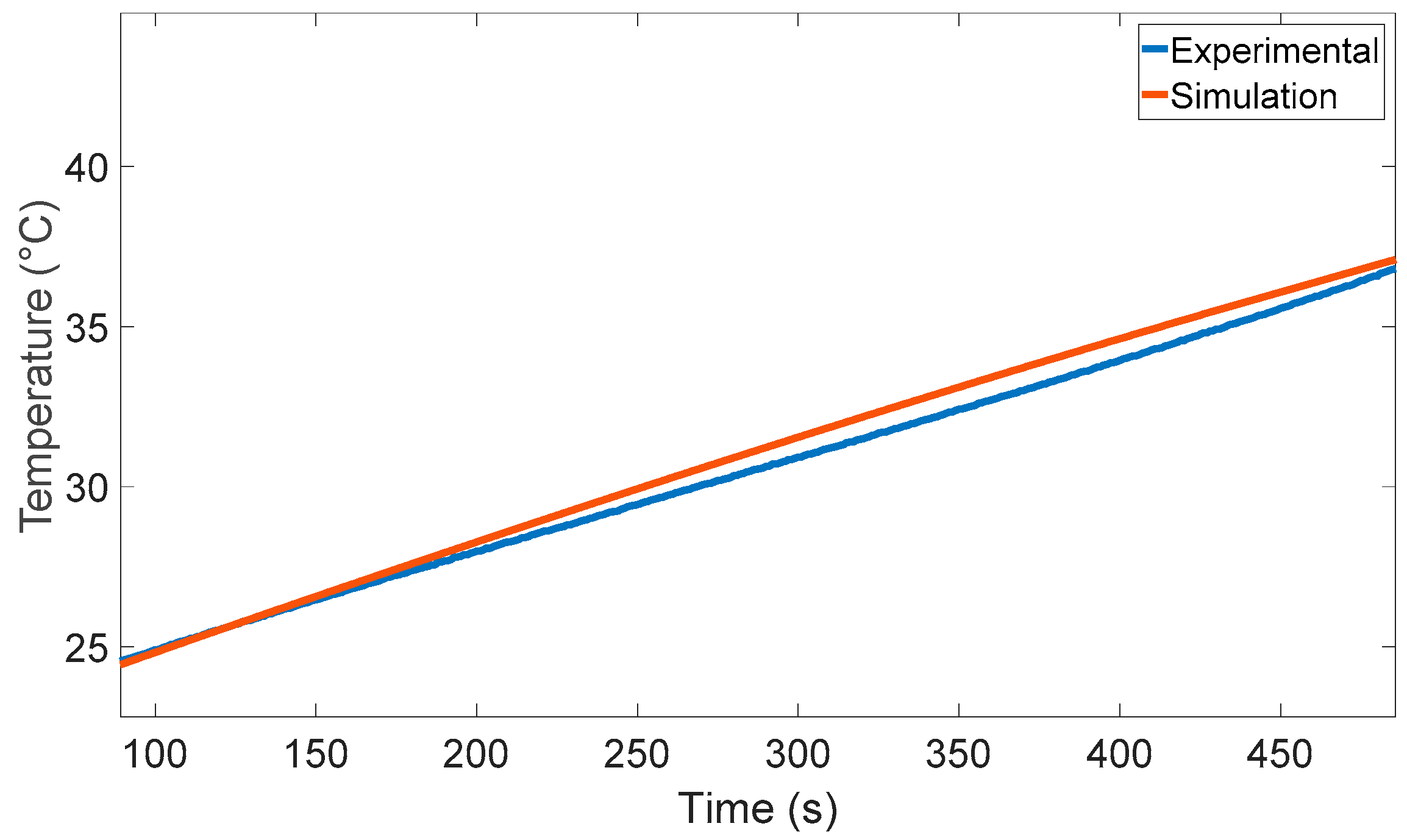
6. Experimental Validation
7. Simulation Results and Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- von Srbik, M.; Marinescu, M.; Martinez-botas, R.F.; Offer, G.J. A physically meaningful equivalent circuit network model of a lithium-ion battery accounting for local electrochemical and thermal behaviour, variable double layer capacitance and degradation. J. Power Sources 2016, 325, 171–184. [Google Scholar] [CrossRef]
- Tian, C.; Lin, F. Electrochemical Characteristics of Layered Transition Metal Oxide Cathode Materials for Lithium Ion Batteries: Surface, Bulk Behavior, and Thermal Properties. Acc. Chem. Res. 2018, 2, 89–96. [Google Scholar] [CrossRef]
- Ortiz, G.F.; Alcántara, R.; Lavela, P.; Tirado, J.L. Optimization of the Electrochemical Behavior of Vapor Grown Carbon Nanofibers for Lithium-Ion Batteries by Impregnation, and Thermal and Hydrothermal Treatments. J. Electrochem. Soc. 2005, 152, A1797–A1803. [Google Scholar] [CrossRef]
- Northrop, P.W.C.; Ramadesigan, V.; De, S.; Subramanian, V.R. Coordinate Transformation, Orthogonal Collocation, Model Reformulation and Simulation of Electrochemical-Thermal Behavior of Lithium-Ion Battery Stacks. J. Electrochem. Soc. 2011, 158, A1461–A1477. [Google Scholar] [CrossRef]
- Northrop, P.W.C.; Pathak, M.; Rife, D.; De, S.; Santhanagopalan, S.; Subramanian, V.R. Efficient Simulation and Model Reformulation of Two-Dimensional Electrochemical Thermal Behavior of Lithium-Ion Batteries. J. Electrochem. Soc. 2015, 162, A940–A951. [Google Scholar] [CrossRef]
- Wang, Z.; Siegel, J.; Garikipati, K. Intercalation Driven Porosity Effects in Coupled Continuum Models for the Electrical, Chemical, Thermal and Mechanical. J. Electrochem. Soc. 2017, 164, A2199–A2212. [Google Scholar] [CrossRef]
- Gu, H. Mathematical Analysis of a Zn/NiOOH Cell R. J. Electrochem. Soc. 1983, 130, A1459–A1464. [Google Scholar] [CrossRef]
- Smith, K.; Wang, C.Y. Solid-state diffusion limitations on pulse operation of a lithium ion cell for hybrid electric vehicles. J. Power Sources 2006, 161, 628–639. [Google Scholar] [CrossRef]
- Kim, U.S.; Shin, C.B.; Kim, C.S. Effect of electrode configuration on the thermal behavior of a lithium-polymer battery. J. Power Sources 2008, 180, 909–916. [Google Scholar] [CrossRef]
- Kim, G.-H.; Smith, K.; Lee, K.-J.; Santhanagopalan, S.; Pesaran, A. Multi-Domain Modeling of Lithium-Ion Batteries Encompassing Multi-Physics in Varied Length Scales. J. Electrochem. Soc. 2011, 158, A955–A969. [Google Scholar] [CrossRef]
- Kwon, K.H.; Shin, C.B.; Kang, T.H.; Kim, C.S. A two-dimensional modeling of a lithium-polymer battery. J. Power Sources 2006, 163, 151–157. [Google Scholar] [CrossRef]
- Yi, J.; Kim, U.S.; Shin, C.B.; Han, T.; Park, S. Modeling the temperature dependence of the discharge behavior of a lithium-ion battery in low environmental temperature. J. Power Sources 2013, 244, 143–148. [Google Scholar] [CrossRef]
- Tang, Y.; Wu, L.; Wei, W.; Wen, D.; Guo, Q.; Liang, W.; Xiao, L. Study of the thermal properties during the cyclic process of lithium ion power batteries using the electrochemical-thermal coupling model. Appl. Therm. Eng. 2018, 137, 11–22. [Google Scholar] [CrossRef]
- Panchal, S.; Mathew, M.; Fraser, R.; Fowler, M. Electrochemical thermal modeling and experimental measurements of 18650 cylindrical lithium-ion battery during discharge cycle for an EV. Appl. Therm. Eng. 2018, 135, 123–132. [Google Scholar] [CrossRef]
- Mastali, M.; Foreman, E.; Modjtahedi, A.; Samadani, E.; Amirfazli, A.; Farhad, S.; Fraser, R.A.; Fowler, M. Electrochemical-thermal modeling and experimental validation of commercial graphite/LiFePO4pouch lithium-ion batteries. Int. J. Therm. Sci. 2018, 129, 218–230. [Google Scholar] [CrossRef]
- Bahrami, M.; Consider, N.C.; Water, S. Natural Convection. Eng. Thermodyn. Heat Transf. 2011, 388, 1–7. [Google Scholar]
- ANSYS, Inc. ANSYS FLUENT Manual; ANSYS, Inc.: Cannonsburg, PA, USA, 2018. [Google Scholar]
- Hentunen, A.; Lehmuspelto, T.; Suomela, J. Time-domain parameter extraction method for thévenin-equivalent circuit battery models. IEEE Trans. Energy Convers. 2014, 29, 558–566. [Google Scholar] [CrossRef]
- Stroe, A.I.; Stroe, D.I.; Swierczynski, M.; Teodorescu, R.; Kær, S.K. Lithium-Ion battery dynamic model for wide range of operating conditions. In Proceedings of the 2017 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM) & 2017 International Aegean Conference on Electrical Machines and Power Electronics (ACEMP), Brasov, Romania, 25–27 May 2017; pp. 660–666. [Google Scholar]
- Madani, S.; Schaltz, E.; Kær, S.K.; Madani, S.S.; Schaltz, E.; Kær, S.K. Heat Loss Measurement of Lithium Titanate Oxide Batteries under Fast Charging Conditions by Employing Isothermal Calorimeter. Batteries 2018, 4, 59. [Google Scholar] [CrossRef]
- Wu, B.; Li, Z.; Zhang, J. Thermal Design for the Pouch-Type Large-Format Lithium-Ion Batteries: I. Thermo-Electrical Modeling and Origins of Temperature Non-Uniformity. J. Electrochem. Soc. 2014, 162, A181–A191. [Google Scholar] [CrossRef]
- Guo, M.; White, R.E. A distributed thermal model for a Li-ion electrode plate pair. J. Power Sources 2013, 221, 334–344. [Google Scholar] [CrossRef]
- Yi, J.; Lee, J.; Shin, C.B.; Han, T.; Park, S. Modeling of the transient behaviors of a lithium-ion battery during dynamic cycling. J. Power Sources 2015, 277, 379–386. [Google Scholar] [CrossRef]





| Parameters | A1 | A2 | A3 | A4 | A5 | A6 |
|---|---|---|---|---|---|---|
| R0-0.25C | −3.5809 × 10−9 | 2.5521 × 10−7 | −6.7798 × 10−6 | 8.3191 × 10−5 | −0.00046957 | 0.0025463 |
| R0-0.5 | −1.866 × 10−8 | 9.4976 × 10−7 | −1.7805 × 10−5 | 0.00015173 | −0.00061228 | 0.0027413 |
| R0-1 | −9.7461 × 10−9 | 5.0726 × 10−7 | −9.8659 × 10−6 | 8.9925 × 10−5 | −0.00041996 | 0.0025851 |
| R0-2 | −6.1113 × 10−8 | 3.5975 × 10−6 | −8.0772 × 10−5 | 0.00086392 | −0.0044514 | 0.01021 |
| R0-4 | −9.1265 × 10−8 | 5.3384 × 10−6 | −0.00011908 | 0.0012635 | −0.0064278 | 0.013877 |
| R1-0.25C | −2.114 × 10−8 | 1.3532 × 10−6 | −3.3195 × 10−5 | 0.00039194 | −0.0022685 | 0.0064137 |
| R1-0.5 | −3.2789 × 10−8 | 1.9467 × 10−6 | −4.4325 × 10−5 | 0.00048576 | −0.0026136 | 0.0068707 |
| R1-1 | −3.9476 × 10−8 | 2.3809 × 10−6 | −5.4759 × 10−5 | 0.00060016 | −0.0031773 | 0.0078591 |
| R1-2 | −6.1113 × 10−8 | 3.5975 × 10−6 | −8.0772 × 10−5 | 0.00086392 | −0.0044514 | 0.01021 |
| R1-4 | −9.1265 × 10−8 | 5.3384 × 10−6 | −0.00011908 | 0.0012635 | −0.0064278 | 0.013877 |
| R2-0.25C | −2.6294 × 10−8 | 1.433 × 10−6 | −2.8897 × 10−5 | 0.00026512 | −0.0010917 | 0.0021711 |
| R2-0.5 | −1.7408 × 10−8 | 1.0479 × 10−6 | −2.3627 × 10−5 | 0.00024636 | −0.0011691 | 0.002445 |
| R2-1 | −2.1097 × 10−8 | 1.1844 × 10−6 | −2.509 × 10−5 | 0.00024926 | −0.0011648 | 0.002562 |
| R2-2 | −4.1644 × 10−8 | 2.4069 × 10−6 | −5.2546 × 10−5 | 0.00053695 | −0.0025564 | 0.0049448 |
| R2-4 | −4.1644 × 10−8 | 2.4069 × 10−6 | −5.2546 × 10−5 | 0.00053695 | −0.0025564 | 0.0049448 |
| C1-0.25C | −0.0092475 | 0.45755 | −7.8046 | 47.083 | 34.95 | 311.78 |
| C1-0.5 | −0.0019811 | 0.067608 | −0.38574 | −12.919 | 240.28 | 158.33 |
| C1-1 | −0.0059824 | 0.25455 | −3.4037 | 6.1343 | 215.73 | 184.13 |
| C1-2 | −0.0054655 | 0.25365 | −3.9189 | 13.296 | 219.94 | 136.56 |
| C1-4 | −0.0079124 | 0.40473 | −7.3001 | 44.494 | 157.33 | 113.13 |
| C2-0.25C | 0.032132 | −1.7143 | 33.427 | −293.41 | 1165.2 | 239.18 |
| C2-0.5 | −0.011611 | 0.35172 | −0.50313 | −72.798 | 747.78 | 550.81 |
| C2-1 | 0.012608 | −0.72394 | 15.828 | −172.34 | 1019.5 | 111.45 |
| C2-2 | −0.01571 | 0.6205 | −6.7757 | −20.924 | 827.98 | −182.01 |
| C2-4 | −0.029829 | 1.5623 | −30.689 | 258.86 | −513.18 | 1515 |
| OCV-0.25C | 6.5341 × 10−8 | −5.1732 × 10−6 | 0.00022863 | −0.0032124 | 0.028214 | 2.0797 |
| OCV-0.5 | −1.963 × 10−8 | −8.8693 × 10−7 | 0.00014772 | −0.0024952 | 0.025067 | 2.0873 |
| OCV-1 | −8.6373 × 10−8 | 2.5889 × 10−6 | 7.9331 × 10−5 | −0.001866 | 0.022391 | 2.0925 |
| OCV-2 | −4.6552 × 10−8 | 6.1797 × 10−7 | 0.00011227 | −0.0020581 | 0.022357 | 2.0958 |
| OCV-4 | −7.1791 × 10−8 | 2.0946 × 10−6 | 7.9307 × 10−5 | −0.0017074 | 0.020533 | 2.101 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madani, S.S.; Schaltz, E.; Knudsen Kær, S. Simulation of Thermal Behaviour of a Lithium Titanate Oxide Battery. Energies 2019, 12, 679. https://doi.org/10.3390/en12040679
Madani SS, Schaltz E, Knudsen Kær S. Simulation of Thermal Behaviour of a Lithium Titanate Oxide Battery. Energies. 2019; 12(4):679. https://doi.org/10.3390/en12040679
Chicago/Turabian StyleMadani, Seyed Saeed, Erik Schaltz, and Søren Knudsen Kær. 2019. "Simulation of Thermal Behaviour of a Lithium Titanate Oxide Battery" Energies 12, no. 4: 679. https://doi.org/10.3390/en12040679
APA StyleMadani, S. S., Schaltz, E., & Knudsen Kær, S. (2019). Simulation of Thermal Behaviour of a Lithium Titanate Oxide Battery. Energies, 12(4), 679. https://doi.org/10.3390/en12040679







