A Data-Driven Predictive Prognostic Model for Lithium-ion Batteries based on a Deep Learning Algorithm
Abstract
:1. Introduction
2. Prognostics and Health Management
2.1. Overview of Data-Driven Prognostics
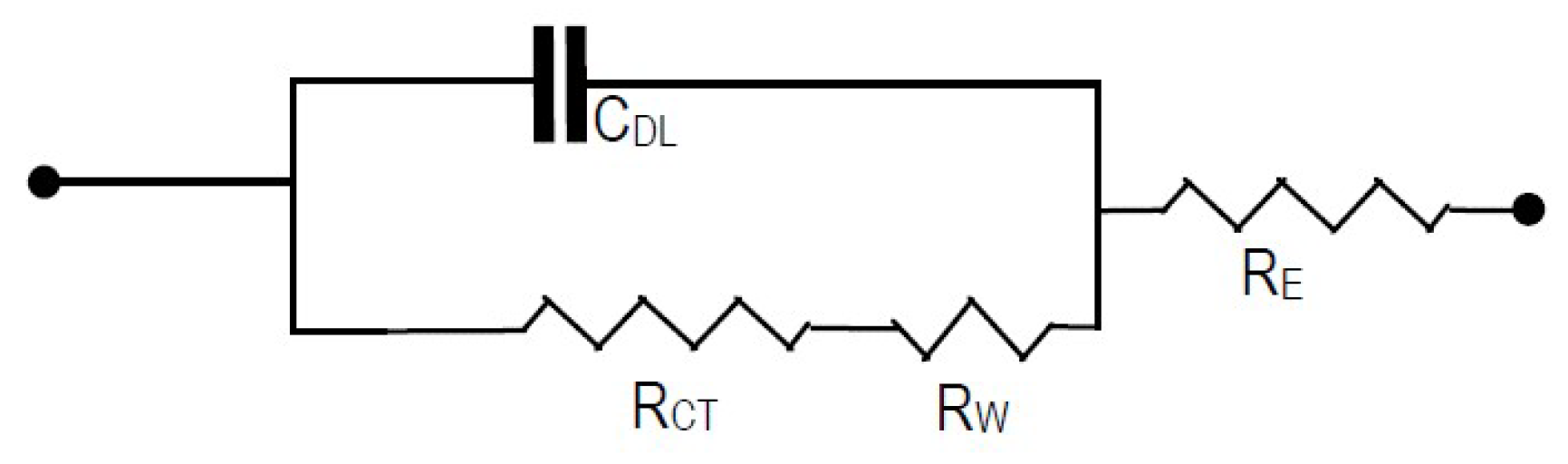
2.2. Prognostics of the Lithium-ion Battery
3. Data-Driven Prognostic Analysis and Modeling
3.1. Artificial Neural Networks
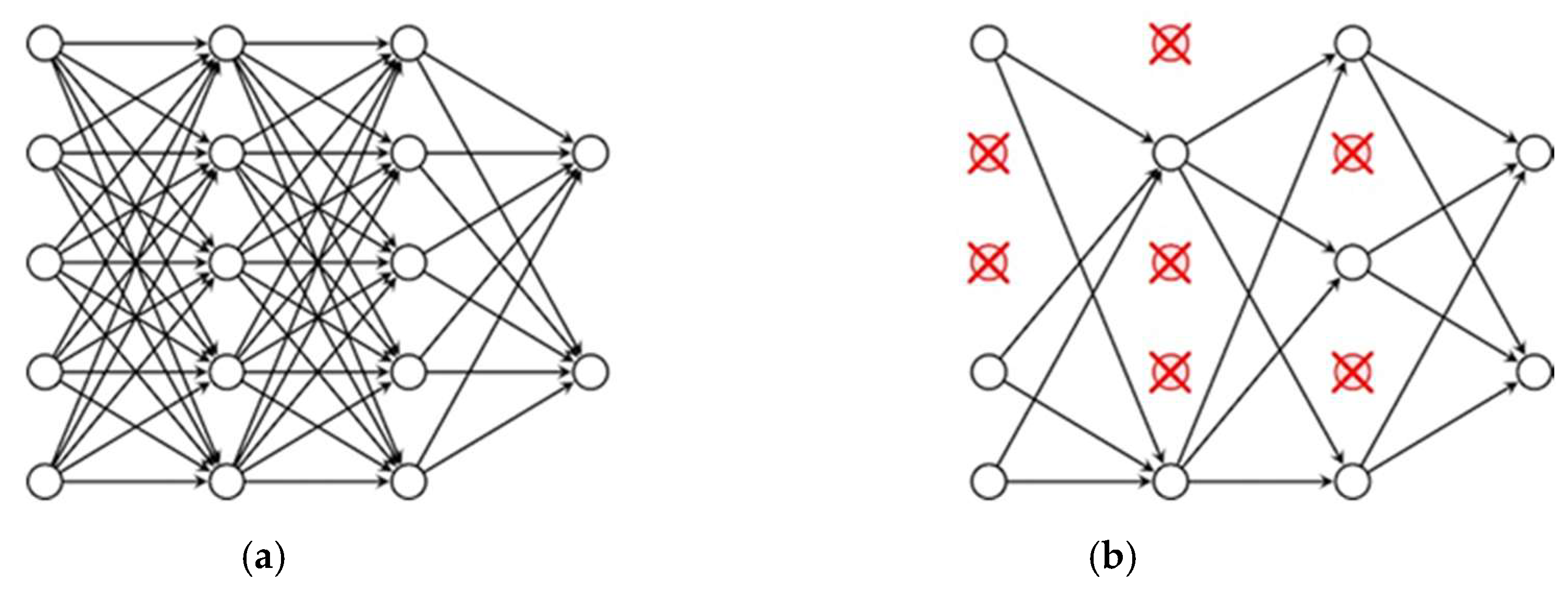
3.2. Overview of the Deep Learning Concept
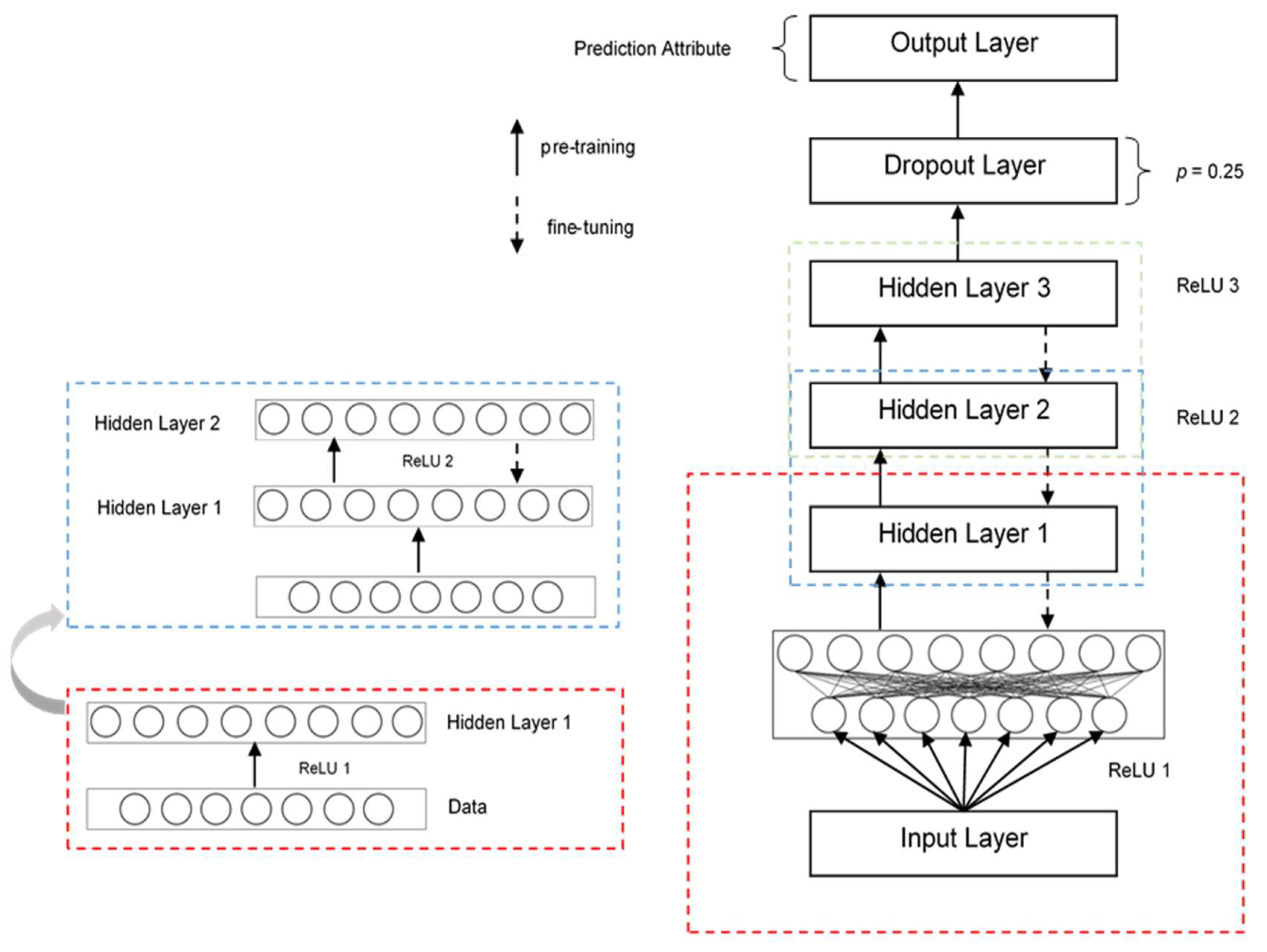
3.3. Employment of Deep Learning to Prognostic Data
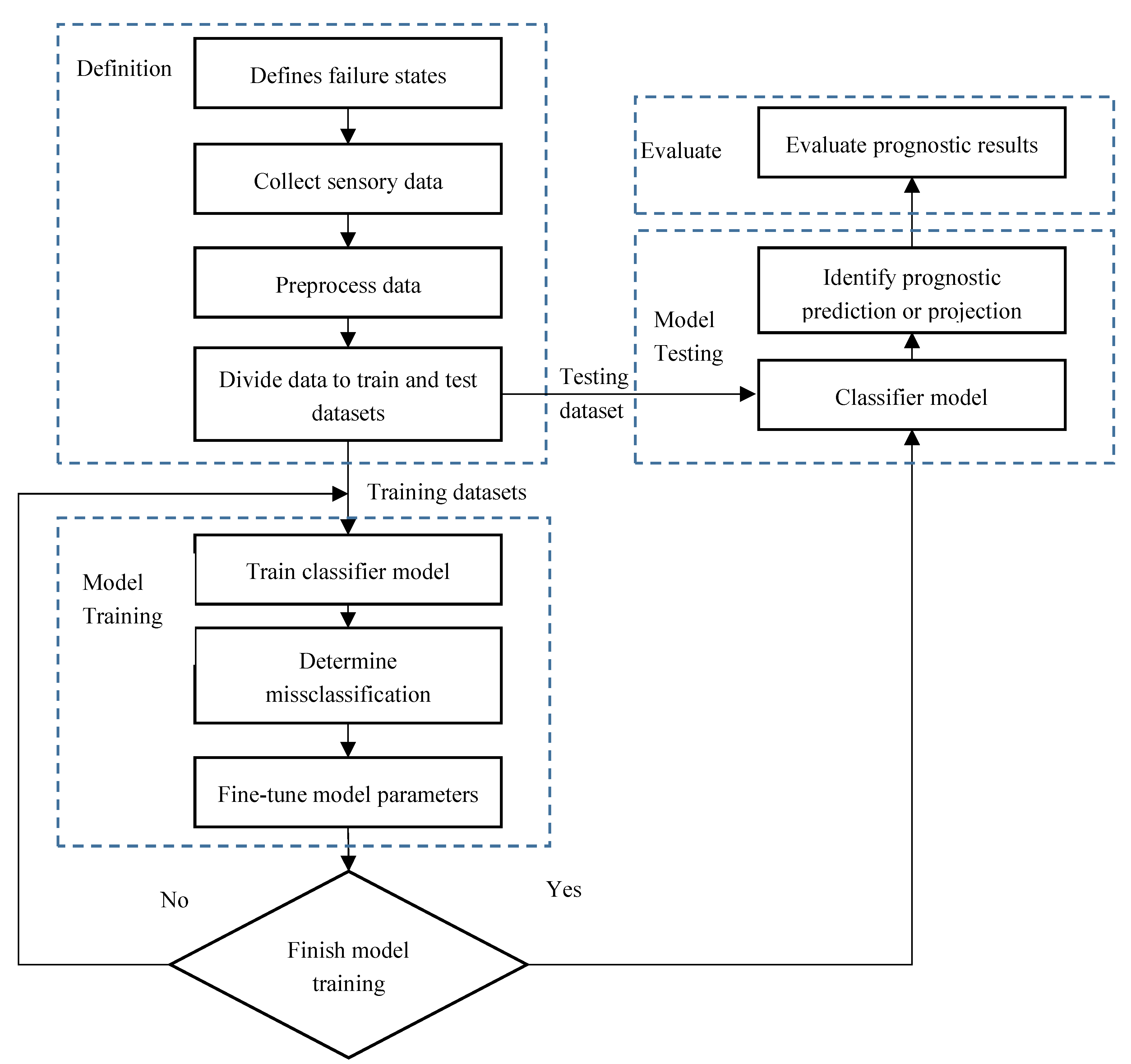
3.4. The Deep Neural Network Framework and Model for Prognostic Data
- Definition states phase. This phase specifically focuses on defining the failure of the system, identifying the prognostic problem, and evaluating system health states.
- Pre-processing phase. In this phase, sensory data are collected according to the predefined health state, in order to build a raw dataset for the experiment. The raw datasets are preprocessed and normalized, and then divided into a training and a testing dataset.
- Training phase. In this phase, initial parameters are developed, and the classification model is trained by the training dataset, based on deep learning theory. It is particularly important to fine-tune the classification model through misclassification errors (such as RSME).
- Testing phase. In this phase, the testing dataset is put into the trained classification model to identify prognostic predictions or projection results.
- Evaluating phase. This phase mainly finishes with computing the accuracy, reporting on, and evaluating the diagnosis results from the final model.
4. Case Study
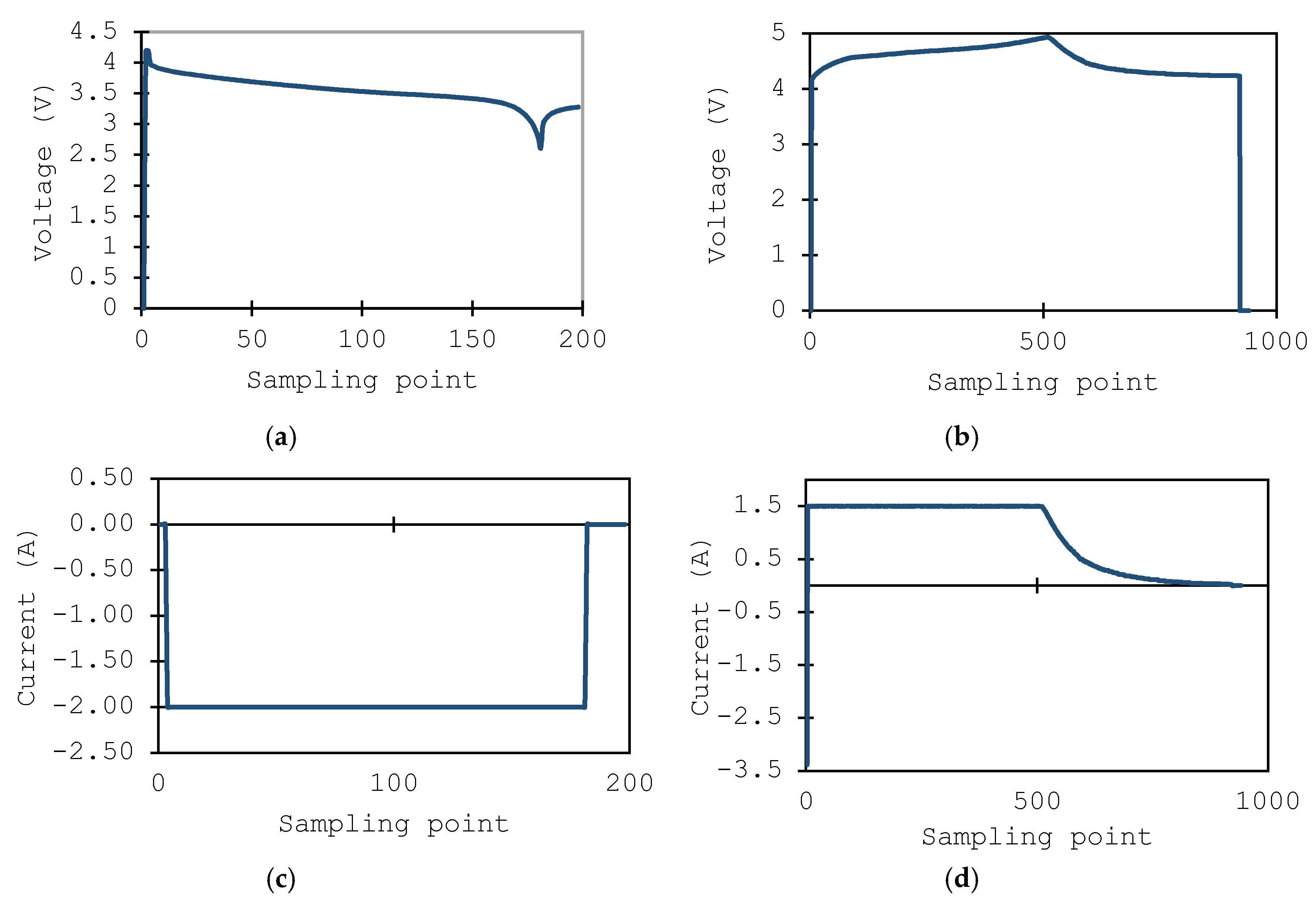
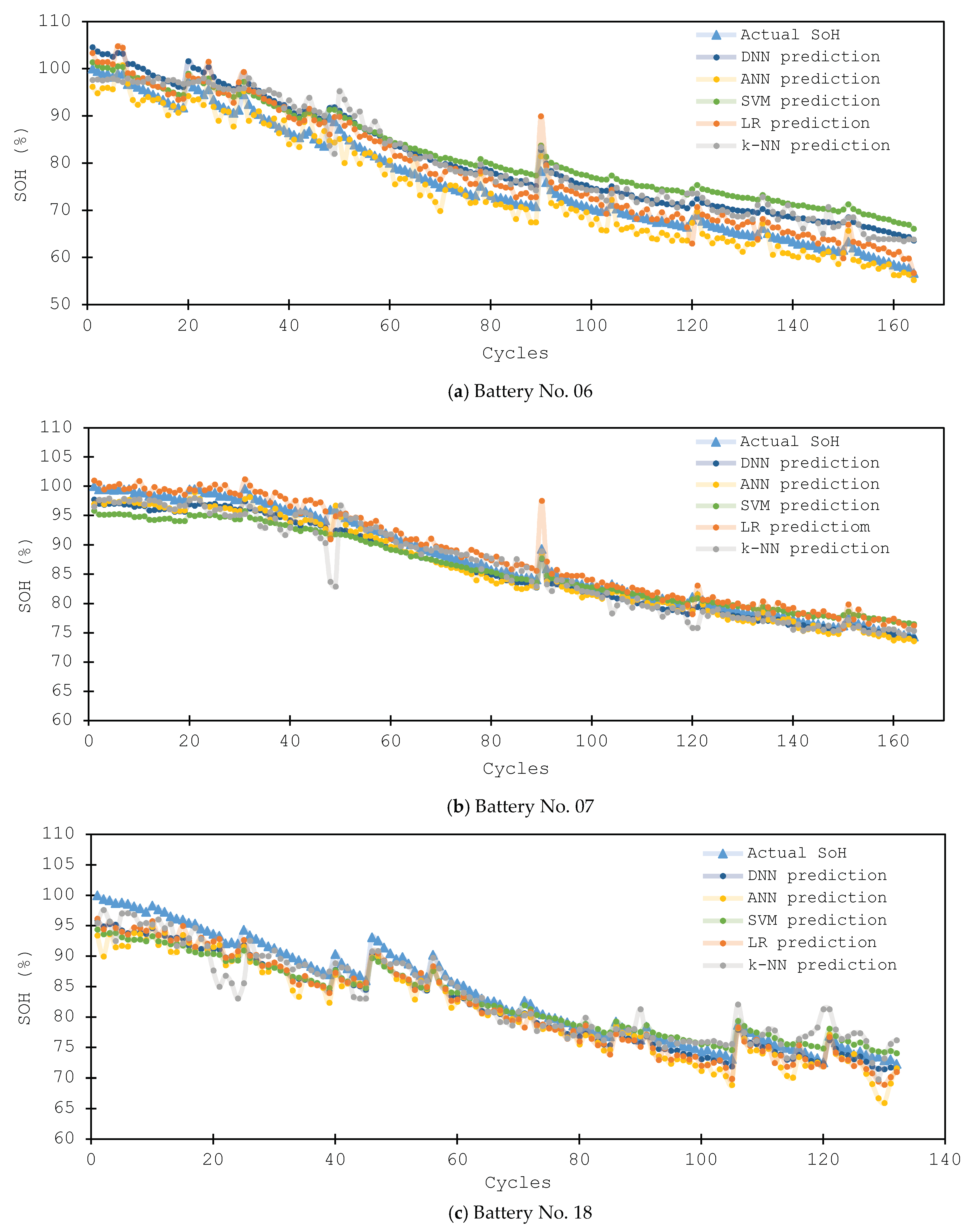
4.1. Results for SoH Estimation
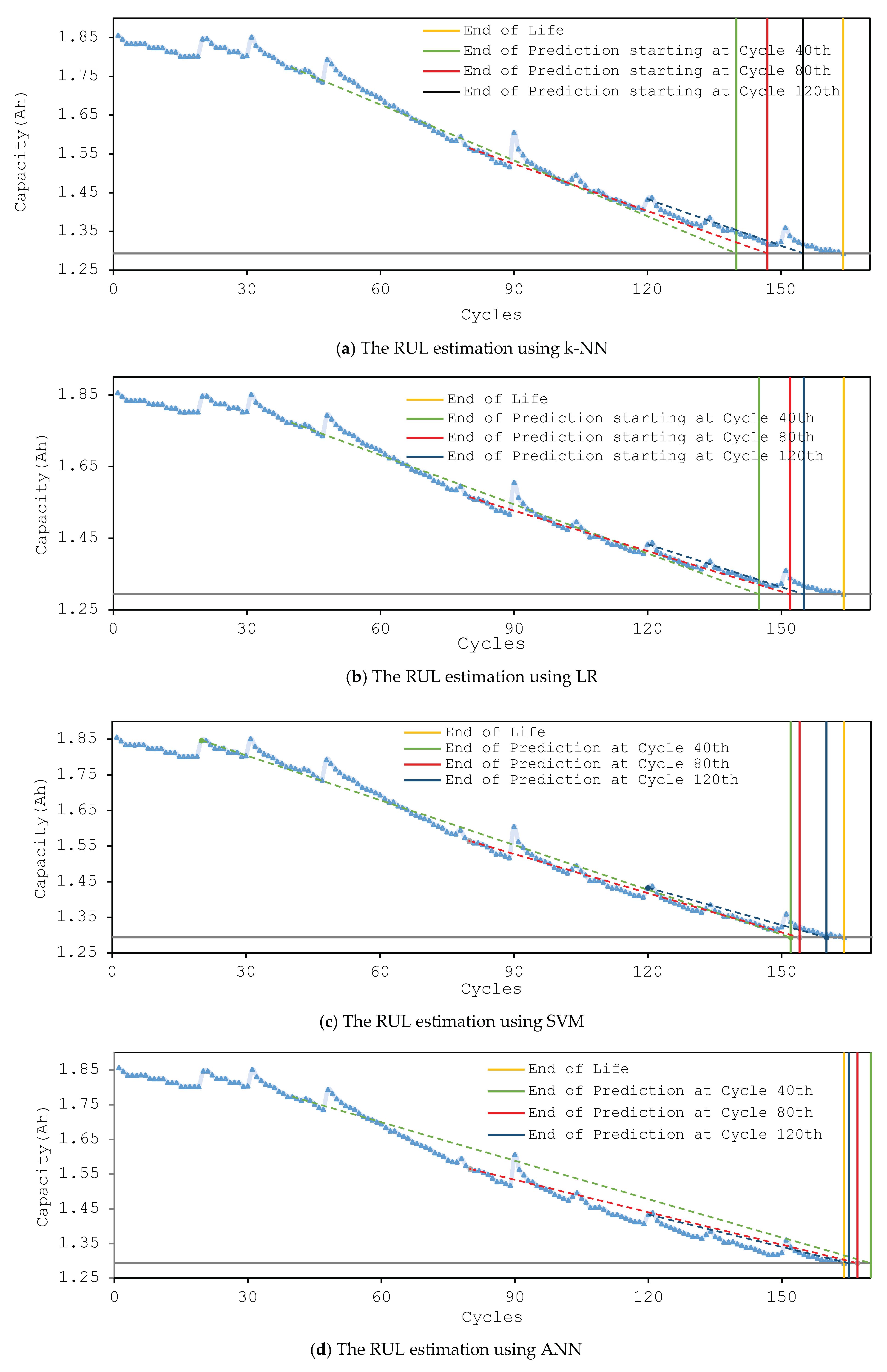
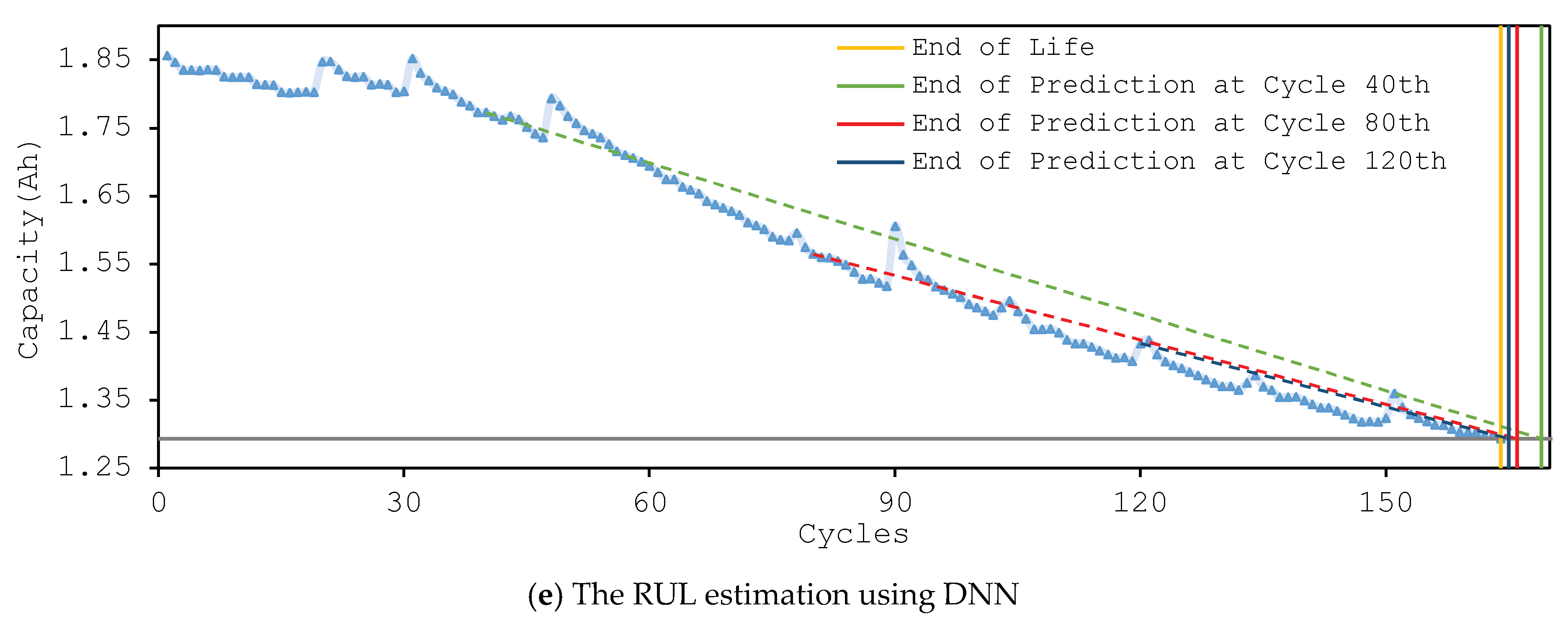
4.2 Results for RUL Estimation
4.3. Discussion and Future Work
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; Van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Corey, G.P. Batteries for stationary standby and for stationary cycling applications part 6: Alternative electricity storage technologies. In Proceedings of the Power Engineering Society General Meeting, Toronto, ON, Canada, 13–17 July 2003; Volume 1, pp. 164–169. [Google Scholar]
- Downey, A.; Lui, Y.H.; Hu, C.; Laflamme, S.; Hu, S. Physics-Based Prognostics of Lithium-Ion Battery Using Non-linear Least Squares with Dynamic Bounds. Reliab. Eng. Syst. Saf. 2019, 182, 1–12. [Google Scholar] [CrossRef]
- Susilo, D.D.; Widodo, A.; Prahasto, T.; Nizam, M. State of Health Estimation of Lithium-Ion Batteries Based on Combination of Gaussian Distribution Data and Least Squares Support Vector Machines Regression. In Materials Science Forum; Trans Tech Publications: Princeton, NJ, USA, 2018; Volume 929, pp. 93–102. [Google Scholar]
- El Mejdoubi, A.; Chaoui, H.; Gualous, H.; Van Den Bossche, P.; Omar, N.; Van Mierlo, J. Lithium-ion Batteries Health Prognosis Considering Aging Conditions. IEEE Trans. Power Electron. 2018. [Google Scholar] [CrossRef]
- Bai, G.; Wang, P.; Hu, C.; Pecht, M. A generic model-free approach for lithium-ion battery health management. Appl. Energy 2014, 135, 247–260. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K. Modeling Li-ion battery capacity depletion in a particle filtering framework. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, San Diego, CA, USA, 27 September–1 October 2009; pp. 2909–2924. [Google Scholar]
- Miao, Q.; Xie, L.; Cui, H.; Liang, W.; Pecht, M. Remaining useful life prediction of lithium-ion battery with unscented particle filter technique. Microelectron. Reliab. 2013, 53, 805–810. [Google Scholar] [CrossRef]
- Li, B.; Peng, K.; Li, G. State-of-charge estimation for lithium-ion battery using the Gauss-Hermite particle filter technique. J. Renew. Sustain. Energy 2018, 10, 014105. [Google Scholar] [CrossRef]
- Wang, D.; Tsui, K.L. Brownian motion with adaptive drift for remaining useful life prediction: Revisited. Mech. Syst. Signal Process. 2018, 99, 691–701. [Google Scholar] [CrossRef]
- Camci, F.; Chinnam, R.B. Health-state estimation and prognostics in machining processes. IEEE Trans. Autom. Sci. Eng. 2010, 7, 581–597. [Google Scholar] [CrossRef]
- Jennions, I.K. (Ed.) Integrated Vehicle Health Management: Perspectives on an Emerging Field; SAE International: Warrendale, PA, USA, 2011. [Google Scholar]
- Eker, Ö.F.; Camci, F.; Jennions, I.K. Major challenges in prognostics: Study on benchmarking prognostic datasets. In Proceedings of the First European Conference of the Prognostics and Health Management Society 2012, Cranfield, UK, 25 May 2012. [Google Scholar]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Robust performance degradation assessment methods for enhanced rolling element bearing prognostics. Adv. Eng. Inform. 2003, 17, 127–140. [Google Scholar] [CrossRef]
- Heng, A.; Zhang, S.; Tan, A.C.; Mathew, J. Rotating machinery prognostics: State of the art, challenges and opportunities. Mech. Syst. Signal Process. 2009, 23, 724–739. [Google Scholar] [CrossRef]
- Jianhui, L.; Namburu, M.; Pattipati, K.; Qiao, A.L.; Kawamoto, M.A.K.M.; Chigusa, S.A.C.S. Model-based prognostic techniques [maintenance applications]. In Proceedings of the AUTOTESTCON 2003 IEEE Systems Readiness Technology Conference, Anaheim, CA, USA, 22–25 September 2003; pp. 330–340. [Google Scholar]
- Zhang, H.; Kang, R.; Pecht, M. A hybrid prognostics and health management approach for condition-based maintenance. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management, Hong Kong, China, 8–11 December 2009; pp. 1165–1169. [Google Scholar]
- Saha, B.; Goebel, K. Battery Data Set, NASA Ames Prognostics Data Repository; NASA Ames: Moffett Field, CA, USA, 2007. Available online: http://ti.arc.nasa.gov/project/prognostic-datarepository (accessed on March 2018).
- Saha, B.; Goebel, K. Uncertainty management for diagnostics and prognostics of batteries using Bayesian techniques. In Proceedings of the Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008; pp. 1–8. [Google Scholar]
- He, W.; Pecht, M.; Flynn, D.; Dinmohammadi, F. A Physics-Based Electrochemical Model for Lithium-Ion Battery State-of-Charge Estimation Solved by an Optimised Projection-Based Method and Moving-Window Filtering. Energies 2018, 11, 2120. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K.; Christophersen, J. Comparison of prognostic algorithms for estimating remaining useful life of batteries. Trans. Inst. Meas. Control 2009, 31, 293–308. [Google Scholar] [CrossRef]
- Meissner, E.; Richter, G. Battery monitoring and electrical energy management: Precondition for future vehicle electric power systems. J. Power Sources 2003, 116, 79–98. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; White, R.E. Online estimation of the state of charge of a lithium ion cell. J. Power Sources 2006, 161, 1346–1355. [Google Scholar] [CrossRef]
- Liu, D.; Pang, J.; Zhou, J.; Peng, Y. Data-driven prognostics for lithium-ion battery based on Gaussian Process Regression. In Proceedings of the 2012 IEEE Conference on Prognostics and System Health Management (PHM), Beijing, China, 23–25 May 2012; pp. 1–5. [Google Scholar]
- Huang, S.C.; Tseng, K.H.; Liang, J.W.; Chang, C.L.; Pecht, M.G. An online SOC and SOH estimation model for lithium-ion batteries. Energies 2017, 10, 512. [Google Scholar] [CrossRef]
- Bianco, A.M.; Martínez, E. Robust testing in the logistic regression model. Comput. Stat. Data Anal. 2009, 53, 4095–4105. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer Science & Business Media: New York, NY, USA, 2003. [Google Scholar]
- Peterson, L.E. K-nearest neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]
- Zhang, Z.; Gu, L.; Zhu, Y. Intelligent Fault Diagnosis of Rotating Machine Based on SVMs and EMD Method. Open Auto. Control Syst. J. 2013, 5, 219–230. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Y.; Zhu, Y. Intelligent fault diagnosis of rolling element bearing based on SVMs and fractal dimension. Mech. Syst. Signal Process. 2007, 21, 2012–2024. [Google Scholar] [CrossRef]
- Samanta, B. Artificial neural networks and genetic algorithms for gear fault detection. Mech. Syst. Signal Process. 2004, 18, 1273–1282. [Google Scholar] [CrossRef]
- Hegazy, T.; Fazio, P.; Moselhi, O. Developing practical neural network applications using back-propagation. Comput. Aided Civ. Infrastruct. Eng. 1994, 9, 145–159. [Google Scholar] [CrossRef]
- Jeon, J. Fuzzy and neural network models for analyses of piles. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2007. [Google Scholar]
- Emsley, M.W.; Lowe, D.J.; Duff, A.R.; Harding, A.; Hickson, A. Data modelling and the application of a neural network approach to the prediction of total construction costs. Constr. Manag. Econ. 2002, 20, 465–472. [Google Scholar] [CrossRef]
- Alex, D.P.; Al Hussein, M.; Bouferguene, A.; Fernando, S. Artificial neural network model for cost estimation: City of Edmonton’s water and sewer installation services. J. Constr. Eng. Manag. 2009, 136, 745–756. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Zhang, G.; Ge, Q.; Liu, X. Research advances in fault diagnosis and prognostic based on deep learning. In Proceedings of the Prognostics and System Health Management Conference (PHM-Chengdu), Chengdu, China, 19–21 October 2016; pp. 1–6. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Graves, A.; Mohamed, A.R.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference On Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- Wirth, R.; Hipp, J. CRISP-DM: Towards a standard process model for data mining. In Proceedings of the 4th International Conference on the Practical Applications of Knowledge Discovery and Data Mining, Manchester, UK, 11–13 April 2000; pp. 29–39. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Schorfheide, F. Loss function-based evaluation of DSGE models. J. Appl. Econom. 2000, 15, 645–670. [Google Scholar] [CrossRef]
- Gupta, S.; Agrawal, A.; Gopalakrishnan, K.; Narayanan, P. Deep learning with limited numerical precision. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1737–1746. [Google Scholar]
- Zhang, Y.; Xiong, R.; He, H.; Liu, Z. A LSTM-RNN method for the lithium-ion battery remaining useful life prediction. In Proceedings of the Prognostics and System Health Management Conference (PHM-Harbin), Harbin, China, 9–12 July 2017; pp. 1–4. [Google Scholar]
- Hahnloser, R.H.; Sarpeshkar, R.; Mahowald, M.A.; Douglas, R.J.; Seung, H.S. Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. Nature 2000, 405, 947. [Google Scholar] [CrossRef]
- Hahnloser, R.H.; Seung, H.S. Permitted and forbidden sets in symmetric threshold-linear networks. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 3–8 December 2001; pp. 217–223. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Orr, G.B.; Müller, K.R. (Eds.) Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]

| Data-Driven Model [15] | Physics-Based Model [16,17] | |
|---|---|---|
| Based on | The empirical lifetime data and the use of previous data of the operation of the system | Physical understanding of the physical rules of the system, the exact formulas that represent the system |
| Advantages | The real behavior of the complex physical system is not required. | Higher accuracy because the model is based on an actual (or near-actual) physical system |
| Models are less complex, easier to employ into a real application | The model represents a real system, the model can be observed and judged in a more realistic manner | |
| Drawbacks | Needs a large amount of empirical data in order to construct a high accuracy model | Highly complex, requires extensive computational time/resources, which may not be very suitable for employment in real-world applications |
| The models do not represent the actual system, it requires more effort to understand the real system behavior based on the collected data | Limitations in modeling, especially in cases of large and complex systems with non-measurable variables |
| Number of Hidden Layers | RMSE |
|---|---|
| 2 | 3.815 |
| 3 | 3.247 |
| 4 | 3.275 |
| Trials | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | 3.917 | 3.877 | 3.667 | 3.507 | 3.487 | 3.321 | 3.296 | 3.253 | 3.249 | 3.247 |
| RMSE | k-NN | LR | SVM | ANN | DNN |
| 5.598 | 4.558 | 4.552 | 4.611 | 3.427 |
| Algorithm | Model Description | |||
|---|---|---|---|---|
| k-NN | 22-Nearest Neighbor model for regression The model contains 624 examples with seven dimensions | |||
| LR | 228.765 * Voltage_measured + 237.439 × Current_measured − 1.495 * Temperature_measured − 1098.506 × Current_charge + 50.156 * Capacity − 918.727 | |||
| SVM | Total number of Support Vectors: 613 Bias (offset): −85.065 w[Voltage_measured] = 42686654.125 w[Current_measured] = –17208.396 w[Temperature_measured] = 243822393.316 w[Current_charge] = 3952.097 w[Voltage_charge] = 0.000 w[Time] = 0.000 w[Capacity] = 16430099.458 number of classes: 2 number of support vectors: 613 | |||
| ANN | Node 1 (Sigmoid) Voltage_measured: –0.172 Current_measured: –0.448 Temperature_measured: 2.894 Current_charge: –1.458 Voltage_charge: 0.005 Time: 0.042 Capacity: –0.155 Bias: –2.726 | Node 2 (Sigmoid) Voltage_measured: 1.954 Current_measured: 0.328 Temperature_measured: –1.124 Current_charge: –0.397 Voltage_charge: 0.036 Time: –0.014 Capacity: 0.943 Bias: –1.930 | Node 3 (Sigmoid) Voltage_measured: 0.406 Current_measured: 1.254 Temperature_measured: 1.472 Current_charge: 1.391 Voltage_charge: –0.049 Time: –0.036 Capacity: 1.107 Bias: –1.055 | |
| Node 4 (Sigmoid) Voltage_measured: –3.468 Current_measured: –0.975 Temperature_measured: 0.080 Current_charge: –0.018 Voltage_charge: 0.044 Time: –0.020 Capacity: 2.457 Bias: –0.108 | Node 5 (Sigmoid) Voltage_measured: –7.072 Current_measured: –0.455 Temperature_measured: 2.095 Current_charge: 2.091 Voltage_charge: –0.004 Time: 0.045 Capacity: –0.464 Bias: –4.078 | Output Regression (Linear) Node 1: 1.278 Node 2: 1.460 Node 3: 0.865 Node 4: 1.214 Node 5: –1.134 Threshold: –0.819 | ||
Neural Network created: | ||||
| DNN | Layer (type) | No. of Hidden Nodes | No. of Parameters | Total parameters: 217 Trainable parameters: 217 Non-trainable parameters: 0 |
| dense_1 (Dense) | 8 | 64 | ||
| dense_2 (Dense) | 8 | 72 | ||
| dense_3 (Dense) | 8 | 72 | ||
| dropout_1 (Dropout) | 8 | 0 | ||
| dense_4 (Dense) | 1 | 9 | ||
| Error of RUL | Starting Points | k-NN | LR | SVM | ANN | DNN |
| 40th cycle | 24 | 19 | 12 | 6 | 5 | |
| 80th cycle | 17 | 12 | 10 | 3 | 2 | |
| 120th cycle | 19 | 9 | 4 | 1 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khumprom, P.; Yodo, N. A Data-Driven Predictive Prognostic Model for Lithium-ion Batteries based on a Deep Learning Algorithm. Energies 2019, 12, 660. https://doi.org/10.3390/en12040660
Khumprom P, Yodo N. A Data-Driven Predictive Prognostic Model for Lithium-ion Batteries based on a Deep Learning Algorithm. Energies. 2019; 12(4):660. https://doi.org/10.3390/en12040660
Chicago/Turabian StyleKhumprom, Phattara, and Nita Yodo. 2019. "A Data-Driven Predictive Prognostic Model for Lithium-ion Batteries based on a Deep Learning Algorithm" Energies 12, no. 4: 660. https://doi.org/10.3390/en12040660
APA StyleKhumprom, P., & Yodo, N. (2019). A Data-Driven Predictive Prognostic Model for Lithium-ion Batteries based on a Deep Learning Algorithm. Energies, 12(4), 660. https://doi.org/10.3390/en12040660





