Adaptive Sliding Mode Control for PMSG Wind Turbine Systems
Abstract
1. Introduction
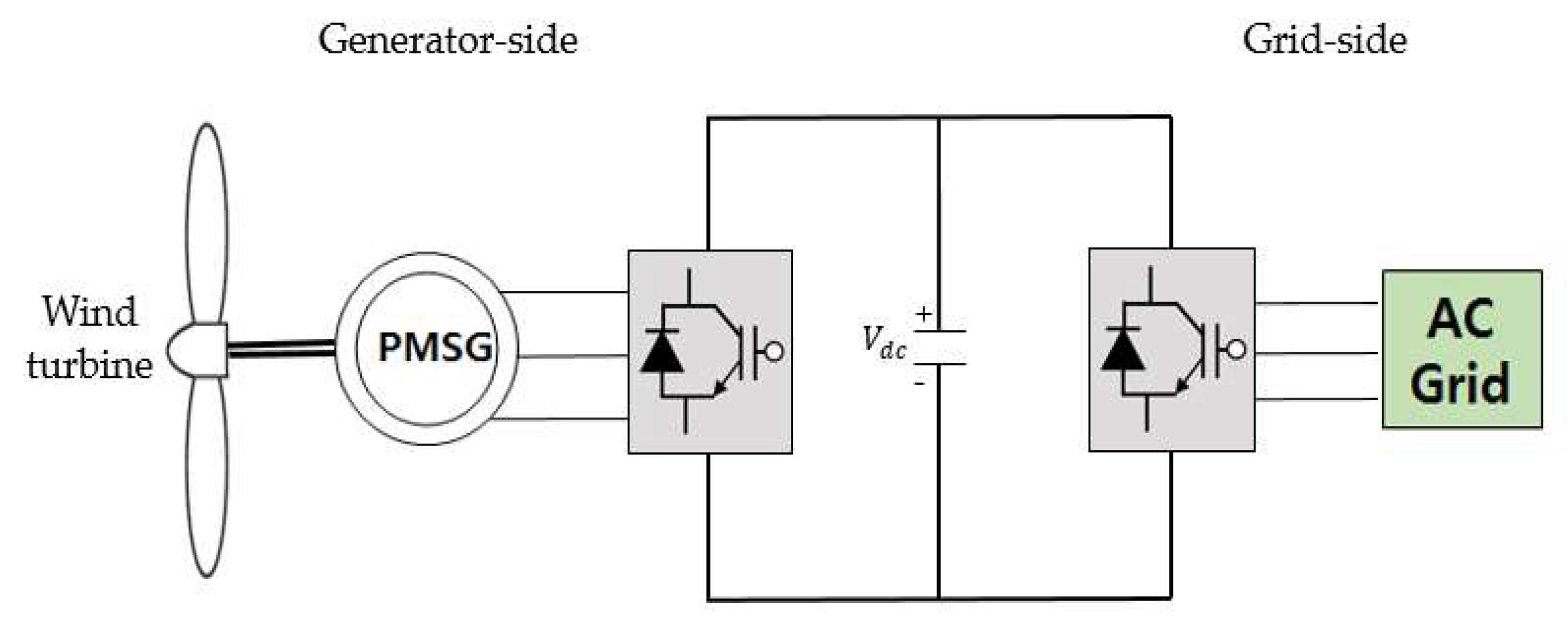
2. Modeling of a Wind Energy Conversion System
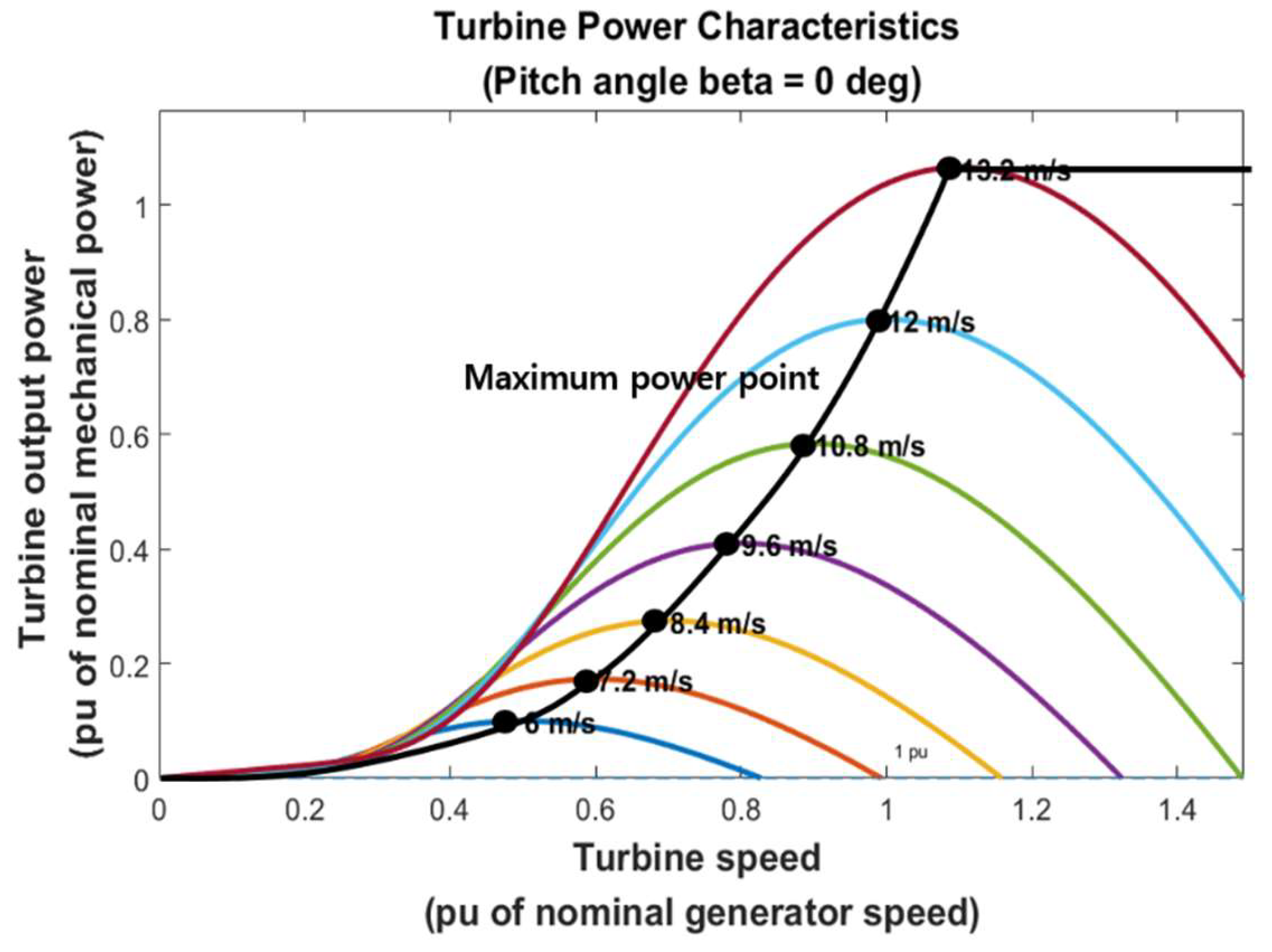
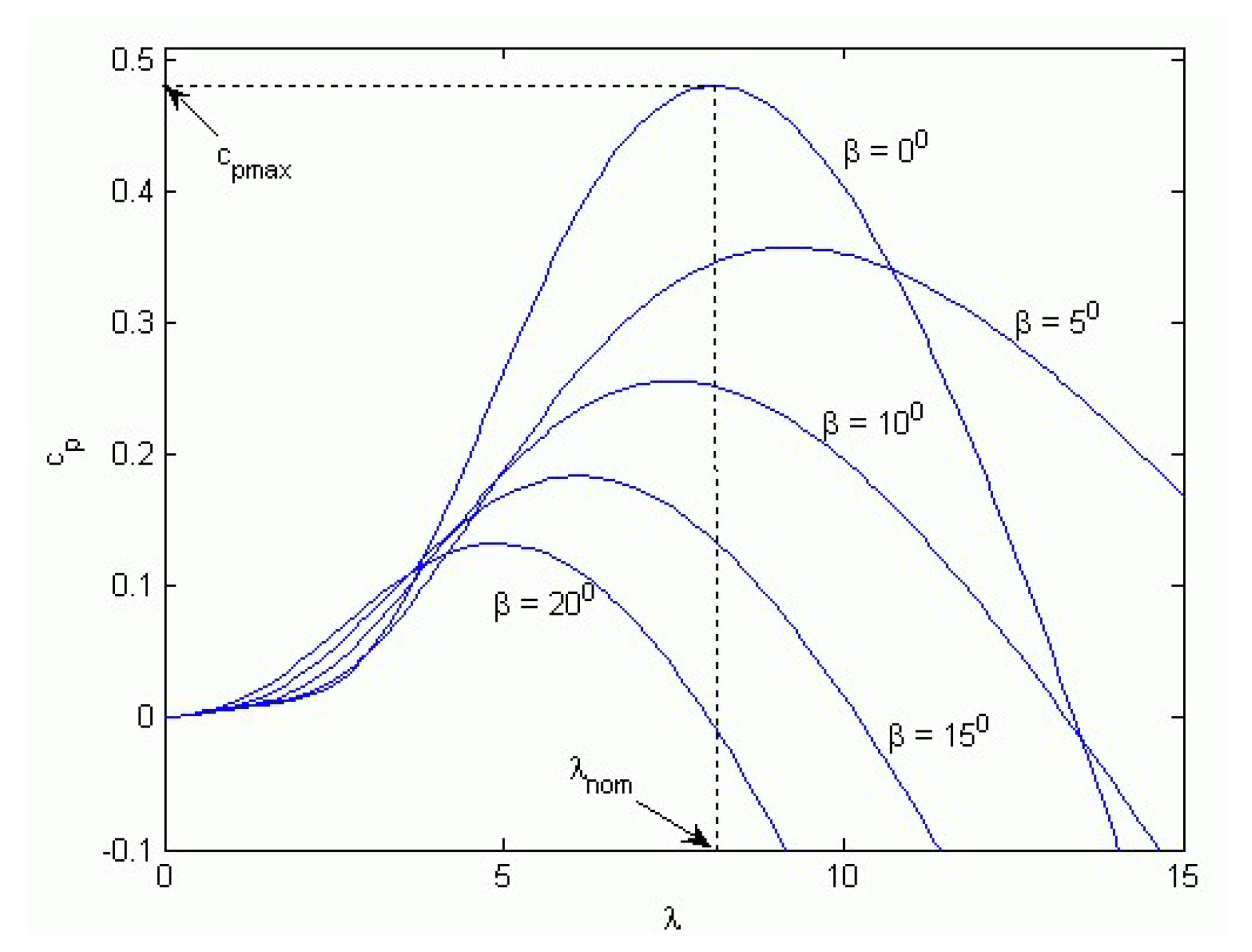
2.1. Wind Turbine Modeling
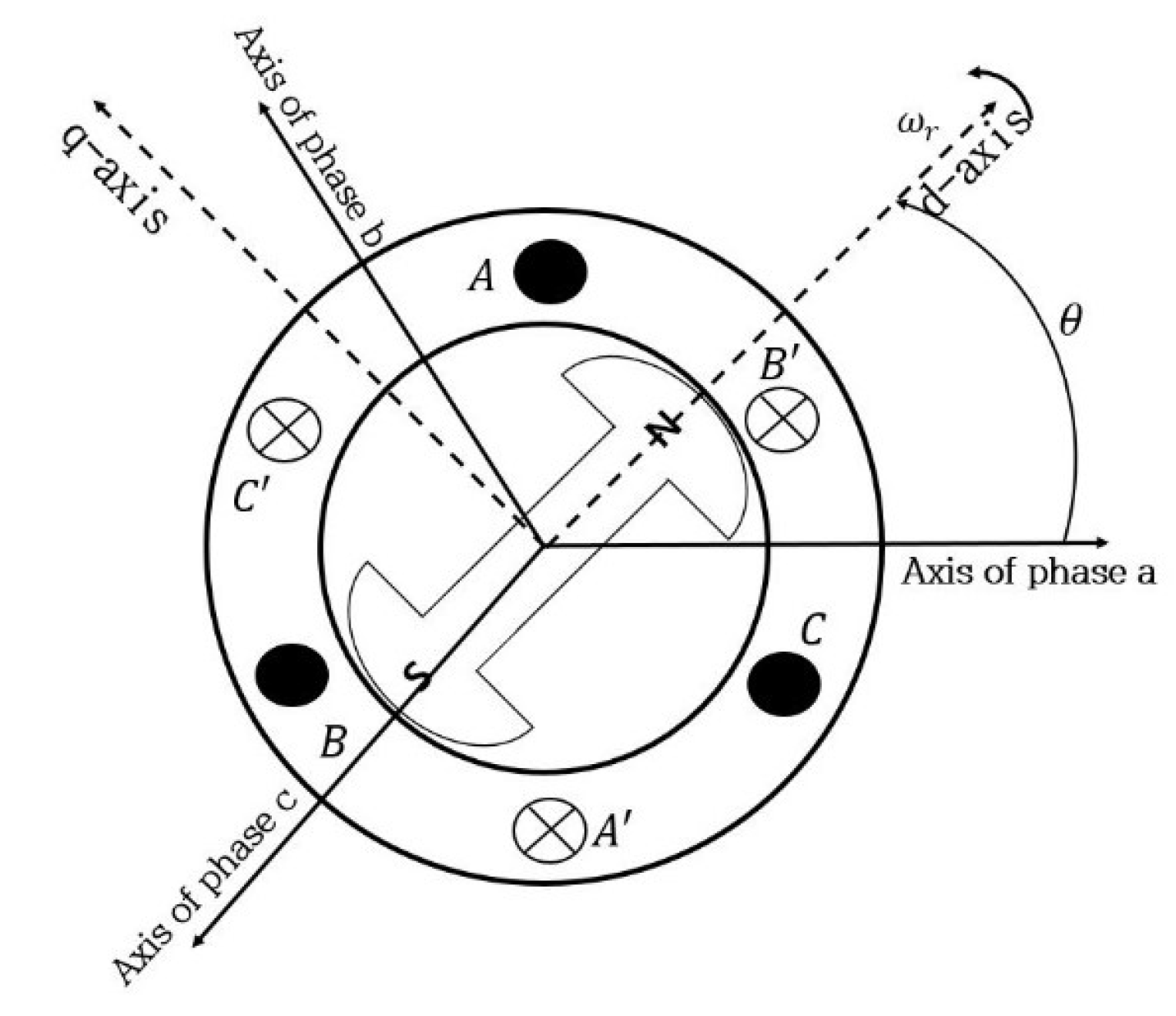
2.2. PMSG Modeling
3. Controller Design
3.1. Sliding Mode Controller Design for the Rotation Speed Error Regulation
3.2. Voltage Controller Design and Adaptative Estimation for Unknown Parameters
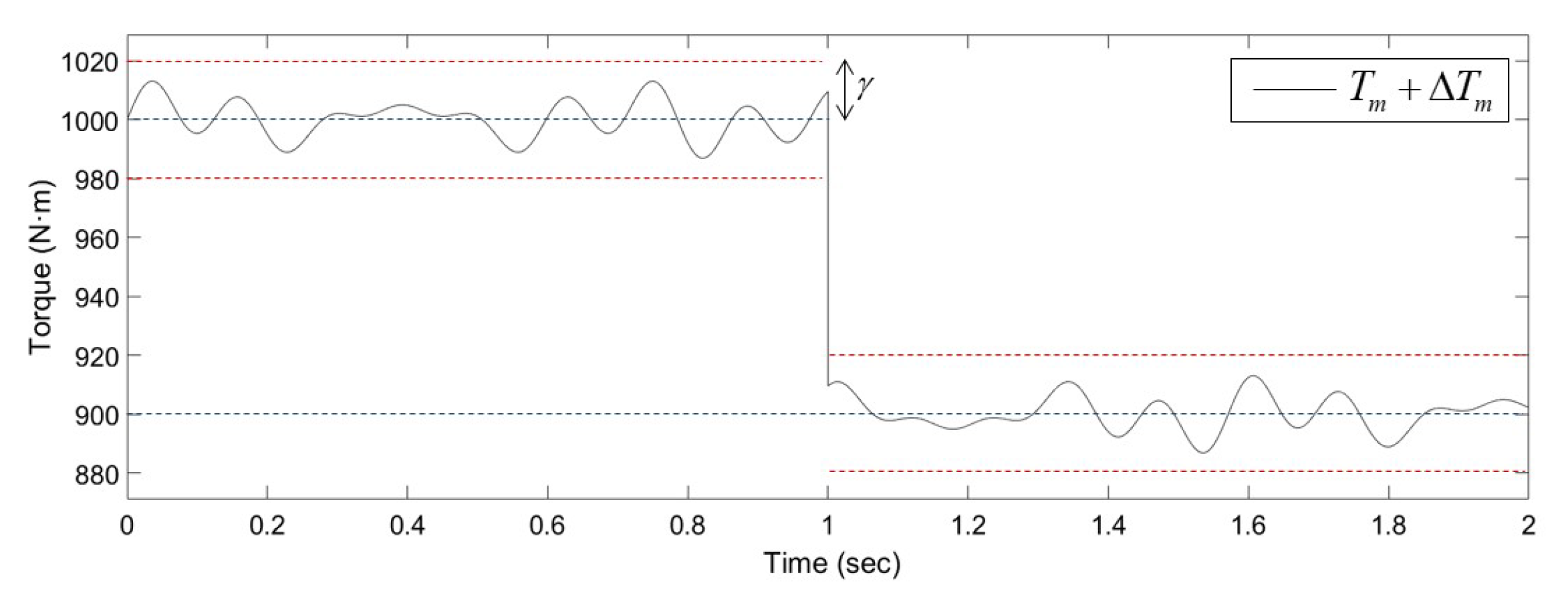
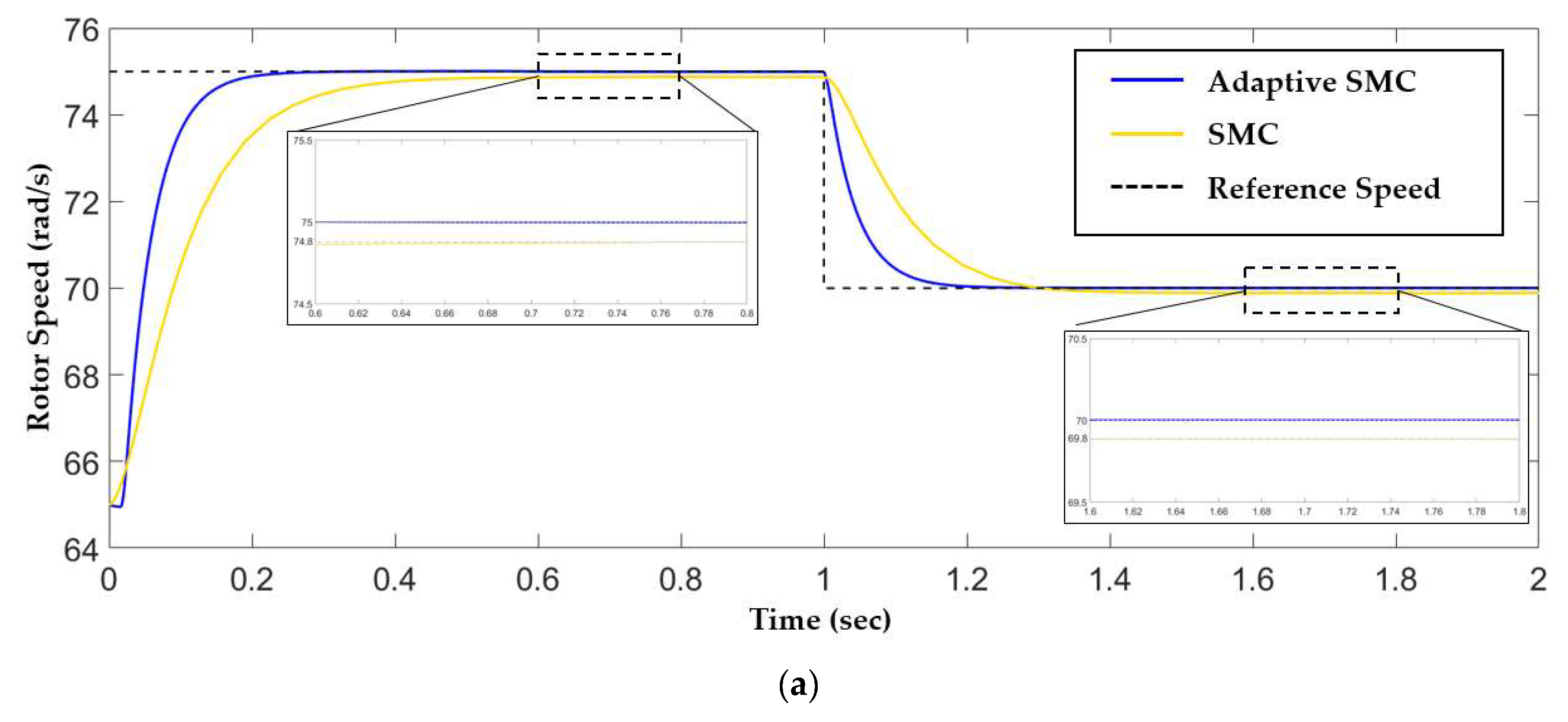
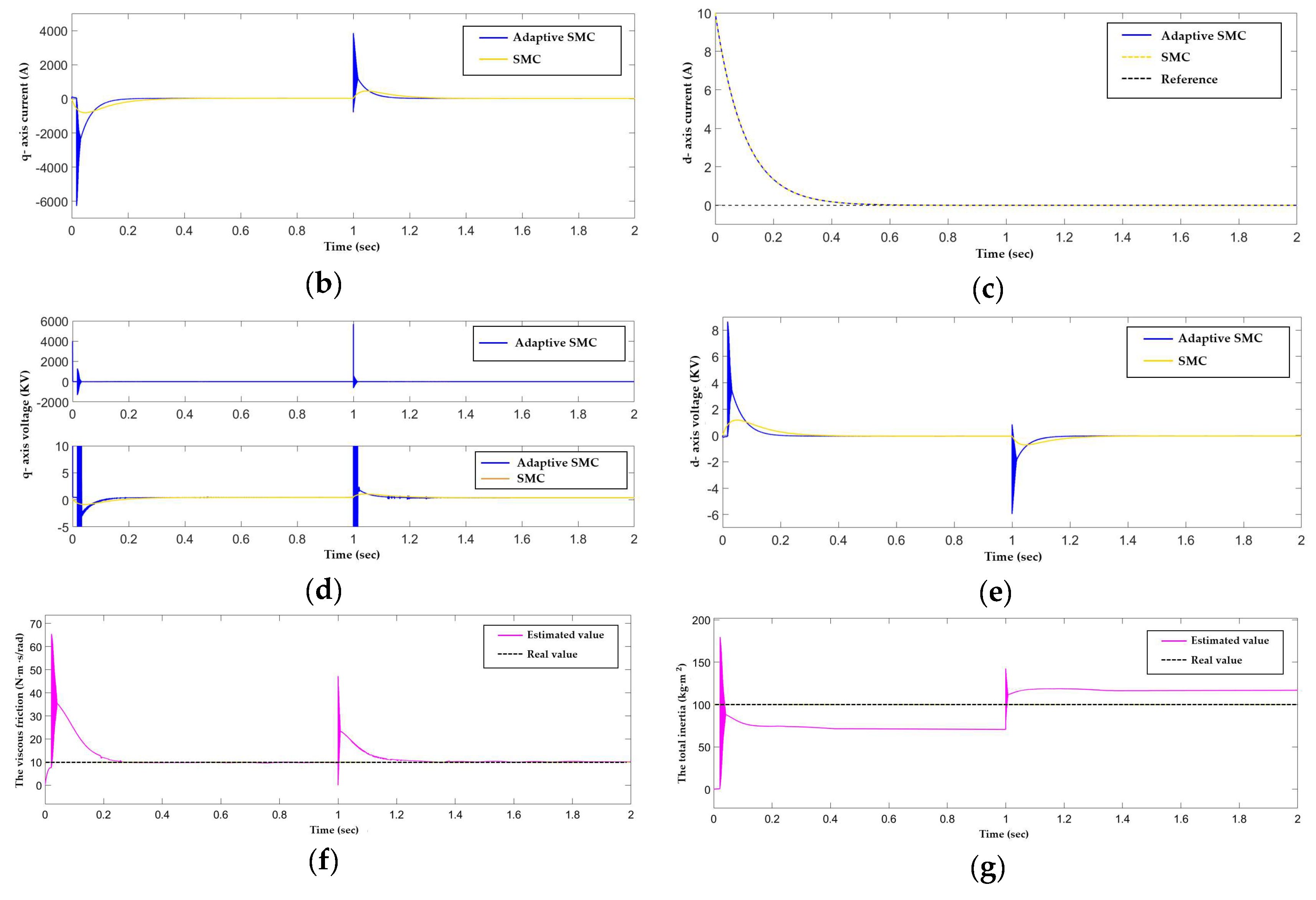
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Chen, Z.; Guerrero, J.M.; Blaabjerg, F. A review of the state of the art of power electronics for wind turbines. IEEE Trans. Power Electron. 2009, 24, 1859–1875. [Google Scholar] [CrossRef]
- Li, S.; Haskew, T.A.; Swatloski, R.P.; Gathings, W. Optimal and direct-surrent vector control of direct-driven PMSG wind turbines. IEEE Trans. Power Electron. 2012, 27, 2325–2337. [Google Scholar] [CrossRef]
- Chinchilla, M.; Arnaltes, S.; Burgos, J.C. Control of permanent-magnet generators applied to variable-speed wind energy systems connected to the grid. IEEE Trans. Energy Convers. 2006, 21, 130–135. [Google Scholar] [CrossRef]
- Grauers, A. Efficiency of three wind energy generator systems. IEEE Trans. Energy Convers. 1996, 11, 650–657. [Google Scholar] [CrossRef]
- Chen, Y.; Pillay, P.; Khan, A. PM wind generator topologies. IEEE Trans. Ind. Appl. 2005, 41, 1619–1626. [Google Scholar] [CrossRef]
- Michalke, G.; Hansen, A.D.; Harkopf, T. Control strategy of a variable speed wind turbine with multipole permanent magnet synchronous generator. In Proceedings of the 2007 European Wind Energy Conference and Exhibition, Milan, Italy, 7–10 May 2007. [Google Scholar]
- Zavadil, R.; Miller, N.; Ellis, A.; Muljadi, E. Making connections: Wind generation challenges and progress. IEEE Power Energy. Mag. 2005, 3, 26–37. [Google Scholar] [CrossRef]
- Li, S.; Haskew, T.A.; Xu, L. Conventional and novel control designs for direct driven PMSG wind turbines. Electr. Power Syst. Res. 2010, 80, 328–338. [Google Scholar] [CrossRef]
- Abdullah, M.A.; Yatim, A.H.M.; Tan, C.W. A study of maximum power point tracking algorithms for wind energy system. In Proceedings of the IEEE First Conference on Clean Energy and Techonology (CET), Kuala Lumpur, Malaysia, 27–29 June 2011; pp. 321–326. [Google Scholar]
- Delfino, F.; Pampararo, F.; Procopio, R.; Rossi, M. A Feedback Linearization Control Scheme for the Integration of Wind Energy Conversion Systems into Distribution Grids. IEEE Syst. J. 2012, 6, 85–93. [Google Scholar] [CrossRef]
- Mao, J.; Wu, A.; Wu, G.; Zhang, X. Maximum power point tracking in variable speed wind turbine system via optimal torque sliding mode control strategy. In Proceedings of the 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 7967–7971. [Google Scholar]
- Mozayan, S.M.; Saad, M.; Vahedi, H.; Fortin-Blanchette, H.; Soltani, M. Sliding mode control of PMSG wind turbine based on enhanced exponential reaching law. IEEE Trans. Ind. Electron. 2016, 63, 6148–6159. [Google Scholar] [CrossRef]
- Merzoug, M.S.; Banalla, H.; Louze, L. Sliding mode control (SMC) of permanent magnet synchronous generators (PMSG). Energy Procedia 2012, 18, 43–52. [Google Scholar] [CrossRef]
- Ciampichetti, S.; Corradini, M.L.; lppoliti, G. Sliding Mode Control of Permanent Magnet Synchronous Generator for Wind Turbines. In Proceedings of the 37th Annual Conference on IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011; pp. 740–745. [Google Scholar]
- Hong, C.-M.; Huang, C.-H.; Cheng, F.-S.; Chih-Ming, H.; Cong-Hui, H.; Fu-Sheng, C. Sliding mode control for variable-speed wind turbine generation system using artificial neural network. Energy Procedia 2014, 61, 1626–1629. [Google Scholar] [CrossRef]
- Beltran, B.; Ahmed-Ali, T.; El Hachemi Benbouzid, M. Sliding mode power control of variable-speed wind energy conversion systems. IEEE Trans. Energy Convers. 2008, 23, 551–558. [Google Scholar] [CrossRef]
- Merabet, A.; Beguenane, R.; Thongam, J.S.; Hussein, I. Adaptive Sliding Mode Speed Control for Wind Turbine Systems. In Proceedings of the on 37th annual conference on IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011; pp. 2461–2466. [Google Scholar]
- Sungwon, L.; Kwanho, C. Adaptive sliding mode controller design for MPPT control in wind turbine PMS generator with torque uncertainties and unknown parameter. J. Inst. Control Robot. Syst. 2018, 24, 532–539. [Google Scholar]
- Barambones, O. Sliding mode control strategy for wind turbine power maximization. Energies 2012, 5, 2310–2330. [Google Scholar] [CrossRef]
- El Magri, A.; Giri, F.; El Fadili, A.; Dugard, L. Adaptive nonlinear control of wind energy conversion system with PMS generator. In Proceedings of the 11th IFAC International Workshop on Adaptation and Learning in Control and Signal Processing, Caen, France, 3–5 July 2013; pp. 318–325. [Google Scholar]
- Tohidi, A.; Hajieghrary, H.; Hsieh, M.A. Adaptive disturbance rejection control scheme for DFIG-based wind turbine: Theory and experiments. IEEE Trans. Ind. Appl. 2016, 52, 2006–2015. [Google Scholar] [CrossRef]
- Plestan, F.; Shtessel, Y.; Bregeault, V.; Poznyak, A. New methodologies for adaptive sliding mode control. Int. J. Control 2010, 83, 1907–1919. [Google Scholar] [CrossRef]
- Plestan, F.; Shtessel, Y.; Bregeault, V.; Poznyak, A. Sliding mode control with gain adaptation—Application to an electropneumatic actuator. Control Eng. Pract. 2013, 21, 679–688. [Google Scholar] [CrossRef]
- Utkin, V.I.; Poznyak, A.S. Adaptive sliding mode control with application to super-twist algorithm: Equivalent control method. Automatica 2013, 49, 39–47. [Google Scholar] [CrossRef]
- Moreno, J.A.; Negrete, D.Y.; Torres-González, V.; Fridman, L. Adaptive continuous twisting algorithm. Int. J. Control 2016, 89, 1798–1806. [Google Scholar] [CrossRef]
- Roy, S.; Kar, I.N. Adaptive robust control of uncertain Euler-Lagrange systems with past data: A time-delayed approach. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 5715–5720. [Google Scholar]
- Roy, S.; Kar, I.N. Adaptive sliding mode control of a class of nonlinear systems with artificial delay. J. Frankl. Inst. 2017, 345, 8156–8179. [Google Scholar] [CrossRef]
- Roy, S.; Kar, I.N.; Jinoh, L.; Tsagarakis, N.G.; Caldwell, D.G. Adaptive-robust control of a class of EL systems with parametric variations using artificially delayed input and position feedback. IEEE Trans. Control Syst. Technol. 2017, 1–13. [Google Scholar] [CrossRef]
- Roy, S.; Kar, I.N.; Jinoh, L.; Maolin, J. Adaptive-Robust Time-Delay Control for a Class of Uncertain Eular-Lagrange Systems. IEEE Trnas. Ind. Electron. 2017, 64, 7109–7119. [Google Scholar] [CrossRef]
- Roy, S.; Roy, S.B.; Kar, I.N. A new design methodology of adaptive sliding mode control for a class of nonlinear systems with state dependent uncertainty bound. In Proceedings of the 15th International Workshop on Variable Structure Systems (VSS), Graz, Austria, 9–11 July 2018; pp. 414–419. [Google Scholar]
- Hau, E. Wind Turbines—Fundamentals, Technologies, Application and Economics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Heier, S. Grid Integration of Wind Energy: Onshore and Offshore Conversion Systems; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Abdullah, M.A.; Yatim, A.H.M.; Tan, C.W.; Saidur, R. A review of maximum power point tracking algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2012, 16, 3220–3227. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Perruquetti, W.; Barbot, J.P. Sliding Mode Control in Engineering; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Utkin, V.; Guldner, J.; Jingxin, S. Sliding Mode Control in Electro-Mechanical Systems; CRC Press: Boca Raton, FL, USA, 2009; pp. 325–355. [Google Scholar]
- Krstic, M.; Kanelakopoulos, I.; Kokotovic, P. Nonlinear and Adaptive Control Design; Wiley: New York, NY, USA, 1995. [Google Scholar]
| Parameter | Value | Unit |
|---|---|---|
| The resistance of the PMSG | 0.15 | |
| The inductance of the PMSG | 5.3 | |
| The magnetic flux of the PMSG | 1.314 | |
| The number of pole pairs | 4 | - |
| The total inertia | 100 | |
| The minimum of inertia | 80 | |
| The viscous friction coefficient | 10 | |
| The upper bound of disturbance () | 17 | - |
| Parameter | Value |
|---|---|
| 20 | |
| 20 | |
| 20 | |
| 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-W.; Chun, K.-H. Adaptive Sliding Mode Control for PMSG Wind Turbine Systems. Energies 2019, 12, 595. https://doi.org/10.3390/en12040595
Lee S-W, Chun K-H. Adaptive Sliding Mode Control for PMSG Wind Turbine Systems. Energies. 2019; 12(4):595. https://doi.org/10.3390/en12040595
Chicago/Turabian StyleLee, Sung-Won, and Kwan-Ho Chun. 2019. "Adaptive Sliding Mode Control for PMSG Wind Turbine Systems" Energies 12, no. 4: 595. https://doi.org/10.3390/en12040595
APA StyleLee, S.-W., & Chun, K.-H. (2019). Adaptive Sliding Mode Control for PMSG Wind Turbine Systems. Energies, 12(4), 595. https://doi.org/10.3390/en12040595





