Seepage Safety Assessment of Concrete Gravity Dam Based on Matter-Element Extension Model and FDA
Abstract
1. Introduction
- (1)
- Dam seepage status is dynamically and continuously varied with time in nature, but most existing evaluation methods can only represent seepage safety status at finite discrete time points.
- (2)
- Dam seepage is affected by various interrelated factors. However, the existing evaluation methods often ignore the correlation among indicators in the process of determining weights and the accuracy of the evaluation results needs improvement.
- (3)
- A concrete gravity dam is composed of several dam blocks, which act against forces both independently and dependently of adjacent blocks. However, the existing evaluation methods often take a single dam block as the research object; the evaluation results cannot easily to reflect the overall seepage safety of the dam.
- (1)
- Establish the D-MEE model based on the MEE model and FDA.
- (2)
- Propose the D-CRITIC method to determine the weights of the indicators.
- (3)
- Construct the spatial weight matrix and assess the overall seepage safety.
2. Methodology
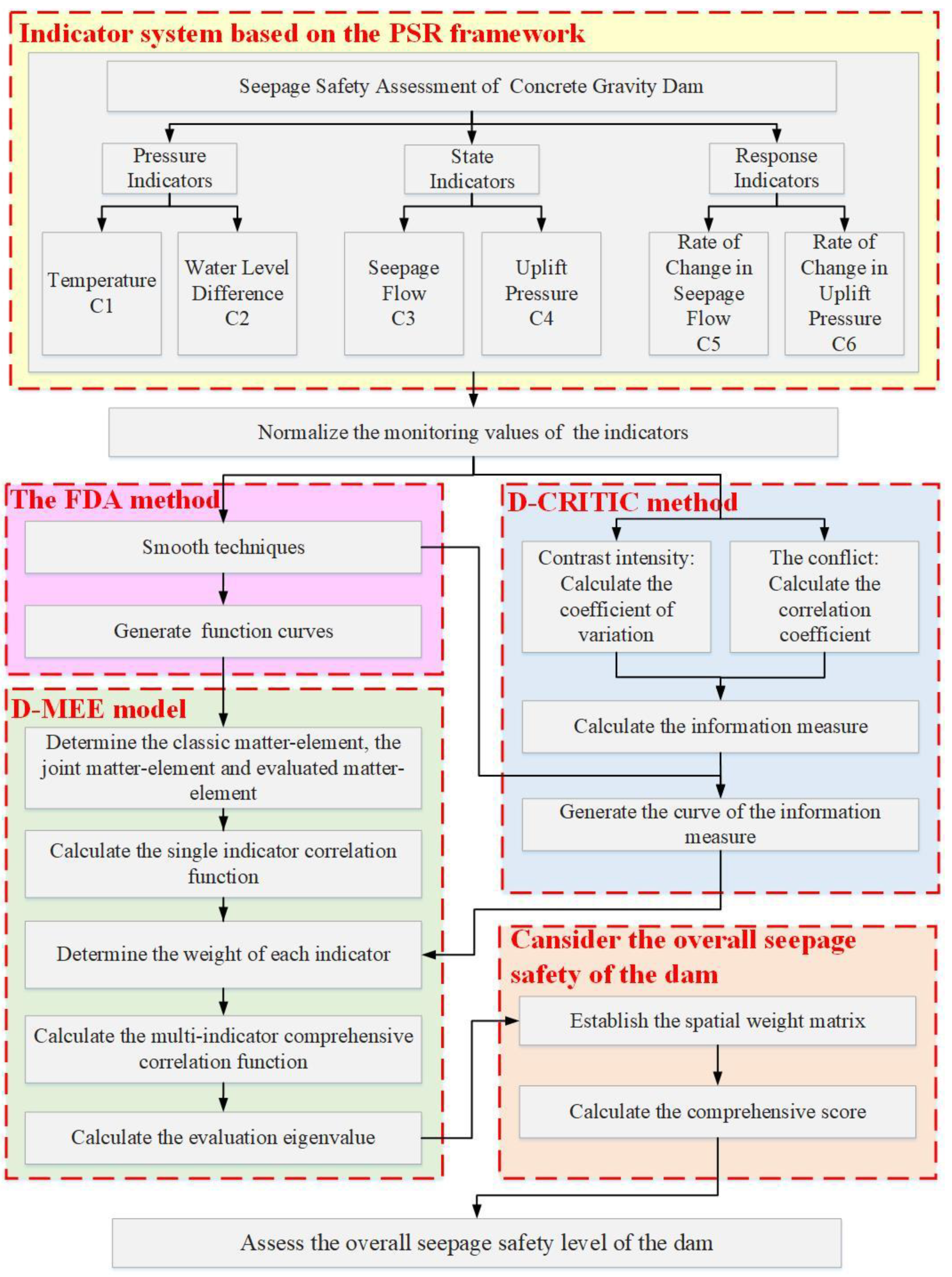
2.1. Research Procedure
2.2. Indicator System Based on the PSR Framework
2.3. D-MEE Model for Seepage Safety Assessment
2.3.1. Functional Data Analysis (FDA)
2.3.2. D-MEE Model
2.4. D-CRITIC Method for Determining the Indicator Weights
2.5. Calculation of the Comprehensive Score by Constructing the Spatial Weight Matrix
3. Case Study
3.1. Project Overview
3.2. Determining the Evaluation Indicators and Criteria
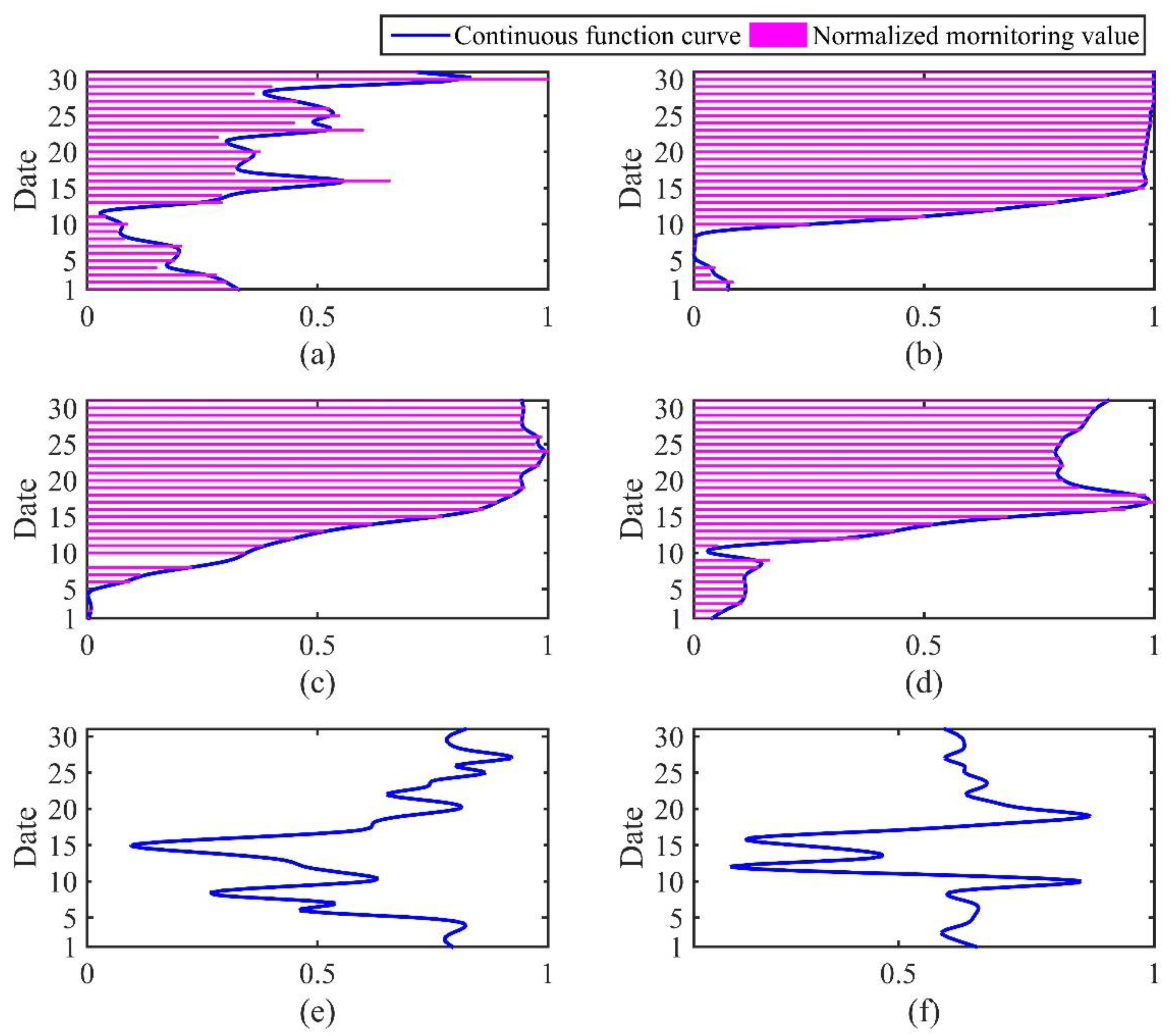
3.3. Generate the Function Curve for Each Indicator Using FDA
3.4. Determine the Classic Matter-Element, the Joint Matter-Element, and Evaluated Matter-Element
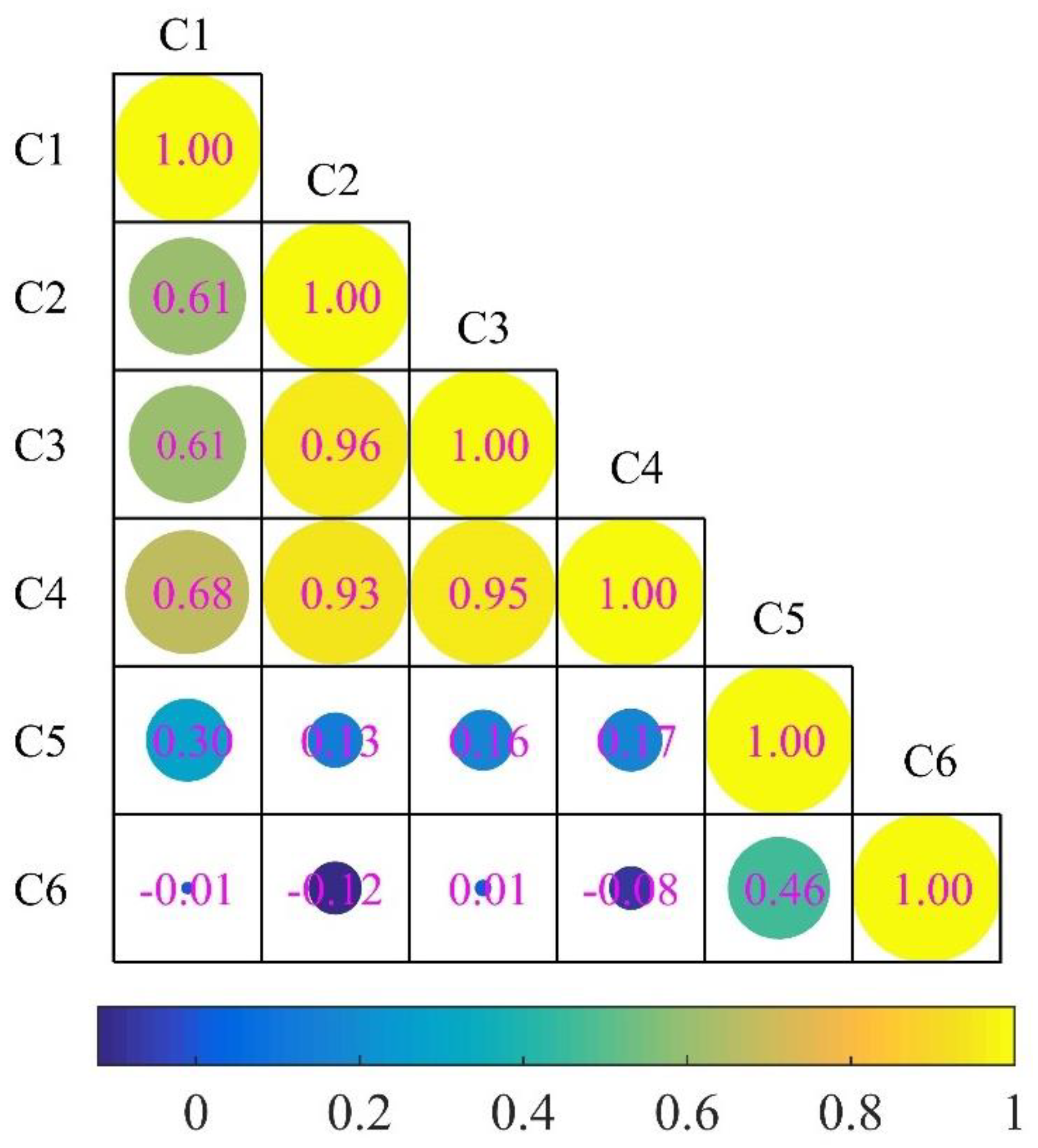
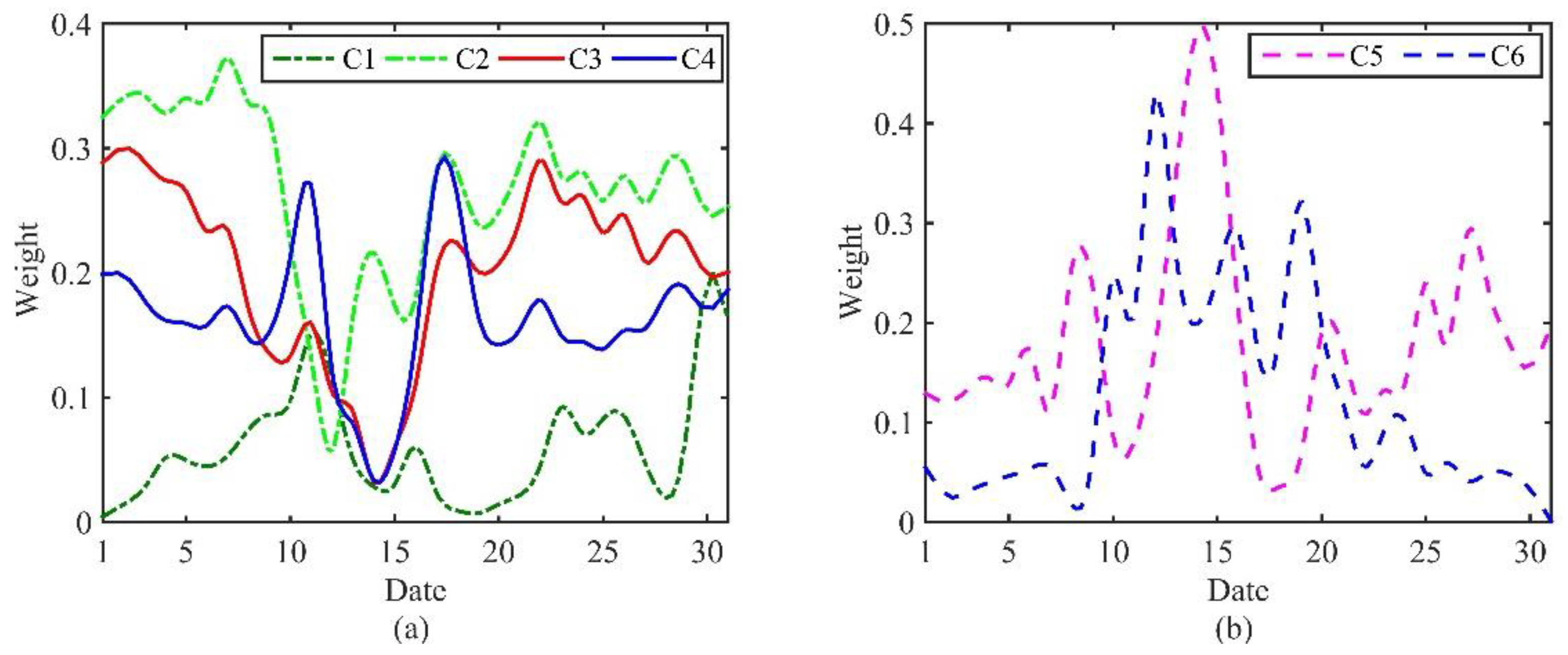
3.5. Determine the Weights of the Indicators Based on the D-CRITIC Method
3.6. Calculate the Comprehensive Score
4. Discussion
5. Conclusions
- The proposed D-MEE model converts the discrete monitoring data into a dynamic and continuous function curve through smoothing technology, which can reflect the dynamic change process of seepage safety more intuitively and comprehensively. In addition, more information can be obtained by the derivative analysis of the function curves. D-MEE can also solve the problems of missing data and unequal sampling.
- The proposed D-CRITIC method effectively considers the correlation among indicators and avoids the overlap of indicator information. At the same time, it determines the weights according to the dynamic change of the indicators, making the weights more accurate.
- The spatial weight integrated with the dynamic evaluation eigenvalues can be effectively used to assess the overall seepage safety and make the evaluation results more reasonable.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhao, H.; Guo, S.; Zhao, H. Comprehensive performance assessment on various battery energy storage systems. Energies 2018, 11, 2841. [Google Scholar] [CrossRef]
- Scott, C.A.; Sugg, Z.P. Global energy development and climate-induced water scarcity—Physical limits, sectoral constraints, and policy imperatives. Energies 2015, 8, 8211–8225. [Google Scholar] [CrossRef]
- General Office of the State Council. Available online: http://www.gov.cn/zhengce/content/2014-11/19/content_9222.htm (accessed on 29 January 2019).
- Nan, D.; Shigemitsu, T.; Zhao, S.D. Investigation and analysis of attack angle and rear flow condition of contra-rotating small hydro-turbine. Energies 2018, 11, 1806. [Google Scholar] [CrossRef]
- Mridha, S.; Maity, D. Experimental investigation on nonlinear dynamic response of concrete gravity dam-reservoir system. Eng. Struct. 2014, 80, 289–297. [Google Scholar] [CrossRef]
- Karastathis, V.K.; Karmis, P.N.; Drakatos, G.; Stavrakakis, G. Geophysical methods contributing to the testing of concrete dams. Application at the Marathon Dam. J. Appl. Geophys. 2002, 50, 247–260. [Google Scholar] [CrossRef]
- Ren, Q.; Xu, L.; Wan, Y. Research advance in safety analysis methods for high concrete dam. Sci. China Ser. E-Technol. Sci. 2007, 50, 62–78. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, X.; Ren, B.; Lv, P.; Zhu, X. Simulation of complex seepage field of a gravity dam foundation using a CFD-based approach. J. Hydraul. Eng. 2018, 144. [Google Scholar] [CrossRef]
- Bretas, E.M.; Lemos, J.V.; Lourenço, P.B. Hydromechanical analysis of masonry gravity dams and their foundations. Rock Mech. Rock Eng. 2013, 46, 327–339. [Google Scholar] [CrossRef]
- Li, M.; Guo, X.; Shi, J.; Zhu, Z. Seepage and stress analysis of anti-seepage structures constructed with different concrete materials in an RCC gravity dam. Water Sci. Eng. 2015, 8, 326–334. [Google Scholar] [CrossRef]
- Ministry of Water Resources of the People’s Republic of China. SL 319—2005 Design Code for Concrete Gravity Dams; China Water Conservancy and Hydropower Press: Beijing China, 2005; pp. 12–13. [Google Scholar]
- Ministry of Water Resources of the People’s Republic of China. SL 601—2013 Technical Specification for Concrete Dam Safety Monitoring; China Water Resources and Hydropower Press: Beijing China, 2013; pp. 15–18. [Google Scholar]
- Ministry of Water Resources of the People’s Republic of China. SL 258—2017 Guidelines on Dam Safety Evaluation; China Water Resources and Hydropower Press: Beijing China, 2017; p. 34. [Google Scholar]
- Zhu, X.; Wang, X.; Li, X.; Liu, M.; Cheng, Z. A new dam reliability analysis considering fluid structure interaction. Rock Mech. Rock Eng. 2018, 51, 2505–2516. [Google Scholar] [CrossRef]
- Jiang, H.; Ma, F.; Wu, S. Comprehensive investigation of leakage problems for concrete gravity dams with penetrating cracks based on detection and monitoring data: A case study. Struct. Control Health Monit. 2017, 25, e2127. [Google Scholar]
- Zhu, K.; Gu, C.; Qiu, J.; Li, H. The analysis of the concrete gravity dam’s foundation uplift pressure under the function of typhoon. Math. Probl. Eng. 2016, 2016, 2834192. [Google Scholar] [CrossRef]
- He, Y.; Zhao, M.; Wang, K.; Liu, P. Fuzzy comprehensive evaluation of earth rockfill dam seepage security risk based on cloud model. Water Resour. Power 2018, 36, 83–86. [Google Scholar]
- Su, H.; Sun, X. Comprehensive evaluation and tendency prediction model for concrete dam seepage behavior. Yangtze River 2013, 44, 95–99. [Google Scholar]
- Mei, Y.; Zhong, Y. Fuzzy extension evaluation model of dam seepage behavior based on entropy weight. Water Resour. Power 2011, 29, 58–61. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inform. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zhao, K. Set pair and set pair analysis-a new concept and systematic analysis method. In Proceedings of the National Conference on System Theory and Regional Planning, Baotou, China, August 1989; pp. 87–91. [Google Scholar]
- Garg, H.; Kumar, K. Distance measures for connection number sets based on set pair analysis and its applications to decision-making process. Appl. Intell. 2018, 48, 3346–3359. [Google Scholar] [CrossRef]
- Cai, W. The extension set and incompatibility problem. J. Sci. Explor. 1983, 1, 81–93. [Google Scholar]
- Ma, L.; Chen, H.; Yan, H.; Li, W.; Zhang, J.; Zhang, W. Post evaluation of distributed energy generation combining the attribute hierarchical model and matter-element extension theory. J. Clean. Prod. 2018, 184, 503–510. [Google Scholar] [CrossRef]
- Tang, J.; Wang, C.; Lin, N.; Li, Z.; Li, H.; Mao, Z. Application of matter-element model in soil nutrient evaluation of ecological fragile region. Chin. Geogr. Sci. 2009, 19, 168–176. [Google Scholar] [CrossRef]
- Li, K.; Hou, K. Dynamic extension evaluation of soil and water environmental quality in metal mine and its improvement measure. Res. J. Chem. Environ. 2012, 16, 97–101. [Google Scholar]
- Wang, J.B. Classification and stability study on surrounding rock of Hipparion red clay in Shi-lou Tunnel. Master’s Thesis, Northwest University, Xian, China, 2014. [Google Scholar]
- Zhao, B.; Xu, W.; Liang, G.; Meng, Y. Stability evaluation model for high rock slope based on element extension theory. Bull. Eng. Geol. Environ. 2015, 74, 301–314. [Google Scholar] [CrossRef]
- Liu, J.; Xu, J.; Bai, E.; Gao, Z. Durability evaluation analysis of reinforced concrete structures based on extension method. Adv. Mater. Res. 2011, 163–167, 3354–3358. [Google Scholar] [CrossRef]
- Xie, D. The researching about evaluation methods that concrete resists sulfate erosion under the freeze thaw-dry wet cycle condition. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2015. [Google Scholar]
- Lian, H. Study and evaluation of concrete durability in the action of carbonization-sulfate attack-dry-wet cycle. Master’s Thesis, North China University of Water Resources and Electric Power, Zhengzhou, China, 2017. [Google Scholar]
- Wang, X.; Wang, G.; Wu, Y.; Xu, Y.; Gao, H. Comprehensive assessment of regional water usage efficiency control based on game theory weight and a matter-element model. Water 2017, 9, 113. [Google Scholar] [CrossRef]
- Li, J.; Wu, F.; Li, J.; Zhao, Y. Research on risk evaluation of transnational power networking projects based on the matter-element extension theory and granular computing. Energies 2017, 10, 1523. [Google Scholar] [CrossRef]
- Liu, D.; Zhao, X. Method and application for dynamic comprehensive evaluation with subjective and objective information. PLoS ONE 2013, 8, e83323. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Guo, L.; Jiang, J.; Hao, L.; Liu, R.; Wang, P. Evaluation and selection of emergency treatment technology based on dynamic fuzzy grey method for chemical contingency spills. J. Hazard. Mater. 2015, 299, 306–315. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Xu, S. Dynamic successive assessment method of water environment carrying capacity and its application. Ecol. Indic. 2015, 52, 134–146. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, L.; Hu, J.; Wang, H.; Li, K. A dynamic and non-linear risk evaluation methodology for high-pressure manifold in shale gas fracturing. J. Nat. Gas Sci. Eng. 2016, 29, 7–14. [Google Scholar] [CrossRef]
- Wu, D.; Ning, S. Dynamic assessment of urban economy-environment-energy system using system dynamics model: A case study in Beijing. Environ. Res. 2018, 164, 70–84. [Google Scholar] [CrossRef]
- Zarei, E.; Azadeh, A.; Khakzad, N.; Aliabadi, M.M.; Mohammadfam, I. Dynamic safety assessment of natural gas stations using Bayesian network. J. Hazard. Mater. 2017, 321, 830–840. [Google Scholar] [CrossRef] [PubMed]
- Ramsay, J.O. When the data are functions. Psychometrika 1982, 47, 379–396. [Google Scholar] [CrossRef]
- Yan, F.; Liu, L. Water quality assessment of the Li Canal using a functional fuzzy synthetic evaluation model. Environ. Sci. Proc. Imp. 2014, 16, 1764–1771. [Google Scholar]
- Yan, F.; Liu, L.; Li, Y.; Zhang, Y.; Chen, M.; Xing, X. A dynamic water quality index model based on functional data analysis. Ecol. Indic. 2015, 57, 249–258. [Google Scholar] [CrossRef]
- Yan, F.; Liu, L.; Zhang, Y.; Chen, M.; Chen, N. The research of dynamic variable fuzzy set assessment model in water quality evaluation. Water Resour. Manag. 2016, 30, 63–78. [Google Scholar] [CrossRef]
- Li, B.; Yang, G.; Wan, R.; Hormann, G. Dynamic water quality evaluation based on fuzzy matter-element model and functional data analysis, a case study in Poyang Lake. Environ. Sci. Pollut. Res. Int. 2017, 24, 19138–19148. [Google Scholar] [CrossRef]
- Aitchison, J. Principal component analysis of compositional data. Biometrika 1983, 70, 57–65. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Pu, Y.; Apel, D.; Xu, H. A principal component analysis/fuzzy comprehensive evaluation for rockburst potential in Kimberlite. Pure Appl. Geophys. 2018, 175, 2141–2151. [Google Scholar] [CrossRef]
- Verma, R.; Suthar, S. Performance assessment of horizontal and vertical surface flow constructed wetland system in wastewater treatment using multivariate principal component analysis. Ecol. Eng. 2018, 116, 121–126. [Google Scholar] [CrossRef]
- Alemi-Ardakani, M.; Milani, A.S.; Yannacopoulos, S.; Shokouhi, G. On the effect of subjective, objective and combinative weighting in multiple criteria decision making: A case study on impact optimization of composites. Expert Syst. Appl. 2016, 46, 426–438. [Google Scholar] [CrossRef]
- Li, L.; Hang, J.; Sun, H.; Wang, L. A conjunctive multiple-criteria decision-making approach for cloud service supplier selection of manufacturing enterprise. Adv. Mech. Eng. 2017, 9, 1–15. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Antucheviciene, J. A new hybrid fuzzy MCDM approach for evaluation of construction equipment with sustainability considerations. Arch. Civ. Mech. Eng. 2018, 18, 32–49. [Google Scholar] [CrossRef]
- Li, Z.; Yang, T.; Huang, C.; Xu, C.; Shao, Q.; Shi, P.; Wang, X.; Cui, T. An improved approach for water quality evaluation: TOPSIS-based informative weighting and ranking (TIWR) approach. Ecol. Indic. 2018, 89, 356–364. [Google Scholar] [CrossRef]
- Rostamzadeh, R.; Keshavarz Ghorabaee, M.; Govindan, K.; Esmaeili, A.; Nobar, H.B.K. Evaluation of sustainable supply chain risk management using an integrated fuzzy TOPSIS-CRITIC approach. J. Clean. Prod. 2018, 175, 651–669. [Google Scholar] [CrossRef]
- Smith, T.E. Estimation bias in spatial models with strongly connected weight matrices. Geogr. Anal. 2010, 41, 307–332. [Google Scholar] [CrossRef]
- Stakhovych, S.; Bijmolt, T.H.A. Specification of spatial models: A simulation study on weights matrices. Pap. Reg. Sci. 2010, 88, 389–408. [Google Scholar] [CrossRef]
- Seya, H.; Yamagata, Y.; Tsutsumi, M. Automatic selection of a spatial weight matrix in spatial econometrics: Application to a spatial hedonic approach. Sci. Urban Econ. 2013, 43, 429–444. [Google Scholar] [CrossRef]
- Rincke, J. Policy diffusion in space and time: The case of charter schools in California school districts. Sci. Urban Econ. 2007, 37, 526–541. [Google Scholar] [CrossRef]
- Moscone, F.; Knapp, M.; Tosetti, E. Mental health expenditure in England: A spatial panel approach. J. Health Econ. 2007, 26, 842–864. [Google Scholar] [CrossRef]
- Tong, T.; Yu, T.-H.E.; Cho, S.-H.; Jensen, K.; Ugarte, D.D.L.T. Evaluating the spatial spillover effects of transportation infrastructure on agricultural output across the united states. J. Transp. Geogr. 2013, 30, 47–55. [Google Scholar] [CrossRef]
- Shi, W.; Lee, L.F. Spatial dynamic panel data models with interactive fixed effects. J. Econom. 2017, 197, 323–347. [Google Scholar] [CrossRef]
- Lesage, J.P.; Ha, C.L. The impact of migration on social capital: Do migrants take their bowling balls with them? Growth Change 2012, 43, 1–26. [Google Scholar] [CrossRef]
- Fingleton, B.; Palombi, S. Spatial panel data estimation, counterfactual predictions, and local economic resilience among British towns in the Victorian era. Sci. Urban Econ. 2013, 43, 649–660. [Google Scholar] [CrossRef]
- Qu, X.; Lee, L.F.; Yu, J.H. QML estimation of spatial dynamic panel data models with endogenous time varying spatial weights matrices. J. Econom. 2017, 197, 173–201. [Google Scholar] [CrossRef]
- Liao, C.; Yue, Y.; Wang, K.; Fensholt, R.; Tong, X.; Brandt, M. Ecological restoration enhances ecosystem health in the karst regions of southwest China. Ecol. Indic. 2018, 90, 416–425. [Google Scholar] [CrossRef]
- Ullah, S.; Finch, C.F. Applications of functional data analysis: A systematic review. BMC Med. Res. Methodol. 2013, 13, 43. [Google Scholar] [CrossRef]
- Chao, K.H.; Li, C.J. An intelligent maximum power point tracking method based on extension theory for PV systems. Expert Syst. Appl. 2010, 37, 1050–1055. [Google Scholar] [CrossRef]
- Su, H.; Yang, M.; Wen, Z. Multi-layer multi-index comprehensive evaluation for dike safety. Water Resour. Manag. 2015, 29, 4683–4699. [Google Scholar] [CrossRef]
- Zhong, D.; Wang, Z.; Zhang, Y.; Shi, M. Fluid–solid coupling based on a refined fractured rock model and stochastic parameters: A case study of the anti-sliding stability analysis of the Xiangjiaba project. Rock Mech. Rock Eng. 2018, 51, 2555–2567. [Google Scholar] [CrossRef]
- Wu, Z.; Su, H. Dam health diagnosis and evaluation. Smart Mater. Struct. 2005, 14, S130–S136. [Google Scholar] [CrossRef]


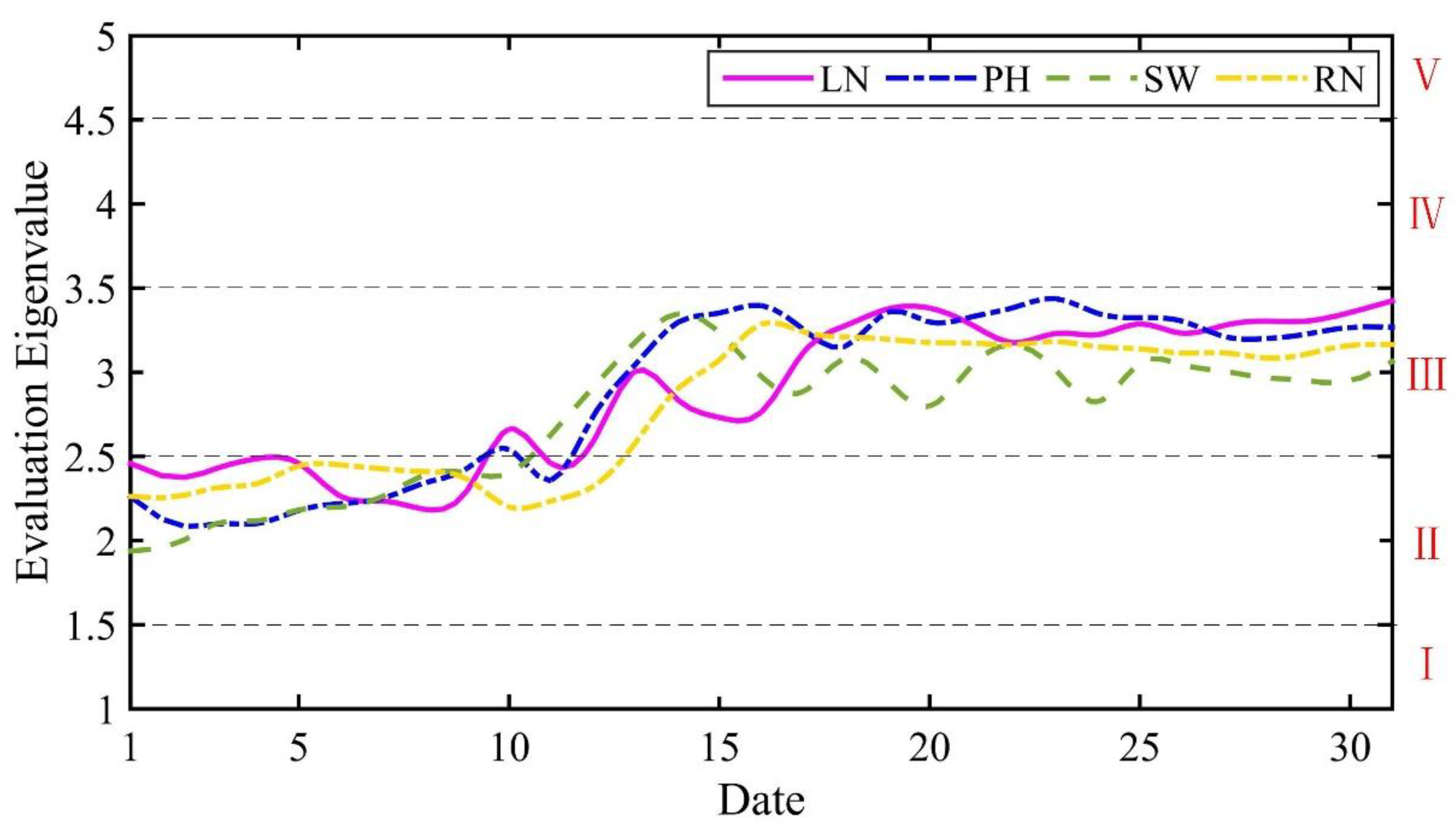
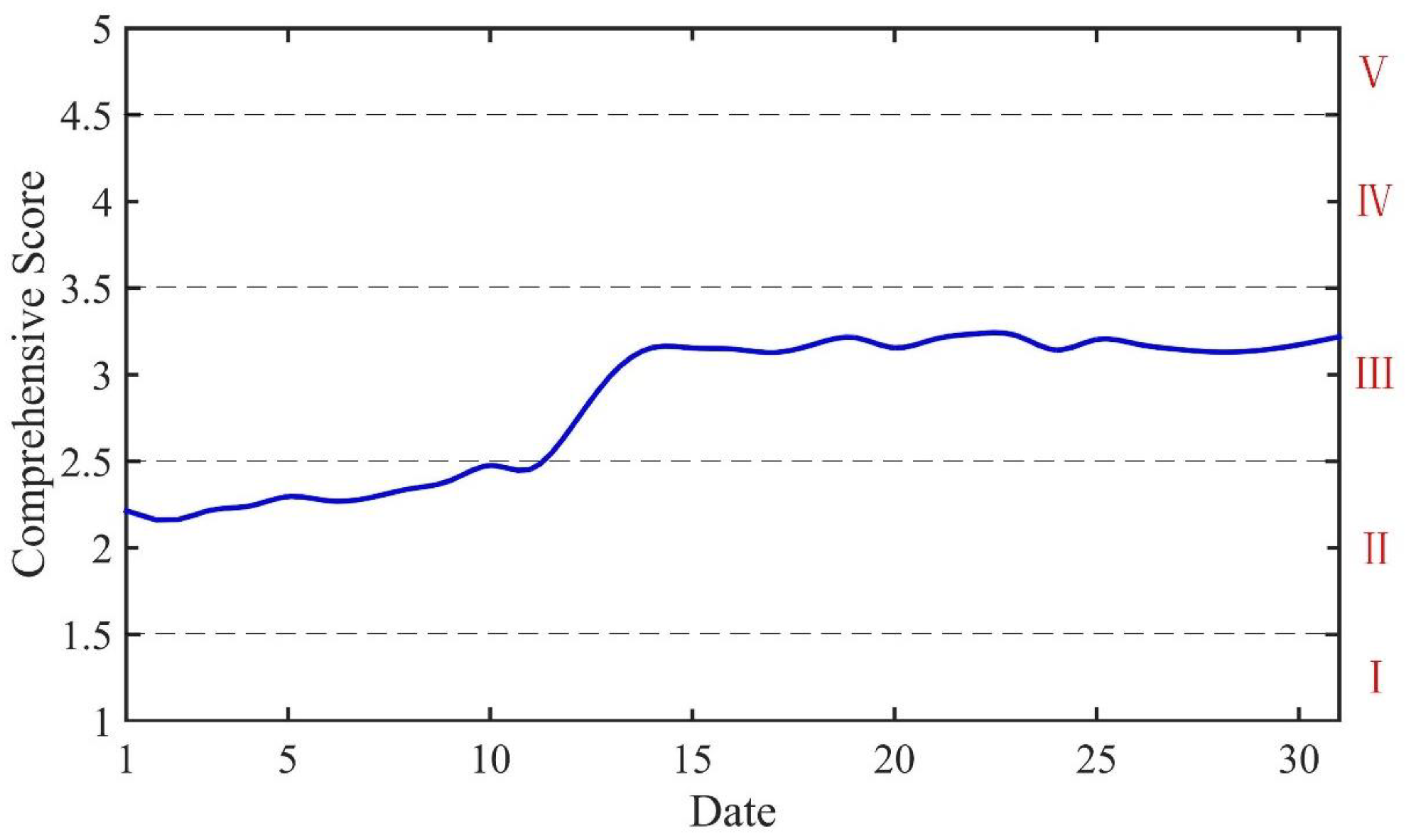
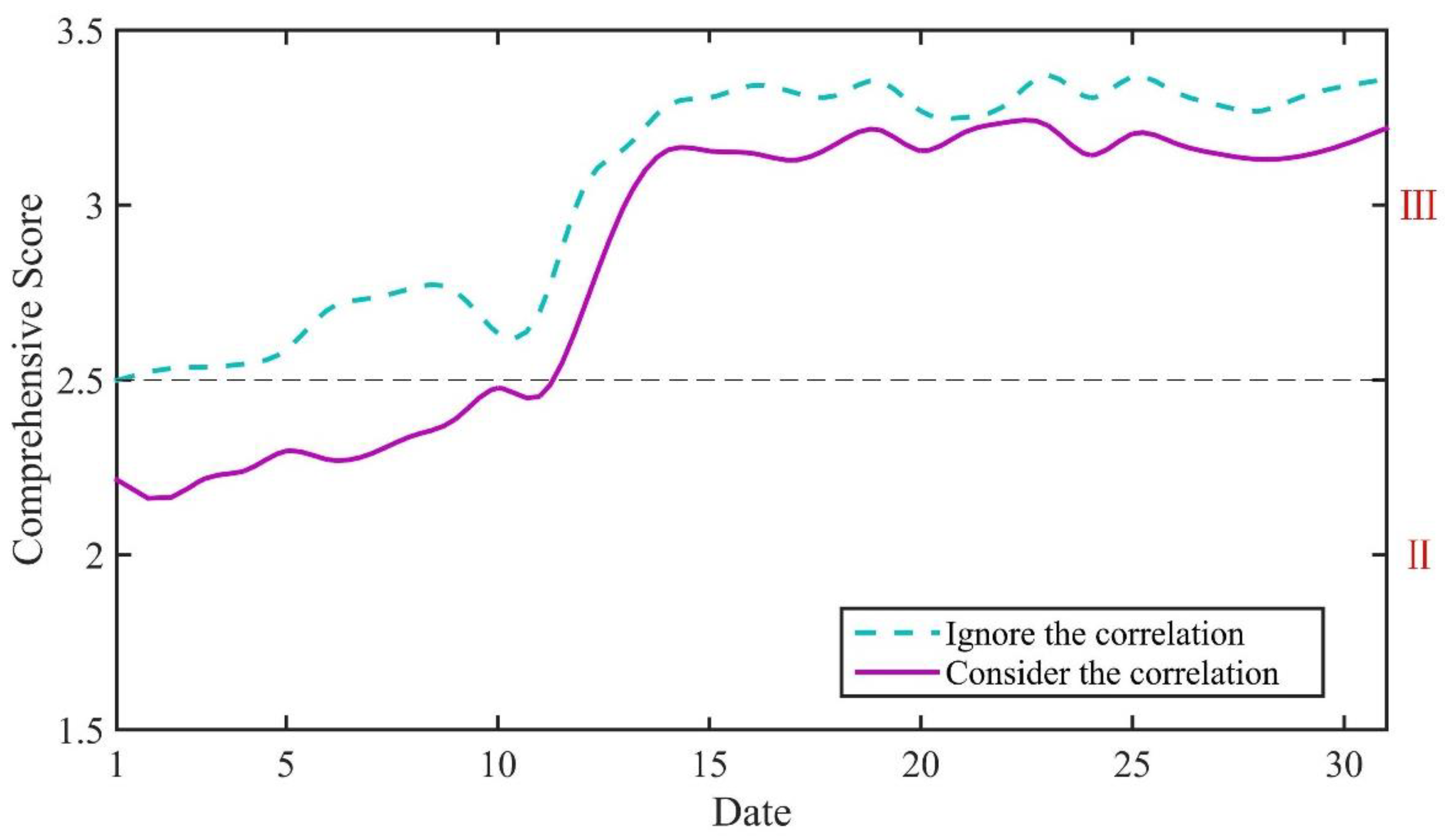
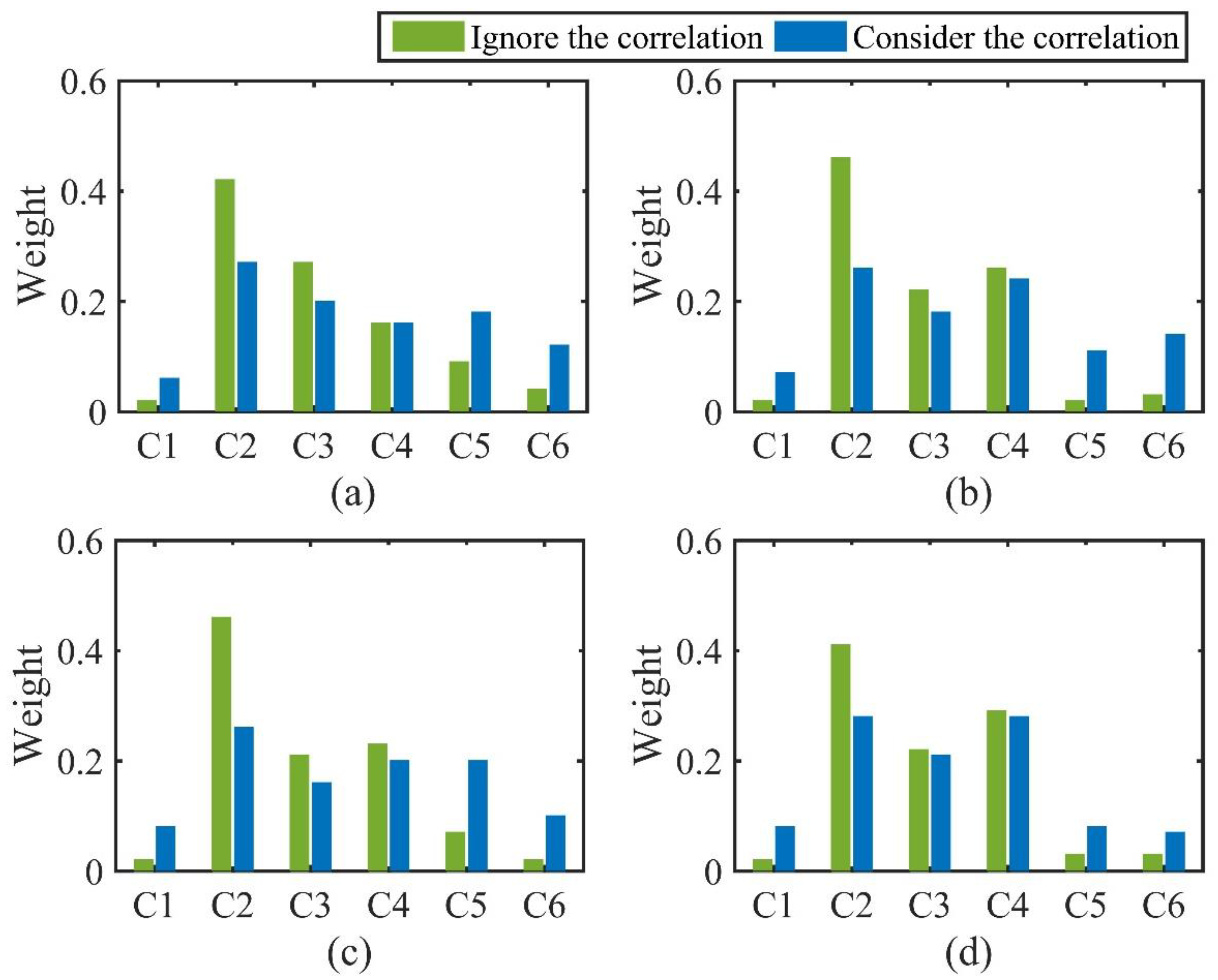
| Classification | Comprehensive Score | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|---|
| I (Normal) | 1–1.5 | 0–0.2 | 0–0.2 | 0–0.2 | 0–0.2 | 0–0.2 | 0–0.2 |
| II (Normal Basically) | 1.5–2.5 | 0.2–0.4 | 0.2–0.4 | 0.2–0.4 | 0.2–0.4 | 0.2–0.4 | 0.2–0.4 |
| III (Little Abnormal) | 2.5–3.5 | 0.4–0.6 | 0.4–0.6 | 0.4–0.6 | 0.4–0.6 | 0.4–0.6 | 0.4–0.6 |
| IV (Abnormal) | 3.5–4.5 | 0.6–0.8 | 0.6–0.8 | 0.6–0.8 | 0.6–0.8 | 0.6–0.8 | 0.6–0.8 |
| V (Dangerous) | 4.5–5 | 0.8–1 | 0.8–1 | 0.8–1 | 0.8–1 | 0.8–1 | 0.8–1 |
| Data | Set Pair Analysis Method | Fuzzy Comprehensive Evaluation Method | Matter-Element Extension Method | D-MEE Method |
|---|---|---|---|---|
| 5 | II | II | III | II |
| 6 | II | II | II | II |
| 7 | II | II | II | II |
| 8 | II | II | II | II |
| 9 | ― | ― | ― | II |
| 10 | II | II | III | III |
| 11 | III | II | II | II |
| 12 | III | III | III | III |
| 13 | III | II | III | III |
| 14 | IV | III | III | III |
| 15 | III | IV | III | III |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Yu, H.; Lv, P.; Wang, C.; Zhang, J.; Yu, J. Seepage Safety Assessment of Concrete Gravity Dam Based on Matter-Element Extension Model and FDA. Energies 2019, 12, 502. https://doi.org/10.3390/en12030502
Wang X, Yu H, Lv P, Wang C, Zhang J, Yu J. Seepage Safety Assessment of Concrete Gravity Dam Based on Matter-Element Extension Model and FDA. Energies. 2019; 12(3):502. https://doi.org/10.3390/en12030502
Chicago/Turabian StyleWang, Xiaoling, Hongling Yu, Peng Lv, Cheng Wang, Jun Zhang, and Jia Yu. 2019. "Seepage Safety Assessment of Concrete Gravity Dam Based on Matter-Element Extension Model and FDA" Energies 12, no. 3: 502. https://doi.org/10.3390/en12030502
APA StyleWang, X., Yu, H., Lv, P., Wang, C., Zhang, J., & Yu, J. (2019). Seepage Safety Assessment of Concrete Gravity Dam Based on Matter-Element Extension Model and FDA. Energies, 12(3), 502. https://doi.org/10.3390/en12030502




