Stochastic Planning of Distributed PV Generation
Abstract
1. Introduction
1.1. Motivation and Context
1.2. Literature Review
1.3. Contributions and Paper Organization
- In line with standard practice based on the PVWatts calculator, an analytical model for PV units is presented that rigorously maps solar irradiance to the injected AC power. It is shown that the analytical model is nonconvex. Two engineering designs are then offered to bypass the non-convexity.
- Based on realistic data, several homes are considered per node of the distribution network. Together with linearized network equations that adequately describe the relationships between powers and voltages of the distribution network, the developed framework is intended as a tool for utility-level studies.
- Extensive numerical studies on the IEEE 34-bus distribution feeder are carried out. It is shown that the degree of freedom between DC and AC sizes can be leveraged to lower installation costs through reduction of the panel area, in comparison to a scheme where the DC and AC sizes are restricted to conform to a known DC:AC ratio.
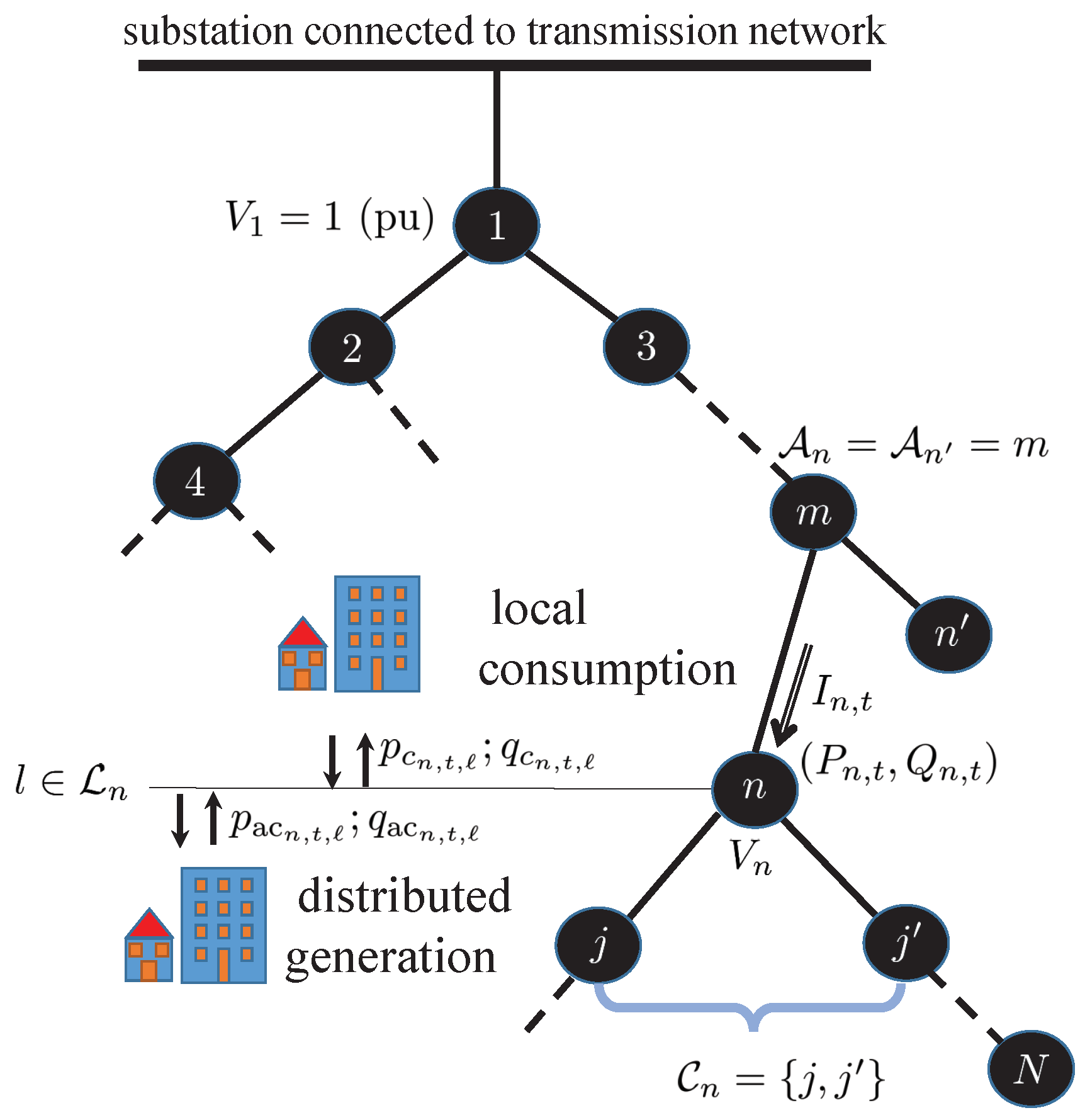
2. Network Model and the Optimization Problem
2.1. PV Module Model
2.2. Inverter Model
2.2.1. Optimal Inverter Sizing
2.2.2. Alternative Inverter Sizing
2.3. Placement and Sizing Constraints
2.4. Real Power and Reactive Power Consumption
2.5. Power Flows
2.6. Objective Function
- PV panel area cost for and . The cost per is represented by .
- Inverter nameplate apparent power capacity cost denoted by for and . The cost per is represented by .
- The term that captures thermal losses [4] multiplied by the price, denoted by , that utility buys from the market.
2.7. Optimization Problem
2.7.1. Placement and Sizing with Optimal Inverter Design
2.7.2. Placement and Sizing with Alternative Inverter Design
3. Numerical Data for Experiments and Design Procedure
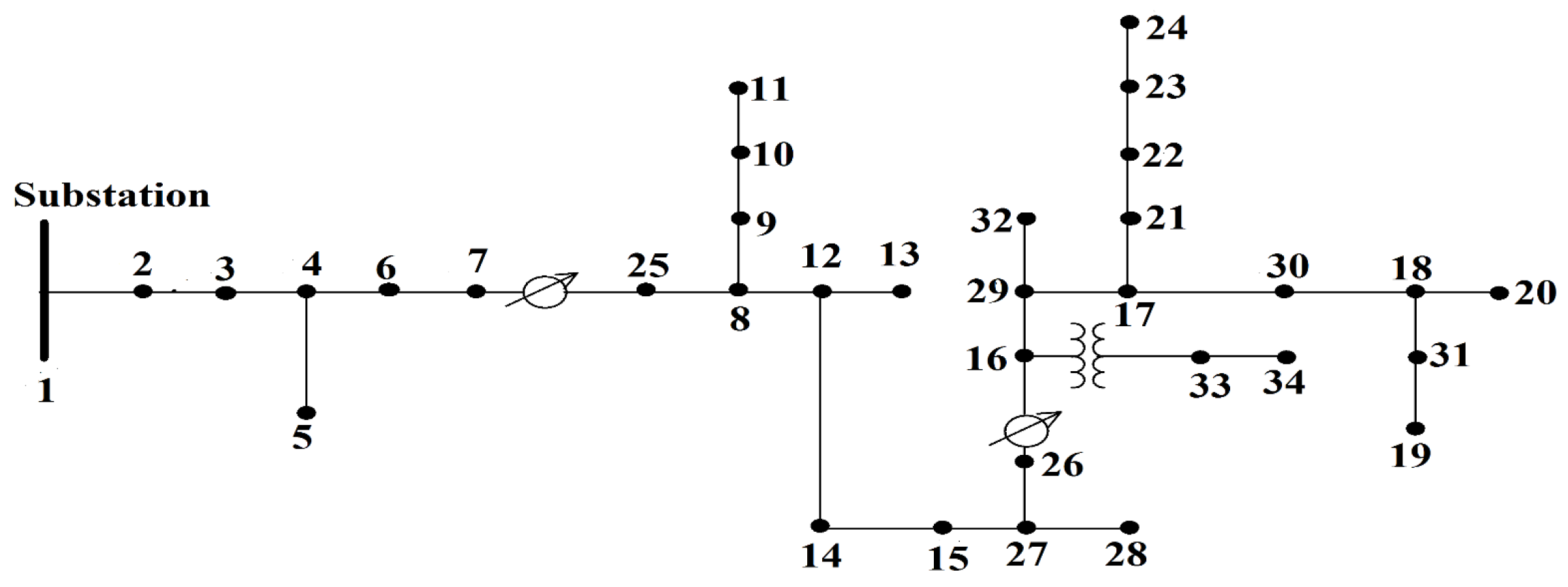
3.1. The Test Network
3.2. Load Scenarios and Allocation of Users per Node
3.3. Irradiance Scenarios
3.4. Installation and Electricity Costs
- Electricity Costs: According to the Wholesale Electricity Market Data of 2016 [41], a representative price of electricity at which the utility buys from the market is .
3.5. Design Procedure
4. Results and Discussion
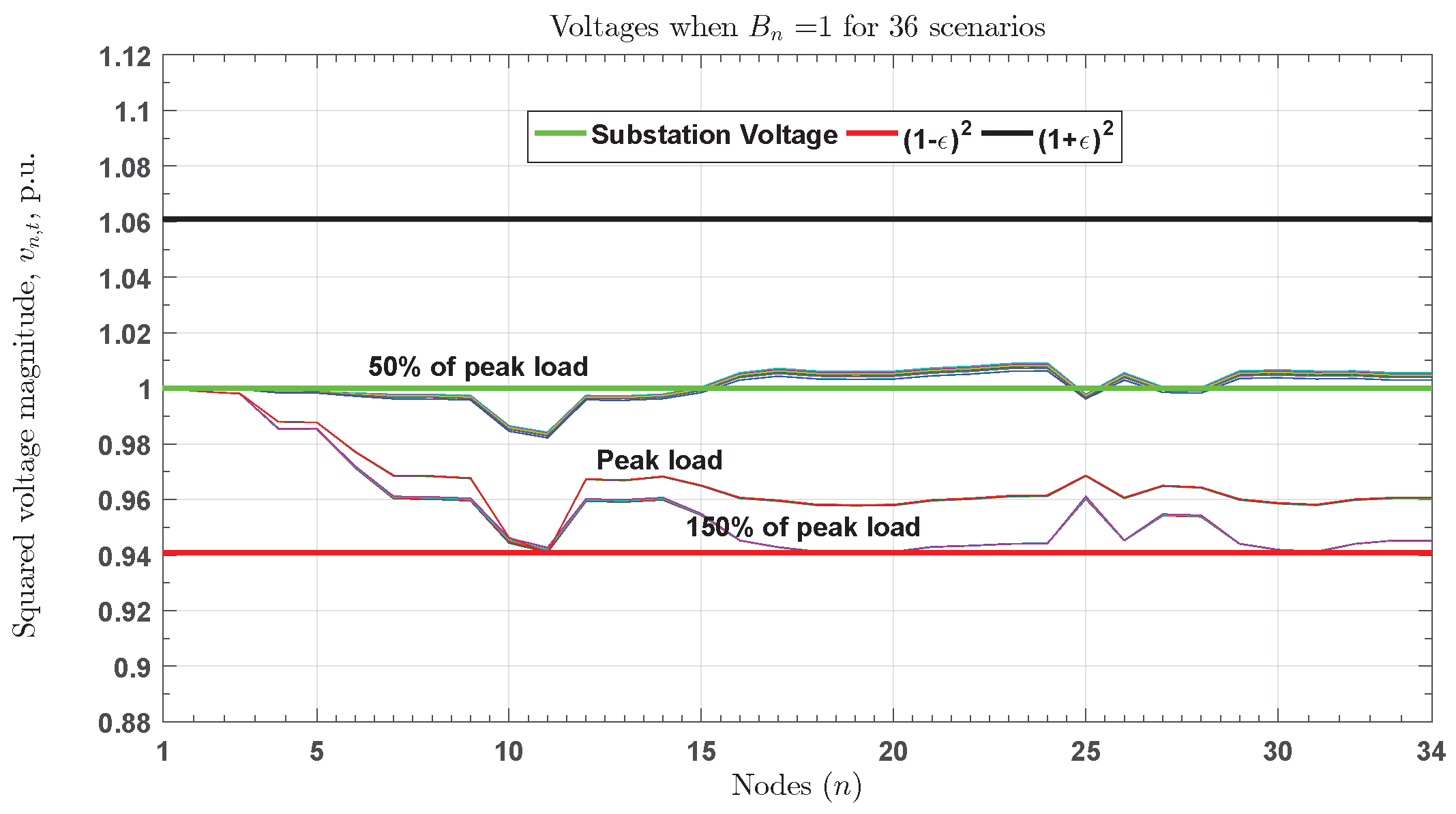
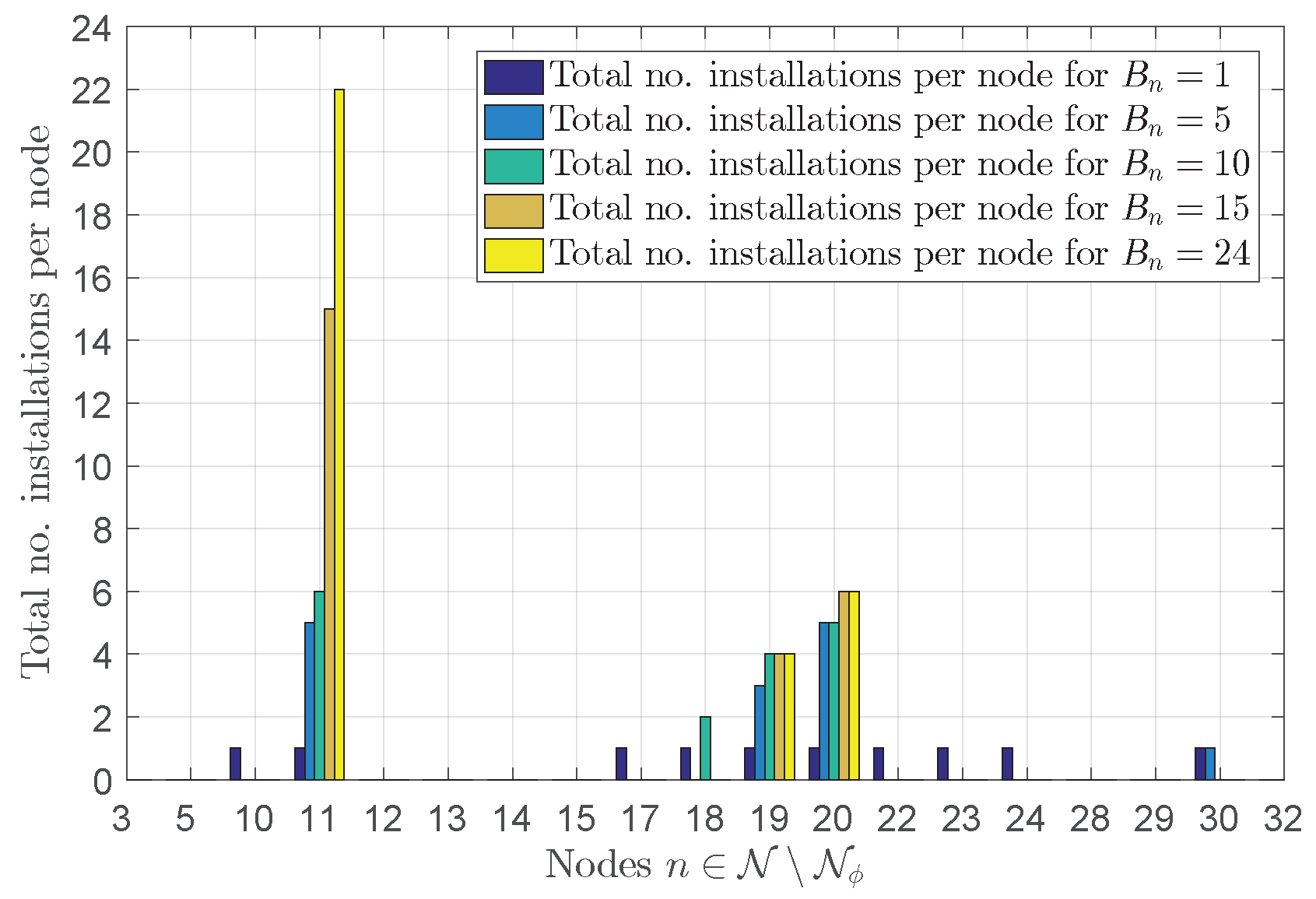
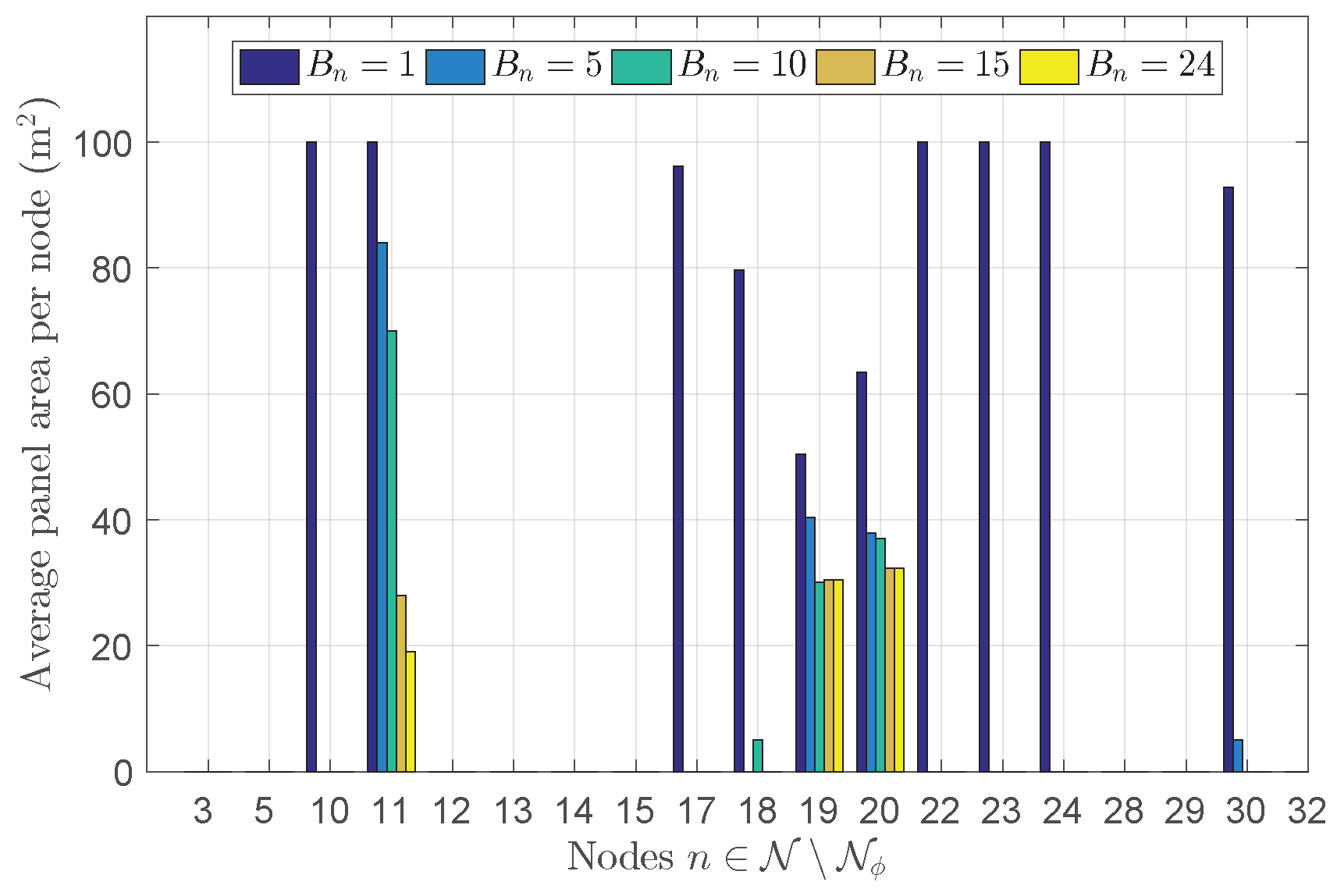
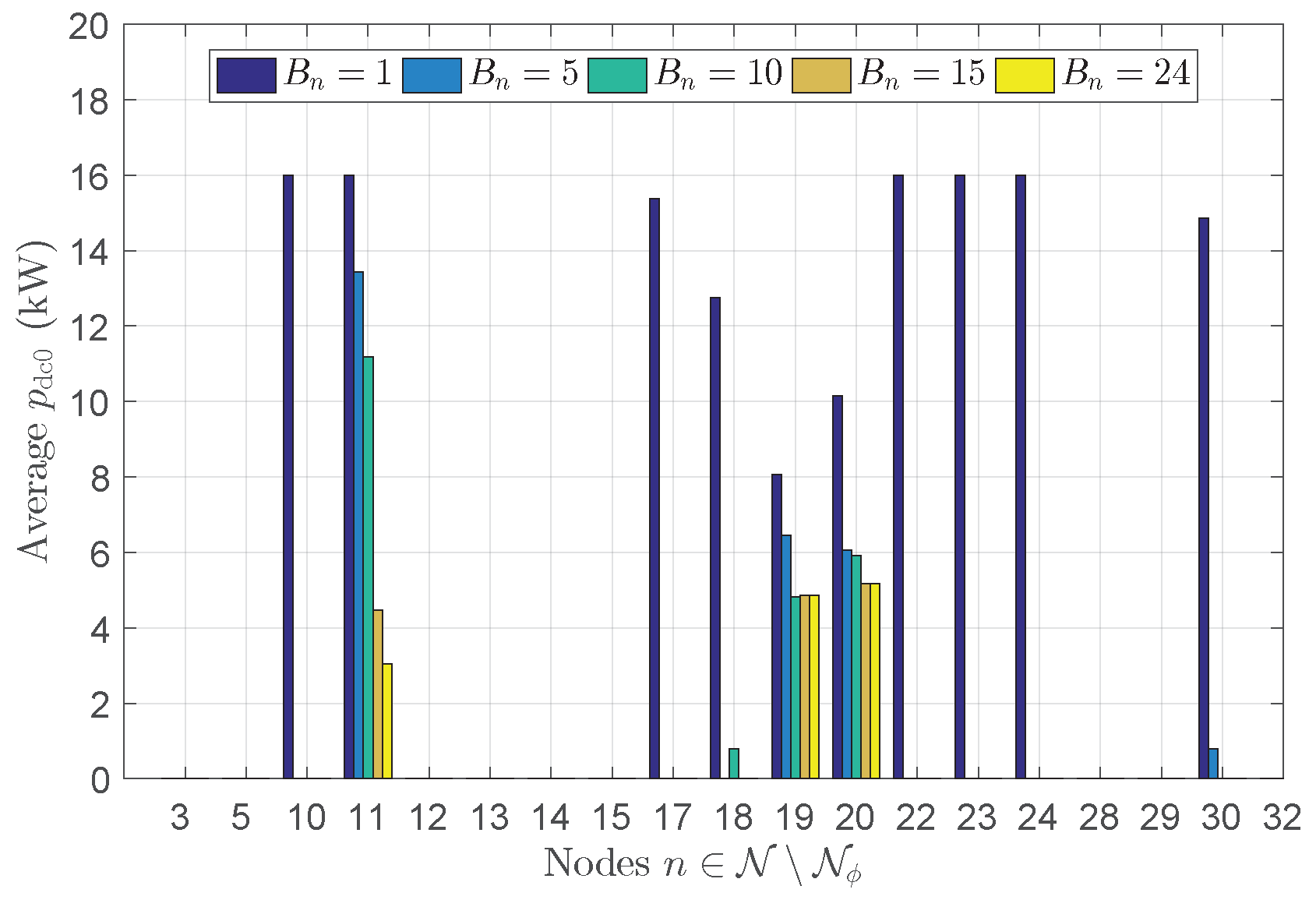
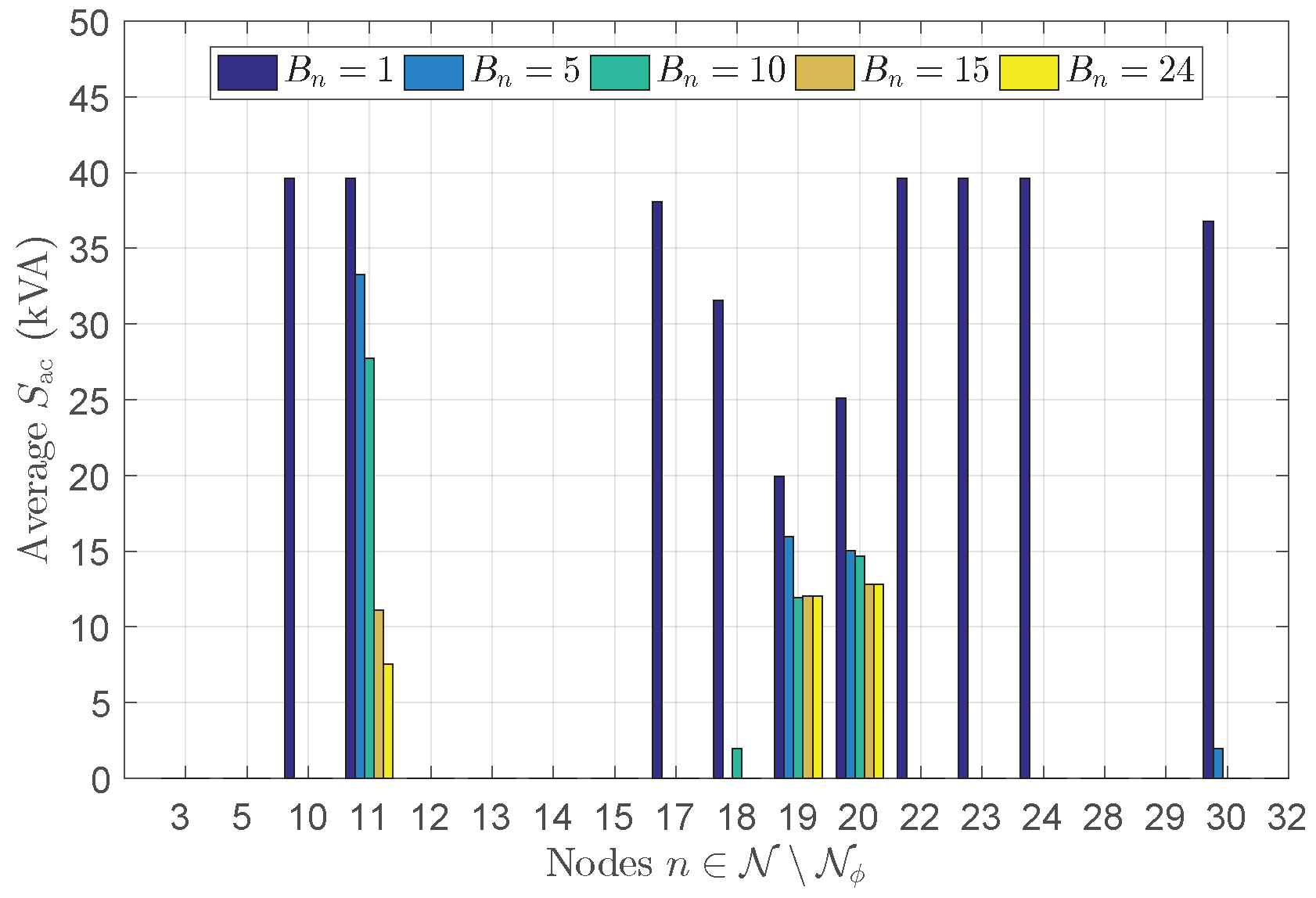
4.1. Results of Placement and Sizing with Optimal Inverter Design
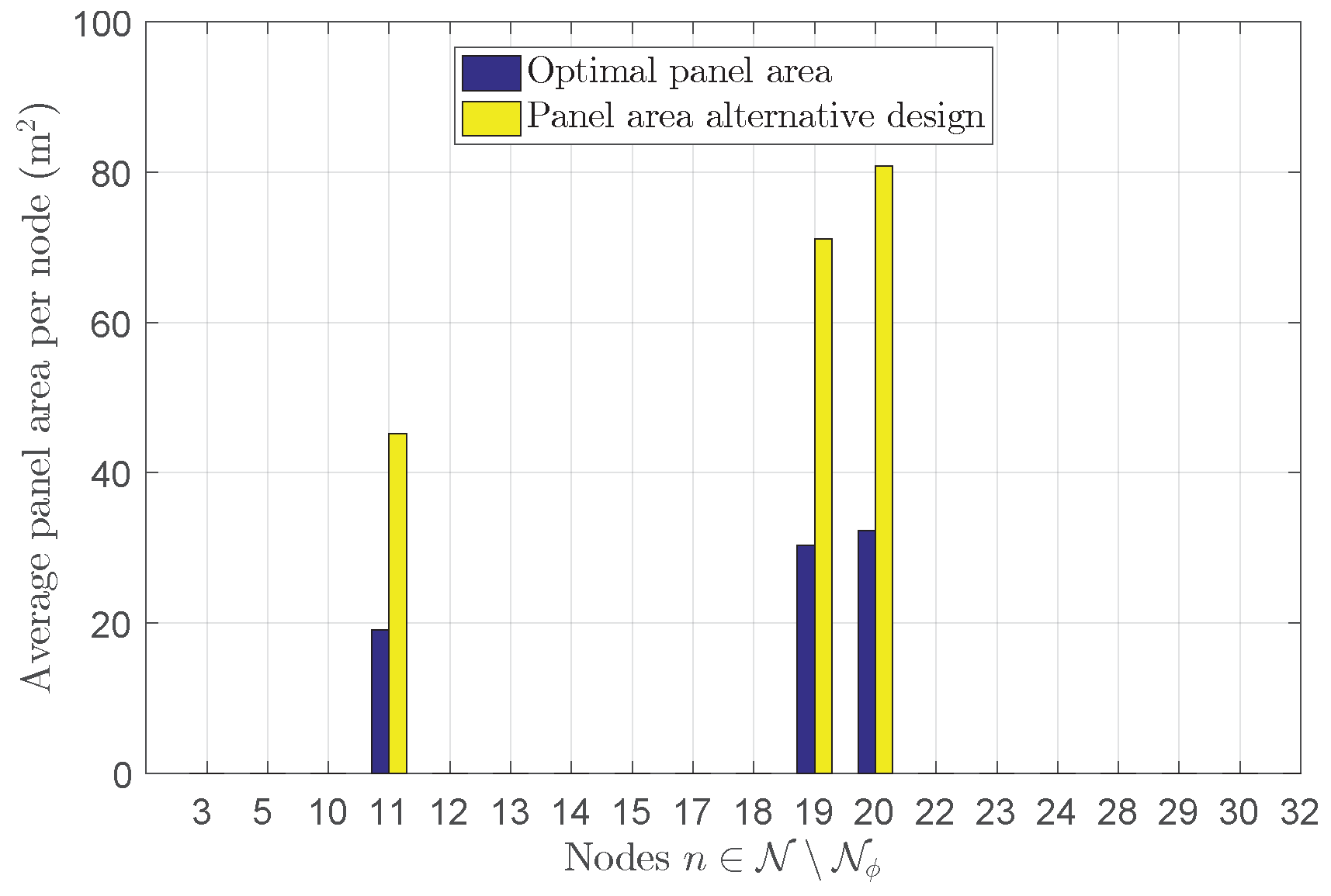
4.2. Comparison between Optimal and Alternative Inverter Design
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pitt, D.; Michaud, G. Analyzing the Costs and Benefits of Distributed Solar Generation in Virginia. Available online: http://mdvseia.org/wp-content/uploads/2014/12/SSG-Value-of-Solar-Study-Final-10-31-14.pdf (accessed on 9 January 2019).
- U.S. Department of Energy. Systems Integration. Available online: https://energy.gov/eere/sunshot/systems-integration (accessed on 9 January 2019).
- CPS Energy. Solar Power. Available online: https://www.cpsenergy.com/en/about-us/programs-services/energy-generation/solar-power.html (accessed on 9 January 2019).
- Xcel Energy Services Inc. Costs and Benefits of Distributed Solar Generation on the Public Service Company of Colorado System Study. Available online: http://www.eei.org/issuesandpolicy/generation/ NetMetering/Documents/Costs%20and%20Benefits%20of%20Distributed%20Solar%20Generation% 20on%20the%20Public%20Service%20Company%20of%20Colorado%20System%20Xcel%20Energy. pdf (accessed on 9 January 2019).
- Kanwar, N.; Gupta, N.; Niazi, K.; Swarnkar, A.; Bansal, R. Simultaneous allocation of distributed energy resource using improved particle swarm optimization. Appl. Energy 2017, 185, 1684–1693. [Google Scholar] [CrossRef]
- Armendáriz, M.; Heleno, M.; Cardoso, G.; Mashayekh, S.; Stadler, M.; Nordström, L. Coordinated microgrid investment and planning process considering the system operator. Appl. Energy 2017, 200, 132–140. [Google Scholar] [CrossRef]
- Silvestre, M.D.; Cascia, D.L.; Sanseverino, E.R.; Zizzo, G. Improving the energy efficiency of an islanded distribution network using classical and innovative computation methods. Util. Policy 2016, 40, 58–66. [Google Scholar] [CrossRef]
- Valdberg, A.J.; Dwyer, M.W. Distribution Resources Plan Rulemaking (R. 14-08-013) Locational Net Benefit Analysis Working Group Final Report. Available online: http://drpwg.org/wp-content/uploads/2016/07/R1408013-et-al-SCE-LNBA-Working-Group-Final-Report.pdf (accessed on 9 January 2019).
- Tonkoski, R.; Turcotte, D.; El-Fouly, T.H.M. Impact of high PV penetration on voltage profiles in residential neighborhoods. IEEE Trans. Sustain. Energy 2012, 3, 518–527. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory. PVWatts Documentation. Available online: http://pvwatts.nrel.gov (accessed on 9 January 2019).
- Dobos, A.P. PVWatts Version 5 Manual. Technical Report NREL/TP-6A20-62641; National Renewable Energy Laboratory, 2014. Available online: http://www.nrel.gov/docs/fy14osti/62641.pdf (accessed on 9 January 2019).
- Georgilakis, P.S.; Hatziargyriou, N.D. Optimal Distributed Generation Placement in Power Distribution Networks: Models, Methods, and Future Research. IEEE Trans. Power Syst. 2013, 28, 3420–3428. [Google Scholar] [CrossRef]
- Keane, A.; Ochoa, L.F.; Borges, C.L.T.; Ault, G.W.; Alarcon-Rodriguez, A.D.; Currie, R.A.F.; Pilo, F.; Dent, C.; Harrison, G.P. State-of-the-Art Techniques and Challenges Ahead for Distributed Generation Planning and Optimization. IEEE Trans. Power Syst. 2013, 28, 1493–1502. [Google Scholar] [CrossRef]
- Kazmi, S.A.A.; Shahzad, M.K.; Shin, D.R. Multi-Objective Planning Techniques in Distribution Networks: A Composite Review. Energies 2017, 10, 208. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. Optimal integration and planning of renewable distributed generation in the power distribution networks: A review of analytical techniques. Appl. Energy 2018, 210, 44–59. [Google Scholar] [CrossRef]
- Naik, S.N.G.; Khatod, D.K.; Sharma, M.P. Analytical approach for optimal siting and sizing of distributed generation in radial distribution networks. IET Gener. Transm. Distrib. 2015, 9, 209–220. [Google Scholar] [CrossRef]
- Al-Sabounchi, A.; Gow, J.; Al-Akaidi, M. Simple procedure for optimal sizing and location of a single photovoltaic generator on radial distribution feeder. IET Renew. Power Gener. 2014, 8, 160–170. [Google Scholar] [CrossRef]
- Vita, V. Development of a Decision-Making Algorithm for the Optimum Size and Placement of Distributed Generation Units in Distribution Networks. Energies 2017, 10, 1433. [Google Scholar] [CrossRef]
- Yammani, C.; Maheswarapu, S.; Matam, S.K. A Multi-objective Shuffled Bat algorithm for optimal placement and sizing of multi distributed generations with different load models. Int. J. Electr. Power Energy Syst. 2016, 79, 120–131. [Google Scholar] [CrossRef]
- Fu, X.; Chen, H.; Cai, R.; Yang, P. Optimal allocation and adaptive VAR control of PV-DG in distribution networks. Appl. Energy 2015, 137, 173–182. [Google Scholar] [CrossRef]
- Li, Y.; Feng, B.; Li, G.; Qi, J.; Zhao, D.; Mu, Y. Optimal distributed generation planning in active distribution networks considering integration of energy storage. Appl. Energy 2018, 210, 1073–1081. [Google Scholar] [CrossRef]
- Sheng, W.; Liu, K.Y.; Liu, Y.; Meng, X.; Li, Y. Optimal Placement and Sizing of Distributed Generation via an Improved Nondominated Sorting Genetic Algorithm II. IEEE Trans. Power Del. 2015, 30, 569–578. [Google Scholar] [CrossRef]
- Bhullar, S.; Ghosh, S. Optimal Integration of Multi Distributed Generation Sources in Radial Distribution Networks Using a Hybrid Algorithm. Energies 2018, 11, 628. [Google Scholar] [CrossRef]
- Kumar, M.; Nallagownden, P.; Elamvazuthi, I. Optimal Placement and Sizing of Renewable Distributed Generations and Capacitor Banks into Radial Distribution Systems. Energies 2017, 10, 811. [Google Scholar] [CrossRef]
- Zhang, S.; Cheng, H.; Li, K.; Tai, N.; Wang, D.; Li, F. Multi-objective distributed generation planning in distribution network considering correlations among uncertainties. Appl. Energy 2018, 226, 743–755. [Google Scholar] [CrossRef]
- Foster, J.D.; Berry, A.M.; Boland, N.; Waterer, H. Comparison of Mixed-Integer Programming and Genetic Algorithm Methods for Distributed Generation Planning. IEEE Trans. Power Syst. 2014, 29, 833–843. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J.; Kim, J.; Begovic, M.M. Robust Optimization Based Optimal DG Placement in Microgrids. IEEE Trans. Smart Grid 2014, 5, 2173–2182. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J.; Begovic, M.M. Stochastic DG Placement for Conservation Voltage Reduction Based on Multiple Replications Procedure. IEEE Trans. Power Del. 2015, 30, 1039–1047. [Google Scholar] [CrossRef]
- Luo, L.; Gu, W.; Zhang, X.P.; Cao, G.; Wang, W.; Zhu, G.; You, D.; Wu, Z. Optimal siting and sizing of distributed generation in distribution systems with PV solar farm utilized as STATCOM (PV-STATCOM). Appl. Energy 2018, 210, 1092–1100. [Google Scholar] [CrossRef]
- Santos, S.F.; Fitiwi, D.Z.; Shafie-Khah, M.; Bizuayehu, A.W.; Cabrita, C.M.P.; Catalão, J.P.S. New Multistage and Stochastic Mathematical Model for Maximizing RES Hosting Capacity—Part I: Problem Formulation. IEEE Trans. Sustain. Energy 2017, 8, 304–319. [Google Scholar] [CrossRef]
- Dall’Anese, E.; Giannakis, G.B. Optimal Distributed Generation Placement in Distribution Systems via Semidefinite Relaxation. In Proceedings of the 2013 Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 2013; pp. 369–373. [Google Scholar] [CrossRef]
- Bazrafshan, M.; Gatsis, N.; Dall’Anese, E. Placement and Sizing of Inverter-Based Renewable Systems in Multi-Phase Distribution Networks. IEEE Trans. Power Systems 2018, in press. [Google Scholar] [CrossRef]
- Conejo, A.J.; Carrión, M.; Morales, J.M. Decision Making under Uncertainty in Electricity Markets; Springer: New York, NY, USA, 2010. [Google Scholar]
- Bazrafshan, M.; Gatsis, N. Risk-averse placement and sizing of photovoltaic inverters in radial distribution networks. In Proceedings of the 2015 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015; pp. 885–889. [Google Scholar] [CrossRef]
- Bazrafshan, M.; Gatsis, N. Placing and sizing distributed photovoltaic generators for optimal reactive power compensation. In Proceedings of the 2015 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Orlando, FL, USA, 14–16 December 2015; pp. 1136–1140. [Google Scholar] [CrossRef]
- Turitsyn, K.; Šulc, P.; Backhaus, S.; Chertkov, M. Options for control of reactive power by distributed photovoltaic generators. Proc. IEEE 2011, 99, 1063–1073. [Google Scholar] [CrossRef]
- IEEE Distribution Planning Working Group. Radial distribution test feeders. IEEE Trans. Power Syst. 1991, 6, 975–985. [Google Scholar] [CrossRef]
- Gomez, J.D.; Elnakat, A.; Wright, M.; Keener, J. Analysis of the energy index as a benchmarking indicator of potential energy savings in the San Antonio, Texas single-family residential sector. Energy Efficien. 2014, 8, 577–593. [Google Scholar] [CrossRef]
- Willis, H.L. Power Distribution Planning Reference Book; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Cameron, C.P.; Goodrichg, A.C. The levelized cost of energy for distributed PV: A parametric study. In Proceedings of the 2010 35th IEEE Photovoltaic Specialists Conference, Honolulu, HI, USA, 20–25 June 2010; pp. 529–534. [Google Scholar] [CrossRef]
- Energy Information Administration. Wholesale Electricity and Natural Gas Market Data. Available online: http://www.eia.gov/electricity/wholesale (accessed on 7 February 2017).
- CVX Research, Inc. CVX: Matlab Software for Disciplined Convex Programming, version 2.0. Available online: http://cvxr.com/cvx/ (accessed on 25 November 2017).
- Grant, M.; Boyd, S. Graph implementations for nonsmooth convex programs. In Recent Advances in Learning and Control; Blondel, V., Boyd, S., Kimura, H., Eds.; Lecture Notes in Control and Information Sciences; Springer-Verlag Limited: Cham, Switzerland, 2008; pp. 95–110. [Google Scholar]




| Line | Line | Line | ||||||
|---|---|---|---|---|---|---|---|---|
| () | () | () | () | () | () | |||
| 1 | 0.0005 | 0.0005 | 12 | 0.0013 | 0.0007 | 23 | 0.0002 | 0.0001 |
| 2 | 0.0004 | 0.0004 | 13 | 0.0002 | 0.0002 | 24 | 0.0000 | 0.0000 |
| 3 | 0.0065 | 0.0066 | 14 | 0.0060 | 0.0044 | 25 | 0.0108 | 0.0080 |
| 4 | 0.0012 | 0.0013 | 15 | 0.0000 | 0.0000 | 26 | 0.0002 | 0.0001 |
| 5 | 0.0076 | 0.0077 | 16 | 0.0017 | 0.0013 | 27 | 0.0068 | 0.0053 |
| 6 | 0.0060 | 0.0061 | 17 | 0.0008 | 0.0006 | 28 | 0.0014 | 0.0011 |
| 7 | 0.0001 | 0.0001 | 18 | 0.0014 | 0.0011 | 29 | 0.0006 | 0.0004 |
| 8 | 0.0007 | 0.0004 | 19 | 0.0003 | 0.0002 | 30 | 0.0001 | 0.0001 |
| 9 | 0.0205 | 0.0109 | 20 | 0.0001 | 0.0001 | 31 | 0.0007 | 0.0004 |
| 10 | 0.0059 | 0.0031 | 21 | 0.0004 | 0.0003 | 32 | 0.0109 | 0.0408 |
| 11 | 0.0030 | 0.0022 | 22 | 0.0011 | 0.0008 | 33 | 0.0021 | 0.0022 |
| Bus | Peak | Peak | Bus | Peak | Peak |
|---|---|---|---|---|---|
| () | () | () | () | ||
| 3 | 0.1100 | 0.0580 | 20 | 0.1340 | 0.0820 |
| 5 | 0.0320 | 0.0160 | 22 | 0.8280 | 0.6400 |
| 10 | 0.0680 | 0.0340 | 23 | 0.0900 | 0.0460 |
| 11 | 0.2700 | 0.1400 | 24 | 0.1660 | 0.1180 |
| 12 | 0.0100 | 0.0040 | 28 | 0.0080 | 0.0040 |
| 13 | 0.0800 | 0.0400 | 29 | 0.0300 | 0.0140 |
| 14 | 0.0080 | 0.0040 | 30 | 0.4120 | 0.2420 |
| 15 | 0.1040 | 0.0460 | 32 | 0.0040 | 0.0020 |
| 17 | 0.0640 | 0.0340 | Shunt Capacitors () | ||
| 18 | 0.1640 | 0.0860 | 22 | 0.6 | |
| 19 | 0.0560 | 0.0280 | 24 | 0.9 | |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 11,540 | |||
| C | |||
| d | |||
| 3 | see Section 4 |
| Bus | Bus | Bus | Bus | Bus | |||||
|---|---|---|---|---|---|---|---|---|---|
| 3 | 9 | 19 | 5 | 13 | 7 | 28 | 1 | 12 | 1 |
| 5 | 3 | 20 | 7 | 14 | 1 | 29 | 3 | 24 | 4 |
| 10 | 5 | 22 | 1 | 15 | 1 | 30 | 24 | 18 | 14 |
| 11 | 22 | 23 | 8 | 17 | 5 | 32 | 1 |
| Month | Average POA | Average no. | Scenario |
|---|---|---|---|
| Irradiance | of Hours with | ||
| Non-Zero Irradiance | |||
| January | 3.91 | 11.19 | 0.349 |
| February | 4.68 | 12 | 0.39 |
| March | 5.32 | 12.77 | 0.41 |
| April | 5.55 | 13.2 | 0.420 |
| May | 5.87 | 14.838 | 0.395 |
| June | 6.29 | 15 | 0.42 |
| July | 6.83 | 14.70 | 0.46 |
| August | 6.57 | 13.77 | 0.477 |
| September | 5.87 | 13 | 0.45 |
| October | 5.40 | 12.45 | 0.43 |
| November | 4.47 | 11.33 | 0.39 |
| December | 3.78 | 11 | 0.34 |
| # of Installations | Max. of Average | Max. of Average |
|---|---|---|
| Allowed per node | Panel Area | Inverter Capacity |
| 100.00 | 39.65 | |
| 83.95 | 33.25 | |
| 69.95 | 27.70 | |
| 32.32 | 12.80 | |
| 32.32 | 12.80 |
| Optimal | Inverter | DC | Thermal | |
|---|---|---|---|---|
| Value | Cost | Cost | Loss Cost | |
| 1,891,670 | 262,230 | 1,629,400 | 57.4959 | |
| 1,576,210 | 218,530 | 1,357,600 | 60.6561 | |
| 1,576,140 | 218,510 | 1,357,600 | 60.6873 | |
| 1,576,090 | 218,520 | 1,357,500 | 60.6467 | |
| 1,576,090 | 218,520 | 1,357,500 | 60.6478 |
| Method | Max. of Average | Max. of Average |
|---|---|---|
| Panel Area | Inverter Capacity | |
| Optimal | 32.32 | 12.8 |
| Alternative | 93.6115 | 13.6 |
| Method | Optimal | Inverter | DC | Thermal Loss |
|---|---|---|---|---|
| Value | Cost | Cost | Cost | |
| Optimal | 1,576,090 | 219,000 | 136,000 | 60.6702 |
| Alternative | 3,361,030 | 187,500 | 3,173,500 | 61.7727 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bazrafshan, M.; Yalamanchili, L.; Gatsis, N.; Gomez, J. Stochastic Planning of Distributed PV Generation. Energies 2019, 12, 459. https://doi.org/10.3390/en12030459
Bazrafshan M, Yalamanchili L, Gatsis N, Gomez J. Stochastic Planning of Distributed PV Generation. Energies. 2019; 12(3):459. https://doi.org/10.3390/en12030459
Chicago/Turabian StyleBazrafshan, Mohammadhafez, Likhitha Yalamanchili, Nikolaos Gatsis, and Juan Gomez. 2019. "Stochastic Planning of Distributed PV Generation" Energies 12, no. 3: 459. https://doi.org/10.3390/en12030459
APA StyleBazrafshan, M., Yalamanchili, L., Gatsis, N., & Gomez, J. (2019). Stochastic Planning of Distributed PV Generation. Energies, 12(3), 459. https://doi.org/10.3390/en12030459





