Numerical Analysis of Dry Ice Blasting Convergent-Divergent Supersonic Nozzle
Abstract
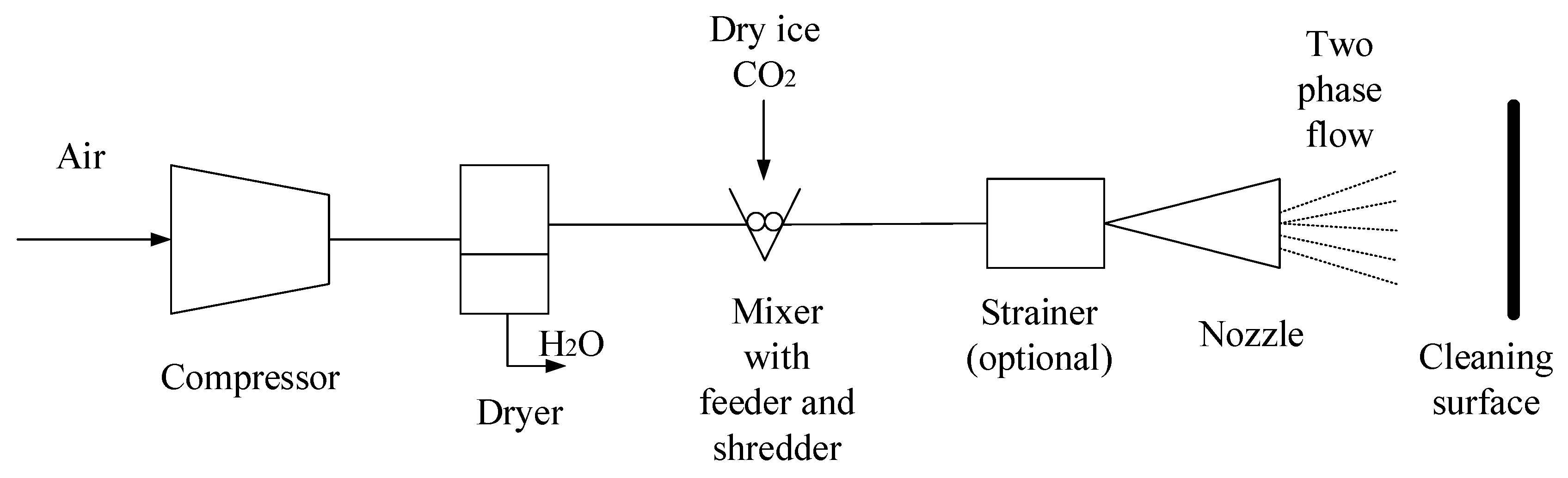
1. Dry Ice Blasting
2. Mathematical Model
2.1. General Equations
2.2. Turbulence Model
2.3. Discrete Phase Model
3. Model Implementation
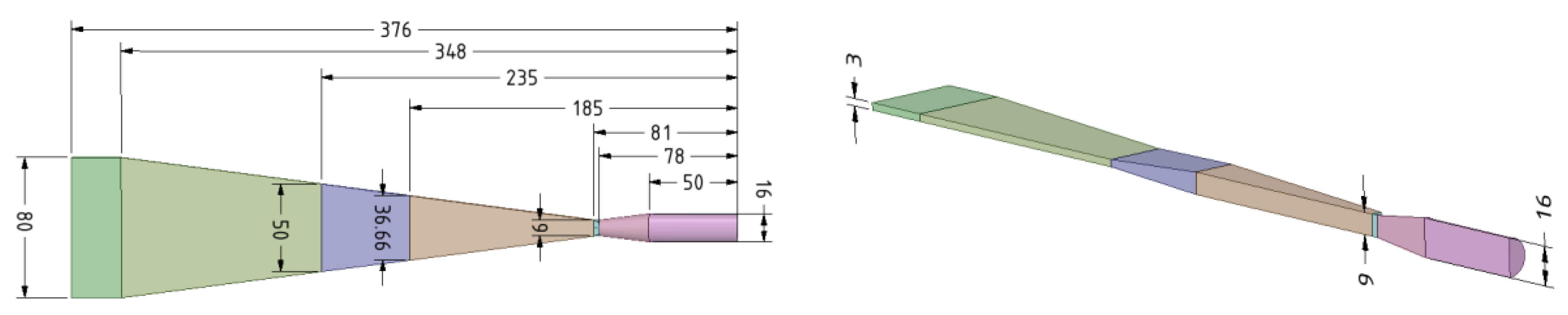
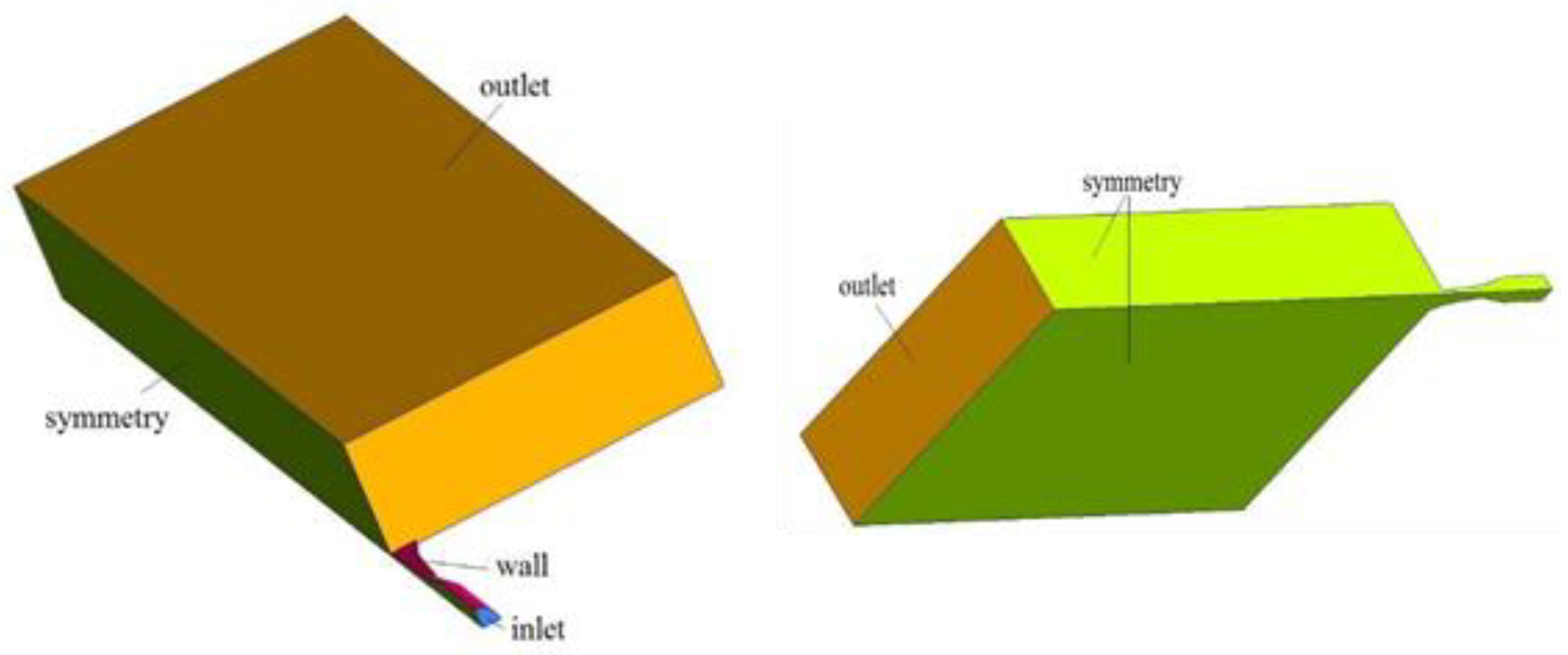
3.1. Geometry
3.2. Computational Fluid Dynamics (CFD) Grid
3.3. Boundary Conditions and General Settings
3.4. Model Validation
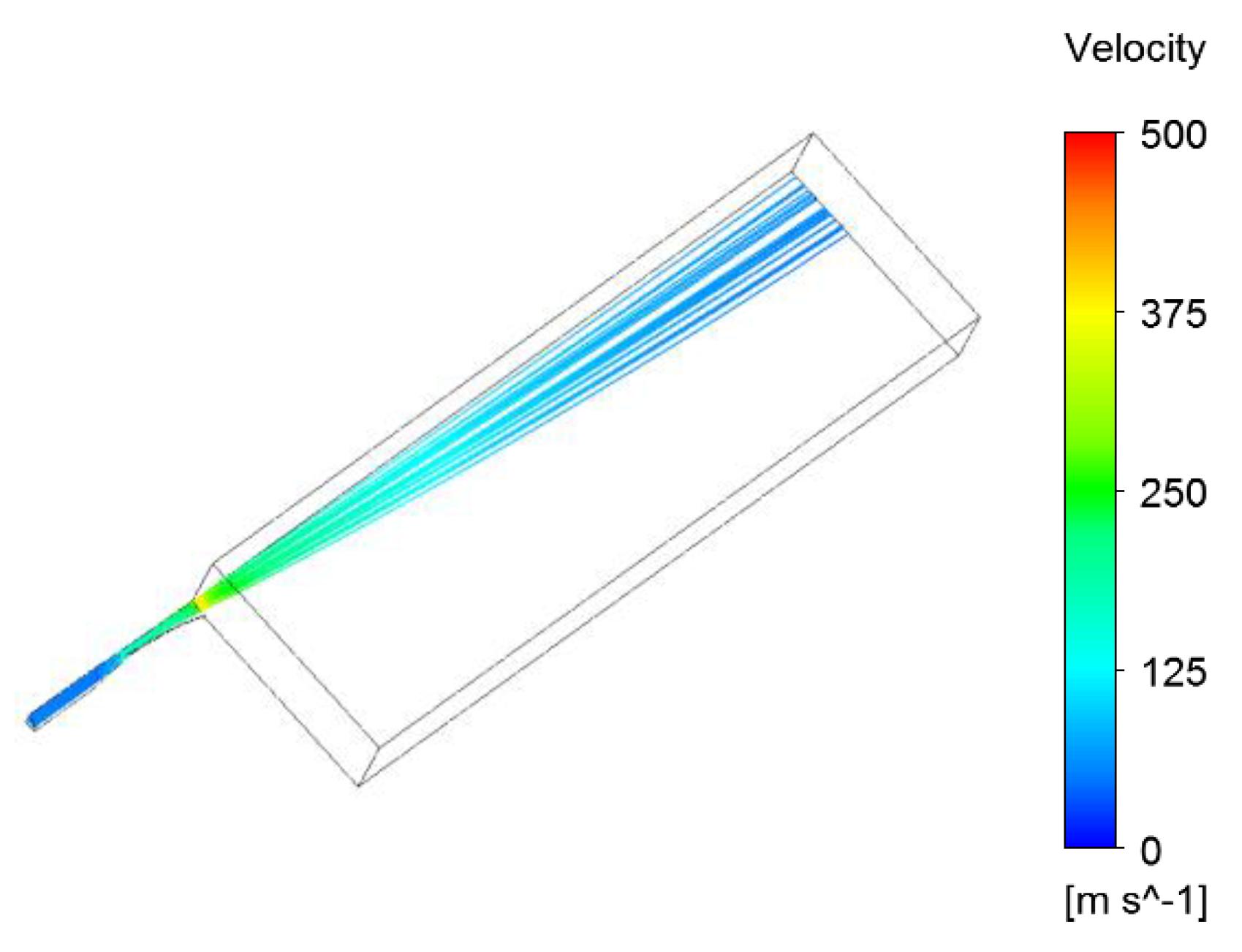
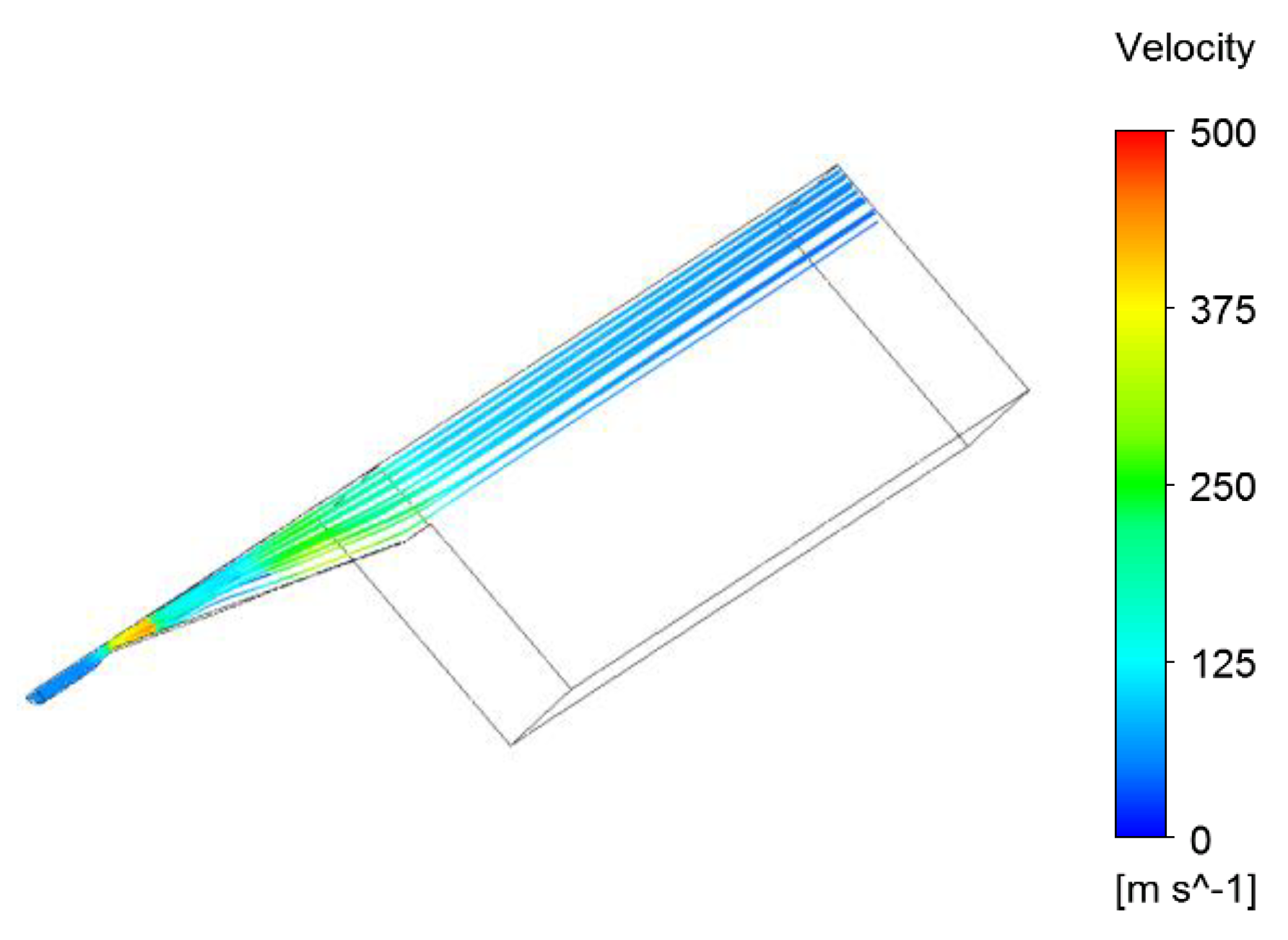
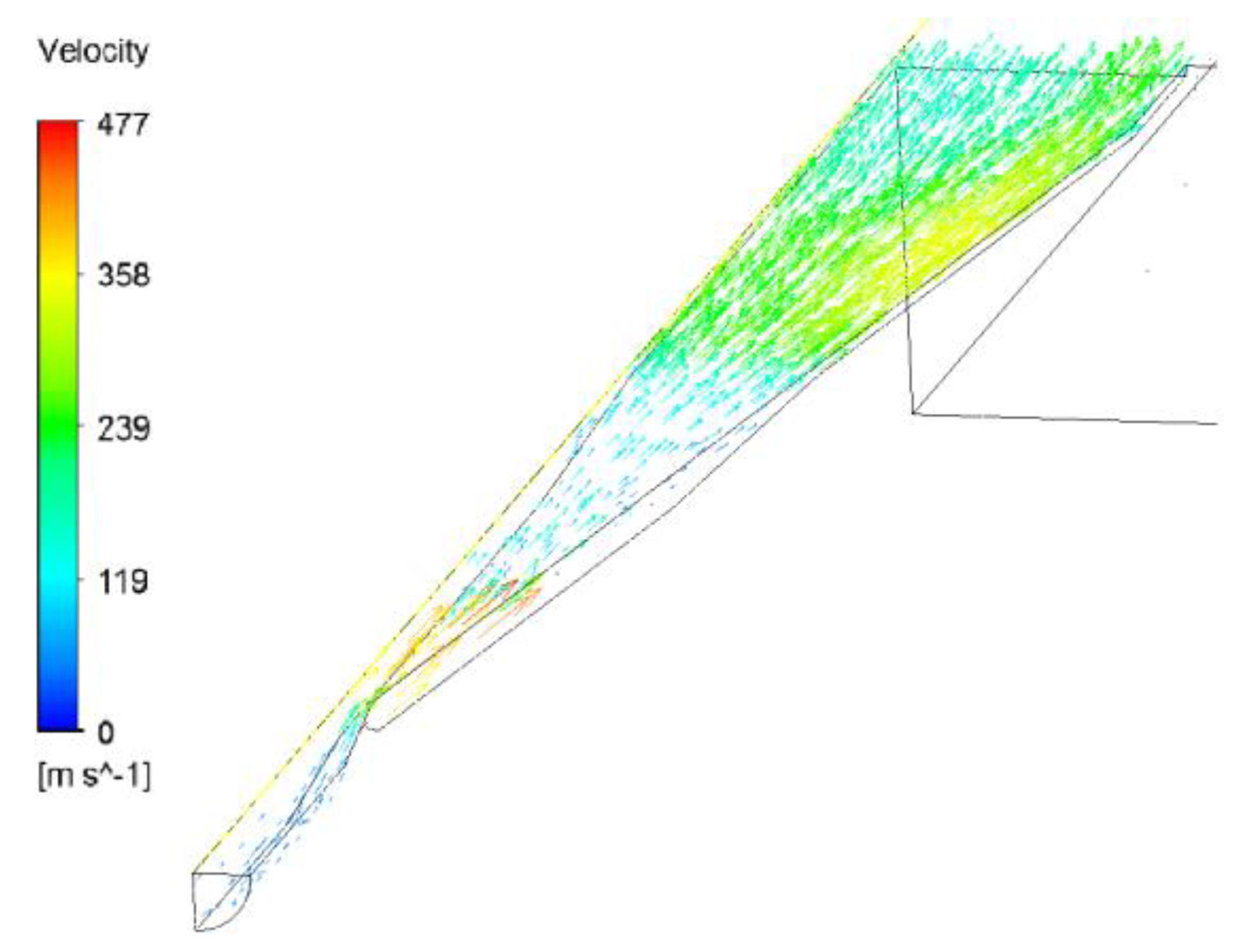
4. Results and Analysis
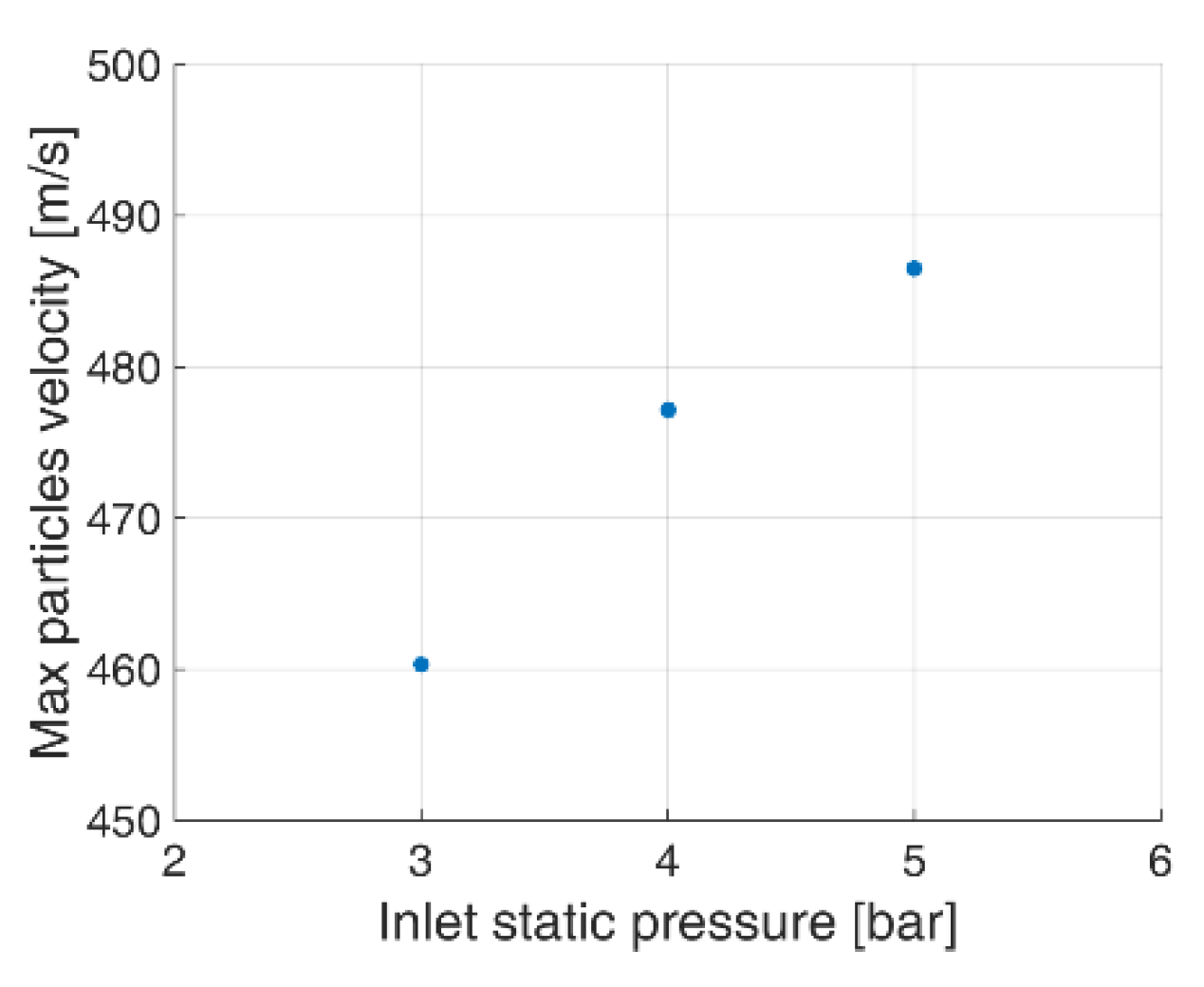
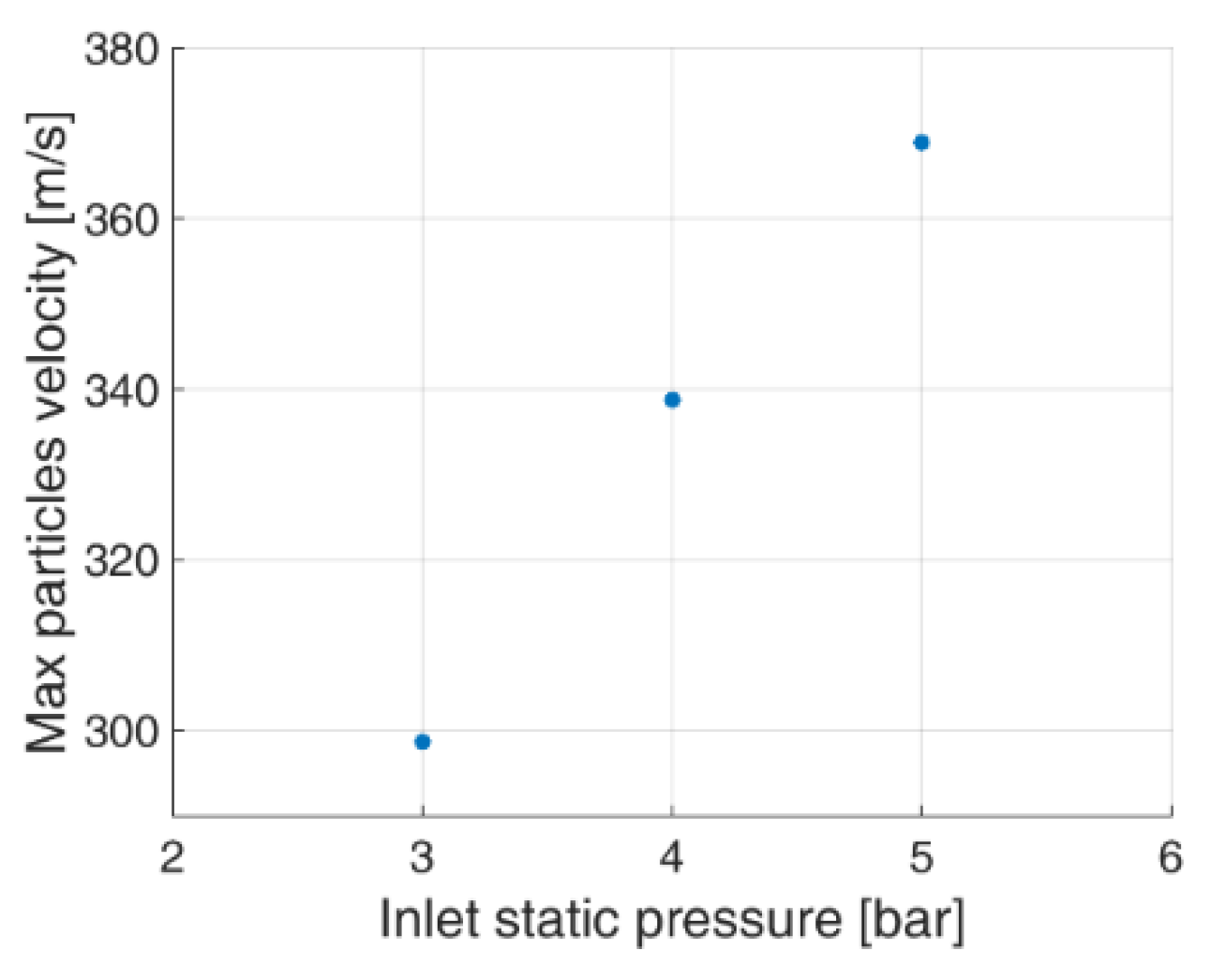
4.1. Inlet Pressure Impact
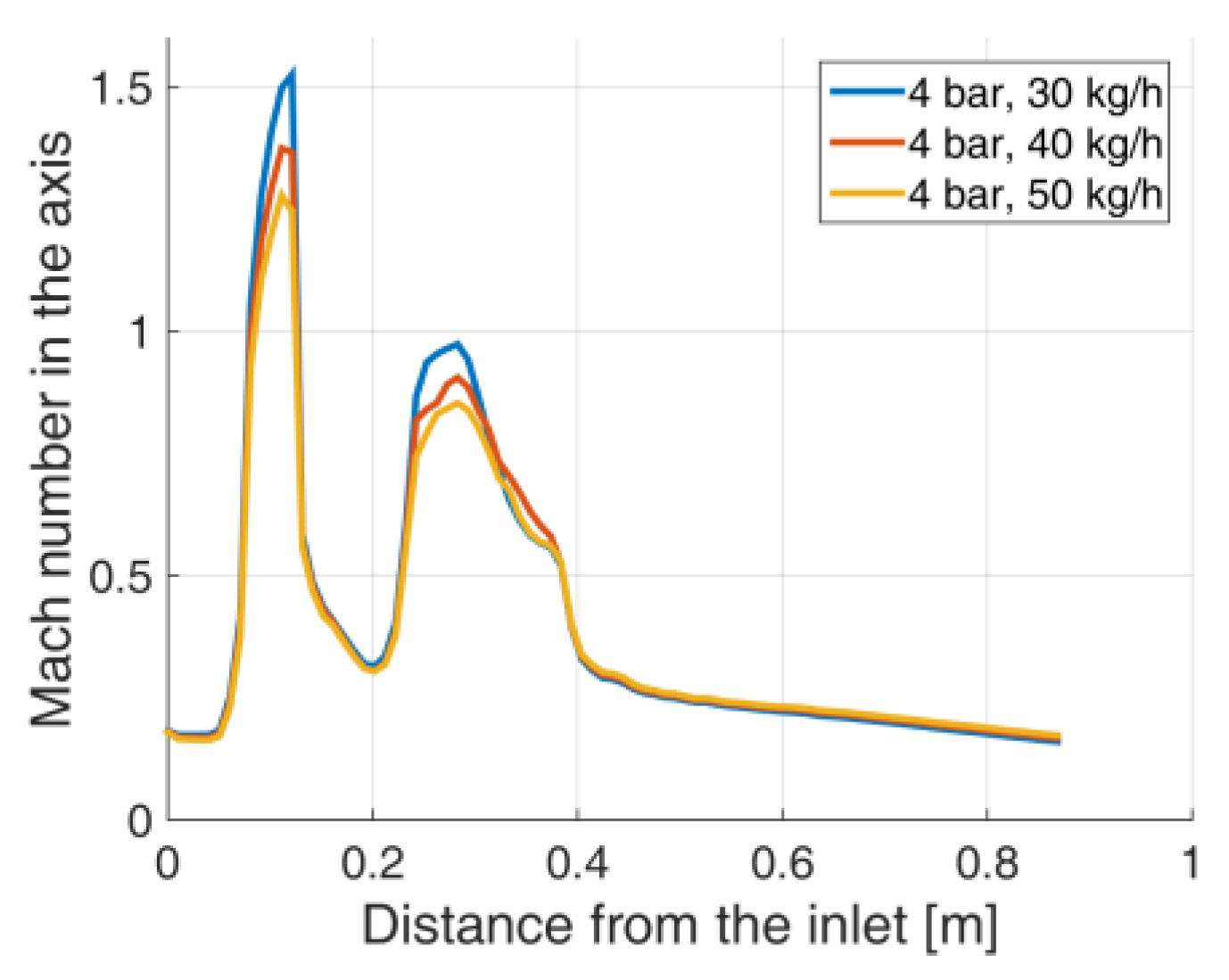
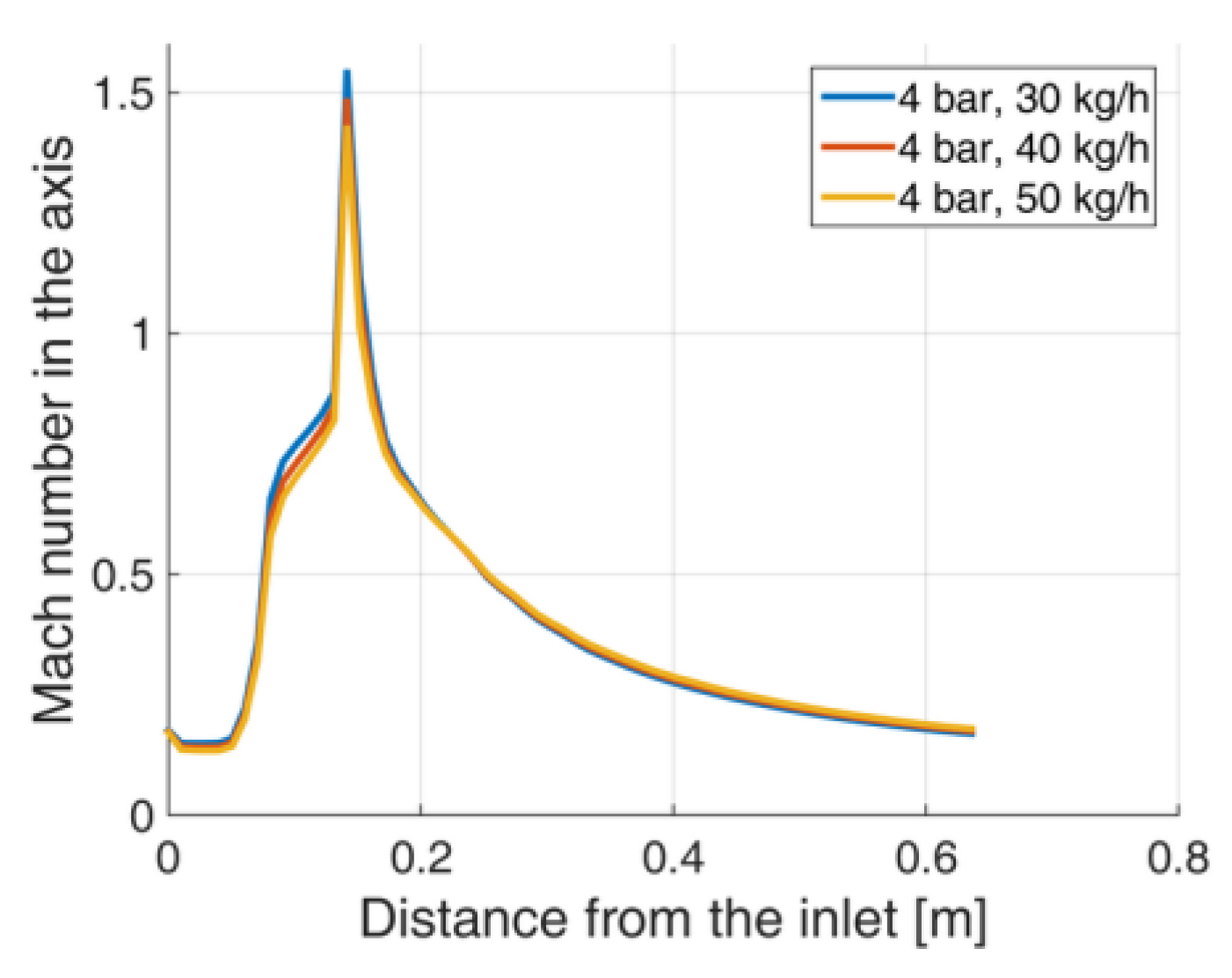
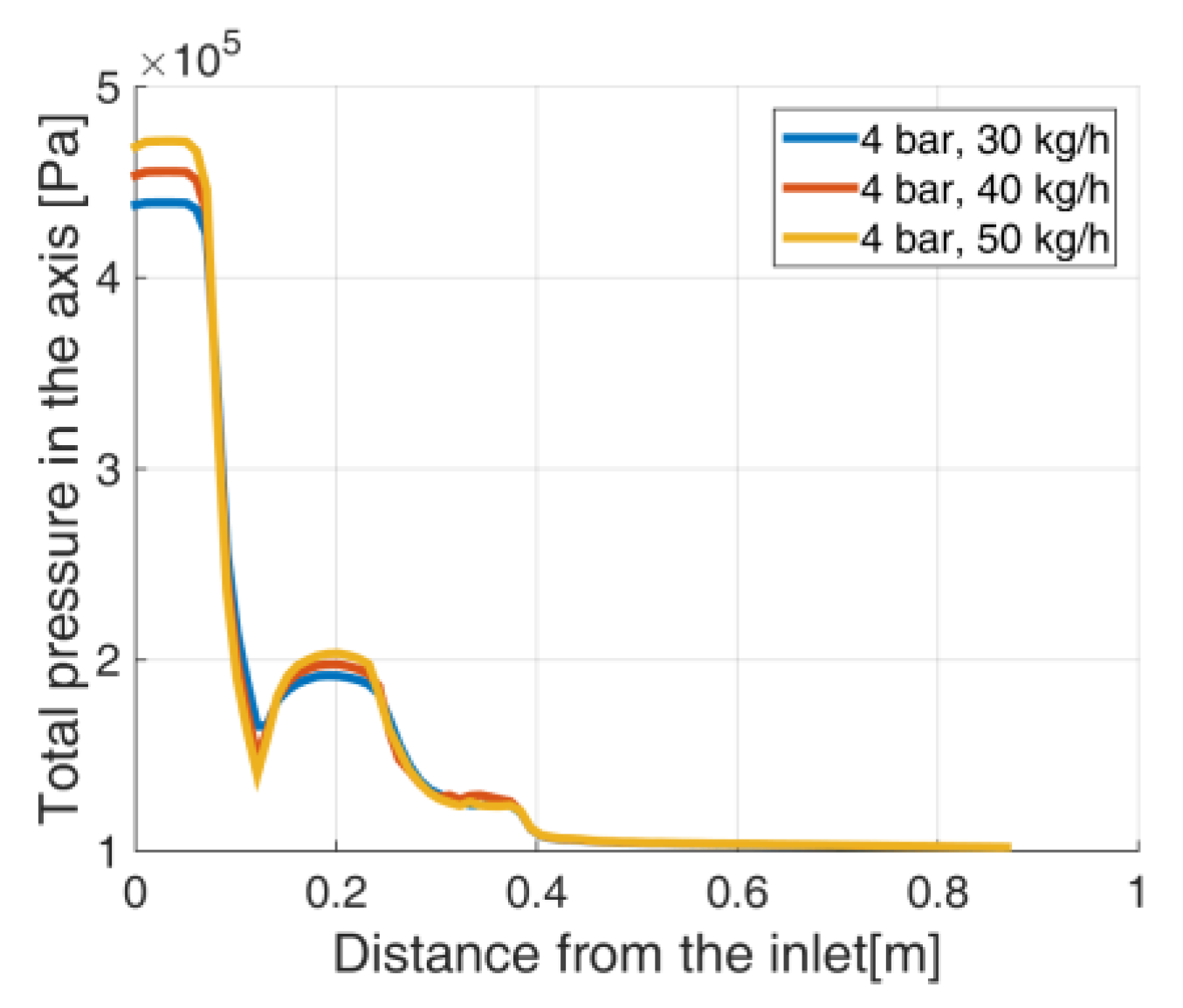
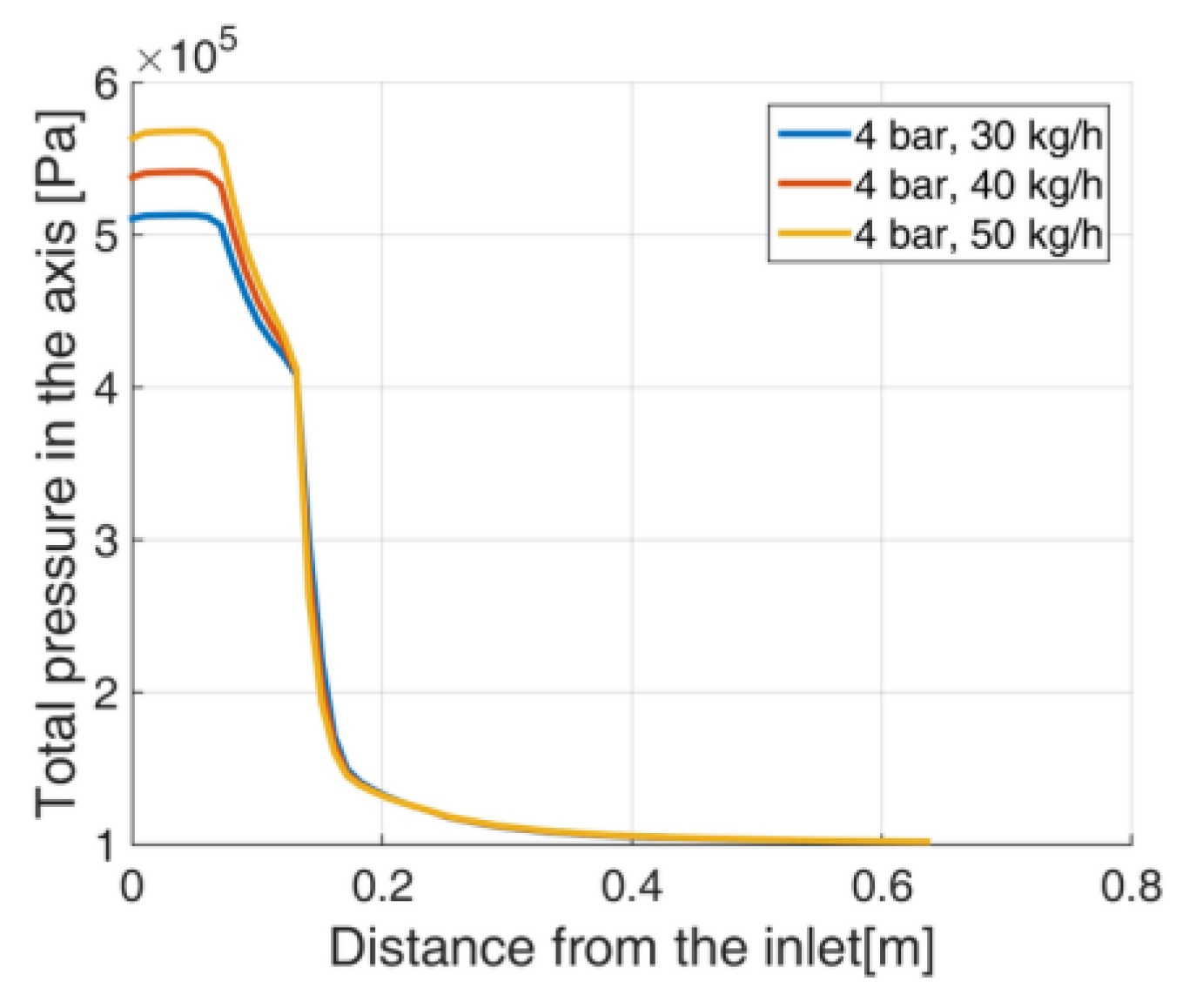
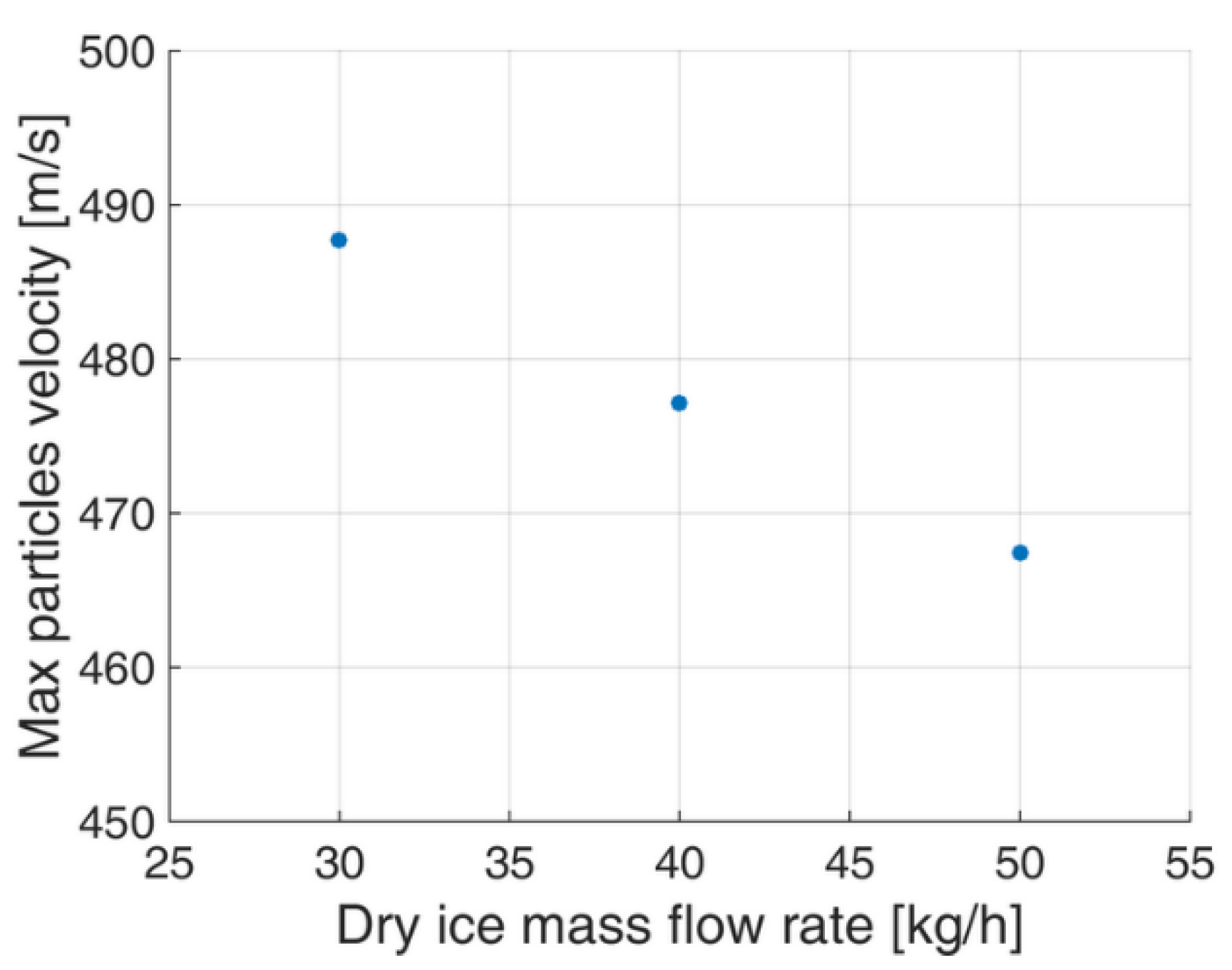
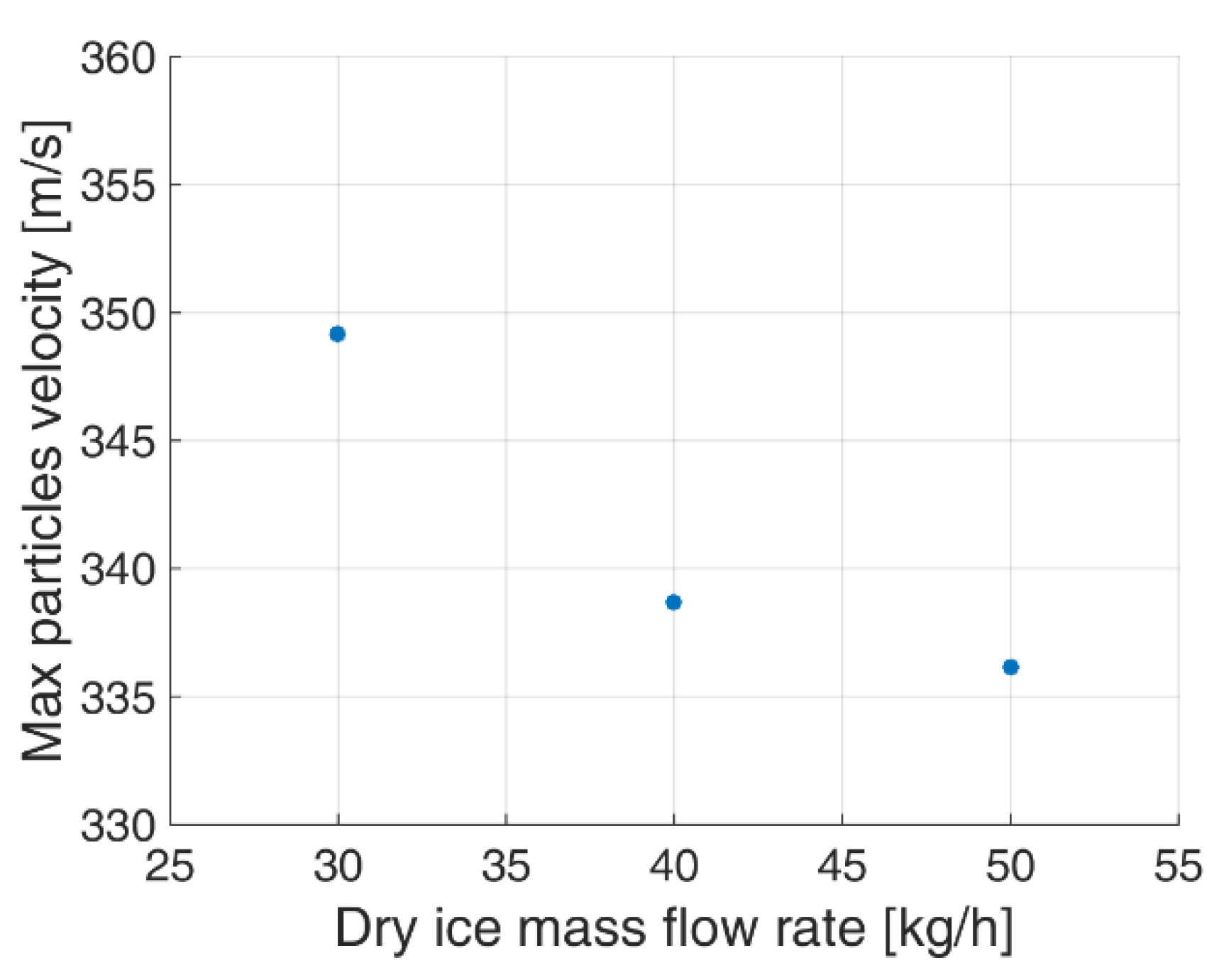
4.2. Dry Ice Mass Flow Rate Impact
5. Outcomes
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Dirac delta function | |
| fluid effective viscosity, [Pa·s] | |
| molecular viscosity, [Pa·s] | |
| turbulent eddy viscosity, [Pa·s] | |
| fluid density, [kg·m−3] | |
| viscous stress tensor, [N·m−2] | |
| inlet cross section area, [m−2] | |
| critical cross section area, [m−2] | |
| total enthalpy, [J·kg−1] | |
| thermal conductivity, [W·m−1·K−1] | |
| drag coefficient | |
| fluid pressure, [Pa] | |
| gas constant, [J·mol−1·K−1] | |
| relative Reynolds number | |
| time, [s] | |
| fluid temperature, [K] | |
| velocity component in the direction, [m·s−1] | |
| local particle–fluid relative velocity, [m·s−1] | |
| Coordinate |
References
- Kumar, P.G.S. Dry Ice Cleaning to Improvise Dielectric Features of High Voltage Windings in Turbine Generators. In Proceedings of the 2013 IEEE 1st International Conference on Condition Assessment Techniques in Electrical Systems (CATCON), Kolkata, India, 6–8 December 2013. [Google Scholar]
- Barnett, D.M. CO2 (DRY ICE) CLEANING SYSTEM. In Proceedings of the Marshall Space Flight Center, Aerospace Environmental Technology Conference 391–398 (SEE N95-31746 11–23), Loganville, GA, USA, 1 March 1995. [Google Scholar]
- Zhou, W.; Liu, M.; Liu, S.; Peng, M.; Yu, J.; Zhou, C. On the mechanism of insulator cleaning using dry ice. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1715–1722. [Google Scholar] [CrossRef]
- Sherman, R. Dry surface cleaning using CO2 snow. J. Vac. Sci. Technol. B 1991, 9, 1970–1977. [Google Scholar] [CrossRef]
- Máša, V.; Kuba, P. Efficient use of compressed air for dry ice blasting. J. Clean. Prod. 2016, 111, 76–84. [Google Scholar] [CrossRef]
- Górecki, J.; Malujda, I.; Wilczyński, D. The influence of geometrical parameters of the forming channel on the boundary value of the axial force in the agglomeration process of dry ice. MATEC Web Conf. 2019, 254, 05001. [Google Scholar] [CrossRef]
- Zhang, X.; Yamaguchi, H. An experimental study on heat transfer of CO 2 solid e gas two phase flow with dry ice sublimation. Int. J. Therm. Sci. 2011, 50, 2228–2234. [Google Scholar] [CrossRef]
- Liu, Y.; Maruyama, H.; Matsusaka, S.; Liu, Y.; Maruyama, H.; Matsusaka, S. Effect of Particle Impact on Surface Cleaning Using Dry Ice Jet Effect of Particle Impact on Surface Cleaning Using. Aerosol Sci. Technol. 2011, 45, 1519–1527. [Google Scholar] [CrossRef]
- Liu, Y.H.; Hirama, D.; Matsusaka, S. Particle removal process during application of impinging dry ice jet. Powder Technol. 2012, 217, 607–613. [Google Scholar] [CrossRef]
- Spur, G.; Elbing, F.; Management, F. Development of flexible automatic disassembly processes and cleaning technologies for the recycling of consumer goods. In Proceedings of the 2001 IEEE International Symposium on Assembly and Task Planning (ISATP2001). Assembly and Disassembly in the Twenty-FIrst Century, Fukuoka, Japan, 29 May 2001; pp. 442–446. [Google Scholar]
- Spur, G.; Uhlmann, E.; Elbing, F. Dry-ice blasting for cleaning: Process, optimization and application. Wear 1999, 233, 402–411. [Google Scholar] [CrossRef]
- Masa, V.; Kuba, P.; Petrilák, D.; Lokaj, J. Decrease in Consumption of Compressed Air in Dry Ice Blasting Machine. Chem. Eng. 2014, 39, 805–810. [Google Scholar]
- Elbing, F.; Anagreh, N.; Dorn, L.; Uhlmann, E. Dry ice blasting as pretreatment of aluminum surfaces to improve the adhesive strength of aluminum bonding joints. Int. J. Adhes. Adhes. 2003, 23, 69–79. [Google Scholar] [CrossRef]
- Dong, S.; Song, B.; Hansz, B.; Liao, H.; Coddet, C. Study on the Mechanism of Adhesion Improvement Using Dry-Ice Blasting for Plasma-Sprayed Al2 O3 Coatings. J. Therm. Spray Technol. 2013, 22, 213–220. [Google Scholar] [CrossRef]
- Dong, S.; Liao, H. Substrate pre-treatment by dry-ice blasting and cold spraying of titanium. Surf. Eng. 2016, 34, 173–180. [Google Scholar] [CrossRef]
- Pougatch, K.; Salcudean, M.; Chan, E.; Knapper, B. Modelling of compressible gas-liquid flow in a convergent-divergent nozzle. Chem. Eng. Sci. 2008, 63, 4176–4188. [Google Scholar] [CrossRef]
- Mat, M.N.H.; Asmuin, N. Optimum design of nozzle geometry of dry ice blasting using CFD for the reduction of noise emission. Int. J. Integr. Eng. 2018, 10, 130–135. [Google Scholar] [CrossRef]
- Mat, M.N.H.; Asmuin, N.Z.; Hasan, N.H.; Zakaria, H.; Rahman, M.F.; Khairulfuaad, R.; Jabbar, B.A. Optimizing Dry Ice Blasting Nozzle Divergent Length using CFD for Noise Reduction. CFD Lett. 2019, 11, 18–26. [Google Scholar]
- Dong, S.J.; Song, B.; Hansz, B.; Liao, H.L.; Coddet, C. Modelling of dry ice blasting and its application in thermal spray. Mater. Res. Innov. 2012, 16, 61–66. [Google Scholar] [CrossRef]
- Bulat, M.P.; Bulat, P.V. Comparison of Turbulence Models in the Calculation of Supersonic Separated Flows. World Appl. Sci. J. 2013, 27, 1263–1266. [Google Scholar]
- Bartosiewicz, Y. Numerical and experimental investigations on supersonic ejectors. Int. J. Heat Fluid Flow 2005, 26, 56–70. [Google Scholar] [CrossRef]
- Innovative Turbulence Modeling: SST Model in ANSYS CFX ®; ANSYS Inc.: Canonsburg, PA, USA, 2006.
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model; Gell Brothers, Inc: Cocoa, FL, USA, 2003. [Google Scholar]
- Bartosiewicz, Y.; Aidoun, Z. CFD-Experiments Integration in the Evaluation of Six Turbulence Models for Supersonic Ejectors Modeling. In Proceedings of the Integrating CFD and Experiments Conference, Glasgow, UK, 8–9 September 2003. [Google Scholar]
- Karunarathne, S.S.; Tokheim, L. Comparison of the Influence of Drag Models in CFD Simulation of Particle Mixing and Segregation in a Rotating Cylinder. In Proceedings of the 58th Conference on Simulation and Modelling (SIMS 58), Reykjavik, Iceland, 25–27 September 2017. [Google Scholar]
- ANSYS. ANSYS FLUENT Theory Guide. Knowl. Creat. Diffus. Util. 2010, 15317, 724–746. [Google Scholar]
- Dzido, A.; Krawczyk, P.; Badyda, K. Operational parameters influence on the dry-ice blasting cleaning efficiency. Rynek Energii 2019, 4, 85–90. [Google Scholar]
- Munday, D.; Gutmark, E.; Liu, J.; Kailasanath, K. Flow structure and acoustics of supersonic jets from conical convergent-divergent nozzles. Phys. Fluids 2011, 23, 116102. [Google Scholar] [CrossRef]
- Mikołajczak, A.; Krawczyk, P.; Stępień, M.; Badyda, K. Preliminary specification of the dry ice blasting converging-divergent nozzle parameters basing on the standard (analytical) methods. Rynek Energii. 2018. Available online: https://yadda.icm.edu.pl/baztech/element/bwmeta1.element.baztech-b8468ec0-87c0-4d32-9d2e-8f130ebb4192 (accessed on 16 December 2019).

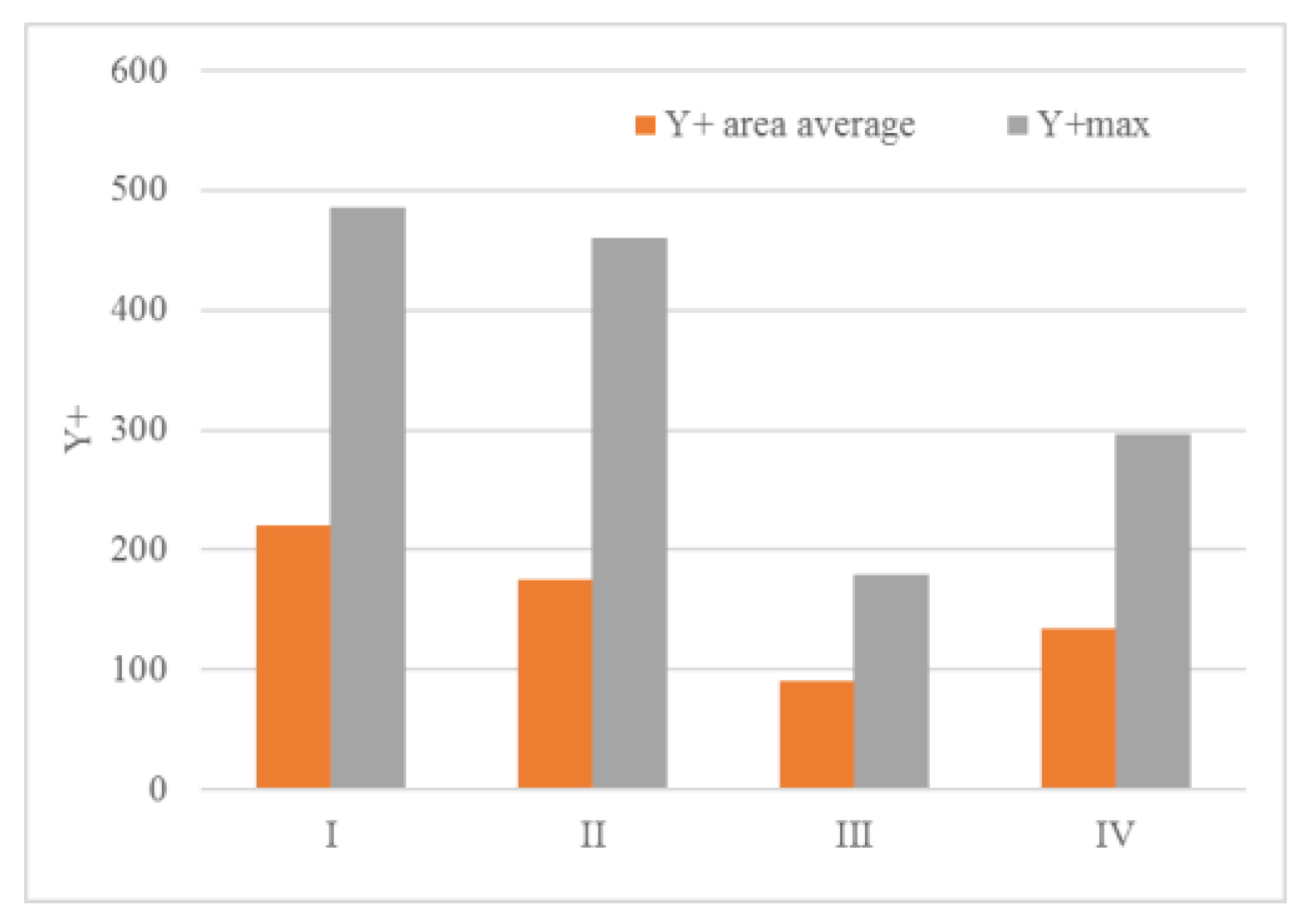
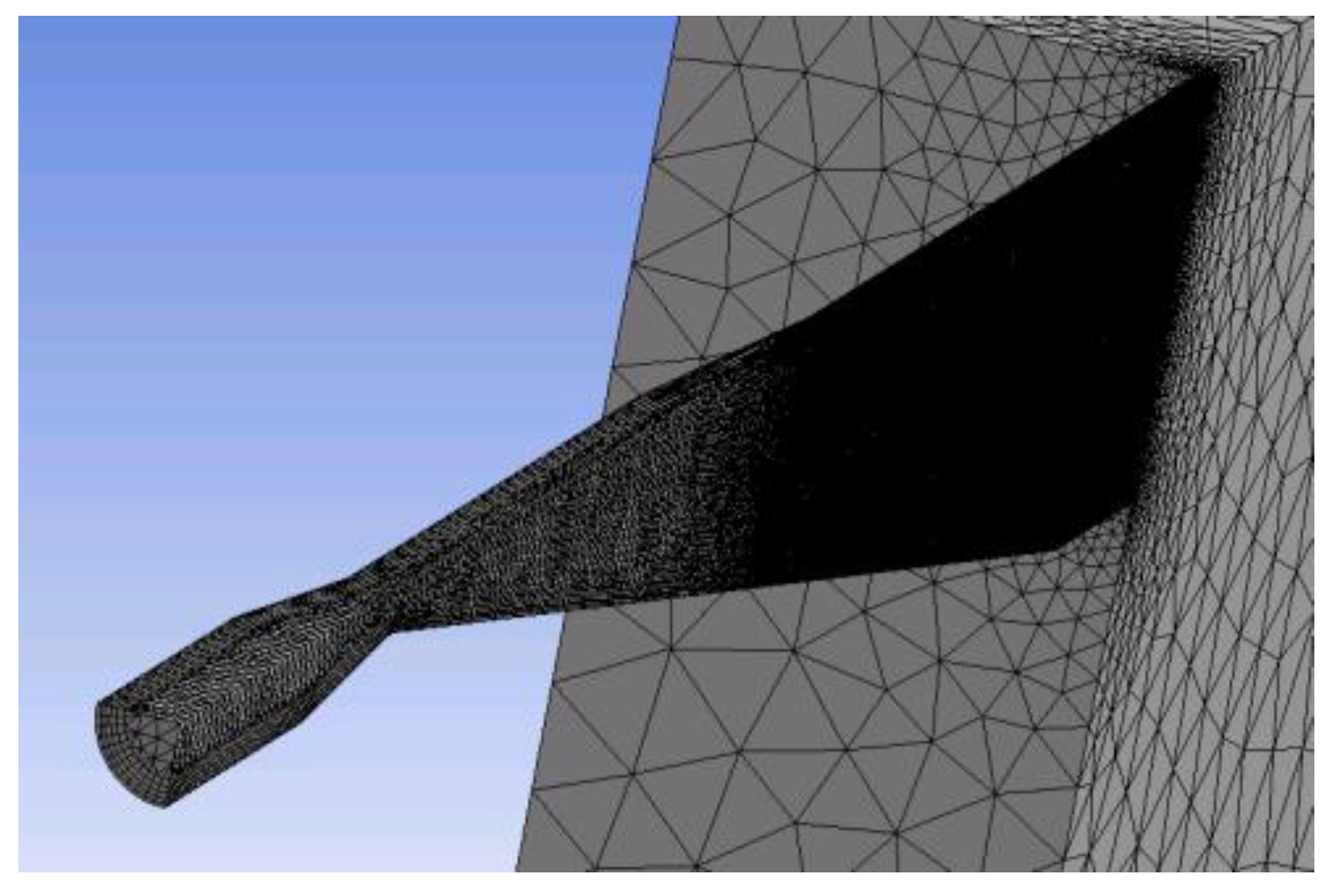








| Grid | Number of Elements | Method |
|---|---|---|
| I | 281,054 | Automatic, nozzle wall sizing |
| II | 473,883 | Automatic, nozzle wall sizing |
| III | 542,757 | Automatic, nozzle wall sizing and inflation |
| IV | 903,234 | Automatic, nozzle wall sizing |
| Geometry | Number of Elements | Number of Nodes | Average Skewness | Average Element Quality | Average Aspect Ratio |
|---|---|---|---|---|---|
| A | 370,365 | 126,681 | 0.24975 | 0.7574 | 2.1583 |
| B | 542,757 | 172,610 | 0.22145 | 0.72519 | 2.5591 |
| Surface | Boundary Condition |
|---|---|
| Inlet | Normal speed and relative static pressure, injection of surface particles |
| Nozzle wall | Adiabatic wall |
| Sym1, Sym2 | Symmetry |
| Outlet | Opening |
| Test | Velocity from the Model [m/s] | Cleaning Speed [cm2/s] | Cleaning Speed/u2 Ratio | ||
|---|---|---|---|---|---|
| 15 cm | 30 cm | 15 cm | 30 cm | ||
| I | 75.77 | 58.94 | 11.95 | 6.63 | 1.09 |
| II | 115.48 | 85.8 | 3.45 | 1.72 | 1.10 |
| No. | Infinite Static Pressure | Inlet Relative Static Pressure | Dry Ice Mass Flow Rate |
|---|---|---|---|
| 1. | 3.0 bar | 292,735.41 Pa | 40.0 kg/h |
| 2. | 4.0 bar | 390,303.93 Pa | 30.0 kg/h |
| 3. | 4.0 bar | 390,303.93 Pa | 40.0 kg/h |
| 4. | 4.0 bar | 390,303.93 Pa | 50.0 kg/h |
| 5. | 5.0 bar | 487,892.35 Pa | 40.0 kg/h |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dzido, A.; Krawczyk, P.; Kurkus-Gruszecka, M. Numerical Analysis of Dry Ice Blasting Convergent-Divergent Supersonic Nozzle. Energies 2019, 12, 4787. https://doi.org/10.3390/en12244787
Dzido A, Krawczyk P, Kurkus-Gruszecka M. Numerical Analysis of Dry Ice Blasting Convergent-Divergent Supersonic Nozzle. Energies. 2019; 12(24):4787. https://doi.org/10.3390/en12244787
Chicago/Turabian StyleDzido, Aleksandra, Piotr Krawczyk, and Michalina Kurkus-Gruszecka. 2019. "Numerical Analysis of Dry Ice Blasting Convergent-Divergent Supersonic Nozzle" Energies 12, no. 24: 4787. https://doi.org/10.3390/en12244787
APA StyleDzido, A., Krawczyk, P., & Kurkus-Gruszecka, M. (2019). Numerical Analysis of Dry Ice Blasting Convergent-Divergent Supersonic Nozzle. Energies, 12(24), 4787. https://doi.org/10.3390/en12244787






