Optimal Timing of Onshore Wind Repowering in Germany under Policy Regime Changes: A Real Options Analysis
Abstract
1. Introduction
2. Related Literature
3. Wind Energy and Repowering in Germany
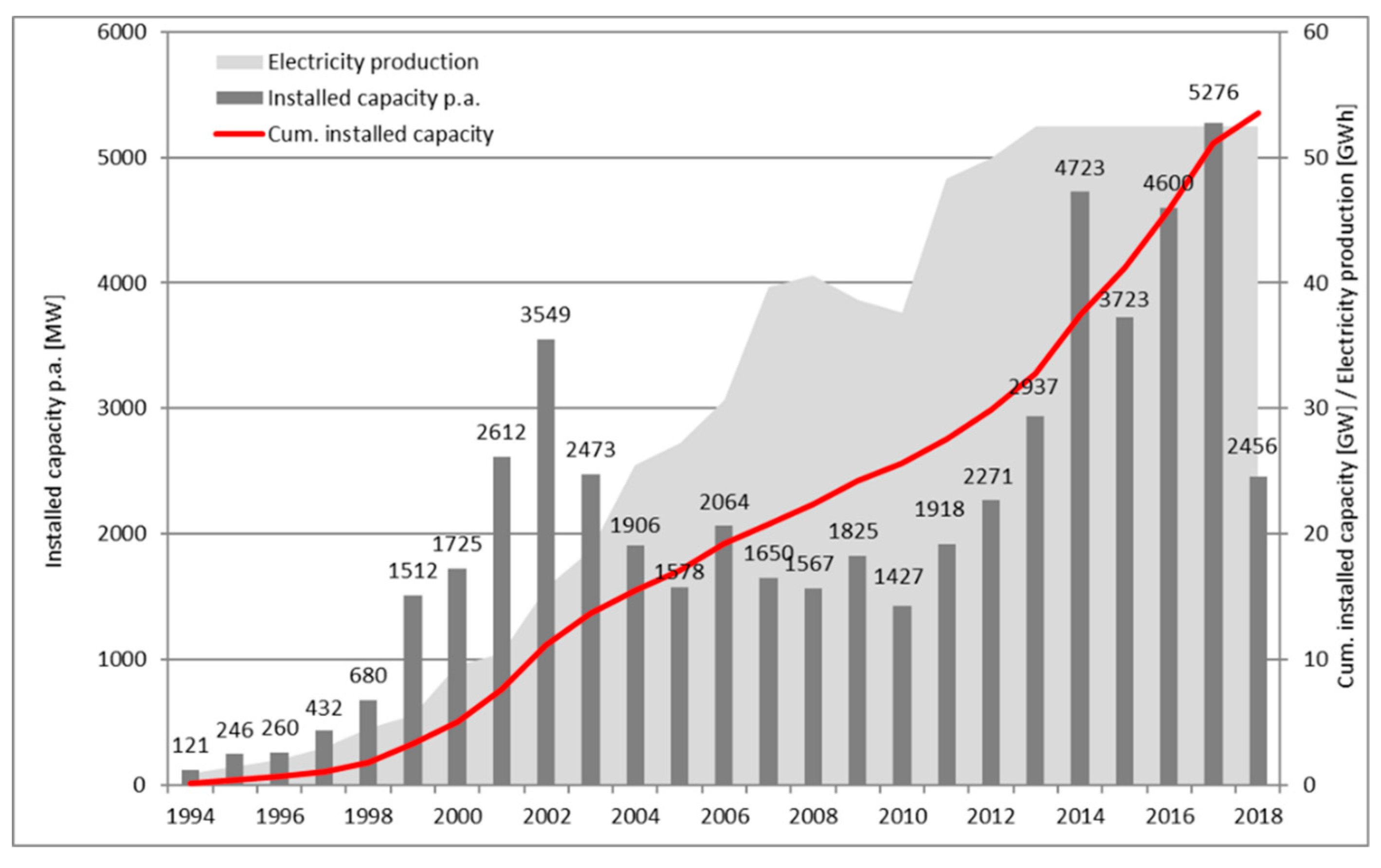
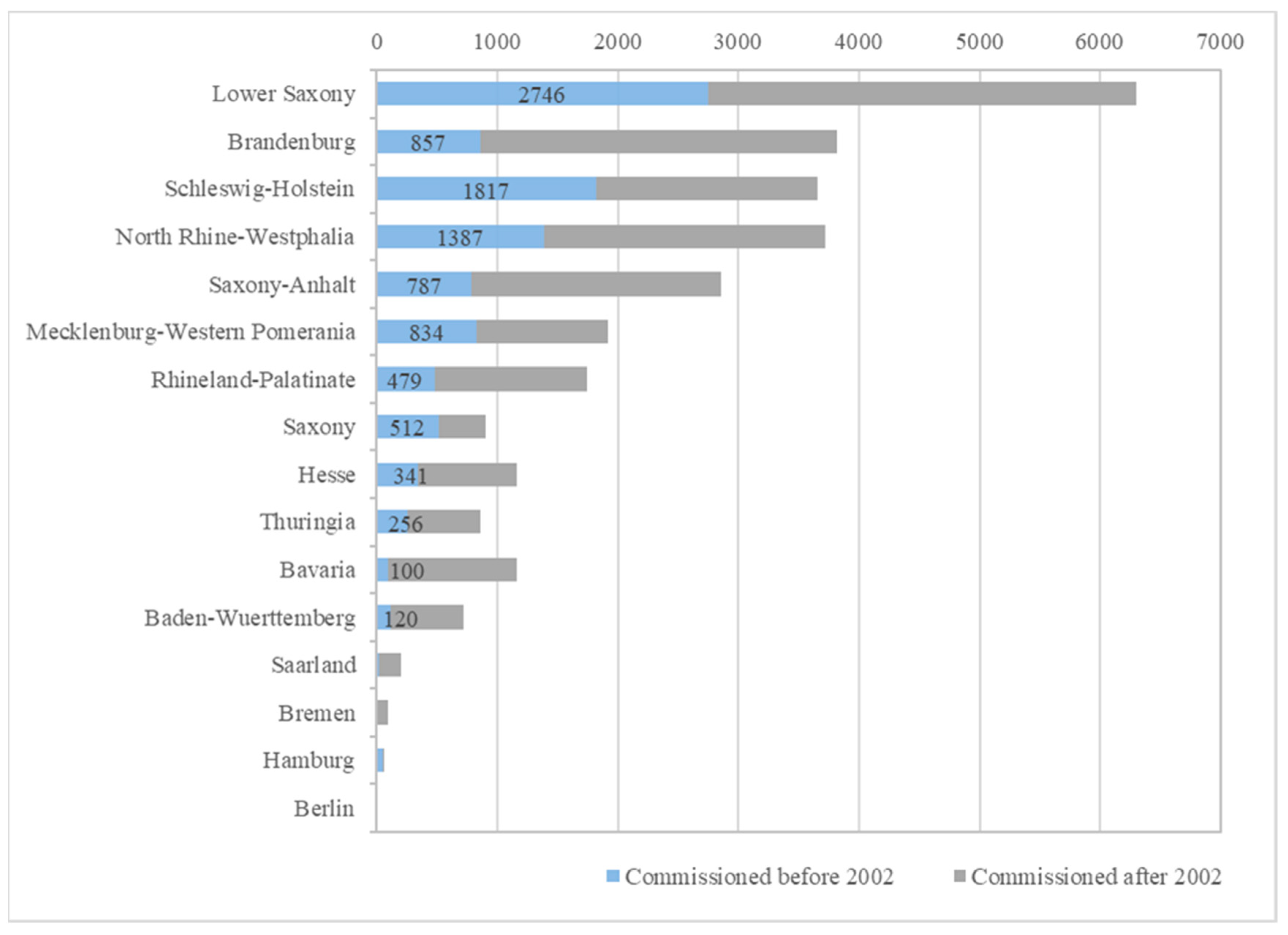
3.1. Installed Onshore Wind Capacity and Technological Development
3.2. Purpose and Effects of Repowering
- ○
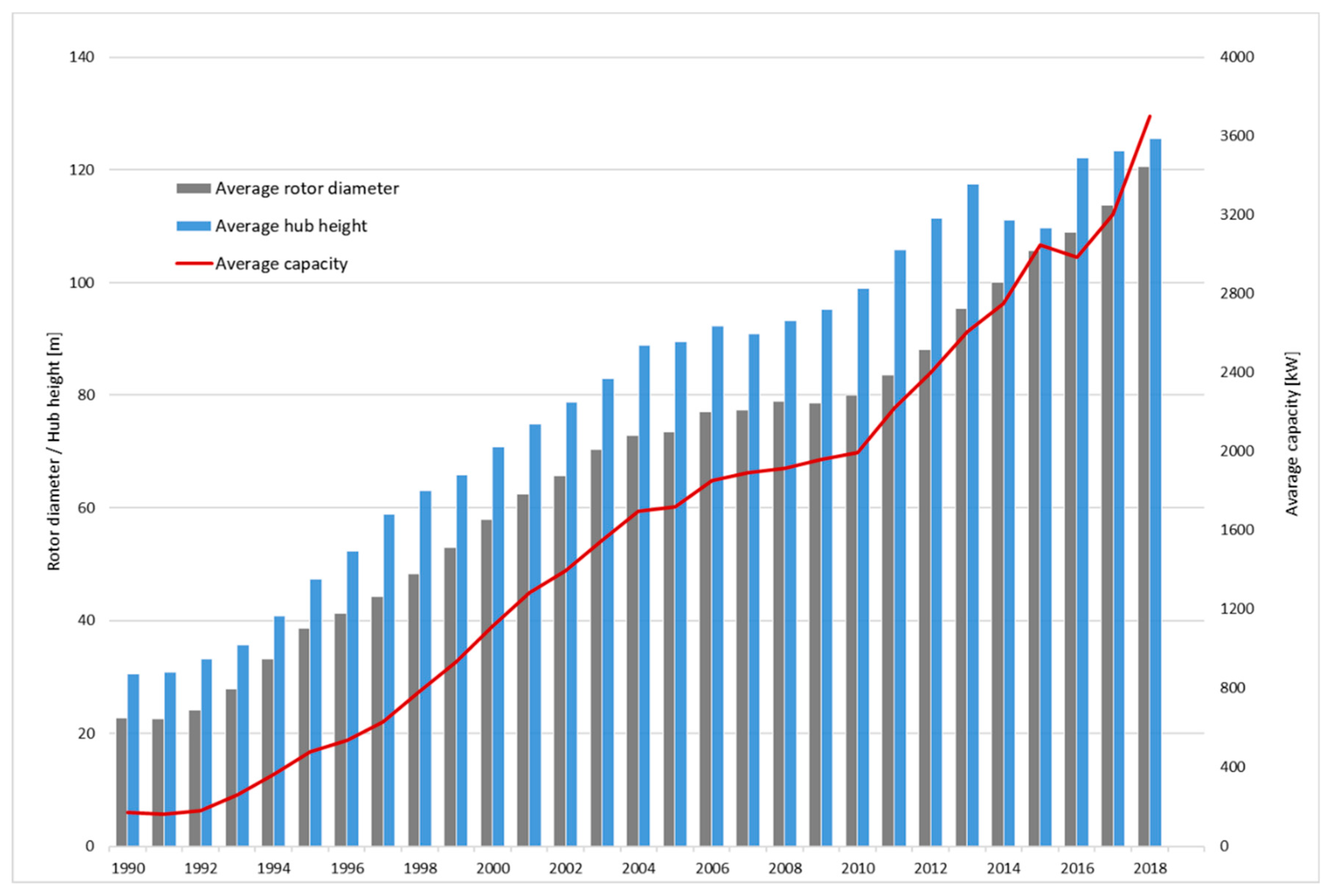
- Higher capacity, production, and efficiency. As seen in Figure 3, there has been an enormous increase in the size and capacity of WTs over the last years, which results in a higher production output. Furthermore, the growth in rotor diameter, improvements in aerodynamics, etc. have led to a much higher availability over a wider range of wind speeds. The example of a repowering project in Galmsbüll (in the federal state of Schleswig-Holstein) illustrates this increase in productivity and the decrease in the number of turbines (see Table 1).
- ○
- O&M costs. According to [27] (p. 1), the operational costs of WTs may increase by 25% after 10 years of operation; LIE [20] (p. 53) also states an increase of 20% in the second half of a WT’s lifetime, which can make repowering attractive. The O&M costs per MWh for new WTs can be expected to be lower than those for old ones, which may be due to the fact that recent projects have used larger turbines with a higher capacity factor ([28]; on the capacity factor see also Section 5.1). The newer machinery also reduces downtimes, since it is less likely to fail.
- ○
- Load factor. Hughes [29] (p. 7) found that the normalized load factors for onshore wind farms in Denmark declined from a peak of 22% at age zero to 18% at age 15 (24% to 11% in the UK). This results in a tremendous decrease in electricity production. The effect on the timing of repowering involved in such a decline is quantified in Section 6.
- ○
- ○
- Grid integration. New WTGs not only produce electricity more steadily (see above), but can also provide grid services, since their maximum active power needs to be remotely controllable by the transmission system operator (TSO), thus supporting grid stability. Also, as discussed in Section 4, regional grid capacity limitations and the rapid expansion of wind power installations may compromise grid stability. Repowering, if properly incentivized, can help to mitigate locational inefficiencies of RES generation and the need for RES curtailments [31].
- ○
- Reduction in the number of WTGs and bundling. Repowering usually helps to significantly decrease the number of installed WTs, while an increase in capacity and production is achieved. Additionally, it offers the opportunity to decommission scattered WTs and to bundle them in designated areas. This allows for the correction of any mistakes that were made in the regional and land-use planning [32]. On top of that, today’s WTs turn more slowly than old ones, which can also help to reduce the visual impact on the surroundings.
- ○
- Tax benefits. Since the trade tax law of 2009 came into effect, the municipalities where WTs are commissioned receive at least 70% of the trade tax yield, the municipality of the asset operator only 30% [33] (Art. 29). Turning local residents into stakeholders of a wind park can additionally increase the acceptance of projects through monetary incentives.
- ○
- Financial risks. The risk of a repowering project might be lower than that of a greenfield development, as good wind data are already available, improving the production forecast accuracy of electricity, thus making it easier to get favorable loan terms and allowing a very high gearing with sometimes less than 10% equity [30]. Also, contact with local communities has already been established [8] and the integration into the planning process might be easier.
- ○
- Availability of favorable sites. As mentioned above, repowering is becoming especially attractive when favorable wind sites are already occupied by old WTGs, and when available sites are scarce.
- ○
- New permitting process. Old WTs have usually been built under different regulatory and environmental frameworks and also, due to the increase in the size of WTs, the permit process can be considered to be as difficult as that of a greenfield project [30]. In contrast, resistance from local communities can often be expected, because of the height of new generation WTs and their visibility from a great distance, especially at night, since constructions higher than 100 m have to be marked with beacons.
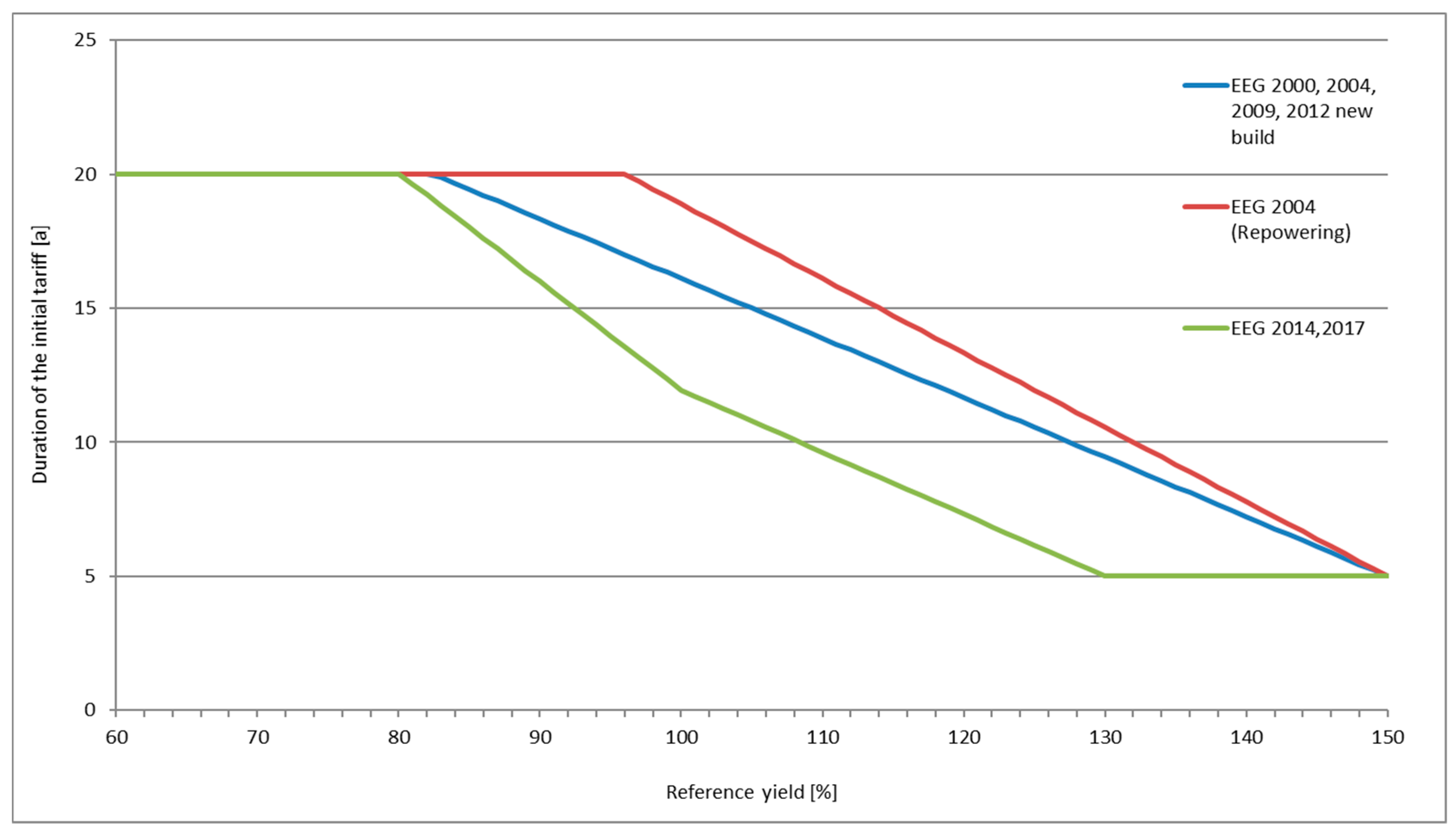
4. Policy Frameworks in Germany from 1991 Until Today
5. Timing of Repowering Under Changing Policy Frameworks
5.1. Optimal Timing of Onshore Wind Repowering
- ○
- Upfront investment costs (capital expenditure). The upfront investment costs for onshore WTs account for approximately 75% of the levelized cost of electricity (LCoE) of wind power over the WTs’ lifetime in Germany [28] (p. 44). They can be divided into the main investment costs and the additional investment costs. The first usually include the wind turbine, rotor, tower, and transportation, while the latter comprise, e.g., grid connection (note that since the increase in capacity of a repowering project is usually significant, the old grid connection is often not sufficient and has to be strengthened), infrastructure, foundation, as well as planning- and permission costs among others. According to [47], the main investment costs for WTs with a tower height of ≥110 m amounted to an average of 1070 €/kW between 2006 and 2013, while WTs with a rotor diameter of ≤95 m cost around 870 €/kW in 2014 (these prices are drawn from projects in Europe, and in North and Latin America). According to [20], the average additional investment costs sum up to 326 €/kW in Germany, while the total investment costs range between 1130–2000 €/kW for 3 MW turbines, with an average of 1570 €/kW. In our base case assumptions for the numerical analysis, we assume a lower value than the average total investment costs stated by [20], since the data provided by [47] suggest lower main investment costs. The effects of higher investment costs are discussed in Section 6.1. Additionally, we assume a slight downward trend of the investment costs, in line with historical data reported in [47] and also used in [9].
- ○
- Decommissioning costs. In the case of repowering, the decommissioning costs of the old WTs have to be considered in the upfront costs as well. According to data from early repowering projects collected by Bloomberg [47], decommissioned WTs can usually be resold, and their residual value covers the dismantling costs or even exceeds them. Himpler and Madlener [9] found that the residual value does not have a significant impact on the repowering decision, though. Additionally, it is difficult to find good quality data about the second-hand turbine market. Hence, for reasons of simplicity, we assume that the residual value equals the dismantling costs, so that the two cancel each other out and can thus be neglected.
- ○
- O&M costs. O&M costs are assumed to account for the remaining 25% of the LCoE of wind power over the total lifetime [28] (p. 44). They include e.g., insurance, regular maintenance, repairs, spare parts, land lease, and administration. Most components can be observed quite easily, such as insurance cost or land lease, which is why the O&M costs are considered to be deterministic in our analysis. Spare parts and repairs can be quite costly, though. Especially if major parts, such as the gearbox, fail in the second half of a WT’s lifetime, it could have a major impact on the decision of repowering, and should be analyzed on a case-by-case basis. Since the experience with WTGs reaching the end of their lifetime is quite limited [49] the O&M costs still provide quite some uncertainty and their actual development, especially at the end of a WT’s lifetime, is an area of further research.
- ○
- Capacity factor and degradation of WTGs. In our study, the load factor is defined as the electricity produced, divided by the electricity that would have been produced by the plant running under full nameplate capacity. Therefore, we refer to it as the capacity factor. The capacity factor of a WT is highly dependent on its location and wind conditions. According to WindEurope [51], gross capacity factors in Germany lie between 22% (onshore) and 36% (offshore). For the numerical analysis, we assume a net capacity factor of 32% following the specifications of the Vestas V90 3 MW turbine with a hub height of 125 m. For the old WTs, a slightly lower initial capacity factor of 26% is assumed due to their age. Since exact historical wind data for the old asset are available over a long period of time, the capacity factor is assumed to be deterministic. According to Hughes [29], the normalized capacity factor of wind farms in the UK declined from a peak of about 24% at age 1 to 11% at age 15, and in Denmark from a peak of 22% to 18% at age 15 (in years). While the study of Hughes does not take into account WTs in Germany, there is no reason to believe that the decrease in the capacity factor should be dissimilar in Germany. Note that the decline of the capacity factor is neglected in the exemplary calculation, but its impact is included in the sensitivity analysis.
- ○
- Construction lead times. For onshore wind farm construction, lead times are relatively short. Small wind parks of up to 10 MW can be built in less than two months, larger wind farms of 50 MW in six months [52]. In Germany, the size of many wind farms lies somewhere in this range. We assume that the investor already holds all the permits necessary for construction, so that construction can start as soon as the economically optimal point in time is reached. Therefore, lead times are neglected.
- ○
- Discount factor. In the model, a risk-free interest rate of 0.5% is used for discounting, which equals the average 10-year German government bond yield (rounded to the next integer; [53]). For the calculation of the NPV, a risk premium of 5% is added to the risk-free rate [54]; this is an arbitrarily chosen value since the discount rate applied depends on the investor’s risk attitude and time preference rate.
- ○
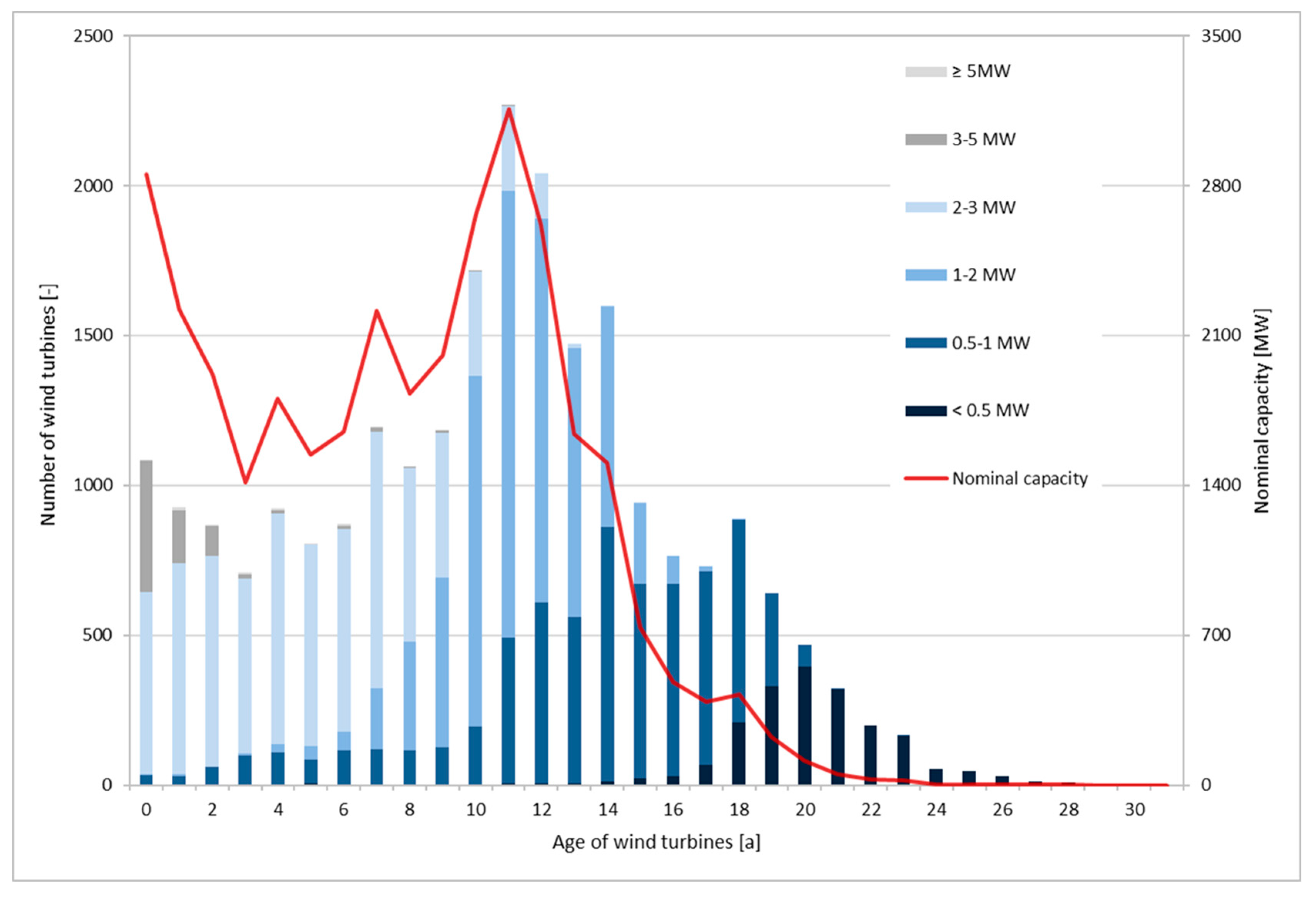
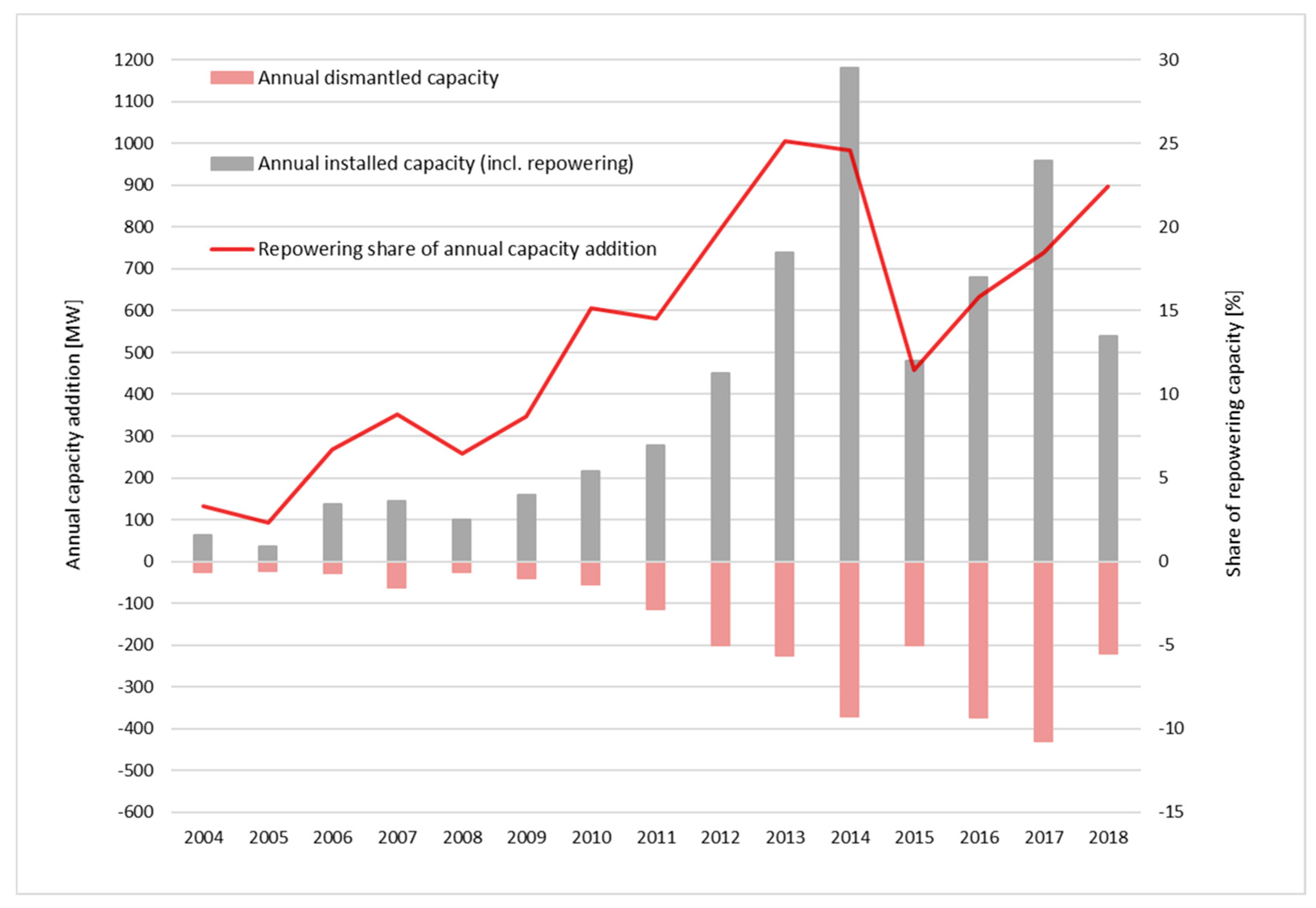
- Repowering factor. The repowering factor describes the ratio between the capacity installed before repowering and afterwards. DEWI [55] lists 11 repowering projects from 2013 in Schleswig-Holstein, with repowering factors varying between 1.2 and 11.3 (average value: 2.67; ignoring the outlier of 11.3, which is uncommonly high not only in the considered data series). The average repowering factor according to Figure 4 in Germany in 2013 was equal to 3.2. Since in the numerical analysis it is assumed that the old asset is 10 years old and one old WT has a capacity of 1 or 2 MW, the resulting repowering factor of 2.3 is smaller than the two average factors described above. However, it still seems reasonable in light of the range of repowering factors described in DEWI [55].
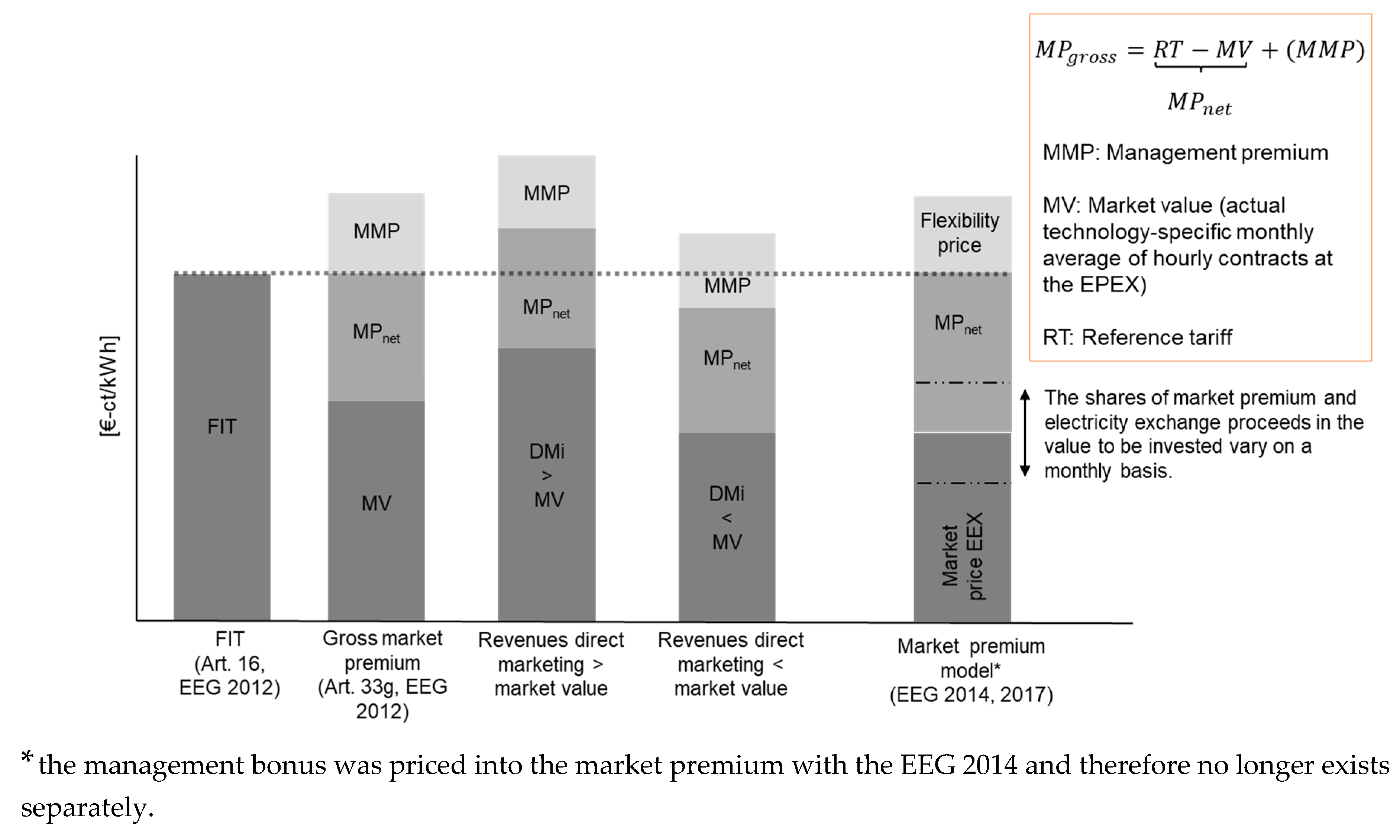
5.2. Repowering Under the Market Premium Model
5.3. Repowering Under A Free Market Regime
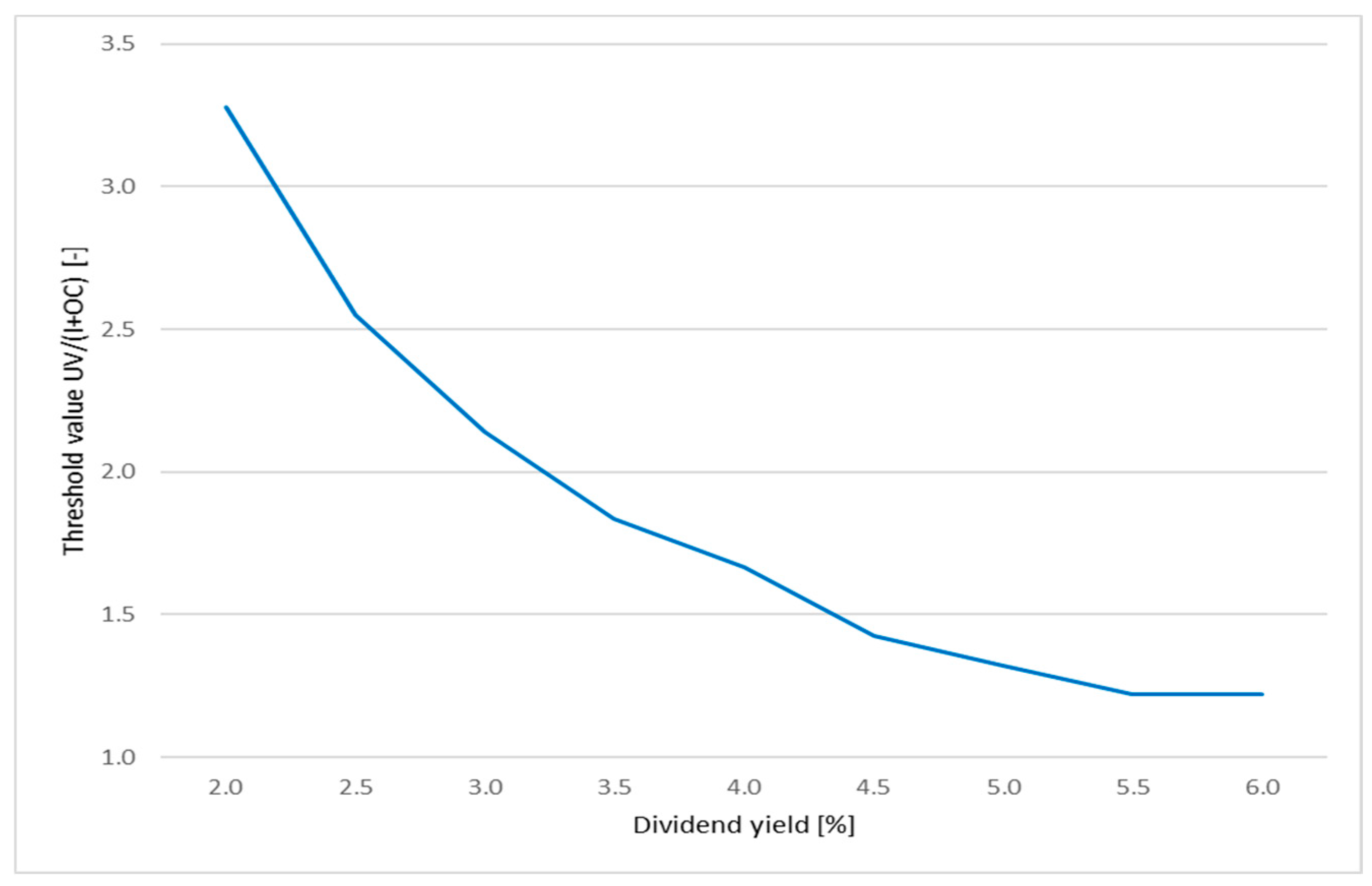
5.4. Repowering Under A Free Market Regime Including the Dividend Yield
6. Model Application and Discussion of Results
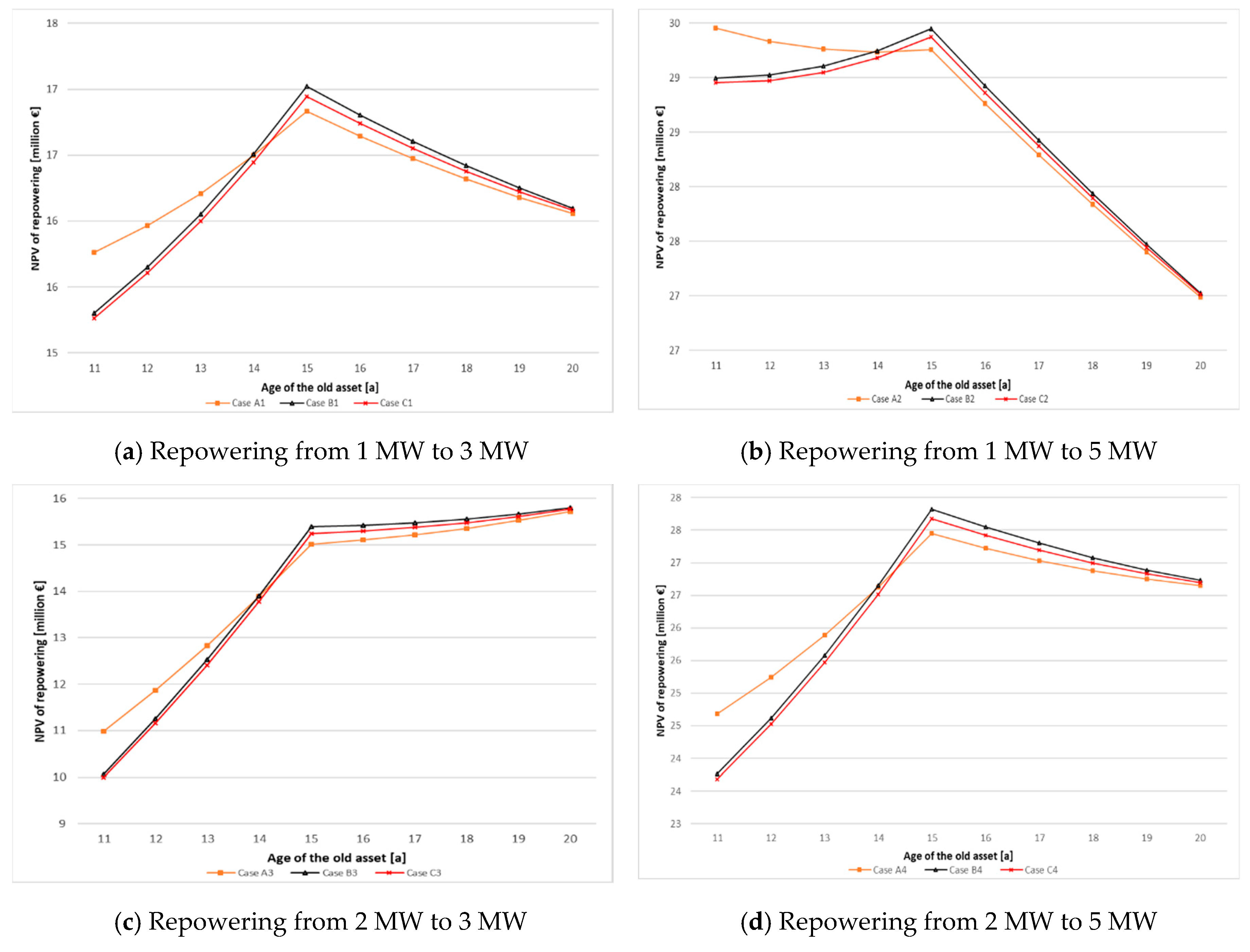
6.1. Repowering Under the Market Premium Model
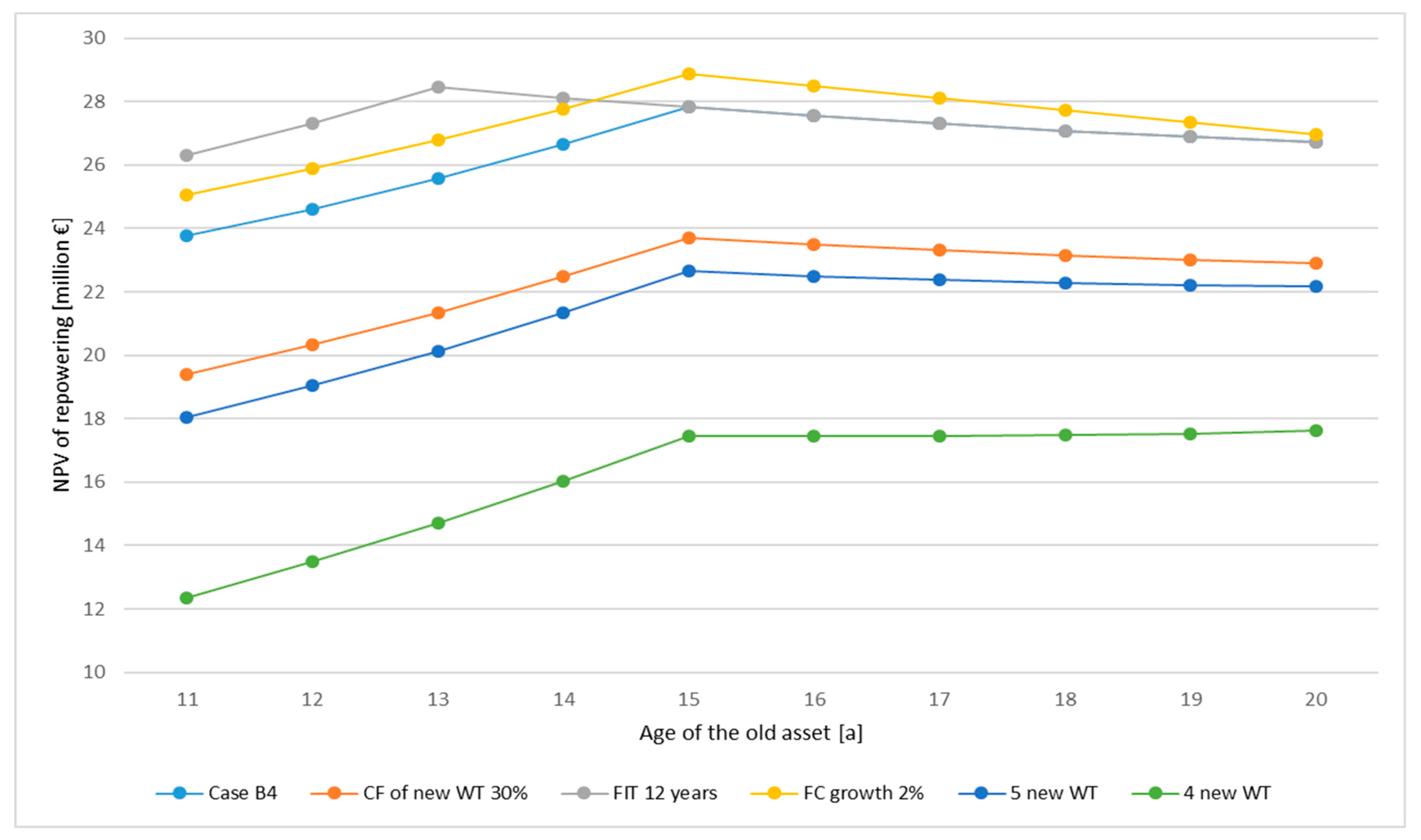
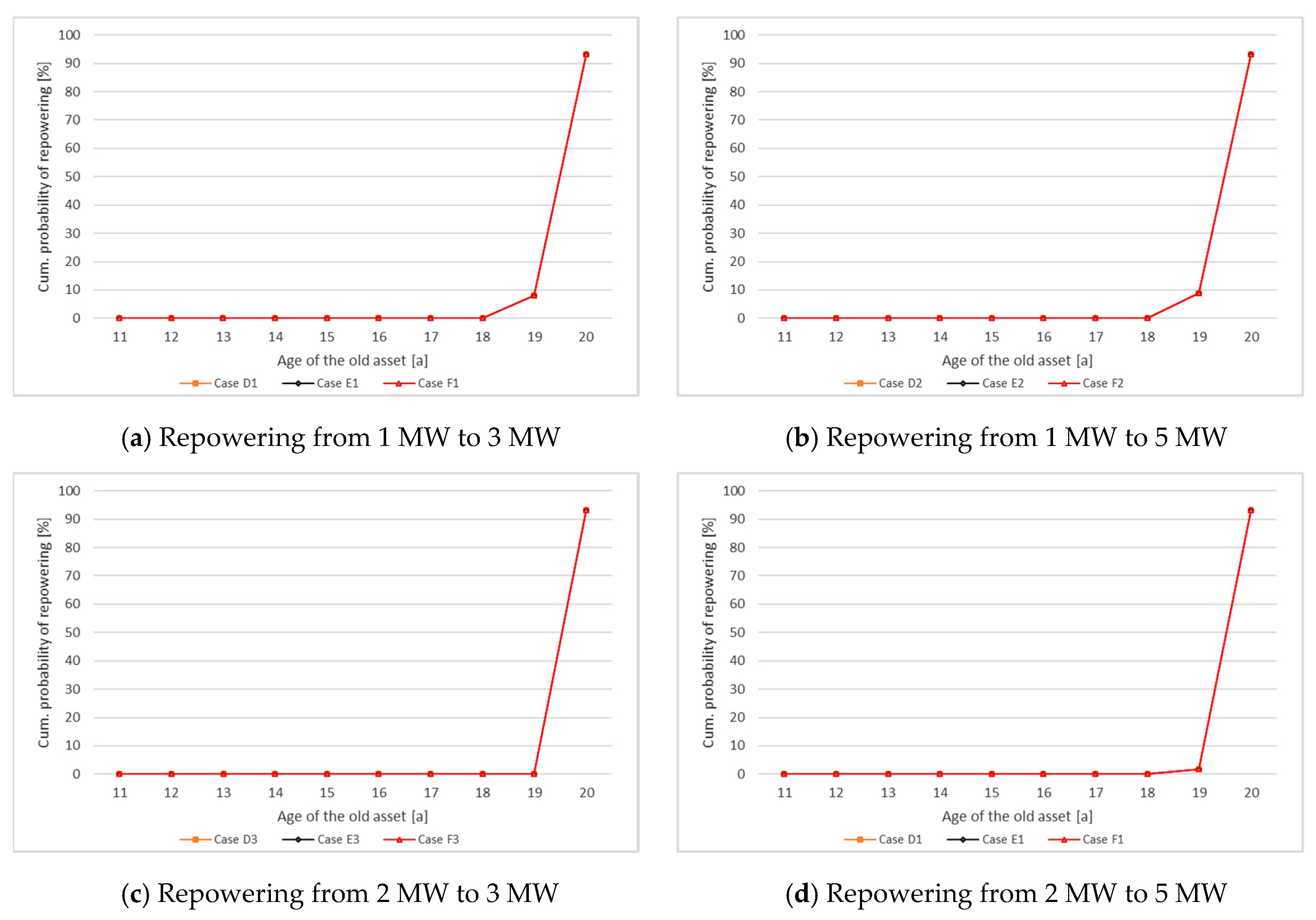
6.2. Repowering Under the Free Market Regime
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations and Symbols Used
| Capi | Capacity of one wind turbine (i = {o, n} for “old” and “new”) |
| DMC | Direct marketing costs |
| EEG | German Renewable Energy Sources Act (Erneuerbare Energien Gesetz) |
| FCap,i | Capacity factor of asset i (i = {o, n} for “old” and “new”) |
| FCi,initial | Initial fixed costs of one wind turbine (i = {o, n} for “old” and “new”) |
| FDeg,i | Performance degradation factor of asset i (i = {o, n} for “old” and “new”) |
| FFC,growth,i | Growth factor of the fixed costs of asset i (i = {o, n} for “old” and “new”) |
| FI | Annual decrease of the investment costs |
| FIT, FITo,high | Feed-in tariff, initial (high) feed-in tariff of the old asset |
| FITo,low | Basic (low) feed-in tariff of the old asset |
| FRT | Digression factor of the reference tariff |
| GBM | Geometric Brownian motion |
| Iinit | Initial investment costs per wind turbine |
| LCoE | Levelized cost of electricity |
| MP | Market premium |
| n | Number of periods per year |
| Ni | Number of wind turbines (i = {o, n} for “old” and “new”) |
| O&M | Operation & maintenance |
| OV | Option value |
| Electricity price | |
| RES, RES-E | Renewable energy sources, electricity from renewable energy sources |
| RET | Renewable energy technologies |
| rf | Risk-free interest rate |
| ROA | Real options, Real options analysis |
| RT | Reference tariff |
| RThigh, initial,RTlow,initial | Initial high (low) reference tariff |
| StrEG | German Electricity Feed-in Act (Stromeinspeisungsgesetz) |
| TD | Decision time horizon |
| TFIT,high | Duration of the initial (high) feed-in tariff of the old asset |
| TL | Assumed lifetime of wind turbines |
| To | Age of the old asset |
| TRT,high | Duration of the high reference tariff |
| TSO | Transmission system operator |
| UV | Underlying variable |
| WT, WTG | Wind turbine, Wind turbine generator |
| δ | Dividend yield |
| μ, σ | Drift and volatility of the electricity price |
Appendix A. EEG Amendments
Appendix A.1. Renewable Energy Sources Act 2000 (EEG 2000)
Appendix A.2. EEG (2004)
Appendix A.3. EEG (2009)
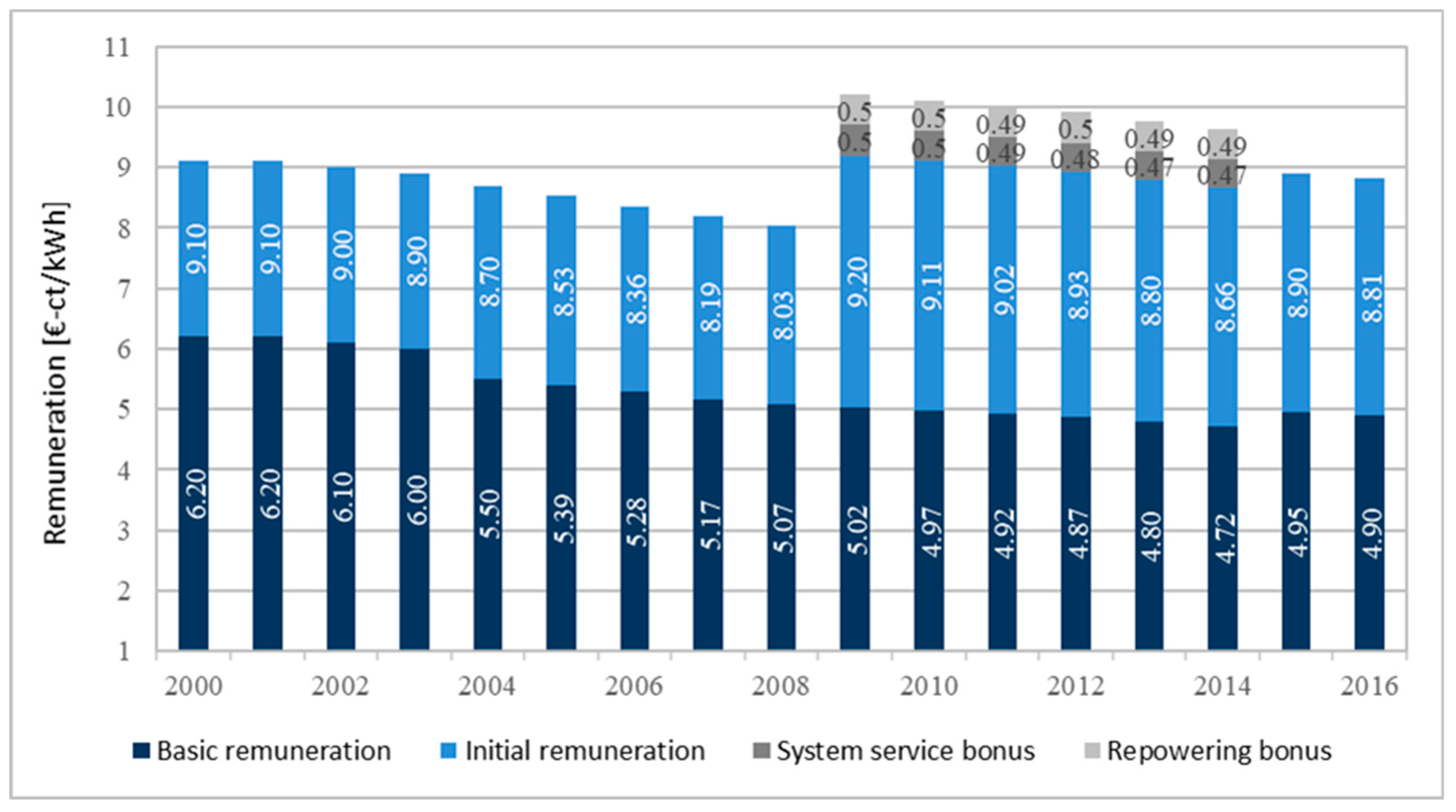
Appendix A.4. EEG (2012) and Market Premium Model
Appendix B. Parametrization
| Input Parameter | Value | Unit | Description |
|---|---|---|---|
| Capo | 1/2 | [MW] | Installed capacity of an old WT |
| FCap,o | 26 | [%] | Capacity factor of the old asset |
| No, To | 8, 10 | [a] | Number of old WTs, Age of the old asset |
| FITo,high, FITo,low | 80.20 / 50.70 | [€/MWh] | Initial / Basic FIT for the old asset (according to EEG 2008) |
| FITo,high, FITo,low | 89.30 / 48.70 | [€/MWh] | Initial / Basic FIT for the old asset (according to EEG 2012) |
| FITo,high, FITo,low | 89.00 / 49.50 | [€/MWh] | Initial / Basic FIT for the old asset (according to EEG 2014) |
| TFIT,high | 14 | [a] | Duration of the initial FIT for the old asset |
| FCo,init | 26.8 | [€/MWh] | O&M costs of an old WTG (in the second operating decade) |
| FFC,growth,o | 1 | [%] | Growth factor of the fixed costs of the old WTs p.a. |
| FDeg,o | 0 | [%] | Performance degradation factor of the old WTs |
| Capn | 3 / 5 | [MW] | Installed capacity of one new WT |
| FCap,n, | 32 | [%] | Capacity factor of the new asset |
| Nn | 6 | Number of new WTs | |
| RThigh, init | 105.86 | [€/MWh] | Initial high reference tariff at t0 |
| RTlow,init | 83.92 | [€/MWh] | Initial low reference tariff at t0 |
| TRT,high | 9 | [a] | Duration of the high reference tariff |
| FRT | 1 | [%] | Digression factor of the reference tariffs |
| DMC | 2 | [€/MWh] | Direct marketing costs |
| FCn,init | 24.1 | [€/MWh] | O&M costs of an old WTG (at beginning of lifetime) |
| FFC,growth,n | 1 | [%] | Growth factor of the fixed costs of the new WTs p.a. |
| Iinit | 1,180 | [€/kW] | Initial investment costs per WT |
| FI | 0.5 | [%] | Annual decrease of Iinit |
| FDeg,n | 0 | [%] | Performance degradation factor of the new WTs |
| TL, TD | 20 / 10 | [a] | Assumed lifetime of a WTG, Decision time horizon |
| N | 4 | Number of periods per year (only for the ROA) | |
| rf, risk premium | 0.5 / 5 | [%] | Risk-free interest rate, Risk premium (the sum of the two is used for discounting) |
| Σ | 16.45 | [%] | Volatility of the electricity price |
| Μ | 25.42 | [%] | Drift rate of the electricity price |
| Δ | 0 | [%] | Dividend yield |
References
- EUR-Lex—European Union. Available online: http://eur-lex.europa.eu/legal-content/DE/TXT/?uri=CELEX:32001L0077 (accessed on 27 September 2019).
- World Energy Council. World Energy Perspective-Cost of Energy Technologies. 2013. Available online: http://www.worldenergy.org/wp-content/uploads/2013/09/ WEC_J1143_CostofTECHNOLOGIES_021013_WEB_Final.pdf (accessed on 27 September 2019).
- Murto, P. Timing of investment under technological and revenue-related uncertainties. J. Econ. Dyn. Control 2007, 31, 1473–1497. [Google Scholar] [CrossRef]
- Kumbaroğlu, G.; Madlener, R.; Demirel, M. A real options evaluation model for the diffusion prospects of new renewable power generation technologies. Energy Econ. 2008, 30, 1882–1908. [Google Scholar] [CrossRef]
- Rohlfs, W.; Madlener, R. Optimal investment strategies in power generation assets: The role of technological choice and existing portfolios in the deployment of low-carbon technologies. Int. J. Greenh. Gas. Control 2014, 28, 114–125. [Google Scholar] [CrossRef]
- Heggedal, A.M.; Linnerud, K.; Fleten, S.E. Uncertain Policy Decisions and Investment Timing: Evidence from Small Hydropower Plants, Norwegian University of Science and Technology, CICERO Center for International Climate and Environmental Research, Oslo. 2011. Available online: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1987701 (accessed on 27 September 2019).
- Boomsma, T.K.; Meade, N.; Fleten, S.E. Renewable energy investments under different support schemes: A real options approach. Eur. J. Oper. Res. 2012, 220, 225–237. [Google Scholar] [CrossRef]
- Madlener, R.; Schumacher, M. Ökonomische Bewertung des Repowering von Onshore-Windenergieanlagen in Deutschland. Z. Energiewirtsch. 2011, 35, 297–320. [Google Scholar] [CrossRef]
- Himpler, S.; Madlener, R. Optimal timing of wind farm repowering: A two-factor real options analysis. J. Energy Mark. 2014, 7, 3–34. [Google Scholar] [CrossRef]
- Ritzenhofen, I.; Spinler, S. Optimal design of feed-in-tariffs to stimulate renewable energy investments under regulatory uncertainty—A real options analysis. Energy Econ. 2016, 53, 76–89. [Google Scholar] [CrossRef]
- Kitzing, L.; Juul, N.; Drud, M.; Boomsma, T.K. A real options approach to analyse wind energy investments under different support schemes. Appl. Energy 2017, 188, 83–96. [Google Scholar] [CrossRef]
- Anatolitis, V.; Welisch, M. Putting renewable energy auctions into action—An agent-based model of onshore wind power auctions in Germany. Energy Policy 2017, 110, 394–402. [Google Scholar] [CrossRef]
- Voss, A.; Madlener, R. Auction schemes, bidding strategies and the cost-optimal level of promoting renewable electricity in Germany. Energy J. 2017, 38, 229–264. [Google Scholar] [CrossRef]
- Moon, Y.; Baran, M. Economic analysis of a residential PV system from the timing perspective: A real option model. Renew. Energy 2018, 125, 783–795. [Google Scholar] [CrossRef]
- Gazheli, A.; van den Bergh, J. Real options analysis of investment in solar vs. wind energy: Diversification strategies under uncertain prices and costs. Renew. Sustain. Energy Rev. 2018, 82, 2693–2704. [Google Scholar] [CrossRef]
- Ruberg, T.; McMillan, D.; Niewczas, P. A decision support tool to assist with lifetime extension of wind turbines. Renew. Energy 2018, 120, 423–433. [Google Scholar] [CrossRef]
- Pescia, D.; Graichen, P. Understanding the Energiewende: FAQ on the Ongoing Transition of the German Power System; Agora Energiewende: Berlin, Gremany, 2015. [Google Scholar]
- Fraunhofer ISE Net Public Electricity Generation in Germany in 2018. 2019. Available online: https://www.energy-charts.de/energy_pie.htm?year=2018 (accessed on 24 October 2019).
- MAKE—Make Consulting. Proprietary database extract for E.ON Climate and Renewables. 2014. Available online: https://www.woodmac.com/our-expertise/capabilities/power-and-renewables/ (accessed on 27 September 2019).
- LIE—Leipziger Institut für Energie. Vorhaben IIe Stromerzeugung aus Windenergie-Wissenschaftlicher Bericht. 2014. Available online: https://www.bmwi.de/BMWi/Redaktion/PDF/XYZ/zwischenbericht-vorhaben-2e,property=pdf,bereich=bmwi2012,sprache=de,rwb=true.pdf (accessed on 27 September 2019).
- WindGuard. Status of Land-based Wind Energy Development in Germany—Year 2018. 2019. Available online: https://www.wind-energie.de/fileadmin/redaktion/dokumente/dokumente-englisch/publications/Factsheet_Status_of_Wind_Energy_Development_in_Germany_-_Year_2018.pdf (accessed on 27 September 2019).
- IWES—Fraunhofer Institute for Wind Energy and System Technology. Wind Energy Report Germany 2013. 2013. Available online: http://windmonitor.iwes.fraunhofer.de/bilder/upload/Windreport_2013_engl (accessed on 27 September 2019).
- Mackensen, R. Windenergie Report Deutschland 2018; Fraunhofer IEE: Stuttgart, Germany, 2019. [Google Scholar]
- IWES—Fraunhofer Institute for Wind Energy and System Technology. Wind Energy Report Germany 2013. 2018. Available online: http://windmonitor.iee.fraunhofer.de /opencms/export/sites/windmonitor/img/Windmonitor-2018/WERD_2018.pdf (accessed on 24 October 2019).
- Hulshorst, W. Repowering and used wind turbines, European Copper Institute. 2008. Available online: http://www.leonardo-energy.org/sites/leonardo-energy/files/root/pdf/2008/repowering-wind.pdf (accessed on 27 September 2019).
- BWE—Bundersverband Windenergie. Repowering von Windenergieanlagen. 2012. Available online: http://www.wind-energie.de/sites/default/files/download/publication/repowering-von-windenergieanlagen/repoweringbroschuere_2012_web.pdf (accessed on 27 September 2019).
- Filgueira, A.; Seijo, M.A.; Muñoz, E.; Castro, L.; Piegari, L. Technical and Economic Study of Two Repowered Wind Farms in Bustelo and San Xoán, 24.7 MW and 15.84 MW, Respectively, ICCEP. 2009. Available online: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=5211998 (accessed on 27 September 2019).
- IRENA—International Renewable Energy Agency. Renewable Energy Technologies: Cost Analysis Series-Wind Power. 2012. Available online: http://www.irena.org/documentdownloads/publications/re_technologies_cost_analysis-wind_power.pdf (accessed on 27 September 2019).
- Hughes, G. The Performance of Wind Farms in the United Kingdom and Denmark, Renewable Energy Foundation (REF), London. 2012. Available online: http://www.ref.org.uk/attachments/article/280/ref.hughes.19.12.12.pdf (accessed on 31 October 2019).
- Bloomberg—Bloomberg New Energy Finance. Wind Research Note-Early Repowering, a Second Spring for Wind Projects? 2014a. Available online: https://www.bnef.com/Insight/10003?fromGlobalSearch=1239852001 (accessed on 27 September 2019).
- Höfer, T.; Madlener, R. Locational (in-) Efficiency of Renewable Power Generation Feeding in the Electricity Grid: A Spatial Regression Analysis; FCN Working Paper No. 6/2019; Institute for Future Energy Consumer Needs and Behavior: Aachen, Germany; RWTH Aachen University: Aachen, Germany, 2019. [Google Scholar]
- Höfer, T.; Sunak, Y.; Siddique, H.; Madlener, R. Wind Farm Siting Using a Spatial Analytic Hierarchy Process Approach: A Case Study of the Städteregion Aachen. Appl. Energy 2016, 163, 222–243. [Google Scholar] [CrossRef]
- Gewerbesteuergesetz (German trade tax act). 2019. Available online: https://dejure.org/gesetze/GewStG/29.html (accessed on 24 October 2019).
- Fachagentur Windenergie, Status des Windenergie-Ausbaus und Repoweringin Schleswig-Holstein. 2016. Available online: https://www.fachagentur-windenergie.de/fileadmin/files/Veroeffentlichungen/FA-Wind_RepoweringSituation_ SH_02-2016.pdf (accessed on 24 October 2019).
- DEWI—DEWI GmbH. Wind Energy Use in Germany—Status 31.12.2013. 2013. Available online: http://www.dewi.de/dewi_res/fileadmin/pdf/publications/Magazin_44/07.pdf (accessed on 27 September 2019).
- Glensk, B.; Madlener, R. Energiewende @ Risk: On the continuation of renewable power generation at the end of public policy support. Energies 2019, 12, 3616. [Google Scholar] [CrossRef]
- IEA—International Energy Agency. Renewable Energy Sources in Figures. 2013. Available online: https://www.erneuerbare-energien.de/EE/Redaktion/DE/Downloads/renewable-energy-sources-in-figures-2014.pdf?__blob=publicationFile&v=3 (accessed on 27 September 2019).
- EEG—Erneuerbare Energien Gesetz 2017. Available online: https://www.clearingstelle-eeg-kwkg.de/files/EEG2017_190513.pdf (accessed on 31 August 2019).
- Grashof, K. Are auctions likely to deter community wind projects? And would it be problematic? Energy Policy 2019, 125, 20–32. [Google Scholar] [CrossRef]
- Lundberg, L. Auctions for all? Reviewing the German wind power auctions in 2017. Energy Policy 2019, 128, 449–458. [Google Scholar] [CrossRef]
- BMWi—Bundesministerium für Wirtschaft. Key Elements of a Revised Renewable Energy Sources Act. 2014. Available online: https://www.bmwi.de/English/Redaktion/Pdf/eeg-reform-eckpunkte-english,property=pdf,bereich=bmwi2012,sprache=en,rwb=true.pdf (accessed on 27 September 2019).
- EEG—Erneuerbare Energien Gesetz. 2014. Available online: https://www.clearingstelle-eeg.de/files/EEG_2014_140721_2.pdf (accessed on 27 September 2019).
- EEG—Erneuerbare Energien Gesetz. 2000. Available online: https://www.clearingstelle-eeg-kwkg.de/sites/default/files/6-EEG00_031222.pdf (accessed on 27 September 2019).
- EEG—Erneuerbare Energien Gesetz. 2004. Available online: https://www.clearingstelle-eeg.de/files/private/active/0/eeg04_061107.pdf (accessed on 27 September 2019).
- EEG—Erneuerbare Energien Gesetz. 2009. Available online: https://www.clearingstelle-eeg.de/files/EEG_2009_juris_Stand_110721.pdf (accessed on 27 September 2019).
- EEG—Erneuerbare Energien Gesetz. 2012. Available online: https://www.clearingstelle-eeg.de/files/EEG2012_juris_120817.pdf (accessed on 27 September 2019).
- Bloomberg—Bloomberg New Energy Finance. Wind Turbine Price Index: H2 2014. 2014. Available online: https://www.bloomberg.com/impact/products/bloombergnef/ (accessed on 27 September 2019).
- Wüstemeyer, C.; Madlener, R.; Bunn, D. A Stakeholder Analysis of Divergent Supply-Chain Trends for the European Onshore and Offshore Wind Installations. Energy Policy 2015, 80, 36–44. [Google Scholar] [CrossRef]
- Liu, P.; Meng, F.; Barlow, C. Wind turbine blade end-of-life options: An eco-audit comparison. J. Clean. Prod. 2019, 212, 1268–1281. [Google Scholar] [CrossRef]
- DWG—Deutsche Wind Guard. Kostensituation der Windenergie an Land in Deutschland. 2013. Available online: http://www.wind-energie.de/sites/default/files/download/publication/kostensituation-der-windenergie-land-deutschland/20140730_kostensituation_windenergie_land.pdf (accessed on 27 September 2019).
- WindEurope. Wind energy in Europe in 2018. 2019. Available online: https://windeurope.org/wp-content/uploads/files/about-wind/statistics/WindEurope-Annual-Statistics-2018.pdf (accessed on 24 October 2019).
- EWEA—European Wind Energy Association (n.d.). Available online: http://www.ewea.org/wind-energy-basics/faq/ (accessed on 27 September 2019).
- Statista—The Statistic Portal. Rendite Zehnjähriger Staatsanleihen Deutschlands bis 2018. 2019. Available online: https://de.statista.com/statistik/daten/studie/200193/umfrage/entwicklung-der-rendite-zehnjaehriger-staatsanleihen-in-deutschland/ (accessed on 27 September 2019).
- Reetz, K.; Gaidosch, D. Hinweis nach Art. 7 Absatz 2 Satz 1 VermAnIG (Vermögensanlagengesetz; German asset investment act), reconcept consulting GmbH, Hamburg, Germany. 2017. Available online: https://www.gesetze-im-internet.de/vermanlg/BJNR248110011.html (accessed on 27 September 2019).
- DEWI—DEWI GmbH. Status of Repowering in 2013. 2014. Available online: http://www.dewi.de/dewi_res/fileadmin/pdf/publications/Magazin_44/08.pdf (accessed on 27 September 2019).
- Gawel, E.; Purkus, A. 2013—Promoting the Market and System Integration of Renewable Energies through Premium Schemes-A Case Study of the German Market. Helmholtz Zentrum für Umweltforschung: Leipzig, Germany. Available online: https://www.ufz.de/export/data/global/46349_4%202013%20Gawel_Purkus_Case%20Study%20Renewable%20Energies_gesamt.pdf (accessed on 27 September 2019).
- DLR—Deutsches Zentrum für Luft-und Raumfahrt. Optionale oder verpflichtende Direktvermarktung für Erneuerbare Energien—wer profitiert wie? 2013. Available online: http://www.dlr.de/blogs/de/desktopdefault.aspx/tabid-6192/10184_read-681/ (accessed on 27 September 2019).
- DIW—Deutsches Institut für Wirtschaftsforschung. Impact of Renewable Energy Act Reform on Wind Project Finance. 2014. Available online: https://www.diw.de/documents/publikationen/73/diw_01.c.466289.de/dp1387.pdf (accessed on 27 September 2019).
- Metcalf, G.E.; Hassett, K.A. Investment under alternative return assumptions-Comparing random walks and mean reversion. J. Econ. Dyn. Control 1995, 19, 1471–1488. [Google Scholar] [CrossRef]
- Fleten, S.E.; Maribu, K.M.; Wangensteen, I. Optimal investment strategies in decentralized renewable power generation under uncertainty. Energy 2007, 32, 803–815. [Google Scholar] [CrossRef]
- Cox, J.; Ross, S.; Rubinstein, M. Option Pricing: A Simplified Approach. J. Financ. Econ. 1979, 7, 229–263. [Google Scholar] [CrossRef]
- Dixit, A.K.; Pindyck, R.S. Investment Under Uncertainty; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Copeland, T.E.; Antikarov, V. Real Options: A Practitioner’s Guide; Texere Publishers: New York, NY, USA, 2003. [Google Scholar]
- Hull, J.C. Options, Futures and Other Derivatives; Pearson Education International: London, UK, 2001. [Google Scholar]
- Mun, J. Real Options Analysis-Tools and Techniques for Valuing Strategic Investment Decisions; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Davis, G.A. Estimating volatility and dividend yield when valuing real options to invest or abandon. Q. Rev. Econ. Finance 1998, 38, 725–754. [Google Scholar] [CrossRef]
- Teisberg, E.O. An option valuation analysis of investment choices by a regulated firm. Manag. Sci. 1994, 40, 535–548. [Google Scholar] [CrossRef]
- Trigeorgis, L. A Real-Options Application in Natural Resource Investments. Adv. Futures Options Res. 1990, 4, 153–164. [Google Scholar]
- Majd, S.; Pindyck, R.S. Time to Build Option Valuation for Arbitrary Stochastic Processes. J. Financ. Econ. 1987, 18, 7–27. [Google Scholar] [CrossRef]
- Guthrie, G. Real Options in Theory and Practice; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Wallasch, A.K.; Lüers, S.; Rehfeldt, K. Kostensituation der Windenergie an Land in Deutschland—Update; Windguard Gmbh: Varel, Germany, 2015. [Google Scholar]
- Wallasch, A.K.; Lüers, S.; Rehfeldt, K. Weiterbetrieb von Windenergieanlagen nach 2020; Windguard Gmbh: Düsseldorf, Germany, 2016. [Google Scholar]
- BNetzA—Bundesnetzagentur. EEG in Zahlen 2017. 2019. Available online: https://www.bundesnetzagentur.de/DE/Sachgebiete/ElektrizitaetundGas/Unternehmen_Institutionen/ErneuerbareEnergien/ZahlenDatenInformationen/zahlenunddaten-node.html (accessed on 27 September 2019).
- Netztransparenz Marktwertübersicht. 2019. Available online: https://www.netztransparenz.de/EEG/Marktpraemie/Marktwerte (accessed on 27 September 2019).
- Next-Kraftwerke. Was ist die Marktprämie? Available online: https://www.next-kraftwerke.de/wissen/ marktpraemie (accessed on 27 September 2019).
- Damodaran, A. The Promise and Peril of Real Options, NYU Working Paper No. S-DRP-05-02. 2005. Available online: https://ssrn.com/abstract=1295849 (accessed on 27 September 2019).
- Beckius, D.; Magnusson, D. The German Wind Energy Market and its Developers-a Study of Sourcing Models, Success Factor and Challenges; Division of Applied Thermodynamics and Refrigeration, KTH School of Industrial Engineering and Refrigeration; Stockholm, Sweden; Available online: http://www.diva-portal.org/smash/get/diva2:644677/FULLTEXT01.pdf (accessed on 27 September 2019).
- BMWi—Bundesministerium für Wirtschaft. Energy Concept for an Environmentally Sound, Reliable and Affordable Energy Supply. 2010. Available online: http://www.germany.info/contentblob/3043402/Daten/3903429/BMUBMWi_Energy_Concept_DD.pdf (accessed on 27 September 2019).
- BDEW—Bundesverband der Energie- und Wasserwirtschaft e.V. 2014. Available online: https://www.bdew.de/internet.nsf/id/83C963F43062D3B9C1257C89003153BF/$file/Energie-Info_Erneuerbare%20Energien%20und%20das%20EEG%20%282014%29_24.02.2014_final_Journalisten.pdf (accessed on 27 September 2019).
| Characteristics | Before Repowering | After Repowering |
|---|---|---|
| Number of wind turbines | 38 | 21 |
| Installed capacity | 12.4 MW | 60 MW |
| Electricity produced | 25,000 MWh/a | 155,000 MWh/a |
| Repowering from–to | Switch to Market Premium Model From | ||
|---|---|---|---|
| EEG 2008 | EEG 2012 | EEG 2014 | |
| 1 MW–3 MW | A1 | B1 | C1 |
| 2 MW–3 MW | A2 | B2 | C2 |
| 1 MW–5 MW | A3 | B3 | C3 |
| 2 MW–5 MW | A4 | B4 | C4 |
| Repowering from–to | Switch to Free Market Regime From | ||
|---|---|---|---|
| EEG 2008 | EEG 2012 | EEG 2014 | |
| 1 MW–3 MW | D1 | E1 | F1 |
| 2 MW–3 MW | D2 | E2 | F2 |
| 1 MW–5 MW | D3 | E3 | F3 |
| 2 MW–5 MW | D4 | E4 | F4 |
| No. of WT After Repowering | Cases | |||
|---|---|---|---|---|
| A1–C1 | A2–C2 | A3–C3 | A4–C4 | |
| 6 | 15.3–17.0 | 27.0–29.5 | 10.0–15.8 | 23.7–27.8 |
| 5 | 11.8–13.9 | 22.4–24.3 | 6.6–13.1 | 18.0–22.7 |
| 4 | 8.4–10.6 | 17.6–18.0 | 3.1–10.3 | 12.3–17.6 |
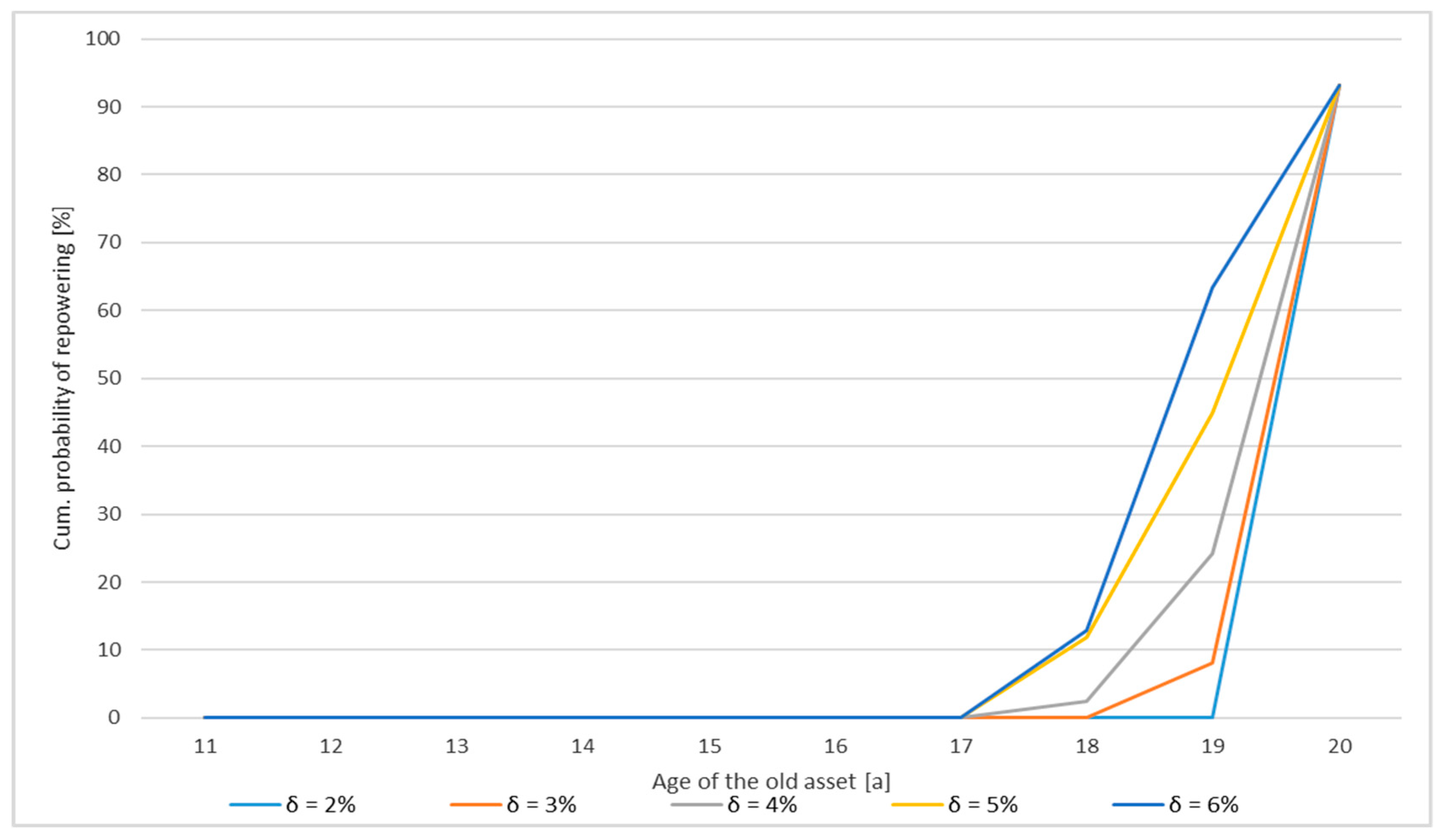
| No. of WT After Repowering | Time of Repowering * | Cumulative Probability of Repowering [in %] For Cases: | |||
|---|---|---|---|---|---|
| D1–F1 | D2–F2 | D3–F3 | D4–F4 | ||
| 6 | 19 | 8.1 | 8.9 | - | 1.7 |
| 20 | 93.1 | 93.1 | 93.1 | 93.1 | |
| 5 | 19 | 1.7 | 8.1 | - | 1.5 (for D4 & F4)1.7 (for E4) |
| 20 | 93.1 | 93.1 | 93.1 | 93.1 | |
| 4 | 19 | 1.5 | 8.1 | - | 1.5 (for E4 & F4) |
| 20 | 93.1 | 93.1 | 93.1 | 93.1 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madlener, R.; Glensk, B.; Gläsel, L. Optimal Timing of Onshore Wind Repowering in Germany under Policy Regime Changes: A Real Options Analysis. Energies 2019, 12, 4703. https://doi.org/10.3390/en12244703
Madlener R, Glensk B, Gläsel L. Optimal Timing of Onshore Wind Repowering in Germany under Policy Regime Changes: A Real Options Analysis. Energies. 2019; 12(24):4703. https://doi.org/10.3390/en12244703
Chicago/Turabian StyleMadlener, Reinhard, Barbara Glensk, and Lukas Gläsel. 2019. "Optimal Timing of Onshore Wind Repowering in Germany under Policy Regime Changes: A Real Options Analysis" Energies 12, no. 24: 4703. https://doi.org/10.3390/en12244703
APA StyleMadlener, R., Glensk, B., & Gläsel, L. (2019). Optimal Timing of Onshore Wind Repowering in Germany under Policy Regime Changes: A Real Options Analysis. Energies, 12(24), 4703. https://doi.org/10.3390/en12244703