Multi-Period Newsvendor Problem for the Management of Battery Energy Storage Systems in Support of Distributed Generation
Abstract
:1. Introduction
- Investigating the analogy between the inventory management of regular commodities and the management of energy storage system;
- Developing a novel variant of the classical newsvendor model for the management of the storage device in the presence of intermittent sources and uncertain loads. A single user’s perspective has been considered in order to optimize the use of the battery energy storage system minimizing its energy cost.
2. Literature Review
2.1. Economic Models for the Electrical Energy Storage Systems
2.2. Inventory Models with Energy Considerations
3. Model Development
3.1. Notation
| Levelized cost of energy for the BESS (€/kWh) | |
| Levelized cost of energy for the photovoltaic system (€/kWh) | |
| Battery degradation per cycle (-) | |
| Energy demand rate at period with probability distribution (kWh) | |
| Depth of discharge (-) | |
| Maximum level of energy stored (kWh) | |
| Minimum level of energy stored (kWh) | |
| Amount of energy stored at time (kWh) | |
| Inventory level at the end of period (kWh) | |
| Charging efficiency of the BESS (-) | |
| Discharging efficiency of the BESS (-) | |
| Energy price for purchasing a kWh from the grid (€/kWh) | |
| Energy price for selling a kWh from the PV system to the grid (€/kWh) | |
| Quantity of energy charged in the BESS (kWh) | |
| Energy production rate of the PV system at period distributed with (kWh) | |
| State of charge (-) | |
| Number of cycles already performed by the BESS (cycles) | |
| Deteriorating rate due to self-discharge (-) | |
| Inventory level at the beginning of period (kWh) |
3.2. Problem Definition
- The conversion losses can be considered into the definition of the relationship between the demand and the production rate as for the production of defective items. Moreover, the energy stored in the BESS continues to perish at a constant rate because of the self-discharge losses and, thus, the model should consider deteriorating items.
- BESS capacity degradation can be modeled as inventory models with space restrictions [30], which may degrade over time.
- Safety stock (SS) are taken into account to prevent issues related to the complete discharge.
- Uncertain and intermittent energy demand, , and production, rates defined through stochastic distributions;
- BESS parameters are fixed over time (i.e., static model);
- The amount of safety stocks corresponds to the lower threshold of energy stored,
- Demand can be satisfied, at least partly, through the energy stored in the BESS and the unsatisfied demand is not backlogged which means that the excess demand cannot be met in a sequent period;
- Shortages are considered as lost sales and should be met with different energy source, such as through energy purchase from the grid. Furthermore, the shortage cost is proportional to the size of the shortage (i.e., the amount of energy demand exceeding the energy available in the BESS);
- Production and order costs are not considered as they are not differential;
- Every cycle can start without delay and thus no lead time are considered;
- Self-discharge losses are linearly proportional to the amount of energy stored in the BESS, , and are evaluated in the model as holding costs;
- The energy produced is first used to meet the demand and, then, the surplus energy is used to charge the BESS;
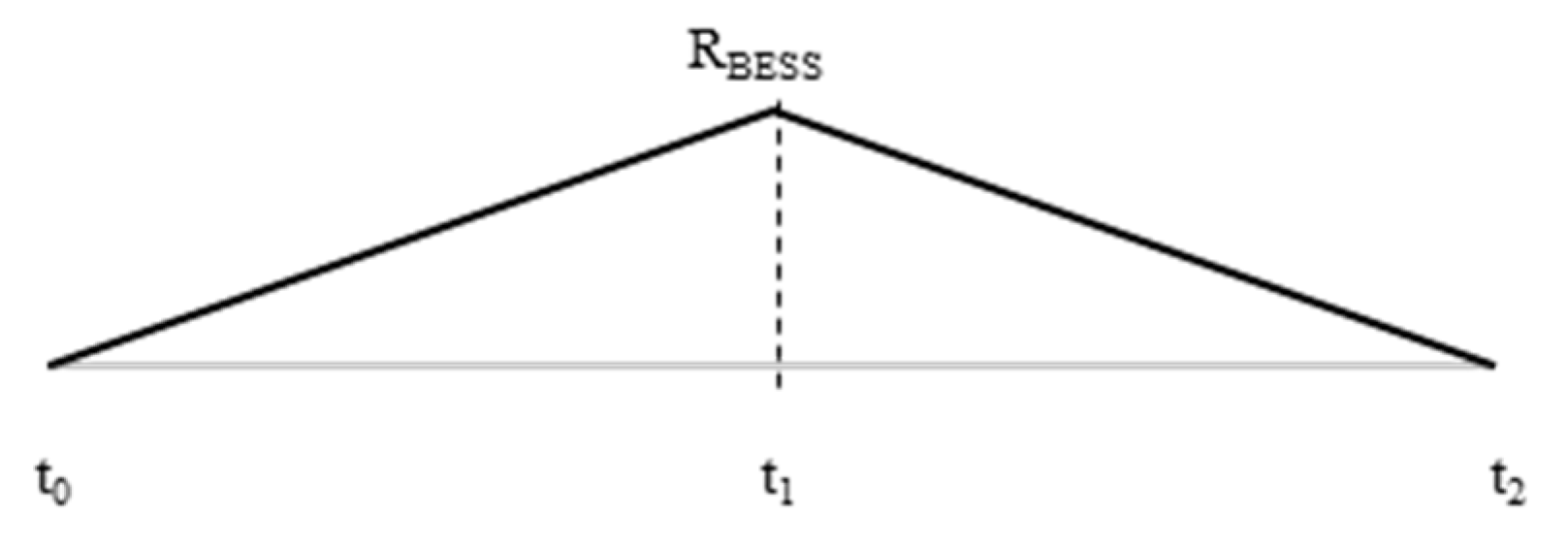
- The energy stored in the battery in period , , is limited between two limits (i.e., and which are defined in Equations (1) and (2), respectively), where the maximum energy that can be stored reduces every cycle because of BESS capacity degradation.
3.3. Model Formulation
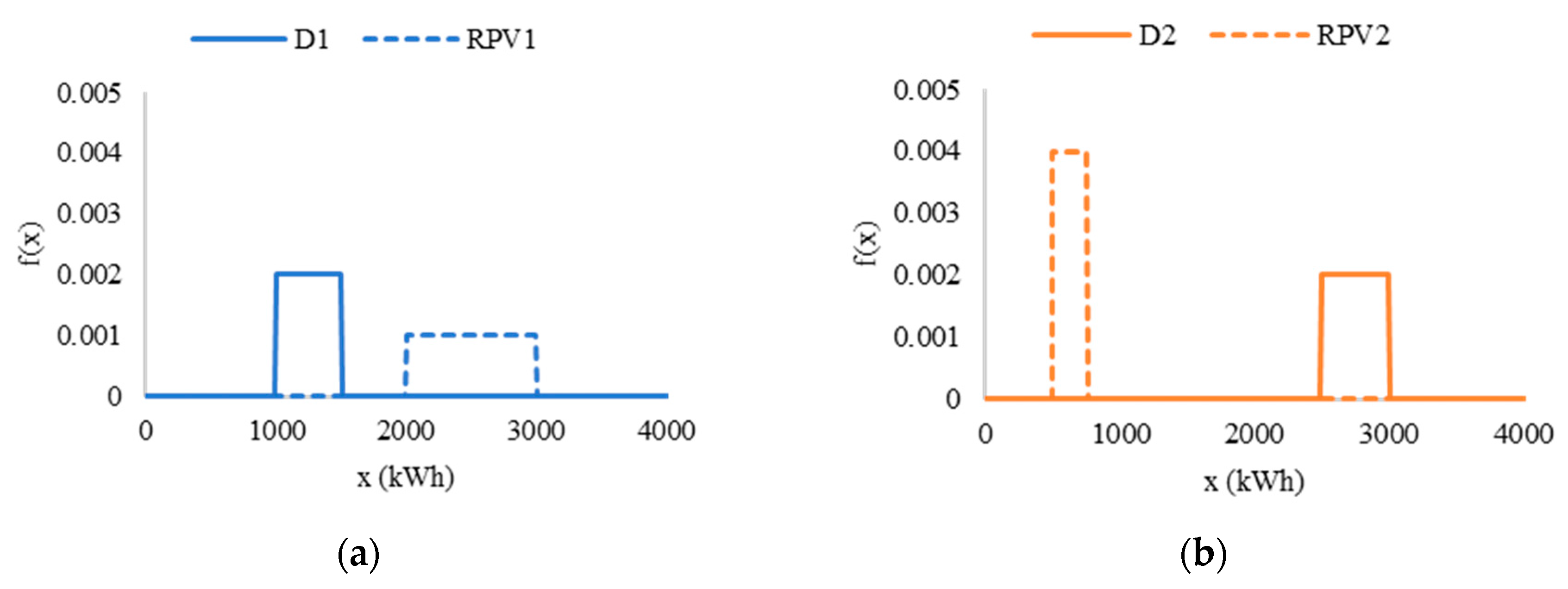
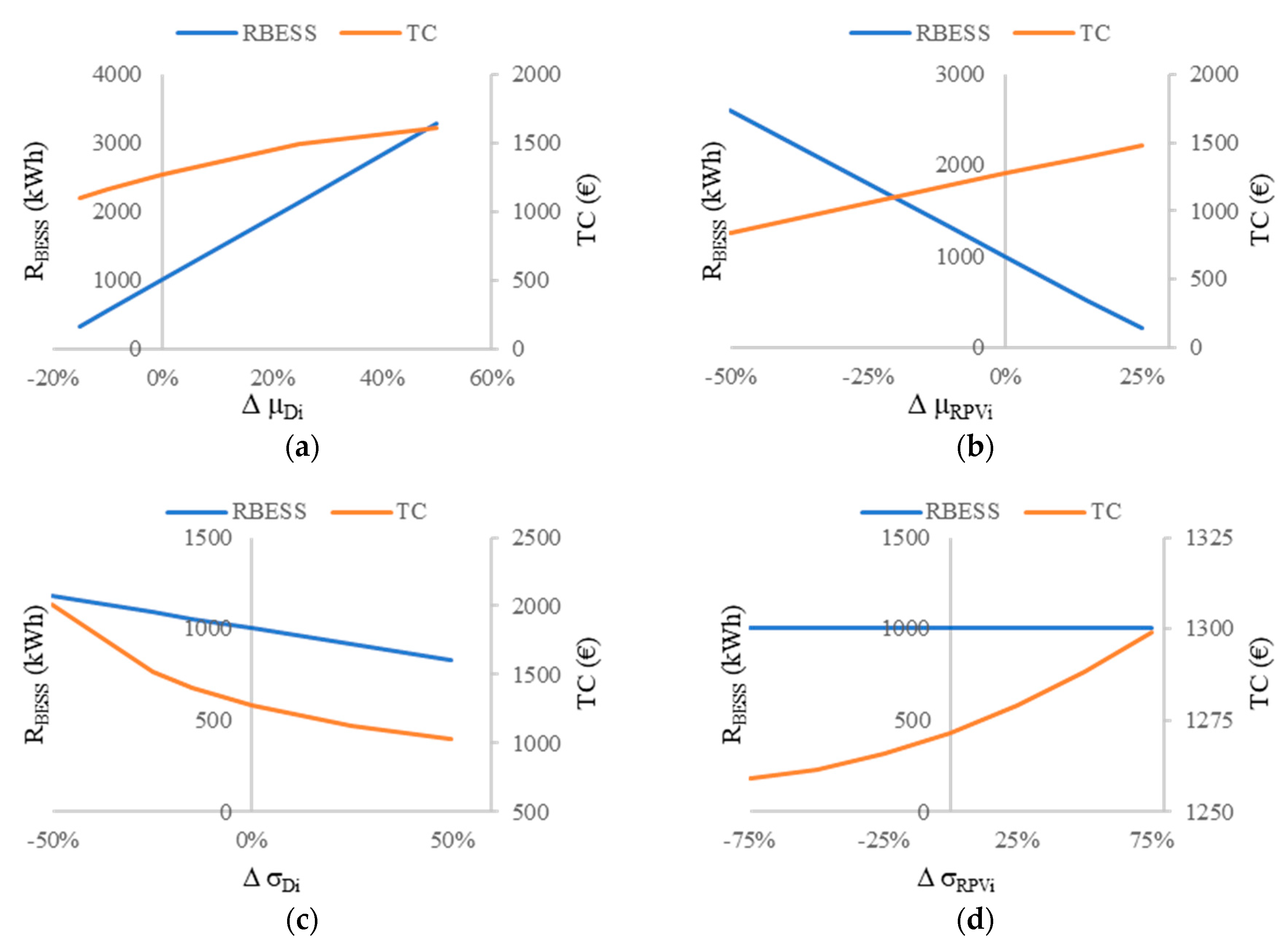
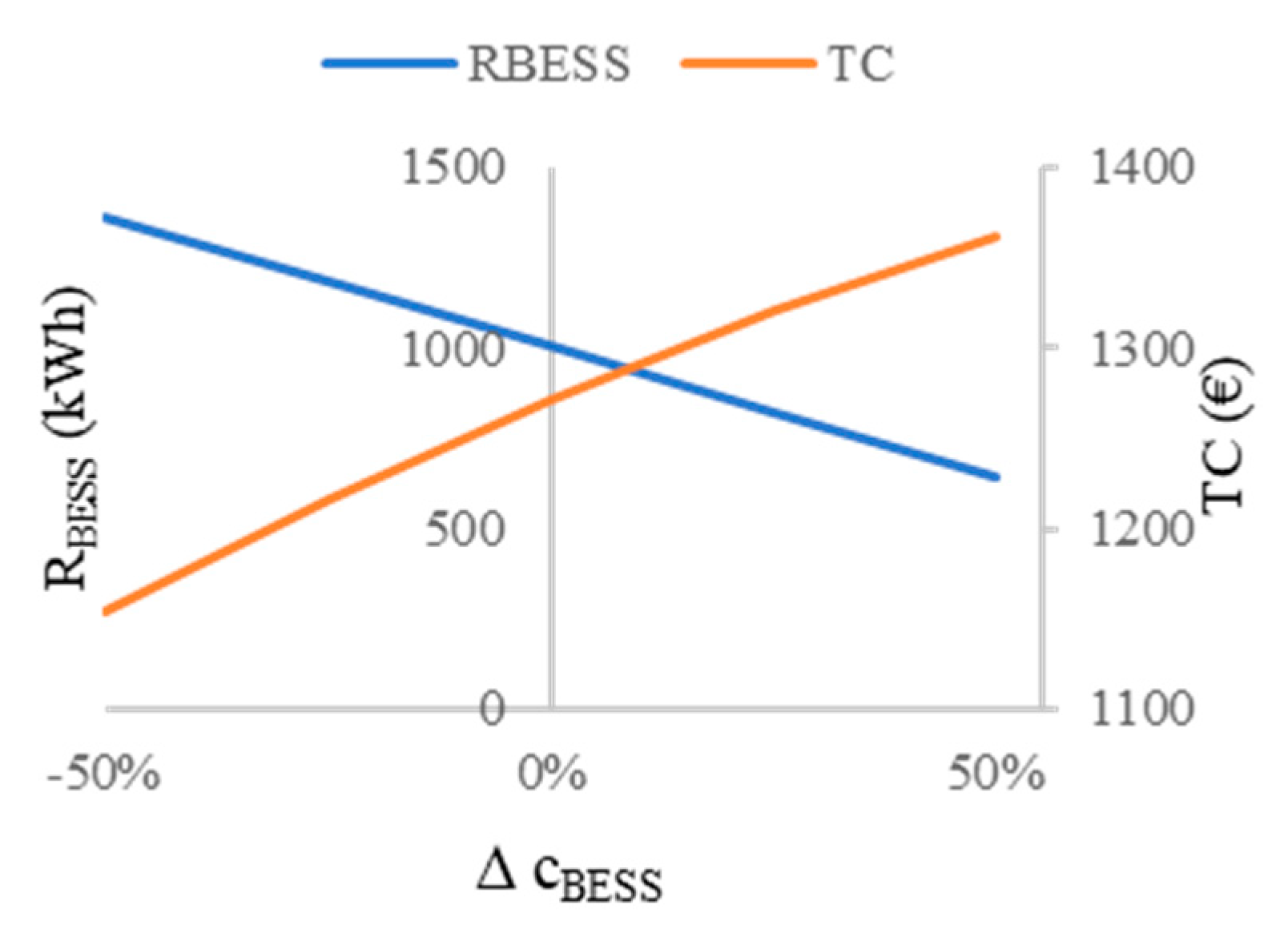
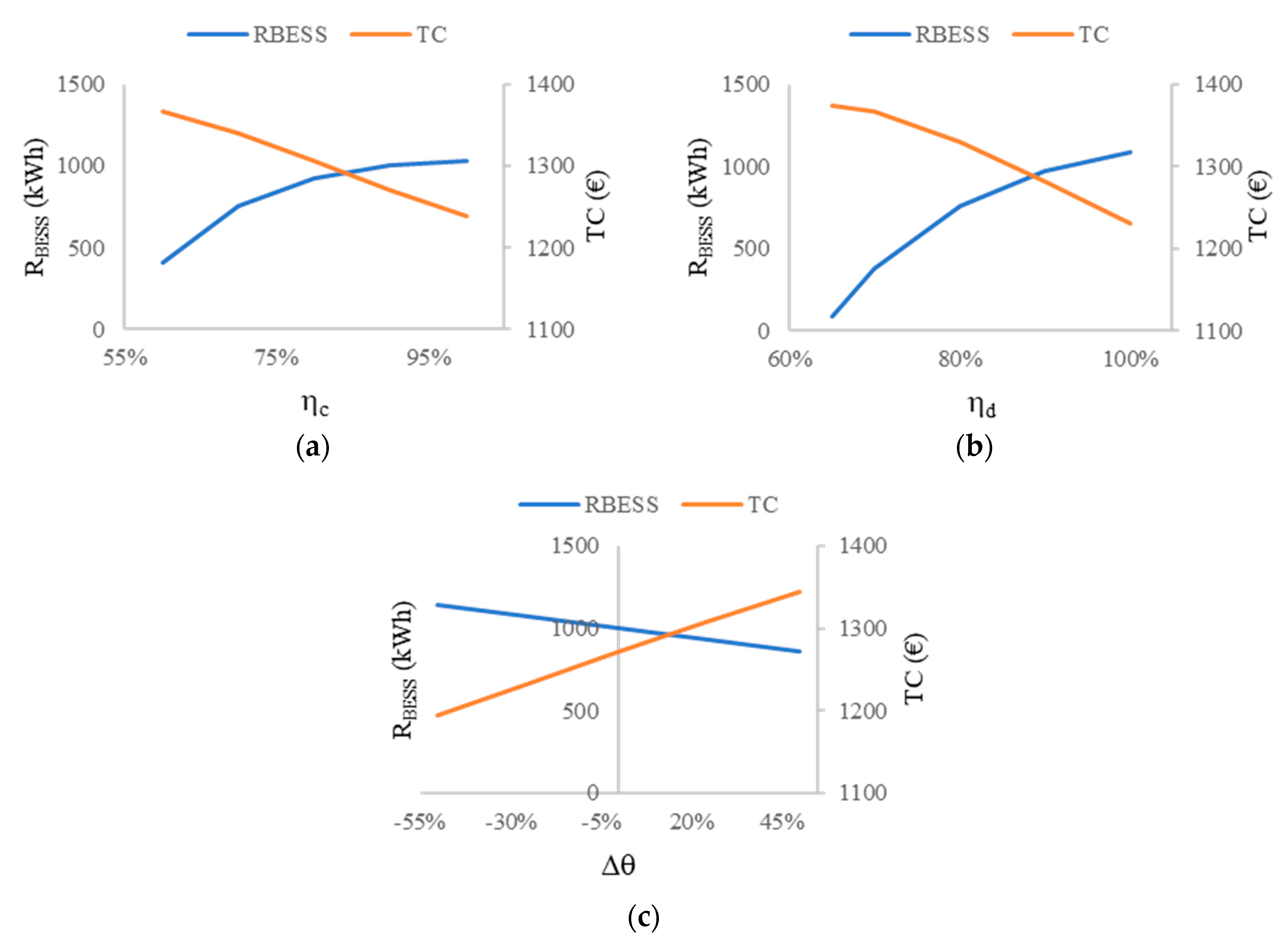
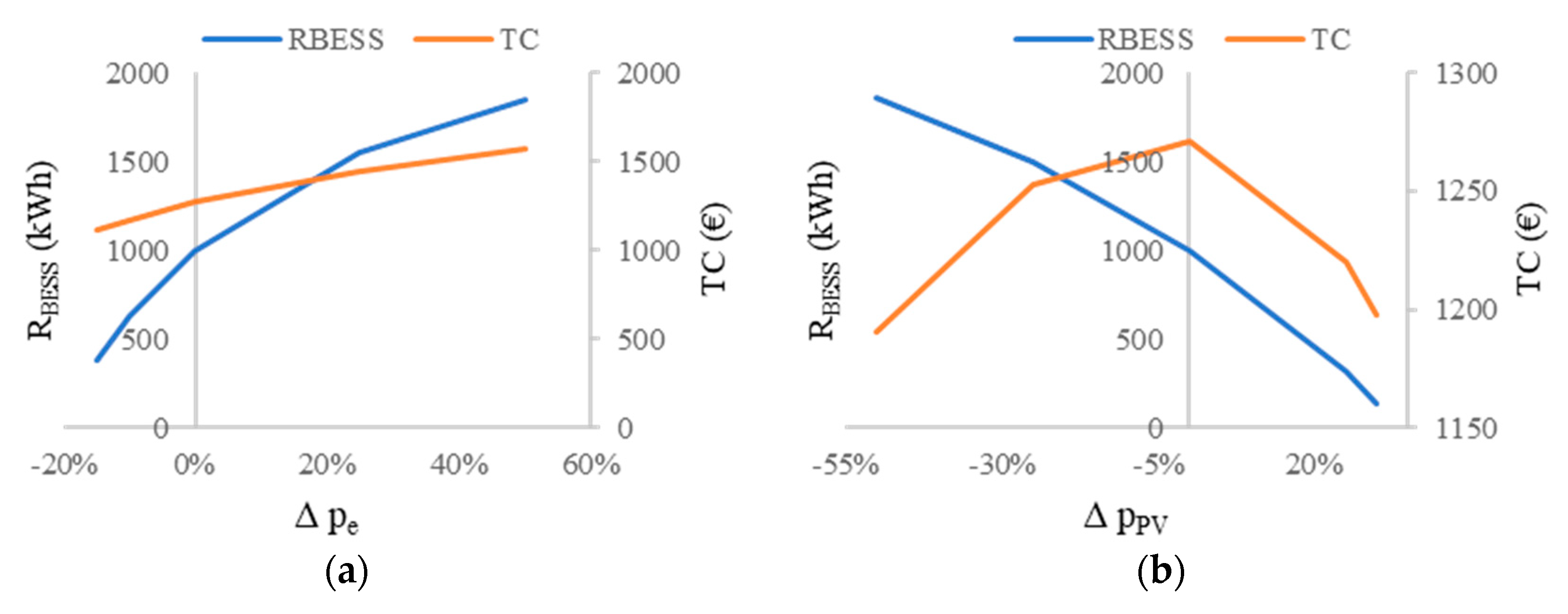
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Electrotechnical Commission (IEC). Electrical Energy Storage; International Electrotechnical Commission: Geneva, Switzerland, 2011. [Google Scholar]
- Marchi, B.; Zanoni, S.; Pasetti, M.; Zavanella, L.E. A queuing theory decision support model and discrete event simulations for the smart charging of electric vehicles. In Proceedings of the Summer School Francesco Turco, Palermo, Italy, 12–14 September 2018. [Google Scholar]
- Weitzel, T.; Glock, C.H. Energy management for stationary electric energy storage systems: A systematic literature review. Eur. J. Oper. Res. 2018, 264, 582–606. [Google Scholar] [CrossRef]
- Office of Electricity Delivery & Energy Reliability DOE Global Energy Storage Database. Available online: http://www.energystorageexchange.org/ (accessed on 01 October 2019).
- Chang, H.H.; Chiu, W.Y.; Sun, H.; Chen, C.M. User-centric multiobjective approach to privacy preservation and energy cost minimization in smart home. IEEE Syst. J. 2019, 13, 1030–1041. [Google Scholar] [CrossRef] [Green Version]
- Muñoz-Delgado, G.; Contreras, J.; Arroyo, J.M. Distribution System Expansion Planning Considering Non-Utility-Owned DG and an Independent Distribution System Operator. IEEE Trans. Power Syst. 2019, 34, 2588–2597. [Google Scholar] [CrossRef]
- Fares, R.L.; Webber, M.E. A flexible model for economic operational management of grid battery energy storage. Energy 2014, 78, 768–776. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Bremner, S.; Menictas, C.; Kay, M. Battery energy storage system size determination in renewable energy systems: A review. Renew. Sustain. Energy Rev. 2018, 91, 109–125. [Google Scholar] [CrossRef]
- Hoppmann, J.; Volland, J.; Schmidt, T.S.; Hoffmann, V.H. The economic viability of battery storage for residential solar photovoltaic systems—A review and a simulation model. Renew. Sustain. Energy Rev. 2014, 39, 1101–1118. [Google Scholar] [CrossRef]
- Nottrott, A.; Kleissl, J.; Washom, B. Energy dispatch schedule optimization and cost benefit analysis for grid-connected, photovoltaic-battery storage systems. Renew. Energy 2013, 55, 230–240. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H.; Aichhorn, A.; Zheng, J.; Greenleaf, M. Sizing Strategy of Distributed Battery Storage System With High Penetration of Photovoltaic for Voltage Regulation and Peak Load Shaving. IEEE Trans. Smart Grid 2014, 5, 982–991. [Google Scholar] [CrossRef]
- Marchi, B.; Zanoni, S.; Pasetti, M. A techno-economic analysis of Li-ion battery energy storage systems in support of PV distributed generation. In Proceedings of the Summer School Francesco Turco, Naples, Italy, 13–15 Septemebr 2016. [Google Scholar]
- Marchi, B.; Pasetti, M.; Zanoni, S. Effect of Demand Tariff Schemes in Presence of Distributed Photovoltaic Generation and Electrical Energy Storage. In Advances in Intelligent System and Computing; Murgul, V., Pasetti, M., Eds.; Springer International Publishing: Berlin, Germany, 2020; Volume 982, pp. 201–215. [Google Scholar]
- Dufo-López, R.; Bernal-Agustín, J.L.; Yusta-Loyo, J.M.; Domínguez-Navarro, J.A.; Ramírez-Rosado, I.J.; Lujano, J.; Aso, I. Multi-objective optimization minimizing cost and life cycle emissions of stand-alone PV -wind-diesel systems with batteries storage. Appl. Energy 2011, 88, 4033–4041. [Google Scholar] [CrossRef]
- Bortolini, M.; Gamberi, M.; Graziani, A. Technical and economic design of photovoltaic and battery energy storage system. Energy Convers. Manag. 2014, 86, 81–92. [Google Scholar] [CrossRef]
- Marchi, B.; Pasetti, M.; Zanoni, S. Life Cycle Cost Analysis for BESS Optimal Sizing. Energy Procedia 2017, 113, 127–134. [Google Scholar] [CrossRef]
- Lai, C.S.; Mcculloch, M.D. Levelized cost of electricity for solar photovoltaic and electrical energy storage. Appl. Energy 2017, 190, 191–203. [Google Scholar] [CrossRef]
- Harris, F.W. How many parts to make once. Fact. Mag. Manag. 1913, 10, 135–136. [Google Scholar] [CrossRef]
- Traft, E.W. The most economical production lot. Iron Age 1918, 101, 1410–1412. [Google Scholar]
- Ardak, P.S.; Borade, A.B. A State of Art on Economic Production Quantity Models. Int. J. Eng. Res. Technol. 2014, 3, 520–523. [Google Scholar]
- Misra, R.B. Optimum production lot size model for a system with deteriorating inventory. Int. J. Prod. Res. 1975, 13, 495–505. [Google Scholar] [CrossRef]
- Bakker, M.; Riezebos, J.; Teunter, R.H. Review of inventory systems with deterioration since 2001. Eur. J. Oper. Res. 2012, 221, 275–284. [Google Scholar] [CrossRef]
- Zavanella, L.E.; Marchi, B.; Zanoni, S.; Ferretti, I. Energy considerations for the economic production quantity and the joint economic lot sizing. J. Bus. Econ. 2019, 89, 845–865. [Google Scholar] [CrossRef]
- Wichmann, M.G.; Johannes, C.; Spengler, T.S. Energy-oriented Lot-Sizing and Scheduling considering energy storages. Int. J. Prod. Econ. 2019, 216, 204–214. [Google Scholar] [CrossRef]
- Abdel-malek, L.; Zanoni, S. Application of the newsvendor model with re-ordering opportunity in two-echelon supply chains. Int. J. Integr. Supply Manag. 2011, 6, 270–283. [Google Scholar] [CrossRef]
- Käki, A.; Liesiö, J.; Salo, A.; Talluri, S. Newsvendor decisions under supply uncertainty. Int. J. Prod. Res. 2015, 53, 1544–1560. [Google Scholar] [CrossRef]
- Saran, P.; Goentzel, J.; Siegert, C.W. Economic Analysis of Wind Plant and Battery Storage Operation using Supply Chain Management Techniques. Policy 2010, 1–8. [Google Scholar] [CrossRef]
- Schneider, M.; Biel, K.; Pfaller, S.; Schaede, H.; Rinderknecht, S.; Glock, C.H. Using inventory models for sizing energy storage systems: An interdisciplinary approach. J. Energy Storage 2016. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Technology Roadmap-Energy Storage; International Energy Agency: Paris, France, 2014. [Google Scholar] [CrossRef]
- Xu, K.; Leung, M.T. Stocking policy in a two-party vendor managed channel with space restrictions. Int. J. Prod. Econ. 2009, 117, 271–285. [Google Scholar] [CrossRef]
- Khouja, M. The single-period (news-vendor) problem: Literature review and suggestions for future research. Omega 1999, 27, 537–553. [Google Scholar] [CrossRef]
- Flammini, A.; Pasetti, M.; Rinaldi, S.; Bellagente, P.; Ciribini, A.C.; Tagliabue, L.C.; Zavanella, L.E.; Zanoni, S.; Oggioni, G.; Pedrazzi, G. A Living Lab and Testing Infrastructure for the Development of Innovative Smart Energy Solutions: The eLUX Laboratory of the University of Brescia. In Proceedings of the 2018 110th AEIT International Annual Conference, Bari, Italy, 3–5 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marchi, B.; Zanoni, S.; Pasetti, M. Multi-Period Newsvendor Problem for the Management of Battery Energy Storage Systems in Support of Distributed Generation. Energies 2019, 12, 4598. https://doi.org/10.3390/en12234598
Marchi B, Zanoni S, Pasetti M. Multi-Period Newsvendor Problem for the Management of Battery Energy Storage Systems in Support of Distributed Generation. Energies. 2019; 12(23):4598. https://doi.org/10.3390/en12234598
Chicago/Turabian StyleMarchi, Beatrice, Simone Zanoni, and Marco Pasetti. 2019. "Multi-Period Newsvendor Problem for the Management of Battery Energy Storage Systems in Support of Distributed Generation" Energies 12, no. 23: 4598. https://doi.org/10.3390/en12234598
APA StyleMarchi, B., Zanoni, S., & Pasetti, M. (2019). Multi-Period Newsvendor Problem for the Management of Battery Energy Storage Systems in Support of Distributed Generation. Energies, 12(23), 4598. https://doi.org/10.3390/en12234598






