An Acoustic Source Model for Applications in Low Mach Number Turbulent Flows, Such as a Large-Scale Wind Turbine Blade
Abstract
1. Introduction
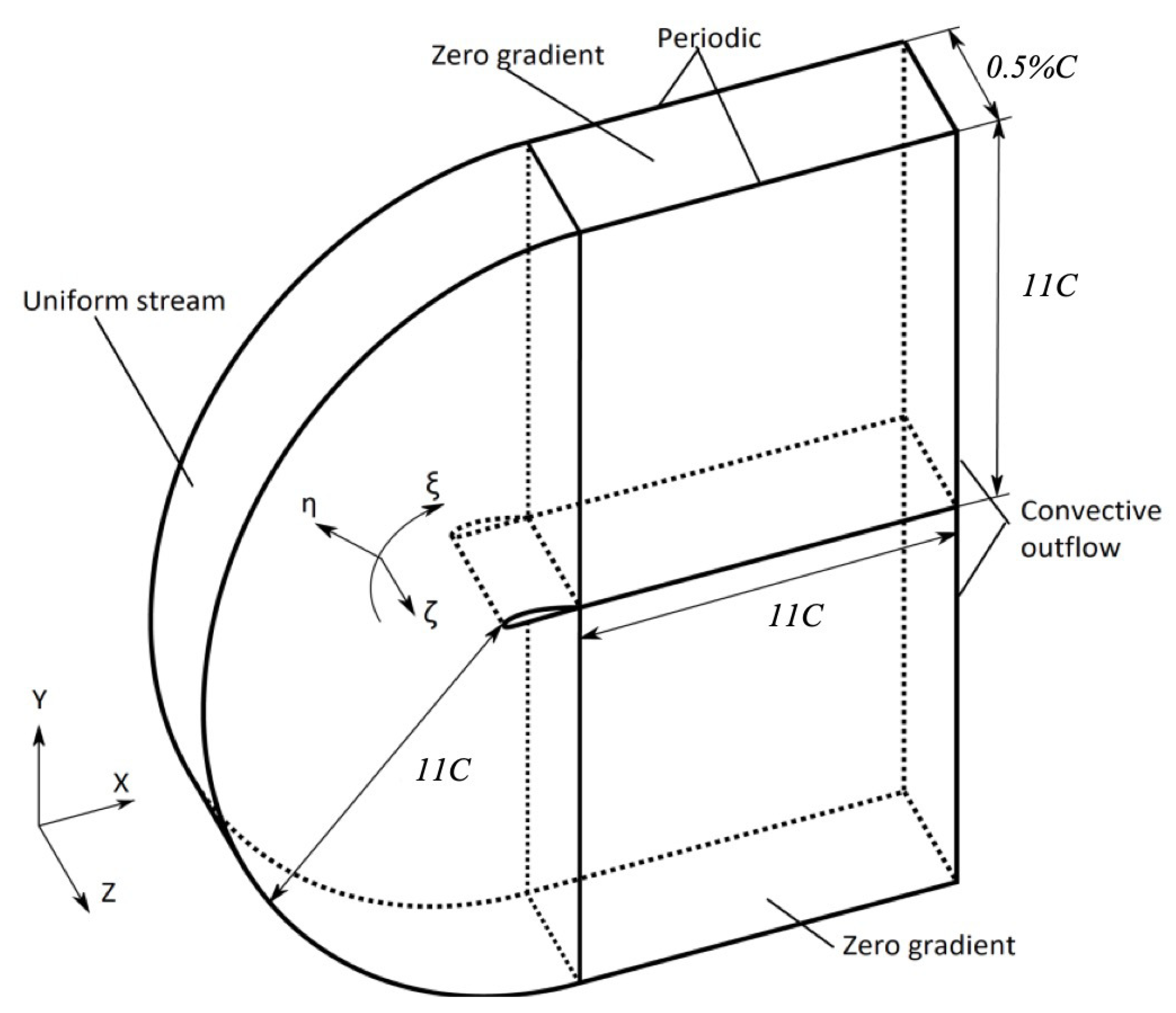
2. LES of Low Mach Number Turbulent Flows around NACA0012 Airfoil
2.1. Basic Equations and Smagorinsky Subgrid Scale (SGS) Model
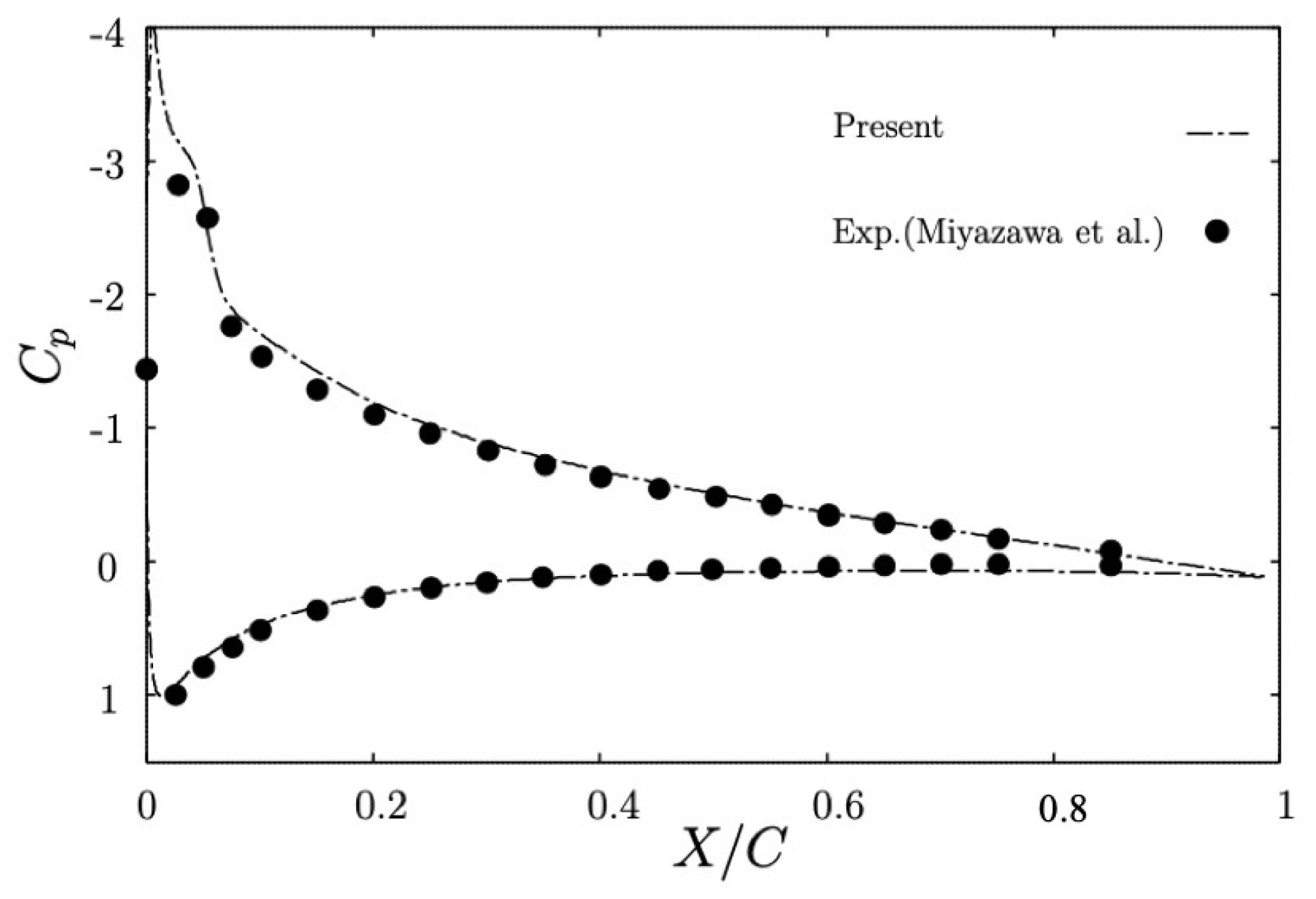
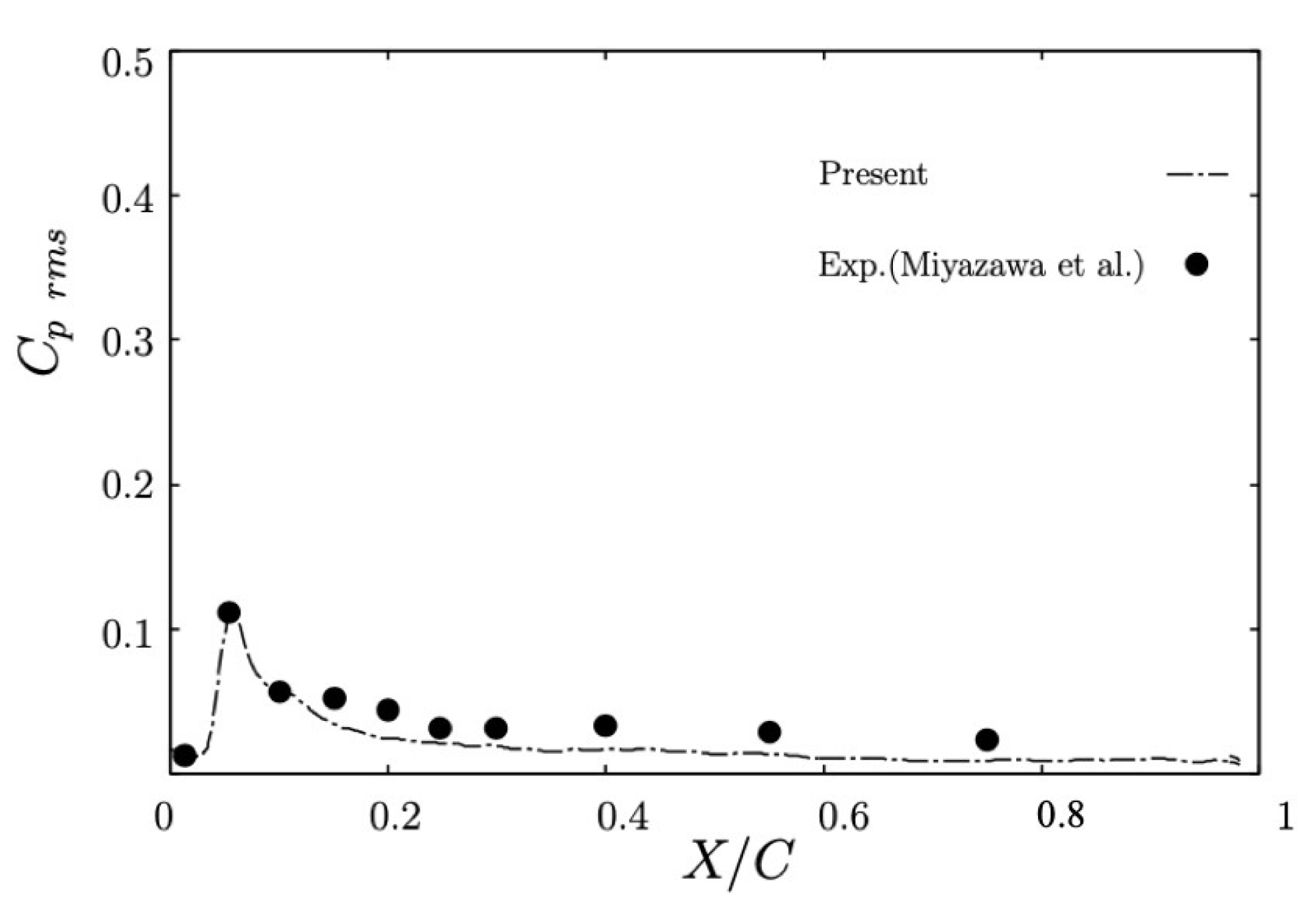
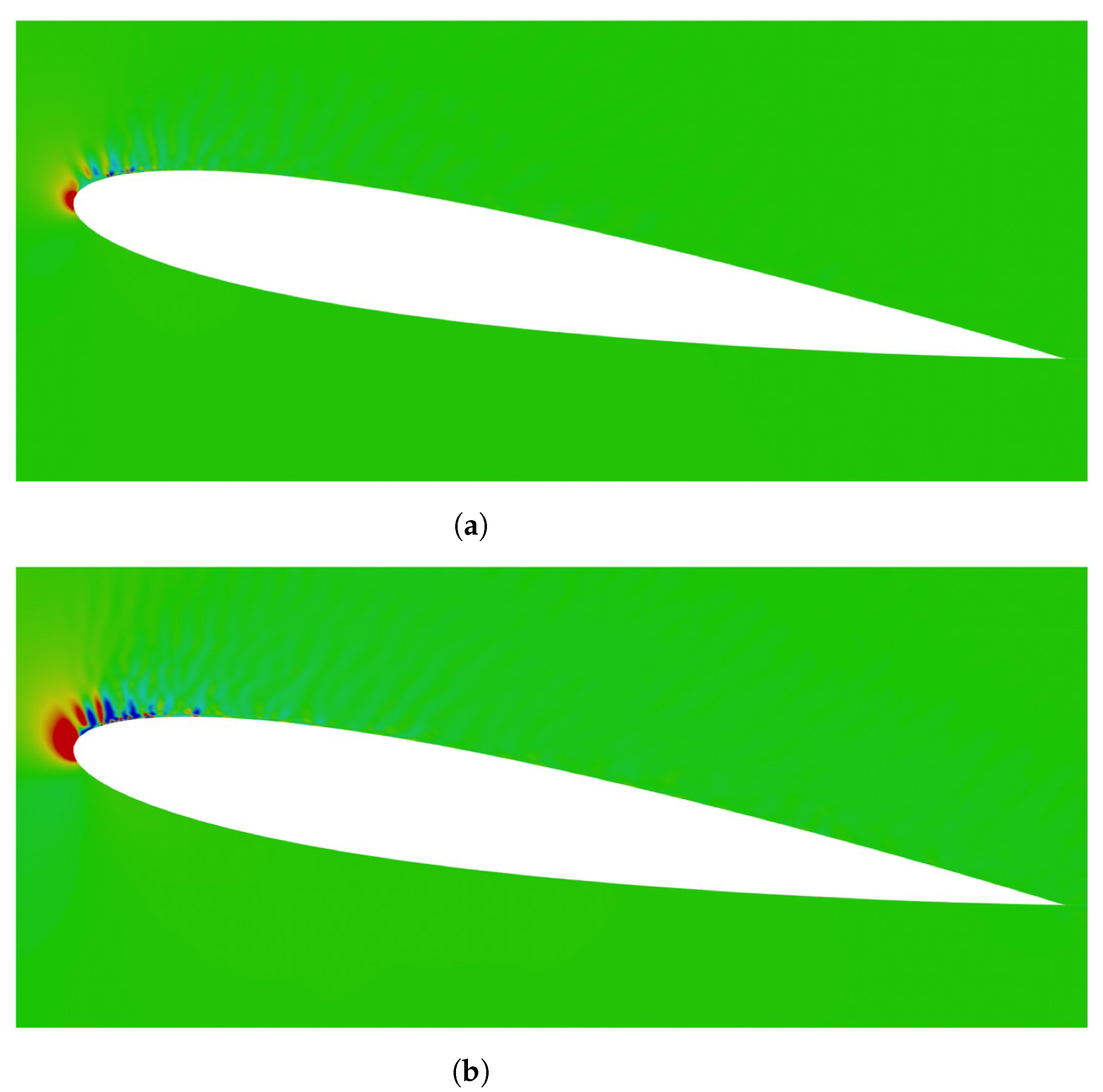
2.2. Validation of LES for Low Mach Number Turbulent Flows around NACA0012 Airfoil
3. Derivation of a New Acoustic Model
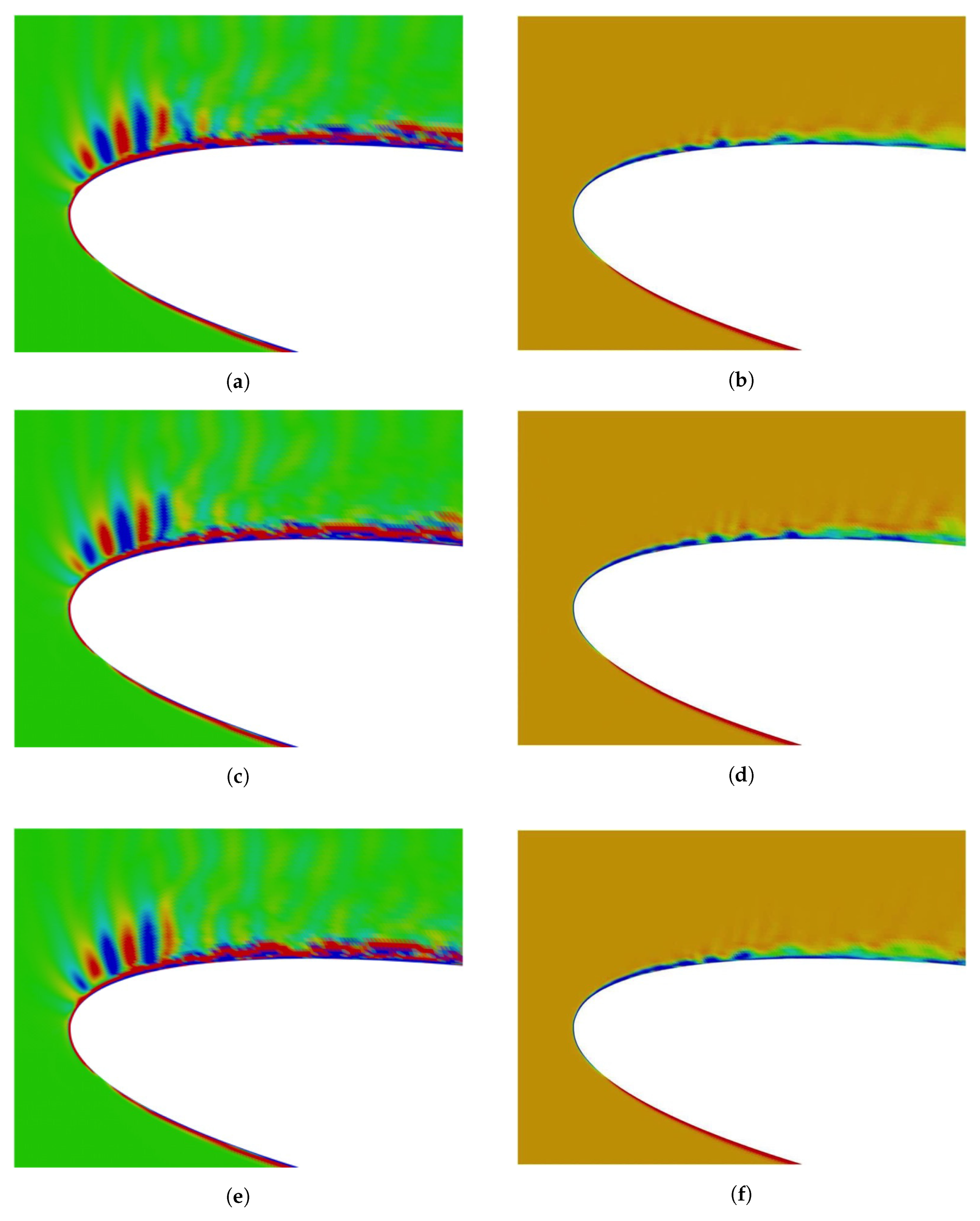
4. Results of the Acoustic Field around NACA0012 Airfoil
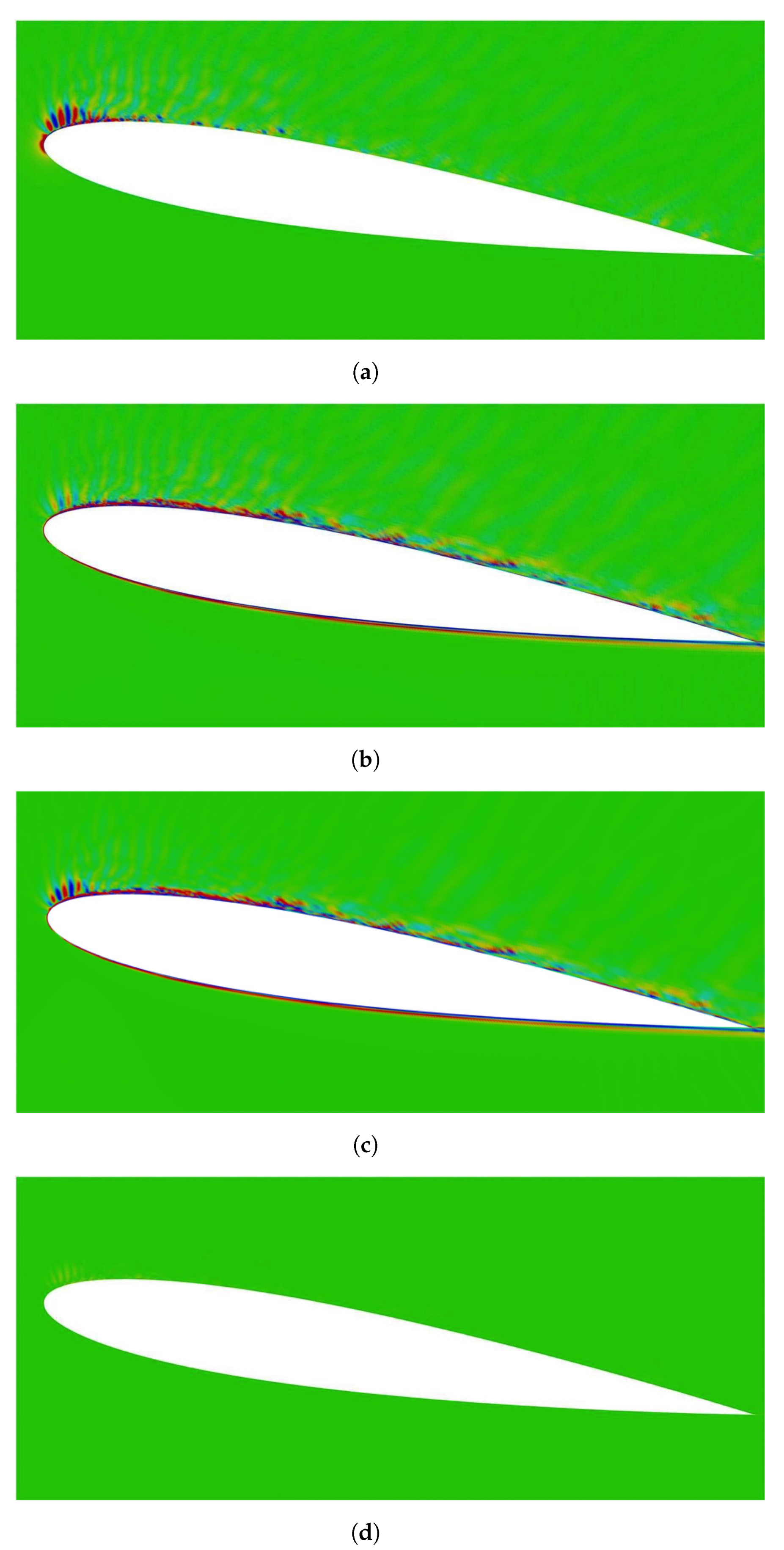
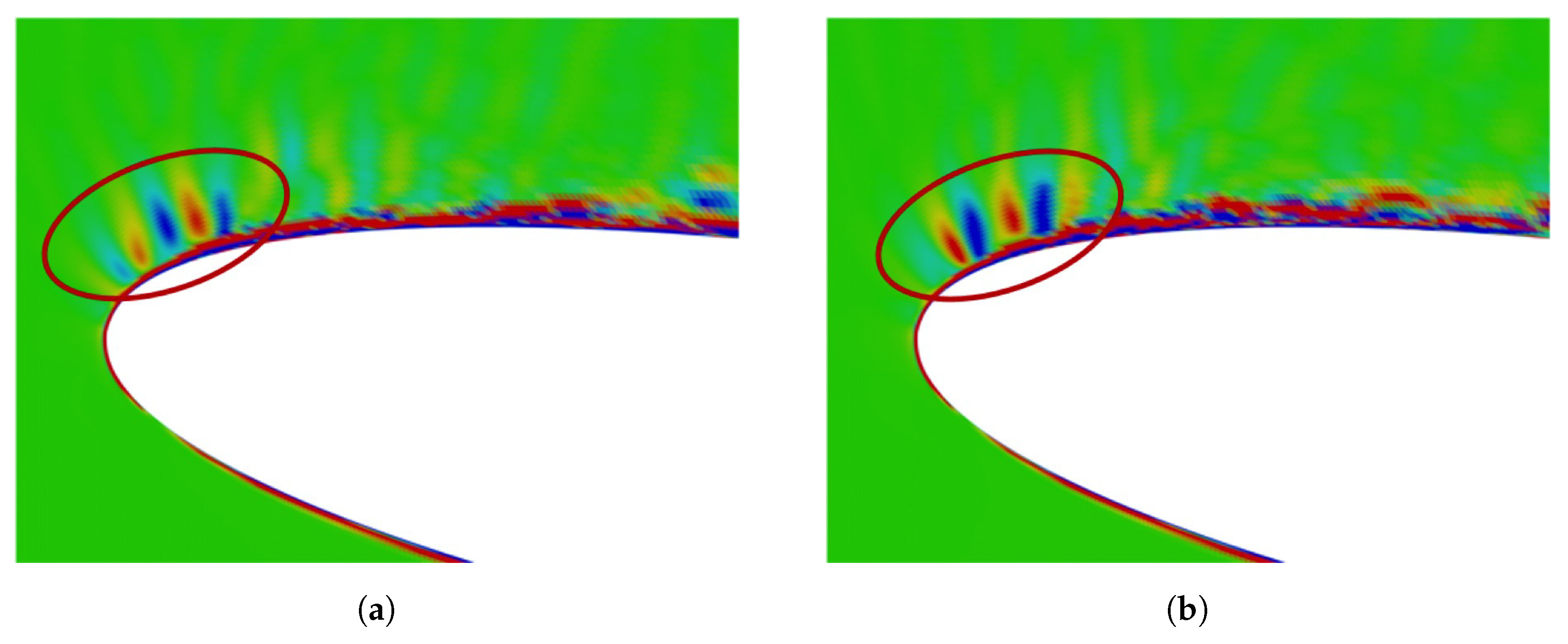
4.1. Comparison of Different Sound Source Detection
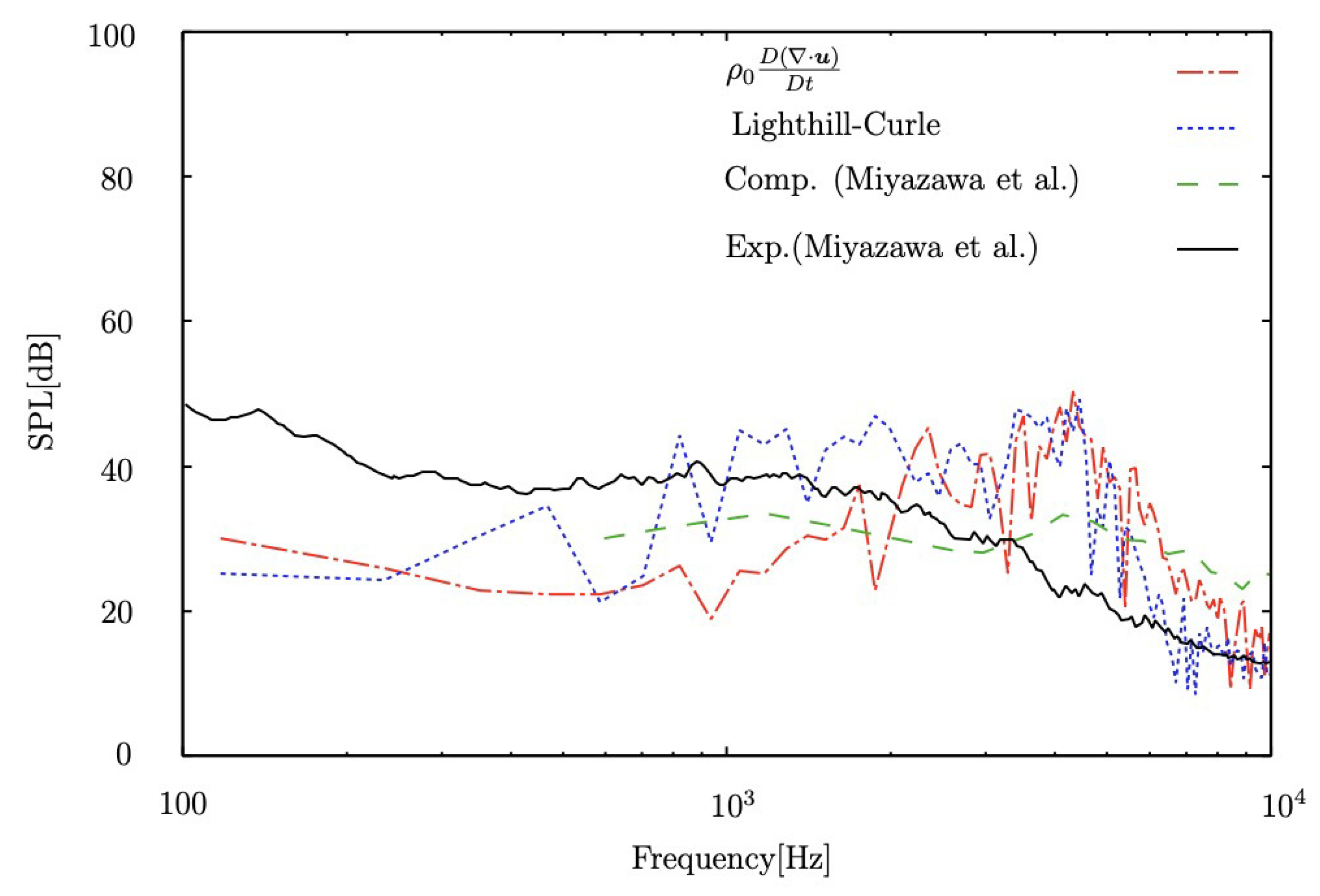
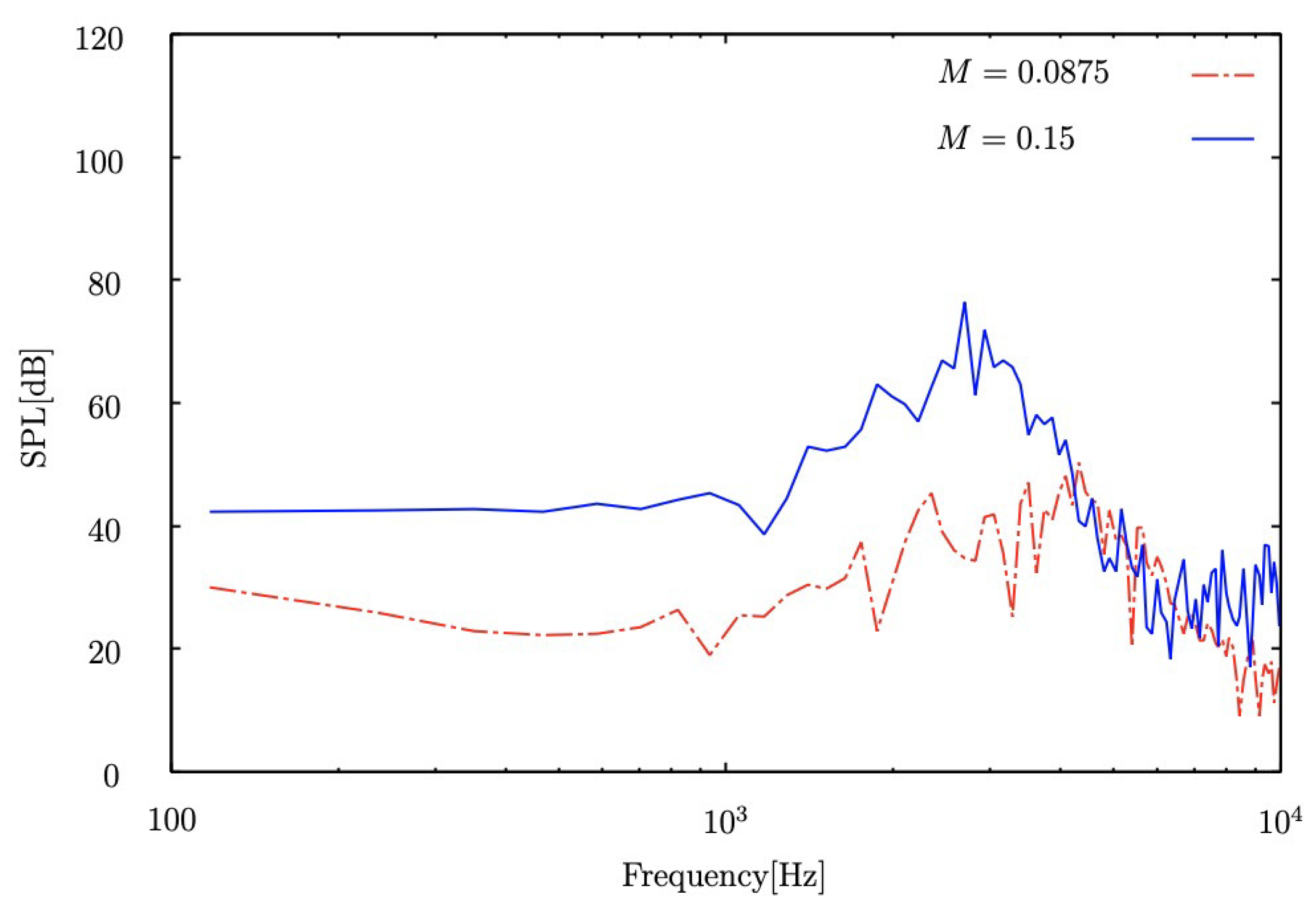
4.2. Comparison of Different Mach Numbers
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | computational Fluid Dynamics |
| CIP | Cubic interpolated pseudo particle |
| DNS | Direct numerical simulation |
| DSM | Dynamic Smagorinsky model |
| EU | European Union |
| LES | Large eddy simulation |
| RANS | Reynolds averaged numerical simulation |
| SGS | Subgrid-scales |
References
- Bai, W.; Lee, D.; Lee, K. Stochastic dynamic AC optimal power flow based on a multivariate short-term wind power scenario forecasting model. Energies 2017, 10, 2138. [Google Scholar] [CrossRef]
- Ageborg Morsing, J.; Smith, M.; Ogren, M.; Thorsson, P.; Pedersen, E.; Forssen, J.; Persson Waye, K. Wind turbine noise and sleep: Pilot studies on the influence of noise characteristics. Int. J. Environ. Res. Public Health 2018, 15, 2573. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.J.; Shen, W.Z.; Barlas, E.; Bertagnolio, F.; Sorensen, J.N. Wind turbine noise generation and propagation modeling at DTU Wind Energy: A review. Renew. Sustain. Energy Rev. 2018, 88, 133–150. [Google Scholar] [CrossRef]
- World Health Organization. Burden of Disease from Environmental Noise: Quantification of Healthy Life Years Lost in Europe; World Health Organization, WHO Regional Office for Europe: Copenhagen, Denmark, 2017. [Google Scholar]
- Onakpoya, I.J.; OSullivan, J.; Thompson, M.J.; Heneghan, C.J. The effect of wind turbine noise on sleep and quality of life: A systematic review and meta-analysis of observational studies. Environ. Int. 2015, 82, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Wagner, S.; Bareiss, R.; Guidati, G. Wind Turbine Noise; Springer Science & Business Media: New York, NY, USA, 1996. [Google Scholar]
- Ghasemian, M.; Ashrafi, Z.N.; Sedaghat, A. A review on computational fluid dynamic simulation techniques for Darrieus vertical axis wind turbines. Energy Convers. Manag. 2017, 149, 87–100. [Google Scholar] [CrossRef]
- Li, Q.A.; Maeda, T.; Kamada, Y.; Murata, J.; Kawabata, T.; Shimizu, K.; Ogasawara, T.; Nakai, A.; Kasuya, T. Wind tunnel and numerical study of a straight-bladed Vertical Axis Wind Turbine in three-dimensional analysis (Part II: For predicting flow field and performance). Energy 2016, 104, 295–307. [Google Scholar] [CrossRef]
- Chen, Y.; Lian, Y. Numerical investigation of vortex dynamics in an H-rotor vertical axis wind turbine. Eng. Appl. Comput. Fluid Mech. 2015, 9, 21–32. [Google Scholar] [CrossRef]
- Oerlemans, S. Reduction of wind turbine noise using blade trailing edge devices. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016. [Google Scholar]
- Lighthill, M.J. On sound generated aerodynamically I. General theory. Proc. R. Soc. Lond. Ser. A 1952, 211, 564–587. [Google Scholar]
- Lighthill, M.J. On sound generated aerodynamically II. Turbulence as a source of sound. Proc. R. Soc. Lond. Ser. A 1954, 222, 1–32. [Google Scholar]
- Sandberg, R.D.; Jones, L.E. Direct numerical simulations of low Reynolds number flow over airfoils with trailing-edge serrations. J. Sound Vib. 2011, 330, 3818–3831. [Google Scholar] [CrossRef]
- Wolf, W.R.; Lele, S.K. Trailing-edge noise predictions using compressible large-eddy simulation and acoustic analogy. AIAA J. 2012, 50, 2423–2434. [Google Scholar] [CrossRef]
- Sandberg, R.D.; Sandham, N.D. Direct numerical simulation of turbulent flow past a trailing edge and the associated noise generation. J. Fluid Mech. 2008, 596, 353–385. [Google Scholar] [CrossRef]
- Bogey, C.; Bailly, C.; Juve, D. Computation of flow noise using source terms in Linearized Euler’s equations. AIAA J. 2002, 40, 235–243. [Google Scholar] [CrossRef]
- Jawahar, H.K.; Lin, Y.; Savill, M. Large eddy simulation of airfoil self-noise using OpenFOAM. Aircraft Eng. Aerosp. Technol. 2018, 90, 126–133. [Google Scholar]
- Curle, N. The influence of solid boundaries upon aerodynamic sound. Proc. R. Soc. Lond. Ser. A 1955, 231, 505–514. [Google Scholar]
- Powell, A. Theory of vortex sound. J. Acoust. Soc. Am. 1964, 36, 177–195. [Google Scholar] [CrossRef]
- Amiet, R.K. Noise due to turbulent flow past a trailing edge. J. Sound Vib. 1976, 47, 387–393. [Google Scholar] [CrossRef]
- Wang, M.; Freund, J.B.; Lele, S.K. Computational prediction of flow-generated sound. Annu. Rev. Fluid Mech. 2006, 38, 483–512. [Google Scholar] [CrossRef]
- Howe, M.S. Theory of Vortex Sound; Cambridge University Press: Cambridge, UK, 2003; Volume 33. [Google Scholar]
- Möhring, W. On vortex sound at low Mach number. J. Fluid Mech. 1978, 85, 685–691. [Google Scholar] [CrossRef]
- Takaishi, T.; Ikeda, M.; Kato, C. Method of evaluating dipole sound source in a finite computational domain. J. Acoust. Soc. Am. 2004, 116, 1427–1435. [Google Scholar] [CrossRef]
- Ewert, R.; Schroder, W. On the simulation of trailing edge noise with a hybrid LES/APE method. J. Sound Vib. 2004, 270, 509–524. [Google Scholar] [CrossRef]
- Hutcheson, F.V.; Brooks, T.F.; Stead, D.J. Measurement of the noise resulting from the interaction of turbulence with a lifting surface. Int. J. Aeroacoust. 2012, 11, 675–700. [Google Scholar] [CrossRef]
- Hutcheson, F.V.; Brooks, T.F. Noise radiation from single and multiple rod configurations. Int. J. Aeroacoust. 2012, 11, 291–333. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Yabe, T.; Wang, P.Y. Unified numerical procedure for compressible and incompressible fluid. J. Phys. Soc. Jpn. 1991, 60, 2105–2108. [Google Scholar] [CrossRef]
- Miyazawa, M. Large eddy simulation of flow around an isolated aerofoil and noise prediction. In Proceedings of the 5th JSME-KSME Joint Fluids Engineering Conference, Nagoya, Japan, 14–18 July 2002; pp. 546–551. [Google Scholar]
- Okita, K.; Kajishima, T. Numerical simulation of unsteady cavitating flows around a hydrofoil. Trans. Jpn. Soc. Mech. Eng. Ser. B 2002, 68, 637–644. [Google Scholar] [CrossRef]
- Kajishima, T.; Ohta, T.; Okazaki, K.; Miyake, Y. High-order finite-difference method for incompressible flows using collocated grid system. JSME Int. J. Ser. B 1998, 41, 830–839. [Google Scholar] [CrossRef]
- Han, C.; Kajishima, T. Large eddy simulation of weakly compressible turbulent flows around an airfoil. J. Fluid Sci. Technol. 2014, 9, JFST0063. [Google Scholar] [CrossRef]
- Tang, H.; Lei, Y.; Li, X.; Fu, Y. Large-Eddy Simulation of an Asymmetric Plane Diffuser: Comparison of Different Subgrid Scale Models. Symmetry 2019, 11, 1337. [Google Scholar] [CrossRef]
- Tang, H.; Lei, Y.; Fu, Y. Noise Reduction Mechanisms of an Airfoil with Trailing Edge Serrations at Low Mach Number. Appl. Sci. 2019, 9, 3784. [Google Scholar] [CrossRef]
- Tang, H.; Lei, Y.; Li, X.; Fu, Y. Numerical Investigation of the Aerodynamic Characteristics and Attitude Stability of a Bio-Inspired Corrugated Airfoil for MAV or UAV Applications. Energies 2019, 12, 4021. [Google Scholar] [CrossRef]
- Tamura, A.; Kikuchi, K.; Takahashi, T. Residual cutting method for elliptic boundary value problems. J. Comput. Phys. 1997, 137, 247–264. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, H.; Lei, Y.; Li, X. An Acoustic Source Model for Applications in Low Mach Number Turbulent Flows, Such as a Large-Scale Wind Turbine Blade. Energies 2019, 12, 4596. https://doi.org/10.3390/en12234596
Tang H, Lei Y, Li X. An Acoustic Source Model for Applications in Low Mach Number Turbulent Flows, Such as a Large-Scale Wind Turbine Blade. Energies. 2019; 12(23):4596. https://doi.org/10.3390/en12234596
Chicago/Turabian StyleTang, Hui, Yulong Lei, and Xingzhong Li. 2019. "An Acoustic Source Model for Applications in Low Mach Number Turbulent Flows, Such as a Large-Scale Wind Turbine Blade" Energies 12, no. 23: 4596. https://doi.org/10.3390/en12234596
APA StyleTang, H., Lei, Y., & Li, X. (2019). An Acoustic Source Model for Applications in Low Mach Number Turbulent Flows, Such as a Large-Scale Wind Turbine Blade. Energies, 12(23), 4596. https://doi.org/10.3390/en12234596




