Model Predictive Control-Based Coordinated Control Algorithm with a Hybrid Energy Storage System to Smooth Wind Power Fluctuations
Abstract
1. Introduction
2. Fluctuation Mitigation Requirements for Wind Power Integration
2.1. Composition of Wind Power Signals
2.2. Fluctuation Mitigation Requirements
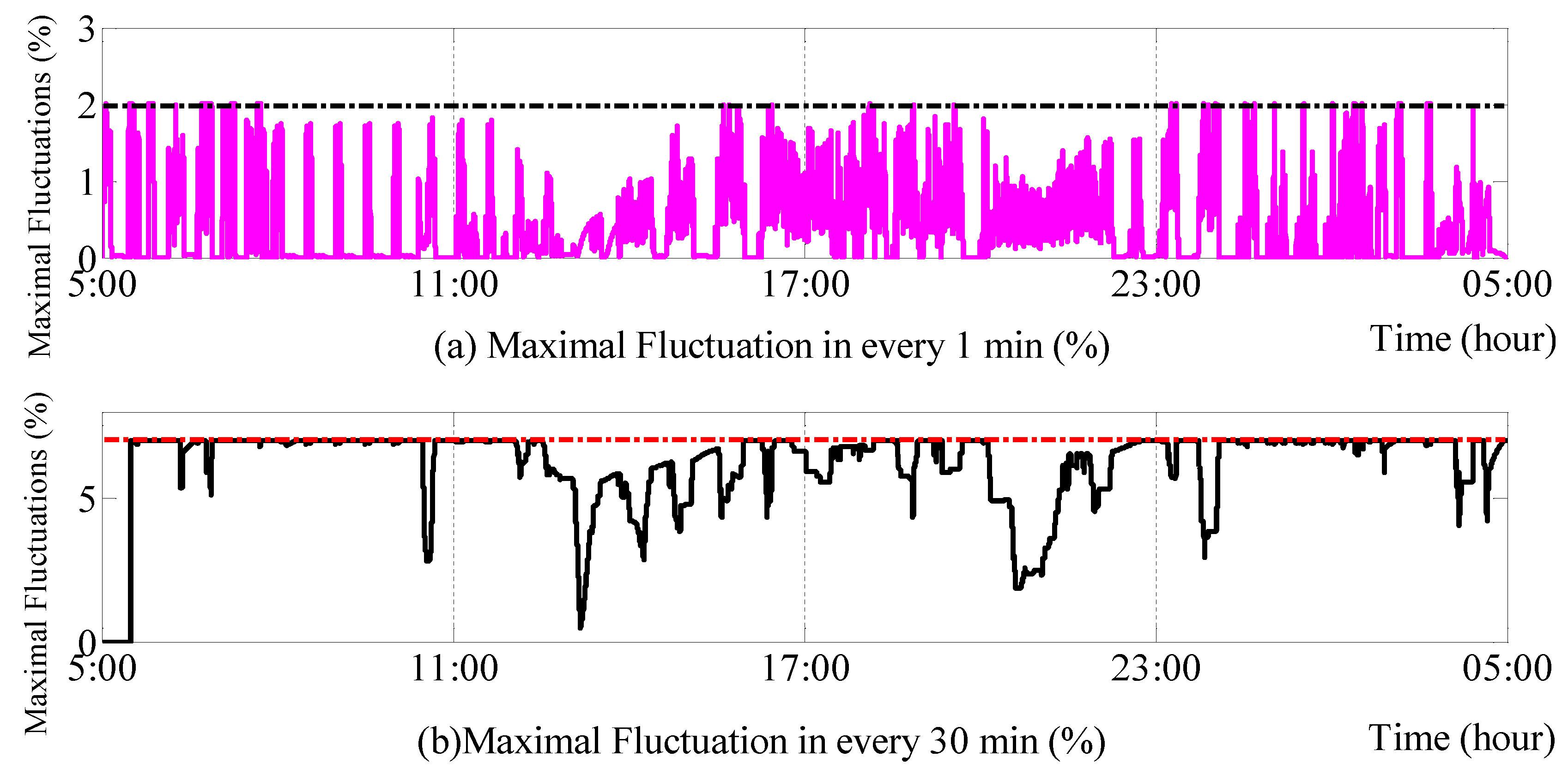
2.2.1. One-Minute Fluctuation Mitigation Requirements
2.2.2. Thirty-Minute Fluctuation Mitigation Requirements
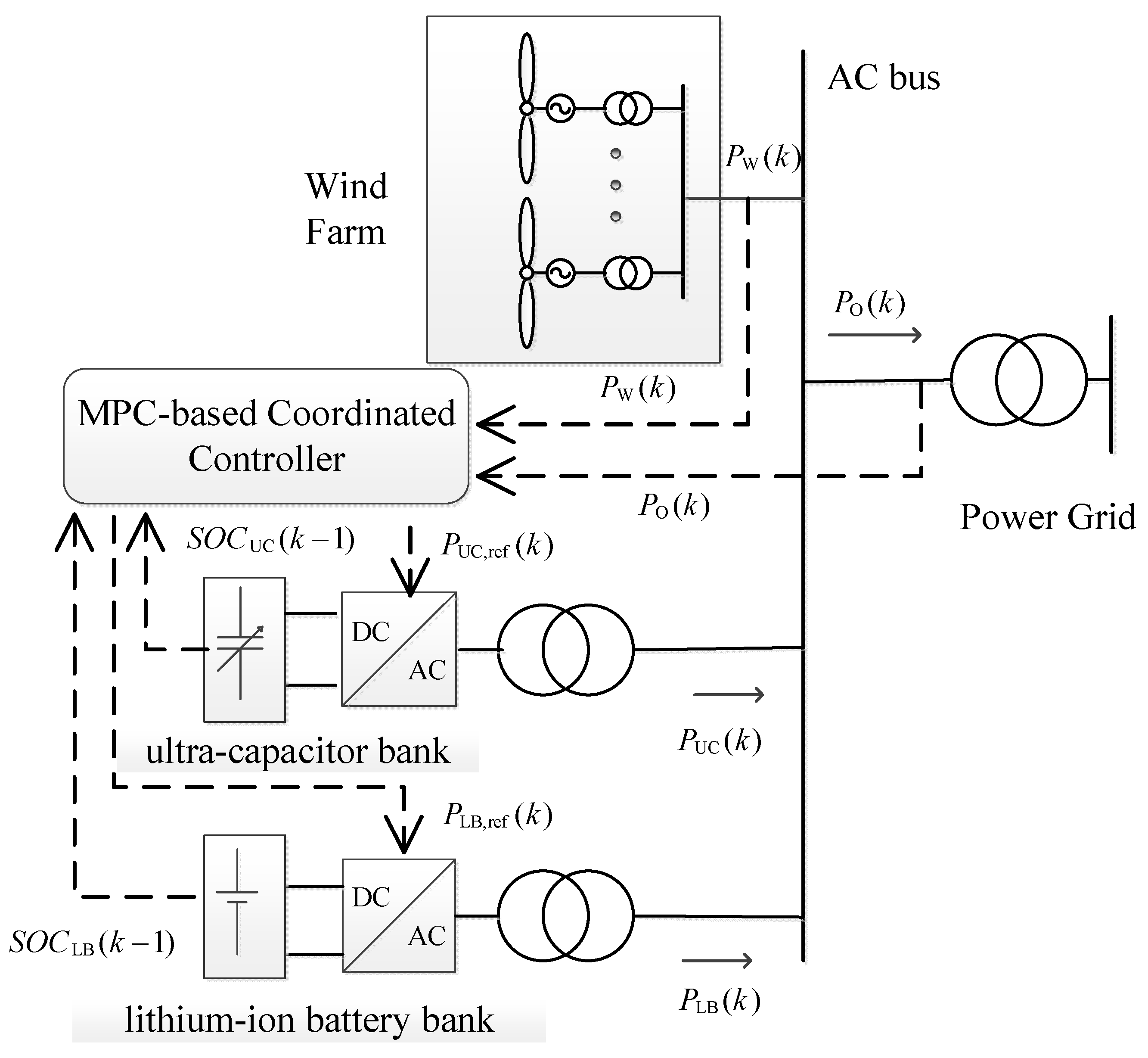
3. MPC-Based Coordination Control Model
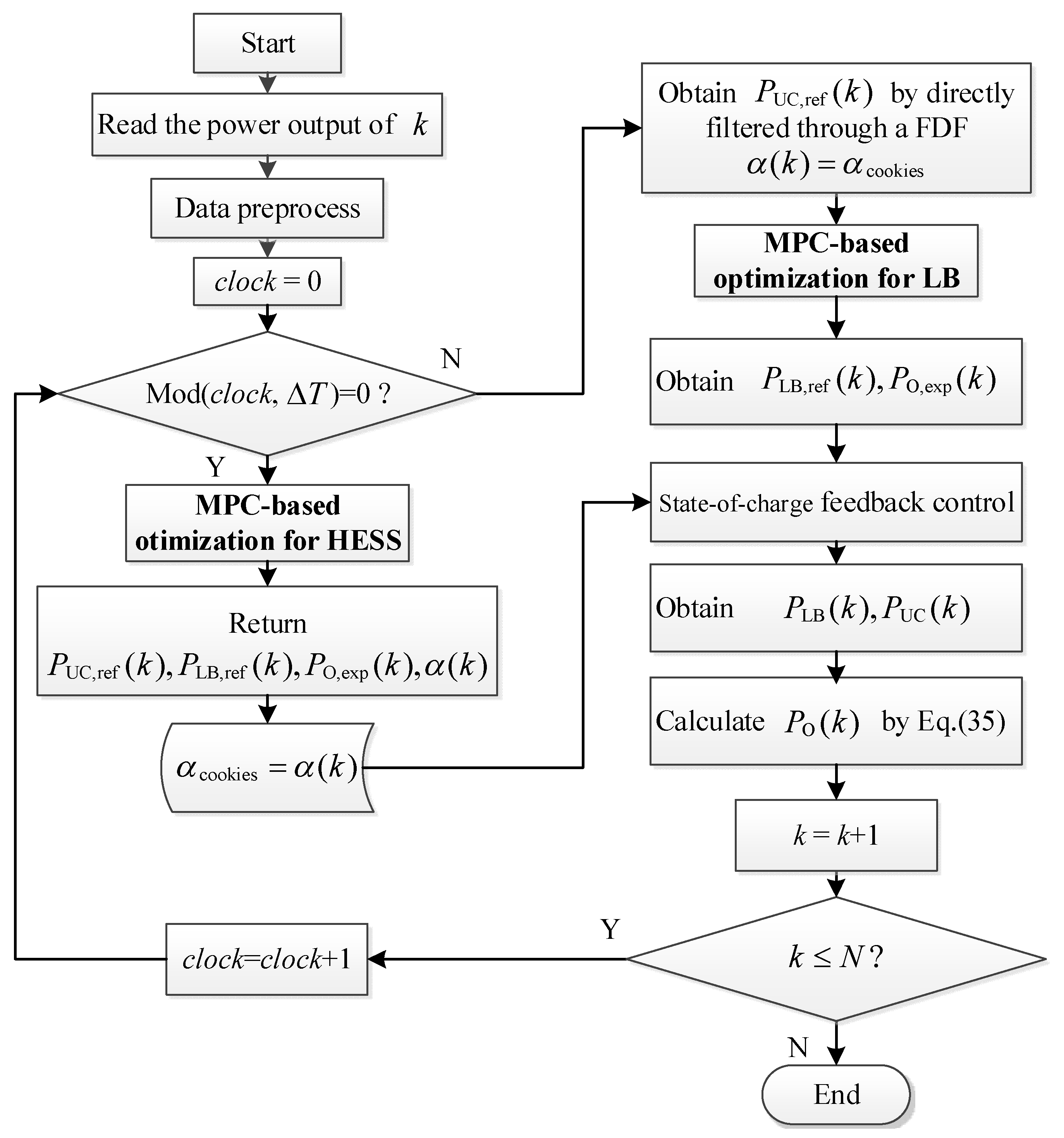
3.1. Flow Chart of MPC-Based Coordination and Optimization Control
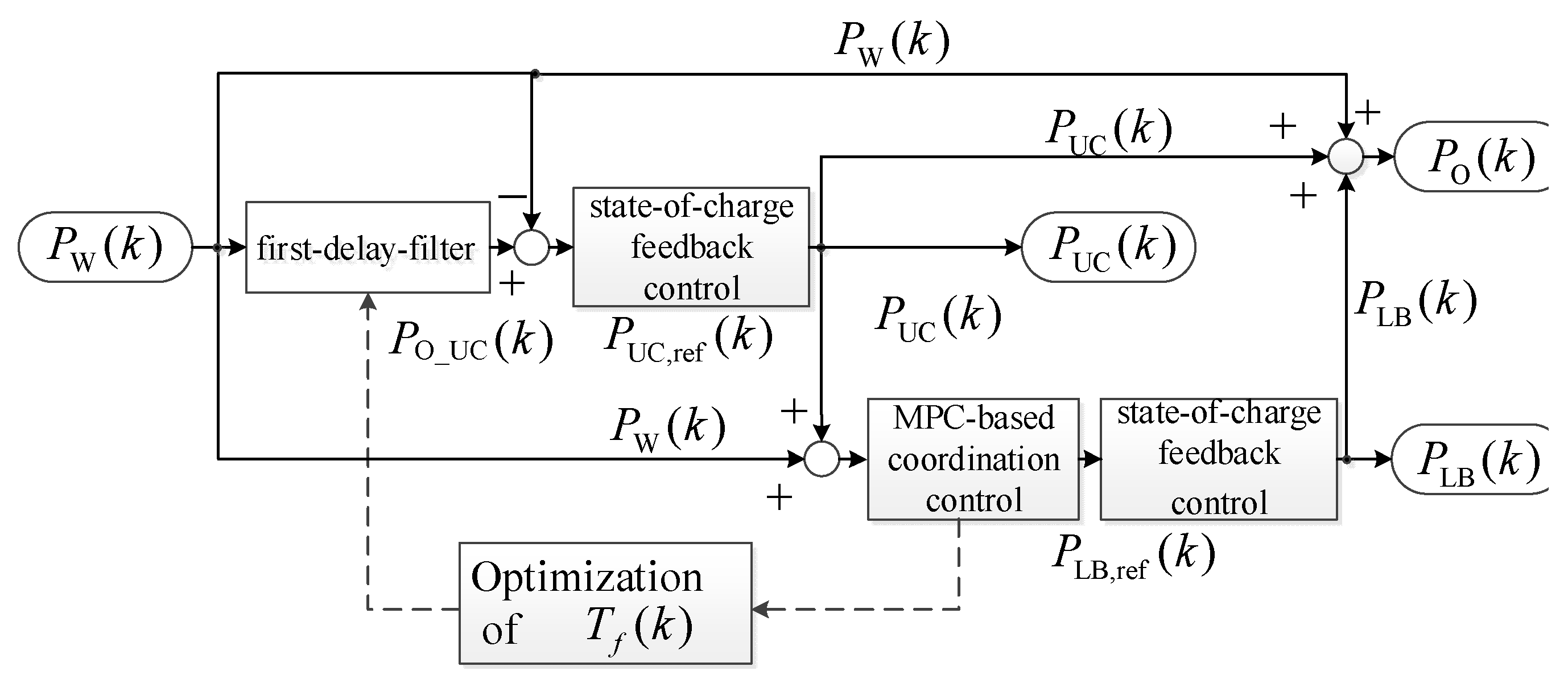
3.2. Flexible First-Delay-Filter with Variable Time Constant
3.3. Capacity Calculation
3.4. MPC-Based Coordination Control Model
3.4.1. MPC-Based Coordination Control Model for the HESS
3.4.2. MPC-based control model for the LB bank
3.5. Transformation of the FMR Constraints
3.6. Model Solution
3.7. Feasibility and Constraints Handling
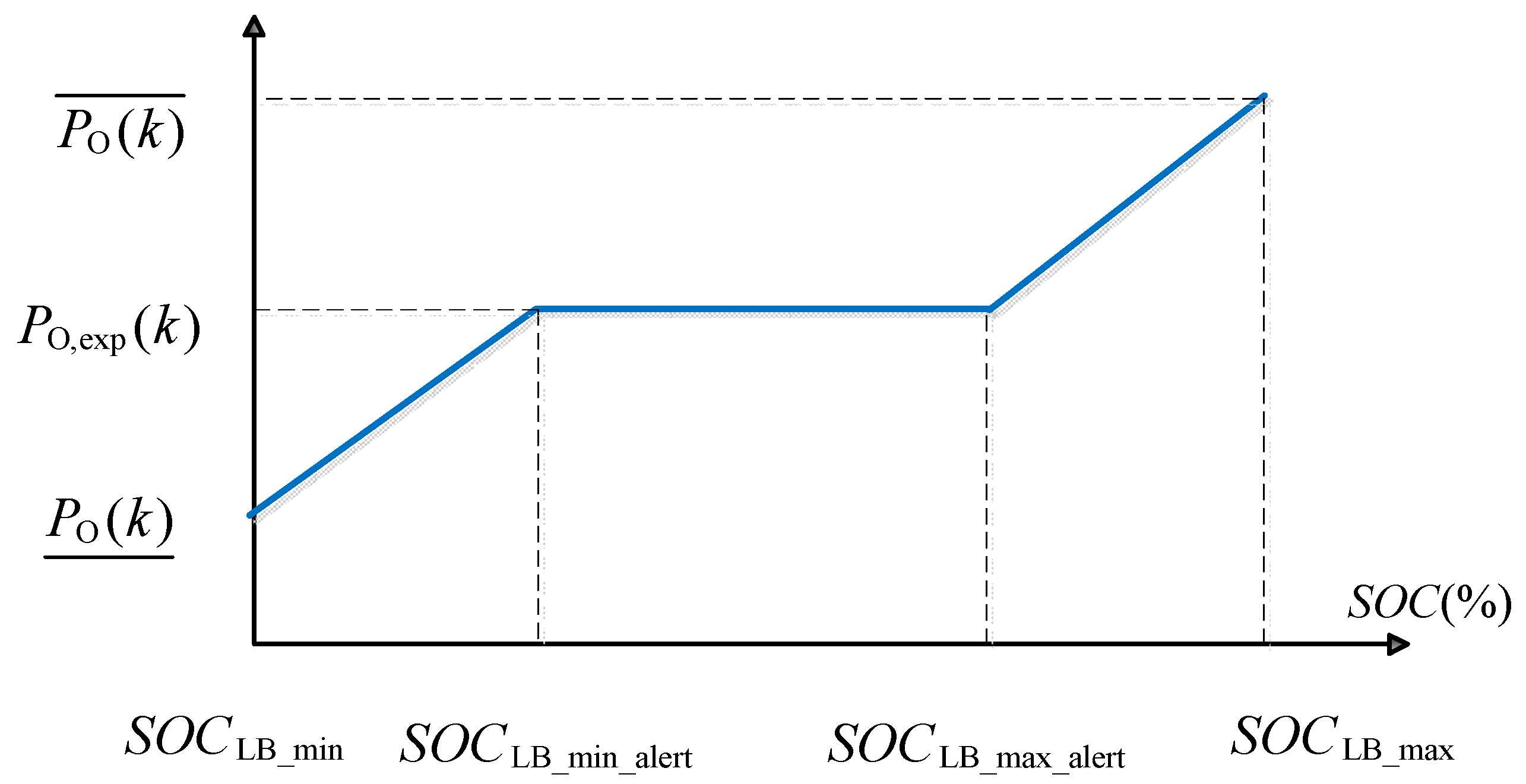
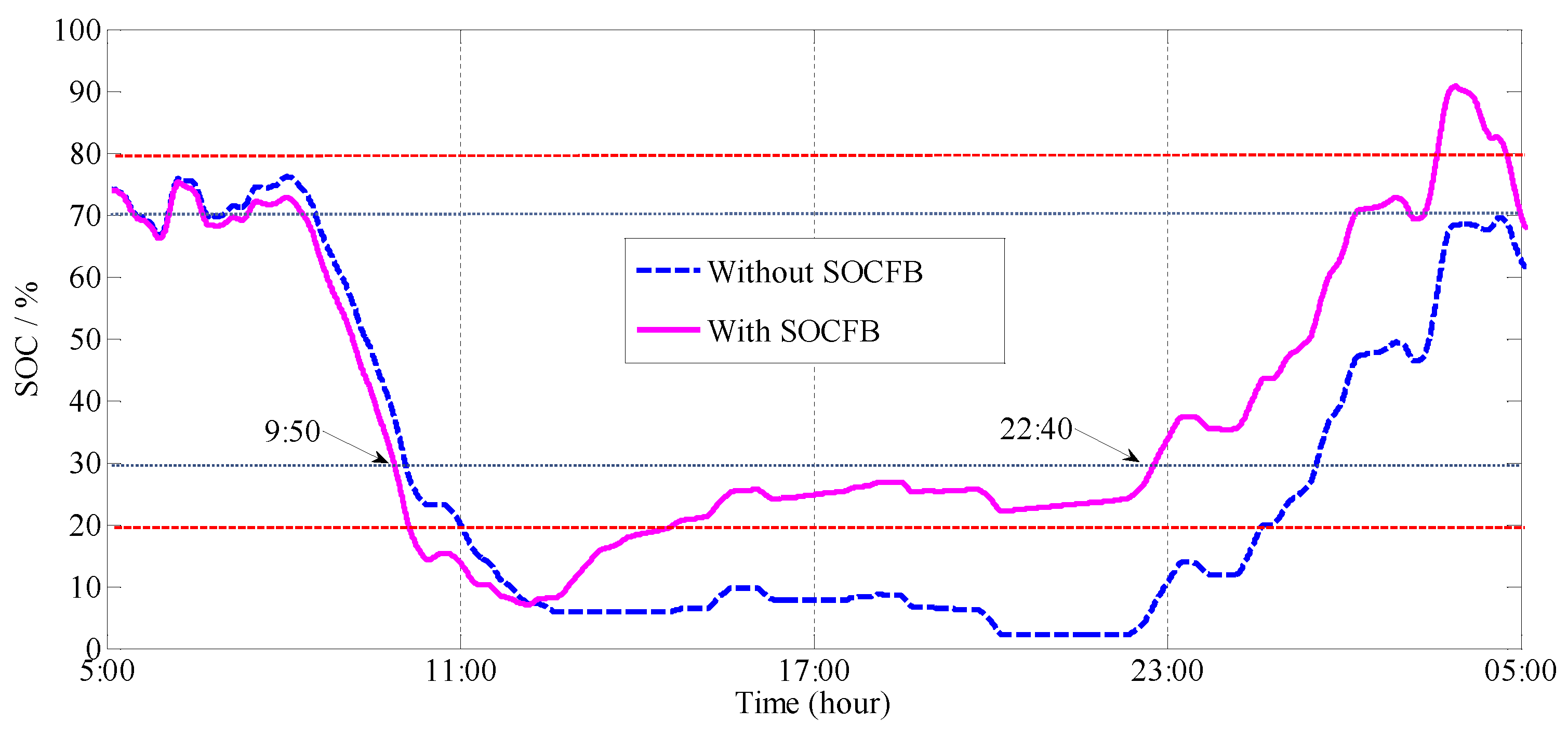
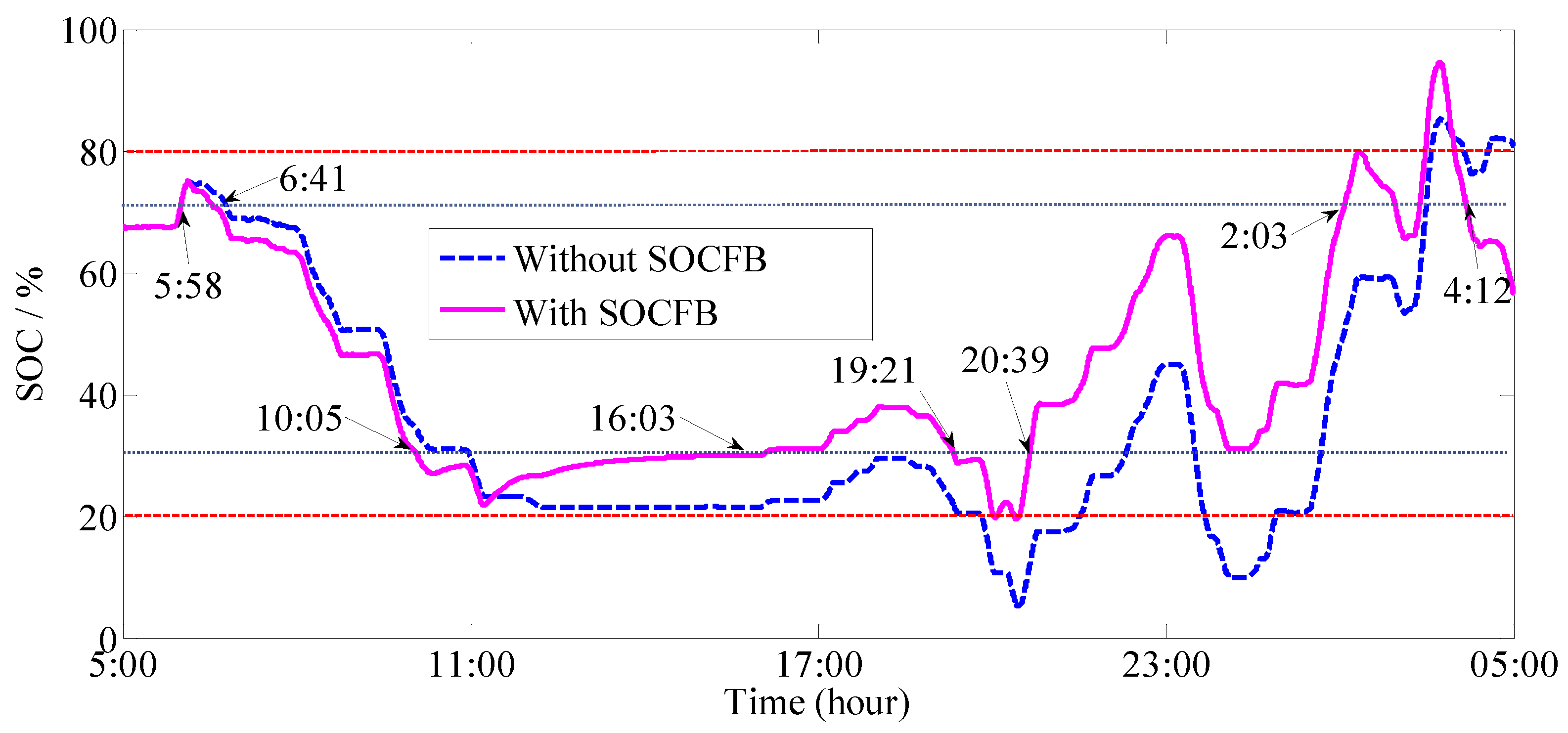
3.8. State-of-Charge Feedback Control
3.8.1. State-of-Charge Feedback Control of the UC
3.8.2. State-of-Charge Feedback Control of the LB
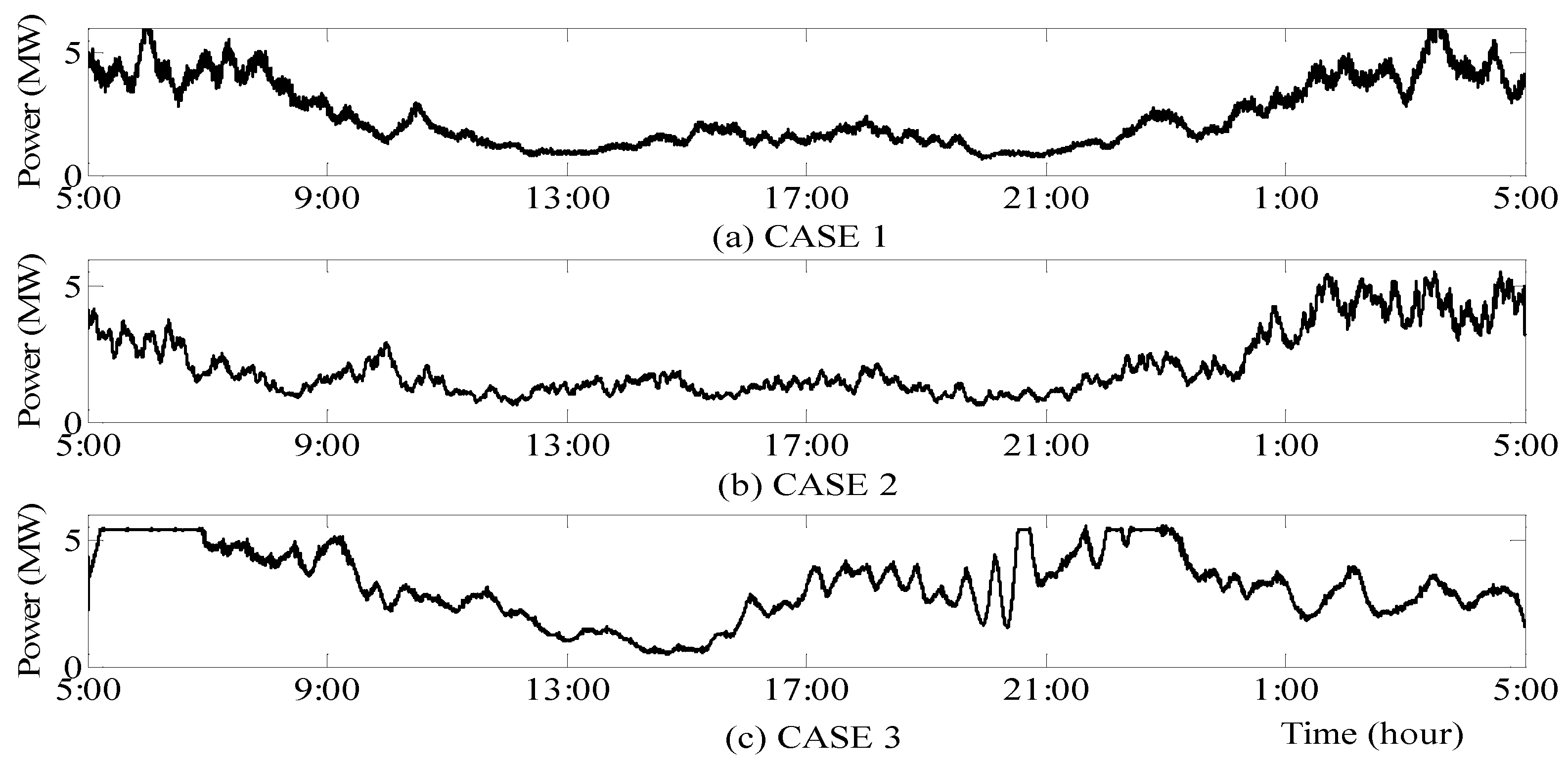
4. Simulation and Analysis
4.1. HESS Capacity and Power Configurations
4.2. Comparison of MPCCC and Conventional Algorithms
4.2.1. Maximum Absolute Value of the Energy Storage Power Output
4.2.2. Energy Storage Capacity Consumed
4.2.3. Battery Health Index
4.2.4. Equivalent Full Cycle
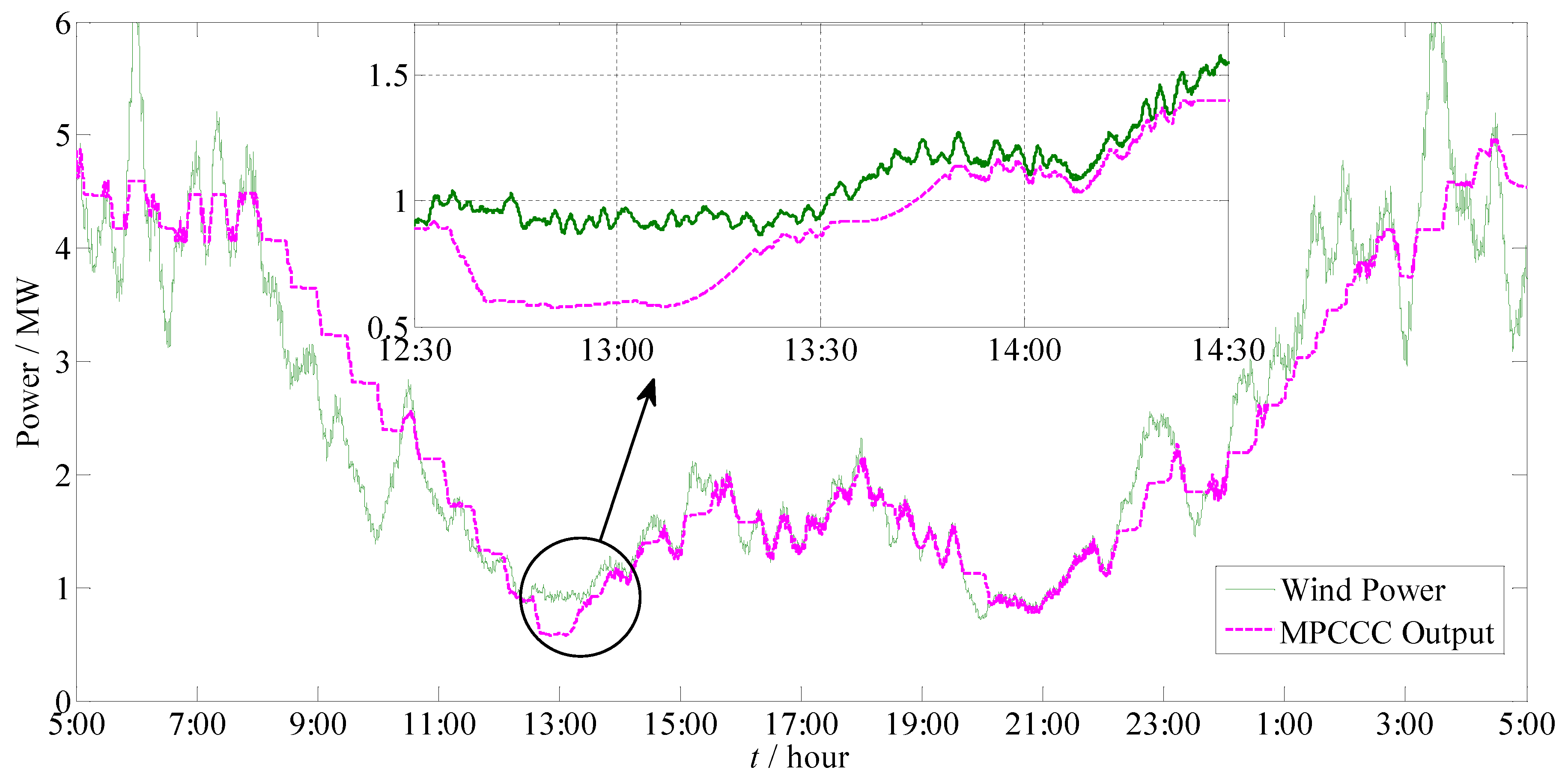
4.3. Verification of the Proposed Control Strategy
5. Conclusions
- A novel MPC-based coordinated control strategy consisting of HESS-computing and LB-computing periods is developed. At each time step, we solve a QCP problem using IPOPT in MATLAB. In the HESS-computing periods, the goal is to minimize the cost of HESS in the next prediction horizon, the optimal power output of LB is obtained, as well as the optimal time constant of first-delay filter for obtaining the power output of UC. In the LB-computing period, the optimal time constant in the last HESS-computing period is kept to directly obtain the power output of UC, the goal of this stage is simplified to minimize the cost of LB utilization in the subsequent control horizon. This control strategy effectively mitigates wind power fluctuations in multiple time scales;
- Adopted a flexible FDF with an optimization of the time constant to obtain the reference value of the UC bank, which can take the full advantage of the high power density of the UC bank;
- Allocated the charge/discharge instruction value of the HESS based on frequency distribution by employing the flexible FDF. This improves the lifetime of both storage devices;
- Deployed a relaxation technique when the MPCCC problem is unsolvable. Thus, the FMR is fulfilled with a large probability even in extreme conditions; and
- Presented a novel SOCFB control scheme that effectively restores the SOCs of the HESS to its proper safety range.
Author Contributions
Funding
Conflicts of Interest
References
- Sahu, B.K. Wind energy developments and policies in China: A short review. Renew. Sustain. Energy Rev. 2018, 81, 1393–1405. [Google Scholar] [CrossRef]
- Yuan, J. Wind energy in China: Estimating the potential. Nat. Energy 2016, 1, 16095. [Google Scholar] [CrossRef]
- Fox, B.; Flynn, D.; Bryans, L.; Jenkins, N.; Milborrow, D.; O’Malley, M.; Watson, R.; Anaya-Lara, O. Wind power integration: Connection and system operation aspects. IET Power Energy Ser. 2006, 50, 2007. [Google Scholar]
- Tanabe, T.; Sato, T.; Tanikawa, R.; Aoki, I.; Funabashi, T.; Yokoyama, R. Generation scheduling for wind power generation by storage battery system and meteorological forecast. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–7. [Google Scholar]
- Jiang, Q.; Hong, H. Wavelet-Based Capacity Configuration and Coordinated Control of Hybrid Energy Storage System for Smoothing Out Wind Power Fluctuations. IEEE Trans. Power Syst. 2013, 28, 1363–1372. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, H. Two-Time-Scale Coordination Control for a Battery Energy Storage System to Mitigate Wind Power Fluctuations. IEEE Trans. Energy Convers. 2013, 28, 52–61. [Google Scholar] [CrossRef]
- Díaz-González, F.; Sumper, A.; Gomis-Bellmunt, O.; Villafáfila-Robles, R. review of energy storage technologies for wind power applications. Renew. Sustain. Energy Rev. 2012, 16, 2154–2171. [Google Scholar] [CrossRef]
- Eyer, J.; Corey, G. Energy Storage for the Electricity Grid: Benefits and Market Potential Assessment Guide; Sandia National Laboratories: Albuquerque, NM, USA, 2010. [Google Scholar]
- Onar, O.C.; Uzunoglu, M.; Alam, M.S. Dynamic modeling, design and simulation of a wind/fuel cell/ultra-capacitor-based hybrid power generation system. J. Power Sources 2006, 161, 707–722. [Google Scholar] [CrossRef]
- Thounthong, P.; Raël, S.; Davat, B. Control Strategy of Fuel Cell and Supercapacitors Association for a Distributed Generation System. IEEE Trans. Ind. Electron. 2007, 54, 3225–3233. [Google Scholar] [CrossRef]
- Henson, W. Optimal battery/ultracapacitor storage combination. J. Power Sources 2008, 179, 417–423. [Google Scholar] [CrossRef]
- Paatero, J.V.; Lund, P.D. Effect of energy storage on variations in wind power. Wind Energy 2005, 8, 421–441. [Google Scholar] [CrossRef]
- Hadjipaschalis, I.; Poullikkas, A.; Efthimiou, V. Overview of current and future energy storage technologies for electric power applications. Renew. Sustain. Energy Rev. 2009, 13, 1513–1522. [Google Scholar] [CrossRef]
- Abbey, C.; Strunz, K.; Joos, G. A knowledge-based approach for control of two-level energy storage for wind energy systems. IEEE Trans. Energy Convers. 2009, 24, 539–547. [Google Scholar] [CrossRef]
- Datta, M.; Senjyu, T.; Yona, A.; Funabashi, T. A fuzzy based method for leveling output power fluctuations of photovoltaic-diesel hybrid power system. Renew. Energy 2011, 36, 1693–1703. [Google Scholar] [CrossRef]
- Richalet, J. Industrial applications of model based predictive control. Automatica 1993, 29, 1251–1274. [Google Scholar] [CrossRef]
- Sorensen, P.; Cutululis, N.A.; Vigueras-Rodriguez, A.; Jensen, L.E.; Hjerrild, J.; Donovan, M.H.; Madsen, H. Power fluctuations from large wind farms. IEEE Trans. Power Syst. 2007, 22, 958–965. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Grid Integration of Large-Capacity Renewable Energy Sources and Use of Large-Capacity Electrical Energy Storage, Market Strategy Board. October 2012. Available online: http://www.iec.ch/whitepaper/pdf/iecWP-gridintegrationlargecapacity-LR-en.pdf (accessed on 1 September 2019).
- Bonneville Power Administration. Renewable Energy Technology Roadmap, Technology Innovation Office. September 2006. Available online: http://www.bpa.gov/corporate/business/innovation/docs/2006/RM-06_Re-newablesFinal.pdf (accessed on 5 September 2019).
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Schoenung, S. Characteristics and Technologies for Long-vs. Short-term Energy Storage; Sandia Report SAND2001-0765; United States Department of Energy: Washington, DC, USA, 2001. [Google Scholar]
- Mehrotra, S. On the implementation of a primal-dual interior point method. SIAM J. Optim. 1992, 2, 575–601. [Google Scholar] [CrossRef]
- Ise, T.; Kita, M.; Taguchi, A. A hybrid energy storage with a SMES and secondary battery. IEEE Trans. Ind. Appl. 2005, 15, 1915–1918. [Google Scholar] [CrossRef]
- Manwell, J.F.; Rogers, A.; Hayman, G.; Avelar, C.T.; McGowan, J.G.; Abdulwahid, U.; Wu, K. Hybrid2: A Hybrid System Simulation Model: Theory Manual; National Renewable Energy Laboratory: Amherst, MA, USA, 1998. [Google Scholar]
- Jiang, Q.; Gong, Y.; Wang, H. A Battery Energy Storage System Dual-Layer Control Strategy for Mitigating Wind Farm Fluctuations. IEEE Trans. Power Syst. 2013, 28, 263–3273. [Google Scholar] [CrossRef]
| Case | F1max (%) | ρ1 | F30max (%) | ρ30 | ||
|---|---|---|---|---|---|---|
| Case 1 | 4.16 | 57.73 | 0.0279 | 17.43 | 72.83 | 0.1060 |
| Case 2 | 2.61 | 65.07 | 0.0216 | 16.79 | 65.07 | 0.0880 |
| Case 3 | 2.35 | 65.87 | 0.0183 | 18.12 | 70.18 |
| Methods | Power Rating of LB (MW) | Capacity Rating of LB (MWh) | Power Rating of UC (MW) | Capacity Rating of UC (MWh) |
|---|---|---|---|---|
| FDF | 3.2 | 10 | 1.5 | 0.2 |
| Rate limiter | 3.0 | 7 | 1.5 | 0.2 |
| Wavelet-based | 2.5 | 5 | 1.5 | 0.2 |
| MPCCC | 2.5 | 3 | 1.5 | 0.2 |
| Case | Methods | D (e−4) | Expected life (y) | EFC (DOD = 60%) | EFC (DOD = 80%) |
|---|---|---|---|---|---|
| Case 1 | First-delay-filter | 9.2887 | 2.9495 | 2.7884 | 2.2183 |
| Rate limiter | 7.1713 | 3.8204 | 2.1528 | 1.7127 | |
| wavelet-based control | 4.2491 | 6.4477 | 1.2756 | 1.0148 | |
| MPC-based control | 3.7222 | 7.3606 | 1.1174 | 0.8889 | |
| Case 2 | First-delay-filter | 8.7497 | 3.1312 | 2.6266 | 2.0896 |
| Rate limiter | 6.8732 | 3.9861 | 2.0633 | 1.6415 | |
| wavelet-based control | 3.9616 | 6.9157 | 1.1892 | 0.9461 | |
| MPC-based control | 3.6579 | 7.4899 | 1.0981 | 0.8736 | |
| Case 3 | First-delay-filter | 11.1701 | 2.4527 | 3.3532 | 2.6677 |
| Rate limiter | 9.7787 | 2.8017 | 2.9355 | 2.3354 | |
| wavelet-based control | 7.9426 | 3.4494 | 2.3843 | 1.8969 | |
| MPC-based control | 6.7711 | 4.0462 | 2.0326 | 1.6172 |
| Case | Methods | Maximum Power of LB (MW) | Capacity Consumed of LB (MWh) | Maximum Power of UC (MW) | Capacity Consumed of UC (MWh) | BHI of LB (%) | BHI of UC (%) |
|---|---|---|---|---|---|---|---|
| Case 1 | First-delay-filter | 2.7266 | 8.9740 | 0.4235 | 0.1401 | 35.14 | 100 |
| Rate limiter | 2.2373 | 4.9405 | 0.4235 | 0.1401 | 45.46 | 100 | |
| wavelet-based control | 1.9220 | 2.9545 | 0.7741 | 0.1276 | 100 | 99.10 | |
| MPC-based control | 2.0476 | 2.2035 | 1.0659 | 0.1501 | 100 | 100 | |
| Case 2 | First-delay-filter | 3.0210 | 7.9200 | 0.5012 | 0.1278 | 56.64 | 100 |
| Rate limiter | 2.6475 | 4.9956 | 0.5012 | 0.1278 | 100 | 100 | |
| wavelet-based control | 2.4580 | 2.9680 | 0.8641 | 0.1200 | 100 | 100 | |
| MPC-based control | 2.4479 | 2.6903 | 1.4594 | 0.1500 | 100 | 100 | |
| Case 3 | First-delay-filter | 2.5284 | 6.8001 | 0.9771 | 0.1312 | 62.51 | 100 |
| Rate limiter | 2.5065 | 5.2008 | 0.9771 | 0.1312 | 98.39 | 100 | |
| wavelet-based control | 2.3564 | 4.1451 | 1.2088 | 0.1226 | 100 | 100 | |
| MPC-based control | 2.3308 | 3.7573 | 1.4899 | 0.1541 | 100 | 100 |
| Methods | Maximum Power of LB(MW) | Capacity Consumed of LB (MWh) | Maximum Power of UC (MW) | Capacity Consumed of UC (MWh) | BHI of LB (%) | BHI of UC (%) |
|---|---|---|---|---|---|---|
| MPCCC-BA (without the state-of-charge feedback) | 2.0644 | 2.2555 | 1.1594 | 0.1552 | 43.73 | 80.62 |
| MPCCC (with the state-of-charge feedback) | 2.0522 | 2.3225 | 1.0784 | 0.1523 | 80.37 | 92.95 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, H.; Jiang, Q. Model Predictive Control-Based Coordinated Control Algorithm with a Hybrid Energy Storage System to Smooth Wind Power Fluctuations. Energies 2019, 12, 4591. https://doi.org/10.3390/en12234591
Hong H, Jiang Q. Model Predictive Control-Based Coordinated Control Algorithm with a Hybrid Energy Storage System to Smooth Wind Power Fluctuations. Energies. 2019; 12(23):4591. https://doi.org/10.3390/en12234591
Chicago/Turabian StyleHong, Haisheng, and Quanyuan Jiang. 2019. "Model Predictive Control-Based Coordinated Control Algorithm with a Hybrid Energy Storage System to Smooth Wind Power Fluctuations" Energies 12, no. 23: 4591. https://doi.org/10.3390/en12234591
APA StyleHong, H., & Jiang, Q. (2019). Model Predictive Control-Based Coordinated Control Algorithm with a Hybrid Energy Storage System to Smooth Wind Power Fluctuations. Energies, 12(23), 4591. https://doi.org/10.3390/en12234591




