Exergetic, Energetic, and Quality Performance Evaluation of Paddy Drying in a Novel Industrial Multi-Field Synergistic Dryer
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
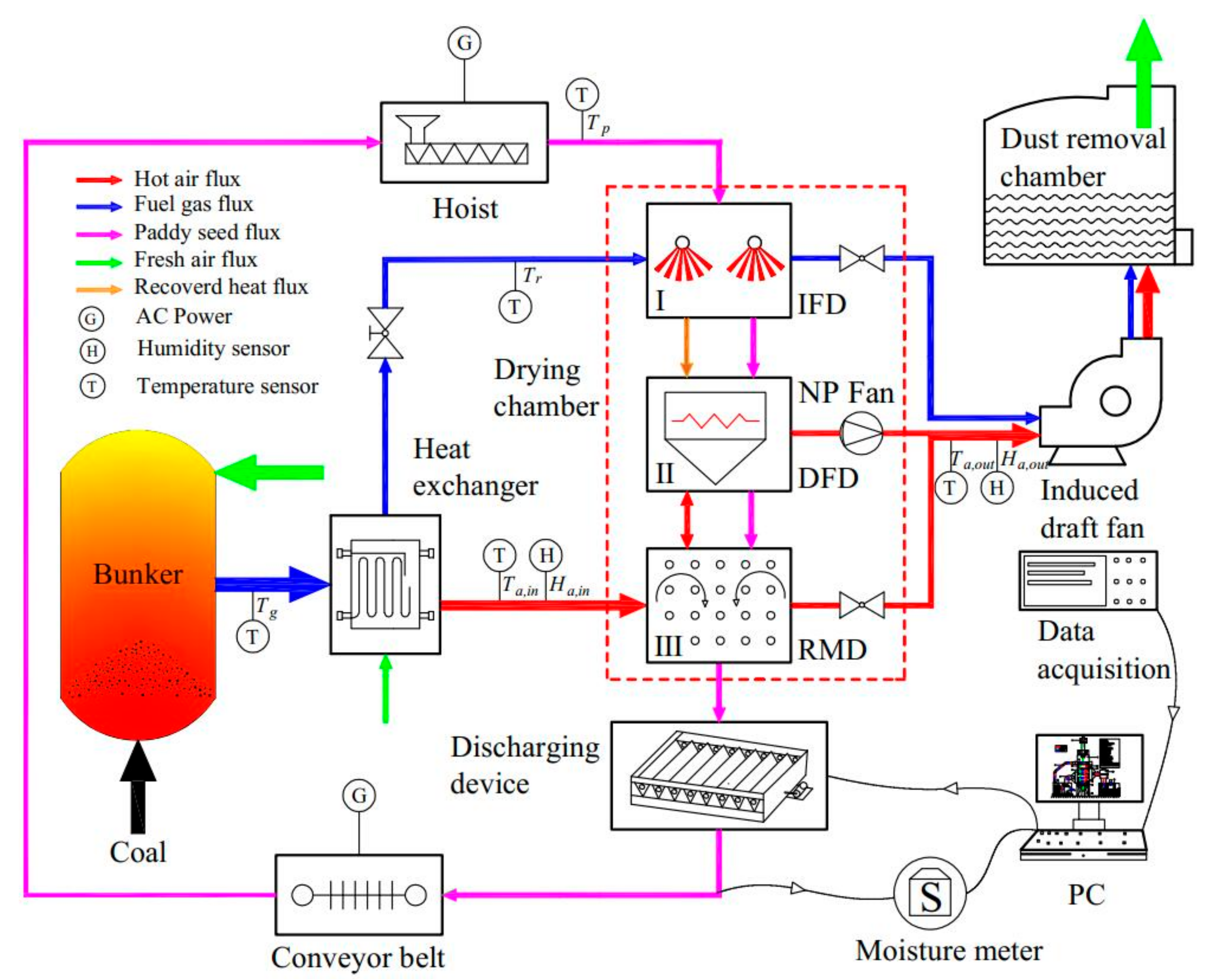
2.2. Equipment Description and the Working Principle
2.3. Energy Performance
2.4. Exergy Analysis
2.5. Drying Kinetics and Quality Performance
2.6. Uncertainty Analysis
3. Results and Discussions
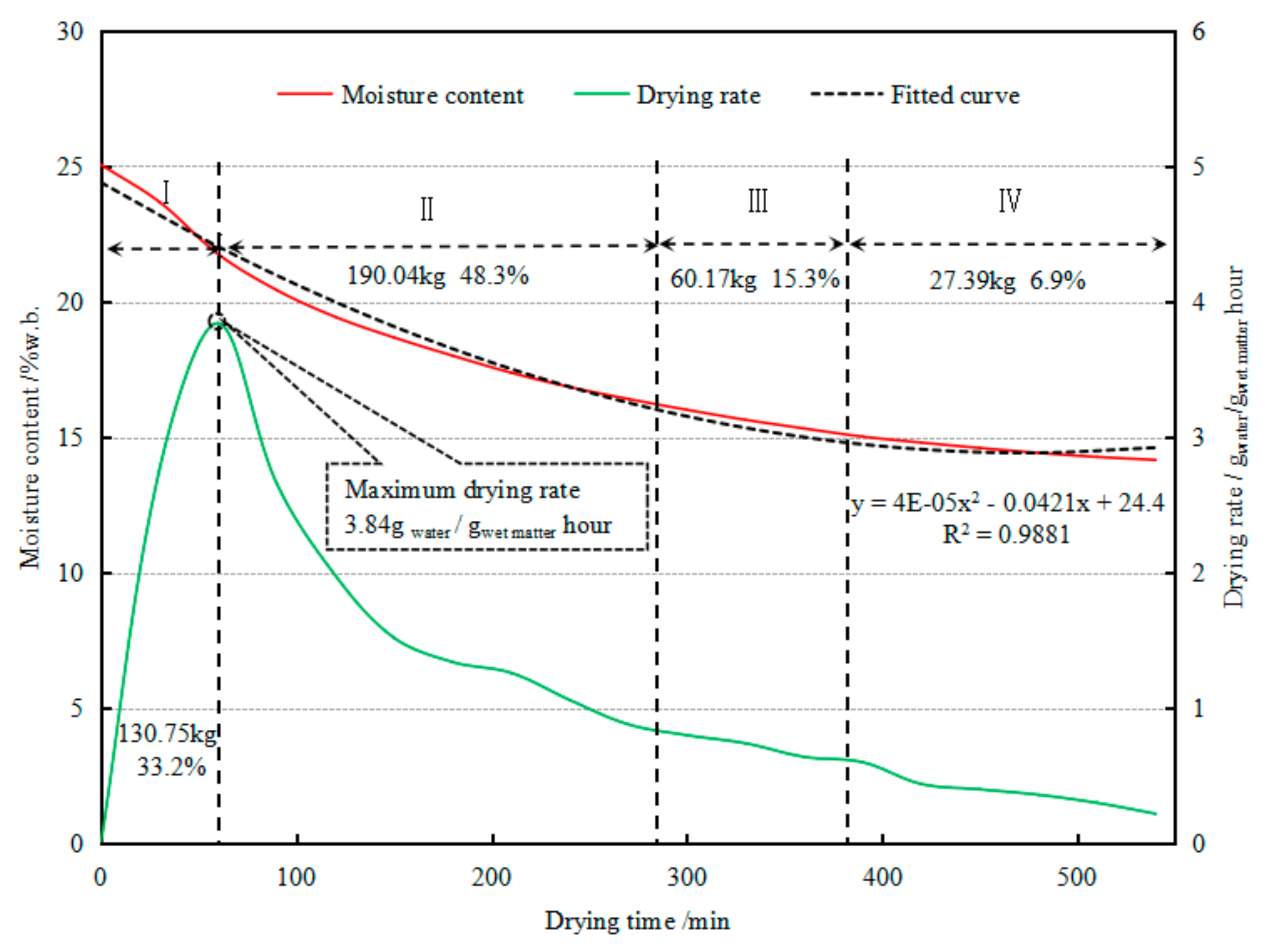
3.1. Drying Performance of the Dryer
3.2. Energy Analysis of the Dryer
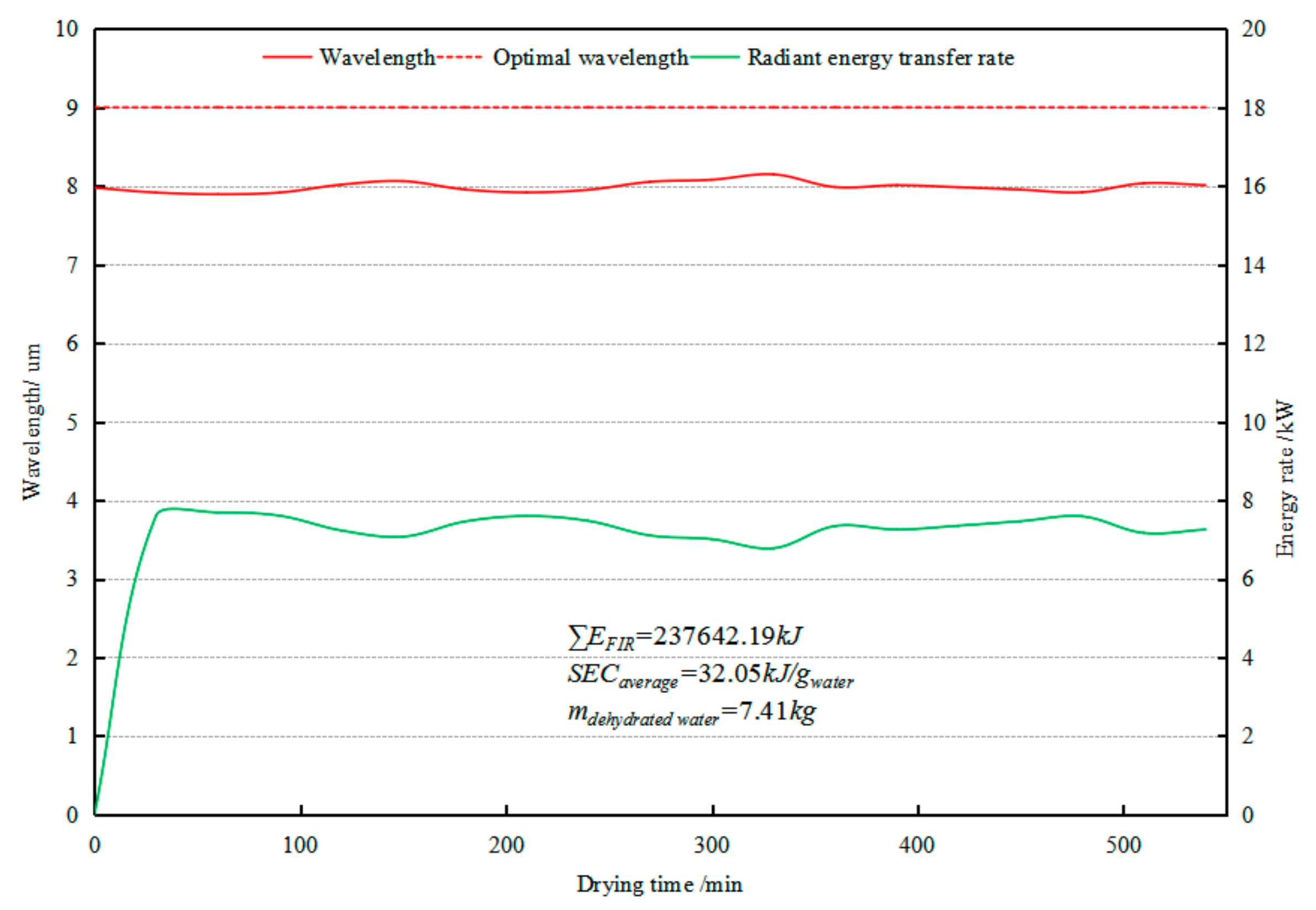
3.2.1. Energy Recovery
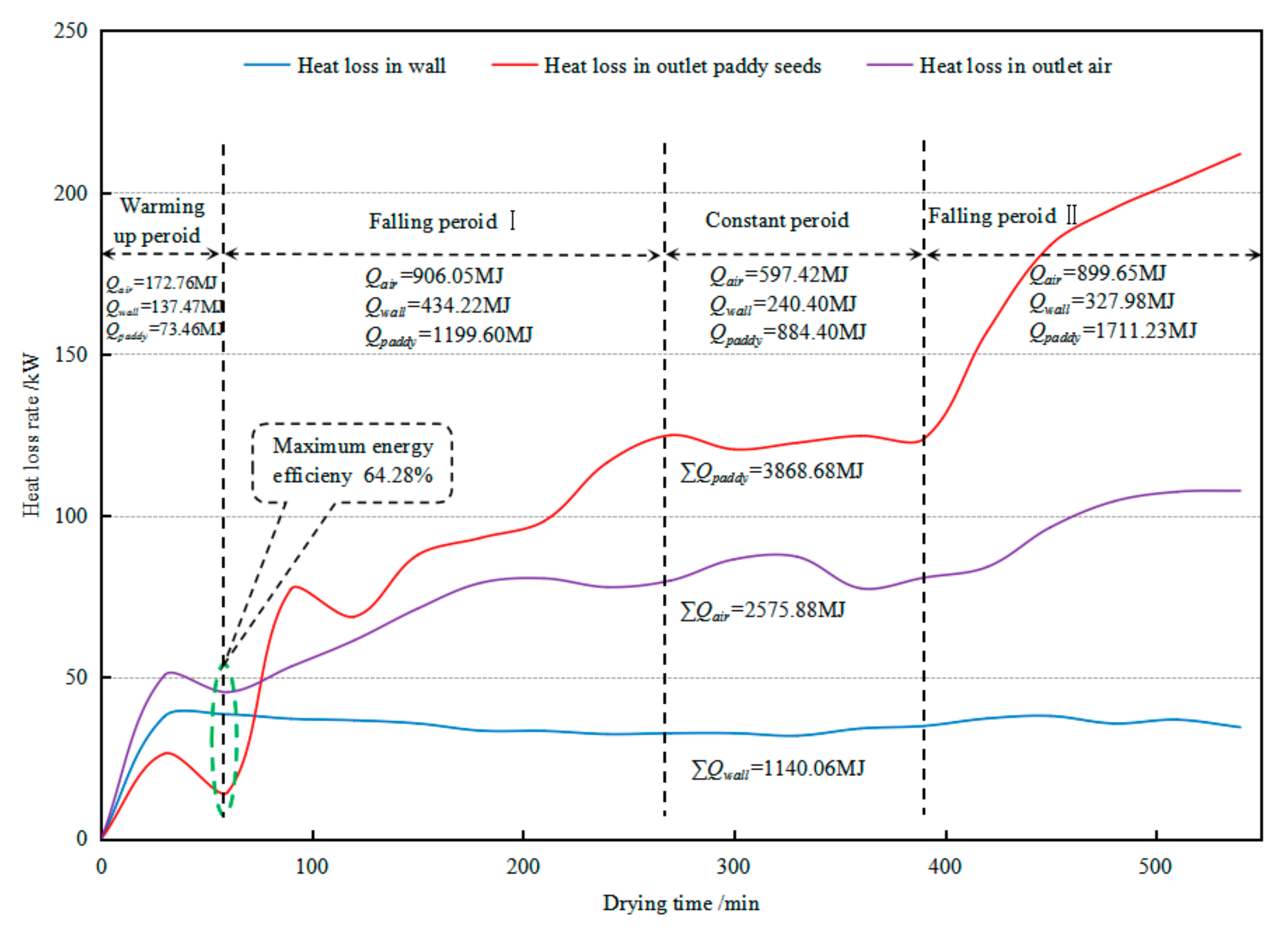
3.2.2. Heat Loss Characteristics
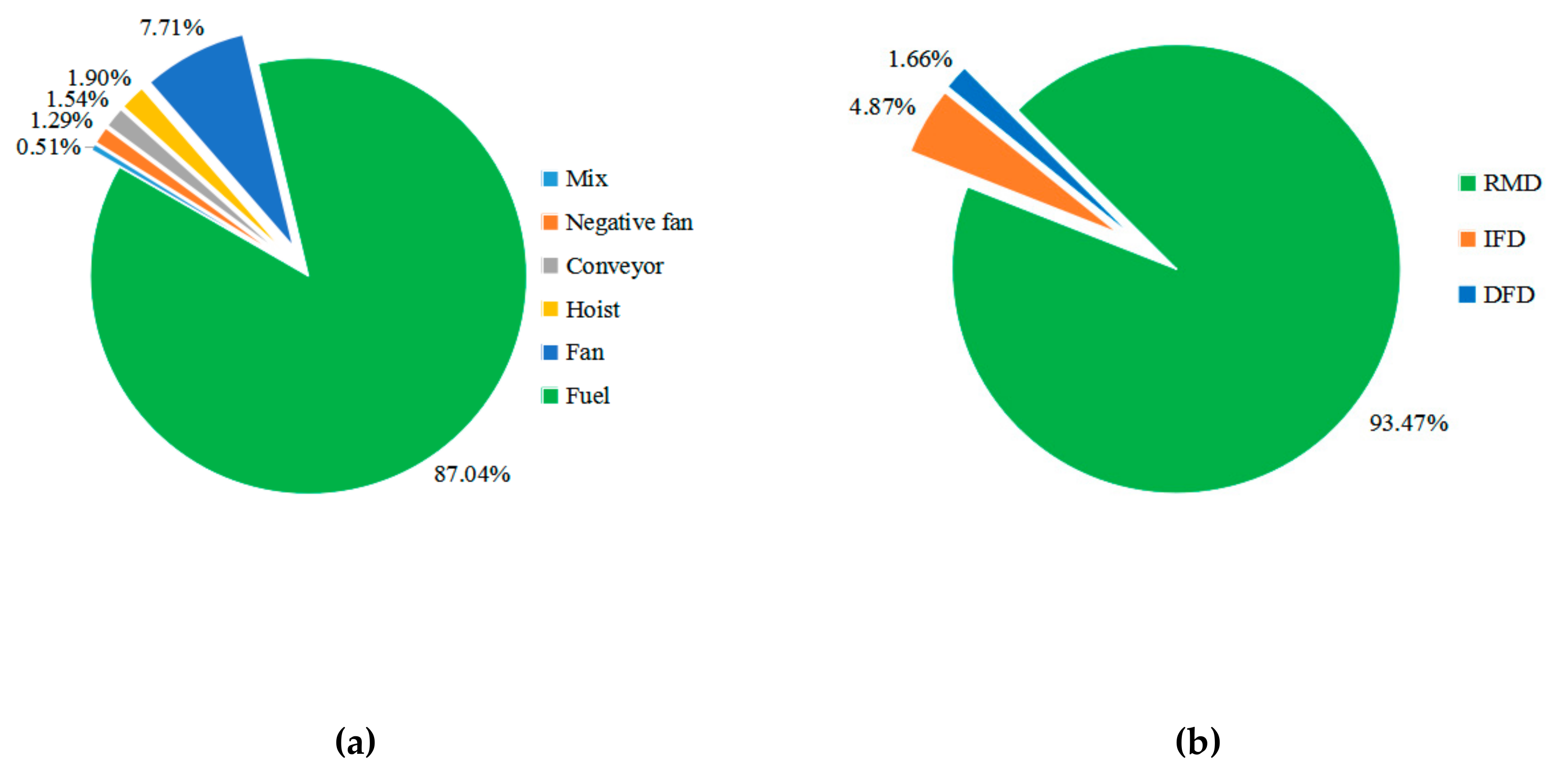
3.2.3. Energy Structure of the Drying System
3.3. Exergy Analysis
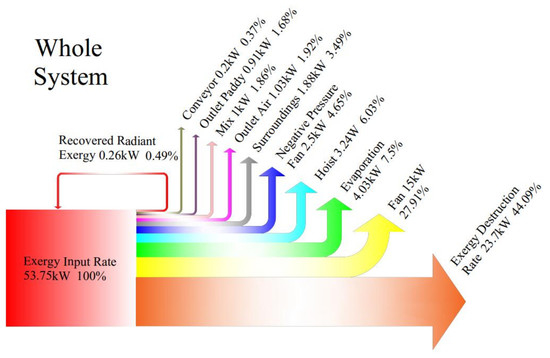
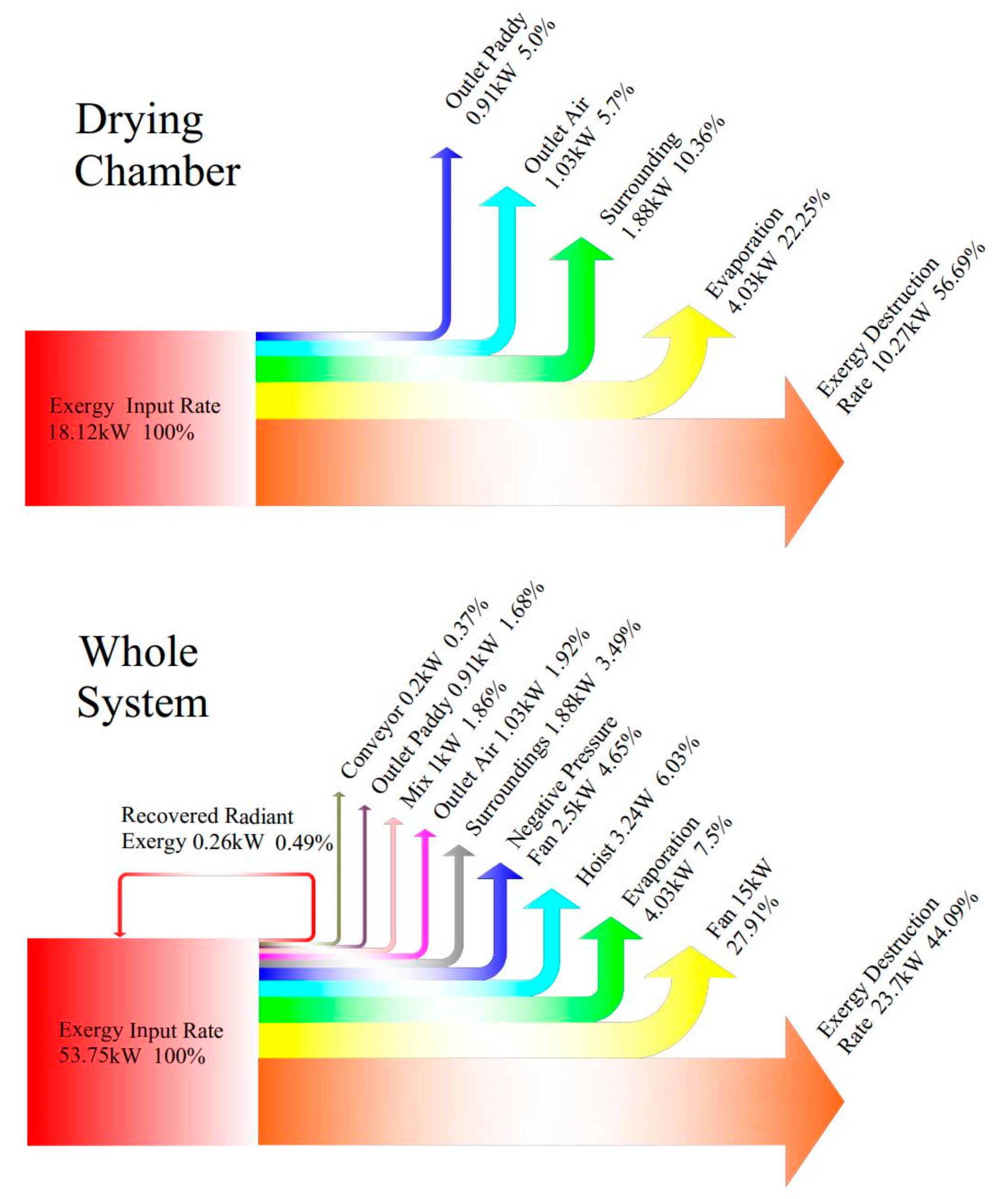
3.3.1. Exergy Structure of the Whole System and the Drying Chamber
3.3.2. Exergetic Performance of the Whole System and the Drying Chamber
4. Conclusions
- The average drying rate for the paddy drying in the present dryer was ascertained to be 1.21 gwater/gwet matter hour, and the drying rate decreased significantly after 390 min, an appropriate drying temperature for maintaining the drying rate with reasonable energy consumption should be further studied.
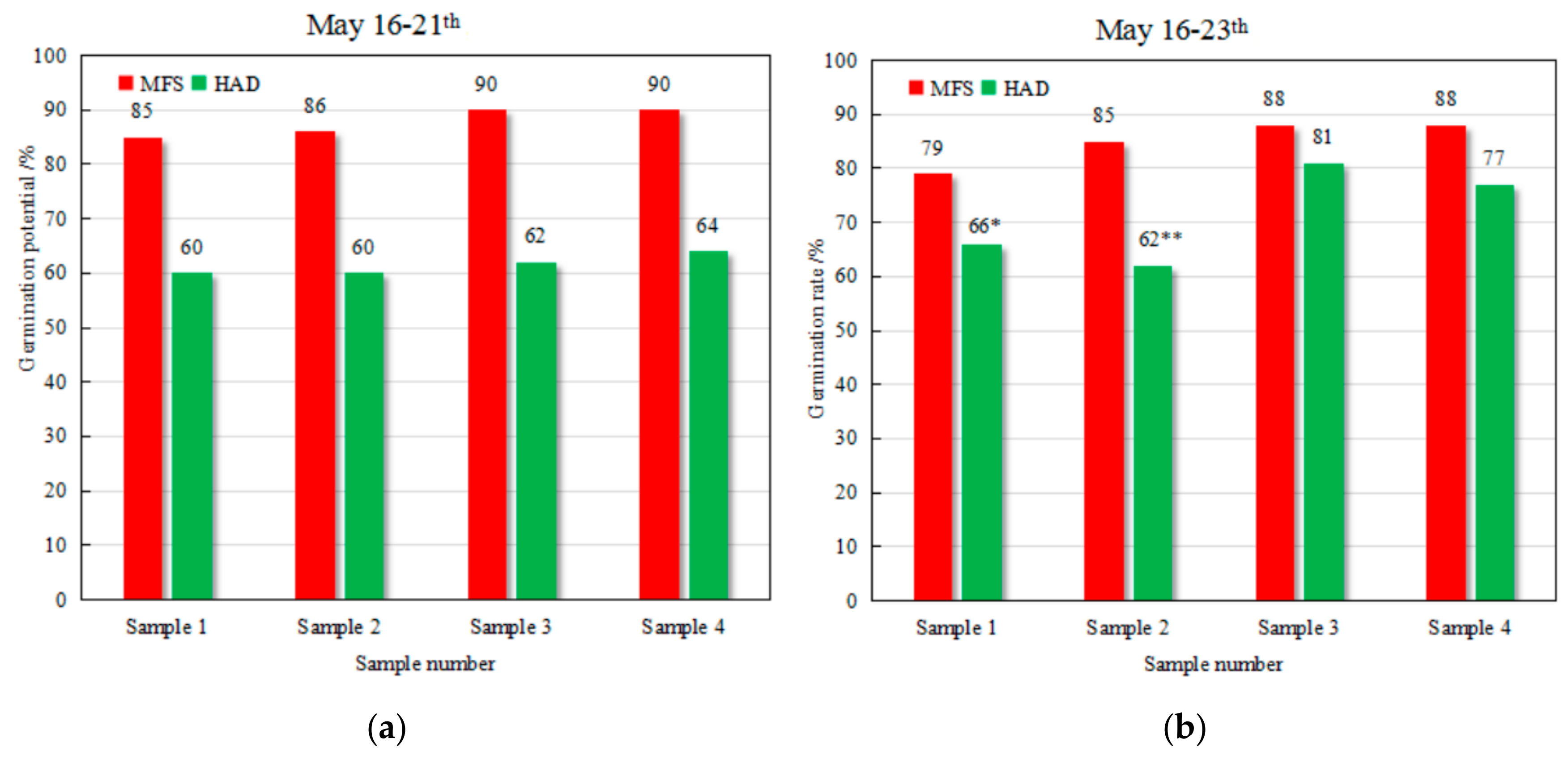
- The quality aspect of the product dried by the present dryer showed a better performance than that by the traditional industrial hot air dryer. The GP and GR of the paddy seeds dried by the present dryer ranged from 75% to 90% and 69% to 88%, respectively, the crackle ratio of the paddy seeds was 1%.
- After 390 min, the heat loss in outlet paddy seeds rapidly increased with the increase of drying time, which indicated that the energy efficiency should be improved in this period. The overall heat loss in outlet air, paddy seeds and in wall were ascertained to be 2575.88, 3868.68, and 1140.06 MJ, respectively.
- The total recovered radiant energy and radiant exergy recover rate were ascertained to be 237.64 MJ and 0.26 kW, respectively. Additionally, the wavelength varied from 7.89 µm to 8.15 µm, which are close to the optimal absorption wavelength of the paddy seeds.
- The overall energy and exergy efficiency of the paddy drying in the multi-field dryer ranged from 13.26% to 56.63% and 39.03% to 60.23%, respectively, indicating that the dryer is designed in an energy efficient manner.
- The improvement potential rates of the drying process varies from the lowest 2.88 kW to the highest 10.59 kW for the drying chamber and accounting for 15.89–58.44% of the total exergy inputted into the drying chamber, indicating that the drying chamber has a high potential to improve the exergetic performance.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| c | specific heat (J·kg−1·K−1) |
| humidity ratio of air (kg water vapor/kg dry air) | |
| mass flow rate (kg·s−1) | |
| energy rate (kW) | |
| x | exergy rate (kW) |
| heat transfer rate (kW) | |
| power rate (kW) | |
| work rate (kW) | |
| R | gas constant (kJ·kg−1·K−1) |
| A | cross-sectional area of the drying chamber (m2) |
| v | velocity (m·s−1) |
| g | gravity acceleration (m·s−2) |
| hfg | latent heat (kJ·kg−1) |
| T | Temperature (K or °C) |
| m | mass (kg) |
| mi | initial wet weight (g) |
| md | final dry weight (g) |
| pi | pressure (Pa) |
| dg | paddy equivalent diameter (m) |
| specific enthalpy (kJ·kg−1) | |
| Abbreviations | |
| DFD | depressurized flash drying section |
| IFD | far-infrared section |
| RMD | reverse mixed drying section |
| MFD | multi-field drying |
| HAD | hot air drying |
| Greek symbols | |
| Ɛ | emissivity |
| ρ | density (kg·m3) |
| μ | dynamic viscosity (kg·m−1·s−1) |
| γ | thermal conductivity (W·m−1·K−1) |
| δ | thickness (m) |
| λ | wavelength (um) |
| Subscripts | |
| a | air |
| p | paddy seeds |
| in | inlet |
| out | outlet |
| l | load |
| v | vapor |
| c | chamber |
| abs | absolute |
| da | dry air |
| ∞ | ambient |
| evap | evaporation |
| r | radiator |
References
- Drying and Wetting of Building Materials and Components; Delgado, J.M.P.Q., Ed.; Springer International Publishing: Basel, Switzerland, 2014; Volume 4. [Google Scholar] [CrossRef]
- Mujumdar, A.S. Handbook of Industrial Drying, 3rd ed.; Taylor & Francis Group, CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar] [CrossRef]
- Kudra, T. Energy aspects in drying. Dry. Technol. 2004, 22, 917–932. [Google Scholar] [CrossRef]
- Kemp, I.C. Fundamentals of Energy Analysis of Dryers. In Modern Drying Technology—Energy Savings; Tsotsas, E., Mujumdar, A.S., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2011; pp. 1–46. [Google Scholar] [CrossRef]
- Sookramoon, K. Design of a Solar Tunnel Dryer Combined Heat with a Parabolic Trough for Paddy Drying. Appl. Mech. Mater. 2016, 851, 239–243. [Google Scholar] [CrossRef]
- Taechapairoj, C.; Dhuchakallaya, I.; Soponronnarit, S.; Wetchacama, S.; Prachayawarakorn, S. Superheated steam fluidised bed paddy drying. J. Food Eng. 2013, 58, 67–73. [Google Scholar] [CrossRef]
- Irfandy, F.; Djaeni, M. Evaluation of paddy quality dried with zeolite under medium temperature. IOP Conf. Ser. Earth Environ. Sci. 2018, 102, 012079. [Google Scholar] [CrossRef]
- Suherman, S.; Djaeni, M.; Kumoro, A.C. Drying Kinetics of Paddy in Fluidized Bed with Immersed Heating Element. Adv. Sci. Lett. 2017, 23, 2364–2366. [Google Scholar] [CrossRef]
- Krissadang, S. Performance Evaluation of a Solar Tunnel Dryer for Paddy Drying at Prathum Tani, Thailand. Appl. Mech. Mater. 2015, 799–800. [Google Scholar] [CrossRef]
- Rordprapat, W.; Nathakaranakule, A.; Tia, W.; Soponronnarit, S. Comparative study of fluidized bed paddy drying using hot air and superheated steam. J. Food Eng. 2005, 71, 28–36. [Google Scholar] [CrossRef]
- Firouzi, S.; Alizadeh, M.R.; Haghtalab, D. Energy consumption and rice milling quality upon drying paddy with a newly-designed horizontal rotary dryer. Energy 2016, 119, 629–636. [Google Scholar] [CrossRef]
- Sarker, M.S.H.; Ibrahim, M.N.; Aziz, N.A.; Punan, M.S. Energy and exergy analysis of industrial fluidized bed drying of paddy. Energy 2015, 84, 131–138. [Google Scholar] [CrossRef]
- Sarker, M.; Ibrahim, M.N.; Ab Aziz, N.; Salleh, P.M. Energy and rice quality aspects during drying of freshly harvested paddy with industrial inclined bed dryer. Energy Convers. Manag. 2014, 77, 389–395. [Google Scholar] [CrossRef]
- Li, C.; Ma, X.; Fang, Z.; Zhang, Y. Thermal energy structure of grain hot air drying and analytical method. Trans. Chin. Soc. Agric. Eng. 2014, 30, 220–228. [Google Scholar] [CrossRef]
- Shen, Q.; Quek, S.Y. Microencapsulation of astaxanthin with blends of milk protein and fiber by spray drying. J. Food Eng. 2014, 123, 165–171. [Google Scholar] [CrossRef]
- Ratti, C. Hot air and freeze-drying of high-value foods: a review. J. Food Eng. 2001, 49, 311–319. [Google Scholar] [CrossRef]
- Beigi, M.; Tohidi, M.; Torki-Harchegani, M. Exergetic Analysis of Deep-Bed Drying of Rough Rice in a Convective Dryer. Energy 2017, 140. [Google Scholar] [CrossRef]
- Folayan, J.A.; Osuolale, F.; Anawe, P. Data on exergy and exergy analyses of drying process of onion in a batch dryer. Data Brief 2018, 21, 1784–1793. [Google Scholar] [CrossRef] [PubMed]
- Tohidi, M.; Sadeghi, M.; Torki-Harchegani, M. Energy and quality aspects for fixed deep bed drying of paddy. Renew. Sustain. Energy Rev. 2017, 70, 519–528. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Song, M.; Li, H.; Sun, Z. Experimental investigation on drying performance of an existed enclosed fixed frequency air source heat pump drying system. Appl. Therm. Eng. 2018, 130, 735–744. [Google Scholar] [CrossRef]
- Aviara, N.A.; Onuoha, L.N.; Falola, O.E.; Igbeka, J.C. Energy and exergy analyses of native cassava starch drying in a tray dryer. Energy 2014, 73, 809–817. [Google Scholar] [CrossRef]
- Aktaş, M.; Khanlari, A.; Amini, A.; Şevik, S. Performance analysis of heat pump and infrared–heat pump drying of grated carrot using energy-exergy methodology. Energy Convers. Manag. 2017, 132, 327–338. [Google Scholar] [CrossRef]
- Hazervazifeh, A.; Nikbakht, A.M.; Moghaddam, P.A. Novel hybridized drying methods for processing of apple fruit: Energy conservation approach. Energy 2016, 103, 679–687. [Google Scholar] [CrossRef]
- Li, C.; Mai, Z.; Fang, Z. Analytical study of grain moisture binding energy and hot air drying dynamics. Trans. Chin. Soc. Agric. Eng. 2014, 30, 236–242. [Google Scholar] [CrossRef]
- Defraeye, T. Advanced computational modelling for drying processes—A review. Appl. Energy 2014, 131, 323–344. [Google Scholar] [CrossRef]
- Akpinar, E.K.; Midilli, A.; Bicer, Y. The first and second law analyses of thermodynamic of pumpkin drying process. J. Food Eng. 2006, 72, 320–331. [Google Scholar] [CrossRef]
- Bejan, A. Advanced Engineering Thermodynamics; John Wiley & Sons: New York, NY, USA, 1988. [Google Scholar] [CrossRef]
- Khanali, M.; Aghbashlo, M.; Rafiee, S.; Jafari, A. Exergetic performance assessment of plug flow fluidised bed drying process of rough rice. Int. J. Exergy 2013, 13, 387–408. [Google Scholar] [CrossRef]
- Dincer, I.; Sahin, A.Z. A new model for thermodynamic analysis of a drying process. Int. J. Heat Mass Transf. 2004, 47, 645–652. [Google Scholar] [CrossRef]
- Yildirim, N.; Genc, S. Energy and exergy analysis of a milk powder production system. Energy Convers. Manag. 2017, 149, 698–705. [Google Scholar] [CrossRef]
- Baird, J.K.; King, T.R. A wien displacement law for impact radiation. Int. J. Impact Eng. 1999, 23, 39–49. [Google Scholar] [CrossRef]
- De Lima, J.A.S.; Santos, J. Generalized Stefan-Boltzmann law. Int. J. Theor. Phys. 1995, 34, 127–134. [Google Scholar] [CrossRef]
- Li, C. Theoretical analysis of exergy transfer and conversion in grain drying process. Trans. Chin. Soc. Agric. Eng. 2018, 34. [Google Scholar] [CrossRef]
- Aghbashlo, M.; Mobli, H.; Rafiee, S.; Madadlou, A. Energy and exergy analyses of the spray drying process of fish oil microencapsulation. Biosyst. Eng. 2012, 111, 229–241. [Google Scholar] [CrossRef]
- Syahrul, S.; Hamdullahpur, F.; Dincer, I. Thermal analysis in fluidized bed drying of moist particles. Appl. Therm. Eng. 2002, 22. [Google Scholar] [CrossRef]
- Skoneczna-Łuczków, J.; Ciesielczyk, W. Exergetic analysis for a complete node of a fluidized bed drying of poppy seeds. Chem. Process. Eng. 2015, 36. [Google Scholar] [CrossRef]
- Li, J.; Chen, K.; Yang, M.; Ji, C. Studies of Paddy’s Increased Crack Percentage and Sprouting Percentage after Being Dried in a Fixed Deep Bed. Cereal Feed Ind. 2001. [Google Scholar] [CrossRef]
- Yogendrasasidhar, D.; Setty, Y.P. Drying kinetics, exergy and energy analyses of Kodo millet grains and Fenugreek seeds using wall heated fluidized bed dryer. Energy 2018. [Google Scholar] [CrossRef]
- Yang, H.; Cai, X.; Chen, Q. Influence of two drying measure with two temperature to rice quality. Grain Storage 2013, 1, 34–38. [Google Scholar]
- Chen, N.; Chen, M.; Fu, B.; Song, J. Far-infrared irradiation drying behavior of typical biomass briquettes. Energy 2017, 121, 726–738. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, Y.; Yue, J.; Liu, Z.; Zheng, Y.; Qian, B.; Zhong, Y.; Zhao, Y. Thermal behavior, microstructure and protein quality of squid fillets dried by far-infrared assisted heat pump drying. Food Control 2014, 36, 102–110. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, Z. Research on characteristics of infrared absorption of grain. Grain Storage 2003, 32, 38–41. [Google Scholar]
- Ma, X.; Fang, Z.; Li, C. Energy efficiency evaluation and experiment on grain counter-flow drying system based on exergy analysis. Trans. Chin. Soc. Agric. Eng. 2017, 33, 285–291. [Google Scholar] [CrossRef]
- Shiun, L.J.; Haslenda, H.; Zainuddin, A.M.; Shariafah, R.A. Optimal design of a rice mill utility system with rice husk logistic network. Ind. Eng. Chem. 2012, 51, 362–373. [Google Scholar] [CrossRef]
- Hepbasli, A. A review on energetic, exergetic and exergoeconomic aspects of geothermal district heating systems (GDHSs). Energy Convers. Manag. 2010, 51, 2041–2061. [Google Scholar] [CrossRef]
- Xiong, S.; Sun, W.; Zhao, L.; Lu, Z.; He, X.; Mao, J.; Zhou, Q. Optimization of three-stage drying of paddy. Food Sci. 2017, 38, 274–281, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Aghbashlo, M.; Mobli, H.; Madadlou, A.; Rafiee, S. Influence of spray dryer parameters on exergetic performance of microencapsulation processs. Int. J. Exergy 2012, 111, 229–241. [Google Scholar] [CrossRef]
- Aghbashlo, M.; Kianmehr, M.H.; Arabhosseini, A. Energy and Exergy Analyses of Thin-Layer Drying of Potato Slices in a Semi-Industrial Continuous Band Dryer. Dry. Technol. 2008, 26, 1501–1508. [Google Scholar] [CrossRef]



| Parameters | Designed Values | Considerations |
|---|---|---|
| Inlet air temperature (Ta,in) | 70 °C | Specific high initial moisture content |
| Outlet air temperature (Ta,out) | 30 °C | To decrease the heat loss in outlet air |
| Outlet paddy temperature (Tp,out) | 30 °C | To decrease the heat loss in outlet paddy |
| Flue gas temperature (Tg) | 400 °C | Empirical |
| Radiator temperature (Tr) | 90 °C | The paddy seed get the optimal absorption wavelength (9 µm) when Tr is 90 °C |
| Devices | Model | Measurement Range | Precision | Uncertainly |
|---|---|---|---|---|
| Thermal resistance | PT100 | −200–450 °C | ±0.1 °C | ±0.133 °C |
| Anemometer | DT-8893 | 0.001–45 m/s | 0.01 m/s | 0.0234 m/s |
| Temperature and humidity sensors | AM2301 | 0–100%/−40–80 °C | ±3%/±0.5 °C | ±3.102%/±0.534 °C |
| Data acquisition system | Self-developed | - | - | - |
| Moisture meter | Self-developed | 10–40% | ±0.5% | ±0.5136% |
| Parameters Name | Value/Equation | Unit | Reference |
|---|---|---|---|
| Ra | 0.287 | kJ·kg−1·K−1 | [19] |
| Rv | 0.462 | kJ·mol−1·K−1 | |
| σ | 5.67 × 10−8 | W·m−2·K−4 | [32] |
| Ɛr | 0.9 | - | |
| Ar | 8.3 | m2 | |
| δ | 0.02 | m | |
| γ | 1.0 | W·m−1·K−1 | |
| S | 18.1 | m·s−1 | |
| A | 0.126 | m2 | |
| 17.223 | kg·s−1 | ||
| Cp | kJ·kg−1·K−1 | [33] | |
| hfg | kJ·kg−1 | [34] | |
| Cv | kJ·kg−1·K−1 | [28] | |
| Ca | kJ·kg−1·K−1 | ||
| Radiator size | D0 = 0.22; Di = 0.2; L = 3 | m |
| Equipment | Power |
|---|---|
| Mix | 1 kW |
| Hoist | 3.7 kW |
| Conveyor | 3 kW |
| Induced fan | 15 kW |
| Negative pressure fan | 2.5 kW |
| Drying Time/min | SEC (kJ/gw) | Drying Chamber | Whole System | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ηex (%) | ηen (%) | (kW) | SI (-) | ηex (%) | ηen (%) | (kW) | SI (-) | ||
| 30 | 6.54 | 57.92 | 50.02 | 4.79 | 2.38 | 54.62 | 45.70 | 10.90 | 2.20 |
| 60 | 4.98 | 76.31 | 64.28 | 2.88 | 4.22 | 60.23 | 56.63 | 8.49 | 2.51 |
| 90 | 7.39 | 51.05 | 43.58 | 5.44 | 2.04 | 52.81 | 41.62 | 11.40 | 2.12 |
| 120 | 9.58 | 36.45 | 30.08 | 7.76 | 1.57 | 52.59 | 35.07 | 10.60 | 2.11 |
| 150 | 12.38 | 27.34 | 22.40 | 8.81 | 1.38 | 51.10 | 29.93 | 10.60 | 2.04 |
| 180 | 15.32 | 23.33 | 18.72 | 9.72 | 1.30 | 46.30 | 25.57 | 13.93 | 1.86 |
| 210 | 16.95 | 22.04 | 18.39 | 8.75 | 1.28 | 44.13 | 23.93 | 15.53 | 1.79 |
| 240 | 20.01 | 18.30 | 15.27 | 8.98 | 1.22 | 43.95 | 22.06 | 14.99 | 1.78 |
| 270 | 22.83 | 14.94 | 12.27 | 9.65 | 1.18 | 46.23 | 21.34 | 12.40 | 1.86 |
| 300 | 24.91 | 13.51 | 11.18 | 9.59 | 1.16 | 46.54 | 20.70 | 11.91 | 1.87 |
| 330 | 25.95 | 12.62 | 10.85 | 8.70 | 1.14 | 48.21 | 20.90 | 10.41 | 1.93 |
| 360 | 33.70 | 10.46 | 8.46 | 10.59 | 1.12 | 42.63 | 17.59 | 15.14 | 1.74 |
| 390 | 35.64 | 9.77 | 7.92 | 10.52 | 1.11 | 43.11 | 17.39 | 14.51 | 1.76 |
| 420 | 49.75 | 7.19 | 5.94 | 9.60 | 1.08 | 41.30 | 15.38 | 15.14 | 1.70 |
| 450 | 56.09 | 6.53 | 5.45 | 8.60 | 1.07 | 40.14 | 14.64 | 15.46 | 1.67 |
| 480 | 63.91 | 5.79 | 4.75 | 8.82 | 1.06 | 39.03 | 13.92 | 15.83 | 1.64 |
| 510 | 71.52 | 4.93 | 4.23 | 7.38 | 1.05 | 41.94 | 14.33 | 12.02 | 1.72 |
| 540 | 99.41 | 3.65 | 3.28 | 6.25 | 1.04 | 40.72 | 13.26 | 12.81 | 1.69 |
| Average | 32.05 | 22.34 | 18.73 | 8.16 | 1.47 | 46.42 | 25.00 | 12.89 | 1.89 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Li, C.; Li, T.; Zeng, Z.; Ou, W.; Li, C. Exergetic, Energetic, and Quality Performance Evaluation of Paddy Drying in a Novel Industrial Multi-Field Synergistic Dryer. Energies 2019, 12, 4588. https://doi.org/10.3390/en12234588
Li B, Li C, Li T, Zeng Z, Ou W, Li C. Exergetic, Energetic, and Quality Performance Evaluation of Paddy Drying in a Novel Industrial Multi-Field Synergistic Dryer. Energies. 2019; 12(23):4588. https://doi.org/10.3390/en12234588
Chicago/Turabian StyleLi, Bin, Changyou Li, Tao Li, Zhiheng Zeng, Wenyan Ou, and Chengjie Li. 2019. "Exergetic, Energetic, and Quality Performance Evaluation of Paddy Drying in a Novel Industrial Multi-Field Synergistic Dryer" Energies 12, no. 23: 4588. https://doi.org/10.3390/en12234588
APA StyleLi, B., Li, C., Li, T., Zeng, Z., Ou, W., & Li, C. (2019). Exergetic, Energetic, and Quality Performance Evaluation of Paddy Drying in a Novel Industrial Multi-Field Synergistic Dryer. Energies, 12(23), 4588. https://doi.org/10.3390/en12234588