1. Introduction
Air traffic especially in Europe and USA delivers a significant contribution to the carbon dioxide emissions of the traffic sector. The vision for future airplanes is to equip them with an electrical drive system powered by batteries (small aircrafts) or hydrogen-based fuel cells. That is why electrical machines for fan drives in aviation are getting into the focus of development engineers. The dominant requirement is an extremely low weight of the drive to gain a competitive advantage with a modern aviation turbofan or propeller turbine. Currently, discussed figures are 10 to 20 kW per kg weight [
1] of the machine, which are only are achievable with intense fluidic cooling and only where the higher value may be achieved with superconducting technologies. Another important figure that is seldom referenced is the drive system weight, respective of the weight of the electrical machine, inverter, and cooling system. All three components compose the drive system for a fan or propeller drive [
2].
The conventional cooling system for electrical machines installed in aircraft, e.g., generators, is oil spray cooling using the oil from the turbine gear. This method is well established and documented in Reference [
3]. In Reference [
4], a heat pump is proposed for an oil spray cooling to raise the temperature level of the cooling fluid and to obtain smaller and lighter heat exchangers. Often the temperature level of the cooling oil is rather high, which requires a huge mass flow of oil and appropriate pumping capacity. Oil spray cooling also causes excessive rotor friction, which reduces the efficiency of the drive.
With industrial and automotive applications, water jacket cooling is a well-established cooling method [
4] with the advantage of a simple mechanical structure and large heat capacity of water. In Reference [
5], a water cooling system for an automotive drivetrain is combined with a heat pump to achieve convenient temperature levels for the cooling of the drive train components under summer and winter conditions.
In the overview paper [
6], focus is set on the most recent progress in thermal management of electric motors for aviation. Besides air cooling, oil bath cooling, water jacket cooling, heat pipe cooling, intra winding cooling channels with a thermal conductive polymer [
7], and direct winding cooling with tube-like conductors are cited. In this case, the problem of large pressure drops in the cooling ducts of six bars or more occurs. As experimental results, current densities of 24.7 A/mm
2 and transient current density of more than 40 A/mm
2 with class F insulation were achieved. With class H insulation even higher, values up to 58 A/mm
2 could be possible. By using conductors with integrated cooling channels, current densities possibly reaching 130 A/mm
2 were anticipated. However, the losses increase with the square of the current density and are linear with the volume of the winding even though the temperature is within the limits of the insulation system. The extremely high copper losses will increase weight and size of the cooling system and the reduced efficiency also requires an increase of the on-board power supply (generators and prime movers, fuel tank or energy storages, wiring, switchgear).
The weight advantages of such machines can be quickly overcompensated by the weight of the cooling system and the increased power supply. Therefore, an accurately balanced design of the drive system is necessary. A proposal for the improvement of this approach is given in
Section 5.
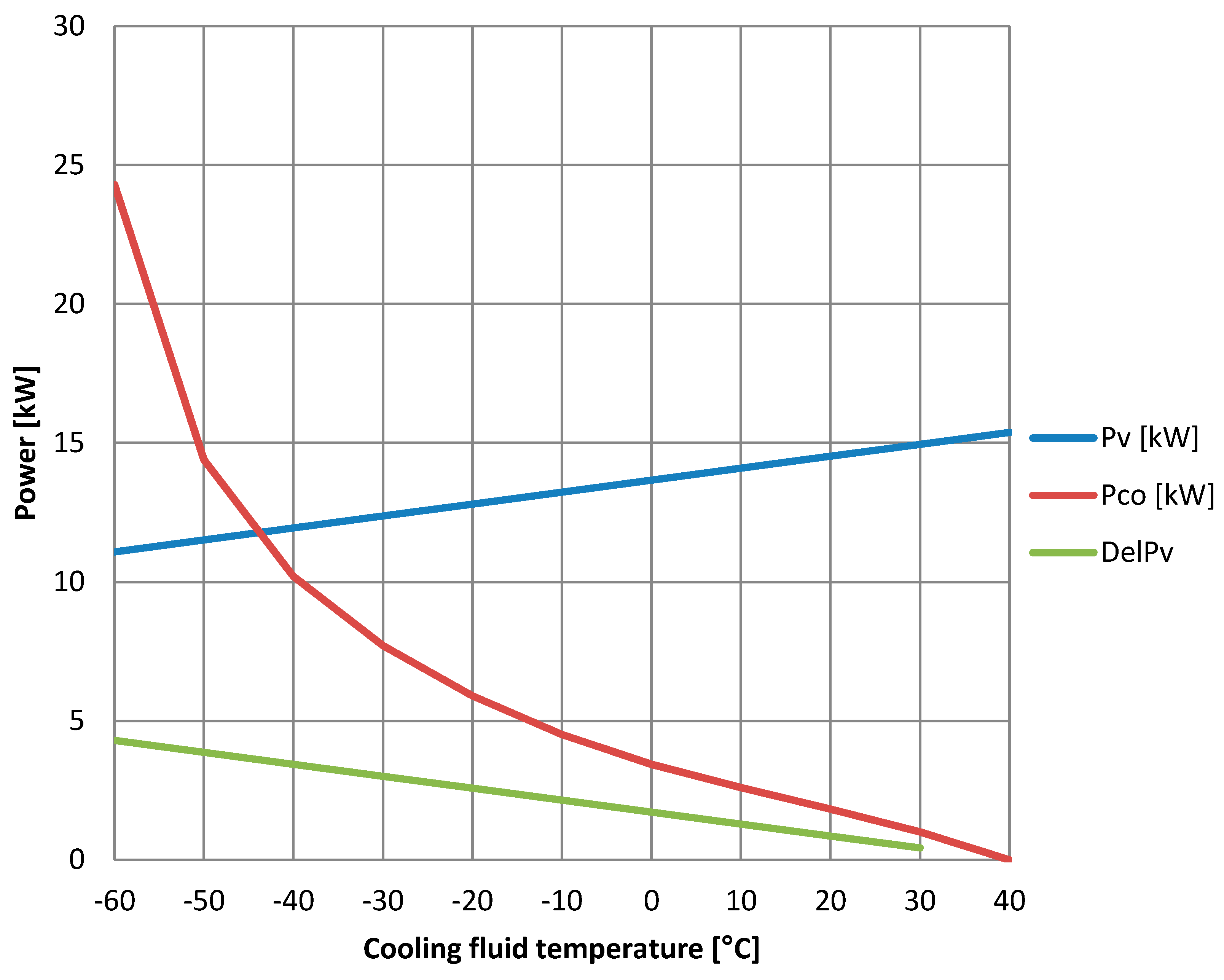
A reduction of the winding temperature level by lowering the coolant temperature below standard ambient temperature promises a reduction of the copper losses in the electrical machine and a longer lifetime of the insulation. The higher effort for such cooling systems may be compensated by the higher efficiency of the drive. Due to the usually high temperature drop between winding and cooling fluid, this requires low ambient temperatures—as given in high cruising altitudes—or the use of refrigerant cooling systems, which allow coolant temperatures below ambient temperatures. In a literature study, no papers dealing with this question for aviation were found.
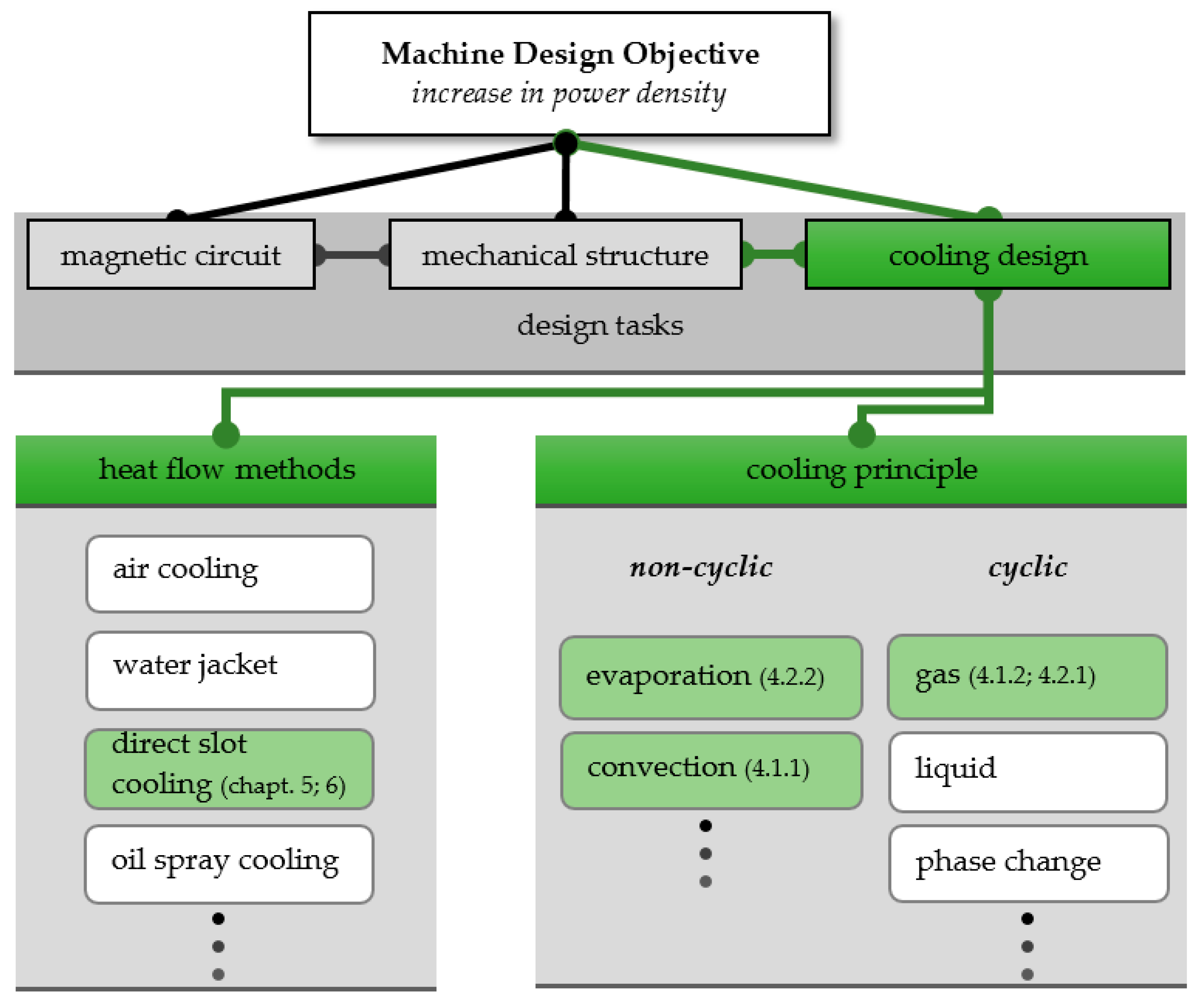
The scope of this paper is illustrated in
Figure 1 as the green path. In this case, the focus is on studying the theoretical potentials of cooling technologies for conventional high-power density machines with one phase fluid cooling applicable to drives of some MW rating for smaller aircrafts or single aisle aircraft. With a new proposal for direct slot cooling, a high potential to improve the cooling system is identified and so this is studied in depth in
Section 5. The results will help develop a design strategy for aviation drives.
2. Holistic Requirements on Machine Design for Aviation Application
The operation profile of a commercial aircraft (mission profile) can be reduced to some worst-case scenarios the drive has to deal with. In Reference [
8], some references are given to the operation modes of an aircraft. It comprises the take-off with overload power at ground pressure and temperature, the subsequent climb flight with nominal power and decreasing ambient temperature, the cruising at high altitude with reduced power and very low ambient temperature of −40 to −60 °C, and the approach for landing with reduced power and increasing ambient temperature. During landing, an electrical drive offers the favorable feature of a short response time if a touch-and-go procedure is required.
The ground temperature can vary from −30 to −40 °C (Alaska, North Canada, Greenland) to +40 °C (Dubai, Caracas) or more. For conventional planes, an ambient temperature of 40 °C requires a significant reduction of take-off weight or a longer runway. That is why we defined 40 °C as the reference temperature for this study.
From the mission profile, a worst-case scenario for the electrical drive and the cooling system can be derived. Take off with overload power from an airport in a tropical region with usually high ambient temperatures can be derived, which the cooling system has to handle reliably. The temperature in the machine windings must be controlled and monitored to ensure a safe climb flight. To illustrate the study conducted in this scenario, we referred to an exemplary small-size aircraft with two 1 MW engines. Regarding efficiency, 96% are assumed to be a realistic value, so losses of 40 kW per engine have to be transferred to the ambient temperature.
5. Methodical Improvement of the Thermal Conductivity Path in the Electrical Machine
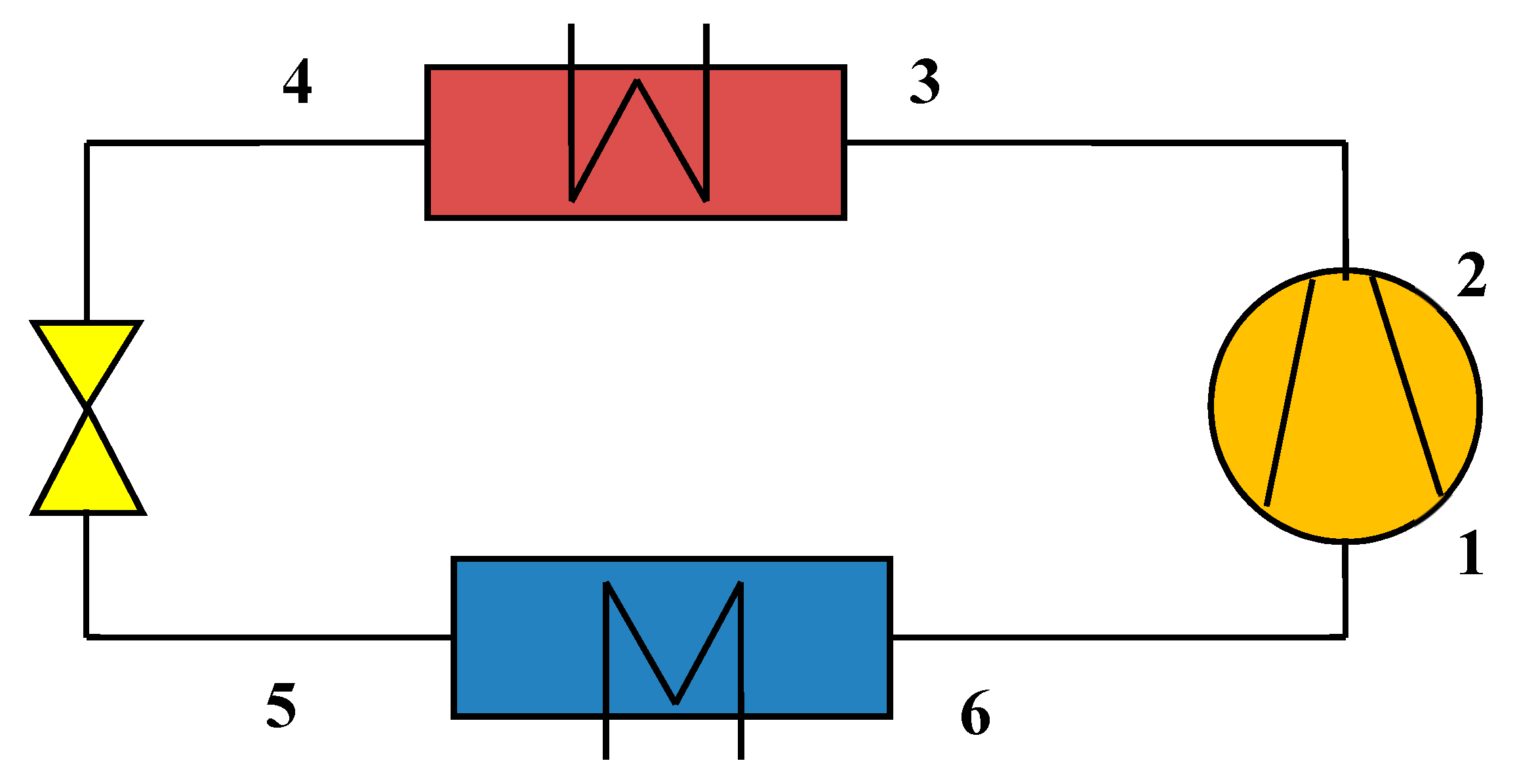
The discussion of cooling systems were based on the assumption of an electrical machine with conventional cooling fluid jacket as used in high power density constructions in industry or automotive drives.
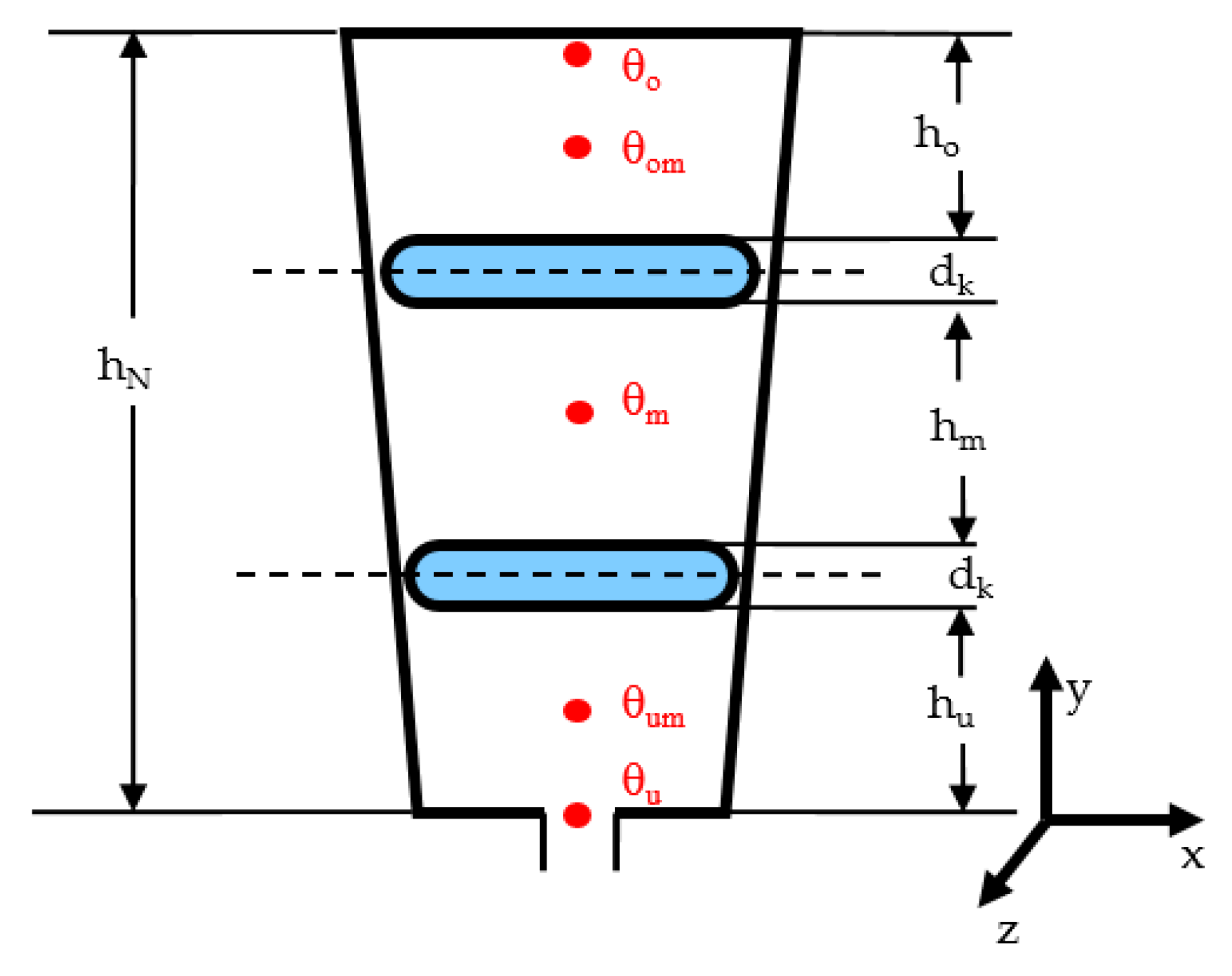
This implicates a certain temperature drop between cooling fluid and winding, which was set in these considerations to approximately 80 to 95 K. As an alternative design, machines with cooling channels placed between the copper conductors in the slots are studied (direct slot cooling).
Figure 10 shows a tested direct slot cooling prototype machine at the IMAB.
Depending on the achieved current density, this may increase the weight of the teeth and yoke, but the losses are then removed where they arise and high current densities under overload and steady state operation can be achieved with a decreased temperature rise in the winding, which allows a low weight design. To overcome the drawbacks of the intra winding cooling mentioned in Reference [
5], all cooling channels are hydraulically in parallel, which reduces the pressure drop significantly. Each slot has at least two or more cooling channels made from thin-walled plastic tubes. To avoid freezing of the cooling fluid at low ambient temperatures, it is advantageous to use a chemical inert fluid with low viscosity even at low temperatures but also with high temperature capability. Fluids on a polysiloxane basis seem to be a good choice [
22]. The current density in the winding is considered to be an optimizable quantity, which can be balanced between machine weight, efficiency, and cooling system weight.
With respect to the probable feeding frequency of 400 to 700 Hz, stranded wires as conductors are a prerequisite. If the machine is appropriately designed, no reduced cooling fluid temperatures are necessary, but the operating temperature of the coolant can be chosen at +60 °C to +90 °C with the option of utilizing the low ambient temperatures at cruising altitudes to reduce losses. In addition, a coupling of this cooling circuit with a chiller operating with a reversed Rankine cycle or an additional boost system, as described in
Section 4.2.2, is possible and may support an optimization in critical environments.
Typical values for the polysiloxane thermo oil [
22] are a thermal capacity of 1.75 kJ/(kgK) at 50 °C and 1.87 kJ/(kgK) at 100 °C as well as fairly low viscosity of 1.19 mPa⋅s at 50 °C, which is close to water. The critical temperature is 350 °C and utilizing these fluids at a temperature range from −82 °C up to 200 °C can be covered, which is more than the range of usual water-glycol mixtures. Thus, no problems even at high cruising altitudes are expected. The fluids are non-toxic and electrically insulating. The environmental impact if accidentally released at high altitudes needs more in-depth studies.
The simplest construction of the electrical machine for this case is a separation of rotor and stator by an air gap sleeve. Consequently, the winding overhangs are immersed in the cooling fluid that is circulating through the overhang spaces, the open slot channels, and a heat exchanger. The classical problem of an air gap sleeve is production of additional eddy current losses and a braking torque if it is made from electrical conducting material. These losses can put severe limits to the machine design. By employing modern construction materials, non-conducting air gap sleeves are possible currently so that this problem can be solved.
A design alternative avoiding the air gap sleeve problems could be distribution channels in both overhang spaces, which are connected with the cooling channels in the slots. This requires an appropriate choice of insulating thermoplastic material and welding technologies but will pose no greater problems to the production process.
A third alternative could be the introduction of heat pipes instead of the cooling channels. The heat exchanger will then be integrated into the overhang spaces. The advantage would be a hermetically sealed cooling system with no risk of leakage. The challenge is the choice of the material. The preferred material for heat pipes is mostly copper that cannot be used in the slot area because of the eddy current losses. Other less conducting materials for the heat pipe may exhibit the risk of hydrogen forming that will block the condensing zone of the pipes.
The calculation of the temperatures of winding and iron can be done with analytical (equivalent heat transfer network) or with numerical methods (finite element method). The method of thermal equivalent networks is well established and described in literature. One of the oldest sources found is reference [
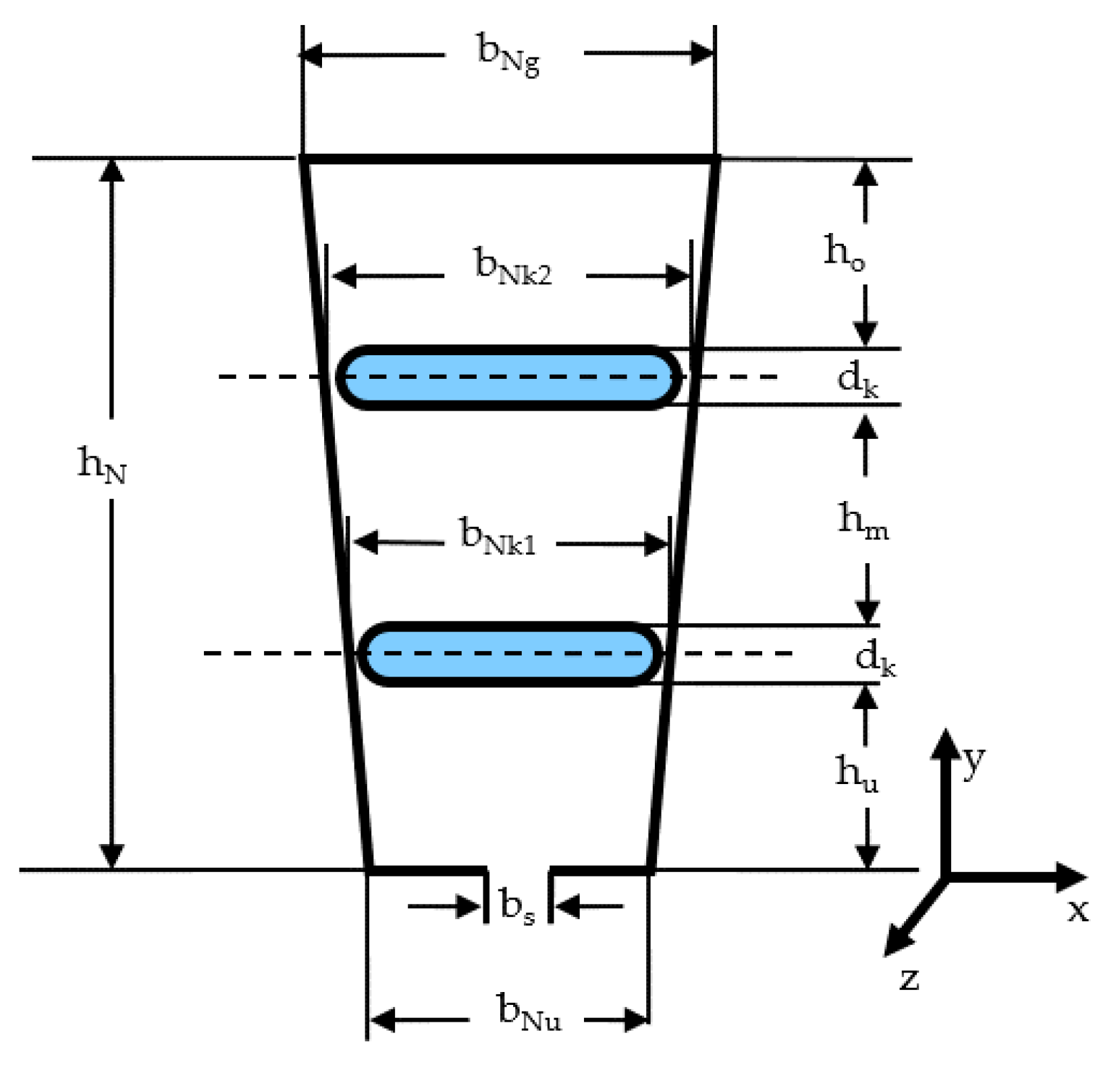
23] dating from 1967. The problem for any calculation method is posed by a sufficient accurate database for the materials used in the machine and an additional challenge for the designer comes with the production experiences. For the first theoretical study, the temperature distribution in an exemplary slot with the dimensions according to
Figure 11 was calculated with analytical and numerical methods as well. The used thermal data are given in
Table 4.
The thermal conductivity of the winding was calculated from the data of a mixture of copper and impregnating resin in all three dimensions. By using this, the winding is represented as a homogenous region.
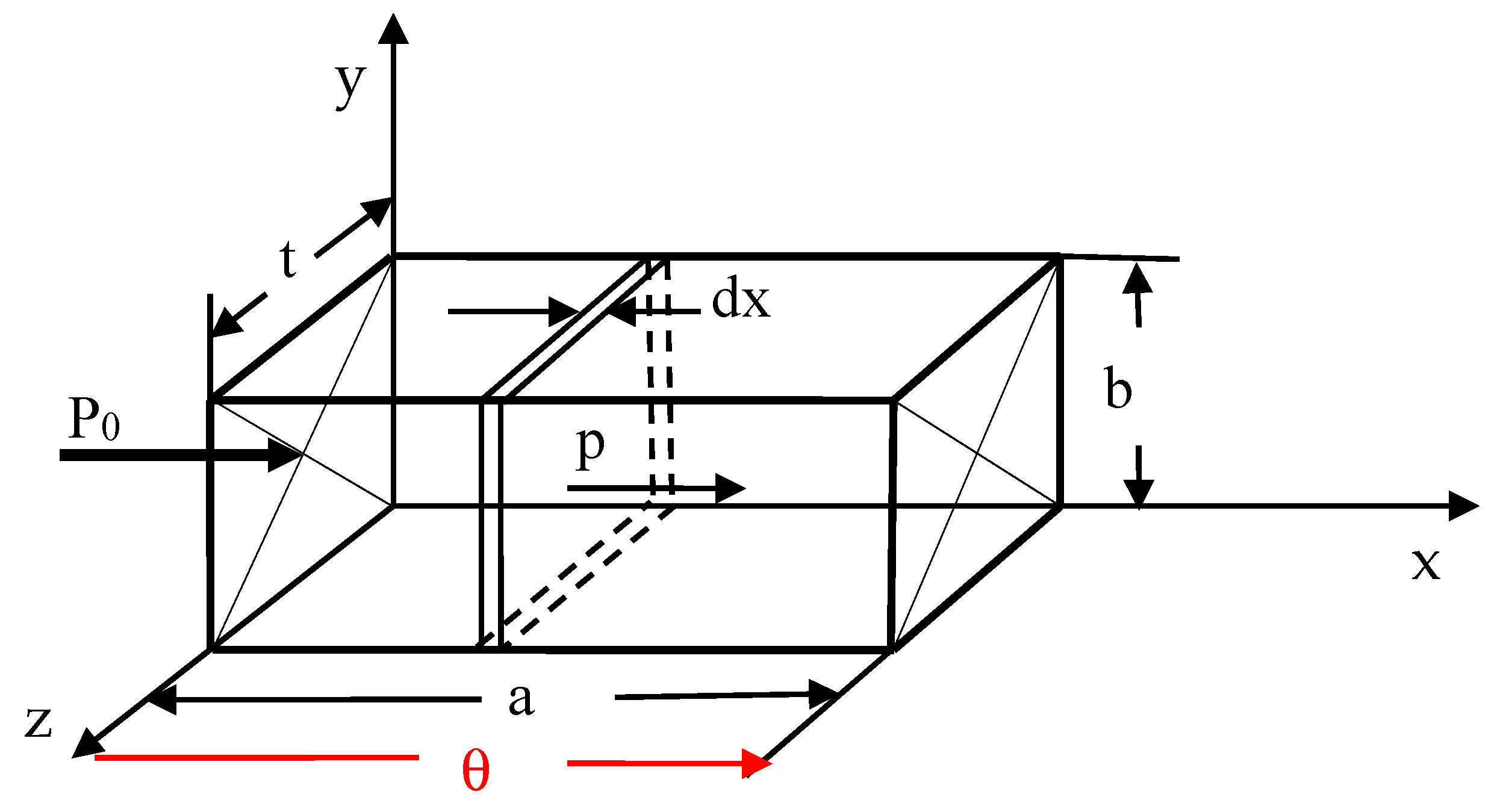
To improve the accuracy of the analytical calculation especially in regions possessing high current densities, a new calculation model for the regions with distributed losses was introduced, as shown in
Figure 12.
The temperature drop
θ in the region of
Figure 12 is composed from the temperature drop due to the external load
P0 and the inner loss density p.
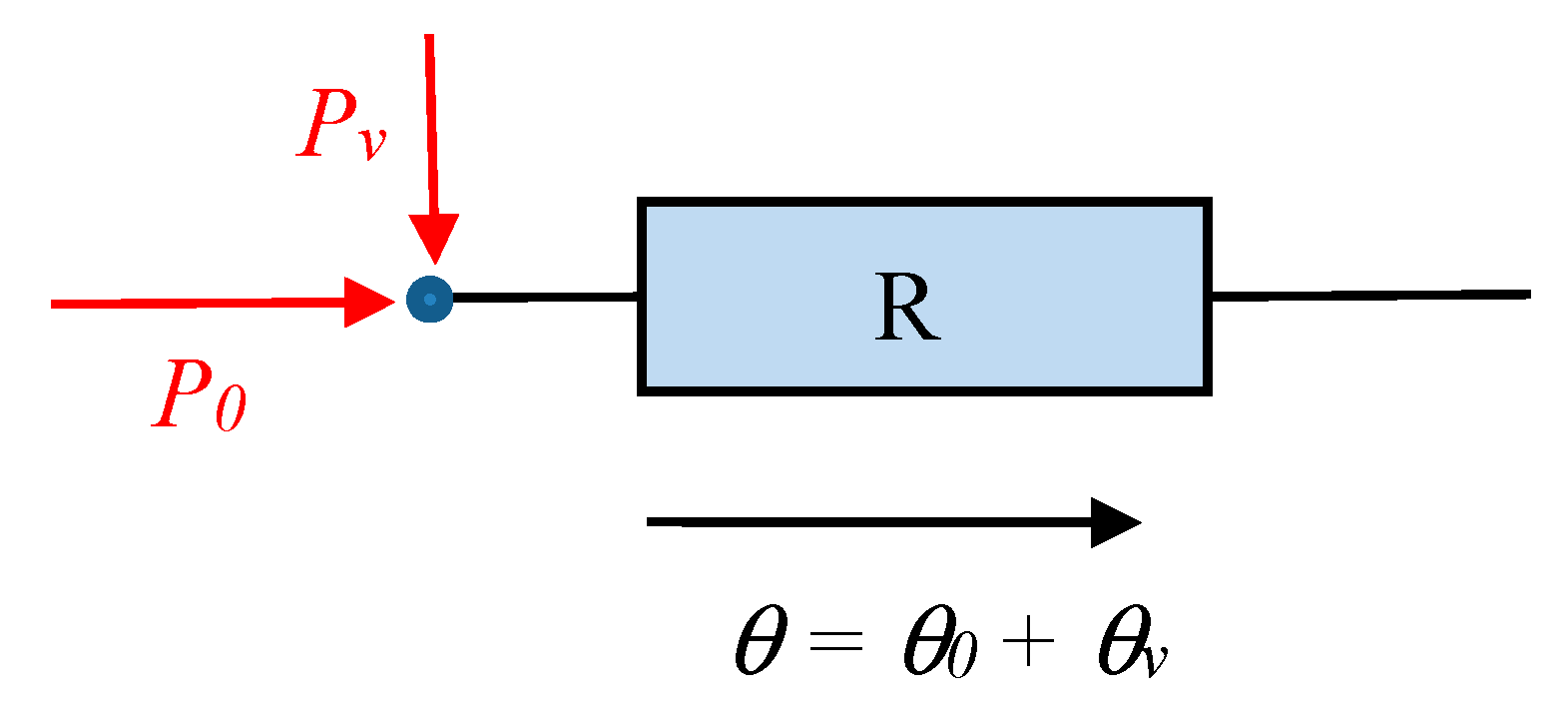
The network element of
Figure 13 gives a representation of a region with distributed losses. The size of the thermal resistance
R now depends on the relation of the distributed losses and the external losses.
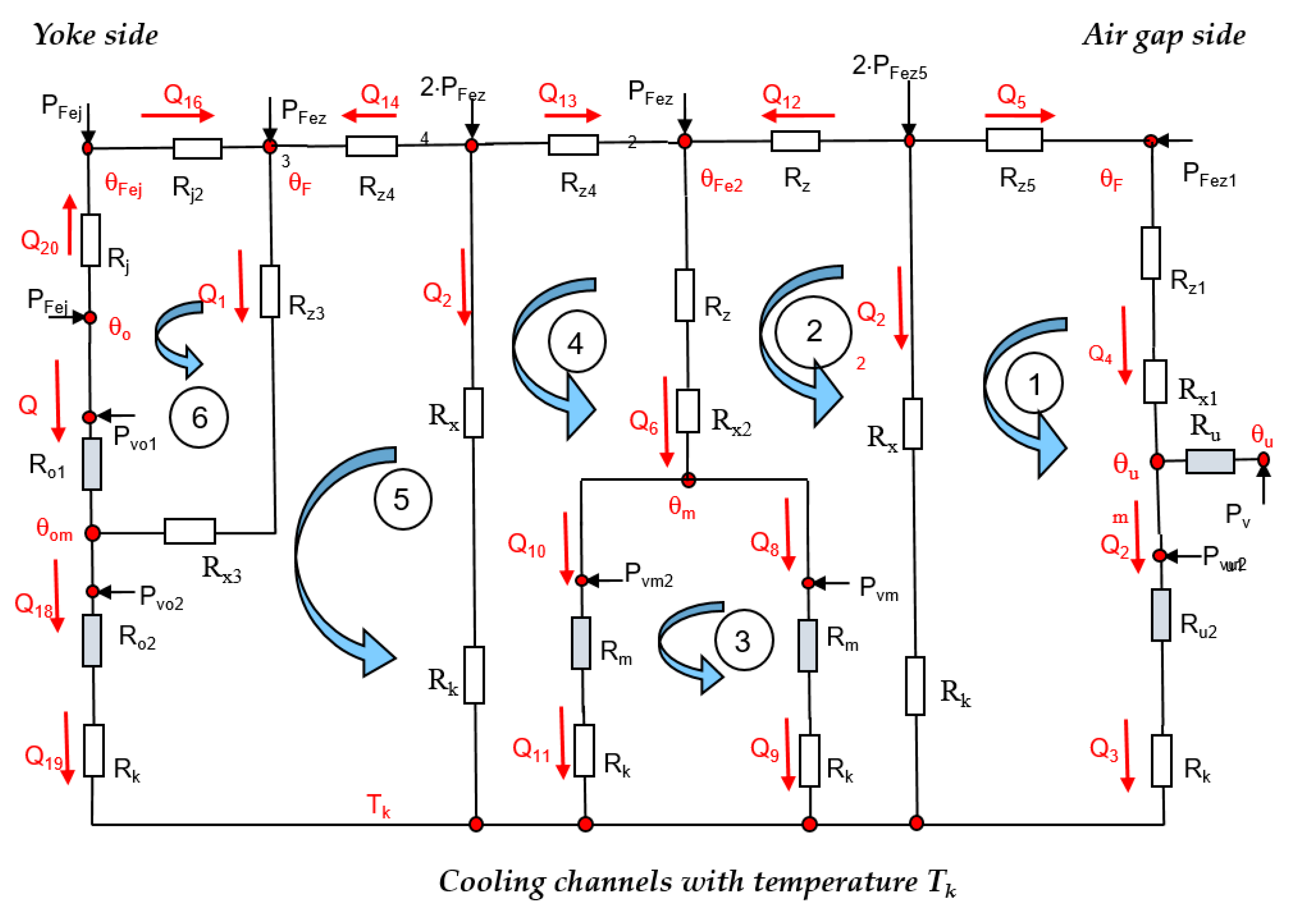
Distributed losses are observed in the winding and in the iron as well. To reduce the calculation effort, only the losses in the winding were calculated as distributed losses—elements with light blue filling in
Figure 14—while the losses in the iron were represented with conventional lumped parameters. Due to the symmetry of the problem, it is sufficient to establish the thermal equivalent network for half of a slot in the x-direction with a symmetry line in the slot middle. All calculations were restricted to a 2-D-Heat flow problem. A heat transfer in the third dimension to the winding overhangs is neglected, so all calculations are on the safe side.
The thermal transfer network of
Figure 14, therefore, represents the implemented calculation model for the analytical calculation. For a more efficient mathematical handling, the network was redrawn. It is assumed that all heat flows are conducted to the cooling channels on the temperature level
Tk. The heat flows in the branches of the network are denoted as Q and the distributed losses are named
Pv. The resistance of the channel walls is named R
k. The iron losses are denoted as P
Fez for the tooth and P
Fej for the yoke sections, respectively.
The system of linear equations derived from the lumped parameter network (six meshes, 22 branches) poses no major problems from the mathematical point of view. The advantage of the lumped parameter network is that it allows the fast and simple calculation of changes in the calculation model and an easy representation of 3-D heat flows if the model is extended by a heat flow to the end windings.
Verification of Analytical Calculations
To verify the results, a numerical finite element calculation model was established with ANSYS software. The hot spots for the comparison of both calculation approaches are given in
Figure 15.
Table 5 displays the calculated values of the temperature drops at the hot spots of the slot resulting from numerical and analytical calculation.
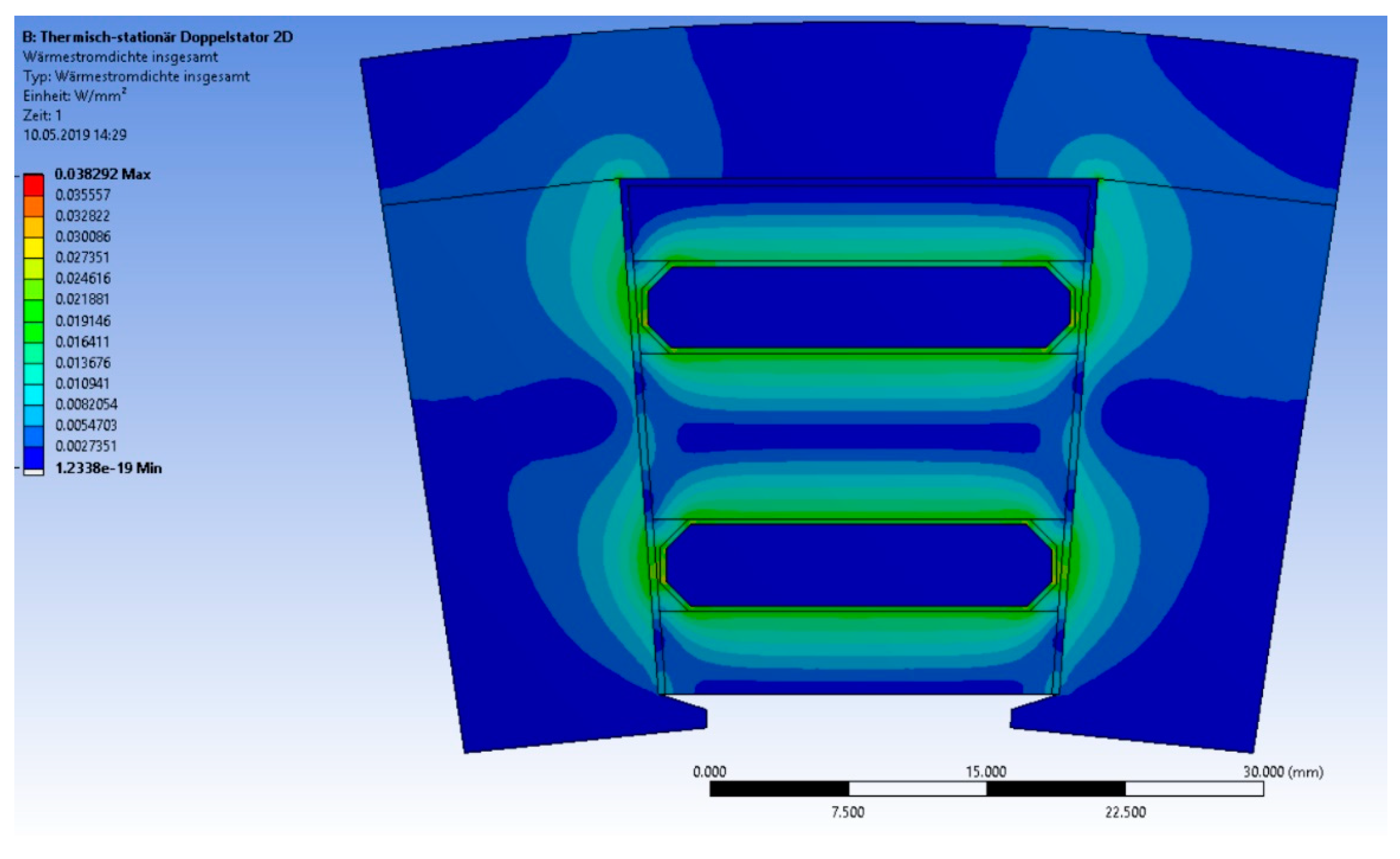
Figure 16 shows the density of the heat flow within a single slot pitch. The main heat flow that goes directly to the cooling channels were assumed to be at a constant temperature of 80 °C. Clearly, there is also a heat flow around the cooling channel edges over the tooth iron, which were not represented in the analytical calculation.
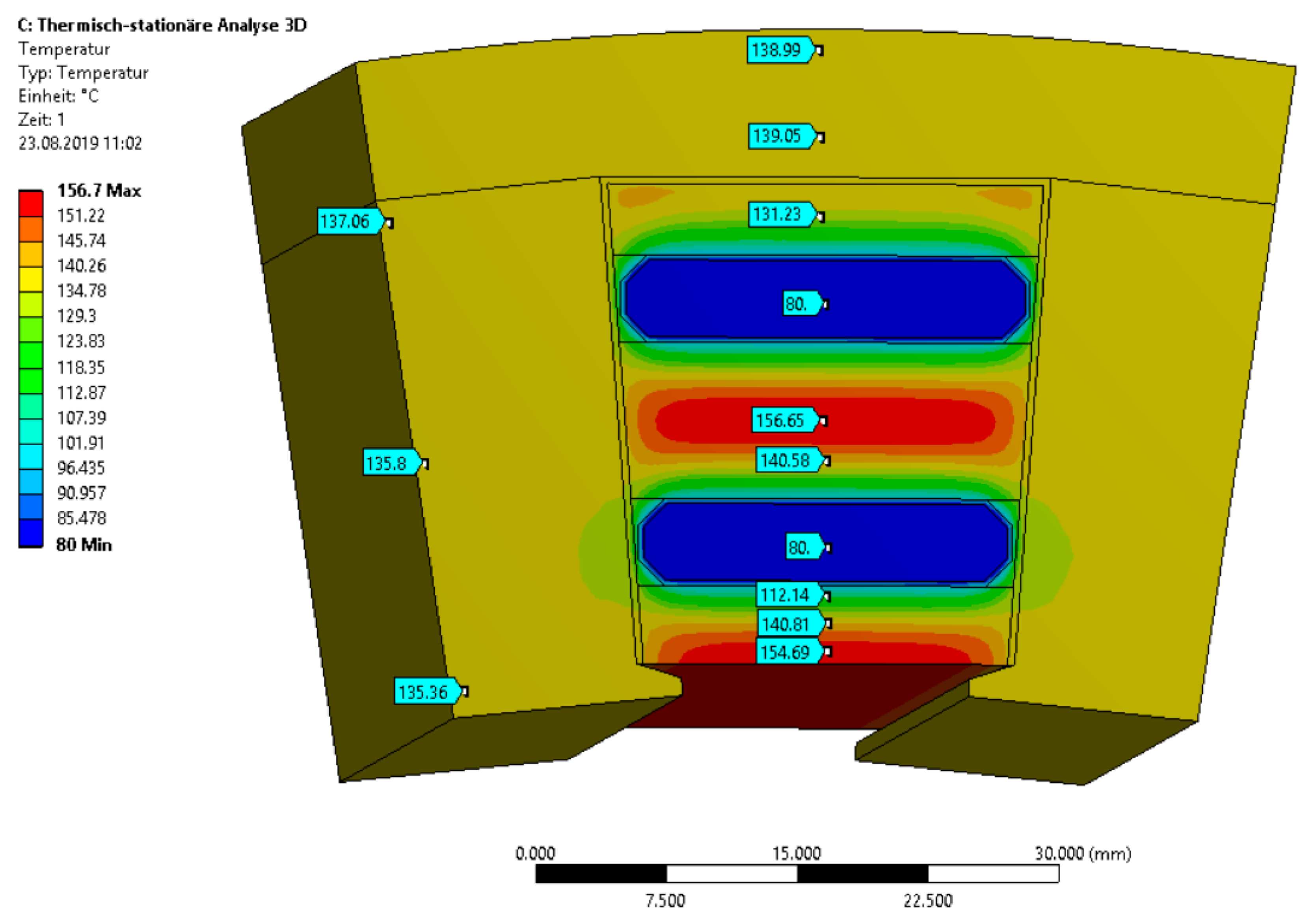
Figure 17 shows the temperature values within a slot pitch (current density of 15 A/mm
2, steady state, copper filling factor of 70%).
The obtained accuracy of the analytical calculation is satisfying the usual uncertainty of the material database. A comparatively high temperature drop in the walls of the cooling channels of 17 K can be observed. In this case, we can identify an optimization potential by choice of material and wall thickness.
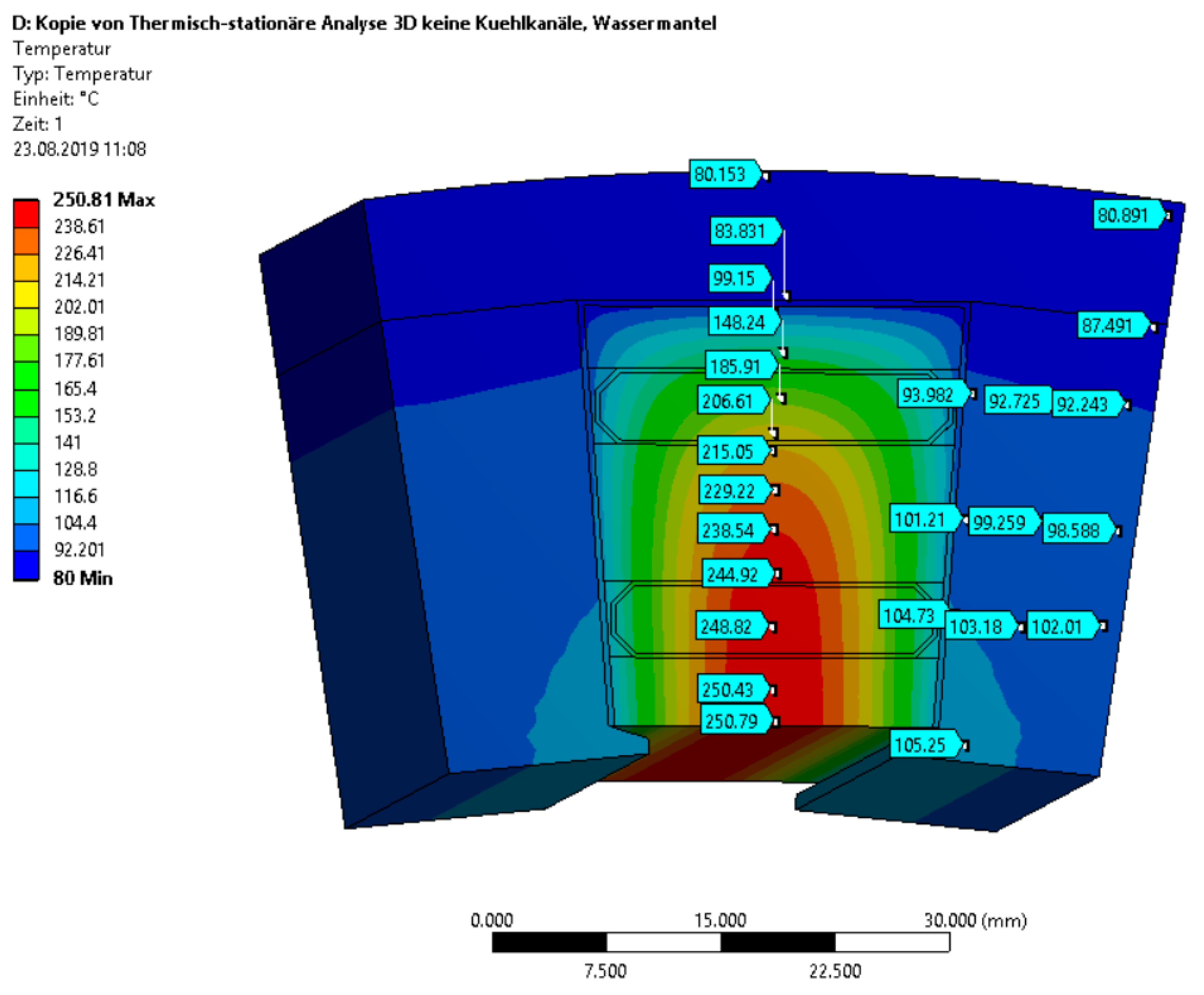
For a further comparison, a calculation for a machine with classical water jacket cooling was made under the same assumptions of the thermal properties as before (
Figure 18). The cooling channels are replaced by copper winding. To achieve the same current loading in the slot, the current density was reduced to 9 A/mm
2. This gives significantly reduced losses but, nevertheless, the calculation shows a temperature rise of 170 K respective of a difference to direct slot cooling of 94 K.
The direct slot cooling exhibits an impressive potential to optimize the current sheet, force density, temperature distribution, and the weight of the machine. Due to the identified potential, experimental investigations are planned in the next steps of the project.
6. Calculation Results on Heat Transfer Channel Wall—Cooling Fluid
Three major temperature drops will dominate the cooling system design of an electric aviation drive.
Temperature drop between winding and cooling channel wall. This can be minimized by direct slot cooling.
Temperature drop between cooling channel wall and coolant (discussed in this section).
Temperature drop between coolant fluid and ambient environment depending on the design of the heat exchanger. Highly effective heat exchangers for aviation will be a topic of further studies.
To calculate the heat transfer from the cooling channel wall to the cooling fluid, one has to solve the hydraulic equations of the cooling system to receive the pressure drop in the cooling channel and the fluid velocity. By estimating the pressure difference in the cooling channel from experience values, a preliminary study of possible problems can be conducted even in an early design stage. The calculations were performed by applying water glycol and a polysiloxane fluid [
22]. Starting values and fluid properties for the calculation are shown in
Table 6 and
Table 7.
6.1. Power Balance and Hydraulic Data
Compared with water, the polysiloxane fluid has an inferior thermal conductivity. Therefore, a higher temperature drop should be expected. The necessary volume flow to remove the losses is calculated from the power balance and the allowed temperature rise ΔTk in the cooling fluid.
In the first step, a pressure difference of Δp = 0.15 bar was assumed.
6.2. Temperature Drop to the Channel Wall and Heating of Cooling Fluid
The temperature drop between the channel wall and fluid is derived from the heat transfer coefficient α, the losses Pv,max, and the surface of channel Aw.
For the calculation of
α, according to Hausens equation [
24], the velocity of the fluid and the Reynolds number are required. Turbulence and large Reynolds numbers are advantageous for a good heat transfer. The calculations were performed for variable channel dimensions with the hydraulic diameter
dh. (A: cross section of channel, U: circumference of the channel).
The exemplary construction of
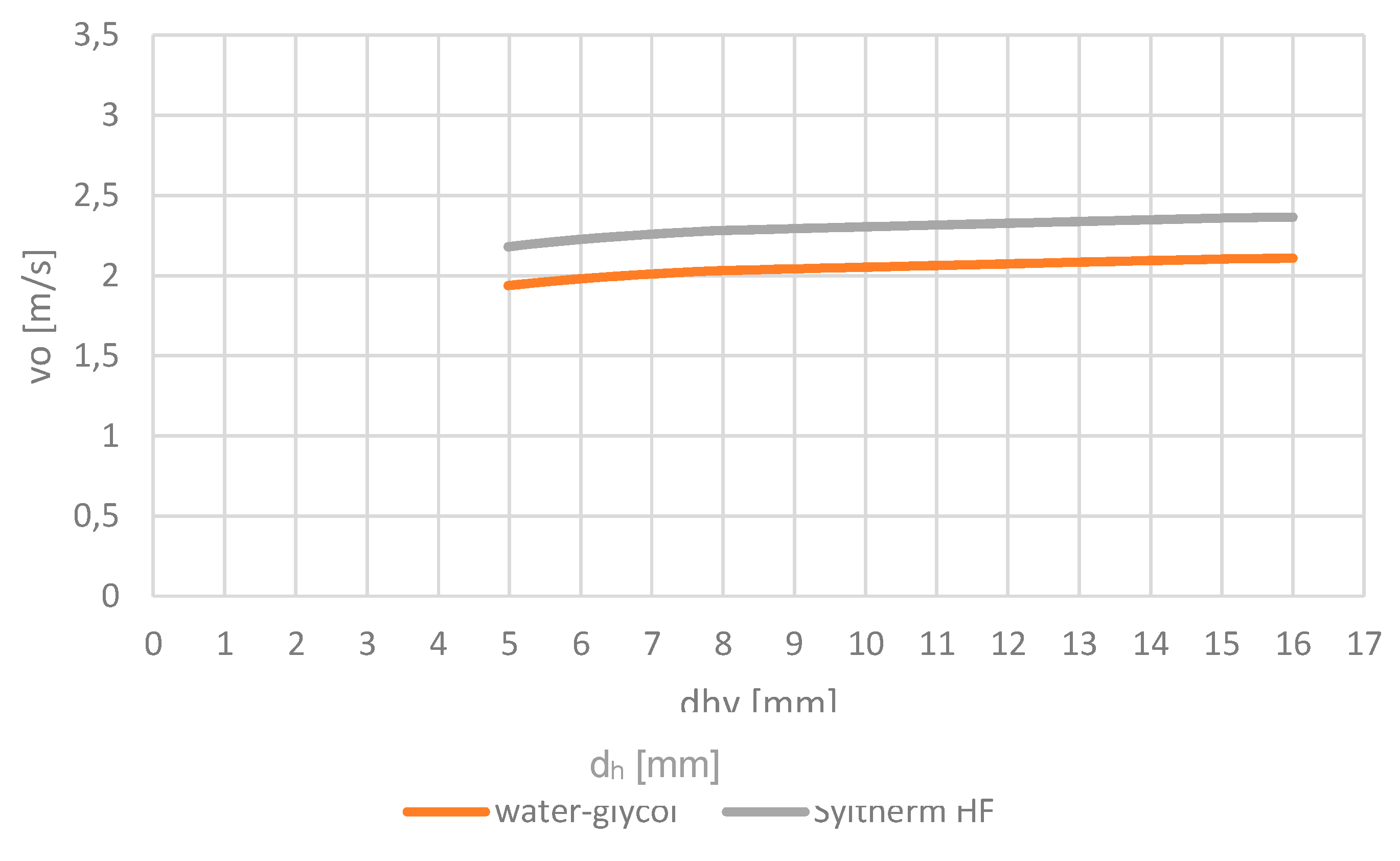
Figure 11 shows a hydraulic diameter of 6.5 mm. The Reynolds number results from the velocity v of the fluid for turbulent flow by numerical solving of the nonlinear Blasius equation (ν
w: Kinematic viscosity, L
k: length of the channel, ρ: Density of the fluid):
The Reynolds numbers for this example are approximate Rey = 104, so turbulent flow can be assumed.
The velocity (
Figure 19) is used to calculate the Nusselts number and the heat transfer coefficient
α [
24] (Pr: Prandtl number, η
w: dynamic Viscosity, λ
w: Thermal conductivity of fluid, cp: specific heat,
K1: Correction factor for the different velocities in the fluid set to 1.1.).
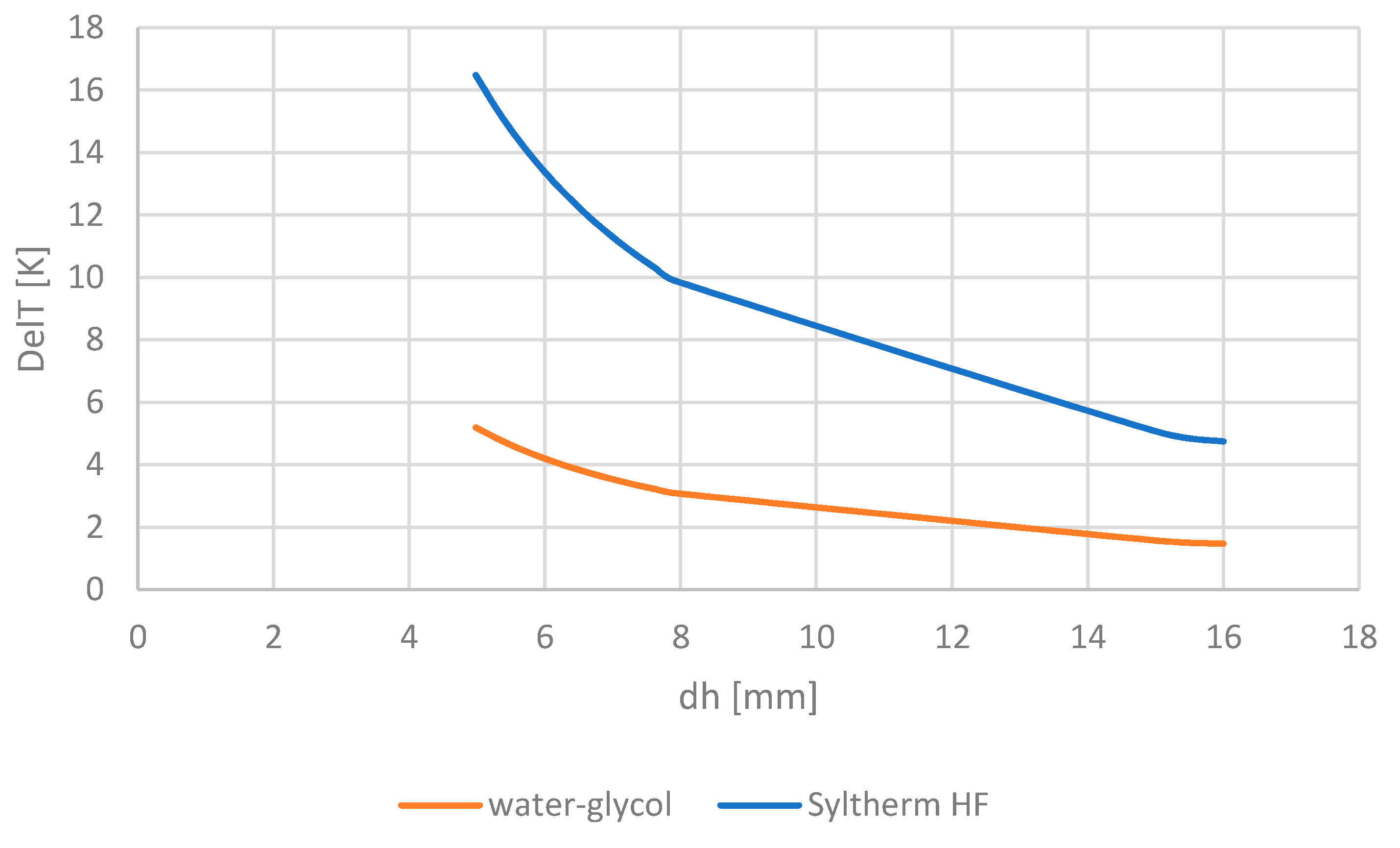
Figure 20 shows that, due to the inferior thermal conductivity of the polysiloxane fluid, we have to assume a much higher temperature difference between the channel wall and fluid than with the water-glycol mixture. The comparatively high temperature drop of 12 K that comes with the polysiloxane fluid has to be taken into account when designing the cooling system.
Furthermore, we can conclude that an increase of the hydraulic diameter or increase of velocity (higher pressure) will have a positive influence on the temperature drop and the heat transfer.
To estimate the power of the pump, the volume flow is an important figure. For this example, the required pump power was estimated with 2.1 l/min per channel and 24 slots and an overall pressure drop of 2 bars to approximately 340 W, which will be a good starting point for the system optimization.
When the cooling fluid itself is heated up by the transfer of the machine losses, the temperature rise in the fluid can be calculated, according to Equation (7). Since both fluids possess a relatively high specific heat, the temperature rises by 0.5 to 1.0 K, which is not dominant for the cooling system design.