4. Procedure of Lead-Acid Battery Selection Based on the Optimization Method
The new LAB selection method using optimization complies fully with the technical criterion regarding the selection of capacity and the number of lead-acid cells connected in series. With the additional variation of factors (temperature and manufacturing constraints) and the number of cells connected in series, we introduced a cost criterion, and criteria for the reliability and operational safety of lead-acid cells in the BR.
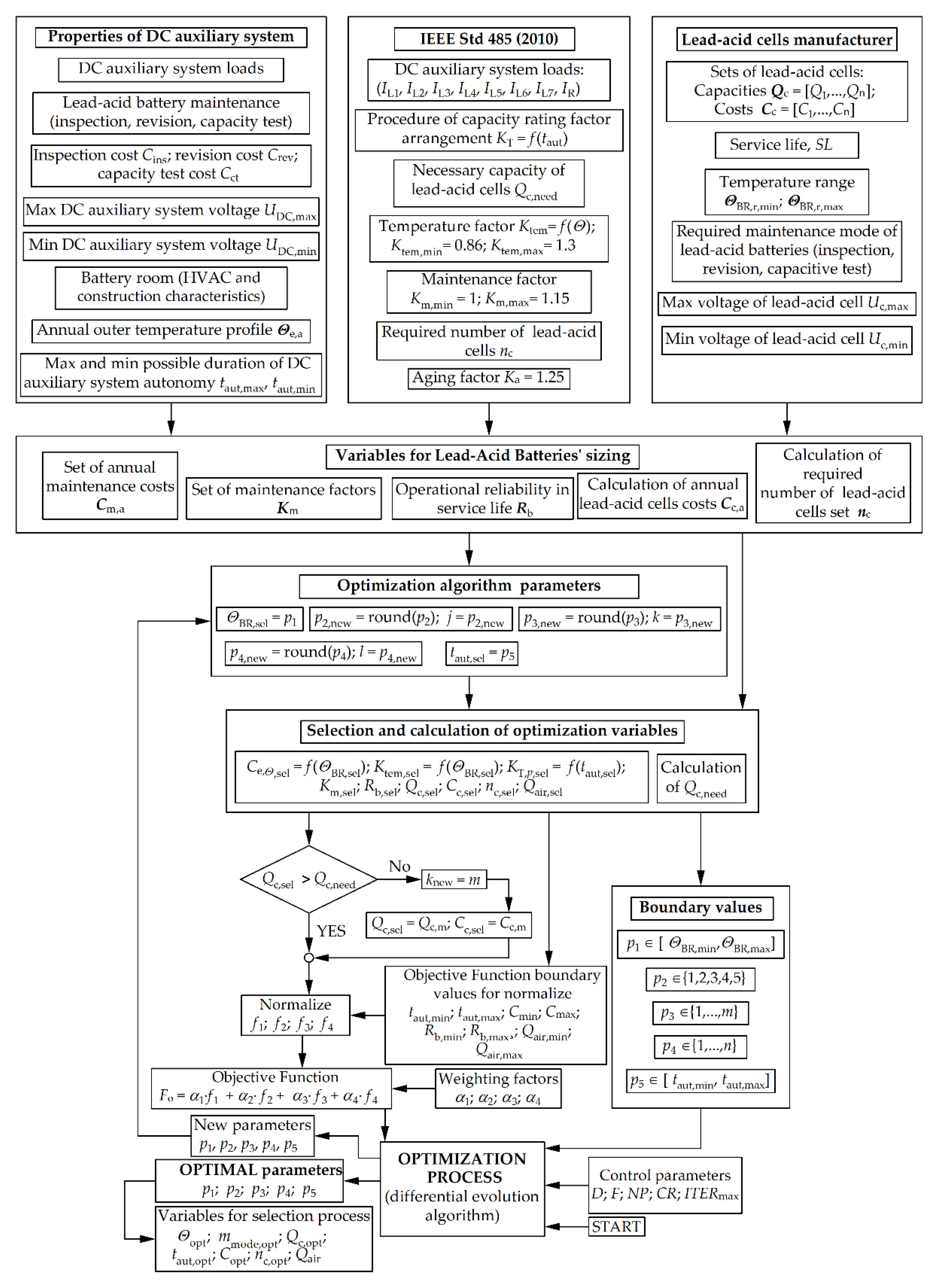
The entire procedure of LAB selection using the optimization method is presented in
Figure 3. DEA was used as an optimization method for the selection of LABs. The basic idea is to use an optimization method that enables selection of the most optimal battery using multiple selection criteria. The flow chart shows several phases of computations and selection. The basic phase is a collection of information and variables that are used in the optimization procedure, as well as Standards, based on the user’s experiences and manufacturer’s data. The flow chart in
Figure 2 presents the entire procedure for the computation of variables that are included in the optimization process.
The elements of IEEE Std 485 (2010) in
Figure 3, properties of a DC auxiliary system, and supplier of LABs, include all necessary input data and procedures for computation of variables that are included in the optimization process. The remaining building blocks of the flow chart are included in the loop of the DEA optimization process algorithm. The selection of optimization parameters influences the selection and computation of variables that are included in the objective function. The DEA requires a normalized objective function and defined limits of optimization parameters. These data are presented in the lower part, since they influence the performance of the algorithm directly. The optimization parameters that are not part of the analytic procedure according to the Standard [
8] are also presented, but have an impact on the DEA’s behavior. The algorithm offers new values of parameters that have an indirect impact on the value of the objective function. This procedure leads to the selection of optimal parameters at the criteria of the highest possible autonomy of supply with the LAB
f1, minimum cost
f2, highest possible operational reliability
f3, and maximum operational safety of LABs in the BR
f4. All elements of this optimization system are presented below.
To include factors KT,p and KT,R in the optimization process, an approximation from three characteristics for three different ways of a lead-acid cell’s discharging was made with the polynomial of the fourth degree. The “grabit” application was used for this purpose, where, for the diagram for each characteristic, the points Ti (xi,yi) were determined (more than 200 points per curve). Since these curves are plotted on a log-log graph, the final points were obtained using x’ = 10x transformation. The transformation is valid for all coordinates. The fourth-degree polynomial coefficients were sought using the approximation process in Equation (5).
where
a1,
a2,
a3,
a4 in
a5 are fourth-degree polynomial coefficients and
taut is the duration of the autonomous supply expressed in minutes.
Table 1 shows the coefficients for three ways of lead-acid cells’ discharge at different
Uc,min.
The Standard defines discrete values of this temperature factor for electrolyte temperatures between θ = 4.4 °C (Ktem = 1.3) and θ = 48.9 °C (Ktem = 0.86). This is also the ambient temperature in the stationary operating conditions. In the optimization process, these boundary conditions are given in a tabular form. For the intermediate temperatures, the factor Ktem is defined by the linear interpolation. Kdm (design margin) is a correction factor that takes into consideration insufficient maintenance and unexpected changes of load. Only the influence of insufficient maintenance is taken into account in the optimization process. The boundary values of this factor lie between Kdm,min = 1.0 and Kdm,max = 1.15. In the subsequent parts of the paper, this factor is addressed to maintenance factor Km = Kdm.
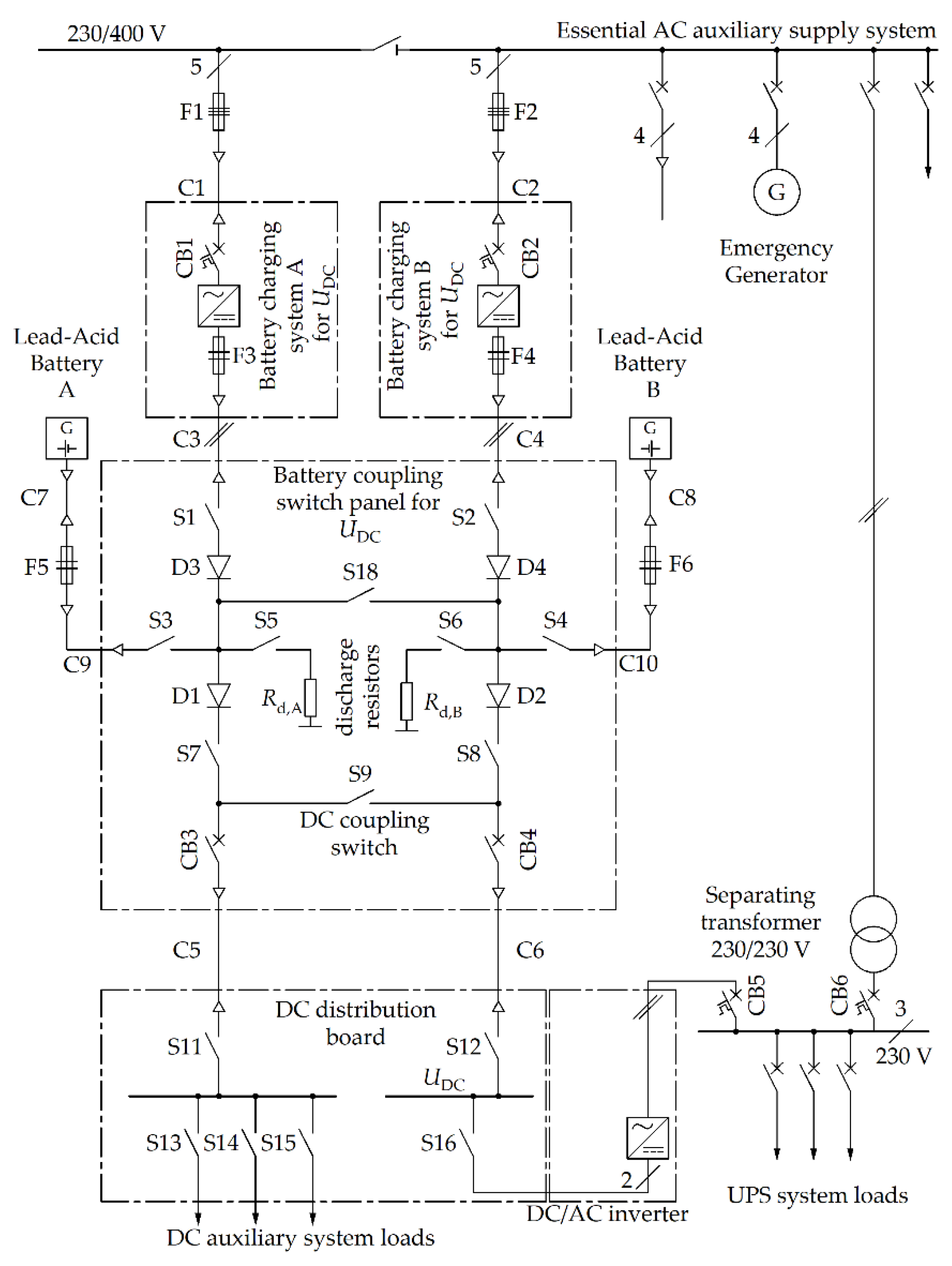
The other important area that influences the selection of a LAB is the DC network supplied by the battery. Below, there is a description of a DC auxiliary system supply in modern substations, although the procedures can be generalized to all DC networks. Voltage levels of DC networks are defined by the types and properties of the connected load. The minimum voltage
UDC,min is the DC network voltage that enables uninterrupted operation of the supplied load. The maximum DC network voltage
UDC,max is the maximum permitted operational voltage of the supplied load. The DC network voltage and, thus, the LAB voltage, depend on the necessary amount of energy stored in the battery. The user has to maintain the LAB and comply with the minimum maintenance requirements defined by the manufacturer. These requirements may be even higher to provide the required level of reliability. An LAB has to undergo inspections, revisions, and capacity tests to maintain its SL. The LAB is not disconnected from the DC network during the inspections. Checked are the general condition of the battery, electrolyte level, and condition of contacts between the lead-acid cells (using a thermovision camera), the sealing, and ventilation of the BR. The battery is switched off during the revisions. This process includes a thorough inspection of contacts, with measurement of contact resistance, battery connections, electrolyte density, and voltage of individual cells. The capacity test is performed in accordance with the IEC 60896-11 Standard [
22], and in accordance with the manufacturer’s instructions. A detailed inspection of the battery is performed. It is loaded with a constant current through the discharging resistor. Voltage is measured until the battery is discharged to 80% of its initial capacity. The intention is to find malfunctioning lead-acid cells. During this process, the electrolyte density is also measured constantly.
The inspection cost is denoted as Cins. The revision cost, on the other hand, is denoted as Crev, while the cost of the capacity test is Cct. The SL of the battery is designated as SL.
The maintenance extent influences the maintenance factor
Km and the maintenance costs
Cm. On the basis of the lead-acid cells’ maintenance method and the manufacturer’s recommendations, five maintenance modes are possible, as described below. Maintenance mode 1: Twice a year, a capacity test is performed; once a year, a revision; and twice a year, an inspection.
Km,mode1 = 1. The cost of maintenance mode 1 is expressed as
Cm,mode1 = (2 ·
Cct +
Crev + 2 ·
Cins) ·
SL. Maintenance mode 2: Once a year, a capacity test; once a year, a revision; and twice a year, an inspection.
Km,mode2 = 1.05. The cost of this mode is defined by
Cm,mode2 = (
Cct +
Crev + 2 ·
Cins) ·
SL. Maintenance mode 3: A capacity test is performed every two years. During the years of the service life, when the capacity test is not performed, a revision is carried out, and, twice a year, an inspection. The cost of this mode is
Cm,mode3 = (0.5 · (
Cct +
Crev) + 2 ·
Cins) ·
SL.
Km,mode3 = 1.075. Service mode 4: A capacity test is performed every five years. During the years of the service life, when the capacity test is not performed, a revision is carried out, and, twice a year, an inspection.
Cm,mode4 = (0.2 ·
Cct + 0.8 ·
Crev + 2 ·
Cins) ·
SL.
Km,mode4 = 1.1. Service mode 5: A capacity test is performed once in the middle of the SL. During years of the service life, when the capacity test is not performed, a revision is carried out, and, twice a year, an inspection.
Km,mode5 = 1.15.
Cm,mode5 =
Cct + (
SL − 1)⋅
Crev + 2 ·
Cins ·
SL. The vectors
Km = [1,1.05,1.075,1.1,1.15] and
Cm = [
Cm,mode1,
Cm,mode2,
Cm,mode3,
Cm,mode4,
Cm,mode5] are formed with the currency unit [CU]. We are interested in the annual maintenance costs. The vector of annual maintenance costs is calculated using
Cm,a = (1/
SL)
· Cm, where SL is the lead-acid cells’
SL. The maintenance of LABs is linked closely with their reliability of operation. A LAB is composed of a large number of cells connected in series. The capacity test gives us an indication of the weak links in this series, and the instruction which cells need to be replaced with new ones. Each weak lead-acid cell can prevent the battery from ensuring it required autonomy time during its operation [
12]. The calculation of reliability depends mainly on the capacity test. A basic level of reliability is ensured by regular revisions if a capacity test is not carried out during the years of service life and inspections twice a year. For mode 1, it was found out that a failure may occur in the last half year of the SL. The reliability of operation is, thus,
Rb,mode1 = 1 − 0.5 ·
SL−1. For mode 2, the reliability of operation is
Rb,mode2 = 1 −
SL−1. For mode 3, the reliability of operation is
Rb,mode3 = 1 − 2 ·
SL−1. For mode 4, the reliability of operation is
Rb,mode4 = 1 − 5 ·
SL−1. For maintenance mode 5, the reliability of operation is expressed as
Rb,mode5 = 1 − 10 ·
SL−1. The reliability of operation vector
Rb = [
Rb,mode1,
Rb,mode2,
Rb,mode3,
Rb,mode4,
Rb,mode5] is formed for the LAB.
The LAB is placed in the BR, which needs to be ventilated forcibly, due to the release of H
2 during battery charging [
18]. For this purpose, a heating, ventilation, and air conditioning (HVAC) device is installed in the BR, which also keeps the room temperature at the desired level. The question is, what are the costs related to the operation of the HVAC device to maintain the desired temperature in the BR? For this purpose, the IEC 12831 Standard [
23] is used, which defines the method of calculating the projected thermal load for buildings. To use this Standard properly, one has to know the properties of the walls, floor, ceilings, windows, and doors of both the building and the BR, as well as the surface areas of all elements. Heat losses due to natural ventilation of the BR and heat transfer through heat bridges can be neglected. It is assumed that the BR is located in a heated building with the temperature of the adjacent rooms amounting to
Θnp. It is also assumed that all the adjacent heated/cooled rooms have the same temperature
Θnp. The heat is transmitted between the building elements with the adjacent rooms, and the outer walls with the exterior. A stationary state of heat transmission is observed. The total heat transmission
ΦBR, expressed in [W], between the BR and the adjacent rooms and the exterior, is defined by Equation (6).
HT,BRnp is the coefficient of transmission heat loss between the BR and the adjacent rooms in [W/K].
HT,BRe is the coefficient of transmission heat loss between the BR and the building exterior.
ΘBR is the temperature inside the BR in [°C], while
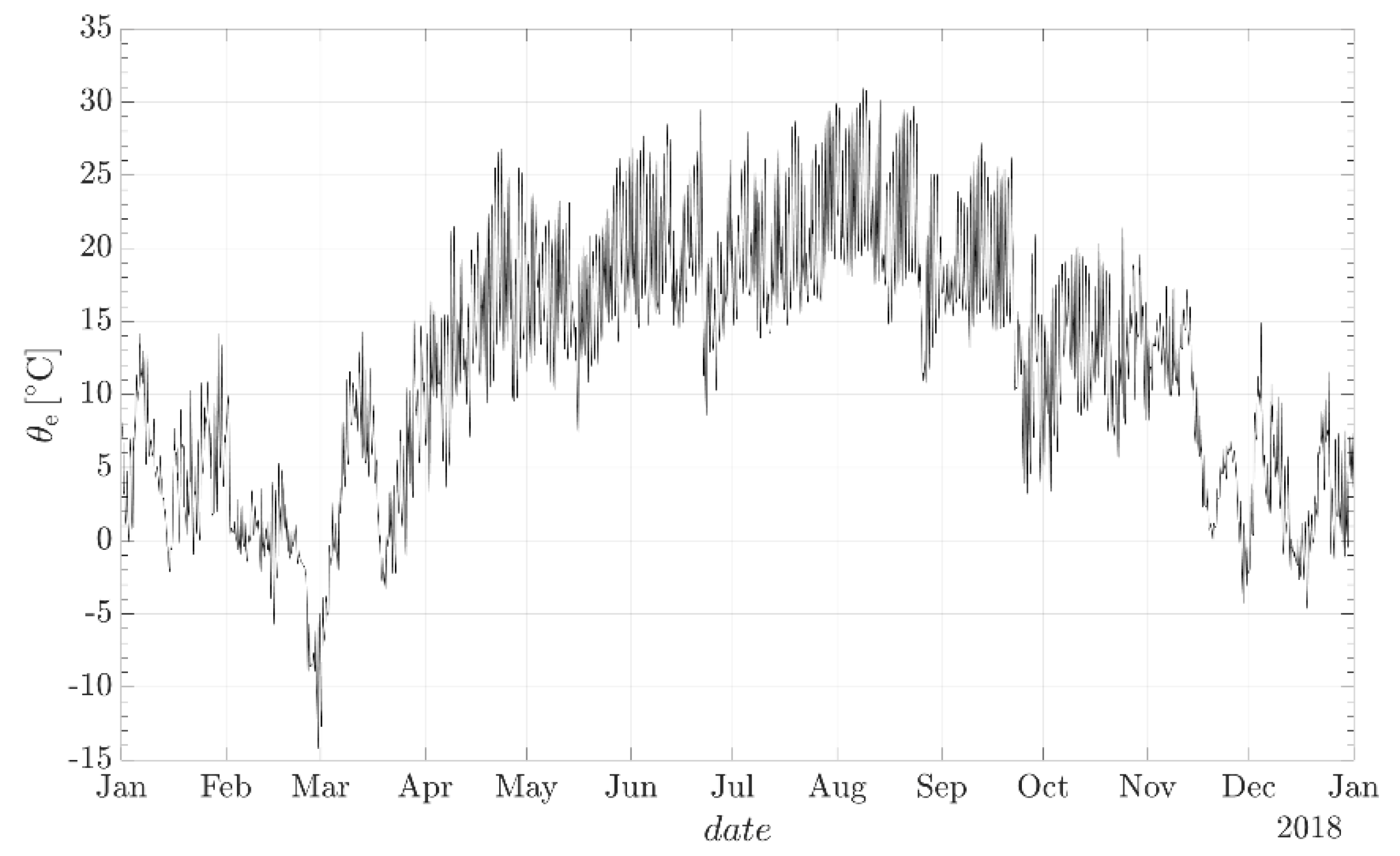
Θe is the exterior temperature. The intention is to know what the levels of heat transmission from the BR are at various outside temperatures. It is assumed that the annual hourly data are known on the exterior temperature around the building. A vector
Θe,a = [
Θe,a,1,…,
Θe,a,i,…,
Θe,a,8760] is formed. The counter of hours
i lies between 1 and
mh = 8760. For a certain BR temperature
ΘBR, a vector of heat transmission from the BR in all hours of the year
ΦBR,T can be defined using Equation (6). This vector is defined as
ΦBR,Θ = [
ΦBR,Θ,1,…,
ΦBR,Θ,i,…,
ΦBR,Θ,8760]. If the heat in a certain hour of the year (
i) is transferred from the BR, the element
ΦBR,Θ,I > 0 is heating, and if it is transferred to it,
ΦBR,Θ,I < 0 it is cooling. The c device covers both ways of heat transmission, and is able to maintain the desired temperature in the BR. To maintain this temperature, the necessary electric power in the hour (
i) in a certain year is calculated using Equation (7).
The factor εHC is the average heating and cooling number of the HVAC device. It is assumed that in the hour (i), the necessary electrical power for air conditioning in the Equation (7) is average. The quantity of electrical energy in this hour is calculated using Equation (8).
The change of time in the observed case amounts to Δt = 1 h. When the necessary energy for all hours in a year is computed, the vector of necessary electrical energy We,Θ can be formed for maintaining the desired temperature in the BR. At the annual level, the hourly contributions of energy are summed up to get the annual electrical energy consumption of the air conditioning device for a certain temperature We,Θ,a using Equation (9).
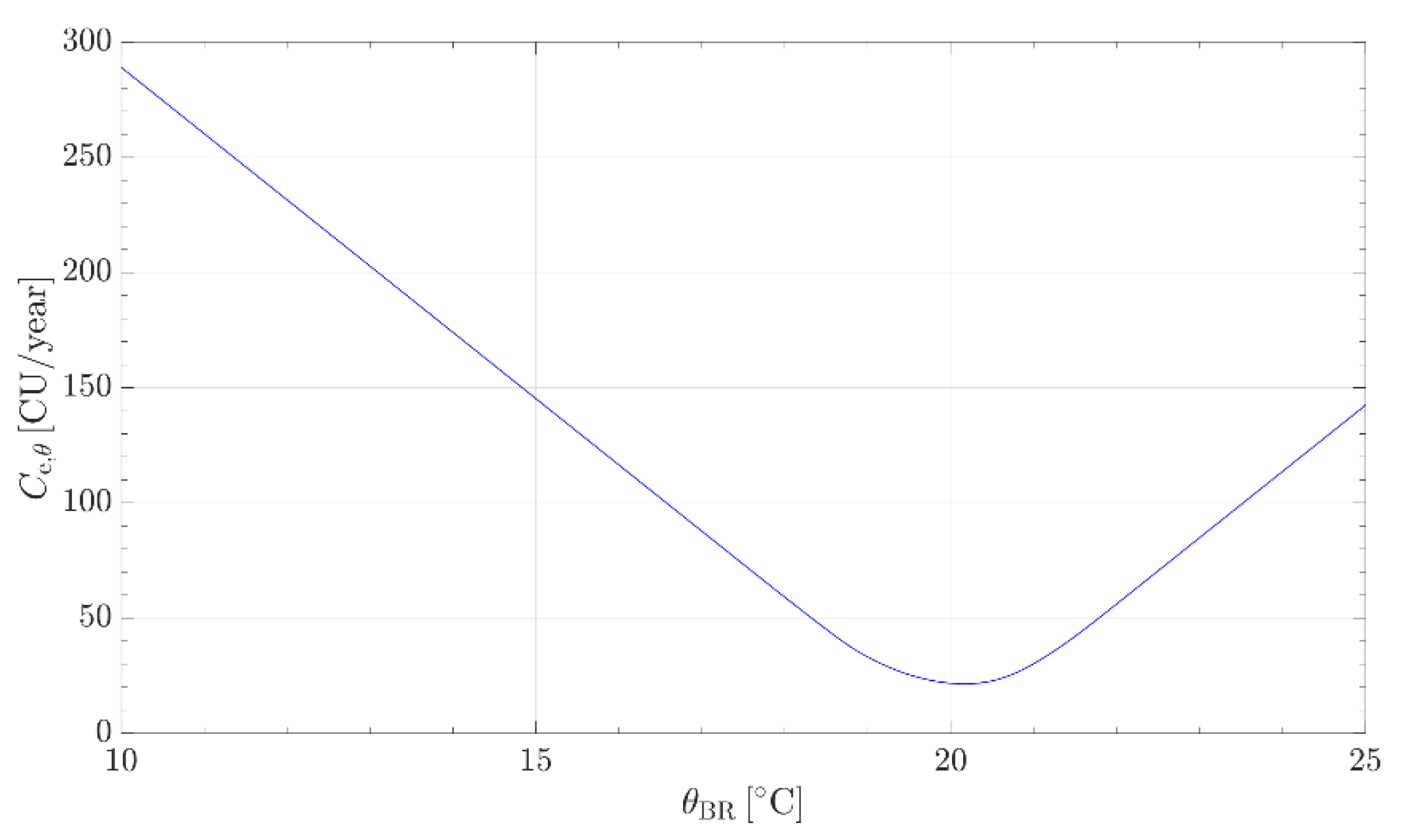
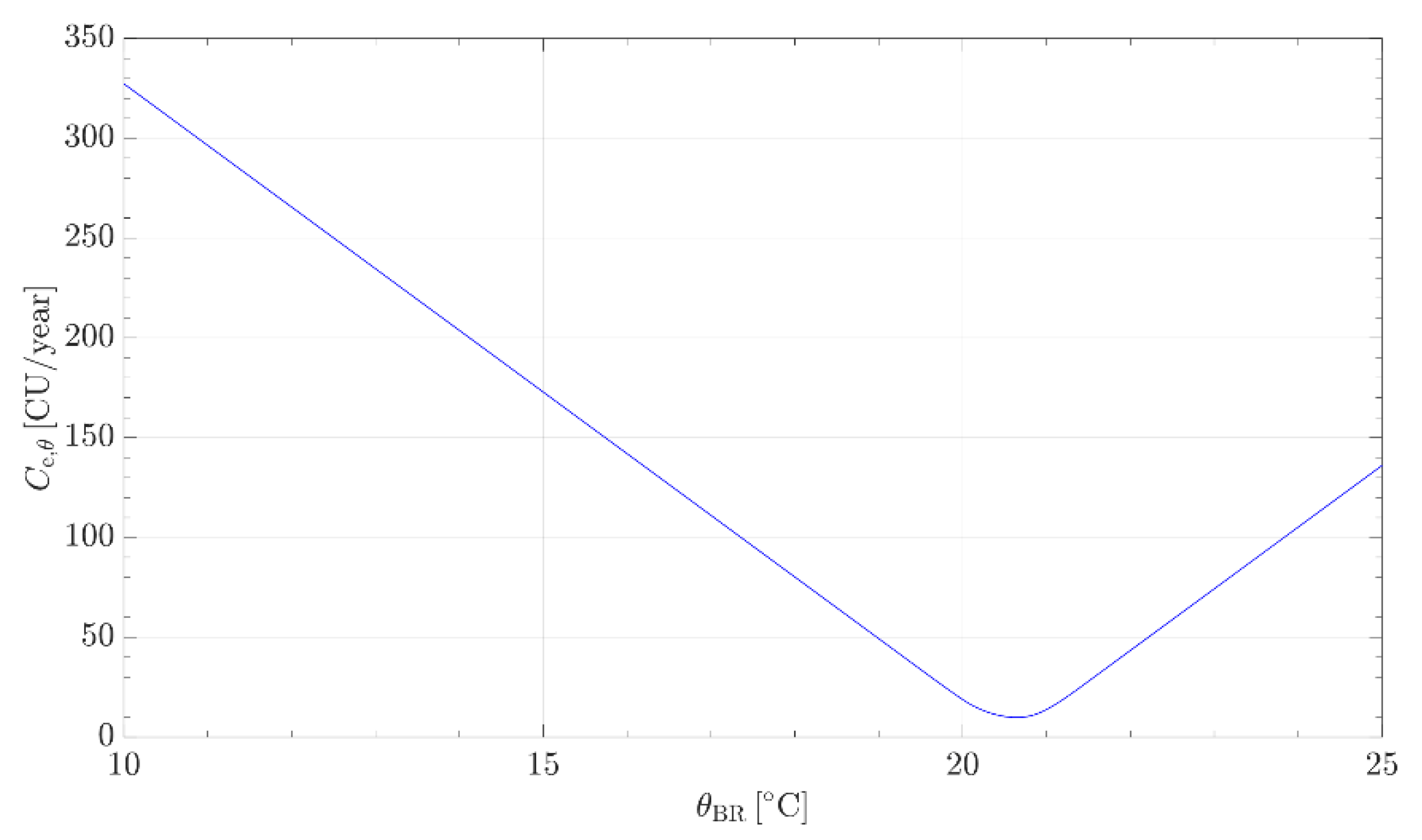
Finally, it is possible to calculate the annual HVAC cost for maintaining the BR temperature at ΘBR by using Equation (10).
The procedure yields that the cost is Ce,Θ = f(ΘBR). This procedure is used in the optimization process.
The user also defines the longest possible time of autonomy of supply by the lead acid battery,
taut,max. This time is defined on the basis of experience. In this task, it is necessary to take into consideration the worst possible case, i.e., when the other battery in the DC network is empty. In the case of a rectifier’s outage, the other network should charge through the mobile emergency generator (
Figure 1). The minimum time needed to recharge the other LAB is, for the optimization process, the highest possible autonomy time of the DC network with a LAB,
taut,max. The user also defines the minimum autonomy of supply time
taut,min, required to remove any problems in most cases and re-establish supply in the other supply network.
The third step in the process of selection of LABs is the battery manufacturer’s data. A set of m possible lead cells is selected from the production program. Thus, the vector Qc = [Qc,1,…,Qc,k,…,Qc,m] is obtained. An important factor in this process is the prices of different types of cells contained in the vector Cc = [Cc,1,…,Cc,k,…,Cc,m]. Since we deal with the annual costs, the vector] is formed of annual procurement costs Cc,a = (1/SL)⋅Cc in a [CU/year]. The manufacturer also gives the technical SL of cells’ SL. Characteristic data are also the maximum lead-acid cell’s voltage Uc,max in [V/cell] and minimum operating voltage that enables its normal operation, Uc,min in [V/cell]. The manufacturer also specifies the recommended temperature range, limited by ΘBR,r,min and ΘBR,r,max. This temperature range is usually narrower than the one defined by the Standard.
The Standard defines the procedure for determining the number of cells connected in series. The procedure was upgraded. The maximum number of cells connected in series is determined using Equation (11).
The natural number nc,max,int is assigned to the maximum number of cells using Equation (12).
The minimum number of cells connected in series is calculated in a similar way. The number nc,min is defined by Equation (13).
The minimum natural number nc,min,int is determined using Equation (14).
The vector of serially connected lead-acid cells nc = [nc,min,int,…,nc,l,…,nc,max,int] can be formed as long as the rule nc,max,int > nc,min,int is in force. The dimension of this vector n is defined by Equation (15).
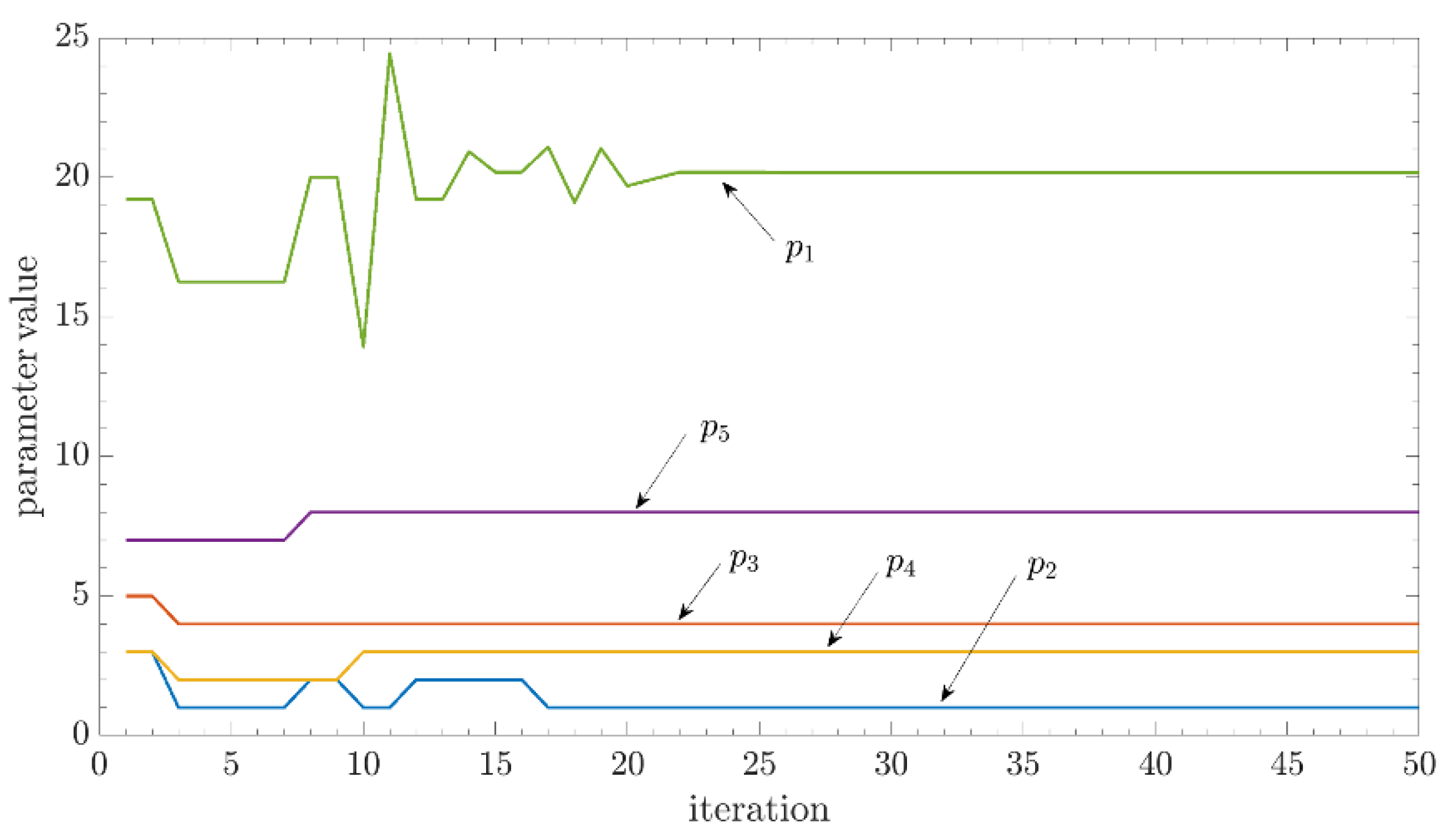
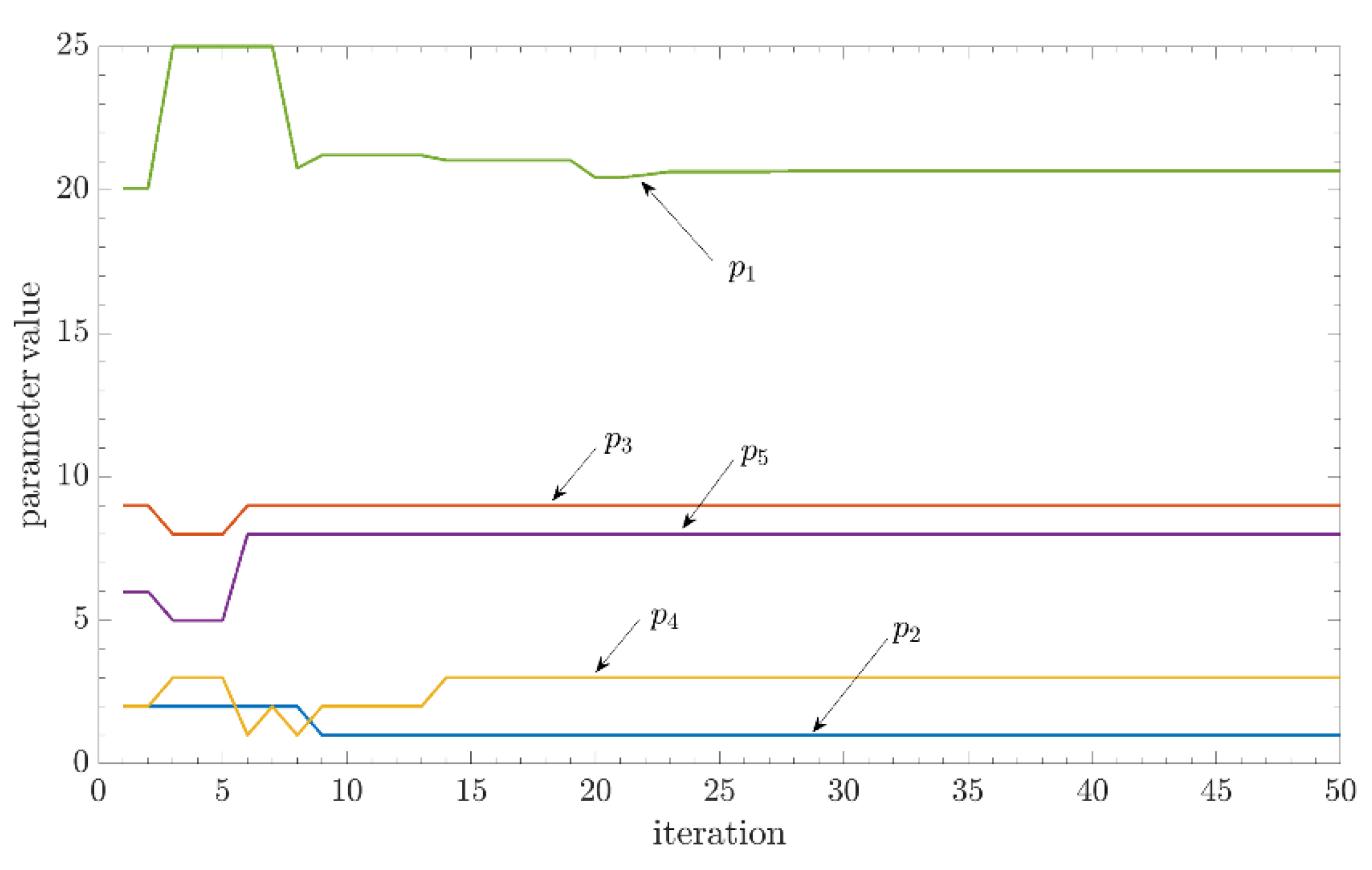
Each number of serially connected cells in the vector nc complies with the technical requirements of the Standard. The size of the vector nc is defined primarily to enable setting of the maximum charging voltage Uc,max. If it is higher, the number of possible cells connected in series is lower. The variables and procedures described so far are input data for the optimization process. In addition to the input data, they are also influenced by the optimization parameters. The output from the DEA is a set of optimization parameter values. They are limited directly in the algorithm. The parameters were not normalized in the concept described in the paper. The limitations are of a physical nature. The optimization algorithm deals with five optimization parameters: Electrolyte temperature (BR) (p1), maintenance mode of the LAB (p2), selection of cells’ capacity from the set of possible ones (p3), selection of the number of lead-acid cells connected in series (p4), and duration of autonomy of supply with the LAB (p5). The first parameter in the optimization process is electrolyte temperature. In stationary operating conditions, this is also the BR temperature. The room temperature takes the value of parameter p1, as ΘBR,sel = p1; p1 ∈ [ΘBR,r,min,ΘBR,r,max]; p1 ∈ ℝ. With the selection of this parameter, the temperature factor Ktem,sel = f(ΘBR,sel) can be determined using linear interpolation, as well as the annual cost of maintaining this temperature with the air conditioning device Ce,Θ,sel using the procedure defined by the set of Equations (6)–(10). The parameter p2 is connected with the battery maintenance. It is an element of the set of natural numbers, p2 ∈ {1,2,3,4,5}; p2 ∈ N. Since the optimization process yields the parameter p2 as a real number, it should be transformed to a natural number using the function round(). This parameter actually represents a counter of possible maintenance modes j = p2. The parameter p2 is used to obtain the maintenance factor Km,sel = Km,j from the vector of maintenance factors Km, reliability of operation of LABs Rb,sel = Rb,j from the vector of reliability of operation Rb, and maintenance-related cost Cm,sel = Cm,j from the vector of maintenance costs Cm. The parameter p3 is related to the selection of lead-acid cells’ capacity, defined by the manufacturer. It represents a counter of selection of cell capacities from the set of products k offered by the manufacturer, k = p3; p3 ∈ {1,2,…,m}; p3 ∈ N. With this parameter, the lead-acid cells’ capacity Qc,sel = Qc,k is selected from the vector Qc, as well as the procurement costs distributed by the years Cc,a,sel = Cc,a,k from the vector of annual costs Cc,a. The parameter p4 represents the counter of selection of the number of cells connected in series. This is the counter l in the vector nc, l = p4; p4 ∈ {1,2,…,n}; p4 ∈ N. The number of cells connected in series nc,sel = nc,l is selected from the vector nc with this parameter,. The parameter p5 represents the duration of battery autonomy in supplying energy to the DC auxiliary network. The duration of autonomy takes the value of the parameter p5 as taut,sel = p5; p5 ∈ [taut,min,taut,max]; p5 ∈ R. This parameter enables calculation of the factor KT,p,sel = f(taut,sel), which makes possible calculation of the needed lead-acid cell’s capacity Qc,need.
When the variables that depend on optimization parameters are selected (Ktem,sel, Ce,Θ,sel, Km,sel, Cm,sel, Rb,sel, Qc,sel, Cc,a,sel, nc,sel, KT,p,sel), it is possible to calculate the needed capacity Qc,need using Equation (4). If Qc,sel ≥ Qc,need, then the capacity was selected properly, and complies with the technical criteria defined by the Standard. If Qc,sel < Qc,need, then the counter k is set at the last place, k = m. The capacity Qc,sel and cost Cc,a,sel are selected once again. After this, we may proceed to the computation of the Objective Function.
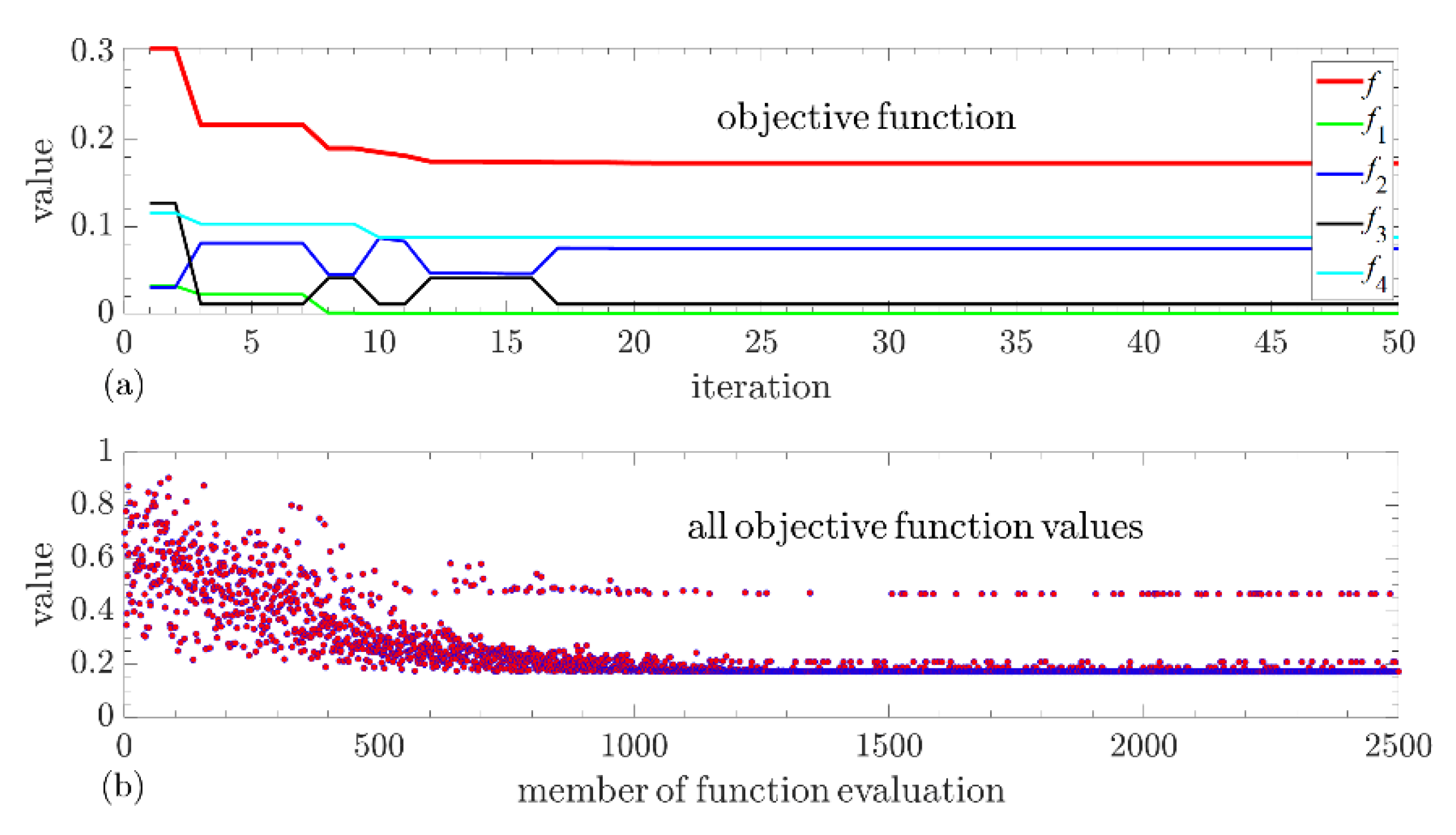
The objective is to select LABs using an optimization procedure by maximizing their duration of autonomy, minimizing costs, and providing maximum reliability of operation of the LAB. This is a multiple-criteria function. The total objective function can be computed using Equation (16). This is a dimensionless variable. In the optimization process it approaches to the minimum.
The functions f1, f2, f3, and f4 are normalized functions for autonomy of supply, costs, reliability of operation, and the operational safety of LABs in a BR. α1, α2, α3, and α4 are weighting factors of the objective function. The normalized function f1 is a normalized objective function for the criterion of autonomy of supply. This function is normalized through the linear transformation in Equation (17).
This objective function is defined only with the duration of supply autonomy. The boundary values of this objective function are also the limits of the parameter p5. The most cost efficient selection of a LAB is sought. This means that the minimum of the objective function f2 is sought. Normalized function f2 is the normalized function for the criterion of cost. Normalization is performed using linear transformation in Equation (18). Since the minimum of this function is sought, it can only be increasing linearly.
The cost criterion was designed on the basis of the procedure in [
14]. The total cost in the optimization procedure
Csel is defined by Equation (19).
The upper limit of cost Cmax is defined by the inequality in Equation (20).
The lower limit of cost Cmin is defined by the inequality in Equation (21).
The third objective function defines the criterion of the maximum reliability of operation. This criterion depends only on the reliability of operation of the LAB. The reliability vector Rb has distributed five probabilities discretely, and each of them has reliability mostly above Rb > 0.5. The normalization of the reliability criterion with linear transformation is, in this case, not adequate. A Gaussian curve is used instead for the normalization of the objective function, assuming that the objective is to ensure the highest possible reliability of operation of the LAB. The function f3 is obtained by Equation (22).
where
ml is the “shape factor” on the left side of the Gaussian curve, calculated for our normalization case using the equation
ml = ln(0.1)/(0.82 − 1)
2.
The last objective function
f4 is the operational safety criterion of LABs in the BR. It refers to the amount of released hydrogen, H
2, into the BR while charging LABs. The Standard [
17] deals with the safety requirements for secondary batteries and installations. An important part of this Standard is explosion hazards and protection against them in the BR. During the charging process of the LAB at
Uc > 2,23 V/cell, a chemical reaction of electrolysis of water is initiated in the electrolyte. The concentration of hydrogen in the air in the BR must not exceed 4%
vol (a potentially explosive mixture). The battery for a DC auxiliary system supply in the substation is recharged all the time. This means the H
2 concentration is increasing regularly. The solution is adequate forced ventilation of the BR. The amount of replaced air in hours is defined by Equation (23).
Igas is a specific equivalent charge current producing H
2 in [mA/Ah]. The thermodynamics of the electrochemical reaction of the electrolysis of water in the electrolyte depends on the charge current density [
18]. With increasing charging current, the amount of H
2 release also increases. The current is dependent on the lead-acid cell’s charge voltage
Uc, since the conductivity is presumed to be constant in this area of charging. In the worst case, the charge voltage of the lead-acid cell is determined as
Uc =
UDC,max/
nc. The limit currents
Igas = 5 mA/Ah at the voltage
Uc = 2.23 V/cell and
Igas = 20 mA/Ah at the voltage
Uc = 2,40 V/cell are specified in the Standard [
17]. Based on the two boundary points, function
Igas =
f(
Uc) is determined by linear interpolation. Inserting this function into Equation (23), Equation (24) is obtained for the ventilation airflow
Qair,sel.
Qc,sel is the selected capacity from vector Qc. Equation (24) is normalized, and the objective function in Equation (25) obtained. As with the normalization for the objective function f3, the Gaussian bell curve function is also applied here.
where
ml is the “shape factor”, defined by
ml = ln(0.01)/50
2. By minimizing the objective function in Equation (25), the amount of H
2 released into the BR is reduced, along with the required airflow for forced ventilation with HVAC.
Figure 3 also presents the control parameters of the DEA, i.e., the algorithm that is used in the optimization. These parameters are the number of optimization variables
D, number of members of population
NP, difference factor
F, crossover control parameter
CR, and the maximum number of iterations
itermax.
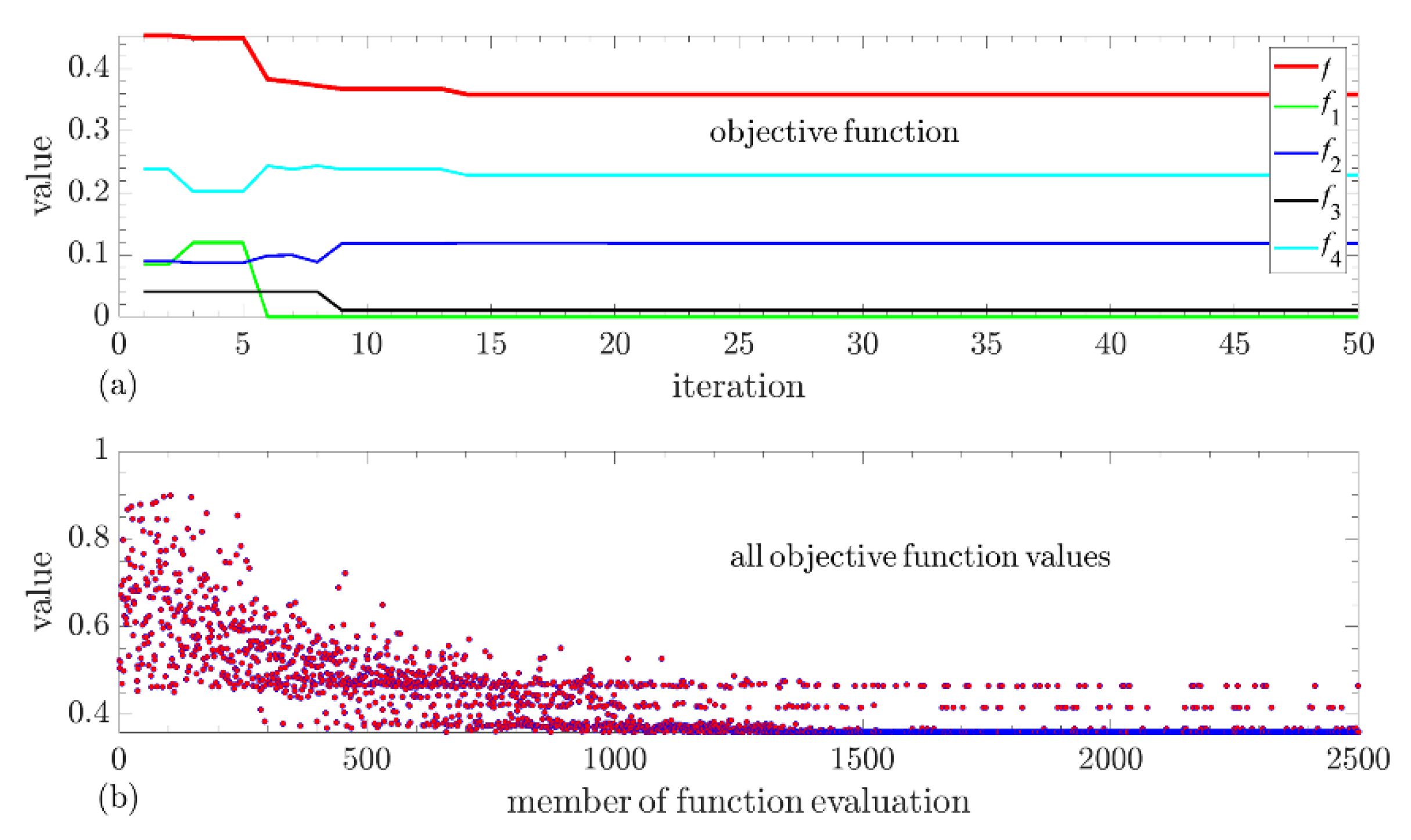
The optimization process terminates when the algorithm reaches the maximum number of iterations, or the deviation of the objective function is lower than ε = 1⋅10−6. The optimization parameters become the optimum parameters. The vector popt = [p1,opt, p2,opt, p3,opt, p4,opt, p5,opt] is obtained as a solution. If the parameters are decoded, we can obtain the optimum operational temperature Θopt = p1,opt, optimum maintenance mode mmode,opt = p2, optimum capacity of the lead-acid cell Qc,opt, optimum number of cells connected in series nc,opt, optimum duration of autonomy taut,opt = p5,opt, and optimum costs Copt, that can be calculated using Equation (19) if optimal costs Ce,Θ,opt, Cm,opt in Cc,a,opt are used as parameters in this equation.