Application of Spectral Clustering Algorithm to ES-MDA with DCT for History Matching of Gas Channel Reservoirs
Abstract
:1. Introduction
2. Methodology
2.1. ES-MDA
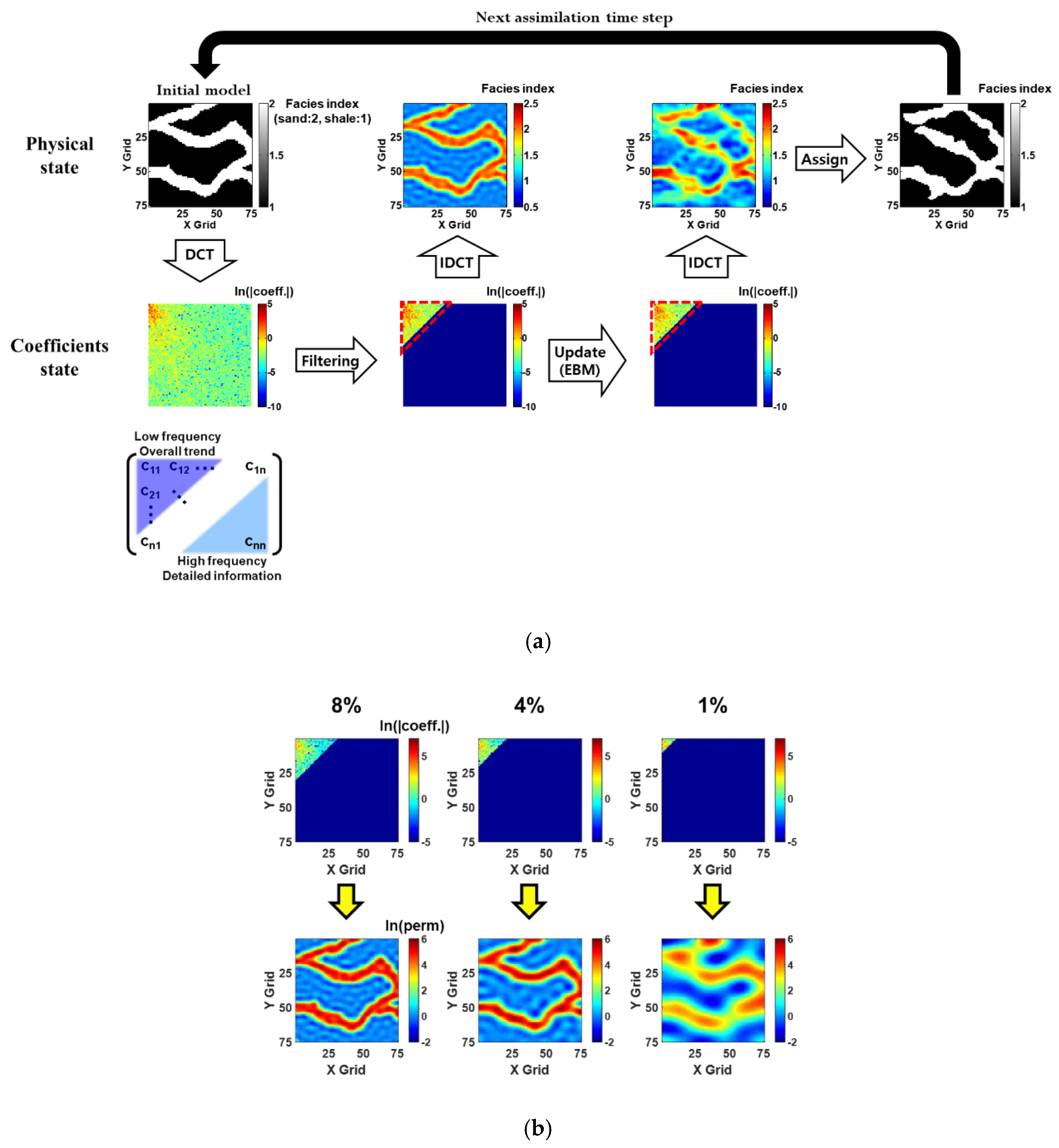
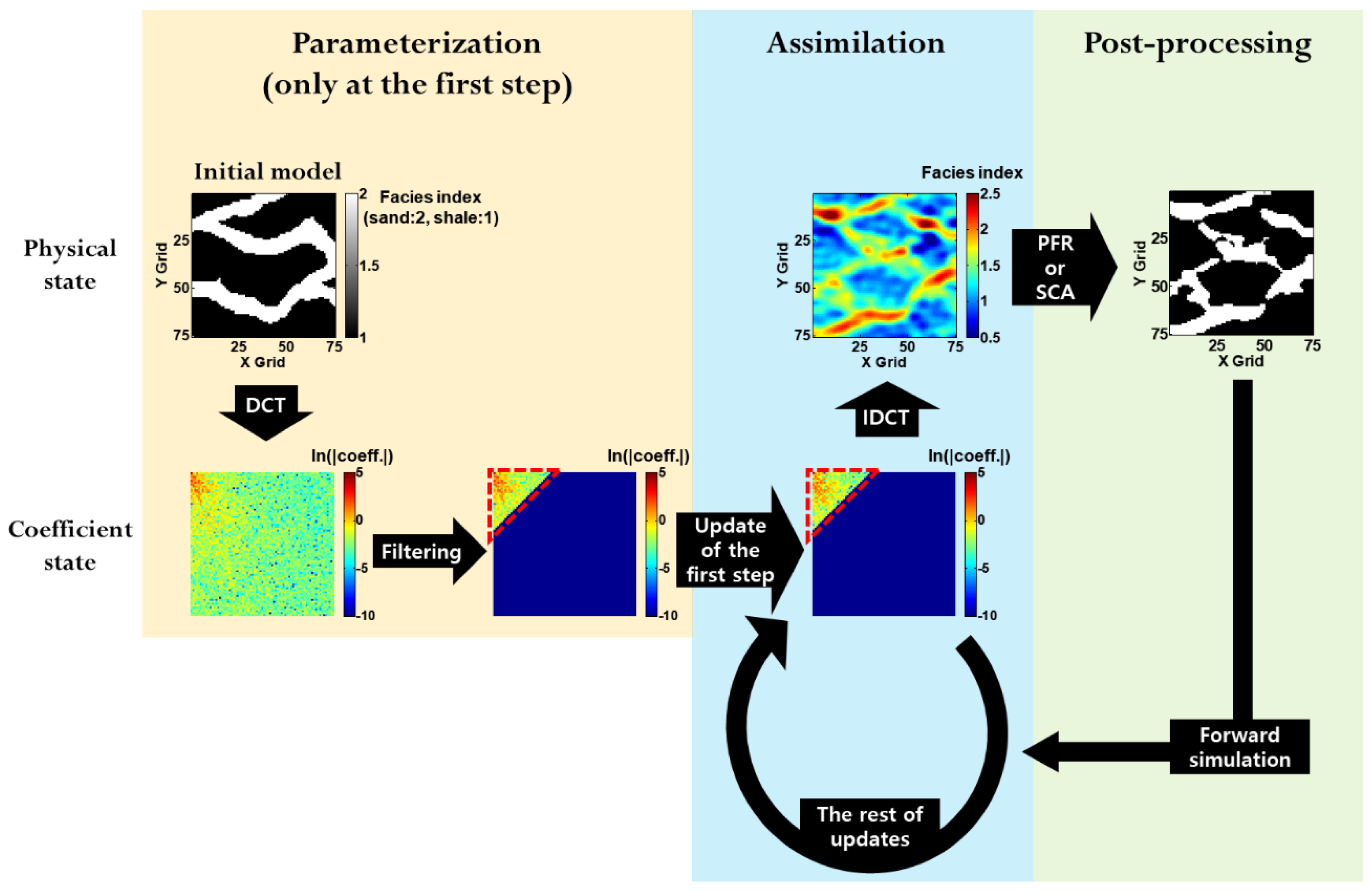
2.2. DCT
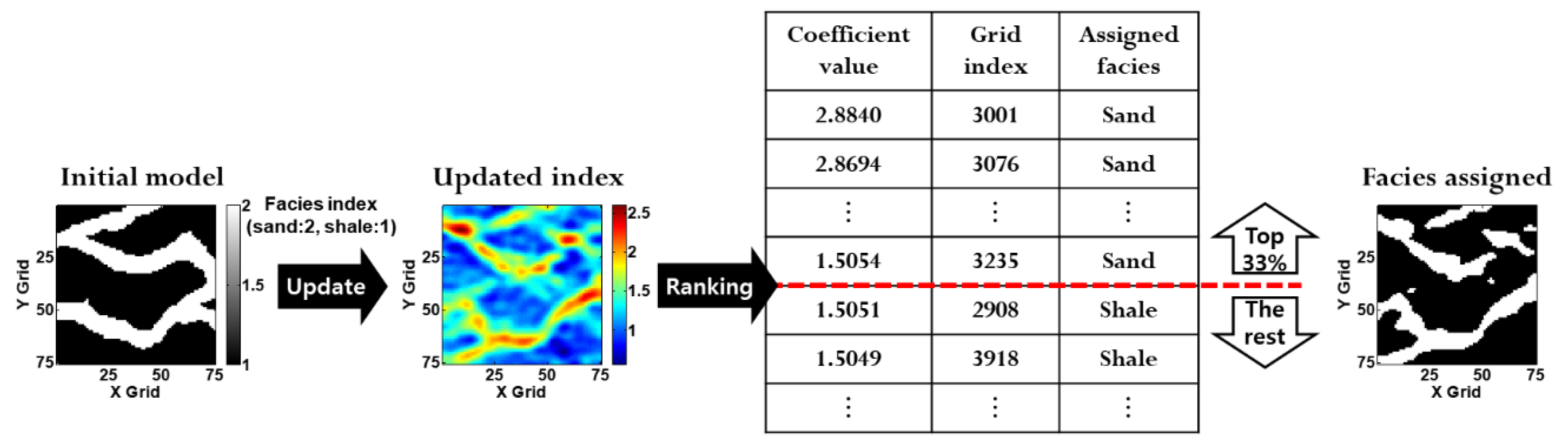
2.3. PFR
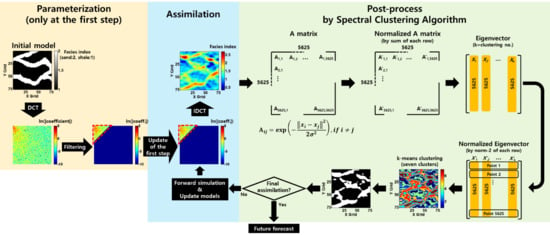
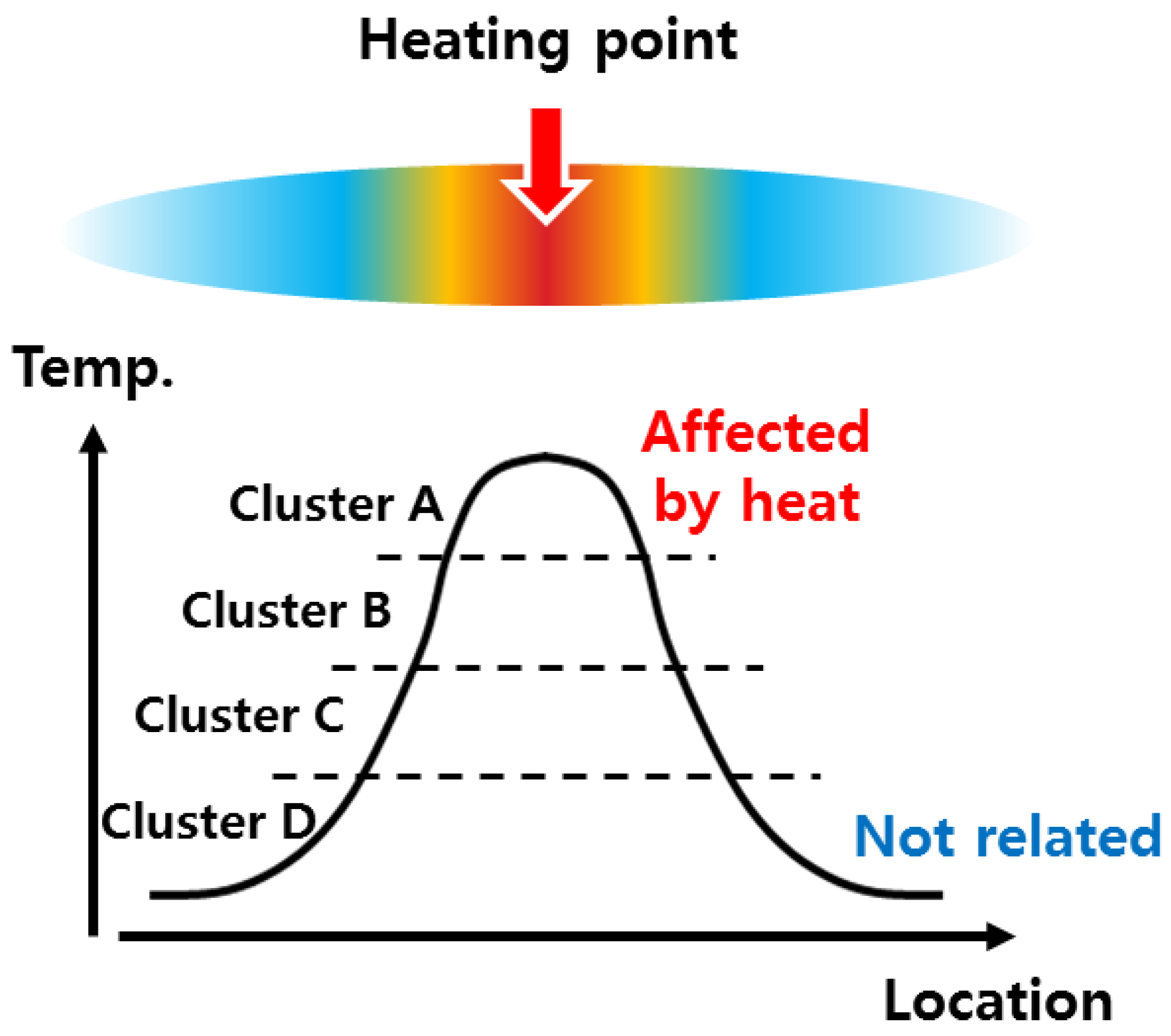
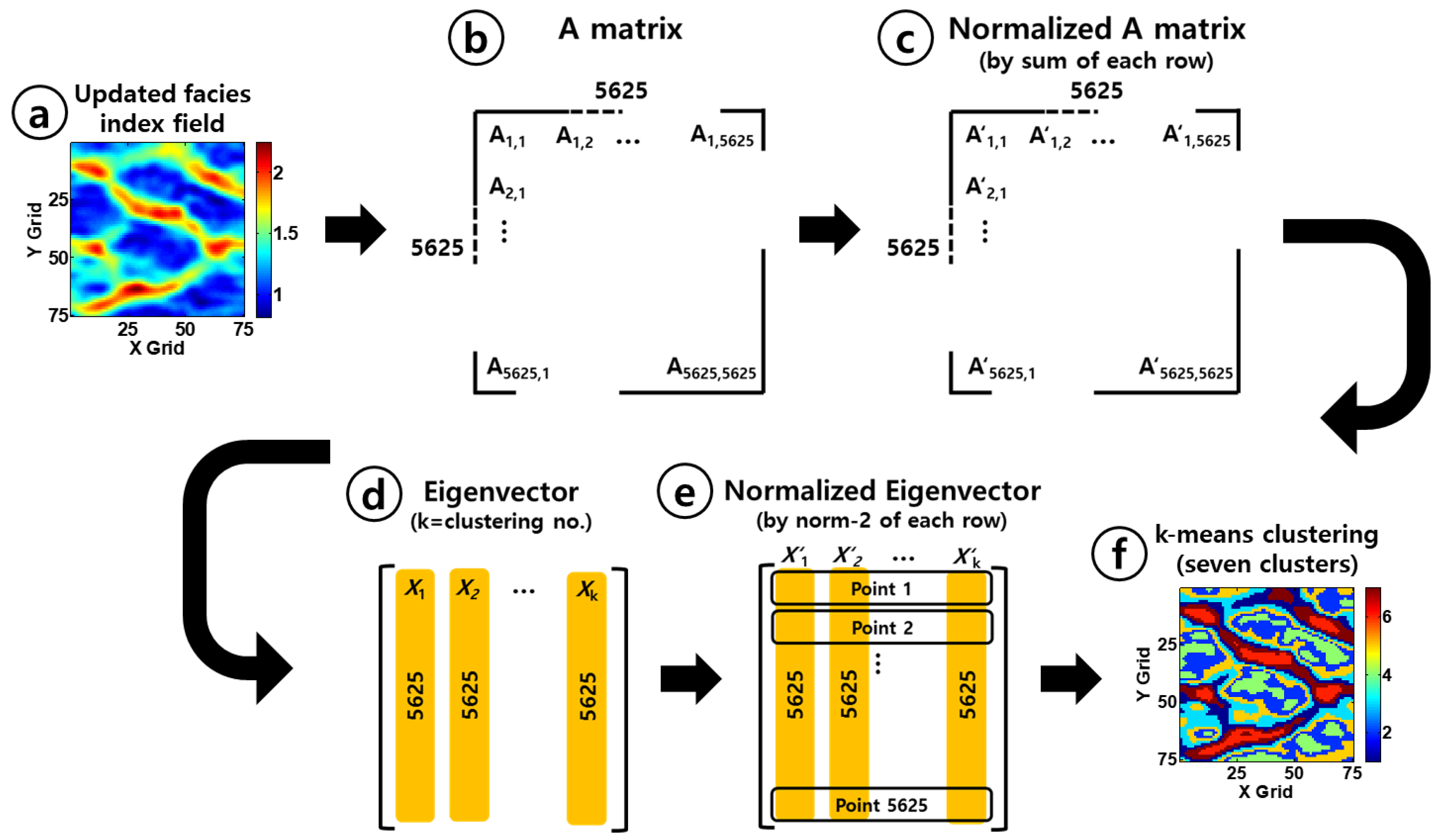
2.4. SCA
2.5. Overall Workflow for History Matching
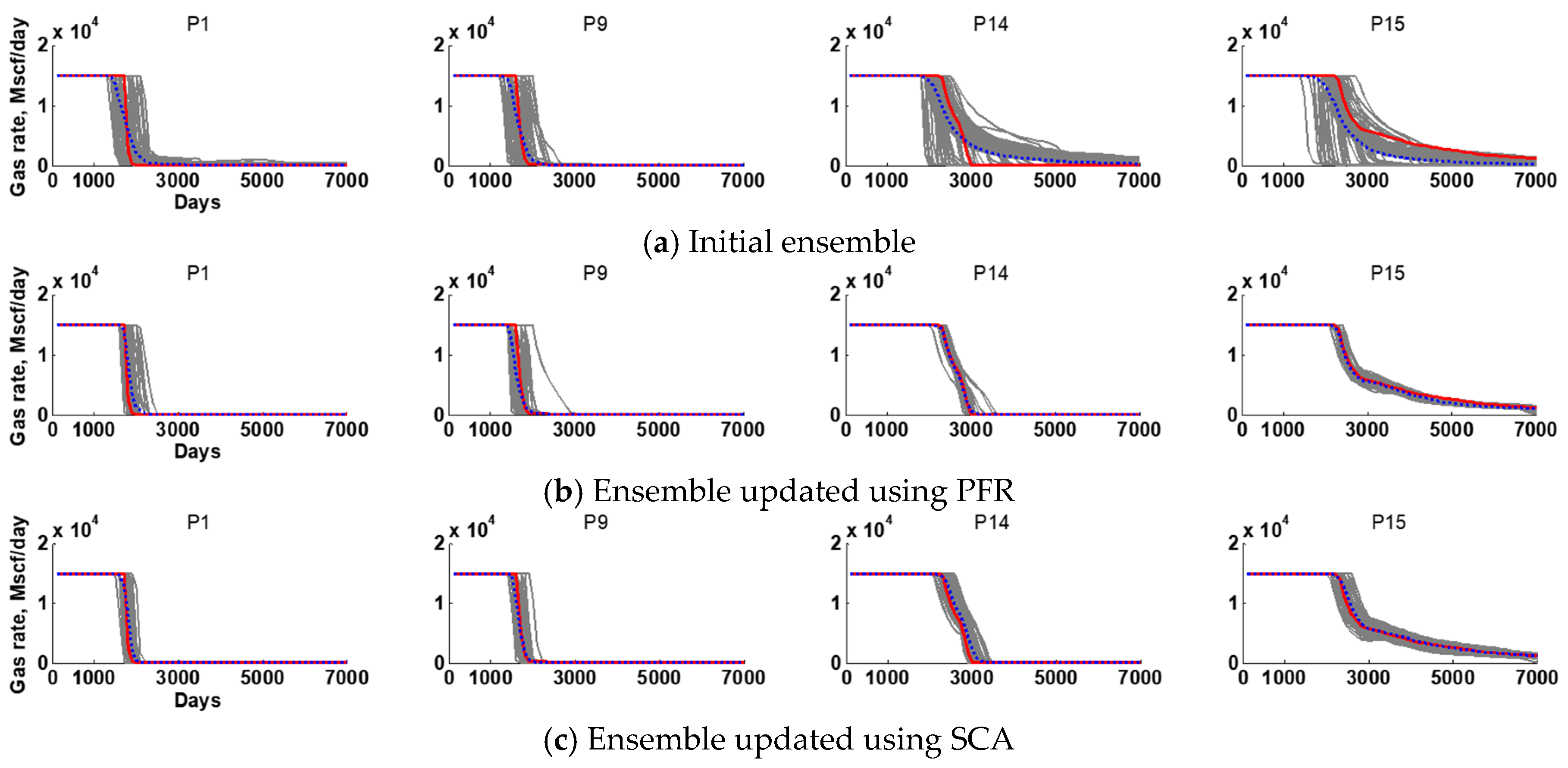
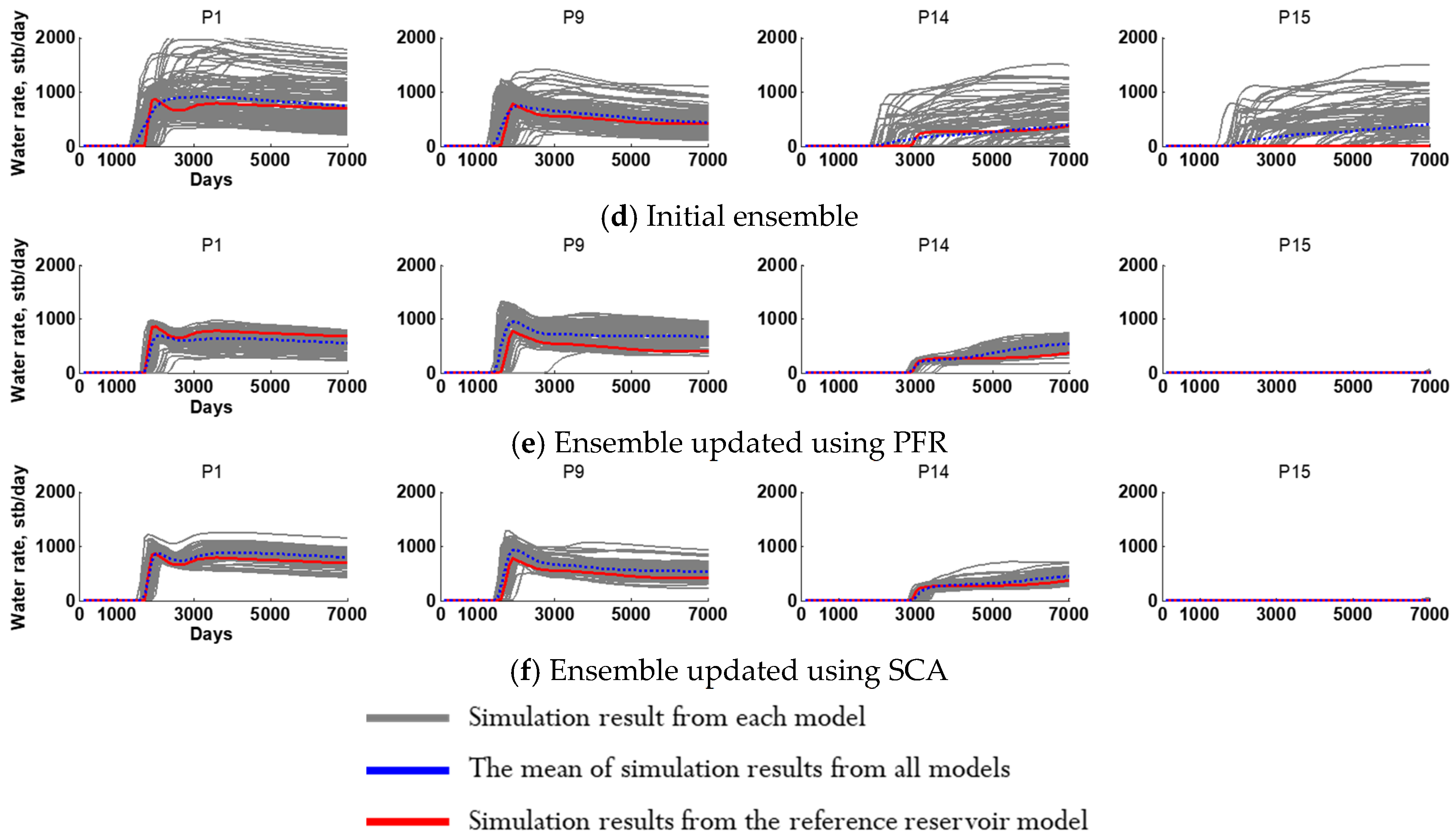
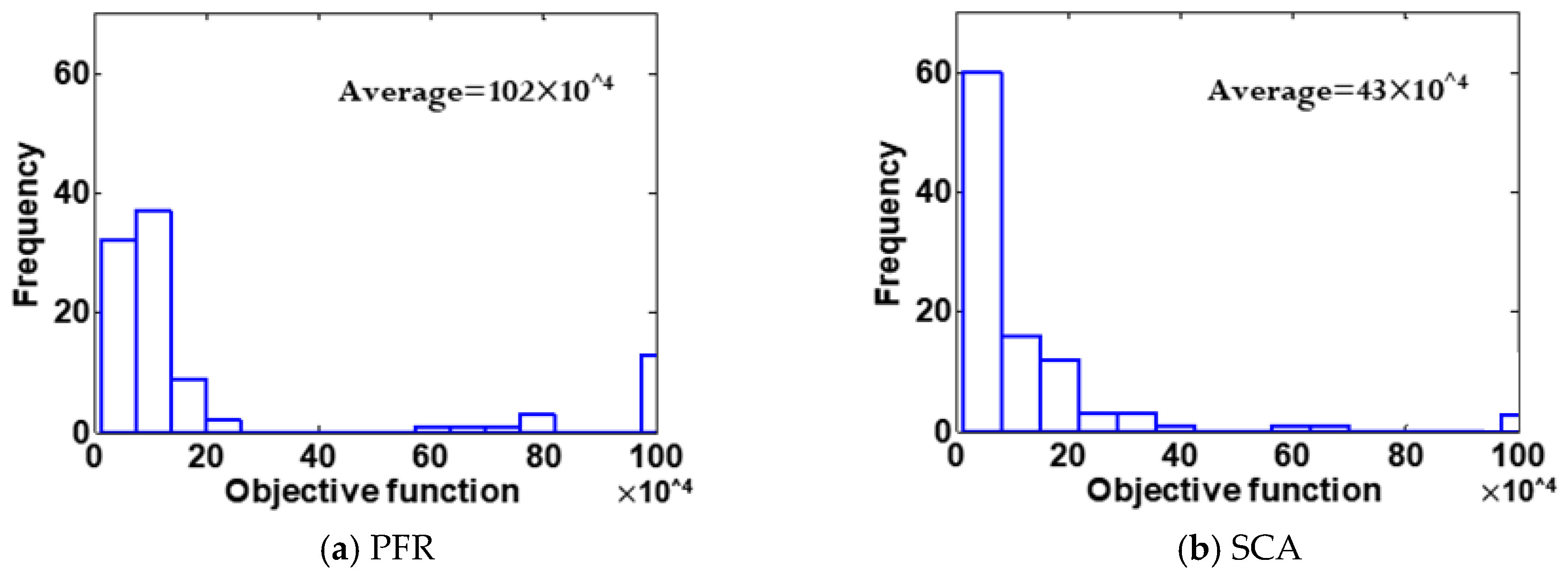
3. Results and Discussion
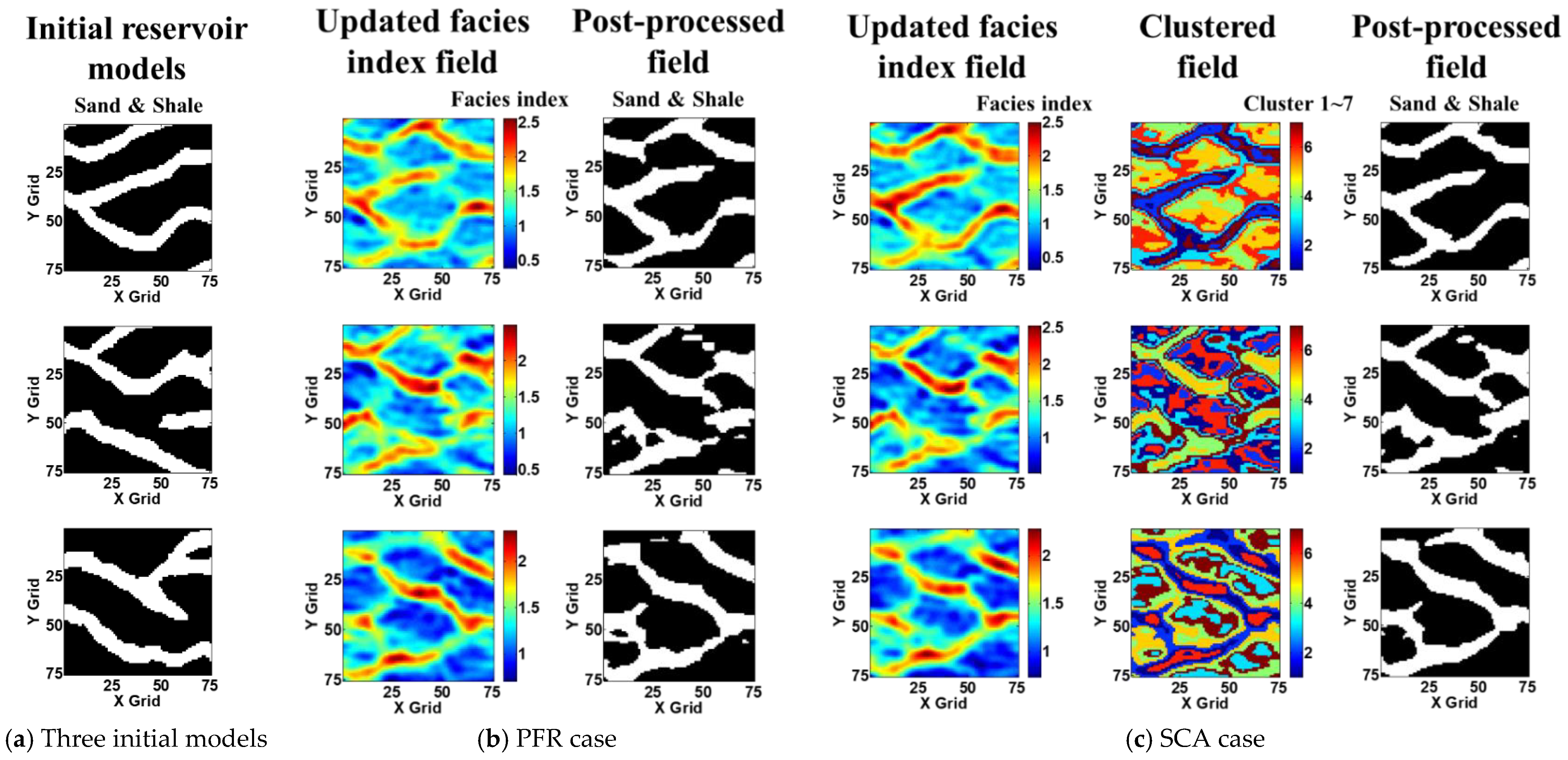
3.1. Facies Distribution
3.2. Gas and Water Productions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jia, B.; Tsau, J.; Ghahfarokhi, R.B. Investigation of Shale-Gas-Production Behavior: Evaluation of the Effects of Multiple Physics on the Matrix. SPE Reserv. Eval. Eng. 2019. [Google Scholar] [CrossRef]
- Jia, B.; Tsau, J.; Barati, R. A review of the current progress of CO2 injection EOR and carbon storage in shale oil reservoir. Fuel 2019, 236, 404–427. [Google Scholar] [CrossRef]
- Evensen, G. Sequential Data Assimilation with a Nonlinear Quasi-Geostrophic Model Using Monte Carlo Methods to Forecast Error Statistics. J. Geophys. Res. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Nævdal, G.; Manneseth, T.; Vefring, E.H. Near-well Reservoir Monitoring Through Ensemble Kalman Filter. In Proceedings of the SPE/DOE Improved Oil Recovery Symposium, Tulsa, OK, USA, 13–17 April 2002. [Google Scholar] [CrossRef]
- Yeo, M.J.; Jung, S.P.; Choe, J. Covariance matrix localization using drainage area in an ensemble Kalman filter. Energy Sour. Part A Recovery Util. Environ. Eff. 2014, 36, 2154–2165. [Google Scholar] [CrossRef]
- Kim, S.; Lee, C.; Lee, K.; Choe, J. Aquifer characterization of gas reservoirs using Ensemble Kalman filter and covariance localization. J. Pet. Sci. Eng. 2016, 146, 446–456. [Google Scholar] [CrossRef]
- Jung, H.; Jo, H.; Lee, K.; Choe, J. Characterization of various channel fields using an initial ensemble selection scheme and covariance localization. J. Energy Resour. Technol. Trans. ASME 2017, 139, 062906. [Google Scholar] [CrossRef]
- Kang, B.; Yang, H.; Lee, K.; Choe, J. Ensemble Kalman filter with principal component analysis assisted sampling for channelized reservoir characterization. J. Energy Resour. Technol. Trans. ASME 2017, 139, 032907. [Google Scholar] [CrossRef]
- Kang, B.; Choe, J. Regeneration of initial ensembles with facies analysis for efficient history matching. J. Energy Resour. Technol. Trans. ASME 2017, 139, 042903. [Google Scholar] [CrossRef]
- Lee, K.; Jeong, H.; Jung, S.P.; Choe, J. Characterization of Channelized Reservoir Using Ensemble Kalman Filter with Clustered Covariance. Energy Explor. Exploit. 2013, 31, 17–29. [Google Scholar] [CrossRef]
- Park, K.; Choe, J. Use of ensemble Kalman filter to 3-dimensional reservoir characterization during waterflooding. In Proceedings of the SPE Europec/EAGE Annual Conference and Exhibition, Vienna, Austria, 12–5 June 2006. [Google Scholar] [CrossRef]
- Jo, H.; Jung, H.; Ahn, J.; Lee, K.; Choe, J. History matching of channel reservoirs using ensemble Kalman filter with continuous update of channel information. Energy Explor. Exploit. 2017, 35, 3–23. [Google Scholar] [CrossRef]
- Skjervheim, J.A.; Evensen, G. An ensemble smoother for assisted history matching. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 21–23 February 2011. [Google Scholar] [CrossRef]
- Van Leeuwen, P.J.; Evensen, G. Data assimilation and inverse methods in terms of a probabilistic formulation. Mon. Weather Rev. 1996, 124, 2898–2913. [Google Scholar] [CrossRef]
- Emerick, A.A.; Reynolds, A.C. Ensemble smoother with multiple data assimilations. Comput. Geosci. 2013, 55, 3–15. [Google Scholar] [CrossRef]
- Lee, K.; Lim, J.; Choe, J.; Lee, H.S. Regeneration of channelized reservoirs using history-matched facies-probability map without inverse scheme. J. Pet. Sci. Eng. 2017, 149, 340–350. [Google Scholar] [CrossRef]
- Lee, K.; Jeong, H.; Jung, S.P.; Choe, J. Improvement of Ensemble Smoother with Clustered Covariance for Channelized Reservoirs. Energy Explor. Exploit. 2013, 31, 713–726. [Google Scholar] [CrossRef]
- Lee, K.; Jung, S.; Lee, T.; Choe, J. Use of Clustered Covariance and Selective Measurement Data in Ensemble Smoother for Three-Dimensional Reservoir Characterization. J. Energy Resour. Technol. Trans. ASME 2017, 139, 022905. [Google Scholar] [CrossRef]
- Kang, B.; Lee, K.; Choe, J. Improvement of ensemble smoother with SVD-assisted sampling scheme. J. Pet. Sci. Eng. 2016, 141, 114–124. [Google Scholar] [CrossRef]
- Kang, B.; Choe, J. Initial model selection for efficient history matching of channel reservoirs using Ensemble Smoother. J. Pet. Sci. Eng. 2017, 152, 294–308. [Google Scholar] [CrossRef]
- Emerick, A.A.; Reynolds, A.C. History matching time-lapse seismic data using the ensemble Kalman filter with multiple data assimilations. Comput. Geosci. 2012, 16, 639–659. [Google Scholar] [CrossRef]
- Fan, Z.; Yang, D.; Chai, D.; Li, X. Estimation of relative permeability and capillary pressure for PUNQ-S3 model using a modified iterative ensemble smoother. J. Energy Resour. Technol. Trans. ASME 2018, 141, 022901. [Google Scholar] [CrossRef]
- Evensen, G. Analysis of iterative ensemble smoothers for solving inverse problems. Comput. Geosci. 2018, 22, 885–908. [Google Scholar] [CrossRef]
- Zhao, Y.; Forouzanfar, F.; Reynolds, A.C. History matching of multi-facies channelized reservoirs using ES-MDA with common basis DCT. Comput. Geosci. 2017, 21, 1343–1364. [Google Scholar] [CrossRef]
- Oliver, D.S.; Chen, Y. Recent Progress on Reservoir History Matching: A Review. Comput. Geosci. 2011, 15, 185–221. [Google Scholar] [CrossRef]
- Kim, S.; Lee, C.; Lee, K.; Choe, J. Characterization of channel oil reservoirs with an aquifer using EnKF, DCT, and PFR. Energy Explor. Exploit. 2016, 34, 828–843. [Google Scholar] [CrossRef]
- Kim, S.; Lee, C.; Lee, K.; Choe, J. Characterization of channelized gas reservoirs using ensemble Kalman filter with application of discrete cosine transformation. Energy Explor. Exploit. 2016, 34, 319–336. [Google Scholar] [CrossRef]
- Kim, S.; Jung, H.; Lee, K.; Choe, J. Initial Ensemble Design Scheme for Effective Characterization of Three-Dimensional Channel Gas Reservoirs with an Aquifer. J. Energy Resour. Technol. Trans. ASME 2017, 139, 022911. [Google Scholar] [CrossRef]
- Jung, H.; Jo, H.; Kim, S.; Lee, K.; Choe, J. Recursive update of channel information for reliable history matching of channel reservoirs using EnKF with DCT. J. Pet. Sci. Eng. 2017, 154, 19–37. [Google Scholar] [CrossRef]
- Lorentzen, R.J.; Flornes, K.M.; Nævdal, G. History Matching Channelized Reservoirs Using the Ensemble Kalman Filter. SPE J. 2012, 17, 137–151. [Google Scholar] [CrossRef]
- Lorentzen, R.J.; Nævdal, G.; Shafieirad, A. Estimating Facies Fields by Use of the Ensemble Kalman Filter and Distance Functions-Applied to Shallow-Marine Environments. SPE J. 2013, 3, 146–158. [Google Scholar] [CrossRef]
- Jafarpour, B.; McLaughlin, D.B. History matching with an ensemble Kalman filter and discrete cosine parameterization. Comput. Geosci. 2008, 12, 227–244. [Google Scholar] [CrossRef]
- Jafarpour, B.; McLaughlin, D.B. Reservoir characterization with the discrete cosine transform. SPE J. 2009, 14, 182–201. [Google Scholar] [CrossRef]
- Panwar, A.; Trivedi, J.J.; Nejadi, S. Importance of distributed temperature sensor data for steam assisted gravity drainage reservoir characterization and history matching within ensemble Kalman filter framework. J. Energy Resour. Technol. Trans. ASME 2015, 137, 042902. [Google Scholar] [CrossRef]
- Mouysset, S.; Noailles, J.; Ruiz, D. On an Interpretation of Spectral Clustering Via Heat Equation and Finite Elements Theory. In Proceedings of the World Congress on Engineering 2010, London, UK, 30 June–2 July 2010. [Google Scholar]
- Mouysset, S.; Noailles, J.; Ruiz, D.; Tauber, C. Spectral Clustering: Interpretation and Gaussian Parameter; Springer: Cham, Germany, 2013; Volume 4, pp. 153–162. [Google Scholar]
- Mouysset, S.; Guivarch, R.; Noailles, J.; Ruiz, D. Segmentation of cDNA Microarray Images using Parallel Spectral Clustering. Adv. Distrib. Comput. Artif. Intell. J. 2013, 2, 1–8. [Google Scholar]
- Ahmed, N.; Natarajan, T.; Rao, K.R. Discrete cosine transform. IEEE Trans. Computers 1974, 100, 90–93. [Google Scholar] [CrossRef]
- Kim, S.; Min, B.; Kwon, S.; Chu, M. History Matching of a Channelized Reservoir Using a Serial Denoising Autoencoder Integrated with ES-MDA. Geofluids 2019, 2019, 3280961. [Google Scholar] [CrossRef]
- Yin, Z.; Feng, T.; MacBeth, C. Fast assimilation of frequently acquired 4D seismic data for reservoir history matching. Comput. Geosci. 2019, 128, 30–40. [Google Scholar] [CrossRef]



| Clusters 1–7 | Average Index Values | Assigned Class |
|---|---|---|
| 6 | 1.9419 | Cluster A |
| 7 | 1.7291 | Cluster B |
| 1 | 1.5202 | Cluster C |
| 3 | 1.3482 | Cluster D |
| 5 | 1.1916 | Cluster E |
| 2 | 1.0533 | Cluster F |
| 4 | 0.9495 | Cluster G |
| Parameters | Values |
|---|---|
| Reservoir grid system | 75 by 75 by 1 |
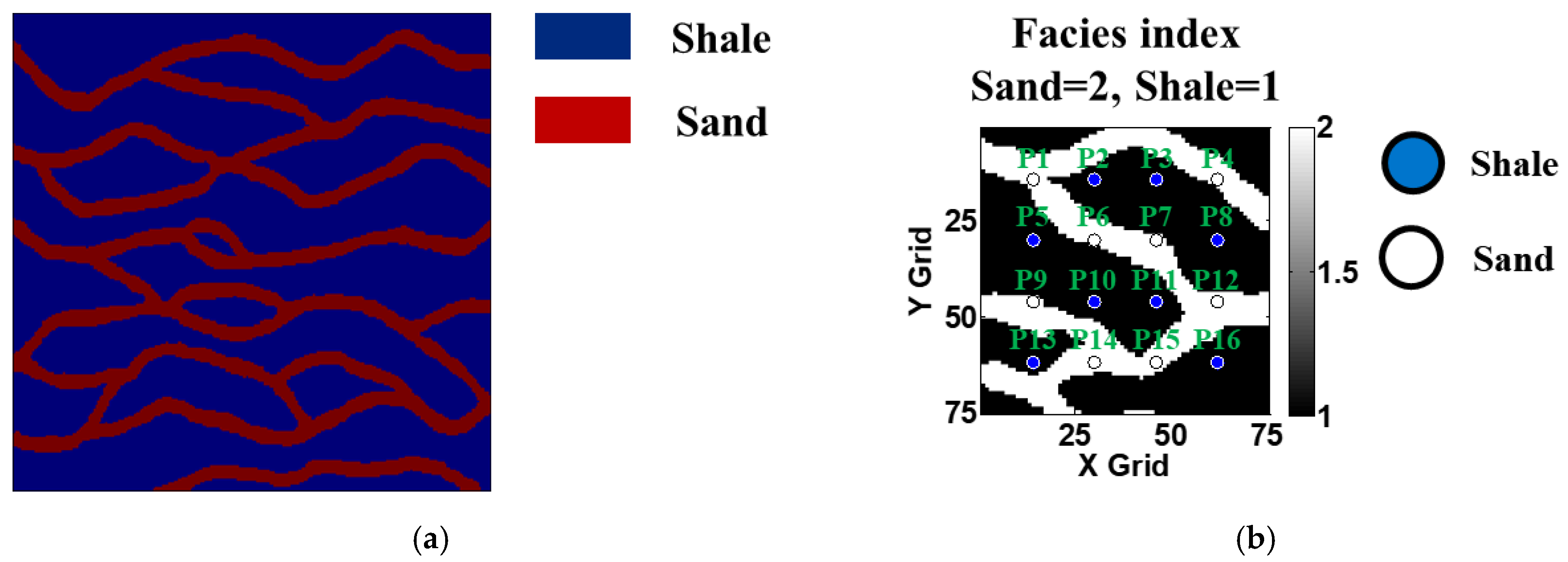
| Well locations, grid coordinate (from the upper left) Well numbering P1–P16 | (14, 14), (30, 14), (46, 14), (62, 14), (14, 30), (30, 30), (46, 30), (62, 30), (14, 46), (30, 46), (46, 46), (62, 46), (14, 62), (30, 62), (46, 62), (62, 62) |
| Observed data types | Well gas production rate, Well bottomhole pressure |
| Porosity, fraction | 0.2 (sandstone), 0.1 (shale) |
| Permeability, md | 100 (sandstone), 1 (shale) |
| Relative permeability, modified Brooks-Corey relation | Connate water saturation = 0.25 Connate gas saturation = 0.2 Sandstone (nw = 3, ng = 2) Shale (nw = 5, ng = 4) |
| Initial water saturation, fraction | 0.25 |
| Initial reservoir pressure, psia | 3000 |
| Bottomhole pressure limit, psia | 1000 |
| The number of DCT coefficients used in a reservoir | 465 (8% of total) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Lee, K. Application of Spectral Clustering Algorithm to ES-MDA with DCT for History Matching of Gas Channel Reservoirs. Energies 2019, 12, 4394. https://doi.org/10.3390/en12224394
Kim S, Lee K. Application of Spectral Clustering Algorithm to ES-MDA with DCT for History Matching of Gas Channel Reservoirs. Energies. 2019; 12(22):4394. https://doi.org/10.3390/en12224394
Chicago/Turabian StyleKim, Sungil, and Kyungbook Lee. 2019. "Application of Spectral Clustering Algorithm to ES-MDA with DCT for History Matching of Gas Channel Reservoirs" Energies 12, no. 22: 4394. https://doi.org/10.3390/en12224394
APA StyleKim, S., & Lee, K. (2019). Application of Spectral Clustering Algorithm to ES-MDA with DCT for History Matching of Gas Channel Reservoirs. Energies, 12(22), 4394. https://doi.org/10.3390/en12224394