Data-Driven Compartmental Modeling Method for Harmonic Analysis—A Study of the Electric Arc Furnace
Abstract
:1. Introduction
2. Data-Driven Compartmental Modeling Method for EAF
2.1. Multi-Mode EAF Harmonic Model
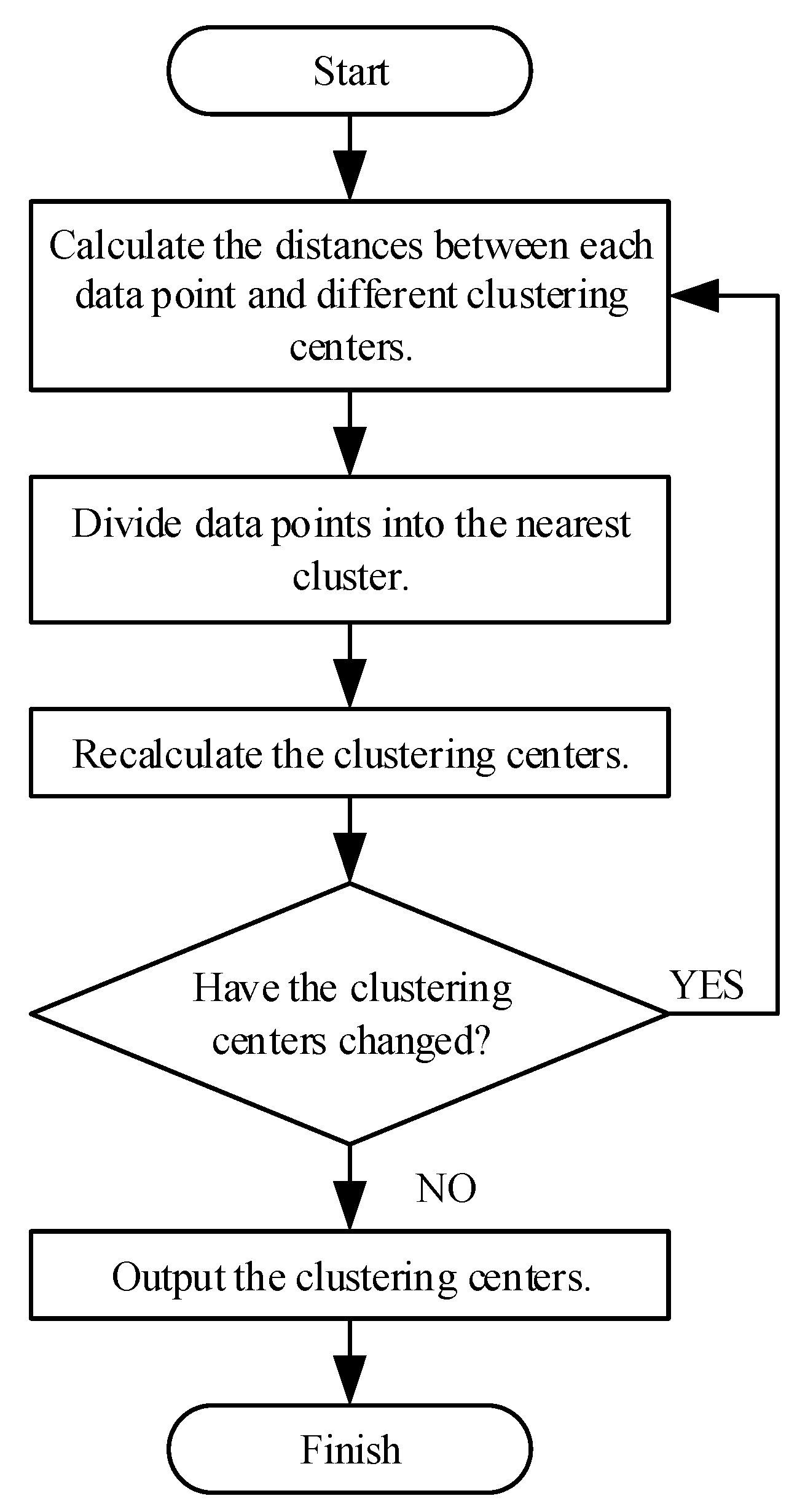
2.2. Data-Driven Compartmental Modeling Method (DCMM)
3. Performance Evaluation
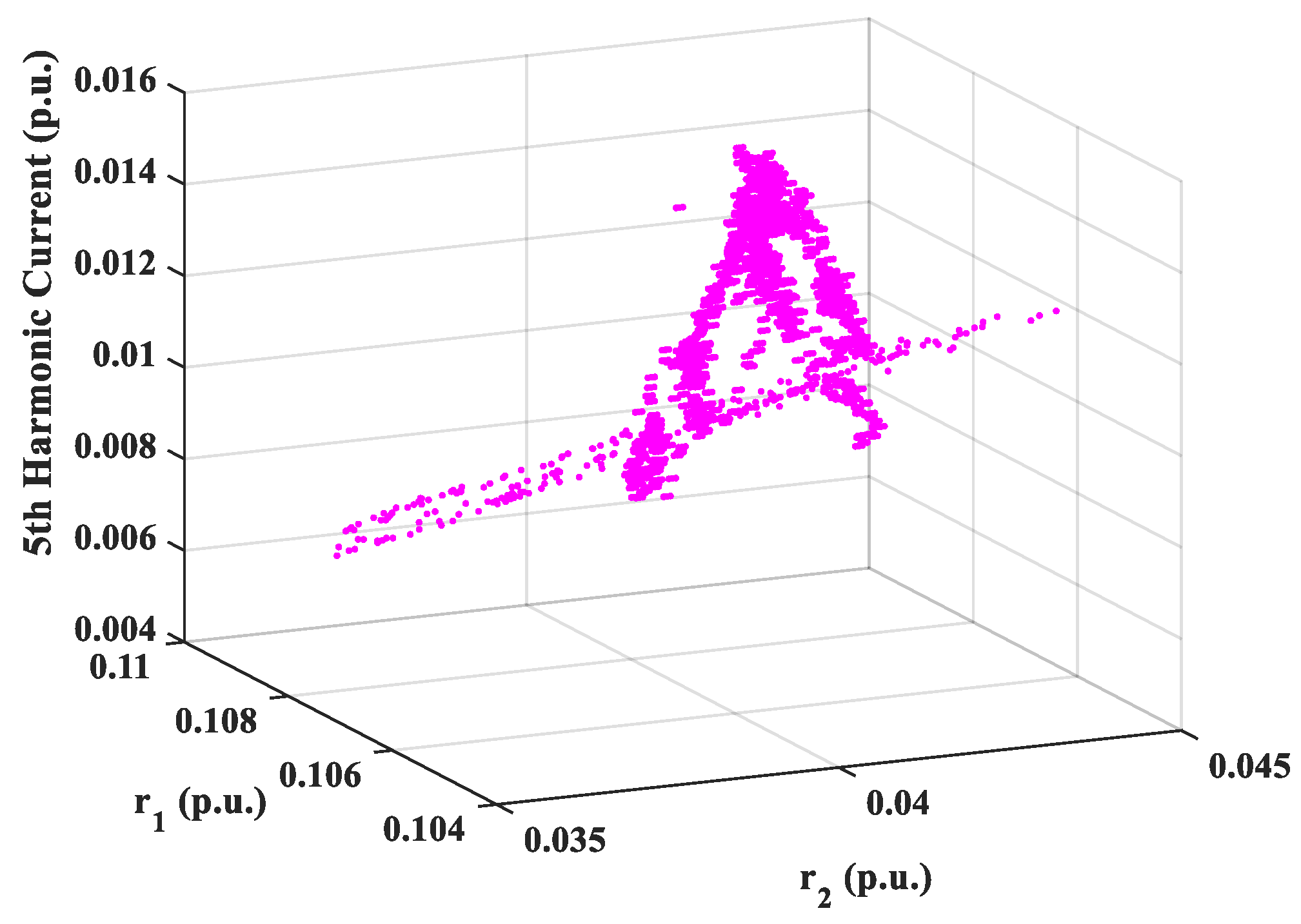
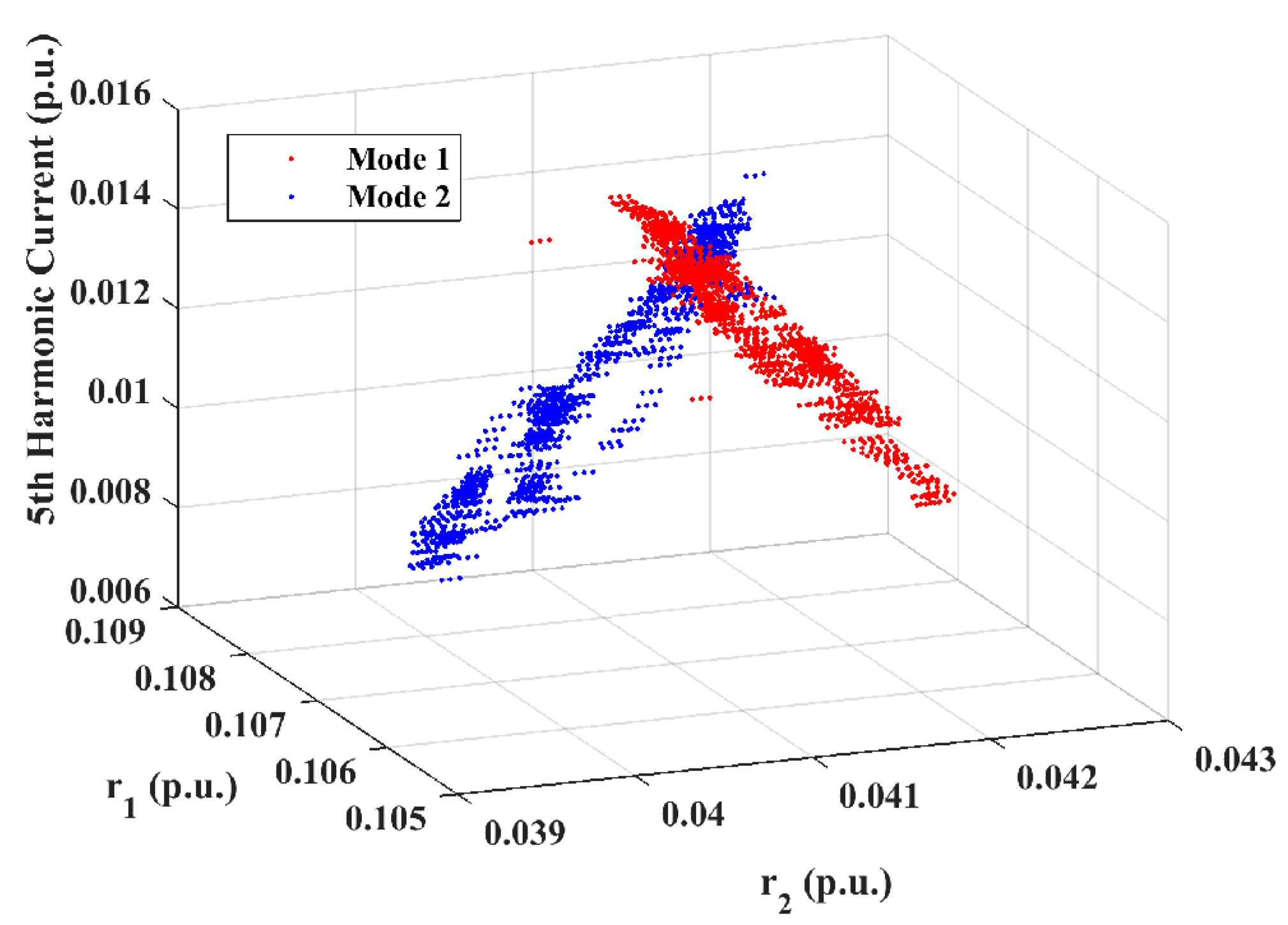
3.1. Case 1: 2880 Data Points, 2 Modes
3.2. Case 2: 3360 Data Points, 3 Modes
3.3. Summary of Case 1 and 2
4. Case Study
4.1. Parameter Identification of Multi-Mode EAF Harmonic Model
4.2. Comparison of Different Models
4.3. Application of Multi-Mode EAF Harmonic Model
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Raul, G.S.; Javier, V.C.; Fernando, M.C.; Longoria-Gandara, O.; Ortegón Aguilar, J. Electric arc furnace modeling with artificial neural networks and arc length with variable voltage gradient. Energies 2017, 10, 1424. [Google Scholar]
- Gajic, D.; Savic-Gajic, I.; Savic, I.; Georgieva, O.; Di Gennaro, S. Modelling of electrical energy consumption in an electric arc furnace using artificial neural networks. Energy 2016, 108, 132–139. [Google Scholar] [CrossRef]
- Kirschen, M.; Badr, K.; Pfeifer, H. Influence of direct reduced iron on the energy balance of the electric arc furnace in steel industry. Energy 2011, 36, 6146–6155. [Google Scholar] [CrossRef]
- Steven, L.; Oyeniyi, O.; Christos, N.M.; Lazova, M.; Kaya, A.; Van den Broek, M.; De Paepe, M. Case study of an organic rankine cycle (ORC) for waste heat recovery from an electric arc furnace (EAF). Energies 2017, 10, 649–664. [Google Scholar]
- Oyeniyi, O.; Christos, M. Thermo-Economic and heat transfer optimization of working-fluid mixtures in a low-temperature organic rankine cycle system. Energies 2016, 9, 448–469. [Google Scholar]
- Horton, R.; Haskew, T.A.; Burch, R.F., IV. A time-domain ac electric arc furnace model for flicker planning studies. IEEE Trans. Power Deliv. 2017, 24, 1450–1457. [Google Scholar] [CrossRef]
- Cano-Plata, E.A.; Ustariz-Farfan, A.J.; Soto-Marin, O.J. Electric arc furnace model in distribution systems. IEEE Trans. Ind. Appl. 2015, 51, 4314–4320. [Google Scholar] [CrossRef]
- Hsu, Y.; Chen, K.; Huang, P.; Lu, C. Electric arc furnace voltage flicker analysis and prediction. IEEE Trans. Instrum. Meas. 2011, 60, 3360–3368. [Google Scholar] [CrossRef]
- Bhonsle, D.C.; Kelkar, R.B. Analyzing power quality issues in electric arc furnace by modeling. Energy 2016, 115, 830–839. [Google Scholar] [CrossRef]
- Chen, X.; Lin, J.; Wan, C.; Song, Y.; Luo, H. A unified frequency-domain model for automatic generation control assessment under wind power uncertainty. IEEE Trans. Smart Grid 2019, 10, 2936–2947. [Google Scholar] [CrossRef]
- Munoz, J.A.; Espinoza, J.R.; Baier, C.R.; Moran, L.A.; Espinosa, E.E.; Melin, P.E.; Sbarbaro, D.G. Design of a discrete-time linear control strategy for a multicell upqc. IEEE Trans. Ind. Electron. 2012, 59, 3797–3807. [Google Scholar] [CrossRef]
- Sezgin, E.; Göl, M.; Salor, Ö. State-Estimation-Based determination of harmonic current contributions of iron and steel plants supplied from PCC. IEEE Trans. Ind. Appl. 2016, 52, 2654–2663. [Google Scholar] [CrossRef]
- Göl, M.; Salor, O.; Alboyaci, B.; Mutluer, B.; Cadirci, I.; Ermis, M. A new field-data-based EAF model for power quality studies. IEEE Trans. Ind. Appl. 2010, 46, 1230–1242. [Google Scholar] [CrossRef]
- Vatankulu, Y.E.; Şentürk, Z.; Salor, O. Harmonics and interharmonics analysis of electrical arc furnaces based on spectral model optimization with high-resolution windowing. IEEE Trans. Ind. Appl. 2017, 53, 2587–2595. [Google Scholar] [CrossRef]
- Illahi, F.; El-Amin, I.; Mukhtiar, M.U. The application of multiobjective optimization technique to the estimation of electric arc furnace parameters. IEEE Trans. Power Deliv. 2018, 33, 1727–1734. [Google Scholar] [CrossRef]
- Mousavi Agah, S.M.; Hosseinian, S.H.; Abyaneh, H.A.; Moaddabi, N. Parameter identification of arc furnace based on stochastic nature of arc length using two-step optimization technique. IEEE Trans. Power Deliv. 2010, 25, 2859–2867. [Google Scholar] [CrossRef]
- Torabian Esfahani, M.; Vahidi, B. A new stochastic model of electric arc furnace based on hidden markov model: A study of its effects on the power system. IEEE Trans. Power Deliv. 2012, 27, 1893–1901. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Y. A neural-network-based data-driven nonlinear model on time- and frequency-domain voltage–current characterization for power-quality study. IEEE Trans. Power Deliv. 2015, 30, 1577–1584. [Google Scholar] [CrossRef]
- Chang, G.W.; Chen, C.; Liu, Y. A neural-network-based method of modeling electric arc furnace load for power engineering study. IEEE Trans. Power Syst. 2010, 25, 138–146. [Google Scholar] [CrossRef]
- Chang, G.W.; Lin, S.; Chen, Y.; Lu, H.; Chang, Y. An advanced EAF model for voltage fluctuation propagation study. IEEE Trans. Power Deliv. 2017, 32, 980–988. [Google Scholar] [CrossRef]
- Naveros, F.; Luque, N.R.; Garrido, J.A.; Carrillo, R.R.; Anguita, M.; Ros, E. A spiking neural simulator integrating event-driven and time-driven computation schemes using parallel CPU-GPU co-processing: A case study. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1567–1574. [Google Scholar] [CrossRef] [PubMed]
- Matsubara, T.; Torikai, H. An asynchronous recurrent network of cellular automaton-based neurons and its reproduction of spiking neural network activities. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 836–852. [Google Scholar] [CrossRef]
- Gao, S.; Li, X.; Ma, X.; Hu, H.; He, Z.; Yang, J. Measurement-Based compartmental modeling of harmonic sources in traction power-supply system. IEEE Trans. Power Deliv. 2017, 32, 900–909. [Google Scholar] [CrossRef]
- Ranade, S. Task force on harmonic modeling and simulation. Modeling and simulation of the propagation of harmonics in electric power networks. I. Concepts, models, and simulation techniques. IEEE Trans. Power Deliv. 1996, 11, 452–465. [Google Scholar]
- Ajaei, F.B.; Afsharnia, S.; Kahrobaeian, A.; Farhangi, S. A Fast and effective control scheme for the dynamic voltage restorer. IEEE Trans. Power Deliv. 2011, 26, 2398–2406. [Google Scholar] [CrossRef]
- Salles, D.; Jiang, C.; Xu, W.; Freitas, W.; Mazin, H.E. Assessing the collective harmonic impact of modern residential loads—Part I: Methodology. IEEE Trans. Power Deliv. 2012, 27, 1937–1946. [Google Scholar] [CrossRef]
- Papaioannou, I.T.; Alexiadis, M.C.; Demoulias, C.S.; Labridis, D.P.; Dokopoulos, P.S. Modeling and field measurements of photovoltaic units connected to LV grid. Study of penetration scenarios. IEEE Trans. Power Deliv. 2011, 26, 979–987. [Google Scholar] [CrossRef]
- Yang, P.; Tsai, J.; Chou, J. PCA-Based fast search method using PCA-LBG-based VQ codebook for codebook search. IEEE Access 2016, 4, 1332–1344. [Google Scholar] [CrossRef]
- Taşkın, G.; Kaya, H.; Bruzzone, L. Feature selection based on high dimensional model representation for hyperspectral images. IEEE Trans. Image Process. 2017, 26, 2918–2928. [Google Scholar] [CrossRef]
- Jia, S.; Tang, G.; Zhu, J.; Li, Q. A novel ranking-based clustering approach for hyperspectral band selection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 88–102. [Google Scholar] [CrossRef]
- Fan, Y.; Gongshen, L.; Kui, M.; Zhaoying, S. Neural feedback text clustering with BiLSTM-CNN-kmeans. IEEE Access 2018, 6, 57460–57469. [Google Scholar] [CrossRef]
- Huang, X.; Ye, Y.; Zhang, H. Extensions of kmeans-type algorithms: A new clustering framework by integrating intracluster compactness and intercluster separation. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1433–1446. [Google Scholar] [CrossRef] [PubMed]
- Peng, K.; Leung, V.C.M.; Huang, Q. Clustering approach based on mini batch kmeans for intrusion detection system over big data. IEEE Access 2018, 6, 11897–11906. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiang, H. A novel consensus-based particle swarm optimization-assisted trust-tech methodology for large-scale global optimization. IEEE Trans. Cybern. 2017, 47, 2717–2729. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X.Q.; Zhan, T.M.; Jiao, Z.Q.; Sun, Y.; Chen, Z.-M.; Yao, Y.; Fang, L.T.; Lv, Y.-D.; Wang, S.-H. Fractal dimension estimation for developing pathological brain detection system based on minkowski-bouligand method. IEEE Access 2016, 4, 5937–5947. [Google Scholar] [CrossRef]









| Case | Mode | Ap | C |
|---|---|---|---|
| Case 1 | Mode 1 | [3.7099, −1.1922] | −0.0115 |
| Mode 2 | [−3.9041, −0.3421] | −0.2107 | |
| Case 2 | Mode 1 | [3.7099, −1.1922] | −0.0115 |
| Mode 2 | [−3.9041, −0.3421] | −0.2107 | |
| Mode 3 | [0.3511, −0.8861] | −0.0904 |
| Case | Mode | Ap′ | C′ |
|---|---|---|---|
| Case 1 | Mode 1 | [3.7338, −1.2106] | −0.0110 |
| Mode 2 | [−3.8913, −0.3801] | −0.2142 |
| Case | Mode | Ap′ | C′ |
|---|---|---|---|
| Case 2 | Mode 1 | [3.7305, −1.2161] | −0.0098 |
| Mode 2 | [−3.8886, −0.790] | −0.2140 | |
| Mode 3 | [0.3510, −0.8861] | −0.0904 |
| Case | Mode | Ap | C |
|---|---|---|---|
| EAF | Mode 1 | [0.1111, −0.0095] | −0.0007 |
| Mode 2 | [0.0283, 0.0099] | 0.0020 | |
| Mode 3 | [−0.0164, 0.1193] | 0.0203 |
| Model | ME | MSE | R2 | FA |
|---|---|---|---|---|
| Proposed model | 1.1369 | 2.0536 | 90.28% | 98.25% |
| Constant-harmonic-ratio-type model | 1.2862 | 2.5837 | 87.78% | 96.80% |
| Norton equivalent model | 1.6345 | 4.2531 | 79.88% | 95.38% |
| Order | Zh (ohms) | Uh (V) |
|---|---|---|
| 3 | 0.039 + 0.882i | 30.4131 |
| 5 | 0.039 + 1.372i | 18.2623 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Shao, Z.; Chen, F. Data-Driven Compartmental Modeling Method for Harmonic Analysis—A Study of the Electric Arc Furnace. Energies 2019, 12, 4378. https://doi.org/10.3390/en12224378
Xu H, Shao Z, Chen F. Data-Driven Compartmental Modeling Method for Harmonic Analysis—A Study of the Electric Arc Furnace. Energies. 2019; 12(22):4378. https://doi.org/10.3390/en12224378
Chicago/Turabian StyleXu, Haobo, Zhenguo Shao, and Feixiong Chen. 2019. "Data-Driven Compartmental Modeling Method for Harmonic Analysis—A Study of the Electric Arc Furnace" Energies 12, no. 22: 4378. https://doi.org/10.3390/en12224378
APA StyleXu, H., Shao, Z., & Chen, F. (2019). Data-Driven Compartmental Modeling Method for Harmonic Analysis—A Study of the Electric Arc Furnace. Energies, 12(22), 4378. https://doi.org/10.3390/en12224378





