1. Introduction
Recently, the adoption of Fuel Cells (FCs) for stationary applications and for combined heat and power plants [
1] has increased, because FCs are clean energy converting devices characterized by very low (even zero) carbon emissions, high conversion efficiency and an inherent decoupling between its power and capacity [
2].
Many projects were funded (for instance, the H2020 HEALTH-CODE project [
3]) with the aim to improve Polymeric Electrolyte Membrane (PEM) FC energy production, reliability and lifetime [
4]. Some of them were focused on the analysis of degradation phenomena [
5] and on the development of appropriate control, diagnostic and prognostic features [
6].
Despite very reliable approaches and accurate results, the main experimental studies in this field use expensive laboratory instrumentation and mainly face offline operating mode, that is, when the FC is disconnected from the load. These studies identify FC stack models by processing the stack voltage and current time-domain waveforms, for example, Reference [
7]. Alternatively, they may operate in the frequency domain through the so-called Electrochemical Impedance Spectroscopy (EIS) [
8]. For a fixed number of frequencies and at a fixed dc operating point of the FC stack, a sine wave current signal, suitably small with respect to the dc current, is injected, perturbing the dc operating point. Then, the following stack voltage perturbation is measured and the ac component at the perturbation frequency is extracted. This allows one to compute the voltage-to-current ratio in the frequency-domain, that is the complex impedance [
9,
10]. More structured waveforms can be used as perturbation signal, for example, the Pseudo Random Binary Sequence (PRBS), which reduces the perturbation times [
11]. Reference [
12] proposes a comprehensive review of EIS applications and critical issues.
The model-based EIS FC diagnosis is often based on parameter identification [
13]. The experimental impedance frequency spectrum is fitted by identifying the parameters of a suitable equivalent electric circuit, namely the impedance model. The set of parameter values characterizing a normal operating condition is taken as the reference set, and the variation of parameters with respect to this reference set is interpreted as an indication of fault or degradation. Impedance parameter identification is not a trivial task. Indeed, both the shape of the impedance spectrum and the frequency of each point in the plot are fundamental information for identification and diagnostic purposes. Moreover, FC frequency-domain models, for example, References [
14,
15] may include the Constant Phase Element (CPE) and the Warburg impedance, with six or more parameters to be identified in total. As a consequence, the identification procedure fits with a laboratory context, so that the experimental data are usually handled by a personal computer, with no significant processing and memory constraints. The same conclusion holds for time-domain identification and diagnostic approaches (see, for instance, Reference [
16]). On the contrary, online/on-board PEM FC diagnosis requires that the experimental stack voltage and current waveforms are (i) acquired through sensors typically used in embedded applications, rather than accurate laboratory equipment, and (ii) processed in a time interval that is suitably shorter than the one needed for the data acquisition. This should be done through cheap and small hardware, whose cost and size is a tiny fraction of the FC system ones.
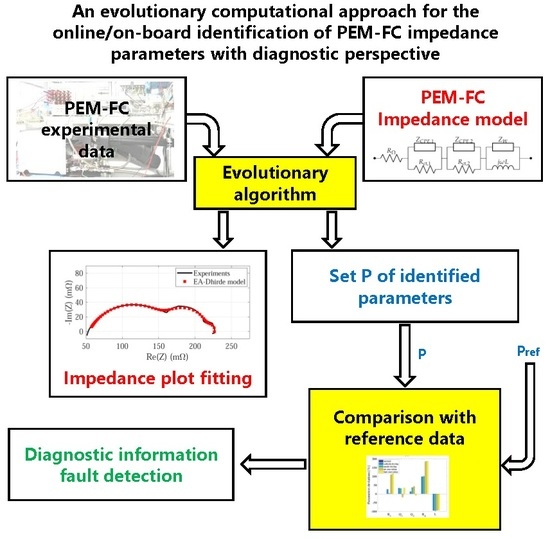
In this context, the main aim of this paper is to show that the PEM FC model-based identification of impedance parameters from an EIS-derived impedance spectrum can be performed online and on-board, with a diagnostic perspective. To this aim, an Evolutionary Algorithm (EA) is used due to its intrinsic ability to explore the search space and find the global optimum among multiple local ones.
EAs have already been used in various PEM FC optimization and identification problems, but very rarely in EIS identification or in online/on-board contexts. The identification problems are often based on the model reported in Reference [
17], or similar ones. Their goal is to fit the FC voltage-to-current (V-I) polarization curve for diagnostic purposes (e.g., Reference [
18] or Reference [
19]). In Reference [
20], an heuristic algorithm named Jaya is used for the optimization of a PEM FC stack design. The Jaya features are exploited to optimize the series/parallel connection of FCs and the cell active areas. This guarantees that the assembly delivers the rated voltage at the rated power, minimizing the overall system cost. In Reference [
21], a stochastic optimization and a multiphysics performance model for the V-I curve are used for parametric identification. In Reference [
22], a dynamic model is preferred and an offline identification is performed using Matlab™ environment. In Reference [
23], an improved particle swarm optimization is utilized for the identification of a very detailed polarization curve model, again in offline mode. A less complex technique, such as a simple genetic algorithm, is used in Reference [
24] for the estimation of parameters of a novel FC model.
The offline EIS data-driven identification of PEM FC equivalent circuits is also discussed in the literature. For instance, in References [
25,
26], least square-based algorithms or Matlab built-in tools are used. Some attempts were also made to extract diagnostic information from EIS time-domain data with a recursive filtering approach [
27,
28,
29]. Few examples of online/on-board identification approaches oriented to FC diagnosis appeared in the literature. In Reference [
30], a mix of evolutionary and deterministic algorithms is used to estimate the fractional order transfer function coefficients from time-domain sample data. This transfer function, which approximates the Warburg impedance, does not allow to obtain a good fit of the frequency-domain curve in healthy and faulty operating conditions. Consequently, poor information oriented to on-board diagnostics can be extracted from such frequency-domain parameters. The aforementioned Reference [
30] does not provide neither a wide validation of the method in various FC operating conditions, nor an implementation of the algorithm on an embedded system. An alternative approach to online/on-board FC diagnostics is presented in Reference [
11]. In that paper, a dimensionless aggregate indicator describes the overall condition of the FC stack. A dc-dc converter injects a PRBS stack current excitation, whose response is analyzed by using an algorithm based on the wavelet transform. This approach prevents the straightforward detection of the failure modes. Moreover, the PRBS sequence requires faster measurements than a sequence of tones at various frequencies but it requires a more significant computational effort.
This paper proposes a computational approach to the identification of the impedance parameters of a PEM FC stack model, based on an EA characterized by limited computational effort. The EA benefits from the use of sub-populations and migration among sub-populations. These features improve the exploration capability of the search space. The impedance parameter identification is formulated as an optimization problem. The objective function is defined as the mismatch between two impedance plots in a normalized plane. The first plot represents the experimental impedance and the second is computed on the basis of the identified parameters using a circuit model. Three kinds of impedance models, characterized by increasing computational complexity, are used depending on the experimental data to be fitted. The first one, a linear model made of resistors and capacitors, is particularly suitable for a low computational burden implementation. The second one is the so-called Fouquet model [
14], that is frequently used in PEM FC literature for its accuracy in frequency-domain representation. The third one, called Dhirde model, extends the Fouquet model capabilities to more complicated impedance plots, characterized by peculiar low frequency behaviors. Preliminary analysis of the experimental impedance spectrum allows one to correlate groups of parameters in each model, or to reduce the initial search space of the algorithm in a valuable way, with beneficial effects on the computational burden. The algorithm is implemented on a low-cost off-the-shelf device, suitable to manage data acquisition in EIS experiments [
3,
31], with a C-language implementation. For the sake of comparison, Matlab implementation results are also shown. The method is validated with literature data in a simulated environment, as well as with experimental data. A good accuracy and low computation times are achieved with commercial embedded system hardware resources, proving that the computational approach fits well with the online/on-board requirements. Finally, from a diagnostic perspective, various experimental impedance plots for a PEM FC stack in normal and faulty conditions are shown. The effects of air and fuel starvation, and of water management issues [
32], are analyzed. Then, a PEM FC diagnostic procedure is outlined on the basis of the identification outcomes.
The paper is organized as follows.
Section 2 briefly recalls three FC stack models used throughout the paper,
Section 3 describes the proposed computation approach to the EA, that is validated in
Section 4 in simulation as well as with experimental results. Then,
Section 5 discusses the diagnostic perspectives of the proposed computational approach. Finally, some conclusions are drawn in
Section 6.
2. Fuel Cell Stack Models
In the neighborhood of a dc operating point, the FC stack can be modeled by various frequency-domain equivalent electric circuits representing the stack impedance. These models are characterized by various capability of reproducing the frequency-domain response of a FC and by various computational complexity, depending on the type of circuit elements included in the circuit.
The simplest circuit model is a linear resistive-capacitive (RC) impedance, that is, an impedance made of a series connection of a linear resistor with a number of RC parallel branches. This number is at least equal to one. The Nyquist-plane impedance plot corresponding to this circuit is characterized by the superposition of some circumference arcs, joined together.
More detailed models, suitable for complex-domain fitting, may include the so-called Warburg impedance and some CPEs in the parallel branches. These complex elements, having no corresponding lumped circuit element in the time-domain, enable one to draw impedance plots characterized by depressed and rectified arcs, typical of electrochemical systems [
9].
Three models for the impedance are described in the following subsections—the RC model, Fouquet model, and Dhirde model. All of them share a linear resistor, , accounting for the losses due to the resistance of the electrolyte to the flow of protons and appearing in series with the rest of the impedance. From a graphical point of view, the presence of this element shifts the impedance plot towards right, for a length equal to . The shape of the plot is determined by the remaining elements appearing in the parallel branches.
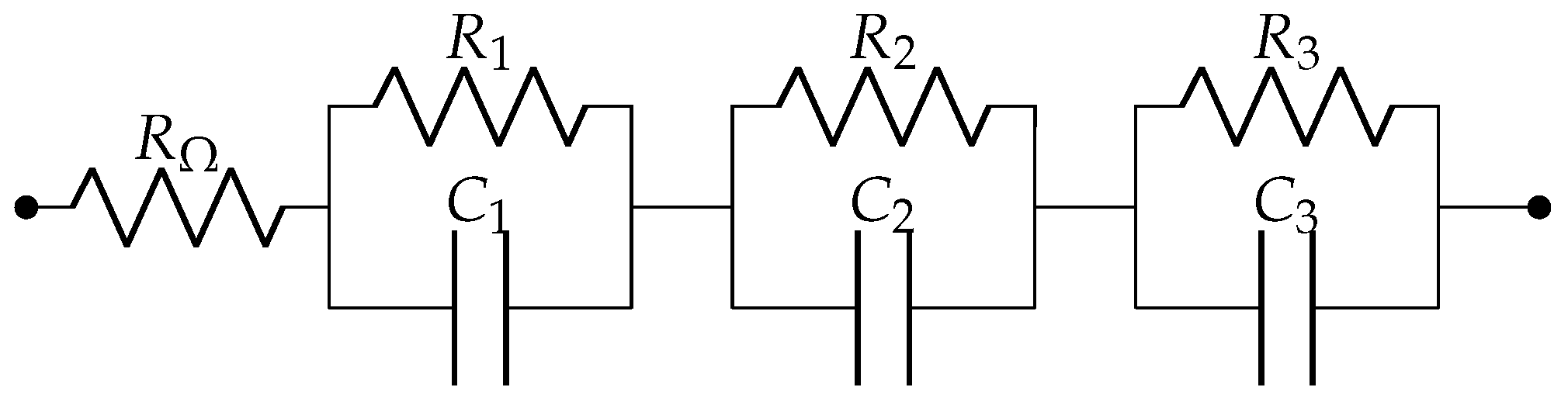
2.1. RC Model
This linear RC model includes the resistor
and a number
of RC parallel branches representing the main system dynamics. The equivalent circuit includes
parameters to be identified on the basis of the experimental impedance measurements at various frequencies. For instance,
Figure 1 shows the third-order linear RC model (
).
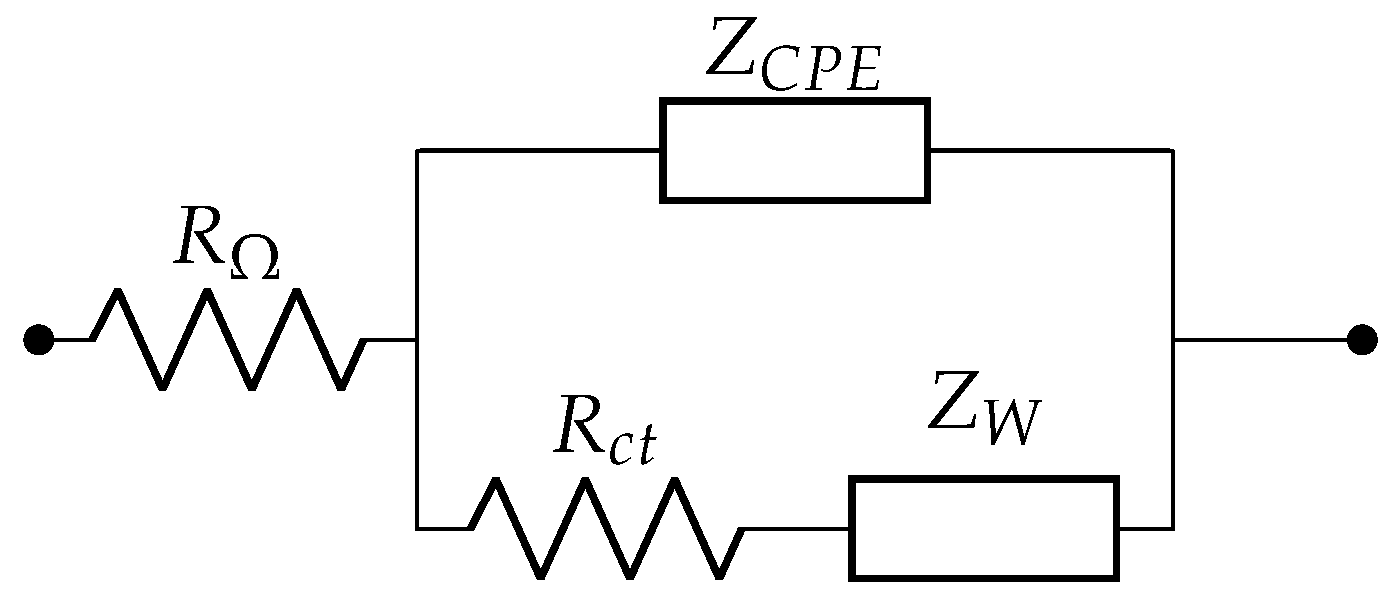
2.2. Fouquet Model
The Fouquet model includes both a CPE:
and a Warburg element:
and neglects anodic phenomena. In (
1) and (
2),
Q and
define the CPE, which represents the behavior of electrodes in the case of rough and porous surfaces. In the Warburg impedance,
accounts for the losses due to the diffusion of reactants, characterized by the time constant
[
14]. The Fouquet impedance is depicted in
Figure 2. Its expression is the following:
Here, is the angular frequency, and is the charge transfer resistance, representing the resistance at the interface electrode/electrolyte to the flow of charges. The Fouquet model is characterized by six parameters ().
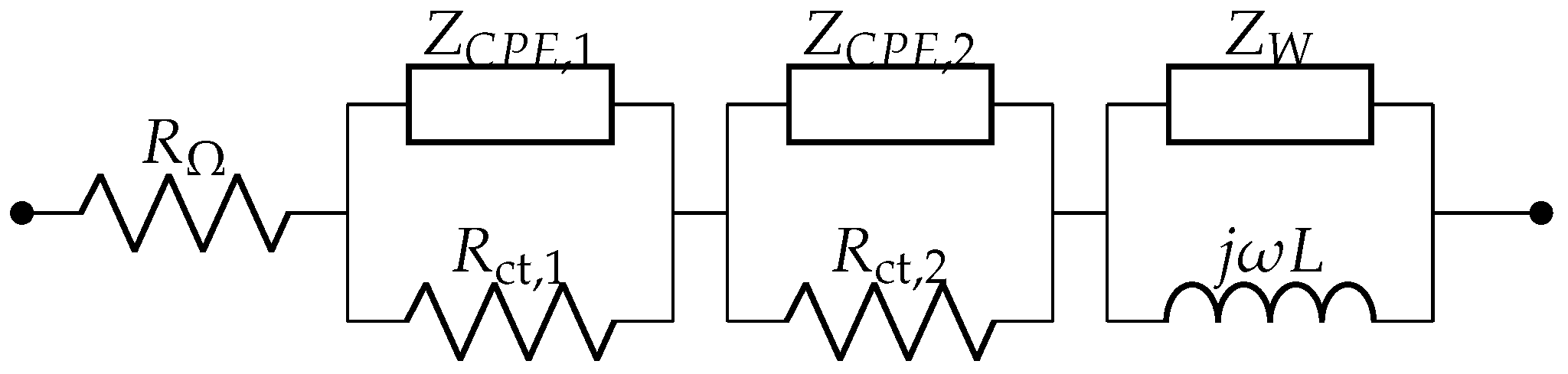
2.3. Dhirde Model
The Dhirde model also includes an inductive element, representing peculiar effects at low frequency. It could be particularly useful to fit a small depressed arc in the low-frequency range of the impedance plot. It was presented for the first time in Reference [
15].
Figure 3 shows the Dhirde impedance, characterized by the presence of a Warburg element connected in parallel with the low frequency inductance and two CPEs. The overall impedance is:
where
is defined in (
2), and
is defined, according to (
1), as:
Here, L represents the low-frequency inductive behavior. The Dhirde model includes parameters.
4. Experimental Results
Two sets of experimental results are used to validate the method. The first set comes from the characterizations of a six-cell assembly with an active area of 150 cm
2, whose results are presented in Reference [
14]. The second set comes from experiments performed in the frame of the H2020 HEALTH-CODE project [
3], characterized by various faults, such as those described in Reference [
40].
The EA runs with a population of
individuals, 4 sub-populations with 50 individuals each, whose
is allowed to migrate from one sub-population to another one. The tournament selection and a single point crossover operators are used, with a crossover probability
. The epoch is fixed at
. The initial mutation probability is
. This value is halved when the population heterogeneity reduces. At each step, given the objective function value
computed for the best individual of the population, the halving is performed as soon as the mean value
of
, computed over the population, falls below the fixed threshold
:
The EA converges when at least one of the following conditions occurs: (i) the number of generations is equal to 10,000; (ii) improvement for 50 successive generations is below ; (iii) the value of the objective function falls below a fixed threshold .
The algorithm is coded both in Matlab and in C language. The latter implementation is aimed at running on an embedded system. Matlab code runs on a PC with Intel Core i7-4720HQ at . The C-language code runs on a Beagle Bone Black (BBB) REV C. The BBB supports a single core AM335x ARM Cortex-A8 processor, and it is equipped with 512 MB DDR3 RAM, 4 GB 8-bit eMMC on-board flash storage, a NEON floating-point accelerator and a 2x PRU 32-bit microcontrollers. Debian 7.9 OS runs on the board. In the tables showing the results, BBB times are reported. Matlab computation times are also included as reference values.
4.1. Validation by Literature Data with RC and Fouquet Model
In this test, the FC behavior is simulated to obtain the set of experimental impedance points
for all
k. To this aim, the Fouquet model is run in
M frequency points by using the following data:
,
,
,
,
,
. These data are taken from Reference [
34].
Once the reference experimental impedance
has been obtained for all
k, the EA is run to identify the parameters of the three models described in
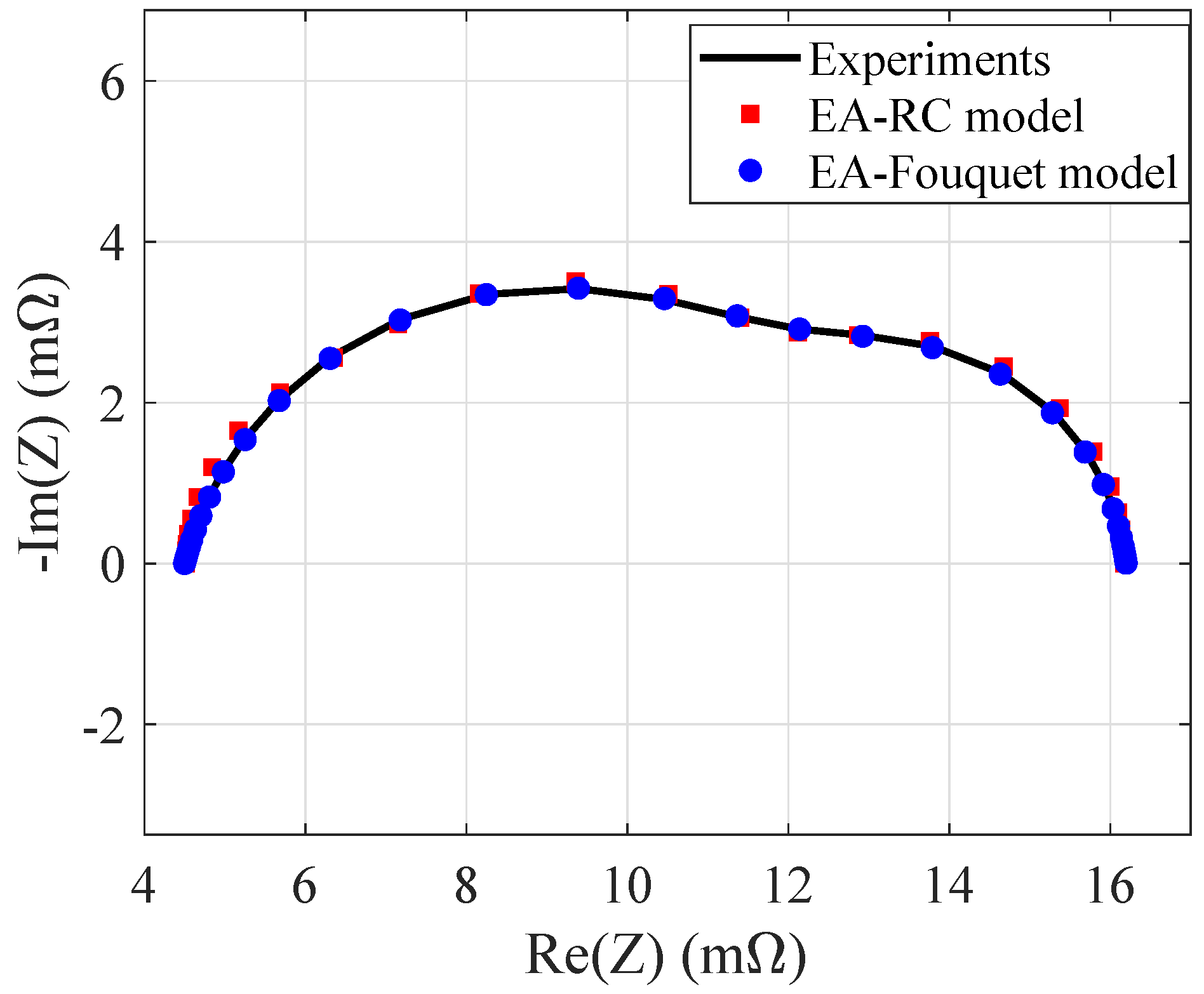
Section 2. The most interesting results are obtained by using the RC model and the Fouquet model. The results reported in
Table 1 (for RC model) and in
Table 2 (for Fouquet model) are graphically shown in
Figure 4. For each parameter, the best individual, the mean one and its standard deviation
are listed. The mean individual and the standard deviation are computed over 100 independent EA runs. These runs are launched by starting from a randomly-generated initial population. Considering the results of the Fouquet model in the best case (see
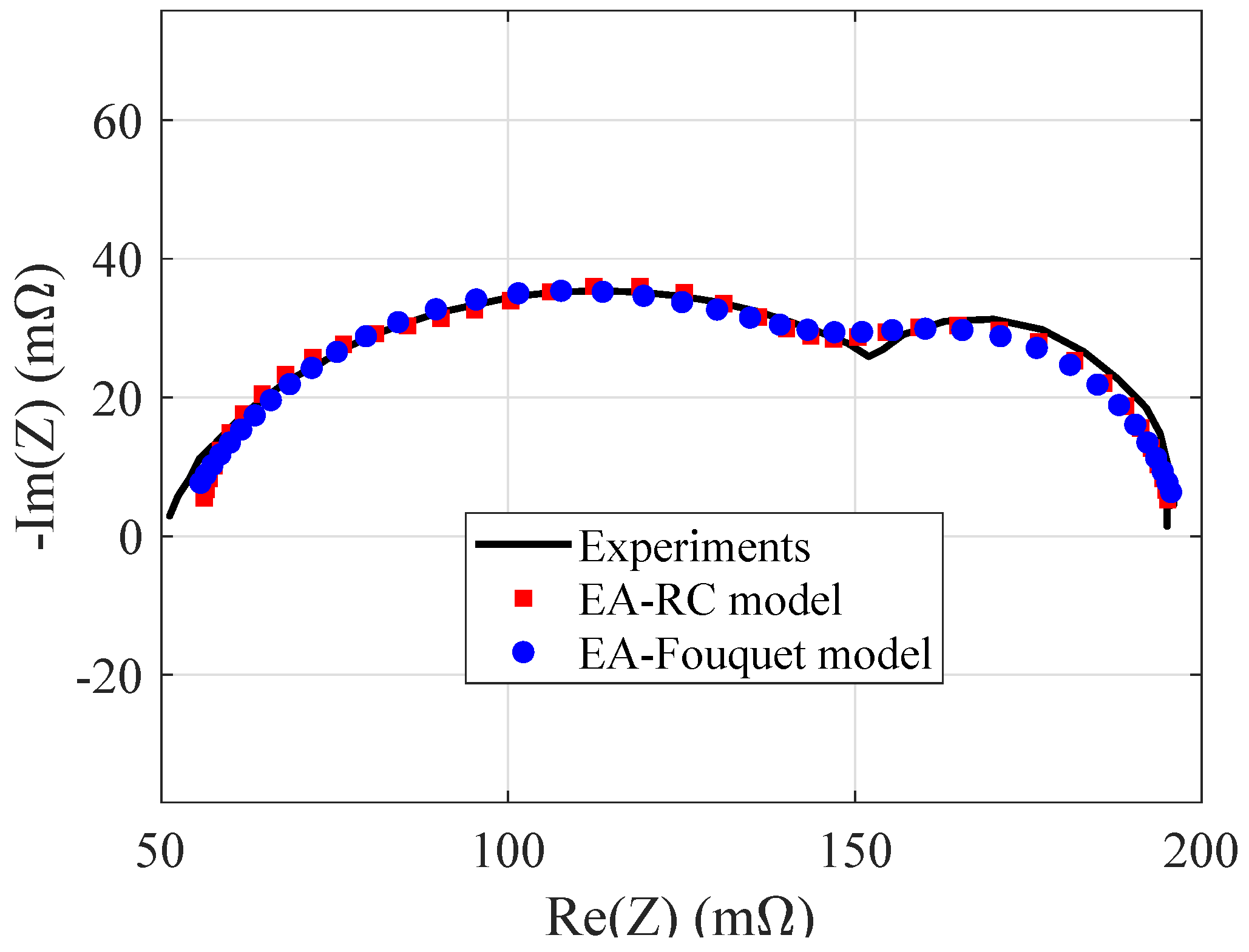
Table 2), they are very close to the ones used to generate the reference plot. The computation time required by the C-language implementation is reported in the second part of the Tables. The Matlab time is also given for comparison purposes. It is worth highlighting that Matlab implementation benefits from many built-in functions.
Figure 4 shows the impedance plots corresponding to the best individuals. The identification results achieved by both models satisfactorily fit the reference plot. The presence of two arcs is correctly detected. The Fouquet model is characterized by higher fitting fidelity, whose measure is the
value. Indeed, in the best Fouquet case,
is lower than the one obtained by means of the RC model. The success rate of the EA is 96% for Fouquet model. This leads to an apparent spread of the solutions over a wide interval, as suggested by the
value affecting
in
Table 2, as well as some parameters. Indeed, in this case, the mean value and the standard deviation are very close to one another. This happens both to the objective function and to some parameters. Excluding the 4 unsuccessful cases over 100, in which the EA shows a premature convergence to a local optimum, the mean value of
becomes very close to the best one, with a standard deviation that drops below
. The standard deviation of the parameters changes accordingly.
Looking at the computation time required by the BBB device to run the EA, the average time required to run the RC model is 70% less than the time required to run the Fouquet model. Indeed, the Fouquet model shows a higher computational burden with respect to the RC model because of its non-linearity, and this aspect has a significant impact especially on the embedded system implementation. Conversely, the RC circuit represents a good compromise between the fitting accuracy of the impedance spectrum and the computation time.
4.2. Validation by Experimental Dataset A with RC and Fouquet Model
Further analyses are performed by using experimental data. The
dataset A collects the data obtained in the framework of the H2020 HEALTH-CODE project [
3], by testing a 46-cell PEM FC stack from Ballard Power System (see
Figure 5). The stack was tested at
, and
, under nominal and faulty conditions: cathode and anode drying, hydrogen starvation, and oxygen starvation are considered. The nominal operating conditions were defined by inlet gases’ relative humidity of 83%, and respective anodic and cathodic overstoichiometric ratios of 1.3 and 2. In all the experiments, the fuel was a mixture of 76% H
, 20% CO
and 4% N
, a composition similar to a reformate gas produced on-board by an alternative carbon-based fuel, such as methanol. The use of reformate gas seems to be more practical than considering pure hydrogen.
Figure 6 shows the good identification performed by both models, with a computation time required by the BBB within
, on average. The two-arcs shape of the impedance plot is quite accurately detected by both models.
Table 3 and
Table 4 report on the results. Again, the computation time required by the RC model is lower than the one obtained with Fouquet model, confirming that C-language implementation suffers from the presence of complex-valued elements, such as the CPEs.
4.3. Validation by Experimental Dataset B with Dhirde Model
The
dataset B is a further set of experimental results used for the validation. The data were acquired by the same test-bed described in
Section 4.2. The low-frequency behavior is characterized by a peculiar shape, which does not allow to achieve low values of
when RC model or Fouquet model are used. To address this problem, the identification of this dataset is carried out by using the Dhirde model, implemented in Matlab. Dhirde model is characterized by
parameters. In this case, the EA runs with a population larger than the ones used before:
individuals.
Compared to previous analyses, considering the valuable increase of both the population and the number of parameters, identification times are expected to be substantially higher.
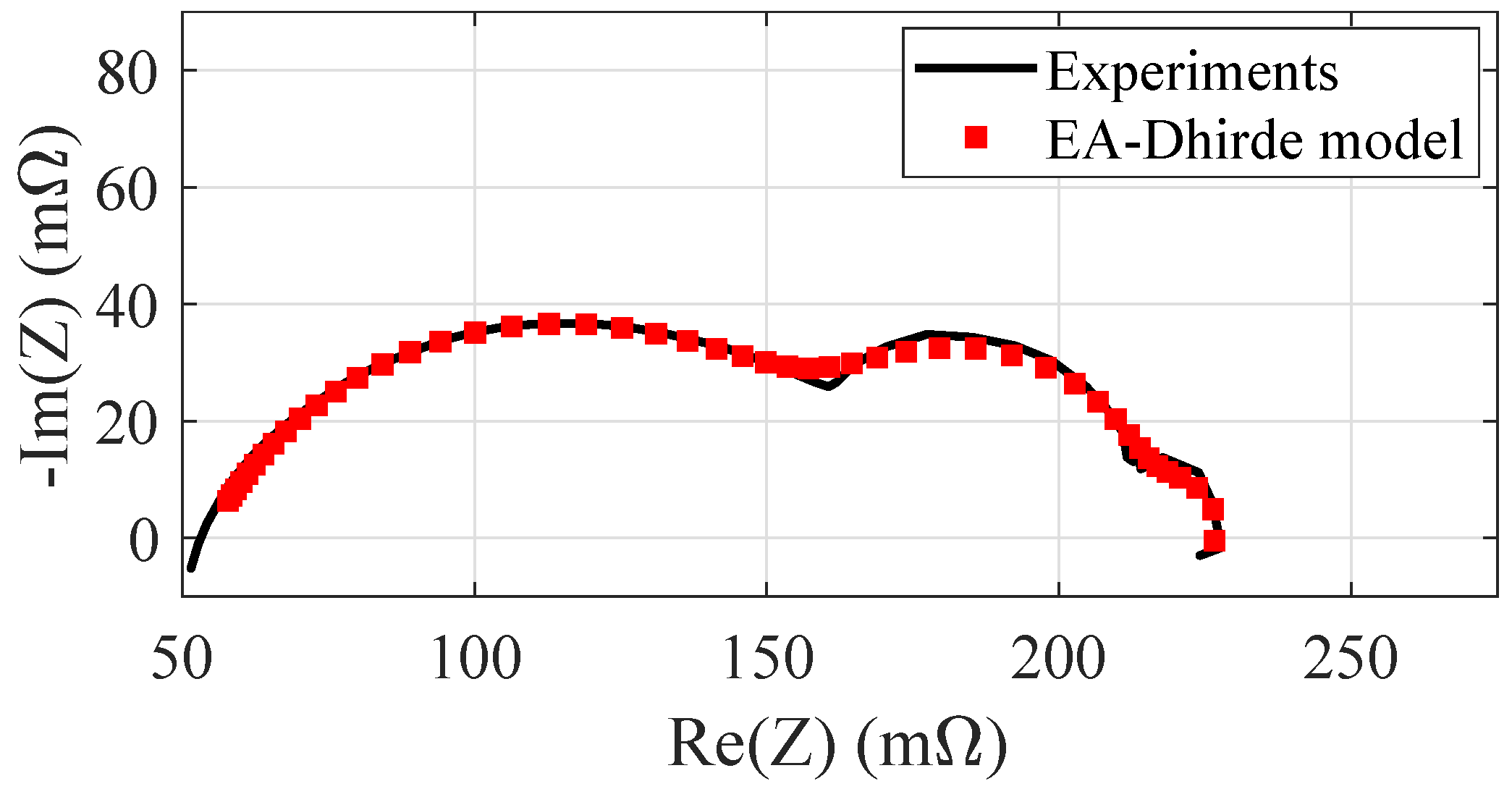
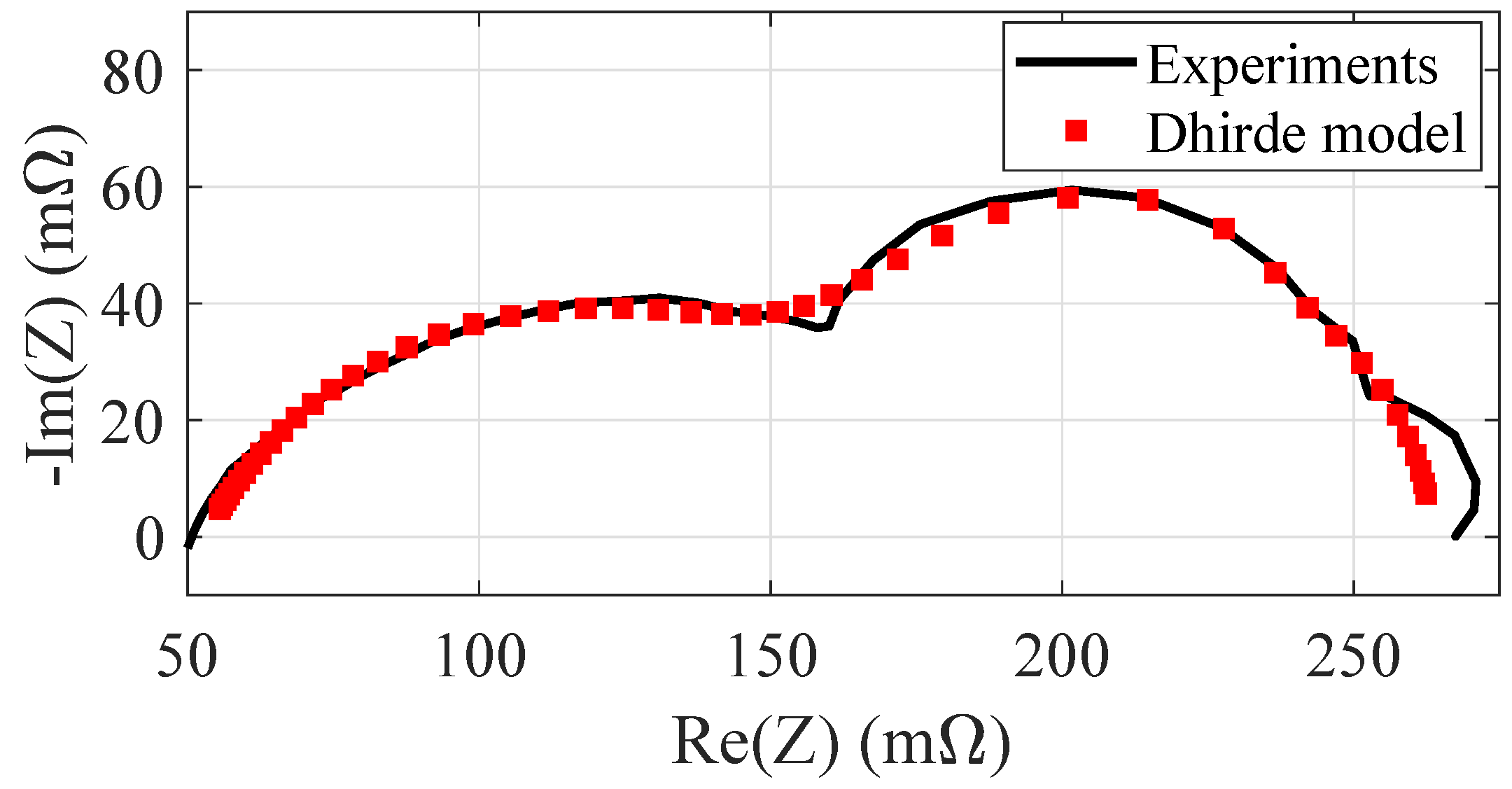
Figure 7 shows the identification results achieved by the Dhirde model when the FC stack works in nominal conditions at
. The right hand side of the plot clearly shows the good fit achieved by the Dhirde model in the presence of a third arc located in the low frequency range.
Table 5 summarizes the identification results over 100 independent EA runs, as already done in previous tables. The computation time required by the EA with Dhirde model is obviously higher than the Fouquet or RC ones. As a future perspective, in order to tackle this point and reduce the computation time, the intrinsic parallel evolution of the sub-populations can be exploited and a part of the EA can be parallelized.
5. Identification Oriented to Diagnostics
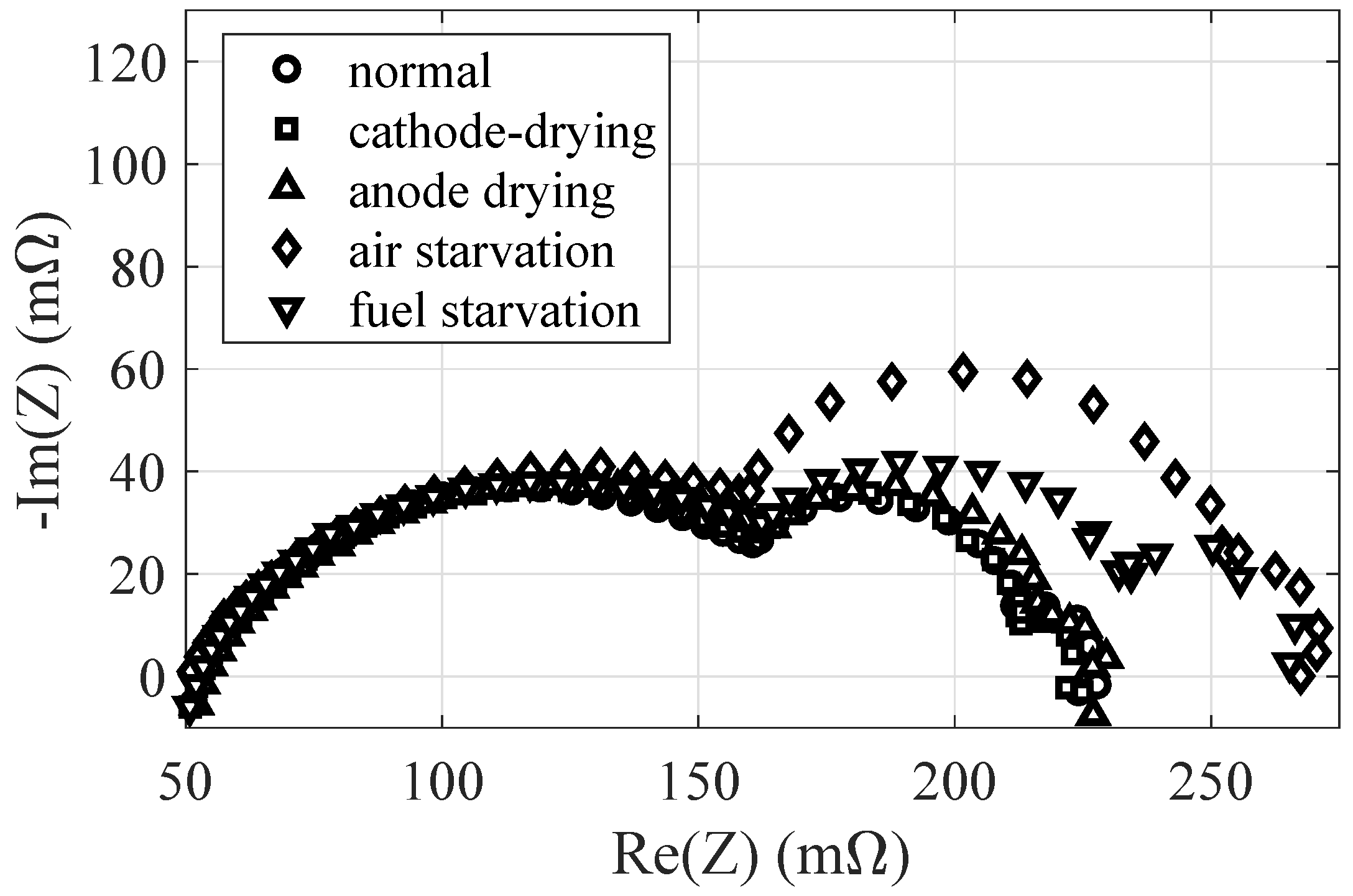
In order to capture how the variations of Dhirde model parameters can be correlated to faults, more spectra are identified both in normal and faulty operating conditions. This is done in a diagnostic perspective. As already mentioned in
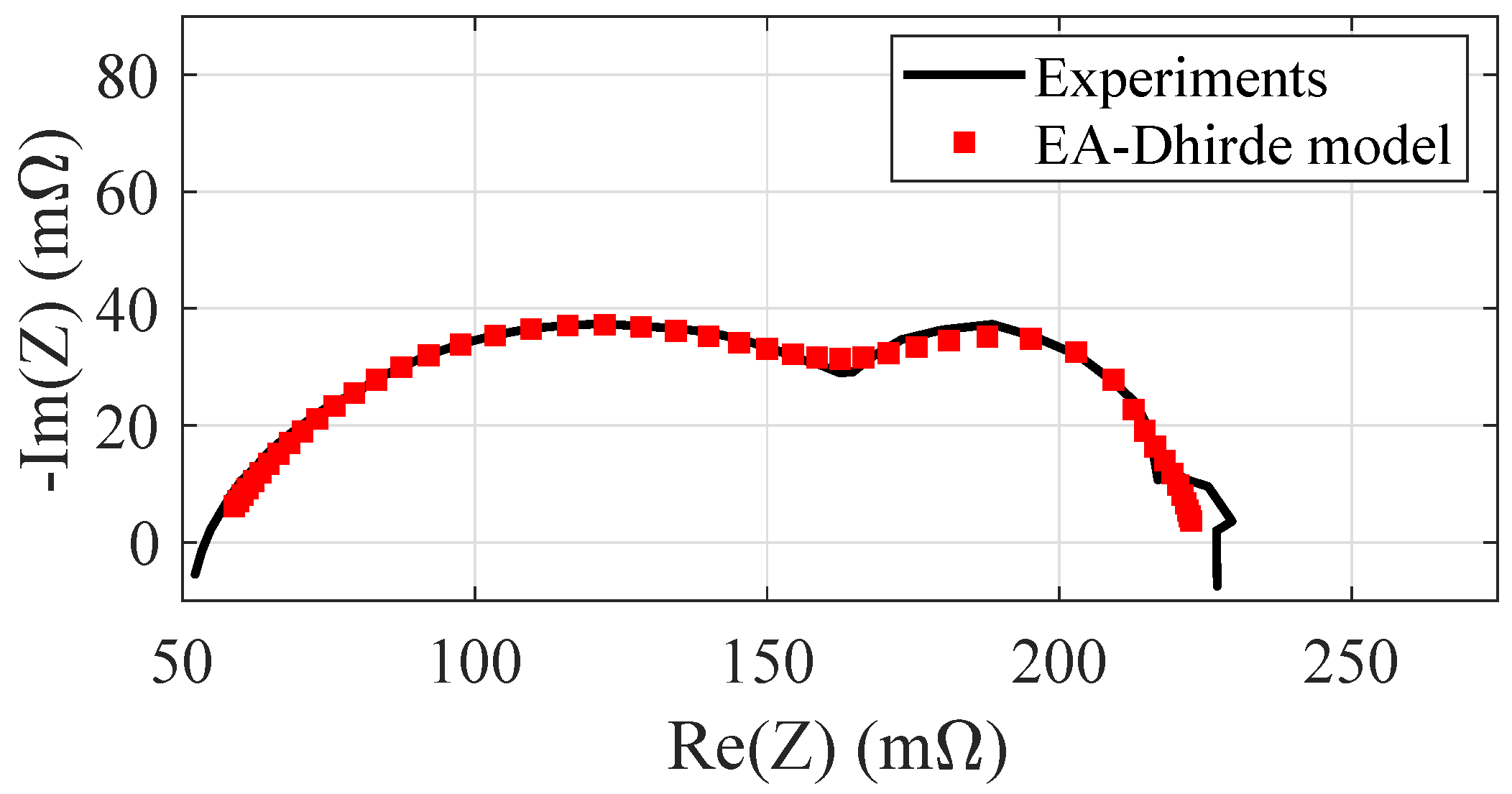
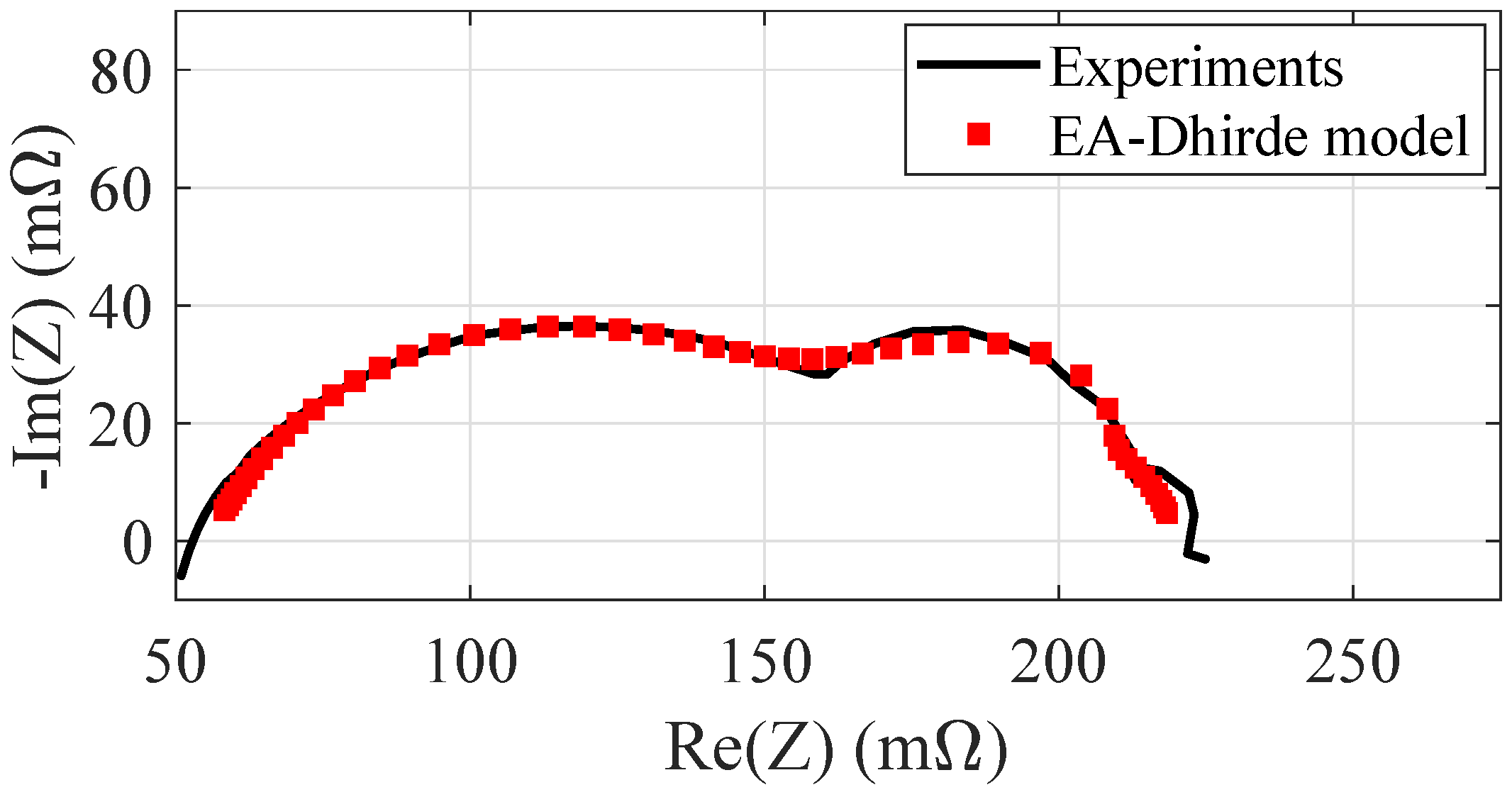
Section 4.3, the Dhirde model appears the most suitable one for this kind of identification problem, having already shown good identification capabilities in the presence of the low-frequency third arc. Here, the following faults are considered—cathode and anode drying (see
Figure 8 and
Figure 9), air and fuel starvation (see
Figure 10 and
Figure 11). In these figures, each identified spectrum is compared to the experimental one. The analysis is carried out again through Matlab only. In order to compare the various behaviors in normal and faulty conditions, the whole set of experimental data is shown in a comprehensive way in
Figure 12. Using the Dhirde model, the parameters are identified by the EA in all faulty cases, ending up with the values reported in
Table 6. The arrows highlight the main parameter variations with respect to the normal condition. The number of arrows is related to the magnitude of variation for each parameter, as detailed in the caption of
Table 6.
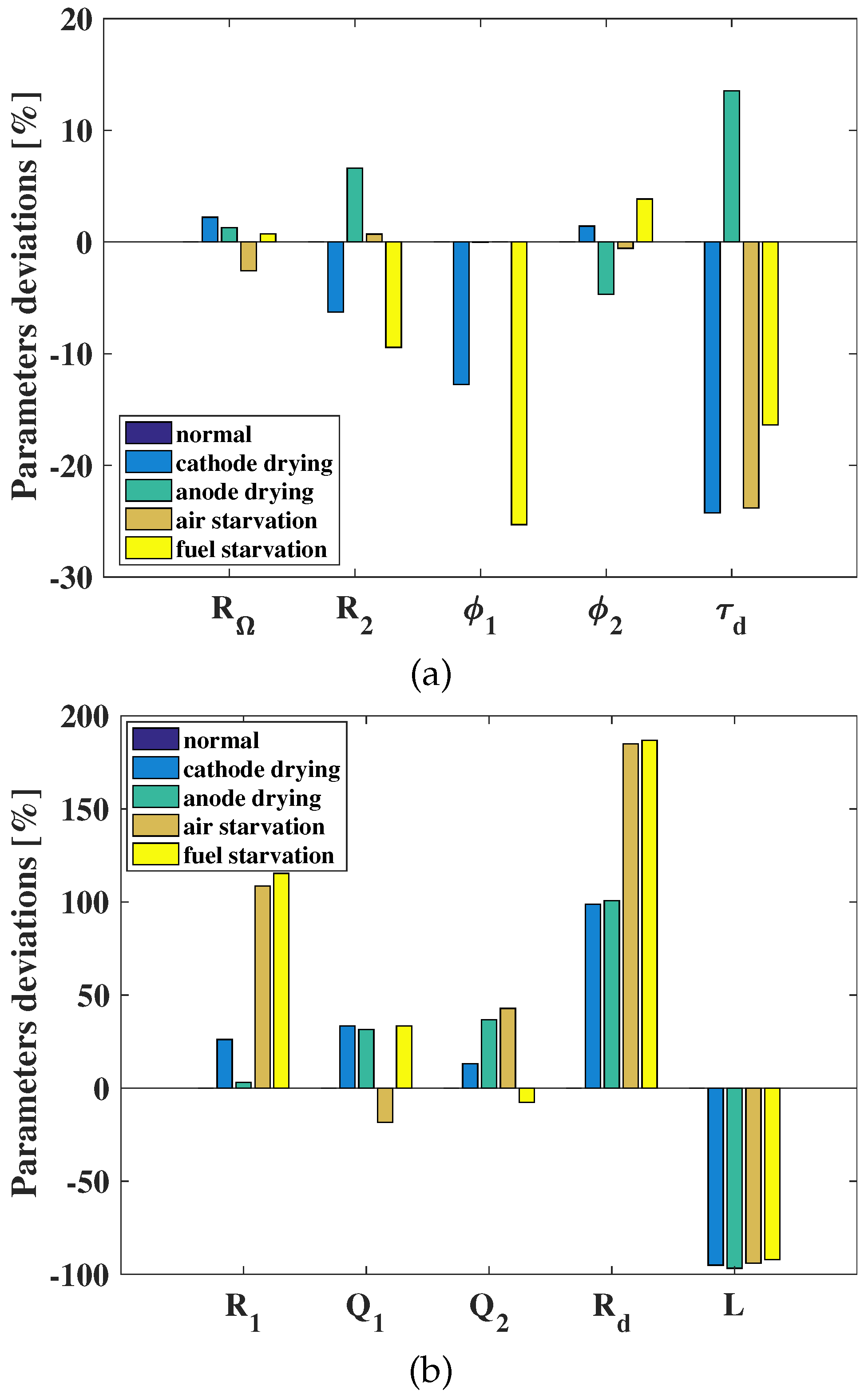
Figure 13 shows the same variation in a pictorial and more intuitive way.
Figure 13a shows the parameters exhibiting low variations, while
Figure 13b shows those ones characterized by high variation. Each bar represents the percent variation of each parameter appearing in the Dhirde model with respect to normal operating conditions. The different colors refer to the analyzed fault conditions. These figures reveal that, according to the Dhirde model, all the faults considered are characterized by a significant reduction of
L and an increase of
. Briefly:
If this happens, and if an increase of occurs, then a drying fault is detected:
Alternatively, in the presence of a strong increase of , a starvation fault is detected:
Moreover, in drying fault conditions, the strong increase or decrease of allows one to distinguish between cathode and anode drying, respectively:
Finally, in starvation conditions, the parameter indicates whether air or fuel starvation is occurring. Briefly:
All the variations highlighted in
Table 6 or
Figure 13 could be used to define fault conditions. Such a method points out the diagnostic potential of the EA computational approach. At present, the diagnostic method is sketched on the basis of very few experiments. Further work is needed to extensively test the identification capability of the EA algorithm, which deeply affects the reliability of the diagnostic procedure. This should be done on the basis of a wider experimental dataset, in which more experimental data are available for each single fault. On the basis of a comprehensive statistics, which is beyond the scope of this paper, the aforementioned methodology should be refined and integrated.
6. Conclusions
In this paper, an evolutionary computation approach to the identification of the impedance parameters of polymeric electrolyte membrane fuel cells is proposed for online/on-board electrochemical impedance spectroscopy experiments. The identification of the impedance parameter is formulated as an optimization problem and solved with an evolutionary algorithm. The knowledge of high- and low-frequency intercepts of the impedance plot with real axis allows one to define some constraints among parameters or to reduce the algorithm search space. The use of sub-populations and migration among sub-populations attain good exploration of the search space and represent a promising solution.
Many tests validate the computational approach by using both simulated and experimental data. Accurate experimental data fitting, with an error lower than , is achieved, especially by using the Fouquet model for fuel cell impedance. A few milliseconds, or even less, are required to identify the set of parameters when the algorithm runs on a low-cost off-the-shelf embedded system. The lowest computation times are achieved by using a linear resistive-capacitive model. The identification time is very short, making this computational approach to the evolutionary algorithm suitable for online and on-board applications.
From the perspective of a fuel cell stack diagnosis based on estimated impedance parameter, both normal and faulty condition data are identified. This is done to study whether the faults can be detected on the basis of parameter variations with respect to normal conditions.
Further work is in progress in order to implement the evolutionary algorithm in an embedded system with hardware parallel computation capabilities, such as a field programmable gate array. This will enable a parallel objective function computation for many individuals or, additionally, a parallel evolution of the sub-population. In this way, a further reduction of the identification time is expected. Concerning the fault detection procedure outlined in this paper, a further effort is aimed at improving it on the basis of more experimental data, in order to increase its robustness and reliability.
References