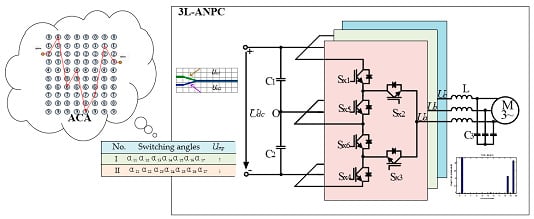
Neutral-Point Potential Balancing Control Strategy for Three-Level ANPC Converter Using SHEPWM Scheme
Abstract
:1. Introduction
2. 3L-ANPC Converter and SHEPWM
2.1. Principle of 3L-ANPC Converter
2.2. Three-Level SHEPWM
3. Chaotic Ant Colony Algorithm and Solving SHEPWM Equation
3.1. Variable-scale Chaotic Ant Colony Algorithm
- (1)
- A chaotic series are embedded into the solutions getting from ACA. After all ants have completed solution construction, the global best ant will be evaluated. The chaos optimization algorithm is used to search within a certain radius of the independent variable of the best ant, and the search radius will be reduced with the iteration. If a better solution is found, it will be decoded into a string of decimal numbers and replaced the best ant.
- (2)
- In order to search only nearby the best ant, the interval of chaotic series is transformed from (0, 1) to (−r, r) by a linear transformation. Then, the transformed series are embedded into the solution getting from the best ant, so new series are found.
- (3)
- The last is a variable radius problem. By adding the variable-scale algorithm to the chaotic ACA, the search scope can expand at the start stage to avoid getting into local optimum, at the same time, it can narrow the search scope at the later stage, so as to improve the search precision.The variable-scale formula is used by Sigmoid formula [23], as follows,
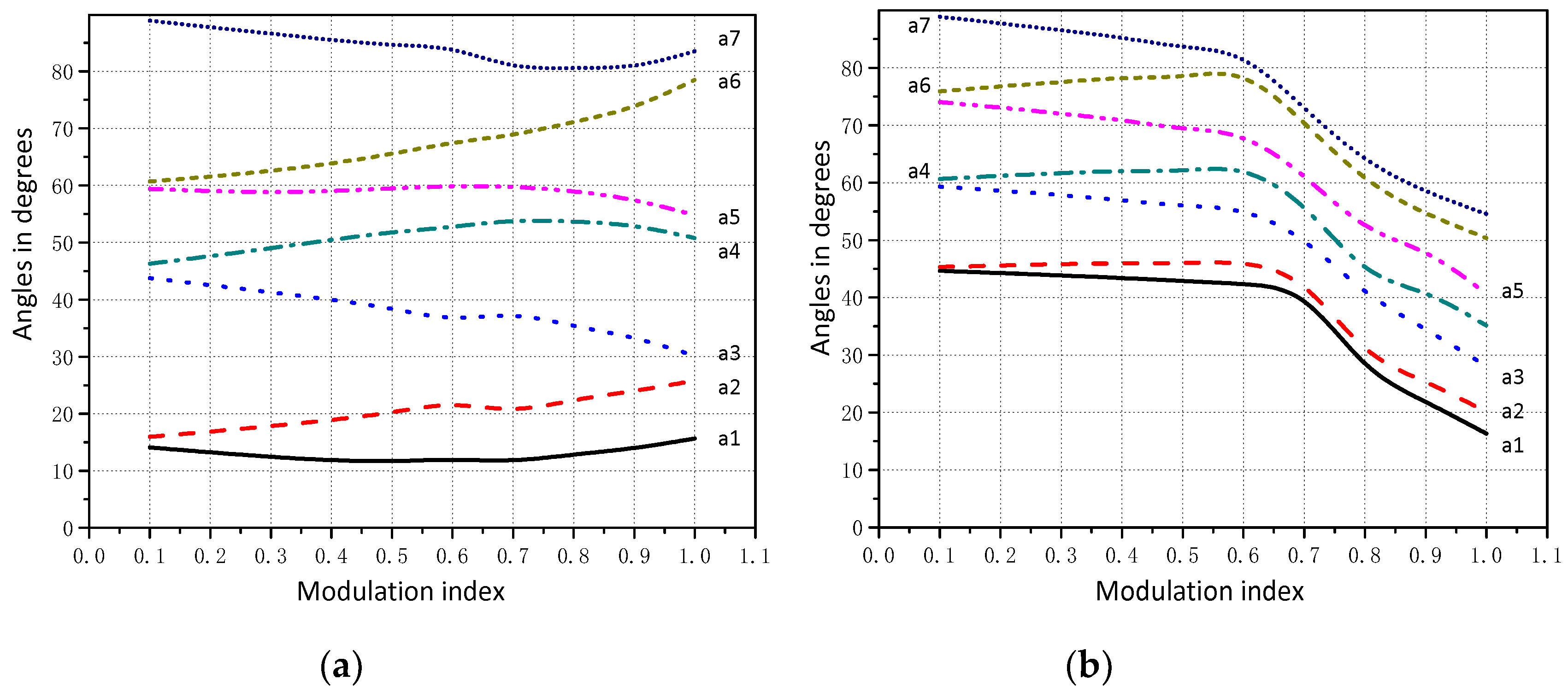
3.2. Solving SHEPWM Nonlinear Equations
4. Control Strategy of NP Balancing
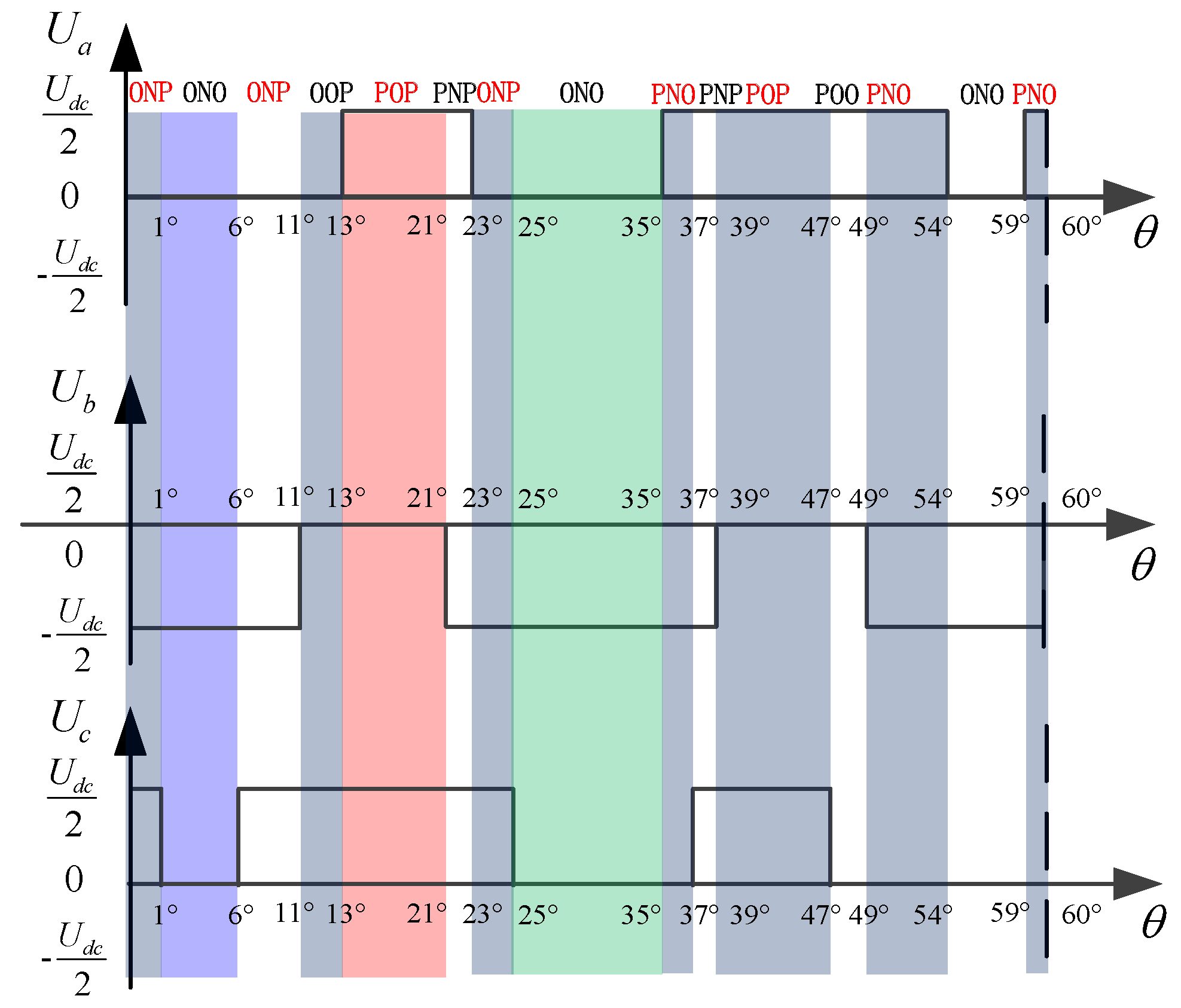
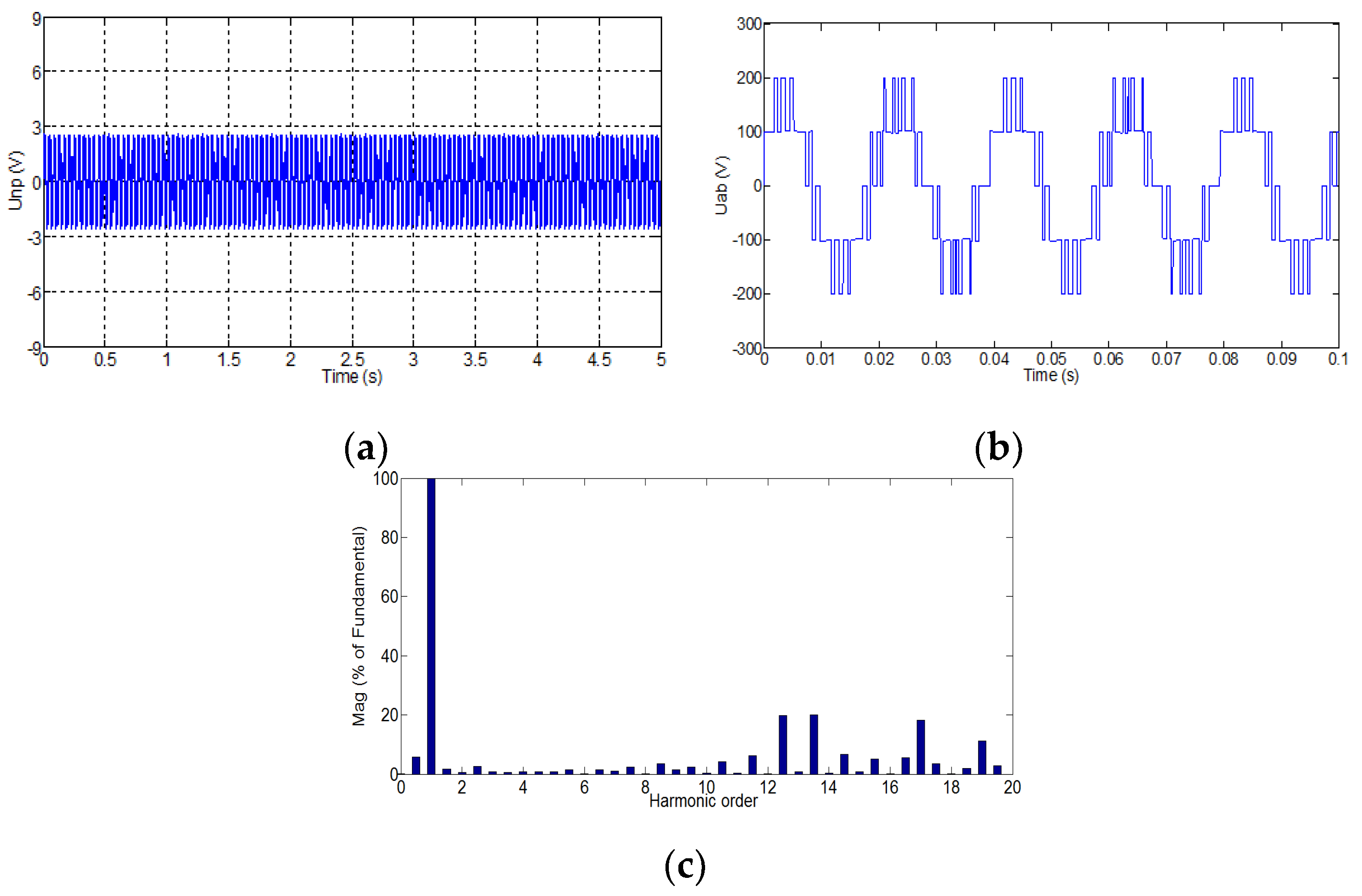
4.1. Effect on NP with Different SHEPWM Switching Angles
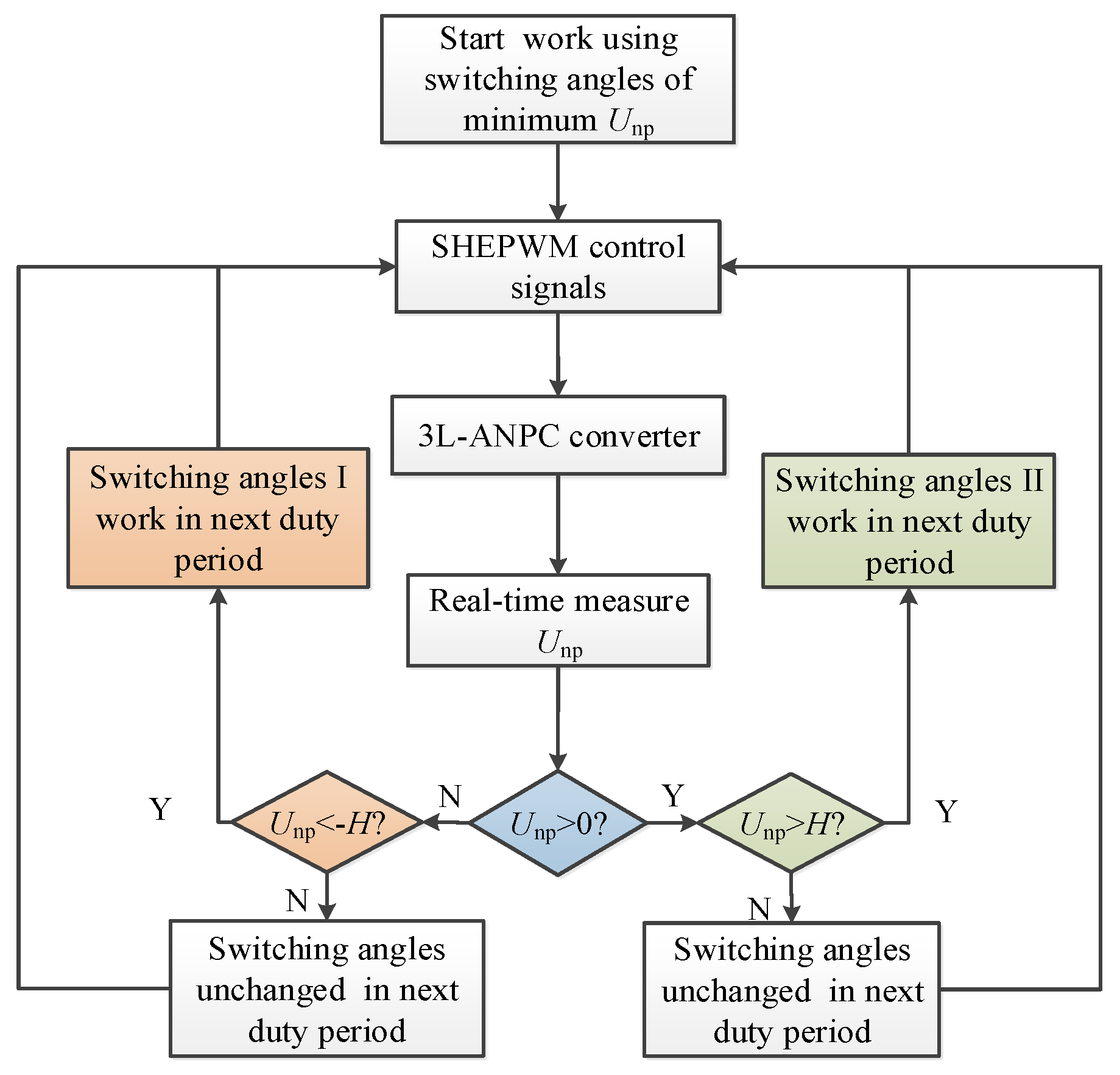
4.2. Voltage Balancing Strategy
- (1)
- When Unp < −H: Select the switching angles I as SHEPWM switching angles in next fundamental period .
- (2)
- When Unp > H: Select the switching angles II as SHEPWM switching angles in next fundamental period.
- (3)
- When |Unp| < H: Switching angles unchanged in next duty period.
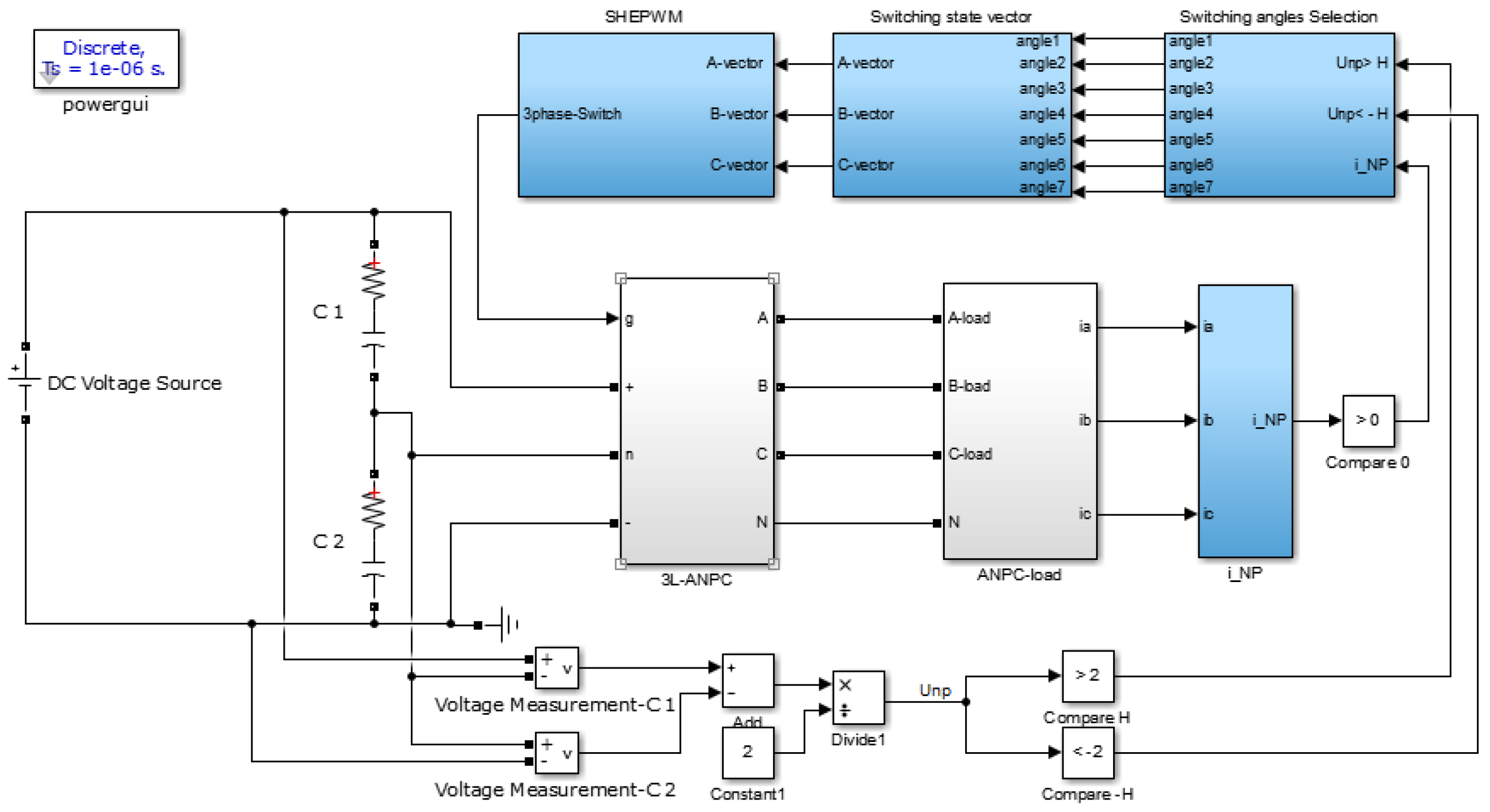
5. Simulation and Experiment
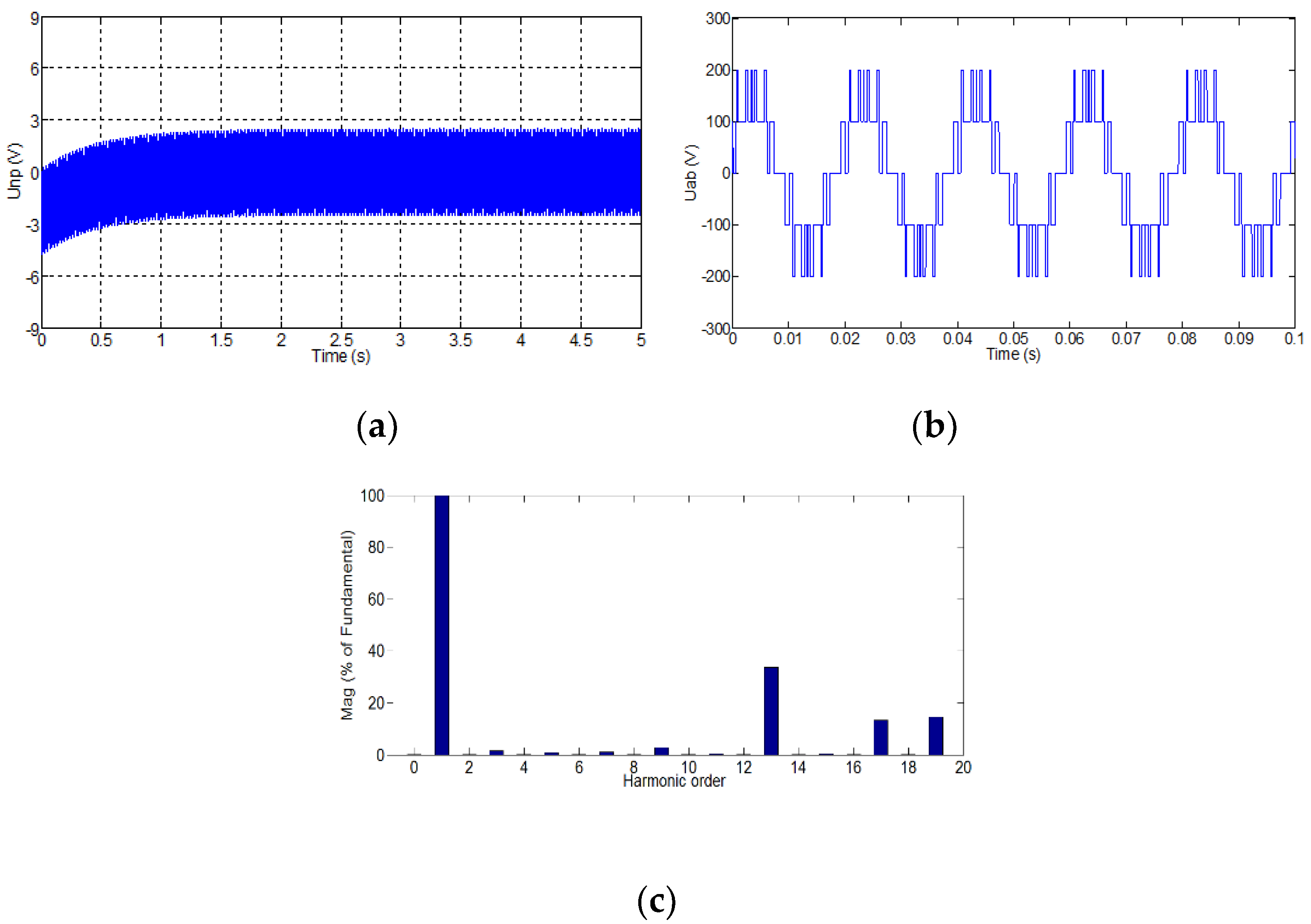
5.1. Simulation Results
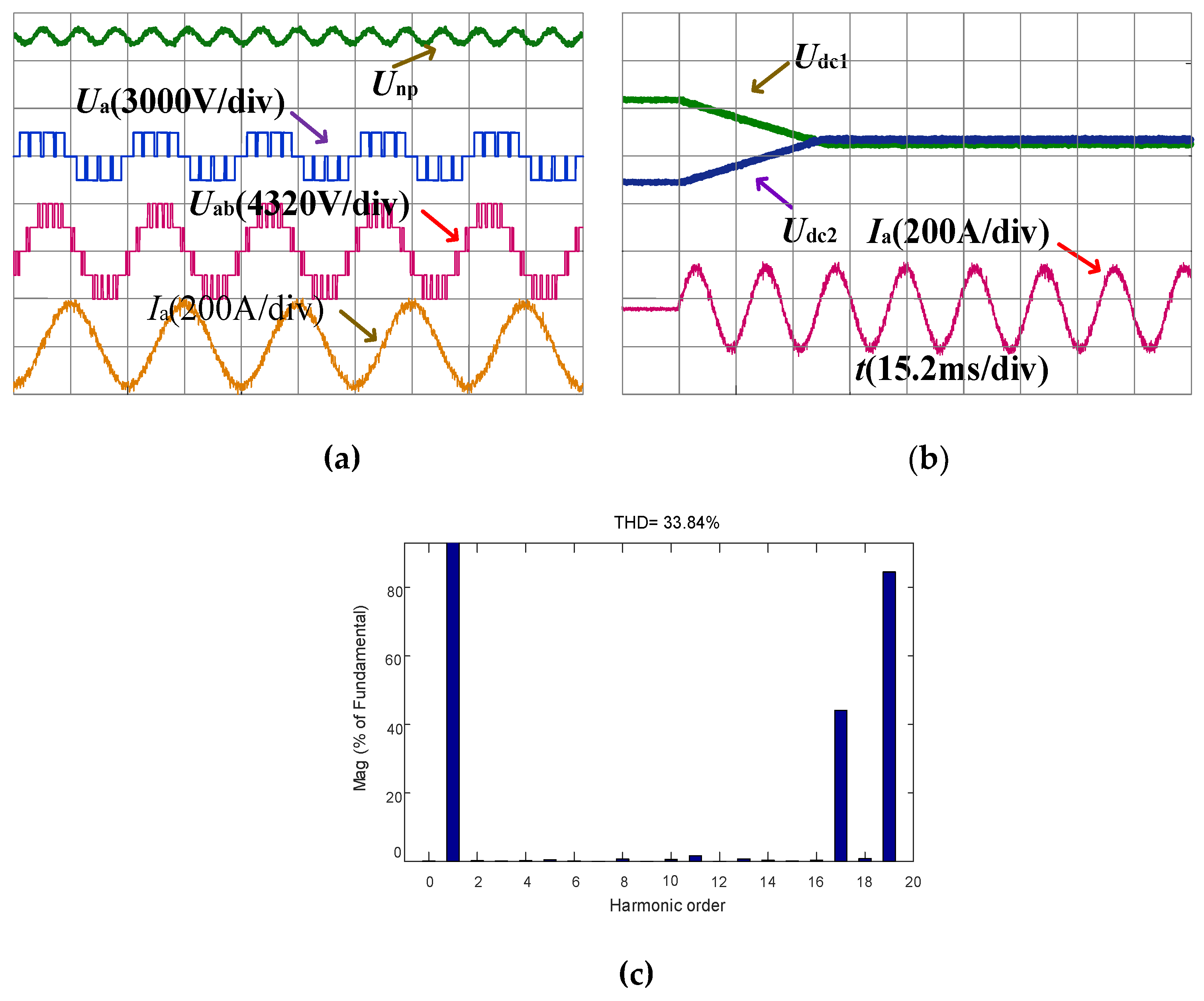
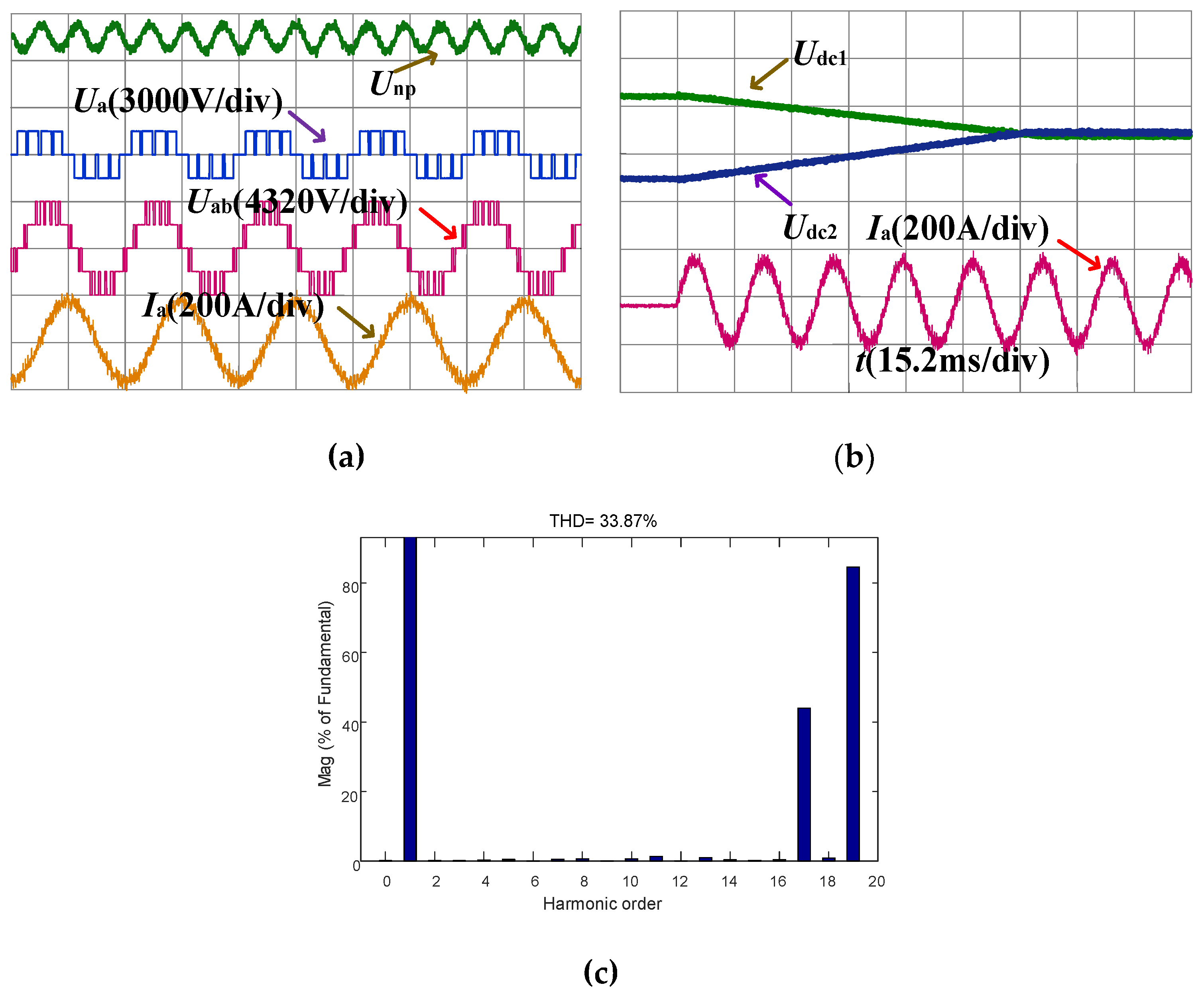
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nabae, A.; Takahashi, I.; Akagi, H. A new neutral-point-clamped PWM inverter. IEEE Trans. Ind. Appl. 1981, 17, 518–523. [Google Scholar] [CrossRef]
- Bruckner, T.; Bernet, S.; Steimer, P. Feedforward loss control of 3L active NPC converters. IEEE Trans. Ind. Appl. 2007, 43, 1588–1596. [Google Scholar] [CrossRef]
- Sayago, J.A.; Bruckner, T.; Bernet, S. Comparison of medium voltage IGBT-based 3L-ANPC-VSCs. In Proceedings of the IEEE PESC, Rhodes, Greece, 15–19 June 2008; pp. 851–858. [Google Scholar]
- Ogasawara, S.; Akagi, H. Analysis of variation of neutral point potential in neutral point clamped voltage source PWM inverters. In Proceedings of the Conference Record of the 1993 IEEE Industry Applications Conference Twenty-Eighth IAS Annual Meeting, Toronto, ON, Canada, 2–8 October 1993; pp. 965–970. [Google Scholar]
- Yazdani, A.; Iravani, R. A generalized state-space averaged model of the 3L NPC converter for systematic dc-voltage-balancer and current-controller design. IEEE Trans. Power Deliv. 2005, 20, 1105–1114. [Google Scholar] [CrossRef]
- Maheshwari, R.; Munk-Nielsen, S.; Busquets-Monge, S. Design of Neutral-Point Voltage Controller of a 3L NPC Inverter with Small DC-Link Capacitors. IEEE Trans. Ind. Electron. 2013, 60, 1861–1871. [Google Scholar] [CrossRef]
- Hornik, T.; Zhong, Q. Parallel PI Voltage–H-infinity Current Controller for the Neutral Point of a Three-Phase Inverter. IEEE Trans. Ind. Electron. 2013, 60, 1335–1343. [Google Scholar] [CrossRef]
- Yamanaka, K.; Hava, A.M.; Kirino, H.; Tanaka, Y.; Koga, N.; Kume, T. A novel neutral point potential stabilization technique using the information of output current polarities and voltage vector. IEEE Trans. Ind. Appl. 2002, 38, 1572–1580. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J. A Method for the Suppression of Fluctuations in the Neutral-Point Potential of a Three-Level NPC Inverter with a Capacitor-Voltage Loop. IEEE Trans. Power Electron. 2017, 32, 825–836. [Google Scholar] [CrossRef]
- Wu, F.; Feng, F.; Duan, J.; Sun, B. Zero Crossing Disturbance Elimination and Spectrum Analysis of Single-Carrier Seven Level SPWM. IEEE Trans. Ind. Electron. 2015, 62, 982–990. [Google Scholar] [CrossRef]
- Xiang, C.; Shu, C. Improved Virtual Space Vector Modulation for Three-Level Neutral-Point-Clamped Converter with Feedback of Neutral-Point Voltage. IEEE Trans. Power Electron. 2018, 33, 5452–5464. [Google Scholar] [CrossRef]
- Wu, X.; Tan, G. Virtual-Space-Vector PWM for a Three-Level Neutral-Point-Clamped Inverter with Unbalanced DC-Links. IEEE Trans. Power Electron. 2018, 33, 2630–2642. [Google Scholar] [CrossRef]
- Hu, C.; Yu, X. An Improved Virtual Space Vector Modulation Scheme for Three-Level Active Neutral-Point-Clamped Inverter. IEEE Trans. Power Electron. 2017, 32, 7419–7434. [Google Scholar] [CrossRef]
- Monge, S.B.; Somavilla, S.; Bordonau, J.; Boroyevich, D. Capacitor voltage balance for the neutral-point-clamped converter using the virtual space vector concept with optimized spectral performance. IEEE Trans. Power Electron. 2007, 22, 1128–1135. [Google Scholar] [CrossRef]
- Du Toit Mouton, H. Natural Balancing of 3L Neutral-Point-Clamped PWM Inverters. IEEE Trans. Ind. Electron. 2002, 49, 1017–1025. [Google Scholar] [CrossRef]
- Memon, M.A.; Mekhilef, S.; Mubin, M. Selective harmonic elimination in multilevel inverter using hybrid APSO algorithm. IET Power Electron. 2018, 11, 1673–1680. [Google Scholar] [CrossRef]
- Memon, M.A.; Mekhilef, S.; Mubin, M.; Aamir, M. Selective harmonic elimination in inverters using bio-inspired intelligent algorithms for renewable energy conversion applications: A review. Renew. Sust. Energy 2018, 82, 2235–2253. [Google Scholar] [CrossRef]
- Yang, K.; Feng, M.; Wang, Y.; Lan, X.; Wang, J.; Zhu, D.; Yu, W. Real-Time Switching Angle Computation for Selective Harmonic Control. IEEE Trans. Power Electron. 2019, 34, 8201–8212. [Google Scholar] [CrossRef]
- Haghdar, K. Optimal DC Source Influence on Selective Harmonic Elimination in Multilevel Inverters Using Teaching-Learning Based Optimization. IEEE Trans. Ind. Electron. 2019, 67, 942–949. [Google Scholar] [CrossRef]
- Colorni, A.; Dorigo, M.; Maniezzo, V. Distributed optimization by ant colonies. In Proceedings of the First European Conference on Artificial Life; Elsevier Science Publisher: Amsterdam, The Netherlands, 1992; pp. 134–142. [Google Scholar]
- Oshaba1, A.S.; Ali, E.S.; Abd Elazim, S.M. Speed control of SRM supplied by photovoltaic system via ant colony optimization algorithm. Neural Comput. Appl. 2017, 28, 365–374. [Google Scholar] [CrossRef]
- Han, Y.; Shi, P. An improved ant colony algorithm for fuzzy clustering in image segmentation. Neurocomputing 2007, 70, 665–671. [Google Scholar] [CrossRef]
- Hu, C.; Wang, Q.; Jiang, W.; Chen, Q.; Xia, Q. Optimization Method for Generating SHEPWM Switching Patterns Using Chaotic Ant Colony Algorithm applied to Three-level NPC Inverter. In Proceedings of the 2007 International Conference on Electrical Machines and Systems (ICEMS), Seoul, Korea, 8–11 October 2007; pp. 149–153. [Google Scholar]
- Li, H.; Wang, S.; Ji, M. An Improved Chaotic Ant Colony Algorithm. Adv. Neural Net. 2012, 7367, 633–640. [Google Scholar]
- Zhang, X.H.; Yue, W.K. Neutral point potential balance algorithm for three-level NPC inverter based on SHEPWM. Electron. Lett. 2017, 53, 1542–1543. [Google Scholar] [CrossRef]
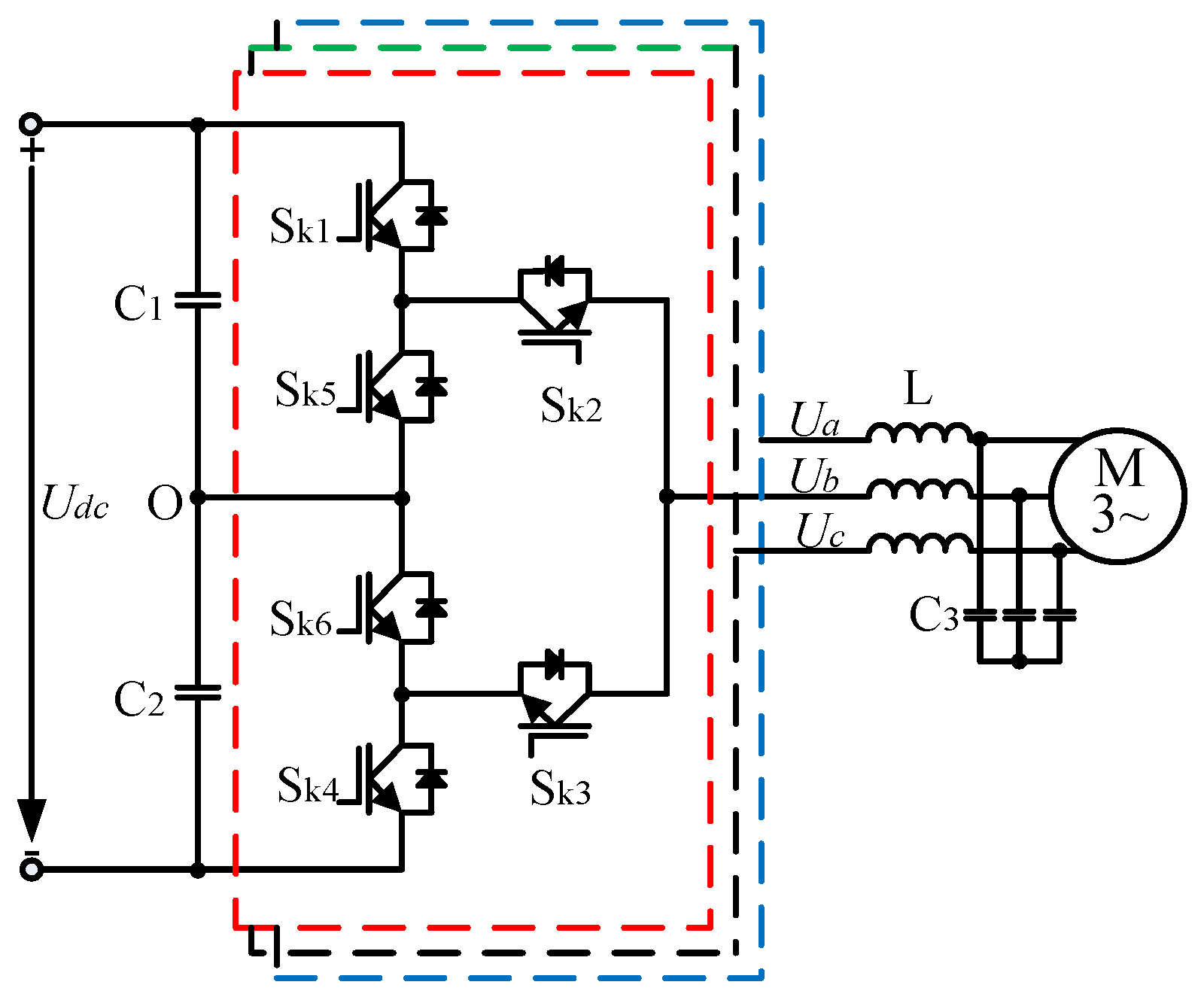
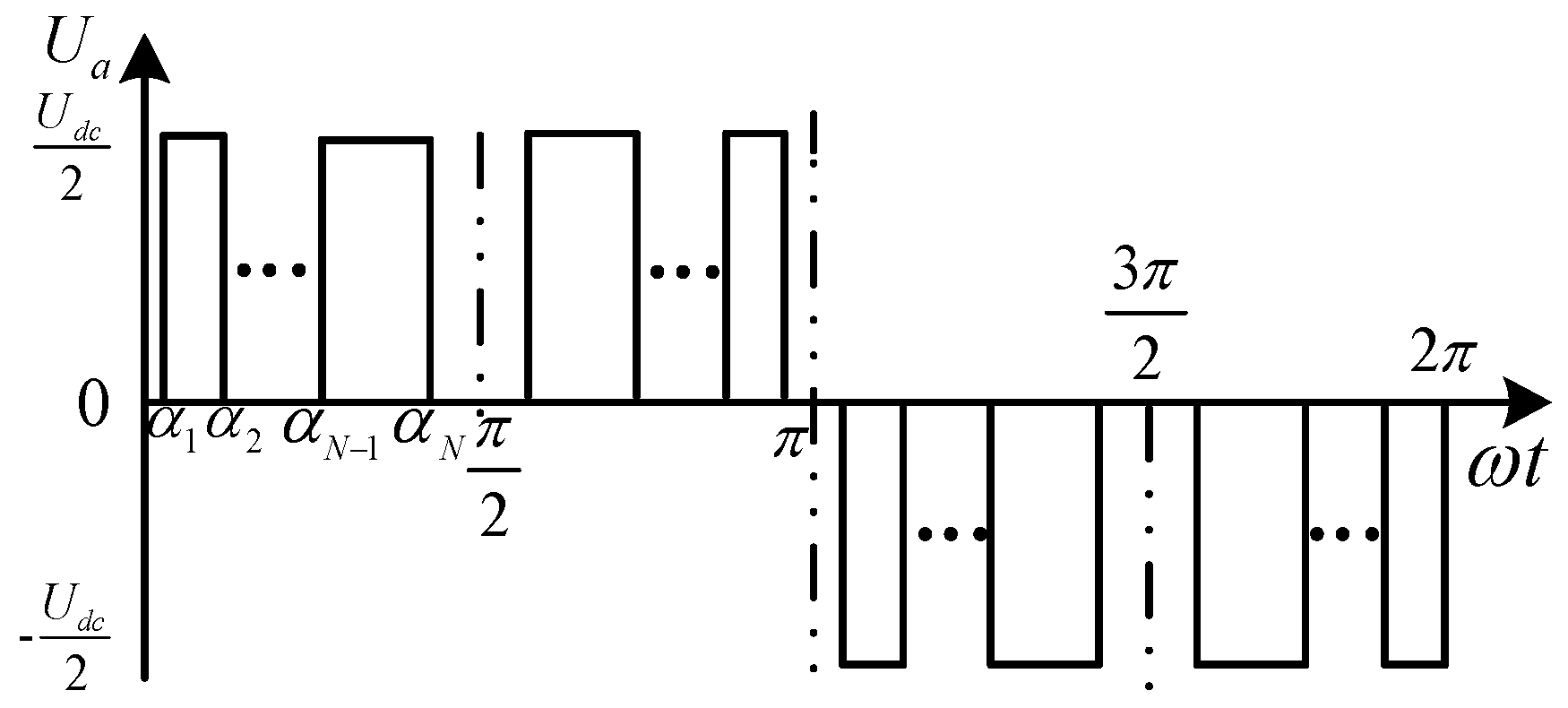



| Switches | Phase Voltage | Switching State | |||||
|---|---|---|---|---|---|---|---|
| Sk1 | Sk2 | Sk3 | Sk4 | Sk5 | Sk6 | ||
| 1 | 1 | 0 | 0 | 0 | 1 | Udc/2 | P |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | OU1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | OU2 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | OL1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | OL2 |
| 0 | 0 | 1 | 1 | 1 | 0 | –Udc/2 | N |
| Duration range | 0°–1° | 1°–6° | 6°–11° | 11°–13° |
| Switching state vector | ONP | ONO | ONP | OOP |
| Duration range | 21°–23° | 23°–25° | 25°–35° | 35°–37° |
| Switching state vector | PNP | ONP | ONO | PNO |
| Duration range | 39°–47° | 47°–49° | 49°–54° | 54°–59° |
| Switching state vector | POP | POO | PNO | ONO |
| Small Vector | Small Vector | Medium Vector | |||
|---|---|---|---|---|---|
| POO | ONN | PON | |||
| PPO | OON | OPN | |||
| OPO | NON | NPO | |||
| OPP | NOO | NOP | |||
| OOP | NNO | ONP | |||
| POP | ONO | PNO |
| Positive Small Vectors | Negative Small Vectors | Medium Vectors | |||
|---|---|---|---|---|---|
| ONN | ↑ | POO | ↓ | PON | ↑ |
| PPO | ↑ | OON | ↓ | OPN | ↑ |
| NON | ↑ | OPO | ↓ | NPO | ↑ |
| OPP | ↑ | NOO | ↓ | NOP | ↑ |
| NNO | ↑ | OOP | ↓ | ONP | ↑ |
| POP | ↑ | ONO | ↓ | PNO | ↑ |
| No. | Switching Angles | Unp | ||||
|---|---|---|---|---|---|---|
| I | … | ↑ | ||||
| II | … | ↓ | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Hu, C.; Wang, Q.; Zhou, Y.; Sun, Y. Neutral-Point Potential Balancing Control Strategy for Three-Level ANPC Converter Using SHEPWM Scheme. Energies 2019, 12, 4328. https://doi.org/10.3390/en12224328
Zhang Y, Hu C, Wang Q, Zhou Y, Sun Y. Neutral-Point Potential Balancing Control Strategy for Three-Level ANPC Converter Using SHEPWM Scheme. Energies. 2019; 12(22):4328. https://doi.org/10.3390/en12224328
Chicago/Turabian StyleZhang, Yunlei, Cungang Hu, Qunjing Wang, Yufei Zhou, and Yue Sun. 2019. "Neutral-Point Potential Balancing Control Strategy for Three-Level ANPC Converter Using SHEPWM Scheme" Energies 12, no. 22: 4328. https://doi.org/10.3390/en12224328
APA StyleZhang, Y., Hu, C., Wang, Q., Zhou, Y., & Sun, Y. (2019). Neutral-Point Potential Balancing Control Strategy for Three-Level ANPC Converter Using SHEPWM Scheme. Energies, 12(22), 4328. https://doi.org/10.3390/en12224328