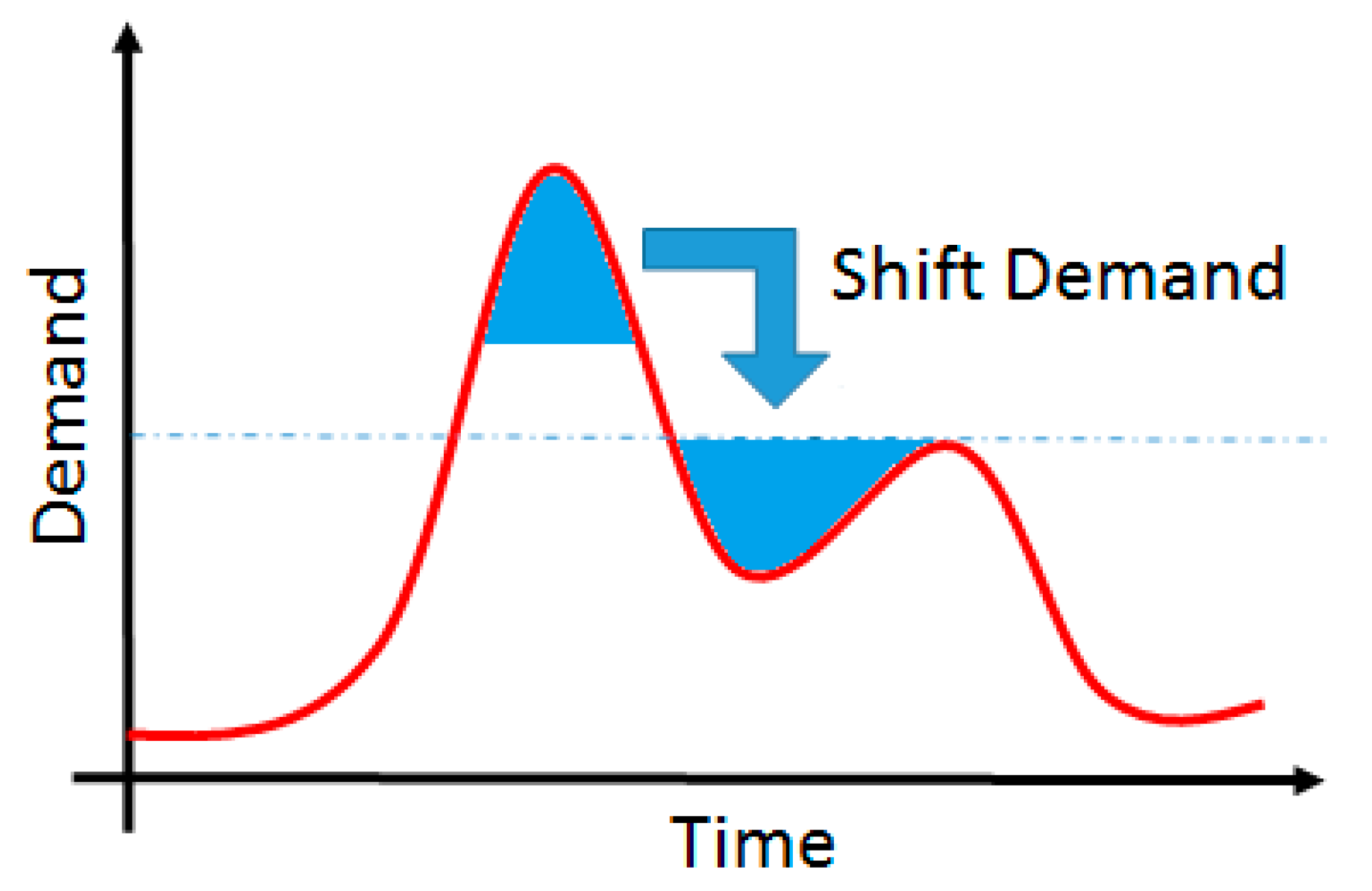
3.1. Individual Unit Dispatch
The legacy mode of operation of an HVAC unit for temperature control is typically through thermostat type controls, i.e., setting the control signal
u(
k) according to the simple ‘relay with hysteresis’ control law [
7,
17,
18]:
where
TR(
k) represents the temperature setpoint at time step
k, and the deadzone of the relay (during which the output is held at its last value) is given by 2Δ. Such a mode of operation is simple to implement; in the following, it is wished to extend the basic relay-based approach to situations in which pre-heating (cooling) can be optimally managed for explicit DR events. For this, a rolling-horizon non-linear MPC employing a finite discrete input set is developed [
20]. The optimization problem to be solved at each discrete-time step
k is the minimization of the following multi-stage quadratic cost function:
Minimize:
with respect to:
subject to:
where
T(
k) represents the zone temperature at time slot
k,
TR(
k) represents the zone temperature reference (setpoint) at time slot
k and
TA(
k) represents the ambient temperature at time slot
k. The binary decision variable
u(
k) represent the control input at time slot
k and Δ is the difference operator such that Δ
u(
k) =
u(
k) −
u(
k − 1). The scalar term
λ is used to penalize changes in the control input and can be considered a ‘move suppression’ or regularization term. Integer
d ≥ 1 represents the time delay and
w(
k) ∊ {0, 1} are indicator variables for defining a demand response window, such that DR is active during time slot
k if
w(
k) is ‘1’ and not active otherwise. The integer
M represents the length of the prediction horizon, and integers
UU and
UL represent upper and lower bounds on the allowed input activity during a defined DR window. Henceforth in this paper, only an upper bound on control activity (e.g., for handling STOR-style DR events) is considered, with the understanding that adding the lower bound (e.g., for DTU-style DR events) follows directly from the described methods. As with other predictive control problems, an appropriate length for the prediction horizon would be the number of samples required to capture the open-loop setting time of the process [
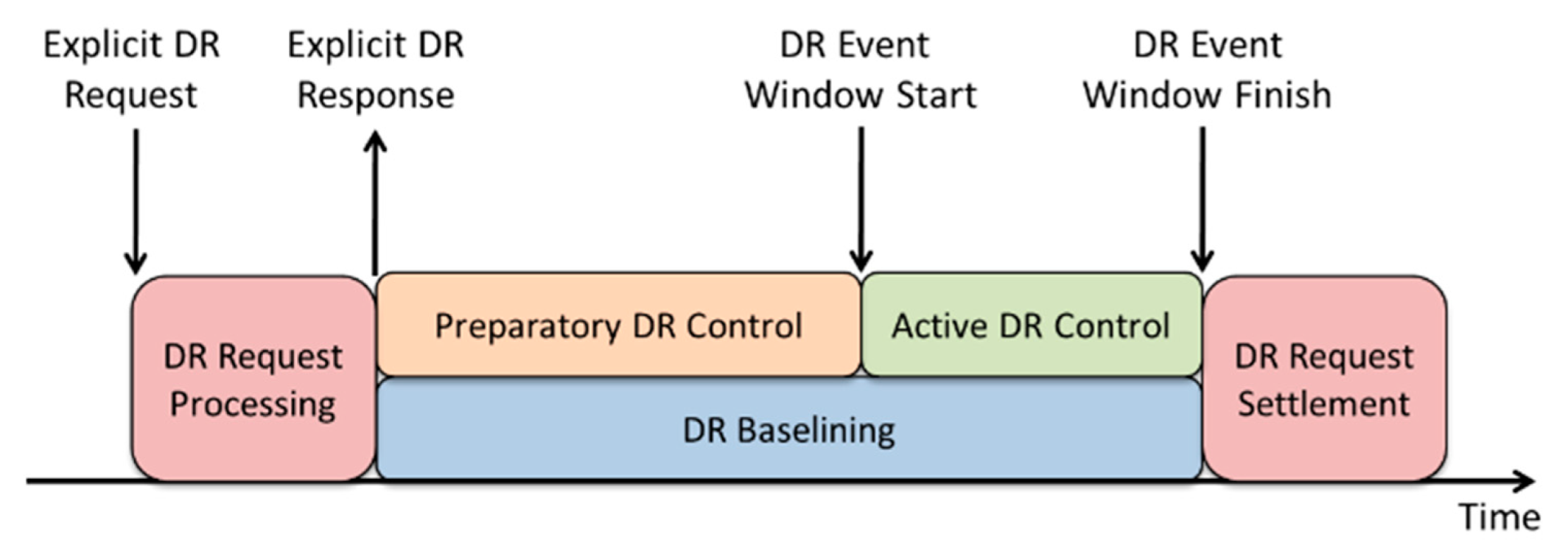
21]. However, with reference to
Figure 2, this should be extended somewhat to allow for preparatory control actions to also take place. For the thermal model, Equation (1), basic systems theory gives the settling time as 4.6
τ, giving a suggested horizon length
M = ⌈(4.6
τ +
W)/
Ts⌉, where
W is the length of time required for preparatory control. For example, a 30-min time constant and preparatory window
W of one hour with time step of 90 s gives a horizon length
M of 132 steps.
The first component of the objective function in Equation (4) is the sum of squared errors between the actual building temperature and its setpoint. A quadratic penalty term is appropriate as it approximately captures the relationship between temperature error and thermal comfort (see, e.g., [
22]). During working hours, this will be typically 22.0 °C in winter and 24.5 °C in summer [
22]. The second component is the sum of squared control moves weighted by the scalar term
λ, which is used to suppress excessive switching of the controls. The indicator weights
w(
k) and bound
UU are used in combination to penalize electricity consumption during a specific defined window of the prediction horizon (corresponding to DR events). DR events are enabled for a particular stage by setting the indicator variable
w(
k) equal to ‘1’. As with all rolling horizon predictive control schemes, once the optimization has been solved for the current time step, only the first control (corresponding to
u(
k)) is applied. At time step
k + 1, the process is repeated with repeated measurement information.
It is quite straightforward to see that for all but prediction horizons of one or two steps in length, and in the absence of any DR activity over the horizon (implying no constraint bounds in Equation (8)), then the control law resulting from the solution of Equations (4)–(7) is a switching surface dependent upon two factors. The first is the predicted difference between the reference temperature
TR(
k +
d) and actual temperature
T(
k +
d) and the second is the previous state of the control input,
u(
k −
d − 1). In this situation, the control defaults to a predictive relay-based controller with deadzone Δ ≈ √
λ(
k). In the presence of upcoming DR events, however, the effective switching surface can change considerably to provide optimal pre-heating (or cooling). In addition, the solution of the optimization problem contains useful predicted quantities regarding upcoming DR events. In particular, since the future control signals can only be ‘1’ or ‘0’, the predicted electricity consumption of the HVAC unit during any upcoming DR event—denoted as
URC(
k)—is easily derived from either inspection of the solution vector, or from the left hand side (l.h.s.) of constraint (8), as follows:
For upcoming DR events, the integer
UU on the right hand side (r.h.s.) of constraint (8) can be used to limit
URC(
k) and specify a load curtailment/reduced consumption from the HVAC unit. These observations will be exploited in the sequel, during which the DR allocation mechanism will be presented. The optimization problem of Equations (4)–(8) is easily formulated as a mixed-integer quadratic program (MIQP), or alternatively as an approximate mixed-integer linear program (MILP) [
16,
21]. In order to improve the run-time efficiency of the approach (and enable bounded worst-case execution times), the DP method is chosen. DP (see Bellman, [
23]) is a computational method for solving optimal control problems with separable additive performance indices. It is based on the recursive application of Bellman’s ‘Principle of Optimality’ [
23,
24]:
‘An optimal policy has the property that whatever the initial state and the initial decision are, the remaining decisions must form an optimal policy with regard to the state resulting from the first decision.’
The mathematical form of this idea can be expressed as a backwards sequence featuring the solution of simpler optimization problems at each stage. Continuing backwards from the end stage
N to the current stage
k—and applying the principle of optimality at each stage—will result in the following recurrence relations for discrete DP [
24]:
where
Jk(
xk) is the cost of entering stage
k with state
xk,
gk(
xk) is the cost for entering stage
k with state
xk,
Uk(
xk) is the set of allowed controls for the input
uk when the state
xk is entered at stage
k, and
fk(
xk,
uk) is a function which maps the state
xk onto state
xk+1 when control
uk is applied at step
k. In discrete DP (DDP), the state vector is mapped onto a grid of size
S and the controls onto a grid of size
U. By iterating through the recursion and trying all admissible control values at each admissible set of state values, a vastly reduced search space is explored when compared to a pure brute-force search; at the end of the minimization, a solution grid is obtained and the optimal control is obtained from the position in the grid corresponding to the current state. In the current context, the state variable is the temperature
T(
k) plus the previous applied control
u(
k − 1). The admissible controls are the current control
u(
k), having two possibilities (
U = 2) at each stage in the absence of DR, but some possibilities may not be admissible if they invalidate constraint (8) when DR is active. In the approach taken in this paper, constraint (8) is translated into a penalty function inserted into the objective; with an iterative tightening of an applied weight upon constraint violation (a maximum of 10 iterations is employed). The temperature is mapped into a discrete grid of over a suitable working range, e.g., 10–30 °C; the control is already discrete in nature. The transition function
fk(
xk,
uk) is given by the linear Equation (6). In the case that the HVAC dynamics are actually non-linear, then this can easily be captured by an appropriate choice of transition function. During the recursion, the minimal cost function is stored for each admissible state along with the corresponding partial sum of the l.h.s of constraint (8). After the recursion, the value of
UDR(
k) is readily computable using Equation (9) and the final value of this partial sum. In many situations, temperature sensors either have 10-bit resolution—or can easily be cast or truncated into this range—giving a full state size
S = 2
11. As the run-time complexity of the DDP algorithm is given by
O(
M.
U.
S), the algorithm runs efficiently even for a relatively large prediction horizon
M, which may be needed for best results. During the backwards recursion, only the current and next stage costs and the partial l.h.s. of constraint (8) are actually required, reducing the memory requirement to
O(
U.
S). As sampling time requirements of approximately one minute are sufficient in many instances (due to the comparatively slow thermal dynamics), then the algorithm is clearly suitable for deployment without undue problems in a small/low-cost embedded system.
3.2. Generation of Predicted Baseline and Reduced Consumption
As discussed earlier, the effective practical implementation of a DR scheme requires the generation of both an accurate and reliable predicted baseline and an accurate and reliable predicted reduced consumption [
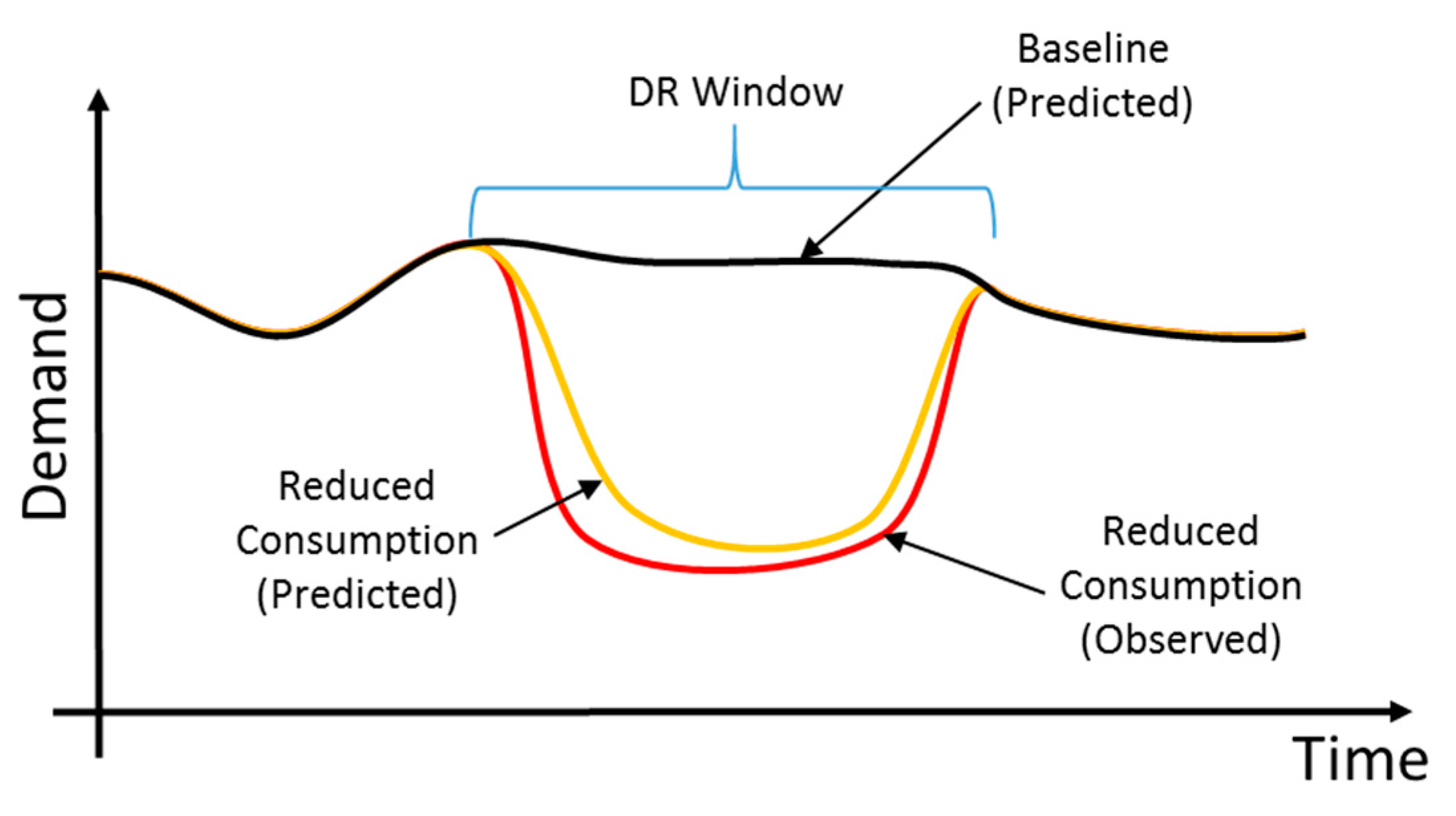
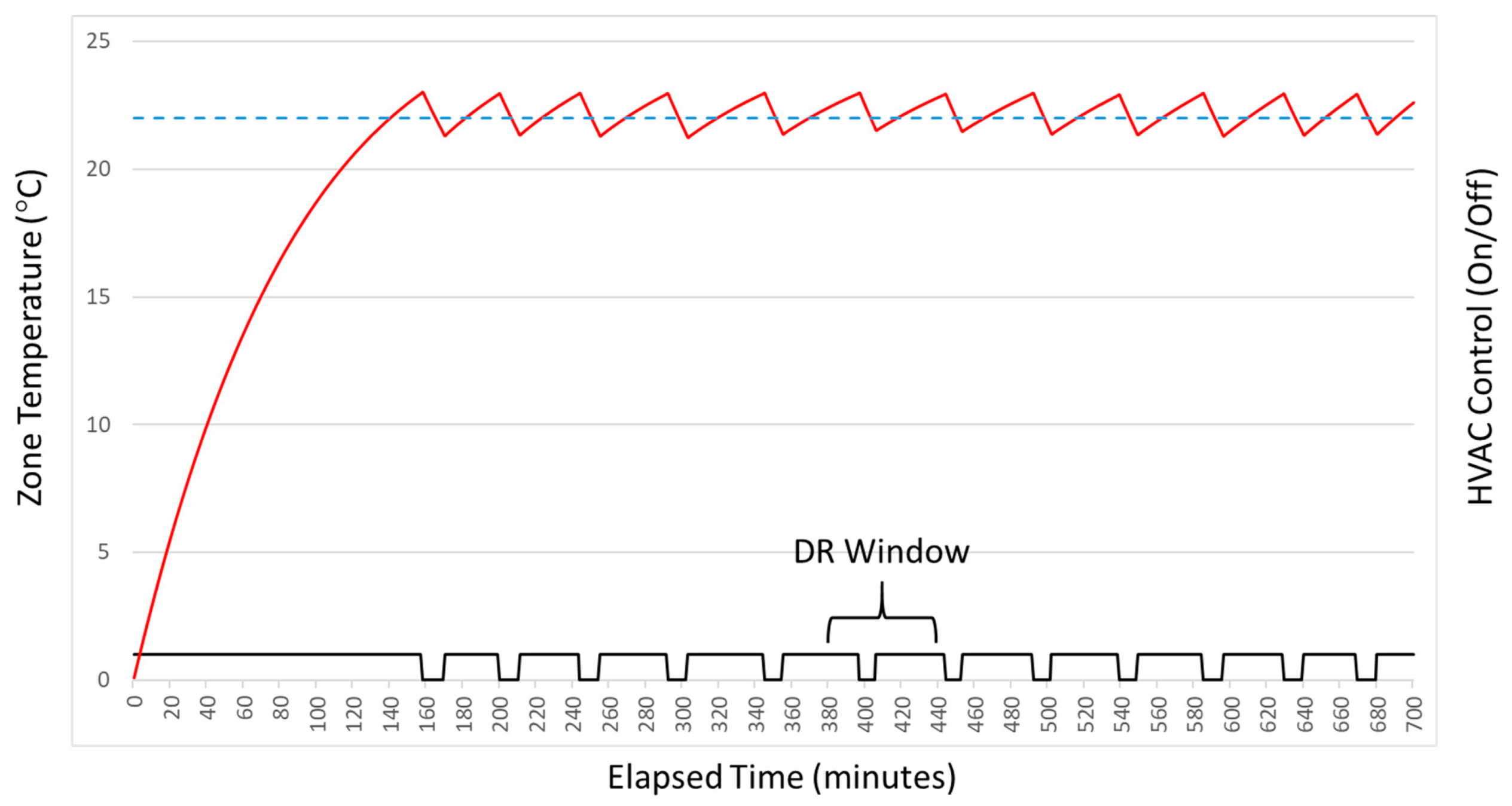
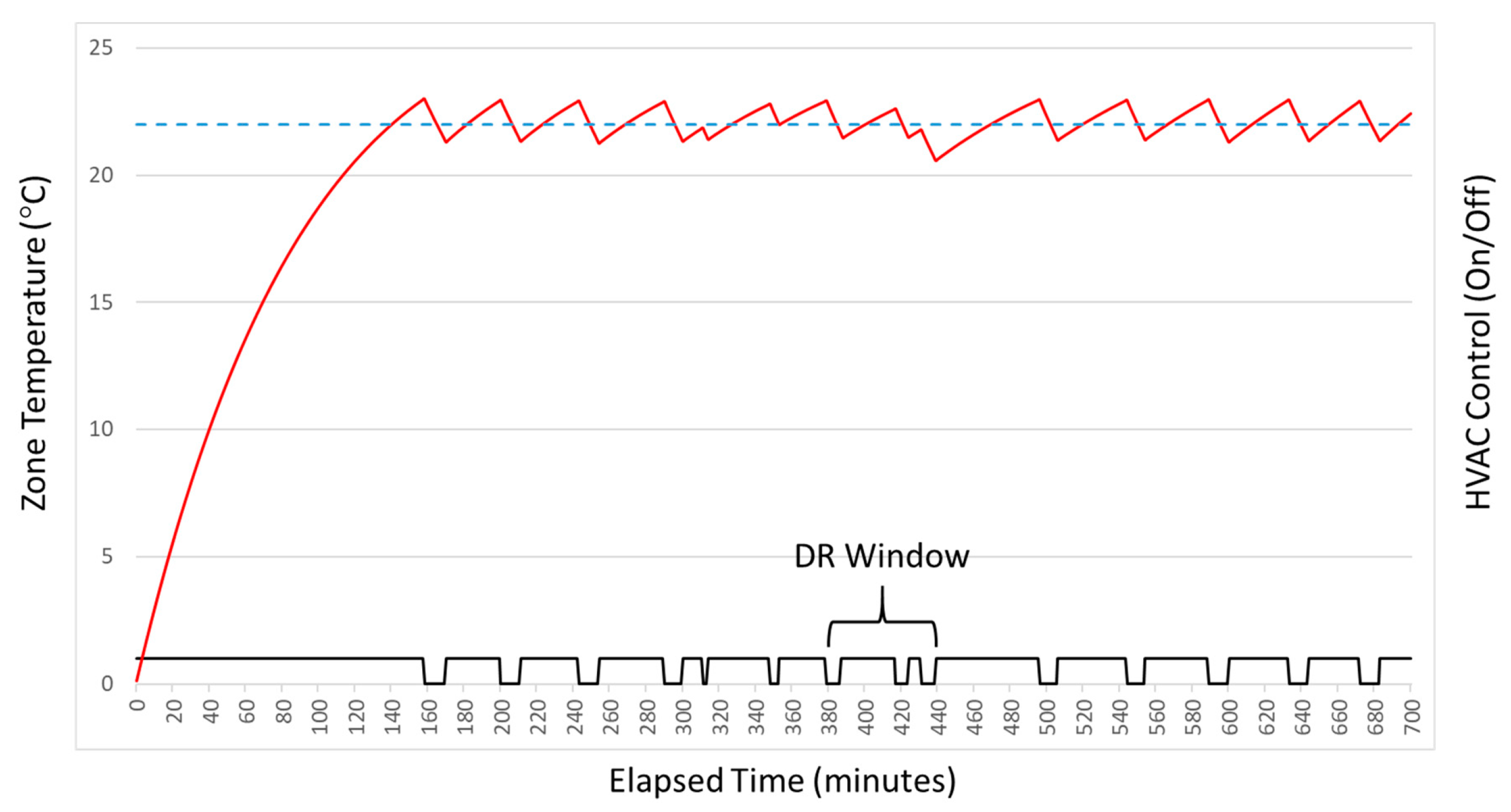
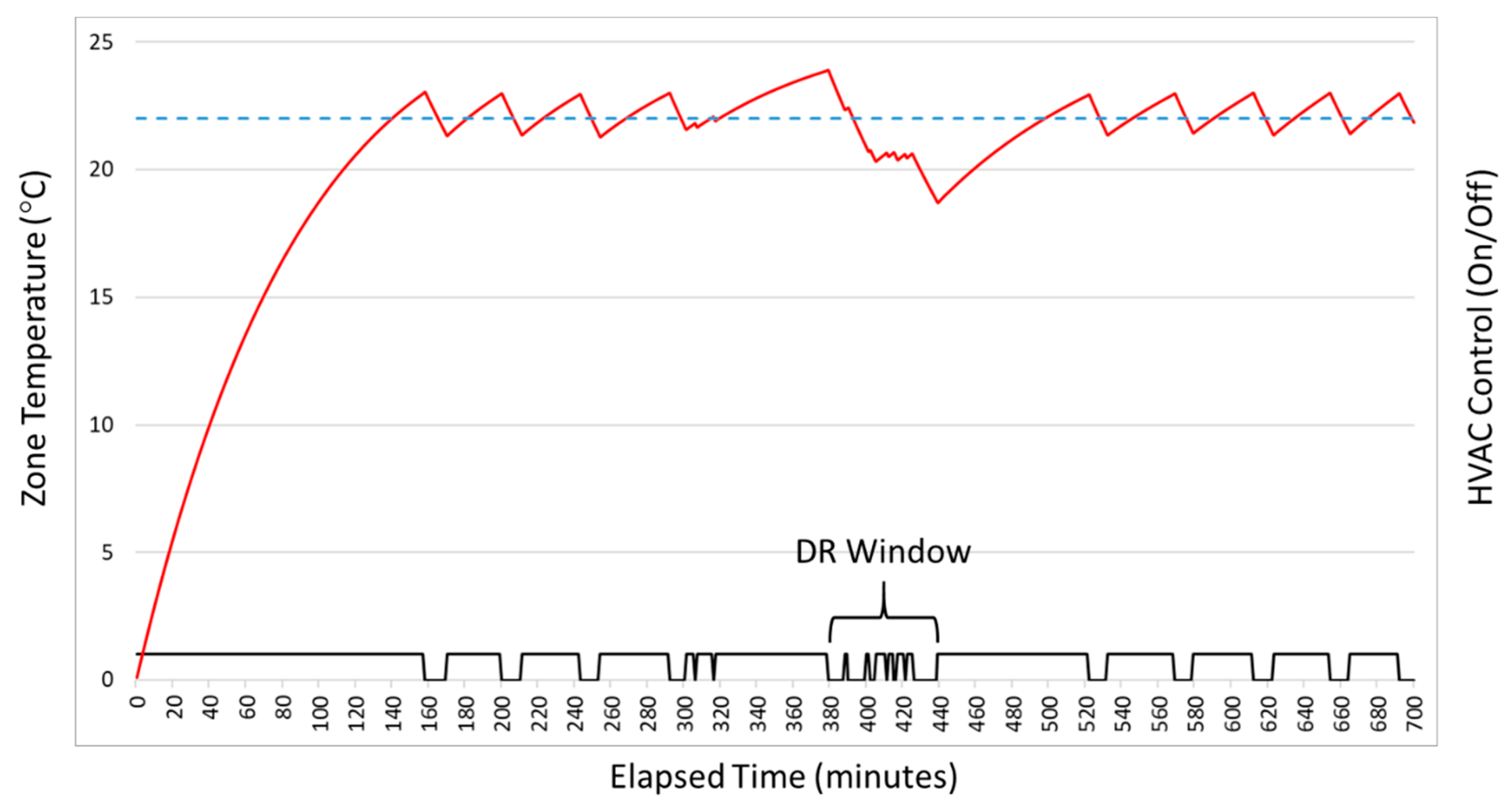
25]. As shown in
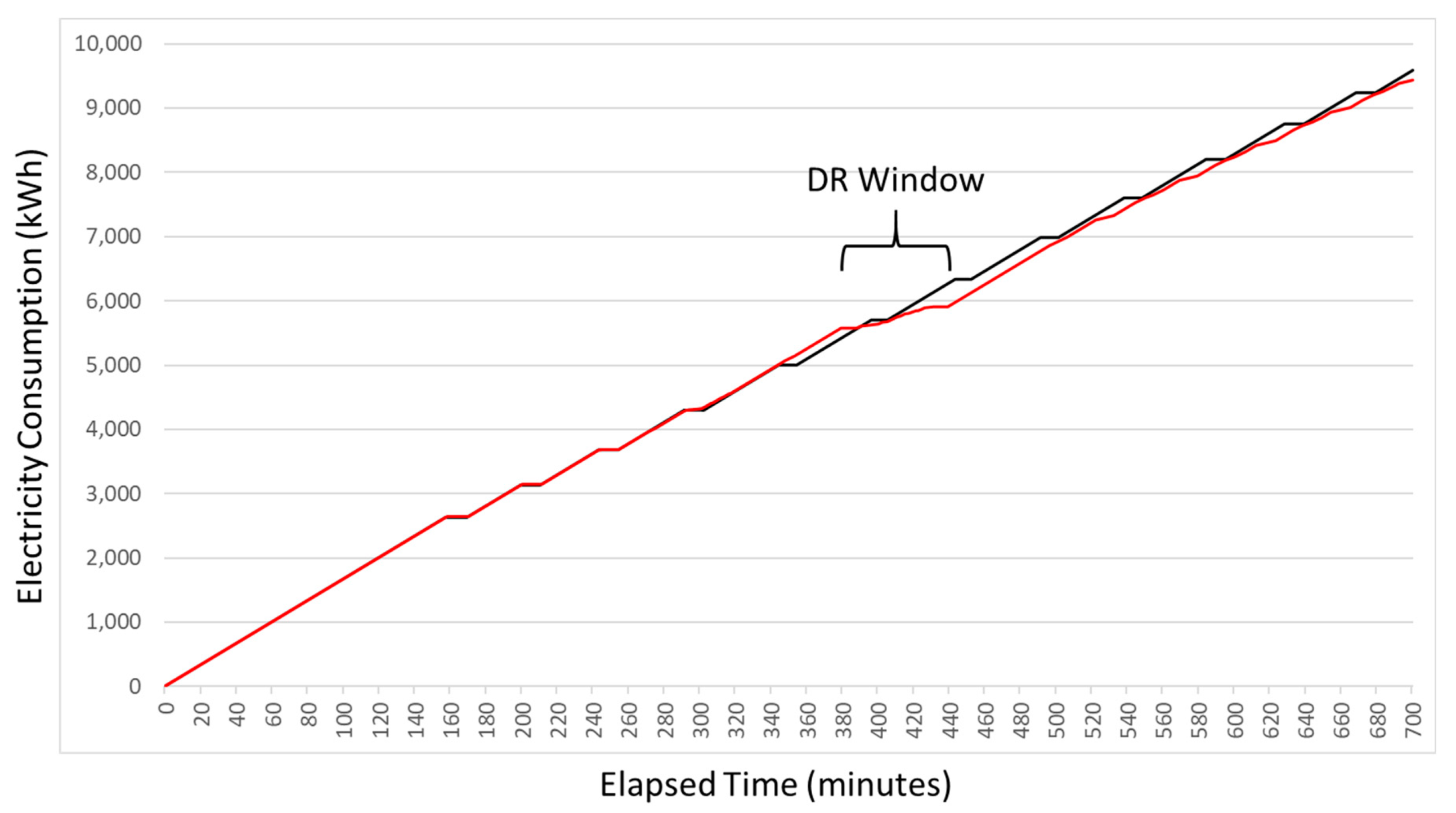
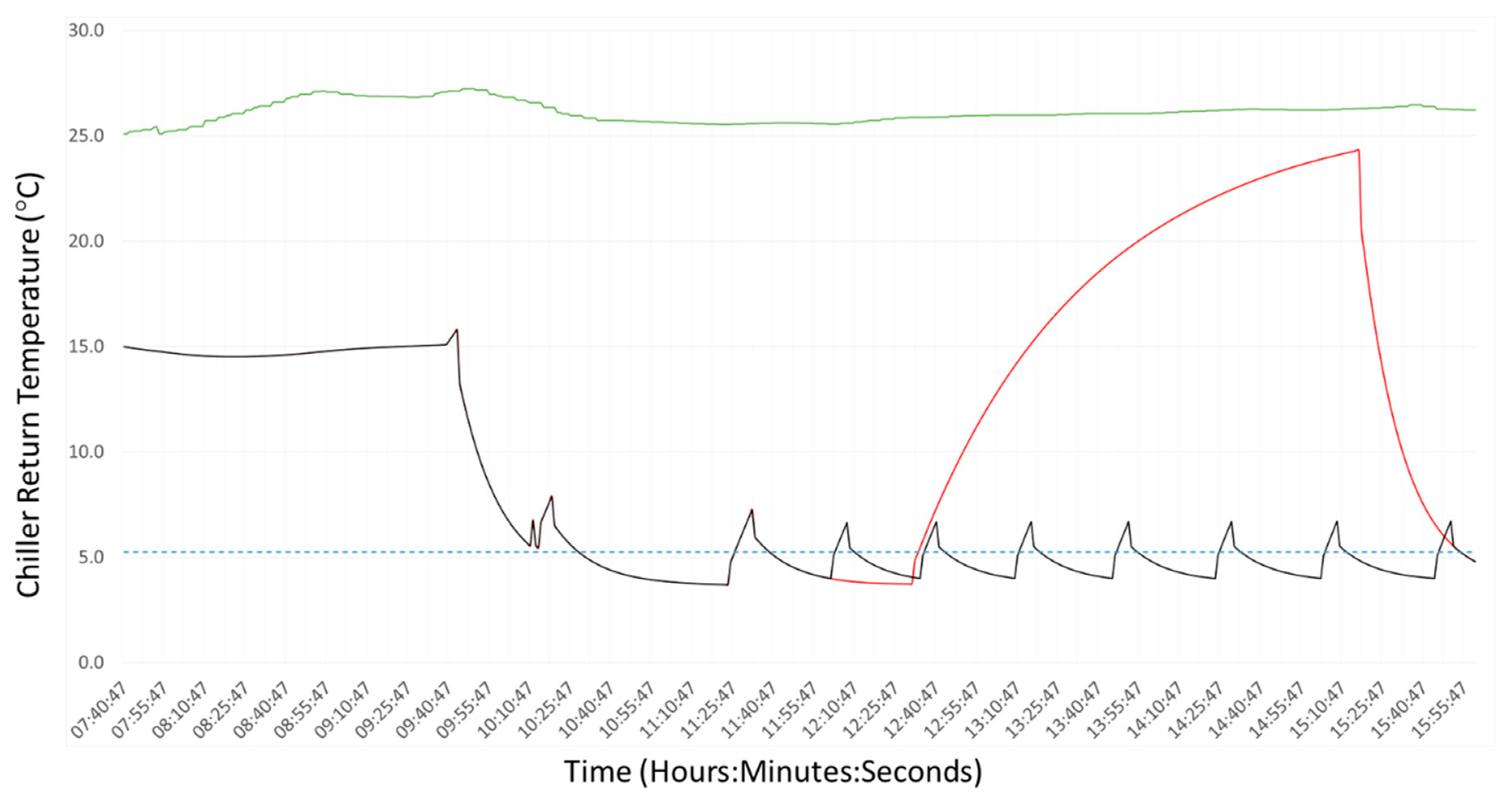
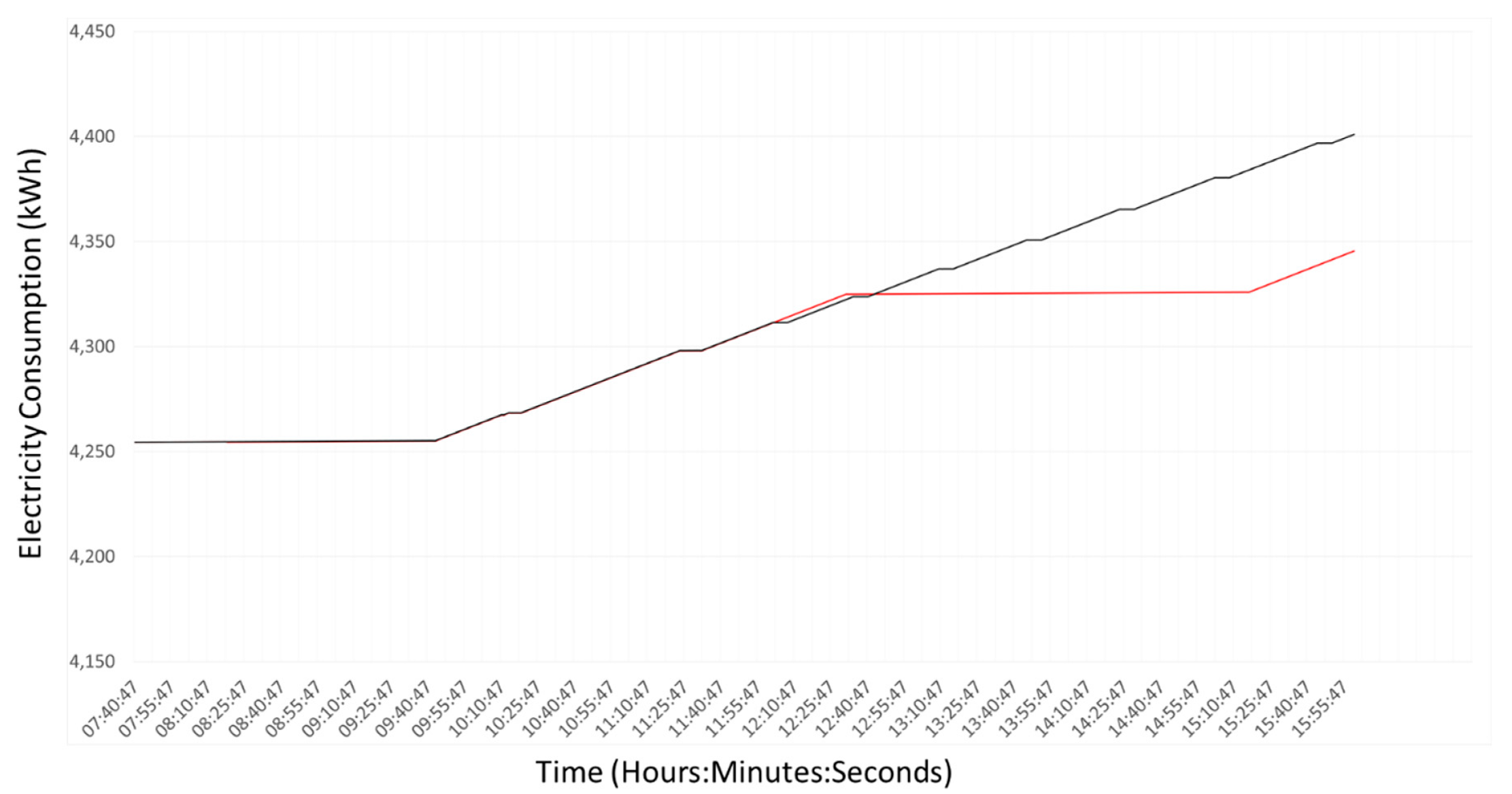
Figure 3, the baseline represents a counterfactual prediction (either forecast or backcast, generated on-line or off-line) of electricity consumption for targeted assets during the time-period corresponding to a DR event, under the assumption that no corrective DR action will be/had been taken. As also shown in
Figure 3, the reduced consumption represents a prediction (forecast, generated on-line) of electricity consumption for targeted assets during the time-period corresponding to a DR event, under the assumption that corrective DR action will be taken. Note that although the observed reduced consumption in
Figure 3 is always lower than predicted, this is not necessarily the case generally, and the accuracy of prediction depends heavily upon the models and methods employed.
Both the predicted baseline and predicted reduced consumption are also dependent upon many factors including occupancy, ambient temperature and weather conditions, and it has proved a challenging and ongoing task to select suitable methods for their implementation [
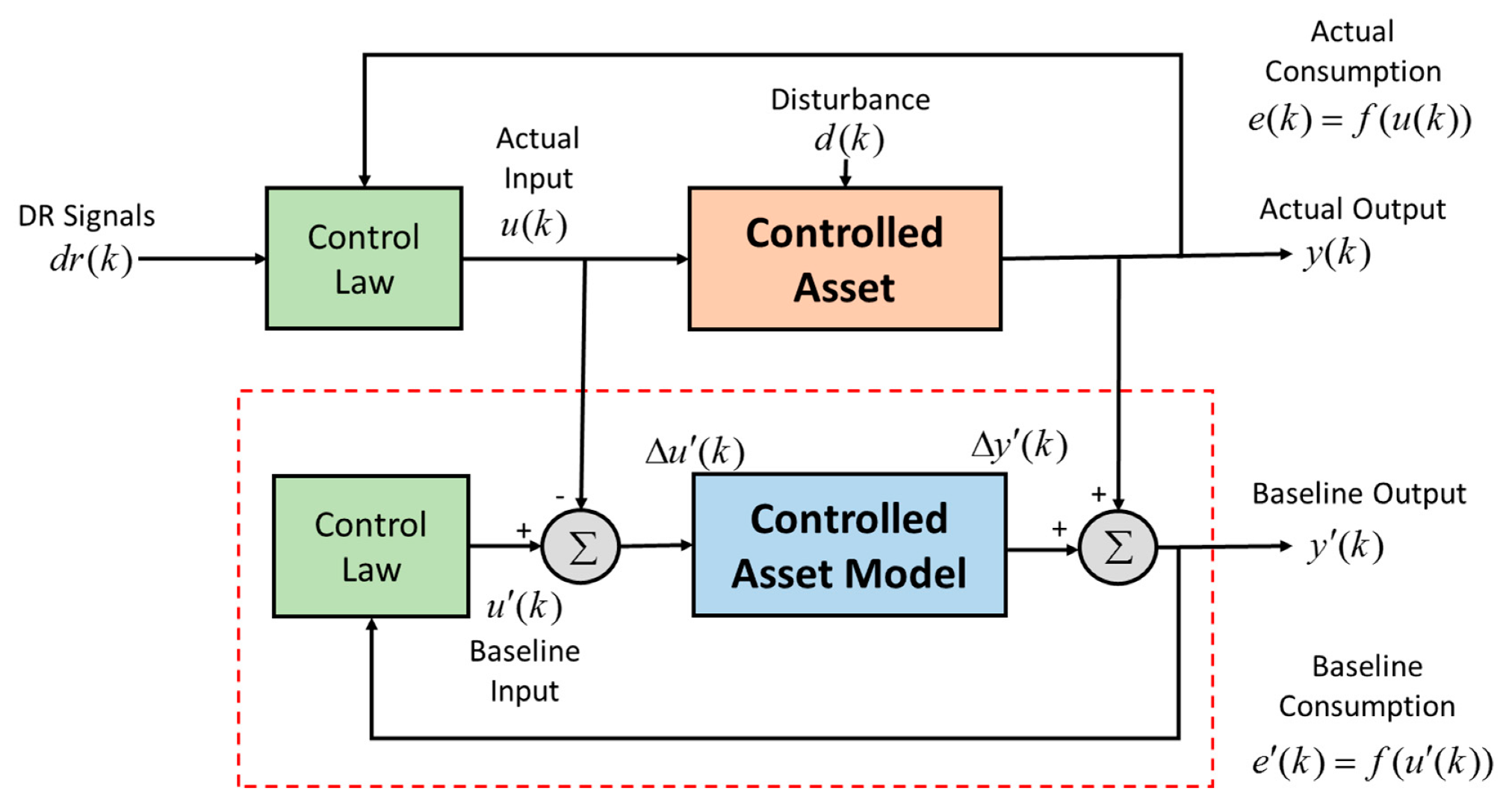
25]. The baseline consumption is needed to gauge performance of controlled assets during a DR event and for post-event financial settlement, where it is compared to the actual measured consumption. Therefore, the baseline should be accurate as possible. In the context of the research presented here, it is required to generate a reliable baseline across the rolling horizon for an HVAC unit in an on-line fashion. The methodology proposed is illustrated in
Figure 4.
As can be seen in
Figure 4, the controlled asset is driven by input
u(
k) and produces output
y(
k), and consumption
E(
k) is derived as a function of the input signal
f(
u(
k)). The controlled asset is also driven by a disturbance sequence
d(
k) which impacts the output
y(
k); this sequence may consist of partially known (measured) values along with unmeasured or stochastic values. The asset input signal
u(
k) is generated by closed-loop feedback controls, which are also driven by external DR signals represented by
r(
k). The baseline is generated on-line (in real-time) by the components contained within the dashed red box; the asset model represents a discrete-time dynamic model of the controlled asset, while the asset model input signal
u’(
k) is given by the same closed-loop feedback algorithm which drives the actual controlled asset. However, the DR signals
r(
k) are suppressed from the control law in the baseline case to ensure the counterfactual sequence of inputs is generated. The baseline consumption sequence
E’(
k) is derived as a function of the baseline input signal
f(
u’(
k)). Since the disturbances
d(
k) and plant-model mismatch can both impact upon the baseline accuracy, the counter-factual baseline output is generated on-line as follows. The actual nominal control input
u(
k) is first subtracted from the baseline input
u’(
k) to generate an input deviation signal Δ
u’(
k), which acts as input to the asset model to produce an output deviation signal Δ
y’(
k). The baseline output
y’(
k) is then produced by adding the deviation signal Δ
y’(
k) to the measured output
y(
k). This ensures that the effects of disturbances and plant-model mismatch on the actual output
y(
k) are contained within the baseline output
y’(
k), which also captures the impact of the baseline control sequence
u’(
k) to ensure accuracy of the baseline. In the context of the current work, the controlled asset is the HVAC system, the controlled asset model is represented by Equation (2) with the measured part of the disturbance sequence being the ambient temperature, and the control law is the rolling-horizon non-linear MPC procedure given by Equations (4)–(8).
For the effective application of aggregated DR, it is required to generate both a predicted baseline and a predicted reduced consumption across the rolling horizon for each individual HVAC unit in an on-line fashion. At each timestep k, let the baseline consumption of the HVAC unit during an upcoming DR window be denoted as UBL(k) and the reduced consumption of the HVAC unit during an upcoming DR window be given as URC(k). Computation of this latter quantity as a by-product of the application of the DP algorithm was detailed in the previous Section. In order to compute the former quantity UBL(k), the DP algorithm can be applied to solve the optimization problem using baseline input u’(k) and output y’(k) as input data and setting constraint (8) r.h.s. UU = ∞. As discussed in the previous section, the control law resulting from the solution of Equations (4)–(8) in the absence of any DR signals is a predictive relay-based controller. Therefore to simplify the process of generating the baseline controls u(k + i|k) and y(k + i|k) (i.e., i-step predictions of the asset input and output, incorporating measured disturbances such as weather forecast), Equation (3) may be employed at each stage with deadzone Δ = λ2/2. Thus, both quantities can be computed in a straightforward procedure integrating both unit DR controls and unit baseline/reduced consumption predictions in an ITU-based edge device.
3.3. Coordinated Dispatch Scheme
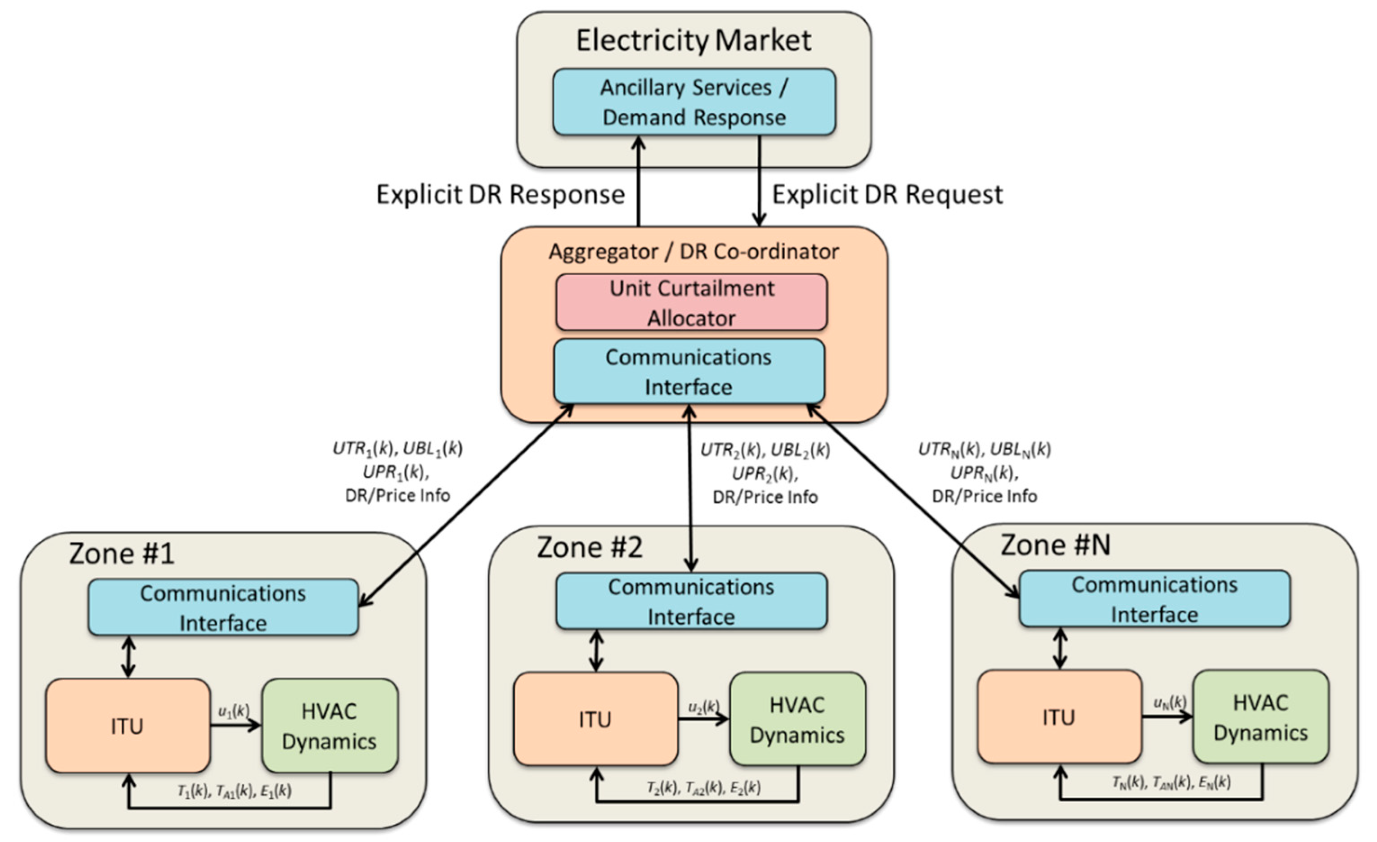
Consider the arrangement of HVAC units (with their edge-based local dispatch optimizers) in the presence of a (cloud-based) aggregator at the network core, in the presence of a wider DR marketplace as shown in
Figure 5. Assume that a flexible IP-based communications infrastructure is employed to interconnect the core and network edges (e.g., using Web Services, OpenADR protocol, etc.), and to provide loose synchronization of their clocks (e.g., using Network Time Protocol (NTP)).
For the aggregated DR coordination scheme, the following approach is employed. In a multiple-zone scenario, let the predicted electricity consumption at time step
k for an upcoming DR event involving HVAC unit
j be given as
URCj(
k). Similarly, let the predicted baseline electricity consumption at time step
k for an upcoming DR event involving HVAC unit
j be given as
UBLj(
k). This quantity is computable as detailed in the last section. Since for each HVAC unit
j and for every time step
k it must hold that
UBLj(
k) ≥
URCj(
k) (i.e., the predicted unit baseline consumption is not less than the unit DR consumption during a DR event), at step
k the explicit unit predicted reduction in load—denoted as
UPRj(
k)—for an upcoming DR event is given by:
UPRj(
k) =
UBLj(
k) −
URCj(
k). This quantity is easily computed in each ITU as detailed in the previous section. Then the predicted aggregated explicit reduction in load for an upcoming DR event at time step
k—denoted
APR(
k)—for
N participating HVAC units can be computed by the aggregator as:
Let the target aggregated electricity reduction consumption for an upcoming DR event be given as ATR(k) ≥ 0, and the target reduction in load for individual HVAC unit j be given as UTRj(k). Since it has been assumed that the HVAC controls are binary in nature, in a given DR window the available load curtailment is limited between zero and the maximum available from the predicted baseline in discrete steps. As such, assume that each HVAC unit j ∊ N offers an agreed price-schedule for load curtailment Xj, such that a specific load Lj,l may be reduced for a price pj,l by selecting one of l ∊ Xj different discrete price/curtailment options. Only one (or none) of the price/curtailment options can be selected for a given HVAC unit, for any given DR event. The objective for the DR coordinator is then to (i) at the start of a preparatory event, allocate individual HVAC unit load curtailments to meet the aggregate DR requirements; and (ii) should an HVAC unit opt-out or become unavailable—or environmental/pricing conditions otherwise change leading to an invalid initial allocation—reallocate curtailments to best suit the new conditions. The allocation/reallocation problem for N available units at time-step k can be written as a variant of a standard integer knapsack problem, as follows:
Minimize:
subject to:
where
xj,l ∊ {0, 1} are binary variables that indicate whether load reduction level
Lj,l is active for HVAC unit
j. Equation (12) defined the main objective, to minimize DR costs while meeting the target reduction in demand (constraint (13)). Constraint (14) allocates load reduction level to individual unit targets, while constraint (15) ensures that individual unit load reductions are not greater than the individual unit baselines for the upcoming event. Constraint (16) enforces mutual exclusion in the choice of load reductions to individual units based upon the available price/curtailment options for that unit. Note that the presence of this constraint allows that any costs for activating a particular HVAC unit for DR purposes can be added into the corresponding costs for discrete load curtailment. The presence of the constraints also suggests that the problem can be efficiently solved using standard DP techniques, using a slight variant of the standard knapsack DP approach [
26]. The time and space complexity of this approach is
O(
N.D.X), where
N is the number of participating units,
D is the level of load curtailment requested and
X is the largest cardinality of curtailment choices among the participating units [
23,
24]. Alternatively, efficient Branch-And-Bound techniques are known and can be applied [
26]. Should the problem defined by Equations (12)–(17) prove infeasible, this will be due a violation of constraint (13), indicating that there is not enough capacity to achieve the aggregated DR value. In this case, either further units should be brought into the DR scenario, or the aggregator should report that it might not be able to deliver the required target to the market.