Parameter Equivalent Method of Stator Anisotropic Material Based on Modal Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Finite Element Model of Stator System
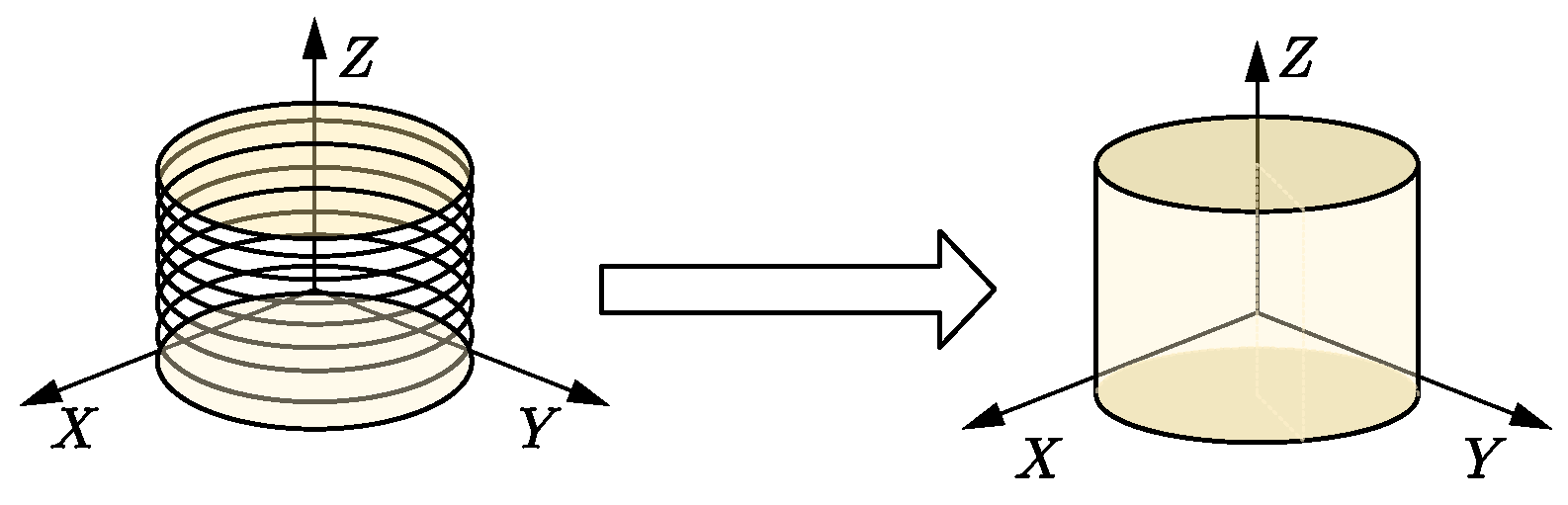
2.1.1. Simplification of Finite Element Model of Stator Core
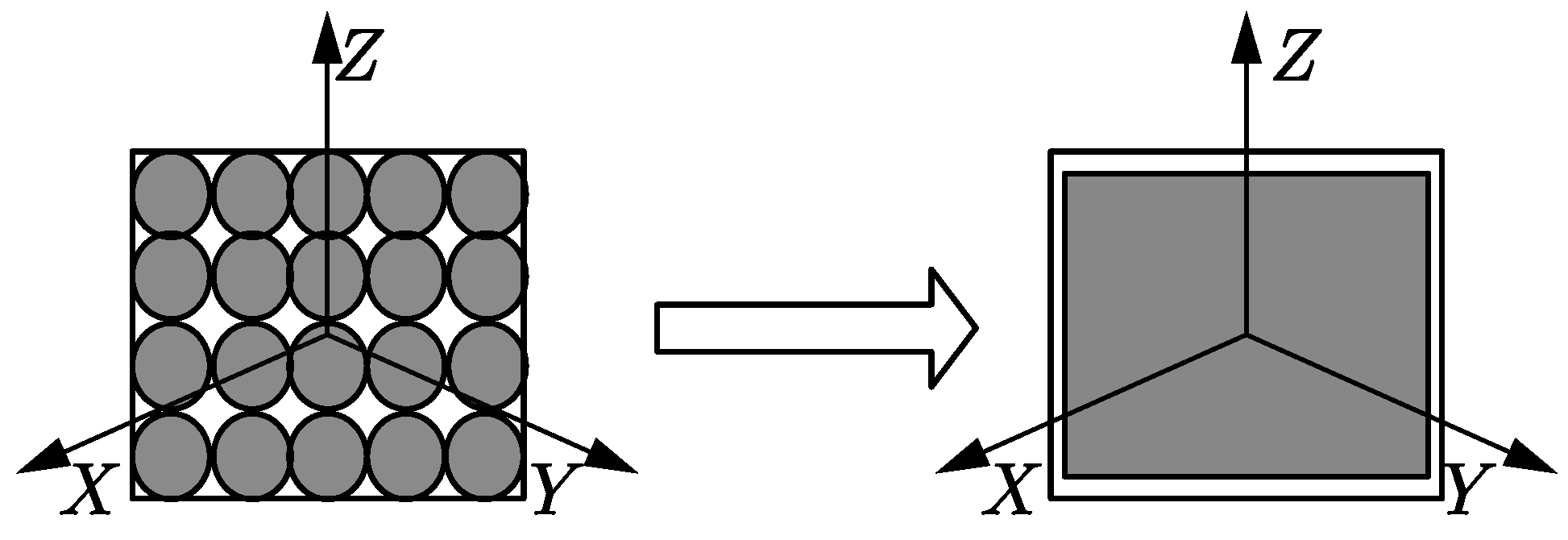
2.1.2. Simplification of Winding Finite Element Model
2.2. Parameter Setting of Stator System Materials
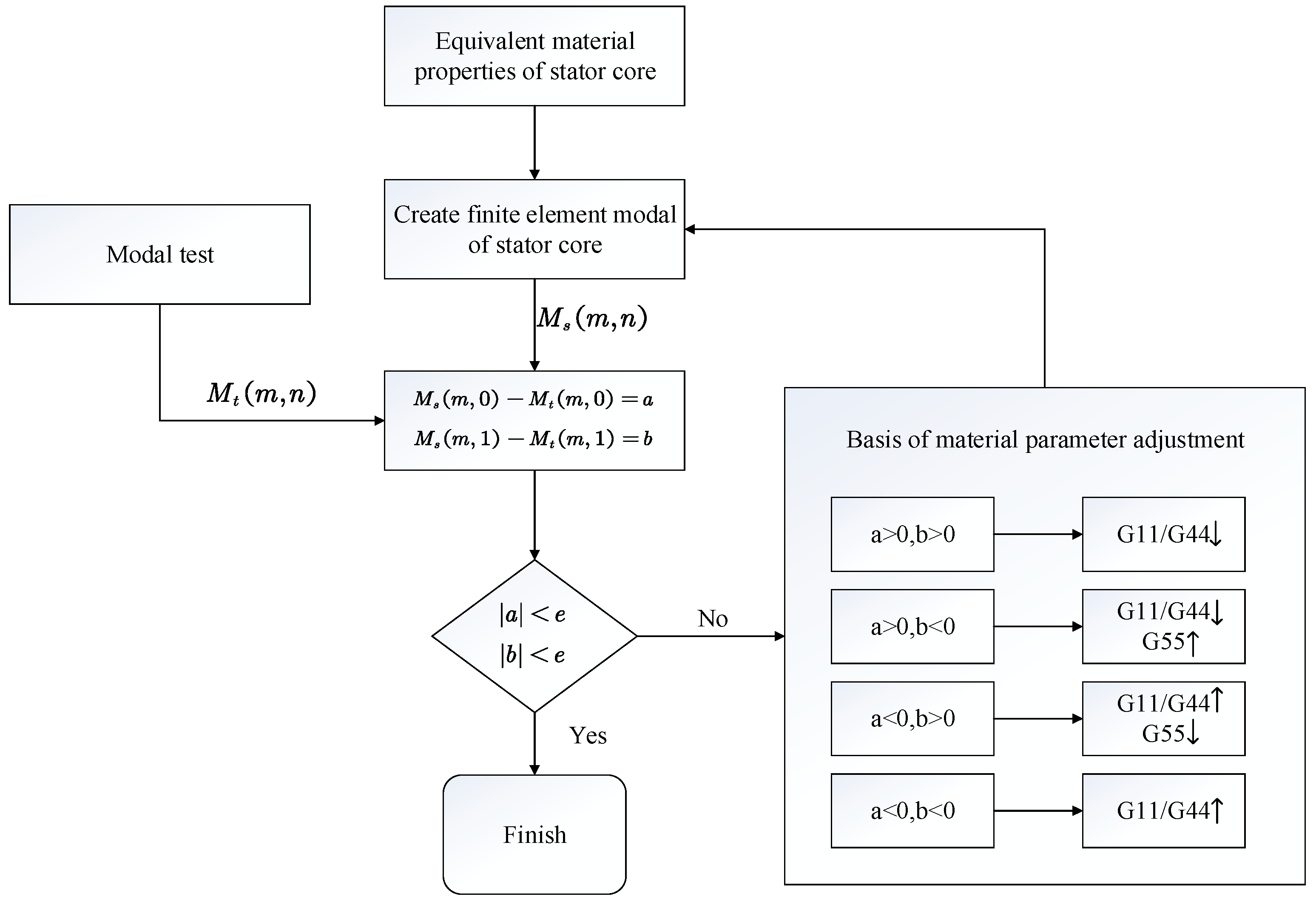
2.3. Stator Core Material Property Equivalent Method
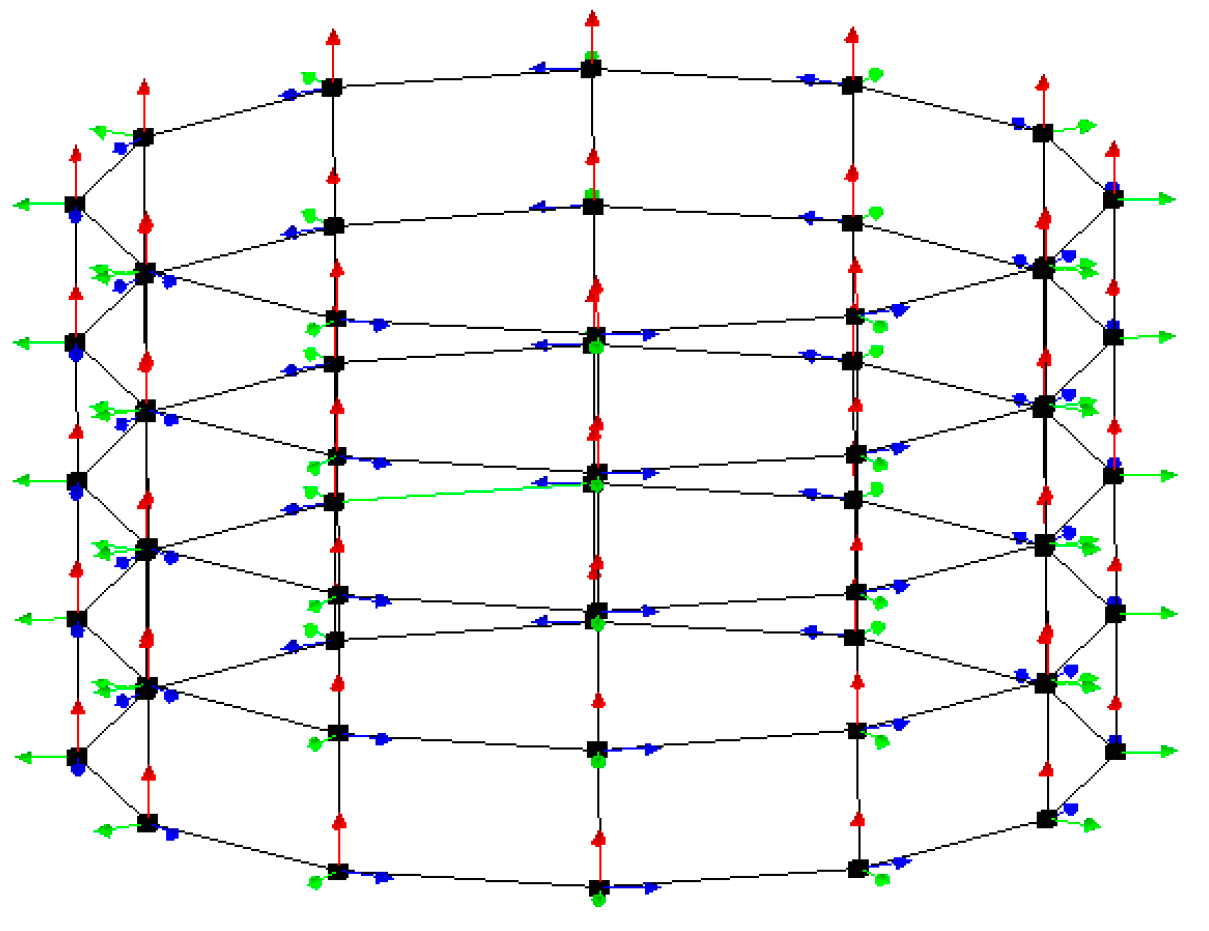
2.4. Modal Testing Analysis
2.4.1. Modal Experiment of Stator Core
2.4.2. Modal Experiment of Stator Winding
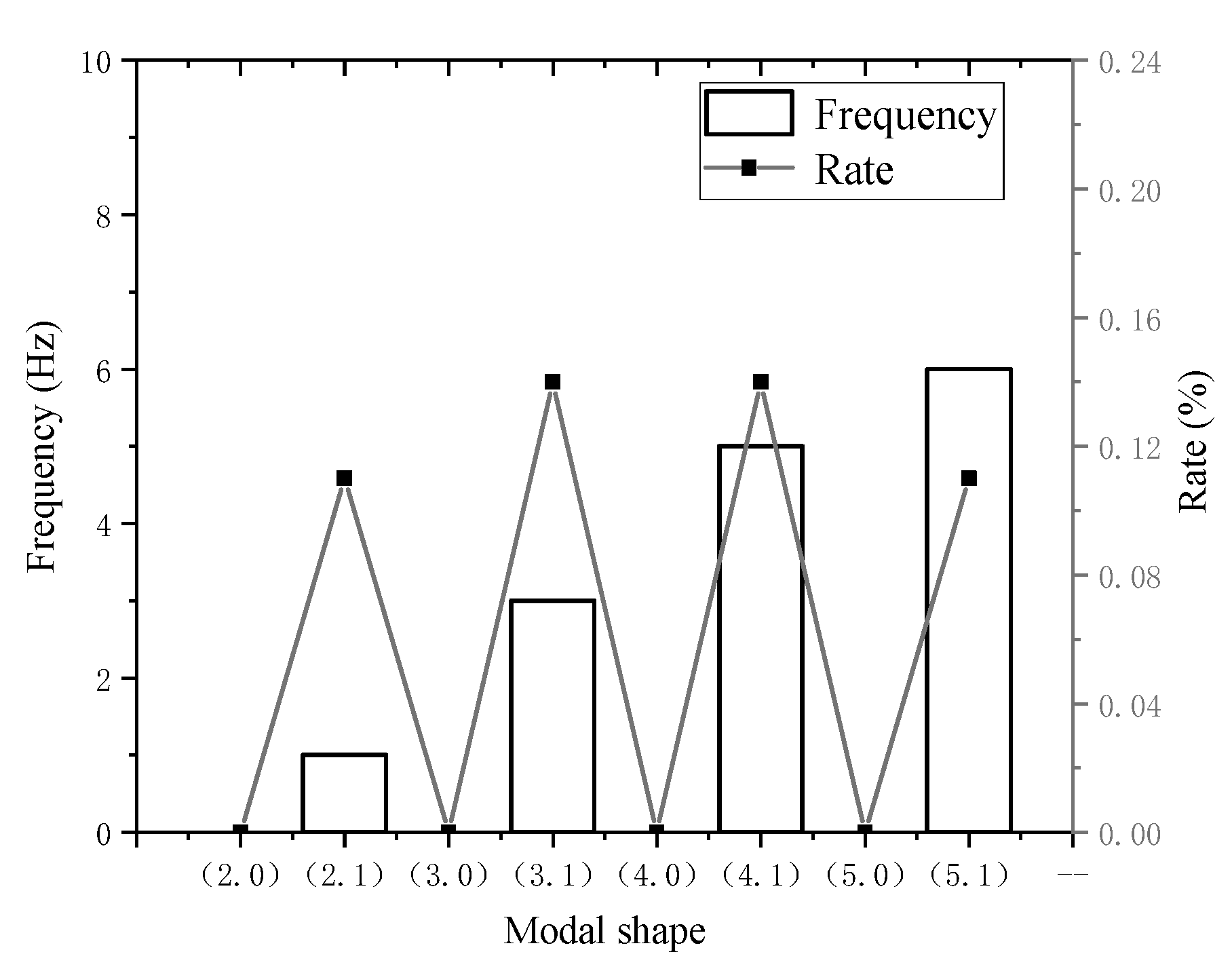
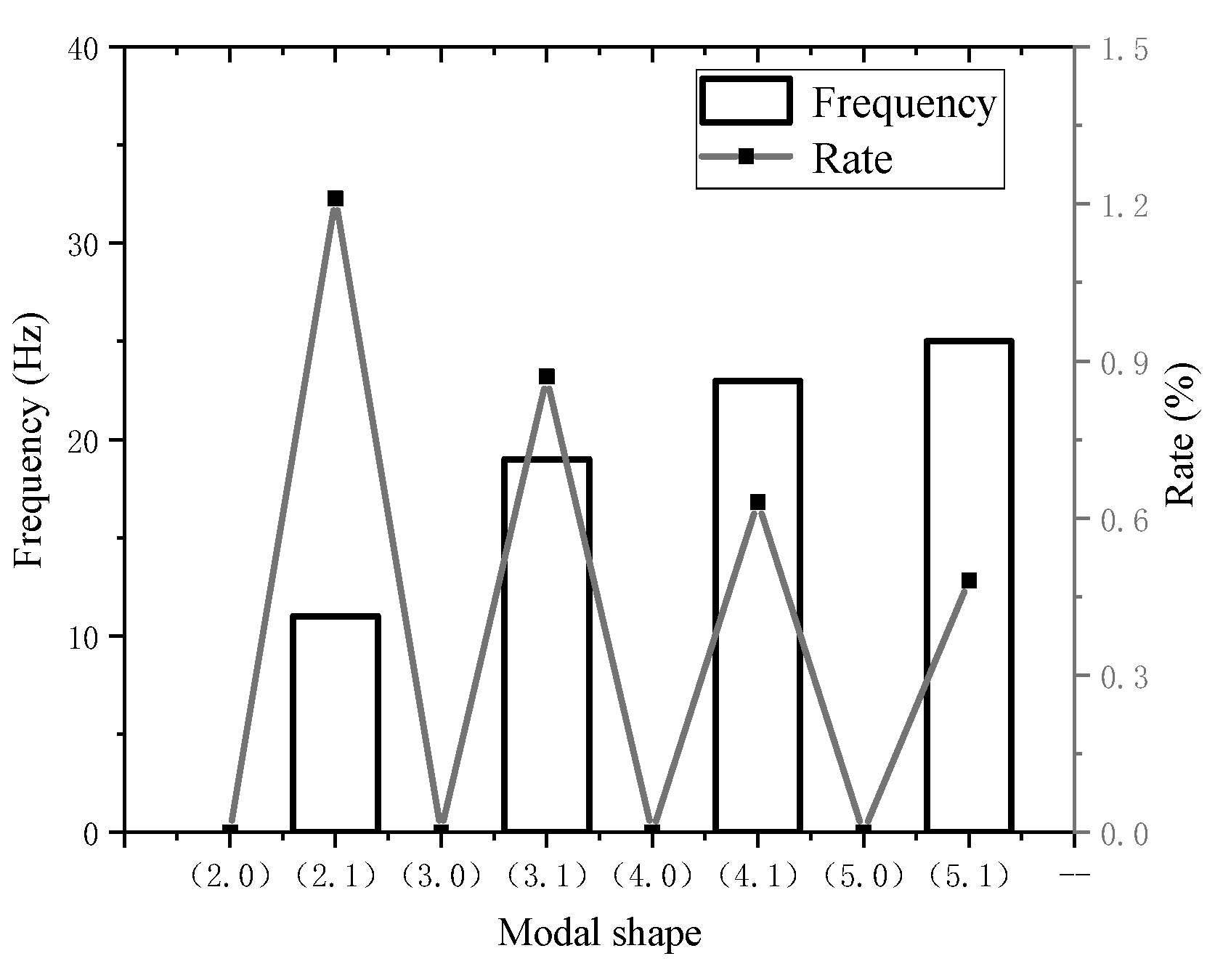
3. Results
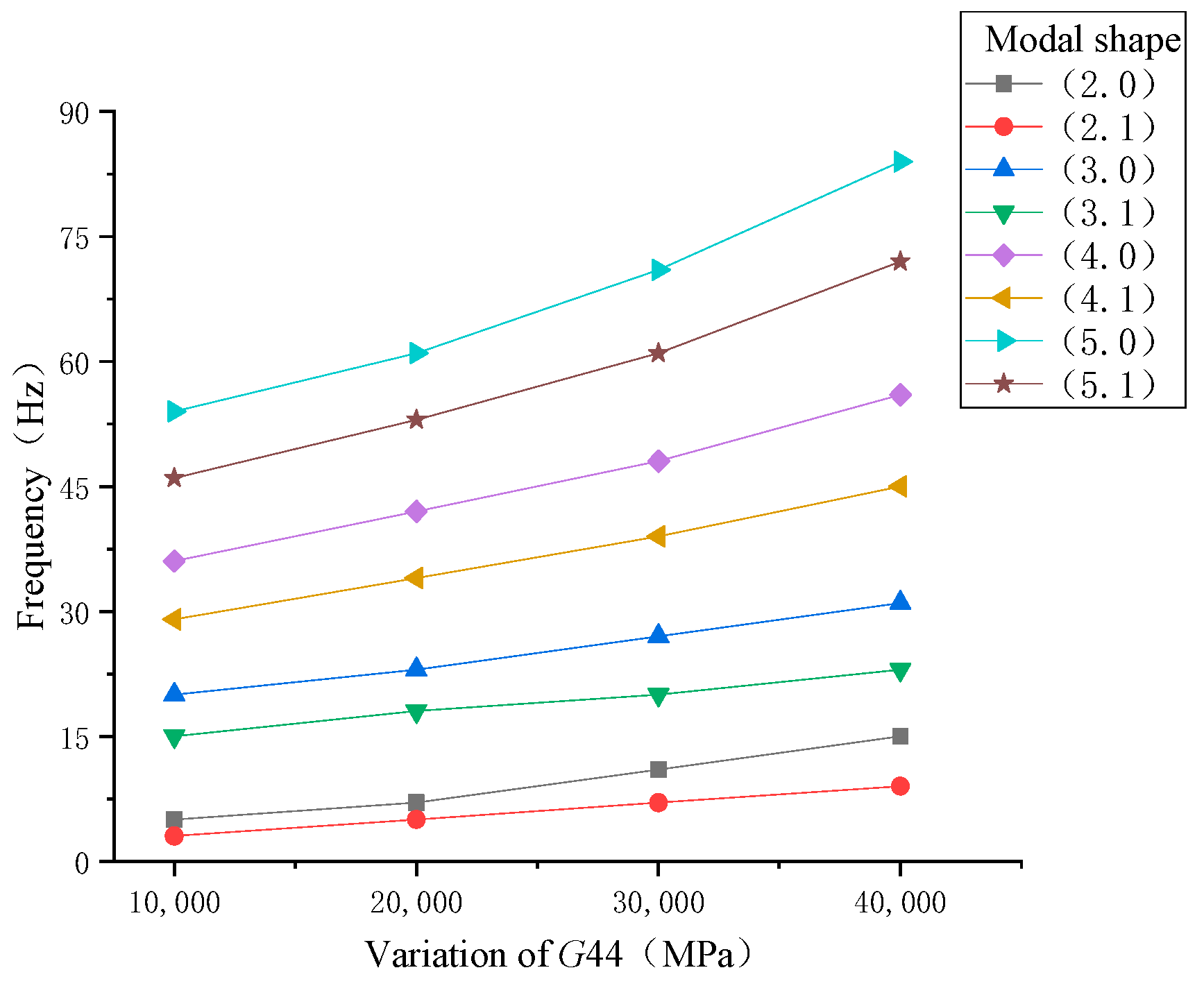
3.1. Correction Method of Anisotropic Material Parameters
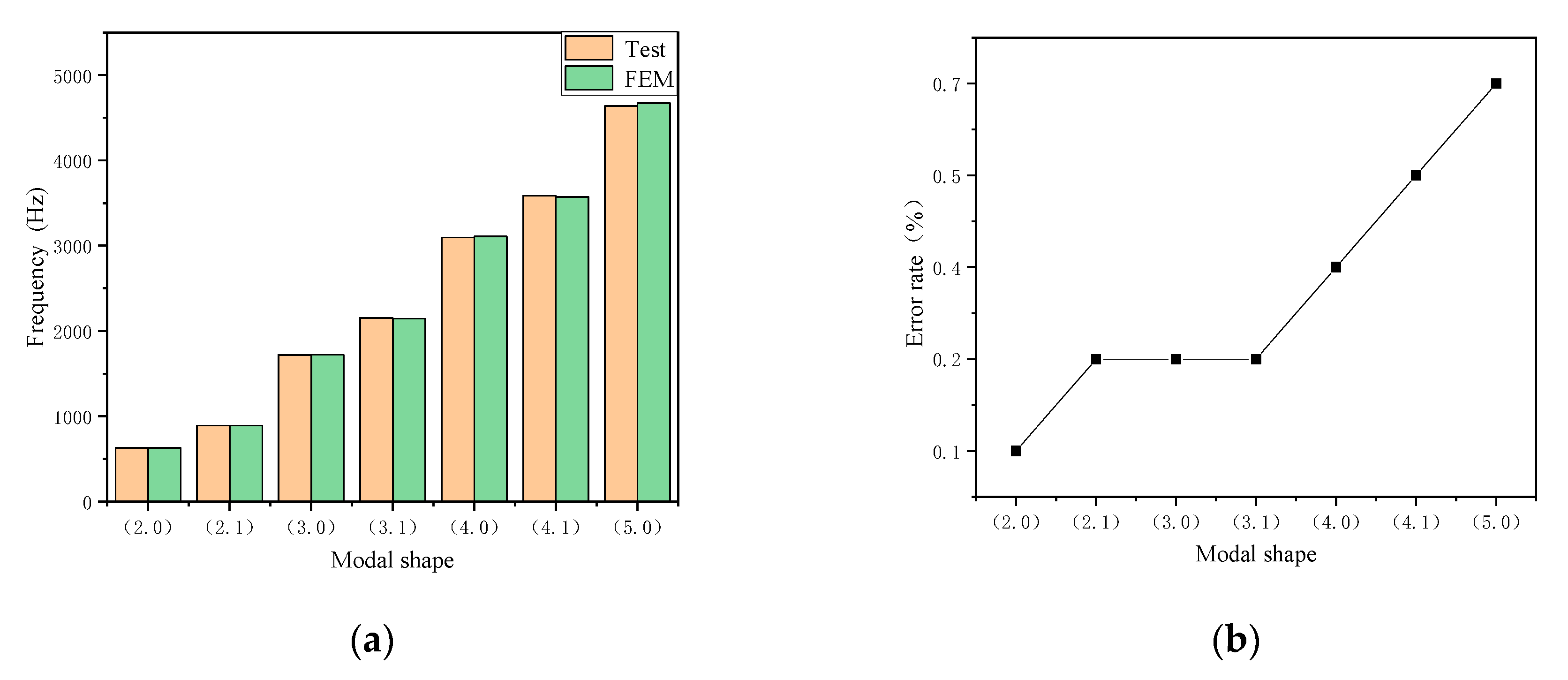
3.2. Modal Testing Results
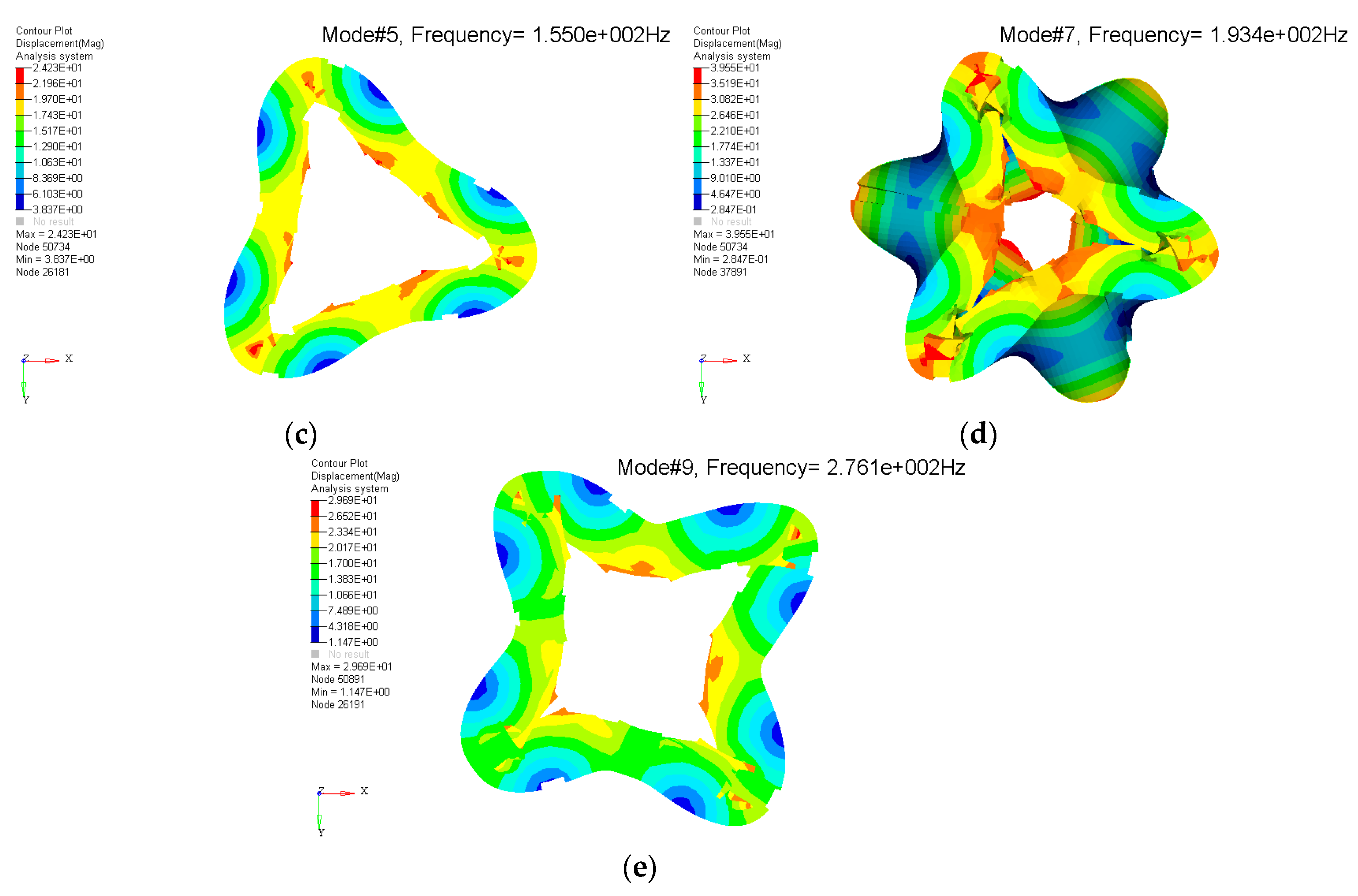
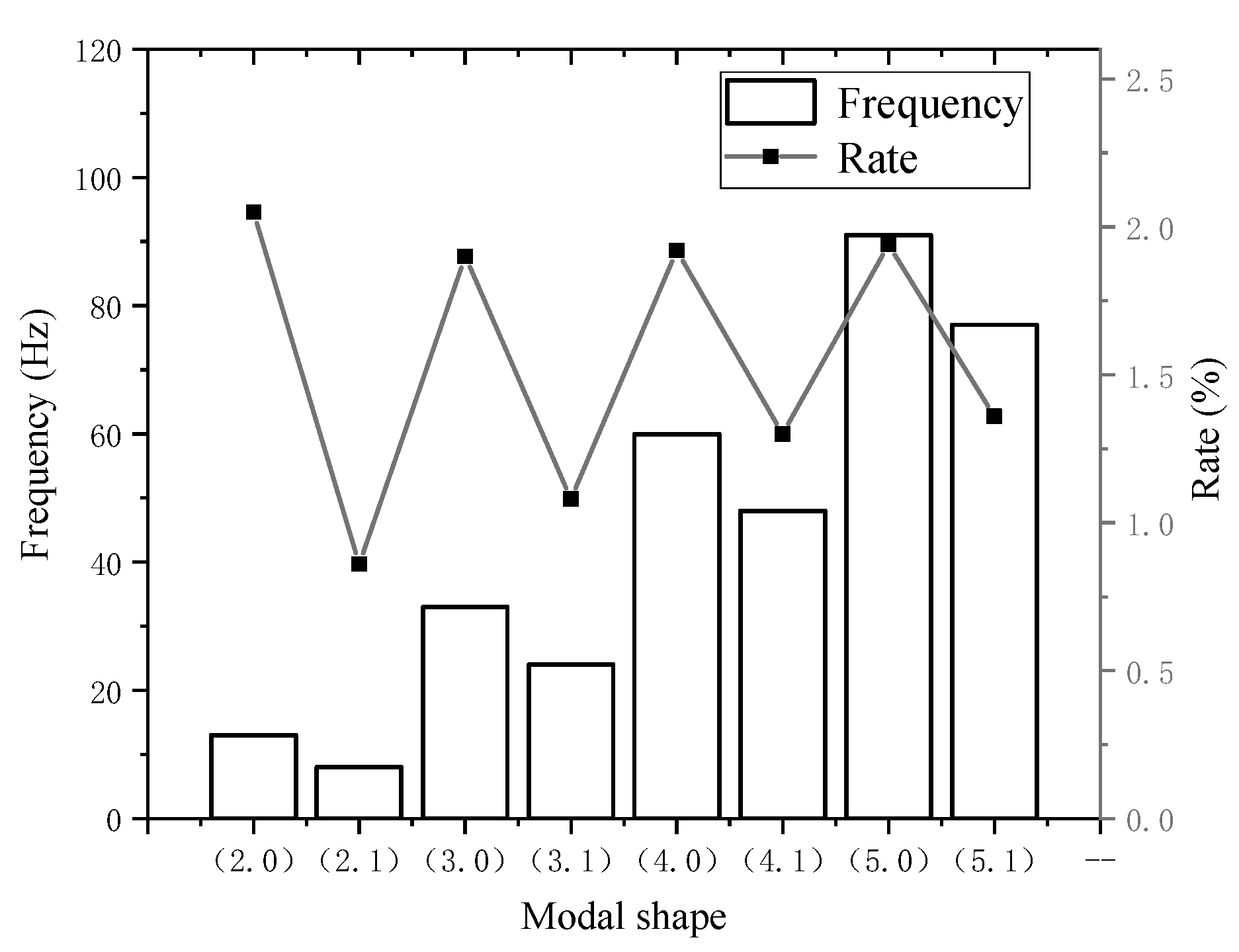
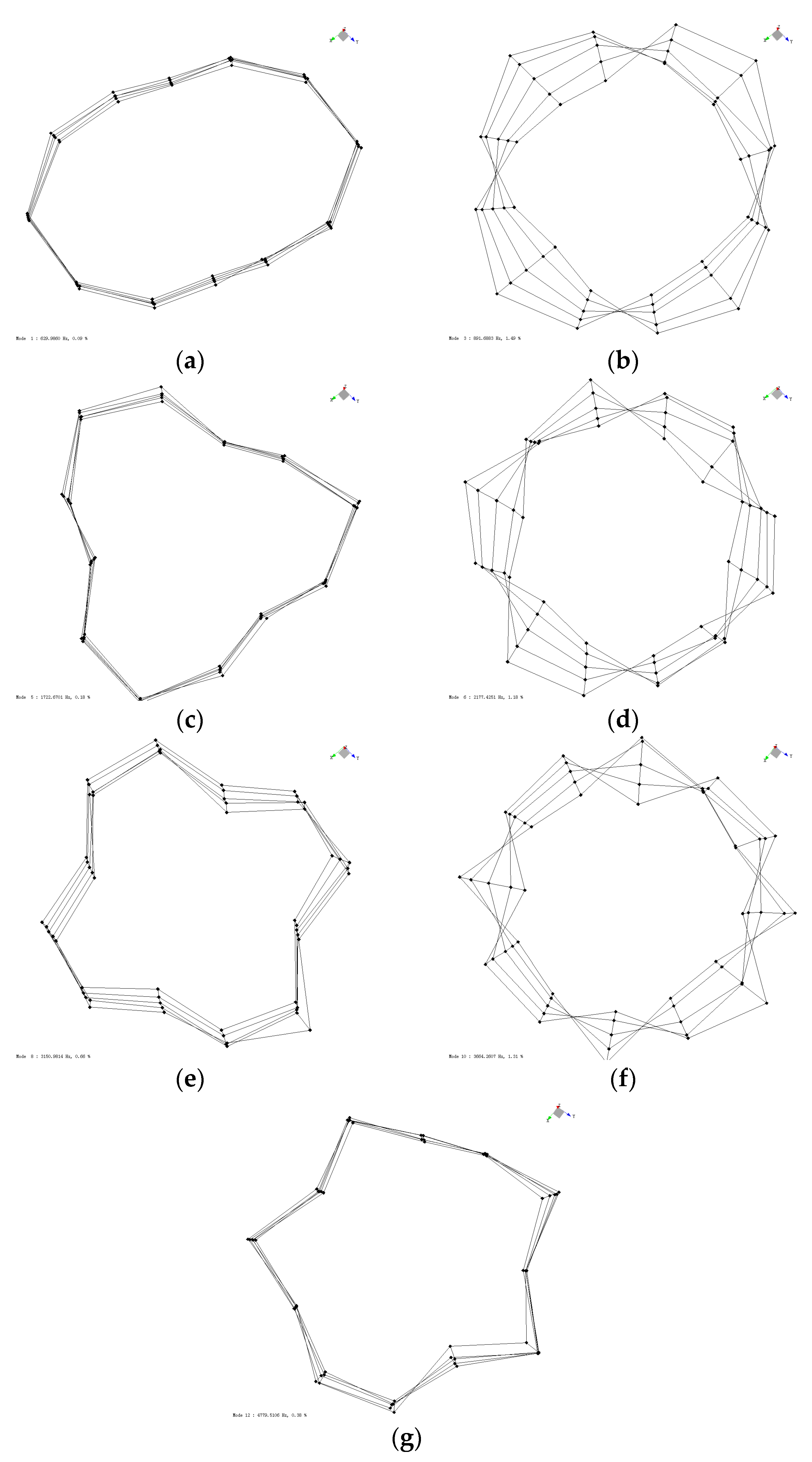
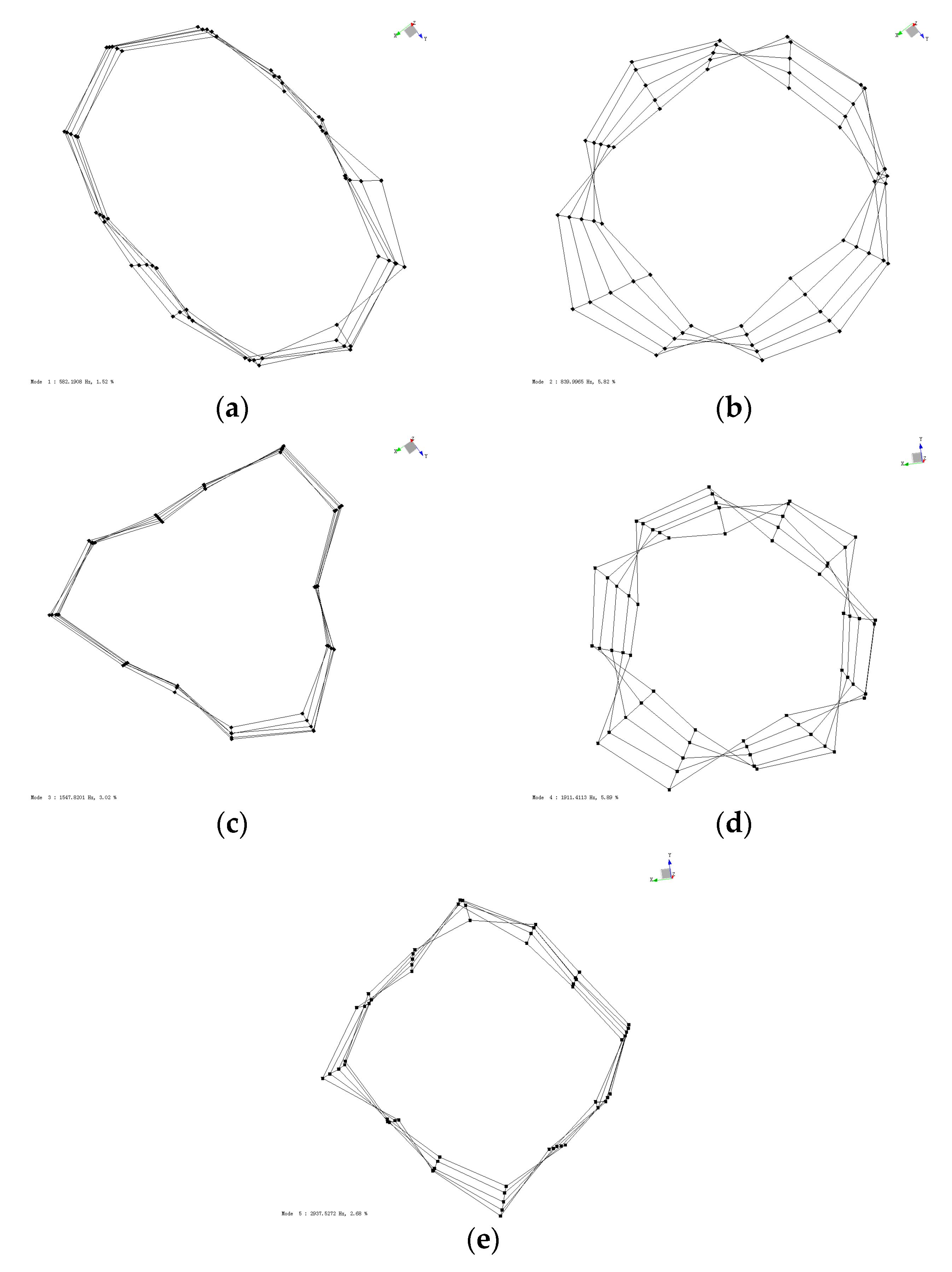
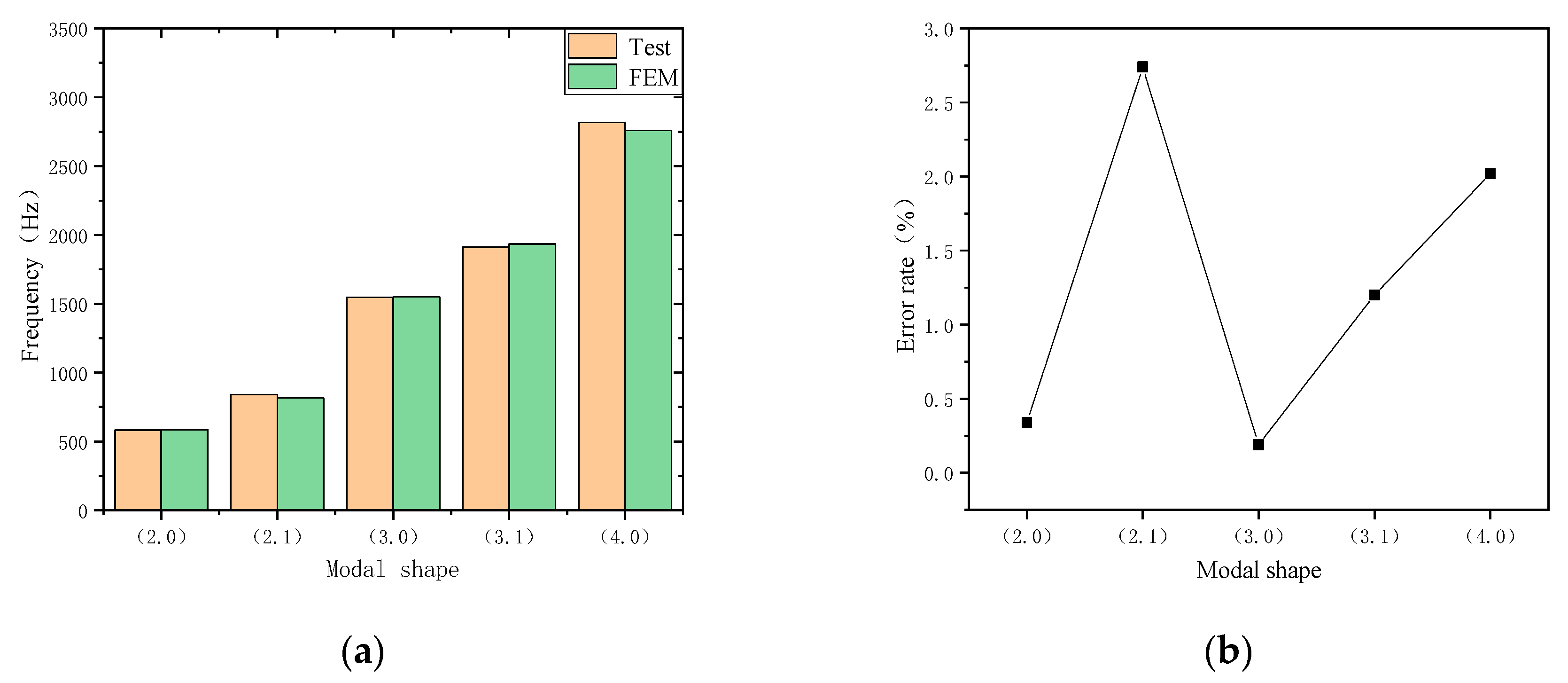
3.2.1. Modal Testing Results of Stator Core
3.2.2. Modal Testing Results of Stator Winding
4. Discussion
- (1)
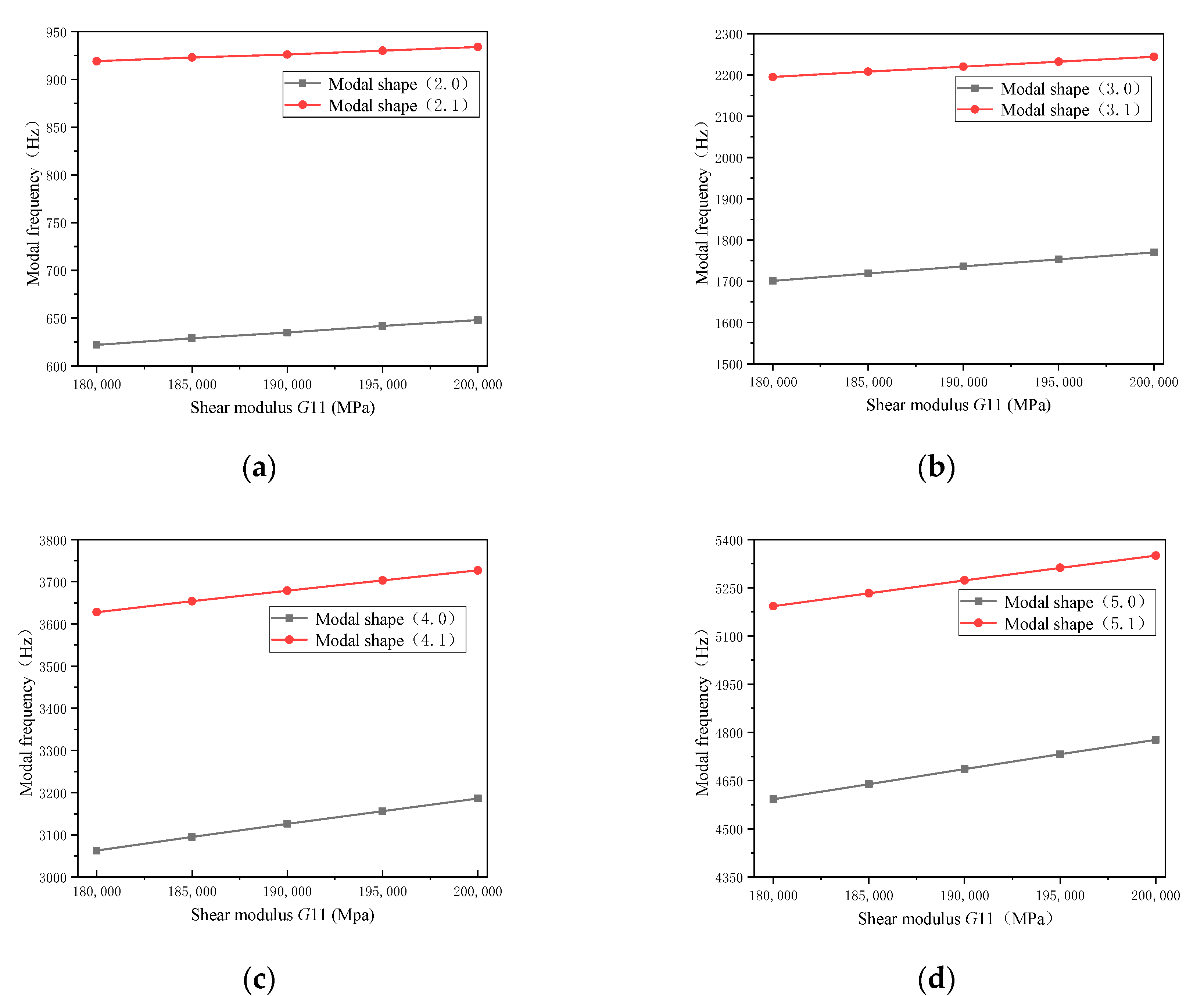
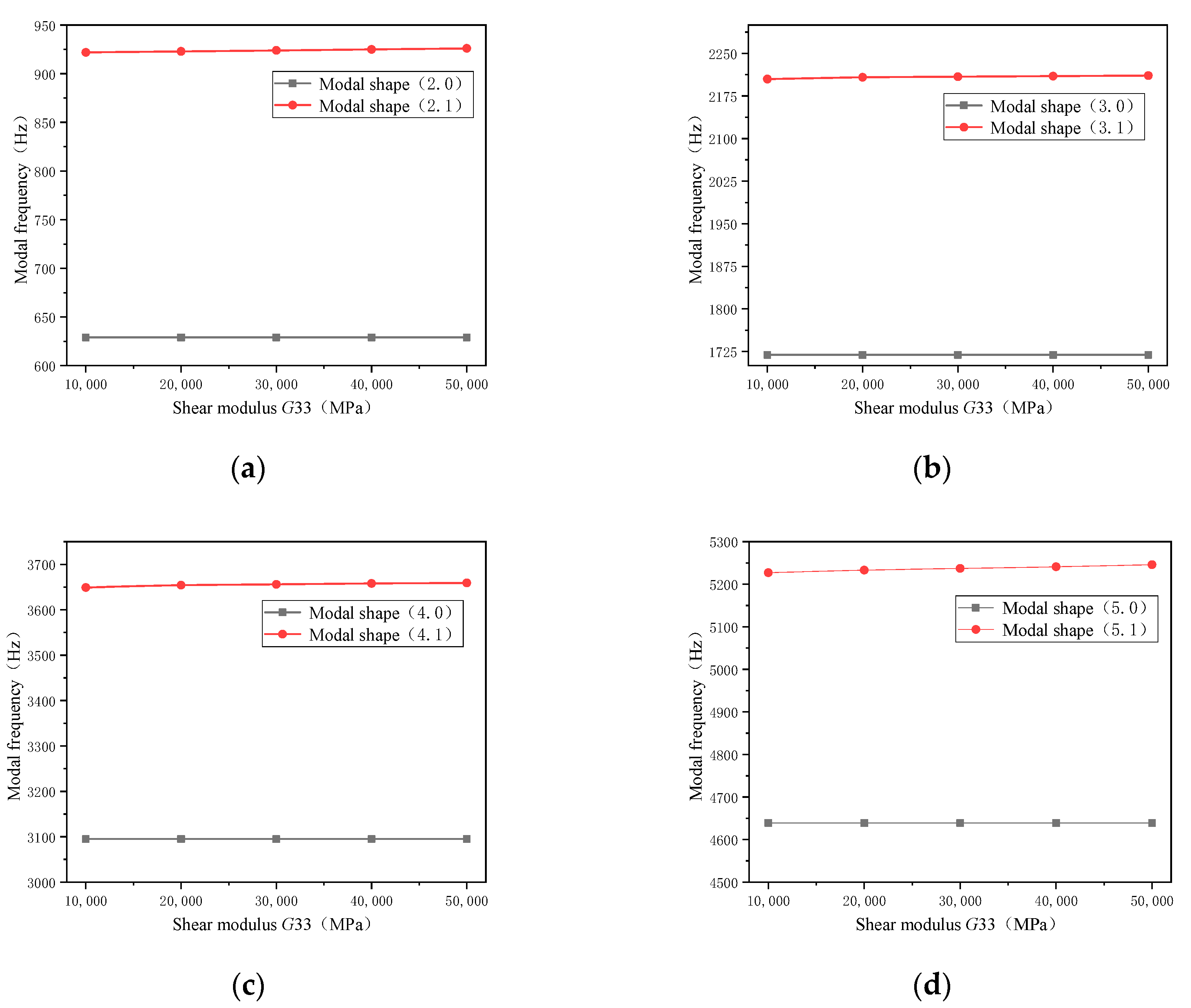
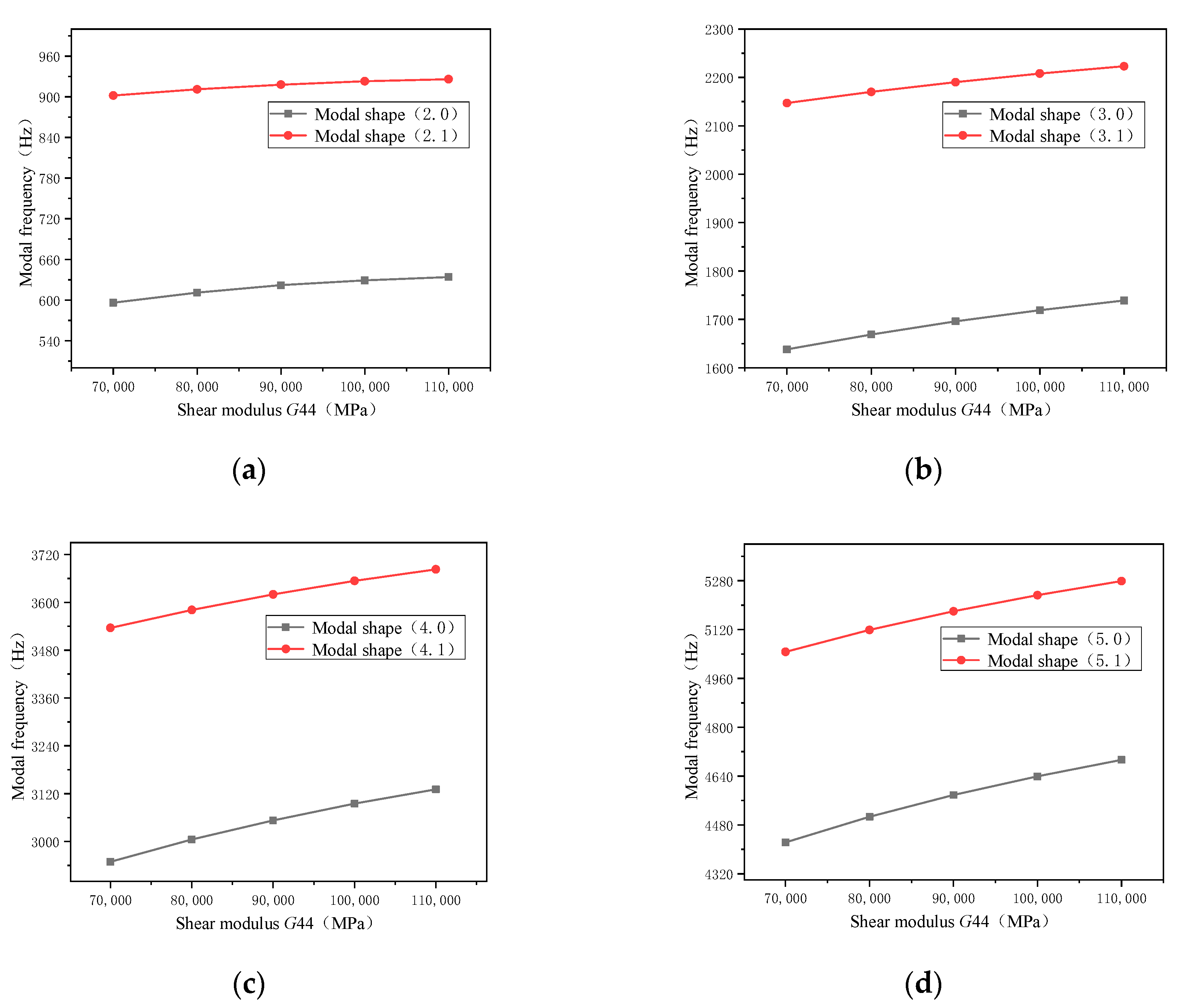
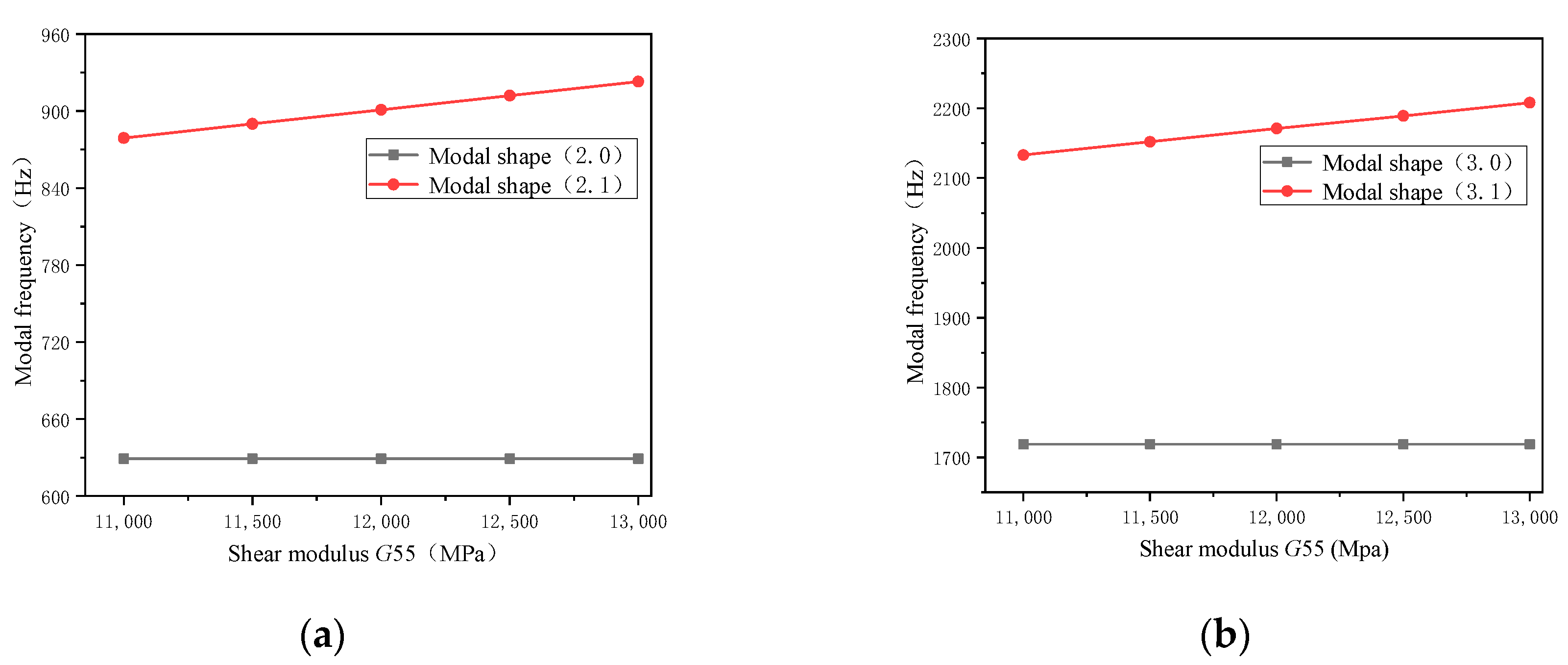
- The analysis showed that the modal frequency was sensitive to material properties. The shear modulus G11 parameter affected the (m, 0) and (m, 1) modal frequencies. The shear modulus G33 parameter affected the (m, 1) modal frequency. The shear modulus G44 parameter affected the (m, 0) and (m, 1) modal frequencies. The shear modulus G55 parameter affected the (m, 1) modal frequency.
- (2)
- The effect of shear modulus G11 on (m, 0) was greater than that on (m, 1), and the effect on the higher order was greater than that on the lower order. The shear modulus G44 had a greater influence on the modal frequency than G11, and the modal frequency changed gradually as the material parameters decreased. The lower order (m, 1) was more sensitive to the shear modulus G55 parameter than the higher order.
- (3)
- The anisotropic material properties of the stator can guarantee the accuracy of the finite element model. The anisotropic material parameter correction method proposed in this paper can quickly determine the equivalent material parameters of a stator and winding.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
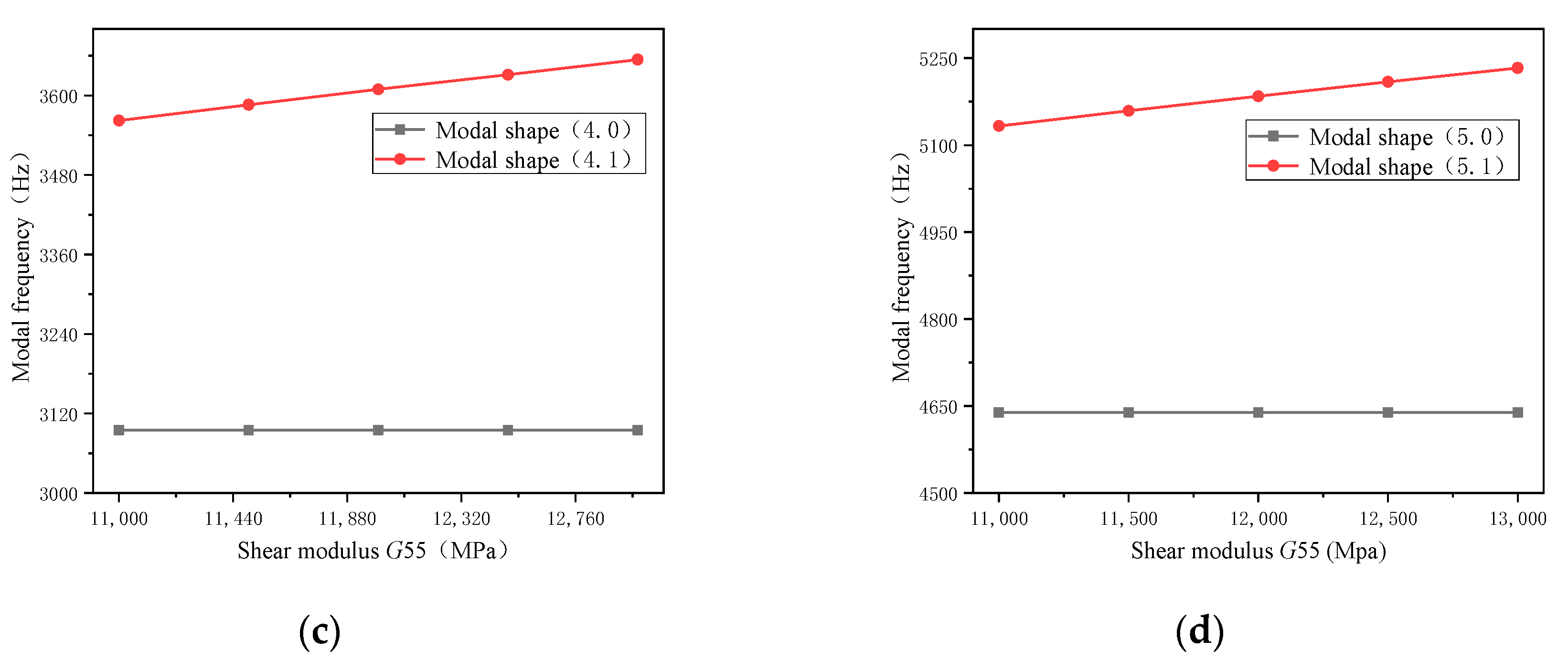
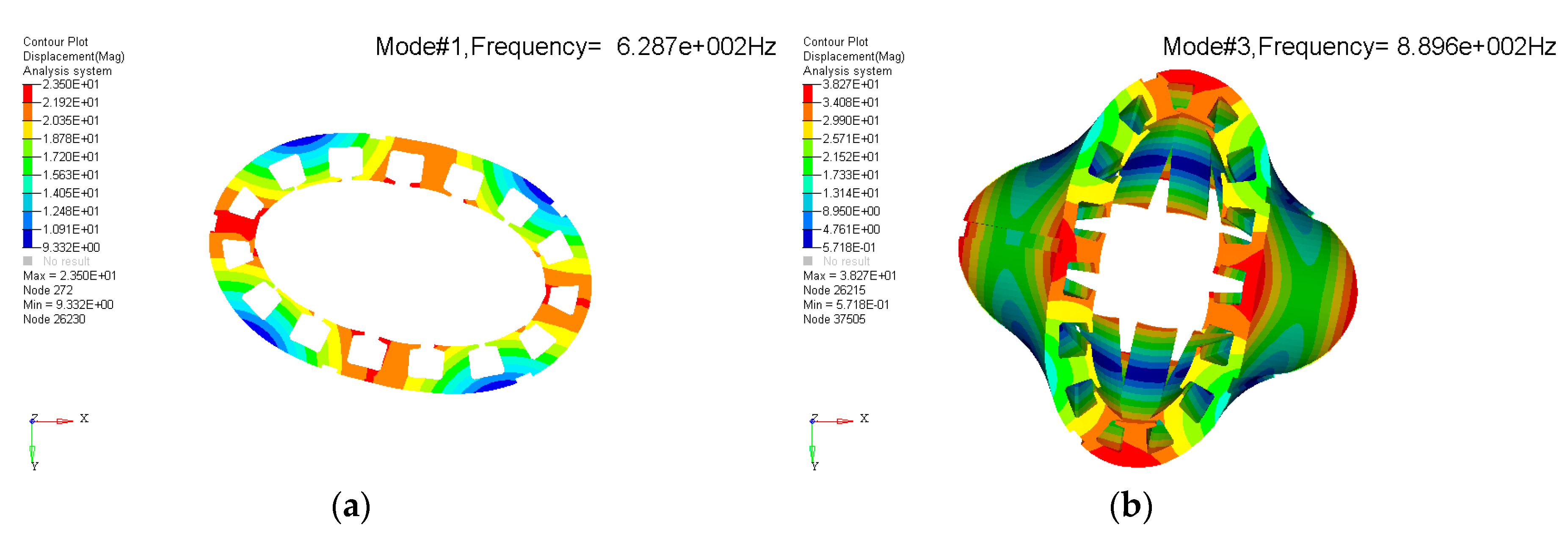
Appendix B
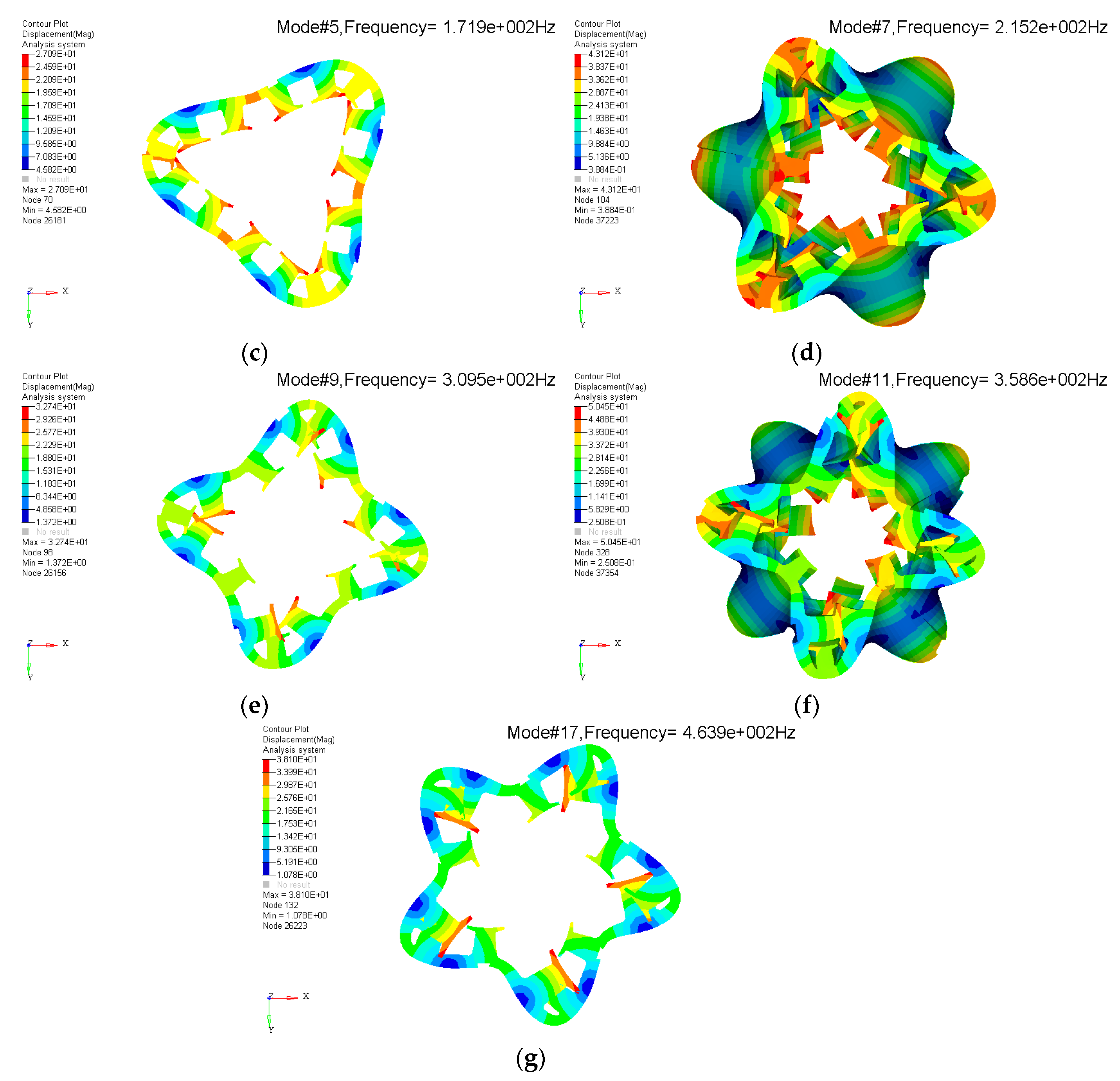
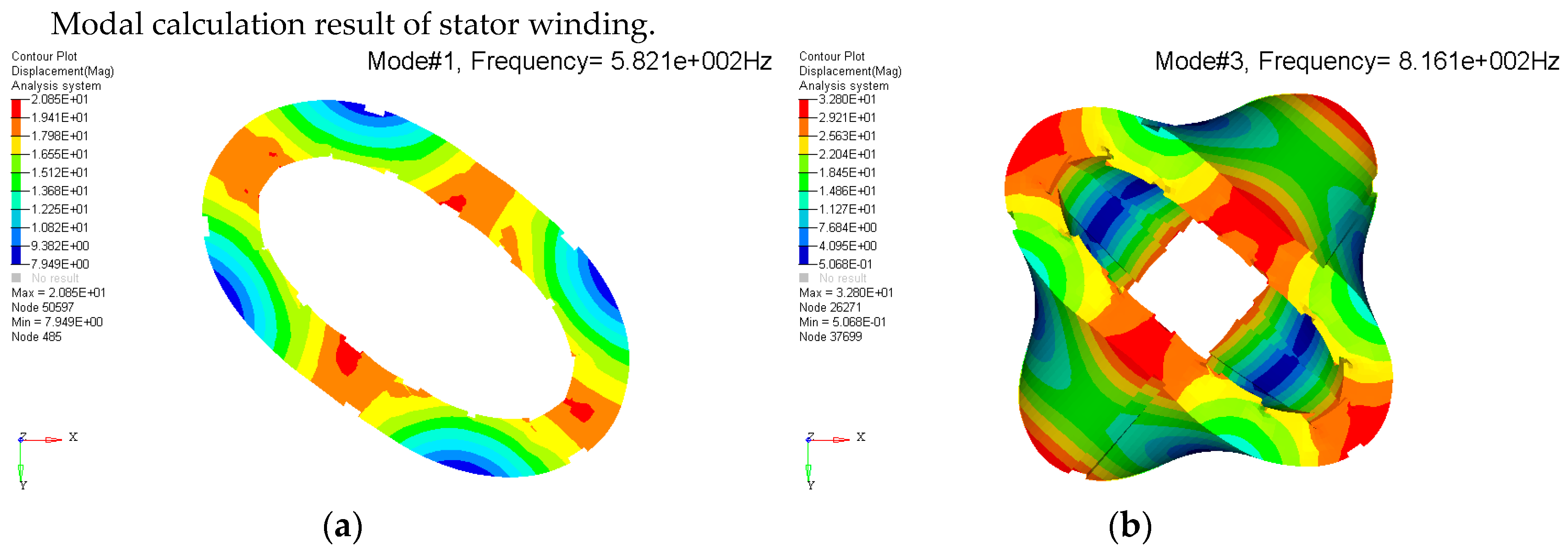
Appendix C
References
- Takeno, M.; Chiba, A.; Hoshi, N.; Ogasawara, S.; Takemoto, M.; Rahman, M.A. Test results and torque improvement of the 50-kw switched reluctance motor designed for hybrid electric vehicles. IEEE Trans. Ind. Appl. 2012, 48, 1327–1334. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, H.; Yang, Z. Design indicators and structure optimisation of switched reluctance machine for electric vehicles. IET Electr. Power Appl. 2015, 9, 319–331. [Google Scholar] [CrossRef]
- Radimov, N.; Ben-Hail, N.; Rabinovici, R. Switched reluctance machines as three-phase AC autonomous generator. IEEE Trans. Magn. 2006, 42, 3760–3764. [Google Scholar] [CrossRef]
- Djelloul-Khedda, Z.; Boughrara, K.; Dubas, F.; Ibtiouen, R. Nonlinear Analytical Prediction of Magnetic Field and Electromagnetic Performances in Switched Reluctance Machines. IEEE Trans. Magn. 2017, 53, 1–11. [Google Scholar] [CrossRef]
- Liang, X.; Li, G.; Ojeda, J.; Gabsi, M.; Ren, Z. Comparative Study of Classical and Mutually Coupled Switched Reluctance Motors Using Multiphysics Finite-Element Modeling. IEEE Trans. Ind. Electron. 2013, 61, 5066–5074. [Google Scholar] [CrossRef]
- Lin, F.; Zuo, S.; Deng, W.; Wu, S. Modeling and Analysis of Electromagnetic Force, Vibration, and Noise in Permanent-Magnet Synchronous Motor Considering Current Harmonics. IEEE Trans. Ind. Electron. 2016, 63, 7455–7466. [Google Scholar] [CrossRef]
- Torregrossa, D.; Khoobroo, A.; Fahimi, B. Prediction of Acoustic Noise and Torque Pulsation in PM Synchronous Machines with Static Eccentricity and Partial Demagnetization Using Field Reconstruction Method. IEEE Trans. Ind. Electron. 2012, 59, 934–944. [Google Scholar] [CrossRef]
- Santos, F.L.M.D.; Anthonis, J.; Naclerio, F.; Gyselinck, J.J.C.; van der Auweraer, H.; Goes, L.C.S. Multiphysics NVH Modeling: Simulation of a Switched Reluctance Motor for an Electric Vehicle. IEEE Trans. Ind. Electron. 2014, 61, 469–476. [Google Scholar] [CrossRef]
- Fleck, N.A.; Deshpande, V.S. The resistance of clamped sandwich beams to shock loading. J. Appl. Mech. 2004, 71, 386–401. [Google Scholar] [CrossRef]
- Rosca, I.C.; Filip, M.; Helerea, E. Three-phase squirrel-cage induction motor modal analyses. Theoretical and experimental aspects. In Proceedings of the 13th International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Brasov, Romania, 24–26 May 2012. [Google Scholar]
- Ying, X.; Yan, W.; Sen, L.; Hongyan, G.; Haisong, L. Modal calculation and test of small asynchronous motor. Transl. China Electrotech. Soc. 2015, 30, 1–9. [Google Scholar]
- Bao, X.; Liu, J.; Ni, Y.; Liu, B. Modal analysis and natural frequency calculation of the stator in automotive claw-pole alternator. Automot. Eng. 2011, 33, 1088–1091. [Google Scholar]
- Zuo, S.G.; Zhang, Y.; Yan, J.; Zhang, G.; Lin, F.; Wu, S. Optimization of vibration and noise in permanent magnet synchronous motor considering stator anisotropy. Xi’an Jiaotong Univ. Xuebao 2017, 51, 60–68. [Google Scholar]
- Guo, X.; Zhong, R.; Zhang, M.; Ding, D.; Sun, W. Fast computation of radial vibration in switched reluctance motors. IEEE Trans. Ind. Electron. 2018, 65, 4588–4598. [Google Scholar] [CrossRef]
- Schlegl, B.; Schönleitner, F.; Marn, A.; Neumayer, F.; Heitmeir, F. Analytical determination of the orthotropic material behavior of stator bars in the range of the end windings and determination of the material characteristics of the orthotropic composite space brackets via experimental modal analysis and FE-calculation. In Proceedings of the International Conference on Electrical Machines, Marseille, France, 2–5 September 2012. [Google Scholar]
- Hu, S.; Zuo, S.; Liu, M.; Wu, H. Method for acquisition of equivalent material parameters considering orthotropy of stator core and windings in SRM. IET Electr. Power Appl. 2019, 13, 580–586. [Google Scholar] [CrossRef]
- Sun, J.J.; Feng, H.J.; Zhu, C.S. Identification of laminated core and winding’s physical parameters by stator’s modal testings. In Proceedings of the 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014. [Google Scholar]
- Mcmeeking, R.; Spuskanyuk, A.; He, M.; Deshpande, V.; Fleck, N.; Evans, A. An analytical model for the response to water blast of unsupported metallic sandwich panels. Int. J. Solids Struct. 2008, 45, 478–496. [Google Scholar] [CrossRef]
- Yin, H.; Ma, F.; Zhang, X.; Gu, C.; Gao, H.; Wang, Y. Research on Equivalent Material Properties and Modal Analysis Method of Stator System of Permanent Magnet Motor with Concentrated Winding. IEEE Access 2019, 7, 64592–64602. [Google Scholar] [CrossRef]
- Kirschneck, M.; Rixen, D.; Polinder, H. Model Reduction Methods for Magnetic Fields Based on Modal Analysis. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Chen, Y.X.; Zhu, Z.Q.; Ying, S.C. Analysis and Control of Motor Noise; Zhejiang University Press: Hangzhou, China, 1987; Volume 1, pp. 36–37. ISBN 7-308-00025-7. [Google Scholar]
- Chai, F.; Li, Y.; Pei, Y.; Li, Z. Accurate modelling and modal analysis of stator system in permanent magnet synchronous motor with concentrated coils for vibration prediction. IET Electr. Power Appl. 2018, 12, 1225–1232. [Google Scholar] [CrossRef]
- Chen, Y.H.; Ding, T.H.; Tian, L. Research on calculation method of motor lamination core vibration characteristics. Electr. Mach. Control 2014, 18, 71–76. [Google Scholar]



| Parameter | Definition |
|---|---|
| RHO | Mass density |
| Gij | The material property matrix |
| Ai | Thermal expansion coefficient vector |
| TREF | Reference temperature |
| GE | Structural element damping coefficient |
| Parameter | Unit | Stator Core |
|---|---|---|
| RHO | g·m-3 | 7680 |
| G11 | MPa | 200,000 |
| G33 | MPa | 20,000 |
| G44 | MPa | 100,000 |
| G55 | Mpa | 13,000 |
| Parameter | Unit | Value |
|---|---|---|
| Number of poles | / | 5 |
| Number of stator slots | / | 15 |
| Number of phases | / | 3 |
| Stator outer/inner diameter | mm | 140/99.6 |
| Rotor outer/inner diameter | mm | 98.6/30 |
| Active axial length | mm | 77.5 |
| Rated power | kW | 2.2 |
| Winding | / | Concentrated |
| Coil turns | / | 3 |
| Parameter | RHO | G11 | G33 | G44 | G55 |
|---|---|---|---|---|---|
| ID | |||||
| 1-1 | 7680 | 200,000 | 20,000 | 100,000 | 13,000 |
| 1-2 | 7680 | 195,000 | 20,000 | 100,000 | 13,000 |
| 1-3 | 7680 | 190,000 | 20,000 | 100,000 | 13,000 |
| 1-4 | 7680 | 185,000 | 20,000 | 100,000 | 13,000 |
| 1-5 | 7680 | 180,000 | 20,000 | 100,000 | 13,000 |
| 2-1 | 7680 | 185,000 | 50,000 | 100,000 | 13,000 |
| 2-2 | 7680 | 185,000 | 40,000 | 100,000 | 13,000 |
| 2-3 | 7680 | 185,000 | 30,000 | 100,000 | 13,000 |
| 2-4 | 7680 | 185,000 | 20,000 | 100,000 | 13,000 |
| 2-5 | 7680 | 185,000 | 10,000 | 100,000 | 13,000 |
| 3-1 | 7680 | 185,000 | 20,000 | 110,000 | 13,000 |
| 3-2 | 7680 | 185,000 | 20,000 | 100,000 | 13,000 |
| 3-3 | 7680 | 185,000 | 20,000 | 90,000 | 13,000 |
| 3-4 | 7680 | 185,000 | 20,000 | 80,000 | 13,000 |
| 3-5 | 7680 | 185,000 | 20,000 | 70,000 | 13,000 |
| 4-1 | 7680 | 185,000 | 20,000 | 100,000 | 13,000 |
| 4-2 | 7680 | 185,000 | 20,000 | 100,000 | 12,500 |
| 4-3 | 7680 | 185,000 | 20,000 | 100,000 | 12,000 |
| 4-4 | 7680 | 185,000 | 20,000 | 100,000 | 11,500 |
| 4-5 | 7680 | 185,000 | 20,000 | 100,000 | 11,000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Jiao, Z.; Xia, H.; Yao, Y. Parameter Equivalent Method of Stator Anisotropic Material Based on Modal Analysis. Energies 2019, 12, 4257. https://doi.org/10.3390/en12224257
Zhang Z, Jiao Z, Xia H, Yao Y. Parameter Equivalent Method of Stator Anisotropic Material Based on Modal Analysis. Energies. 2019; 12(22):4257. https://doi.org/10.3390/en12224257
Chicago/Turabian StyleZhang, Zeyu, Zhiyong Jiao, Hongbing Xia, and Yuhan Yao. 2019. "Parameter Equivalent Method of Stator Anisotropic Material Based on Modal Analysis" Energies 12, no. 22: 4257. https://doi.org/10.3390/en12224257
APA StyleZhang, Z., Jiao, Z., Xia, H., & Yao, Y. (2019). Parameter Equivalent Method of Stator Anisotropic Material Based on Modal Analysis. Energies, 12(22), 4257. https://doi.org/10.3390/en12224257




