4.1. Concept of D–S Evidence Theory
D–S evidence theory can fuse information from different data sources. It is an effective method of information fusion. It has achieved good results in many fields.
Suppose Θ is the identification framework and 2Θ is the power set of Θ. If the mapping relationship m: 2Θ→[0, 1] satisfies , , then m is called the basic probability assignment (BPA) function and m(A) is the basic reliability of evidence to A. If and m (A) > 0, then A is named the focal element of BPA.
However, when there is a high conflict between evidences, the Dempster rule has a big defect in the process of synthesis [
39]. The synthesis results may be even completely contrary to the actual situation. In order to solve this problem, this paper introduces weight coefficient to readjust BPA. The specific process is as follows:
- (1)
Calculate the conflict extent
kij between evidence
Ei and
Ej (
j = 1, 2, …,
i − 1,
i + 1, …
n) to form the collision vector
Ki.
- (2)
Standardize the collision vector
Ki.
- (3)
Calculate the entropy value
Hi of
KiN- (4)
Calculate the reciprocal of
Hi- (5)
Calculate the weight coefficient
wi of
Ei.
Through above five steps, we can get the weight coefficients of each evidence, and combine them to obtain the weight vector Wi = {w1, w2, …, wn}.
Let the maximum weight be
wmax = max{
w1,
w2, …,
wn}, and the relative values of weight coefficients can be obtained as:
W* = (
w1,
w2, …,
wn)/
wmax. Discount coefficient is introduced into the basic probability assignment function, shown as:
where
k = 1, 2, …,
di, and
di is the number of non-Θ focal elements in the identification framework. Therefore, the value of BPA can be adjusted as
mi*(
Ak),
k = 1, 2, …,
di.
To construct the complete BPA, the concept of uncertainty is defined as:
A complete BPA function can be constructed by Formulas (24) and (25).
4.2. Transformer Fault Diagnosis Based on Improved D–S Evidence Theory
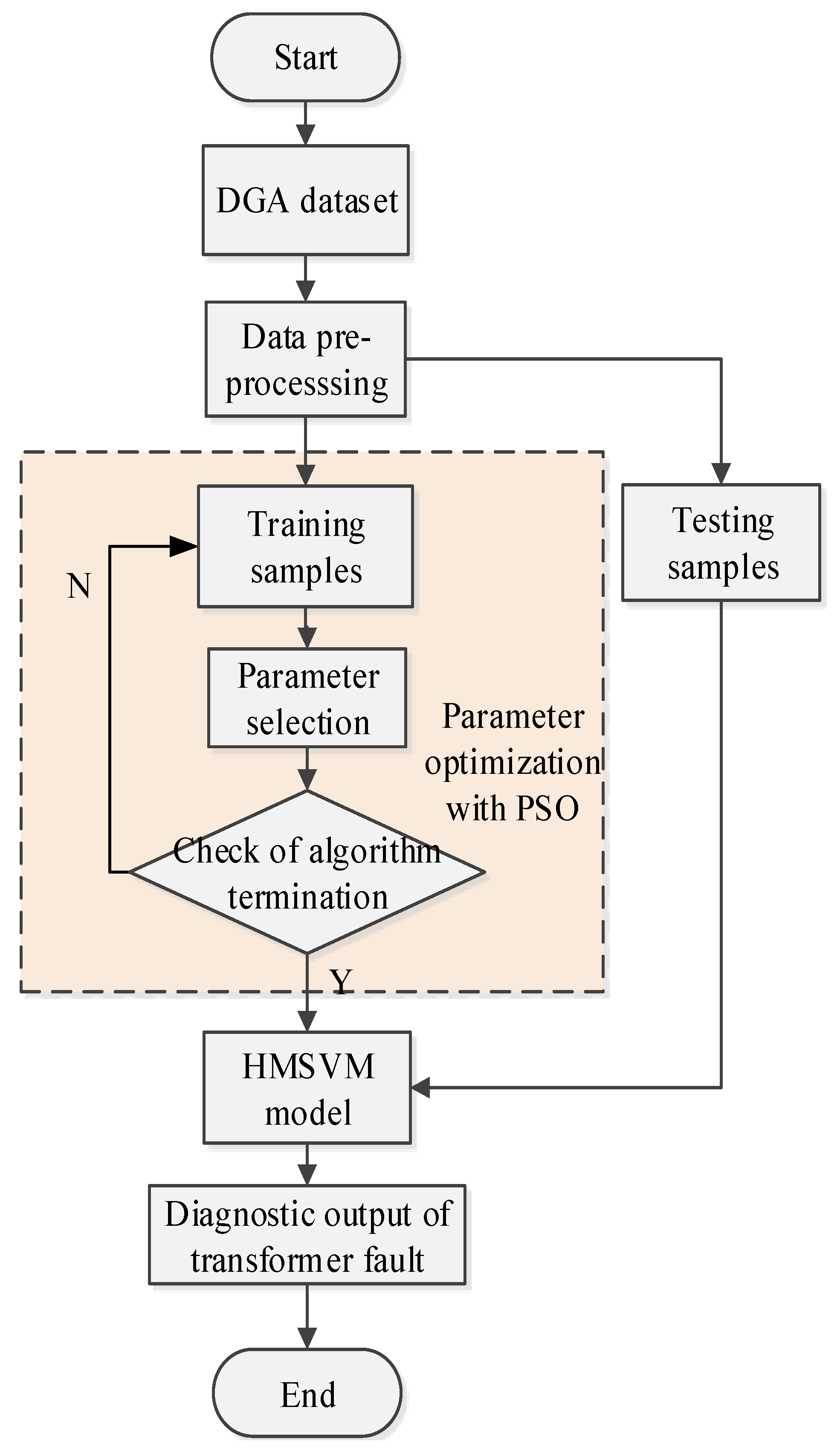
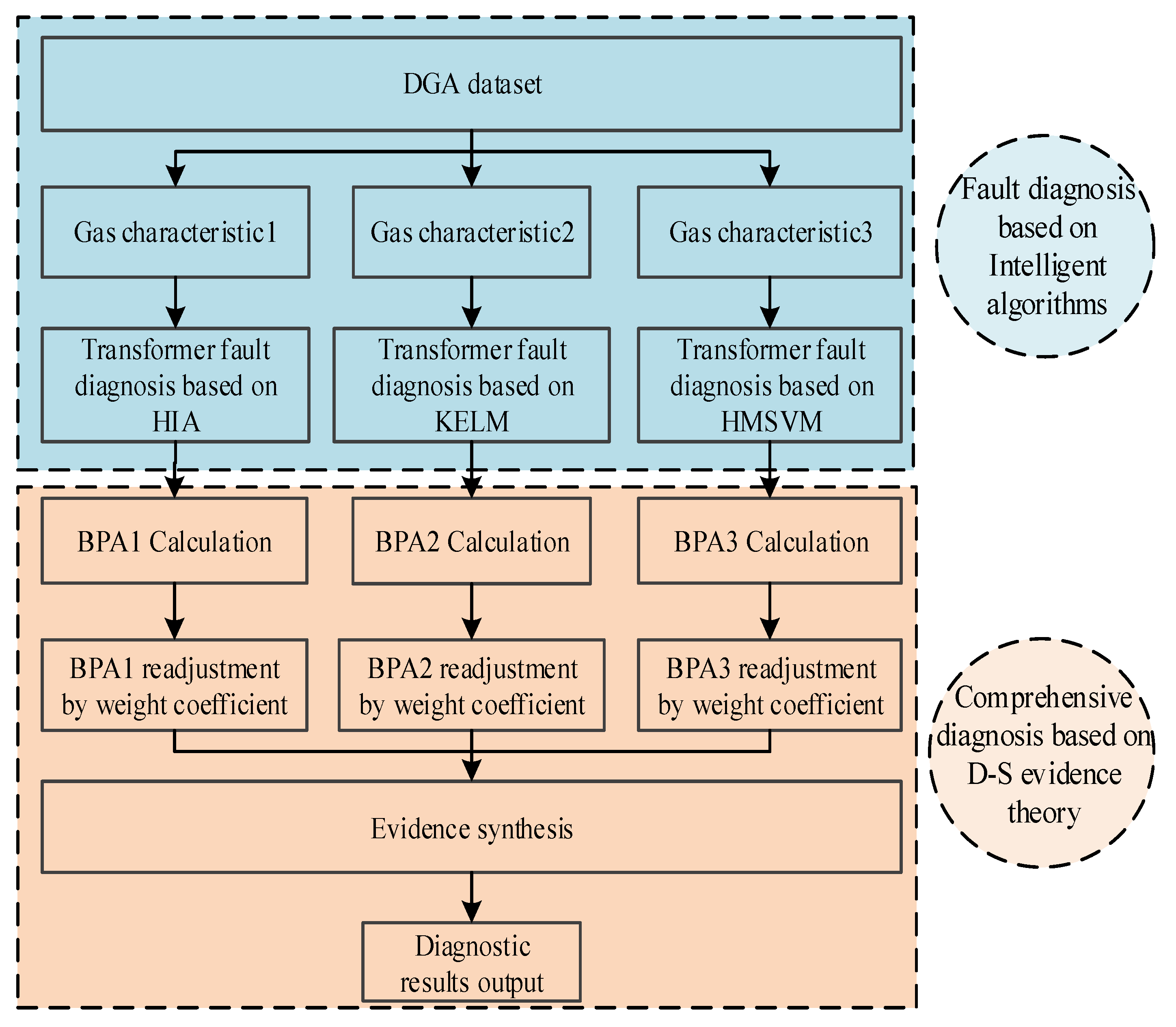
In order to enrich information sources in transformer fault diagnosis and improve the diagnostic efficiency, D–S evidence theory is employed to merge HIA, KELM, and HMSVM together. In this section, a diagnostic fusion model of power transformer fault is constructed based on improved D–S evidence theory. The diagnostic procedure is as follows.
- (1)
Three fault diagnosis models are used to test DGA samples and make a preliminary diagnosis. If a unanimous conclusion is obtained, then stop the operation and output the result directly. Otherwise continue the following steps.
- (2)
Different BPA of three diagnostic approaches are constructed as follows.
a. HIA
In the recognition framework Θ, the Euclidean distances from
Ag to all memory antibodies are calculated. Assuming that the minimum Euclidean distance between
Ag and
Bi is
di, if
di >
σ, and then let
xi = 0, otherwise
xi = 1/
di, where
σ is the affinity threshold,
i = 1, 2, …, 6. In HIA [
40], the BPA of
Ag can be described as follows:
b. KELM
There are 6 kinds of transformer fault states in this paper, that is, the number of recognition types of KELM is 6. If
fi(
x) is used to represent the output function for the
ith state of transformer faults, then the output function
f(
x) of KELM is expressed as [
41]:
The numerical output of KELM is transformed into probabilistic output.
For Sample x, the BPA of KELM is defined as:
c. HMSVM
m3(
Bi) denotes the BPA of HMSVM that a group of DGA samples belong to fault
Ai.
where
P(
Ai) can be calculated by Formula (14).
The above three groups of BPAs are satisfied:
- (3)
The weight coefficient is used to adjust the BPA.
- (4)
The synthesized BPA is discriminated according to the following rules.
Let
A1 and
A2 belong to U, satisfying
where
A1 is the judgment result. Further,
ε1 and
ε2 are preset thresholds, which are set to be 0.2 after repeated comparison.
The fault diagnosis model based on improved evidence theory is shown in
Figure 10.
4.3. Case Analysis and Discussion
In this section, 5 sets of DGA samples are collected from Hebei north electric power company, with actual fault labels attached, shown in
Table 8.
The DGA samples are processed and input into the transformer fault diagnosis model based on HMSVM. The output membership values of five groups of samples are obtained, as shown in
Table 9. The value appears in bold in
Table 9 means the highest membership of each sample.
According to the diagnostic principle of HMSVM, if the sample is located inside the hypersphere, the value of membership is greater, otherwise, the value of membership is smaller.
Table 9 shows that except for Sample 3, the maximum membership of DGA samples is much greater than that of other fault states. This is because the four samples belong to only one state hypersphere, so the diagnosis conclusion is clear, and the membership value is usually greater than 0.5. For T
12 and T
3, the membership values of Sample 3 are greater than 0.5, and close to each other. This is because the sample is located in the overlapping area of hyperspheres, which is prone to misjudgment. According to HMSVM diagnostic criteria, the diagnosis conclusion of this sample is T
3, which is not consistent with the actual fault.
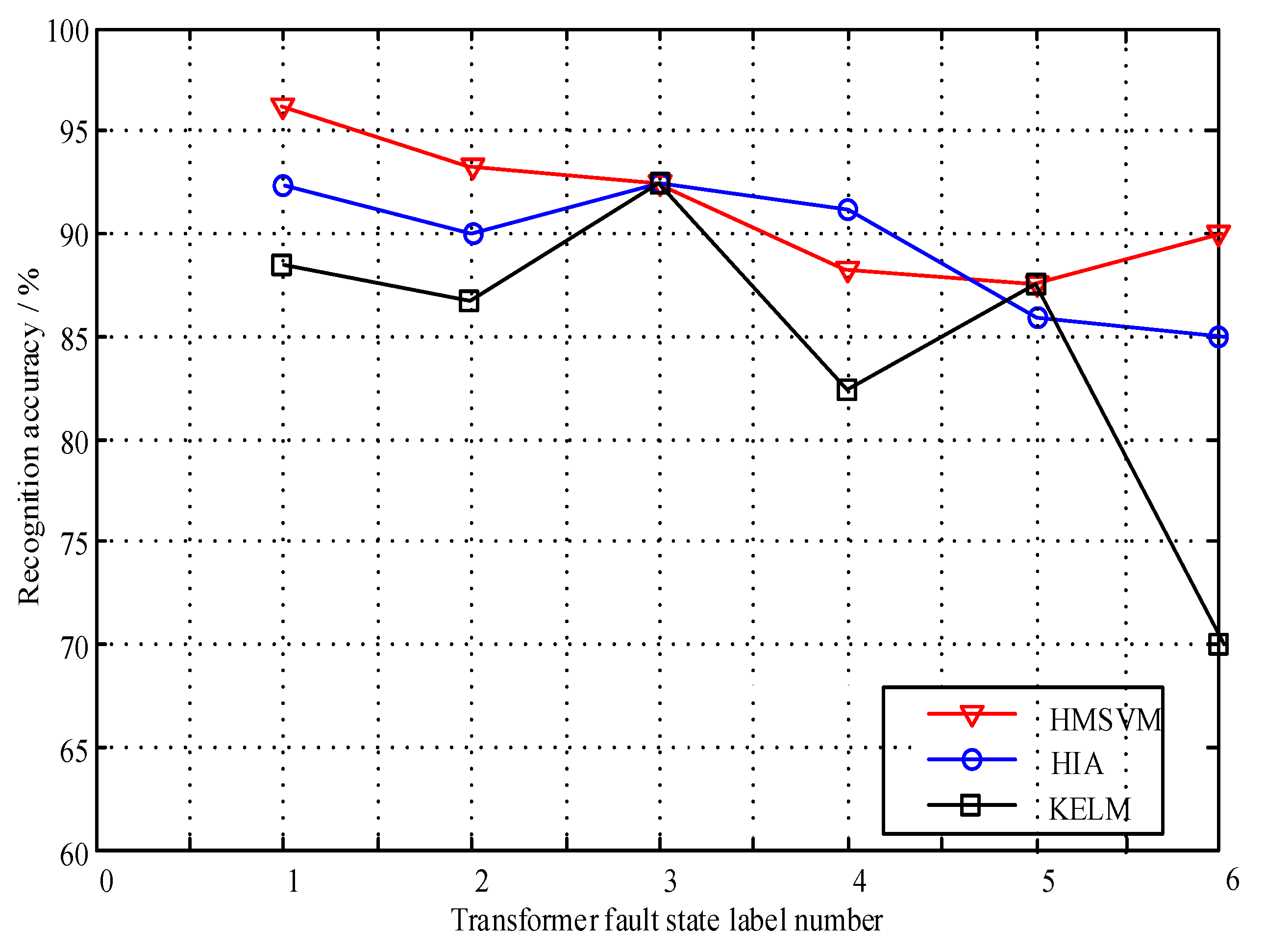
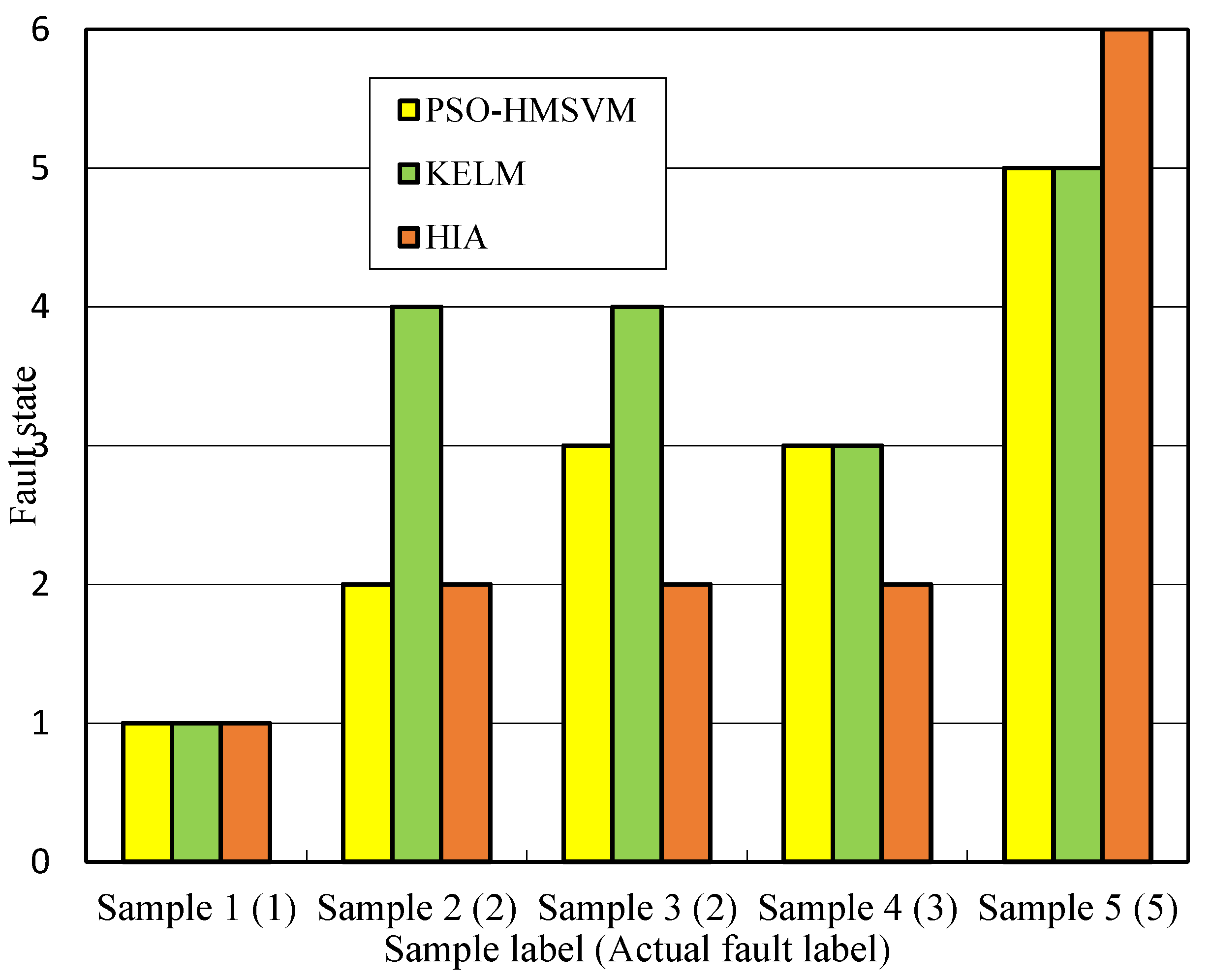
HIA and KELM are employed to analyze above typical samples. The diagnostic results using three intelligent algorithms are shown in
Figure 11.
As can be seen from
Figure 11, for the five sets of fault samples, the diagnostic results obtained by three intelligent algorithms are quite different. Among them, the HMSVM method has the best diagnostic effect, and only Sample 3 is not recognized correctly. The reason is this sample is located in the overlapping area of hyperspheres, which results in misjudgment. The KELM method has some problems in the diagnosis of Sample 2 and Sample 3, which shows that it is easy to misjudge the overheating fault. The HI method has misjudged Sample 4 and Sample 5, which indicates that this method is not effective for the distinction between high energy discharge and high temperature superheating faults. According to above analysis, except for normal samples, three intelligent methods have great difference in the diagnosis effect of transformer faults. For Sample 3, the diagnostic conclusions given by the three intelligent methods are completely different. Therefore, this paper chooses Sample 3 as the high conflict data for detailed analysis. Afterwards, the evidence theory fusion method is used for comprehensive diagnosis.
In this section, the proposed fusion algorithm is utilized to analyze the high-conflict DGA sample. First of all, the characteristics of the sample are extracted. Then, three different intelligent approaches are employed for preliminary diagnosis. According to the BPA construction method of three different algorithms, the BPA to each fault state is obtained shown in
Table 10. In the table,
E1,
E2,
E3 represent the evidence of KELM, HIA, and HMSVM respectively, and
m denotes the basic probability assignment.
Table 10 shows that the reliability to T
3 is the highest for KELM and HMSVM, and the reliability to T
12 is the highest for HIA. The conflictive degree of evidences is calculated, defined as
k.
k12 denotes the conflictive degree between KELM and HIA.
k13 means the conflictive degree between KELM and HMSVM. Lastly,
k23 denotes the conflictive degree between HMSVM and HIA. After multiple calculations, the values of
k12,
k13,
k23 are obtained, which are 0.9827, 0.1721, and 0.9700. This indicates that the conflictive degree between HIA and each other evidence is higher.
In order to solve the problem of high conflict between evidences, the weight coefficient is introduced for BPA readjustment. With the degree of conflict
k12,
k13,
k23, the weight coefficient
wi can be obtained by Formulas (20)–(23) as
wi = (0.3845, 0.2335, 0.3819). Due to the serious conflict between E
2 and the other evidence, HIA has smaller weight coefficient. Different weight coefficient values can distinguish the importance degree of each evidence. The uncertainty
m(Θ) is introduced in the process of BPA adjustment. The adjusted BPA based on weight coefficients is obtained in
Table 11.
With the BPA in
Table 11, the diagnostic decision can be made by formula (24) and (25). After calculation,
m(T
12) and
m(T
3) are the first and second maximum of basic probability assignment. The difference between these two values is 0.466, which is greater than
ε1(0.2). In addition, the value of uncertainty
m(Θ) is 0.0201, which is much less than
ε2(0.2). Above all, the final diagnostic result is T
12, which is the same as the actual state.
Using above 253 testing DGA samples, the diagnostic results based on different algorithms are shown in
Table 12.
It can be seen from
Table 12 that, due to the superior performance in processing nonhomogeneous and small samples, the total diagnostic accuracy of HMSVM reaches 90.9%, which is better than KELM and HIA. However, for
D1, HIA performs better than HMSVM. In addition, HMSVM gets worse results for
PD than both HIA and KELM. It indicates that three intelligent algorithms have diverse performances for different transformer fault states. For each transformer fault state, the diagnostic accuracy of the fusion method based on improved D–S evidence theory is no less than 90.0%. In total, the proposed fusion method has the highest diagnostic accuracy, which is obviously better than the other three single approaches. It shows that IDET can fuse the advantages of each single algorithm together and recognize transformer fault states effectively.