Abstract
Finding cost efficient earthing system design with acceptable level of safety might be quite tedious work. Thus, many earthing system engineers try to find the most suitable design either by employing only their best experience or taking advantage of some more complex optimisation programs. Although both approaches might work well under certain circumstances, they might fail either due to counter-intuitiveness of the specific situation or by misunderstanding of the applied optimisation method, its limitations etc. Thus, in this paper, the earthing system design optimisation problem was addressed by analysing optimisation simulation results together with conducted sensitivity analysis. In the paper, a simple double ring earthing system was optimised while using five different optimisation methods. The earthing system was placed in different horizontally stratified soil models and the earthing system was optimised by minimising touch voltages instead of commonly minimised earth potential rise. The earthing system was modelled by Ansys Maxwell software. Apart from using Ansys Maxwell built-in optimisers, the possible solution space has also been mapped by performing sensitivity analysis with changing the earthing system design dimensions and the results of optimisation were compared and validated. It was found out that the Sequential Non-Linear Programming Optimisation technique was quite superior to the other techniques. Additionally, in most cases, the Ansys Maxwell optimiser was able to found optimal solution; however, in some cases, based on the initial conditions, it might get stuck in local minima or the results might be influenced by the solution noise. Additionally, some quite non intuitive dependencies of earthing system electrodes positions had been found when different spatial dimensions constraints are used.
1. Introduction
The earthing system (ES) is one of the necessary parts of distribution and transmission power networks. The basic requirements on ES are stated in standards EN 50522:2010 [1] or e.g., in its American counterpart IEEE 80 [2]. Apart from other requirements, the designing engineer must ensure that step voltages (SV) and touch voltages (TV) in the vicinity of the ES shall not exceed the safety limits defined by [1], or [2] respectively. Thus, the proposed design by the engineer is always compliant with safety requirements, e.g., permissible touch voltage curve of EN 50522, however it might not be the best possible design for this desired specific site and its constraints. It might be quite common that the initial approach by the engineer is to apply some universal ES design recommendations (e.g., for distribution transformation station use double ring earthing system). The spatial layout of this initial design is usually the same for every such proposed design. Once this initial design is not compliant with the safety requirements, the designing engineer makes some adjustments to this initial design to find a solution that is compliant with the safety limits. However, the final proposed design by the engineer is not optimised within the specific site constraints and there might be still room for finding better design layout by employing a more complex optimisation approach, i.e., decrease the TV, decrease used material, etc. This designing approach might be especially true in case of the great number of built distribution transformer stations supplying the low voltage distribution networks. In the case of these ESs, the designing engineer very often uses the simplified formulas of an Annex J [1] to get the ES resistance to earth (e.g., ES ring Equation (1))
where ρ is soil resistivity, D is diameter of earthing ring, and d is the diameter of ring electrode cross section.
Once the resistance to earth is obtained, the safety assessment is quite straight forward, as the failure current might be obtained from simplified equivalent electrical circuit with the equivalent voltage source method [3]. The ES is then assessed based on the prospective permissible touch voltage that is taken as one half of entire earth potential rise (EPR) [1].
Basically, the abovementioned approach is kind of optimization technique with an objective function
Subject to design spatial dimension constraints
where d1…dn are appropriate ES dimensions and g1…gn, h1…hn are the spatial dimension constraints. This is because the designing engineer should mainly focus on decreasing the overall EPR to lower the corresponding touch voltages as much as possible. Decreasing the EPR is most effectively done through decreasing the resistance to earth of the ES design. The described procedure of (2) and (3) in all situations would mean lengthening the ES horizontal dimensions up to the outer boundary of the horizontal constraints and burying the ES near the burial depth lower constraint. This procedure might be also expected, regardless of most often used horizontally stratified soil model if the simplified formula of (1) is used.
Usually, the ES horizontal dimensions are constrained by utility owner limited land. Additionally, burying the ES to greater depth might get costly due to more excavation work needed. Thus, many researchers have been dealing with the ES design optimization problem. Some of the papers were dealing with finding/proposing a method to optimize the design by appropriate ES conductor allocation in the soil with reducing earthing system total EPR only [4]. Other works are aimed on the optimization by minimising the total length of used ES horizontal and vertical conductors [5,6]. Some other researchers also included into the optimization the costs that are connected with the installation process, i.e., the excavation costs as well as the ES conductor material costs [5,7,8]. Another, quite a different approach to ES design optimisation can be found in [9,10]. It is proposed by these papers to optimize the ES by using low resistivity materials. This optimization method is based on the fact that by applying different chemicals near or next to ES rods and strips, the fault current is more effectively driven into the ground due to increased effective surface area of the ES rods. By this method, the ES resistance might be influenced either temporarily or permanently. Lastly, but not used very often might be the optimisation by finding optimal distance to some other external grounding grid [11].
Generally, two things are necessary for the optimization procedure. The first thing is some objective function that is used to quantify if the so-called optimum has been reached. The second necessary thing is some kind of step direction function that determines the direction towards the so-called optimum. The usage of some different objective functions has been described in the previous paragraph. However, in the case of the step direction function, the aforementioned papers [4,5,6,7,8,9,10,11] mainly use two different approaches or their combination. The first approach is by performing parametric analysis (i.e., sensitivity analysis). This approach is based on the fact that, if there are only expected smooth changes in the solution, by choosing appropriate parametric step, the whole solution space can be mapped and this solution space is later searched for the so-called optimal solution according to the objective function. The results of this parametric analysis can be also used as a recommendation for the designing engineer if properly depicted [12]. The second approach that was identified in the reference is the use of some more complex optimization approach e.g., using non-linear programming optimization methods, like genetic algorithm optimization, particle swarm optimization, and hybrid particle swarm genetic algorithm optimization. In general, ES design optimization is a spatial problem where the use of the mentioned methods can decrease the overall time that is needed for the parametric analysis. In some cases, performing parametric analysis with fine steps might get quite tedious and time consuming.
Quite a novel approach to earthing system optimization problem might be the optimization through Quantified Risk Analysis [13,14,15]. The objective function of this approach is the quantified real risk (i.e., the resulting risk of death consisting of the probability of hazardous TVs level and the coincidence probability [13]). This approach is mostly assumed as an alternative to the conventional ‘worst case’ earthing system approach [1], which might be more strict or more loose, depending on the situation. However, the authors are yet unaware of publication using this approach together with some kind of step direction function and, also, the so-called ‘optimum’ for this method might be questionable due to diverse risk perception and acceptable risk level laws.
Not many papers have been dealing with the earthing system optimisation through the minimisation of TVs in case of horizontally stratified soil model. For example, in paper [4] the total EPR together with the TV was analysed. The ‘compression ratio’ function was proposed as a step direction function. The proposed approach is best suited for horizontal earthing mats with parallel and perpendicular conductors and it can be easily used for conducting parametric analysis. In the case of searching for optimal compression ratio, a more sophisticated step direction function different from simple first or second order gradient based approach might be necessary. Additionally, only the horizontal separation of parallel earthing conductors is optimised without any mean of incorporating earthing mat or separate electrodes burying depth.
Thus, in this paper, an optimisation analysis is introduced for the allocation of separate earthing system electrodes in earth through using Ansys Maxwell Optimetrics Component [16]. The Optimetrics Component allows for the user to search for ES design optimal dimensions. The prospective TV was assumed as the source of real associated risk with the earthing system design and it was chosen as the objective function of the optimisation. A comprehensive parametric/sensitivity analysis was also carried out with changing some of the model parameters to assess the correctness of obtained results by the built-in optimisers in Ansys Maxwell [16]. By this approach, the solution space was searched first and the results that were obtained from sensitivity analysis were compared with results from the built-in Maxwell optimisers.
2. Ansys Maxwell Optimisers
Ansys Maxwell [16] is a software module incorporated in the whole simulation software ANSYS. Ansys Maxwell is software for the simulation of low frequency quasi stationary electromagnetic fields (EMF). The EMF can be determined for general spatial electromagnetic problems as well as for only two-dimensional problems. The solution of Maxwell equations is managed through the finite element method. Basically, the user has to define/import the required design model, define sources, boundary and meshing condition, and the solution is determined by approximating the EMF distribution through the mesh of finite elements [17]. Additionally, with the use of the built-in field calculator a user defined quantities might be obtained from postprocessing of solved EMF data.
Ansys Maxwell presents an Optimetrics component that enables the user to perform parametric/sensitivity/sweep analysis. Furthermore, a component for optimisation is available. For the Optimetrics analysis it is necessary to define user defined variables, i.e., model length and any other dimensions, and user defined EMF quantities, like electric potentials at certain points, etc. The user defined variables are later used in the optimisation analysis as the parameters that are changed in iterative manner to find optimum design. The user defined EMF quantities are used for definition of objective function of the optimisation. The software features six different options for model optimisation [16]:
2.1. Quasi Newton (QN)
The Quasi Newton optimizer is a gradient based optimizer numerically determining the derivatives of quadratically approximated higher order functions of actual local objective function dependency. This optimizer suffers from the possibility of stucking in local minima, and due to finite element method nature of the results also stucking due to high level of solution noise. As the Hessian matrix increase rapidly with the number of optimised design variables the computational time might increase rapidly and thus this optimizer is recommended for optimisation of 1–2 design variables only.
2.2. Pattern Search (PS)
The Pattern Search optimizer uses the grid based simplex search with simplices in the form of tetrahedrons. It is non-gradient based optimisation search, thus it is less dependent on the solution noise. However, it might take longer to find the optimum. The use of only three optimised design variables is recommended.
2.3. Sequential Non-Linear Programming (SNLP)
The SNLP optimizer is more complex one. Basically, the optimizer creates a response surface by using Taylor series approximation of finite element analysis. By this approximation, the optimizer can find locations of improving points and determine next step direction. The SNLP optimizer is supposed to be more accurate and reliable because it is not constrained by the problem of stucking in local minima like QN. That is also caused by the possibility to overcome the local minima by taking larger steps within the optimisation variable constraints limits.
2.4. Sequential Mixed Integer Non-Linear Programming (SMINLP)
SMINLP optimizer is basically same as SNLP. However, this optimizer allows for mixing discrete and continuous optimised design variables.
2.5. Genetic Algorithm (GA)
The GA optimizer is stochastic optimizer. It runs many iterations with random selection of next searched points. It uses an iterative process with initial generation/parents/children and mutated population. The better performing individuals are chosen for the generation of the next generation in each iteration. Through this random search process, the solution space is searched in a structured manner and the optimum is found. However, the disadvantage is also that the non-improving designs are searched in the random selection process and thus this approach takes many more iterations and is thus slow.
2.6. Matlab Optimiser (MO)
Ansys Maxwell also facilitates the possibility to pass parameters to Matlab software (Matlab 2016b, MathWorks, Natick, USA) and invokes Matlab built-in optimisation functions and uses them to optimize the Ansys Maxwell design.
3. Earthing System Optimised Model
The feasibility of using Ansys Maxwell software for earthing system design optimisation was assessed on simple double ring earthing system, as in Figure 1. The first inner ring with a diameter D1 was buried at depth h1 and the outer ring with diameter D2 was buried at depth h2. The earthing system was made of FeZn strip with cross section 30 × 4 mm2. The earthing system was modelled in Ansoft Maxwell [16,17] with horizontally stratified soil model with two layers—the surface one with resistivity ρ1 and thickness H and the bottom layer with resistivity ρ2. The soil was modelled by semi-sphere with radius of 200 m and the analysis percent error was set to 1%. For the illustrative purpose, the earthing system model in Figure 1a,c is depicted with an improper soil scale. The earthing system was excited by a DC current [17] of 30 A (red arrow in bottom right picture of Figure 1c) injected at the centre of the ES, where the ES conductor is brought up above the ground and it is considered as accessible for touch.
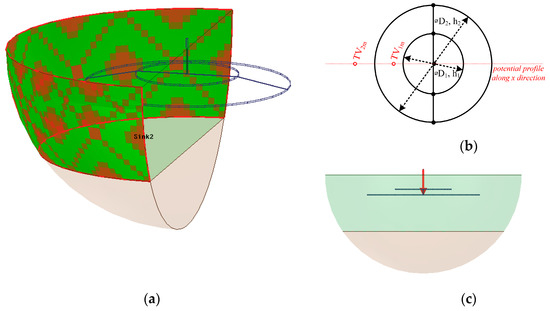
Figure 1.
Earthing system model, spatial view (a), top view (b), and side view (c).
4. Earthing System Sensitivity Analysis Results
A comprehensive sensitivity analysis was carried out before the optimisation of ES design by Ansys Maxwell. In this analysis, the ES was placed in seven different soil models, including ‘High on Low’ (HoL), Uniform, and ‘Low on High’ (LoH) soil models, as in Table 1.

Table 1.
Sensitivity analysis soil models.
For each of used soil model in the sensitivity analysis, the diameters of the ES were changed as inner ring D1 = 1, 2, and 3 m, and outer ring always greater than inner ring D2 = 4 and 5 m. In the case of burial depths of both rings h1 and h2, seven burial depths were used for each ring as 0.3–1.5 m with step of 0.2 m. I.e., for one set combination of ES rings diameters D1 and D2 all 49 combinations of ES design burial depths were modelled by Ansys Maxwell and the results were used in the sensitivity analysis. By this way, about 2000 ES design variations were analysed in this analysis. For each of these ES design variations, the potential profile on the earth surface along x direction (Figure 1b) was read and the TV distribution have been determined in the vicinity of the ES. Although the potential profile was read with step of 0.25 m, for the purpose of optimisation evaluation throughout this paper four main performance values have been determined—TV1m, TV2m and TV3m as TV 1, 2, and 3 m apart from the centre of the earthing system, respectively (i.e., potential difference between EPR and point 1, 2 and 3 m apart). Additionally, the total EPR was read. For set diameter D2 (used here to represent the dimensional constraint), the optimum burial depth was manually searched whilst changing other three dimensions D1, h1, and h2. Incorporating the optimisation of inner ring diameter D1 whilst manually searching for optimum design is quite challenging as the number of analysed variations increase rapidly. The results of the sensitivity analysis are introduced in Figure 2, Figure 3, Figure 4 and Figure 5 and Table 2, Table 3, Table 4 and Table 5.
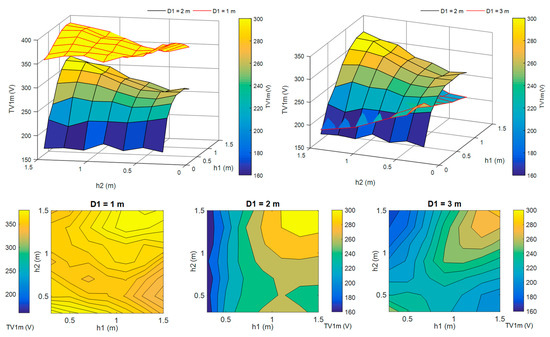
Figure 2.
TV1m solution surfaces for ES with diameters D1 = 1–3 m, D2 = 4 m, ρ1 = 500 Ωm, ρ2 = 100 Ωm, H = 2 m.
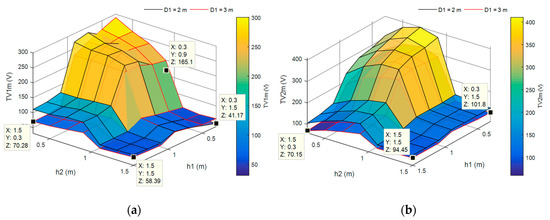
Figure 3.
Touch voltage (TV) surfaces, 500 Ωm/100 Ωm/1 m, D2 = 4 m, (a) TV1m surface; (b) TV2m surface.
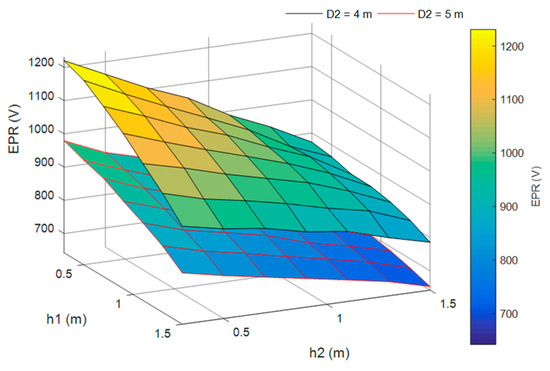
Figure 4.
EPR, 500 Ωm/ 100 Ωm/ 2 m, D1 = 2 m, D2 = 4 and 5 m.
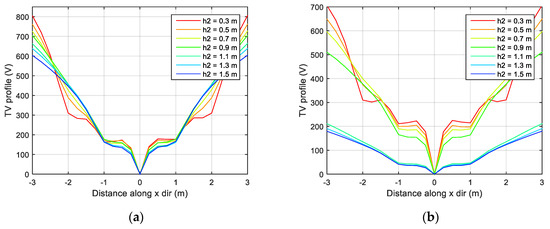
Figure 5.
TV profiles along x direction for HoL model ρ1 = 500 Ωm, ρ2 = 100 Ωm, D1 = 2 m, D2 = 4 m, h1 = 0.3 m; (a) surface layer thickness H = 2 m; and, (b) Surface layer thickness H = 1 m.

Table 2.
Sensitivity analysis results for ρ1 = 500 Ωm, ρ2 = 100 Ωm, H = 2 m, D2 = 4 m, D1 = 2 m.

Table 3.
Sensitivity analysis results for ρ1 = 500 Ωm, ρ2 = 100 Ωm, H = 2 m, D2 = 4 m, D1 = 3 m.

Table 4.
Sensitivity analysis results for ρ1 = 100 Ωm, ρ2 = 500 Ωm, H = 2 m, D2 = 4 m, D1 = 2 m.

Table 5.
Sensitivity analysis results for ρ1 = 500 Ωm, ρ2 = 100 Ωm, H = 2 m, D2 = 5 m, D1 = 2 m.
In Figure 2, the general overview of the results of sensitivity analysis is depicted. For set dimensional constraint D2 = 4 m, three TV1m surfaces are depicted for different inner ring diameter D1 and each surface is consisting of results of all 49 burial depth variations. In this compact form, the optimum burial depth of both rings can be immediately read. Within the dimensional constraints of h1, h2 (being in range of 0.3–1.5 m) and D2 (being fixed as 4 m), the ‘global’ minimum of the solution surface can be expected for D1 = 2 m, h1 = 0.3 m, and h2 = 1.5 m. In case of D1 = 3 m, a remarkable saddle point (h1 = 0.7 m, h2 = 0.6 m) is formed by a significant change in slope direction, where two areas with local (h1 = 1.5, h2 = 0.5 m) and global (h1 = 0.3, h2 = 1.5 m) minima are formed. Although this saddle point might not be as much remarkable for all simulated inner ring diameters, it is still present among all the surfaces.
Similar TV surfaces were also obtained for other objective functions in form of TV2m and TV3m. The results of these analysis are summarized in tabular form in Table 2, Table 3, Table 4 and Table 5. In this compact tabular form, only the remarkable points of the sensitivity analysis surfaces are listed for different soil models and for different ES dimensions whilst preserving the clarity of the results. The burial depths of ES designs were selected for two extreme cases and for all three analysed TVxm objective functions:
- Min TV where the burial depth of the design is selected for lowest TVxm.
- Max TV where the burial depth of the design is selected for the highest TVxm.
In this way, six different ES designs for set dimensional constraints of D1, D2, and selected soil model are listed and they can be compared for different objective functions TVxm, EPR objectives etc.
In Table 2 and Table 3, a slight difference in TVs for HoL soil model might be observed when changing the inner ring diameter D1 from 2 m to 3 m and with set constraint of outer ring D2 = 4 m. Even though the best possible design assessed based on EPR would be with both rings in the bottom layer h1 = h2 = 1.5 m and D1 = 2 m, based on TV1m the best design would be a different one with only the outer ring in the bottom layer and the inner ring in the surface layer h1 = 0.3 m, h2 = 1.5 m and D1 = 2 m. Additionally, if TV2m and TV3m objectives would be assessed a completely different designs are optimal. These findings might not be as much intuitive. However, with the increasing number of possible assessed option, the situation might get even more tricky.
For example, if additional constraints (i.e., different objective function or less favourable soil model) would be solved, a kind of unexpectable design solution might have been found. This can be apparent from Figure 3a,b, where the TV surface of HoL soil model with surface layer thickness of only 1 m is depicted for objectives TV1m and TV2m and for constraint of outer ring diameter D2 = 4 m. As it might be expected by some experienced engineers, the better designs are with an outer ring burial depth greater than the thickness of the surface layer. The overall best design, as already stated in the previous paragraph, is with D1 = 2 m, h1 = 0.3 m, and h2 = 1.5 m. However, this might not be true if other constraints are applied, e.g., dimensional constraint of both rings maximum burial depth of only 0.9 m and both TV1m and TV2m should be assessed. In the region of constraint burial depth of only 0.9 m, there is an evident change of pattern in optimal burial depths (between (a) and (b) of Figure 3) where the optimum design depending on the objective function is either for inner ring close to the surface with h1 = 0.3 m and h2 close to bottom layer, or the inner ring close to bottom layer and outer ring close to the surface, respectively. Additionally, design with increased inner ring diameter of 3 m gives better results than 2 m as in the case of TV1m objective. From both figures it is evident that if both TV1m and TV2m objectives need to be evaluated, the contradiction of the solution will need some sort of more complicated addressment, e.g., weighting of risk, etc.
Additionally, based on the results of depicted sensitivity surfaces, as in Figure 3a, the positive effect of earthing electrode grading can be assessed. For example, for the analysed arrangement and objective of TV1m, burying the inner ring only to a shallow depth of 0.3 m led to decreasing the risk. The rest of the designs are either comparable, or even worse. Burying both rings to the bottom layer is worse by slightly more than 40% than the optimal shallow inner ring placement (h1 = 0.3 and h2 = 1.5 m). The TV surface for inner ring diameter of 1 m for HoL has yielded in almost all cases to higher TVs and is thus excluded here.
The Uniform and LoH soil models are almost excluded from presented results, as the optimisation of ES design through changing design dimensions had greater observable dependency in TVs and EPRs for HoL soil model. Table 4 presents the results for LoH soil model. In case of LoH and Uniform soil models the TV differences between the min and max TV options are of small values and thus no big difference was found while searching for optimal solution. Additionally, the EPRs of different designs are almost identical. The abovementioned findings are true if the outer ring diameter is kept constant as a dimensional constraint. If that diameter would be even larger, the differences in TVs would smoothen even more. It is worth pointing out that, in the case of Uniform soil model, the results are even more convenient than in the case of the LoH model.
Increasing the outer ring diameter would of course lead to more suitable ES design, as might be apparent from Table 5, in comparison to Table 2 and Table 3, where design with increased outer ring diameter of 5 m is presented (compared to 4 m in Table 2 and Table 3). To complete the ES behaviour overview, Figure 4 depicts the EPR surface for different burial depths and outer ring diameters.
Figure 5a,b depict a kind of complementary and expanding overview of ES behaviour. In these figures the potential profiles along the x direction (Figure 1b) on the surface is depicted for ES designs with changing only the outer ring burial depth while keeping the rest of the dimensions constant. From the figures the TV1m, TV2m, and TV3m can be obtained. From Figure 5a, it is obvious that the optimum design in case of objective TV1m is with deep outer ring h2 = 1.5 m and with shallow inner ring h1 = 0.3 m. However, this chosen design is by no means also optimal when also assessed to TV2m.
From Figure 5b the positive effect of burying the outer ring into the bottom layer in HoL soil model with H = 1 m is observable, where the TV profile had dramatically flattened.
5. Ansys Maxwell Earthing System Optimisation Results
The optimisation of the ES design was also carried out by Ansys Maxwell Optimetrics component for soil models number 1, 3, 4, and 5 (Table 1). The ES was always modelled with some ‘initial’ dimensions, denoted by the subscript ‘i’ (i.e., the D1, h1, and h2 as D1i, h1i and h2i) and through the optimisation the ‘optimised’ dimensions have been obtained and are denoted by the subscript ‘o’ (i.e., D1o, h1o, h2o). The outer ring diameter D2 was set as a dimensional constraint equal to 4 m in most of the simulations. The burial depth constraint was set as in region 0.3–1.5 m for both rings and the maximum inner ring diameter constraint was set as D1max = 0.9xD2, thus so the inner ring is always smaller than the outer ring. The minimization of TV1m was set as the optimisation objective. The optimisation was carried out by five different optimisers—QN, SNLP, SMINLP, PS, GA. After the optimisation process some other parameters have been also recorded for possible comparison and benchmarking of different optimisers. I.e., TV2m, TV3m, the total EPR of optimised ES design, total time needed for finding the optimal design t, the number of performed simulations in total ItN (optimisation iterations), and a number of iterations (out from total of ItN iterations) where the optimal design was found ItO. As an optimisation analysis stopping criterion was also set the maximum number of optimisation iteration that was in most cases 300, or in some cases only 100. The optimisation results, together with the performed stopping option, are listed in Table 6 (Parts 1 and 2). The stopping option is in the last column ‘Status’ as either one of the following three options:
- S—for solved, stopped by finding minimum by Ansys Maxwell optimizer, the obtained result is expected to be the global minimum.
- M—for stopped by maximum number of iterations, not necessary global minimum found, the best suiting result was selected.
- F—for simulation failed. Again, the best suiting result was selected, however the optimisation ended prematurely. The failure might had happened due to more different problems. Either Ansys Maxwell adaptive mesher failed to build the mesh of finite elements, or the optimizer failed in finding the dimensions of the next design or the optimizer generally failed without description.
For HoL soil model 1, it was expected that the optimum burial depth for both rings with fixed outer ring diameter D2 = 4 m (Figure 2) should be 0.3 and 1.5 m for h1 and h2, respectively, and inner ring D1 = 2 m (as was found in sensitivity analysis Table 2, Table 3 minimum TV1m). For simplicity and comparability, first two optimisation analysis had been performed just with only burial depths h1 and h2 being optimised (lines 26, 27 of Table 6). This is also due to the fact that the simulated designs in sensitivity analysis were simulated with quite great step of inner ring diameter of 1 m, as the possible number of designs rapidly increase when a lower step would had been used. These two optimisation analysis were performed with different initial conditions. In both cases, Ansys Maxwell found ES design close to the expected optimal solution. In the second case, the outer ring depth was only 1.4 m where the optimiser evaluated visiting the depth of 1.5 m as unnecessary. This might be caused by the level of solution noise, i.e., with the set analysis percent error of 1% (Section 3) the changes in solution data of 5–15 V might be expectable due to randomness of creation of finite element mesh and also due to not sufficiently fine mesh elements. Better results might be expected for percent error of about 0.3% [17], however this will cause about three times or even greater increase in solution time.
In the rest of the simulation, the inner ring diameter was also optimised. As the sensitivity analysis was only done with 1 m step of the inner ring diameter, the results of optimisation cannot be really matched to sensitivity analysis results. However, from the comparison of TV1m surfaces from Figure 2 it can be expected that the optimal design should has inner ring diameter in 2–3 m region, and the burial depths as h1 = 0.3 m and h2 = 1.5 m. This expectation had been met in most of the results for SNLP optimiser. However, in case of the other optimisers, kind of invalid and different results had been found. This might have happened in some cases due to stucking in actual local minima, stucking in local minima caused by the solution noise, failing due to Ansys Maxwell Adaptive Mesher, etc.
In the case of GA optimiser, more extensive analysis of correct setting of the optimiser might lead to better results. For example, out of four different settings of the optimiser, the optimal design was found in only one (line 10). However, this optimisation had been stopped by user after more than two days of continuous simulation. From the optimisation results it had been found that the optimiser visited the location of global minimum (D1 ~ 2 m, h1 ~ 0.3 m, h2 ~ 1.5 m) only about three times out of total 1134 optimisation iterations. The optimal design was already found after about the first half of all iterations in the 664th iteration, however the optimiser did not evaluate it as the global optimum and was further searching for better solution.
The QN and SMINLP optimisers only found a local minima or did not find the expected optimum design at all in their all 8 performed simulation. Even though the suggested results by the optimisers are quite close to the global optimum, the global optimum still was not reached. The PS optimiser reached the global optimum in only one case out of three and the results seemed to be heavily reliable on the design initial condition. In case of all these three QN, PS, and SMINLP optimisers, there are not many options in Ansys Maxwell software that the user can change to improve the performance of the optimiser. One possible way might be to decrease the analysis percent error, which might help to overcome the optimiser problem of stucking in local minima also caused by solution noise. However, a corresponding increase in solution time is expectable.
The SNLP optimiser tended to give more reliable results, so a more extensive analysis was conducted for this optimiser only focusing mainly on the optimiser immunity to setting different initial conditions of the simulation. An outer ring diameter constraint of 4 m was set in most of the simulations. It was found out that the local minimum becomes significant once the inner ring diameter is close to 3.5 m when a saddle point (Figure 2, comments in Section 4) separates it from the global minimum. This assumption was also clarified by performing additional sensitivity analysis with inner ring diameters of 1.5, 2.5 and 3.5 m (Figure 6 solution surface for D1 = 3.5 m). However, in case of this local minimum the TV1m value is about 15–25 V higher that the expected global minimum in the region of D1 = 2–2.5 m. Thus, from results of lines 24 and 28 in (and also 2 QN and 5 PS) Table 6, it can be seen that, in the case of unfavourable initial conditions, the global minimum is not always found and the optimiser might be unable to overcome this problem on its own.
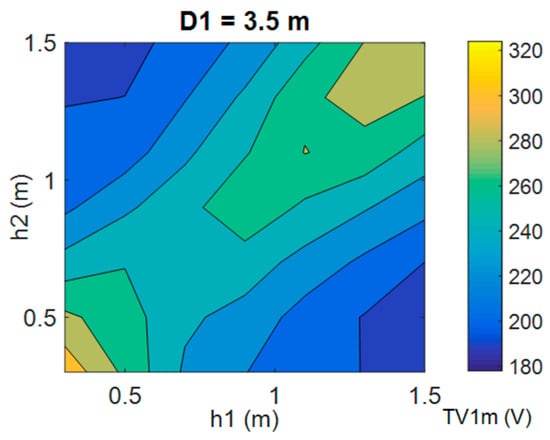
Figure 6.
TV1m solution surfaces for ES: 500 Ωm/100 Ωm/2m, D1 = 3.5 m, D2 = 4 m.
Lastly, in most cases, the maximum number of 300 optimisation iterations was enough to find the optimal design. In the case of SNLP optimiser, usually slightly more than 100 iterations were necessary to find the global minimum of the optimisation problem. However, if for example the maximum number was set only to 100 iterations, only a solution close to global optimum was found and the 100 iterations limit might be too restricting, i.e., in case of line 16.
6. Conclusions
In this paper, the appropriateness of using the Ansys Maxwell optimizer to optimize ES design was demonstrated on couple of examples. The use of the SNLP optimiser might be assessed as satisfactory and superior to other Ansys Maxwell optimisers. In most cases, the SNLP method found the optimum design, however in the case of unfavourable initial conditions it is still prone to stucking in local minima. This problem can be overcome by conducting the optimisation analysis for different initial conditions to see whether the found result is kind of reliable. In the case of other compared optimisers, different settings might lead to more reliable results, however the increase in solution time as well as more experienced engineer (user) might be necessary.
Another novel approach that is presented in this paper is the optimisation of the design by minimising touch voltages instead of most often used EPR. Unlike simple EPR minimisation would lead to burying of ES in greater depth it was pointed out that this approach might not necessarily lead to optimal layout also assessed based on actual touch voltages. As the real risk that is associated with the ES is driven by the touch voltages instead of EPR, using of touch voltages is more precise than simple optimisation of EPR. However, when the design is optimised to minimise TVs, it was found out that the optimum ES design might get quite counter intuitive considering the wide variety of options, like different dimensional constraints, different soil models, or even different objective functions ~ transferred voltages, step voltages. Thus, as was presented in this paper, the use of software with more complex optimisation methods (non-linear programming, like SNLP method) might be beneficial, if not even necessary.
Author Contributions
Conceptualization, V.V.; Funding acquisition, P.T.; Investigation, V.V.; Supervision, D.T. and P.T.; Validation, M.P. and D.T.; Writing—original draft, V.V.; Writing—review & editing, M.P., D.T. and P.T.
Funding
Authors gratefully acknowledge financial support from the Technology Agency of the Czech Republic (project No. TN01000007).
Acknowledgments
Authors gratefully acknowledge the Centre for Research and Utilization of Renewable Energy (CVVOZE) where this research work was carried out.
Conflicts of Interest
The authors declare no conflict of interest.
References
- CENELEC. Earthing of Power Installation Exceeding 1 kV a.c.; CENELEC Standard EN 50522:2010; European Committee for Electrotechnical Standardization (CENELEC): Brussels, Belgium, 2010. [Google Scholar]
- IEEE Guide for Safety in AC Substation Grounding; IEEE Std 80-2013; IEEE Standard: Piscataway, NJ, USA, 2015.
- Short-Circuit Currents in Three Phase a.c. Systems: Part 0: Calculation of Currents; IEC 60909-0; International Electrotechnical Commision (IEC): Geneva, Switzerland, 2016.
- Lee, H.-S.; Kim, J.-H.; Dawalibi, F.P.; Ma, J. Efficient Ground Grid Designs in Layered Soils. IEEE Trans. Power Deliv. 1998, 13, 745–751. [Google Scholar]
- Taher, A.; Said, A.; Eliyan, T.; Hafez, A. Optimum Design of Substation Grounding Grid Based on Balancing Parameters using Genetic Algorithm. In Proceedings of the (MEPCON)—Twentieth International Middle East Power Systems Conference, Cairo, Egypt, 18–20 December 2018; pp. 352–360. [Google Scholar]
- Silva, C.L.B.; Oliveira, D.n.; Pires, T.G.; Nerys, J.W.L.; Calixto, W.P.; Alves, A.J. Optimization of Grounding Grid’s Multidesign Geometry. In Proceedings of the IEEE (EEEIC) 16th International Conference on Environment and Electrical Engineering, Florence, Italy, 7–10 June 2016; pp. 1–6. [Google Scholar]
- Alik, B.; Teguar, M.; Mekhaldi, A. Minimization of Grounding System Cost Using PSO, GAO, and HPSGAO Techniques. IEEE Trans. Power Deliv. 2015, 30, 2561–2569. [Google Scholar] [CrossRef]
- Perng, J.-W.; Kuo, Y.C.; Lu, S.-P. Grounding System Cost Analysis Using Optimization Algorithms. Energies 2018, 11, 1–19. [Google Scholar] [CrossRef]
- Al-Arainy, A.A.; Khan, Y.; Quereshi, M.I.; Malik, N.H.; Pazheri, F.R. Optimized Pit Configuration for Efficient Grounding of Power System in High Resistivity Soils using Low Resistivity Materials. In Proceedings of the Fourth International Conference on Modeling, Simulation and Applied Optimization, Kuala Lumpur, Malaysia, 19–21 April 2011; pp. 1–5. [Google Scholar]
- Boualegue, A.; Ghodbane, F. A new Parametric Approach for Grounding Analysis in Multilayered Soils with Finite Volumes. In Proceedings of the First International Conference on Renewable Energies and Vehicular Technology, Hammamet, Tunisia, 26–28 March 2012; pp. 274–278. [Google Scholar]
- Pan, W.; Sun, H.; Chai, S.; Zhou, J. Research of Optimal Distance of External Grounding Grid. In Proceedings of the IEEE (POWERCON) International Conference on Power System Technology, Wollongong, Australia, 28 September–1 October 2016; pp. 1–4. [Google Scholar]
- Datta, A.J.; Taylor, R.; Ledwich, G. Earth Grid Safety Criteria Determination with Standards IEEE-80 and IEC-60479 and Optimization of Installation Depth. In Proceedings of the (AUPEC) Australian Universities Power Engineering Conference, Wollongong, Australia, 28 September–1 October 2015; pp. 1–5. [Google Scholar]
- Carman, B.; Palmer, S.; Fickert, L.; Griffiths, H.; Moller, C.; Toman, P. Substation Earthing System Design Optimisation Through the Application of Quantified Risk Analysis, 1st ed.; Cigre—International Council on Large Electric Systems: Paris, France, 2018; ISBN 978-2-85873-451-1. [Google Scholar]
- Topolanek, D.; Vycital, V.; Toman, P.; Carman, B. Application of the probabilistic approach for earthing system evaluation in distribution network. Int. J. Electr. Power Energy Syst. 2018, 20, 268–279. [Google Scholar] [CrossRef]
- National Annexes NA and NB of British Adopted European Standard Earthing of Power Installations Exceeding 1 kV a.c.; BS EN 50522:2010; British Standards Instituiton (BSI): London, UK, 2012.
- EMF Simulating Software, Version 18, Ansys Maxwell Package; Ansys: Canonsburg, PA, USA, 2017.
- Vycital, V.; Toman, P. Modelling of Electrical Installations Earthing Systems in Ansoft Maxwell. In Proceedings of the 24th Conference STUDENT EEICT 2018, Brno, Czech Republic, 26 April 2018; pp. 487–491. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).