1. Introduction
To ensure a sustainable and decarbonized future, the number of electric vehicles (EVs) is increasing steadily in the transport sector. Global EV penetration is estimated to grow up to 20 million units by 2020 [
1]. This increase is expected to continue since several countries are developing supporting regulatory schemes that make EVs more attractive for potential buyers.
On the other hand, the EU is setting targets to significantly reduce greenhouse gas emissions by 2050 [
2]. To accomplish this goals, the share of renewable energy sources must increase significantly. Challenges related to maintaining a high security of supply have increased with the increasing share of intermittent renewable electricity generation.
Distributed Energy Resources (DER), such as automic loads (AL), electric vehicles (EVs), thermostatically controlled loads (TCLs) could assist cost-optimal integration of renewable energy sources (RES) that offer flexibility. The possible gain from the DER integration on the whole system is investigated in detail in [
3,
4,
5]. The potential benefits are also acknowledged by the European Commission, which in turn updates the legislation that encourages market operators to open electricity markets for DER units.
In particular, depending on their charging plans, EVs can potentially assist efficient and secure functioning of the power system. To enable the access of this type of small-scale flexibility to a large electricity market and ensure efficient resource allocation, an aggregation agent might be required. This coordination might be achieved by offering flat rate prices to EV owners. In this case, the aggregator as a business entity dominates the decision-making process by defining optimal power set points [
6,
7,
8,
9]. This coordination might not be attractive enough to motivate end users to get involved.
On the other hand, the coordination can be accomplished by preparing retail price incentives for the final customers. In this way more than one player influences on the decision making process. For example, apart from the aggregator, an EV owner also decides when and how much to consume based on the offered retail price rate. Hence, it becomes extremely relevant to study the strategic interaction between EV aggregator and EV owners, while coordinating cost-optimal resource allocation in multi-settlement day-ahead, intra-day and real-time markets.
In power system research, complementarity models, specifically, mathematical models with equilibrium constrains (MPECs) are useful for modeling strategic interaction between players [
10]. This mathematical tool has wide applications in the power system context. For instance, the application of MPECs in the generation expansion problems is studied in [
11,
12]. The coordination of transmission expansion planning, where generation investments are considered strategic, is proposed in [
13]. A bilevel optimization tool is not only used to model the decision-making processes related to dealing with the problems producers face, but also to model such processes related to dealing with the problems consumers face. Reference [
14] models the strategic behavior of hydropower producers, whereas the market power of thermal power producer is studied in [
15] by applying bilevel program based on the Stackelberg game. In both references the upper level represents strategically acting producer (hydropower or thermal power), called a Stackelberg leader, while the second level represents the market operator, also called a Stackelberg follower.
The decision making problem of demand-side agents using bilevel optimization is studied in [
4]. The reference [
4] analyzes the strategic behavior of a DER aggregator who participates in a wholesale market.
The application of bilevel optimization formulation to the EV scheduling problems is limited in the literature. In most cases the bilevel formulation is used to investigate the EV aggregator’s strategic behavior modeling the market-clearing algorithm in the lower level [
16,
17]. EV-scheduling problems, where different market players interact to reach a retail price interface equilibrium are thin on the ground. In this context, the reference [
18] applies a deterministic bilevel optimization approach to reach an equilibrium point of retail price interface. In [
18] the EV aggregator commits in competitive wholesale day-ahead market to purchase charging power for its fleet of EVs.
An EV aggregator needs to forecast underlying market prices as well as the electric power needs of its fleets of EVs. The increasing integration of intermittent renewable generation makes the forecasting levels less reliable. This requires proper stochastic programming techniques [
19,
20] to model uncertainties involved in the EV aggregation problem. Uncertainties are counted in [
21], where authors develop a stochastic bilevel optimization model for an EV aggregator in a competitive day-ahead and balancing market environment.
According to Nord Pool’s key statistics [
22], Nord Pool experiences gradual growth of intra-day market trading. This growth might be due to the continuous increase in the integration of intermittent renewable energy sources. As the penetration of renewable energy sources in the EU is expected to increase further to meet the EU decarbonization target [
2], it is logical to assume that the use of intra-day adjustment markets will increase regularly.
The aggregator faces a significant level of uncertainty when performing in highly uncertain market conditions and due to the uncertain nature of fleet characteristics. Hence, the aggregator is motivated to become involved in intra-day and balancing markets that are closer to real-time to gain from correcting measures taken on the day-ahead obligations. Therefore, controlled by intra-day and real-time volatile market prices, EVs can be planned in hourly intra-day selling/buying and balancing up/down-regulating positions. These correcting actions are necessary to quantify the errors stemming from the availability and price prediction [
7].
Even though in an EV aggregation context, where a stochastic bilevel optimization approach is taken in which different players act strategically to reach equilibrium was proposed in [
21], the application of this kind of approach to trade energy in three sequential day-ahead, intra-day and real-time markets has not been explored. This paper proposes a stochastic bi-level optimization framework based on the Stackelberg game for an EV aggregator to prepare profit optimal retail price incentives to attract more end users to support the secure operation of the power grid relying on EVs optimal charging plans. The aggregator trades in day-ahead, intra-day and real-time markets. This formulation determines endogenously the profit-maximizing retail price levels constraint by cost-minimizing EV charging plans.
The contributions of the paper are threefold:
The development of a stochastic bi-level optimization framework based on the Stackelberg game for an aggregator who operates many batteries (stationary and EVs) and trades electric power in three markets. The model addresses carefully the lack of certainty in market prices and fleet characteristics as well as accounts for the existing market rules. This model enables market trading regardless of (1) generation or consumption technology and (2) mobile or immobile battery unit.
The extraction of optimal trading quantities for three-settlement markets with reasonable calculation time by employing a proper scenario-reduction technique.
The uncertainty modeling in all three market prices as well as EV mobility parameters.
The next sections of the paper are organized in the following manner:
Section 2 outlines the problem statement, describes the proposed stochastic bilevel formulation of an aggregator based on the Stackelberg game and derives a stochastic one-level problem by replacing the lower level problem with its optimality conditions.
Section 3 discusses the results from the studied cases and
Section 4 concludes the paper.
2. Problem Statement and Methodology
First, a short description of the underlying market places is provided. Then, the decision process framework is presented. Finally, the involved uncertainties are characterized.
2.1. Market Places
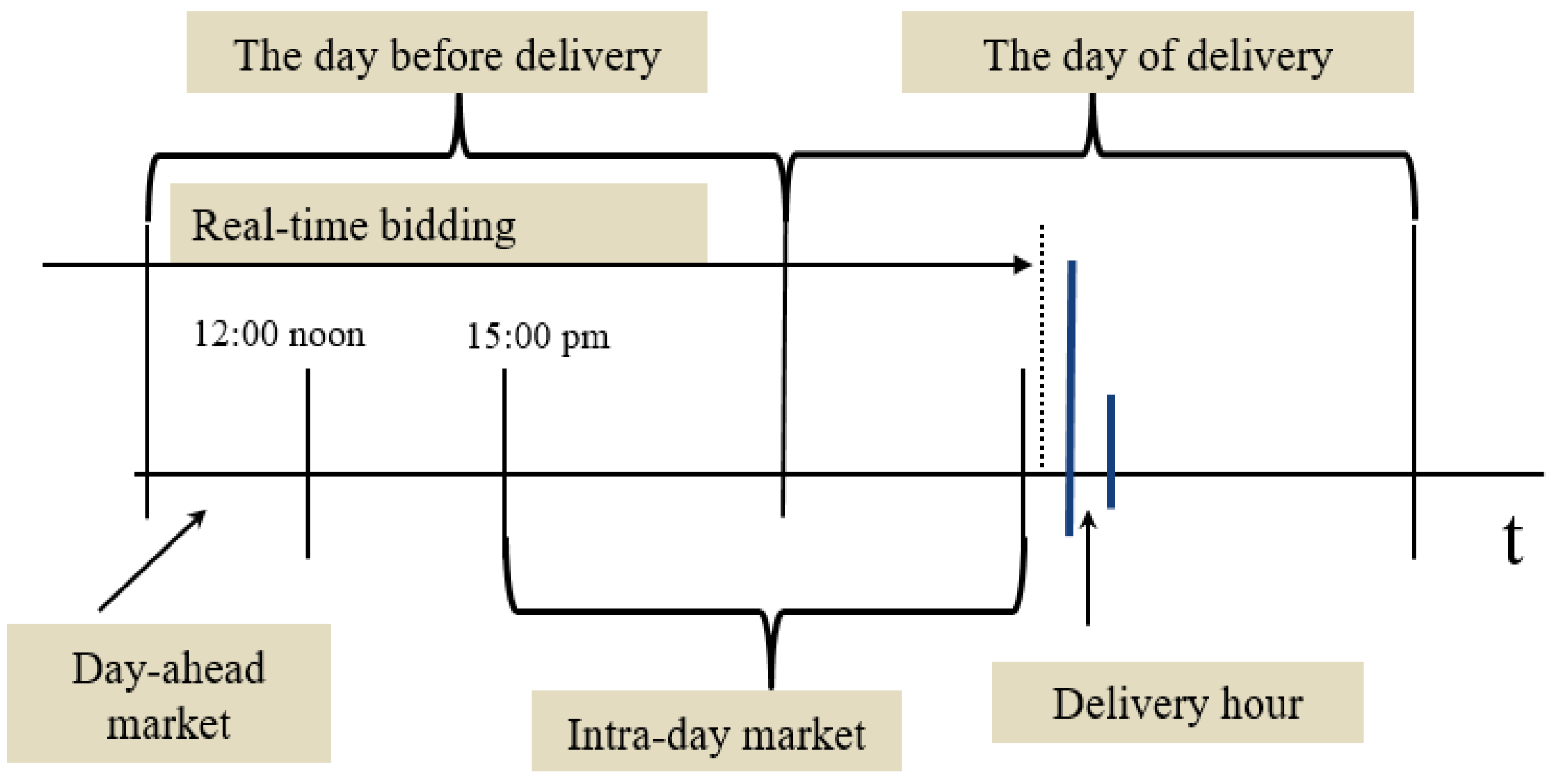
Liberalized electricity markets, irrespective of geographic location, are multi-settlement structured and usually include a day-ahead market, an intra-day market and a real-time market. Unpredictable events can be balanced in the intra-day or the real-time markets. In a day-ahead market, players trade electric power with hourly increments the day before, for energy delivery of the following day. In this market, hourly demand and supply bids for the next 24 hours are submitted at once before the gate closure. In the Nordic power system, the day-ahead market gate closes at noon the day before the delivery day (see
Figure 1). For day-ahead markets, gate-closure time might vary slightly in different markets. After the closure of the day-ahead market, for every hour aggregated demand and supply curves are built. The intersection point of those curves defines the day-ahead market prices and traded volumes; in other words the day-ahead market clearing takes place. In the Nordic power system, the day-ahead market clears at 3 p.m. Again, the market clearing time might vary a little in different power systems.
Intra-day markets are open directly after the clearing process of the day-ahead market. In contrast, intra-day markets are continuous and the gate closure takes place shortly before the actual delivery of that hour (in the Nordic system this is one hour before the delivery).
Similar to an intra-day market, in a real-time market the gate closes very close to the actual delivery time step (in the Nordic market the real-time market closes 45 min before the delivery). However, the real-time market is open two weeks before the delivery hour. Both producers and consumers submit upwards and downwards bids for a specific hour indicating prices and volumes. Then, system operator clears the real-time market based on the received information.
Figure 1 depicts the time line for physical electricity trading in all three market floors. The gate closure and market clearing times are based on the Nordic power system case.
As an aggregator of a flexible power source, the EV aggregator faces the need for making optimal decisions based on uncertain data. Thus, the multilevel stochastic programming tool is appropriate in this circumstance.
2.2. Decision Process Framework
The decision making process is expressed by providing a brief description of the involved actors (an EV aggregator and end users) together with their aims, as well as the interaction between the actors through the well-known Stackelberg game.
2.2.1. End Users: Consumers
An EV owner aims at recharging their vehicle at the lowest possible cost. This means that EV owners are motivated to choose the most competitive aggregator from whom to buy the energy volume they need.
2.2.2. Aggregators
The usual decision-making mechanism of an EV aggregator shares some of the common characteristics of the decision-making skeleton of a typical consumer/retailer. On the one hand, the EV aggregator competes with other market players for electricity purchase at the least possible cost and for ancillary service provision in a profit-optimal way. On the other hand, the aggregator competes against other aggregators or retailers who provide similar services in an attempt to attract more end users.
The aggregator aims at maximizing its operating profit. In this context, such an agent determines its optimal involvement in different sequentially cleared market floors like day-ahead, intra-day and real-time markets, while offering competitive incentive prices for the end users. The aggregator’s revenue is based on the consumption volume of the EV owners and the offered retail price. However, the aggregator’s cost depends on the cleared prices of the day-ahead, intra-day and real-time markets. These prices are uncertain and are determined exogenously. Thus, it is assumed that the EV aggregator is a price taker and does not have marker power when participating in the above-mentioned markets.
2.2.3. Interaction between the Agents: Stackelberg Game
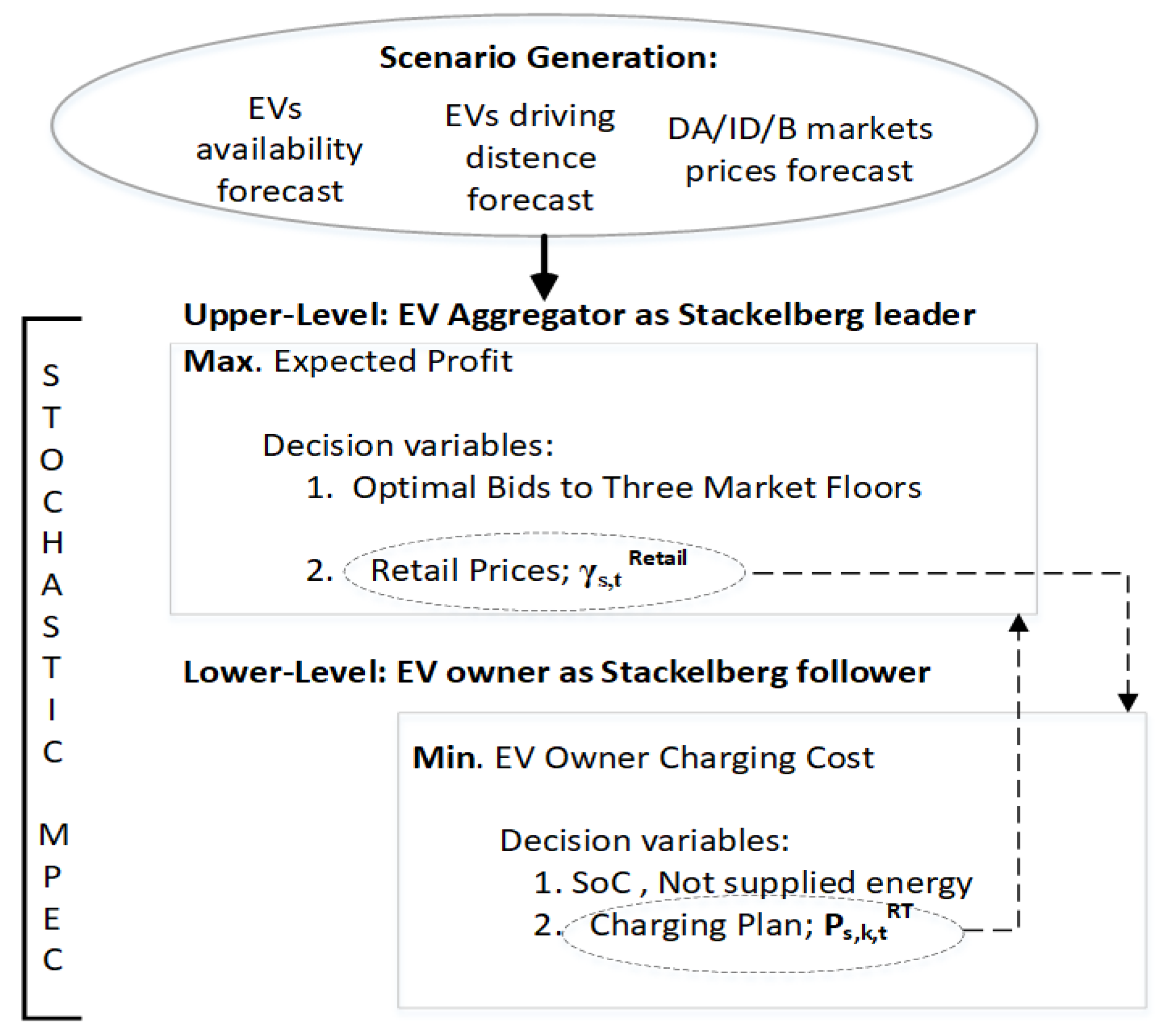
A bilevel optimization framework is suggested for an EV aggregator to construct retail price incentives for its EV owners. The aggregator (the Stackelberg game leader) determines its position in day-ahead, intra-day and real-time markets and defines non-flat price incentives for EV owners (the Stackelberg game followers) taking into consideration expected market outcomes and EV charging patterns.
A bilevel decision making mechanism of an EV aggregator in interaction with EV owners is illustrated in
Figure 2. The upper level (UL) formulates the EV aggregator’s challenge of maximizing revenues from retail, while the lower level (LL) develops the end users (EV owner) problem, where the EV owner aims at minimizing the charging cost subject to the technical constraints as well as EV availability patterns. In addition,
Figure 2 shows the information exchange between UL and LL problems. Accordingly, the UL sends retail price signals to the LL. Consequently, based on the price signals it receives, the LL determines the cost optimal charging plans, which are then submitted to the UL problem.
The uncertainties related to the aggregator’s expectations for day-ahead, intra-day, real-time market price outcomes as well as EV availability patterns are represented through a scenario-based stochastic programming tool.
2.3. Uncertainty Characterization
2.3.1. Methodology for Generation and Reduction of Market Price Scenarios
Modeling and prediction of electricity market prices are complicated due to its complex structure. There is a dynamic dependency among three sequential markets, which complexifies the forecasting process even further. A huge amount of work has been done in the field of modeling and forecasting of day-ahead market prices [
23,
24]. Despite this, the existent literature on intra-day and real-time price modeling and forecasting is very sparse [
25,
26,
27]. The Markov-based HW model for modeling and predicting the day-ahead, intra-day and real-time prices is presented below. According to reference [
28], the Markov-based HW model is one of the best performing predicting tool for electricity market prices. The suggested model is described in the following steps.
2.3.1.1. Step I: The HW Model Parameters’ Estimation
The references [
29,
30] present the general description of the HW model for a time series with a unique seasonal pattern. The HW model is employed to predict the electricity load and imbalance cost in [
31,
32]. The typical HW model for a time series of prices
is as follows [
33]:
where
is the exponential element,
is the trend and
is the seasonal element with period
.
,
, and
∈ [0,1] are smoothing parameters.
is the h-hour forward prediction.
2.3.1.2. Step II: The transition probability matrix estimation of the Markov model for different states of real-time market prices
The forecasting process of the day-ahead market prices includes the estimation of the price magnitude for the entire prediction period. In contrast to day-ahead market prices, both intra-day and real-time market prices, in addition to the price magnitude, also have a discrete mode. This implies that the price states for the intra-day and real-time markets need to be forecasted as well. The magnitude of day-ahead, intra-day and real-time electricity prices can be estimated using the HW forecasting tool. We describe the forecasting process of the price states for the real-time market. Because the forecasting process for intra-day market price states is very similar to that of real-time market, we do not include a detailed description here.
The real-time market prices may have one of the following four states in each bidding interval t: (1) No up-/down-regulating price exists, (2) Only down-regulating price exists, (3) Only up-regulating price exists, and (4) Both up-/down-regulating prices exist. A four-state Markov process can be employed to model the state of real-time market prices.
The transition matrix probabilities for real-time Markov model are evaluated based on real-time market price series. Derived from the real-time price peculiarities, for each bidding period
t, the binary pair
is defined as follows like in reference [
26].
is a parameter, which defines the state of the real-time price at period
t as in (
6).
Let
, then element (i,j) of transition probability matrix
for
can be computed as:
As stated above, the state of intra-day market prices can also be modeled using a four-state Markov process. The intra-day market price series can be used for that purpose.
2.3.1.3. Step III: The scenario generation and reduction procedures for day-ahead, intra-day and real-time market prices
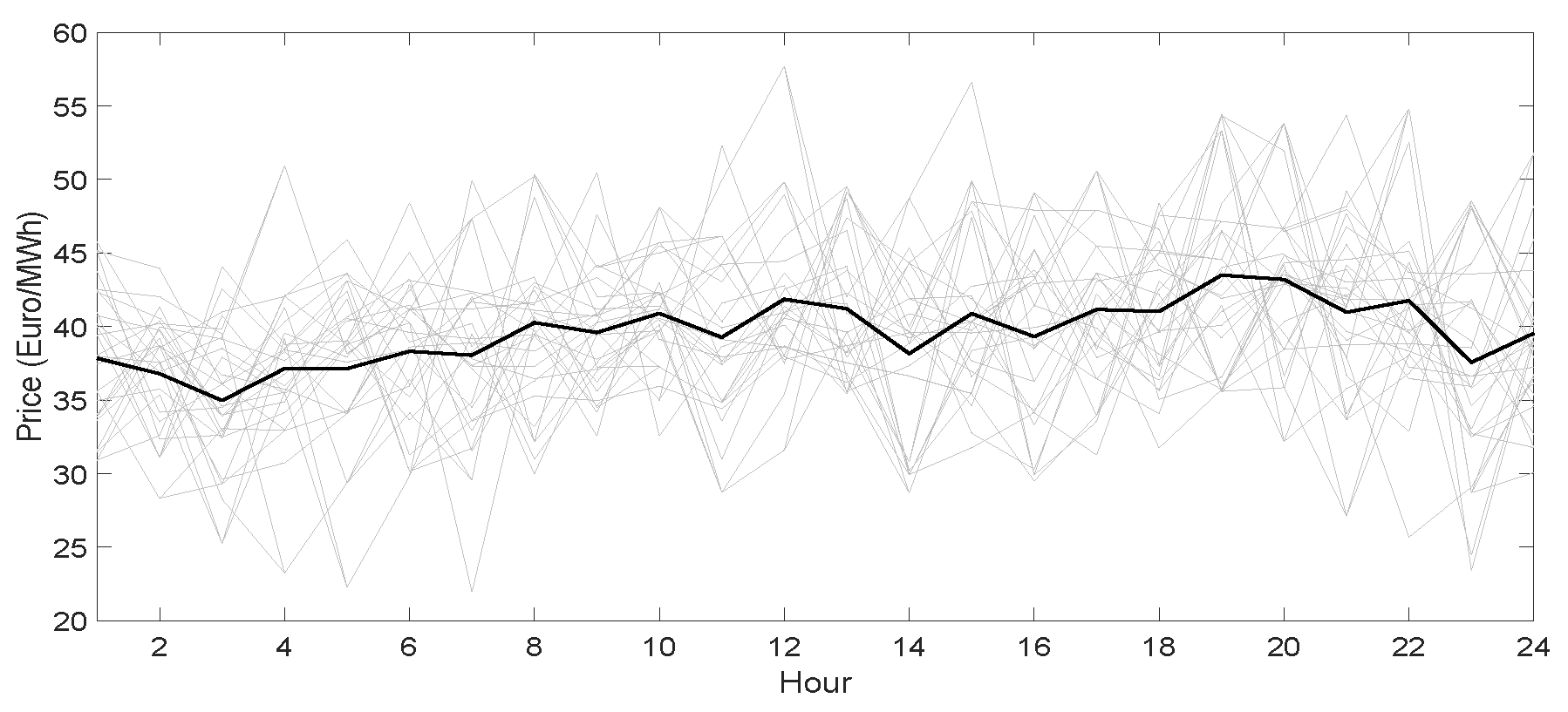
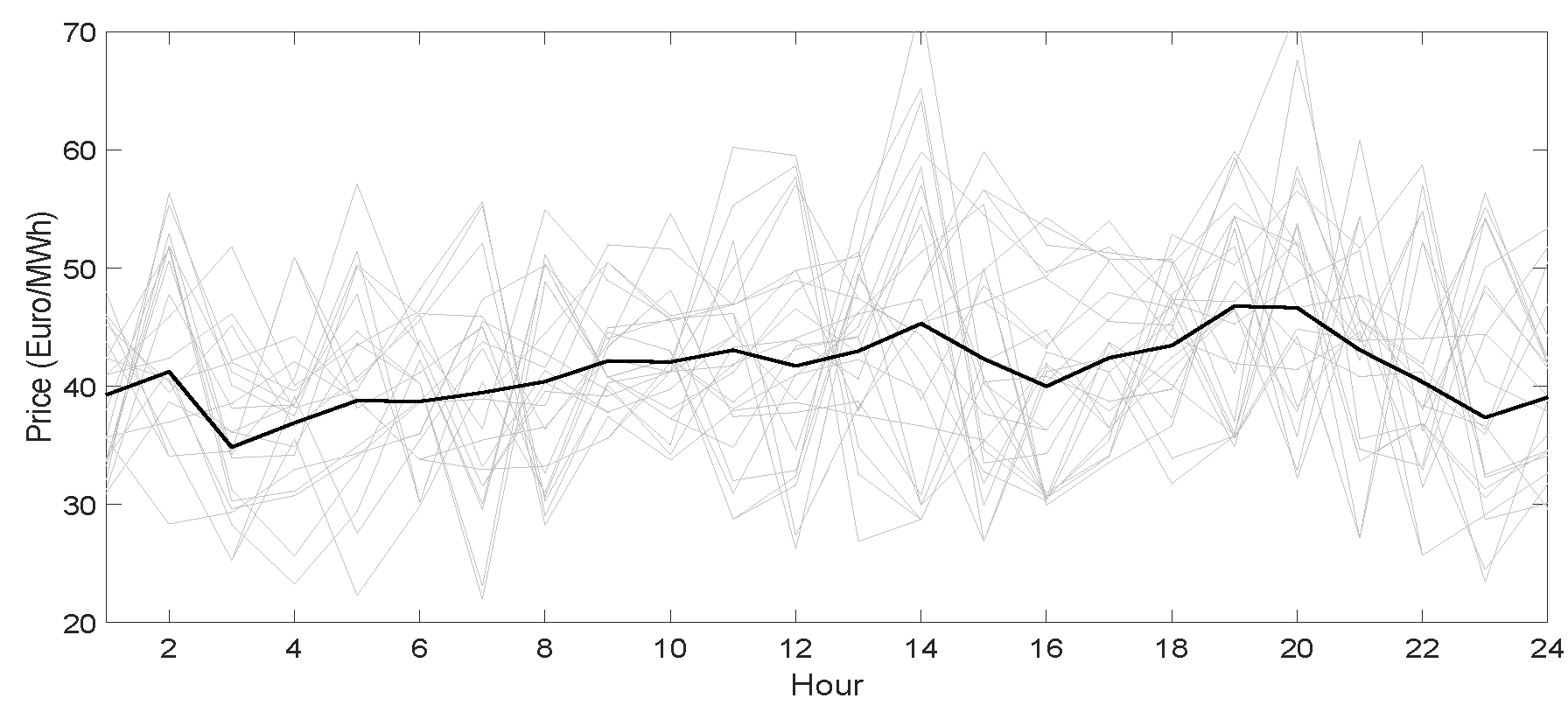
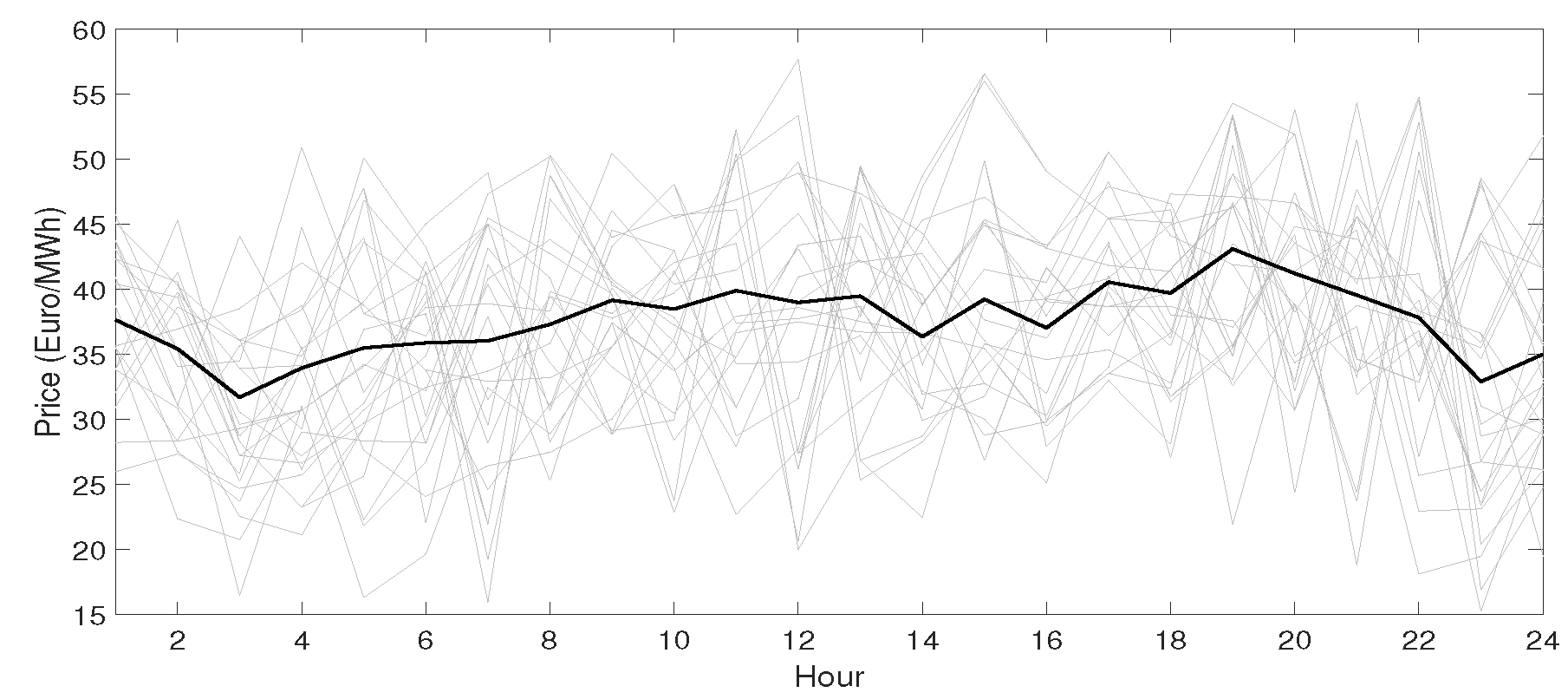
The day-ahead market price magnitude is predicted using the historical prices with the hourly resolution reported in [
34] and applying the prediction technique explained in step I. Afterwards, the day-ahead market price scenarios are produced (1) using the expected values and the variances of day-ahead market prices and (2) assuming normal distribution.
As explained in step II, both price magnitude and market state have to be predicted for intra-day and real-time markets. Historical price time series are needed for this purpose. Analogous to day-ahead market prices, the real-time market hourly price series is available from the Nord Pool website [
34]. In contrast, intra-day market prices are not available on the Nord Pool website. Therefore, we contacted Nord Pool to obtain the intra-day market .csv excel files containing intra-day market trading activities. The preprocessing of the intra-day market .csv excel data resulted in the desired hourly price series. More precisely, this data was preprocessed in the following way: (1) the data was grouped as buying and selling trading within each hour, (2) then a buying and selling price series with an hourly resolution was designed taking the average of all buying and all selling trading prices within each hour correspondingly.
To predict intra-day and real-time price magnitude, the forecasting tool in step I is employed. The price direction for both intra-day and real-time markets was grasped applying the Markov model provided in step II. The intra-day and real-time market price scenarios were produced based on the forecasted price magnitude, direction and assuming normal distribution. Several scenarios have been generated to capture accurately the probabilistic information on random prices. Then the initial number of scenarios was diminished carefully, while preserving the probability information at most. The optimal scenario reduction problem can be expressed as in (
8) and (9), [
35].
The optimisation problem (
8) and (9) can be solved approximately applying the backward reduction method. In this method, a price scenario
is removed such that
,
35].
2.3.2. Availability Simulation
To address the uncertain driving behavior, we need to produce mobility scenarios. A Monte Carlo simulation tool is used in that regard. The following probability measures are considered to derive discrete cumulative distribution functions (cdf), which is employed to generate mobility scenarios;
the probability of travel on a specific day,
the probability that a trip starts in a specific hour,
the probability that a trip covers a certain distance.
Mutually independent distributions are assumed as in [
7].
2.4. Proposed Stochastic Bilevel Formulation
2.4.1. Upper-Level: EV Aggregator as a Stackelberg Game Leader
The stochastic optimization problem stated in (
10) maximizes the scenario-weighted expected profits from day-ahead energy trading, intra-day and real-time power exchange. Hourly resolution is assumed for all three market places.
where the expected profit of the aggregator
+
) can be calculated as in (
11). The first term in (
11) is aggregators revenue from supplying
power to EV owners, while the other terms are potential costs/benefits for the aggregator trading in day-ahead, intra-day and real-time markets.
The objective function in (
10) is subject to the power balance constraint expressed in (
12). Equation (
12) ensures that power bought in day-ahead, intra-day and real-time markets fulfill the need for all individual charging.
In addition, the EV aggregator defines hourly price incentives for EV owners as in (
13), where
is calculated as the average of day-ahead, intra-day and real-time market prices and
n is a constant margin.
2.4.2. Lower-Level: EV Owners as Stackelberg Game Followers
On the lower level the potential customers aim at optimizing their charging schedule at the lowest cost possible (
14).
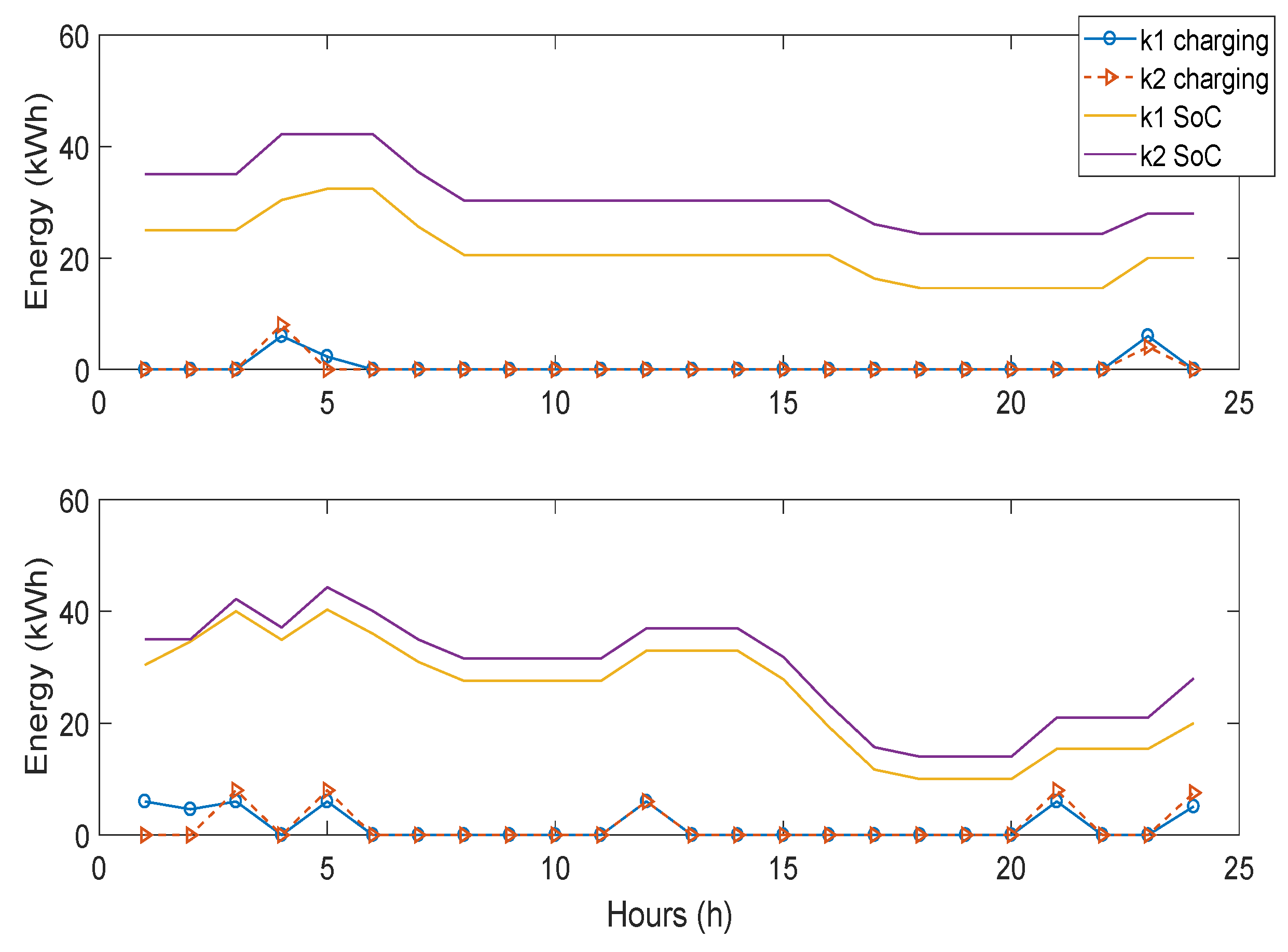
The state of charge balance constraint can be modeled as:
The new battery content for each trading period is calculated considering its previous content, energy inflow and energy outflow. This thought is stated in (
15). Both mobile and immobile batteries can be modeled using Equation (
15). This implies that, for immobile batteries,
availability matrix is always 1. For EVs, the availability matrix is either 0 or 1 depending on whether the EV is available or on a trip. The battery level is bounded by its minimum and maximum levels (
16) and (
17).
Charging activities in the periods of unavailability is prevented by the constraints (
18) and (
19). Finally, the constraint (
20) and (
21) stress the end SoC condition.
The dual variables for equalities h and inequalities g are denoted and correspondingly and are written next to the respective constraint.
The stochastic bi-level problem for developing profit-maximizing price levels while trading in day-ahead, intra-day and real-time markets for an EV aggregator is defined by:
where
=
is the set of decision variables for the upper level problem and
=
is the set of decision variables for the lower level problem.
2.4.3. The Stochastic Convex Reformulation of the Bilevel Program
The LL optimization problem stated in (25)–(32) is a linear program, thus convex. Therefore, it can be replaced by its KKT optimality conditions, which are both necessary and sufficient. To this end, the LL problem KKT conditions can be directly included as constraints for the UL problem stated in (
22)–(24). The bilevel problem is thus presented by its MPEC formulation: UL problem (
22)–(24), LL constraints (26)–(32), KKT stationary equations and complementary slackness constraints (the complementary slackness constraints are derived in
Appendix A.2).
The first order stationary conditions are derived by building the Lagrangian function of the LL problem and taking partial derivative of it with respect to the primal variables (
33). The Lagrange function is derived in
Appendix A.1.
The complementary slackness constraints
cause non-linearity. To avoid non-linearity resulting from the complementary slackness constraints, this formulation uses the strong duality condition [
36] as derived in (
34). With this last transformation equivalent one-level convex formulation is achieved. Hence, a global optimal solution can be reached.
4. Conclusions
This paper studies the interaction between EV aggregator and EV owner, aiming to maximize the aggregator’s profit and to provide EV owners with the most cost-optimal charging method. We develop a stochastic bilevel program based on the Stackelberg game to optimize the EV aggregator’s decisions. The model allows us to determine endogenously the profit-optimal price incentives, which in turn generates the cost-optimal charging schedules of the final customers. By incorporating strong duality theorem the bilevel model is transformed to a single level convex mathematical program.
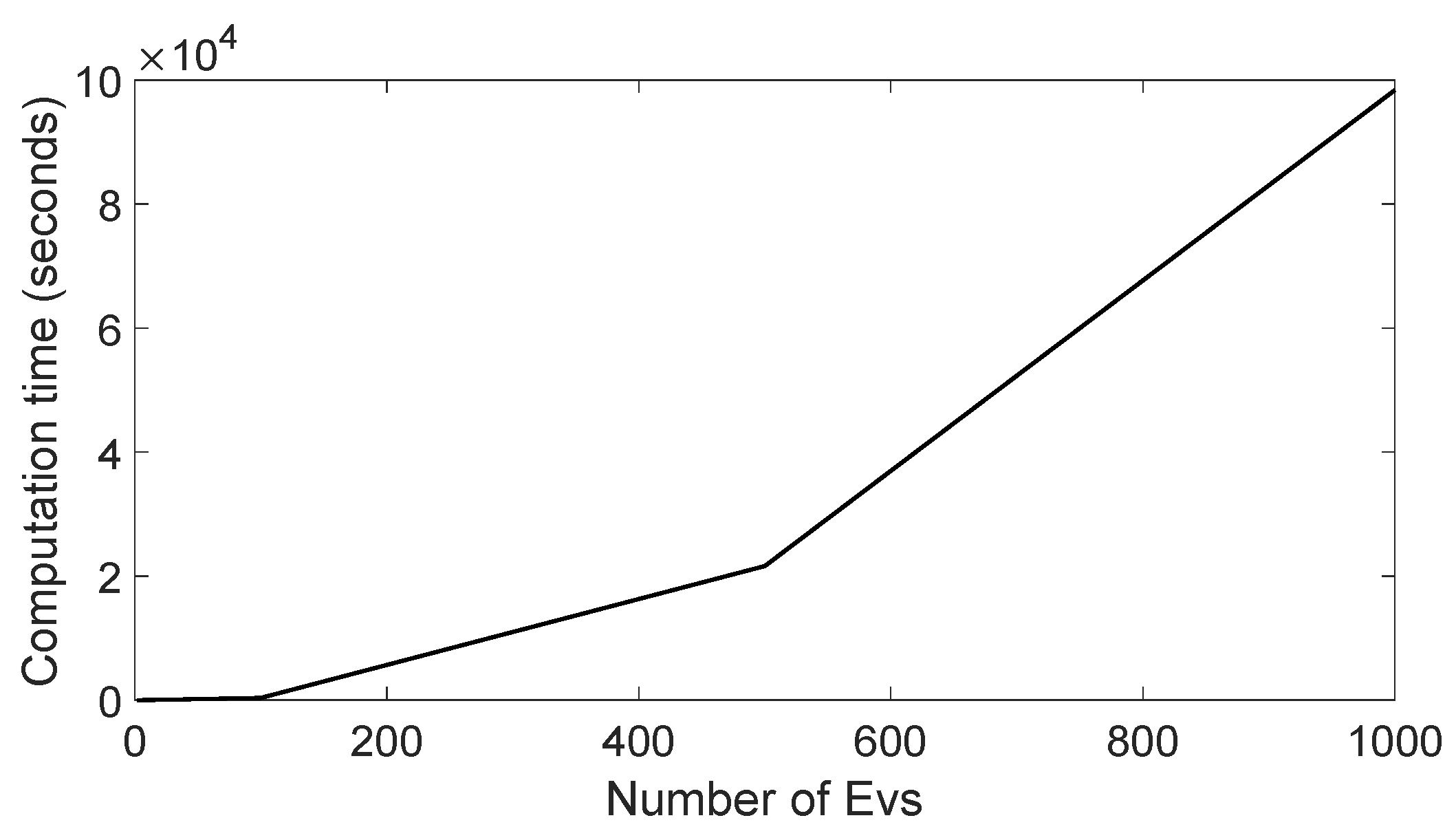
The work creates solid ground to analyze the strategic interaction in a leader-follower game highlighting that aggregators with solid knowledge of the physical features of local EVs’ can behave strategically to increase their profit. Using the developed formulation, the optimal energy economics are achieved for both aggregator on the upper level and EV owners on the lower level in both small and large case studies. The study results show how uncertainties related to market prices and fleet characteristics influence the EV charging plans. In addition, we show how the aggregator selects the optimal retail price margin to keep its customers satisfied. Moreover, the results indicate an economic gain is achieved from coordinated planning when the aggregator trades energy in three day-ahead, intra-day and real-time markets. Large-scale study simulation results indicate that, in order to make the model computationally tractable and applicable for big cases (more than 1000 EVs), a decomposition is required. The developed methodology may be directly included in the everyday scheduling activities of the EV aggregators or retailers. Alternatively, the model might be useful for stakeholders and policy makers to assess the overall added value by coupling the power and transport sectors. This work can be extended by applying a suitable decomposition technique.