Maintenance Models Applied to Wind Turbines. A Comprehensive Overview
Abstract
1. Introduction
- Strategy: Resource requirements, planning, planning horizon, objectives.
- Tactics: Planning; scheduling; inventory management; statistical processing of the information; legal aspects; compliance with the standards; status of the work orders, process and control the processes; selection of the methodology to monitor, detect, diagnose and repair failures; financial indicators; safety; production; etc.
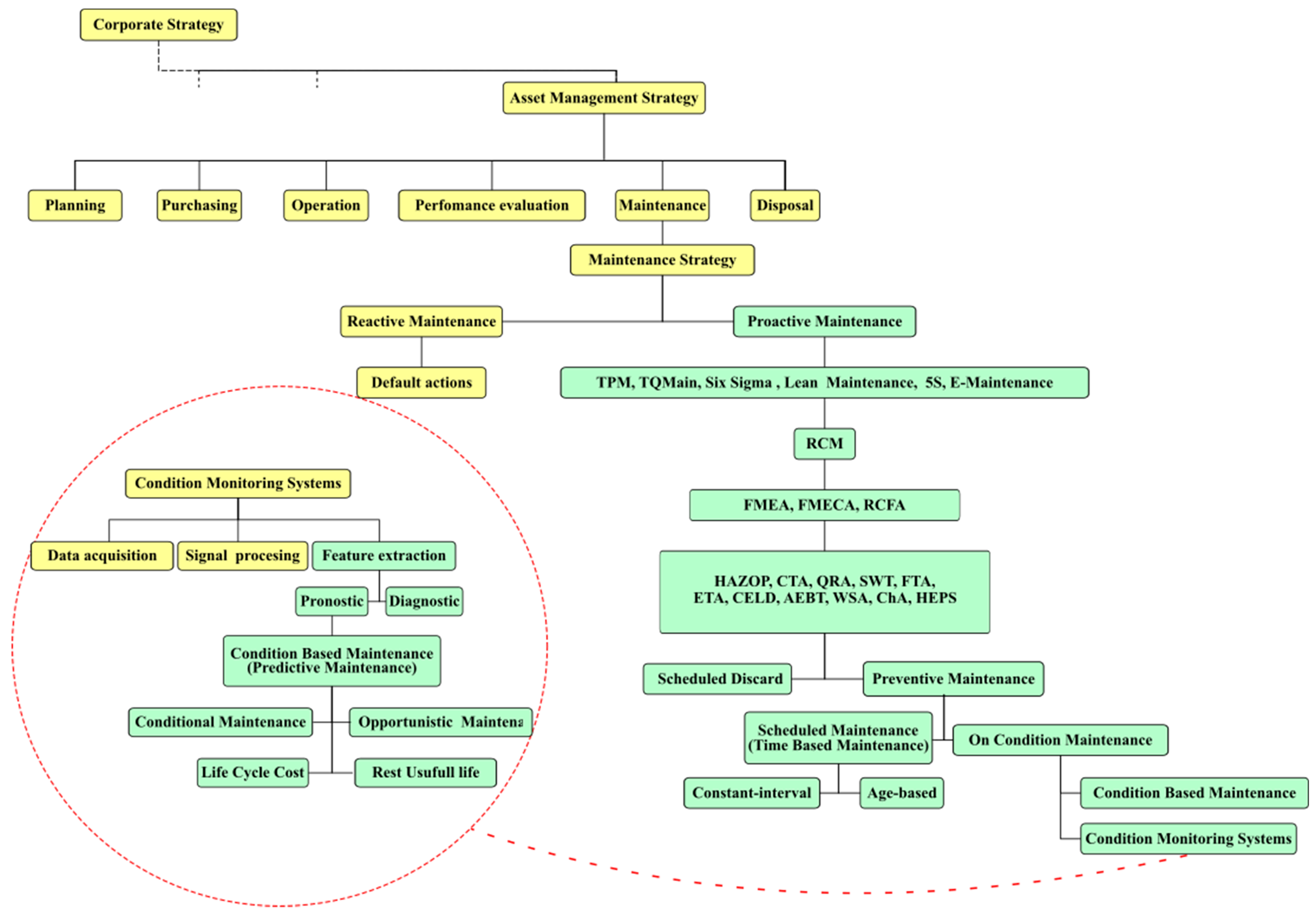
- Continuous improvement: This is done through Total Productive Maintenance (TPM) and Reliability-Centered Maintenance (RCM).
2. Types of Models Applied at the Strategic and Tactical Levels
- What are the functions and associated desired standards of performance of the asset in its present operating context?
- In what manners can it fail to fulfill its functions?
- What causes each functional failure?
- What happens when each failure occurs?
- In what manner does each failure matter?
- What should be done to predict or prevent each failure?
- What should be done if a suitable proactive task cannot be found?
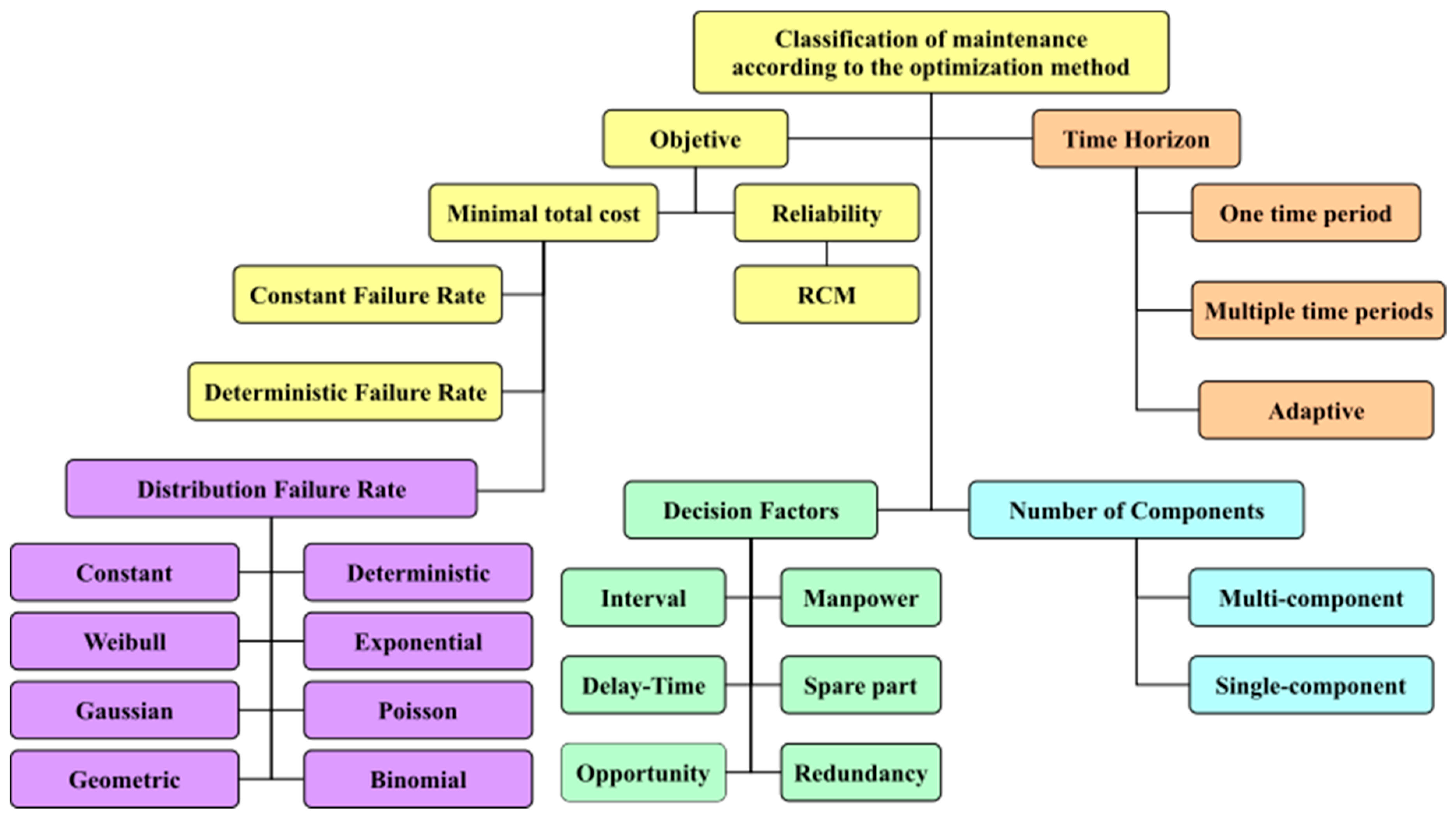
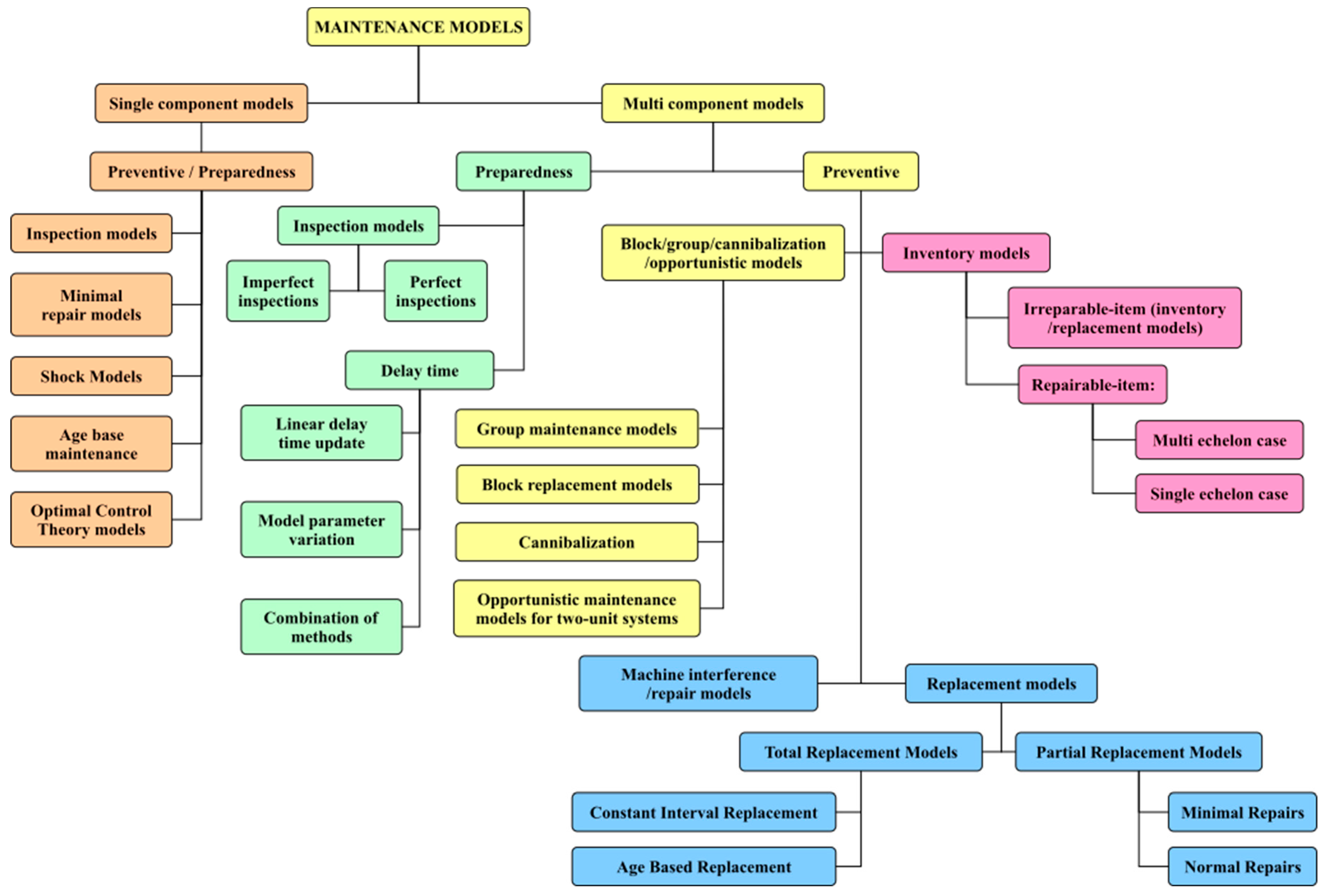
3. Maintenance Types and Associated Mathematical Models
3.1. Replacement Models
- The failure rate is an increasing function.
- The minimal repairs do not affect the failure rate of the system.
- The minimal repair cost is lower than the cost of replacing the entire system.
- The total PR of the equipment is performed after (k − 1) PPRs.
- hi is the length of the i-th time interval (i = 1, 2,..., N − 1) in which the IPM will be performed.
- The IPM is performed at times h1, h1 + h2,…
- The PR is performed after interval N.
- If an unexpected failure occurs between two IPMs, a minimal repair is applied.
- After a PR, the equipment recovers its original failure rate.
- λ(t) is continuous and increases with time.
- The times that minimal repairs, PR and IPM have to be performed at are ignored.
- After N intervals, the cycle ends with a PR.
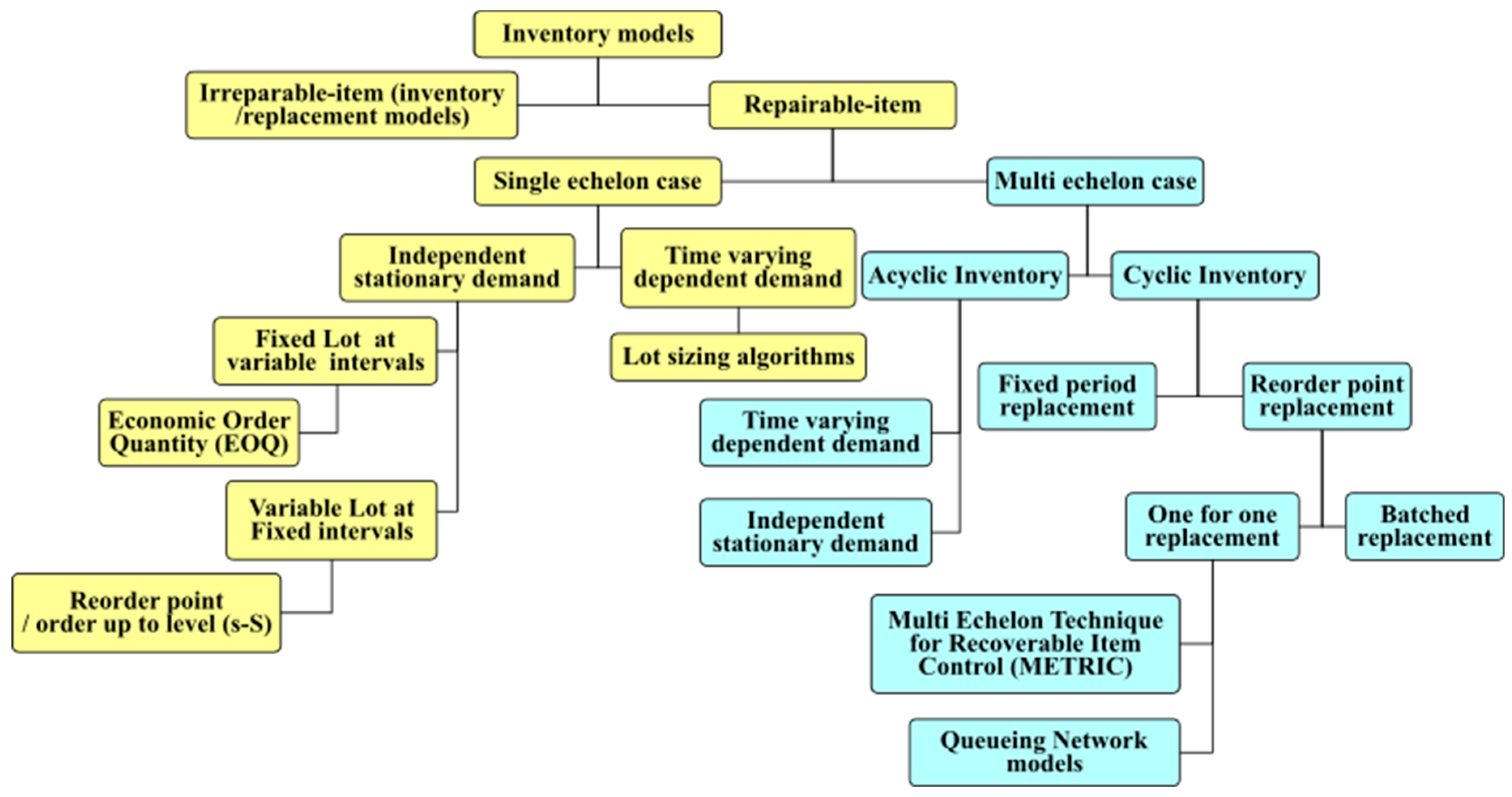
3.2. Models According to the Number of Components
3.3. Impact Models
- The system is subjected to random impacts.
- Each impact causes a random amount of damage.
- The failure is cumulative.
- The time between impacts and the damage caused are random variables with distribution functions FX(t) and GX(t), respectively, and depend on the cumulative damage at time t, X(t).
- After a failure, the system is replaced by an identical and new system at a cost c(Δ). Δ refers to the failure.
- If the deterioration reaches a certain value X, then the replacement can be performed prior to the failure at a lower cost compared to if it is performed after the failure.
- The age at which the maintenance must be performed is ignored.
- It is assumed that the time that it takes to perform the replacements is negligible.
- A new cycle begins with each replacement.
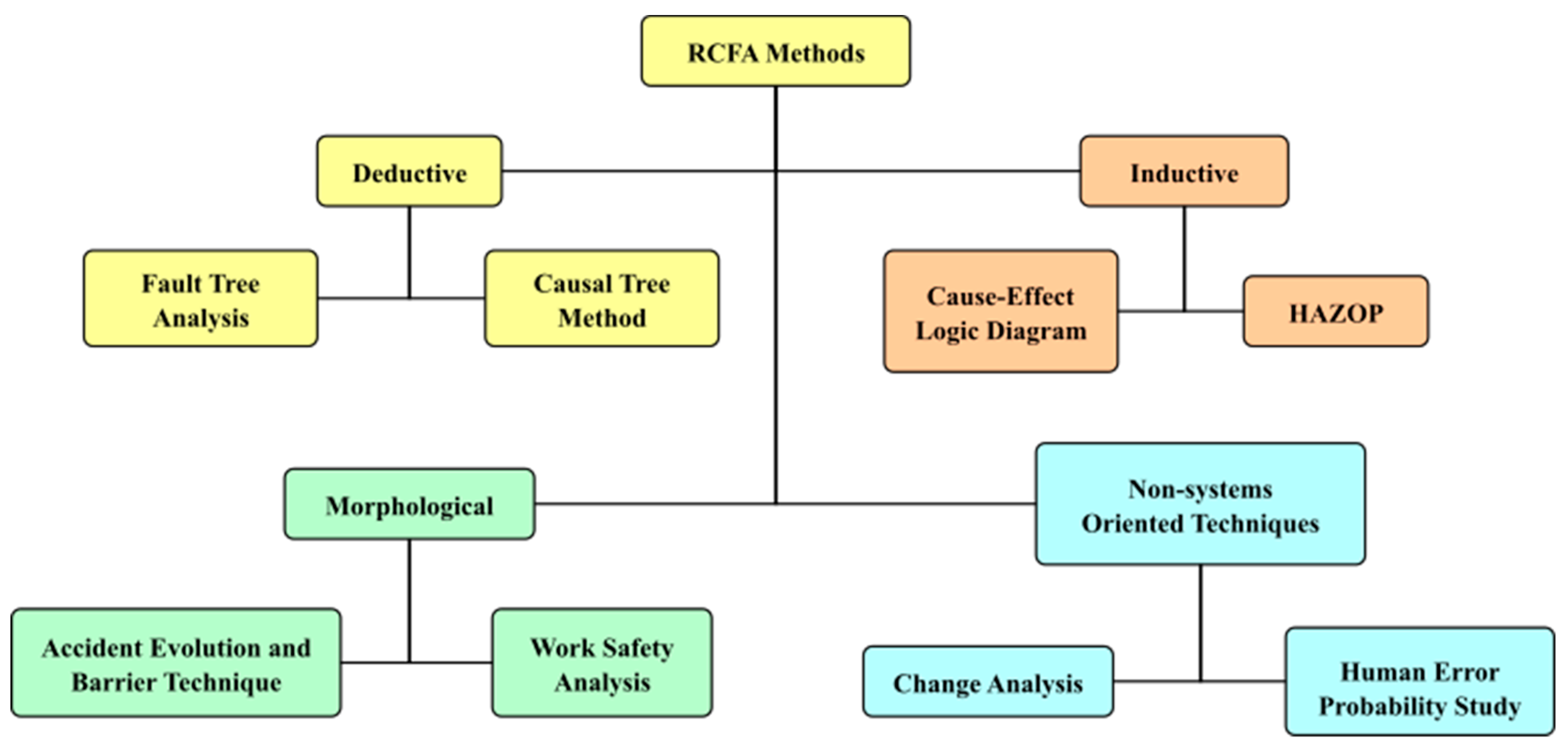
3.4. Inspection Models
- (1)
- Partial inspections detect without error only some types of system failures.
- (2)
- Imperfect inspections can detect some types of system failures (assuming that a failure is detectable by imperfect inspections).
- (3)
- Perfect inspections detect all system failures without error.
- Inspections are performed at times x1, x2, x3,…,xn.
- When a failure is found, the equipment is replaced, and the cycle begins again.
- The equipment failure is only known after the inspection.
- The inspections do not deteriorate the equipment.
- Each inspection has a cost Ci.
- The cost per unit time associated with an undetected failure is Cf.
- The corrective replacement (CR) cost is C.
- When an unexpected failure occurs between inspections, at time ti, the inspection cycle cost is given by Equation (16), and the replacement is performed when the next xn is reached. The cost of this cycle is given by Equation (17).
- The TEC of the maintenance model is obtained by Equation (18); the goal is to find the number of inspections that minimizes the cost:
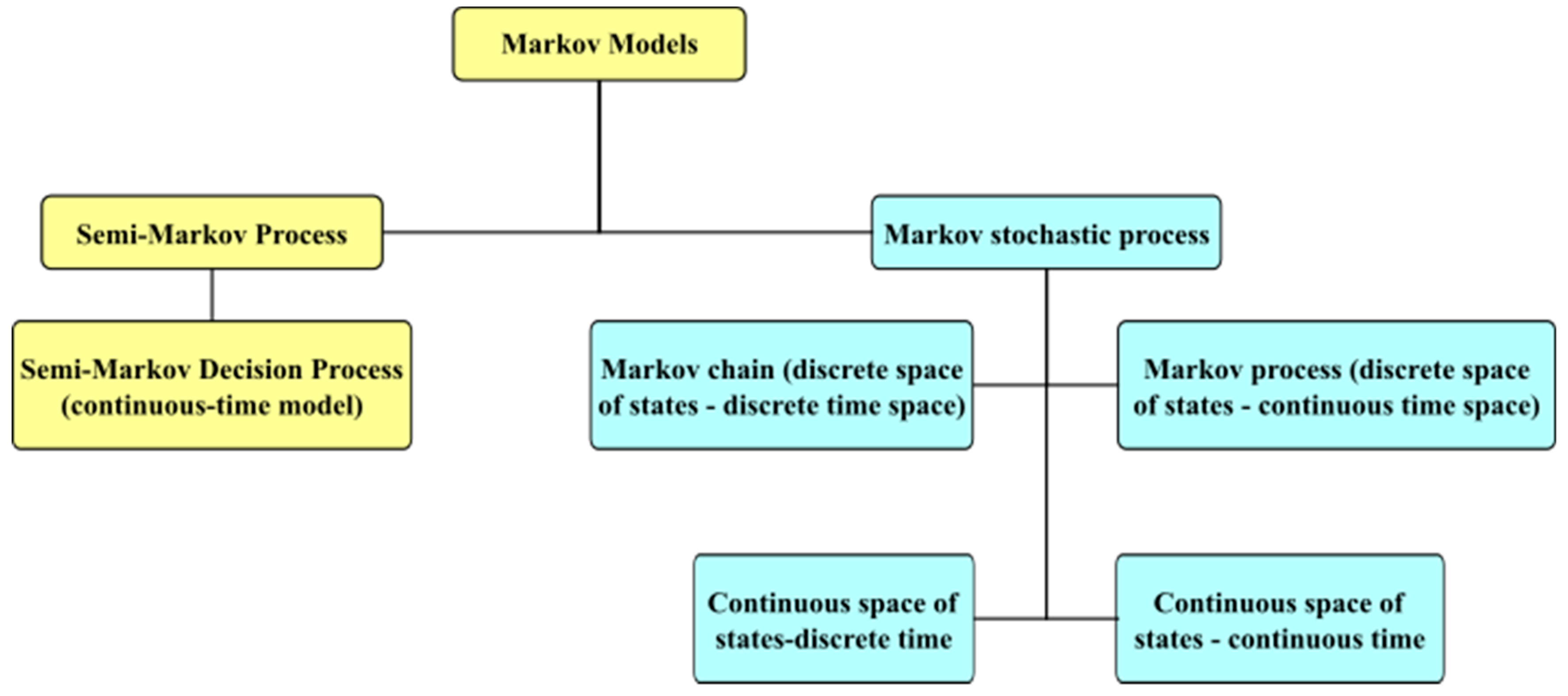
3.5. Maintenance Models Based on Markov Models
3.6. Models Applied to the Logistics of Operation and Maintenance
4. Methodologies and Mathematical Models Applied to the Detection, Diagnosis and Prognosis of Failures
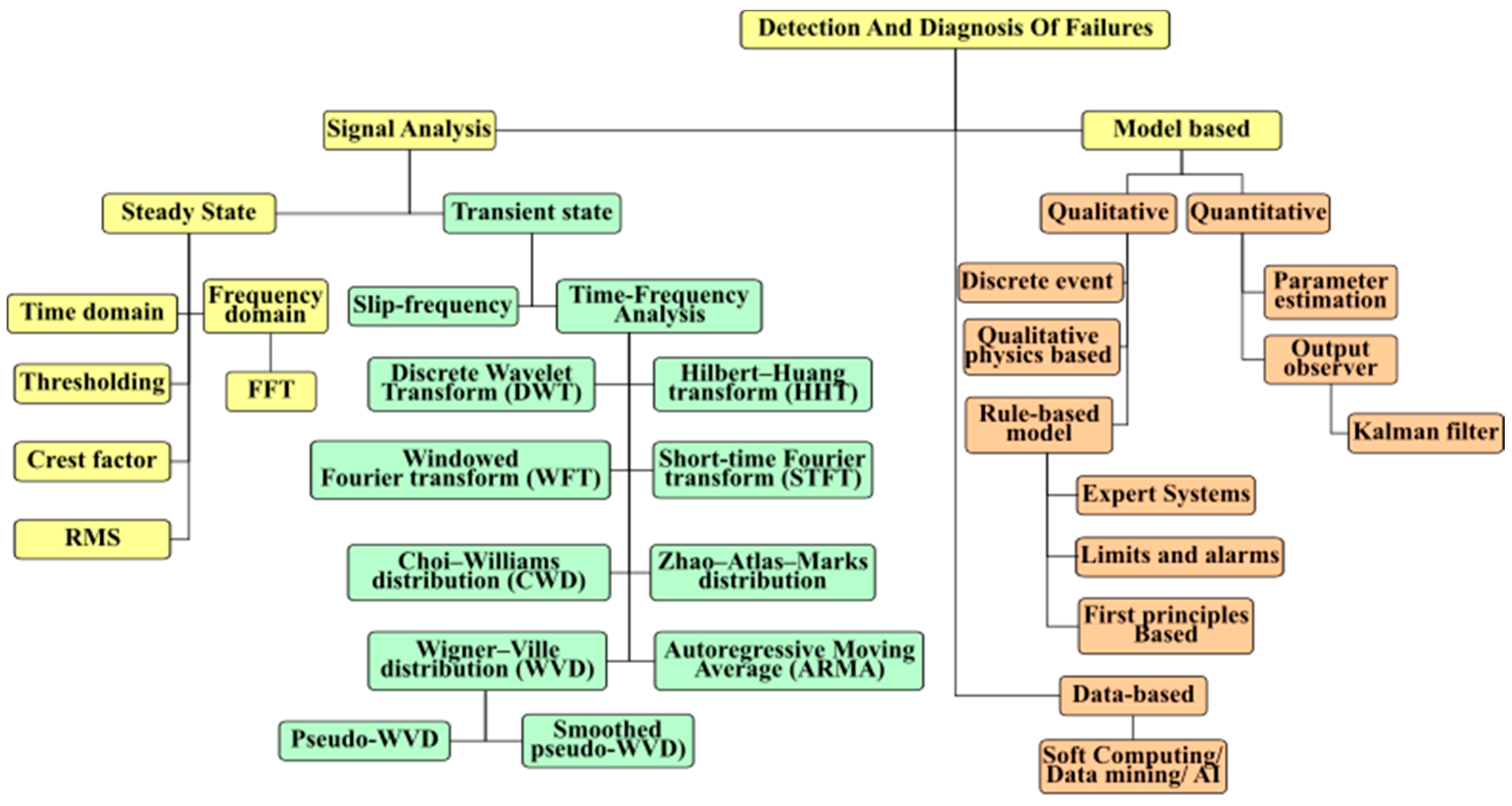
4.1. Detection and Diagnosis
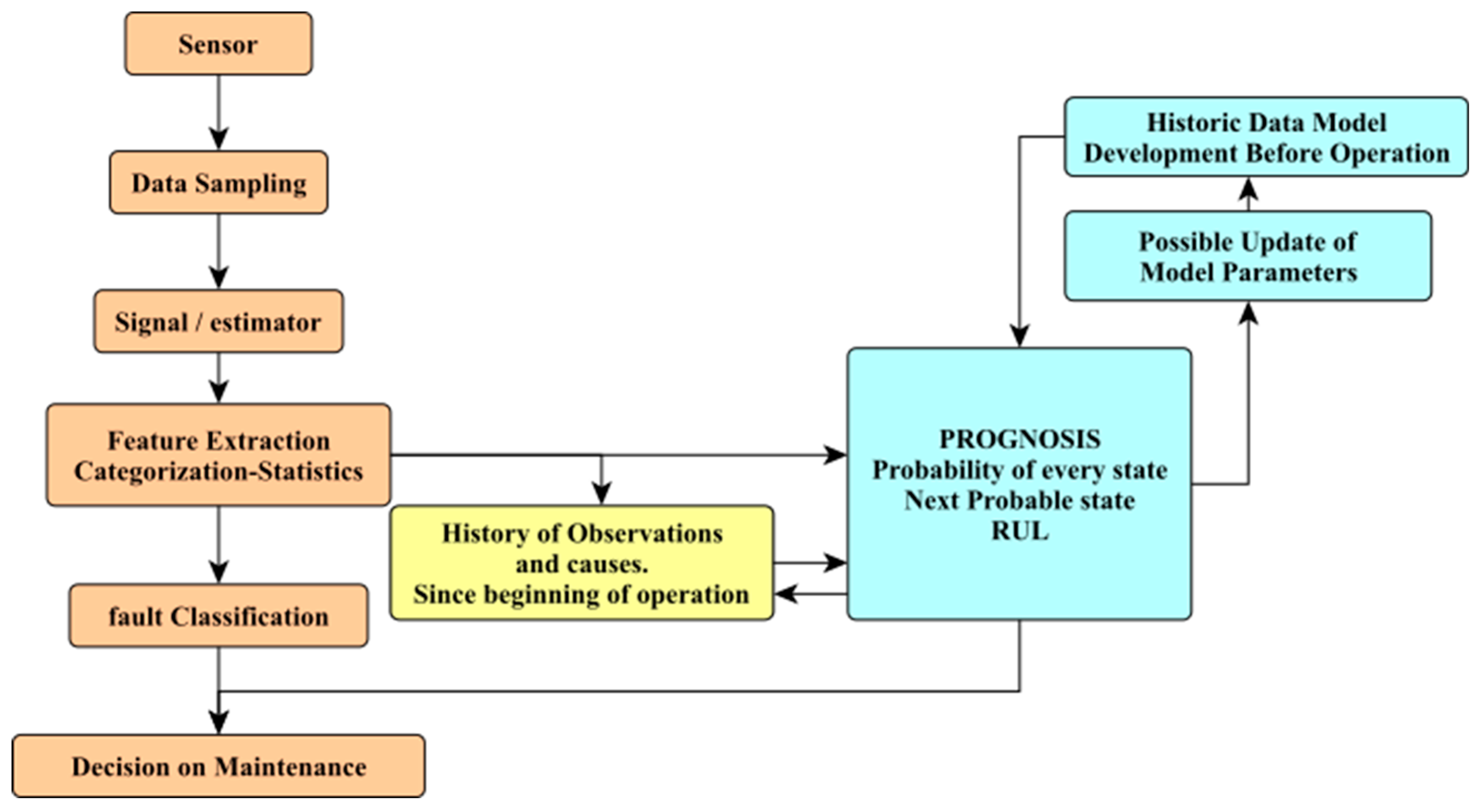
4.2. Prognosis of Failures
4.2.1. Support Vector Machines (SVMs)
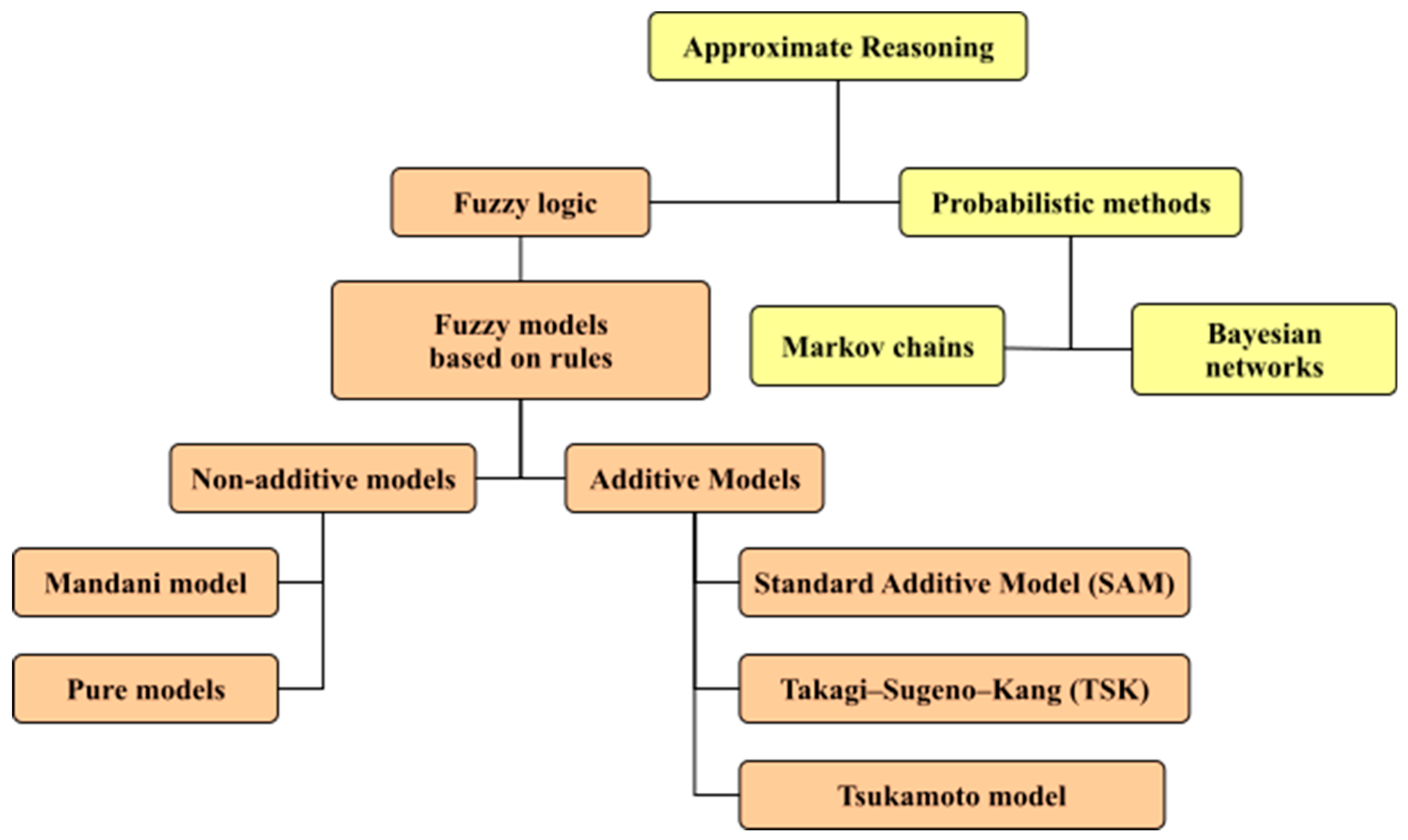
4.2.2. Bayesian Networks
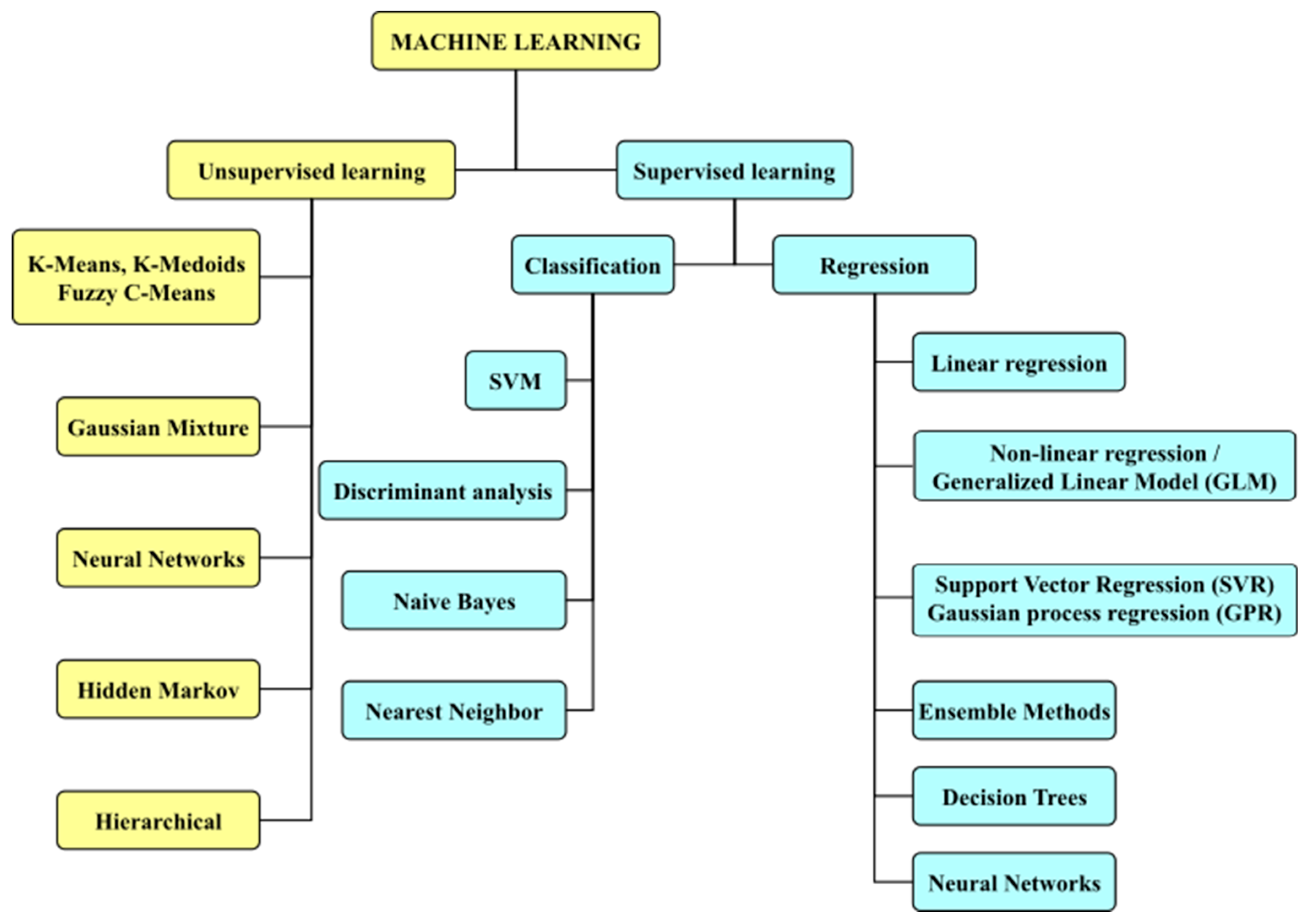
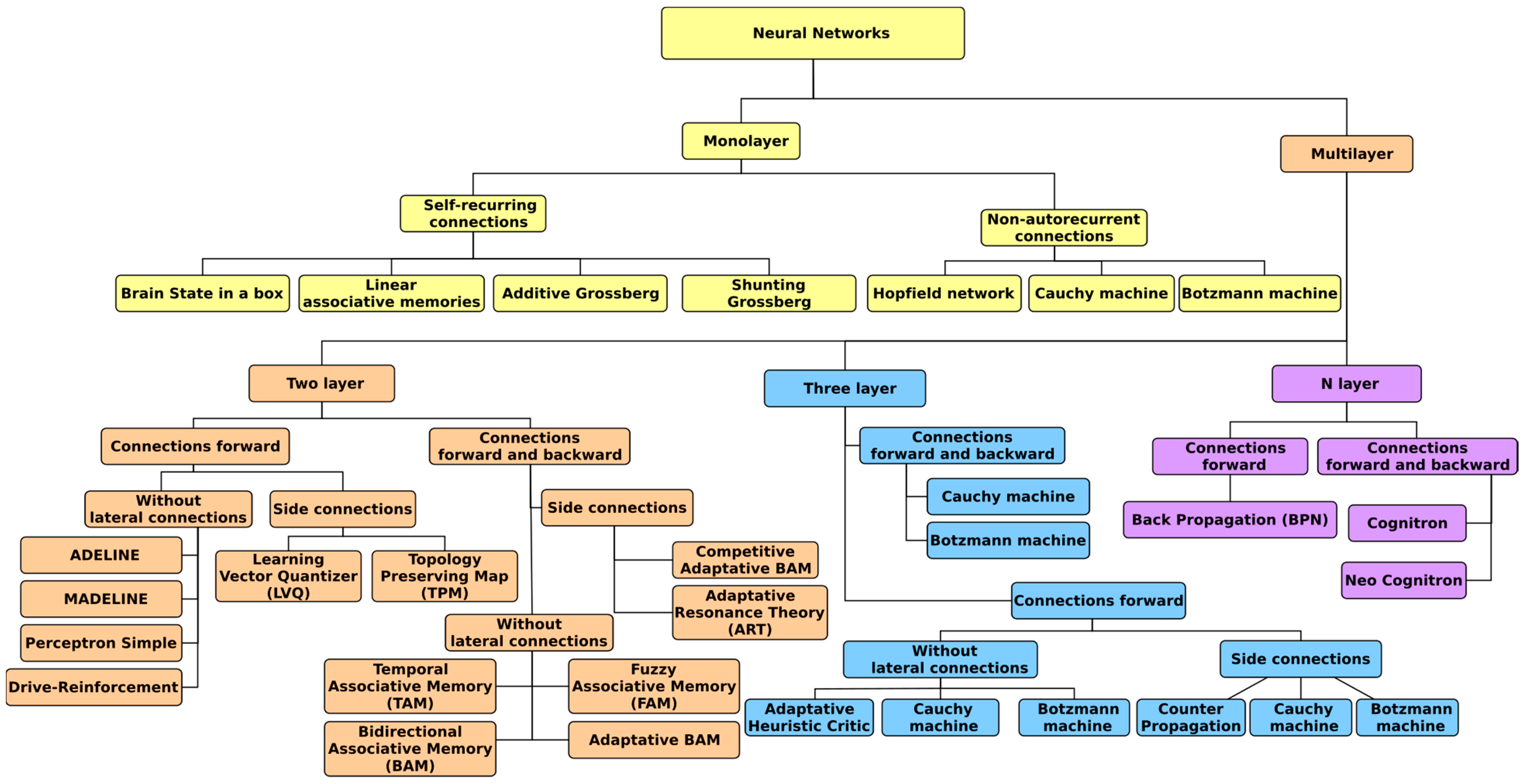
4.2.3. Artificial Neural Networks (ANNs)
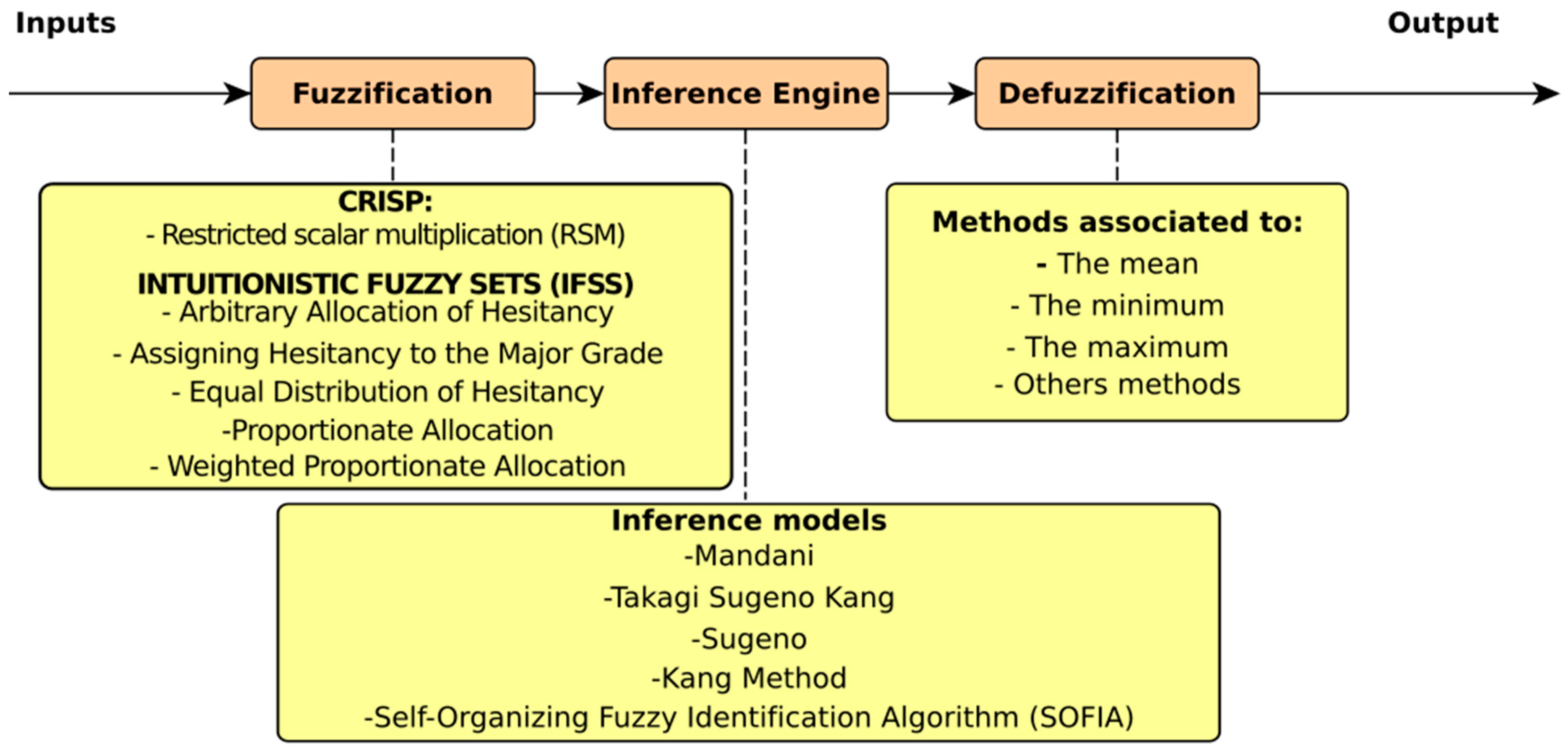
4.2.4. Fuzzy Logic
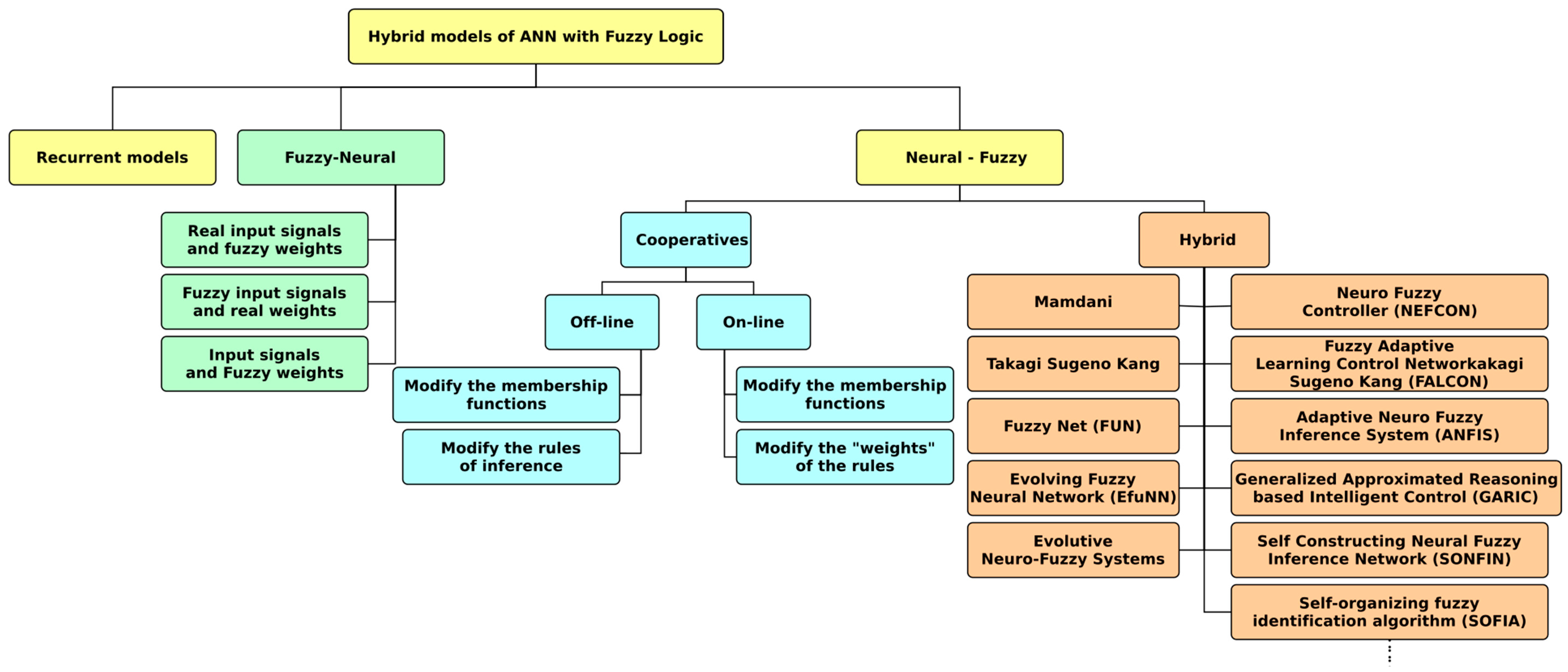
4.2.5. Hybrid Models
5. Conclusions and Recommendations
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AEBT | Accident Evolution and Barrier Technique |
| AHP | Analytical Hierarchy Process |
| ANNs | Artificial Neural Networks |
| ANFIS | Adaptive Neuro Fuzzy Inference System |
| AAKR | Autoassociative Kernel Regression |
| ARMA | Autoregressive Moving Average |
| ARIMA | Autoregressive Integrated Moving Average |
| BDD | Binary Decision Diagram |
| BN | Bayesian Networks |
| CA | Criticality Analysis |
| CBM | Condition Based Maintenance |
| CAPEX | Into Capital Expenditure |
| CELD | Cause Effect Logic Diagram |
| ChA | Change Analysis |
| CMS | Condition Monitoring System |
| CM | Corrective Maintenance |
| COE | Cost of Energy |
| CPM | Critical Path Method |
| CR | Corrective Replacement |
| CTA | Critical Task Analysis |
| DAG | Directed Acyclic Graph |
| DFIG | Doubly Fed Induction Generator |
| DFMEA | Design Failure Mode and Effects Analysis |
| DTS | Degradation-Threshold-Shock |
| DTM | Delay Time Model |
| ETA | Event Tree Analysis |
| FFT | Fast Fourier transform |
| FMEA | Failure Mode and Effects Analysis |
| FMECA | Failure Mode Effects and Criticality Analysis |
| FT | Fault Tree |
| FTA | Fault Tree Analysis |
| GSPN | Generalized Stochastic Petri Nets |
| HAZOP | Hazard and Operability Studies |
| HEPS | Human Error Probability |
| HPP | Homogeneous Poisson Process |
| IPM | Imperfect Preventive Maintenance |
| JESS | Java Expert Shell System |
| k-NN | k-Nearest neighbor |
| kW | kilo Watts |
| LCCA | Life Cycle Cost Analysis |
| MatMs | Mathematical Models |
| MLP | Multilayer Perceptron |
| MILP | Mixed Integer Linear Programming |
| MRP | Material Requirements Planning |
| MTBF | Mean Time Between Failure |
| MTTF | Mean Time To Failure |
| MTTR | Mean Time To Repair |
| MW | Mega Watts |
| NHPP | Non Homogeneous Poisson Process |
| NR | Normal Replacement |
| O&M | Operation and Maintenance |
| OPEX | Operating Expenditure |
| PAM | Physical Asset Management |
| PERT | Program Evaluation and Review Techniques |
| PF | Particle Filtration |
| PFMEA | Production Failure Mode and Effects Analysis |
| PLP | Power Law Process |
| PM | Preventive Maintenance |
| POMDP | Partially Observed Markov Decision Process |
| PPR | Preventive Partial Replacement |
| PREMO | Preventive Maintenance Optimization |
| QRA | Quantified Risk Analysis |
| RCFA | Root Cause Failure Analysis |
| RCM | Reliability Centered Maintenance |
| RPN | Risk Priority Number |
| RUL | Remaining Useful Life |
| SCADA | Supervisory Control and Data Acquisition |
| SCM | Supply Chain Management |
| SLT | Statistical Learning Theory |
| SRM | Structural Risk Minimization |
| SVM | Support Vector Machines |
| SWT | Structured What if Technique |
| TEC | Total Expected Cost per Unit Time |
| TPM | Total Productive Maintenance |
| TQM | Total Quality Management |
| TQMain | Total Quality Maintenance |
| WF | Wind Farm |
| WSA | Work Safety Analysis |
| WT | Wind Turbine |
| MMs | Maintenance Models |
References
- Igliński, B.; Iglińska, A.; Koziński, G.; Skrzatek, M.; Buczkowski, M. Wind energy in Poland–History, current state, surveys, Renewable Energy Sources Act, SWOT analysis. Renew. Sustain. Energy Rev. 2016, 64, 19–33. [Google Scholar] [CrossRef]
- Erguido, A.; Crespo Márquez, A.; Castellano, E.; Gómez Fernández, J. A dynamic opportunistic maintenance model to maximize energy-based availability while reducing the life cycle cost of wind farms. Renew. Energy 2017. [Google Scholar] [CrossRef]
- Al-Najjar, B. Total quality maintenance. J. Qual. Maint. Eng. 2017, 2, 4–20. [Google Scholar] [CrossRef]
- Jardine, A.; Tsang, A. Maintenance, Replacement, and Reliability—Theory and Applications, 2nd ed.; Taylor and Francis, Boka: Boca Raton, FL, USA, 2006; ISBN 0-8493-3966-9. [Google Scholar]
- Xing, B.; Marwala, T. Smart Maintenance for Human–Robot Interaction, 1st ed.; Springer International Publishing: Gewerbestrasse, Switzerland, 2018; ISBN 978-3-319-67480-3. [Google Scholar]
- Al-Turki, U. Methodology and Theory A framework for strategic planning in maintenance. J. Qual. Maint. Eng. 2011, 17, 150–162. [Google Scholar] [CrossRef]
- Bertling, L.; Wennerhag, P. Wind Turbine Operation and Maintenance. 2012. Available online: https://www.coursehero.com/file/17068791/12-41-rapport-screen-1-OM/ (accessed on 2 January 2018).
- Shafiee, M. Maintenance logistics organization for offshore wind energy: Current progress and future perspectives. Renew. Energy 2015, 77, 182–193. [Google Scholar] [CrossRef]
- Velmurugan, R.; Dhingra, T. Maintenance strategy selection and its impact in maintenance function. Concept. Framew. 2015, 35, 1622–1661. [Google Scholar] [CrossRef]
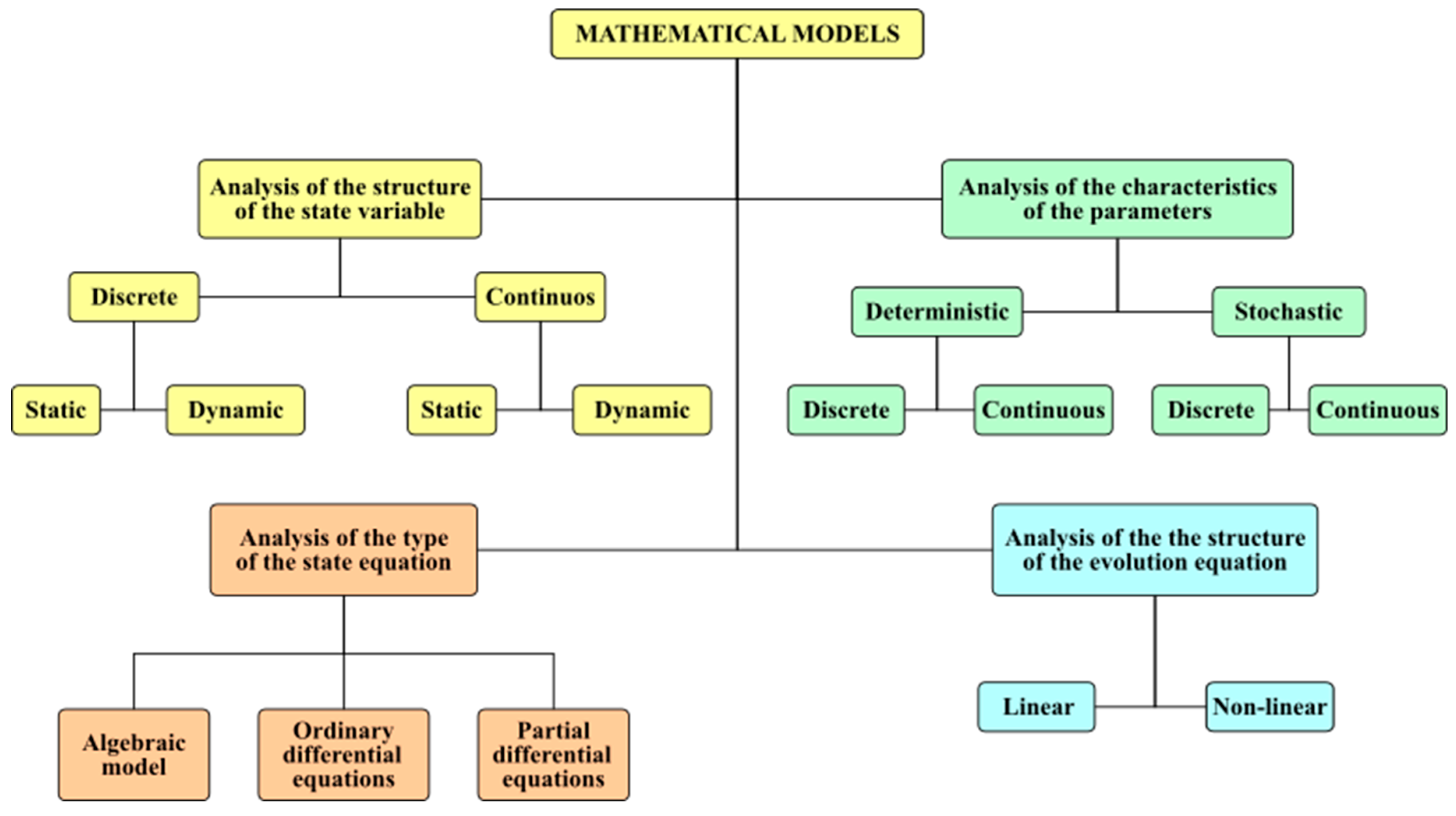
- Veltem, K. Mathematical Modelling and Simulation. Introduction for Scientists and Engineers, 1st ed.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2009; ISBN 978-3-527-40758-8. [Google Scholar]
- Bellomo, N.; Preziosi, L. Modelling Mathematical Methods and Scientific Computation, 1st ed.; CRC Press: Boca Raton, FL, USA, 1995; ISBN 0-8493-8331-5. [Google Scholar]
- Campbell, J.; Reyes-Picknell, J. Uptime: Strategies for Excellence in Maintenance Management, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2016; ISBN 9781482252378. [Google Scholar]
- Endrenyi, J.; Aboresheid, S.; Allan, R.; Anders, G.; Asgarpoor, S.; Billinton, R.; Chowdhury, N.; Dialynas, E.; Fipper, M.; Fletcher, R.; et al. The Present Status of Maintenance Strategies and the Impact of Maintenance on Reliability. IEEE Trans. Power Syst. 2001, 16, 638–646. [Google Scholar] [CrossRef]
- Andrawus, J. Maintenance Optimisation for Wind Turbines. Ph.D. Thesis, School of Engineering, Robert Gordon University, Aberdeen, Scotland, UK, 2008. Available online: https://openair.rgu.ac.uk/bitstream/handle/10059/268/AndrawusThesis.pdf (accessed on 10 January 2017).
- Walford, C. Wind Turbine Reliability: Understanding and Minimizing wind Turbine Operation and Maintenance Costs; Sandia National Laboratories: Alburquerque, NM, USA, 2006; Available online: prod.sandia.gov/techlib/access-control.cgi/2006/061100.pdf (accessed on 4 January 2018).
- Crespo-Márquez, A. The Maintenance Management Framework. Models and Methods for Complex Systems Maintenance; Springer International Publishing: New York, NY, USA, 2007; ISBN 978-1-84628-821-0. Available online: https://link-springer-com.ponton.uva.es/content/pdf/10.1007%2F978-1-84628-821-0.pdf (accessed on 18 February 2018).
- Pires, G.; Araújoa, A.; Carvalho, P. Prognostic techniques applied to maintenance of wind turbines: A concise and specific review. Renew. Sustain. Energy Rev. 2017, in press. [Google Scholar] [CrossRef]
- McCarthy, D.; Rich, N. Lean TPM: A Blueprint for Change; Elsevier Butterworth-Heinemann: Burlington, UK, 2004; ISBN 0750658576. Available online: https://ebookcentral.proquest.com/lib/uguayaquil-ebooks/detail.action?docID=226761 (accessed on 18 January 2018).
- Ahuja, I.; Khamba, J. Total Productive Maintenance Implementation in a manufacturing organization. Int. J. Product. Qual. Manag. 2017, 3, 360–381. [Google Scholar] [CrossRef]
- Nakajima, S. Introduction to TPM: Total Productive Maintenance; Productivity Press: Minnesota, USA, 1988; ISBN 0915299232. [Google Scholar]
- Aldairi, J.; Khan, M.; Munive-Hernandez, E. Knowledge-based Lean Six Sigma maintenance system for sustainable buildings. Int. J. Lean Six Sigma 2017, 8, 109–130. [Google Scholar] [CrossRef]
- Osada, T. The 5S’s: Five Keys to a Total Quality Environment; Asian Productivity Organization: Tokyo, Japan, 1991; ISBN 978-9283311164. [Google Scholar]
- Iung, B.; Levrat, E.; Crespo, A.; Erbe, H. Conceptual framework for e-Maintenance: Illustration by e-Maintenance technologies and platforms. Annu. Rev. Control 2009, 33, 220–229. [Google Scholar] [CrossRef]
- Ricky, S.; Bruce, H. Lean Maintenance: Reduce Costs; Improve Quality and Increase Market Share: Burlington, UK, 2004; ISBN 9780750677790. Available online: https://ebookcentral.proquest.com/lib/uguayaquil-ebooks/detail.action?docID=226703 (accessed on 18 January 2018).
- Ramakrishnan, V.; Nallusamy, S. Implementation of Total Productive Maintenance Lean Tool to Reduce Lead Time-A Case Study. Int. J. Mech. Eng. Technol. 2017, 8, 295–306. [Google Scholar]
- Sherwin, D.; Jonsson, P. TQM, maintenance and plant availability. J. Qual. Maint. Eng. 1995, 1, 15–19. [Google Scholar] [CrossRef]
- Sherwin, D. A review of overall models for maintenance management. J. Qual. Maint. Eng. 2000, 6, 138–164. [Google Scholar] [CrossRef]
- Rausand, M.; Hsyland, A. Systems Reliability Theory, 2nd ed.; John Wiley & Sons, Inc. Publication: Hoboken, NJ, USA, 2004; ISBN 0-471-47133-X. [Google Scholar]
- Moubray, J. Reliability-Centered Maintenance, 1st ed.; Redd Educational and Professional Publishing Ltd.: Woburn, MA, USA, 1997; ISBN 0750633581. [Google Scholar]
- Andrawus, J.; Watson, J.; Kishk, M.; Adam, A. The Selection of a Suitable Maintenance Strategy for Wind Turbines. Wind Eng. 2006, 30, 471–486. [Google Scholar] [CrossRef]
- Arabian-Hoseynabadi, H.; Oraee, H.; Tavner, P. Failure Modes and Effects Analysis (FMEA) for wind turbines. Electr. Power Energy Syst. 2010, 32, 817–824. [Google Scholar] [CrossRef]
- Anleitner, M. Power of Deduction: Failure Modes and Effects Analysis for Design, 2nd ed.; ProQuest Ebook Central; ASQ Quality Press: New York, NY, USA, 2010; ISBN 978-0-87389-796-9. Available online: https://ebookcentral.proquest.com/lib/uguayaquil-ebooks/detail.action?docID=3002651 (accessed on 14 February 2018).
- Tazi, N.; Châtelet, E.; Bouzidi, Y. Using a Hybrid Cost-FMEA Analysis for Wind Turbine Reliability Analysis. Energies 2017, 10, 276. [Google Scholar] [CrossRef]
- Dinmohammadi, F.; Shafiee, F. An economical FMEA-based risk assessment approach for wind turbine systems. In Proceedings of the European Safety and Reliability Conference, ESREL 2013, Amsterdam, The Netherlands, 29 September–2 October 2013. [Google Scholar]
- Crespo Márquez, A. Criticality Analysis for Maintenance Purposes: A Study for Complex In-service Engineering Assets. Qual. Reliabil. Eng. Int. 2015. [Google Scholar] [CrossRef]
- Zhou, A.; Yu, D.; Zhang, W. A research on intelligent fault diagnosis of wind turbines based on ontology and FMECA. Adv. Eng. Inform. 2014, 29, 115–125. [Google Scholar] [CrossRef]
- Rui, J.; Kaili, Z.; Zhiyong, M.; Dameng, W. Fault mode, effects and criticality analysis for overheating fault of wind turbines gearbox and generator. In Proceedings of the International Conference on Renewable Power Generation (RPG 2015), Beijing, China, 17–18 October 2015. [Google Scholar]
- Li, J.; Xu, H. Reliability analysis of aircraft equipment based on FMECA method. Phys. Procedia 2012, 25, 1816–1822. [Google Scholar] [CrossRef]
- Du, Y.; Liao, L.; Wang, L. Failure Mode, Effects and Criticality Analysis of Remanufactured Machine Tools in Service. Int. J. Precis. Eng. Manuf. 2017, 18, 425–434. [Google Scholar] [CrossRef]
- Carpitella, S.; Certa, A.; Izquierdo, J. A combined multi-criteria approach to support FMECA analyses: A real-world case. Reliab. Eng. Syst. Saf. 2017. [Google Scholar] [CrossRef]
- Seebregts, A.; Rademakers, L.; Van den Horn, B. Reliability Analysis In Wind Turbine Engineering. Microelectron Reliab. 1995, 35, 1285–1307. [Google Scholar] [CrossRef]
- García-Marquez, F.; Pinar-Perez, J.; Pliego-Marugan, A.; Papaelias, M. Identification of critical components of wind turbines using FTA over the time. Renew. Energy 2015, 56, 1–15. [Google Scholar] [CrossRef]
- Chou, J.; Tu, W. Failure analysis and risk management of a collapsed large wind turbine tower. Eng. Fail. Anal. 2011, 18, 295–313. [Google Scholar] [CrossRef]
- Tian, Z.; Jin, T.; Wu, B.; Ding, F. Condition based maintenance optimization for wind power generation systems under continuous monitoring. Renew. Energy 2011, 36, 1502–1509. [Google Scholar] [CrossRef]
- García, F.; Mark, A.; Pinar, J.; Papaelias, M. Condition monitoring of wind turbines: Techniques and methods. Renew. Energy 2012, 46, 169–178. [Google Scholar] [CrossRef]
- Tchakoua, P.; Wamkeue, R.; Ouhrouche, M.; Slaoui-Hasnaoui, F.; Tameghe, T.; Ekemb, G. Wind Turbine Condition Monitoring: State-of-the-Art Review, New Trends, and Future Challenges. Energies 2014, 7, 2595–2630. [Google Scholar] [CrossRef]
- Nilsson, J.; Bertling, L. Maintenance Management of Wind Power Systems Using Condition Monitoring Systems—Life Cycle Cost Analysis for Two Case Studies. Ieee Trans. Energy Convers. 2007, 2, 223–229. [Google Scholar] [CrossRef]
- Hilber, P. Maintenance Optimisation Power Distribution Systems. Ph.D. Thesis, Electrical Engineering, Royal Institute of Technology, Stockholm, Sweden, 2008. Available online: https://www.diva-portal.org/smash/get/diva2:13421/FULLTEXT01.pdf (accessed on 30 January 2018).
- Sánchez, A. MatMs Para la Obtención de Políticas Óptimas de Mantenimiento Caracterización y Aplicación Práctica. Ph.D. Thesis, Department of Industrial Organization and Business Management, University of Sevilla, Sevilla, Spain, 2002. Available online: https://dialnet.unirioja.es/servlet/tesis?codigo=23020 (accessed on 19 December 2017).
- Valdez-Flores, C.; Felman, R. A survey of preventive maintenance models for stochastically deteriorating single-unit systems. Nav. Res. Logist. Q. 1989, 36, 419–446. [Google Scholar] [CrossRef]
- Dekker, R. Applications of maintenance optimization models: A review and analysis. Reliab. Eng. Syst. Saf. 1996, 51, 229–240. [Google Scholar] [CrossRef]
- Pierskalla, W.; Voelker, A. A survey of maintenance models: The control and surveillance of deteriorating systems. Nav. Res. Logist. Q. 1976, 23, 353–388. [Google Scholar] [CrossRef]
- Sherif, Y.; Smith, M. Optimal maintenance models for system subject to failure. A review. Nav. Res. Logist. Q. 1981, 28, 47–74. [Google Scholar] [CrossRef]
- Tuan-Huynh, K.; Castro, I.; Barros, A.; Bérenguer, C. Modeling age-based maintenance strategies with minimal repairs for systems subject to competing failure modes due to degradation and shocks. Eur. J. Oper. Res. Elsevier 2012, 218, 140–151. [Google Scholar] [CrossRef]
- Qiu, Q.; Cui, L.; Shen, J.; Yang, L. Optimal maintenance policy considering maintenance errors for systems operating under performance-based contracts. Comput. Ind. Eng. 2017, 112, 147–155. [Google Scholar] [CrossRef]
- Cho, D. A survey of maintenance models for multi-unit systems. Eur. J. Oper. Res. 1991, 51, 1–23. [Google Scholar] [CrossRef]
- Lopez, R.; Cavalcante, C.; Alencar, M. Delay-time inspection model with dimensioning maintenance teams: A study of a company leasing construction equipment. Comput. Ind. Eng. 2015, 88, 341–349. [Google Scholar] [CrossRef]
- Osakiz, S. Stochastics Models in Reliability and Maintenance; Springer International Publishing: New York, NY, USA, 2002; ISBN 978-3-642-07725-8. [Google Scholar]
- Christer, A.; Redmond, D. Revising models of maintenance and inspection. Int. J. Prod. Econ. 1992, 24, 227–234. [Google Scholar] [CrossRef]
- Díaz, A.; Fu, M. Multi Echelon Models for Repairable Items: A review. Available online: https://drum.lib.umd.edu/bitstream/handle/1903/2300/review.pdf?sequence=1&isAllowed=y (accessed on 21 February 2018).
- Ben-Daya, M.; Duffuaa, S.; Raouf, A. Maintenance Modeling and Organization, 1st ed.; Springer International Publishing: Gewerbestrasse, Switzerland, 2000; ISBN 978-1-4613-6944-9. [Google Scholar]
- Hauth, J. Grey-Box Modelling for Nonlinear Systems. Ph.D. Thesis, Fachbereich Mathematik, Universität Kaiserslautern, Kaiserslautern, Germany, 2008. Available online: https://kluedo.ub.uni-kl.de/frontdoor/deliver/index/docId/2045/file/diss.pdf (accessed on 25 January 2018).
- Sarbaz, Y.; Pourakbari, H. A review of presented mathematical models in Parkinson’s disease: Black‑ and gray‑box models. Med. Biol. Eng. Comput. 2017. [Google Scholar] [CrossRef] [PubMed]
- Cherkassky, V.; Dhar, S. Interpretation of Black-Box Predictive Models, 1st ed.; Springer Science + Business Media: Singapore, 2015. [Google Scholar]
- Besnard, F. On maintenance Optimization for Offshore Wind Farms. Ph.D. Thesis, Division of Electric Power Engineering, Chalmers University of Technology, Gothenburg, Sweden, 2013. Available online: https://pdfs.semanticscholar.org/a039/1bde8226ea173fbc8c85104059c565e2bb13.pdf (accessed on 9 January 2017).
- Sindareh-Esfahani, P.; Sepehr, S.; Pieper, J. Model Predictive Control of a Heat Recovery Steam Generator during Cold Start-up Operation Using Piecewise Linear Models. Appl. Therm. Eng. 2016. [Google Scholar] [CrossRef]
- Scaarf, P. On the application of mathematical model in maintenance. Eur. J. Oper. Res. 1997, 99, 493–506. [Google Scholar] [CrossRef]
- Lindquist, T. On reliability Modelling og Ageing Equipment in Electric Power Systems with Regrad to the Effect of Maintenance. Licentiate Thesis, School of Electrical Engineering, Royal Institute of Technology, Stockholm, Sweden, 2005. Available online: http://www.diva-portal.org/smash/get/diva2:8439/FULLTEXT01.pdf (accessed on 8 May 2018).
- Herbert, G.; Iniyan, S.; Goinc, R. Performance, reliability and failure analysis of wind farm in a developing Country. Renew. Energy 2010, 35, 2739–2751. [Google Scholar] [CrossRef]
- Poore, R.; Lettenmaier, T. Alternative Design Study Report: windPACT Advanced Wind Turbine Drive Train Designs Study; Contract No. DE-AC36-99-GO10337; National Renewable Energy Laboratory: Golden, CO, USA, 2002; Available online: www.nrel.gov/docs/fy03osti/33196.pdf (accessed on 25 February 2018).
- Huang, L.; Fu, Y.; Mi, Y.; Cao, J.; Wang, P. A Markov-Chain-Based Availability Model of Offshore Wind Turbine Considering Accessibility Problems. IEEE Trans. Sustain. Energy 2017, 8, 1592–1600. [Google Scholar] [CrossRef]
- Yang, W.; Jiang, J. Wind turbine condition monitoring and reliability analysis by SCADA information. In Proceedings of the 2011 Second International Conference on Mechanic Automation and Control Engineering (MACE), Hohhot, China, 15–17 July 2011. [Google Scholar]
- Roy, A.; Chatterjee, K. Availability estimation of a multi-state wind farm in fuzzy environment. Int. J. Green Energy 2018, 15, 80–95. [Google Scholar] [CrossRef]
- Alhmouda, L.; Wang, B. A review of the state of the art in wind energy reliability analysis. Renew. Sustain. Energy Rev. 2017, in press. [Google Scholar] [CrossRef]
- Santos, F.; Teixeira, A.; Guedes Soares, C. Maintenance planning of an offshore wind turbine using stochastic Petri nets with predicates. J. Offshore Mech. Arct. Eng. 2018, 140, 2539–2549. [Google Scholar] [CrossRef]
- Leigh, J.; Dunnett, S. Use of Petri Nets to Model the Maintenance of Wind Turbines. Qual. Reliab. Eng. Int. 2016, 32, 167–180. [Google Scholar] [CrossRef]
- Sarker, B.; Faiz, T. Minimizing maintenance cost for offshore wind turbines following multi-level opportunistic preventive strategy. Renew. Energy 2016, 85, 104–113. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, W.; Guo, S.; Li, Y.; Yang, T. Opportunistic maintenance for wind turbines considering imperfect, reliability-based maintenance. Renew. Energy 2017, 103, 606–612. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, Y.; Ma, X. An inspection model for a multi-component system subject to 2 types of failures. Qual. Reliab. Eng. Int. 2017, 33, 2539–2549. [Google Scholar] [CrossRef]
- Shafiee, M.; Finkelstein, M.; Bérenguer, C. An opportunistic condition-based maintenance policy for offshore wind turbine blades subjected to degradation and environmental shocks. Reliab. Eng. Syst. Saf. 2016, 142, 463–471. [Google Scholar] [CrossRef]
- Pazouki, E.; Bahrami, H.; Choi, S. Condition based maintenance optimization of wind turbine system using degradation prediction. In Proceedings of the IEEE Power and Energy Society General Meeting, Boston, MA, USA, 27–31 July 2016. [Google Scholar]
- Le, B.; Andrews, J. Modelling wind turbine degradation and maintenance. Wind Energy 2016, 19, 571–591. [Google Scholar] [CrossRef]
- Arts, J.; Basten, R. Design of multi-component periodic maintenance programs with single-component models. IISE Trans. 2018, 50, 606–615. [Google Scholar] [CrossRef]
- Su, C.; Chen, W. Optimization of condition-based maintenance for wind turbine system considering economic dependence among components. J. Southeast Univ. 2016, 46, 1007–1012. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, Y.; Ma, X.; Qiu, Q. An optimal inspection and replacement policy for a two-unit system. J. Risk Reliab. 2018, in press. [Google Scholar] [CrossRef]
- Su, C.; Zhou, X. Maintenance optimization for multi-component of wind turbine based on effective age. J. Southeast Univ. 2012, 42, 1100–1104. [Google Scholar] [CrossRef]
- Santos, F.; Teixeira, A.; Guedes Soares, C. Assessing progressive failure in long wind turbine blades under quasi-static and cyclic loads. Renew. Energy 2018, 219, 754–766. [Google Scholar] [CrossRef]
- Tao, H.; Zhou, B. Condition-based maintenance modeling of wind turbine based on stochastic process. Comput. Integr. Manuf. Syst. 2014, 20, 1416–1423. [Google Scholar] [CrossRef]
- Zequeira, R.; Berenguer, C. Optimal scheduling of non-perfect inspections. IMA J. Manag. Math. 2006, 17, 187–207. [Google Scholar] [CrossRef]
- Christer, H.; Waller, W. Delay Time Models of Industrial Inspection Maintenance Problems. J. Oper. Res. Soc. 1984, 35, 401–406. [Google Scholar] [CrossRef]
- Wang, W. An overview of the recent advances in delay-time-based maintenance modelling. Reliab. Eng. Syst. Saf. 2012, 106, 165–178. [Google Scholar] [CrossRef]
- Ossai, C.; Boswell, B.; Davies, I. A Markovian approach for modelling the effects of maintenance on downtime and failure risk of wind turbine components. Renew. Energy 2016, 96, 775–783. [Google Scholar] [CrossRef]
- Tzioiutzias, T.; Platis, A.; Koutras, V. Markov Modeling of the Availability of a Wind Turbine Utilizing Failures and Real Weather Data. In Proceedings of the 2016 Second International Symposium on Stochastic Models in Reliability Engineering, Life Science and Operations Management (SMRLO), Beer-Sheva, Israel, 15–18 February 2016. [Google Scholar] [CrossRef]
- Wu, Y.; Zhao, H. Optimization Maintenance of Wind Turbines Using Markov Decision Processes. In Proceedings of the IEEE Stochastic Models in Reliability Engineering, International Conference on Power System Technology, Hangzhou, China, 24–28 October 2010. [Google Scholar]
- Memarzadeh, M.; Pozzi, M.; Zico Kolter, J. Season-Dependent Condition-Based Maintenance for a Wind Turbine Using a Partially Observed Markov Decision Process. IEEE Trans. Power Syst. 2010, 25, 1823–1834. [Google Scholar] [CrossRef]
- Water, D. Logistics: An Introduction to Supply Chain Management, 1st ed.; Palgrave, MacMillan: New York, NY, USA, 2003; ISBN 0-333-96369-5. [Google Scholar]
- Taha, A. Operations Research: An Introduction, 8th ed.; Pearson, Prentice Hall: Upper Saddle River, NY, USA, 2016; ISBN 0131889230. [Google Scholar]
- Takuba, R. The Effect of Wind Turbine Transportation on Wind Farm Development in South Africa. Master’s Thesis, Energy Research Center, University of Cape Town, Cape Town, South Africa, 2014. Available online: https://open.uct.ac.za/bitstream/handle/11427/13261/thesis_ebe_2014_takuba_r.pdf?sequence=1 (accessed on 27 December 2018).
- Bierbooms, W.; van Bussel, G. The impact of different means of transport on the operation and maintenance strategy for offshore wind farms. Int. J. Math. Models Methods Appl. Sci. 2011, 5, 371–378. [Google Scholar]
- Scholz-Reiter, B.; Heger, J.; Lütjen, M.; Schweiz, A. A milp for installation scheduling of offshore wind farms. Int. J. Math. Models Methods Appl. Sci. 2011, 5, 371–378. [Google Scholar]
- Santos, F.; Teixeira, A.; Soares, C. Maintenance planning of an offshore wind turbine using stochastic petri nets with predicates. Proceedings of International Conference on Ocean, Offshore and Arctic Engineering, Nantes, Francia, 9–14 June 2013. [Google Scholar] [CrossRef]
- Obdam, T.; Rademakers, L.; Braam, H.; Eecen, P. Estimating Costs of Operation& Maintenance for Offshore Wind Farms. In Proceedings of the European Wind Energy Conference and Exhibition, Brussels, Belgium, 31 March–3 April 2008; ISBN 978-161567115-1. [Google Scholar]
- Dalgic, Y.; Lazakis, I.; Turan, O. Vessel charter rate estimation for offshore wind O&M activities. In Proceedings of the 15th International Congress of the International Maritime Association of the Mediterranean, Coruna, Espain, 14–17 October 2014; ISBN 978-113800162-6. [Google Scholar]
- Nielsen, J.; Sørensen, J. On Risk-Based Operation and Maintenance of Offshore Wind Turbine Components. Reliab. Eng. Syst. Saf. 2011, 96, 218–229. [Google Scholar] [CrossRef]
- Henao, H.; Capolino, G.; Fernandez-Cabanas, M.; Filippetti, F.; Bruzzese, C.; Strangas, E.; Pusca Estima, R.; Riera-Guasp, M.; Hedayati-Kia, S. Trends in Fault Diagnosis for Electrical Machines: A Review of Diagnostic Techniques. IEEE Ind. Electron. Mag. 2014, 8, 31–42. [Google Scholar] [CrossRef]
- Katipamula, S.; Brambley, R. Review Article: Methods for Fault Detection, Diagnostics, and Prognostics for Building Systems—A Review, Part I. HvacR Res. 2005, 11, 3–25. [Google Scholar] [CrossRef]
- Joshuva, A.; Sugumaran, V. Fault diagnostic methods for wind turbine: A review. Arpn J. Eng. Appl. Sci. 2016, 11, 4654–4668. [Google Scholar]
- Alarcón, C. Aportación al Mantenimiento Predictivo de Motores de Inducción Mediante Modernas Técnicas de Análisis de la Señal. Ph.D. Thesis, Institute of Energy Engineering, Universitat Politècnica de València, Valencia, Spain, 2012. Available online: https://riunet.upv.es/bitstream/handle/10251/15915/tesisUPV3825.pdf?sequence=1 (accessed on 17 March 2018).
- Faiz, J.; Mahdi-Moosavi, M. Detection of mixed eccentricity fault in doubly-fed induction generator based on reactive power spectrum. IET Electr. Power Appl. 2017, 11, 1076–1084. [Google Scholar] [CrossRef]
- Ibrahim, R.; Tautz-Weinert, J.; Watson, S. Neural networks for wind turbine fault detection via current signature analysis. In Proceedings of the Wind Europe Summit 2016, Hamburg, Germany, 27–29 September 2016; Available online: https://dspace.lboro.ac.uk/dspace-jspui/bitstream/2134/23014/1/WindEurope2016-RIbrahim JTautzWeinert-published.pdf (accessed on 7 March 2018).
- Rifat-Shahriar, M.; Borghesani, P.; Ledwich, G.; Tan, A. Performance analysis of electrical signature analysis-based diagnostics using an electromechanical model of wind turbine. Renew. Energy 2017, 1–27. [Google Scholar] [CrossRef]
- Entezami, M.; Hillmansen, S.; Weston, P.; Papaelias, M. Fault detection and diagnosis within a wind turbine mechanical braking system using condition monitoring. Renew. Energy 2012, 47, 175–182. [Google Scholar] [CrossRef]
- Cambell, P.; Adamson, K. Identification of blade vibration causes in wind turbine generators. In Proceedings of the 4th International Conference Data Mining Including Building Applications for CRM & Competitive Intelligence, Rio de Janeiro, Brazil, 1–3 December 2003; Volume 29, pp. 149–158, ISBN 1853128309. [Google Scholar]
- Gonzalez-Carrato, R. Sound and vibration-based pattern recognition for wind turbines driving mechanisms. Renew. Energy 2017, 109, 262–274. [Google Scholar] [CrossRef]
- Chen, J.; Pan, J.; Li, Z.; Zi, Y.; Chen, X. Generator bearing fault diagnosis for wind turbine via empirical wavelet transform using measured vibration signals. Renew. Energy 2016, 89, 80–92. [Google Scholar] [CrossRef]
- Bangalore, P.; Letzgus, S.; Karlsson, D.; Patriksson, M. An artificial neural network-based condition monitoring method for wind turbines, with application to the monitoring of the gearbox. Wind Energy 2017. [Google Scholar] [CrossRef]
- Wang, X.; Makis, V.; Yang, M. A wavelet approach to fault diagnosis of a gearbox under varying load conditions. J. Sound Vib. 2010, 329, 1570–1585. [Google Scholar] [CrossRef]
- Tang, B.; Liu, W.; Song, T. Wind turbine fault diagnosis based on Morlet wavelet transformation and Wigner-Ville distribution. Renew Energy 2010, 35, 2862–2866. [Google Scholar] [CrossRef]
- Chen, F.; Tang, B.; Chen, R. A novel fault diagnosis model for gearbox based on wavelet support vector machine with immune genetic algorithm. Measurement 2013, 46, 220–232. [Google Scholar] [CrossRef]
- Barszcz, T.; Randall, R. Application of spectral kurtosis for detection of a tooth crack in the planetary gear of a wind turbine. Mech Syst Signal Process 2009, 23, 1352–1365. [Google Scholar] [CrossRef]
- Saravanan, N.; Cholairajan, S.; Ramachandran, K.I. Vibration based fault diagnosis of spur bevel gear box using fuzzy technique. Expert Syst. Appl. 2009, 36, 3119–3135. [Google Scholar] [CrossRef]
- Durbhaka, G.; Selvaraj, P. Predictive Maintenance for Wind Turbine Diagnostics using Vibration Signal Analysis based on Collaborative Recommendation Approach. In Proceedings of the Advances in Computing. Communications and Informatics (ICACCI), Jaipur, India, 21–24 September 2016. [Google Scholar]
- Gou, P.; Infield, D. Wind Turbine Tower Vibration modeling and Monitoring by the Nonlinear State Estimation Technique. Energies 2012, 5, 5279–5293. [Google Scholar] [CrossRef]
- Kusiak, A.; Verma, A. Analyzing bearing faults in wind turbines: A data-mining approach. Renew. Energy 2012, 48, 110–116. [Google Scholar] [CrossRef]
- Astolfi, D.; Castellani, F.; Tersi, L. Fault Prevention and Diagnosis Through Scada Temperature Data Analysis of An Onshore Wind Farm. Diagnostyka 2014, 15, 71–78. [Google Scholar]
- Leahy, K.; Lily-Hu, R.; Konstantakopoulos, I.; Spanos, C.; Agogino, A. Diagnosing wind turbine faults using machine learning techniques applied to operational data. In Proceedings of the Prognostics and Health Management (ICPHM), IEEE International Conference, Ottawa, ON, Canada, 22–26 June 2016. [Google Scholar] [CrossRef]
- Kusiak, A.; Verma, A. A data-driven approach for monitoring blade pitch faults in wind turbines. IEEE Trans. Sustain. Energy 2011, 2, 87–96. [Google Scholar] [CrossRef]
- Besnard, F.; Bertling, L. An Approach for Condition-Based Maintenance Optimization Applied to Wind Turbine Blades. IEEE Trans. Sustain. Energy 2010, 1, 77–83. [Google Scholar] [CrossRef]
- Byon, E.; Ding, Y. Wind Turbine Gearbox Condition Monitoring with AAKR and Moving Window Statistic Methods. Energies 2011, 4, 2077–2093. [Google Scholar] [CrossRef]
- Schlechtingen, M.; Santos, I.F. Comparative analysis of neural network and regression-based condition monitoring approach for wind turbine fault detection. Mech. Syst. Signal Process. 2011, 25, 1849–1875. [Google Scholar] [CrossRef]
- Gómez-Muñoz, C.; Arcos-Jiménez, A.; García Márquez, F. Wavelet transforms and pattern recognition on ultrasonic guides waves for frozen surface state diagnosis. Renew. Energy 2017. [Google Scholar] [CrossRef]
- González-Carrato, R.; García-Márquez, F. Maintenance management of wind turbines structures via MFCs and wavelet transforms. Renew. Sustain. Energy Rev. 2015, 48, 472–482. [Google Scholar] [CrossRef]
- Anicic, O.; Petković, D.; Cvetkovic, S. Evaluation of wind turbine noise by softcomputing methodologies: A comparative study. Renew. Sustain. Energy Rev. 2016, 56, 1122–1128. [Google Scholar] [CrossRef]
- Bellini, A.; Filippetti, F.; Tassoni, C.; Capolino, G. Advances in diagnostic techniques for induction machines. IEEE Trans. Ind. Electron. 2008, 55, 4109–4126. [Google Scholar] [CrossRef]
- Benbouzid, M.; Vieira, M.; Theys, C. Induction motors’ faults detection and localization using stator current advanced signal processing techniques. IEEE Trans. Power Electron. 1999, 14, 14–22. [Google Scholar] [CrossRef]
- Benbouzid, M.; Kliman, G. What stator current processing-based technique to use for induction motor rotor faults diagnosis? IEEE Trans. Energy Convers. 2003, 18, 238–244. [Google Scholar] [CrossRef]
- Merizalde, Y.; Hernández-Callejo, L.; Duque-Perez, O. State of the Art and Trends in the Monitoring, Detection and Diagnosis of Failures in Electric Induction Motors. Energies 2007, 10, 1056. [Google Scholar] [CrossRef]
- Ciang, C.; Lee, J.; Bang, H. Structural health monitoring for a wind turbine system: A review of damage detection methods. Meas. Sci. Technol. 2008, 19, 12. [Google Scholar] [CrossRef]
- Schubel, P.; Crossley, R.; Boateng, E.; Hutchinson, J. Review of structural health and cure monitoring techniques for large wind turbine blades. Renew. Energy 2013, 51, 113–123. [Google Scholar] [CrossRef]
- Thomson, W.; Fenger, M. Current Signature Analysis to Detect Induction Motors faults. IEEE Ind. Appl. Mag. 2001, 7, 26–34. [Google Scholar] [CrossRef]
- Suganthi, L.; Iniyan, S.; Samuel, A. Applications of fuzzy logic in renewable energy systems—A review. Renew. Sustain. Energy Rev. 2015, 48, 585–607. [Google Scholar] [CrossRef]
- Hasan, A.; Manchanda, P.; Bhardwaj, R. Mathematical Models, Methods and Applications; Springer International Publishing: New York, NY, USA, 2003; ISBN 978-3-540-77481-5. Available online: https://link.springer.com/content/pdf/10.1007%2F978-981-287-973-8.pdf (accessed on 12 March 2018).
- Chaturvedi, D. Soft Computing: Techniques and Its Applications in Electrical Engineering; Springer International Publishing: New York, NY, USA, 2003; ISBN 978-3-540-77480-8. Available online: https://link.springer.com/content/pdf/10.1007%2F978-3-540-77481-5.pdf (accessed on 12 March 2018).
- Byon, E.; Ntaimo, L.; Ding, Y. Optimal Maintenance Strategies for Wind Turbine Systems Under Stochastic Weather Conditions. IEEE Trans. Reliab. 2010, 59, 393–404. [Google Scholar] [CrossRef]
- Piu-Lau, B.; Man-Ma, E.; Pecht, M. Review of offshore wind turbine failures and fault prognostic methods. In Proceedings of the IEEE 2012 Prognostics and System Health Management Conference, Beijing, China, 23–25 May 2012. [Google Scholar] [CrossRef]
- Petkovic, D.; Pavlovic, N.; Cojbašic, Z. Wind farm efficiency by adaptive neuro-fuzzy strategy. Electr. Power Energy Syst. 2016, 81, 215–221. [Google Scholar] [CrossRef]
- Chong, W.; Gwani, M.; Shamshirband, S.; Muzammil, W.; Tan, C.; Fazlizan, A.; Poh, S.; Petkovic, D.; Wong, K. Application of adaptive neuro-fuzzy methodology for performance investigation of a power-augmented vertical axis wind turbine. Energy 2016, 102, 630–636. [Google Scholar] [CrossRef]
- Shamshirband, S.; Petković, D.; Wen-Tong, C.; Tamah, E. Trend detection of wind speed probability distribution by adaptive neuro-fuzzy methodology. Flow Meas. Instrum. 2015, 45, 43–48. [Google Scholar] [CrossRef]
- Hameed, Z.; Wang, K. Development of Optimal Maintenance Strategies for Offshore Wind Turbine by using Artificial Neural Network. Wind Eng. 2012, 36, 353–364. [Google Scholar] [CrossRef]
- De Acevedo, H.; Maurício, A.; Bouchonneau, N. A review of wind turbine bearing condition monitoring: State of the art and challenges. Renew. Sustain. Energy Rev. 2016, 56, 368–379. [Google Scholar] [CrossRef]
- Mohandes, M.; Reham, S.; Halawani, T. A neural networks approach for wind speed prediction. Renew. Energy 1998, 13, 3–345. [Google Scholar] [CrossRef]
- Barbounis, T.; Theocharis, J.; Alexiadis, M.; Dokopoulos, P. Long-term wind speed and power forecasting using local recurrent neural network models. IEEE Trans. Energy Convers. 2006, 21, 273–284. [Google Scholar] [CrossRef]
- Li, S.; Wunsch, D.; O’Hair, E. Using neural networks to estimate wind turbine power generation. IEEE Trans. Energy Convers. 2001, 16, 276–282. [Google Scholar] [CrossRef]
- Zhi-Ling, Y.; Bin, W.; Xing-Hui, D.; Hao, L. Expert system of fault diagnosis for gear box in wind turbine. Syst. Eng. Procedia 2012, 4, 189–195. [Google Scholar] [CrossRef]
- Watson, S.; Xiang, B.; Yang, W.; Tavner, P.; Crabtree, C. Condition monitoring of the power output of wind turbine generators using wavelets. IEEE Trans. Energy Convers. 2010, 25, 715–721. [Google Scholar] [CrossRef]
- Gonzáles, J. Herramientas de Soft Computing para la Comparación de Estructuras de Proteínas. Ph.D. Thesis, E.T.S. Ingenierías Informática y de Telecomunicación University of Granada, Granada, Spain, 2008. Available online: https://es.scribd.com/document/131279901/Tesis-Doctoral-Sintesis-de-Sistemas-de-Control-Borroso-Estables-Por-Diseno (accessed on 10 February 2018).
- Barragán, A. Síntesis de Sistemas de Control Borroso Estables por Diseño. Ph.D. Thesis, Department of Electronic Engineering, Computer Systems and Automation, University of Huelva, Huelva, Spain, 2009. Available online: https://es.scribd.com/document/131279901/Tesis-Doctoral-Sintesis-de-Sistemas-de-Control-Borroso-Estables-Por-Diseno (accessed on 9 February 2018).
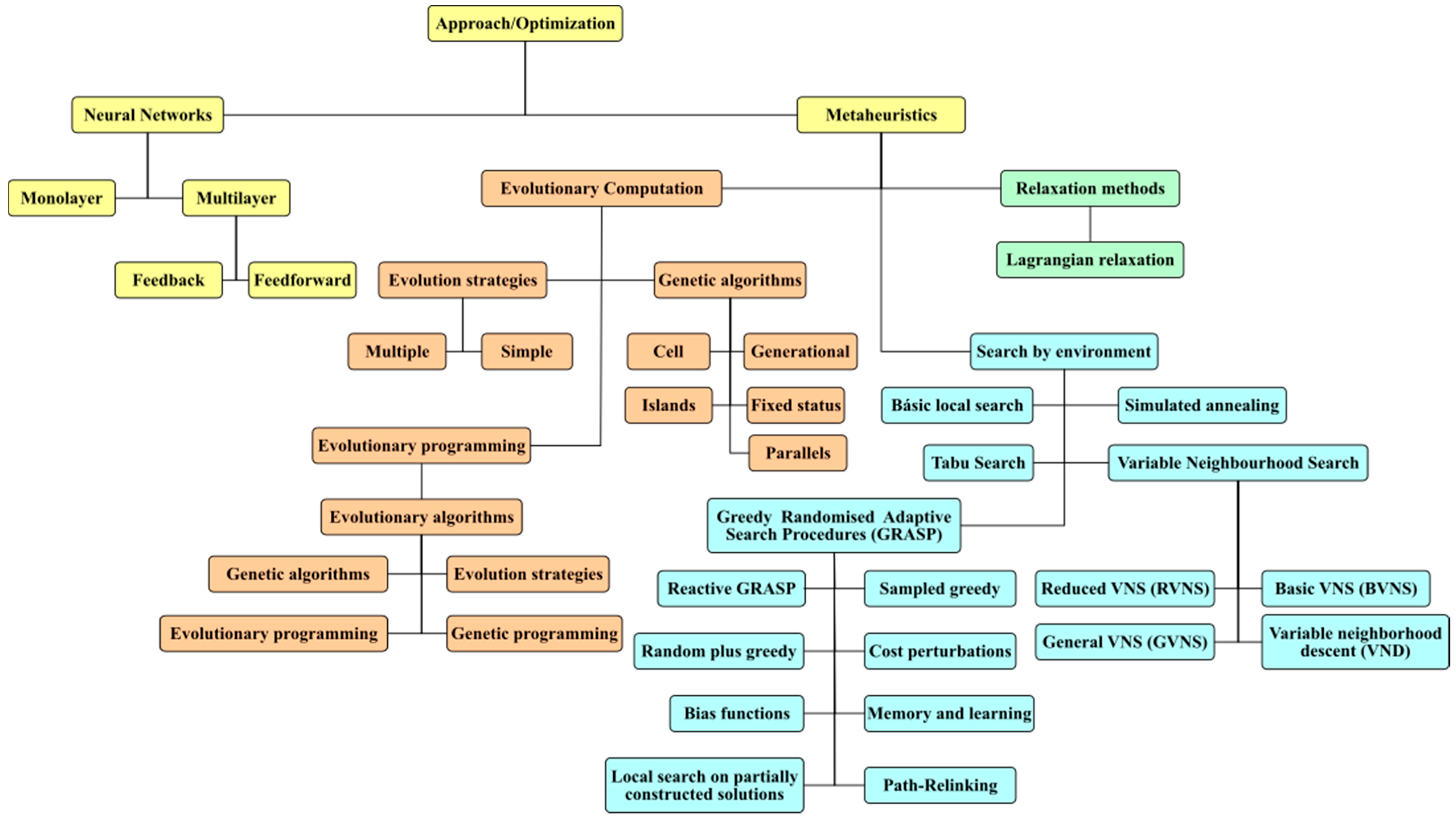
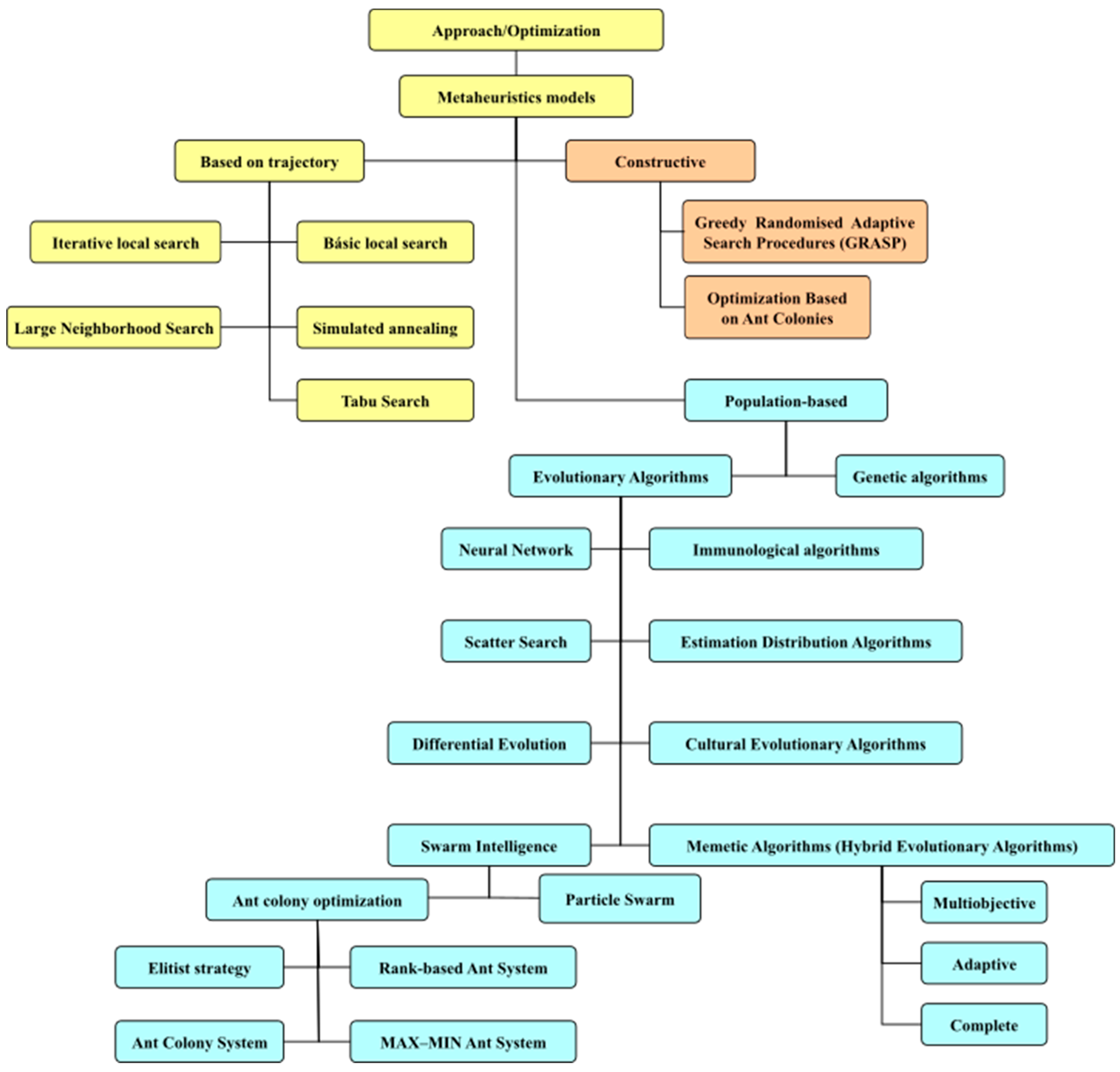
- Gendreau, M.; Potvin, J. Handbook of Metaheuristics, 2nd ed.; Springer International Publishing: New York, NY, USA, 2016; ISBN 978-1-4419-1665-5. Available online: https://link-springer-com.ponton.uva.es/content/pdf/10.1007%2F978-1-4419-1665-5.pdf (accessed on 12 February 2018).
- Stützle, T. Local Search Algorithms for Combinatorial Problems-Analysis, Improvements and New Applications. Ph.D. Thesis, Department of Computer Science, Technical University of Darmstadt, Darmstadt, Germany, 2002. Available online: http://iridia.ulb.ac.be/~stuetzle/publications/Thesis.ThomasStuetzle.pdf (accessed on 12 February 2018).
- Bonabeau, E.; Dorigo, M.; Theraulaz, G. Swarm Intelligence. From Nature to Artificial Systems; Oxford University Press: New York, NY, USA, 1999; ISBN 0195131584. [Google Scholar]
- Dorigo, M.; Stuetzle, T. Ant Colony Optimization; The MIT Press: Cambridge, CA, USA, 2004; ISBN 9780262042192. [Google Scholar]
- Yang, X.; Cui, Z.; Xiao, R.; Gandomi, A.; Karamanoglu, M. Swarm Intelligence and Bio-Inspired Computation: Theory and Applications, 1st ed.; Elsevier Press: London, UK, 2013; ISBN 9780124051638. [Google Scholar]
- Eiben, A.; Smith, J. Introduction to Evolutionary Computation, 2nd ed.; Springer International Publishing: New York, NY, USA, 2003; ISBN 9783662448748. Available online: https://link-springer-com.ponton.uva.es/content/pdf/10.1007%2F978-3-662-44874-8.pdf (accessed on 12 February 2018).
- Gupta, G.; Mishra, R. A Failure Mode Effect and Criticality Analysis of Conventional Milling Machine Using Fuzzy Logic: Case Study of RCM. Qual. Reliab. Eng. Int. 2017, 33, 347–356. [Google Scholar] [CrossRef]
- Pillay, A.; Wang, J. Modified failure mode and effects analysis using approximate reasoning. Reliability Eng. Syst. Saf. 2003, 79, 69–85. [Google Scholar] [CrossRef]
- Djeziri, M.; Benmoussa, S.; Sanchez, R. Hybrid method for remaining useful life prediction in wind turbine systems. Renew. Energy 2017, 116, 173–187. [Google Scholar] [CrossRef]
- Qian, P.; Ma, X.D.; Cross, P. Integrated data-driven model-based approach to condition monitoring of the wind turbine gearbox. IET Renew. Power Gener. 2017, 11, 1177–1185. [Google Scholar] [CrossRef]
- Yang, Z.X.; Wang, X.B.; Zhong, J.H. Representational Learning for Fault Diagnosis of Wind Turbine Equipment: A Multi-Layered Extreme Learning Machines Approach. Energies 2016, 9, 379. [Google Scholar] [CrossRef]
- Introducing Machine Learning, Mat Lab Inc. Available online: https://www.mathworks.com/content/dam/mathworks/tagteam/Objects/i/88174_92991v00_machine_learning_section1_ebook.pdf (accessed on 13 March 2018).
- Stoean, C.; Stoean, R. Support Vector Machines and Evolutionary Algorithms for Classification; Springer International Publishing: New York, NY, USA, 2014; ISBN 978-3-319-06941-8. Available online: https://link-springer-com.ponton.uva.es/content/pdf/10.1007%2F978-3-319-06941-8.pdf (accessed on 7 June 2018).
- Kecman, V. Support Vector Machines–An Introduction. In Support Vector Machines: Theory and Applications. Studies in Fuzziness and Soft Computing; Wang, L., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 177, ISBN 978-3-540-32384-6. Available online: https://link-springer-com.ponton.uva.es/chapter/10.1007/10984697_1 (accessed on 7 June 2018).
- Soualhi, A.; Medjaher, K.; Zerhouni, N. Bearing Health Monitoring Based on Hilbert–Huang Transform, Support Vector Machine, and Regression. IEEE Trans. Instrum. Meas. 2015, 64, 52–62. [Google Scholar] [CrossRef]
- Darwiche, A. Modeling and Reasoning with Bayesian Networks; Cambridge University Press: New York, NY, USA, 2009; ISBN 9780511811357. Available online: https://www.cambridge.org/core/terms (accessed on 5 August 2018). [CrossRef]
- Dougherty, G. Pattern Recognition and Classification. An Introduction; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-5323-9. Available online: https://link-springer-com.ponton.uva.es/content/pdf/10.1007%2F978-1-4614-5323-9.pdf (accessed on 5 August 2018).
- Borunda, M.; Jaramillo, O.; Reyes, A.; Ibargüengoytia, P. Bayesian networks in renewable energy systems: A bibliographical survey. Renew. Sustain. Energy Rev. 2016, 62, 32–45. [Google Scholar] [CrossRef]
- Memarzadeh, M.; Pozzi, M.; Zico Kolter, J. Optimal Planning and Learning in Uncertain Environments for the Management of Wind Farms. J. Comput. Civ. Eng. 2015, 29, 1592–1600. [Google Scholar] [CrossRef]
- Nielsen, J.; Sørensen, J. Bayesian Estimation of Remaining Useful Life for Wind Turbine Blades. Energies 2017, 10, 664. [Google Scholar] [CrossRef]
- Pattison, D.; Segovia, M.; Xie, W.; Quail, F.; Revie, M.; Whitfield, R.; Irvine, I. Intelligent integrated maintenance for wind power generation. Wind Energy 2016, 19, 547–562. [Google Scholar] [CrossRef]
- Reder, M.; Melero, J. A Bayesian Approach for Predicting Wind Turbine Failures based on Meteorological Conditions. In Proceedings of the 7th Science of Making Torque from Wind, TORQUE 2018, Milan, Italy, 20–22 June 2018. [Google Scholar] [CrossRef]
- Nguyen, H.; Prasad, N.; Walker, C.; Walker, E. A First Course in Fuzzy and Neural Control; CRC Press LLC: Boca Raton, FL, USA, 2002; ISBN 1-58488-244-1. [Google Scholar]
- Hilera-González, J.; Martínez-Hernando, V. Redes Neuronales Artificiales: Fundamentos, Modelos y Aplicaciones; Editorial RA-MA: Madrid, España, 1995; ISBN 84-7897-155-6. [Google Scholar]
- Zilouchian, A.; Jamshidi, M. Intelligent Control Systems Using Soft Computing Methodologies; CRC Press LLC: Boca Raton, FL, USA, 2001; ISBN 0-8493-1875-0. [Google Scholar]
- Ponce, P. Inteligencia Artificial con Aplicaciones a la Ingeniería; Alfaomega: México D. F., México, 2010; ISBN 978-607-7854-83-8. [Google Scholar]
- Hongshan, Z.; Huihai, L.; Wenjing, H.; Xihui, Y. Anomaly Detection and Fault Analysis of Wind Turbine Components Based on Deep Learning Network. Renew. Energy 2018, 127, 825–834. [Google Scholar] [CrossRef]
- Alfonso Ballesteros, Enrique Dominguez. Clasificación de las Redes Neuronales Artificiales. Available online: http://www.redes-neuronales.com.es/tutorial-redes-neuronales/clasificacion-de-las-redes-neuronales-artificiales.htm (accessed on 13 August 2018).
- Pliego, A.; García, F.; Pinar, J.; Ruiz, D. A survey of artificial neural network in wind energy systems. Appl. Energy 2018, 228, 1822–1836. [Google Scholar] [CrossRef]
- Teng, W.; Zhang, X.; Liu, Y.; Kusiak, A.; Ma, Z. Prognosis of the Remaining Useful Life of Bearings in a Wind Turbine Gearbox. Energies 2016, 10, 32. [Google Scholar] [CrossRef]
- Nguyen, H.; Sugeno, M. Fuzzy Systems. Modeling and Control; Springer: Nueva York, NY, USA, 1998; ISBN 978-1-4615-5505-6. Available online: https://link-springer-com.ponton.uva.es/content/pdf/10.1007%2F978-1-4615-5505-6.pdf (accessed on 14 August 2018).
- García, B.; Villamizar, E. Sistemas Neuro Difusos Aplicados Al Control Automático. Engineering Thesis, Faculty of Engineering, Department of Electrical and Electronic Engineering, Tecnology University of Bolivar, Cartagena de Indias, Colombia, 2005. Available online: http://biblioteca.unitecnologica.edu.co/notas/tesis/0030354.pdf (accessed on 14 August 2018).
- Talon, A.; Curt, C. Selection of appropriate defuzzification methods: Application to the assessment of dam performance. Expert Syst. Appl. 2017, 10, 160–174. [Google Scholar] [CrossRef]
- Shodhganga, A reservoir of Indian Theses. Fuzzification, Defuzzification and I-Fuzzification Methods. Available online: http://shodhganga.inflibnet.ac.in/bitstream/10603/111418/2/11_chapter3.pdf (accessed on 27 August 2018).
- Civelek, Z.; Lüy, M.; Çam, E.; Mamur, H. A new fuzzy logic proportional controller approach applied to individual pitch angle for wind turbine load mitigation. Renew. Energy 2017, 111, 708–717. [Google Scholar] [CrossRef]
- Simani, S.; Castaldi, P. Data-driven and adaptive control applications to a wind turbine benchmark model. Renew. Energy 2013, 21, 1678–1693. [Google Scholar] [CrossRef]
- Ouanas, A.; Medoued, A.; Mordjaoui, M.; Lebaroud, A.; Sayad, D. Fault diagnosis in yaw drive induction motor for wind turbine. Wind Eng. 2018, in press. [Google Scholar] [CrossRef]
- De la Hermosa González, R.R. Wind farm monitoring using Mahalanobis distance and fuzzy clustering. Renew. Energy 2018, 123, 526–540. [Google Scholar] [CrossRef]
- Cordón, O.; Herrera, F.; Hoffmann, F.; Magdalena, L. Genetic Fuzzy Systems. Evolutionary Tuning and Learning of Fuzzy Knowledge Bases, 1st ed.; World Scientific Publishing: London, UK, 2001; ISBN 978-9810240172. [Google Scholar]
- Hoffmann, F. Evolutionary Algorithms for Fuzzy Control System Design. Proc. IEEE 2001, 89, 1318–1333. [Google Scholar] [CrossRef]
- Cheng, F.; Qu, L.; Qiao, W. Machine Condition Prediction Based on Adaptive Neuro–Fuzzy and High-Order Particle Filtering. IEEE Trans. Ind. Electron. 2011, 58, 157–167. [Google Scholar] [CrossRef]
- Cheng, F.; Qu, L.; Qiao, W. Fault Prognosis and Remaining Useful Life Prediction of Wind Turbine Gearboxes Using Current Signal Analysis. IEEE Trans. Sustain. Energy 2018, 9, 157–167. [Google Scholar] [CrossRef]
- Arcos, A.; Gómez, C.; García, F. Machine Learning for Wind Turbine Blades Maintenance Management. Energies 2017, 11, 13. [Google Scholar] [CrossRef]
| Term | Time | Model |
|---|---|---|
| Long | 3 months–1 year | MRP, CPM |
| Medium | Weekly | PERT, CPM |
| Short | Daily | - |
| Part of the Wind Turbine | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Signal | Model | Blades | Shaft | Bearing | Gearbox | Braking System | Electric Generator | Converter | Tower |
| Current | Finite elements | [109] | |||||||
| Artificial neural network (ANN) | [110] | ||||||||
| Electromechanical model | [111] | [111] | [111] | [111] | [112] | [111] | [111] | ||
| Vibration | Rule induction ANN | [113] | |||||||
| Fast Fourier transform (FFT) Wavelets | [114,115] | [114] | |||||||
| Mahalanobis distance ANN | [116] | ||||||||
| Morlet continuous Wavelet Wigner-Ville distribution | [117,118] | ||||||||
| Wavelets Immune genetic algorithm | [119] | ||||||||
| Spectral kurtosis | [120] | ||||||||
| Fuzzy logic | [121] | ||||||||
| k-Nearest neighbor (k-NN) | [122] | ||||||||
| Support vector machine (SVM) | [119,122] | ||||||||
| k-Means | [122] | ||||||||
| Nonlinear state estimation technique | [123] | ||||||||
| Thermal | Data mining | [124,125] | [125] | [41,124,125] | [125] | ||||
| Autoregressive model ANN | [126] | ||||||||
| Bagging, ANN, kNN Genetic programming | [127] | ||||||||
| Continuous time Markov chain Monte Carlo | [128] | ||||||||
| Autoassociative Kernel Regression (AAKR) Moving window statistic | [129] | ||||||||
| ANN | [130] | ||||||||
| Acoustic | Continuous time Markov chain Monte Carlo | [127] | |||||||
| Wavelet transforms Wigner-Ville distribution Hilbert transforms | [131] | [132] | |||||||
| Support vector regression (SVR) | [133] | ||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merizalde, Y.; Hernández-Callejo, L.; Duque-Perez, O.; Alonso-Gómez, V. Maintenance Models Applied to Wind Turbines. A Comprehensive Overview. Energies 2019, 12, 225. https://doi.org/10.3390/en12020225
Merizalde Y, Hernández-Callejo L, Duque-Perez O, Alonso-Gómez V. Maintenance Models Applied to Wind Turbines. A Comprehensive Overview. Energies. 2019; 12(2):225. https://doi.org/10.3390/en12020225
Chicago/Turabian StyleMerizalde, Yuri, Luis Hernández-Callejo, Oscar Duque-Perez, and Víctor Alonso-Gómez. 2019. "Maintenance Models Applied to Wind Turbines. A Comprehensive Overview" Energies 12, no. 2: 225. https://doi.org/10.3390/en12020225
APA StyleMerizalde, Y., Hernández-Callejo, L., Duque-Perez, O., & Alonso-Gómez, V. (2019). Maintenance Models Applied to Wind Turbines. A Comprehensive Overview. Energies, 12(2), 225. https://doi.org/10.3390/en12020225