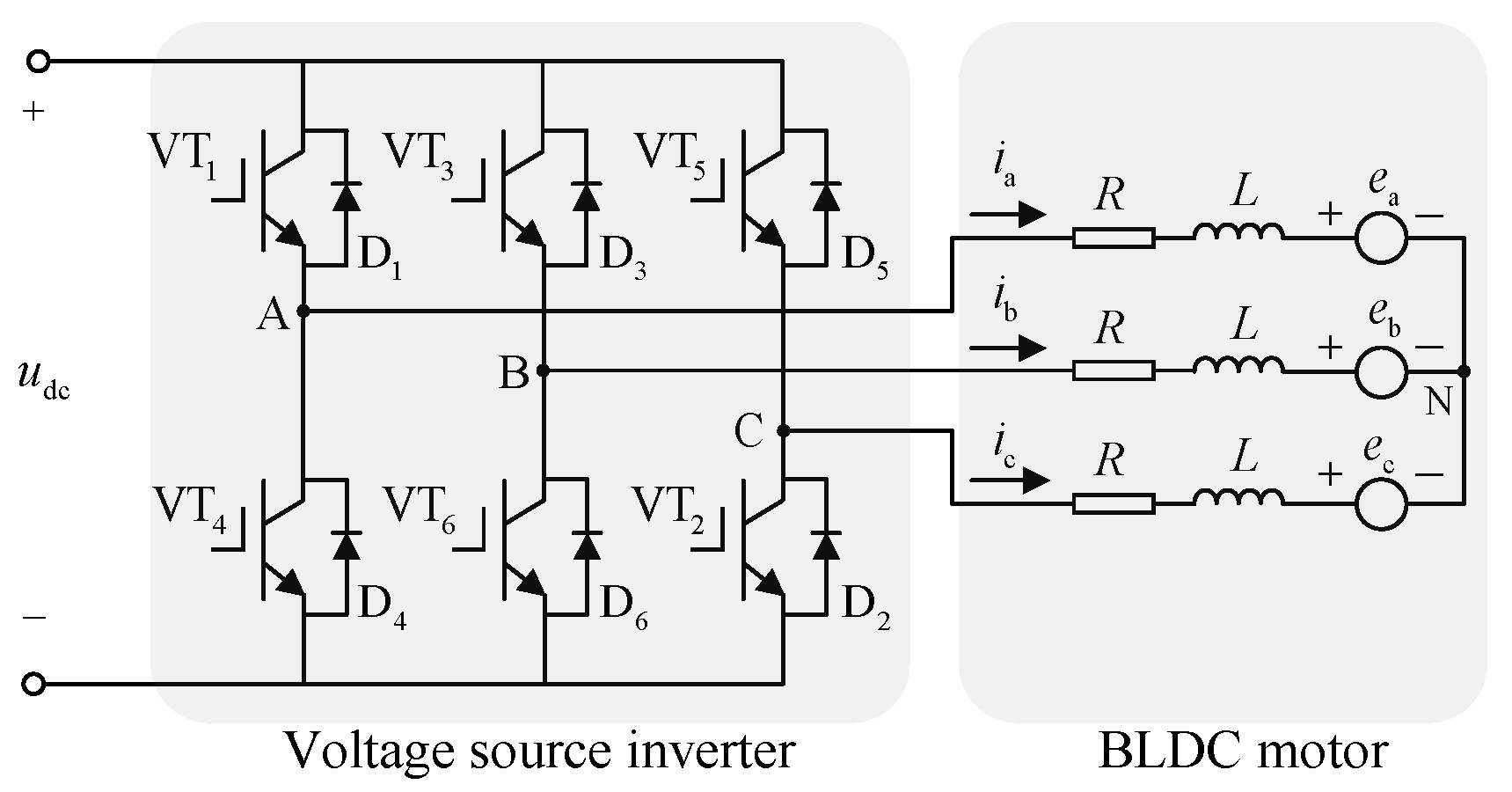
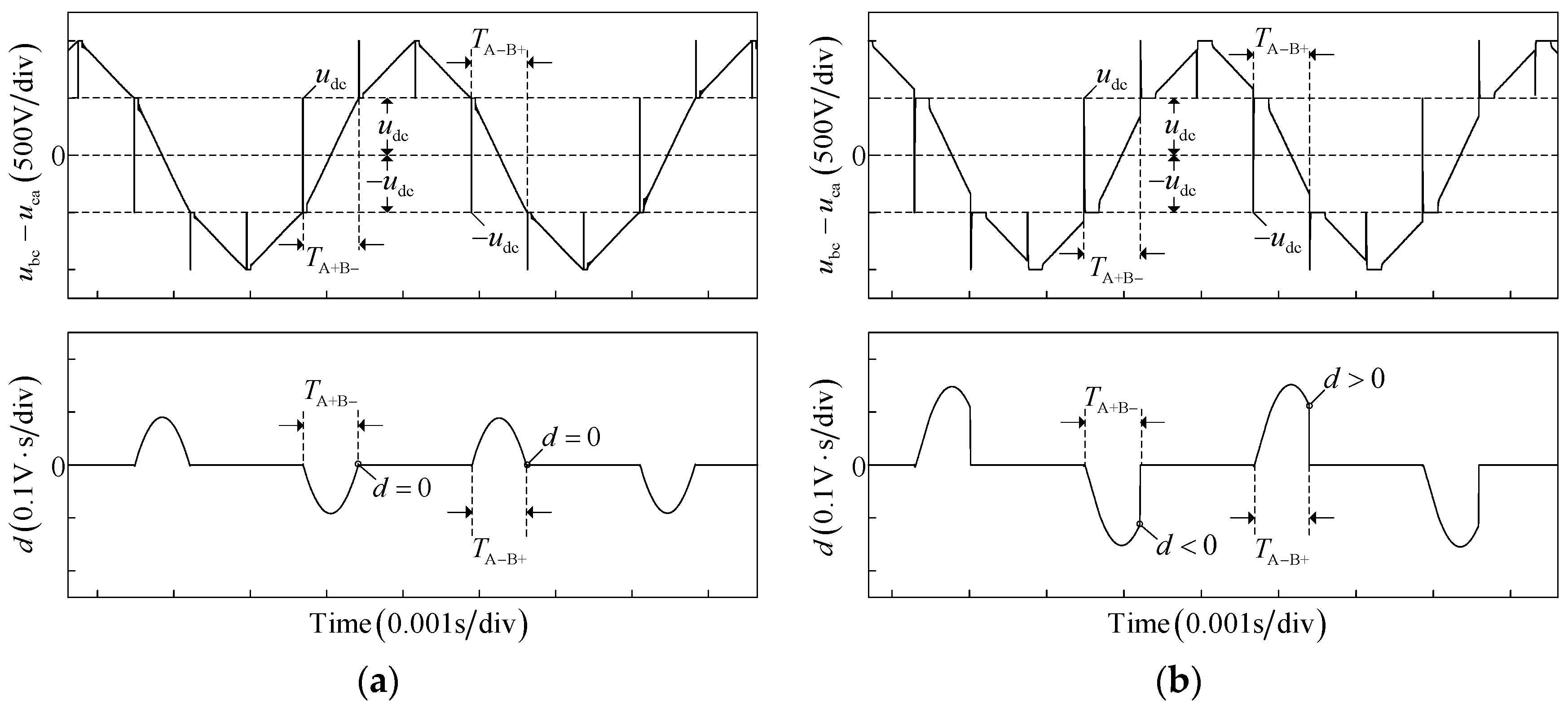This paper presents a commutation error compensation strategy based on the line voltage difference integral. In this section, the relationship between the line voltage difference integral and the commutation error is theoretically analyzed. Then, a feedback compensation strategy with the line voltage difference integral is presented. Finally, an incremental PI controller is designed to regulate the commutation error.
2.2. Line Voltage Difference Integral without Consideration of Freewheeling Period
For a BLDC motor, there are six operation modes and every operation modes last 60 electrical degrees. In the 60 electrical degree conduction interval, two periods are included: the freewheeling period and the normal conduction period. In the freewheeling period , the incoming phase current begins to rise, the un-commutated current remains conducting, and the outgoing phase current gradually decays due to the existence of phase inductance. When the outgoing phase current drops to zero, the freewheeling period is over and the motor starts operating in the normal conduction period.
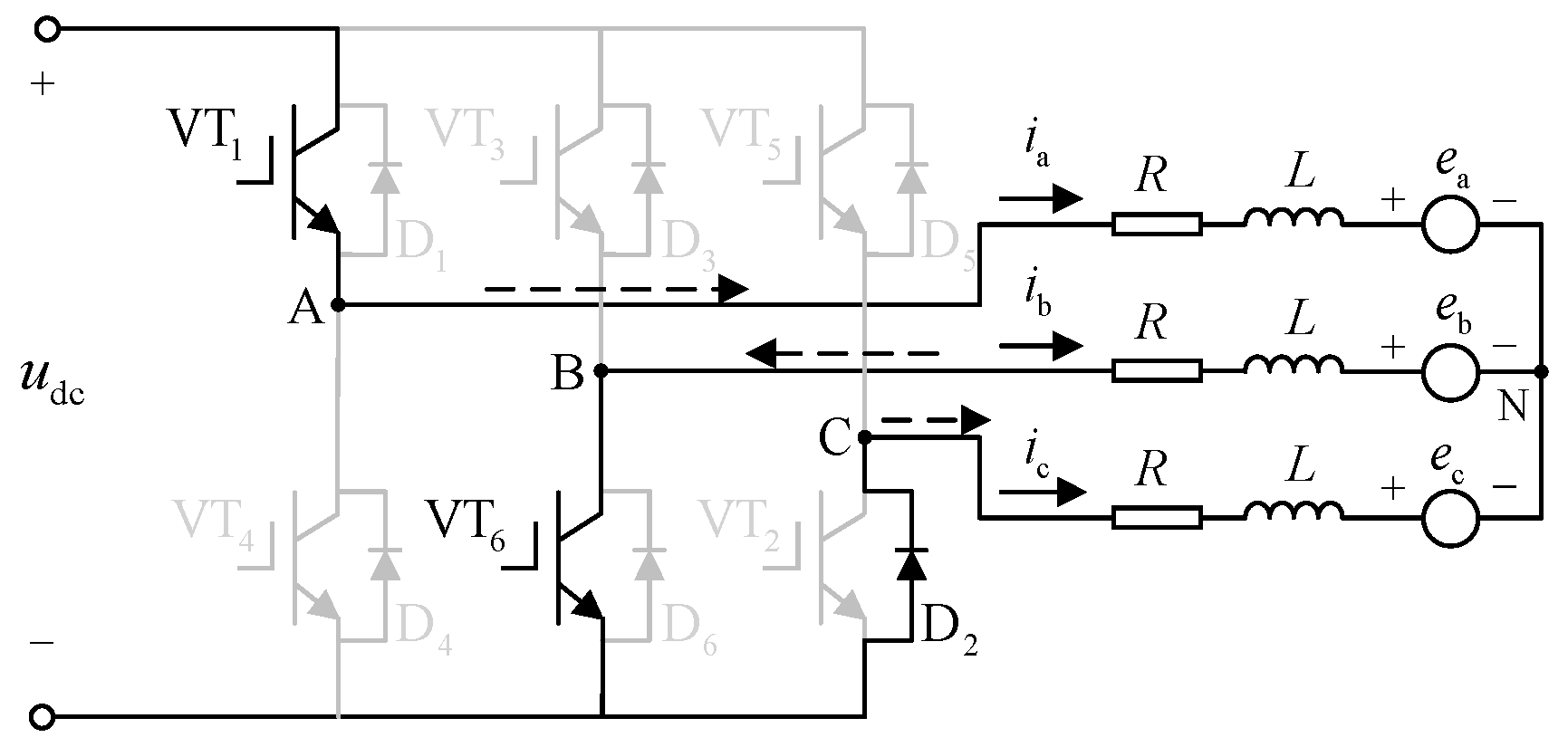
Assume at some step that VT
1 and VT
6 are conducting, while VT
5 is floating. The line voltage difference
is expressed as
Considering a BLDC motor with a negligible freewheeling period
, the current equation satisfies
and
during the entire 60-electrical degree period when
, as shown in
Figure 2. Substituting the current equation into (4), the line voltage difference
is simplified as
By integrating (5), the line voltage difference integral
is achieved as follows:
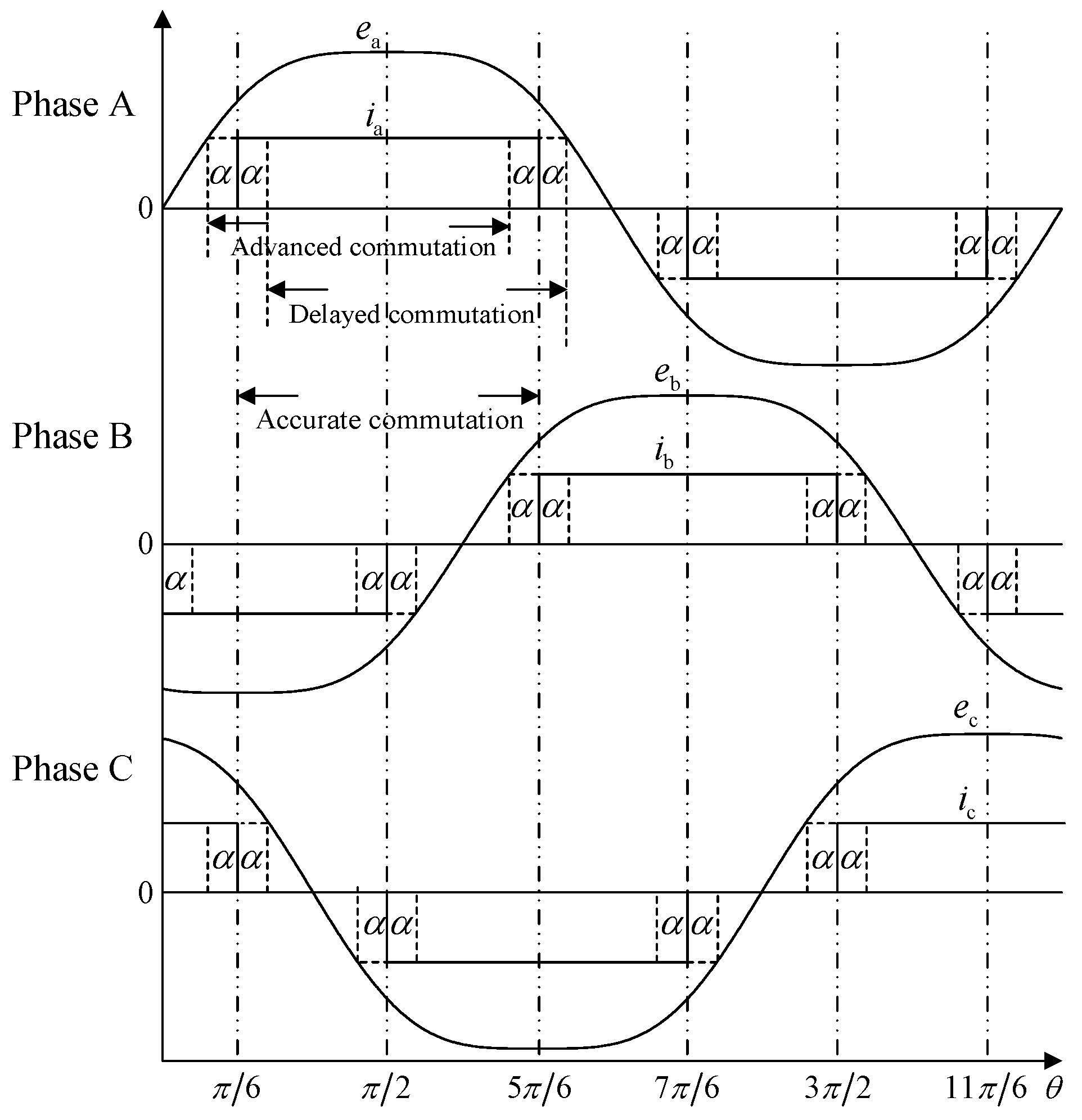
Figure 3 shows the three-phase back-EMF under accurate, delayed, and advanced commutation; the shadowed areas in each subfigure represent the integral of each back-EMF. As seen in
Figure 3a, the integral of the back-EMFs
and
yields equal amplitudes but opposite signs, i.e.,
; hence, the sum of the integrated back-EMFs
and
is zero in the interval. Similarly, the integral of the back-EMF
is zero, i.e.,
, due to the AC symmetry of the back-EMF
. From this analysis, (6) satisfies the condition
The line voltage difference integral
under accurate commutation yields a value of zero. When the commutation instants are delayed or advanced by
, the conduction period of VT
1 and VT
6 lasts for the interval
, and the line voltage difference integral
is written as
where
,
.
Since the third harmonics of the three three-phase back-EMFs are equal,
. Then, (8) is simplified as
Solving and simplifying the definite integral gives
As the back-EMF harmonic coefficients satisfy the condition
, the high-order terms of the back-EMF in (10) are negligible, and (10) can be simplified as
As seen in (11), the three-phase back-EMF integral is a function of the commutation error . The relationship between the three-phase back-EMF integral and the commutation error will be discussed in the following section.
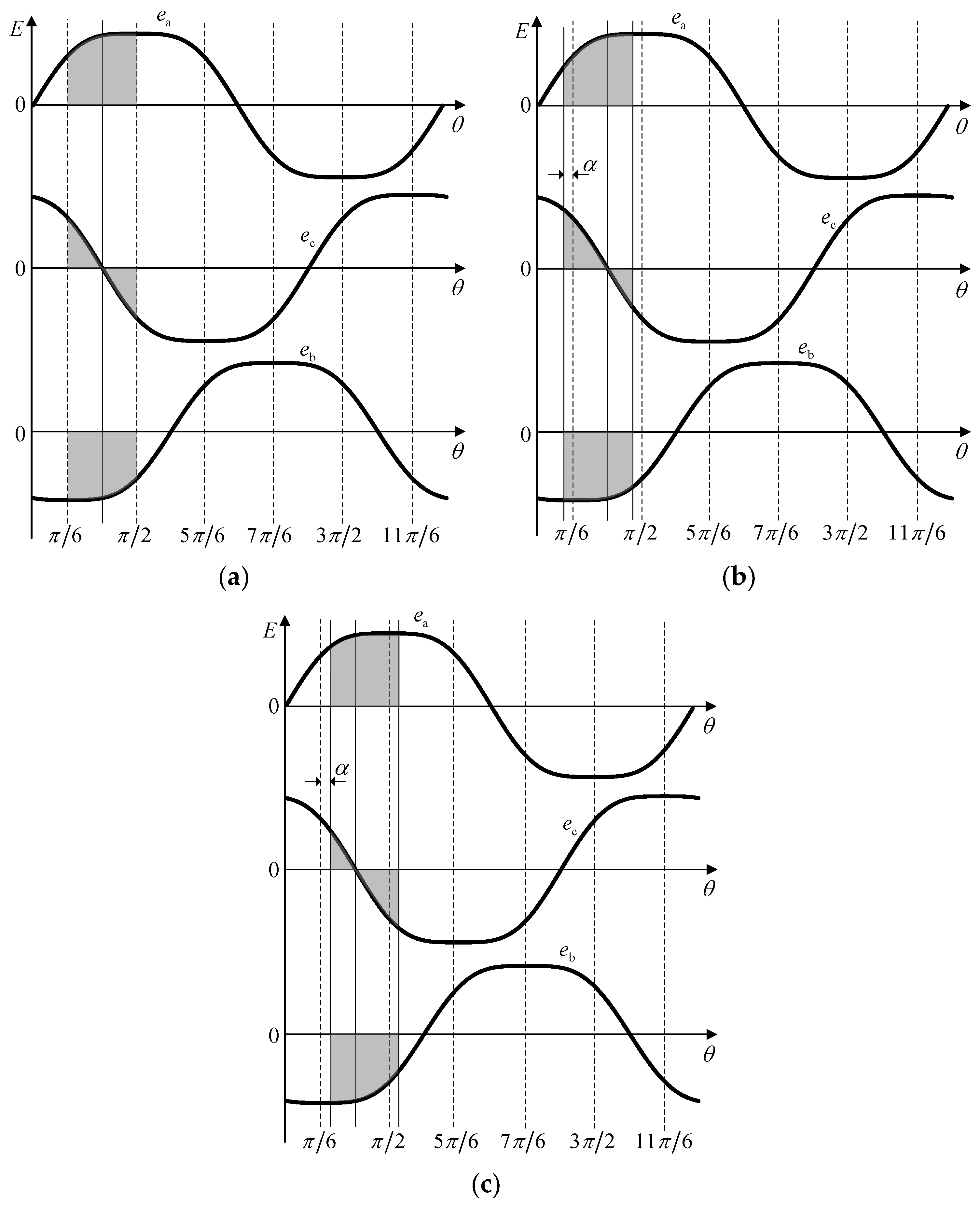
Accurate commutation: when the commutation error
, the motor works under accurate commutation, as shown in
Figure 3a, and the back-EMF integral
.
Advanced commutation: when the commutation error
, the motor works under advanced commutation, as shown in
Figure 3b, and the three-phase back-EMF integral
.
Delayed commutation: when the commutation error
, the motor works under delayed commutation, as shown in
Figure 3c, and the three-phase back-EMF integral
.
Similarly, when VT3 and VT4 are in conduction state, the phase current flows in opposite direction compared with the direction during the conduction period of VT1 and VT6. The three-phase back-EMF integral under accurate commutation, under delayed commutation, and under advanced commutation.
From previous research on three-phase back-EMF integral and the line voltage difference integral expression in (7), when the freewheeling period is negligible, the line voltage difference integral is proportional to the commutation error and can be used as an indicator of commutation errors.
The relationship between the conduction switch, the line voltage difference integral, and the commutation information is shown in
Table 1; here,
and
are the lower and upper limits of integral, respectively.
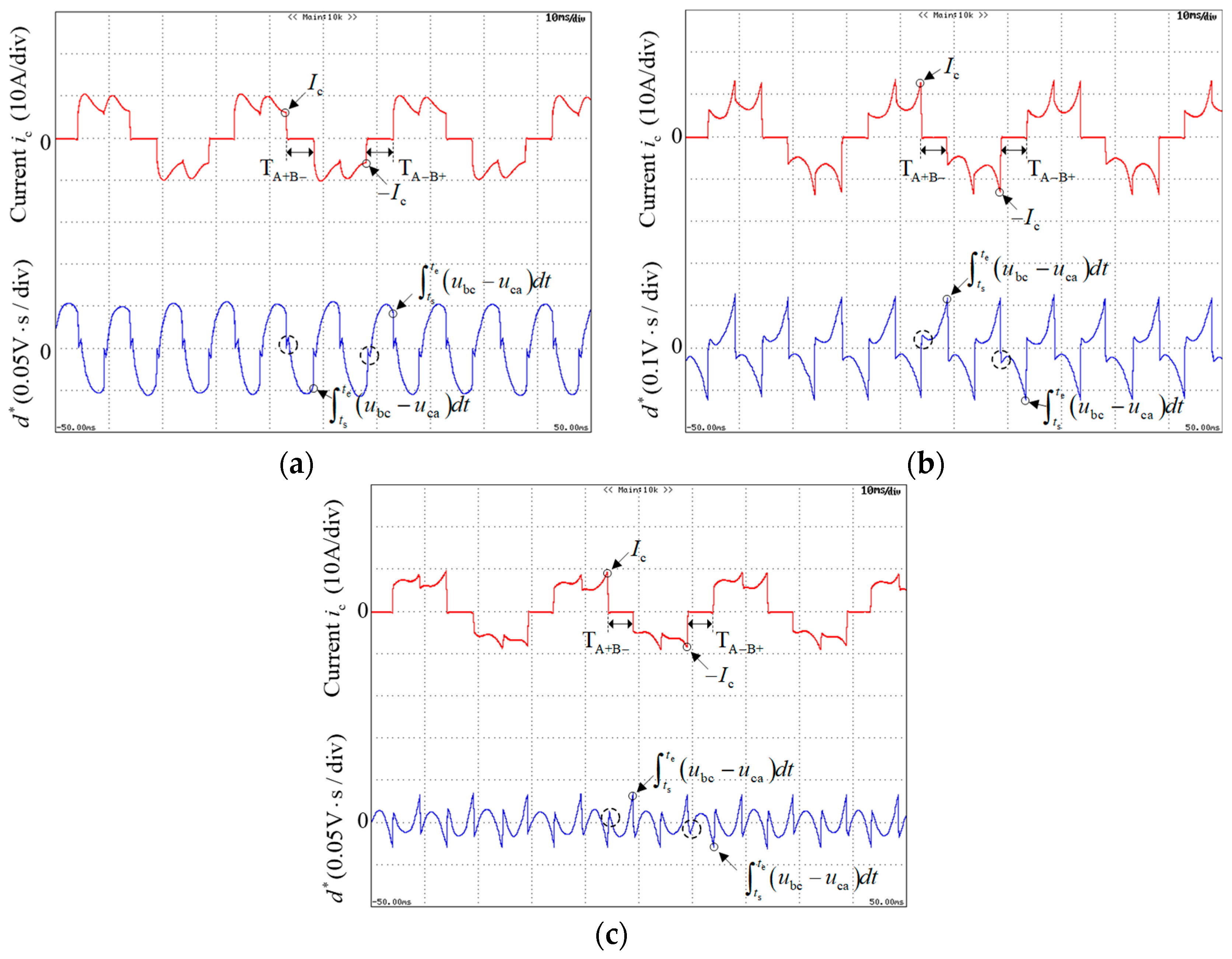
When the motor is in no-load state, the effect of the freewheeling period
is negligible.
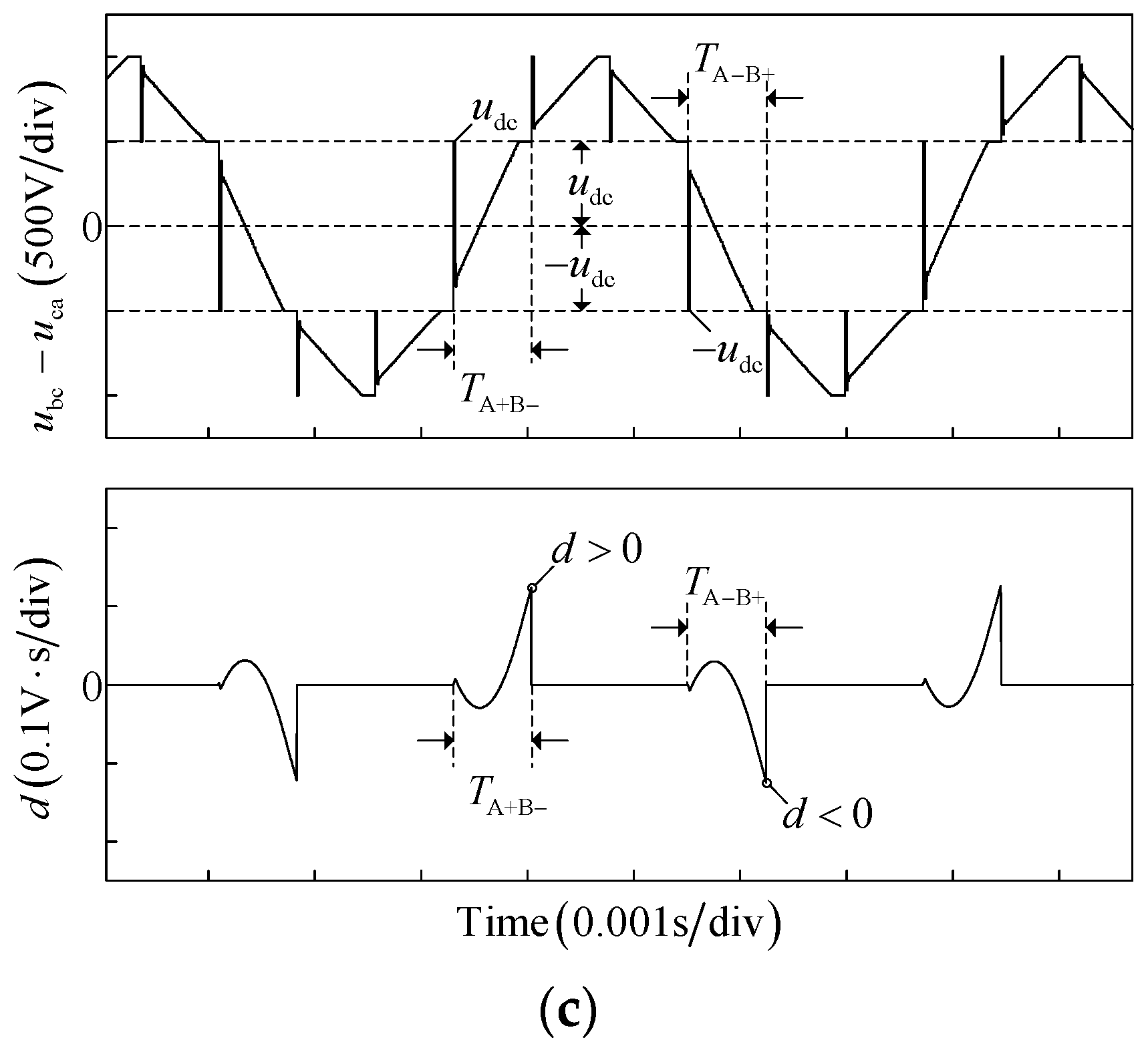
Figure 4 shows the diagram of the line voltage difference integral
in the 60-electrical degree interval of A+B− and A−B+, where
and
represents the conduction period of phase A+B− and A−B+, respectively. The integral
in the A+B− conduction interval is zero under accurate commutation (
Figure 4a), negative under advanced commutation (
Figure 4b), and positive under delayed commutation (
Figure 4c). In the A−B+ conduction interval, the integral
is opposite compared with that in the A+B− conduction interval. These results agree with the theoretical analysis.
2.3. Line Voltage Difference Integral Considering Freewheeling Period
During the freewheeling period , the line voltage difference is distorted by the DC-link voltage and clamped at the level of the DC-link voltage . When line voltage difference integral is performed, the distorted line voltage difference in the interval is also integrated, which will cause the line voltage difference integral to deviate from the accurate line voltage difference integral. In this section, the line voltage difference integral of a BLDC motor considering the freewheeling period will be discussed.
Assume that the commutation error is
and the conduction interval of VT
1 and VT
6 lasts for the period when
, as shown in
Figure 2. In the conduction period, the line voltage difference integral
can be expressed as
Figure 5 shows the equivalent circuit when the commutation occurs from VT
5 to VT
1. In the commutation period
, VT
5 is turned off, VT
1 is turned on, and VT
6 continues conducting. The three phase voltages are expressed as
The line voltage difference meets the condition
, and the line voltage difference integral during the freewheeling period
is reformulated as
In (14), the line voltage difference is equal to the DC-link voltage in the freewheeling period ; hence, the line voltage difference integral shows a trend of linear growth in the freewheeling period .
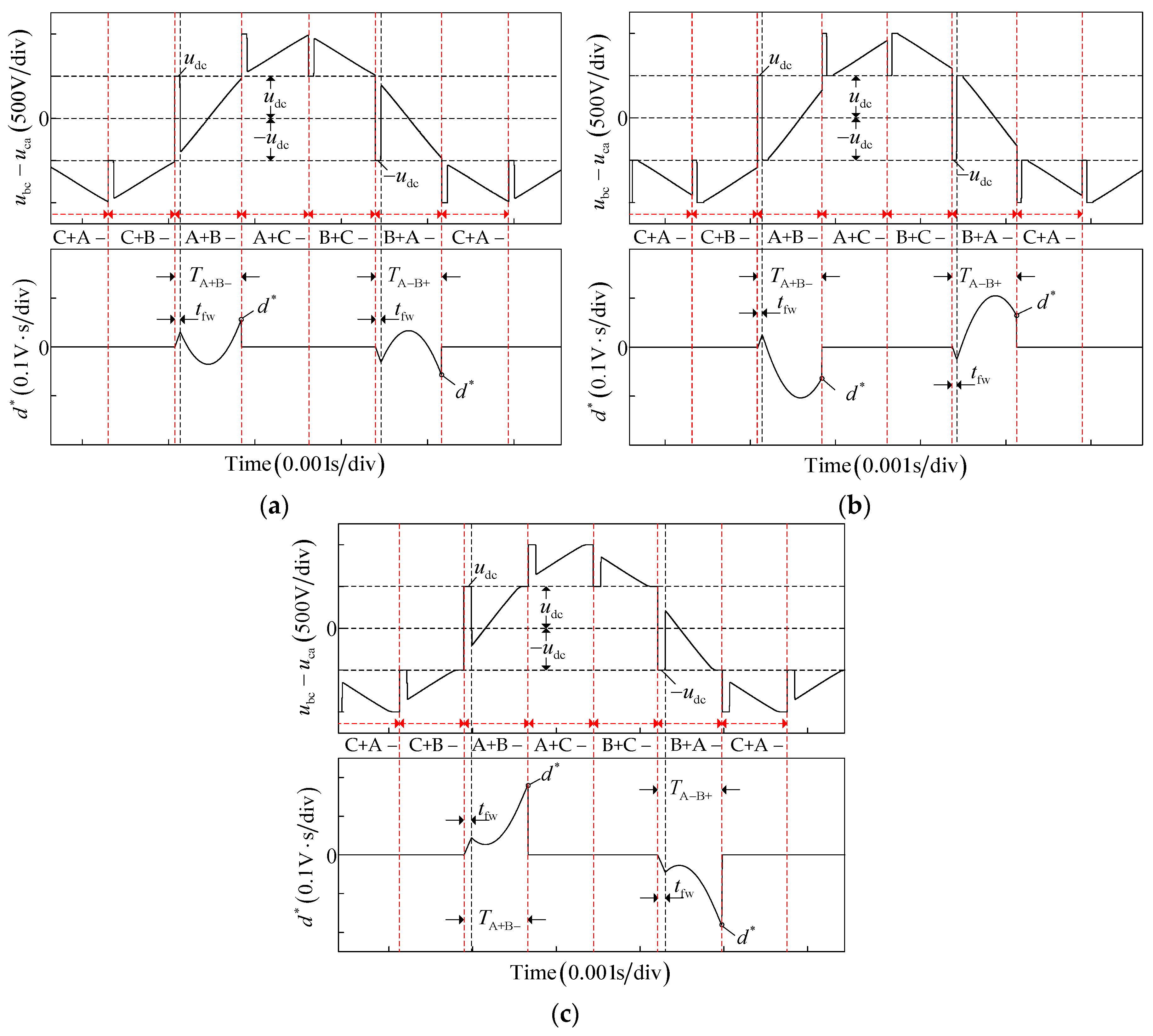
Figure 6 shows the diagram of the line voltage difference
and its integral
in the conduction period of phase A+B− and A−B+. The as seen in
Figure 6, the line voltage difference
is equal to the DC-link voltage
in the freewheeling period
and the corresponding integral
linearly increases in the interval. Compared with that in
Figure 4, since the disturbed voltage difference is integrated in the freewheeling period
, the integral
under different commutation produces an amplitude deviation. Especially under accurate commutation, for example, the integral
deviates from zero, and becomes positive and negative in the conduction period of phase A+B− and A−B+, respectively.
The other voltage spikes in
Figure 6 are analyzed as followed. When the commutation occurs, the outgoing phase current continues conducting through the anti-parallel diode, so the terminal voltage is clamped at the level of 0 V or
. When the motor commutates between different phases, the clamped voltage value of three-phase voltage changes, hence the line voltage difference
will also change accordingly. The cause of the voltage spikes is the same under delayed, advanced, and accurate commutation. To facilitate the analysis, the voltage spike under the accurate commutation is taken as an example.
(1) When commutation occurs from A+B− to A+C−, it meets , , and in the freewheeling period . Therefore, , and it corresponds to the positive spike whose magnitude exceeds .
(2) When commutation occurs from B+A− to C+A−, it meets , , and in the freewheeling period . Therefore, , and it corresponds to the negative spike whose magnitude exceeds .
(3) When commutation occurs from A+C− to B+C−, it meets , , and in the freewheeling period . Therefore, , and it corresponds to the positive spike whose magnitude is equal to .
(4) When commutation occurs from C+A− to C+B−, it meets , , and in the freewheeling period . Therefore, , and it corresponds to the negative spike whose magnitude is equal to .
The voltage spikes of the line voltage difference
in 360-degree electrical angle are listed in
Table 2.
In the normal conduction period, when
, the phase currents
ia and
ib conduct, while the outgoing phase current
remains zero, i.e.,
and
. Substituting the current equation and (2) into the second item of (12), the line voltage difference integral
is rewritten as
By decomposing (15) into a combination of two items, it is reformulated as
Substituting (14) and (16) into (12), and (12) is rewritten as
The phase current satisfies
in the freewheeling period
. Substituting the phase current relationship, (13) into the second item of (17), it is simplified as
where
is the final value of the outgoing phase current before commutation.
During the commutation period
, the outgoing phase current drops from the final value
to zero, the integral item
can be approximated by
, and (18) is rewritten as
From (13), the phase current
in the freewheeling period
is solved as
where
.
From (20), the freewheeling period
for the outgoing phase current
dropping from final value
to zero is solved as
Substituting (21) into (19), and (19) is shown as
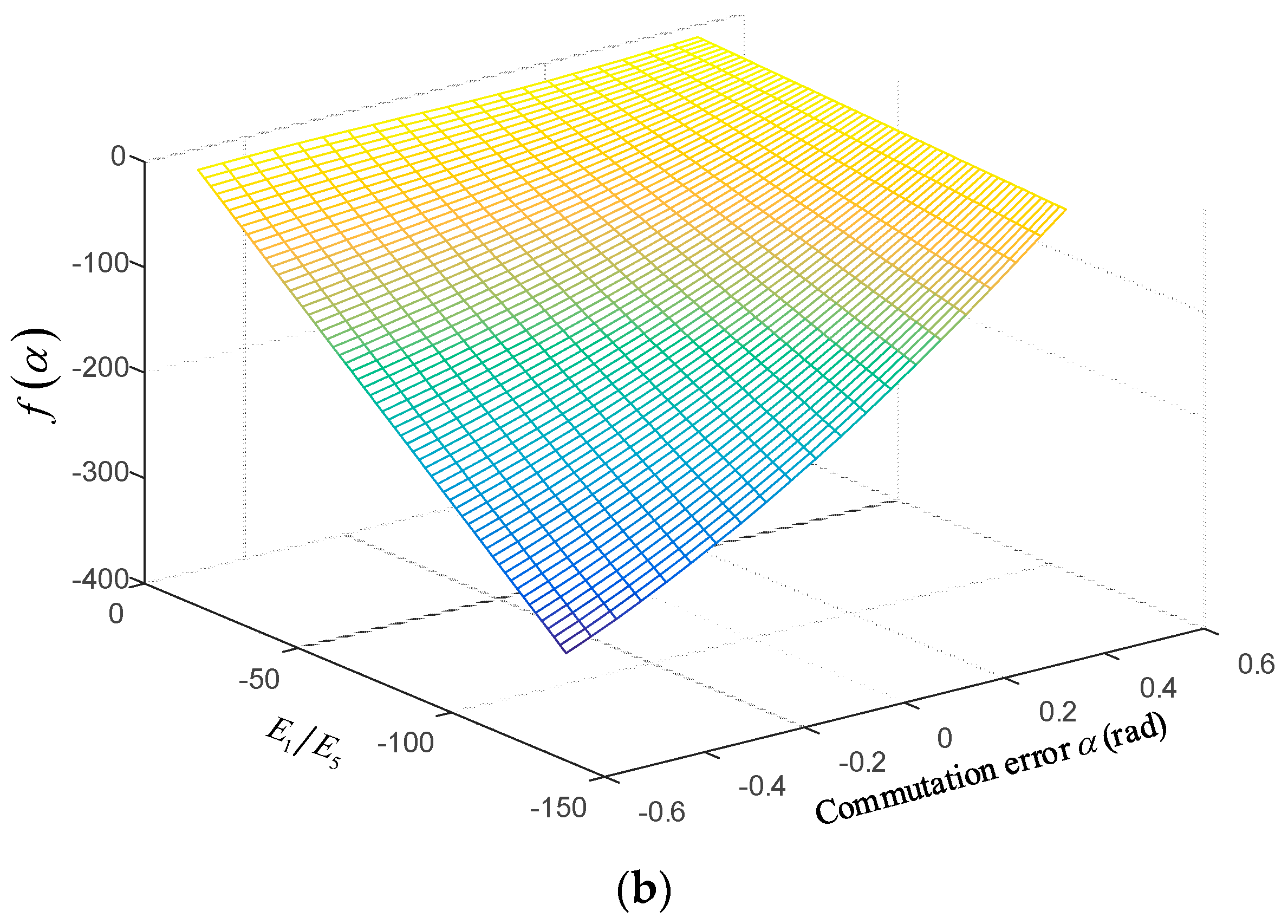
In (22), is related to . Next, the effect of will be discussed.
In the freewheeling period when
,
is expressed as
Considering
, the high-order terms of the back-EMF in (23) are negligible, and (23) can be simplified as
By calculating the trigonometric functions, (24) is simplified as
Both sides of (25) are multiplied by
, and refined as
In general, the EMF harmonic coefficients of a BLDC motor with a trapezoidal back EMF [
25]
. The relationship between
,
, and the commutation error
during the freewheeling period
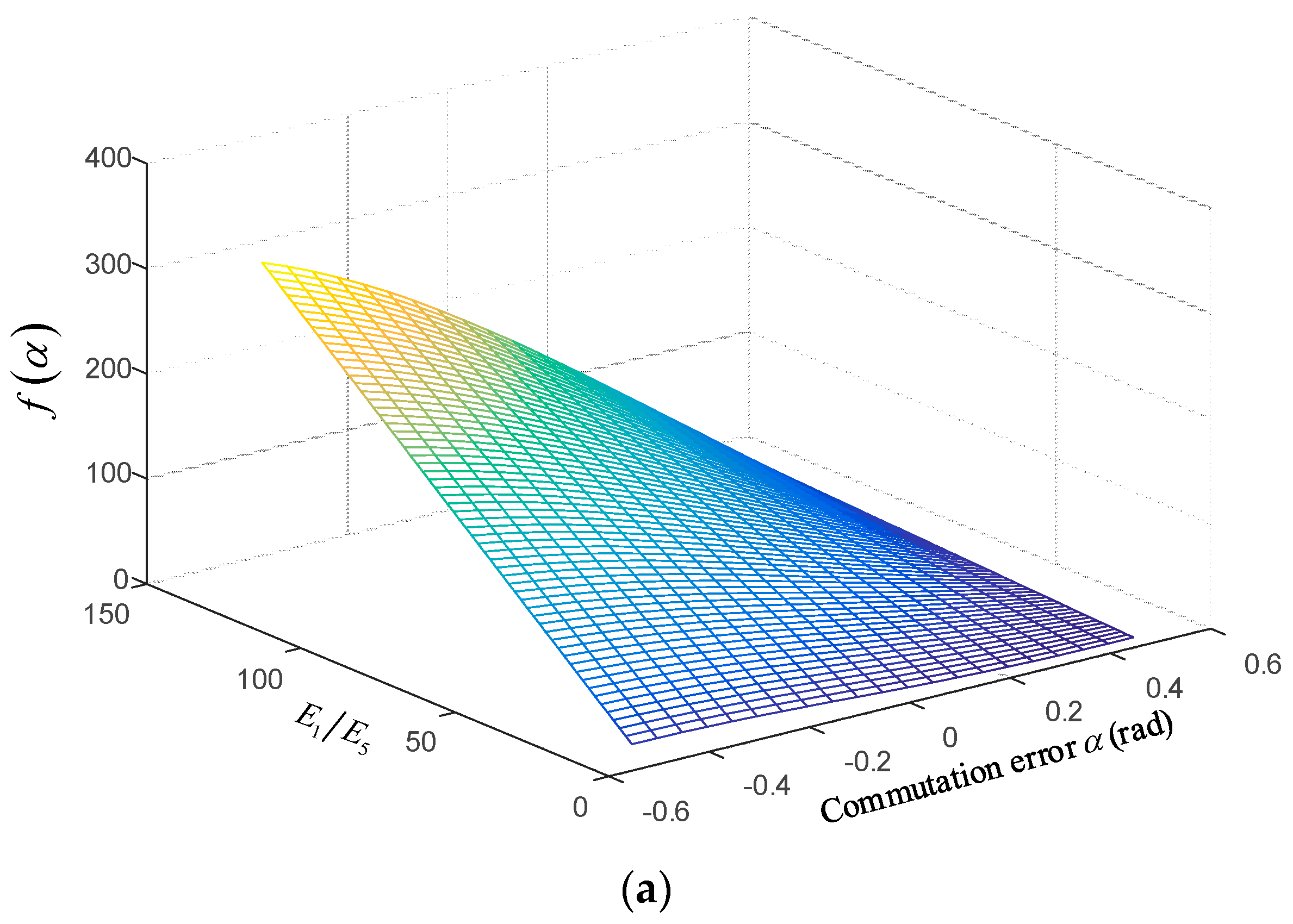
can be obtained in (26). When
,
, and the corresponding 3-D graph is shown in
Figure 7a. It is observed that with respect to
,
is greater than zero when the commutation error
, so
. When
,
, and the corresponding 3-D graph is shown in
Figure 7b.
is less than zero when the commutation error
, and
. Based on the relationship, it is derived that
and
. Both sides of
are multiplied by
, and the item
is represented as
, where
denotes copper loss and
.
denotes the input power of the motor and
. In general, the copper loss
is negligible, hence it satisfies
, which implies
Therefore, (19) is simplified as
Combining (27) and (17), the latter is reformulated as
According to the previous analysis, the general function of the line voltage difference integral
is given as
where the subscripts x and y represent the active phase, and z represents the inactive phase.
and
are the lower and upper limits of integral, respectively.
2.4. Commutation Error Compensation Strategy
In
Section 2.2 and
Section 2.3, the respective line voltage difference integrals
and
without and with consideration of the freewheeling period
are discussed. Next, the commutation error compensation strategy is described based on the analysis of the line voltage difference integral.
From (29), the three-phase back-EMF integral is rewritten as
According to the research in
Section 2.2, three-phase back-EMF integral can reflect commutation errors. In (30), three-phase back-EMF integral can be obtained from the combination of the integral
and
to determine commutation errors when the freewheeling period
is considered.
In general, the commutation instants are obtained by delaying ZCPs by 30 electrical degrees in the sensorless technique and reactivating the motor windings according to the predefined commutation sequence. The predefined commutation sequences are shown in
Table 3; here,
,
, and
are virtual hall signals.
In
Table 1, the sign of the three-phase back-EMF integral changes according to the direction of the phase current. The three-phase back-EMF integral
can be updated as
where
denotes the rotation direction of the motor rotor. When
, the motor runs in the anti-clockwise rotation, and when
, the motor rotates in the opposite one. When the sensorless BLDC motor runs, the windings are excited in according with the predefined commutation sequence listed in
Table 3, and the conduction switches are obtained. Then the line voltage difference integral
is calculated with
Table 1, and the outgoing phase current
before commutation is sampled. By using (30), the three-phase back-EMF integral
can be given. Considering the rotation direction
of the motor rotor is known, the three-phase back-EMF integral
is converted to a positive value under delayed commutation and to a negative one under advanced commutation with (31), which also makes PI controller available.
Here, a PI regulator is also designed to compensate commutation errors, and the PI regulator is defined as
where three-phase back-EMF integral error
, and the reference value
.
is the proportional coefficient, and
is the integral coefficient.
is the integral period and
.
is the
kth output value of the PI regulator,
is the
th output value of the PI regulator. Here,
k represents the number of iterations.
For the sensorless BLDC motor based on ZCP detection of the back-EMF, the accurate commutation instants are obtained by 30 electrical degrees delayed shift of ZCPs. Therefore, after the commutation error is determined, the commutation shift is updated as
where
.
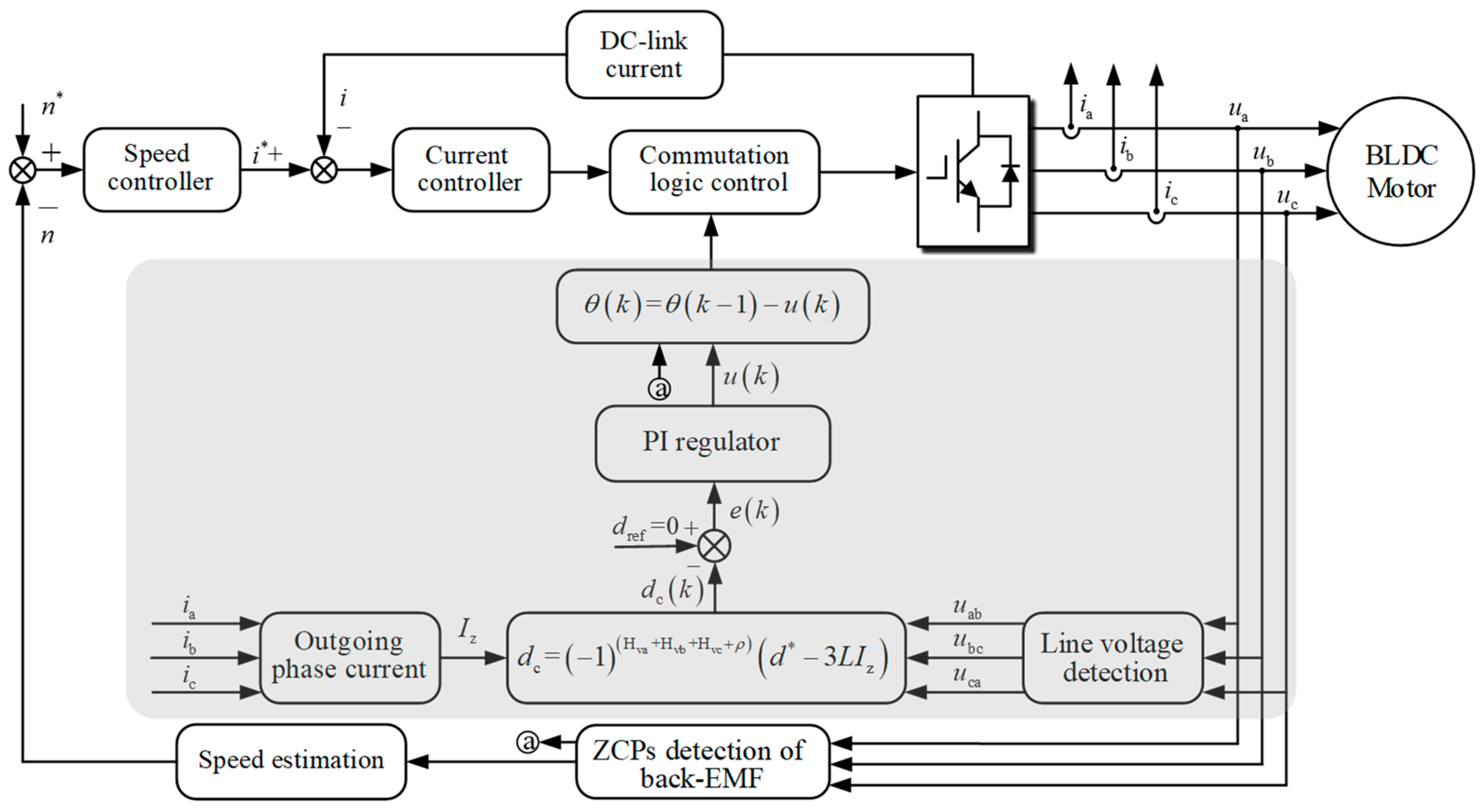
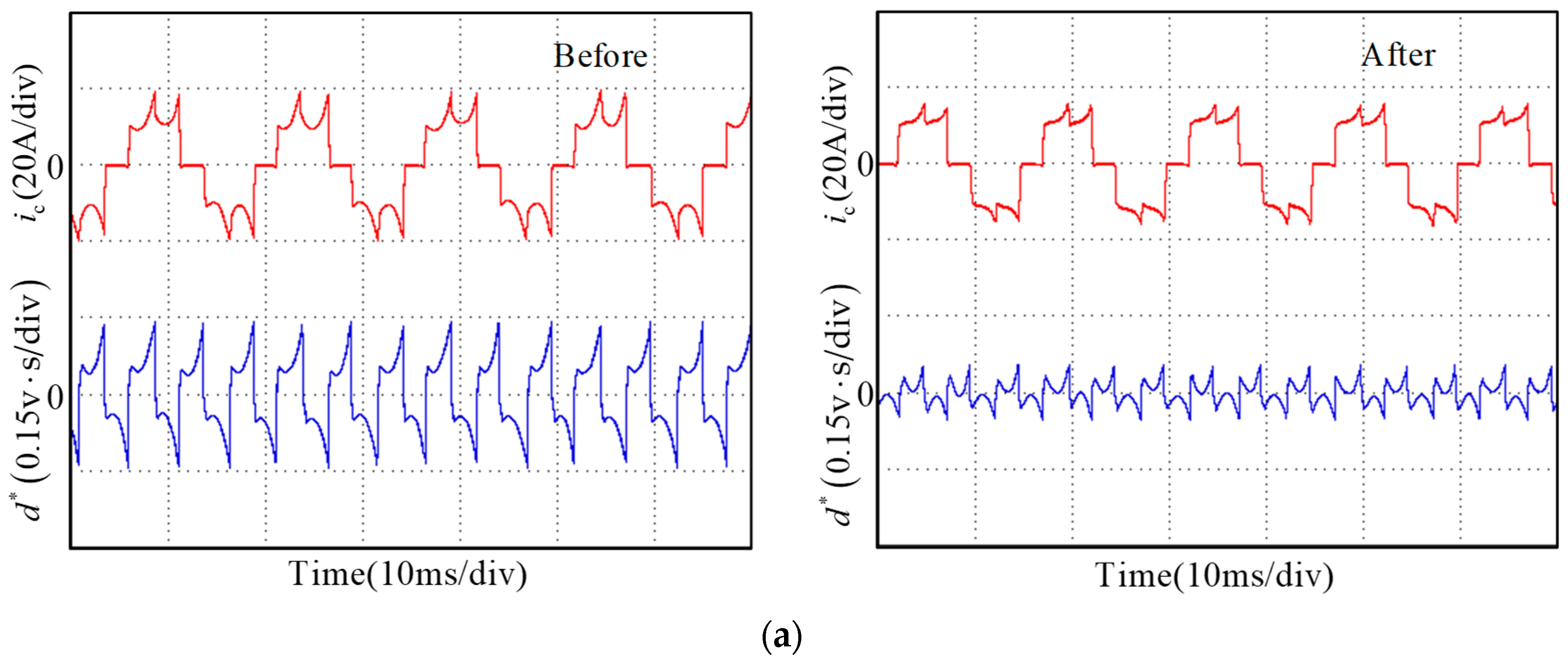
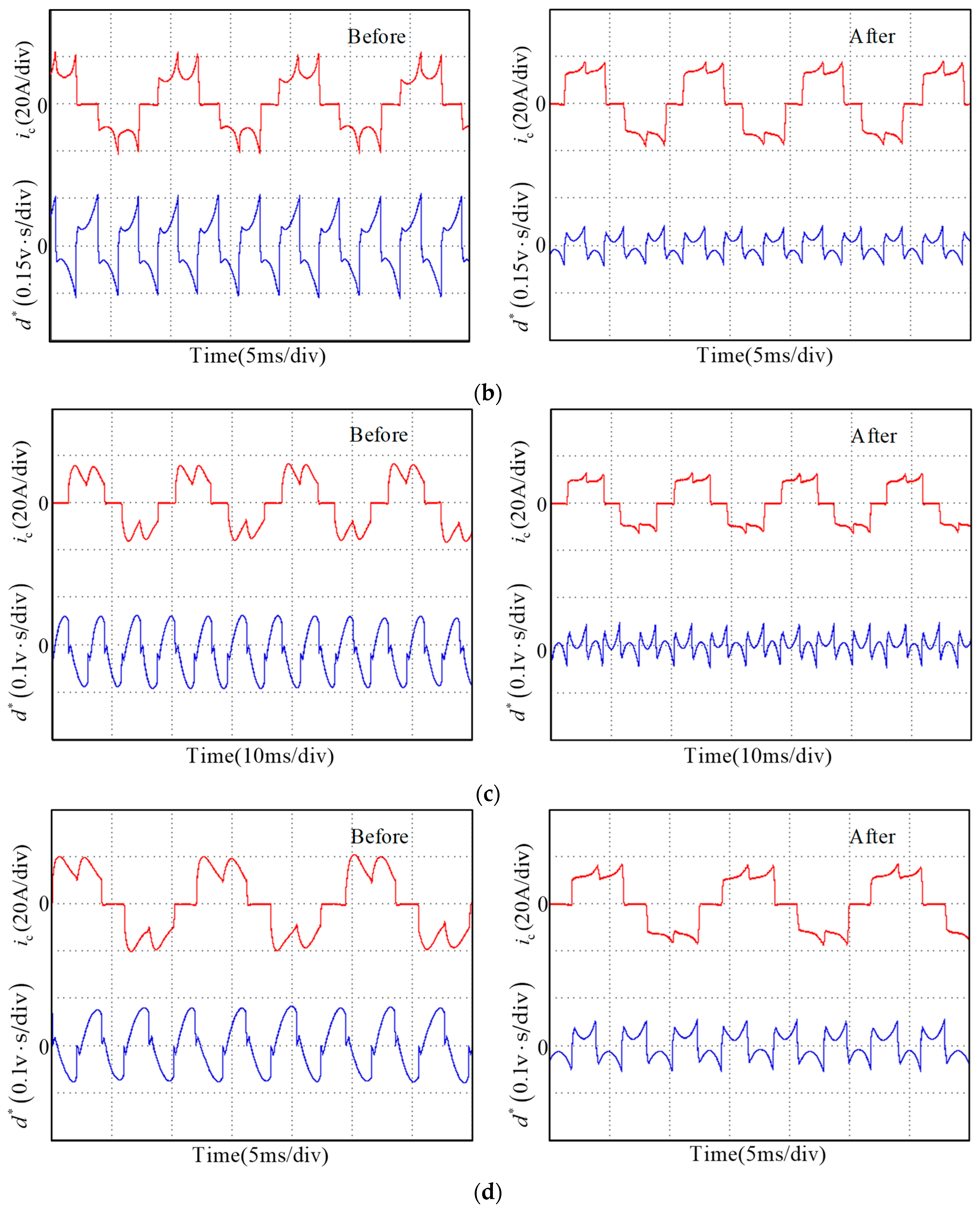
Figure 8 shows the block diagram of a sensorless BLDC motor drive system and the proposed commutation error compensation strategy is shown in the shadowed area. The system contains a speed-loop controller, a current-loop controller, and a commutation error compensation link. In the commutation error compensation link, when commutation signals are detected, the outgoing phase current final value
is sampled and the line voltage difference is integrated until the commutation occurs again. Then, the line voltage difference integral
is recorded, and the three-phase back-EMF integral
is calculated from the sampled current value
and the line voltage difference integral
. The entire compensation process is then resumed. A flowchart of the proposed method is shown in
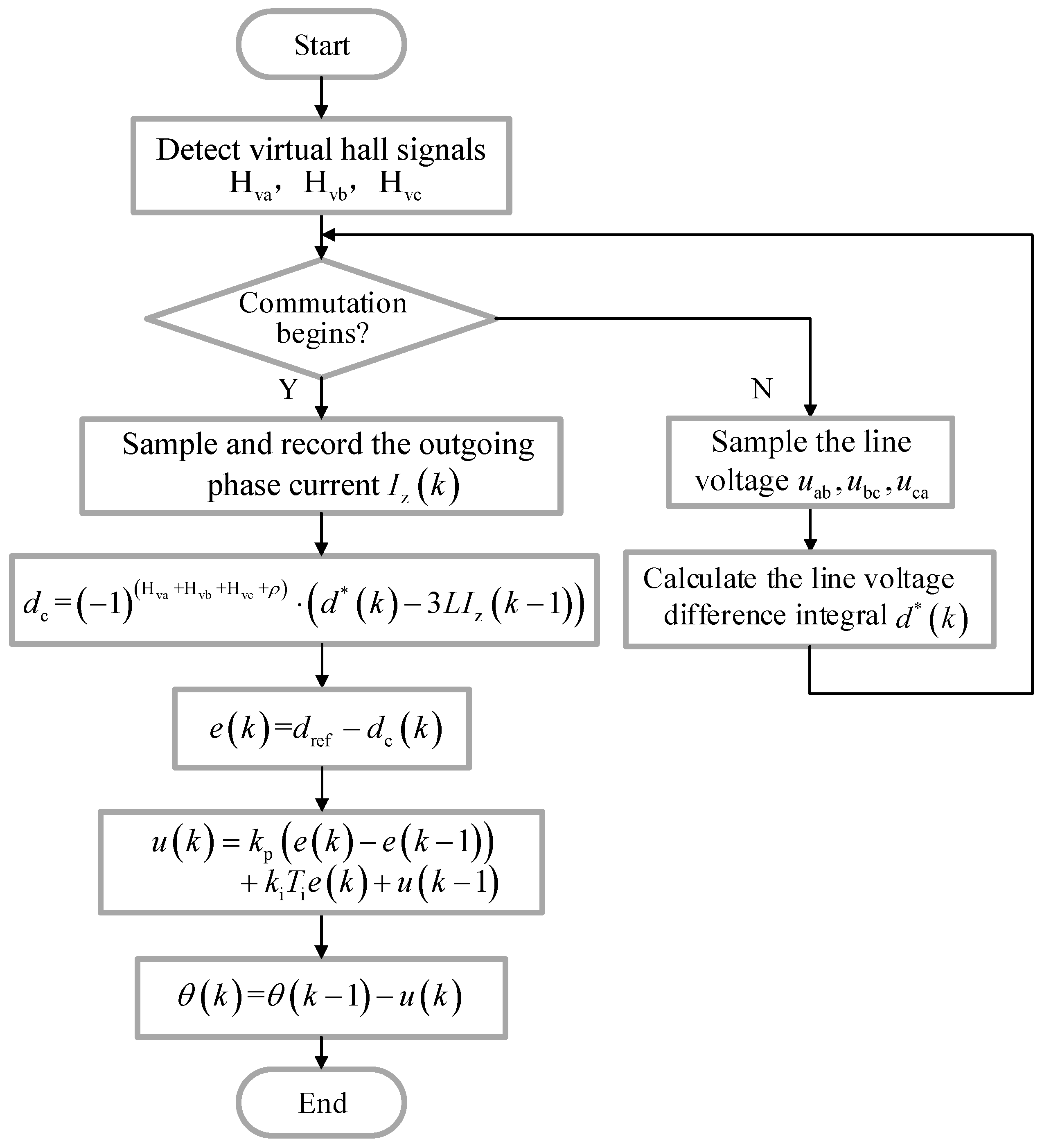
Figure 9.
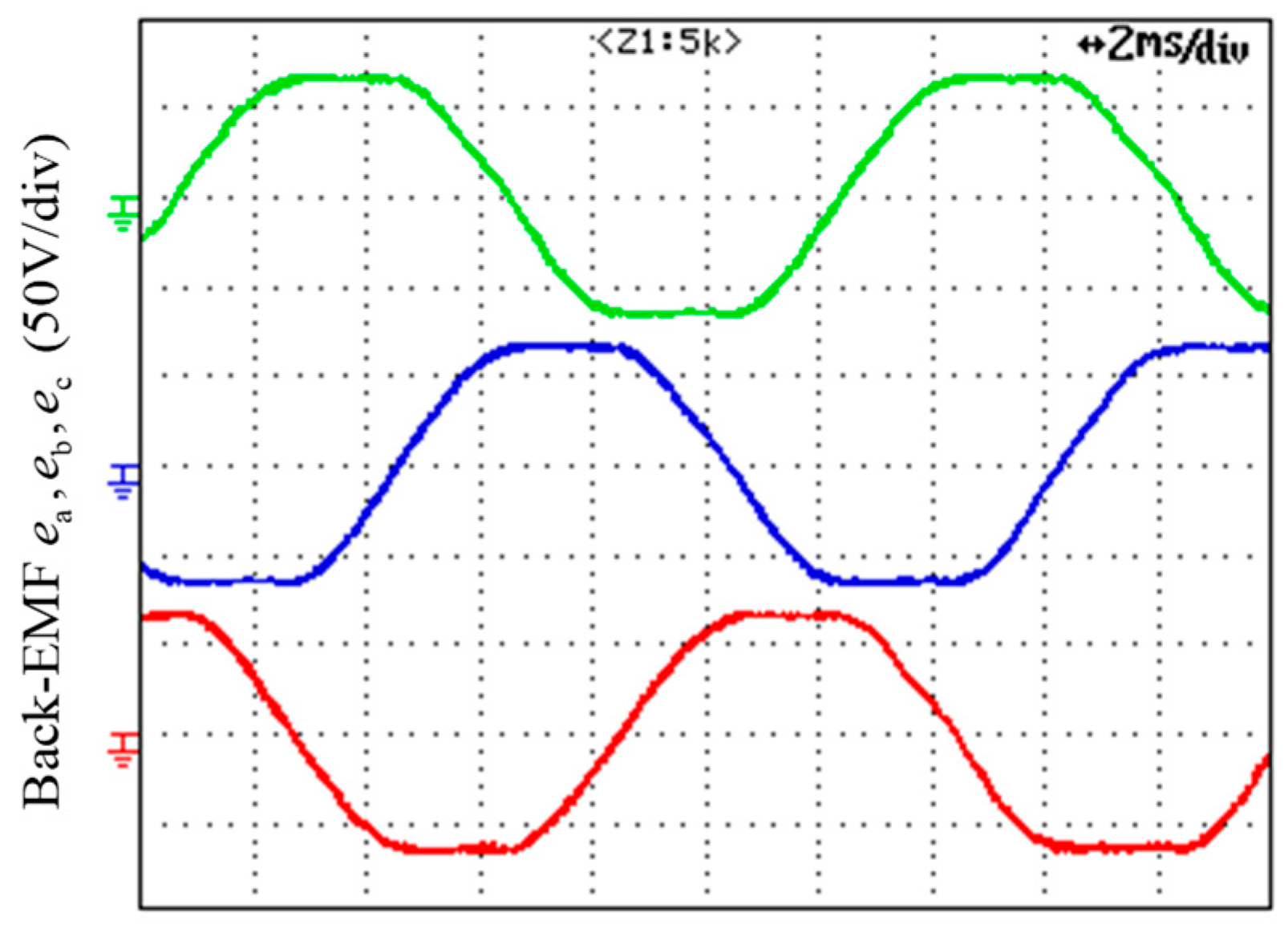
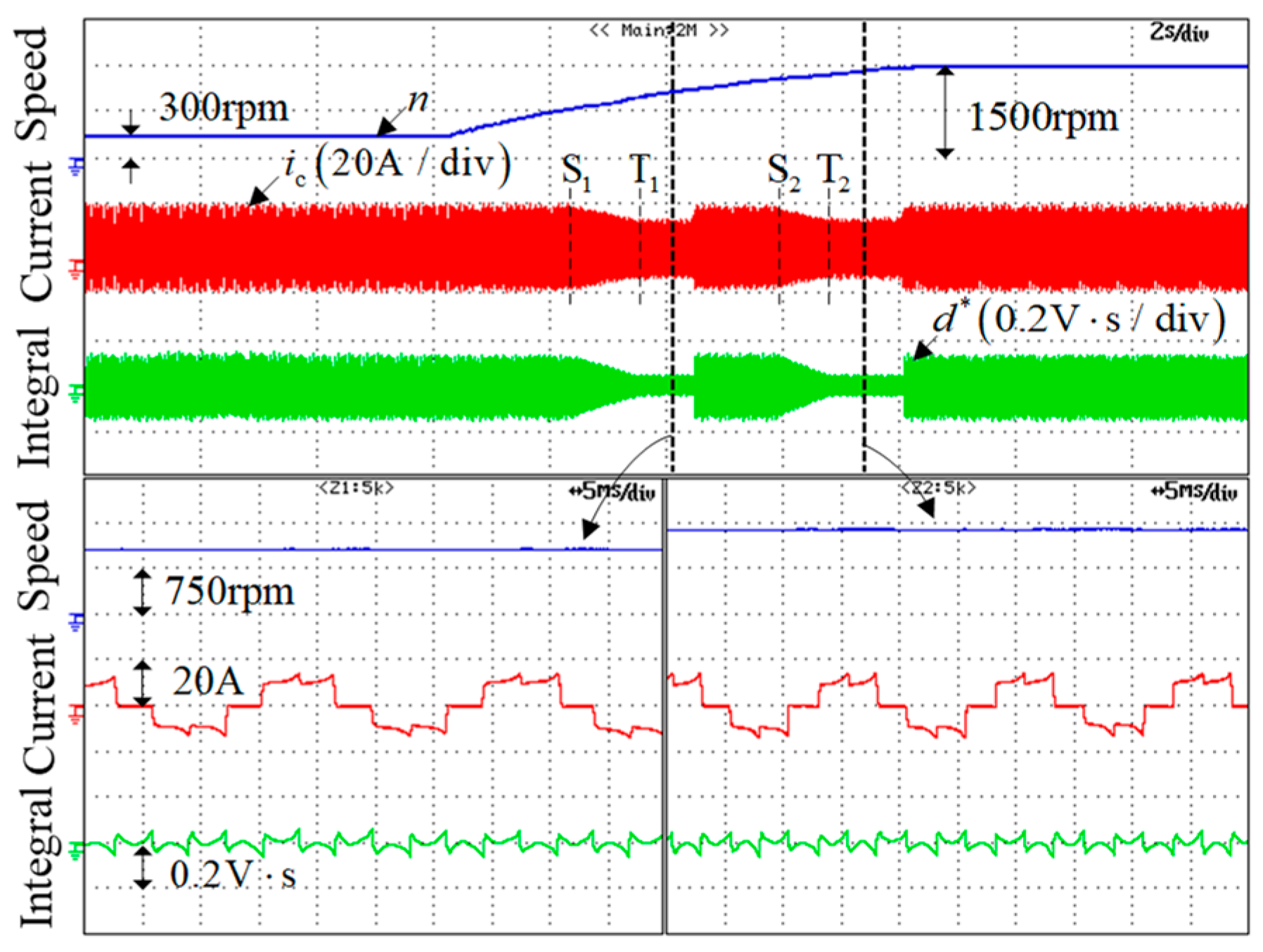
Figure 10 shows the back-EMF waveforms by the constant speed test of 1200 rpm.