A Novel Rotor Eddy Current Loss Estimation Method for Permanent Magnet Synchronous Machines with Small Inductance and a Conductive Rotor Sleeve
Abstract
1. Introduction
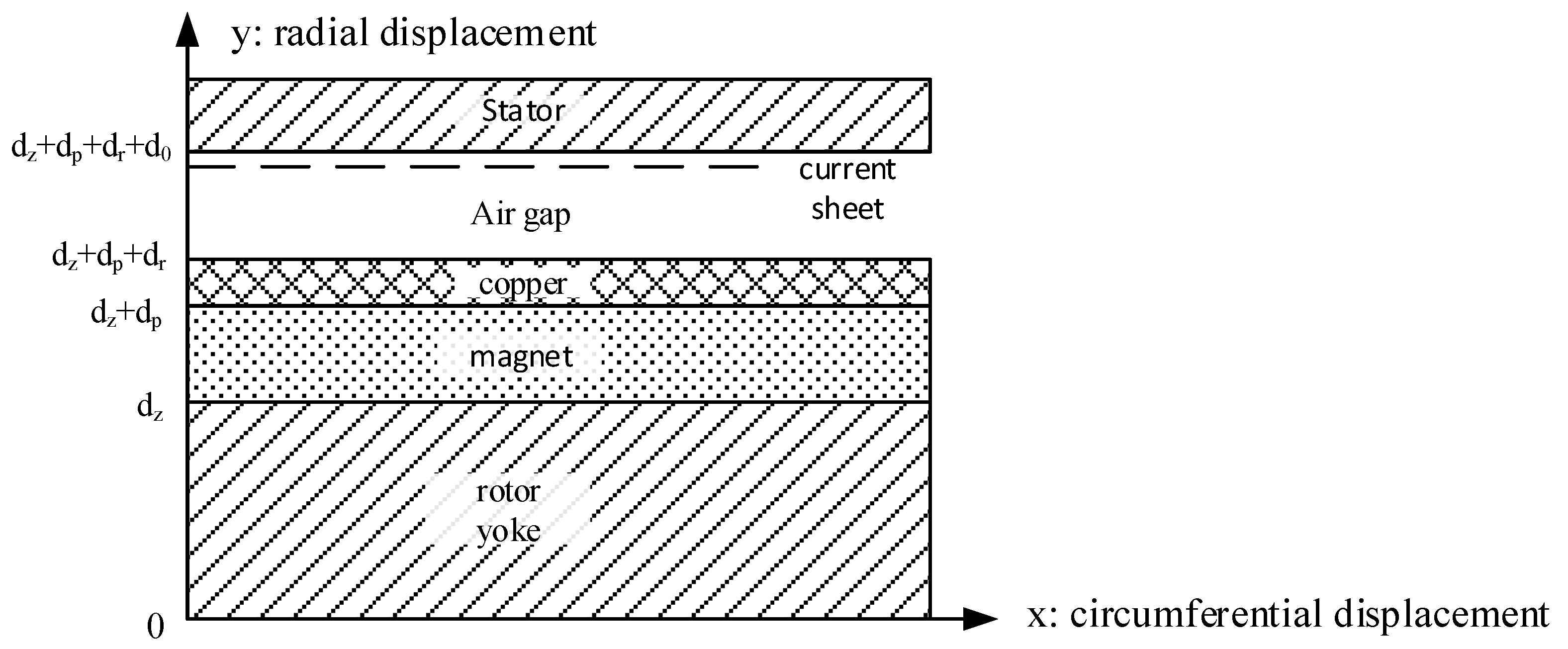
2. Problem Statement
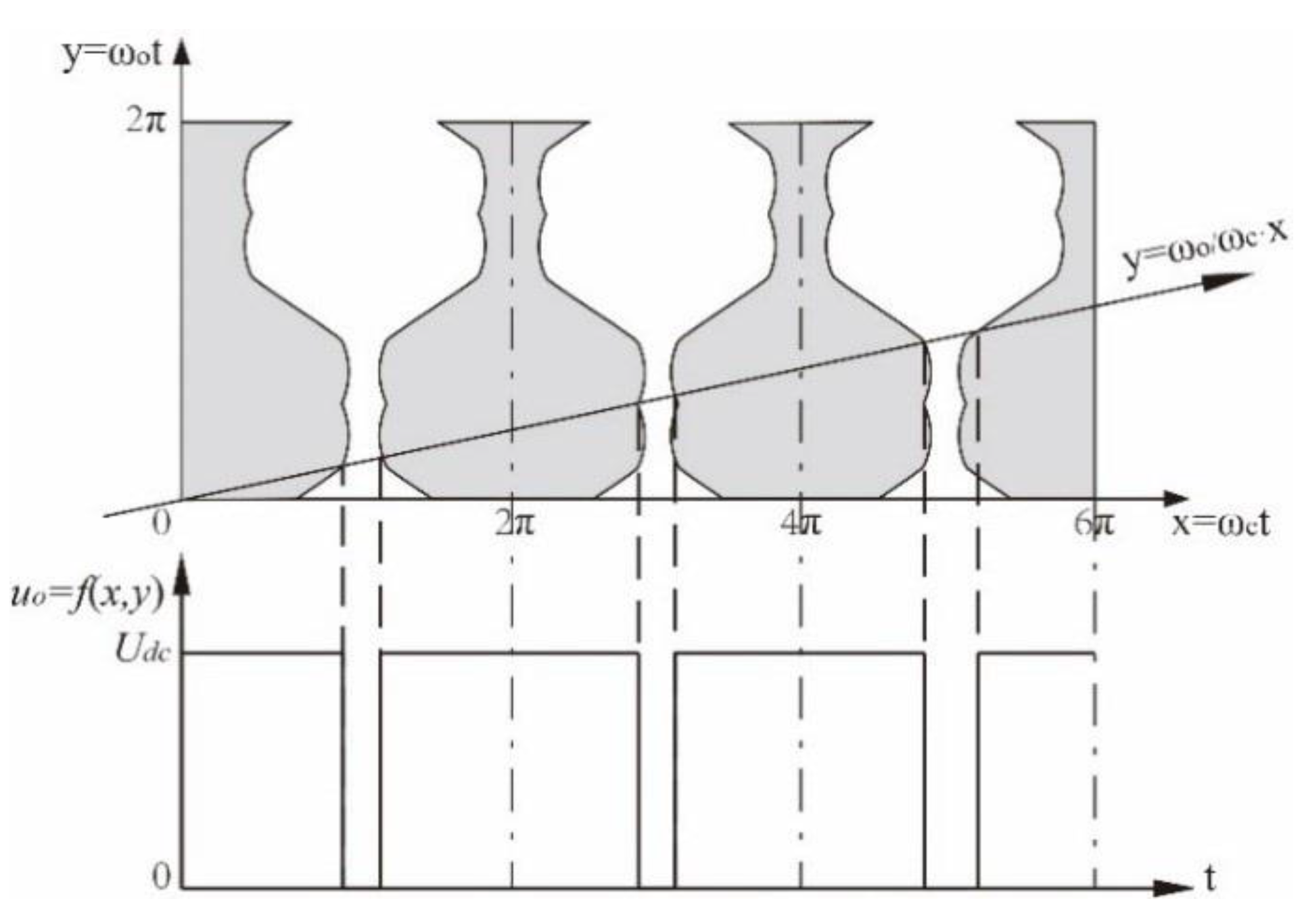
3. SVPWM Working Principle and Expression Deduction of Modulation Wave Per Phase
4. Refined SVPWM Frequency Spectrum Structure
- When n = 3k, the coefficients in fa(t), fb(t) and fc(t) are the same. Thus, the harmonic voltage does not produce a respective resulting harmonic current.
- Switching harmonics does not exist in phase currents; i.e., the voltage harmonics bearing the form in Equation (20)do not produce current harmonics. This is because the coefficients of such voltage harmonics are the same in all three phases.
- Voltage harmonics with m ± n being even do not produce current harmonics either. The reasons for this are as follows.Components bearing the form in Equation (21)will not produce current harmonics because =0.Components bearing the form in Equation (22)will not produce current harmonics because = 0 when m and n are both even or odd, which is a synonym of m ± n being even.Components bearing the form in Equation (23)will not produce current harmonics because = 0 when m and n are both even or odd, which is another synonym of m ± n being even.Components bearing the form in Equation (24)will not produce current harmonics; the reason for this is similar.
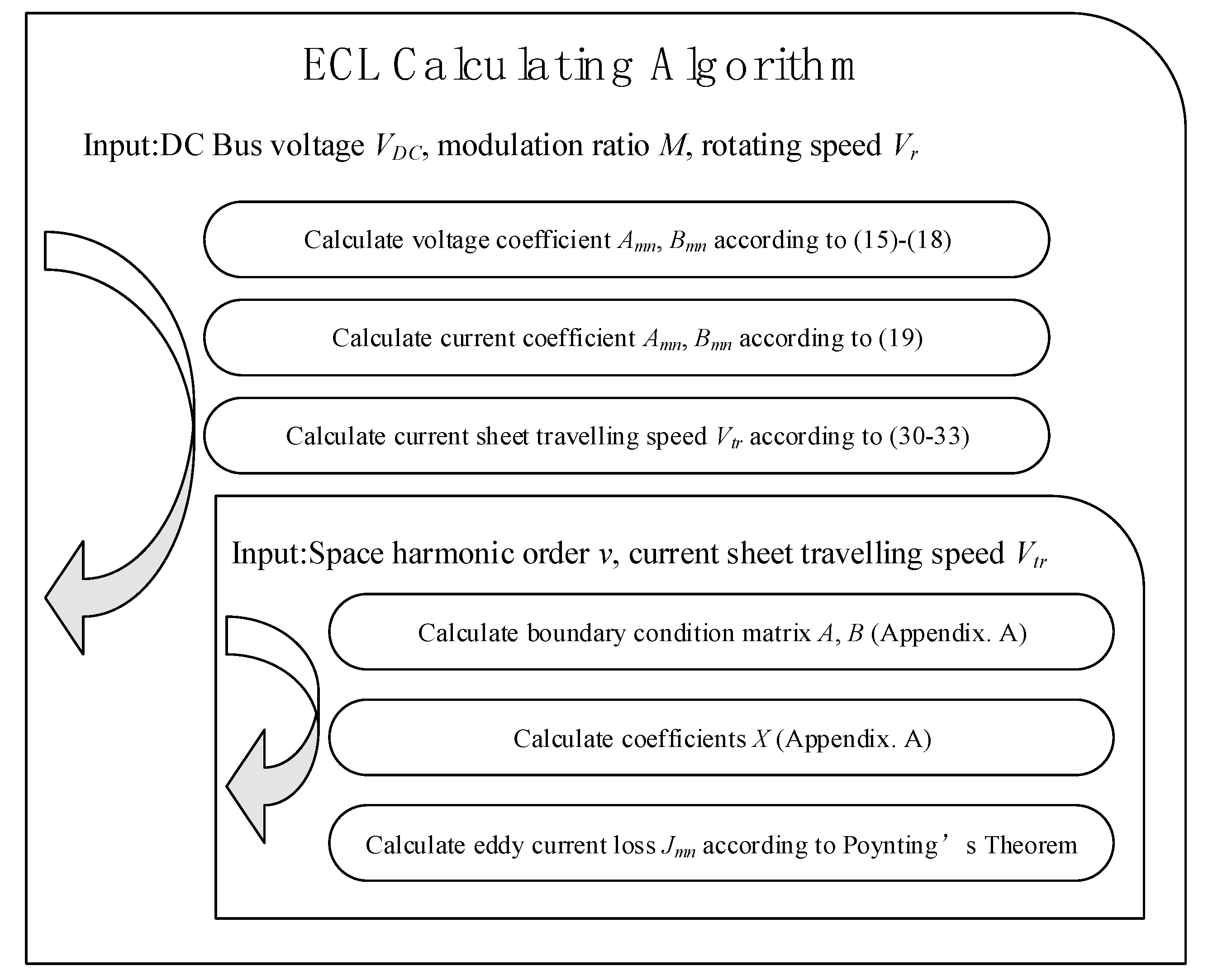
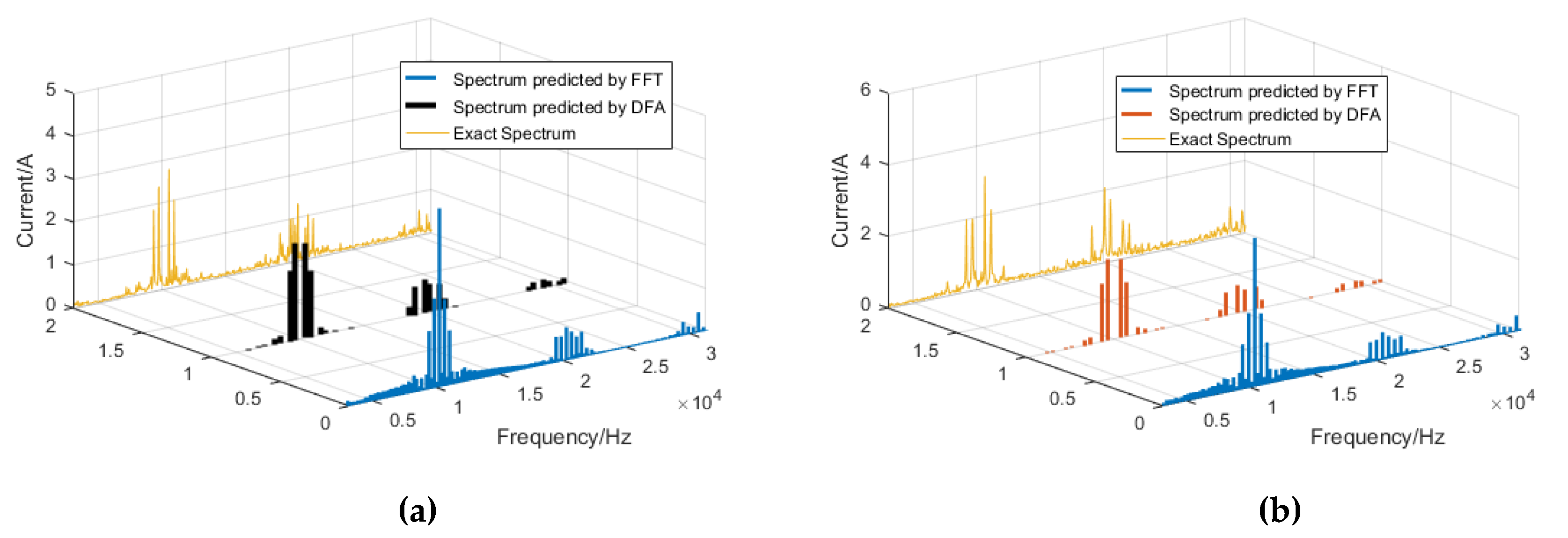
5. ECL Estimation Algorithm with Different Travelling Current Sheet Direction Judgement Methods
- (v+n) can be divided by three, while (v-n) cannot:In this situation, the travelling wave travels backwards with regard to the rotor. Suppose the velocity of the outer rotor of the permanent magnet synchronous machine is vr; then, the travel velocity vtr of the travelling current sheet is expressed as in Equation (31):
- (v-n) can be divided by three, while (v+n) cannot:
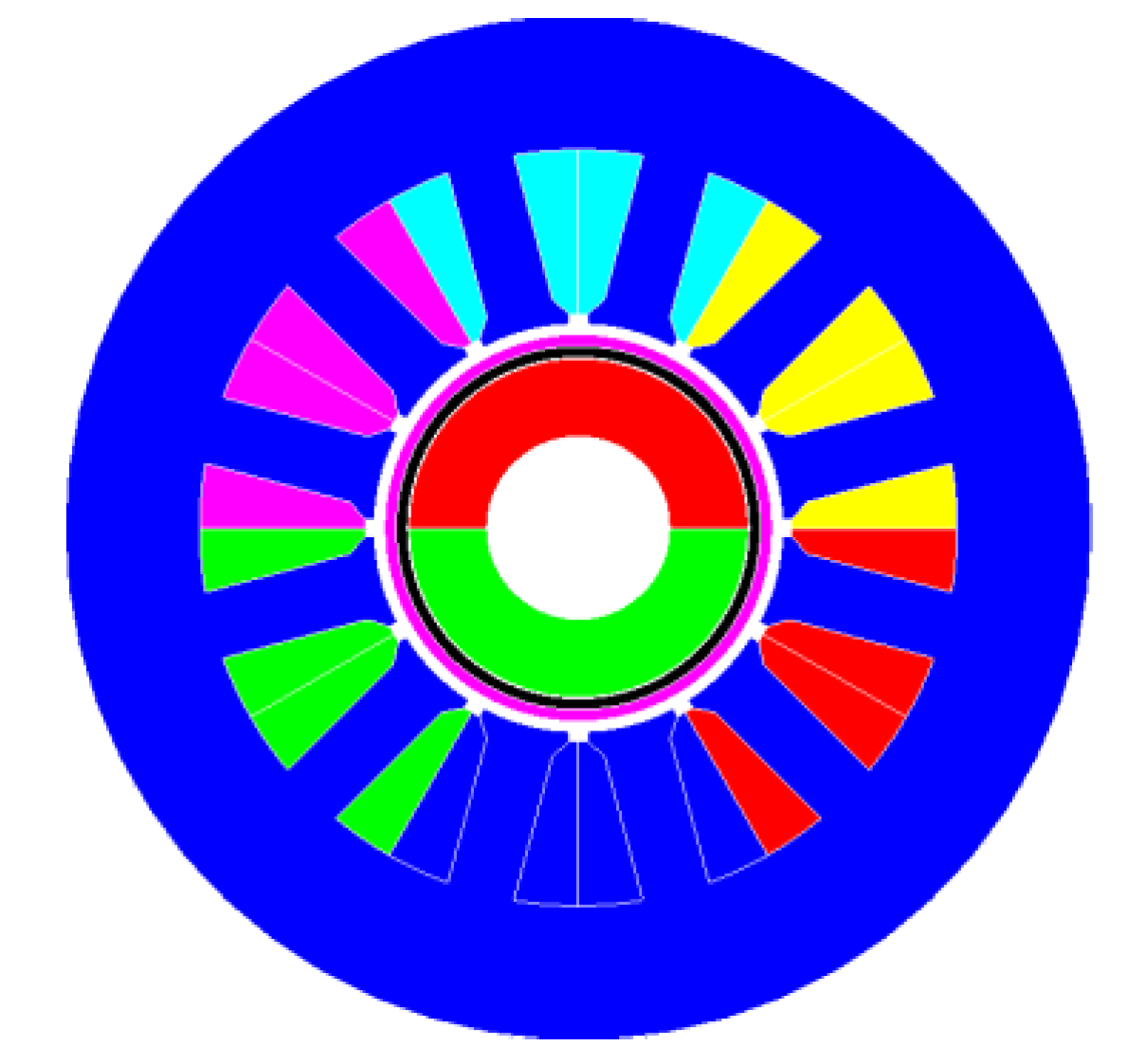
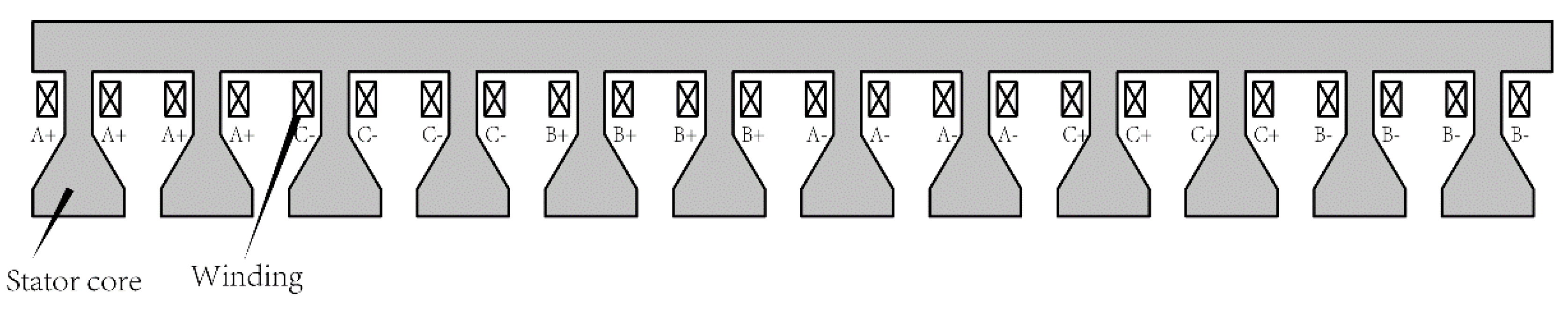
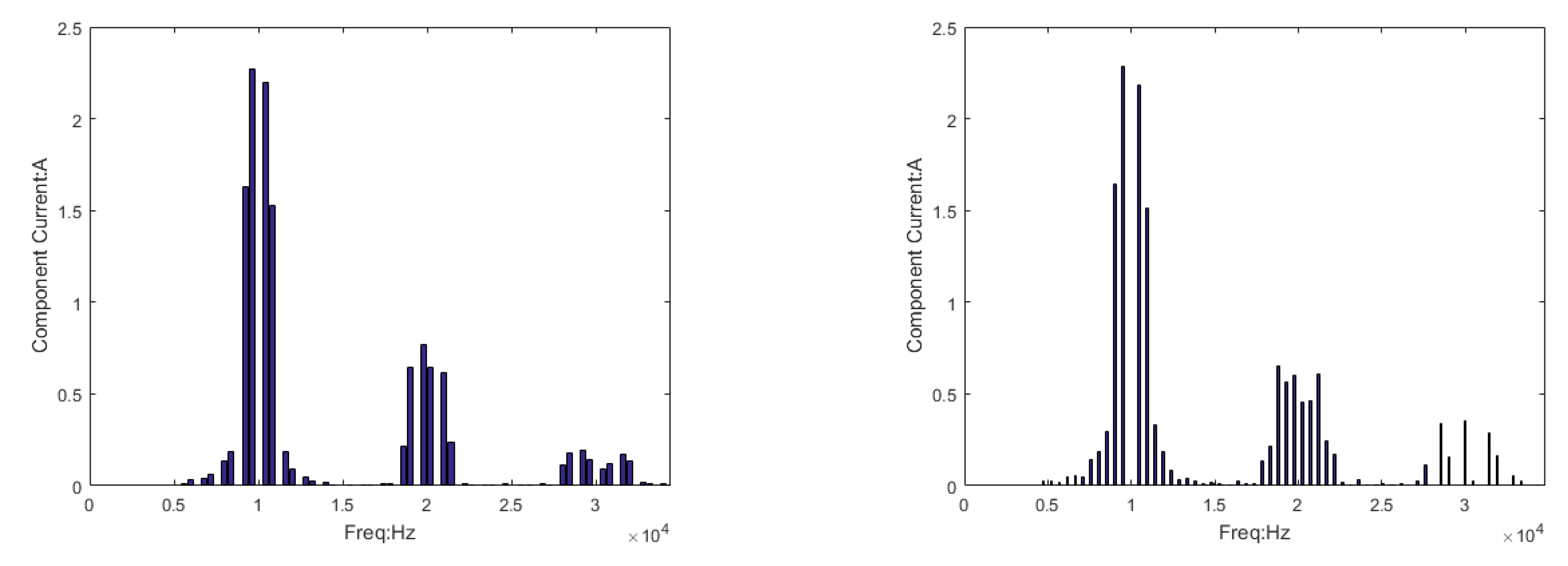
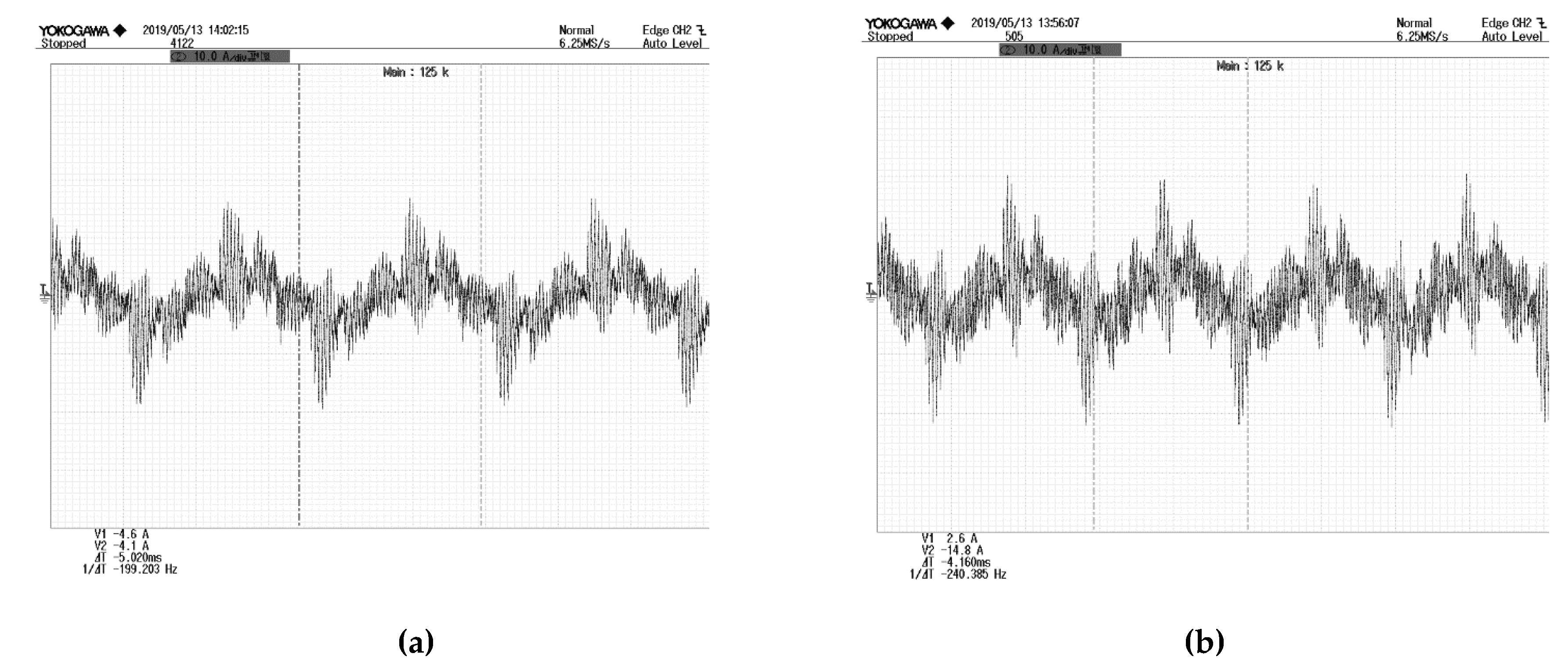
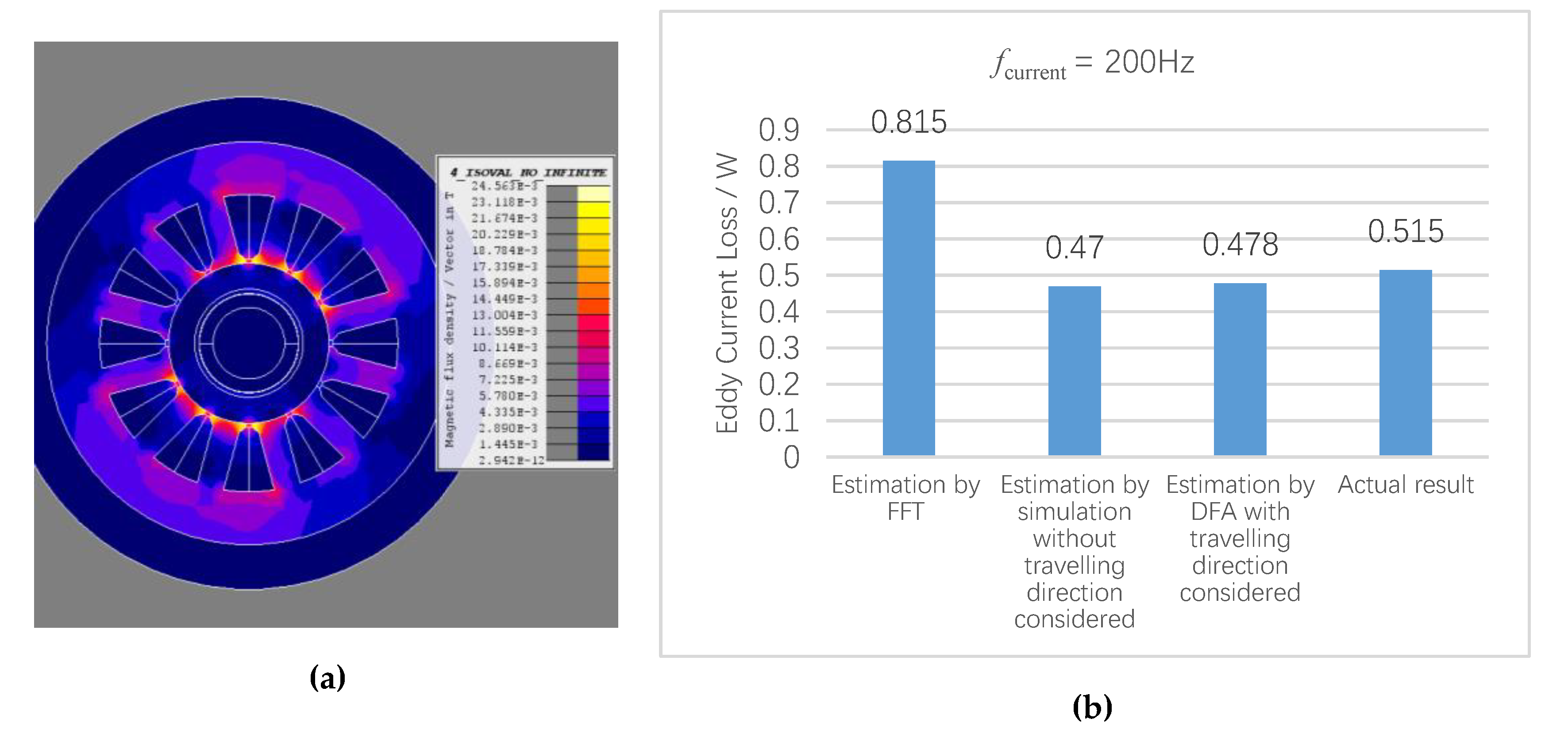
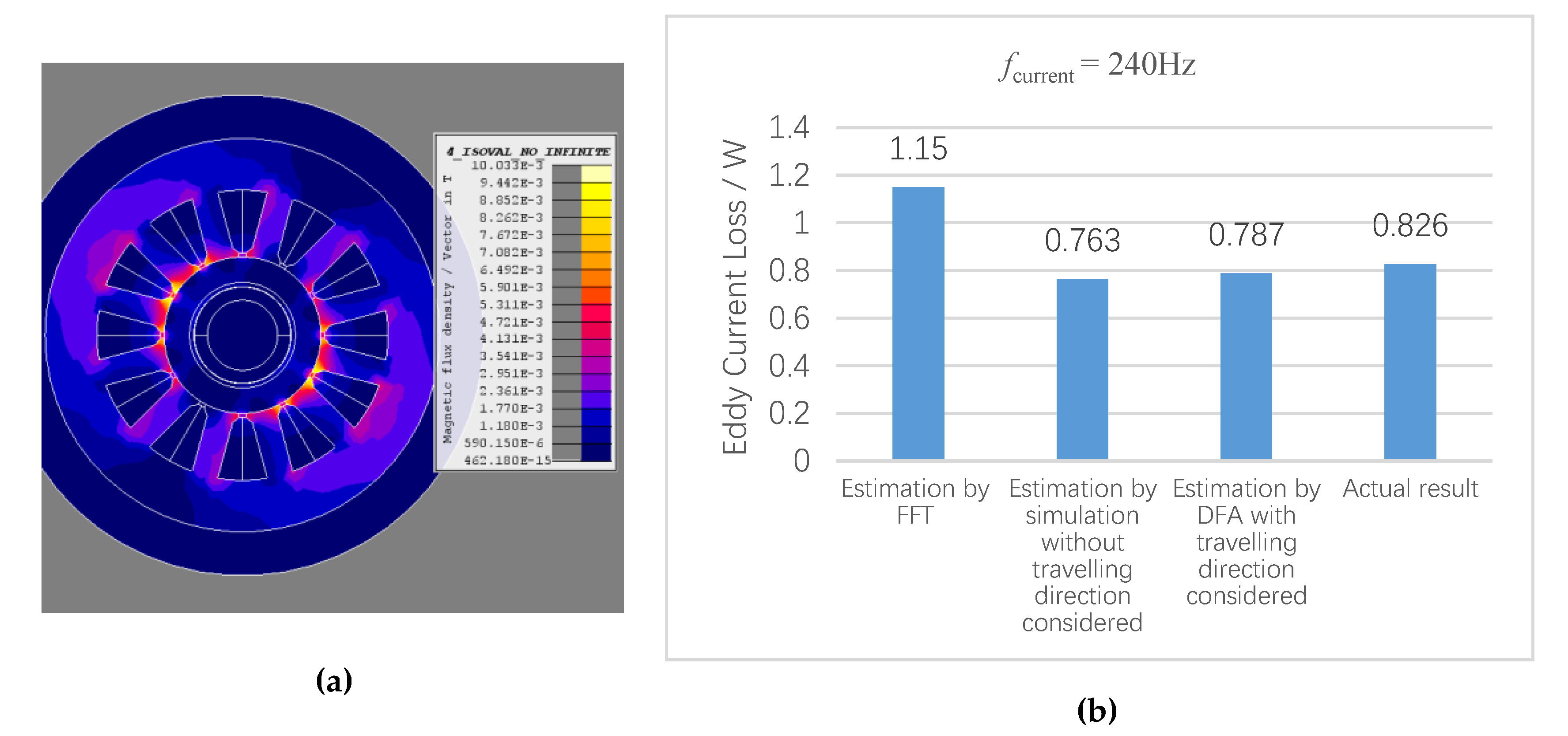
6. Simulation Study and Experiments
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Details of the Analytical Model for the Eddy Current Loss Estimation
References
- Hannon, B.; Sergeant, P.; Dupré, L. Evaluation of the Rotor Eddy-Current Losses in High-Speed PMSMs With a Shielding Cylinder for Different Stator Sources. IEEE Trans. Magn. 2019, 55, 1–10. [Google Scholar] [CrossRef]
- Riemer, B.; Lebmann, M.; Hameyer, K. Rotor design of a high-speed permanent magnet synchronous machine rating 100,000 rpm at 10 kW. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 3978–3985. [Google Scholar]
- Weili, L.; Hongbo, Q.; Xiaochen, Z.; Ran, Y. Influence of copper plating on electromagnetic and temperature fields in a high-speed permanent-magnet generator. IEEE Trans. Magn. 2012, 48, 2247–2253. [Google Scholar] [CrossRef]
- Li, W.; Qiu, H.; Zhang, X.; Cao, J.; Yi, R. Analyses on electromagnetic and temperature fields of superhigh-speed permanent-magnet generator with different sleeve materials. IEEE Trans. Ind. Electron. 2014, 61, 3056–3063. [Google Scholar] [CrossRef]
- Li, L.; Czarkowski, D.; Liu, Y.; Pillay, P. Multilevel space vector PWM technique based on phase-shift harmonic suppression. In Proceedings of the Fifteenth Annual IEEE Applied Power Electronics Conference and Exposition (Cat. No. 00CH37058), New Orleans, LA, USA, 6–10 February 2000; Volume 1, pp. 535–541. [Google Scholar]
- Yu, F.; Zhang, X.; Wang, S. Five-phase permanent magnet synchronous motor vector control based on harmonic eliminating space vector modulation. In Proceedings of the 2005 International Conference on Electrical Machines and Systems, Nanjing, China, 27–29 September 2005; Volume 1, pp. 392–396. [Google Scholar]
- Zhou, C.; Yang, G.; Su, J. PWM strategy with minimum harmonic distortion for dual three-phase permanent-magnet synchronous motor drives operating in the overmodulation region. IEEE Trans. Power Electron. 2015, 31, 1367–1380. [Google Scholar] [CrossRef]
- Li, X.; Chen, G. An Approach to Harmonic Suppression Based on Triple Harmonics Injection with Passive Circuit. Autom. Electr. Power Syst. 2007, 14, 61–65. [Google Scholar]
- Zhang, Y.; Li, Y.W. Investigation and suppression of harmonics interaction in high-power PWM current-source motor drives. IEEE Trans. Power Electron. 2014, 30, 668–679. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Ng, K.; Schofield, N.; Howe, D. Analytical prediction of rotor eddy current loss in brushless machines equipped with surface-mounted permanent magnets. I. Magnetostatic field model. In Proceedings of the Fifth International Conference on Electrical Machines and Systems, Shenyang, China, 18–20 August 2001; Volume 2, pp. 806–809. [Google Scholar]
- Zhu, Z.Q.; Ng, K.; Schofield, N.; Howe, D. Analytical prediction of rotor eddy current loss in brushless machines equipped with surface-mounted permanent magnets. II. Accounting for eddy current reaction field. In Proceedings of the Fifth International Conference on Electrical Machines and Systems, Shenyang, China, 18–20 August 2001; Volume 2, pp. 810–813. [Google Scholar]
- Fang, D.; Nehl, T.W. Analytical modeling of eddy-current losses caused by pulse-width-modulation switching in permanent-magnet brushless direct-current motors. IEEE Trans. Magn. 1998, 34, 3728–3736. [Google Scholar] [CrossRef]
- Bellara, A.; Bali, H.; Belfkira, R.; Amara, Y.; Barakat, G. Analytical Prediction of Open-Circuit Eddy-Current Loss in Series Double Excitation Synchronous Machines. IEEE Trans. Magn. 2011, 47, 2261–2268. [Google Scholar] [CrossRef]
- Paradkar, M.; Bocker, J. 2D analytical model for estimation of eddy-current loss in the magnets of IPM machines considering the reaction field of the induced eddy currents. In Proceedings of the 2015 IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 1096–1102. [Google Scholar]
- Atallah, K.; Howe, D.; Mellor, P.; Stone, D. Rotor loss in permanent-magnet brushless AC machines. IEEE Trans. Ind. Appl. 2000, 36, 1612–1618. [Google Scholar]
- Wang, J.; Atallah, K.; Chin, R.; Arshad, W.M.; Lendenmann, H. Rotor Eddy-Current Loss in Permanent-Magnet Brushless AC Machines. IEEE Trans. Magn. 2010, 46, 2701–2707. [Google Scholar] [CrossRef]
- Ishak, D.; Zhu, Z.; Howe, D. Eddy-current loss in the rotor magnets of permanent-magnet brushless machines having a fractional number of slots per pole. IEEE Trans. Magn. 2005, 41, 2462–2469. [Google Scholar] [CrossRef]
- Markovic, M.; Perriard, Y. A simplified determination of the permanent magnet (PM) eddy-current losses due to slotting in a PM rotating motor. In Proceedings of the International Conference on Electrical Machines and Systems (ICEMS), Wuhan, China, 17–20 October 2008; pp. 309–313. [Google Scholar]
- Wu, L.J.; Zhu, Z.Q.; Staton, D.; Popescu, M.; Hawkins, D. Analytical model for predicting magnet loss of surface-mounted permanent magnet machines accounting for slotting effect and load. IEEE Trans. Magn. 2012, 48, 107–117. [Google Scholar] [CrossRef]
- Wu, L.J.; Zhu, Z.Q.; Staton, D.; Popescu, M.; Hawkins, D. Analytical modeling of eddy current loss in retaining sleeve of surface-mounted PM machines accounting for influence of slot opening. In Proceedings of the 2012 IEEE International Symposium on Industrial Electronics, Hangzhou, China, 28–31 May 2012; pp. 611–616. [Google Scholar]
- Rahideh, A.; Korakianitis, T. Analytical magnetic field distribution of slotless brushless permanent magnet motors—Part I. Armature reaction field, inductance and rotor eddy-current loss calculations. IET Electr. Power Appl. 2012, 6, 628. [Google Scholar] [CrossRef]
- Yamazaki, K.; Kanou, Y. Rotor Loss Analysis of Interior Permanent Magnet Motors Using Combination of 2D and 3D Finite Element Method. IEEE Trans. Magn. 2009, 45, 1772–1775. [Google Scholar] [CrossRef]
- Fang, Z.X.; Zhu, Z.Q.; Wu, L.J.; Xia, Z.P. Simple and accurate analytical estimation of slotting effect on magnet loss in fractional-slot surface-mounted PM machines. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; Volume 37, pp. 464–470. [Google Scholar]
- Jaffar, M.Z.M.; Husain, I. Path permeance based analytical inductance model for IPMSM considering saturation and slot leakage. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–7. [Google Scholar]
- Wang, J.; Papini, F.; Chin, R.; Arshad, W.M.; Lendenmann, H. Computationally efficient approaches for evaluation of rotor eddy current loss in permanent magnet brushless machines. In Proceedings of the 2009 International Conference on Electrical Machines and Systems, Tokyo, Japan, 15–18 November 2009. [Google Scholar]
- Bode, C.; Canders, W.R. Advanced calculation of eddy-current losses in PMSM with tooth windings. In Proceedings of the XIX International Conference on Electrical Machines, Rome, Italy, 6–8 September 2010; Volume 1, pp. 1–6. [Google Scholar]
- Pyrhonen, J.; Jussila, H.; Alexandrova, Y.; Rafajdus, P.; Nerg, J. Harmonic Loss Calculation in Rotor Surface Permanent Magnets—New Analytic Approach. IEEE Trans. Magn. 2012, 48, 2358–2366. [Google Scholar] [CrossRef]
- Dubas, F.; Rahideh, A. Two-Dimensional Analytical Permanent-Magnet Eddy-Current Loss Calculations in Slotless PMSM Equipped With Surface-Inset Magnets. IEEE Trans. Magn. 2014, 50, 54–73. [Google Scholar] [CrossRef]
- Martin, F.; Zaim, M.E.H.; Tounzi, A.; Bernard, N. Improved Analytical Determination of Eddy Current Losses in Surface Mounted Permanent Magnets of Synchronous Machine. IEEE Trans. Magn. 2014, 50, 1–9. [Google Scholar]
- Arumugam, P.; Hamiti, T.; Gerada, C. Estimation of Eddy Current Loss in Semi-Closed Slot Vertical Conductor Permanent Magnet Synchronous Machines Considering Eddy Current Reaction Effect. IEEE Trans. Magn. 2013, 49, 5326–5335. [Google Scholar] [CrossRef]
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation for Power Converters: Principles and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2003; pp. 215–257. [Google Scholar]

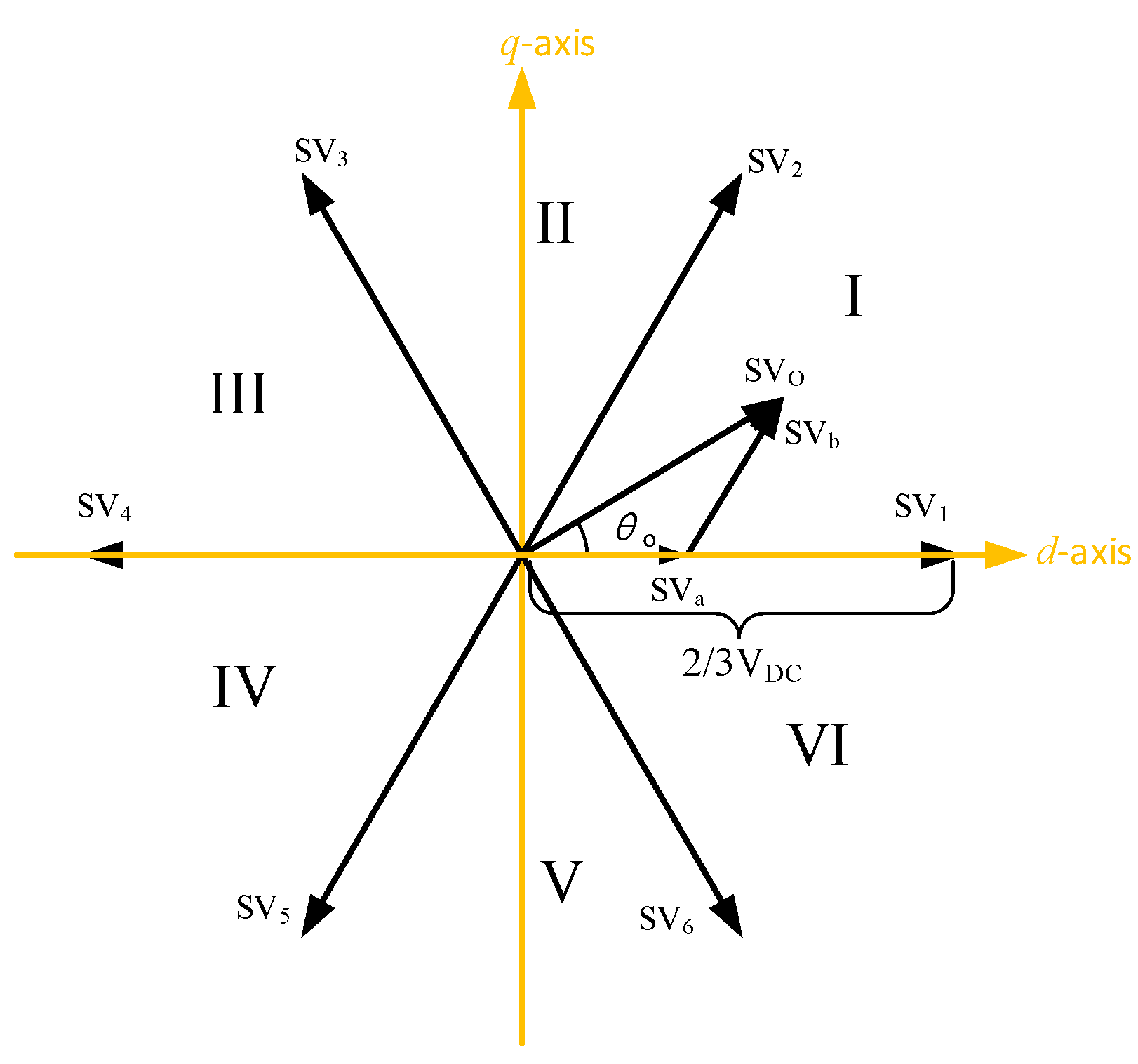
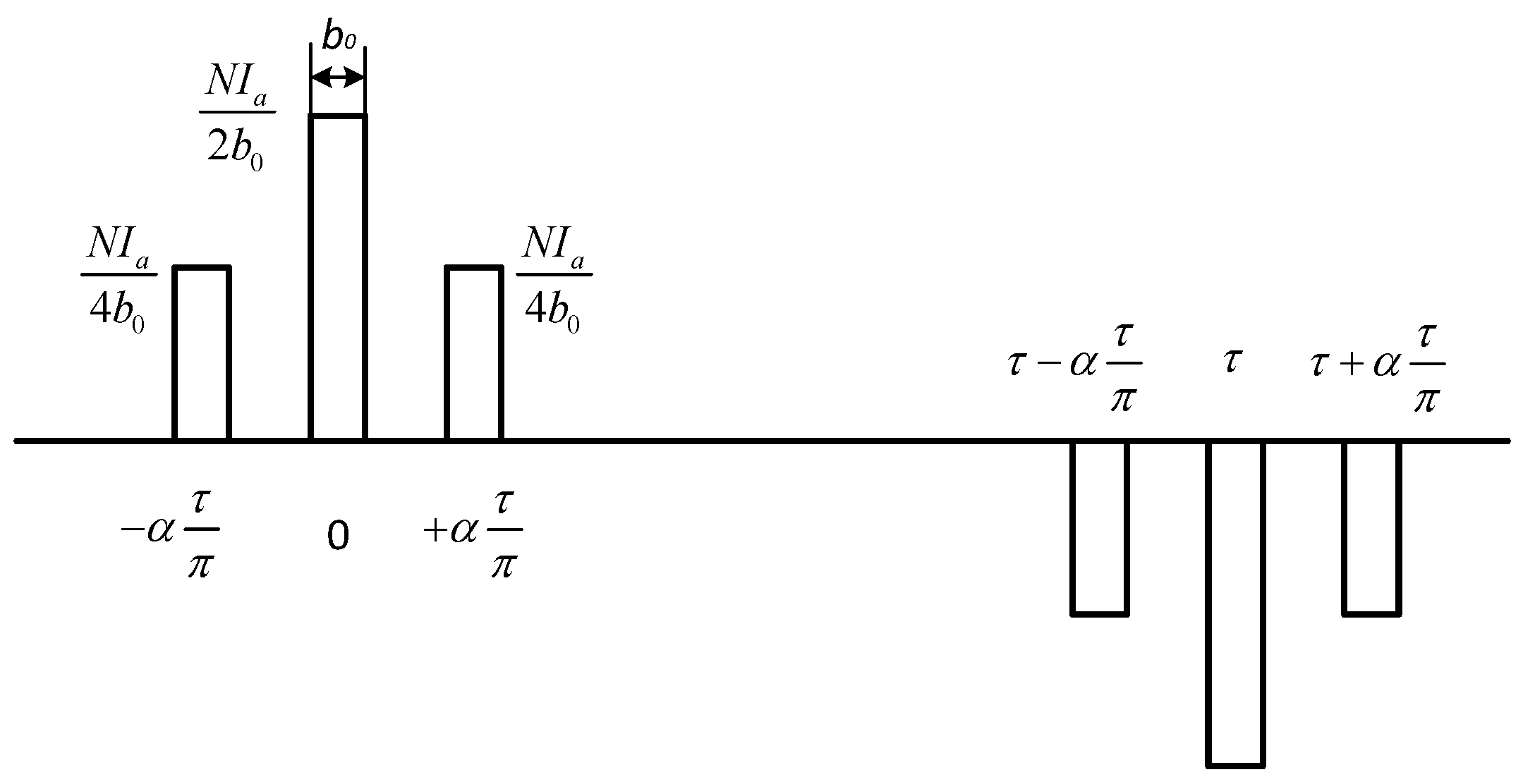


| θo = ωot | Active Space Vectors | Effect Time Span |
|---|---|---|
| 0 < θo ≤ π/3 | ||
| π/3 < θo ≤ 2π/3 | ||
| 2π/3 < θo ≤ π | ||
| π < θo ≤ 4π/3 | ||
| 4π/3 < θo ≤ 5π/3 | ||
| 5π/3 < θo ≤ 2π |
| θo = ωot | fA(θo) |
|---|---|
| 0 < θo ≤ π/3 | |
| π/3 < θo ≤ 2π/3 | |
| 2π/3 < θo ≤ π | |
| π < θo ≤ 4π/3 | |
| 4π/3 < θo ≤ 5π/3 | |
| 5π/3 < θo ≤ 2π |
| i | ys(i) | ye(i) | xr(i) | xf(i) |
|---|---|---|---|---|
| 1 | 0 | π/3 | ||
| 2 | π/3 | 2π/3 | ||
| 3 | 2π/3 | π | ||
| 4 | π | 4π/3 | ||
| 5 | 4π/3 | 5π/3 | ||
| 6 | 5π/3 | 2π |
| Parameter | Value |
|---|---|
| Poles/slots | 2/12 |
| Stator inner diameter | 36 mm |
| Rotor outer diameter | 30.2 mm |
| Air gap flux density | 0.4 T |
| Effective length | 50 mm |
| Magnet material | N40EH |
| Phase inductance | 48 μH |
| Parameter | Value |
|---|---|
| Width of slot opening | 0.8 mm |
| Winding turns of a single phase | 12 |
| Electrical angle between adjacent slot opening | 30° |
| Pole pitch | 56.6 mm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, L.; Li, L.; Guo, Q.; Yang, R.; Du, P. A Novel Rotor Eddy Current Loss Estimation Method for Permanent Magnet Synchronous Machines with Small Inductance and a Conductive Rotor Sleeve. Energies 2019, 12, 3760. https://doi.org/10.3390/en12193760
Pei L, Li L, Guo Q, Yang R, Du P. A Novel Rotor Eddy Current Loss Estimation Method for Permanent Magnet Synchronous Machines with Small Inductance and a Conductive Rotor Sleeve. Energies. 2019; 12(19):3760. https://doi.org/10.3390/en12193760
Chicago/Turabian StylePei, Le, Liyi Li, Qingbo Guo, Rui Yang, and Pengcheng Du. 2019. "A Novel Rotor Eddy Current Loss Estimation Method for Permanent Magnet Synchronous Machines with Small Inductance and a Conductive Rotor Sleeve" Energies 12, no. 19: 3760. https://doi.org/10.3390/en12193760
APA StylePei, L., Li, L., Guo, Q., Yang, R., & Du, P. (2019). A Novel Rotor Eddy Current Loss Estimation Method for Permanent Magnet Synchronous Machines with Small Inductance and a Conductive Rotor Sleeve. Energies, 12(19), 3760. https://doi.org/10.3390/en12193760





