Fractional Calculus-Based Processing for Feature Extraction in Harmonic-Polluted Fault Monitoring Systems
Abstract
1. Introduction
2. Foundations
2.1. Induction Motor Faults
- Bearing fault due to the thermal and electrical burden, insufficient lubrication, etc.;
- Air–gap eccentricity fault caused by a significant variation in the rotor-to-stator spacing; and
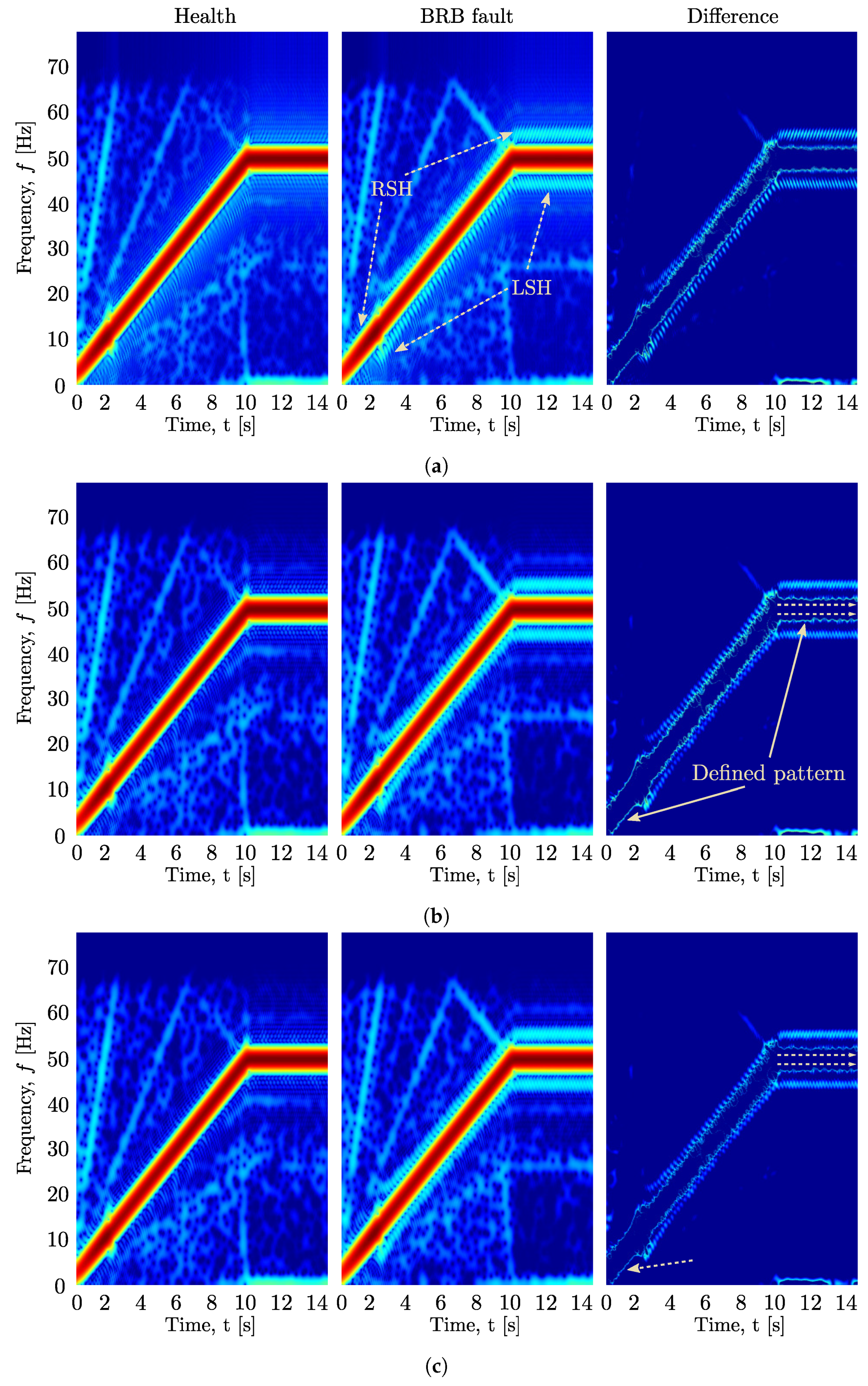
- Broken Rotor Bars (BRBs) fault mainly produced by mechanical, thermal, magnetic, electrical, and environmental stresses.
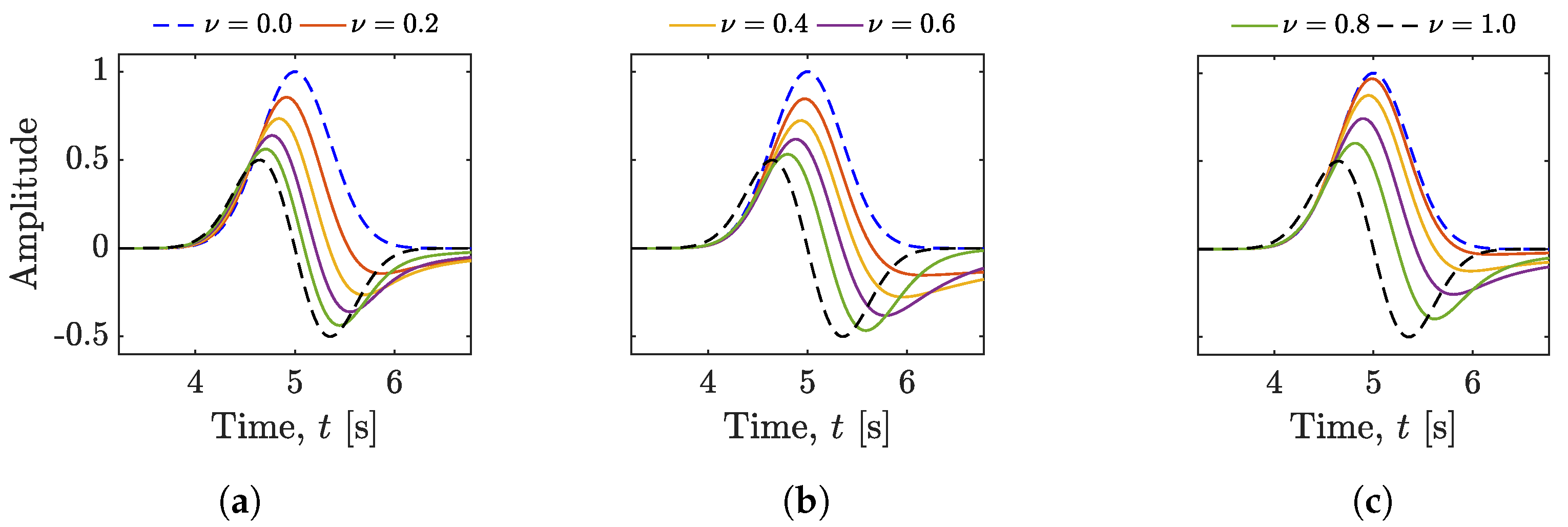
2.2. Fractional Gaussian Windows
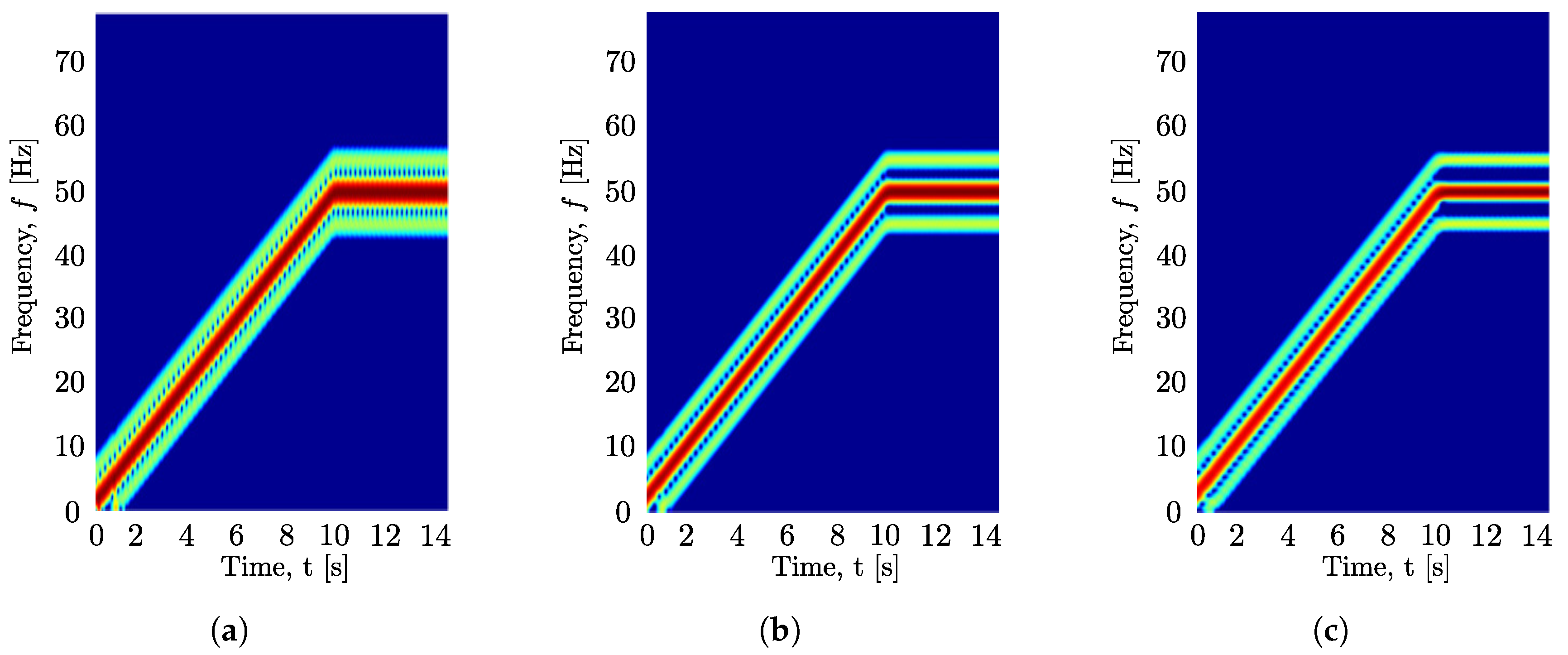
2.3. Windowed Fourier Transform
3. Methodology
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Siddique, A.; Yadava, G.; Singh, B. A review of stator fault monitoring techniques of induction motors. IEEE Trans. Energy Convers. 2005, 20, 106–114. [Google Scholar] [CrossRef]
- Mehrjou, M.R.; Mariun, N.; Marhaban, M.H.; Misron, N. Rotor fault condition monitoring techniques for squirrel-cage induction machine—A review. Mech. Syst. Signal Process. 2011, 25, 2827–2848. [Google Scholar] [CrossRef]
- Hassan, O.E.; Amer, M.; Abdelsalam, A.K.; Williams, B.W. Induction motor broken rotor bar fault detection techniques based on fault signature analysis—A review. IET Electr. Power Appl. 2018, 12, 895–907. [Google Scholar] [CrossRef]
- Saddam, B.; Ahmed, B.S.; Aissa, A.; Ali, T. Squirrel Cage Induction Motor under Stator and Rotor Bars Faults Modeling and Diagnosis. In Proceedings of the International Conference on Communications and Electrical Engineering (ICCEE), El Oued, Algeria, 17–18 December 2018; pp. 1–6. [Google Scholar]
- Liu, Y.; Bazzi, A.M. A review and comparison of fault detection and diagnosis methods for squirrel-cage induction motors: State of the art. ISA Trans. 2017, 70, 400–409. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Grant, B.; Defour, R.; Sharma, C.; Bahadoorsingh, S. A review of induction motor fault modeling. Electr. Power Syst. Res. 2016, 133, 191–197. [Google Scholar] [CrossRef]
- Martin-Diaz, I.; Morinigo-Sotelo, D.; Duque-Perez, O.; Arredondo-Delgado, P.A.; Camarena-Martinez, D.; Romero-Troncoso, R.J. Analysis of various inverters feeding induction motors with incipient rotor fault using high-resolution spectral analysis. Electr. Power Syst. Res. 2017, 152, 18–26. [Google Scholar] [CrossRef]
- Demenko, A.; Kołodziejek, P.; Bogalecka, E. Broken rotor bar impact on sensorless control of induction machine. Int. J. Comput. Math. Electr. Electron. Eng. 2009, 28, 540–555. [Google Scholar]
- Bednarz, S. Rotor fault compensation and detection in a sensorless induction motor drive. Power Electron. Drives 2017, 2, 71–80. [Google Scholar]
- Iqbal, A.; Husain, M.A. MRAS based Sensorless Control of Induction Motor based on Rotor Flux. In Proceedings of the International Conference on Computational and Characterization Techniques in Engineering & Sciences (CCTES), Lucknow, India, 14–15 September 2018; pp. 152–155. [Google Scholar]
- Gritli, Y.; Zarri, L.; Rossi, C.; Filippetti, F.; Capolino, G.A.; Casadei, D. Advanced diagnosis of electrical faults in wound-rotor induction machines. IEEE Trans. Ind. Electron. 2012, 60, 4012–4024. [Google Scholar] [CrossRef]
- Saidi, L.; Fnaiech, F.; Henao, H.; Capolino, G.; Cirrincione, G. Diagnosis of broken-bars fault in induction machines using higher order spectral analysis. ISA Trans. 2013, 52, 140–148. [Google Scholar] [CrossRef]
- Quiroz, J.C.; Mariun, N.; Mehrjou, M.R.; Izadi, M.; Misron, N.; Radzi, M.A.M. Fault detection of broken rotor bar in LS-PMSM using random forests. Measurement 2018, 116, 273–280. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Dybkowski, M.; Kowalski, C.T. Rotor fault analysis in the sensorless field oriented controlled induction motor drive. Autom. Časopis Autom. Mjer. Elektron. Računarstvo I Komun. 2010, 51, 149–156. [Google Scholar] [CrossRef]
- Zając, M.; Sułowicz, M. Wavelet detectors for extraction of characteristic features of induction motor rotor faults. In Proceedings of the International Conference on Signals and Electronic Systems (ICSES), Krakow, Poland, 5–7 September 2016; pp. 212–218. [Google Scholar]
- Lamim Filho, P.; Baccarini, L.; Batista, F.; Alves, D. Broken rotor bar detection using empirical demodulation and wavelet transform: Suitable for industrial application. Electr. Eng. 2018, 100, 2253–2260. [Google Scholar] [CrossRef]
- Skowron, M.; Wolkiewicz, M.; Orlowska-Kowalska, T.; Kowalski, C.T. Application of Self-Organizing Neural Networks to Electrical Fault Classification in Induction Motors. Appl. Sci. 2019, 9, 616. [Google Scholar] [CrossRef]
- Orłowska-Kowalska, T.; Kowalski, C.T.; Dybkowski, M. Fault-Diagnosis and Fault-Tolerant-Control in Industrial Processes and Electrical Drives. In Advanced Control of Electrical Drives and Power Electronic Converters; Springer: Cham, Switzerland, 2017; pp. 101–120. [Google Scholar]
- Martin-Diaz, I.; Morinigo-Sotelo, D.; Duque-Perez, O.; Romero-Troncoso, R.D.J. An Experimental Comparative Evaluation of Machine Learning Techniques for Motor Fault Diagnosis under Various Operating Conditions. IEEE Trans. Ind. Appl. 2018, 54. [Google Scholar] [CrossRef]
- Razik, H.; de Rossiter Corrêa, M.B.; da Silva, E.R.C. A novel monitoring of load level and broken bar fault severity applied to squirrel-cage induction motors using a genetic algorithm. IEEE Trans. Ind. Electron. 2009, 56, 4615–4626. [Google Scholar] [CrossRef]
- Bellini, A.; Yazidi, A.; Filippetti, F.; Rossi, C.; Capolino, G.A. High frequency resolution techniques for rotor fault detection of induction machines. IEEE Trans. Ind. Electron. 2008, 55, 4200–4209. [Google Scholar] [CrossRef]
- Kowalski, C.T.; Wolkiewicz, M. Converter-fed induction motor diagnosis using instantaneous electromagnetic torque and power signals. In Proceedings of the IEEE Eurocon 2009, St. Petersburg, Russia, 18–23 May 2009; pp. 811–816. [Google Scholar]
- Benbouzid, M.E.H.; Kliman, G.B. What stator current processing-based technique to use for induction motor rotor faults diagnosis? IEEE Trans. Energy Convers. 2003, 18, 238–244. [Google Scholar] [CrossRef]
- Neild, S.; McFadden, P.; Williams, M. A review of time-frequency methods for structural vibration analysis. Eng. Struct. 2003, 25, 713–728. [Google Scholar] [CrossRef]
- Yang, Y.; Peng, Z.; Zhang, W.; Meng, G. Parameterised time-frequency analysis methods and their engineering applications: A review of recent advances. Mech. Syst. Signal. Process. 2019, 119, 182–221. [Google Scholar] [CrossRef]
- Yang, S.; Qin, H.; Liang, X.; Gulliver, T. Clutter Elimination and Harmonic Suppression of Non-Stationary Life Signs for Long-Range and Through-Wall Human Subject Detection Using Spectral Kurtosis Analysis (SKA)-Based Windowed Fourier Transform (WFT) Method. Appl. Sci. 2019, 9, 355. [Google Scholar] [CrossRef]
- Grédiac, M.; Blaysat, B.; Sur, F. Extracting Displacement and Strain Fields from Checkerboard Images with the Localized Spectrum Analysis. Exp. Mech. 2019, 59, 207–218. [Google Scholar] [CrossRef]
- Delgado-Arredondo, P.A.; Garcia-Perez, A.; Morinigo-Sotelo, D.; Osornio-Rios, R.A.; Avina-Cervantes, J.G.; Rostro-Gonzalez, H.; Romero-Troncoso, R.D.J. Comparative Study of Time-Frequency Decomposition Techniques for Fault Detection in Induction Motors Using Vibration Analysis during Startup Transient. Shock Vib. 2015, 2015, 1–14. [Google Scholar] [CrossRef]
- Lima, M.F.M.; Machado, J.A.T.; Crisostomo, M. Windowed Fourier Transform of Experimental Robotic Signals with Fractional Behavior. In Proceedings of the IEEE International Conference on Computational Cybernetics, Budapest, Hungary, 20–22 August 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Lima, M.F.M.; Machado, J.A.T. A.T. A Statistical Approach for Tuning the Windowed Fourier Transform. In Mathematical Methods in Engineering; Fonseca Ferreira, N.M., Tenreiro Machado, J.A., Eds.; Springer: Dordrecht, The Netherlands, 2014; Volume 1, pp. 269–281. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus; World Scientific Publishing Company: Singapore, 2016. [Google Scholar]
- Hristov, J. Steady-state heat conduction in a medium with spatial non-singular fading memory: Derivation of Caputo–Fabrizio space–fractional derivative from Cattaneo concept with Jeffrey’s Kernel and analytical solutions. Therm. Sci. 2017, 21, 827–839. [Google Scholar] [CrossRef]
- Capelas de Oliveira, E.; Tenreiro Machado, J. A review of definitions for fractional derivatives and integrals. Math. Prob. Eng. 2014, 2014, 238459. [Google Scholar] [CrossRef]
- Uchaikin, V. Fractional Derivatives for Physicists and Engineers; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Cruz-Duarte, J.M.; Rosales-Garcia, J.; Correa-Cely, C.R.; Garcia-Perez, A.; Avina-Cervantes, J.G. A closed form expression for the Gaussian-based Caputo–Fabrizio fractional derivative for signal processing applications. Commun. Nonlinear Sci. Numer. Simul. 2018, 61, 138–148. [Google Scholar] [CrossRef]
- Kochubei, A.N. General Fractional Calculus, Evolution Equations, and Renewal Processes. Integral Equ. Oper. Theory 2011, 71, 583–600. [Google Scholar] [CrossRef]
- Tarasov, V.E. No nonlocality. No fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2018, 62, 157–163. [Google Scholar] [CrossRef]
- Ortigueira, M.; Tenreiro Machado, J. A critical analysis of the Caputo–Fabrizio operator. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 608–611. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T. What is a fractional derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- Algahtani, O.J.J. Comparing the Atangana–Baleanu and Caputo–Fabrizio derivative with fractional order: Allen Cahn model. Chaos Solitons Fractals 2016, 89, 552–559. [Google Scholar] [CrossRef]
- Liu, Z.; Li, X. A novel second order finite difference discrete scheme for fractal mobile/immobile transport model based on equivalent transformative Caputo formulation. arXiv 2017, arXiv:1701.01283. [Google Scholar]
- Duarte Ortigueira, M. Fractional Calculus for Scientists and Engineers; Springer: Berlin/Heidelberg, Germany, 2011; p. 159. [Google Scholar]
- Atangana, A.; Alqahtani, R. Numerical approximation of the space-time Caputo–Fabrizio fractional derivative and application to groundwater pollution equation. Adv. Differ. Equ. 2016, 2016. [Google Scholar] [CrossRef]
- Losada, J.; Nieto, J.J. Properties of a New Fractional Derivative without Singular Kernel. Prog. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar] [CrossRef]
- Henao, H.; Capolino, G.A.; Fernandez-Cabanas, M.; Filippetti, F.; Bruzzese, C.; Strangas, E.; Pusca, R.; Estima, J.; Riera-Guasp, M.; Hedayati-Kia, S. Trends in Fault Diagnosis for Electrical Machines: A Review of Diagnostic Techniques. IEEE Ind. Electron. Mag. 2014, 8, 31–42. [Google Scholar] [CrossRef]
- Schwab, J.; Pereverzyev, S.; Haltmeier, M. A Galerkin least squares approach for photoacoustic tomography. SIAM J. Numer. Anal. 2016, 56, 160–184. [Google Scholar] [CrossRef]
- Boashash, B. Time-Frequency Signal Analysis and Processing: A Comprehensive Reference, 2nd ed.; Academic Press: London, UK, 2016. [Google Scholar]

| Parameter (Unit) | Value | Parameter (Unit) | Value |
|---|---|---|---|
| (A/A) | 1.0 | (s) | 5.0 |
| (A/A) | 0.3 | (s) | 15 |
| (Hz) | 0.0 | (ms) | 6.4 |
| (Hz) | 50 | (s) | 10 |
| (Hz) | 5.0 | SNR (dB) | 25 |
| Parameter | Set of Values |
|---|---|
| 80, 100, 120, 150, 180, and 220 | |
| 0.1, 0.2, 0.3, ⋯, 1.0 | |
| 0.01, 0.02, 0.03, ⋯, 0.90 |
| Feature | Fractional Gaussian Windows | Traditional Windows | ||||
|---|---|---|---|---|---|---|
| CD | CF | ABC | Rectangular | Hanning | Hamming | |
| Mean | 5.0 | 5.0 | 5.0 | – | – | – |
| Standard Deviation | 0.3 | 0.2 | 0.3 | – | – | – |
| Non-integer order | 0.03 | 0.015 | 0.1 | – | – | – |
| Main-lobe width | 21.5 | 2.15 | 21.5 | 11.7 | 18.6 | 16.6 |
| Side-lobe Attenuation | −51.3 | −58.9 | −58.3 | −13.3 | −31.5 | −42.6 |
| Leakage factor | 0.00 | 0.00 | 0.00 | 9.37 | 0.05 | 0.04 |
| –metric | 1.624 | 1.631 | 1.633 | 0.615 | 1.358 | 1.220 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murcia-Sepúlveda, N.; Cruz-Duarte, J.M.; Martin-Diaz, I.; Garcia-Perez, A.; Rosales-García, J.J.; Avina-Cervantes, J.G.; Correa-Cely, C.R. Fractional Calculus-Based Processing for Feature Extraction in Harmonic-Polluted Fault Monitoring Systems. Energies 2019, 12, 3736. https://doi.org/10.3390/en12193736
Murcia-Sepúlveda N, Cruz-Duarte JM, Martin-Diaz I, Garcia-Perez A, Rosales-García JJ, Avina-Cervantes JG, Correa-Cely CR. Fractional Calculus-Based Processing for Feature Extraction in Harmonic-Polluted Fault Monitoring Systems. Energies. 2019; 12(19):3736. https://doi.org/10.3390/en12193736
Chicago/Turabian StyleMurcia-Sepúlveda, Nathaly, Jorge M. Cruz-Duarte, Ignacio Martin-Diaz, Arturo Garcia-Perez, J. Juan Rosales-García, Juan Gabriel Avina-Cervantes, and Carlos Rodrigo Correa-Cely. 2019. "Fractional Calculus-Based Processing for Feature Extraction in Harmonic-Polluted Fault Monitoring Systems" Energies 12, no. 19: 3736. https://doi.org/10.3390/en12193736
APA StyleMurcia-Sepúlveda, N., Cruz-Duarte, J. M., Martin-Diaz, I., Garcia-Perez, A., Rosales-García, J. J., Avina-Cervantes, J. G., & Correa-Cely, C. R. (2019). Fractional Calculus-Based Processing for Feature Extraction in Harmonic-Polluted Fault Monitoring Systems. Energies, 12(19), 3736. https://doi.org/10.3390/en12193736







