Evaluating the Potential of Hosting Capacity Enhancement Using Integrated Grid Planning modeling Methods

Abstract

Connection of a significant amount of distributed generation, such as solar photovoltaic (PV) capacity, may lead to problems in distribution networks due to violations of distribution network hosting capacity (HC) limits. HC enhancement techniques, such as energy storage, could increase the allowable PV penetration level in the distribution network, reducing the need for transmission and large-scale generation expansion. However, current approaches for transmission and generation expansion planning do not account for distribution network HC limits. As a consequence, it is hard to quantify the impact and benefits of HC enhancement in the context of long-term grid expansion planning. This paper presents a novel integrated planning approach, combining a two-stage transmission and generation expansion planning model with a distribution network hosting capacity assessment, which allows for inclusion of detailed distribution network constraints We test this method on a stylized representation of the Malaysian grid. Our results show that distribution constraints have a significant impact on optimal transmission expansion plans and significantly increase overall system costs. HC enhancement in the form of battery storage does not significantly mitigate this but does lead to a cost decrease regardless of distribution network constraints. We also show how our approach can identify the key interactions between transmission and distribution networks in systems with high levels of renewable and storage technologies. In particular, HC enhancement with battery storage can act as a substitute or complement to line investment, depending on the renewable energy penetration, the storage location and the level of coordination in the network.

1. Introduction

Renewable generation capacity is growing significantly as a result of technology advancement and policies that aim to reduce the $\left(C{O}_2\right)$ emissions, including carbon prices and renewable targets. Solar photovoltaic (PV) generation capacity has increased particularly quickly and in many places, it is now among the cheapest forms of electricity generation. Solar PV capacity comes in different forms. Large solar photovoltaic (LPV) plants may be connected to transmission networks, as other types of renewable capacity, including wind, tend to be. However, in most markets, a large fraction of solar PV capacity is connected to distribution networks (distributed solar photovoltaic, DPV), beyond the transmission system operator’s control. This DPV capacity can cause significant problems in distribution networks, including reverse power flows, voltage excursions and frequency issues. Distribution networks, therefore, have a limited hosting capacity (HC) for renewable capacity. Hosting capacity (HC) is the network’s capacity to integrate distributed energy resources (DER) without compromising the overall network performance limits [1,2,3].

This presents a challenge to grid planners, operators and investors in other types of generation capacity, which will only increase as the amount of DPV grows. However, current approaches for high-level transmission and generation expansion planning do not generally account for distribution network constraints [4,5,6,7,8,9]. As a consequence, high-level planning results likely overstate the amount of DPV that can be safely integrated into distribution networks without significant infrastructure expansion or underestimate generation expansion costs [10]. Moreover, we do not fully understand how distribution and transmission-level investments interact.

Energy storage presents a similar challenge. Storage can play a vital role in accommodating variable renewable generation into the electricity system [5,11,12,13,14,15] and therefore act as HC enhancement that enables various applications in demand-side management and flexible loads [16]. But, like solar PV, a large fraction of storage capacity will likely be connected to distribution networks and is therefore invisible to transmission system operators and beyond the scope of high-level expansion planning models.

In light of these issues, a new modeling framework for optimizing system expansion is needed, which must be able to jointly model transmission and distribution networks; in the latter, detailed distribution grid operating constraints should be included to accurately model distribution network issues resulting from DPV and storage installations. Such a modeling framework would need to be able to identify how congestion in distribution and transmission networks interacts and how storage or other HC enhancement techniques at different levels affect infrastructure planning.

There is extensive literature on integrated modeling approaches that jointly consider transmission and distribution systems operations. However, applications of these models to grid expansion planning are limited [17,18,19,20]. Joint modeling of transmission and distribution networks for planning purposes is a significant challenge, as it requires a large geographic scale, a long time horizon and a large amount of detail. Distribution network constraints are nonlinear, so the framework proposed above would be a large-scale nonlinear multi-stage optimization problem, which would be extremely computationally expensive for large networks. Inclusion of different technologies at different levels, including storage, in such a non-linear model, would only increase its complexity.

In this paper, we therefore simply the problem by breaking it down into two components—a two-stage optimization transmission and generation expansion model and a detailed distribution network hosting capacity (HC) assessment. Both of these models are already in use and are not highly computationally expensive. We solve these two models iteratively to heuristically find a fixed point. Although this does not guarantee convergence, we find that convergence is achieved in less than ten iterations in all cases we examine and multi-starts do not produce different fixed points. We apply this model to a stylized representation of the Malaysian grid, which is expected to have to integrate a large amount of DPV capacity over the coming decade.

We find that, first of all, the inclusion of distribution network constraints significantly changes optimal transmission and generation capacities, not just in distribution networks but also at the transmission level. We show that interactions between distribution and transmission networks are important and not always straightforward. In particular, at lower solar penetration levels, distributed small-scale storage substitutes for line investment, while at higher solar penetration levels, small-scale storage instead complements line investment. Distribution network hosting capacity enhancement techniques, using distribution connected storage, can significantly reduce the overall costs of meeting a renewable target and increase distributed solar PV (DPV) penetration in the distribution network. However, the correct mix of distribution-connected and transmission-connected storage is crucial. Finally, this paper demonstrates that combined transmission and distribution network modeling is possible and practical to evaluate the potential whole-system benefits of HC enhancement to achieve renewable objectives.

The rest of the paper is organized as follows. In Section 2, we propose an integrated grid expansion planning approach that accounts for distribution network constraints and we discuss the assumptions and data sources used in the case study. Section 3 presents results and analysis. Section 4 discusses limitations, suggestions for future work and conclusions.

2. Materials and Methods

2.1. Model Overview

The nomenclature for our model is listed in

Table 1. Nomenclature.

	Set and indices		Parameters
L	Corridor, l	$C{Y}_{ek}$	Capital cost of new generation k ($/MW)
$L^D$	Corridor, l connected to distribution node, $N^D$	$C{X}_e$	Transmission investment cost ($/MW/km)
N	Nodes, n	$C{V}_{ek}$	Generation cost type k (USD/MWh)
K	Generator types, k	$C{Z}_{eb}$	Capital cost of new battery storage b($/MW)
E	Model stages, e	$C{D}_{eb}$	ESS discharge cost type b (USD/MWh)
T	Years, t	$C{P}_e$	Carbon price ($/t)
P	Time block (hour), p	i	Discount rate (1/yr)
$N^D$	Distribution nodes	N	Model horizon (hours)
$K^C$	Conventional generator types	$Q_{enp}$	Electricity demand at node n (MW)
$K^S$	Solar PV generator	${\gamma }_{el}$	Susceptance of corridor l
$K^{DS}$	Distributed solar PV generator	$E_k$	Carbon emission by plant type k (t/MWh)
B	Battery storage, b	$X_l$	Initial transmission capacity (MW)
$B^{DS}$	Domestic battery storage, b	$Z_l$	Initial battery capacity (MW)
	Variables	$Y_{nk}$	Initial generators at node n (MW)
$t{c}_e$	Total cost at stage e ($)	$L{F}_k$	Load factor for each generator type k
$x_{el}$	New transmission investment $e=1,2$ (MW)	$S{P}_p$	Hourly solar pattern (per unit)
$y_{enk}$	Capacity of new plant stage $e=1,2$ (MW)	$R{E}_e$	Renewable target (%)
$g_{enpk}$	Generation of plant stage $e=2,3$ (MW)	$S{M}_n$	Allowed DPV (%) at node $n=N^D$
$g_{enpk}^S$	Generation of Solar plant stage $e=2,3$ (MW)	$S{B}_n$	Allowed ESS (%) at node $n=N^D$
$f_{elp}$	Reactive power flow stage $e=2,3$ (MW)	$R{L}_k$	Ramping limit by technology, k (MW/hour)
${\theta }_{np}$	Voltage angle between nodes (radian)	$R{T}_b$	Roundtrip efficiency of battery storage type, b
$ns{e}_{enp}$	Energy not supplied (load shed) at node n, period e (MW)	$H_b$	Energy capacity of battery storage b
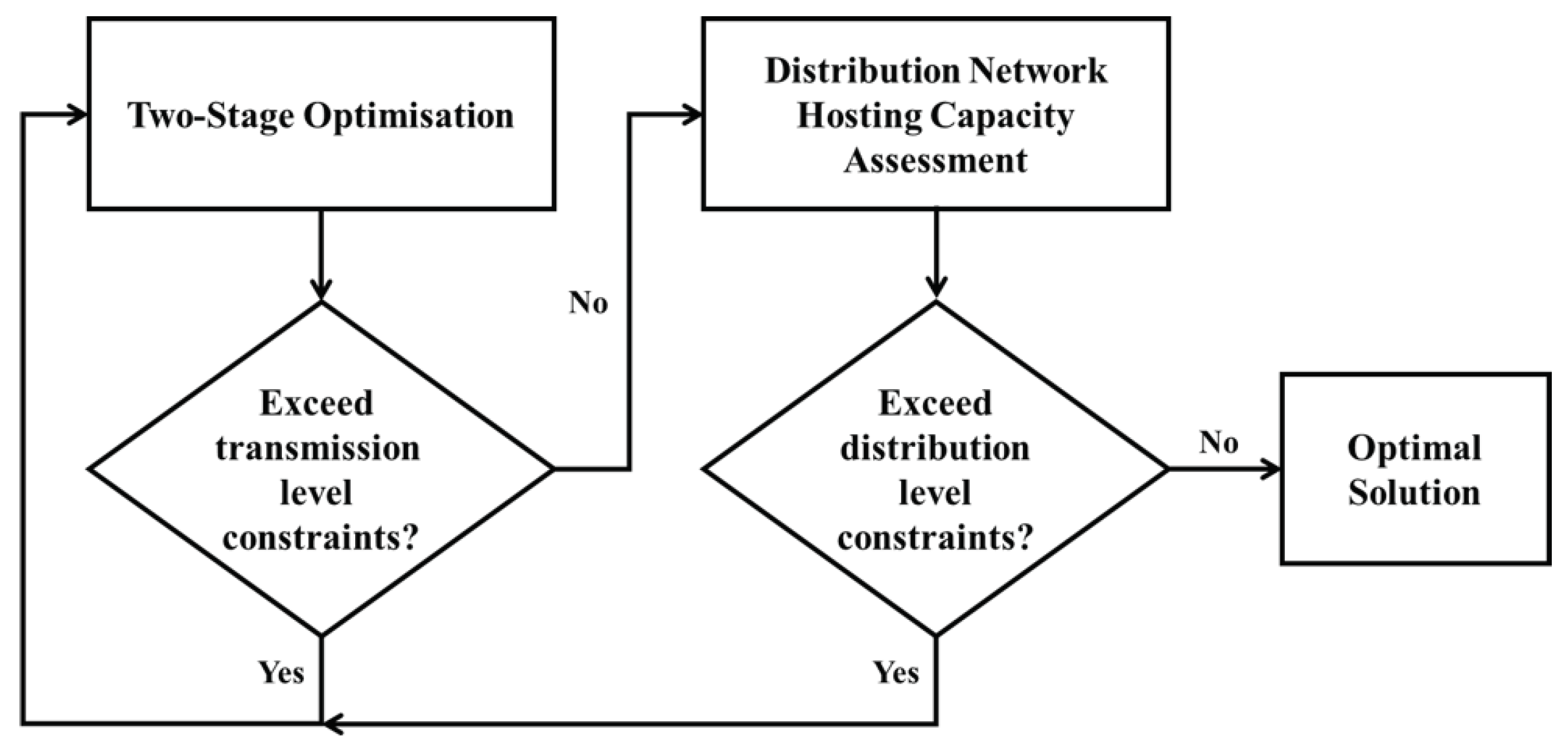
$s_{enpk}$	Solar energy spillage (MW)	$V_n$	Voltage limits at distribution node $n=N^D$

. The model combines a high-level two-stage transmission and generation expansion planning model with a distribution network hosting (HC) capacity assessment. First, we determine the optimal level of transmission and generation expansion considering only transmission-level constraints. This optimal solution includes the amount of distributed generation and distribution-connected storage at each bus. We then assess the viability of the proposed distributed solar PV (DPV) capacity, considering detailed distribution network constraints, including reverse power flow and voltage constraints. If these constraints are violated at one or more buses, the upper-level model is re-run with tightened constraints on the allowed maximum DPV capacity in these locations. We iterate between the two models until we find a fixed point where all transmission and distribution network constraints are satisfied, as shown schematically in Figure 1.

The upper-level transmission and generation planning model is an optimization model that uses a linearized DC approximation of power flows, while the distribution network HC assessment is performed using a non-linear steady state power flow model. We introduce a set of corridors between each transmission node and a corresponding distribution network to link the two. To evaluate the effect of an increasing solar PV penetration, we classify solar PV into two technologies: dispatchable large-scale solar (LPV), which is connected to the transmission network and dispatched together with all other power plants and distributed solar (DPV) which is connected to the distribution network. DPV is non-dispatchable and effectively reduces energy demand. In addition, we include three types of battery storage; grid-scale storage which is directly connected to the transmission network, controllable Distribution Service Operator (DSO) operated storage and uncontrollable distribution-connected domestic storage. We conduct a sensitivity analysis for different configurations of battery types in the network.

2.2. Timeline and Model Objective

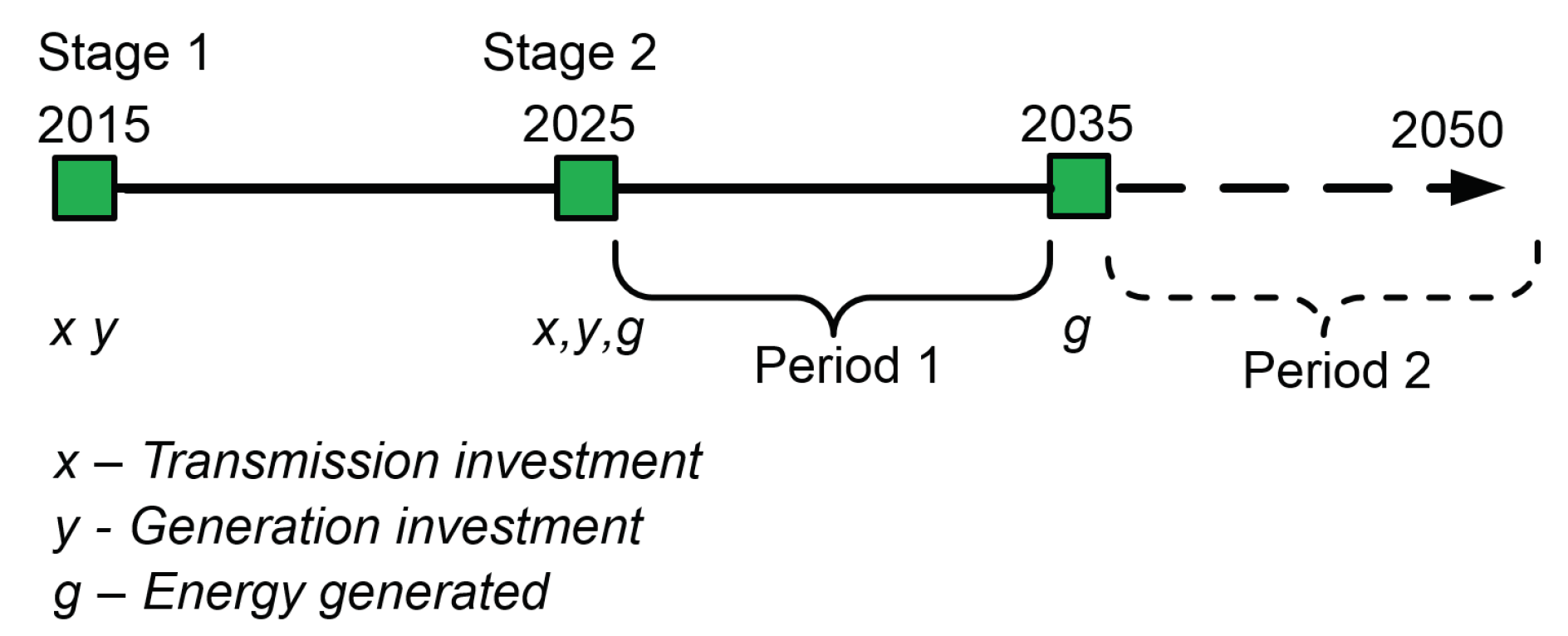
Our model assumes that investment and operational decisions are taken in two periods, followed by a final set of operational decisions. Figure 2 gives an overview of the model timeline. In 2015, the model decides on transmission and generation capacity investment, which is assumed to become on-line at the start of 2025. (Alternatively, generation investment can be seen as a decision by separate generation investors in a perfectly competitive market). The second set of investment decisions takes place in the year 2025, with new assets coming into operation in the year 2035. Note that, after the second set of decisions in 2025, we assume that there is no further investment. To avoid end-of-timeline effects, we model dispatch decisions for the next 25 years until 2050, such that the total model horizon is 35 years.

The model minimizes the total expected cost of grid investment and operations taking into account flow constraints on all lines, maximum capacity constraints, resource limitations and a solar generation target. In this paper, the total expected cost includes capital expenses for new transmission, generation and battery storage investment, as well as operational costs including generation costs, battery losses and a carbon tax. The overall model objective function is formulated in (1) and consist of total cost for each stage, e, defined in (2)–(4).

$$min\left\{t{c}_1+{\left(\frac{1}{1+i}\right)}^{10}t{c}_2+{\left(\frac{1}{1+i}\right)}^{10}t{c}_3\right\}$$

(1)

where

$$t{c}_1=\sum C{X}_1{x}_1+\sum _{nk}C{Y}_{1k}{y}_{1nk}+\sum _{nb}C{Z}_{1b}{z}_{1nb}$$

(2)

$$\begin{array}{cc}\hfill t{c}_2=\sum C{X}_2{x}_2+\sum _{nk}C{Y}_{2k}{x}_{2nk}& +\sum _{nb}C{Z}_{2b}{z}_{1nb}\hfill \\ & +\frac{8760}{N}\sum _{t=1}^{10}{\left(\frac{1}{1+i}\right)}^{t-1}\sum _{npk}(C{V}_{2k}+E_{k}C{P}_2)g_{2npk}+\sum _{nkp}C{D}_{2b}{r}_{2npb}^d\hfill \end{array}$$

(3)

$$t{c}_3=\frac{8760}{N}\sum _{t=1}^{15}{\left(\frac{1}{1+i}\right)}^{t-1}\sum _{npk}(C{V}_{3k}+E_{sk}C{P}_3)g_{3npk}+\sum _{nkp}C{D}_{3b}{r}_{3npb}^d$$

(4)

2.3. Model Constraints

2.3.1. Transmission Network and Generators

Linearized DC power flow constraints are defined in (5) and (6). Each transmission line is represented by a single bi-directional corridor l. The active power flow on each corridor is limited to the total available capacity in (7) and (8). The voltage angle is set to zero for one slack bus such that there is a uniquely defined solution. Transmission and generation investments cannot be negative.

$$\begin{array}{c}\hfill \sum _{k\notin K^s}{g}_{enpk}+\sum _{k\in K^s}(g_{enpk}-s{p}_{enpk})+\sum _{b\in B}{r}_{enpb}^d-\sum _{l}f{}_{ep}-Q_{enp}-\sum _{b\in B}{r}_{enpb}^c+ns{e}_{enp}=0\end{array}$$

(5)

$$f_{epl}-{\gamma }_{el}({\theta }_{enp}-{\theta }_{emp})=0$$

(6)

$$-(X_l+x_{1l})\le f_{2lp}\le (X_l+x_{1l})\forall l,p$$

(7)

$$-(X_l+x_{1l}+x_{2lp})\le f_{3lp}\le (X_l+x_{1l}+x_{2lp})\forall l,p$$

(8)

The output of conventional generators is constrained simply to the amount of available capacity, which is derated using the generators’ average availability factor $LF$ in (9) and (10).

$$0\le g_{2npk}\le (Y_{nk}+y_{1nk})LF{}_k\forall n,p,k\in K^C$$

(9)

$$0\le g_{3npk}\le (Y_{nk}+y_{1nk}+y_{2nk})L{F}_k\forall n,p,k\in K^C$$

(10)

We include a security or reserve margin in (11) and (12) to ensure enough reserve capacity is installed; this is a common approximation of more detailed security constraints which would drastically increase the size of the model without yielding significant additional insight.

$$\sum _{nk}(Y_{nk}+y_{1nf})\ge \sum Q_{2np}(1+RM)\forall s,p=peak$$

(11)

$$\sum _{nk}(Y_{nk}+y_{1nf}+y_{2nf})\ge \sum Q_{3np=peak}(1+RM)\forall s,p=peak$$

(12)

In addition, to properly evaluate the effect of intermittent PV generators generation, ramping limits (13), (14) are considered. Energy spillage (15) is allowed and load shedding (16) at each bus, at a high value of lost load, is included to maintain feasibility.

$$g_{enpk}-g_{en,p-1,k}\le RL{}_k\forall e,p,n,k$$

(13)

$$g_{en,p-1k}-g_{en,p-1,k}\le RL{}_k\forall e,p,n,k$$

(14)

$$0\le s{p}_{enpk}\le g_{enpk}\forall e,p,n,k\in K^s$$

(15)

$$0\le ns{e}_{enp}\le Q_{enp}\forall e,n,p$$

(16)

Finally, constraint (17) defines a solar generation target at every stage e.

$$\sum _{npk}{g}_{enpk}\ge R{E}_e\sum _{np}{Q}_{enp}\forall e,k\in K^s$$

(17)

Generation from solar PV and battery storage are limited by the availability of resources, siting and maximum capacity constraints.

2.3.2. Solar Photovoltaic (PV)

We consider two distinct types of solar PV generation capacity which represent the different technologies that are currently being used. The first is dispatchable large solar PV (LPV), which is treated the same as other large-scale generation with the exception of its variable load factor. The second is distribution-connected PV (DPV). DPV generation is not centrally controlled and therefore indistinguishable from a local reduction in demand. These differences in technology are reflected in (18), (19) for LPV and DPV generation limits are formulated in (20) and (21). In this model, LPV is connected to the transmission grid and DPV is installed only in the distribution network.

$$0\le g_{2npk}^S\le (Y_{nk}+y_{1nk})S{P}_{ep}\forall n,p,k\in K^s$$

(18)

$$0\le g_{3npk}^S\le (Y_{nk}+y_{1nk}+y_{2nk})S{P}_{ep}\forall n,p,k\in K^s$$

(19)

$$0\le g_{2npk}^S=(Y_{nk}+y_{1nk})S{P}_{ep}\forall n,p,k\in K^s$$

(20)

$$0\le g_{3npk}^S=(Y_{nk}+y_{1nk}+y_{2nk})S{P}_{ep}\forall n,p,k\in K^s$$

(21)

2.3.3. Battery Storage

Next, we add battery storage modeling components and for practical reasons, we consider only Li-ion battery storage which is one of the most common technologies currently in use. We consider three types of battery storage to represent grid scale battery, controllable Distribution Service Operator (DSO) owned storage and uncontrollable distribution-connected domestic storage. The controllable grid scale battery is connected to the transmission network and co-optimized with generators at the dispatch stage. The other two types of battery (DSO owned and domestic) are connected to the distribution network. We use a generic mathematical representation of storage, which decouples energy capacity (MWh) and power generation (MW) [5,21,22,23]. In general, storage can provide energy arbitrage to improve load factors of generation technologies with lower variable costs, discharging during peak periods and charging when renewable generation is high or demand is low. The characteristic of storage are modeled in (22)–(27). Note that battery storage is not constrained by ramp rates as it is sufficiently flexible at our temporal resolution.

$$r_{enpb}=r_{enpb}^d-r_{enpb}^c$$

(22)

$$-(Z_{nb}+z_{1nb})\le r_{2npb}\le Z_{nb}+z_{1nb}$$

(23)

$$-(Z_{nb}+z_{1nb}+z_{2snb})\le r_{3npb}\le Z_{nb}+z_{1nb}+z_{2nb}$$

(24)

$$r_{enpb}^s=r_{enp-1b}^s-r_{enpb}^d+R{T}_b{r}_{enpb}^c$$

(25)

$$r_{2npb}^s\le (Z_{nb}+z_{1nb})H_b$$

(26)

$$r_{3npb}^s\le (Z_{nb}+z_{1nb}+z_{2nb})H_b$$

(27)

2.3.4. Distribution Network Hosting Capacity (HC) Assessment

As Figure 1 shows, the proposed DPV and storage capacity at each distribution node of the high-level grid planning model is assessed using a distribution network hosting capacity (HC) assessment. The HC is evaluated using the solar penetration level, $S{M}_n$ and home storage level $S{B}_n$ from the upper-level model subject to reverse power flow and voltage constraints in the distribution network.

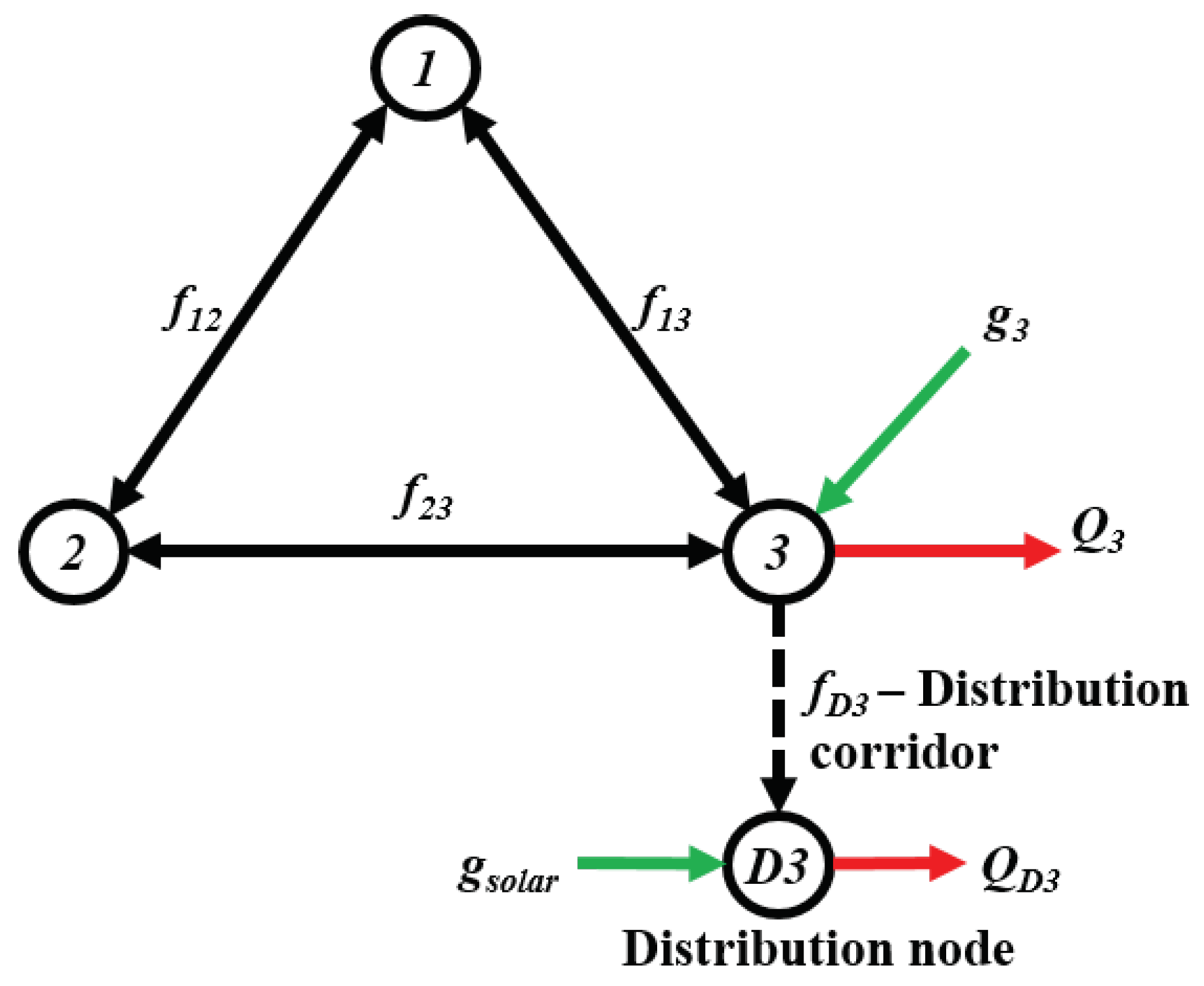
To evaluate the firm level effect of DPV and small scale storage, we introduce an additional corridor that connects each transmission node to a corresponding distribution node as shown in Figure 3. The negative effects caused by solar generation include voltage violations and back-feed to the transmission network, which can cause instability and security problems. Thus, we constrain power flows to the transmission node to be non-negative in (28), while voltage limits are set to typical values of 0.95 pu and 1.05 pu as a minimum and maximum, respectively (29); these are common regulatory constraints in current distribution networks.

$$f_{elp}\le 0,l\in L^D$$

(28)

$$0.95pu\le V_{n=N^D}\le 1.05pu$$

(29)

In our model, hosting capacity (HC) assessment is performed heuristically until the DPV and home storage levels satisfy distribution network constraints; that is, reverse power flow and voltage limits. However, applying this heuristic approach will likely cause the iteration process to diverge. To solve this and find a fixed point, the model will successively decrease the allowable DPV level and if necessary, will reduce or increase the amount of domestic battery storage to determine a new limit for each distributed PV and domestic storage in the optimization model as shown in Figure 4.

The allowable home storage and distributed solar penetration in distribution nodes are enforced in (30) and (31) respectively. In addition, domestic battery storage capacity is limited by the amount of DPV in the distribution network as in (32). Relevant assumptions and parameters applied to the established distribution network are detailed in the next section.

$$\sum _{npk}{g}_{enpk}\ge S{M}_n\sum _{np}{Q}_{enp}\forall e,n\in N^D,k\in K^{DS}$$

(30)

$$\sum _{npb}{r}_{enpb}^d\ge S{B}_n\sum _{np}{Q}_{enp}\forall e,n\in N^D,b\in B^{DS}$$

(31)

$$\sum _{nz}(Z_{nb}+z_{1nb}+z_{2nb})\ge \sum _{nk}(Y_{nk}+y_{1nf}+y_{2nf})n\in N^D,b\in B^{DS},k\in K^{DS}$$

(32)

2.4. Model Outputs

The above model calculates the optimal expansion plan by minimizing the total cost of transmission and generation expansion and operation. We consider two scenarios for battery storage coordination namely ‘grid-size’ and ‘all-storage’. In the former, only transmission-connected storage is available, while in the latter, where all storage type including distributed small-scale storage are incorporated in grid planning. First, we demonstrate the effect of distribution network constraints (HC limits). Then, we analyze the optimal result for solar PV integration with only grid size storage and integration of solar PV with all storage types; grid size, DSO owned and home storage (HC enhancement).

2.4.1. Impact of Hosting Capacity (HC) Limit on Grid Investment

Our model combines a two-stage planning model with a distribution hosting capacity (HC) assessment. To demonstrate the importance of distribution network constraints in grid planning we, first of all, obtain the expected total system cost without HC limit using only a two-stage optimization model. Then, we integrate both the two-stage optimization model and the HC assessment model to determine the optimal solution after HC limit is imposed. The difference in total system costs between the two cases illustrates the effect of HC limits.

2.4.2. Effects of Battery Storage Integration and Hosting Capacity (HC) Enhancement

Storage technology can be utilized as a HC enhancement method, complementing renewable generation and also potentially substituting the transmission line investment [12]. To demonstrate the effect of different levels of storage coordination for different solar penetration levels, we first obtain an optimal solution allowing for only grid-size storage and then add small-scale storage (HC enhancement) into the integrated planning model.

In the real world, there are other options for HC enhancement. Depending on the problem, HC enhancement techniques varies from active network management (ANM), network reinforcement, application of on-load tap changers (OLTC) to energy storage and harmonics mitigation [1,24,25]. In this paper, we only apply hosting capacity (HC) enhancement techniques resulting from the connection of small scale Li-ion battery storage in the distribution network; controllable Distribution Service Operator (DSO) owned storage and uncontrollable distribution-connected domestic storage; however, other methods would likely yield similar results.

2.5. Assumptions and Data

2.5.1. Transmission and Generation Characteristics

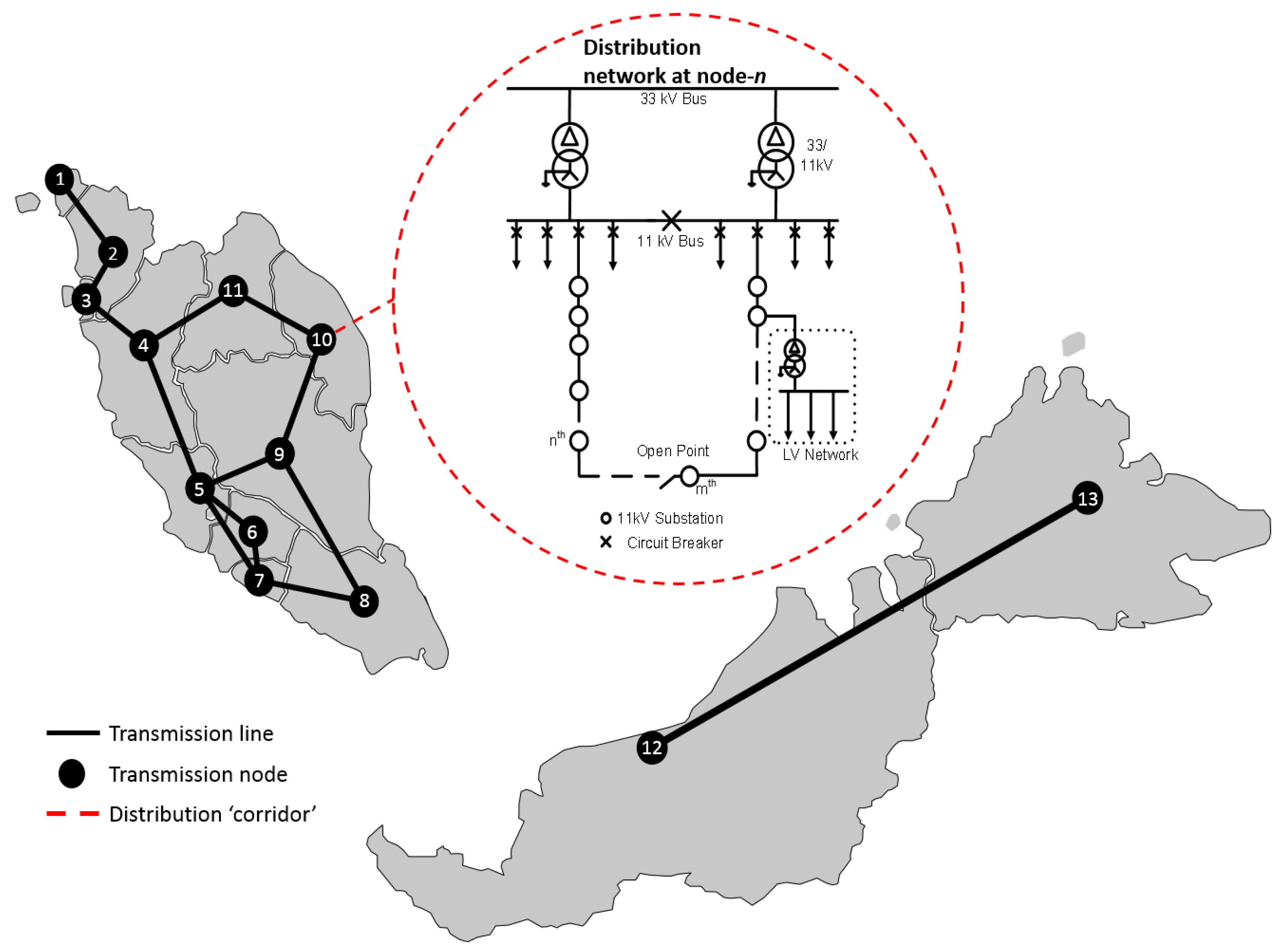
The transmission network in Malaysia is operated at 132 kV, 275 kV, and 500 kV. For simplicity, and because the most important constraints are on higher-voltage corridors, we ignore the 132 kV network. We condense the remaining 275 kV and 500 kV network to 13 transmission nodes, one for each of the main cities. This representation is also widely used by the Malaysian regulator and in industry [26,27,28]. Transmission losses would introduce nonlinearities without adding significant insight and are therefore not considered. As explained above, we extend the network with a set of corridors that connect a distribution node to each transmission node. This corridor is a representation of the multiple cables that connect distribution substations and transmission grid supply points. As congestion on these lines is uncommon, they are assumed to have unlimited capacity.

All generators are assigned to the nearest nodes, using their actual generation capacity while distance between nodes is based on the direct distances between the main cities, as shown in Figure 5. Asset retirement is not considered in our model and we assume that new generation capacity built in 2025 and 2035 will continue to be in operation until the end of the timeframe modeled.

Generator efficiency, technical and cost parameters for the power plants are obtained from References [7,29] and own assumptions which are listed in

Table 2. Power plant cost and technical characteristic—2015.

Plant Type	Load Factor (%)	${\mathit{CO}}_2$ Emission (tonne/MWh)	Operation Cost ($/MWh)	Capital Cost ($Million/MW)	Ramping Rate (MW/hr)
Biomass	38	0.093	40.28	2.26	240
CCGT	59	0.353	39.46	0.82	960
Coal	46	0.748	23.15	2.08	240
Diesel	55	0.54	49.7	1.14	420
Hydro	64	0	2.14	3.54	9000
OCGT	32	0.53	72.4	0.68	3000
LPV	17	0	2	2.43	N/A
DPV	17	0	0	2.43	N/A

. Note that the ramping rate of solar PV is assumed to be infinite, as PV generation is driven by renewable resource availability. Capital costs include construction cost and fixed costs discounted to the year construction starts; for batteries, this includes degradation costs. Only solar, hydro and biomass plants are considered to be renewable and both types of solar PV contribute towards solar target. Only solar energy is intermittent.

The existing generation capacities are taken from References [27,28] and summarised in

Table 3. Generator installed capacity (MW).

Node	Biomass	CCGT	Coal	Diesel	Hydro	OCGT	LPV	DPV
1		650
2								5.41
3								3.95
4	14.13	660	3080					9.77
5	14.39	1943	1486		900	820		54.02
6	23.4	1584	1400		2.2	436.4		34.41
7		1411				434		15.57
8	17.85	1042	2100			210		10.4
9	16.83	275						7.31
10					6.38			20.89
11		1029			650			5.62
12	44.3		480	171.96	614.8	867.6		0.3
13	54.19	1034.2		332.8	97.86			18.14

.

2.5.2. 11 kV Distribution

To model the distribution network, we formulate a typical 11 kV Malaysian distribution network Open Distribution Simulation Software (OpenDSS) [30]. This network is shown in Figure 5.

Generally, there will be two 33/11 kV power transformers operating in parallel in most 33 kV substations in peninsular Malaysia. For operational reasons, the system planner would plan for peak demand to be capped at 50% to 75% of the network total capacity. The reason for this is to ensure demand is fully or at least partially transferable to another transformer within the same substation in case of a failure in one power transformer. This will ensure fast restorations of supply and prudent asset management by having a longer lifespan of power transformers. However, for simplicity, and because we do not consider outages here, this typical redundant configuration is omitted in the network model used for this paper. We assume instead that only one power transformer is connected to the modeled network.

For the 11 kV outgoing feeder, we model a single radial feeder to further simplify the analysis; actual feeders are usually interconnected in mesh. At each 11 kV substation, voltages will be stepped down from 11 kV to 400 V by distribution transformers. This study covers the 11 kV distribution network, where most power issues occur; low voltage networks are therefore excluded from this network model. The effects of aggregation for each case of reverse power flows, voltage rises and network losses have been validated at the preliminary stage of this research, showing minimal and insignificant differences between the simplified model and a more complex, realistic model, giving confidence that our results are not affected by these simplifications.

The network is modeled based on an 11 kV distribution network in a highly populated area in Malaysia where the average distance between substations is 1 km to 2 km. Therefore, it is assumed that all buses are connected by 300 mmp three-core 11kV armored cables (aluminum conductor) and the distance between buses is 2 km. Due to data limitations, electrical properties of the power transformer and cables are set according to technical specification manuals from major suppliers of those equipment in Malaysia. The final network model is based on the characteristics summarized in

Table 4. Distribution network characteristics.

Characteristic	Quantity
Power Transformer Rating	30 MVA
Total Load	17.1 MW
Power Factor	0.97
Average Cable Length	1 km–2 km

. The same distribution network representation is repeated at each transmission bus.

2.5.3. Demand

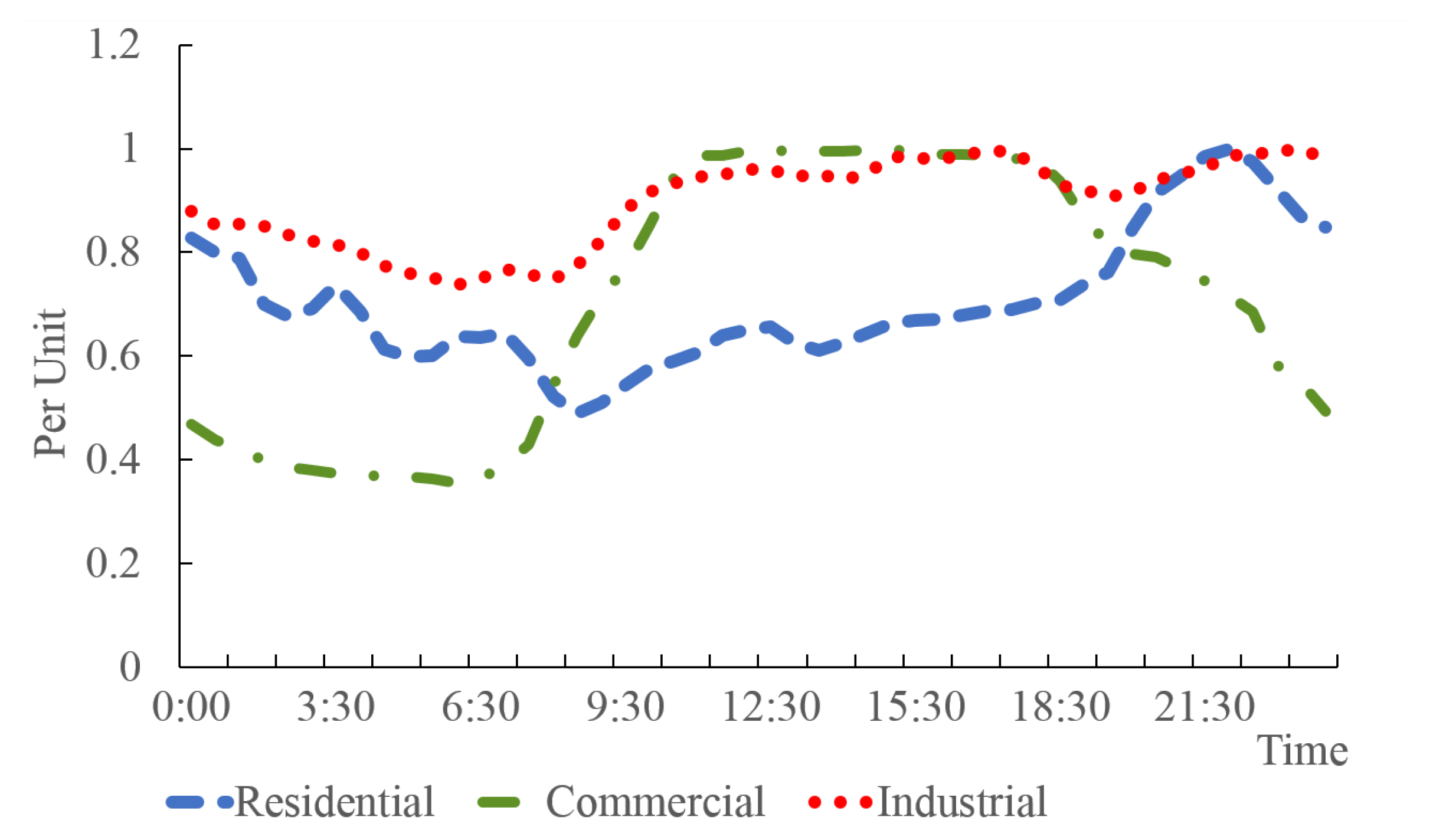
Peak demand for each transmission node is taken from measured data [27] and disaggregated to the distribution nodes in the connected distribution network based on own assumptions. Then, each node is assigned a demand pattern based on three typical demand categories identified in Malaysia. Demand aggregations and classifications are established based on the economic and demographic of each state. We use three sets of actual hourly demand data from the 5th of September 2016, extracted from energy meters installed at the major substations in Klang Valley, Malaysia. Demand is categorized based on the patterns of the extracted data and locations of each substation and defined as residential, commercial and industrial, representing the three typical demand types in Malaysia depicted in Figure 6.

The main characteristic of residential demand in Malaysia is the low energy consumption between 7 am until 6.30 pm during working hours and rush hours. Energy usage starts to increase after 7.00 pm and gradually decreases around 10.30 pm. In contrast, commercial demand patterns will reach their peak consistently for a few hours after 10 am, when most business transactions take place and are subsequently reduced after 6.30 pm. On the other hand, industrial demand patterns appear to be flat with minor fluctuations within 0.75–1 per unit value; this data was extracted from the main substation which supplies an area of heavy industries that operates 24 h a day. It is possible that other industrial areas will have different demand patterns but it is impossible to consider all of those. We therefore, focus on this representative case study.

In the distribution network hosting capacity (HC) assessment model, total peak demand is assumed to be evenly distributed at each phase and node, for lack of more detailed information about the distribution of demand over the network. The total demand is set at 17.1 MW or 60% of the total transformer capacity which, as explained above, is a realistic level. Also, residential demand patterns are assigned to all distribution nodes and buses with an average power factor of 0.97, corresponding to the actual demand data mentioned above. Resource availability and demand parameters for each node are listed in

Table 5. Demand and resource availability.

Node	Peak Demand (MW)			Demand Category		Resource Availability
	Total	Tx Node	Dx Node	Tx Node	Dx Node	B	Cc	Co	D	H	O	L	D
1	92.29	4.61	87.67	I	R		1				1	1	1
2	1033.18	103.32	929.86	I	R							1	1
3	1633.90	490.17	1143.73	I	R							1	1
4	1464.51	366.13	1098.38	I	R	1	1	1		1	1	1	1
5	7291.07	2916.43	4374.64	C	R	1	1	1			1	1	1
6	769.92	115.49	654.43	I	R	1	1	1			1	1	1
7	697.09	34.85	662.24	I	R		1				1	1	1
8	2927.71	731.93	2195.78	I	R	1	1	1			1	1	1
9	720.41	144.08	576.33	I	R	1						1	1
10	402.73	60.41	342.32	I	R		1			1	1	1	1
11	428.20	42.82	385.38	R	R					1		1	1
12	2288.00	343.20	1944.80	C	R	1	1	1	1	1	1	1	1
13	914	91.40	822.60	C	R	1	1		1	1	1	1	1
Tx-Transmission			R-Residential			Co-Coal			L-Large PV
Dx-Distribution						D-Diesel			D-Distributed PV
I-Industrial			1-Available			H-Hydro			Cc-CCGT
C-Commercial			Blank-Not Available			O-OCGT			B-Biomass

are extracted from References [27,28] and aggregated based on own assumptions.

2.5.4. Solar PV and Battery Storage Characteristic

As a result of the current Malaysian Feed-in Tariff (FiT), most solar PV systems are connected within distribution networks and in many cases are rooftop solar installations in residential areas connected to end-users. In this paper, we use modeled solar generation data from a mesoscale weather model [31] for all major cities in Malaysia and normalize this to a per unit value shown in Figure 7. Solar generation starts at sunrise, on average around 7.30 am, peaks in the afternoon between 12 pm and 3 pm. It is similar to generation patterns used in previous research [32,33]. To assess the impact of solar penetration on the network, the built-in OpenDSS solar PV model is used to represent a cluster of solar PV connected within the distribution network. For practical reasons, in both models (transmission and distribution network) we only use a 48-hour solar pattern representing the highest and lowest weekly average in a typical year.

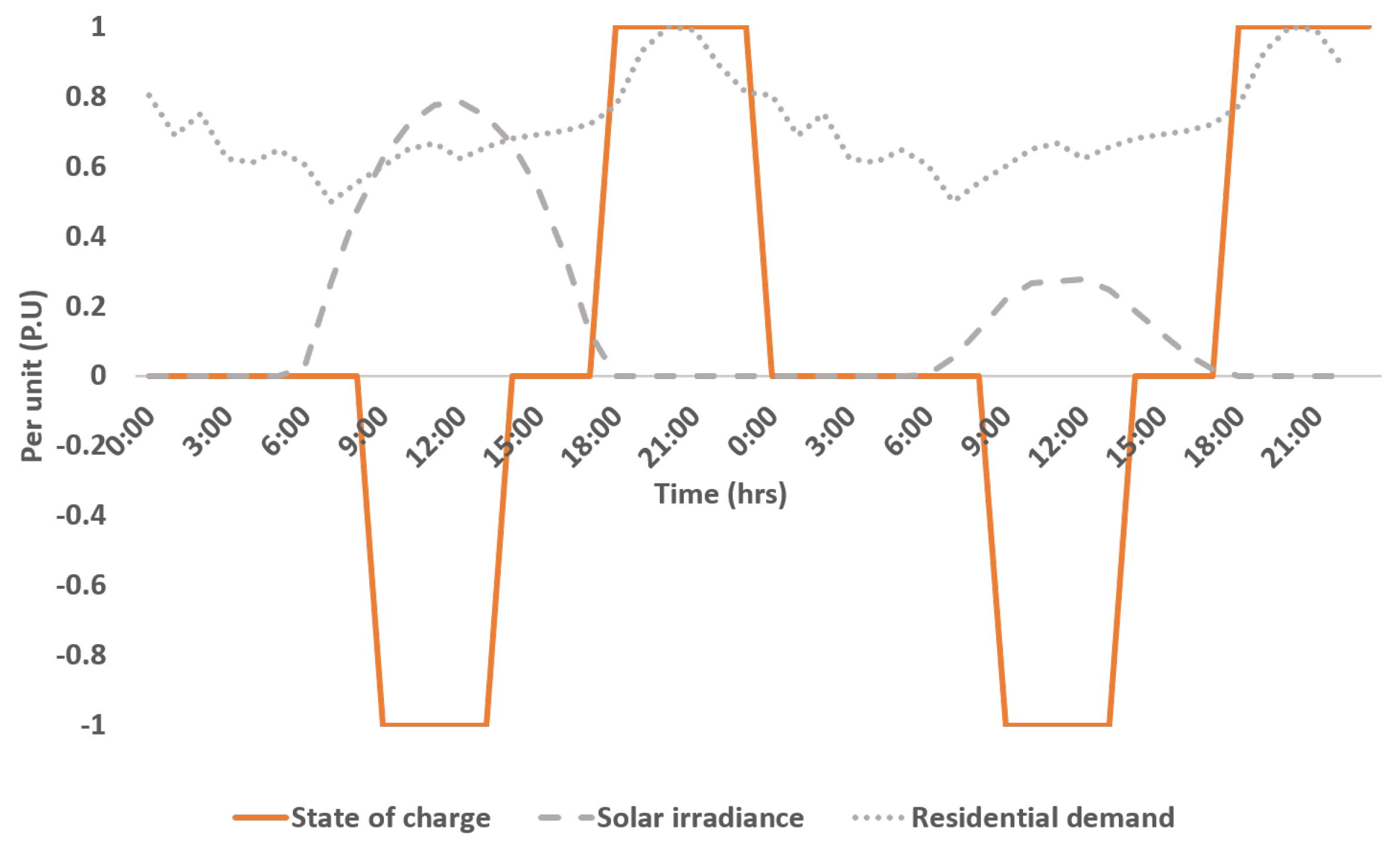
Also, using a built-in OpenDSS storage model, the uncontrolled domestic storage is set to charge between 9 am to 1 pm to match the period of high solar irradiance while in the night-time when the demand starts increasing, the battery will begin to discharge as depicted in Figure 8. Although it is known that battery production contributes significantly to $C{O}_2$ emissions [34,35], we do not account for this in our model. Hence, only $C{O}_2$ emissions from grid operation are considered. Also, similar to generation assets, battery storage is assumed to last until the end of planning period while the effects of state of charge (SOC) on battery life-cycle and calendar aging are not explicitly modeled but included in the capital cost of batteries. However, we suggest that the aging effect of battery and generation assets retirement should be incorporated in future studies.

Technical and economic parameters for the storage technologies are obtained from References [5,14,36] and own assumptions which are listed in

Table 6. Battery storage characteristics.

Battery Type	Battery Hour	Roundtrip Efficiency (%)	Operation Cost ($/MWh)	Capital Cost ($Million/MW)
Large-scale	4	0.8	6	2.43
DSO-owned	2	0.8	5	1.53
Domestic	3	0.8	0	0.94

.

2.6. Planning Scenario

We consider a planning scenario summarized in

Table 7. Summary of planning scenario.

Year	Operating Cost	Capital Cost	Line Investment Cost	Demand Growth	Carbon Price (USD/tonne)	RE Target (% of Total Electricity Production)
2025	Conv & Hydro −15%	Conv & Hydro −10%	−30%	50%	15	20%
	Bio −30%, LPV −30%	Bio −20%, LPV −20%
	DPV −30%, Gs −30%	DPV −30%, Gs −20%
	Ds −30%	Ds −30%, Hs −35%
2035	Conv & Hydro −20%	Conv & Hydro −15%	−50%	70%	30	40%
	Bio −35%, LPV −35%	Bio −25%, LPV −30%
	DPV −40%, Gs −35%	DPV −50%, Gs −30%
	Ds −40%	Ds −50%, Hs −55%
Conv-conventional plant			Gs- Grid size battery storage
RE-renewable plant			Ds-DSO owned battery storage
LPV-Large PV			Hs-Domestic battery storage
DPV-Distributed PV

that emphasizes a decrease in operating and investment costs resulting from technological advancement and industrialization; simultaneously, these factors translate into high demand growth (50–70%) [27,37,38,39]. Consequently, the projected cost for all generating plants and transmission investment are significantly reduced after the first modeling stage. As compared to the conventional generators, new technologies see especially significant decreases in costs, to reflect the fact that, for these technologies, learning curves are still steep [36,40,41,42].

3. Results and Discussion

3.1. Impact of Hosting Capacity (HC) Limits on Grid Investment

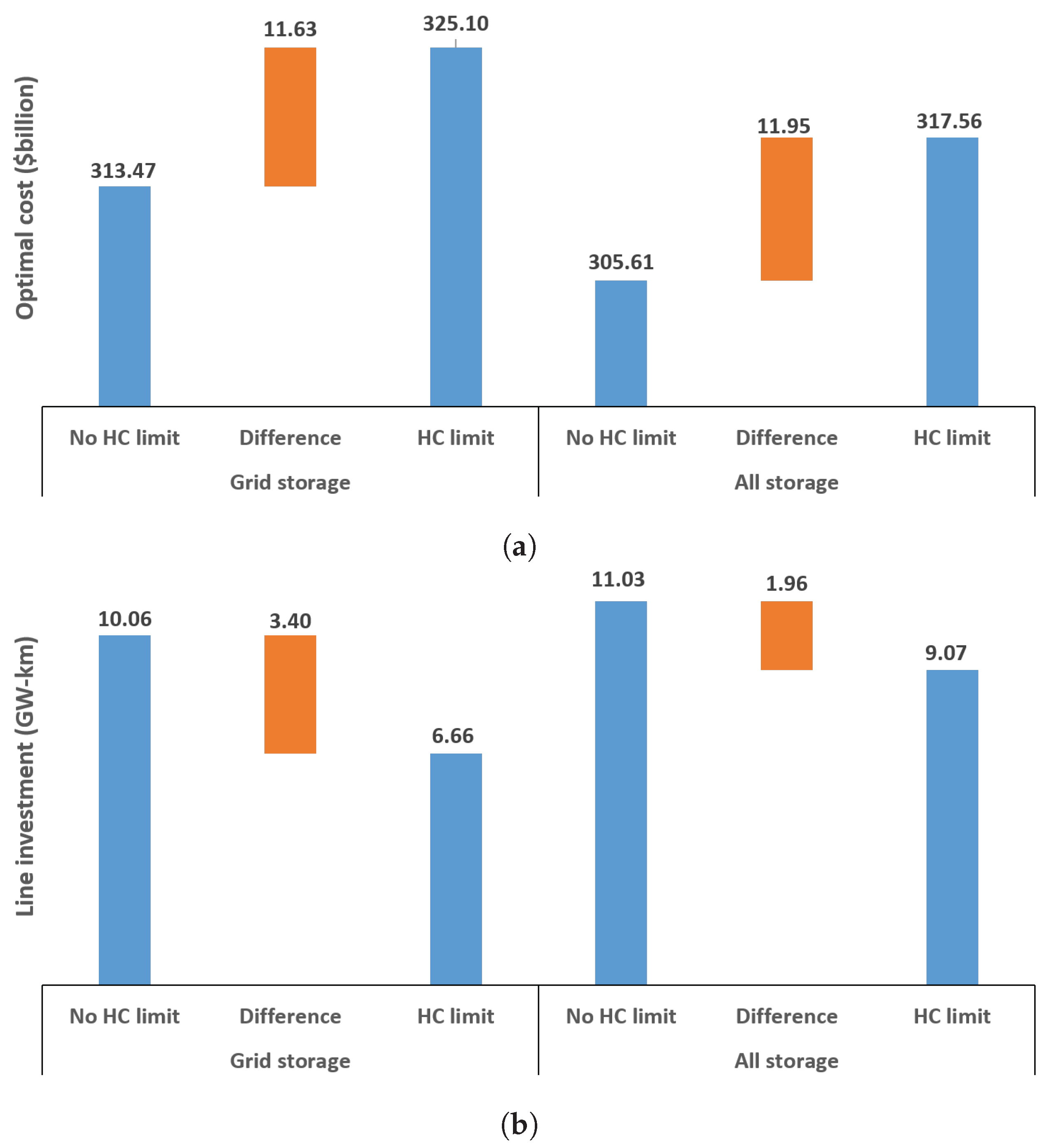
Figure 9 shows the total expected system costs (in $ billion) and total line (in GW) investment for two scenarios; one with grid-size storage only and one with all three types of storage. In each case, a high 80% solar target is enforced. As this figure shows, hosting capacity limits impose significant additional costs.

As shown in Figure 9, in the absence of distribution network constraints, the model proposes a significant amount of line investment to fully utilize the cheaper energy generated by both large solar PV (LPV) and distributed solar PV (DPV) located in the buses with the best solar resource. After distribution HC limits (reverse power flow constraints and voltage limits) are imposed, reverse power flows from distribution network are constrained, resulting in a significant reduction in DPV investment at the high-resource distribution nodes that exceed the HC limit. 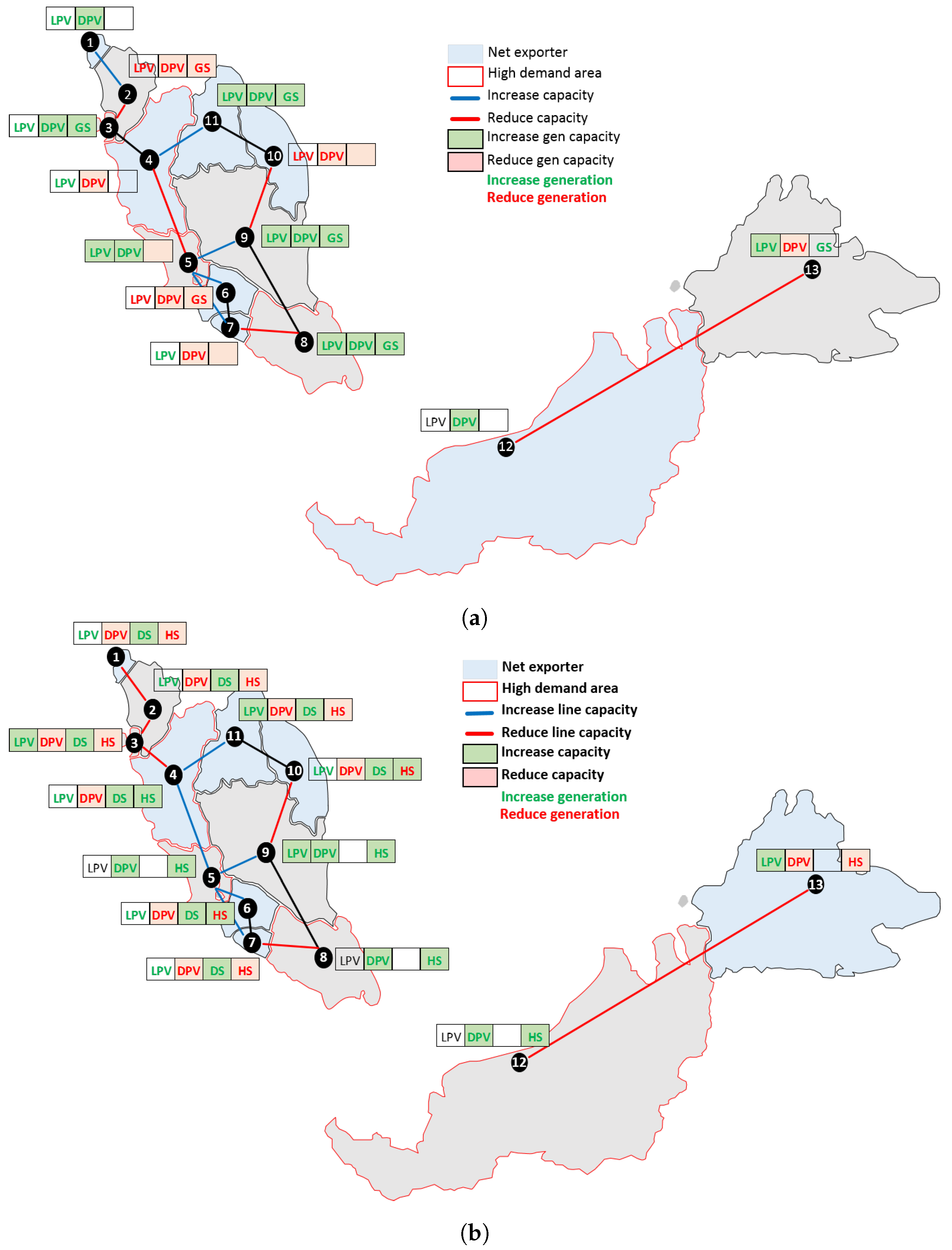However, due to the fixed solar target, a significant amount of DPV investment has to be shifted to other distribution nodes with lower solar resources as depicted in Figure 10a. This increases costs.

Also, due to the non-dispatchable characteristic of DPV and in absence of small-scale battery storage to mitigate negative distribution network effects, more expensive LPV is proposed instead of DPV, which also increases the overall cost. However, because the solar capacity is now more evenly distributed across the networks, less transmission reinforcement is necessary. The 3.4 GW reduction in transmission capacity somewhat offsets but does not negate, the cost increase due to the decreased average solar capacity factor.

If we include cheaper small-scale storage (DSO owned and distributed domestic storage) into the model, this decreases overall costs substantially, as it increases the allowable solar penetration level in the distribution network. Nevertheless, the additional costs of HC limits do not decrease substantially.

Detailed changes and spatial distributions of solar and storage investment after considering HC limits are shown in Figure 10. The spatial distribution of solar and storage capacities in Figure 10 are different for both cases which at is, to some extent, driven by our cost parameters, solar availability and demand profiles at each node.

In Figure 10a, due to the set solar target, a significant amount of solar PV investment is shifted to the lower-resource nodes (node 5, 8, 9 and 10) and re-allocation of LPV, DPV and grid-size storage takes place regionally. Meanwhile, if small-scale storage technology is included, re-allocation decisions have more flexible and most investment is shifted locally, at the same node, resulting in a different mix of distributed solar and battery storage. In order words, HC limits have limited spatial investment effects if a range of storage technologies is available; on the other hand, if only large-scale storage is available, HC limits require much larger spatial shifts in investment. Note especially that an increase in DSO owned storage in Figure 10b is proposed at many nodes to maintain a high level of DPV penetration after HC limit is imposed.

In addition, changes in transmission investment decisions are affected by the type of storage that is available. This will be discussed further in the next section.

3.2. Effects of Battery Storage Integration and Hosting Capacity (HC) Enhancement

3.2.1. Cost Implication and $C{O}_2$ Emission from Grid Operation

The results above were obtained assuming a very high solar penetration level. In this section, we evaluate the benefit of different types of battery storage at different solar targets. Note that, in this simulation, in contrast to the previous sections, the base case is a setting with solar PV integration without any battery storage and that, for each simulation, battery storage technology is only utilized for load shifting and peak shaving.

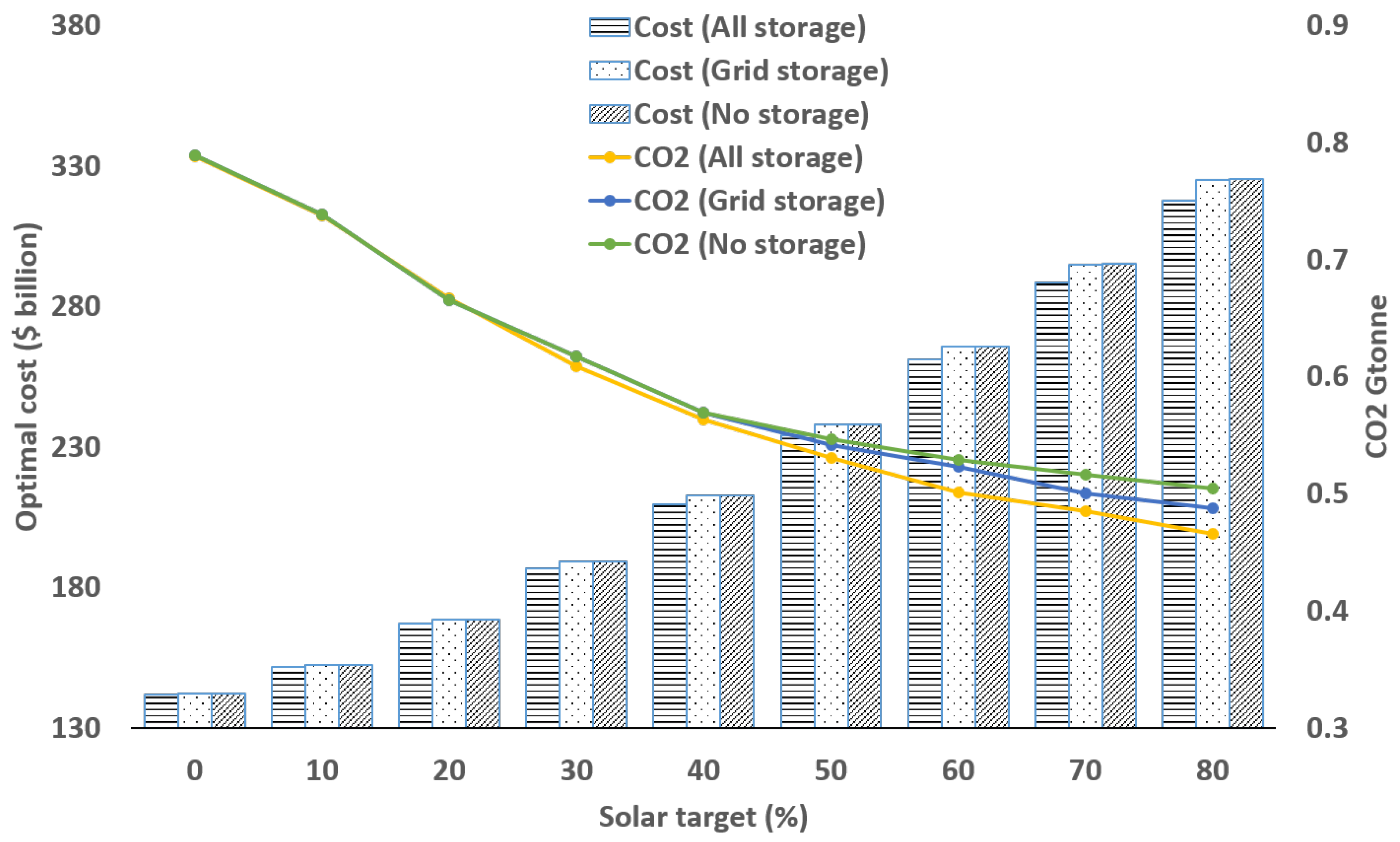
As shown in Figure 11, in the ‘no-storage’ and ‘grid-storage’ scenarios, the observed trends in total costs and $C{O}_2$ emission are similar at solar penetration levels below 60%. With a higher solar target, the overall cost gradually increases while $C{O}_2$ emission is significantly reduced, as is expected. The more storage technologies are available, the faster $C{O}_2$ emissions decrease and the lower costs are, as they allow solar capacity to be integrated more efficiently and in locations with a better solar resource.

Table 8. Cost savings ($ billion).

Solar Target (%)	All Storage	Grid Storage
0	0.29	0
10	0.72	0
20	1.15	0
30	2.3	0
40	3.02	0
50	3.96	0
60	4.72	0.02
70	6.37	0.22
80	7.76	0.22

presents the cost savings that result from including distribution-connected storage. This shows a significant cost saving which increases monotonically with the solar target. At an 80% solar target, the cost is reduced by $7.5 billion in the ‘all-storage’ case while much lower savings of around ($0.22 billion) are obtained by integrating only grid-size storage. This observation indicates the benefits of co-locating small-scale battery storage with distributed solar PV (DPV) in the distribution network. Grid-scale storage by itself does not have significant benefits, because without distribution-connected storage the most economical solar capacity is simply not available.

3.2.2. Transmission Investment

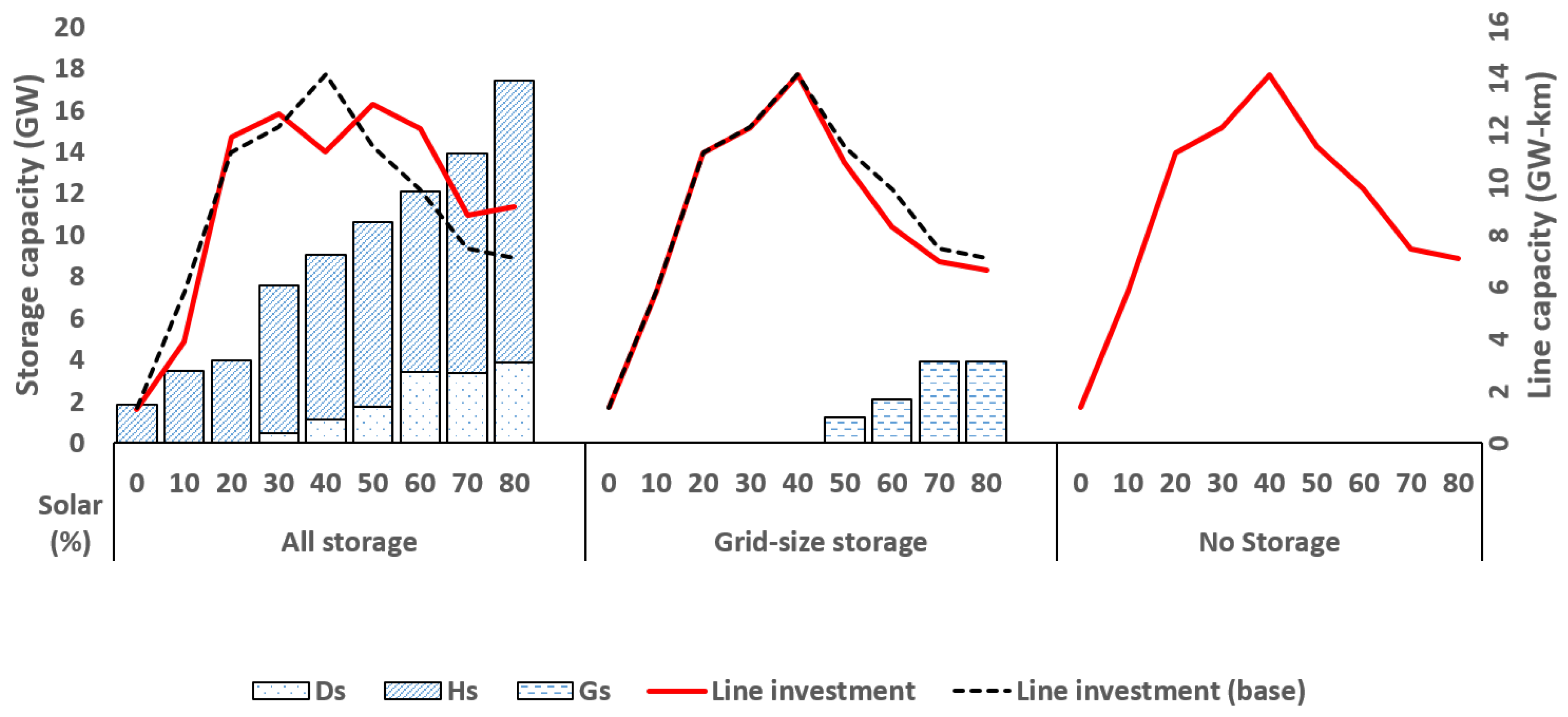
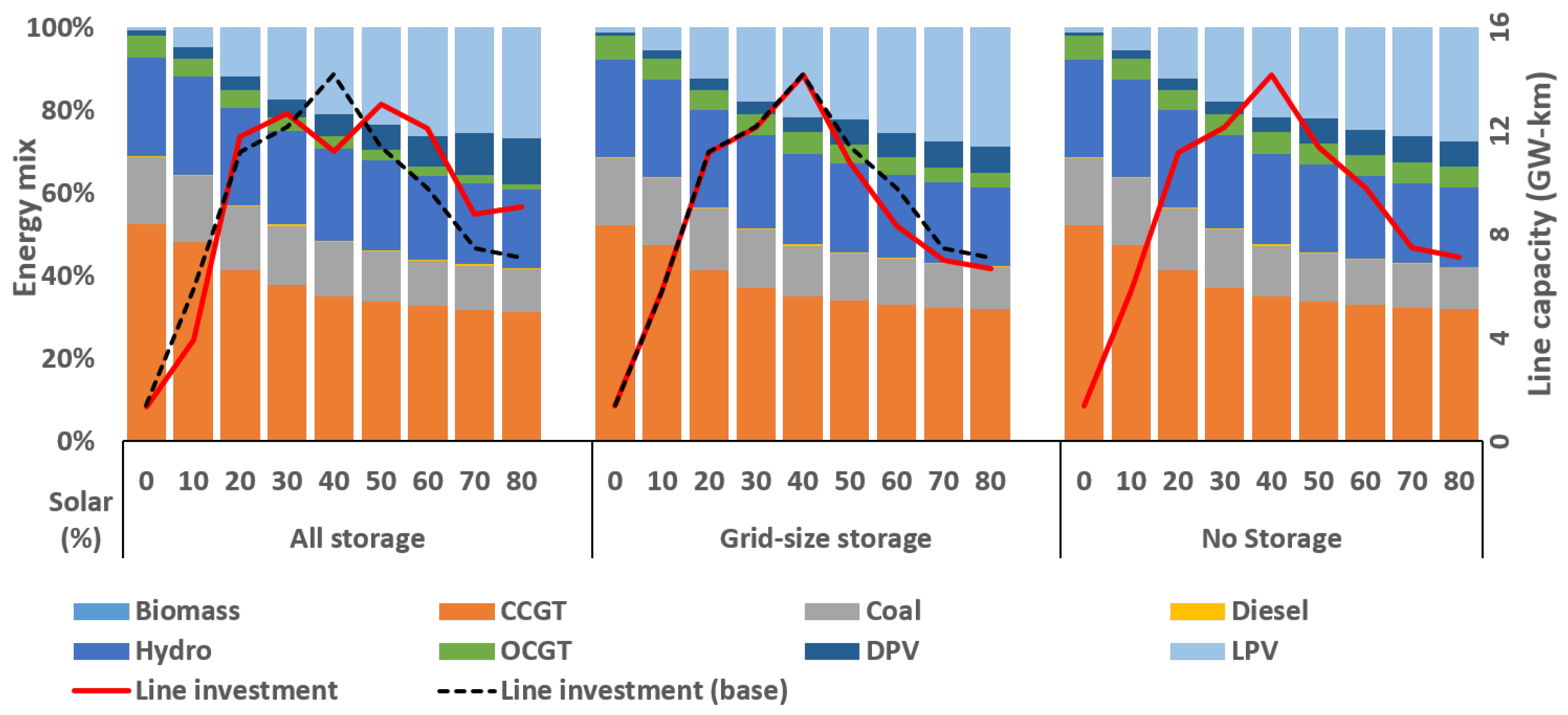
Next, we demonstrate the impact of battery storage HC enhancement on line investment, comparing the ‘grid-only’ and ‘all-storage’ scenarios. Figure 12 shows the relationship between transmission line reinforcement and battery storage investment. In both scenarios (‘grid-only’ and ‘all-storage’) we observe a non-linear trend. When the solar target is low, little line investment is necessary, as the current system suffices. As the solar target increases, line investment helps integrate solar energy more efficiently; storage and solar technologies complement each other. However, very high solar penetration levels can only be achieved with a more evenly distributed amount of solar capacity, helped by some investment in storage, in which case the additional value of line investment is lower. Hence, at a solar penetration level exceeding 60% solar penetration battery grid-scale storage becomes a substitute for line investment—storage enables a more local energy system, requiring less large-scale transmission investment.

However, an opposite trend can be observed in the ’all-storage’ scenario. First of all, note that grid-size storage is not invested in here, for two reasons. Firstly, its cost is comparatively higher than the combined cost of small scale storage and DPV. Secondly, small scale battery storage allows higher utilization of cheaper solar energy by increasing the HC limit. As a result, significant DSO owned and home storage are connected to the low-level network. At a low solar target (10–40%), connecting more small-scale battery storage in the network enables deferring line investment but at a higher solar penetration, line investment and battery storage are complementing each other to ensure system flexibility in the transmission and distribution network, respectively.

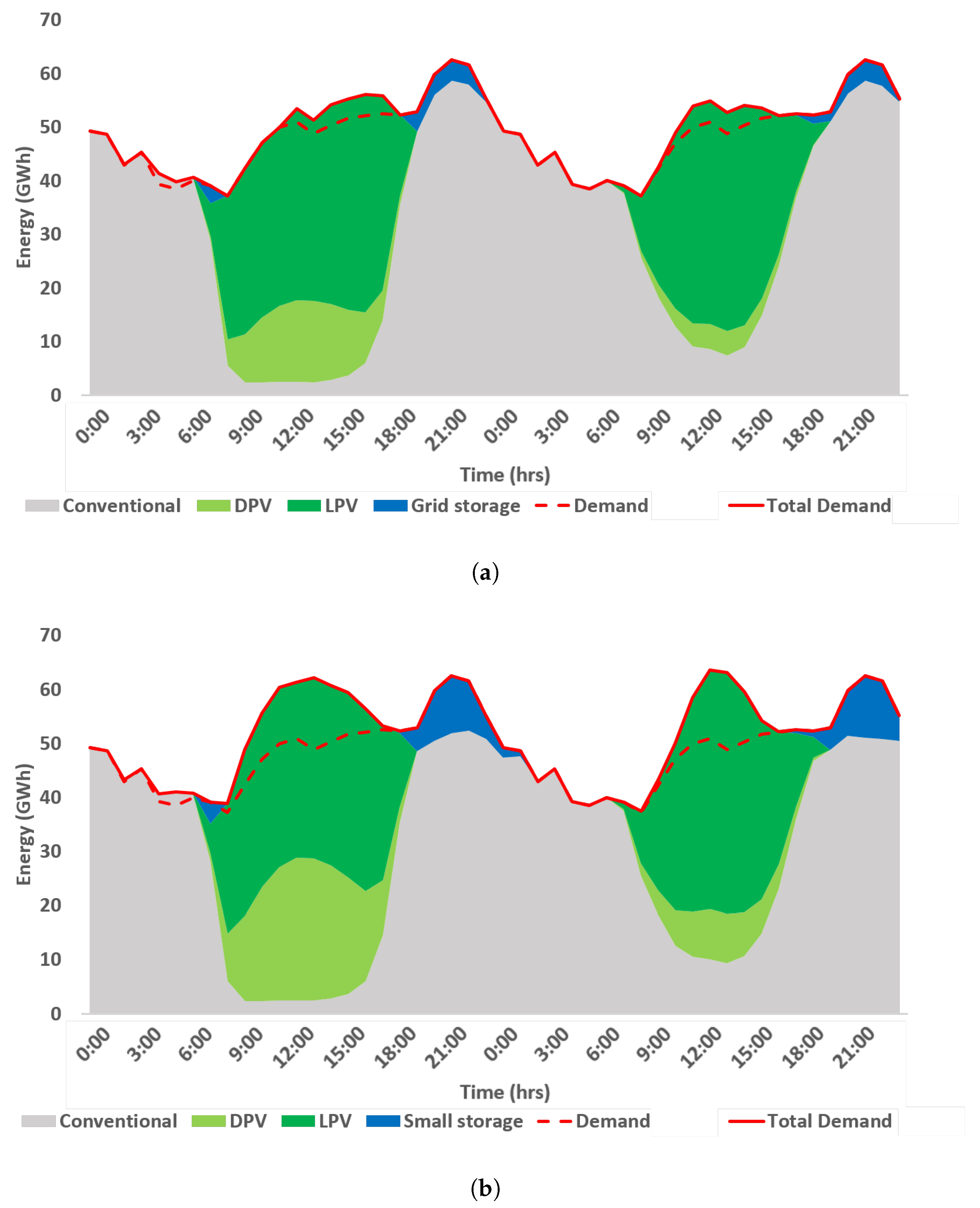
This opposite effect requires a more detailed explanation. In the ’all-storage’ case, the excess solar energy from DPV is stored either in DSO owned or home storage which reduces the intermittent effect of non-dispatchable solar generation in the network. The stored energy is discharged from these small-scale stores (DSO owned and distributed domestic storage) during the peak demand period. In this scenario, a significant load shifting and demand clipping within the peak period occurs, as is shown in Figure 13.

For this reason, new OCGT generators, which are generally utilized as peaker plant, are not as necessary in this scenario.

Table 9. Optimal solution at 80% solar target.

Technology	Grid Storage					All Storage
	Energy st 3 (GWh)	Energy (%)	New Capacity (GW)	Total Capacity (GW)	ACF	Energy st 3 (GWh)	Energy (%)	New Capacity (GW)	Total Capacity (GW)	ACF
Biomass	0.00	0.00	0.00	0.19	0.00	0.00	0.00	0.00	0.19	0.00
CCGT	387.60	22.21	15.37	25.00	0.32	385.72	22.60	15.37	25.00	0.32
Coal	107.79	6.18	0.00	8.55	0.26	108.06	6.33	0.00	8.55	0.26
Diesel	3.39	0.19	0.00	0.50	0.14	3.42	0.20	0.00	0.50	0.14
Hydro	204.14	11.70	3.27	9.00	0.47	205.61	12.05	3.27	9.00	0.48
OCGT	47.81	2.74	2.89	5.66	0.18	9.09	0.53	0.00	2.77	0.07
LPV	855.13	48.99	115.02	115.02	0.15	740.07	43.36	97.68	97.68	0.16
DPV	139.58	8.00	19.78	19.96	0.15	254.67	14.92	34.69	34.88	0.15

shows the optimal mix for both scenarios at 80% solar penetration; this clearly shows that the OCGT utilization level in ‘all-storage’ scenario is much lower than the other scenario. Also, as shown in Figure 14, investment in OCGT and LPV is significantly reduced as more DPV and distributed small-scale battery storage are connected to the distribution network. Instead, additional line capacity is constructed to fully utilize cheaper energy generated from LPV and non-OCGT conventional (new and existing) generators including hydro, coal and CCGT. This explains why a relatively higher transmission investment is observed in this scenario.

4. Conclusions

In this paper, we have proposed and demonstrated an integrated planning model that allows distribution network hosting capacity (HC) constraints to be included in long term grid planning. This is important especially in countries such as Malaysia where distribution-connected solar PV capacity is expected to play a large role in the energy mix. Current grid planning methods generally do not consider distribution network constraints and, as a result, distribution system operators are facing increasing difficulties managing voltages and reverse power flows. Our model quantifies the effects of these distribution network constraints, their interactions with transmission and distribution level investment. Furthermore, we demonstrate the impact of integrating a large amount of distributed small-scale battery storage for use as hosting capacity enhancement in the distribution network to quantify its benefit in terms of overall system costs. We apply our model to a stylized representation of the Malaysian grid, where solar energy is expected to play a particularly large role.

From our findings, we conclude that distribution network constraints (HC limits) have a significant impact on the overall grid planning outcome and increase the cost by almost $12 billion which does not depend significantly on the level of storage integration. Omitting HC limits would allow reverse power flows from distribution network to the transmission network which does not represent the actual practice in network planning and operation.

Considering distribution network constraints (HC limit), we evaluate the effect of integrating battery storage at different network levels (distribution and transmission) on the optimal solution. Although the benefit of incorporating battery storage in grid planning has been widely covered, our integrated approach provides additional evidence on the substitutability and complementary of storage and line investment. At a higher solar penetration level, incorporating only grid-size battery storage in grid planning results in significant line investment deferral which means that battery storage substitutes for investment. However, the inclusion of small-scale battery storage (DSO owned and distributed domestic storage) in grid planning produces a different result. Like large-scale storage, small-scale battery storage substitutes for investment at a lower solar penetration level (10–40%). However, above 40% solar target, small-scale battery storage acts as a complement the line investment.

Finally, we quantify a cost saving of up to $7.76 billion depending on solar target from using distributed small-scale battery storage (HC enhancement). In this paper, we show that different levels of battery storage in the network have a different impact on the optimal grid planning, and we explicitly quantify the benefit of connecting small-scale battery storage (HC enhancement) in the distribution network.

These results were obtained with a simplified model under a range of restrictive assumptions, and more research is necessary to generalize these. Firstly, we assume the objectives of transmission planners and generators are perfectly aligned which reflects the current setting in Malaysia but not necessarily elsewhere. A full bi-level optimization can address a different setting where both parties (transmission planner and generators) have different objectives. Secondly, future research should incorporate asset retirement including battery life-cycle restrictions, which may have a significant influence on the optimal planning solutions. Thirdly, a larger set of distribution network constraints could be considered, as well as a longer time horizon. Fourthly, as many model parameters are uncertain, a stochastic modeling approach could properly account for this—this would increase the model size but could be realized within our modeling framework. Finally, using the proposed framework, the benefits of integrating solar and storage systems can be further analyzed considering their interaction with demand-side management and load flexibility in smart grid systems.

However, although the results described above were obtained using a simplified representation of real-world networks and decisions, they do show the importance of distribution network constraints (HC limits) in grid planning and explicitly quantify the benefits of integrating distributed battery storage (HC enhancement). We expect our qualitative results to carry over to more complex settings.