Nonlinear Viscoelastic–Plastic Creep Model Based on Coal Multistage Creep Tests and Experimental Validation

Abstract

The development of fractures, which determine the complexity of coal creep characteristics, is the main physical property of coal relative to other rocks. This study conducted a series of multistage creep tests to investigate the creep behavior of coal under different stress levels. A negative elastic modulus and a non-Newtonian component were introduced into the classical Nishihara model based on the theoretical analysis of the experimental results to propose a nonlinear viscoelastic–plastic creep model for describing the non-decay creep behavior of coal. The validity of the model was verified by experimental data. The results show that this improved model can preferably exhibit decelerating, steady state, and accelerating creep behavior during the non-decay creep process. The fitting accuracy of the improved model was significantly higher than that of the classical Nishihara model. Given that acceleration creep is a critical stage in predicting the instability and failure of coal, its successful description using this improved model is crucial for the prevention and control of coal dynamic disasters.

1. Introduction

With the gradual depletion of mineral resources in the shallow, most mines begin the trend of deep mining [1,2]. The rheological characteristics of coal become more significant with the increase in strata stress, thereby decreasing its mechanical strength under long-term static load, which causes deep mining to face many time-related problems [3,4], such as aggravated roadway deformation, collapse of gas extraction boreholes, and gas and coal outburst delay [5,6,7]. All of these problems pose serious threats to underground safety. Therefore, exploring the creep characteristics of coal and presenting an applicable creep model are crucial for the underground engineering design, mining construction, and safe production of coal mines.

Research methods for the rheological model are mainly divided into empirical equation and component combination [8,9]. Logarithmic, exponential, and power functions are adopted in the empirical equation to describe the strain–time relation with few fitting parameters and strong pertinence based on the creep test results. However, this method has some defects, such as long experiment time, unclear physical meaning, and difficult extrapolation of research results [10,11]. The component combination method uses Hooker (H), Newton (N), and plastic (Y) units to establish rheological constitutive models, such as Burgers and Nishihara models, to reflect the rheological behavior of rocks with clear physical significance. However, these models cannot reproduce the accelerating creep stage because of the use of linear components in the models [12]. Shao et al. [13,14] proposed constitutive models that could represent the induced plastic deformation, damage, and creep characteristics of brittle rocks to describe nonlinear creep characteristics. Ping [15] developed a new nonlinear-damage creep constitutive model that combined the Burgers, Hooke, and St. Venant models, and the applicability of this model was verified by a series of uniaxial compression creep tests. Kang [16] established a fractional nonlinear creep model that considered the viscoelastic–plastic characteristic and damage effects of coal; moreover, he also conducted several uniaxial creep tests under different axial stress conditions to verify the model. Cai [17,18] presented an improved hardening damage creep model by introducing hardening and damage functions based on the uniaxial creep test of lean coal. Furthermore, Wang [19] deduced a nonlinear creep constitutive model of coal under three-dimensional (3D) stress condition and achieved satisfactory fitting results with the experimental data of coal unloading confining pressure creep.

Coal, a natural organic mineral, has undergone a long geological period of evolution and is affected by mining stress, which results in the generation of abundant fractures with poor homogeneity inside the coal, and determines the complexity of its creep behavior under different loads. However, only limited research has focused on the creep characteristics of coal. Thus, a suitable creep model must be proposed. Motivated by the aforementioned facts, we conducted a series of multistage creep tests on coal specimens and analyzed coal creep behaviors under different loading conditions to develop a new nonlinear viscoelastic–plastic creep model using empirical equations and component combinations. The accuracy and applicability of this model were verified by model identification, and the effects of model parameters on creep behavior were also discussed in detail. The results obtained in this work are expected to provide some scientific basis for the study of coal instability failure and dynamic disasters.

2. Multistage Creep Tests

High development degree of microfissures (with the aperture less than 0.1 mm), which is the principal factor that affects coal creep behavior, is the main physical characteristic of coal. Figure 1 shows the micromorphology of anthracite coal samples collected from Jiulishan Coal mine using a JSM-6390/LV scanning electron microscope (SEM), where several fractures can be clearly observed. The data of the industrial analysis and basic parameters of coal sample are also listed in

Table 1. Industrial analysis and basic parameters of coal sample.

Parameter	Value	Parameter	Value
Adsorption constant a	29.412 m3/t	Mad	0.44%
Adsorption constant b	2.252 MPa−1	Ad	8.12%
True density	1.56 g·cm−3	Vdaf	10.58%
Apparent density	1.49 g·cm−3	FCad	80.86%

. These fractures are affected by the influence of coal-forming and geological processes, and a large number of intricate fissure networks were generated. Stress concentration will be firstly formed around fractures during the loading process, thereby causing local damage and inhomogeneous deformation inside the coal, and further inducing a weakening effect on the mechanical strength. When this weakening effect accumulates to a certain extent, the fractures will expand rapidly, thereby accelerating the instability and failure of the coal. Especially for newly exposed coals affected by pressure relief, massive secondary fractures were generated and resulted in significant creep characteristics. To determine the special physical properties of coal, this study performed a series of triaxial compression creep tests with stepwise loading on coal specimens and analyzed the creep laws under different stress levels to introduce a new model suitable for describing coal creep behavior.

2.1. Specimen Preparation and Experimental Set-Up

The coal samples used in the multistage creep tests were selected from an underground mining face in Jiulishan Coal mine (Figure 2a,b). In accordance with the experimental specification recommended by the International Society for Rock Mechanics (ISRM) [20], the specimens were cored from intact coal blocks and prepared to the standard cylindrical dimensions with a diameter and height of 50 mm and 100 mm, respectively (Figure 2c). The triaxial creep tests were performed on the RLW-500G coal–rock triaxial creep experimental system (Figure 2d), which is equipped with features, such as axial loading, confining pressure loading, pore pressure loading, servo system, control system, data acquisition, and automatic drawing system. The digital servo controller is used in the control part of the axial loading and confining pressure loading systems, which can automatically complete the triaxial creep tests.

The main technical parameters of the RLW-500G experimental device are presented as follows:

(a)

The main engine adopts a framework structure with stiffness of more than 5000 kN/mm.

(b)

The maximum axial capacity is 500 kN, with measure resolution and precision less than 2.5 N and 1%, respectively. The maximum confining pressure is 50 MPa, with a measure resolution and precision of less than 0.001 MPa and ±1%, respectively.

(c)

Axial and radial extensometer deformation measuring ranges are 0–15 mm and 0–7 mm, respectively; and the measuring accuracy is ±0.5%.

(d)

Limit control system: When the parameters of axial deformation, radial deformation, or test time reach a preset value, or the specimen split, oil pipe blockage, and oil temperature too high, the device can be automatically stopped for self-protection.

2.2. Experimental Scheme

The loading methods used in the creep test include single-stage and multistage loading. Multistage loading, which has the advantages of convenient operation and a high adoption rate, was applied in this work for the triaxial compressive creep tests of coal specimens.

Because the low gas pressure and small confining pressure of collected coal sample taken from the mining face in the Jiulishan mine are low, the experimental conditions were set during the experimental process to simulate the real underground field conditions: 1 MPa confining pressure, 0.2 MPa gas pressure, and 25 °C ambient temperature. The specific experimental procedures are presented as follows:

First, initial axial and confining pressures were applied to 1 MPa at a rate of 200 N/s. Second, the cylinder intake valve was opened to introduce methane gas into the triaxial-gripper of the specimen until the inlet pressure reached the preset experimental value. Third, the adsorption state was maintained for 24 h to simulate the original adsorption of gas-filled coal. Subsequently, axial stress was loaded at a rate of 100 N/s to the preset value of 5 MPa. Each axial stress stage was maintained for a sufficient time until axial strain trended to be stable. Afterwards, the next stage of axial stress was loaded again, in which the gradient of axial compression is 10 MPa, until the specimen failed. Finally, the next coal specimen was replaced for testing. The axial strain data were recorded during the experiment.

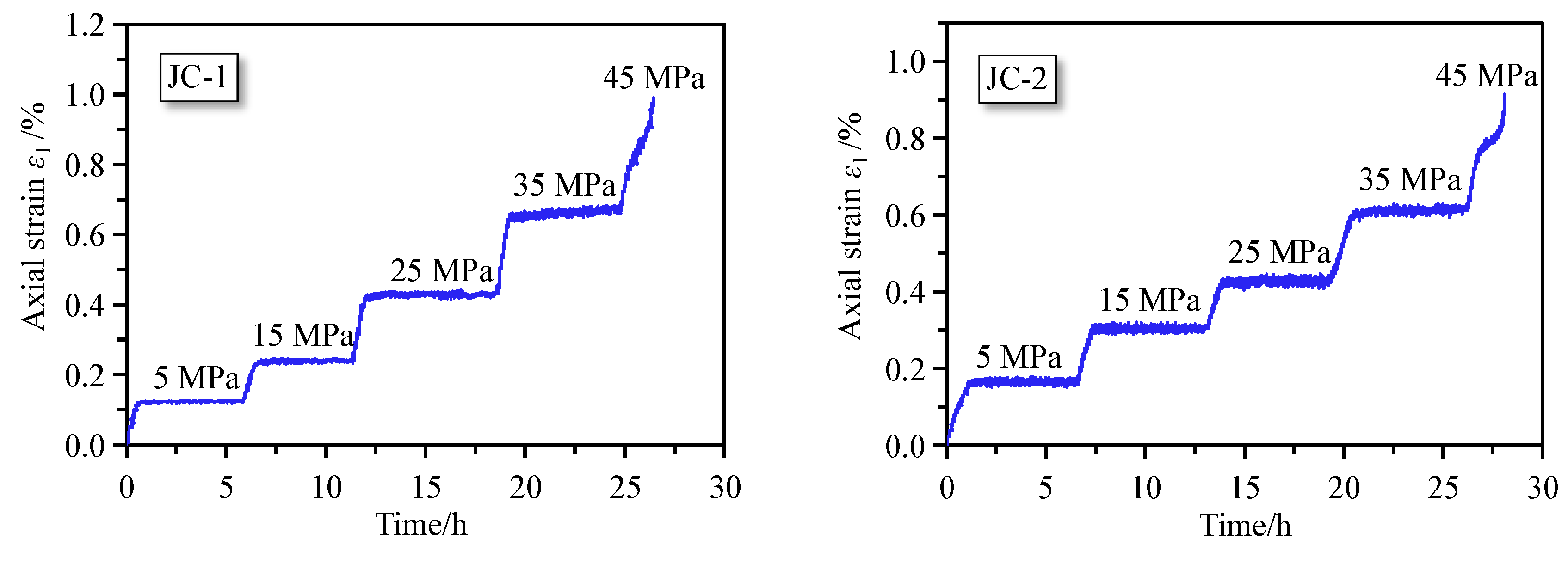
2.3. Experimental Results

The creep curves of increased deviatoric stress gradings on coal specimens can be obtained from multistage loading creep tests. However, the experimental results present differences owing to the complexity of fractures in different coal specimens. Therefore, JC-1 and JC-2, which are the most representative coal specimens, are analyzed in Figure 3.

To further investigate the creep behavior of coal specimens under different stress levels, the whole creep curves were transformed into multiple curves with various creep loads according to the data processing method for multistage loading creep test proposed on the basis of comprehensive superposition principle [21]. The results are shown in Figure 4.

Figure 4 shows that the creep characteristics of coal specimens greatly varied under different stress levels. Axial strain continuously increased with stress during the graded loading process. The test results show that when stress was less than 35 MPa, the creep rate of specimens JC-1 and JC-2 (i.e., both underwent decelerating and steady state creeps) decreased with time. Finally, coal strain tended to a certain value. When the load reached 45 MPa, the creep rate decreased first and then increased with time. For example, specimen JC-1 was developed directly from decelerating creep to accelerating creep stage at 1.0 h. Specimen JC-2 also experienced a short period of steady state creep and swiftly developed into accelerating creep. During the accelerating creep, the coal specimens easily exhibited inconsistent deformations owing to the sharp increase in axial strain, thereby aggravating the formation and convergence of fractures inside the coal, leading to the complete failure of the whole specimen. The failure characteristics of the coal specimens in Figure 5 show that the failure of coal specimens was mainly caused by a dominant crack that split the whole specimen into several thin sheets. Therefore, the monitoring of coal creep characteristics in the process of underground mining is of great engineering significance.

The multistage creep test results show that the coal creep characteristics under different stress levels are significant. According to the stress on coal specimen, the creep types can be divided into decay and non-decay creeps (Figure 6).

If the stress level is less than the yield stress of the coal, then coal presents decay creep, which is only characterized by decelerating (I) and steady state creep (II). However, when the stress level is larger than the yield stress, the coal exhibits non-decay creep performance, which includes decelerating (I), steady state (II), and accelerating (III) creep stages.

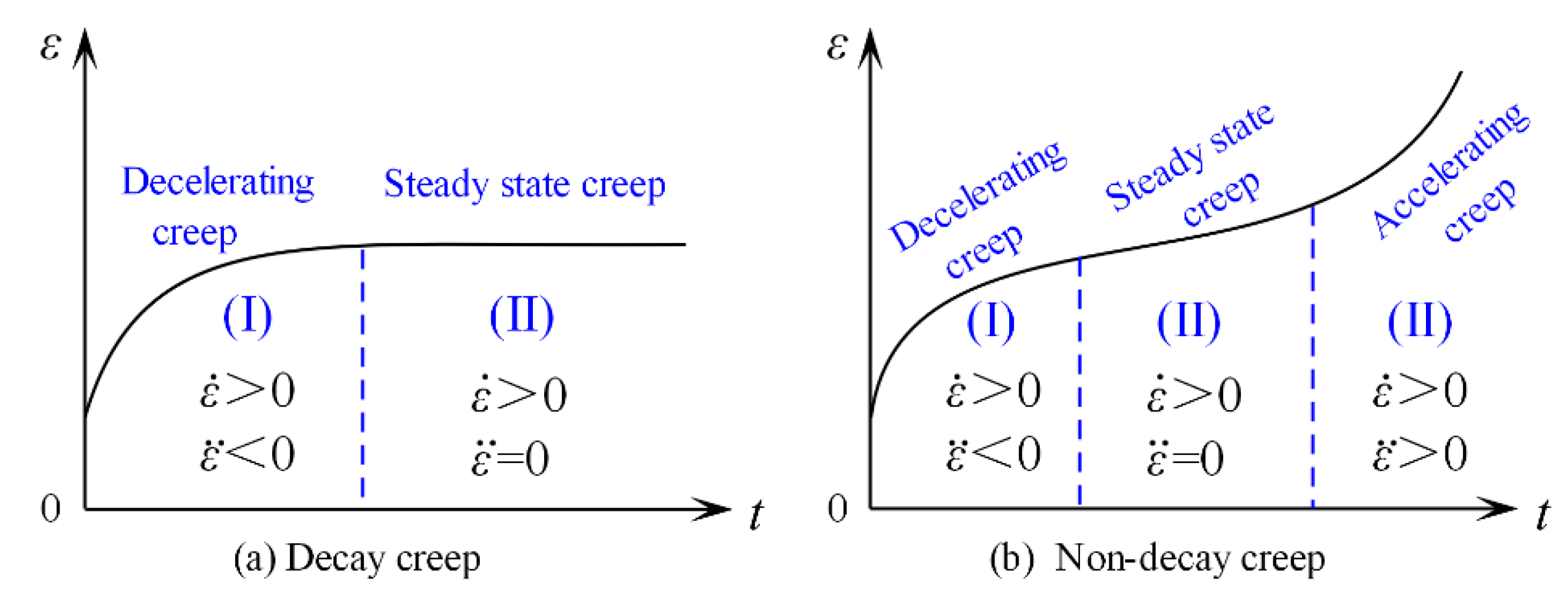
(1)

In decelerating creep, creep rate decreases with the increase in axial strain, that is, creep rate $\dot{\epsilon }$ > 0 and creep acceleration $\ddot{\epsilon }$ < 0. The creep curve in this stage presents a convex shape.

(2)

In steady state creep, the coal strain tends to be constant along with time, that is, creep rate $\dot{\epsilon }$ > 0 and creep acceleration $\ddot{\epsilon }$ = 0, with a linear change tendency of creep curve.

(3)

In accelerating creep, when the coal strain goes beyond the yield point, the axial strain and creep rate increase rapidly, that is, creep rate $\dot{\epsilon }$ > 0 and creep acceleration $\ddot{\epsilon }$ > 0, and the creep curve is presented as a concave shape.

The aforementioned analysis shows that the convex–concave features of a coal creep curve will be changed only when non-decay creep occurs. Therefore, the coal creep types can be recognized by the convex–concave variation. We assume that the coal strain ε(t) is a function of time. Thus, if the inflection point of the creep curve does not appear, then only decelerating and steady state creep occur, and the curve is convex. The coal will only enter the accelerating creep stage when the inflection point appears. At this time, the concave–convex property of the creep curve also changes. Therefore, the existence of an inflection point in the creep curve is a necessary and sufficient condition to judge the occurrence of accelerating creep of coal. If the occurrence time of the inflection point can be accurately predicted, then some effective protective measures can be considered in time to control the potential safety hazards of coal instability and failure. For this reason, finding the creep inflection point by establishing a creep mathematical model that can describe the nonlinear change characteristic of coal strain with time is important.

3. Analysis of Classical Nishihara Model

As for the study in the creep models of coal and rock, the classical Nishihara model (Figure 7), which consists of a generalized Kelvin and ideal viscoplastic body, is characterized by a simple model structure and can fully reflect the elastic–viscoelastic–viscoplastic characteristics of rock. Therefore, the model has been widely used in rock rheology.

The Nishihara model is only suitable for describing the decelerating and steady state creep characteristics of soft rock, because all the components used in this model are linear [22,23]. We assume that the volume change of coal is elastic, and coal deformation is caused by deviatoric stress. Thus, if deviatoric stress is less than yield stress, that is, (σ₁ − σ₃) < S_h, then the creep equation of the classical Nishihara model under equal confining pressure conditions is given by the following [24]:

$$\epsilon =\frac{\left({\sigma }_1-{\sigma }_3\right)}{3G_1}+\frac{\left({\sigma }_1-{\sigma }_3\right)}{3G_2}\left[1-\exp \left(-\frac{G_2}{{\eta }_1}t\right)\right]+\frac{\left({\sigma }_1-{\sigma }_3\right)-S_h}{3{\eta }_2}t,\left({\sigma }_1-{\sigma }_3\right)<S_h,$$

(1)

where ε is the strain of the model; σ₁ and σ₃ are the first and third principal stresses, respectively; G₁ and G₂ are the shear modulus of generalized Kelvin and ideal viscoplastic body, respectively; η₁ and η₂ are the viscosity coefficients; S_h is the deviatoric yield stress of the model; and t is the creep time.

In accordance with Equation (1), the analytical software MATLAB was used to fit the creep test data of coal specimens with decay creep characteristic under 35 MPa.

Table 2. Parameter values of classical Nishihara model.

Specimen	σ1/MPa	G1/GPa	G2/GPa	η1/(GPa·h)	R2
JC-1	5	15.049	39.493	5.339	0.963
	15	24.120	102.695	18.413	0.969
	25	23.091	97.723	16.608	0.956
	35	18.025	286.917	352.267	0.934
JC-2	5	9.814	44.575	6.066	0.937
	15	17.452	128.684	9.252	0.925
	25	20.630	194.027	33.941	0.931
	35	19.599	317.160	136.092	0.953

shows the fitting results of the model parameters, and Figure 6 depicts the comparison results between fitting curves and test data.

Table 2 shows that all coefficients of determination R² of the model parameters are above 0.925, which indicates that the classical Nishihara model is well fit to the data of decay creep of coal. The data from Table 2 are substituted into Equation (1) to obtain the creep curves of coal specimens (Figure 8). The fitting curves coincide with the creep test data, indicating that the classical Nishihara model can describe the decelerating and steady state creep behavior satisfactorily. Thus, fitting decay creep characteristic using the classical Nishihara model is appropriate.

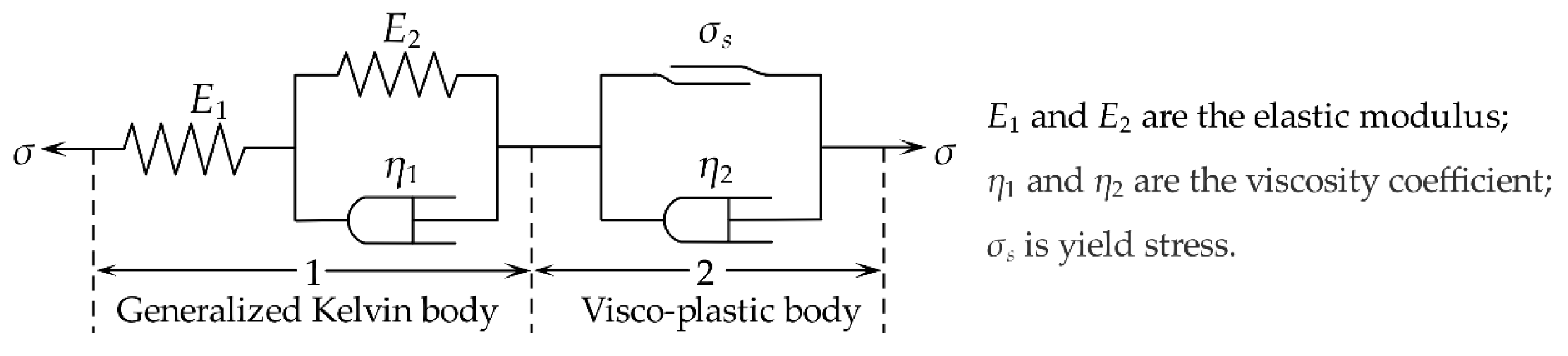
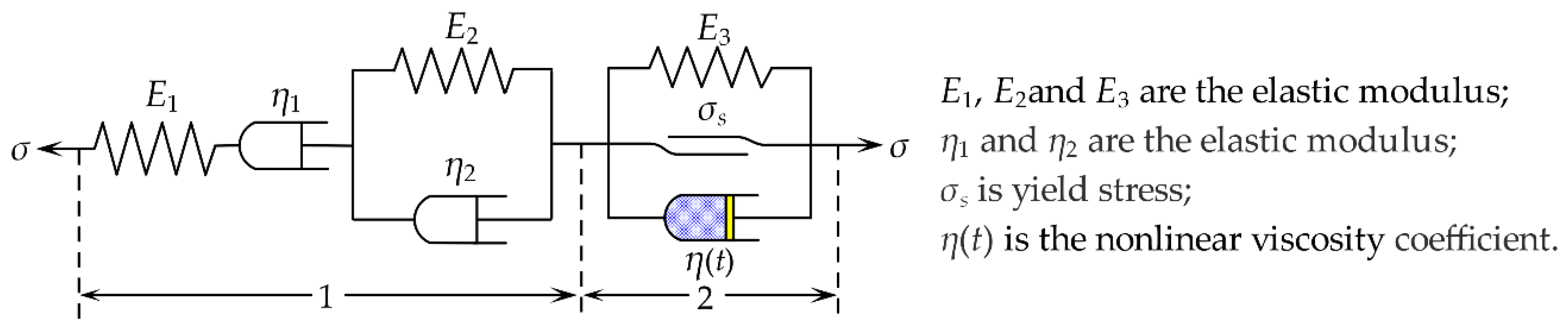
4. Establishment of Nonlinear Viscoelastic–Plastic Creep Model

Considering that linear units are used in the classical Nishihara model, it cannot accurately reflect the nonlinear increase in strain with time in the accelerating creep stage. At present, the nonlinear creep model can be established using two approaches. One is the nonlinear revision of the traditional linear component, and the other is to build a nonlinear relationship between strain and time using damage mechanics or fracture mechanics theory. This study selected the first method to propose a new nonlinear viscoelastic–plastic creep model to enhance the applicability of the creep model in reflecting coal creep behavior. The concrete ideas are presented as follows:

At first, the accelerating creep curve was analyzed by empirical formula, and a non-Newtonian component with exponential variation law was presented. The non-Newtonian component was connected with elastic and plastic components in parallel by stress triggering to compose a nonlinear viscoelastic–plastic body to reflect the creep characteristic of coal in the accelerating creep stage. Subsequently, it was replaced with the ideal viscoplastic body in the classical Nishihara model to establish the nonlinear creep model.

4.1. Model Development

4.1.1. Improvement of Non-Newtonian Component

Remarkable nonlinear change tendencies that existed between coal strain and creep time were detected through the creep tests. Therefore, a non-Newtonian component can be used to characterize the direct proportional relation between stress and strain acceleration. Here, we used the exponential function to fit the creep test data of the accelerating creep stage, and the function equation is described as follows:

$$\epsilon ={\epsilon }_0+A\exp \left(nt\right),$$

(2)

where ε₀ is the initial strain of the accelerating stage; A is the fitting parameter; and n is the acceleration index, n > 0.

The comparison results between the test data and fitting curves of accelerated creep stage of coal specimens shown in Figure 9 can be obtained on the basis of Equation (2), and the parameter fitting results are listed in

Table 3. Parameter identification of accelerating creep stage

Specimen	ε0	A	n	R2
JC-1	0.8306	1.658×10−3	3.1724	0.9656
JC-2	0.7946	2.24×10−5	6.4569	0.9765

.

Table 3 shows that the square of correlation coefficient R² of the fitting results reaches up to 0.96, demonstrating that the use of the exponential function is a feasible method for describing the accelerating creep stage curve of coal. Hence, this non-Newtonian component with exponential change law can be used instead of the ideal viscous component of the classical Nishihara model, which has a constitutive equation as follows:

$$\sigma =\eta \left(t\right)\frac{\mathrm{d}\epsilon }{\mathrm{d}t}=\eta \left(t\right)\dot{\epsilon }.$$

(3)

Coal strain can be calculated by integrating Equation (3) as follows:

$$\epsilon =\frac{\sigma }{\eta \left(t\right)}t+C.$$

(4)

The non-Newtonian component expression can be obtained by equating Equation (2) to Equation (3) and taking A = σ/η₀, C = ε₀ as follows:

$$\eta \left(t\right)=\frac{{\eta }_{0}t}{\exp \left(nt\right)},$$

(5)

where η(t) and η₀ are the nonlinear and initial viscosity coefficients of non-Newtonian unit, respectively.

4.1.2. Introduction of Negative Elastic Modulus E₃ (Shear Modulus G₃)

For the rheological mechanics of rock engineering, when the visco–elastic flow develops to a certain extent, it will transform into a visco-plastic flow state. The correlation research indicates that accelerating creep may occur in coal and other strain-softening materials [25]. Thus, the elastic potential energy will gradually decrease as creep deformation develops. At this time, the flow rule of coal and rock mass should be similar to that of viscoelastic–plastic flow. Thus, a negative elastic modulus, E₃ (corresponding to the shear modulus G₃ under 3D stress condition), can be introduced parallel with the viscoplastic component to construct a new nonlinear viscoelastic–plastic body (Figure 10). This viscoelastic–plastic body characterizes the yield that weakens with the increase in coal strain in the accelerating creep stage. It also indicates the process of releasing elastic potential energy.

According to a series of rules, the nonlinear viscoelastic–plastic body in the one-dimensional (1D) case obeys the following relationships:

$$\{\begin{array}{l}\epsilon ={\epsilon }_1={\epsilon }_2={\epsilon }_3\\ \sigma ={\sigma }_1+{\sigma }_2+{\sigma }_3\end{array}.$$

(6)

Consequently, the constitutive relation of this nonlinear viscoelastic-plastic body is described as follows:

$$\sigma -{\sigma }_s=E_3\epsilon +\eta \left(t\right)\dot{\epsilon }.$$

(7)

On the basis of the initial condition, t = 0, ε = 0, the creep solution of the nonlinear viscoelastic–plastic body can be obtained by integrating constitutive Equation (7):

$$\epsilon =\frac{\sigma -{\sigma }_s}{E_3}\left[1-\exp \left(-\frac{E_3}{\eta \left(t\right)}t\right)\right]=\frac{\sigma -{\sigma }_s}{E_3}\left\{1-\exp \left[-\frac{E_3}{{\eta }_0}\exp \left(nt\right)\right]\right\}.$$

(8)

The creep rate and creep acceleration of the nonlinear viscoelastic–plastic body are solved by taking the first and the second derivatives of Equation (8) as follows:

$$\{\begin{array}{l}\dot{\epsilon }=n\frac{\sigma -{\sigma }_s}{{\eta }_0}\exp \left[nt-\frac{E_3}{{\eta }_0}\exp \left(nt\right)\right]\\ \ddot{\epsilon }=n^2\frac{\sigma -{\sigma }_s}{{\eta }_0}\exp \left[nt+1-2\frac{E_3}{{\eta }_0}\exp \left(nt\right)\right]\end{array},$$

(9)

where $\dot{\epsilon }$ is the creep rate and $\ddot{\epsilon }$ is the creep acceleration.

Equations (8) and (9) show that strain ε is the function of time t during the coal creep process. Only when E₃ < 0 can the creep rate and creep acceleration be above zero, because the acceleration index n, yield stress σ_s, and nonlinear viscosity coefficient η(t) are the constants that are greater than zero, indicating that the strain of the nonlinear viscoelastic–plastic body will increase over time. Therefore, E₃ < 0 not only has mathematical significance, but also has definite physical meaning that describes the process of releasing elastic potential energy in the accelerating creep stage. Therefore, this non-linear viscoelastic–plastic unit can be used to capture the changing regularity of accelerating creep.

4.2. Nonlinear Viscoelastic–Plastic Creep Model

The nonlinear viscoelastic–plastic body in Figure 10 can be replaced by the ideal viscoplastic body in the classical Nishihara model to establish a new nonlinear viscoelastic–plastic creep model with six elements, because its accelerating creep characteristics are improved. Figure 11 shows the improved method for describing the non-decay creep characteristic of coal mass.

According to the improved model in Figure 11, if the value of constant stress σ is less than σ_s, then the model is in a viscoplastic state, that is, Part 2, is rigid and only Part 1 deforms in the model. Therefore, the improved model degenerates into a generalized Kelvin body. However, if the constant stress σ is more than σ_s, Part 1 and Part 2 both deform in the model, and the nonlinear viscoelastic–plastic creep model meets the following formulation:

$$\{\begin{array}{ll}\epsilon ={\epsilon }_1+{\epsilon }_2+{\epsilon }_3,& \sigma ={\sigma }_1={\sigma }_2={\sigma }_3\\ {\sigma }_1=E_1{\epsilon }_1,& {\sigma }_2=E_2{\epsilon }_2+{\eta }_2{\dot{\epsilon }}_2\\ {\sigma }_3={\sigma }_s+E_3{\epsilon }_3+\eta \left(t\right){\dot{\epsilon }}_3& \end{array}.$$

(10)

The creep equations of the improved model under 1D stress state can be expressed on the basis of Equation (10) as follows:

$$\{\begin{array}{ll}\epsilon =\frac{\sigma }{E_1}+\frac{\sigma }{E_2}\left[1-\exp \left(-\frac{E_2}{{\eta }_1}t\right)\right],& \sigma <{\sigma }_s\\ \epsilon =\frac{\sigma }{E_1}+\frac{\sigma }{E_2}\left[1-\exp \left(-\frac{E_2}{{\eta }_1}t\right)\right]+\frac{\sigma -{\sigma }_s}{E_3}\left\{1-\exp \left[-\frac{E_3}{{\eta }_0}\exp \left(nt\right)\right]\right\},& \sigma \ge {\sigma }_s\end{array}.$$

(11)

Underground coal and rock masses are usually subject to complex 3D stress states. Therefore, deducing the creep model under 3D conditions is of great engineering significance. In the 3D stress state, the coal stress tensor σ_ij can be decomposed as a spherical stress tensor σ_m and deviatoric stress tensor S_ij, which can be represented as follows [26]:

$${\sigma }_{ij}=S_{ij}+{\delta }_{ij}{\sigma }_m,$$

(12)

where δ_ij is the Kronecker function.

Generally, a spherical stress tensor σ_m only changes the volume of an object, and deviatoric stress tensor S_ij only changes the shape. Similarly, strain tensor ε_ij can also be divided into spherical strain tensor ε_m and partial strain tensor e_ij. Thus, ε_m and e_ij are given by the following:

$${\epsilon }_{ij}=e_{ij}+{\delta }_{ij}{\epsilon }_m.$$

(13)

Typically, coal and rock masses can be regarded as isotropic media in the mechanical analysis. On the basis of the broad sense of Hook’s law, the constitutive relationship under the 3D stress state can be defined as follows:

$${\sigma }_m=3K{\epsilon }_m,S_{ij}=2G{e}_{ij},$$

(14)

where K and G are the bulk and shear moduli, respectively.

For simplicity, we assumed that the creep deformation is only caused by deviatoric stress tensor S_ij. Thus, the 3D creep equation can be described as follows:

$$\{\begin{array}{ll}\epsilon =\frac{S_{ij}}{2G_1}+\frac{S_{ij}}{2G_2}\left[1-\exp \left(-\frac{G_2}{{\eta }_1}t\right)\right],& \sigma <{\sigma }_s\\ \epsilon =\frac{S_{ij}}{2G_1}+\frac{S_{ij}}{2G_2}\left[1-\exp \left(-\frac{G_2}{{\eta }_1}t\right)\right]+\frac{\sigma -{\sigma }_s}{2G_3}\left\{1-\exp \left[-\frac{G_3}{{\eta }_0}\exp \left(nt\right)\right]\right\},& \sigma \ge {\sigma }_s\end{array}.$$

(15)

However, most conventional triaxial compression tests are conducted under constant confining pressure conditions, in which case σ₂ = σ₃. By substituting S_ij = (σ₂ − σ₃) into Equation (14), the axial strain in nonlinear viscoelastic–plastic creep model can be deduced as follows:

$$\{\begin{array}{ll}\epsilon =\frac{{\sigma }_1-{\sigma }_3}{3G_1}+\frac{{\sigma }_1-{\sigma }_3}{3G_2}\left[1-\exp \left(-\frac{G_2}{{\eta }_1}t\right)\right],& \sigma <{\sigma }_s\\ \epsilon =\frac{{\sigma }_1-{\sigma }_3}{3G_1}+\frac{{\sigma }_1-{\sigma }_3}{3G_2}\left[1-\exp \left(-\frac{G_2}{{\eta }_1}t\right)\right]+\frac{\left({\sigma }_1-{\sigma }_3\right)-{\sigma }_s}{3G_3}\left\{1-\exp \left[-\frac{G_3}{{\eta }_0}\exp \left(nt\right)\right]\right\},& \sigma \ge {\sigma }_s\end{array}.$$

(16)

5. Model Validation and Parametric Analysis

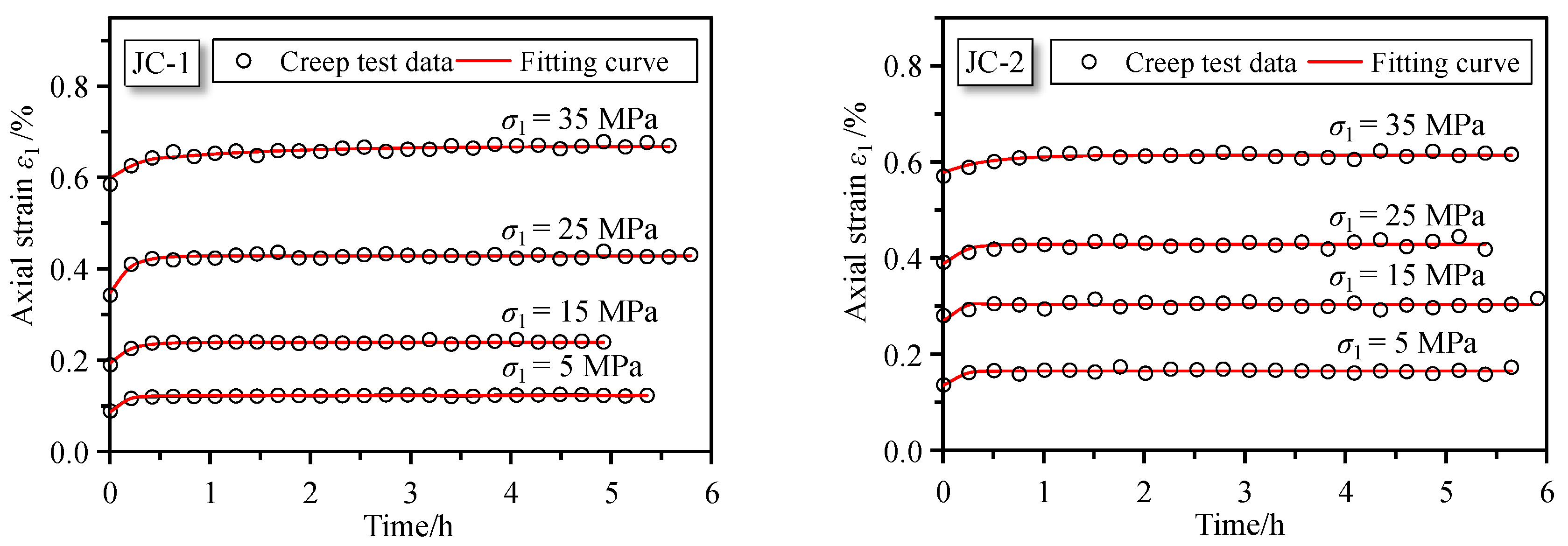
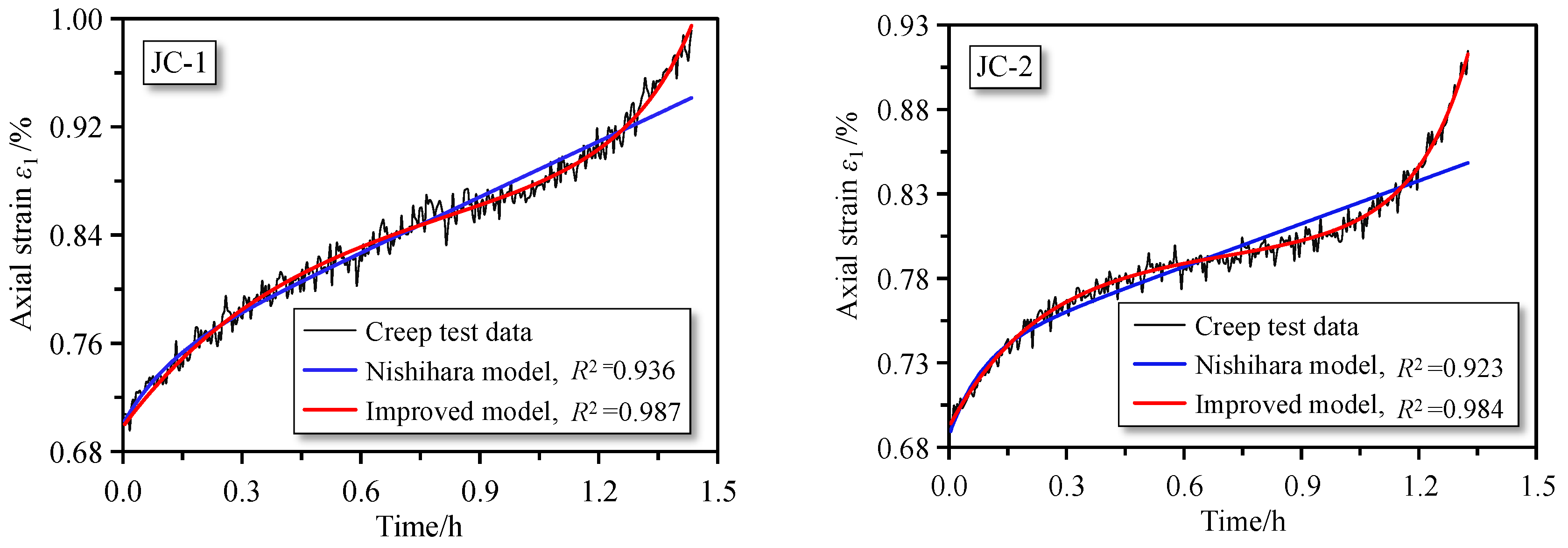
5.1. Model Validation

At present, the main methods used to determine model parameters include regression analysis, least squares, rheological curve decomposition, and the optimization separation method [27]. Among these methods, the least squares method is the most widely used in identifying creep parameters. However, it cannot perfectly address nonlinear problems. Thus, the final result will not converge or may converge to the local minimum if the selection of the iterative initial value is unreasonable. In addition, this method has a slow convergence rate. For this reason, the universal global optimization algorithm (UGO) in 1stop analysis software was used in this study to fit the non-decay creep curves in coal creep tests. The greatest advantage of this method is that the initial value of parameters is randomly given by the program, and the optimal solution can be found through its UGO algorithm, which can avoid the selection of initial parameters, thus enabling the rapid and precise identification of the model parameters [28].

Because the non-linear viscoelastic–plastic creep model proposed in this work was improved for the accelerating creep characteristics, the experimental data under 45 MPa with non-decay creep characteristics were used to validate the improved model using 1stop in accordance with the second item (σ ≥ σ_s) in Equation (15). Meanwhile, the fitting results were also compared with the classical Nishihara model. The parameter fitting results of different creep models are listed in

Table 4. Parameter fitting results of different creep models.

Model	Specimen	G1/GPa	G2/GPa	G3/GPa	η1/(GPa·h)	η0/(GPa·h)	η2/(GPa·h)	n	Sh/MPa	R2
Improved model	JC-1	20.080	86.918	−164.902	37.604	451.877	-	1.507	41.027	0.987
	JC-2	21.213	144.289	−11.506	34.096	8.211	-	1.114	43.991	0.984
Nishihara model	JC-1	20.815	455.497	-	47.673	-	0.010	-	43.999	0.936
	JC-2	21.326	305.679	-	24.715	-	0.361	-	43.969	0.923

Notes: G₁, G₂, and G₃ are the shear modulus; η₁ and η₂ are the viscosity coefficient, respectively; η₀ and η(t) are the initial and nonlinear viscosity coefficients, respectively; n is the acceleration index; S_h is the deviatoric yield stress of the model.

, and the comparison results of the fitting curves and test data are shown in Figure 12.

Table 4 shows that all the squares of correlation coefficient R² of the nonlinear viscoelastic–plastic creep model are above 0.98, which is higher than those of the classical Nishihara model, thereby showing good agreement with the experimental data. Combining the comparison results in Figure 12, the classical Nishihara model can reflect the decelerating creep and steady state creep stages, but the fitting curves still maintain a linear tendency during the accelerating creep, thus deviating from the experimental data and resulting in a large discrepancy. By contrast, the fitting curves obtained by the improved model basically coincide with the experimental data and exhibit an exponential increasing law that can describe the full creep stage of coal, especially the accelerating creep stage, in which the coal strain gradually increased with time. Furthermore, the fitting results demonstrate the high applicability and superiority of the proposed nonlinear viscoelastic–plastic creep model.

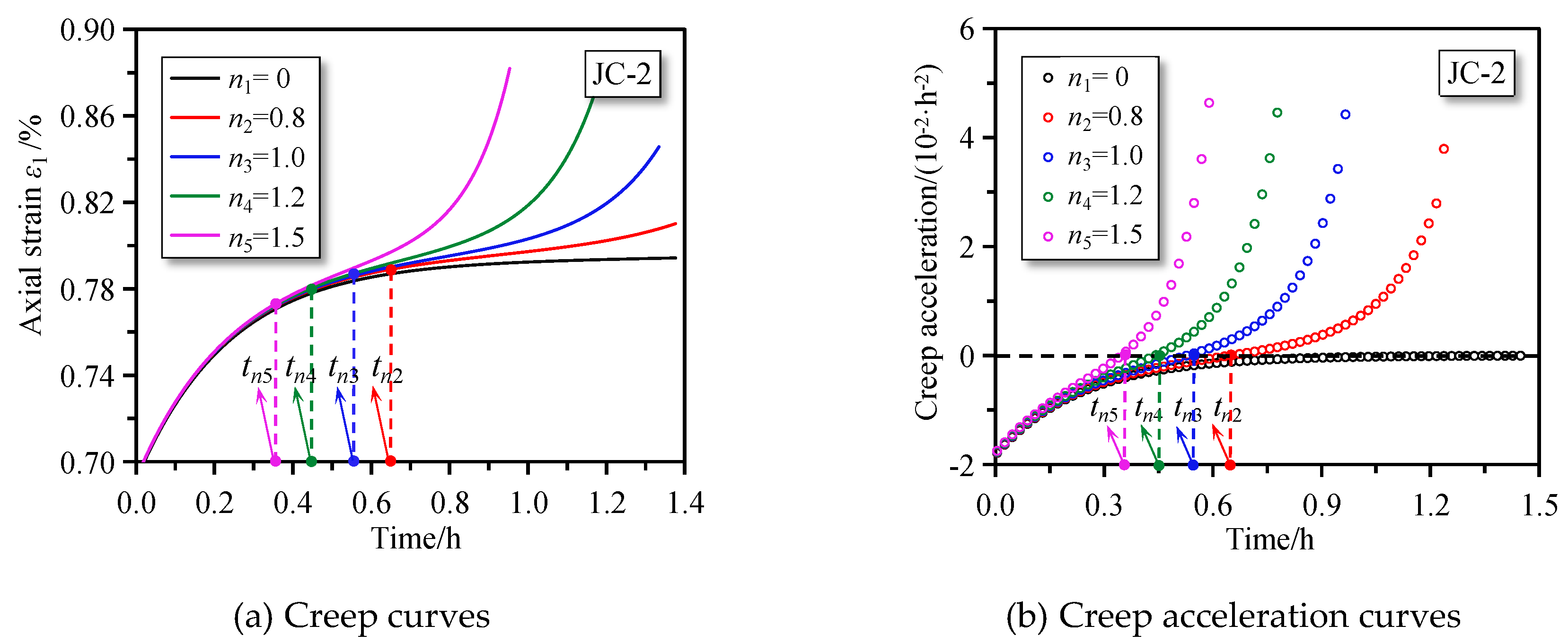
5.2. Parametric Sensitivity Analysis

A negative elastic modulus E₃ (corresponding to the shear modulus G₃) and a non-Newtonian component with exponential change laws are introduced in the improved model. The introduction is necessary to describe the non-decay creep characteristics of coal, among which the negative elastic modulus E₃ represents the release of elastic potential energy during the accelerating creep stage. In addition, the acceleration creep index n of the non-Newtonian component can embody the accelerated creep rate. To further analyze the sensitive effect of n value on coal creep deformation, the creep acceleration equation can be deduced from Equation (15), as shown in Equation (16). With specimen JC-2 as a sample, the creep curves and creep acceleration curves with different acceleration creep indexes n (n = n₁, n₂, n₃, n₄, n₅) are shown in Figure 13.

$$\ddot{\epsilon }=-\frac{\left({\sigma }_1-{\sigma }_3\right)G_2}{3{\eta }_1^2}\exp \left(-\frac{G_2}{{\eta }_1}t\right)+n^2\frac{\left[\left({\sigma }_1-{\sigma }_3\right)-{\sigma }_s\right]}{3{\eta }_0}\exp \left[nt+1-\frac{2G_3}{{\eta }_0}\exp \left(nt\right)\right],\sigma \ge {\sigma }_s.$$

(17)

Figure 13a shows that when n = 0, the relationship between axial strain and creep time is linear. Thus, the non-Newtonian component degenerates into an ideal Newtonian unit. While n > 0, the concavity–convexity of the coal creep curve will be changed, and the axial strain increases nonlinearly and presents non-decay creep characteristic. When the value of acceleration creep index n is large, the increasing rate of coal strain is fast, and the corresponding creep inflection point also appears early.

Subsequently, further analysis on creep acceleration in accordance with Figure 13b shows that if n = 0, then creep acceleration gradually increases to the zone, that is, $\underset{t\to \infty }{\lim }\ddot{\epsilon }=0$. However, if n > 0, then the creep acceleration of coal tends to be infinite along with time in the non-decay creep process, that is, $\underset{t\to \infty }{\lim }\ddot{\epsilon }=+\infty$. The corresponding creep inflection point only appears when $\ddot{\epsilon }=0$. The creep instability condition, that is, $\ddot{\epsilon }$ > 0, suggests that coal will fail once it enters into the accelerating creep stage. In other words, the value of accelerating creep index n is directly proportional to the instability level, that is, a large n value results in the early occurrence of coal failure.

If we can accurately predict the occurrence time of the instability failure of coal and take effective protective measures in time during the actual underground production process, then various geologic hazards and potentially fatal accidents can be reduced to a large extent. The aforementioned analysis suggests that the linear viscoelastic–plastic creep model proposed in this study can accurately reflect the non-decay creep characteristics of coal. Thus, the occurrence time of the creep inflection point can be predicted via model calculation. If the creep inflection point does not appear, then coal instability will not occur. Conversely, once the creep inflection point emerges, the accelerating creep of coal will happen. Then, the occurrence time can be deduced to judge whether or not coal failure, which is crucial for the prevention and control of coal and rock dynamic disasters, will happen.

6. Conclusions

This study aims at developing a nonlinear model to describe the viscoelastic–plastic creep behavior of coal. The proposed model consisted of a generalized Kelvin and improved viscoelastic–plastic body using the method of empirical equation and component combination. The validity of the proposed model and the sensitivity of the model parameters were verified and analyzed on the basis of the experimental data. The main conclusions of this study are presented as follows:

(1)

A series of multistage creep tests was performed on coal specimens with different stress levels and found that the concavity–convexity in creep curves will be changed when coal enters accelerating creep stage. That is, a creep inflection point is found on the creep curve. If the occurrence time of the creep inflection point can be accurately predicted, then some effective protective measures can be taken in time to avoid the potential safety hazards caused by coal instability and failure.

(2)

The exponential function was used to fit the accelerating creep data of coal specimens and achieved the desired results. Thus, a non-Newtonian component was proposed to replace the ideal Newtonian component. Furthermore, a negative elastic modulus E₃ (shear modulus G₃) was introduced to establish a nonlinear viscoelastic–plastic body to describe the accelerating creep characteristics of coal. Therefore, a new nonlinear viscoelastic–plastic creep model that consists of a generalized Kelvin and improved viscoelastic–plastic body was proposed, and the creep equation of the improved model under constant confining pressure was also derived.

(3)

1 stop analysis software was used to fit the experimental data of the non-decay creep characteristics in the coal multistage creep tests based on the proposed nonlinear viscoelastic–plastic creep model. The results show that the fitting correlation coefficients have R² values above 0.98, and the fitting curves are highly consistent with the experimental data, which can accurately describe the non-decay creep characteristic of coal and verify the correctness and applicability of the model.

(4)

The analyses of creep rate and creep acceleration curves using different acceleration creep indexes n show that if n = 0, then the non-Newtonian component will degenerate into the ideal Newtonian body, and only the decelerating and steady-state creeps of coal will occur. If n > 0, then coal specimens will present non-decay creep characteristic. When the acceleration creep index n is large, the level of creep acceleration increases, and the occurrence of coal instability appears earlier.