Weighting Factor Selection of the Ensemble Model for Improving Forecast Accuracy of Photovoltaic Generating Resources
Abstract
1. Introduction
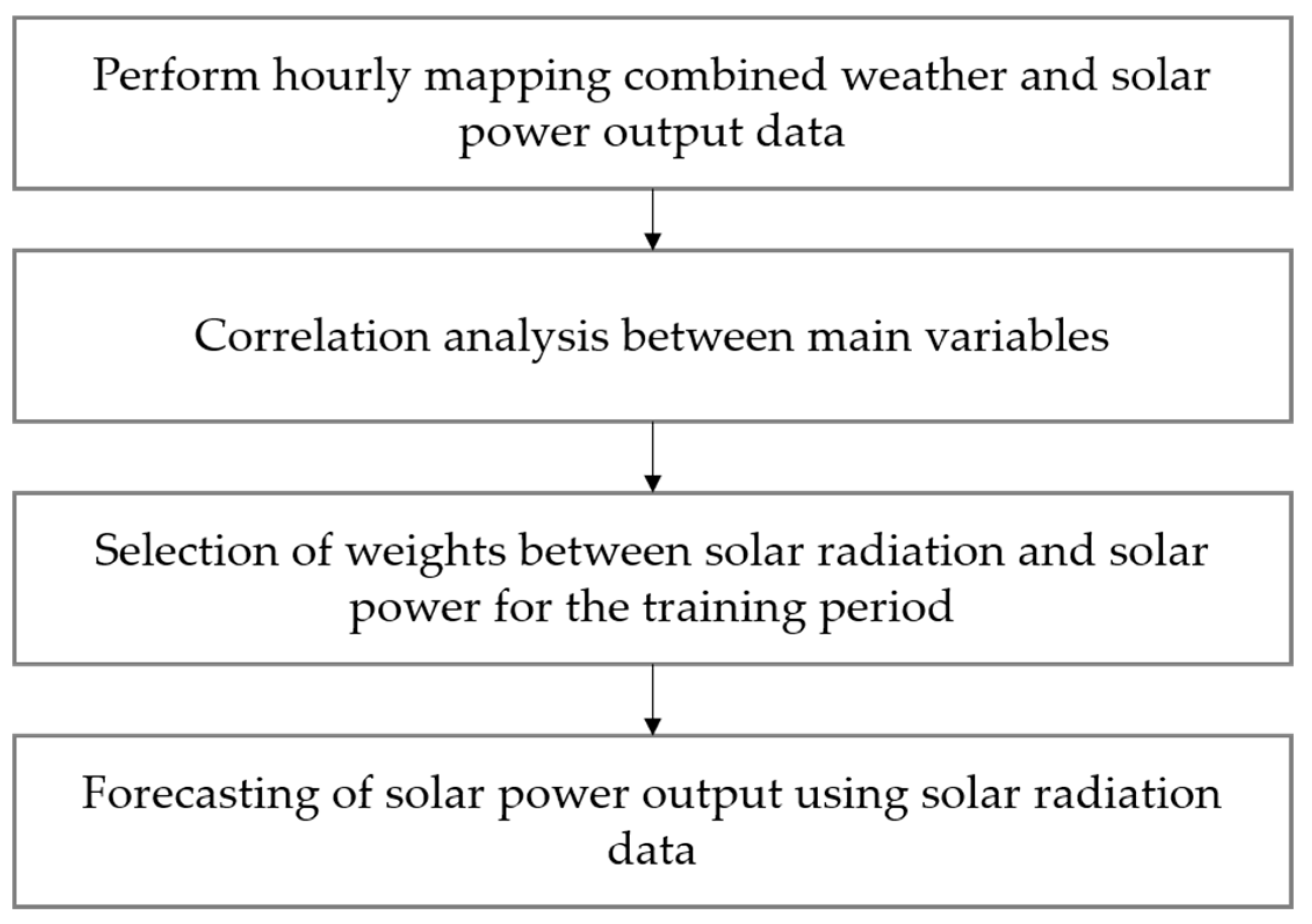
2. Power Output Forecasting Model of Photovoltaic Generating Resources
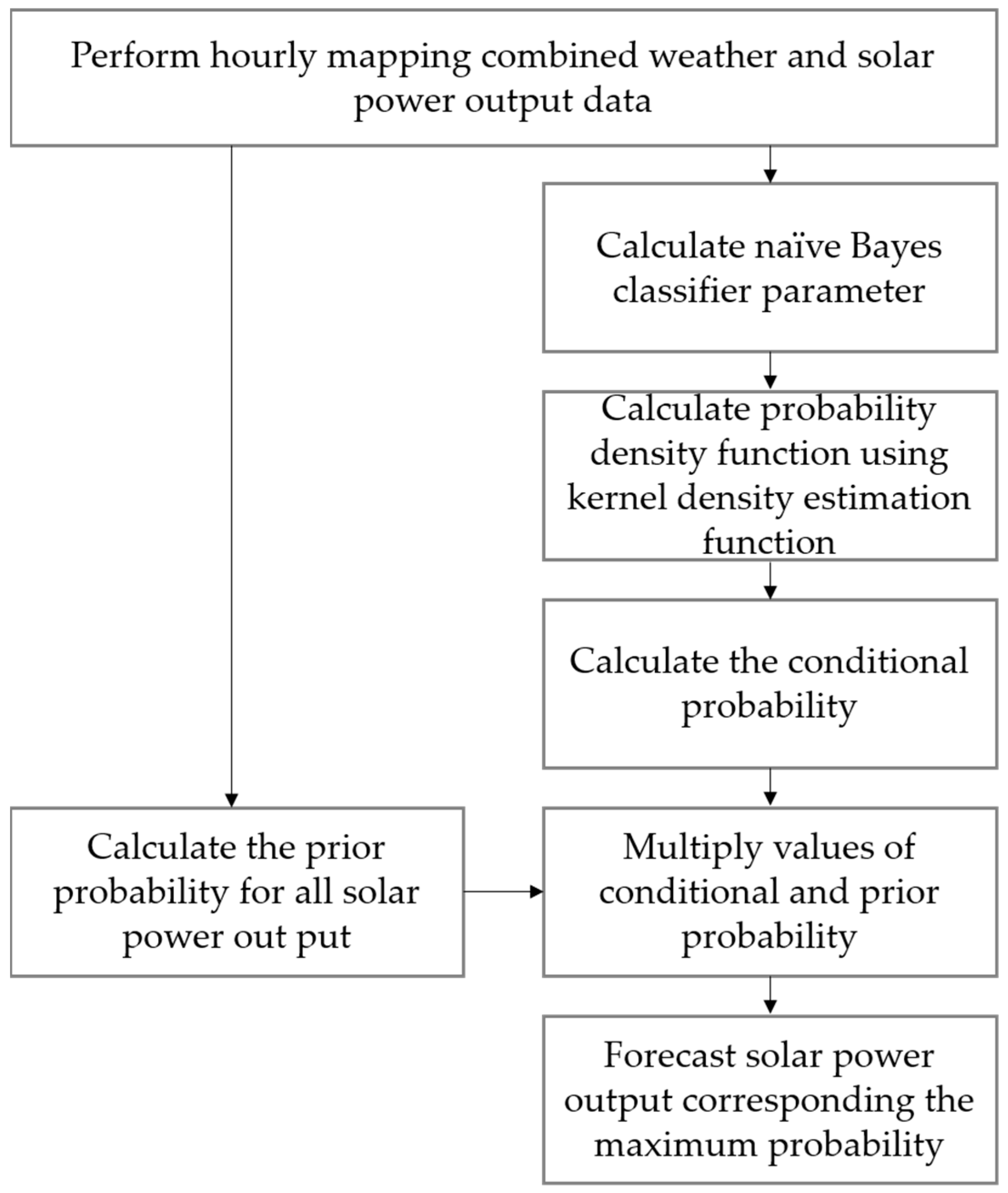
2.1. NBC Model
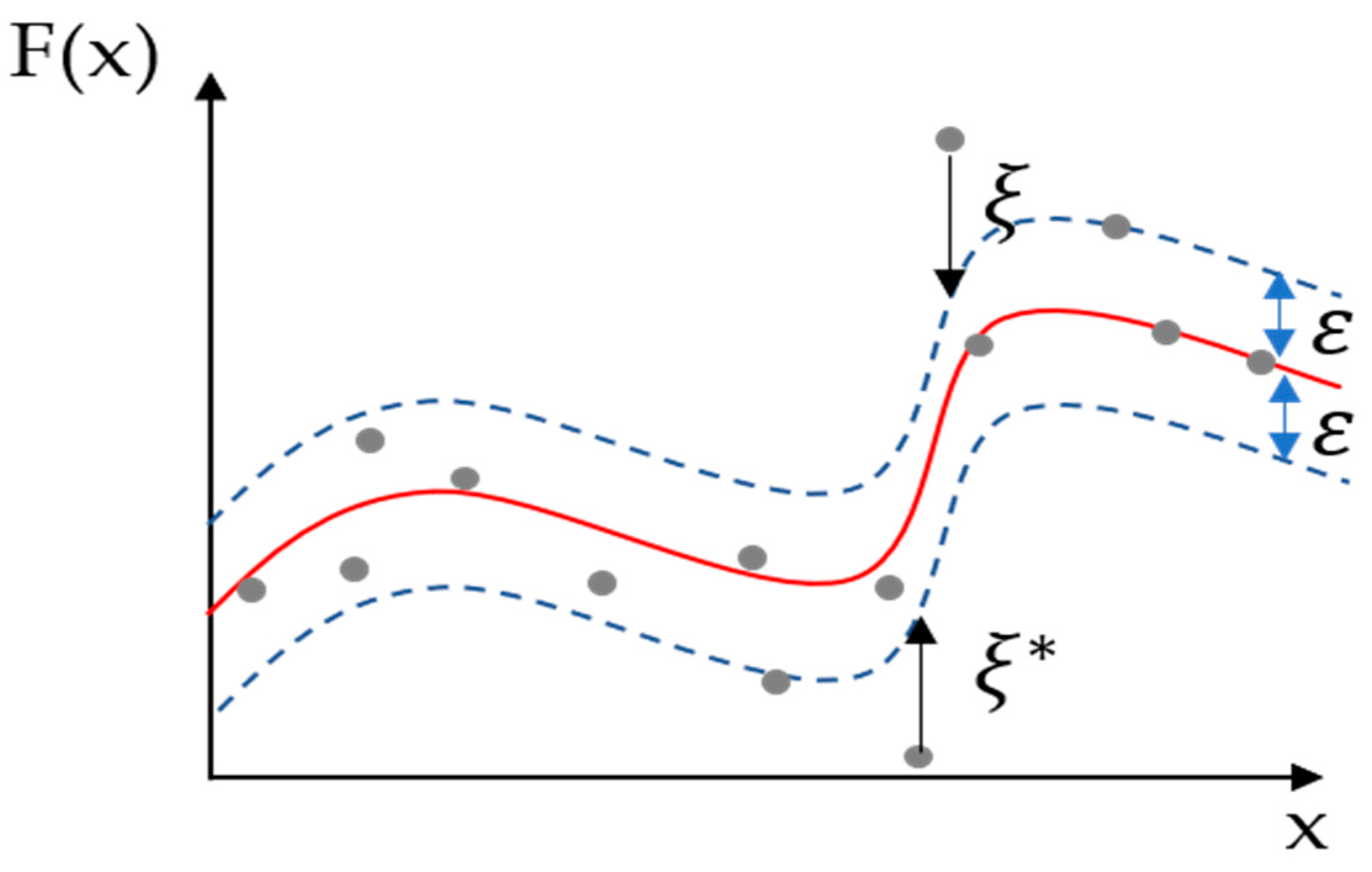
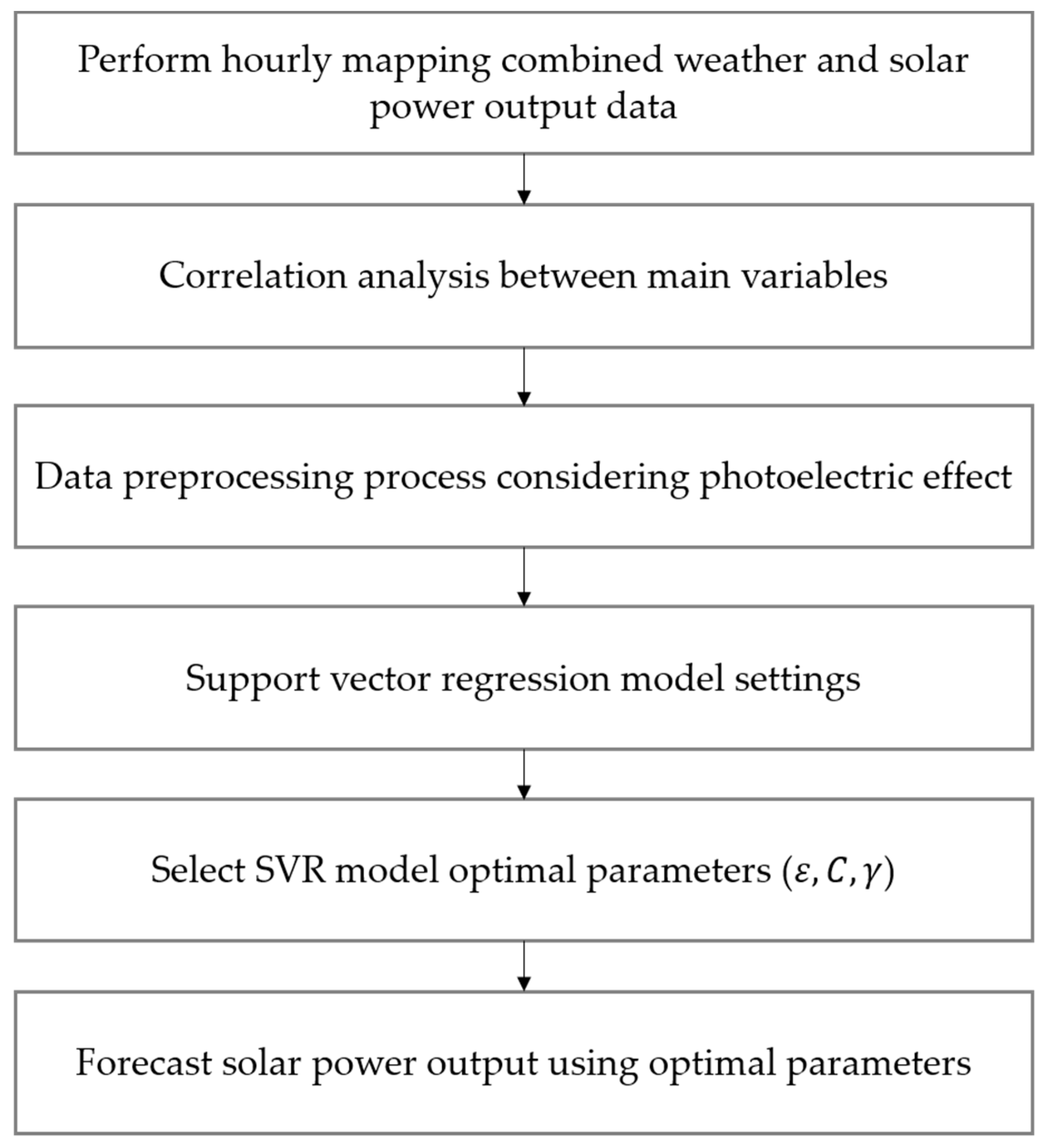
2.2. SVR Model
2.3. Hourly Regression Model
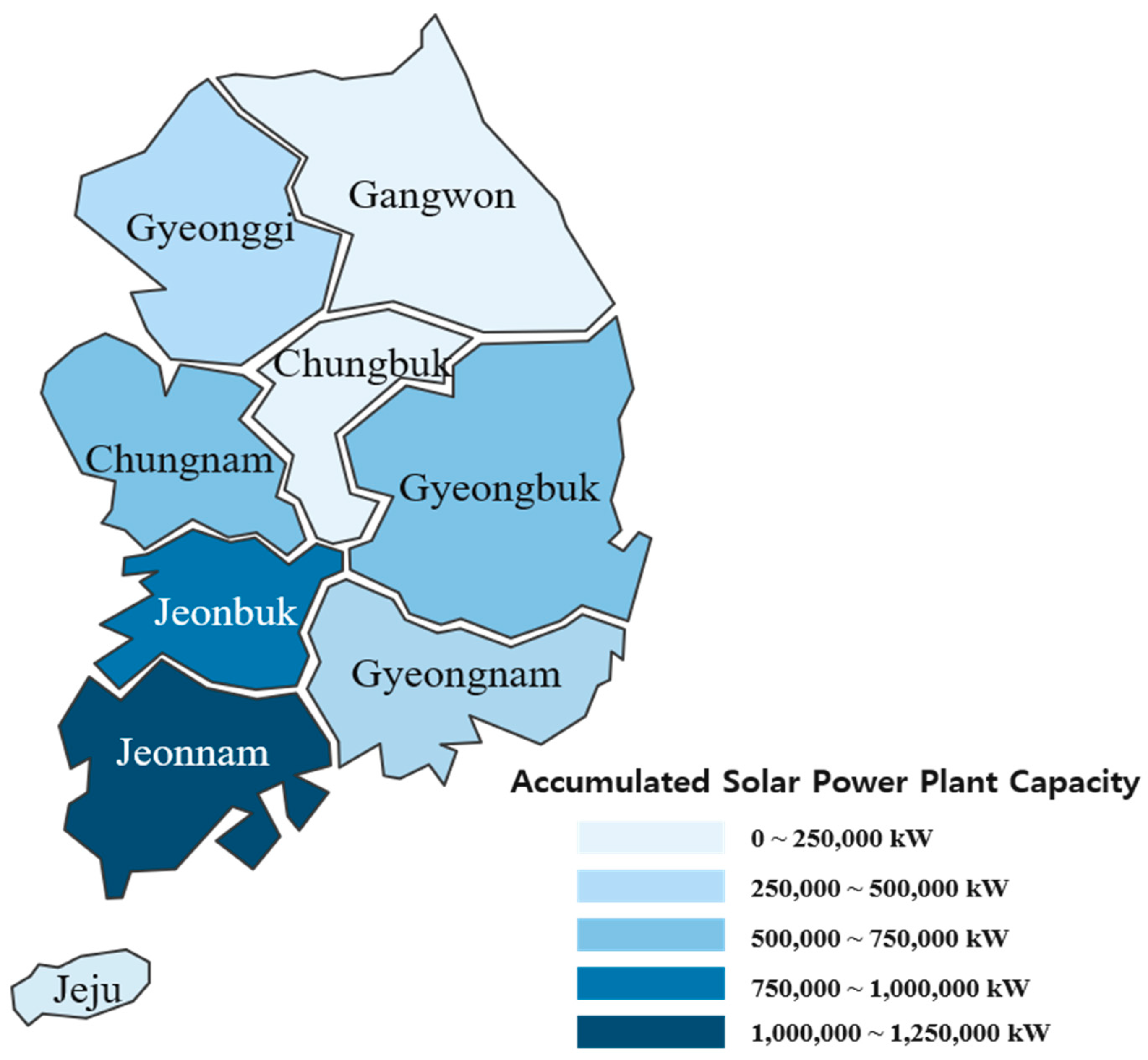
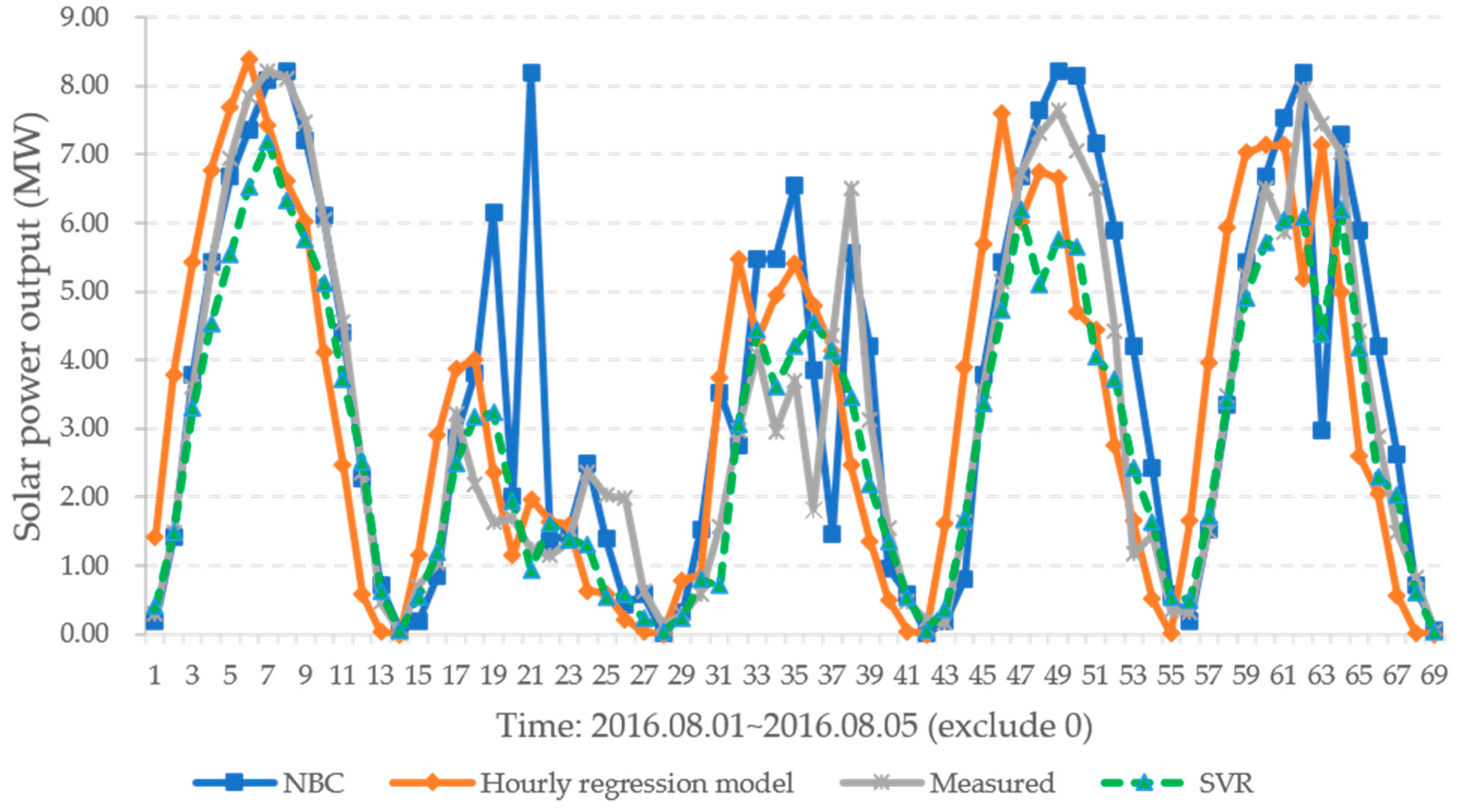
3. Forecasting Simulation of Photovoltaic Power Using Empirical Data
4. Enhancement of Photovoltaic Power Forecasting through Ensemble
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Symbols
| NBC | Naïve Bayes Classifier |
| NMAE | Normalized Mean Absolute Error |
| ARMA | Auto Regressive Moving Average |
| k-NN | k-Nearest Neighbors |
| NWP | Numerical Weather Prediction |
| RBF | Radial basis function |
| MAE | Mean Absolute Error |
| SVR | Support Vector Regression |
| AR | Auto-regressive |
| ANN | Artificial Neural Network |
| AI | Artificial Intelligence |
| SVM | Support Vector Machine |
| RMSE | Root Mean Square Error |
References
- International Renewable Energy Agency. Renewable Capacity Highlights 2018. Available online: https://www.irena.org/media/Files/IRENA/Agency/Publication/2018/Mar/RE_capacity_highlights_2018.pdf (accessed on 1 August 2019).
- Korea Energy Corporation’s Renewable Energy Center. Renewable Energy Supply Statistics 2017. Available online: http://www.index.go.kr/potal/main/EachDtlPageDetail.do?idx_cd=1171 (accessed on 1 August 2019).
- Ela, E.; Diakov, V.; Ibanez, E.; Heaney, M. Impacts of Variability and Uncertainty in Solar Photovoltaic Generation at Multiple Timescales (NREL/TP-5500-58274); National Renewable Energy Lab (NREL): Golden, CO, USA, 2013.
- Lew, D.; Milligan, M.; Jordan, G.; Piwko, R. Value of Wind Power Forecasting (No. NREL/CP-5500-50814); National Renewable Energy Lab (NREL): Golden, CO, USA, 2011.
- Monteiro, C.; Santos, T.; Fernandez-Jimenez, L.; Ramirez-Rosado, I.; Terreros-Olarte, M. Short-term power forecasting model for photovoltaic plants based on historical similarity. Energies 2013, 6, 2624–2643. [Google Scholar] [CrossRef]
- Lorenz, E.; Hurka, J.; Karampela, G.; Heinemann, D.; Beyer, H.; Schneider, M. Qualified Forecast of ensemble power production by spatially dispersed grid-connected PV systems. In Proceedings of the 23rd European Photovoltaic Solar Energy Conference and Exhibition, Valencia, Spain, 1–5 September 2008; pp. 3285–3291. [Google Scholar] [CrossRef]
- Huang, R.; Huang, T.; Gadh, R.; Li, N. Solar generation prediction using the ARMA model in a laboratory-level micro-grid. In Proceedings of the IEEE 3rd International Conference on Smart Grid Communications on Smart Grid Communications, Tainan, China, 5–8 November 2012; pp. 528–533. [Google Scholar] [CrossRef]
- David, M.; Ramahatana, F.; Trombe, P.J.; Lauret, P. Probabilistic forecasting of the solar irradiance with recursive ARMA and GARCH models. Sol. Energy 2016, 133, 55–72. [Google Scholar] [CrossRef]
- Yang, D.; Jirutitijaroen, P.; Walsh, W.M. Hourly solar irradiance time series forecasting using cloud cover index. Sol. Energy 2012, 86, 3531–3543. [Google Scholar] [CrossRef]
- Wang, F.; Mi, Z.; Su, S.; Zhao, H. Short-term solar irradiance forecasting model based on artificial neural network using statistical feature parameters. Energies 2012, 5, 1355–1370. [Google Scholar] [CrossRef]
- Sözen, A.; Arcaklioǧlu, E.; Özalp, M.; Çaǧlar, N. Forecasting based on neural network approach of solar potential in Turkey. Renew. Energy 2005, 30, 1075–1090. [Google Scholar] [CrossRef]
- Ashraf, I.; Chandra, A. Artificial neural network based models for forecasting electricity generation of grid connected solar PV power plant. Int. J. Glob. Energy Issues 2004, 21, 119–130. [Google Scholar] [CrossRef]
- Pedro, H.T.C.; Coimbra, C.F.M. Assessment of forecasting techniques for solar power production with no exogenous inputs. Sol. Energy 2012, 86, 2017–2028. [Google Scholar] [CrossRef]
- Marquez, R.; Pedro, H.T.C.; Coimbra, C.F.M. Hybrid solar forecasting method uses satellite imaging and ground telemetry as inputs to ANNs. Sol. Energy 2013, 92, 176–188. [Google Scholar] [CrossRef]
- Wan, C.; Zhao, J.; Song, Y.; Xu, Z.; Lin, J.; Hu, Z. Photovoltaic and solar power forecasting for smart grid energy management. CSEE J. Power Energy Syst. 2015, 1, 38–46. [Google Scholar] [CrossRef]
- Abedinia, O.; Amjady, N.; Ghadimi, N. Solar energy forecasting based on hybrid neural network and improved metaheuristic algorithm. Comput. Intell. 2018, 34, 241–260. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de-Pison, F.J.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Ahlstrom, M.; Bartlett, D.; Collier, C.; Duchesne, J.; Edelson, D.; Gesino, A.; De La Torre Rodríguez, M. Knowledge is power: Efficiently integrating wind energy and wind forecasts. IEEE Power Energy Mag. 2013, 11, 45–52. [Google Scholar] [CrossRef]
- Widiss, R.; Porter, K. A Review of Variable Generation Forecasting in the West. Available online: https://www.nrel.gov/docs/fy14osti/61035.pdf (accessed on 1 August 2019).
- Bracale, A.; Caramia, P.; Carpinelli, G.; Fazio, A.R.D.; Ferruzzi, G. A Bayesian Method for Short-Term Probabilistic Forecasting of Photovoltaic Generation in Smart Grid Operation and Control. Energies 2013, 6, 733–747. [Google Scholar] [CrossRef]
- Visscher, R.D.; Delouille, V.; Dupont, P.; Deledalle, C.A. Supervised classification of solar features using prior information. J. Space Weather Space Clim. 2015, 5. [Google Scholar] [CrossRef]
- Quek, Y.T.; Woo, W.L.; Logenthiran, T. A naïve Bayes Classification Approach for Short-Term Forecast of Photovoltaic System. In Proceedings of the 6th Annual International Conference on Sustainable Energy and Environmental Sciences (SEES 2017), Singapore, 6–7 May 2017. [Google Scholar]
- Davig, T.; Hall, A.S. Recession forecasting using Bayesian classification. Int. J. Forecast. 2019, 35, 848–867. [Google Scholar] [CrossRef]
- Raschka, S. Naïve Bayes and Text Classification 1–Introduction and Theory. 2014. Available online: https://arxiv.org/abs/1410.5329 (accessed on 1 August 2019).
- Nam, S.; Hur, J. Probabilistic Forecasting Model of Solar Power Outputs Based on the Naïve Bayes Classifier and Kriging Models. Energies 2018, 11. [Google Scholar] [CrossRef]
- Kim, S.B.; Han, K.S.; Rim, H.C.; Myaeng, S.H. Some Effective Techniques for Naïve Bayes Text Classification. IEEE Trans. Knowl. Data Eng. 2006, 18, 1457–1466. [Google Scholar] [CrossRef]
- Gayathri, A.; Revathi, M.; Velmurugan, J. A survey on Weather forecasting by Data Mining. Int. J. Adv. Res. Comput. Commun. Eng. 2016, 5, 298–300. [Google Scholar] [CrossRef]
- Bhargavi, P.; Jyothi, S. Applying Naive Bayes Data Mining Technique for Classification of Agricultural Land Soils. Int. J. Comput. Sci. Netw. Secur. 2009, 9, 117–122. [Google Scholar]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Lu, C.J.; Lee, T.S.; Chiu, C.C. Financial time series forecasting using independent component analysis and support vector regression. Decis. Support Syst. 2009, 47, 115–125. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004. [Google Scholar] [CrossRef]
- Drucker, H.; Surges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1998; pp. 155–161. [Google Scholar]
- Basak, D.; Pal, S.; Patranabis, D.C. Support vector regression. Neural Inf. Process. Lett. Rev. 2007, 11, 203–224. [Google Scholar]
- Das, U.; Tey, K.; Seyedmahmoudian, M.; Idna Idris, M.; Mekhilef, S.; Horan, B.; Stojcevski, A. SVR-based model to forecast PV power generation under different weather conditions. Energies 2017, 10. [Google Scholar] [CrossRef]
- Samanta, M.J.; Srikanth, B.K.; Yerrapragada, J.B. Short-Term Power Forecasting of Solar PV Systems Using Machine Learning Techniques. Available online: https://pdfs.semanticscholar.org/c1e5/7d5b888d8347dfc831c255bd1f374ee397a6.pdf (accessed on 1 August 2019).
- Dolara, A.; Grimaccia, F.; Leva, S.; Mussetta, M. Comparison of training approaches for photovoltaic forecasts by means of machine learning. Appl. Sci. 2018, 8. [Google Scholar] [CrossRef]
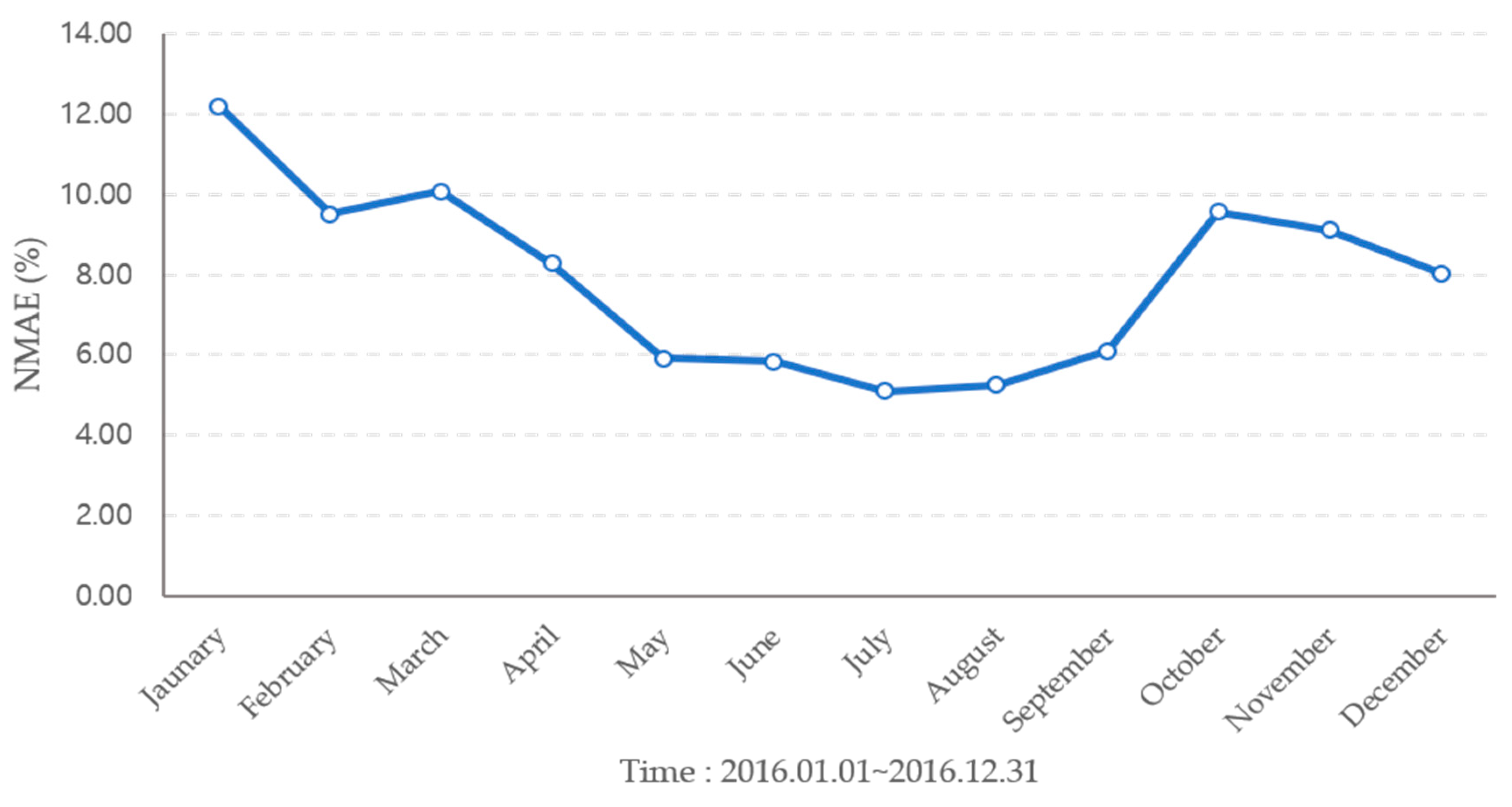
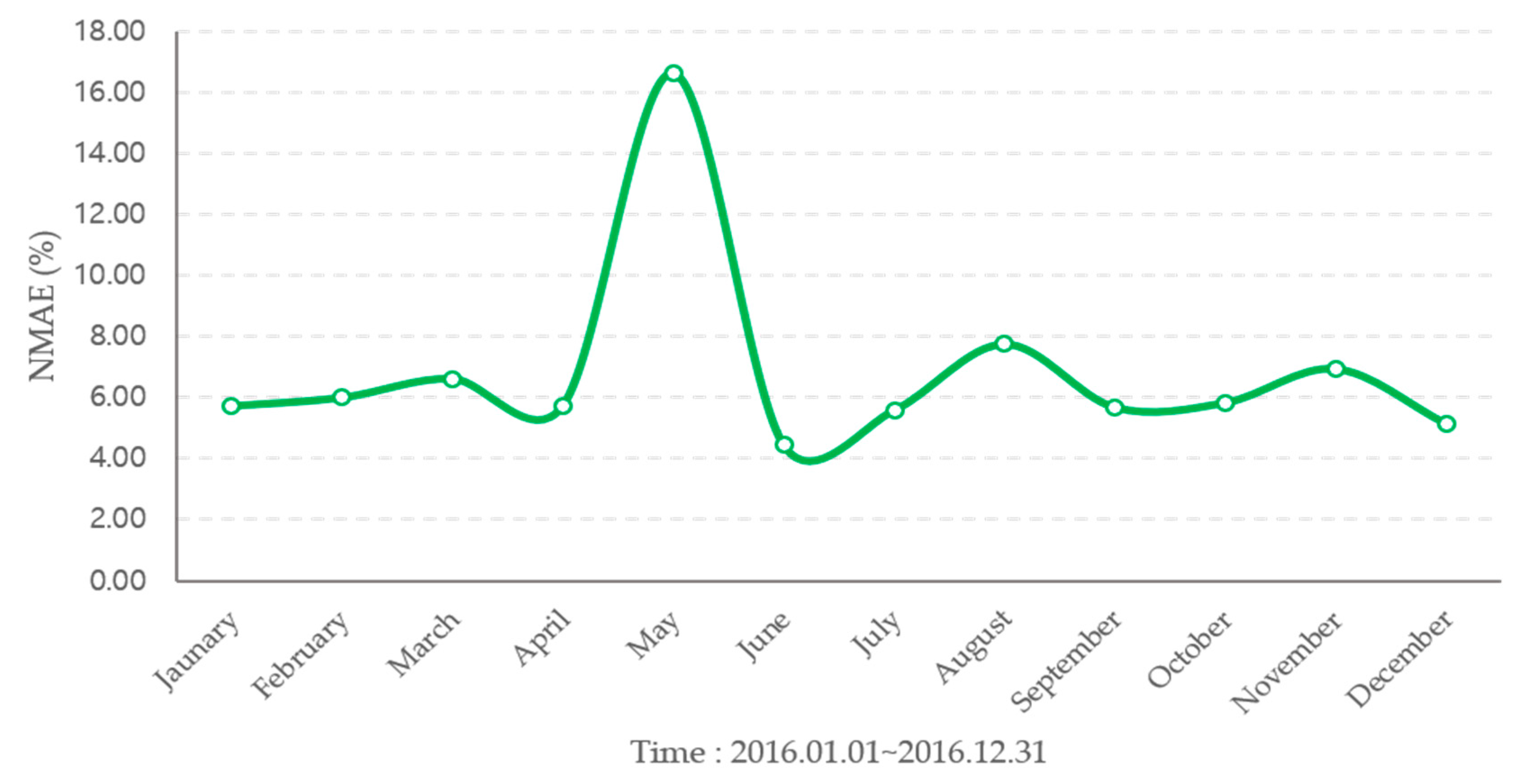
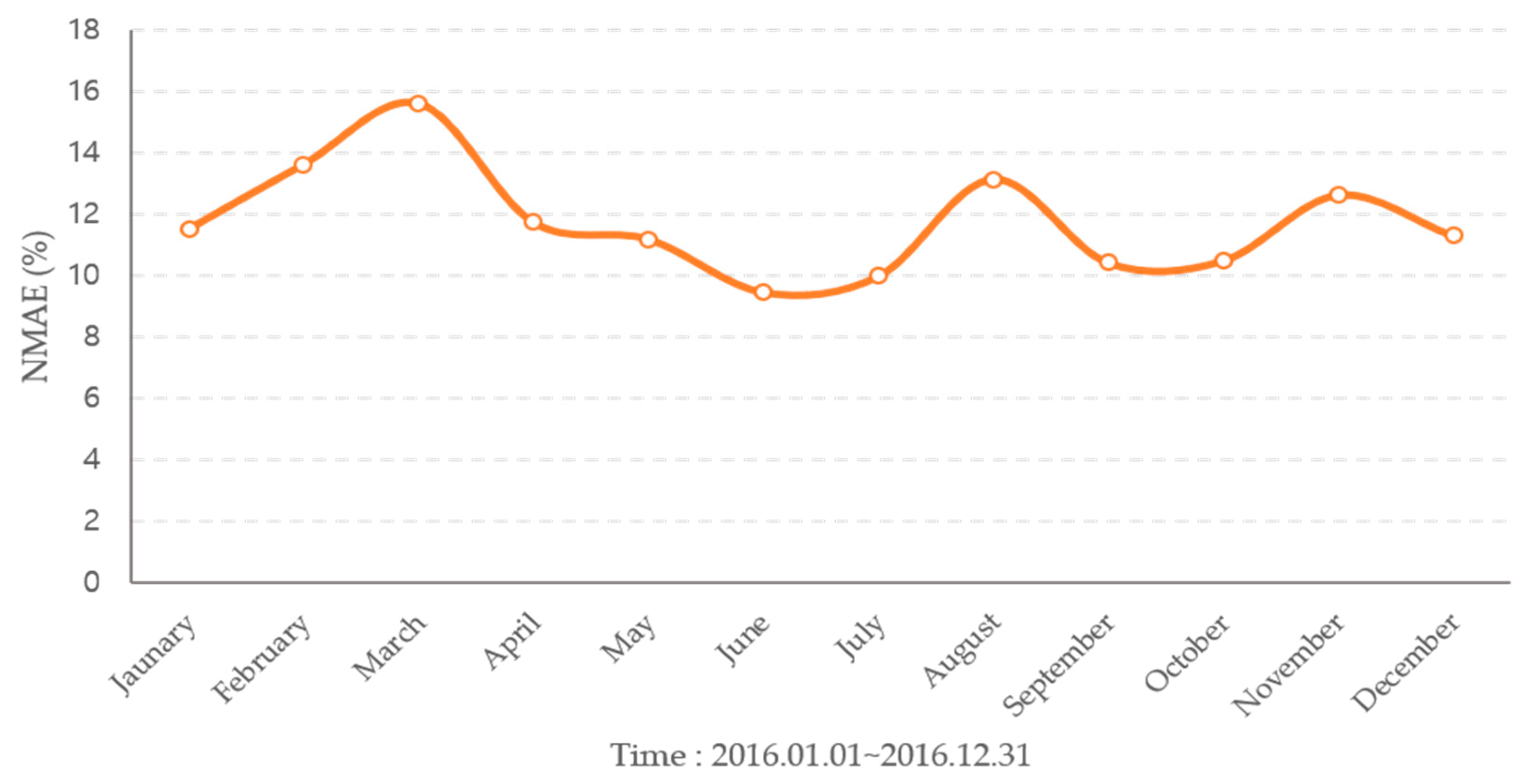

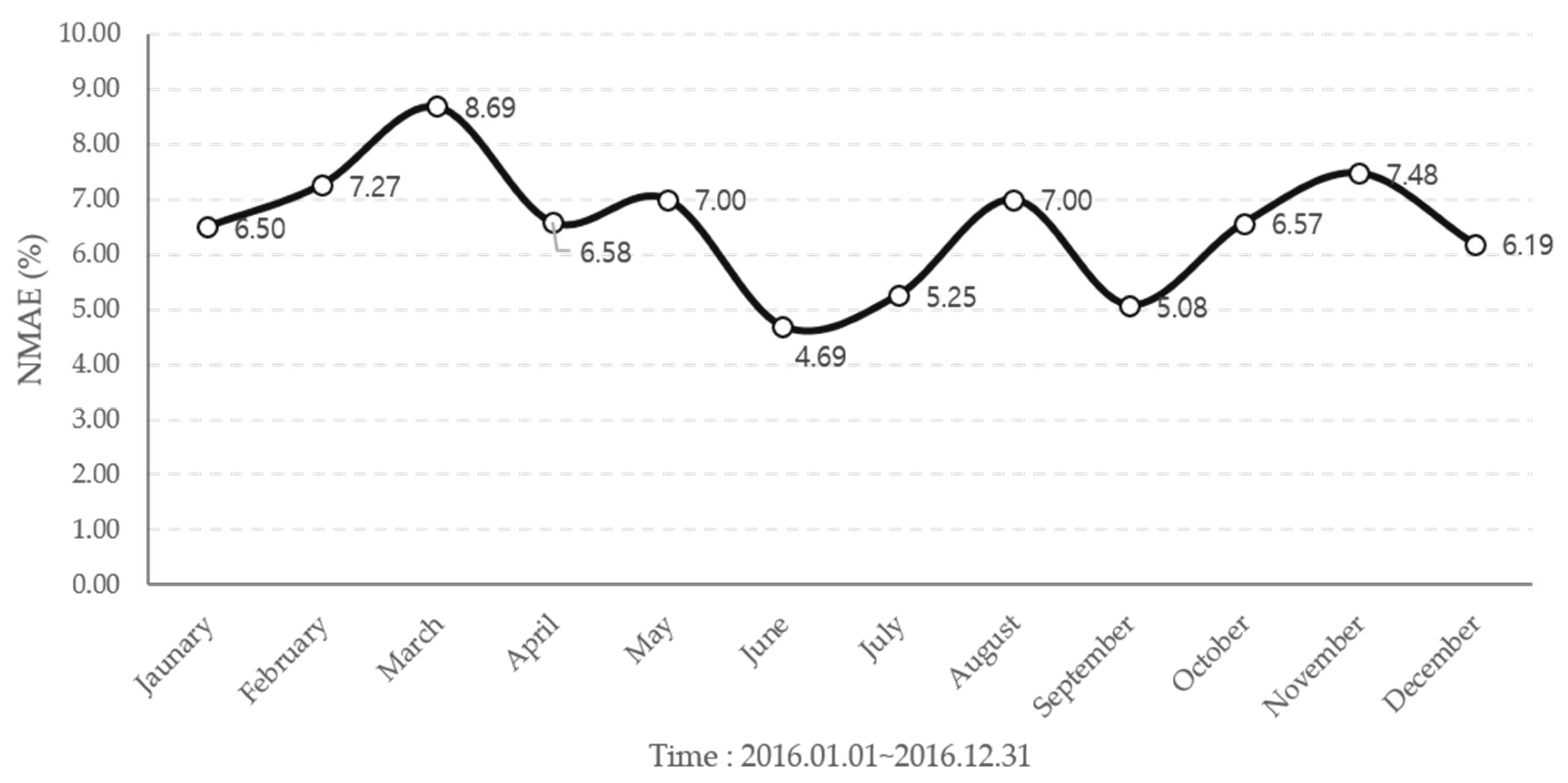

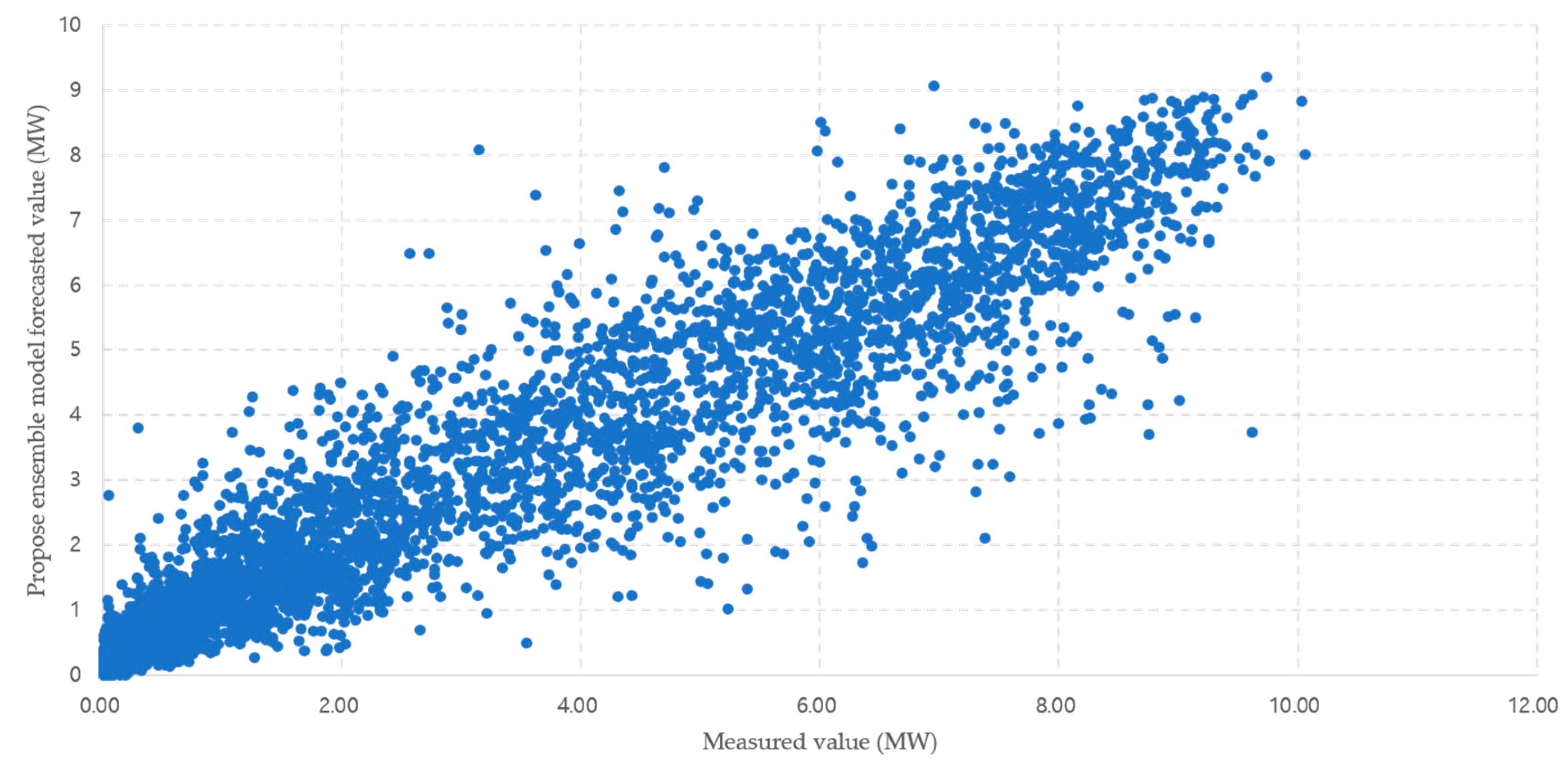
| Month | NBC Model (%) | SVR Model (%) | Hourly Regression Model (%) |
|---|---|---|---|
| January | 12.19 | 5.71 | 11.52 |
| February | 9.50 | 5.99 | 13.62 |
| March | 10.08 | 6.61 | 15.60 |
| April | 8.28 | 5.73 | 11.73 |
| May | 5.90 | 16.60 | 11.18 |
| June | 5.83 | 4.43 | 9.46 |
| July | 5.08 | 5.57 | 9.98 |
| August | 6.09 | 7.74 | 13.13 |
| September | 9.57 | 5.66 | 10.41 |
| October | 9.56 | 5.82 | 10.48 |
| November | 9.10 | 6.93 | 12.61 |
| December | 8.03 | 5.13 | 11.29 |
| Month | Mean (%) | Propose Method (%) |
|---|---|---|
| January | 7.31 | 6.50 |
| February | 8.80 | 7.27 |
| March | 9.97 | 8.69 |
| April | 6.62 | 6.58 |
| May | 8.02 | 7.00 |
| June | 4.93 | 4.69 |
| July | 5.42 | 5.25 |
| August | 7.12 | 7.00 |
| September | 5.23 | 5.08 |
| October | 6.75 | 6.57 |
| November | 7.75 | 7.48 |
| December | 6.63 | 6.19 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.; Hur, J. Weighting Factor Selection of the Ensemble Model for Improving Forecast Accuracy of Photovoltaic Generating Resources. Energies 2019, 12, 3315. https://doi.org/10.3390/en12173315
Kim K, Hur J. Weighting Factor Selection of the Ensemble Model for Improving Forecast Accuracy of Photovoltaic Generating Resources. Energies. 2019; 12(17):3315. https://doi.org/10.3390/en12173315
Chicago/Turabian StyleKim, Kihan, and Jin Hur. 2019. "Weighting Factor Selection of the Ensemble Model for Improving Forecast Accuracy of Photovoltaic Generating Resources" Energies 12, no. 17: 3315. https://doi.org/10.3390/en12173315
APA StyleKim, K., & Hur, J. (2019). Weighting Factor Selection of the Ensemble Model for Improving Forecast Accuracy of Photovoltaic Generating Resources. Energies, 12(17), 3315. https://doi.org/10.3390/en12173315





