Analysis of Subsynchronous Resonance Characteristics and Influence Factors in a Series Compensated Transmission System
Abstract
1. Introduction
2. Eigenvalue Analysis and System Modeling
2.1. Eigenvalue Analysis
- A detailed mathematical model is established for various components of the SSR system and the power network, and the differential equations describing the transient process is obtained.
- By linearizing the differential equations near stable values and writing out the standard form , the state-space representation is acquired, which is suitable for eigenvalue analysis.
- The initial values of the studied system under stable operation are calculated.
- The eigenvalues of characteristic equations are solved, and the stability and damping characteristics of the system are analyzed based on the results.
2.2. System Modeling
2.2.1. Turbine Speed Governing System
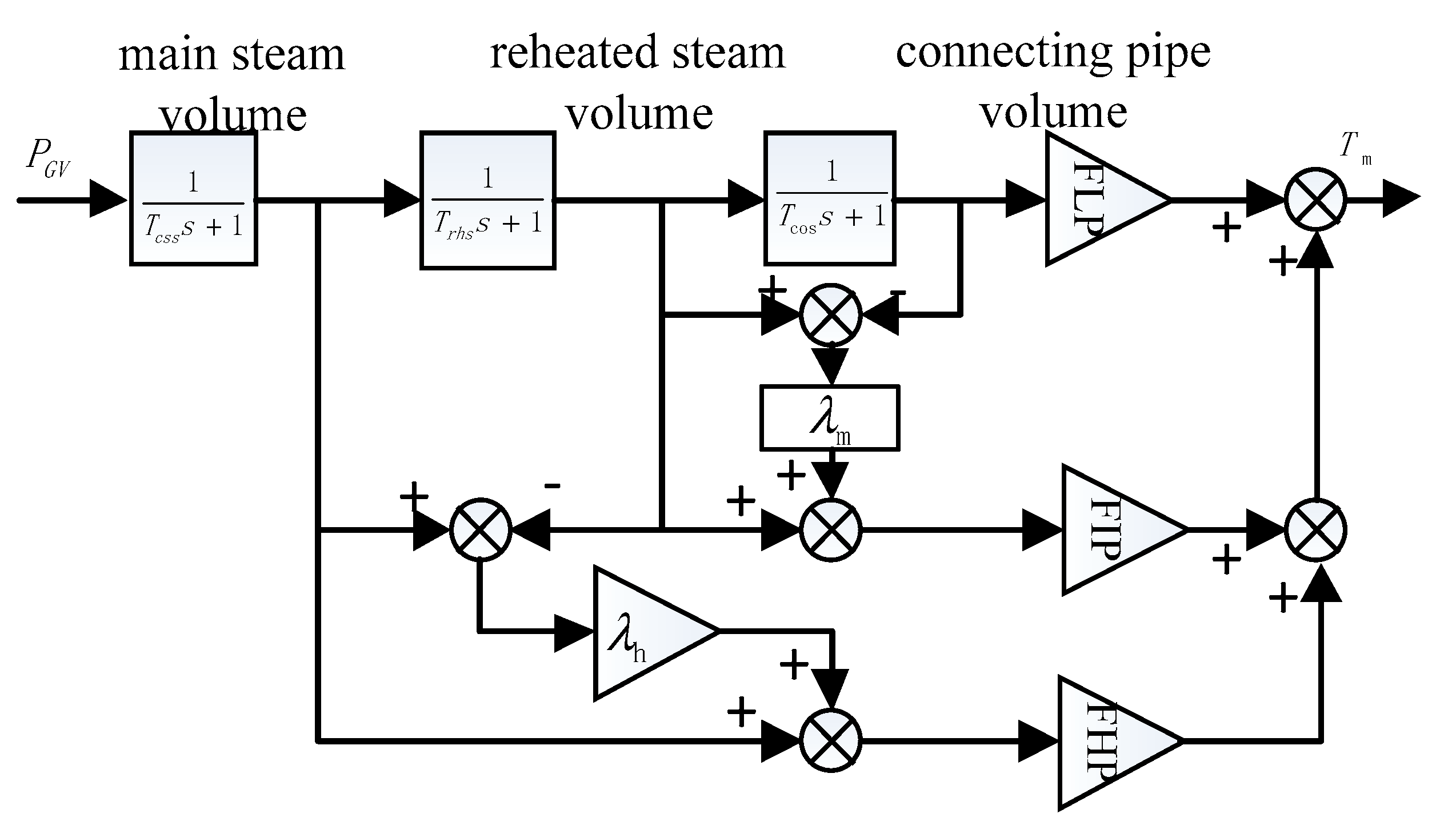
2.2.2. Turbine Prime Mover Model
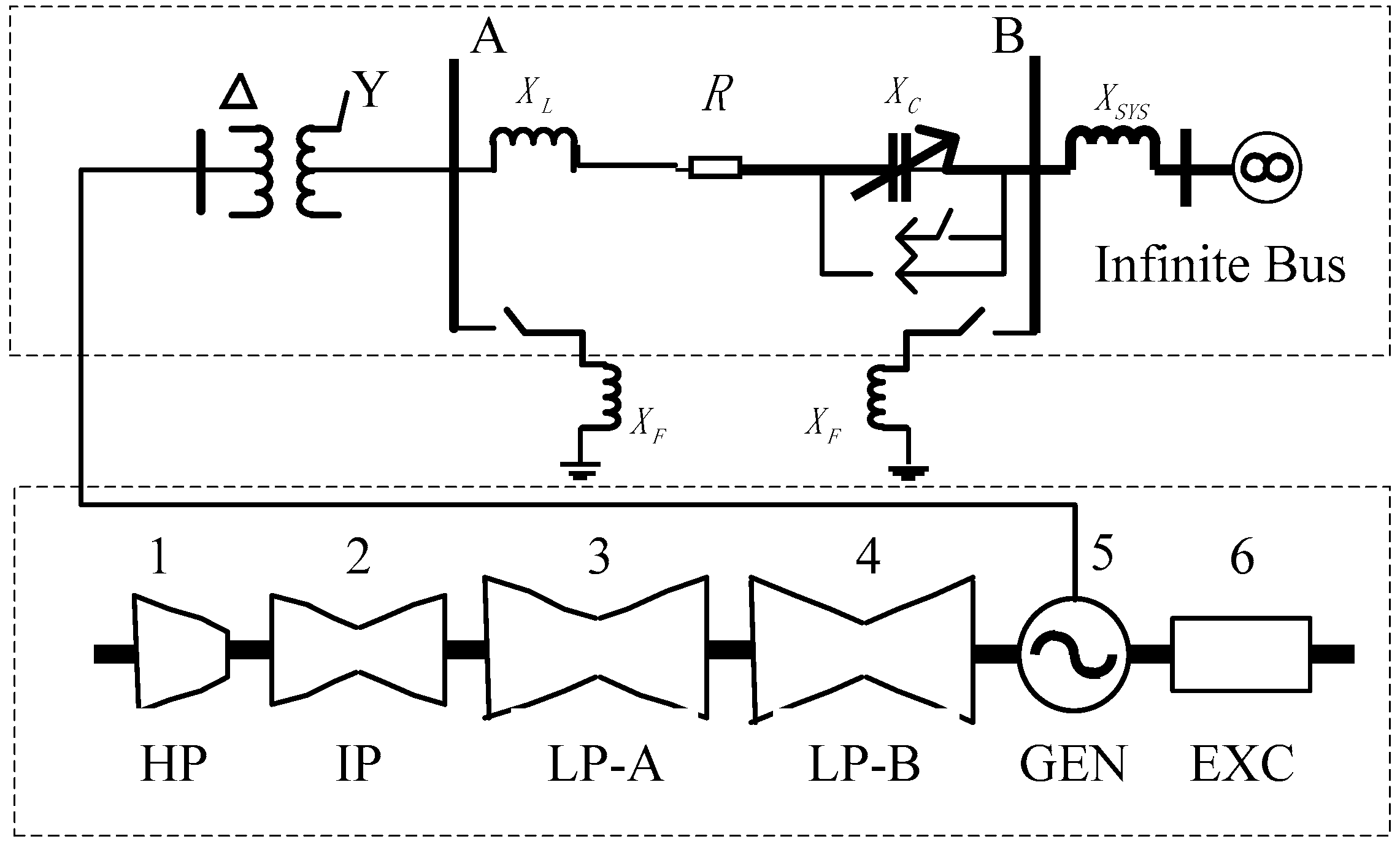
3. Case Analysis
3.1. Model Parameters
3.2. Eigenvalue Calculation Results
4. Analysis of Influence Factors of SSR
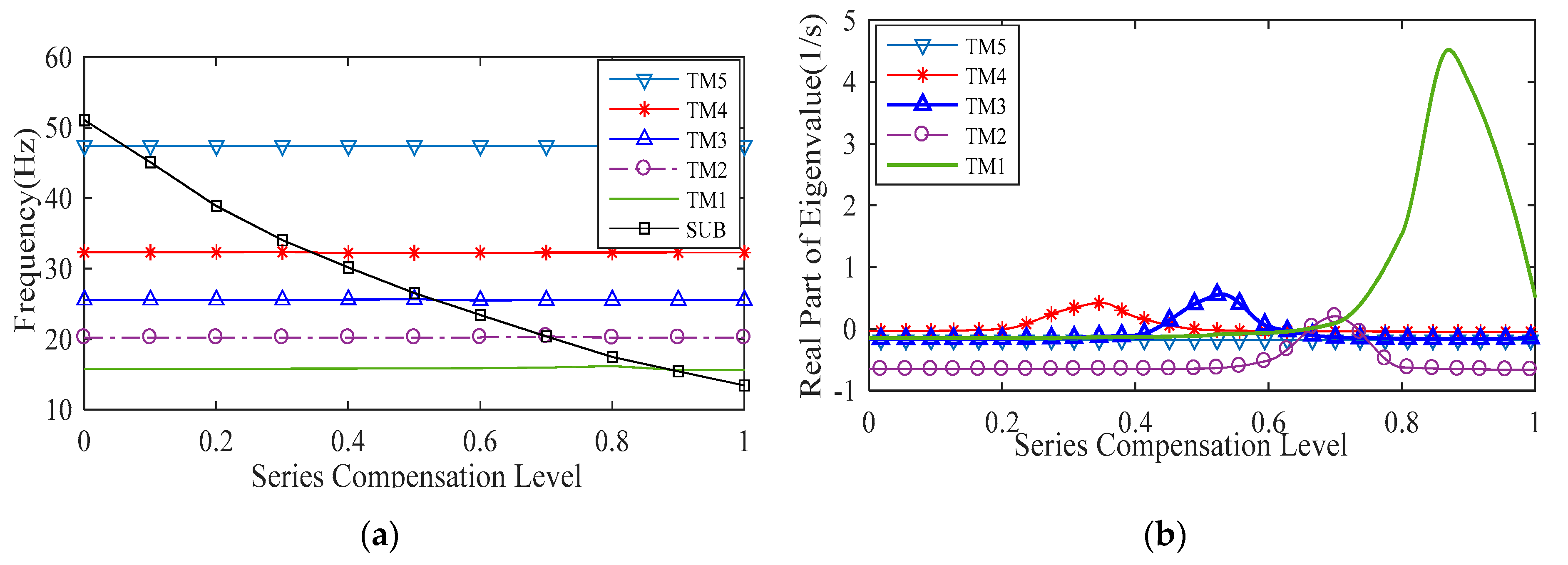
4.1. Influence of Compensation Level
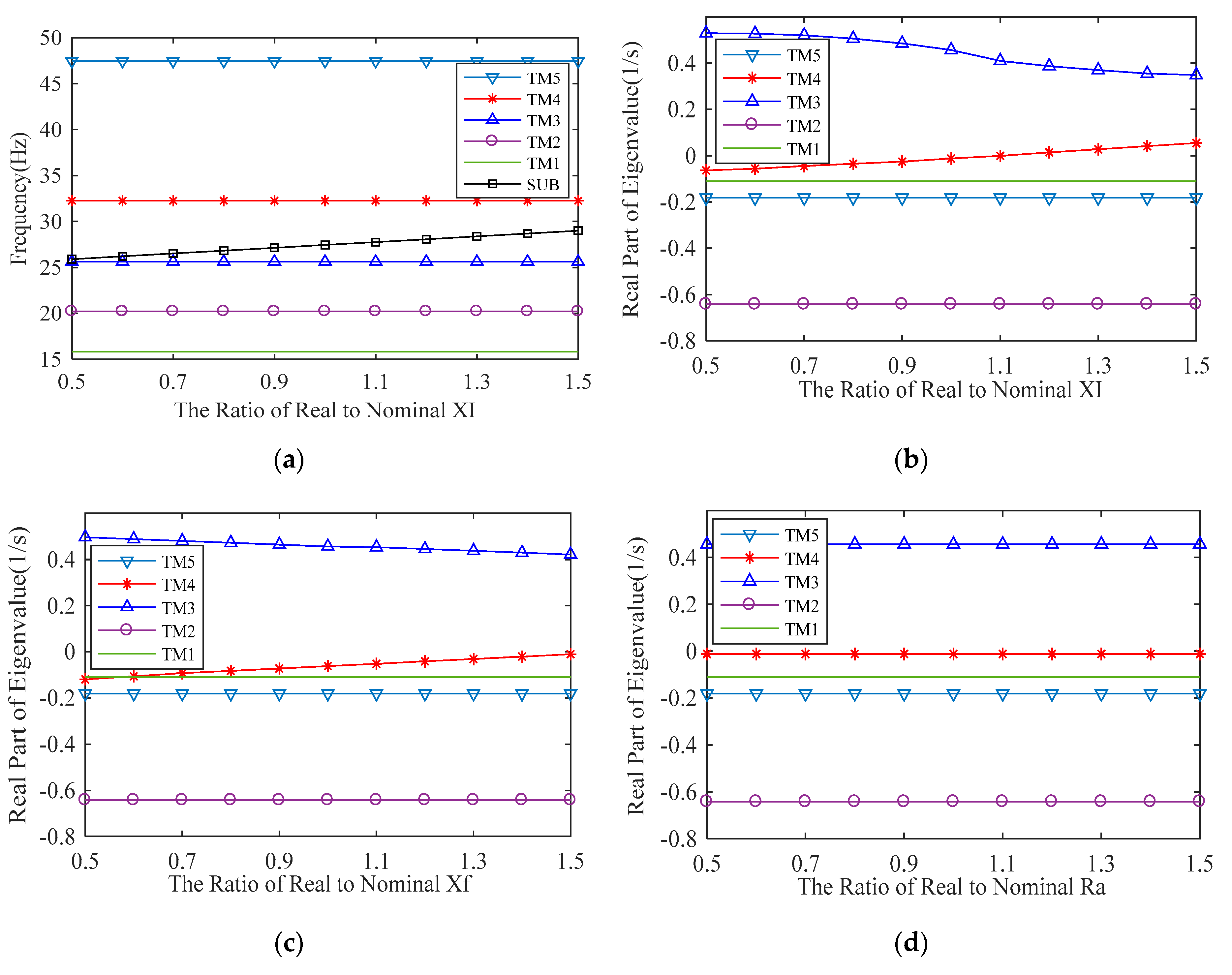
4.2. Influence of Synchronous Generator Parameters
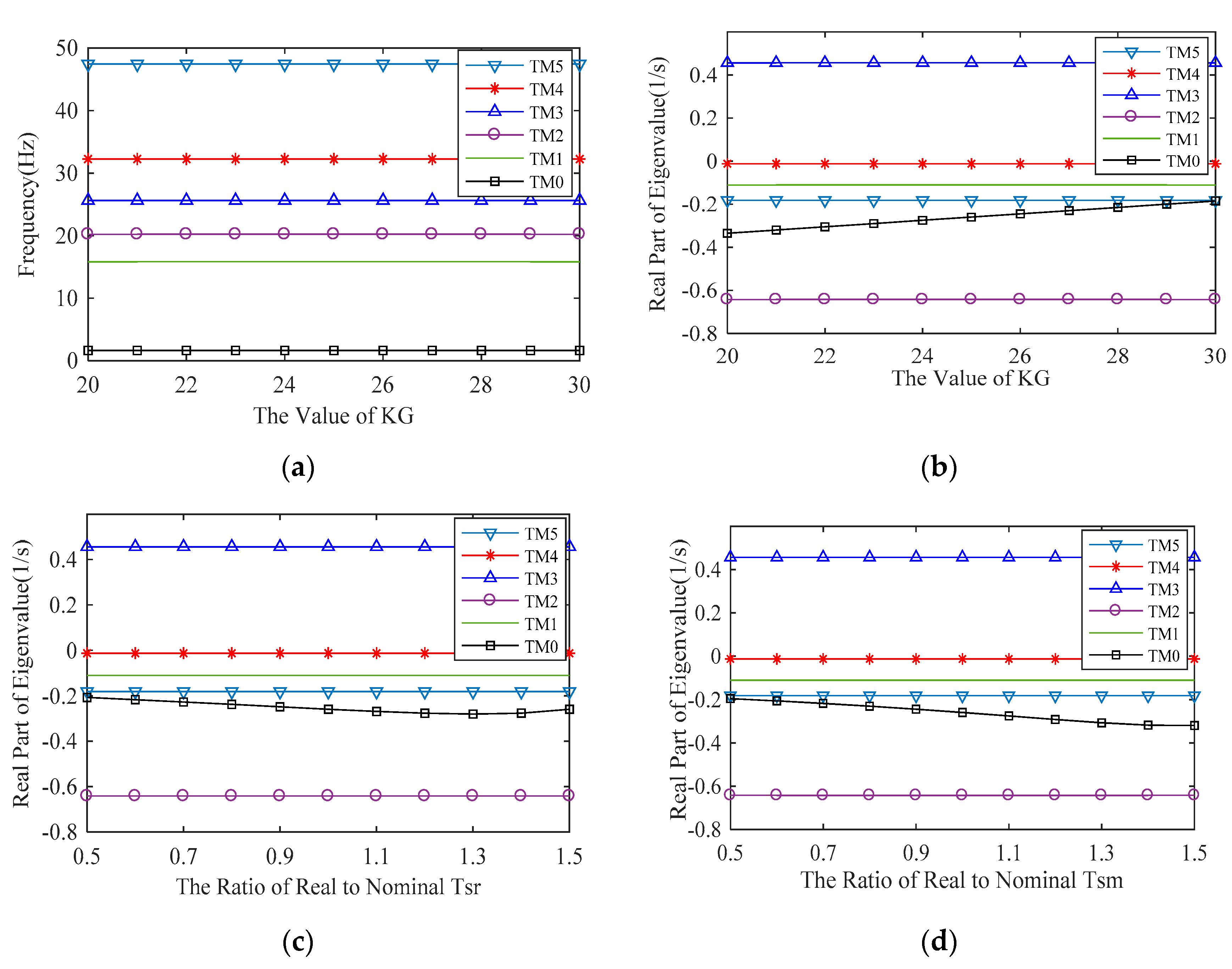
4.3. Influence of Speed Governing System Parameters
4.3.1. With or Without Speed Governing System
4.3.2. Influence of Speed Governing System Parameters
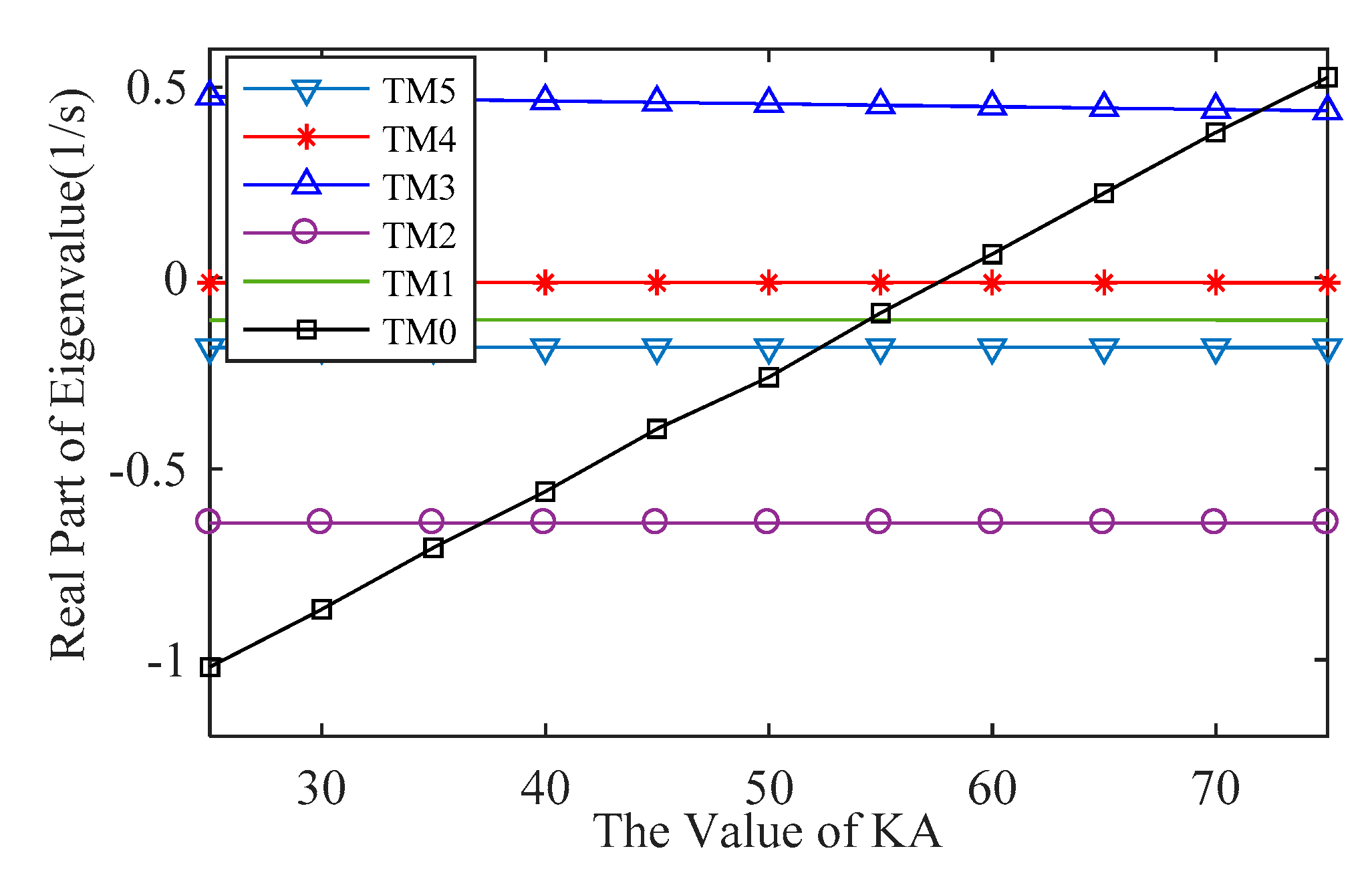
4.4. Influence of Excitation System Parameters
5. Conclusions
- The series compensation level has the greatest influence on the torsional mode damping of the system. With the increase of , one or more torsional mode damping will appear negative, indicating that the system may have a single mode or multimode SSR, and the greater is, the lower the torsional mode frequency is, but the change of does not affect total damping of the system, that is, the total damping of the system is conserved.
- The parameters of the synchronous generator will not affect torsional mode frequencies of the turbogenerator shaft, and the reactance parameters of generators have a certain influence on torsional mode damping of the system. The variation of the reactance parameters may lead to instability of the torsional mode when and become close. However, the damping of adjacent torsional modes will be increased, which is beneficial to its stability. In addition, the resistance parameters of synchronous generator have little effect on the damping of each torsional mode, which can be ignored.
- Speed governing system parameters , and have a great influence on TM0 damping, and slightly affect other torsional modes damping. Excitation system parameter significantly affects TM0 damping, and has little effect on other torsional modes damping.
Author Contributions
Funding
Conflicts of Interest
References
- Bizzarri, F.; Brambilla, A.; Milano, F. Simplified model to study the induction generator effect of the subsynchronous resonance phenomenon. IEEE Trans. Energy Conver. 2018, 33, 889–892. [Google Scholar] [CrossRef]
- Kumar, R.; Harada, A.; Merkle, M.; Miri, A.M. Investigation of the influence of series compensation in AC transmission systems on the bus connected parallel generating units with respect to subsynchronous resonance (SSR). In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; pp. 1083–1088. [Google Scholar]
- Li, J.; Zhang, P.X. Impact of increased wind power generation on subsynchronous resonance of turbine-generator units. J. Mod. Power Syst. Clean Energy. 2016, 4, 219–228. [Google Scholar] [CrossRef]
- Virulkar, V.B.; Gotmare, G.V. Sub-synchronous resonance in series compensated wind farm: A review. Renew. Sustain. Energy Rev. 2016, 55, 1010–1029. [Google Scholar] [CrossRef]
- Xie, X.R.; Zhang, X.; Liu, H.K.; Liu, H.; Li, Y.H.; Zhang, C.Y. Characteristic analysis of subsynchronous resonance in practical wind farms connected to series-compensated transmissions. IEEE Trans. Energy Conver. 2017, 32, 1117–1126. [Google Scholar] [CrossRef]
- Zhu, B.C.; Hu, M.; Wu, Z. Parameters impact on the performance of a double-fed induction generator-based wind turbine for subsynchronous resonance control. IET Renew. Power Gener. 2012, 6, 92–98. [Google Scholar] [CrossRef]
- Chen, W.H.; Xie, X.R.; Wang, D.H. Probabilistic stability analysis of subsynchronous resonance for series compensated DFIG-based wind farms. IEEE Trans. Sustain. Energ. 2018, 9, 400–409. [Google Scholar] [CrossRef]
- Park, J.K.; Kim, C.H.; Cho, G.J.; Sohn, S.H.; Chung, S.J. A Novel Reclosing Algorithm Considering Turbine-Generator Shaft Torque. IEEE Trans. Power Deliv. 2017, 32, 703–712. [Google Scholar] [CrossRef]
- Dong, D.Y.; Chen, W.H.; Zhang, J.; Tan, L.N. Subsynchronous resonance modeling method for real systems. Power Syst. Tech. 2015, 39, 1059–1066. [Google Scholar]
- Johansson, N.; Ängquist, L.; Nee, H.P. A comparison of different frequency scanning methods for study of subsynchronous resonance. IEEE Trans. Power Syst. 2011, 26, 356–363. [Google Scholar] [CrossRef]
- Li, H.F.; Liu, C.R.; Han, M.X. Analysis on subsynchronous resonance caused by series compensation in AC system based on frequency-scanning and eigenvalue. Power Syst. Tech. 2012, 36, 107–112. [Google Scholar]
- IEEE Subsynchronous Resonance Task Force. First benchmark model for computer simulation of subsynchronous resonance. IEEE Trans. Power Appar. Syst. 1977, 96, 1565–1572. [Google Scholar] [CrossRef]
- Yu, Y.X.; Li, J. The power system subsynchronous oscillations were studies based on eigenvalue analysis. Electr. Eng. 2017, 18, 44–48. [Google Scholar]
| SSR Analysis Methods | Features | Advantages | Disadvantages |
|---|---|---|---|
| Eigenvalue analysis | It is also called state-space analysis method, which is a quantitative analysis method based on the small disturbance linearization model and obtains SSR-related information by solving eigenvalues. |
| Higher order model parameters are required for the entire system, which is difficult to analyze. |
| Electromagnetic transient analysis | Using a step-by-step numerical integration method, a set of differential equations of the system are solved. The mathematical model can be linear or nonlinear. |
| Only time domain response results can be given. It is difficult to directly give SSR reasons and the mechanism of instability. |
| Complex torque coefficient analysis | Frequency scanning of the mechanical and electrical complex torque coefficients of the shaft system in the subsynchronous frequency range to determine whether the system will undergo subsynchronous oscillation. |
|
|
| Frequency scanning | It is an approximate linear method to calculate the equivalent impedance for a specific frequency and filter out the system conditions with potential SSR. |
|
|
| Mass Block | Inertia Constant, (s) | Shaft Segment | Elastic Constant, K (p.u.) |
|---|---|---|---|
| HP | 0.185794 | - | - |
| IP | 0.311178 | HP-IP | 19.303 |
| LPA | 1.717340 | IP-LPA | 34.929 |
| LPB | 1.768430 | LPA-LPB | 52.038 |
| GEN | 1.736990 | LPB-GEN | 70.858 |
| EXC | 0.068433 | GEN-EXC | 2.822 |
| Eigenvalue | Torsional Mode | Real Part (1/s) | Imaginary Part (rad/s) | Frequency (Hz) |
|---|---|---|---|---|
| 1,2 | TM0 | −0.5073 | ±11.66 | 1.86 |
| 3,4 | TM1 | 0.0931 | ±100.28 | 15.96 |
| 5,6 | TM2 | 0.2034 | ±128.08 | 20.38 |
| 7,8 | TM3 | −0.1352 | ±160.34 | 25.52 |
| 9,10 | TM4 | −0.0404 | ±202.78 | 32.27 |
| 11,12 | TM5 | −0.1818 | ±298.17 | 47.46 |
| Eigenvalue | Torsional Mode | KC = 0.1 | KC = 0.3 | KC = 0.5 | KC = 0.7 | KC = 0.9 |
|---|---|---|---|---|---|---|
| 1,2 | TM0 | 0.0693 ± j8.46 | −0.0748 ± j9.31 | −0.2597 ± j10.35 | −0.5073 ± j11.66 | −0.8623 ± j13.41 |
| 3,4 | TM1 | −0.1487 ± j99.13 | −0.1422 ± j99.27 | −0.1106 ± j99.52 | 0.0931 ± j100.28 | 3.9947 ± j98.05 |
| 5,6 | TM2 | −0.6549 ± j127.02 | −0.6525 ± j127.03 | −0.6423 ± j127.07 | 0.2034 ± j128.08 | −0.6522 ± j126.92 |
| 7,8 | TM3 | −0.1627 ± j160.62 | −0.1479 ± j160.69 | 0.4564 ± j161.08 | −0.1351 ± j160.34 | −0.1644 ± j160.46 |
| 9,10 | TM4 | −0.0301 ± j203.01 | 0.3233 ± j203.43 | −0.0125 ± j202.68 | −0.0404 ± j202.78 | −0.0449 ± j202.84 |
| 11,12 | TM5 | −0.1819 ± j298.17 | −0.1819 ± j298.17 | −0.1819 ± j298.17 | −0.1819 ± j298.17 | −0.1819 ± j298.17 |
| 13,14 | SUB | −7.1191 ± j283.35 | −7.1702 ± j213.94 | −7.0882 ± j166.68 | −6.5888 ± j128.06 | −9.1422 ± j96.86 |
| 15,16 | SUPER | −7.5026 ± j470.47 | −7.5806 ± j539.24 | −7.6238 ± j586.55 | −7.6543 ± j624.99 | −7.6778 ± j658.22 |
| 17,18 | −4.6872 ± j0.6335 | −4.7382 ± j0.3856 | −4.8737 ± j0.2566 | −4.9573 ± j0.1521 | −3.4114 ± j0.5459 | |
| 19 | −1.8966 | −1.8446 | −1.7833 | −1.6996 | −1.5619 | |
| 20 | −24.7628 | −24.7842 | −24.8113 | −24.8466 | −24.8939 | |
| 21 | −30.8793 | −31.5042 | −32.3627 | −33.6064 | −35.5306 | |
| 22 | −8.5726 | −8.3123 | −7.9786 | −7.5383 | −6.9382 | |
| 23 | −101.8931 | −101.7953 | −101.648 | −101.4514 | −101.1882 | |
| 24 | −499.9582 | −499.9821 | −499.9783 | −499.9742 | −499.9713 | |
| 25 | −2.9453 | −3.1215 | −3.4887 | −3.4828 | −3.9244 | |
| 26 | −0.1417 | −0.1417 | −0.1418 | −0.1419 | −0.1419 | |
| 27 | −4.6223 | −4.3293 | −3.6731 | −3.5842 | −4.1051 | |
| sum | −696.0893 | −696.1123 | −696.1281 | −696.0932 | −696.1024 |
| Torsional Mode | With Speed Governing System | Without Speed Governing System | ||
|---|---|---|---|---|
| Real Part (1/s) | Imaginary Part (rad/s) | Real Part (1/s) | Imaginary Part (rad/s) | |
| TM0 | −0.2597 | 10.35 | −0.3099 | 10.56 |
| TM1 | −0.1818 | 298.17 | −0.1828 | 298.17 |
| TM2 | −0.0125 | 202.68 | −0.0153 | 202.68 |
| TM3 | 0.4564 | 161.08 | 0.4453 | 161.08 |
| TM4 | −0.6423 | 127.07 | −0.6505 | 127.07 |
| TM5 | −0.1106 | 99.52 | −0.1224 | 99.52 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, C.; Sun, D.; Song, L.; Ma, L. Analysis of Subsynchronous Resonance Characteristics and Influence Factors in a Series Compensated Transmission System. Energies 2019, 12, 3282. https://doi.org/10.3390/en12173282
He C, Sun D, Song L, Ma L. Analysis of Subsynchronous Resonance Characteristics and Influence Factors in a Series Compensated Transmission System. Energies. 2019; 12(17):3282. https://doi.org/10.3390/en12173282
Chicago/Turabian StyleHe, Chengbing, Dakang Sun, Lei Song, and Li Ma. 2019. "Analysis of Subsynchronous Resonance Characteristics and Influence Factors in a Series Compensated Transmission System" Energies 12, no. 17: 3282. https://doi.org/10.3390/en12173282
APA StyleHe, C., Sun, D., Song, L., & Ma, L. (2019). Analysis of Subsynchronous Resonance Characteristics and Influence Factors in a Series Compensated Transmission System. Energies, 12(17), 3282. https://doi.org/10.3390/en12173282





