Modified Rotor Flux Estimators for Stator-Fault-Tolerant Vector Controlled Induction Motor Drives
Abstract
1. Introduction
- A comprehensive state of the art review about FTC systems for stator winding faults of induction machines;
- Detailed analysis of the impact of an ITSC on the accuracy of IM rotor flux estimation by open-loop estimators (analytical substantiation included);
- Analysis of an impact of an ITSC on the performance of a closed-loop control scheme (DFOC) with open-loop rotor flux estimators;
- A new FTC unit for ITSCs is proposed, based on modified rotor flux estimators.
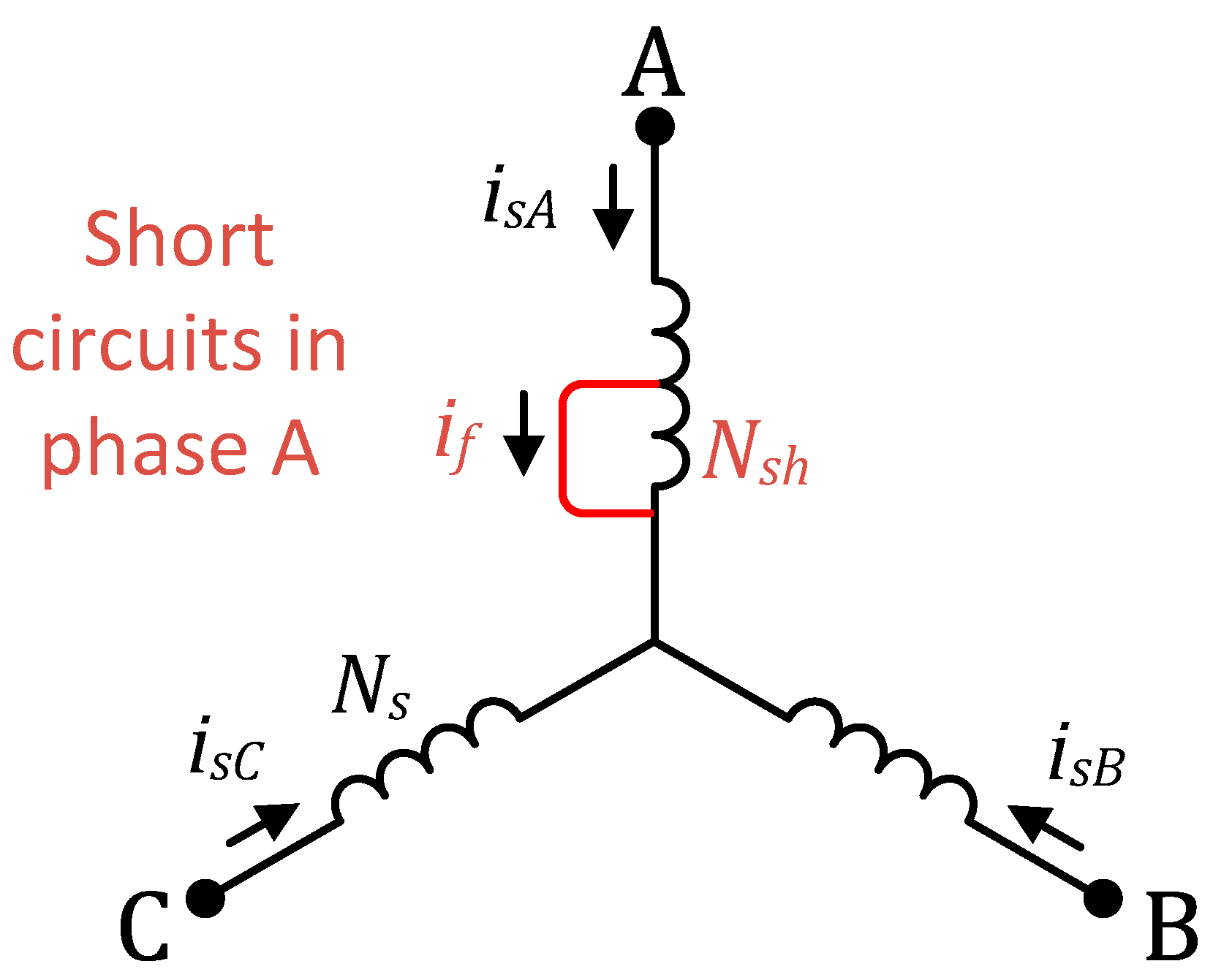
2. Mathematical Model of Induction Motor with Short Circuits in Stator Windings
3. Mathematical Models of Rotor Flux Estimators
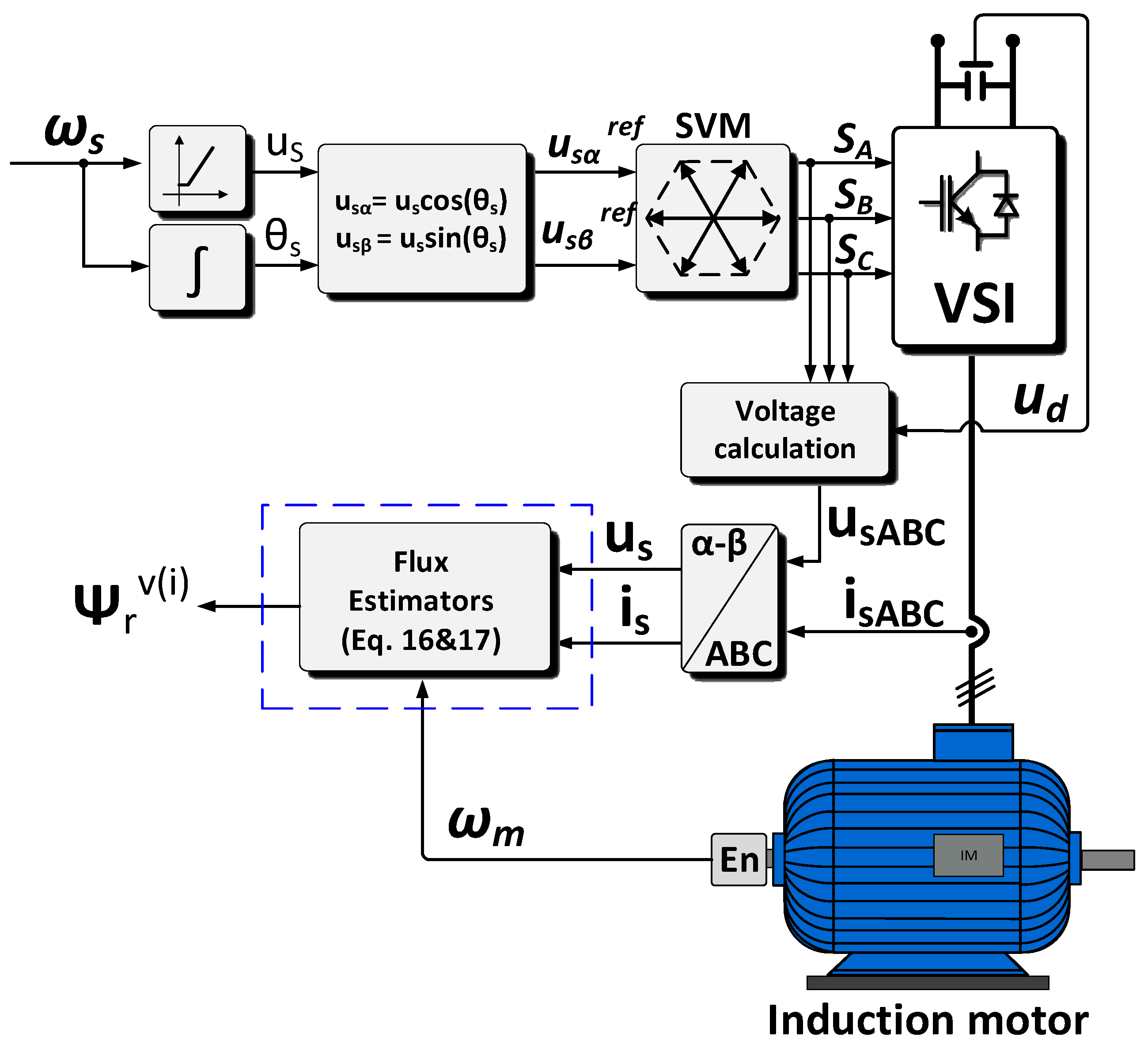
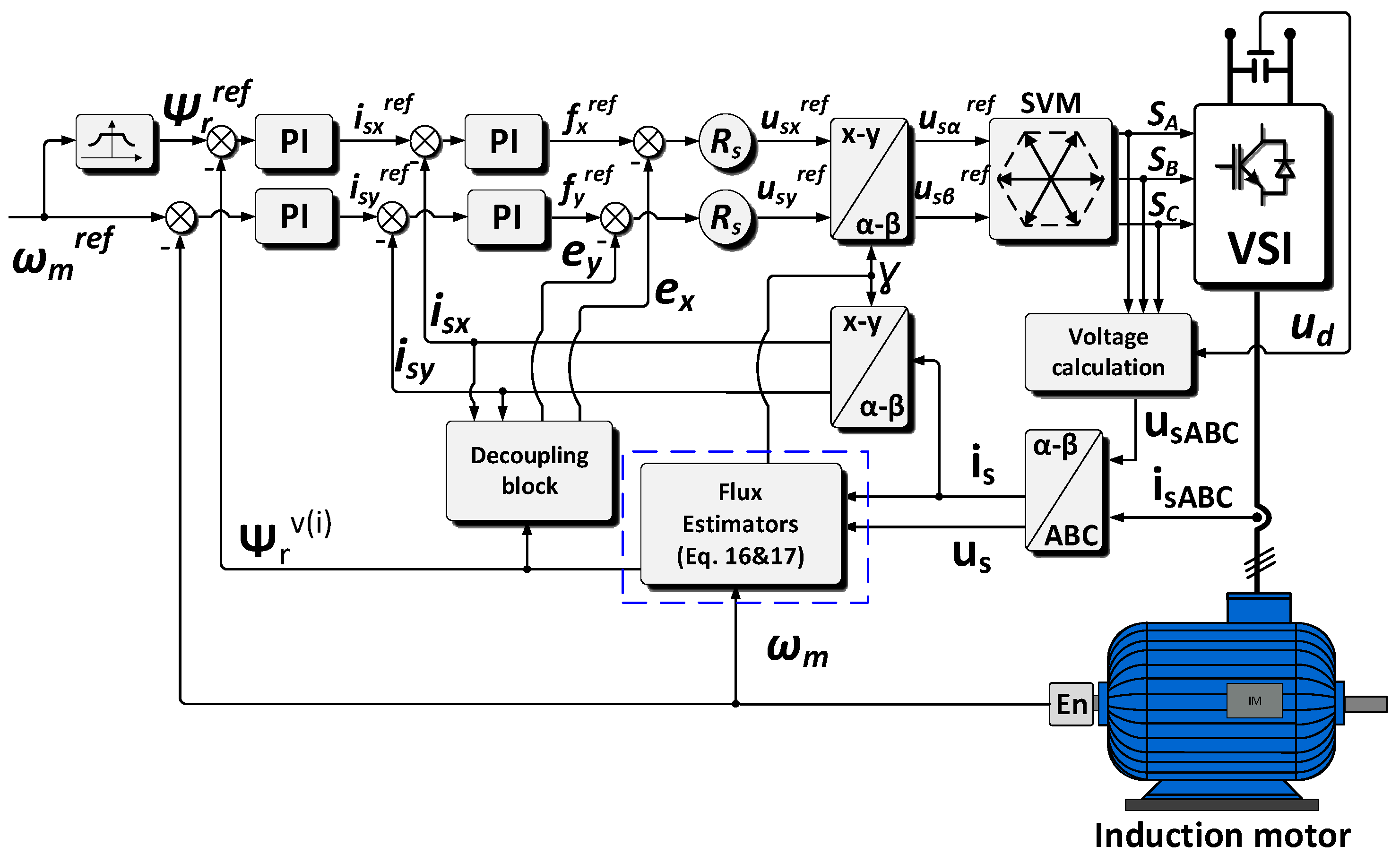
4. Description of Control Structures of Induction Motor
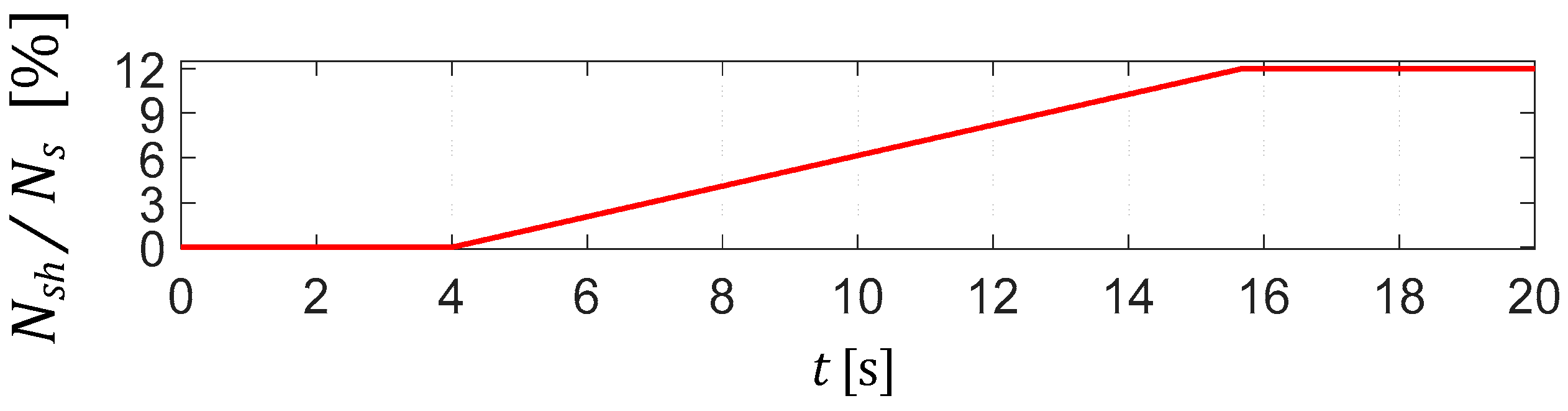
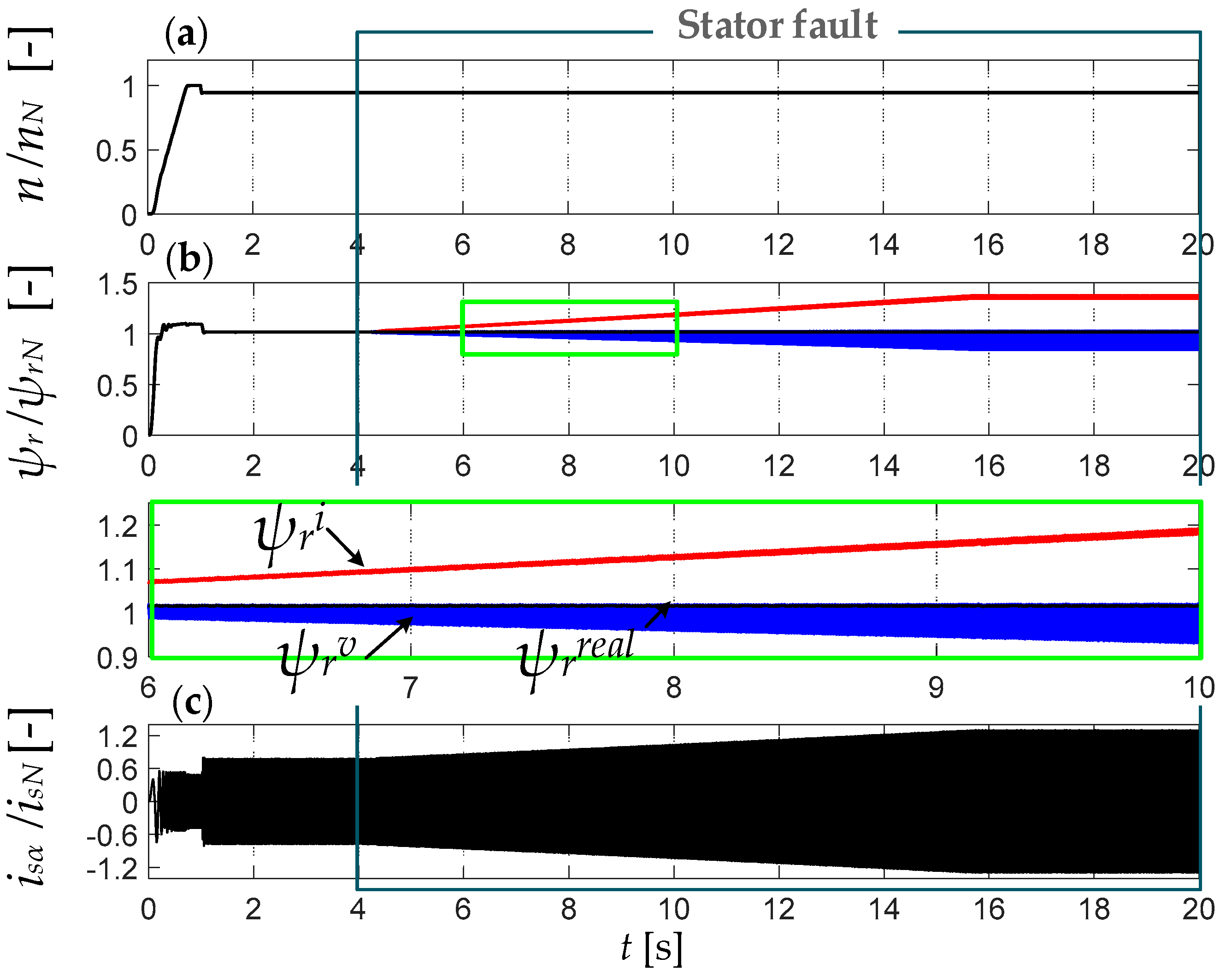
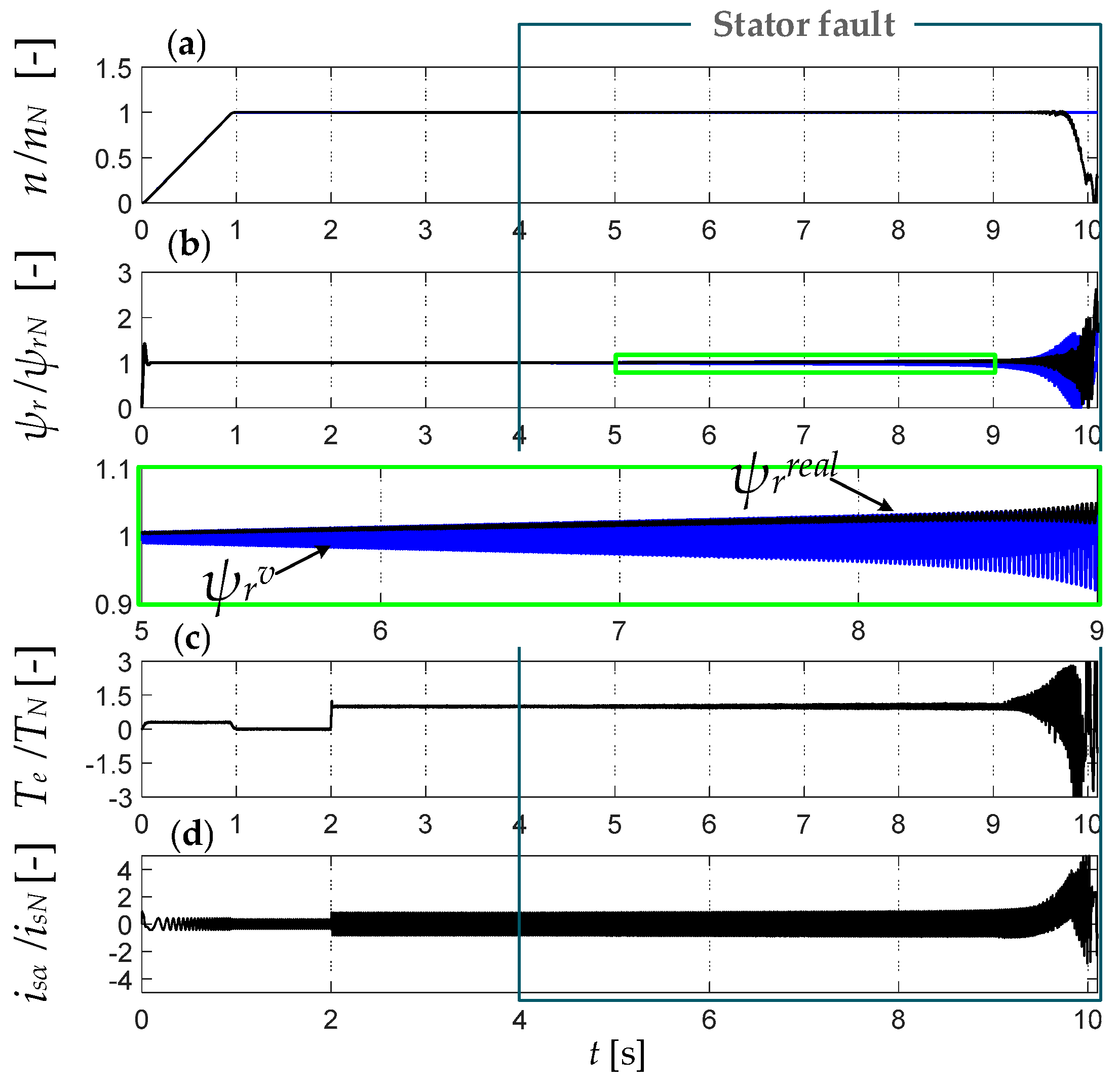
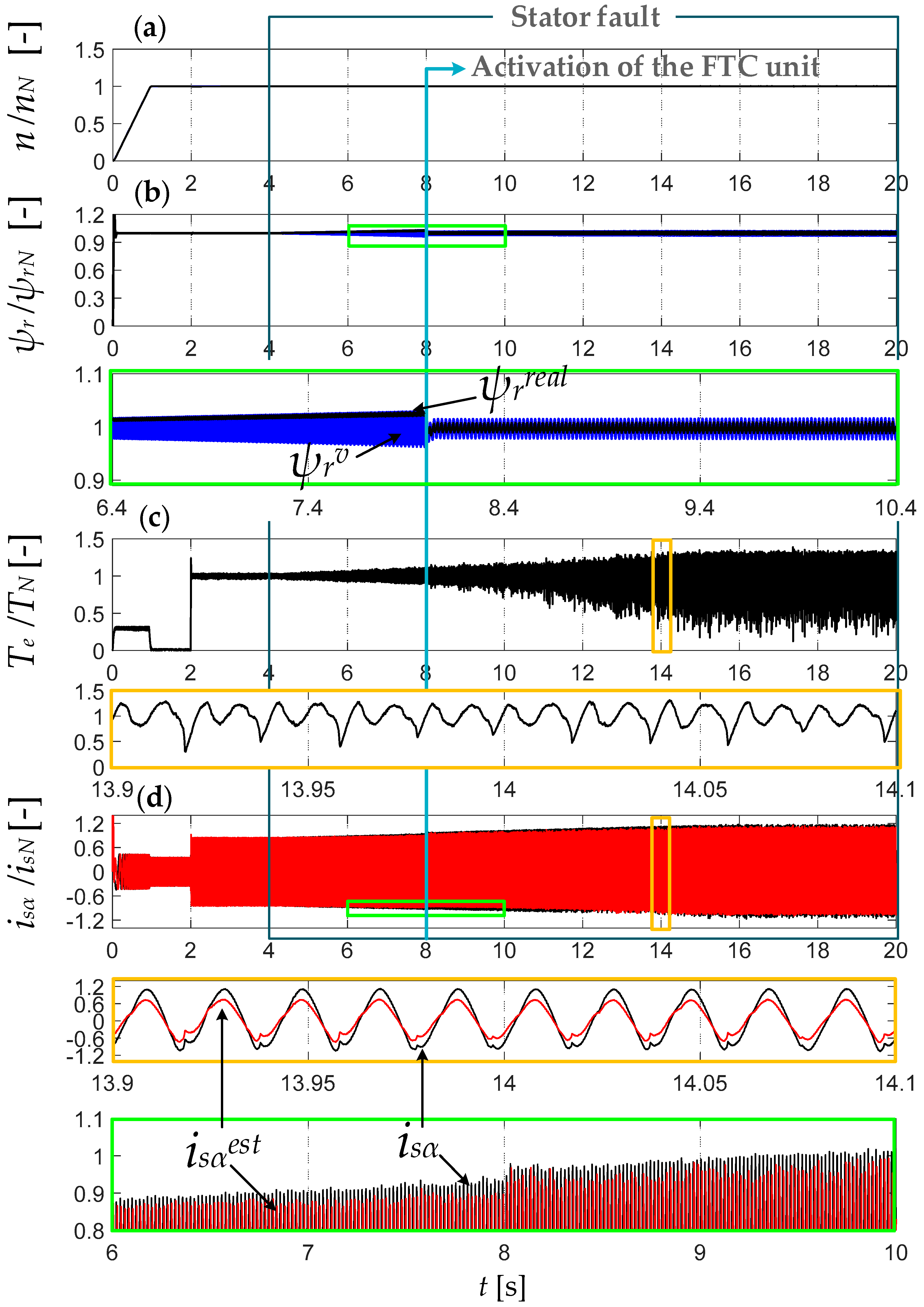
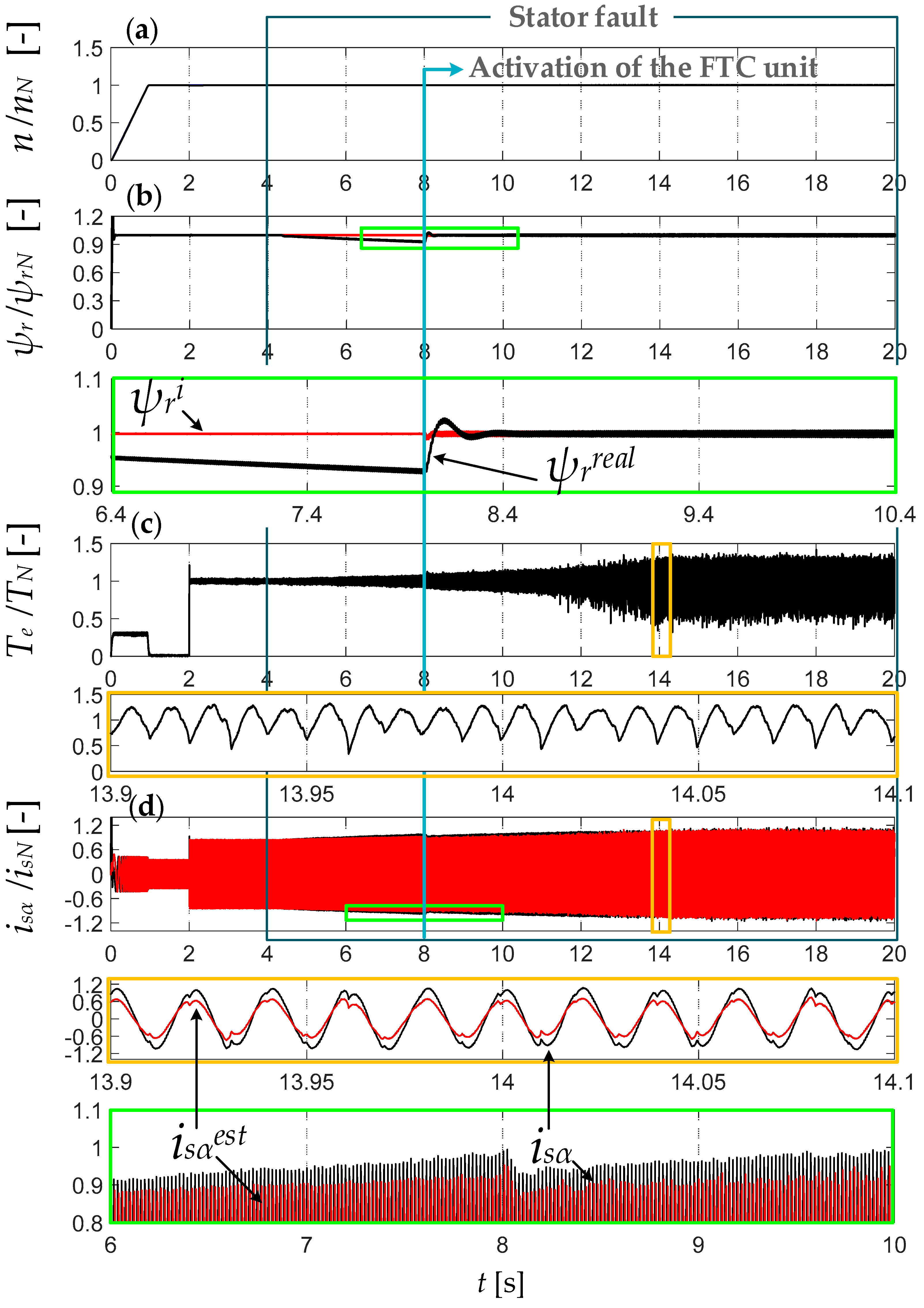
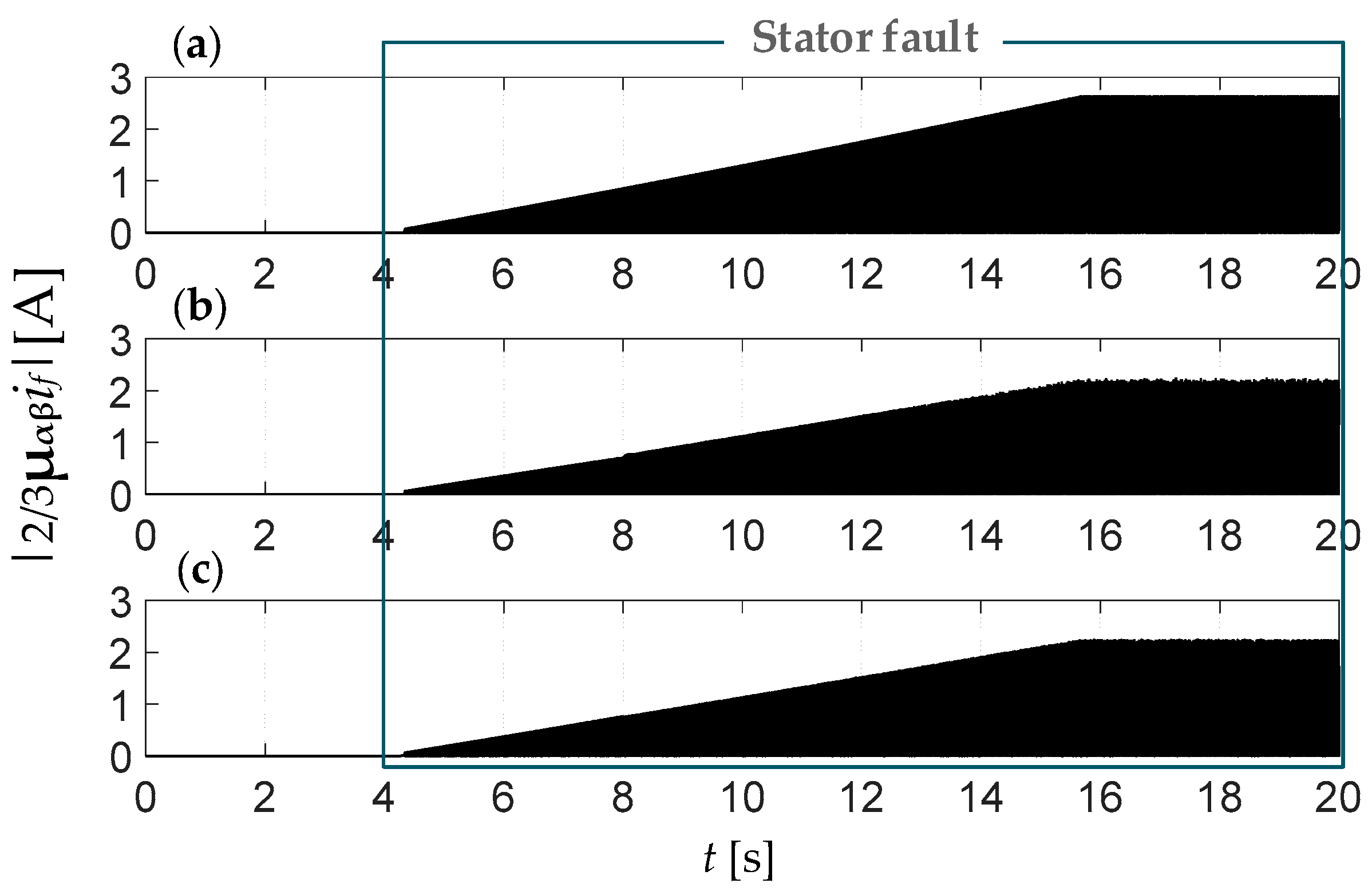
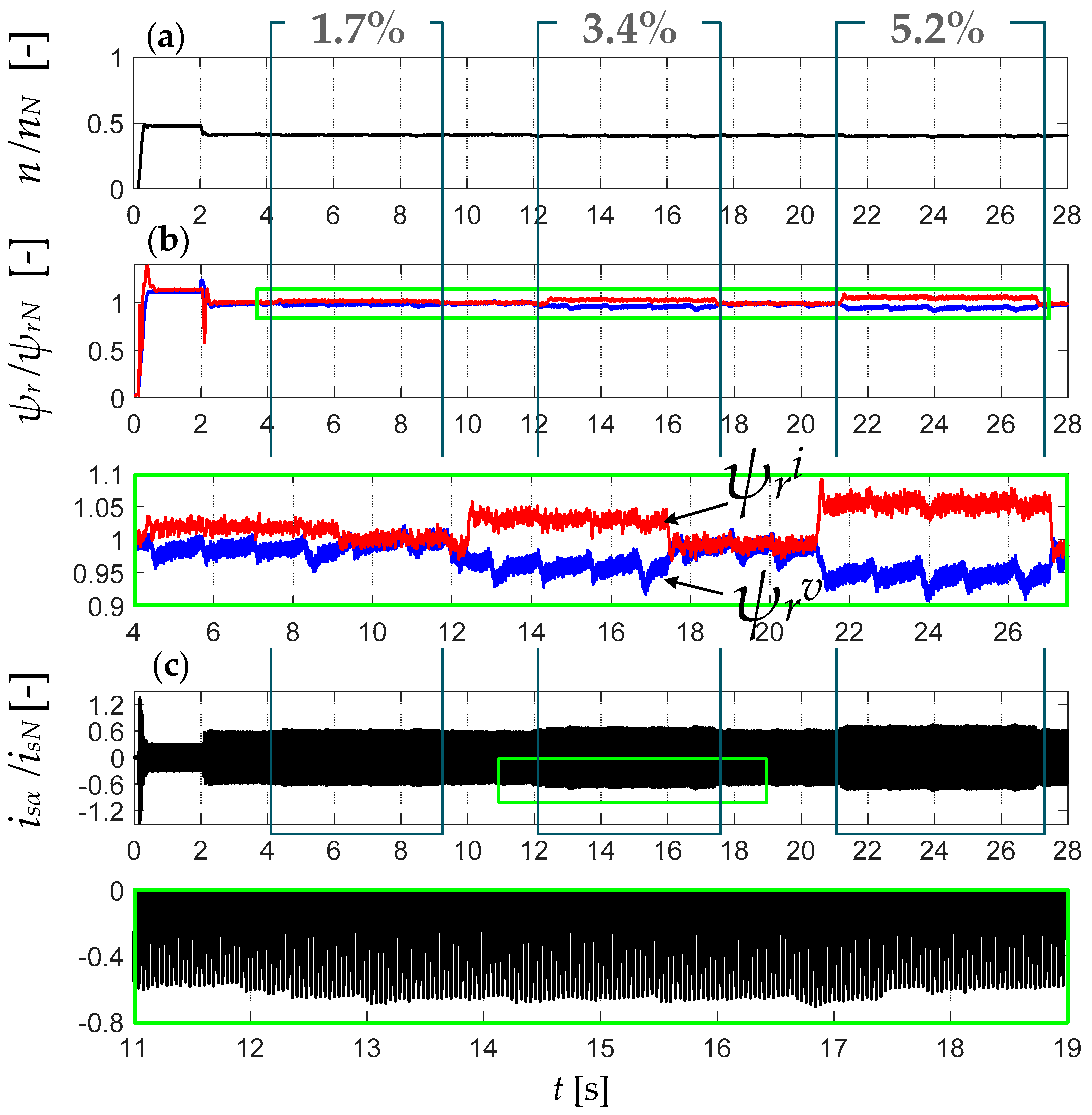
5. Impact of Inter-Turn Short Circuits (ITSCs) on Rotor Flux Estimation Accuracy and Drive Performance
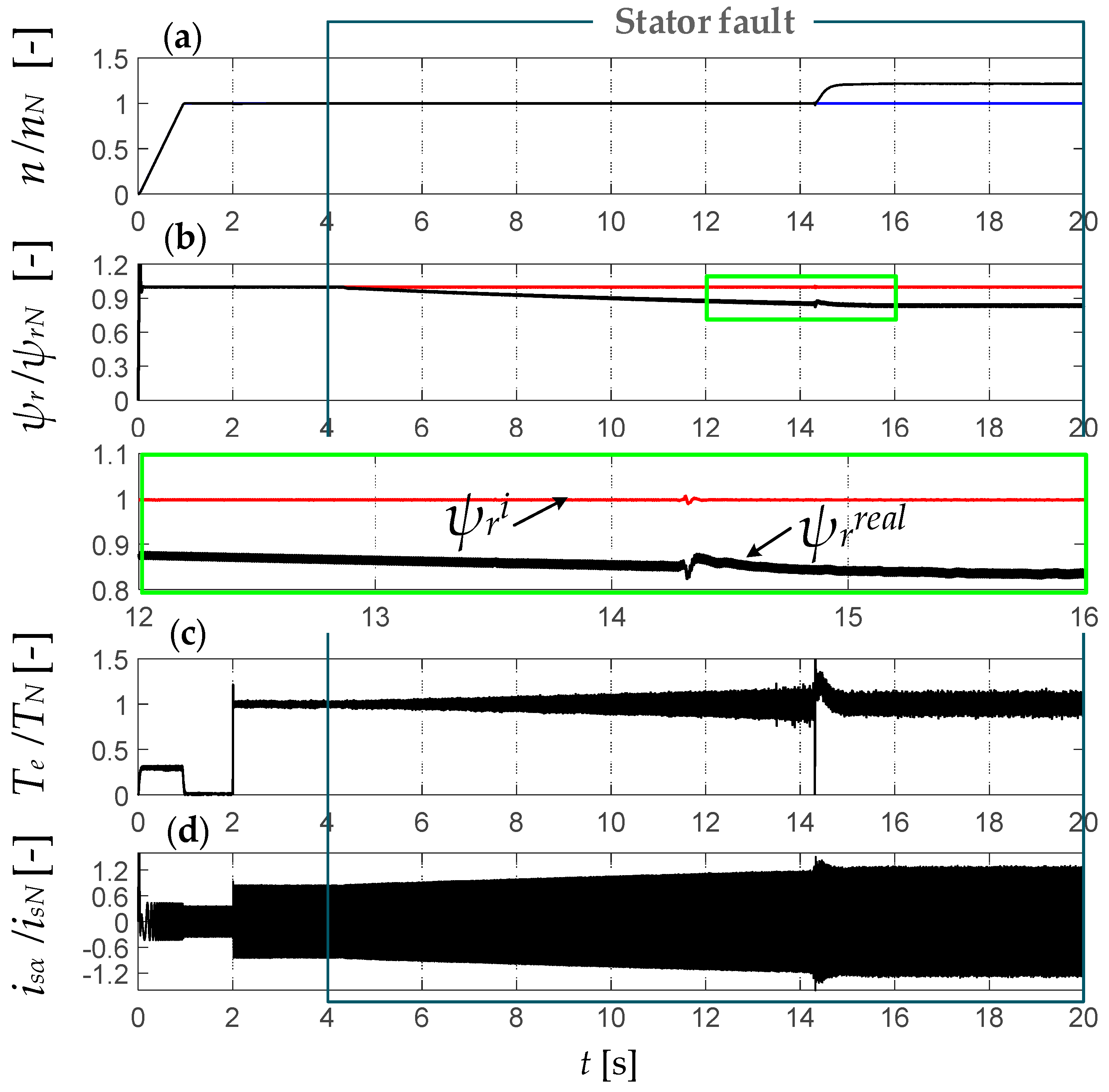
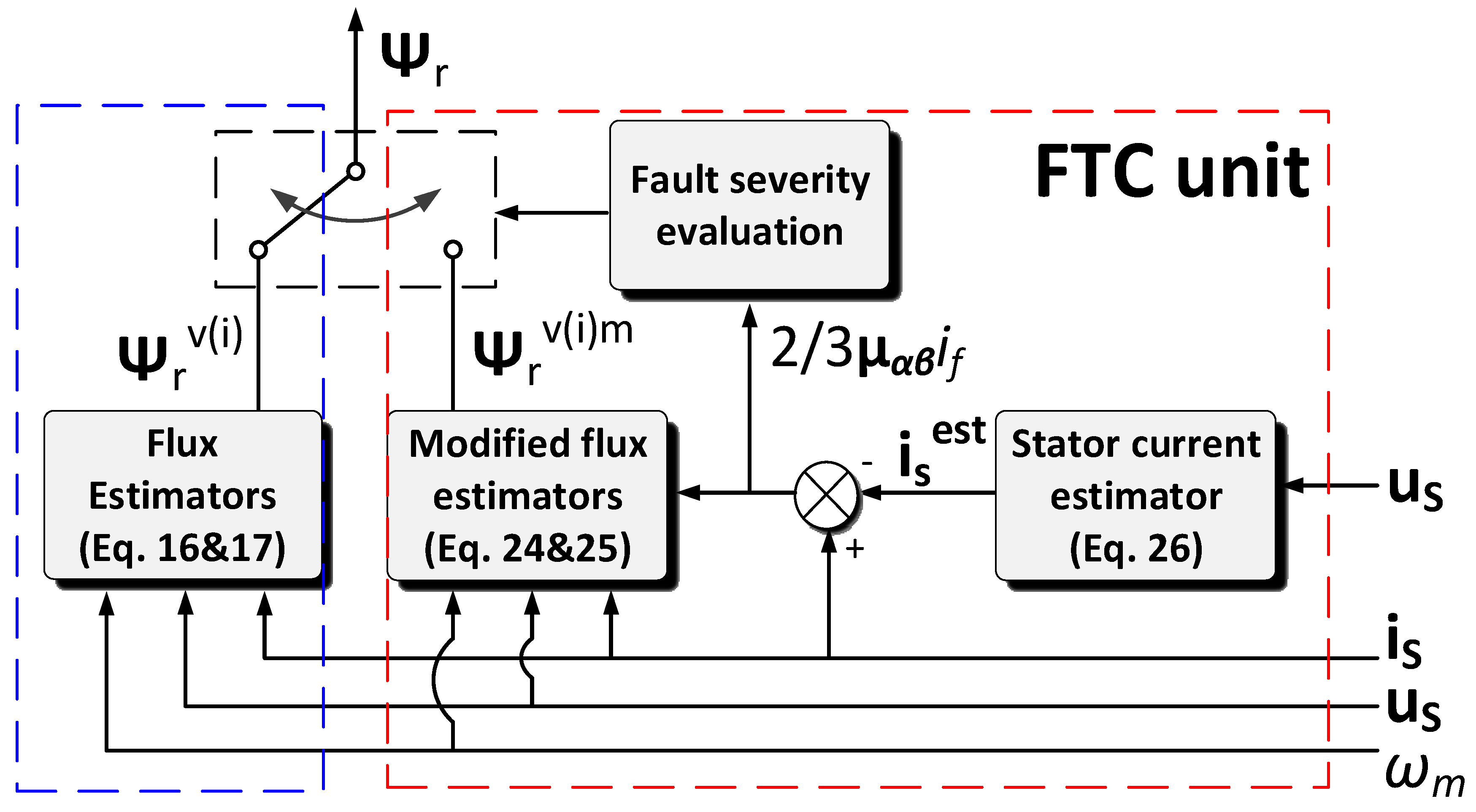
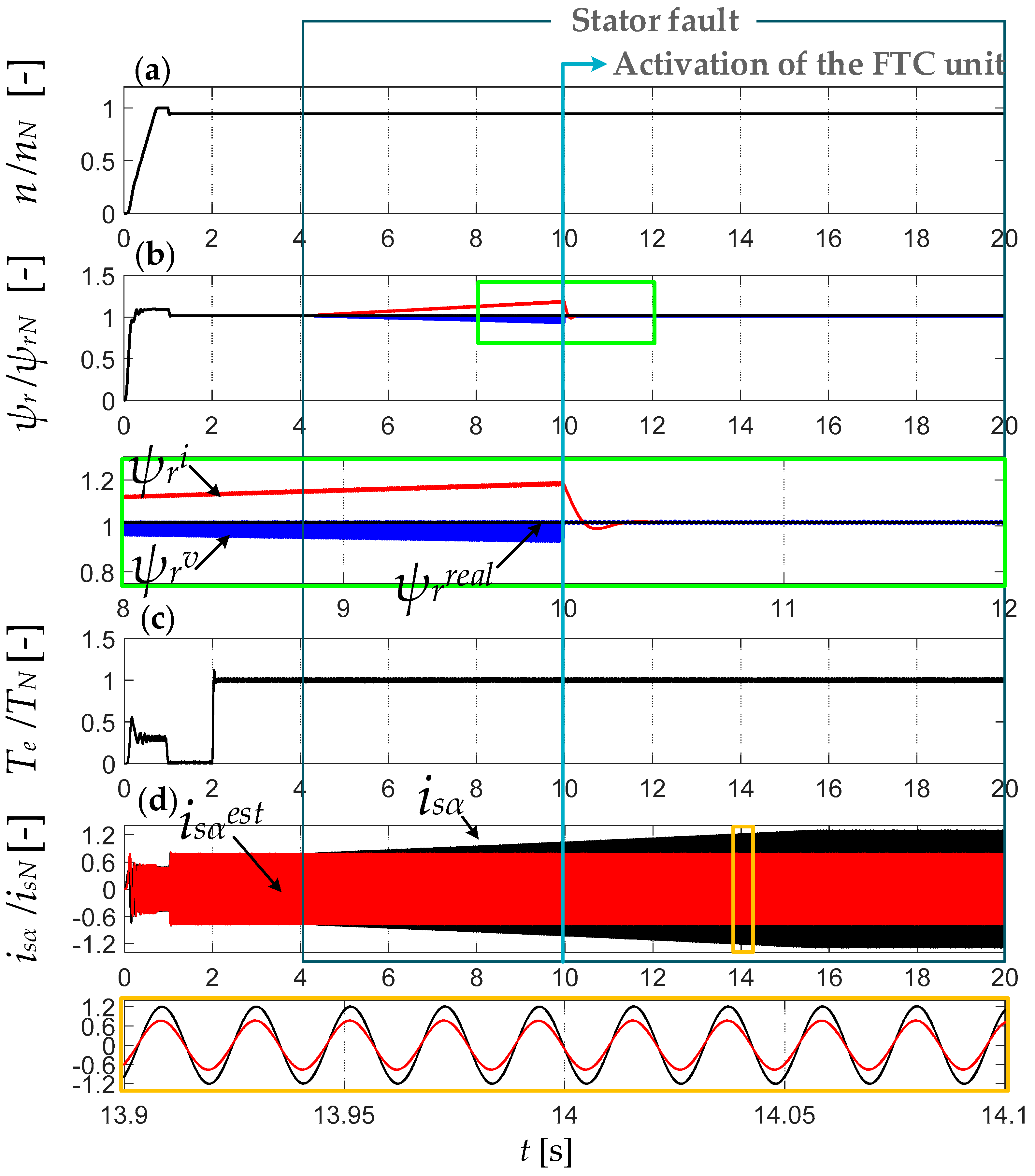
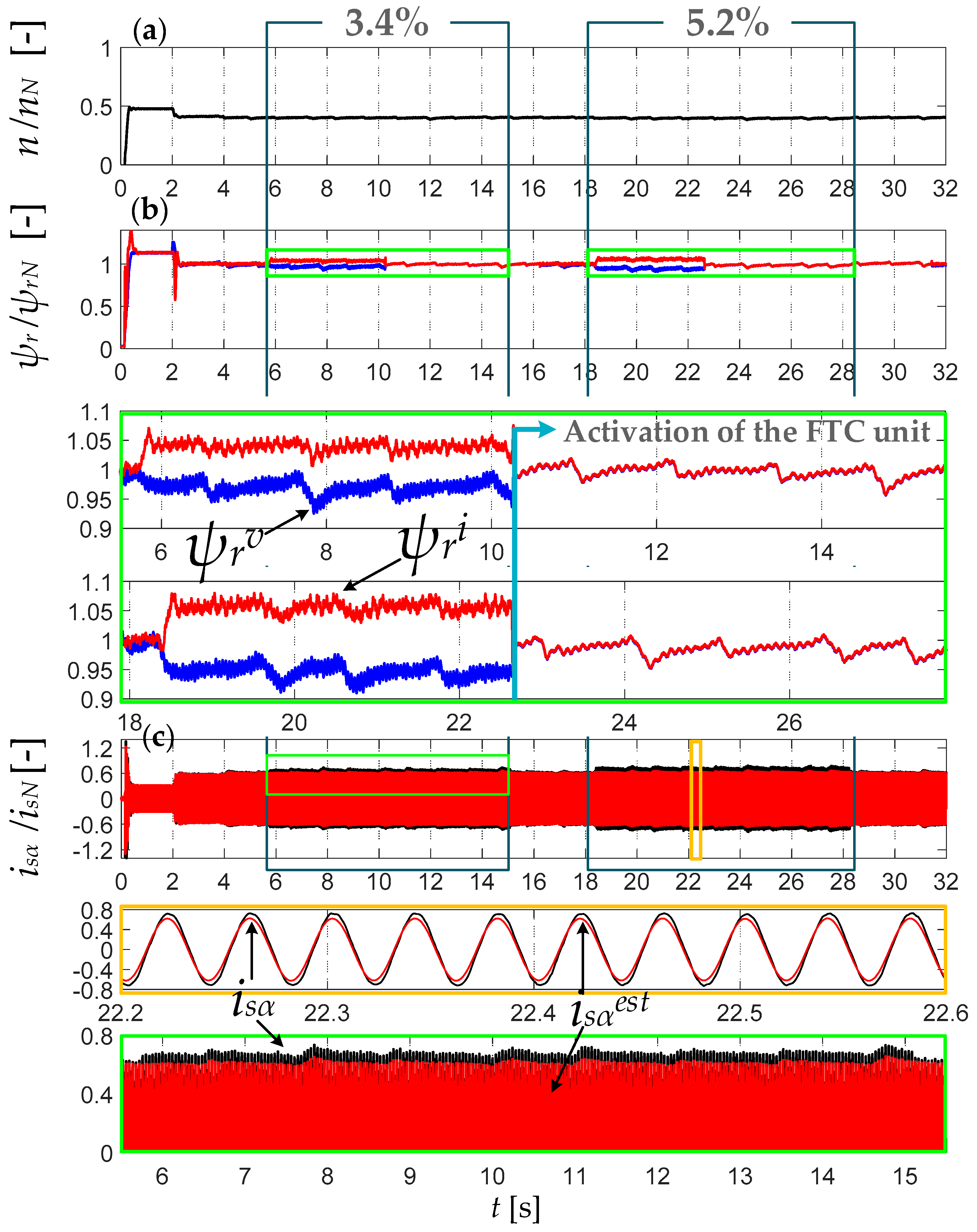
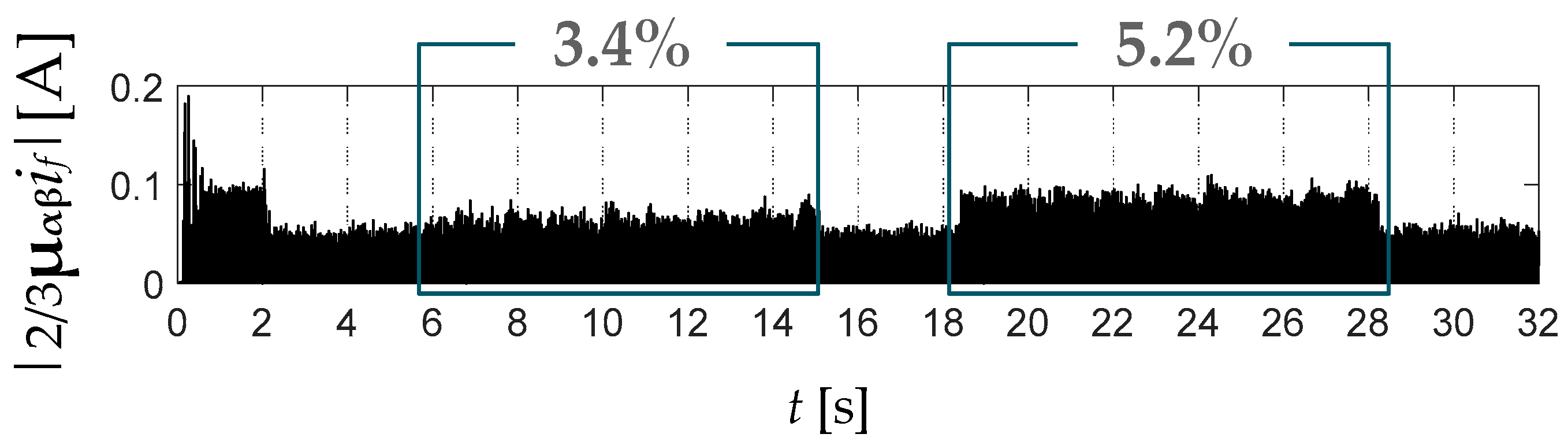
6. Improvement of the Drive Performance during ITSC by an FTC Unit with Modified Rotor Flux Estimators
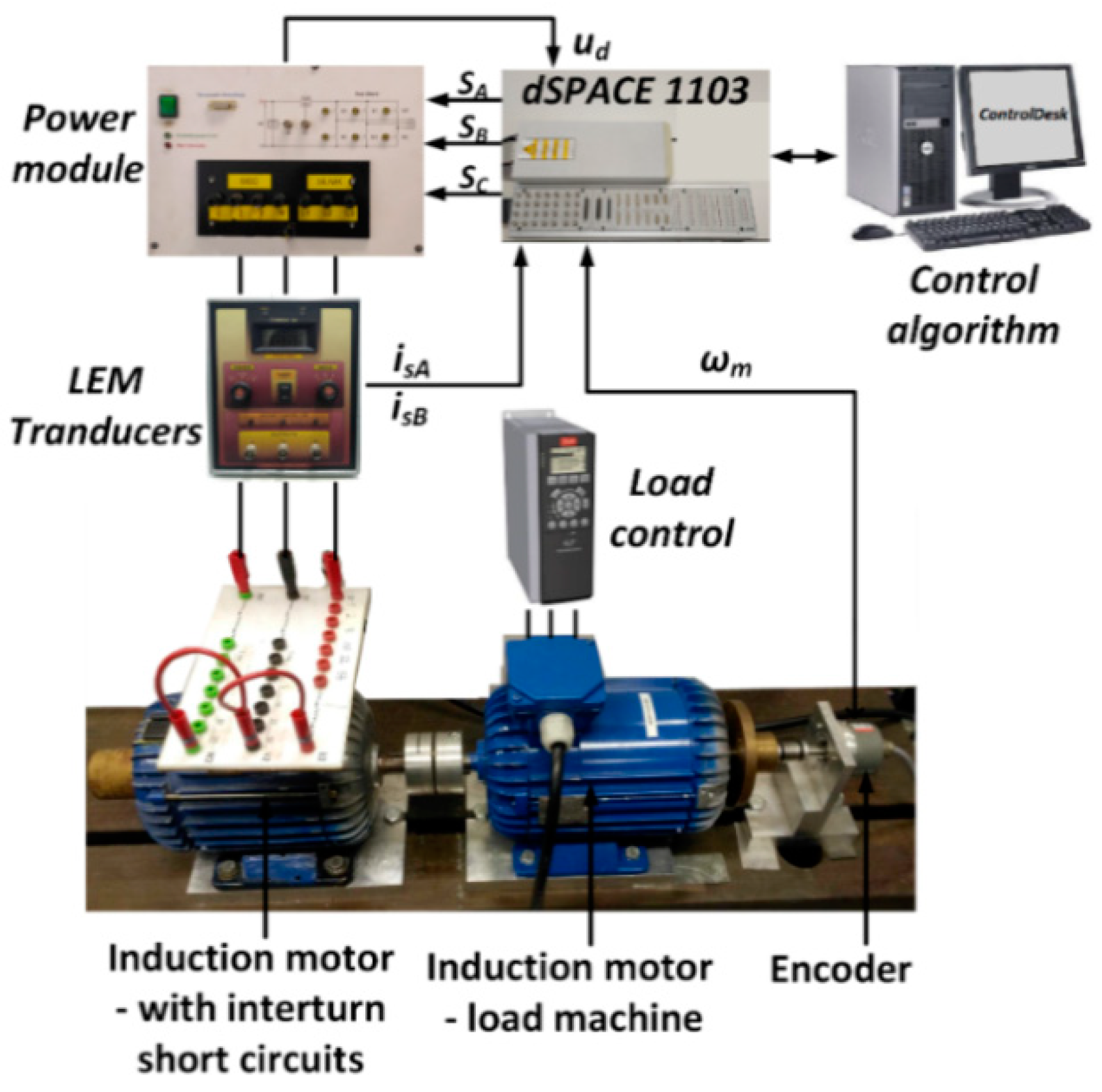
7. Experimental Verification
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Symbol | Rated Data | Value | Unit |
|---|---|---|---|
| PN | Power | 1.5 | kW |
| UN | Stator voltage | 220/380 | V |
| IN | Stator current | 5.0/2.9 | A |
| nN | Mechanical speed | 1400 | rpm |
| TN | Torque | 7.5 | Nm |
| Rs | Stator resistance | 5.9 | Ω |
| Rr | Rotor resistance | 4.6 | Ω |
| Ls | Stator inductance | 417.3 | mH |
| Lr | Rotor inductance | 417.3 | mH |
| Lm | Magnetizing inductance | 392.5 | mH |
| pb | Pole pairs | 2 | - |
| Ns | Turns per phase | 292 | - |
References
- Bose, B.K. Power Electronics and Motor Drives: Advances and Trends, 1st ed.; Academic Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Kazmierkowski, M.P.; Krishann, F.; Blabjerg, F. Control in Power Electronics: Selected Problems, 1st ed.; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Holtz, J. Sensorless Control of Induction Motor Drives. Proc. IEEE 2002, 90, 1359–1394. [Google Scholar] [CrossRef]
- Barut, M.; Demir, R.; Zerdali, E.; Inan, R. Real-time implementation Speed-sensorless, of bi input-extended Kalman filter-based estimator for control of induction motors. IEEE Trans. Ind. Electron. 2012, 59, 4197–4206. [Google Scholar] [CrossRef]
- Syam, P.; Kumar, R.; Das, S.; Chattopadhyay, A.K. Review on model reference adaptive system for sensorless vector control of induction motor drives. IET Electr. Power Appl. 2015, 9, 496–511. [Google Scholar] [CrossRef]
- Lascu, C.; Boldea, I.; Blaabjerg, F. A class of speed-sensorless sliding-mode observers for high-performance induction motor drives. IEEE Trans. Ind. Electron. 2009, 56, 3394–3403. [Google Scholar] [CrossRef]
- Toliyat, H.A.; Levi, E.; Raina, M. A review of RFO induction motor parameter estimation techniques. IEEE Trans. Energy Convers. 2003, 18, 271–283. [Google Scholar] [CrossRef]
- Bellini, A.; Filippetti, F.; Tassoni, C.; Capolino, G.A. Advances in Diagnostic Techniques for Induction Machines. IEEE Trans. Ind. Electron. 2008, 55, 4109–4126. [Google Scholar] [CrossRef]
- Campos-Delgado, D.U.; Espinoza-Trejo, D.R.; Palacios, E. Fault-tolerant control in variable speed drives: A survey. IET Electr. Power Appl. 2008, 2, 121–134. [Google Scholar] [CrossRef]
- Riera-Guasp, M.; Antonino-Daviu, J.A.; Capolino, G.A. Advances in Electrical Machine, Power Electronic, and Drive Condition Monitoring and Fault Detection: State of the Art. IEEE Trans. Ind. Electron. 2015, 62, 1746–1759. [Google Scholar] [CrossRef]
- Merizalde, Y.; Hernández-Callejo, L.; Duque-Perez, O. State of the art and trends in the monitoring, detection and diagnosis of failures in electric induction motors. Energies 2017, 10, 1056. [Google Scholar] [CrossRef]
- Bednarz, S.A.; Dybkowski, M. Induction Motor Windings Faults Detection Using Flux-error Based MRAS Estimators. Diagnostyka 2019, 20, 87–92. [Google Scholar] [CrossRef]
- Zhang, P.; Du, P.; Habetler, T.G.; Lu, B. A Survey of Condition Monitoring and Protection Methods for Medium-Voltage Induction Motors. IEEE Trans. Ind. Appl. 2011, 47, 34–46. [Google Scholar] [CrossRef]
- Gandhi, A.; Corrigan, T.; Parsa, L. Recent Advances in Modeling and Online Detection of Stator Interturn Faults in Electrical Motors. IEEE Trans. Ind. Electron. 2011, 58, 1564–1575. [Google Scholar] [CrossRef]
- Maraaba, L.; Al-Hamouz, Z.; Abido, M. An Efficient Stator Inter-Turn Fault Diagnosis Tool for Induction Motors. Energies 2018, 11, 653. [Google Scholar] [CrossRef]
- Bazan, G.H.; Scalassara, P.R.; Endo, W.; Goedtel, A.; Palácios, R.H.C.; Godoy, W.F. Stator Short-Circuit Diagnosis in Induction Motors Using Mutual Information and Intelligent Systems. IEEE Trans. Ind. Electron. 2019, 66, 3237–3246. [Google Scholar] [CrossRef]
- Zamudio-Ramirez, I.; Osornio-Rios, R.A.; Trejo-Hernandez, M.; Romero-Troncoso, R.D.J.; Antonino-Daviu, J.A. Smart-Sensors to Estimate Insulation Health in Induction Motors via Analysis of Stray Flux. Energies 2019, 12, 1658. [Google Scholar] [CrossRef]
- Skowron, M.; Wolkiewicz, M.; Orlowska-Kowalska, T.; Kowalski, C.T. Application of Self-Organizing Neural Networks to Electrical Fault Classification in Induction Motors. Appl. Sci. 2019, 9, 616. [Google Scholar] [CrossRef]
- Tallam, R.M.; Habetler, T.G.; Harley, R.G. Stator winding turn-fault detection for closed-loop induction motor drives. IEEE Trans. Ind. App. 2003, 39, 1553–1557. [Google Scholar] [CrossRef]
- Cheng, S.; Zhang, P.; Habetler, T.G. An impedance identification approach to sensitive detection and location of stator turn-to-turn faults in a closed-loop multiple-motor drive. IEEE Trans. Ind. Electron. 2011, 58, 1545–1554. [Google Scholar] [CrossRef]
- Wolkiewicz, M.; Tarchała, G.; Kowalski, C.T.; Orłowska-Kowalska, T. Stator Faults Monitoring and Detection in Vector Controlled Induction Motor Drives—Comparative Study. In Advanced Control of Electrical Drives and Power Electronic Converters; Kabźiński, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Tarchała, G.; Wolkiewicz, M. Performance of the Stator Winding Fault Diagnosis in Sensorless Induction Motor Drive. Energies 2019, 12, 1507. [Google Scholar] [CrossRef]
- Cruz, S.M.A.; Cardoso, A.J.M. Diagnosis of Stator Inter-Turn Short Circuits in DTC Induction Motor Drives. IEEE Trans. Ind. Appl. 2004, 40, 1349–1360. [Google Scholar] [CrossRef]
- Berzoy, A.; Mohammed, O.A.; Restrepo, J. Analysis of the Impact of Stator Interturn Short-Circuit Faults on Induction Machines Driven by Direct Torque Control. IEEE Trans. Energy Convers. 2018, 33, 1463–1474. [Google Scholar] [CrossRef]
- Sobański, P.; Orłowska-Kowalska, T. IGBT Open-Circuit Fault Diagnostic Methods for SVM-VSI Vector-Controlled Induction Motor Drives. In Advanced Control of Electrical Drives and Power Electronic Converters; Kabźiński, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Dybkowski, M.; Klimkowski, K. Fault Tolerant Control Structure for Induction Motor Drive System. Automatika 2016, 57, 638–647. [Google Scholar] [CrossRef]
- Isermann, R. Fault-Diagnosis Applications, Model-Based Condition Monitoring: Actuators, Drives, Machinery, Plants, Sensors, and Fault-tolerant Systems, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Muenchhof, M.; Beck, M.; Isermann, R. Fault Diagnosis and Fault Tolerance of Drive Systems: Status and Research. Eur. J. Control 2009, 15, 370–388. [Google Scholar] [CrossRef]
- Levi, E. Multiphase electric machines for variable-speed applications. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M. Diagnosis and Fault-Tolerant Control, 2st ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Jiang, J.; Yu, X. Fault-tolerant control systems: A comparative study between active and passive approaches. Annu. Rev. Control 2012, 36, 60–72. [Google Scholar] [CrossRef]
- Bonivento, C.; Isidori, A.; Marconi, L.; Paoli, A. Implicit fault-tolerant control: Application to induction motors. Automatica 2004, 40, 355–371. [Google Scholar] [CrossRef]
- Roubache, T.; Chaouch, S.; Naït Saïd, M.S. Backstepping fault tolerant control for induction motor. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Ischia, Italy, 18–20 June 2014. [Google Scholar]
- Roubache, T.; Chaouch, S.; Naït Saïd, M.S. Backstepping design for fault detection and FTC of an induction motor drives-based EVs. Automatika 2017, 57, 736–748. [Google Scholar] [CrossRef]
- Djeghali, N.; Ghanes, N.; Djennoune, S.; Barbot, J.P.; Tadjine, M. Fault tolerant control for induction motors using sliding mode observers. In Proceedings of the 11th International Workshop on Variable Structure Systems (VSS), Mexico City, Mexico, 26–28 June 2010. [Google Scholar]
- Kouchih, D.; Hachelaf, R.; Boumalha, N.; Tadjine, M.; Boucherit, M.S. Vector fault tolerant control of induction motor drives subject to stator interturn faults. In Proceedings of the 16th International Power Electronics and Motion Control Conference and Exposition (PEMC), Antalya, Turkey, 21–24 September 2014. [Google Scholar]
- Abdelmadjid, G.; Ahmed, S.; Mohamed, B.S.; Mohamed, T. Sliding mode observer for fault tolerant control of induction motor. In Proceedings of the 2nd International Symposium On Environment Friendly Energies And Applications, Newcastle, UK, 25–27 June 2012. [Google Scholar]
- Roubache, T.; Chaouch, S.; Naït Saïd, M.S. Sensorless Fault-Tolerant Control of an Induction Motor Based Electric Vehicle. J. Electr. Eng. Technol. 2016, 11, 1423–1432. [Google Scholar] [CrossRef]
- Toumi, D.; Boucherit, M.; Tadjine, M. Observer-based fault diagnosis and field oriented fault tolerant control of induction motor with stator inter-turn fault. Arch. Electr. Eng. 2012, 61, 165–188. [Google Scholar] [CrossRef]
- Kallesøe, C.S.; Izadi-Zamanabadi, R.; Vadstrup, P.P.; Rasmussen, H. Observer-based estimation of stator-winding faults in delta-connected induction motors: A linear matrix inequality approach. IEEE Trans. Ind. Appl. 2007, 43, 1022–1031. [Google Scholar] [CrossRef]
- Sellami, T.; Berriri, H.; Jelassi, S.; Darcherif, A.M.; Mimouni, M.F. Short-Circuit Fault Tolerant Control of a Wind Turbine Driven Induction Generator Based on Sliding Mode Observers. Energies 2017, 10, 1611. [Google Scholar] [CrossRef]
- Refaat, S.S.; Abu-Rub, H.; Iqbal, A. ANN-based system for inter-turn stator winding fault tolerant DTC for induction motor drives. In Proceedings of the 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015. [Google Scholar]
- Diallo, D.; Benbouzid, M.E.H.; Makouf, A. A Fault-Tolerant Control Architecture for Induction Motor Drives in Automotive Applications. IEEE Trans. Veh. Technol. 2004, 53, 1847–1855. [Google Scholar] [CrossRef]
- Gaeid, K.S.; Ping, H.W.; Khalid, M.; Masaoud, A. Sensor and sensorless fault tolerant control for induction motors using a wavelet index. Sensors 2012, 12, 4031–4050. [Google Scholar] [CrossRef] [PubMed]
- Youngkook, L.; Habetler, T.G. A Stator Turn Fault Tolerant Strategy for Induction Motor Drives in Safety Critical Applications. In Proceedings of the 37th IEEE Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006. [Google Scholar]
- Refaat, S.S.; Abu-Rub, H.; Saad, M.S.; Aboul-Zahab, M.S.; Iqbal, A. Fault tolerance of stator turn fault for three phase induction motors star-connected using artificial neural network. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013. [Google Scholar]
- De Angelo, C.H.; Bossio, G.R.; Giaccone, S.J.; Valla, M.I.; Solsona, J.A.; Garcia, G.O. Online Model-Based Stator-Fault Detection and Identification in Induction Motors. IEEE Trans. Ind. Electron. 2009, 56, 4671–4680. [Google Scholar] [CrossRef]
- Rassmusen, H.; Knudsen, M.; Tonnes, M. Parameter estimation of inverter and motor model at standstill using measured currents only. In Proceedings of the IEEE International Symposium on Industrial Electronics (ISIE), Warsaw, Poland, 17–20 June 1996. [Google Scholar]
- Dybkowski, M.; Orłowska-Kowalska, T.; Wierzbicki, R. Self-commissioning sensorless induction motor drive with new MRAS estimator: Experimental tests. Pozn. Univ. Technol. Acad. J. Electr. Eng. 2007, 55, 59–71. [Google Scholar]
- Zorgrani, Y.A.; Jouili, M.; Koubaa, Y.; Boussak, M. A very-low speed sensorless control induction motor drive with online rotor resistance tuning by using MRAS scheme. Power Electron. Drives. 2018, 3, 171–186. [Google Scholar] [CrossRef]
- Hu, J.; Wu, B. New integration algorithms for estimating flux over a wide speed range. IEEE Trans. Power. Electron. 1998, 13, 969–977. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dybkowski, M.; Bednarz, S.A. Modified Rotor Flux Estimators for Stator-Fault-Tolerant Vector Controlled Induction Motor Drives. Energies 2019, 12, 3232. https://doi.org/10.3390/en12173232
Dybkowski M, Bednarz SA. Modified Rotor Flux Estimators for Stator-Fault-Tolerant Vector Controlled Induction Motor Drives. Energies. 2019; 12(17):3232. https://doi.org/10.3390/en12173232
Chicago/Turabian StyleDybkowski, Mateusz, and Szymon Antoni Bednarz. 2019. "Modified Rotor Flux Estimators for Stator-Fault-Tolerant Vector Controlled Induction Motor Drives" Energies 12, no. 17: 3232. https://doi.org/10.3390/en12173232
APA StyleDybkowski, M., & Bednarz, S. A. (2019). Modified Rotor Flux Estimators for Stator-Fault-Tolerant Vector Controlled Induction Motor Drives. Energies, 12(17), 3232. https://doi.org/10.3390/en12173232






