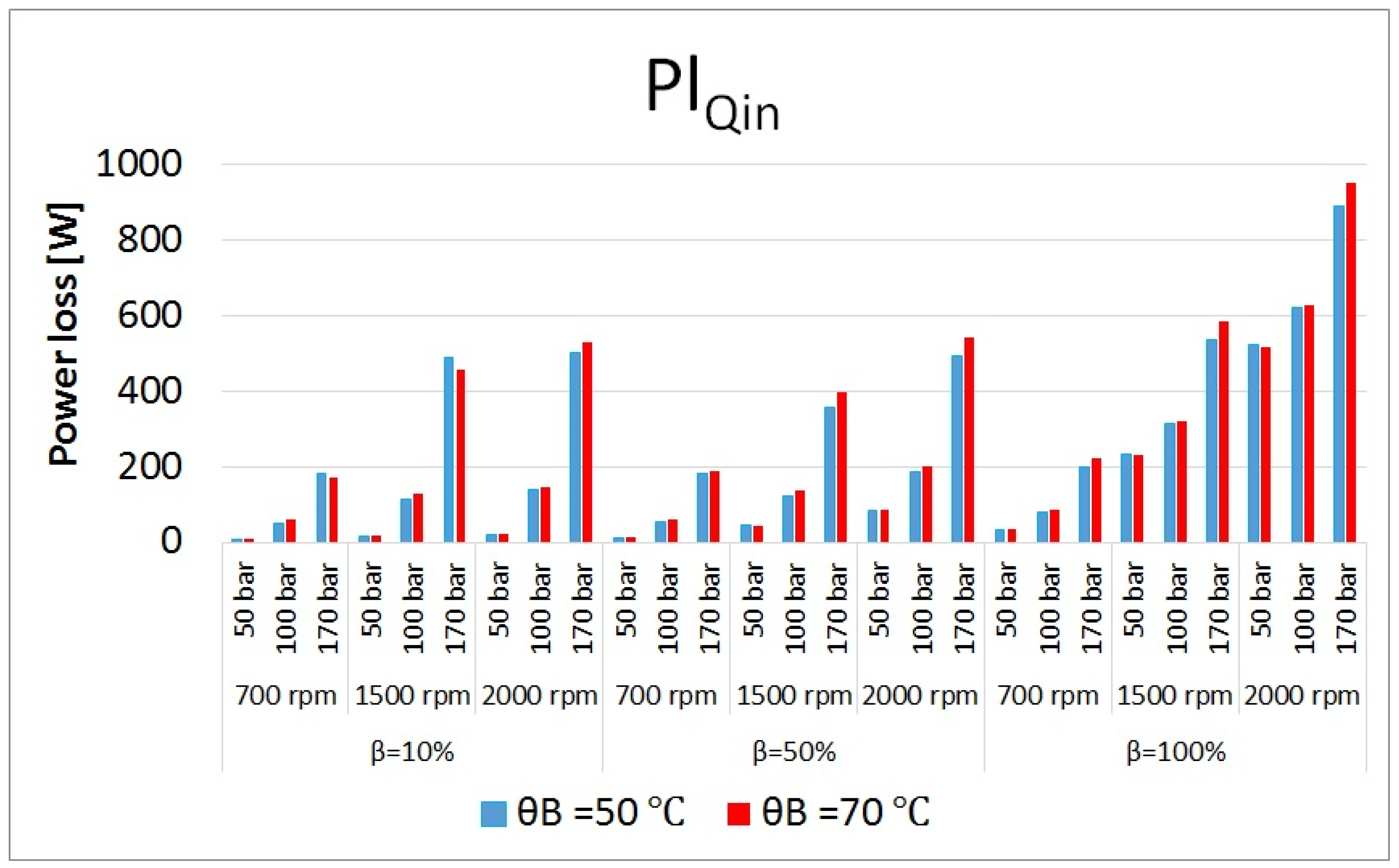
Figure 1.
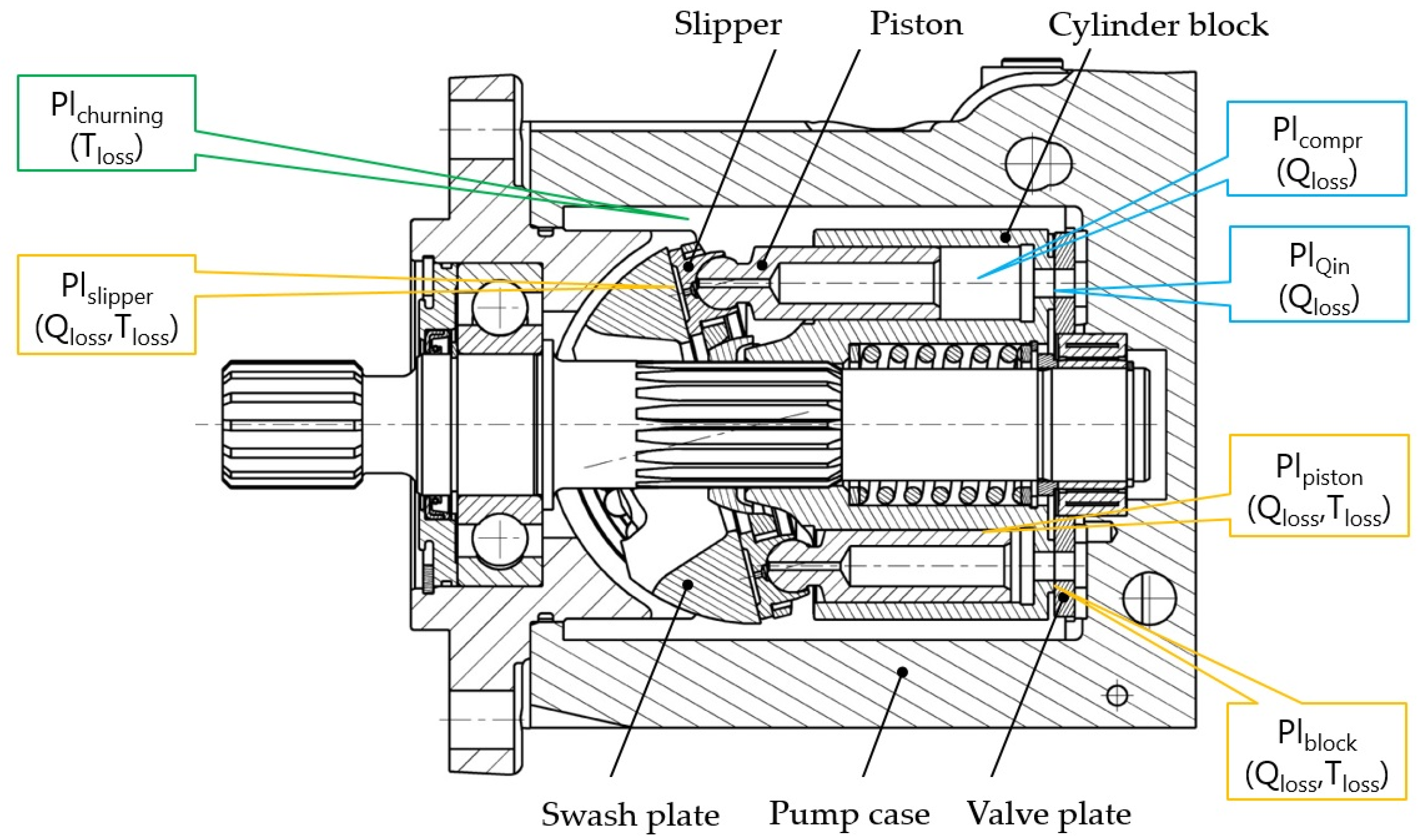
Power losses in an S-APP.
Figure 1.
Power losses in an S-APP.
Figure 2.
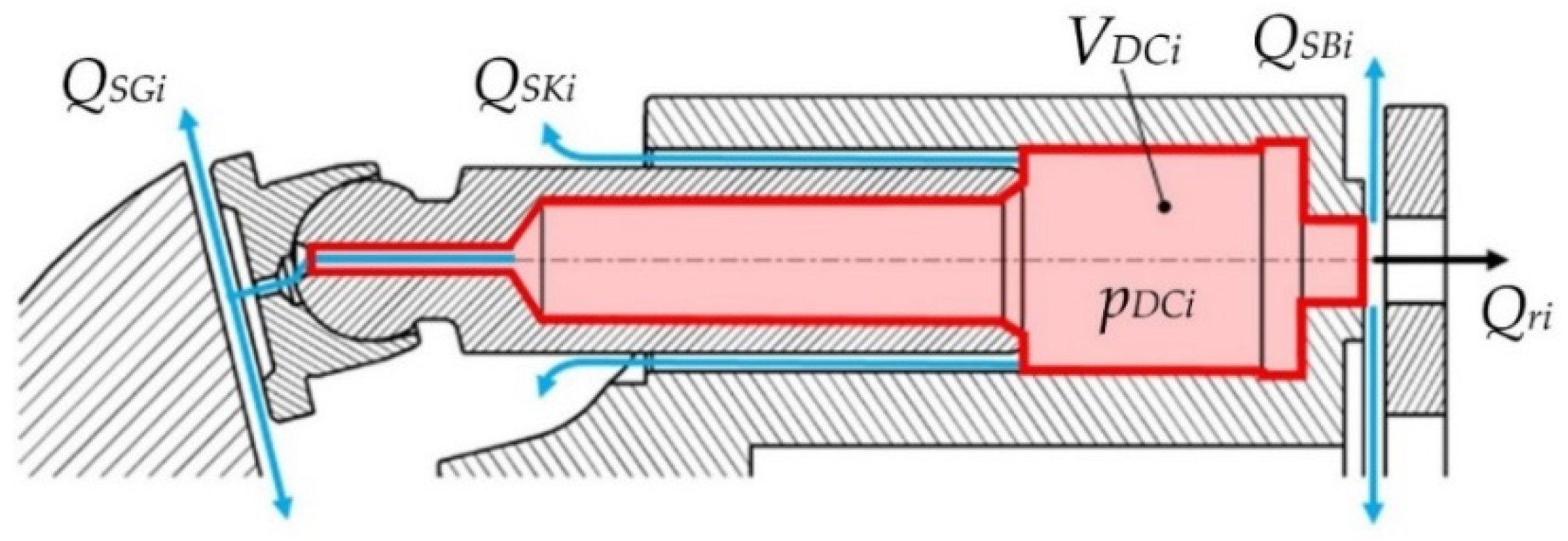
The schema of a displacement chamber.
Figure 2.
The schema of a displacement chamber.
Figure 3.
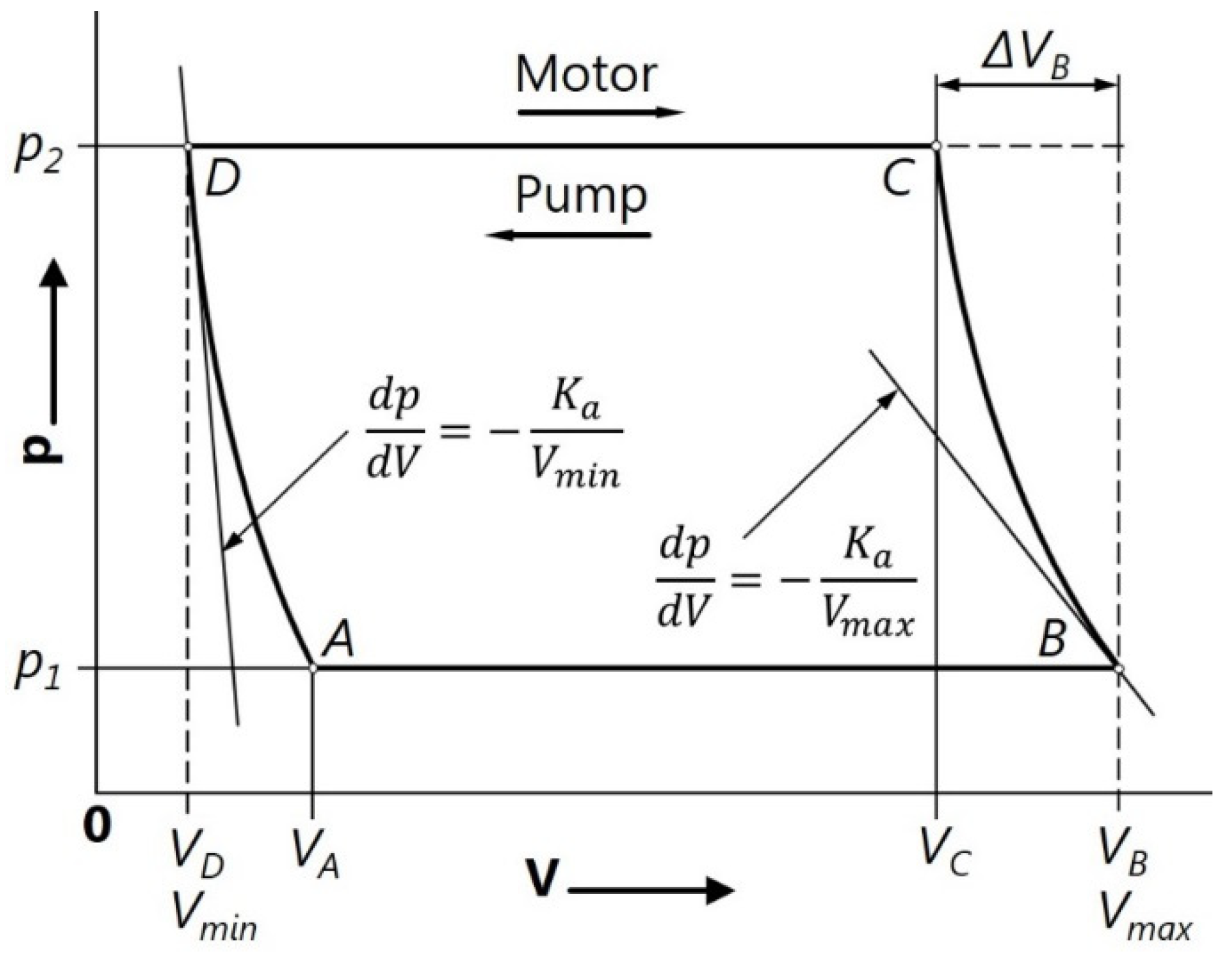
Diagram of an ideal displacement machine with a compressible fluid.
Figure 3.
Diagram of an ideal displacement machine with a compressible fluid.
Figure 4.
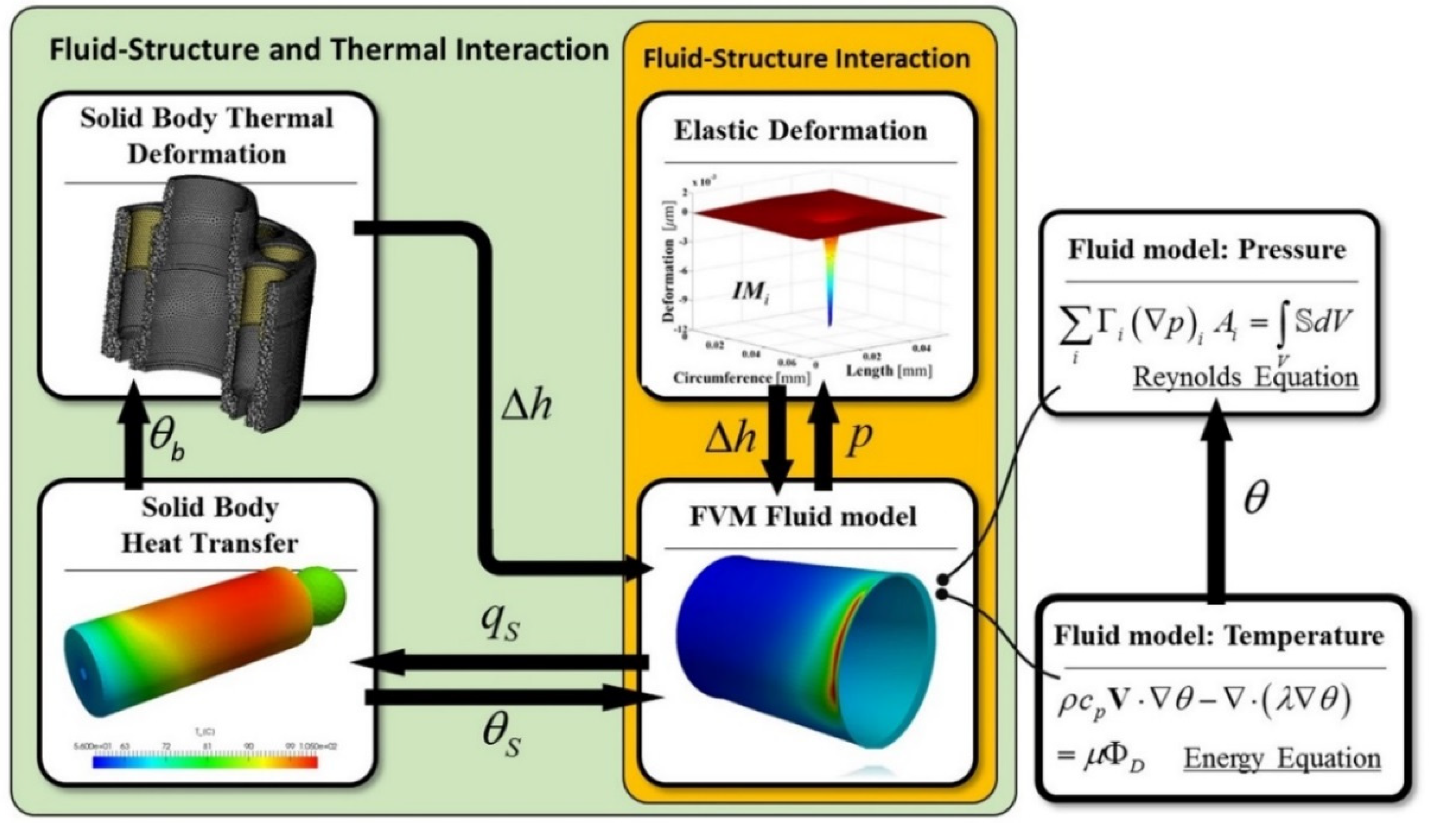
Structure of the simulation model for the prediction of lubricating interface performance.
Figure 4.
Structure of the simulation model for the prediction of lubricating interface performance.
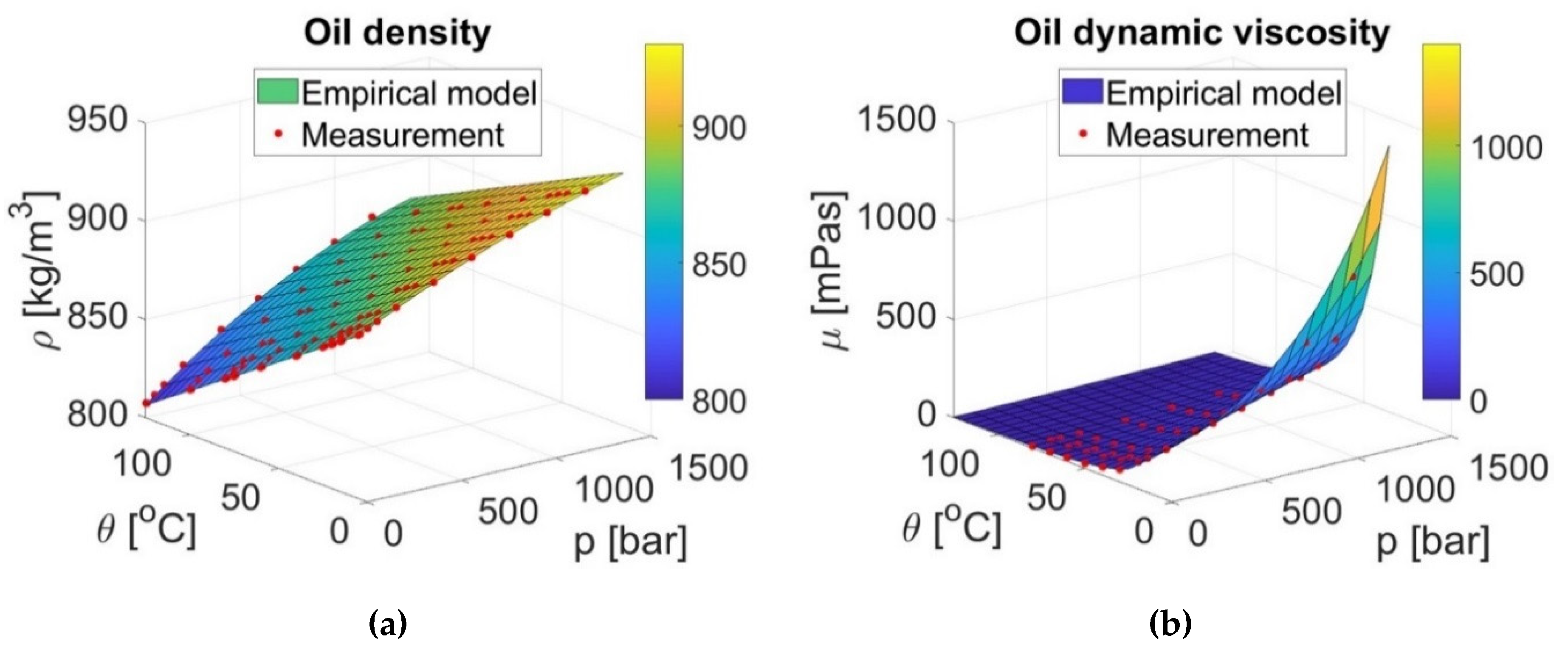
Figure 5.
(a) Dependence of the density on the pressure and temperature for the oil an ISO 46 viscosity grade; (b) dependence of the viscosity on the pressure and temperature for the oil an ISO 46 viscosity grade.
Figure 5.
(a) Dependence of the density on the pressure and temperature for the oil an ISO 46 viscosity grade; (b) dependence of the viscosity on the pressure and temperature for the oil an ISO 46 viscosity grade.
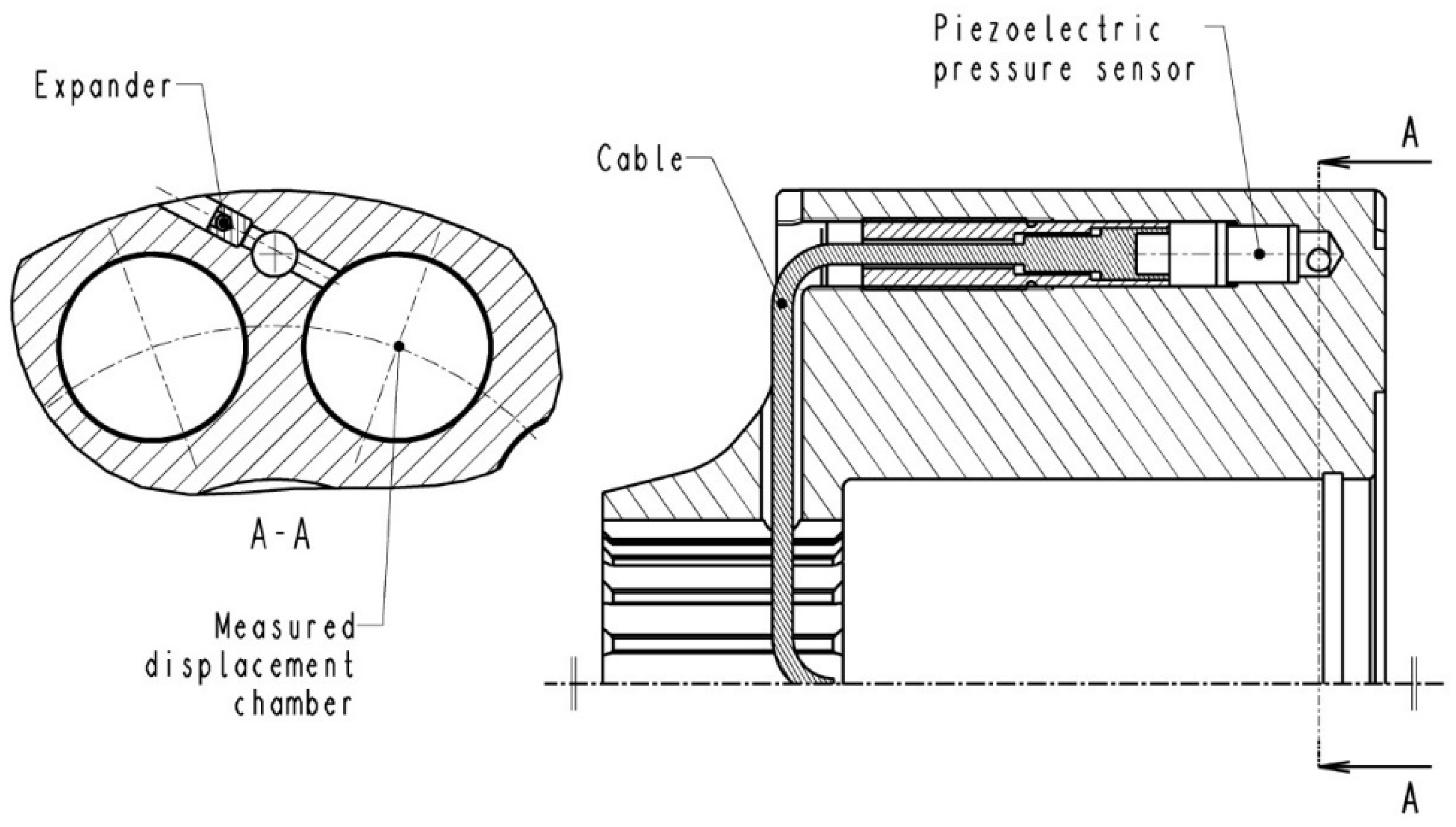
Figure 6.
Implementation of the pressure transducer into the cylinder block.
Figure 6.
Implementation of the pressure transducer into the cylinder block.
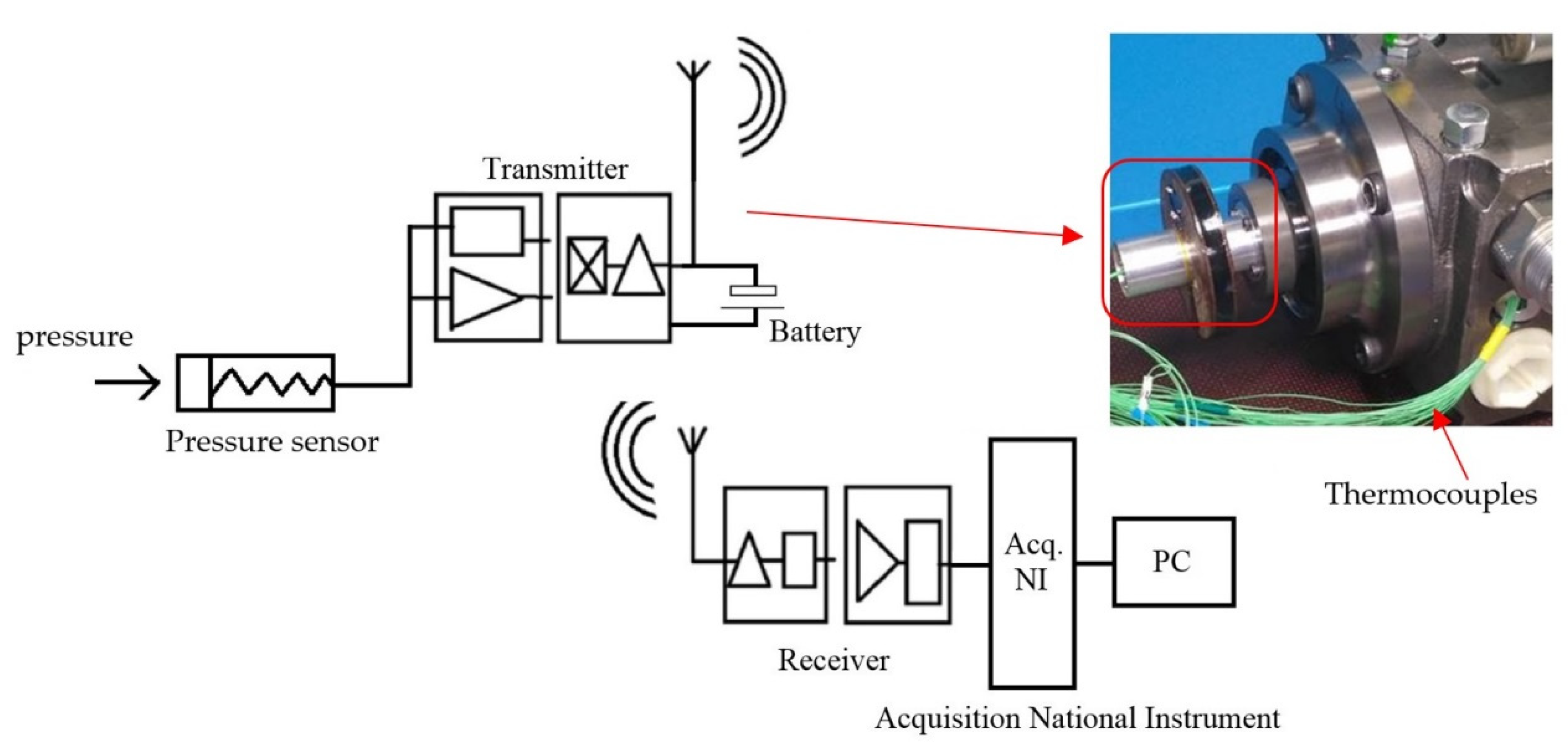
Figure 7.
The principle schema of telemetry system and its installation on the pump.
Figure 7.
The principle schema of telemetry system and its installation on the pump.
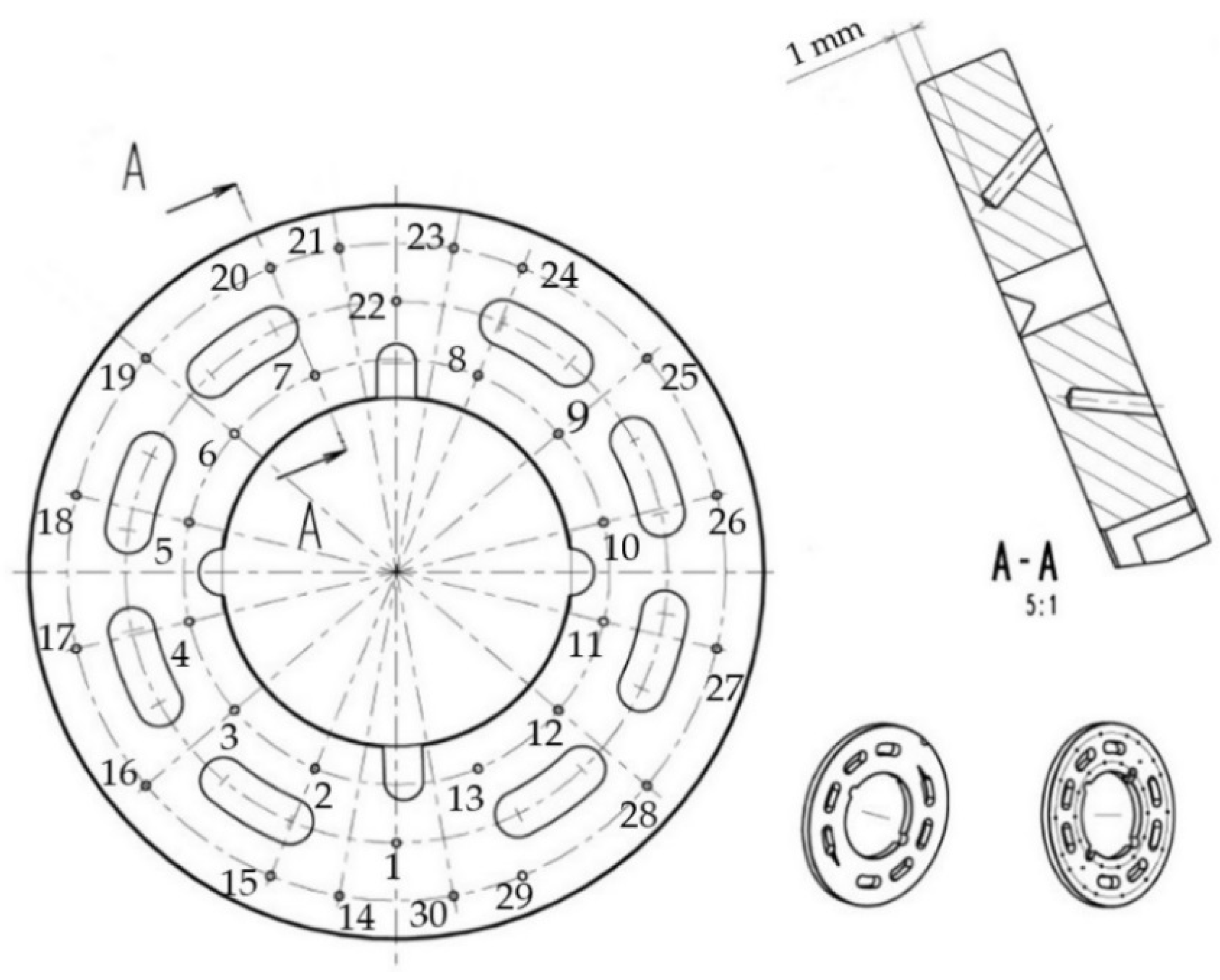
Figure 8.
Position of the thermocouples in the valve plate.
Figure 8.
Position of the thermocouples in the valve plate.
Figure 9.
Valve plate in the end case of the pump.
Figure 9.
Valve plate in the end case of the pump.
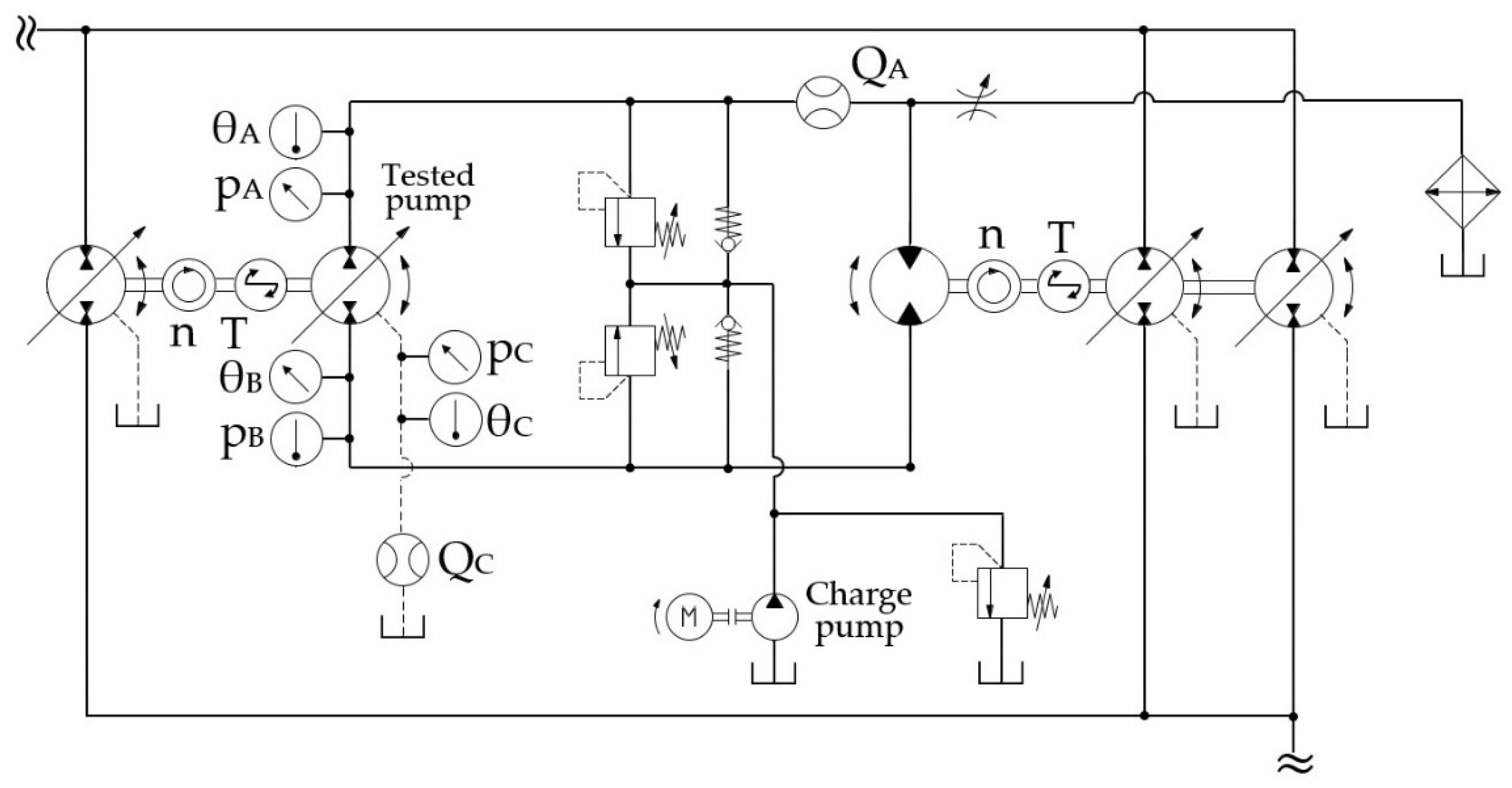
Figure 10.
Hydraulic schematic of the test rig.
Figure 10.
Hydraulic schematic of the test rig.
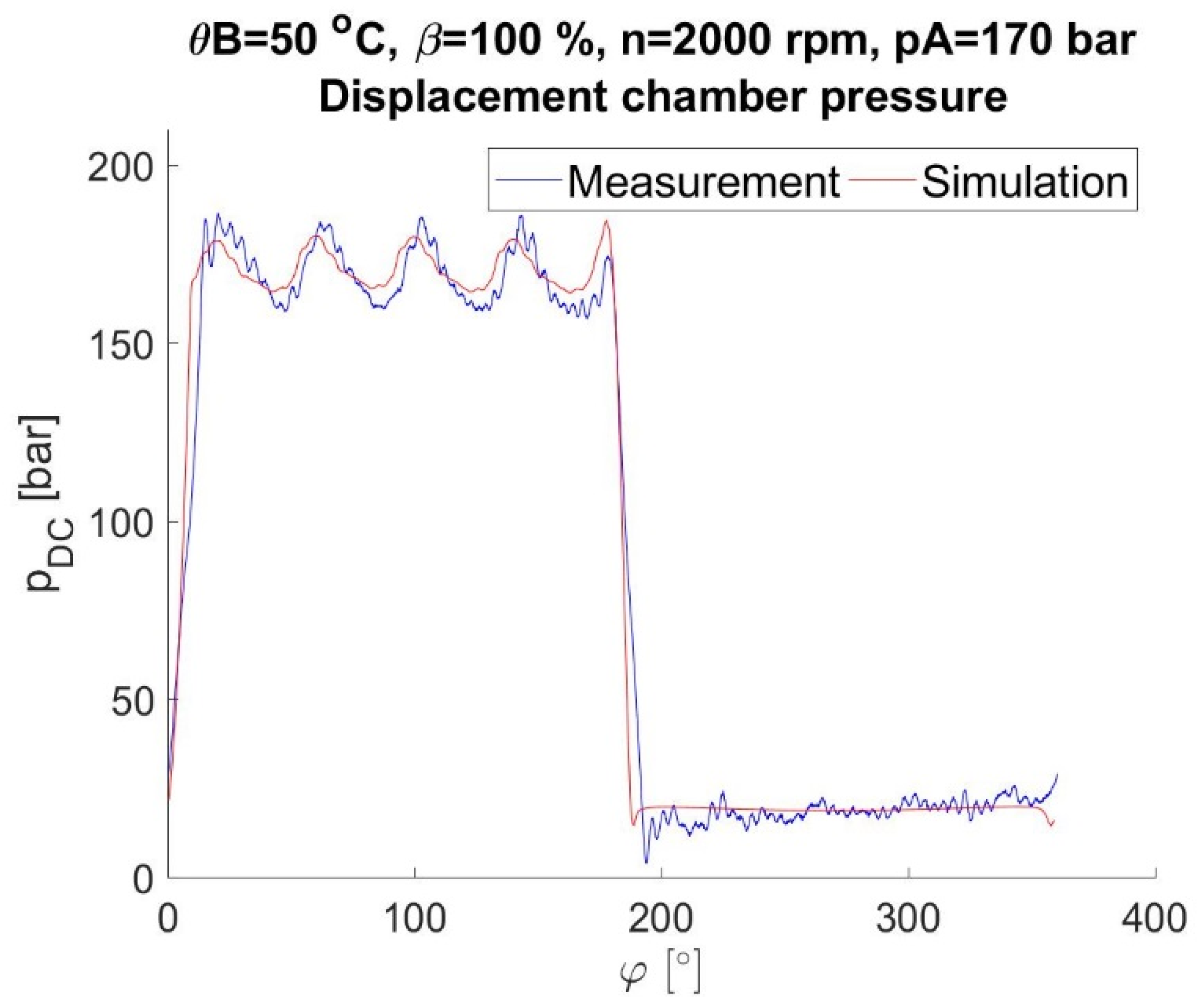
Figure 11.
Prediction vs. measurement; displacement chamber pressure.
Figure 11.
Prediction vs. measurement; displacement chamber pressure.
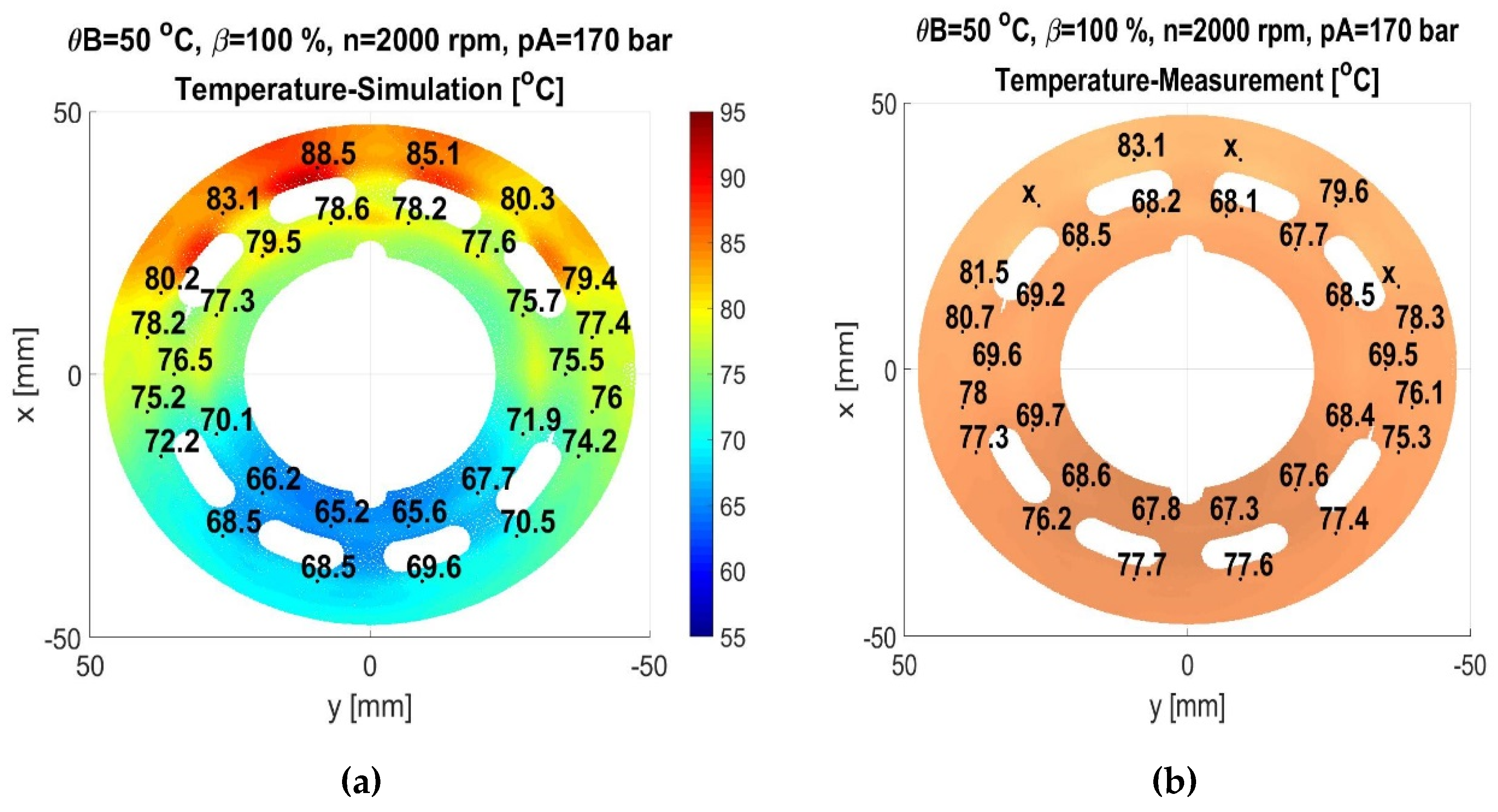
Figure 12.
(a) Simulated temperature of valve plate; (b) measured temperature of valve plate.
Figure 12.
(a) Simulated temperature of valve plate; (b) measured temperature of valve plate.
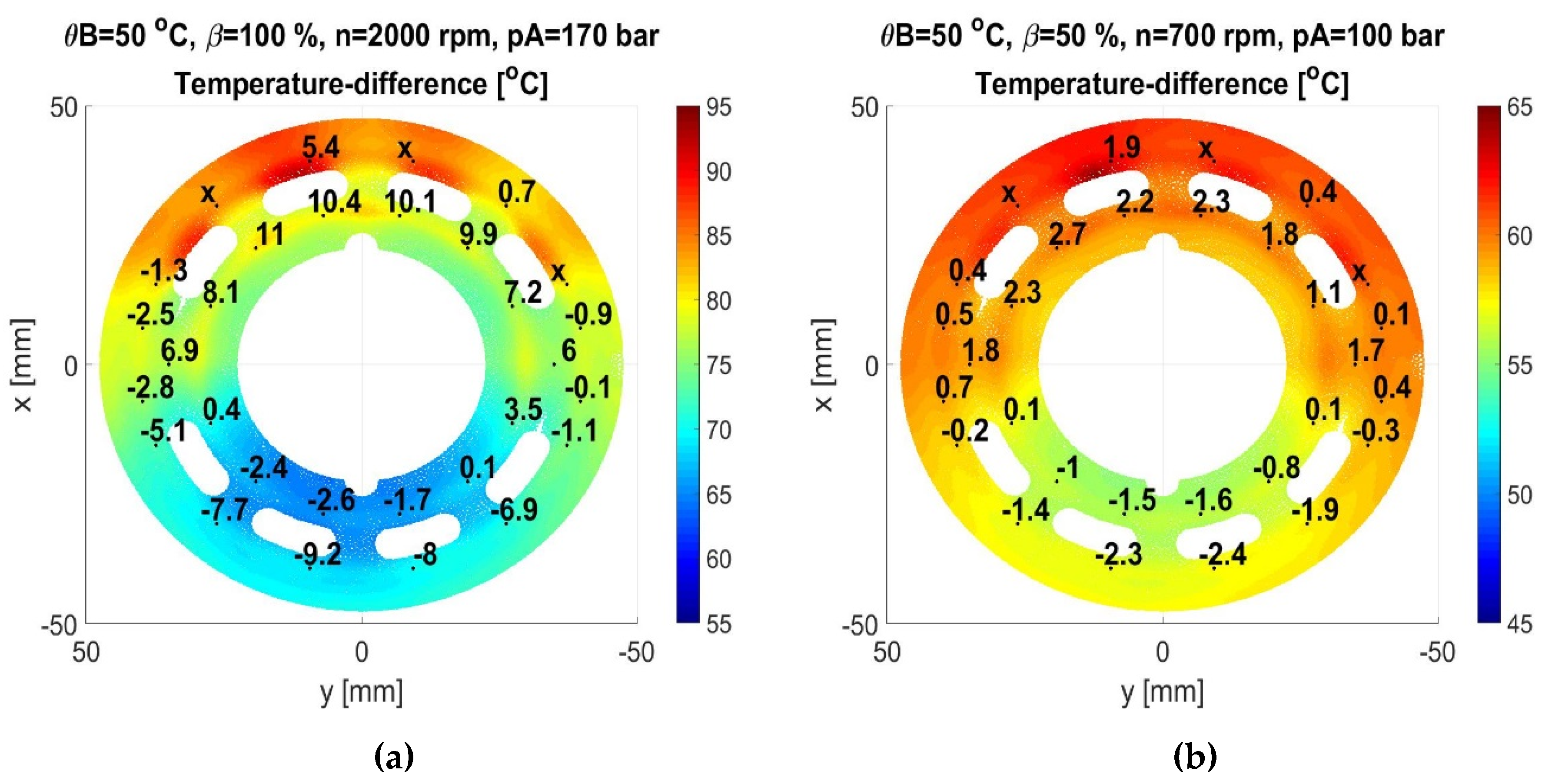
Figure 13.
(a) Difference between simulation and measurement at high power operating condition; (b) difference between simulation and measurement at low power operating condition.
Figure 13.
(a) Difference between simulation and measurement at high power operating condition; (b) difference between simulation and measurement at low power operating condition.
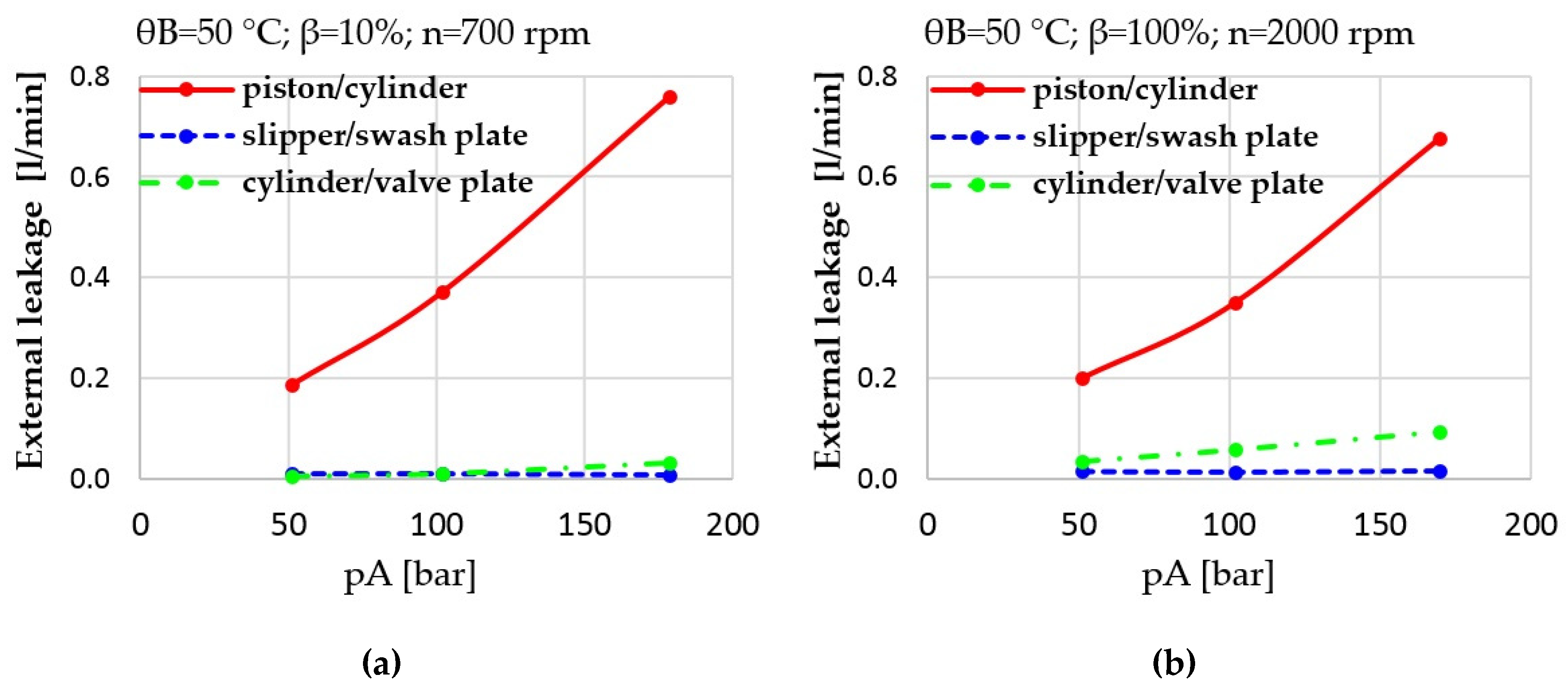
Figure 14.
(a) Prediction of the leakage flow through the individual lubricating interfaces at low power operating condition; (b) prediction of the leakage flow through the individual lubricating interfaces at high power operating condition.
Figure 14.
(a) Prediction of the leakage flow through the individual lubricating interfaces at low power operating condition; (b) prediction of the leakage flow through the individual lubricating interfaces at high power operating condition.
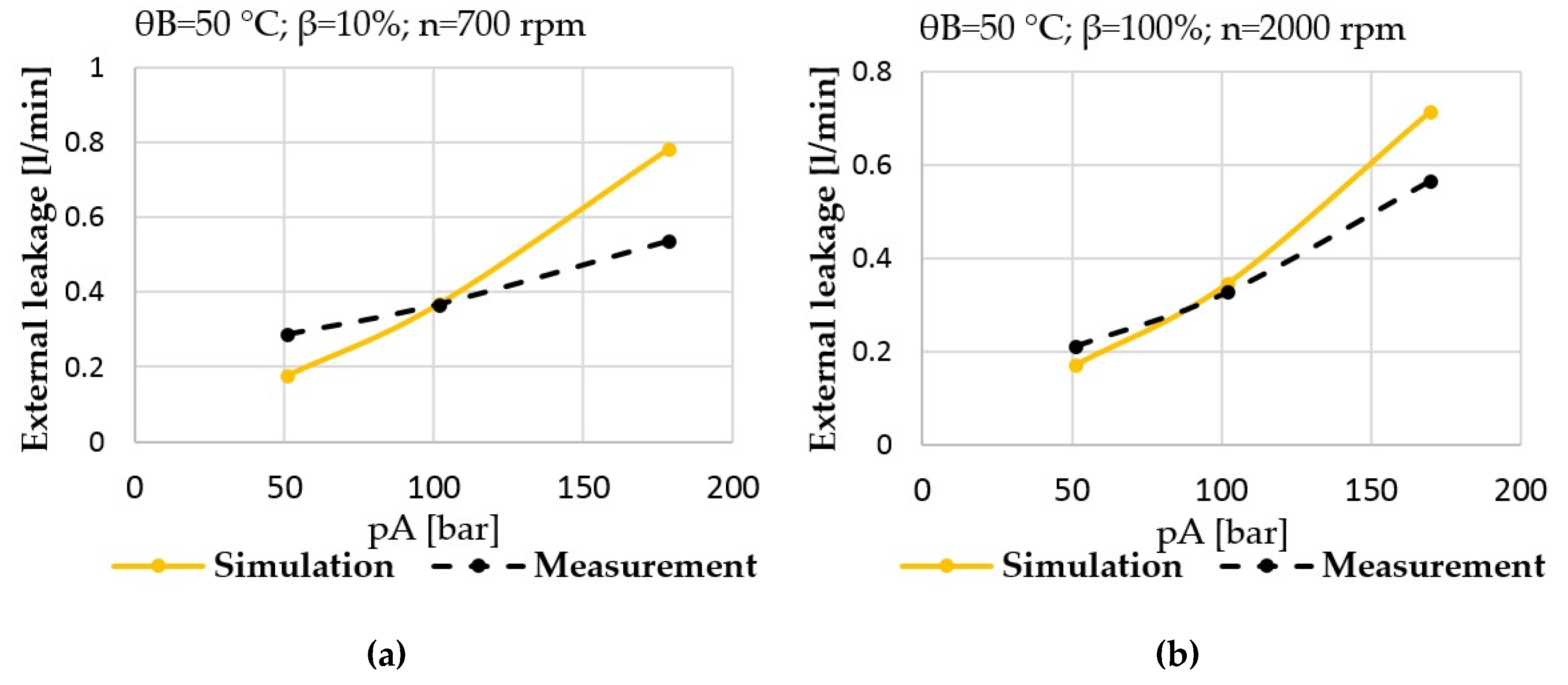
Figure 15.
(a) Prediction vs. measurement; total external leakage of the pump at low power operating condition; (b) prediction vs. measurement; total external leakage of the pump at high power operating condition.
Figure 15.
(a) Prediction vs. measurement; total external leakage of the pump at low power operating condition; (b) prediction vs. measurement; total external leakage of the pump at high power operating condition.
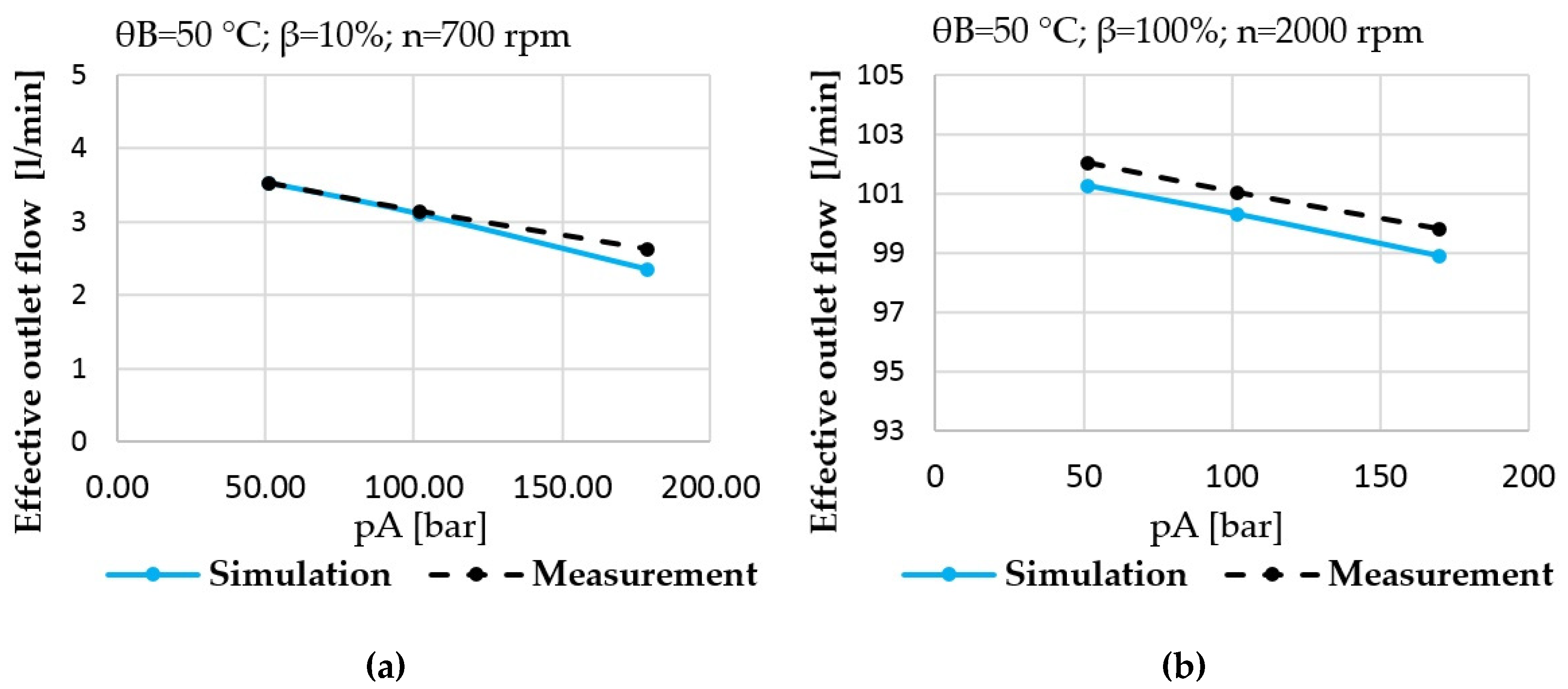
Figure 16.
(a) Prediction vs. measurement; effective outlet flow of the pump at low power operating condition; (b) prediction vs. measurement; effective outlet flow of the pump at high power operating condition.
Figure 16.
(a) Prediction vs. measurement; effective outlet flow of the pump at low power operating condition; (b) prediction vs. measurement; effective outlet flow of the pump at high power operating condition.
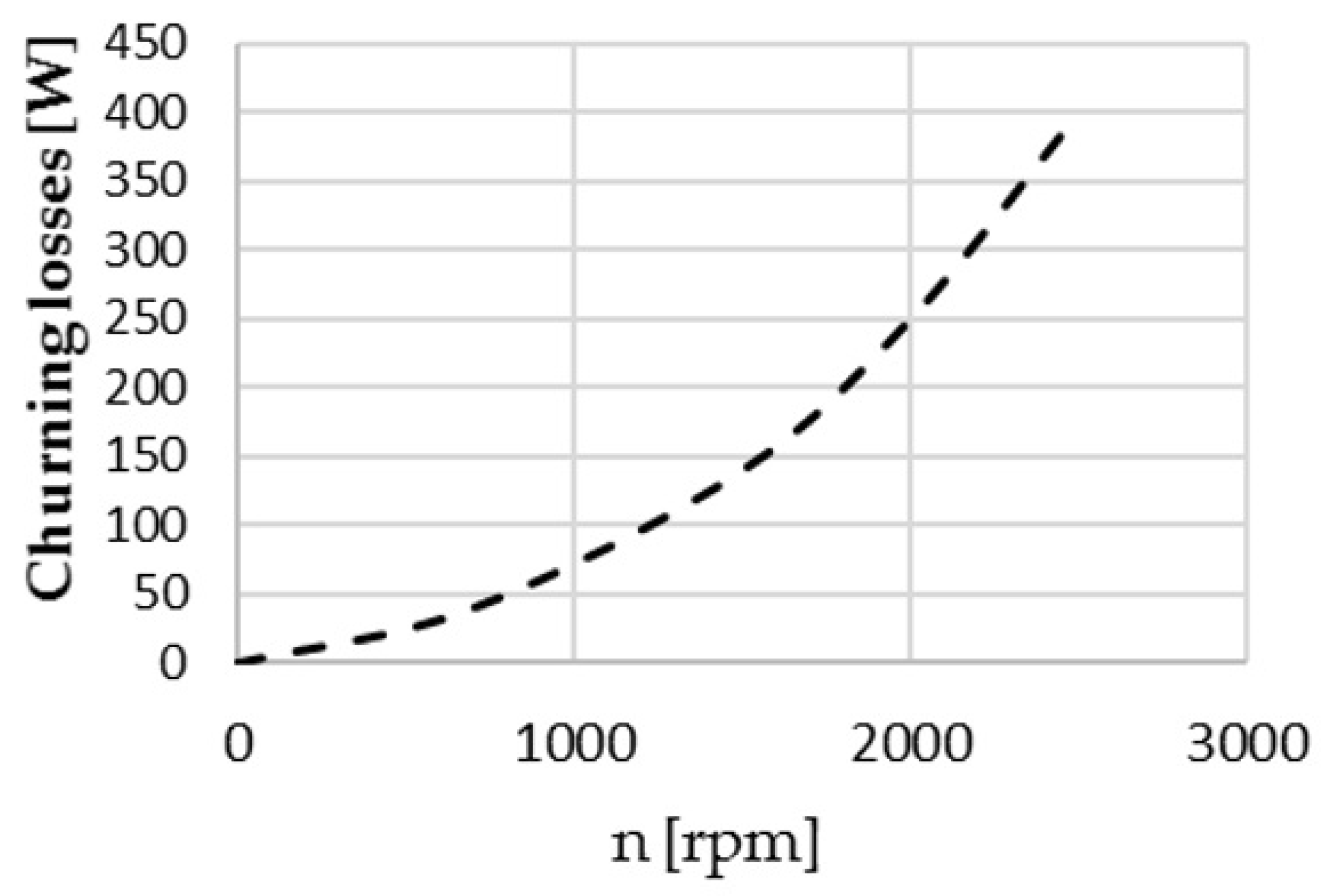
Figure 17.
Churning losses of a 52 cc S-APP.
Figure 17.
Churning losses of a 52 cc S-APP.
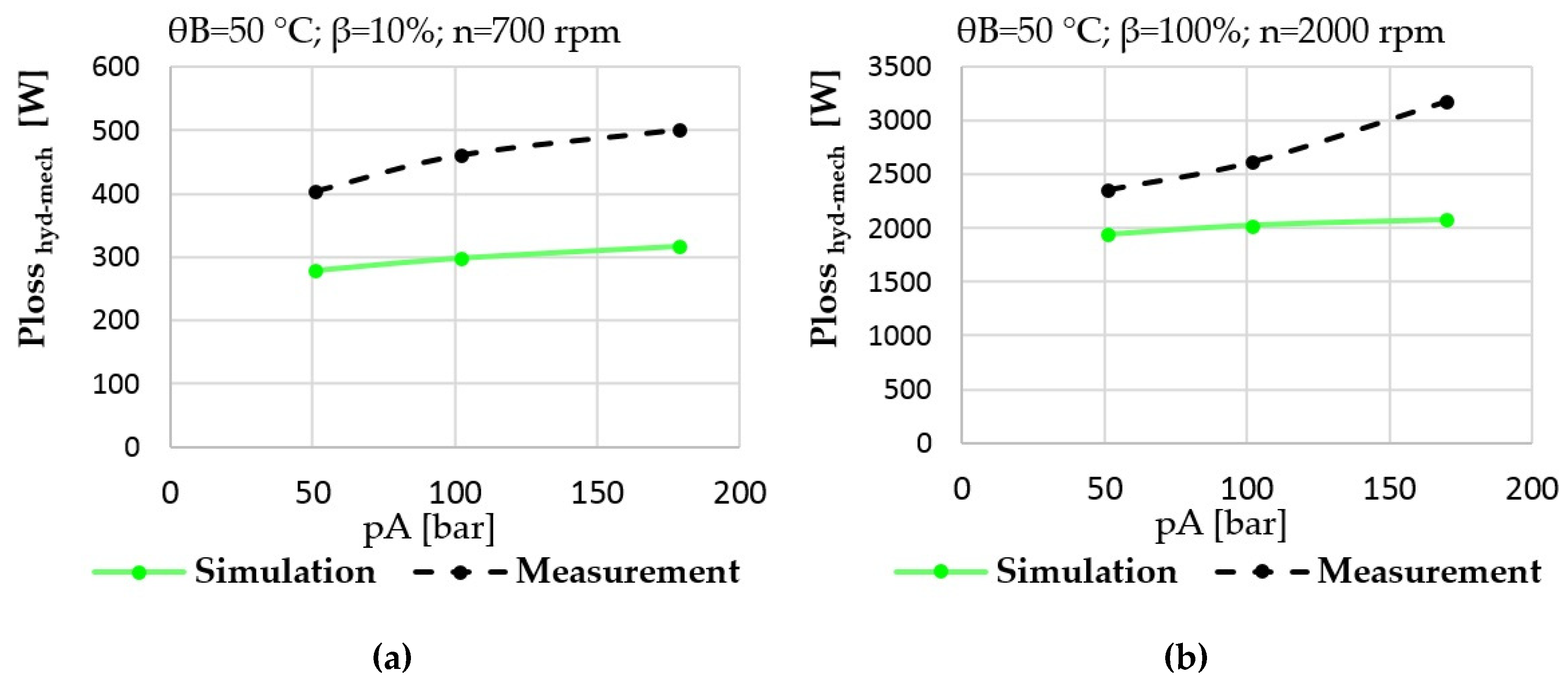
Figure 18.
(a) Prediction vs. measurement; hydraulic-mechanical losses of the pump at low power operating condition; (b) prediction vs. measurement; hydraulic-mechanical losses of the pump at high power operating condition.
Figure 18.
(a) Prediction vs. measurement; hydraulic-mechanical losses of the pump at low power operating condition; (b) prediction vs. measurement; hydraulic-mechanical losses of the pump at high power operating condition.
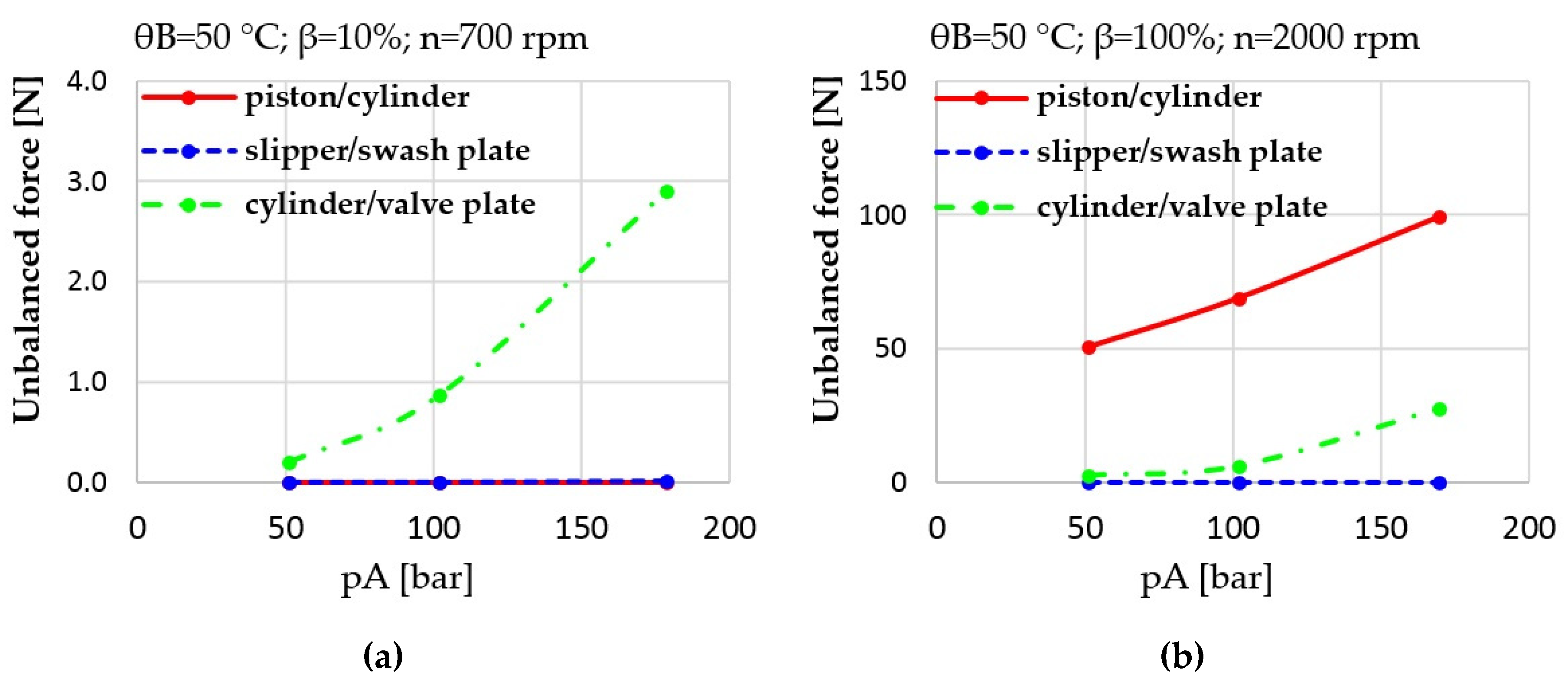
Figure 19.
(a) Unbalanced forces in the individual lubricating interfaces at low power operating condition; (b) unbalanced forces in the individual lubricating interfaces at high power operating condition.
Figure 19.
(a) Unbalanced forces in the individual lubricating interfaces at low power operating condition; (b) unbalanced forces in the individual lubricating interfaces at high power operating condition.
Figure 20.
Power losses due to internal leakage at different operating conditions.
Figure 20.
Power losses due to internal leakage at different operating conditions.
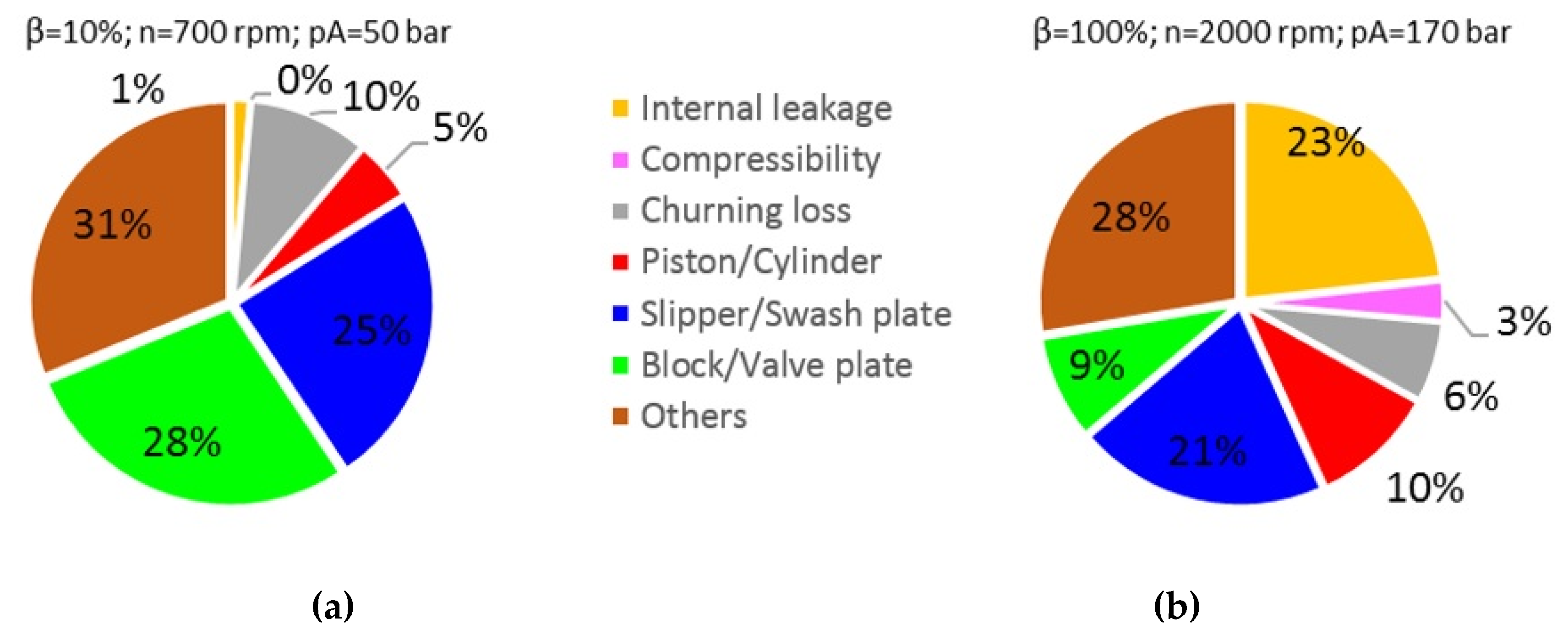
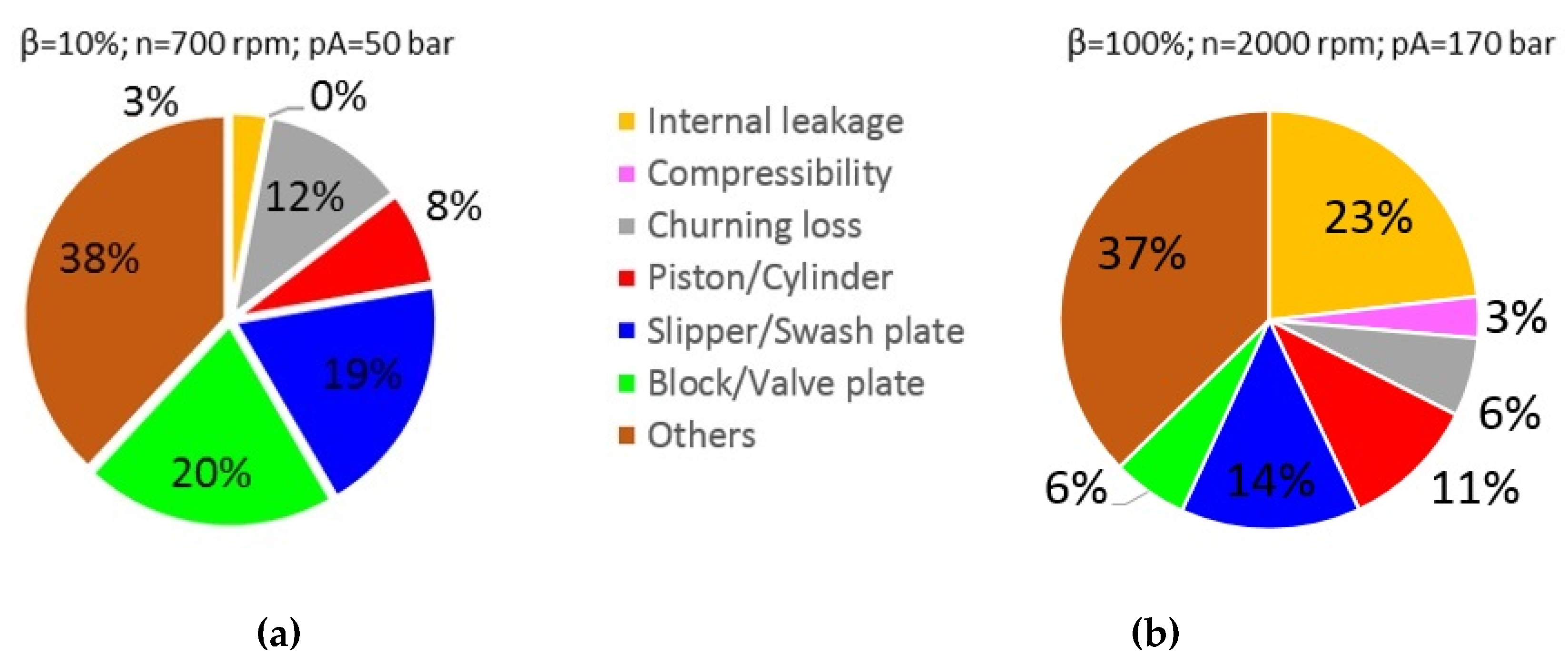
Figure 21.
(a) Distribution of power losses at low power operating condition and θB = 50 °C; (b) distribution of power losses at high power operating condition and θB = 50 °C.
Figure 21.
(a) Distribution of power losses at low power operating condition and θB = 50 °C; (b) distribution of power losses at high power operating condition and θB = 50 °C.
Figure 22.
(a) Distribution of power losses at low power operating condition and θB = 70 °C; (b) distribution of power losses at high power operating condition and θB = 70 °C.
Figure 22.
(a) Distribution of power losses at low power operating condition and θB = 70 °C; (b) distribution of power losses at high power operating condition and θB = 70 °C.
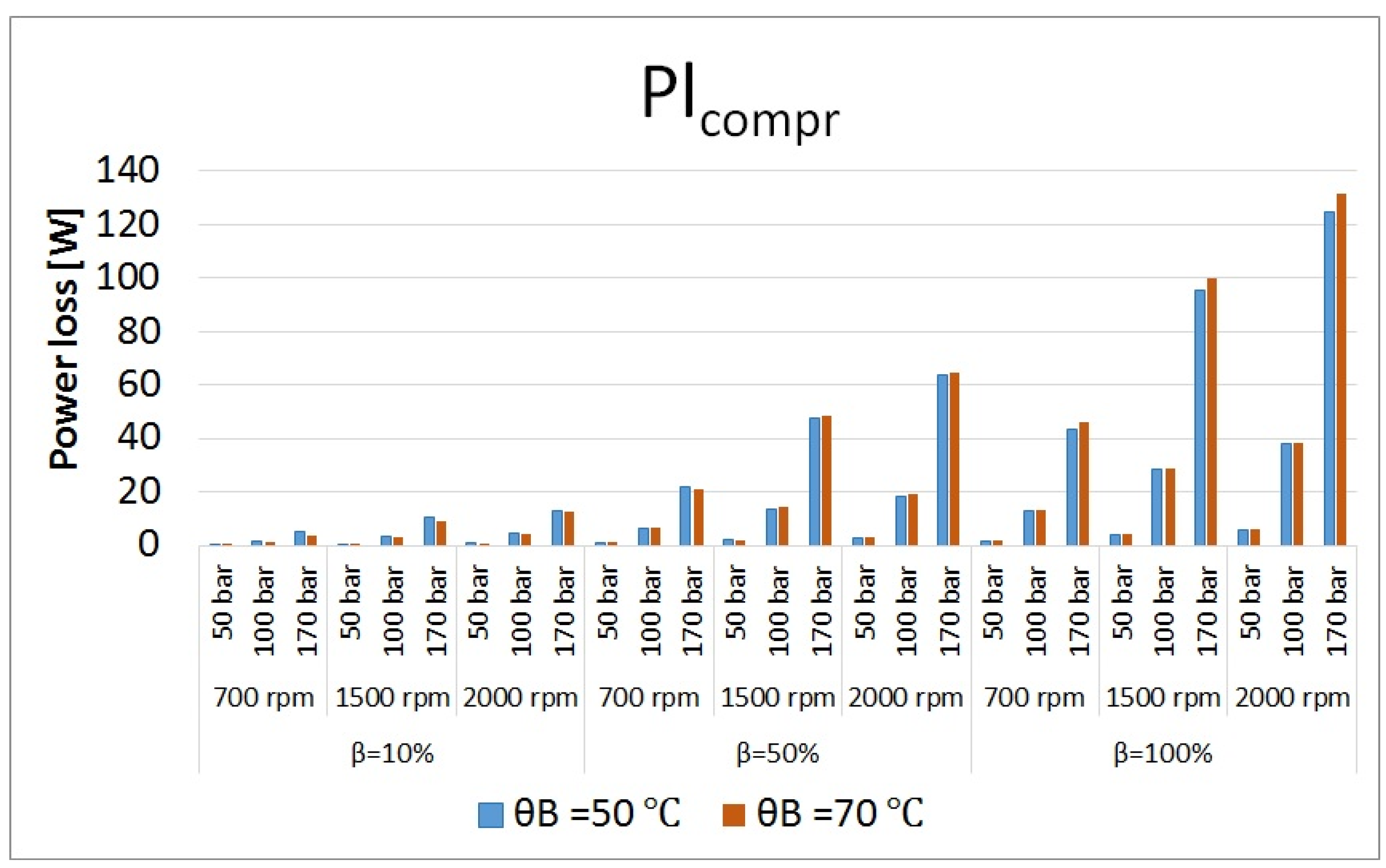
Figure 23.
Compression power losses at different operating conditions.
Figure 23.
Compression power losses at different operating conditions.
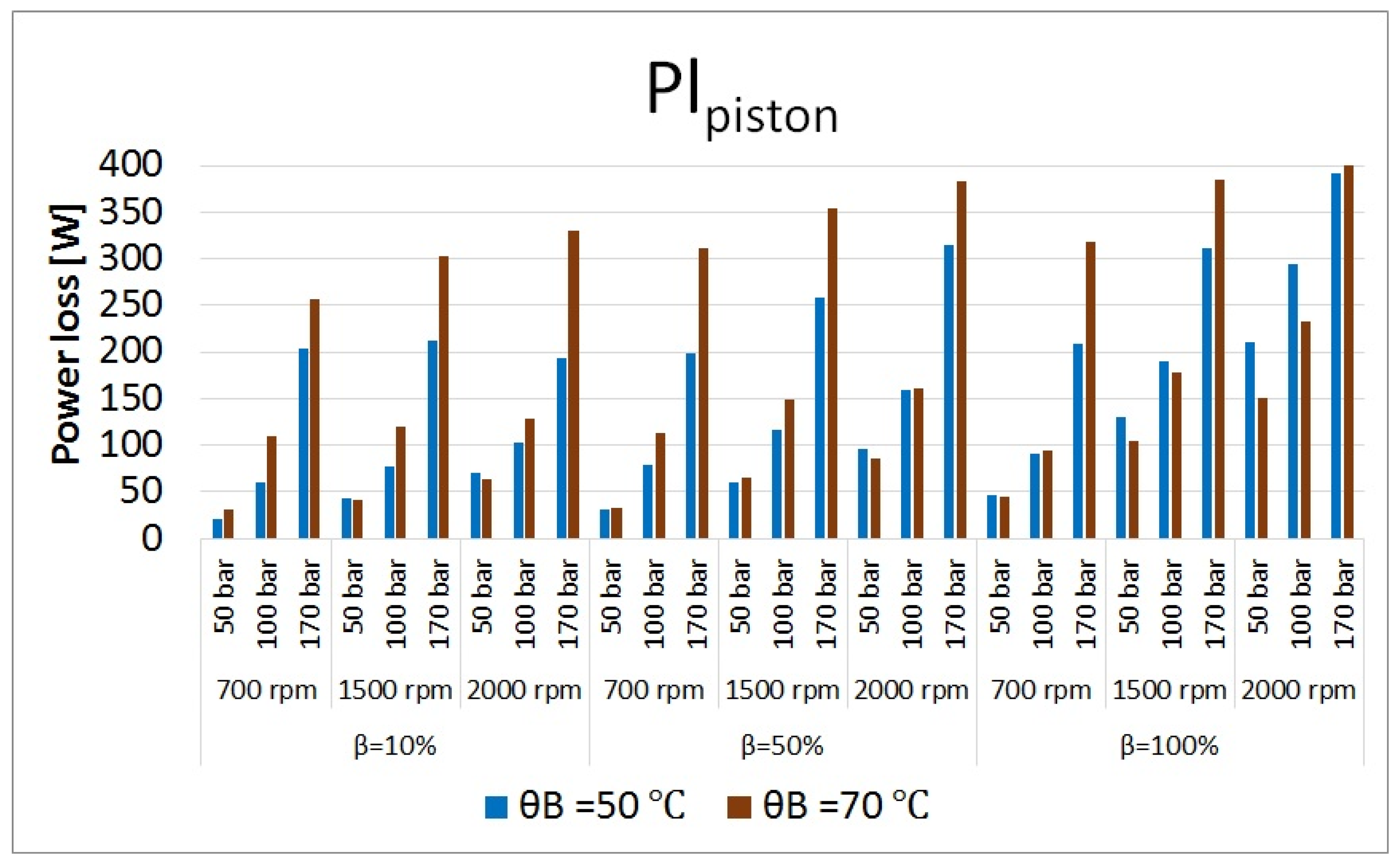
Figure 24.
Total power losses in piston/cylinder bore interfaces at different operating conditions.
Figure 24.
Total power losses in piston/cylinder bore interfaces at different operating conditions.
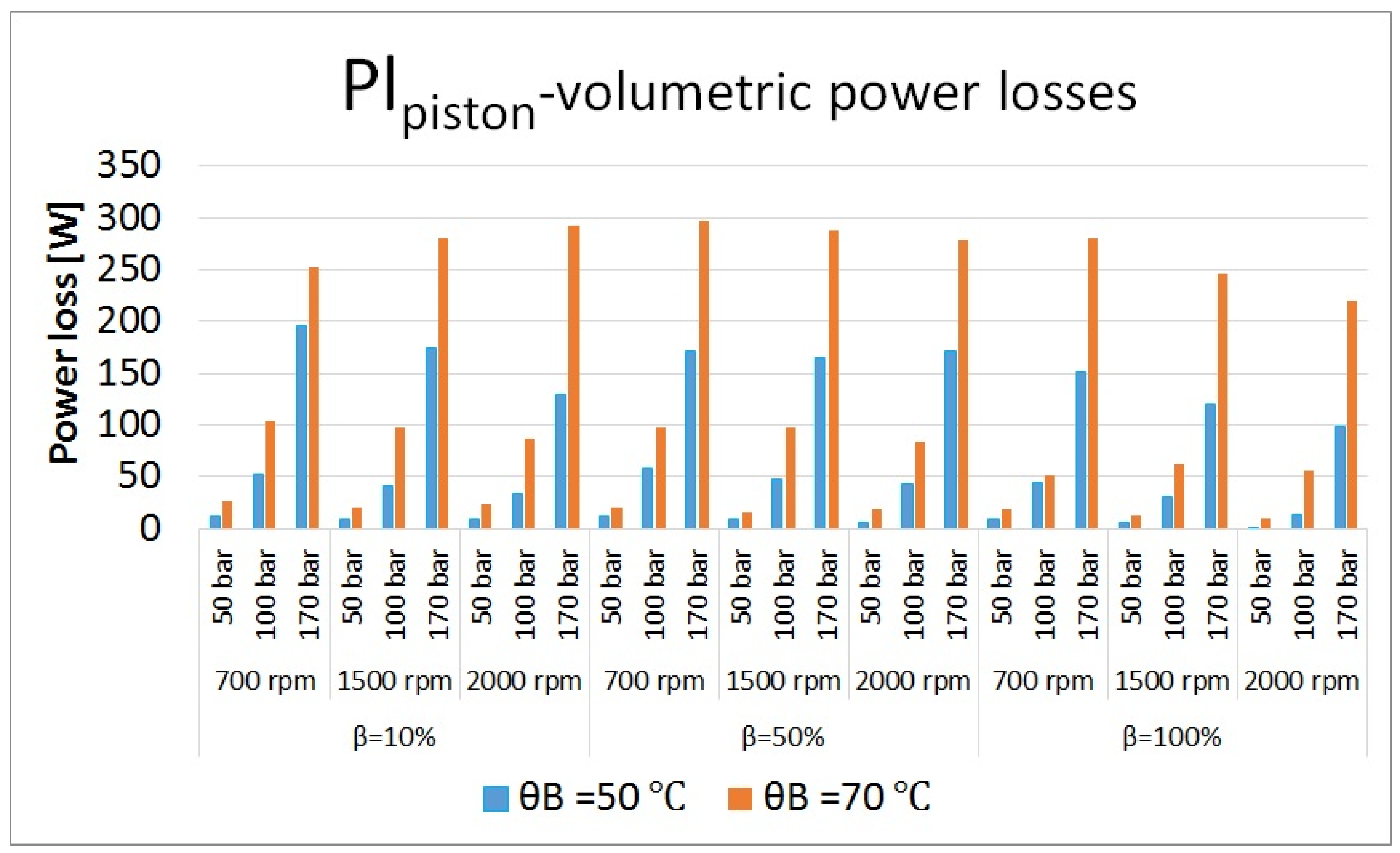
Figure 25.
Volumetric power losses in piston/cylinder bore interfaces at different operating conditions.
Figure 25.
Volumetric power losses in piston/cylinder bore interfaces at different operating conditions.
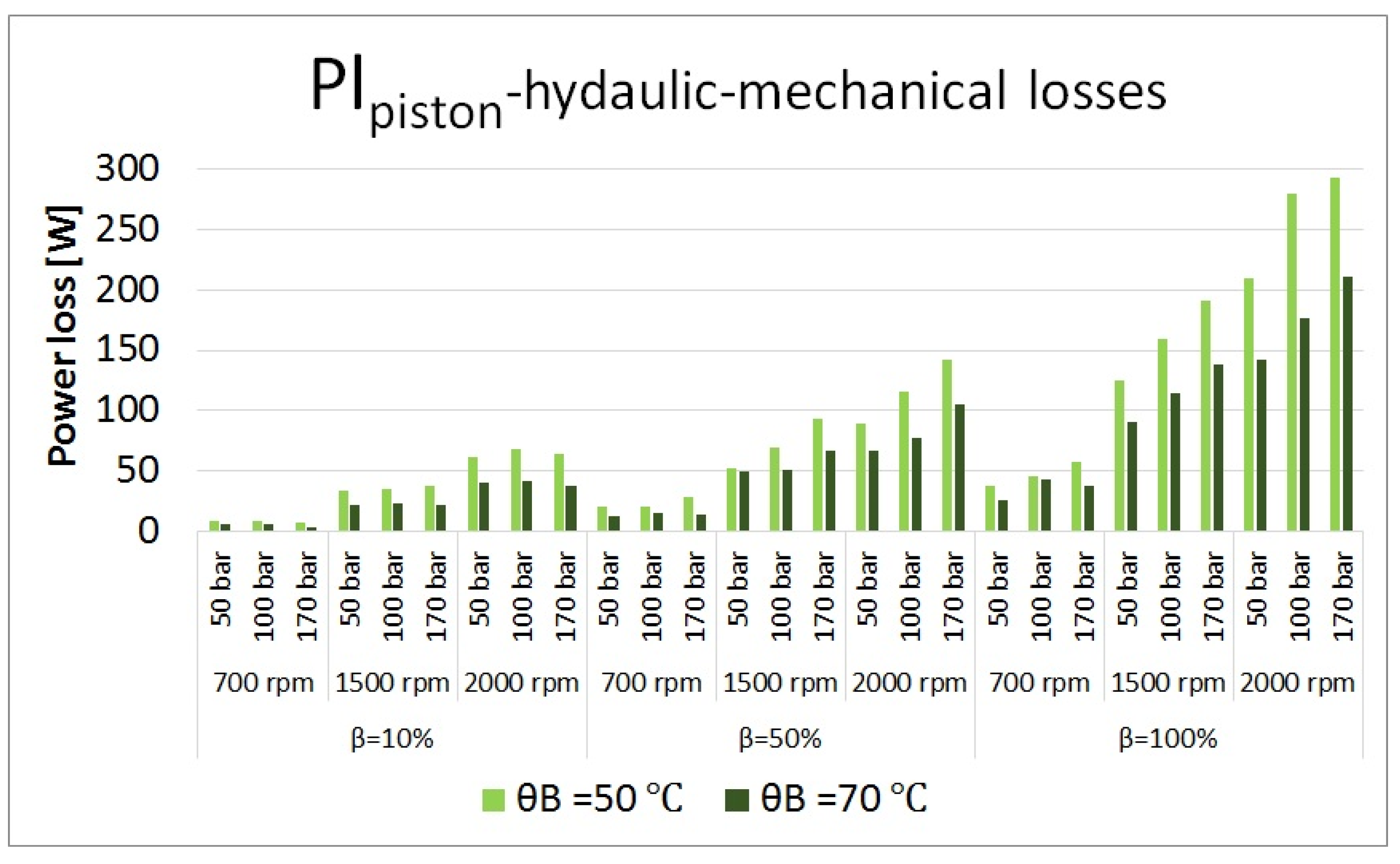
Figure 26.
Hydraulic-mechanical losses in piston/cylinder bore interfaces at different operating conditions.
Figure 26.
Hydraulic-mechanical losses in piston/cylinder bore interfaces at different operating conditions.
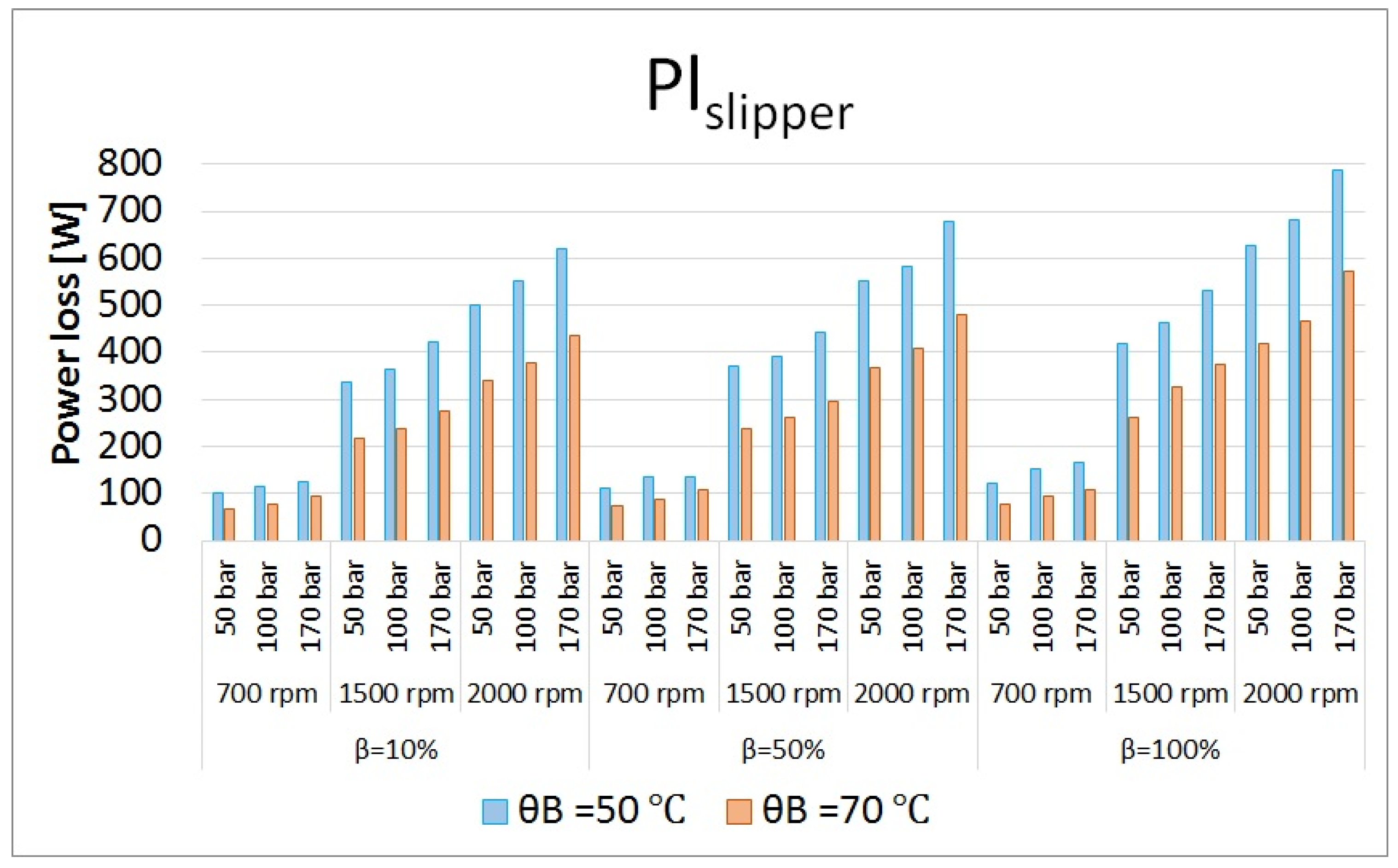
Figure 27.
Total power losses in slipper/swash plate interface at different operating conditions.
Figure 27.
Total power losses in slipper/swash plate interface at different operating conditions.
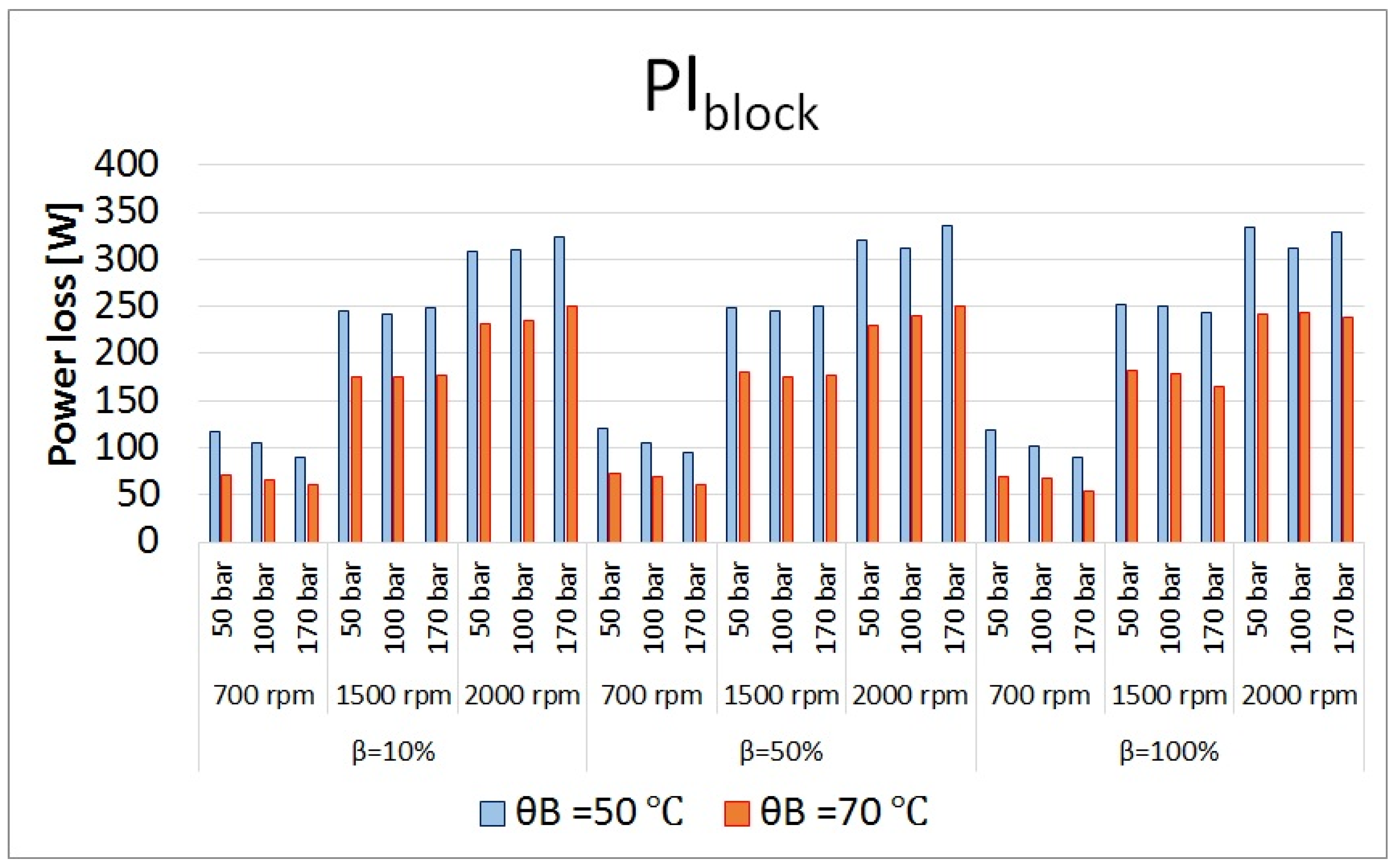
Figure 28.
Total power losses in cylinder block/valve plate interface at different operating conditions.
Figure 28.
Total power losses in cylinder block/valve plate interface at different operating conditions.
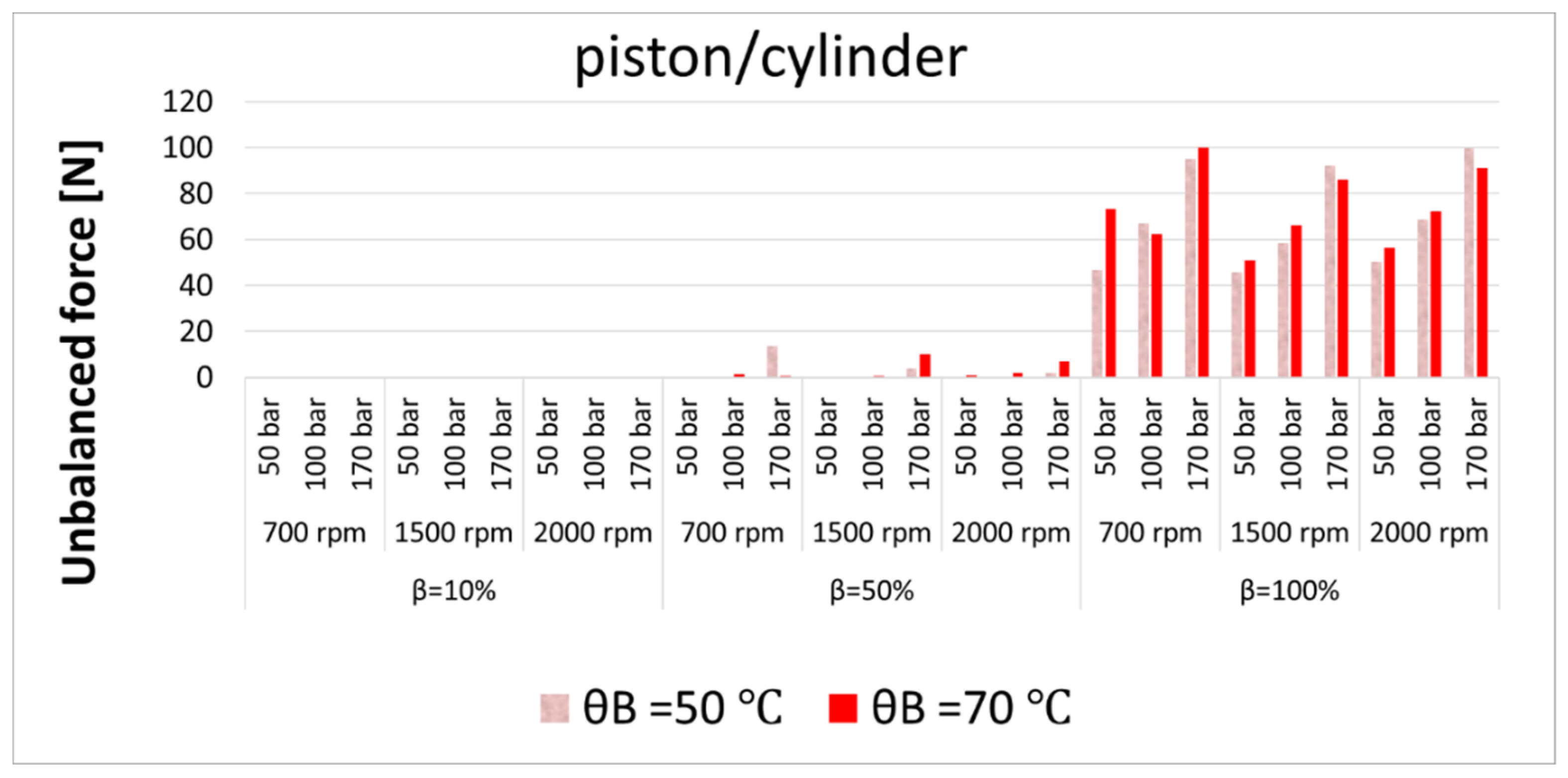
Figure 29.
Unbalanced forces in the piston/cylinder interfaces at different operating conditions.
Figure 29.
Unbalanced forces in the piston/cylinder interfaces at different operating conditions.
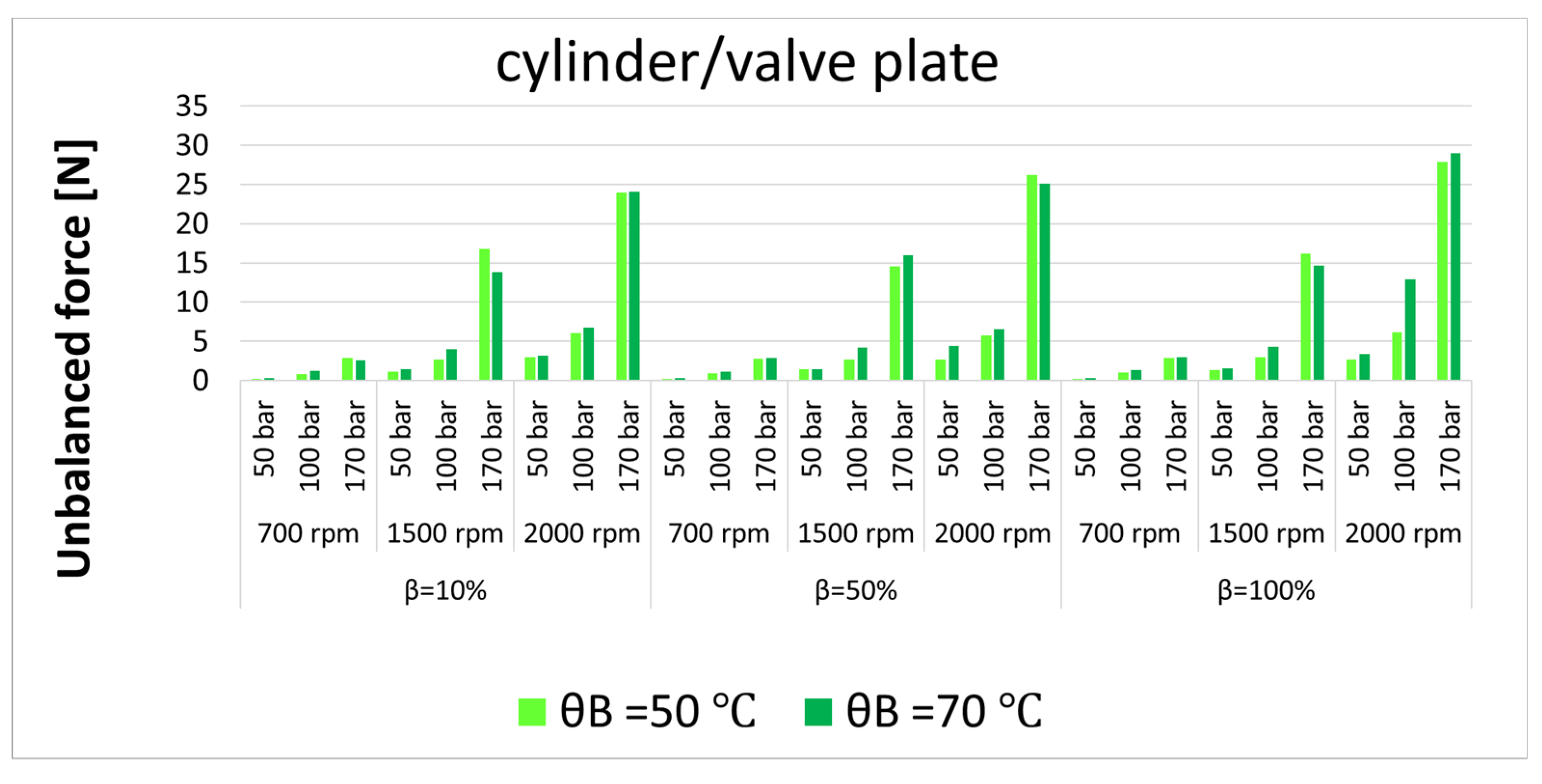
Figure 30.
Unbalanced forces in the cylinder/valve plate interfaces at different operating conditions.
Figure 30.
Unbalanced forces in the cylinder/valve plate interfaces at different operating conditions.
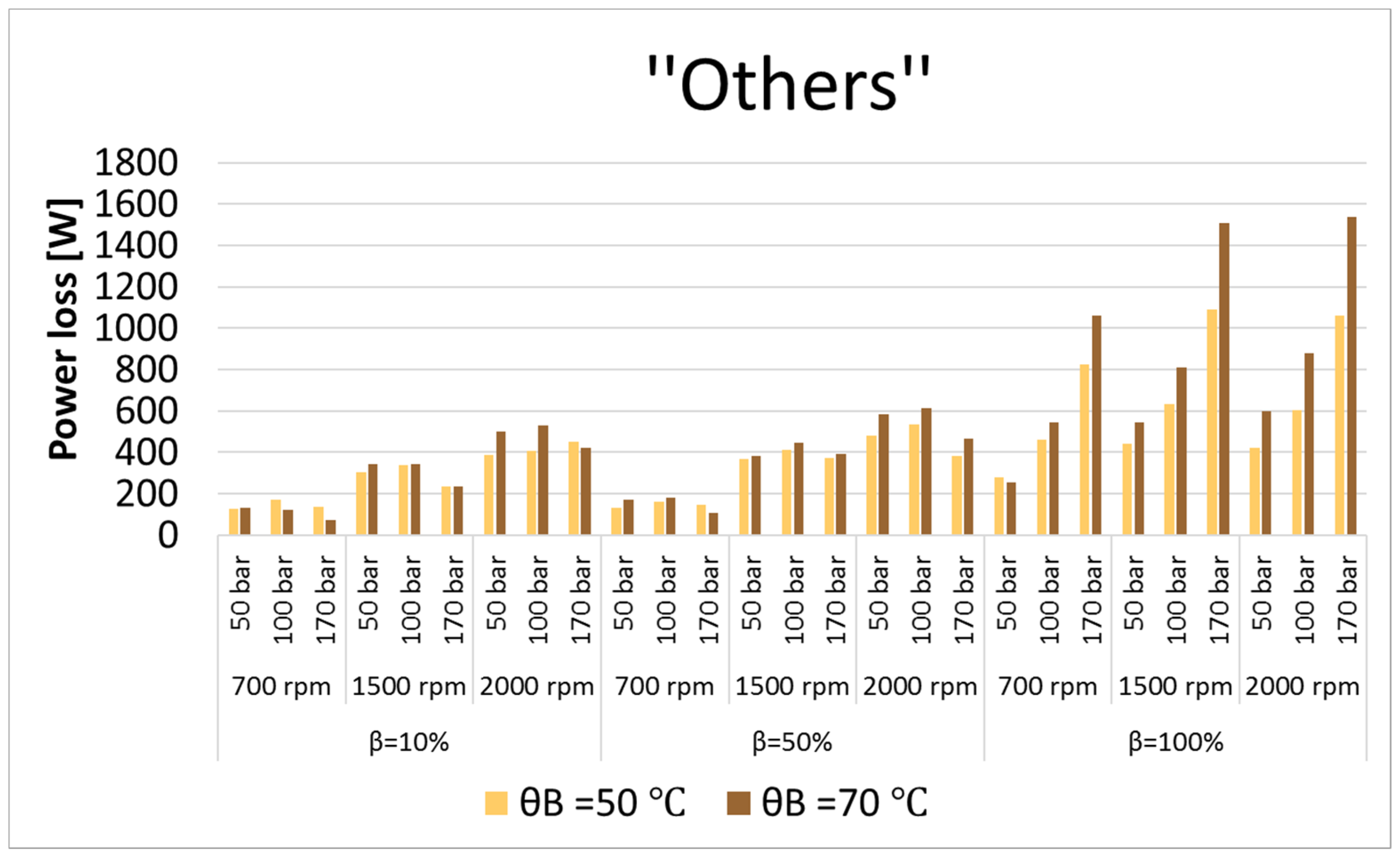
Figure 31.
Undefined losses at different operating conditions.
Figure 31.
Undefined losses at different operating conditions.
Table 1.
Data of the reference S-APP.
Table 1.
Data of the reference S-APP.
| Parameter | Value | Unit |
|---|
| Number of pistons | | 9 | (-) |
| Max displacement | | 52 | (cc/rev) |
| Speed ratings | min | 700 | (rpm) |
| max | 3400 |
| System pressure | rated | 300 | (bar) |
| max | 400 |
| min low loop | 15 |
Table 2.
Steady-state measurement sensors.
Table 2.
Steady-state measurement sensors.
| Sensor | Parameter | Specification | Accuracy |
|---|
| T, n | torque, speed | HMB T40B/500 Nm | class 0.05 |
| QA | flow | KEM SRZ 400 KL | +/−0.31% |
| QC | case flow | KEM SRZ 100 KL | +/−0.36% |
| pA, pB | pressure in A, B line | HBM P3ICP/500 bar | +/−0.033% |
| pC | case pressure | HBM P3ICP/50 bar | +/−0.092% |
| θA, θB, θC | temperature | Omega K Type Thermocouple | +/−1.1 °C |
| θi | valve plate temperature | Omega K Type Thermocouple | +/−1.1 °C |
| pDC | displ. chamber pressure | Kistler 603CA | +/−0.04% |
| φ | shaft angular position | ROS-W 1906009; 1–250,000 RPM | NA |
Table 3.
The operating conditions considered in this study.
Table 3.
The operating conditions considered in this study.
| Inlet Temperature θB | Displacement β | Speed n | Outlet Port Pressure pA |
|---|
| 50 °C | 10% | 700 rpm | 50 bar |
| 70 °C | 50% | 1500 rpm | 100 bar |
| - | 100% | 2000 rpm | 170 bar |
Table 4.
Average error of the valve plate temperature.
Table 4.
Average error of the valve plate temperature.
| | | | Average Error (°C) |
|---|
| β | n | pA | θB = 50 °C | θB = 70 °C |
|---|
| 10% | 700 rpm | 50 bar | 2.0 | 1.3 |
| 100 bar | 1.3 | 1.1 |
| 170 bar | 2.4 | 1.6 |
| 1500 rpm | 50 bar | 3.7 | 3.0 |
| 100 bar | 3.7 | 2.9 |
| 170 bar | 3.6 | 2.5 |
| 2000 rpm | 50 bar | 4.5 | 2.1 |
| 100 bar | 4.6 | 3.4 |
| 170 bar | 4.9 | 4.0 |
| 50% | 700 rpm | 50 bar | 2.4 | 1.2 |
| 100 bar | 1.3 | 1.1 |
| 170 bar | 1.5 | 1.5 |
| 1500 rpm | 50 bar | 4.1 | 3.4 |
| 100 bar | 3.8 | 3.1 |
| 170 bar | 3.5 | 2.8 |
| 2000 rpm | 50 bar | 5.4 | 4.1 |
| 100 bar | 4.8 | 4.2 |
| 170 bar | 5.1 | 4.2 |
| 100% | 700 rpm | 50 bar | 1.9 | 1.1 |
| 100 bar | 1.5 | 2.3 |
| 170 bar | 3.6 | 4.5 |
| 1500 rpm | 50 bar | 4.5 | 3.5 |
| 100 bar | 3.7 | 2.7 |
| 170 bar | 3.8 | 3.3 |
| 2000 rpm | 50 bar | 5.9 | 4.7 |
| 100 bar | 4.7 | 4.2 |
| 170 bar | 4.3 | 4.1 |
Table 5.
Distribution of power losses in the S-APP a 52 cc size; θB = 50 °C.
Table 5.
Distribution of power losses in the S-APP a 52 cc size; θB = 50 °C.
| | | | Power Losses (W) |
|---|
| β | n | HP | Pltotal | PlQin | Plcompr | Plchurning | Plpiston | Plslipper | Plblock | ‘’Others’’ |
|---|
| 10% | 700 rpm | 50 bar | 413.6 | 6 | 0.3 | 40.0 | 20.5 | 101.2 | 116.8 | 128.8 |
| 100 bar | 537.2 | 47.8 | 1.5 | 40.0 | 60.3 | 113.2 | 105.7 | 168.6 |
| 170 bar | 782.1 | 183.2 | 4.9 | 40.0 | 203.7 | 124.5 | 89.9 | 135.9 |
| 1500 rpm | 50 bar | 1084.1 | 16.1 | 0.6 | 140.0 | 42.3 | 337.0 | 245.9 | 302.2 |
| 100 bar | 1279.1 | 115.0 | 3.1 | 140.0 | 77.0 | 364.1 | 241.4 | 338.5 |
| 170 bar | 1755.6 | 490.9 | 10.5 | 140.0 | 211.8 | 420.6 | 248.7 | 233.1 |
| 2000 rpm | 50 bar | 1536.9 | 18.6 | 0.8 | 250.0 | 70.8 | 500.7 | 308.2 | 387.8 |
| 100 bar | 1767.0 | 139.4 | 4.4 | 250.0 | 102.2 | 552.3 | 310.2 | 408.4 |
| 170 bar | 2352.4 | 501.7 | 13.2 | 250.0 | 193.7 | 619.7 | 324.5 | 449.6 |
| 50% | 700 rpm | 50 bar | 452.3 | 12.2 | 1.0 | 40.0 | 31.8 | 112.8 | 120.5 | 134.0 |
| 100 bar | 581.5 | 55.0 | 6.3 | 40.0 | 79.8 | 135.2 | 104.5 | 160.7 |
| 170 bar | 819.1 | 182.6 | 22.1 | 40.0 | 198.4 | 134.5 | 95.2 | 146.3 |
| 1500 rpm | 50 bar | 1232.4 | 43.5 | 2.1 | 140.0 | 60.8 | 371.6 | 248.1 | 366.3 |
| 100 bar | 1439.2 | 121.5 | 13.6 | 140.0 | 116.4 | 390.9 | 244.5 | 412.4 |
| 170 bar | 1868.8 | 357.6 | 47.5 | 140.0 | 258.4 | 443.8 | 249.7 | 371.9 |
| 2000 rpm | 50 bar | 1788.4 | 84.6 | 2.9 | 250.0 | 95.9 | 552.0 | 320.8 | 482.3 |
| 100 bar | 2040.7 | 184.1 | 18.3 | 250.0 | 158.6 | 583.9 | 311.4 | 534.4 |
| 170 bar | 2519.7 | 492.6 | 63.9 | 250.0 | 313.9 | 679.4 | 335.3 | 384.6 |
| 100% | 700 rpm | 50 bar | 643.9 | 33.3 | 1.8 | 40.0 | 46.9 | 121.0 | 119.4 | 281.5 |
| 100 bar | 936.1 | 79.8 | 13.1 | 40.0 | 90.8 | 151.0 | 102.6 | 458.8 |
| 170 bar | 1570.0 | 197.3 | 43.4 | 40.0 | 209.3 | 165.6 | 89.3 | 825.1 |
| 1500 rpm | 50 bar | 1615.8 | 233.6 | 4.1 | 140.0 | 130.0 | 417.6 | 251.4 | 439.0 |
| 100 bar | 2018.0 | 312.4 | 28.2 | 140.0 | 190.6 | 463.4 | 249.5 | 634.0 |
| 170 bar | 2944.6 | 534.7 | 95.4 | 140.0 | 311.3 | 531.1 | 243.8 | 1088.4 |
| 2000 rpm | 50 bar | 2372.8 | 524.6 | 5.6 | 250.0 | 209.9 | 627.8 | 334.3 | 420.6 |
| 100 bar | 2804.9 | 621.7 | 38.3 | 250.0 | 294.2 | 682.9 | 312.1 | 605.7 |
| 170 bar | 3828.8 | 888.4 | 124.4 | 250.0 | 391.8 | 786.6 | 328.3 | 1059.3 |
Table 6.
Distribution of power losses in the S-APP a 52 cc size; θB = 70 °C.
Table 6.
Distribution of power losses in the S-APP a 52 cc size; θB = 70 °C.
| | | | Power losses (W) |
|---|
| β | n | HP | Pltotal | PlQin | Plcompr | Plchurning | Plpiston | Plslipper | Plblock | ‘’Others’’ |
|---|
| 10% | 700 rpm | 50 bar | 351.8 | 10.4 | 0.3 | 40.0 | 31.9 | 67.1 | 70.3 | 131.8 |
| 100 bar | 473.3 | 59.3 | 1.5 | 40.0 | 109.3 | 77.4 | 65.9 | 119.8 |
| 170 bar | 698.3 | 169.7 | 3.9 | 40.0 | 256 | 94.8 | 60.4 | 73.5 |
| 1500 rpm | 50 bar | 935.1 | 17.1 | 0.6 | 140.0 | 42.1 | 216.5 | 175.4 | 343.4 |
| 100 bar | 1148.3 | 130.0 | 3.2 | 140.0 | 120.2 | 238.5 | 174.5 | 341.9 |
| 170 bar | 1595.8 | 458.6 | 9.2 | 140.0 | 302.4 | 273.8 | 177.1 | 234.7 |
| 2000 rpm | 50 bar | 1404.3 | 20.5 | 0.7 | 250.0 | 62.8 | 338.9 | 231.6 | 499.8 |
| 100 bar | 1671.0 | 146.1 | 4.4 | 250.0 | 129.3 | 379.2 | 234.4 | 527.6 |
| 170 bar | 2232.2 | 530.8 | 12.7 | 250.0 | 330.8 | 436.5 | 249.9 | 421.6 |
| 50% | 700 rpm | 50 bar | 403.0 | 13.2 | 1.0 | 40.0 | 32.9 | 73.2 | 72.4 | 170.4 |
| 100 bar | 559.4 | 62.3 | 6.5 | 40.0 | 113.2 | 85.8 | 69.4 | 182.2 |
| 170 bar | 834.5 | 189.6 | 20.9 | 40.0 | 311.1 | 106.3 | 60.0 | 106.6 |
| 1500 rpm | 50 bar | 1049.6 | 44.3 | 2.1 | 140.0 | 65 | 236.1 | 180.2 | 381.9 |
| 100 bar | 1326.5 | 138.0 | 14.5 | 140.0 | 148.6 | 263.0 | 176.0 | 446.4 |
| 170 bar | 1803.5 | 397.3 | 48.5 | 140.0 | 354.7 | 295.7 | 176.2 | 391.0 |
| 2000 rpm | 50 bar | 1603.3 | 84.9 | 2.8 | 250.0 | 85.8 | 367.9 | 230.2 | 581.6 |
| 100 bar | 1890.6 | 199.7 | 19.0 | 250.0 | 161.1 | 406.8 | 240.8 | 613.2 |
| 170 bar | 2437.8 | 540.8 | 64.8 | 250.0 | 383.6 | 479.8 | 251.1 | 467.8 |
| 100% | 700 rpm | 50 bar | 524.8 | 34.1 | 2.0 | 40.0 | 44.4 | 77.7 | 69.7 | 256.9 |
| 100 bar | 936.3 | 83.9 | 13.3 | 40.0 | 93.9 | 92.9 | 66.8 | 545.6 |
| 170 bar | 1851.2 | 222.7 | 46.2 | 40.0 | 317.7 | 108.0 | 54.7 | 1061.8 |
| 1500 rpm | 50 bar | 1468.4 | 232.8 | 4.5 | 140.0 | 103.8 | 261.3 | 182.5 | 543.4 |
| 100 bar | 1982.0 | 320.7 | 28.9 | 140.0 | 177.2 | 327.0 | 178.3 | 809.8 |
| 170 bar | 3255.5 | 585.0 | 100.0 | 140.0 | 383.9 | 374.9 | 164.7 | 1507.0 |
| 2000 rpm | 50 bar | 2182.1 | 517.6 | 5.8 | 250.0 | 151.2 | 417.4 | 241.9 | 598.2 |
| 100 bar | 2736.4 | 627.0 | 38.6 | 250.0 | 232.7 | 467.6 | 244.1 | 876.4 |
| 170 bar | 4112.5 | 953.6 | 131.3 | 250.0 | 431.2 | 571.8 | 239.1 | 1535.4 |