1. Introduction
Transmission lines are at the core of power systems, serving as an asset that allows the transfer of electrical energy from where it is generated to where it is consumed. Their existence gives the system operators flexibility to commit different generator units in different locations in the system, and this process leads the operation of power systems in an economical manner by adopting production cost minimization while committing and dispatching the generation fleet. However, due to the aging grid and the time it takes to complete maintenance tasks, transmission line maintenance rates have been increasing. The current process of transmission maintenance schedule is not centralized at the operator level, and it gives full control to the transmission owner to select the date, time, and duration. The loss of a transmission line with no consideration on the optimality tends to increase production costs and decrease reliability. This paper intends to fill this gap by introducing a co-optimized mathematical model of transmission maintenance scheduling and the production cost minimization. To address both objectives, traditionally used models of unit commitment, optimal topology control, and scheduling are discussed throughout this paper.
The traditional unit commitment (UC) is a mathematical model that commits a generator’s capacity to meet the power demand while minimizing the production cost of the system [
1,
2]. It is generally formulated in the form of mixed integer linear programming (MILP) and several solution techniques are discussed in the literature [
3,
4,
5,
6], including Lagrangian relaxation [
7,
8], Branch and Bound [
9,
10,
11], heuristic methods [
12,
13] and their comparisons [
14,
15,
16]. Extended surveys of unit commitment studies are also presented in References [
17,
18]. However, a profit-based unit commitment (PBUC) may be found in the literature, in which the objective of the problem is switched to maximize the profit of the generation companies. A shuffled frog leaping algorithm [
19] and swarm intelligence technique [
20] have been proposed to solve such a problem in power networks, yet a microgrid solution is also proposed with security constraints [
21].
Transmission switching, or optimal topology control (OTC), is another mathematical model that identifies transmission lines to be in service while minimizing the production cost [
22,
23]. Like the UC problem, OTC is also formulated in the form of MILP. Although its theoretical background is studied and published by several groups [
24,
25,
26,
27,
28,
29,
30,
31], there is no reported use of OTC in business as of today. However, possible sub-applications of OTC in deregulated markets are discussed in Reference [
32].
One of the sub-applications of OTC is related to transmission maintenance scheduling (TMS). Instead of looking for one or more transmission assets to switch off out of all transmission lines in the system, a TMS problem only looks at a limited number of transmission assets waiting for maintenance. In other words, the proposed model in this study schedules short-term maintenance of transmission lines in a centralized way so that maintenance is completed at the optimal time, reducing the production cost of the system.
The main difference of the proposed model is the way it treats the TMS problem. As discussed in Reference [
33], transmission line scheduling studies are generally presented from a transmission operator’s (TO) perspective, and whose objectives are to either maximize profit and/or minimize maintenance costs [
34,
35]. Because of this, problems are solved by a self-scheduling method [
36,
37], which means no central coordination has been considered in the literature. This study, however, fills this gap by introducing a single objective optimization problem that co-optimize the benefits of unit commitment, maintenance scheduling, and transmission switching in a production cost simulation framework, known as the scheduling maintenance for reliable transmission systems (SMaRTS) model.
While the proposed model focuses on the maintenance schedule, the proposed formulation is also flexible to cover the OTC problem. It reveals that the cardinality of the OTC problem is significantly reduced compared to Hedman’s first development [
38]. The reason is a new approach taken for N-1 reliability constraints by eliminating the separate binary variable for contingencies. This contribution is later detailed in
Section 4 by discussing the simple changes to convert the proposed TMS model to an OTC model.
The rest of the paper is structured as follows. The proposed problem formulation and thorough discussion around the details of each constraint are given in
Section 3.
Section 4 discusses the flexibility of the proposed formulation and introduces the steps to convert the SMaRTS model into other well-known mathematical models of power systems such as security constraint unit commitment (SCUC) and OTC.
Section 5 includes a case study covering a modified IEEE-30 bus system with all the details that allow an interested party to duplicate the work done in this study. It also covers the comparison of a proposed model with business-as-usual (BaU) transmission maintenance schedule.
Section 6 introduces additional case studies, including a renewable integration study, heavy loaded system study, and OTC study to address the impact of the variability of renewables, less reliability on the system, and full control of all assets on the system, respectively.
Section 7 concludes the study with the final remarks on the findings.
2. Problem Formulation
This section covers the dense mathematical representation of the proposed model. Definitions of the variables are given in the nomenclature. Generally, variables are denoted with three subscripts, denoting index, time, and contingency state parameters respectively. Other variables are denoted with two subscripts, which are index and time parameters. Finally, if the value of a parameter does not change with respect to time, it has only one subscript for indexing.
The formulation includes linear equality and inequality constraints on power flow definitions, power balance equations, unit commitment, technical limits, and maintenance scheduling constraints. The objective is to minimize total production costs of the system. It is a summation of four different terms, as shown in Equation (1).
2.1. Objective Function
Minimize total production cost, including the cost of generation, no-load cost, startup cost, and partial maintenance cost (no cost is allocated if the maintenance is completed with no interruption).
The first term in Equation (1) is the production cost at a steady-state, and the second term is no load cost. Together, they represent the total cost of generation. The third term is startup cost (SU), which depends on the binary startup decision variable, s. The last term is the partial maintenance (PM) cost. It treats all maintenance requests equally if they are scheduled in a block timeframe. However, if scheduling the maintenance in two or more time windows leads to a better solution, then the model captures this tradeoff.
2.2. Power Flow-Related Constraints
Power flow definition, maximum power transfer on transmission lines
Constraints (2a), (2b), and (3a), (3b) define the amount of power flowing on a transmission line. The maximum flow limit of transmission lines is modeled in (2c) and (2d). Constraints (3e) and (3f) define the power balance at each bus.
One of the contributions of this study is to reduce the size of the problem by eliminating a binary variable previously used in other studies [
38]. Our observation is that a transmission line being ON or OFF does not change in any contingency states but for its own. Secondly, if the line is out due to a contingency, then its transfer capability is zero, which means it is mathematically already known and not a variable to be determined in the program. By introducing a parameter, we can avoid introducing a separate variable as represented in the Constraint (3b).
2.3. Contingency-Related Constraints and Power Balance Constraint
Due to the adaptation of a lossless model in this study, the amount of power flowing from Bus i to Bus j is equal to the flow from Bus j to Bus i. The set of k ∈ (i,*) in (3e) and (3f) includes branches having Bus i as their “From Bus,” and the set of k ∈ (*,i) in (3e) and (3f) includes branches having Bus i as their “To Bus”. Voltage angle for the reference bus set to zero to get a unique angle tensor at the optimal solution.
2.4. Generator-Related Constraints
Min and max generation limits, ramping limits, minimum uptime, and downtime limits
Several studies [
6,
7,
8,
9,
10,
11,
14,
15,
16] use constraints (4a–4f) to model the security-constrained unit commitment. Constraint (4a) is for maximum and minimum generation capacity, (4b) is for a secure transition from a steady state to a contingency state, and (4c) is for the secure transition of generation dispatches between two consecutive time periods in a steady state. Two inequality constraints (4d), (4e) satisfy the minimum up and downtime limits of each generator unit. Constraint (4f) is a valid constraint if, and only if, either
s or
h appears in the objective function with a positive coefficient in front as the third term in Equation (1) denoting the startup cost of generators.
2.5. Maintenance Scheduling-Related Constraints
Start time of maintenance, flag for partial maintenance allowed, and completion of maintenance in the study horizon
The last section of the model includes constraints on centralized maintenance scheduling. It is worthwhile to note that the set Ψ includes the transmission lines pending maintenance approval. All constraints on this section are defined solely for the set Ψ. Constraint (5a) defines the binary variable with respect to a change in the status of Branch k. It is valid if, and only if, m appears in the objective function with a positive coefficient.
Constraints (5b) and (5c) are included to add more flexibility in maintenance scheduling. A partial maintenance task may have a predetermined minimum time, the value of which may not be equal to the total duration required to complete the maintenance. Due to the fact that the model can split the total maintenance duration into partial timeframes, constraint (5b) ensures Branch k is kept open during the minimum timeframe denoted by . However, it may not be possible to split a maintenance task, though some tasks may be divided into one-hour intervals. To address this issue, constraint (5c) is included to create this flexibility by changing the maintenance value of . For example, if , then the maintenance duration for Branch k cannot be divided into partial timeframes. However, if then the minimum partial maintenance window becomes a one-hour interval. Constraint (5d) ensures that if the maintenance is approved, it has to be fully completed in the planning time horizon.
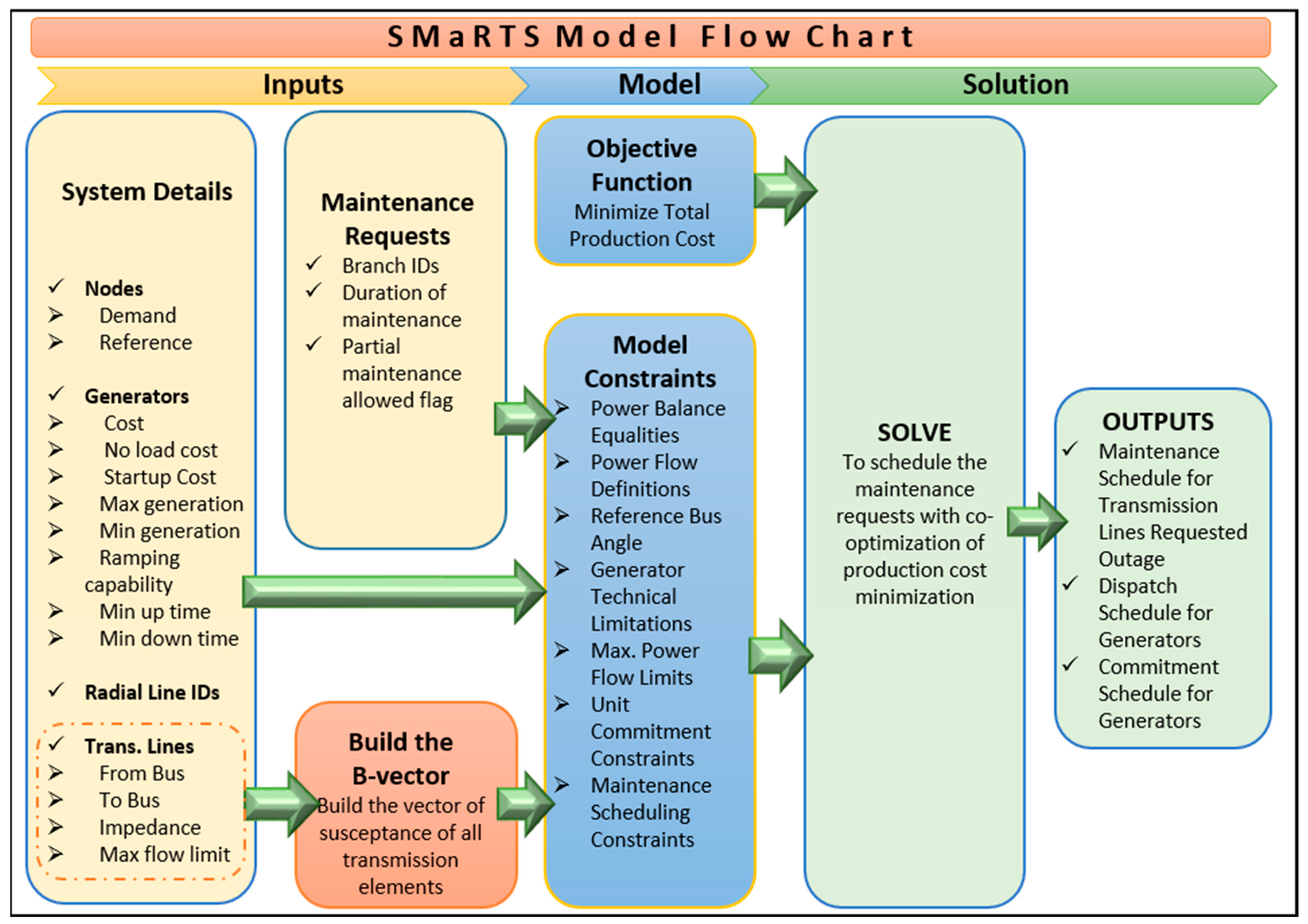
The final model can be created as a single objective optimization problem that minimizes (1) subject to the constraints of Equations (2a–2d), (3a–3f), (4a–4f), and (5a–5d). All necessary information to complete a nodal system-level study with the SMaRTS model is summarized in
Figure 1 with the subsections of Inputs, Model, and Solution.
3. Model Flexibility and Convertibility
The proposed model is developed to co-optimize generation unit commitment with transmission switching from an outage coordination perspective. Cost savings are achieved by shifting the maintenance duration to an optimal timeframe when the loss of this transmission line reduces the total operating cost of the system. The model captures the impact of a transmission line status on the production cost, which means the optimal solution will always yield a better solution than the BaU model.
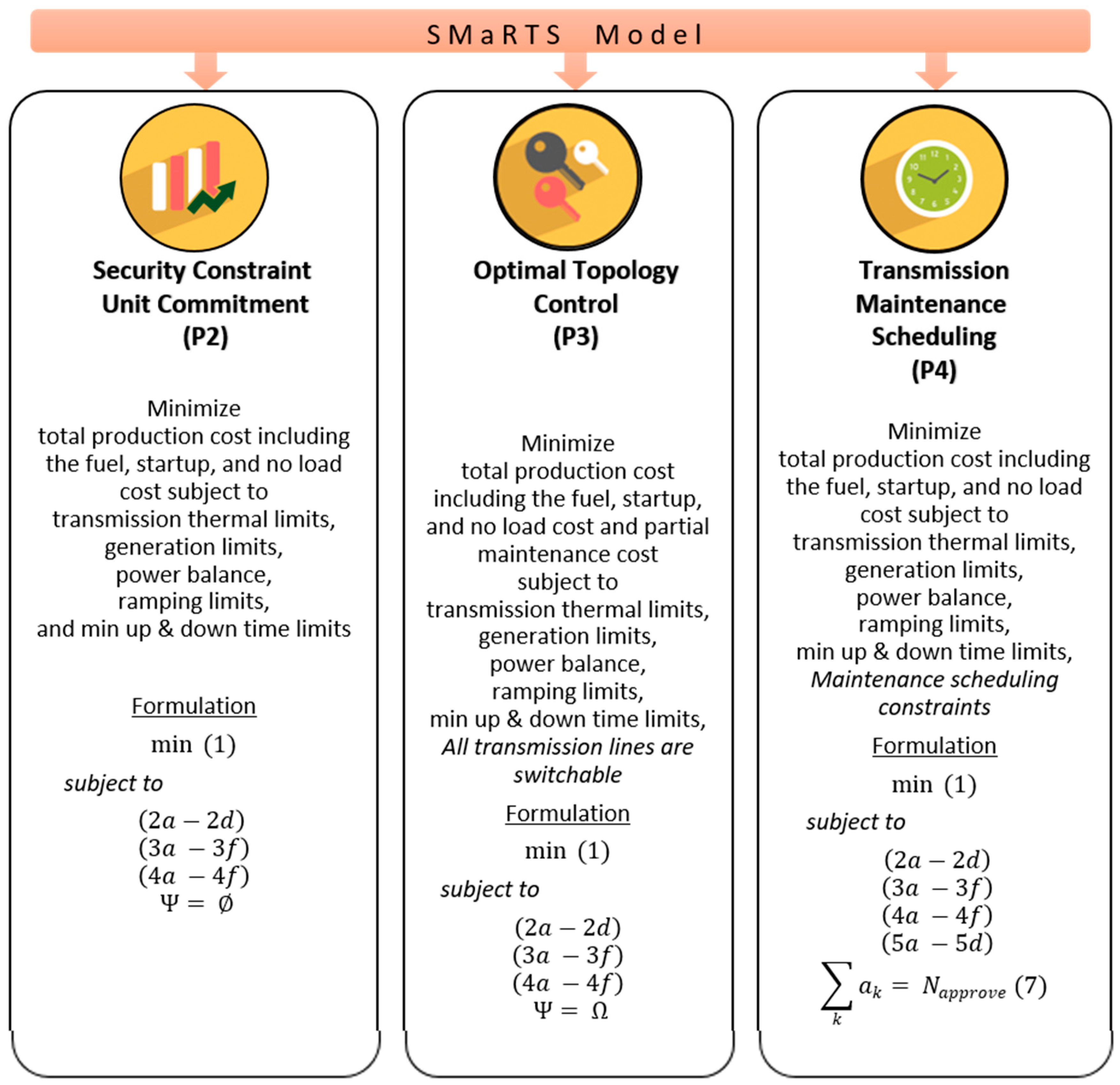
The model includes all constraints of a SCUC problem. To convert the model to a SCUC, as given in (P2), we drop the maintenance scheduling constraints given in Equations (5a–5d) from the constraint set, and then set no pending maintenance requests (Ψ = ∅). Moreover, the proposed model can also be modified to be the exact problem of co-optimization of generation unit commitment and transmission switching with N-1 reliability [
38]. Dropping the maintenance scheduling constraints given in Equations (5a–5d) from the constraint set and selecting all transmission lines for maintenance (Ψ = Ω) converts the model to an OTC-SCUC, as presented in (P3).
In our context, SCUC does not consider transmission switching, OTC-SCUC includes all transmission lines and generators in the commitment procedure, yet in a different meaning than SMaRTS. In a simplistic manner, one SCUC corresponds to one topology. If we consider M topologies, solving M SCUCs and selecting the best one would give us the cheapest schedule as the same as OTC-SCUC. In branch and bound, we prune a branch as the process goes. As a branching point goes down, feasibility is enhanced, but optimality becomes reduced. Therefore, the SCUC is higher since no maintenance is scheduled. The OTC-SCUC is lowest since strict maintenance schedules are taken into consideration. However, SMaRTS exist in between in terms of optimality and feasibility since a “flexible” maintenance schedule is considered because we allow the maintenance schedules to split into multiple pieces.
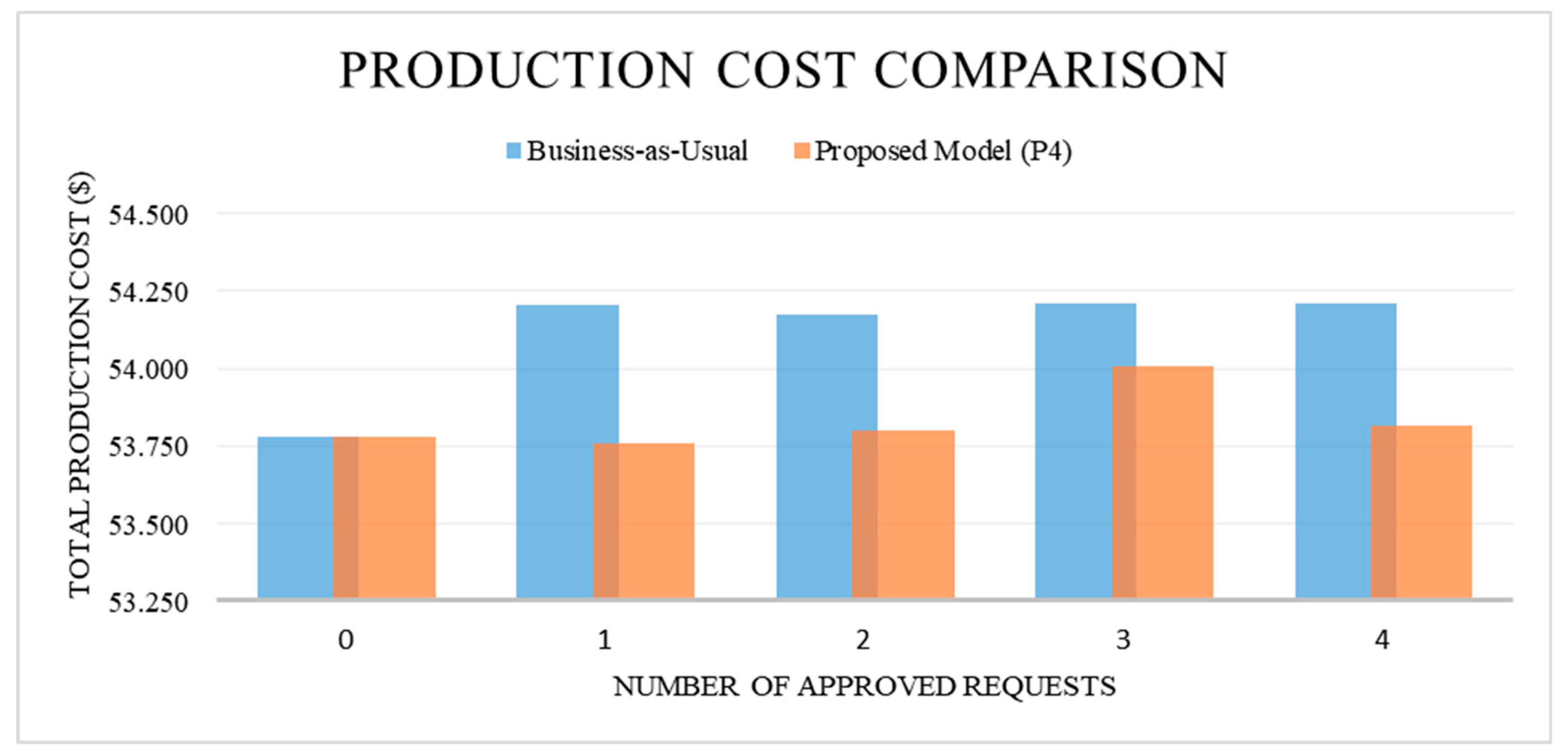
The model can also be modified to show the tradeoff between total operating costs and the approval of one more request from the maintenance waiting list. This capability is unique and may be used to identify the Pareto optimal solutions from a multi-objective optimization perspective. The modified problem is given in (P4) by adding a linear equality constraint as shown in Equation (7) on
Figure 2. The summation of request status variable a can be bounded by the total number of the approval parameter,
. The scalar value of
may be selected from the set of {0, 1,…,
n(Ψ)} where
n(Ψ) denotes the number of elements in Set Ψ. The difference between the two objective values may give an opportunity to the system operator to analyze the impact of maintenance on the total operating cost.
4. Numerical Example
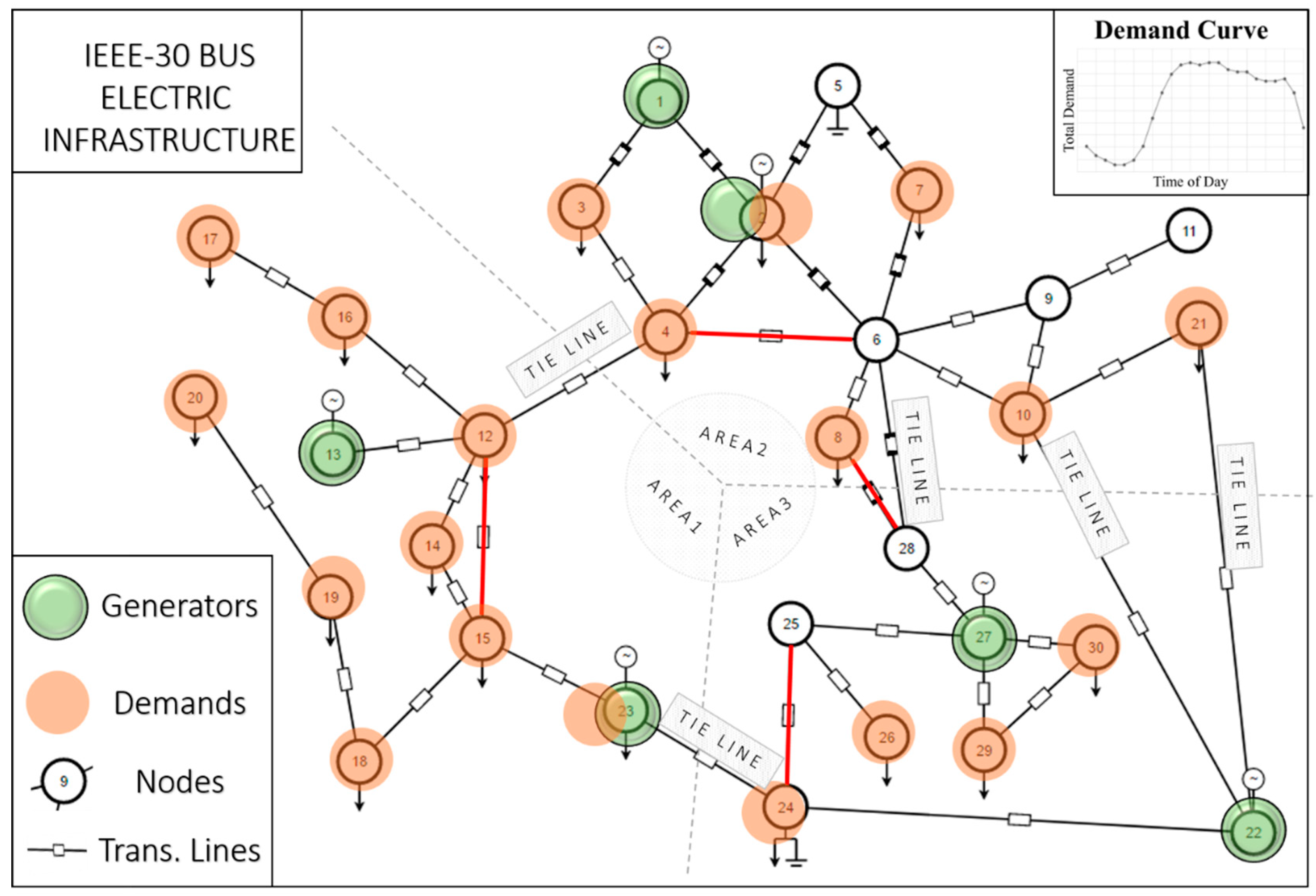
A modified 30-bus system included in MATPOWER [
39] is used in this study with minor modifications given in
Table 1. The dataset of the system is adopted from MATPOWER (v6.0, PSERC, Ithaca, NY, USA). However, additional parameters like startup cost, ramp rates, minimum up- and downtime parameters are assumed to be given in
Table 2. Six transmission lines out of 39 are assumed requesting maintenance (
Table 3). Hourly peak load in percent of total load (
Table 4) is adopted from IEEE-reliability test system [
40]. The 24-hour time period of interest is assumed to be a summer weekday with a total peak load of 189.20 MW. Per-unit basis [
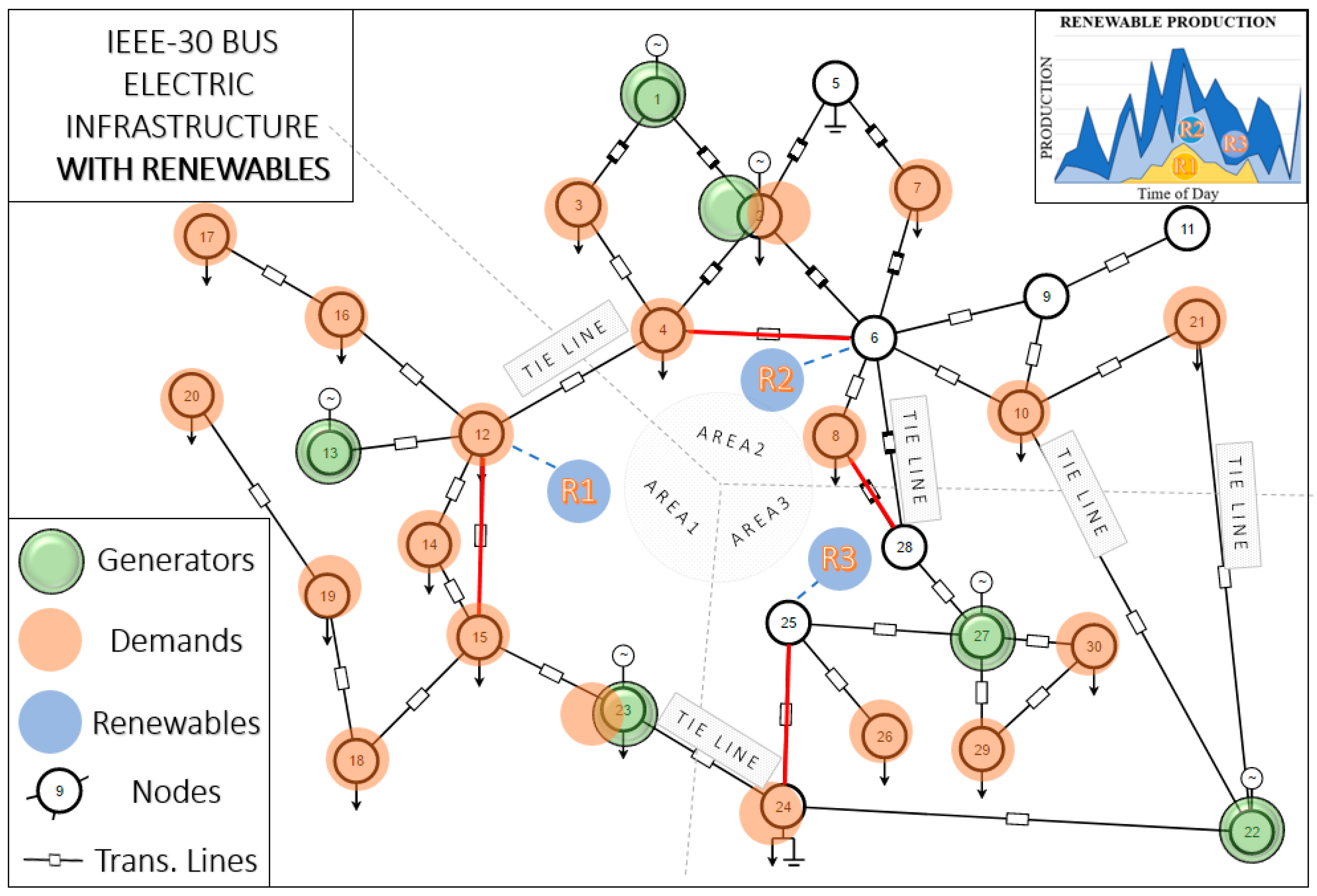
41], BaseMW, is set to 100 MW. The final electric infrastructure of the modified 30-bus system is illustrated in
Figure 3.
The proposed model is implemented in MATLAB 2017a (The MathWorks, Inc, Natick, MA, USA) with the YALMIP toolbox [
42] and solved by an academic version of a commercial optimization solver, CPLEX. It is noteworthy to mention that YALMIP is an intermediate toolbox in MATLAB between the user and the solver. It can detect what kind of a problem the user has defined, and selects a suitable solver based on this analysis [
42]. While convenient, it has a large overhead and tends to get slower for bigger size optimization problem just because it is an unnecessary intermediate process. The SMaRTS problem is a mixed-integer linear programming (MILP) that is an
NP-hard problem. Therefore, the computational complexity is difficult to address, and it is a topic of research activities. For an example, a study on the scalability of an MILP [
43] shows that the computation time critically depends on the number of binary variables and implies that the proposed algorithm would be applicable to a real-world power system with on the order of 10
3 binary variables. The novelty in the proposed model lies in reducing them by a new approach to N-1 contingency and commitment modeling.
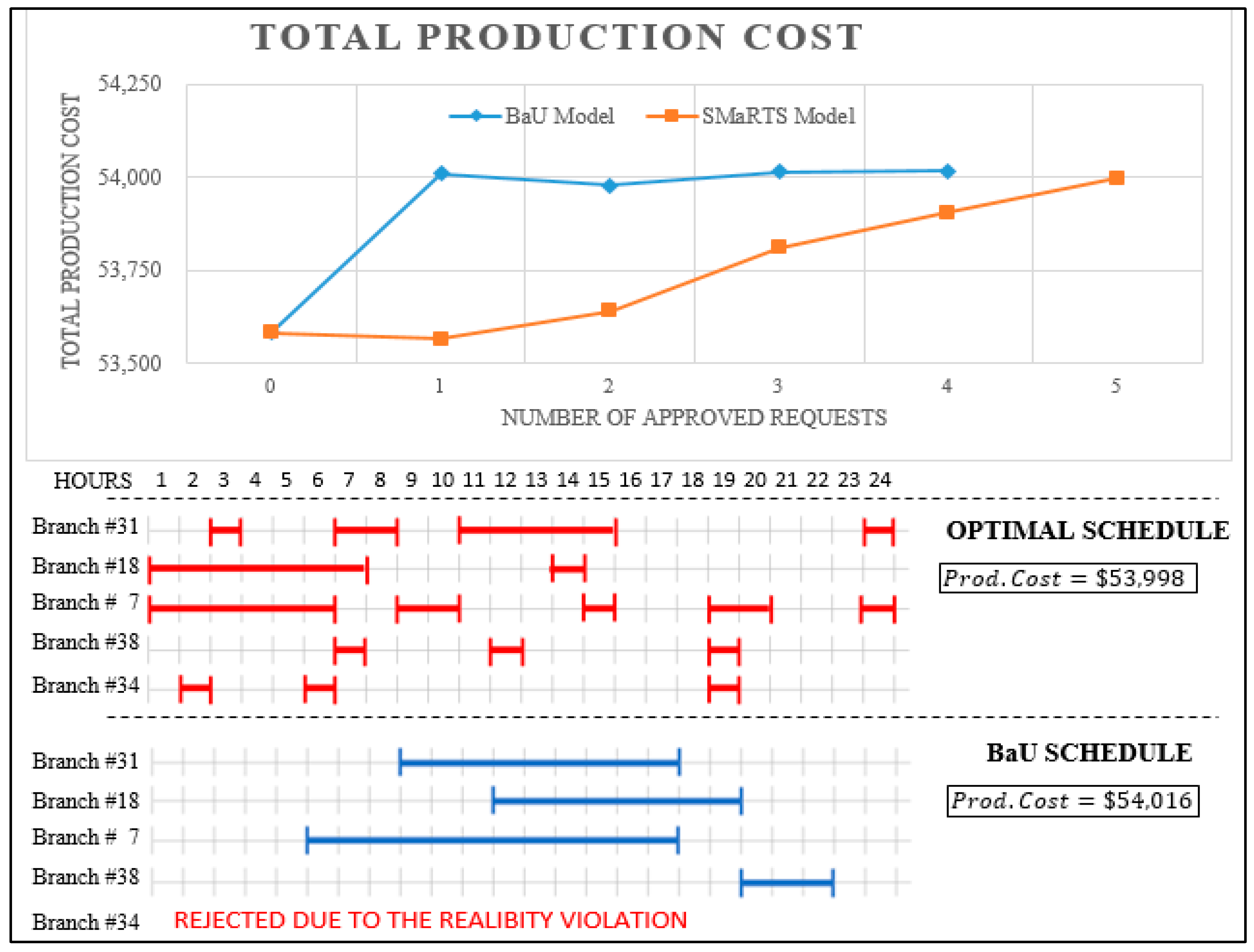
The optimal operating cost of the system is
$53,757.78, with the approval of one maintenance out of four requests. The hourly status of the transmission line that is approved for maintenance (variable
z) and the unit commitment decisions (variables
u) at the optimal solution are given in
Table 5. Two generators are committed fully in the planning period, and the other four are committed partially to meet the hourly power demand, as needed.
The BaU model as currently adopted by the system operators does not consider the tradeoff between the decision on maintenance requests and the total operating costs. Instead, the BaU model has a priority list of maintenance requests based on their submission dates. As long as the first request is N-1 reliable for the system with no consideration on the financials, the operator approves the request. Then the next request from the priority list is studied and the decision is made based on the previously approved outage request(s).
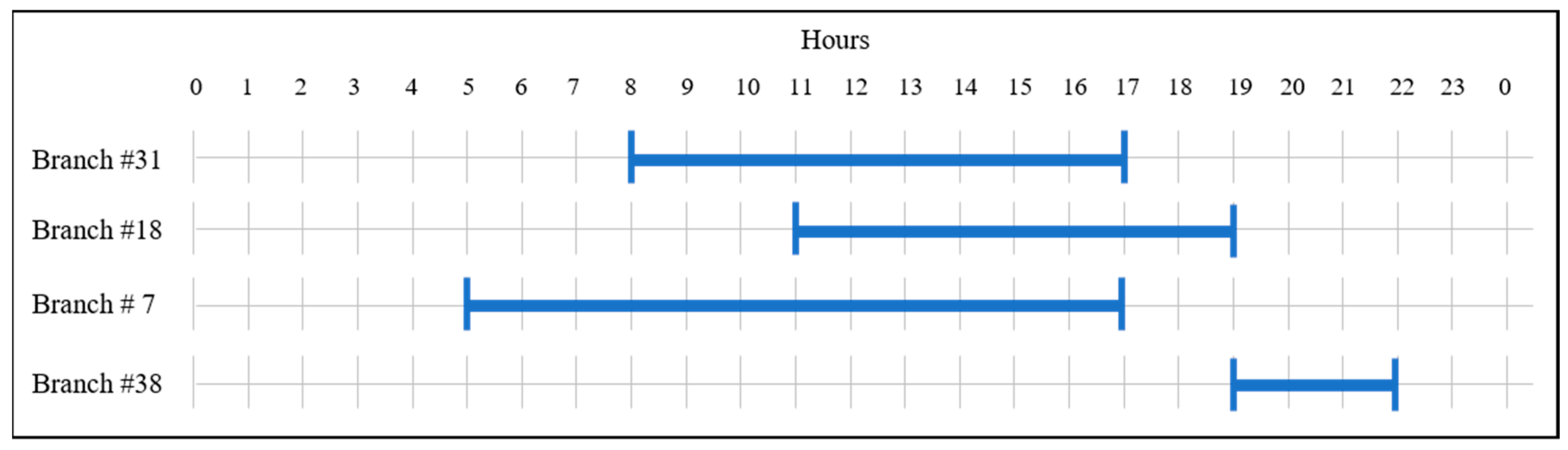
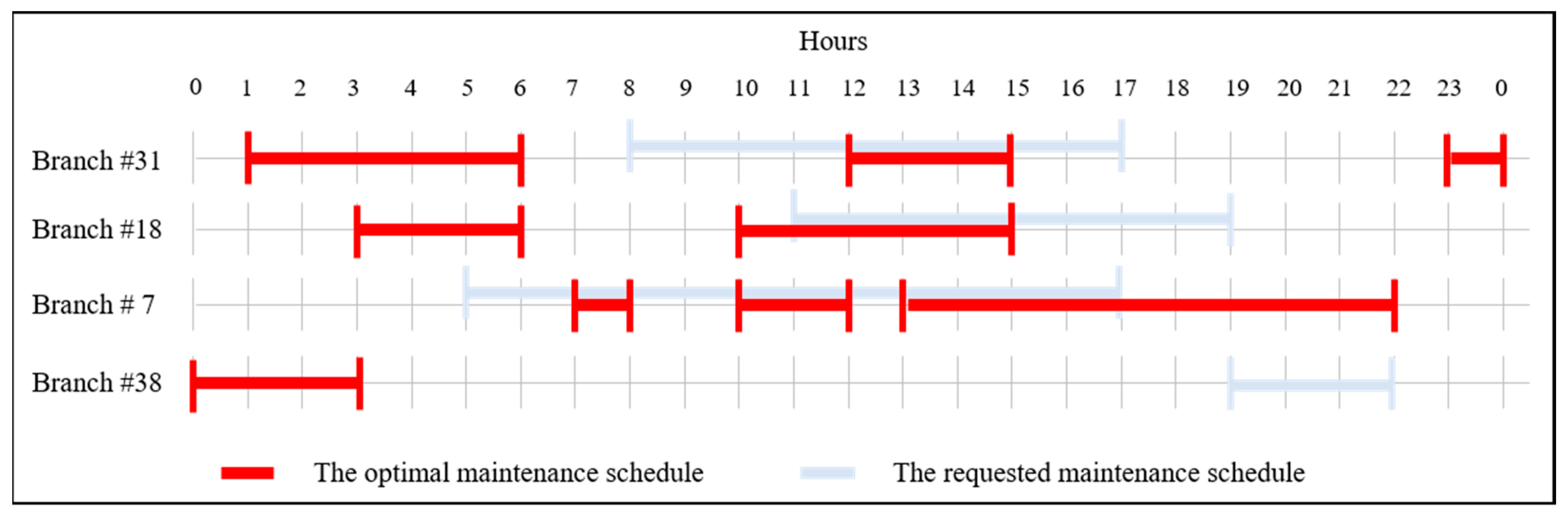
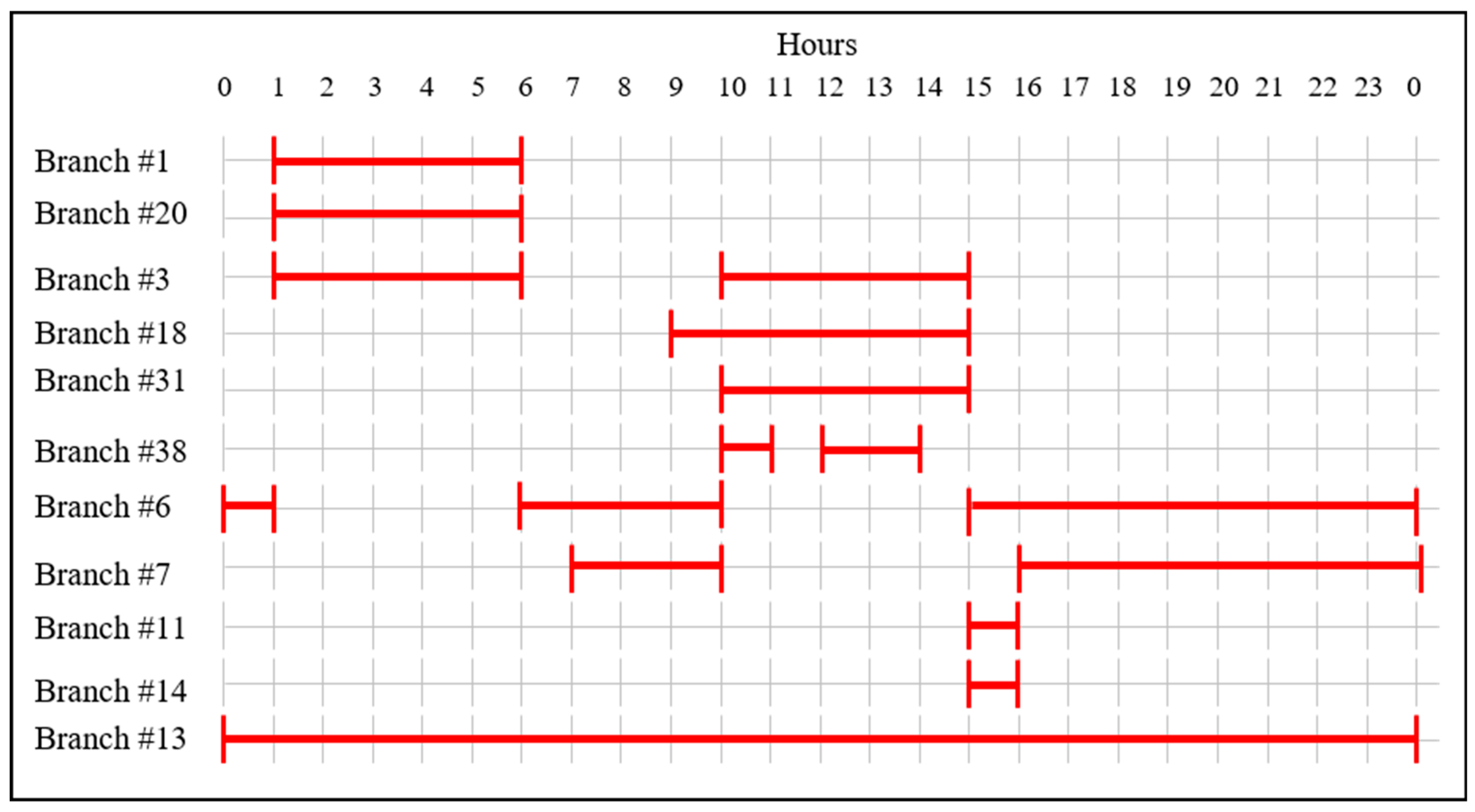
In this part of the study, the financial savings of the proposed model in comparison to the BaU is discussed. The priority list is assumed to be in the order of Line 31-18-7-38. The starting time of day for maintenance requests is assumed to be 8 a.m., 11 a.m., 5 p.m., and 8 p.m., respectively. The expected duration to complete maintenance for these lines are assumed to 9, 8, 12, and 3 hours, respectively. An illustrative time windows for each maintenance requests is given in
Figure 4.
As discussed earlier, the only approval criteria for maintenance requests is to verify that the loss of that transmission line does not violate the N-1 operation criteria, and the order of approval must coincide with the priority of those requests. Therefore, a simulation is performed with the loss of the first transmission line in the rank during the requested maintenance window. If there is no violation of the N-1 criteria at the time of maintenance, then the second simulation is performed with the loss of the first and second transmission lines in the rank. The process is continued until all four maintenance requests are complete. The case study shows that even after approval of four maintenance tasks, the system is still satisfying the N-1 criteria. However, the total production cost of the system increases as each maintenance request is introduced to the system.
Table 6 shows the total production cost of the system for the study horizon with each additional approval.
This information lets us show the effectiveness of the proposed co-optimized maintenance scheduling with the production cost minimization (Model P4) by comparing the cost of BaU model and the TMS model. The proposed model schedules the maintenance time windows optimally at each approval level and provides better-operating conditions that yield to lower production cost for the system. Even after approval of all four maintenance requests, the proposed model yields 1% cost savings with while holding the exact same N-1 contingency criteria as shown in
Figure 5. The optimal schedule of maintenance timeframes is given in
Figure 6 with the timeframe used in the BaU as a reference.
5. Case Studies
Case studies are always helpful to simulate different operating conditions and different system structures. Although it is possible to create various scenarios on the interesting subject of transmission line maintenance schedule, this section focusses on two important topics: (1) Renewable energy utilization and delivery, and (2) system reliability in terms of service interruption. Maintenance schedule has a direct impact on the network topology that can cause sudden changes in the available energy transfer capability of the system. The change on the transfer capability may have a local or system-wide impact based on the location of the transmission line. The starting time of two different maintenance operations may conflict each other in the currently used maintenance scheduling approval process, which may lead to the rejection of one to maintain the system reliability. However, the proposed optimal maintenance scheduling with co-optimization of production cost may provide a schedule that fits for each request. The increased acceptance rate of regular maintenance requests evidently reduces the forced outage of those lines due to the delay caused by inefficient scheduling processes. To show the effectiveness of centralized maintenance scheduling on systems (1) with high penetration of renewables and (2) with a heavy load, two additional case studies are provided in this section. The first case study introduces renewable generators into the system used in
Section 5 to enhance the reliable operation of power systems in the presence of uncertainty, while the transmission maintenance scheduling is co-optimized with the production cost minimization. The second case study is performed on the same system used in
Section 5 but has higher demand on each node in comparison to the original to simulate the effectiveness of centralized maintenance scheduling on the unserved energy level.
For the first case study where renewables are introduced into the system, three new generators are included and their locations are selected to be physically close to the transmission lines waiting for the maintenance approval. The first one is located on Bus 12 and it is a solar generator. The second and third are located at Bus 6 and Bus 25, respectively, and they are wind generators. The production profile of each generator is illustrated in the top right portion of
Figure 7.
A new three-hour long maintenance request on line 34 connecting Bus 27 and 28 is introduced with a starting time of 6 p.m. Its priority is assumed to be right after the request of Line 38, which connects the Bus 8 and 28 starting at 8 p.m. Based on the location of these two lines, it is not possible to approve both requests. The loss of these two lines at the same time leaves Bus 28 isolated from the grid, which violates the approval criteria in the BaU scheduling process. This kind of conflicting event is the result of the self-scheduling approach by the transmission owners in today’s operations. However, the proposed centralized scheduling approach may find a suitable schedule for both transmission lines while minimizing the production cost of the system.
The analysis of the simulation results shows that the new maintenance request is rejected due to the approval of the request from Line 38. The approved maintenance starts at 8 p.m. and continues for three hours. During this time, Line 34 is a must-run line to provide electric service to Bus 28. The requested timeframe for maintenance on Line 34 begins at 6 p.m. and ends at 9 p.m. Due to the schedule conflict between 8 p.m. and 9 p.m., the BaU process for scheduling rejects the request for Line 34. However, the proposed centralized scheduling method with co-optimization of production costs finds the optimal schedule for all five requests within the study horizon. Although the production cost is increasing after the approval of the second request, it is lower than the cost found by BaU model as shown in
Figure 8, as well as the generation mix and the optimal maintenance schedule after approval of all five requests.
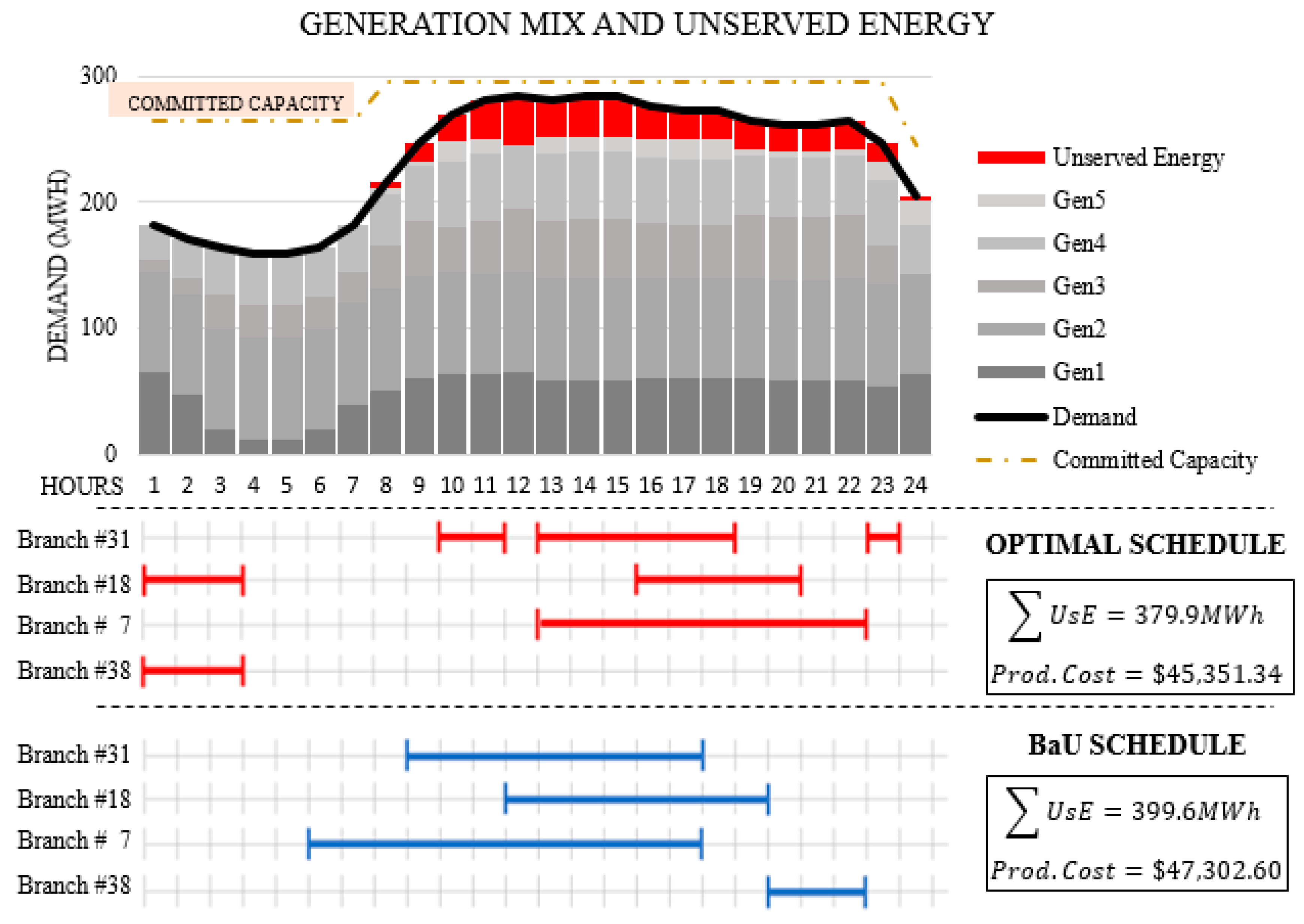
The second case study simulates heavily loaded system conditions by increasing the original demand by 50% for each hour of the day at each bus. A new variable is introduced to the mathematical model to address the possible unserved energy conditions while meeting the high demand. The motivation of this case study is to reveal the positive impact of optimal maintenance scheduling on the reliability of the system by reducing the total unserved energy within the study horizon. Although the system is facing heavy load, the proposed scheduling method can find the optimal timeframe for transmission maintenance requests while providing more economical generation dispatch. Generally, unserved energy variables are introduced in production cost simulations to relax the power balance equality constraints that are difficult to satisfy. This can also be treated as a reliability index of the system. The tradeoff of violating the power balance equation for each node, the unserved energy variable, is penalized in the objective function by the value of loss load (VoLL). $1000/MWh is used as VoLL throughout this study. To address those changes in the mathematical model, three modifications are made on (1) objective function, (2) power balance equalities, (3) additional constraints to have contingency cases not worse than the base case in terms of unserved energy.
Objective function: Equation (1) is switched with Equation (6) to reflect the penalty on unserved energy.
Power balance constraints, including unserved energy: Equations (3e) and (3f) are also switched with Equations (7a) and (7b) to reflect the relaxation of power balance equality constraints. The introduction of unserved energy variable for each node also represents the reliability index of the system, including the capability of meeting power demand at all times.
Additional constraints: All unserved energy variables must be positive, and total unserved energy under the contingency cases should be less than the base case.
Having heavily loaded power systems tends to create reliability issues in terms of not able to meet the required electrical demand due to either lack of supply or lack of available transfer capability. This case study is created to address the impact of centralized transmission maintenance scheduling on the total unserved energy within the study horizon, and also the production cost of the system. The results of the simulations with the BaU model, and also with the TMS model, reveal that the optimal scheduling of maintenance requests have positive impacts on both conditions. In the following case study, all four maintenance requests are approved in both models. However, similar results are observed in other cases.
Figure 9 includes the committed generation capacity, the demand, and the unserved energy on the same chart for each hour of the day. The total unserved energy within the study horizon with the optimal maintenance schedule is reduced by 20 MWh compared to the BaU schedule. Furthermore, the total production cost is also reduced by
$1951, which is equivalent to a 4% cost savings by the proposed model.
6. Optimal Topology Control
As discussed earlier in this paper, the transmission maintenance schedule is a sub-application of the OTC problem. The OTC mainly searches for a better topology that leads to greater savings in terms of production cost. While the proposed scheduling model is developed, it is observed that the model can be converted into a full OTC problem, and the resulting problem is an advancement on the current OTC formulation with consideration of N-1 contingency criteria.
This section is devoted to showing the impact of OTC on the same test case used in the earlier sections. Due to the expanded feasible region by adopting the OTC idea, it is expected to observe cost savings in comparison to the base case in which all transmission assets are active. The total production cost in the base case is
$53,781, but it is
$53,532 in the OTC case, which is about %0.5 cost reduction. An interesting observation is made on the selection of transmission lines to switch off with the OTC model.
Figure 10 shows the selected lines and the time of day they are switched off. Instead of showing the lines in their ID order, lines with similar schedules are plotted next to each other, revealing that two or more lines are actually selected together for different times of the day. Branch #1, #20, and #3 are switched off together between 1 a.m. and 6 a.m. Similarly, Branch #3, #18, #31, and #38 are switched off together between 10 a.m. and 3 p.m. Moreover, two other lines, Branch #6 and #7 are switched off when the other selected lines are switched back on. Completing this kind of analysis for days and throughout a year may help system operators understand the correlation of lines in reducing the system’s production cost.
This observed correlation is also consistent with the findings in
Section 5 and
Section 6 where the maintenance requested to Branch #7 is actually scheduled at times the other lines are online as shown in
Figure 6, and Branch #18 and #38 are scheduled together as shown in
Figure 9.
7. Conclusions
The consequences of aging infrastructure have become visible in recent years. The maintenance rates and forced outage rates of transmission lines that play a key role in maintaining the stable and reliable power systems have increased in the last decade. With the increasing need of maintenance on the transmission side, the current procedure of scheduling those tasks will soon be cumbersome for operations due to the length of time the maintenance takes and the negative impact on the production cost when the schedule is not fully optimized with real-time information. This paper aims to help smooth and optimize this process by proposing a new, co-optimized mathematical model to schedule transmission maintenance requests with the production cost minimization, all while maintaining the N-1 contingency criteria and other necessary technical constraints of power systems.
A novel model is developed to centralize the maintenance scheduling process at the system operator level. Central scheduling benefits the operator in terms of production cost savings. Cost savings are achieved by optimally scheduling the transmission requests at the time of their loss, leading to a lower production cost of the system. The model promises production cost savings by shifting a maintenance time window to one that is optimal for both operator and transmission owner. To address different types of maintenance tasks, the proposed model is flexible and able to differentiate block or partial maintenance. The model can split the full maintenance duration into several smaller timeframes if they lead to a lower production cost for the system.
Although the focus of the study is on maintenance schedules, the new formulation of contingency events in the mathematical program can be further developed for the OTC problem since its first introduction by Hedman [
38]. With a few changes on the proposed model, a small-size problem related to variables and constraints is introduced in this study.
The impacts of the proposed approach on the production cost, reliability, unserved energy, and transfer capability are tested on a modified IEEE-30 bus system in three different case studies. The proposed model shows up to 4% production cost savings, as well as a reduction on the unserved energy while maintaining the N-1 contingency criterion for the system. Use of the optimal schedule can also replace the additional commitment of a generator and increase the renewable generation in the fuel mix. The findings on the test cases suggest that further research on optimal transmission maintenance scheduling is justified for realistic networks. Further studies may also include the VAr scheduling and voltage control to fully support the operation of power systems.