Modeling and Design of the Vector Control for a Three-Phase Single-Stage Grid-Connected PV System with LVRT Capability according to the Spanish Grid Code
Abstract
1. Introduction
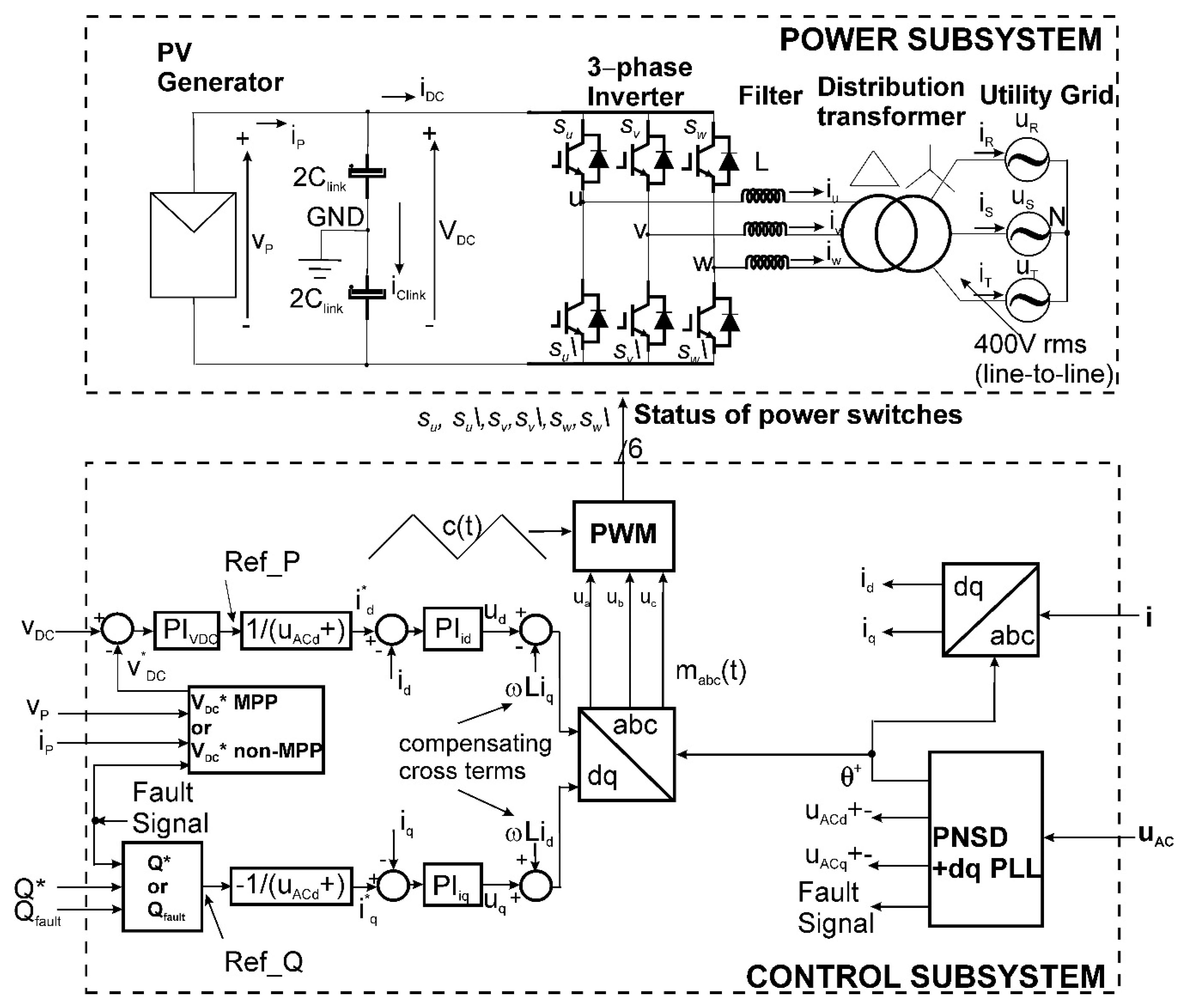
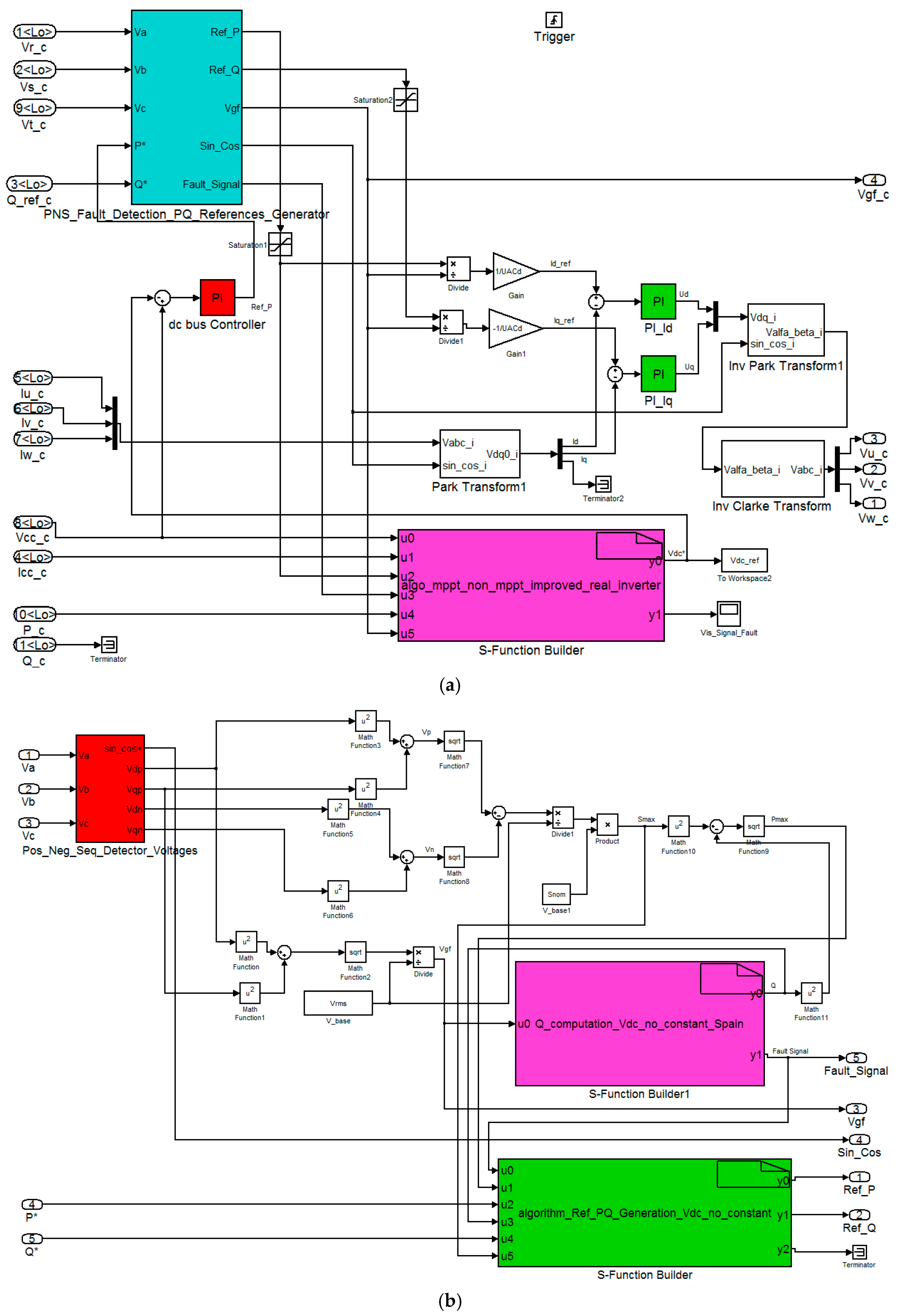
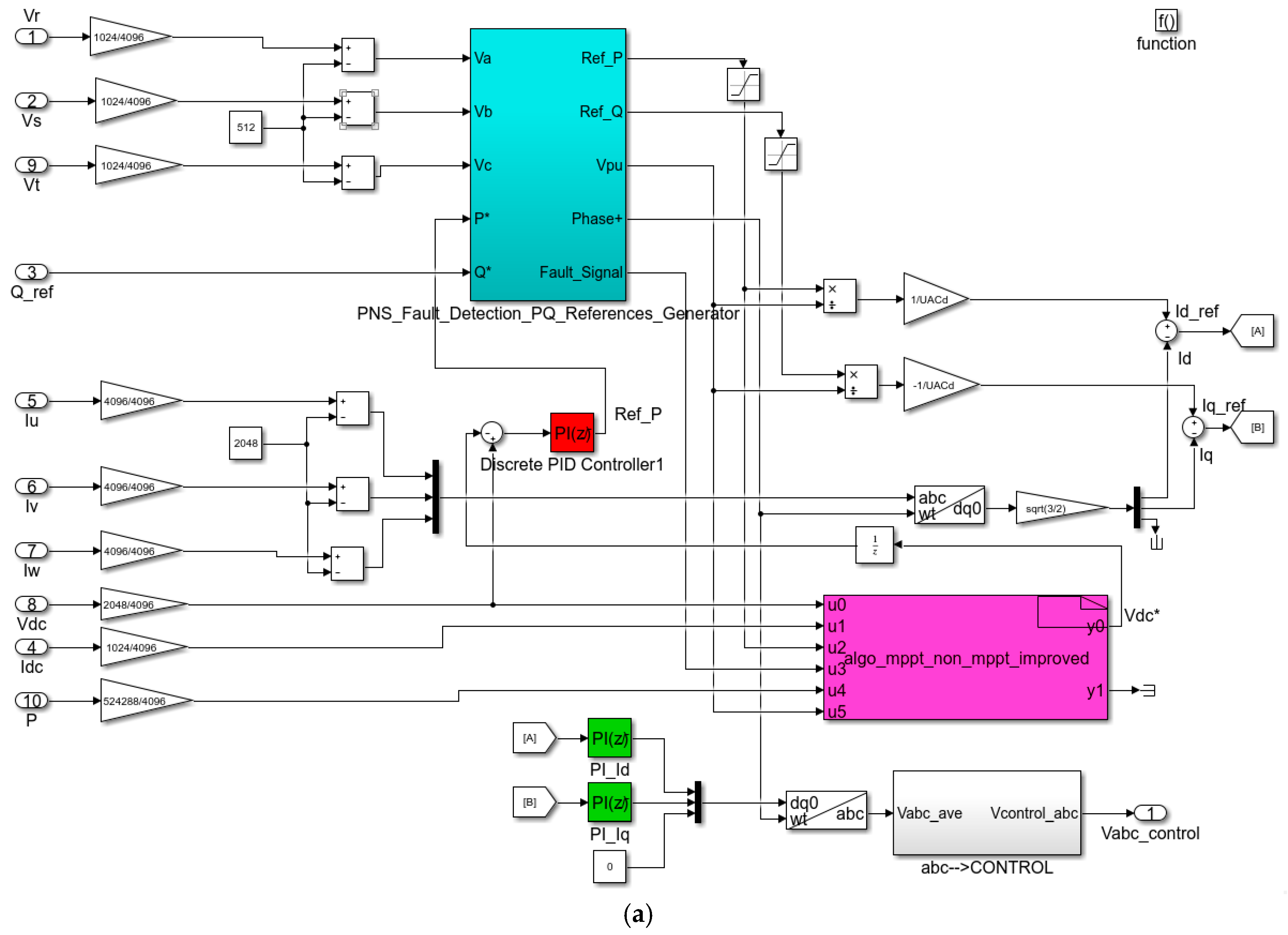
2. Control of the PV System
2.1. Control of the Inverter Currents
2.2. Control of the DC Bus Link Voltage
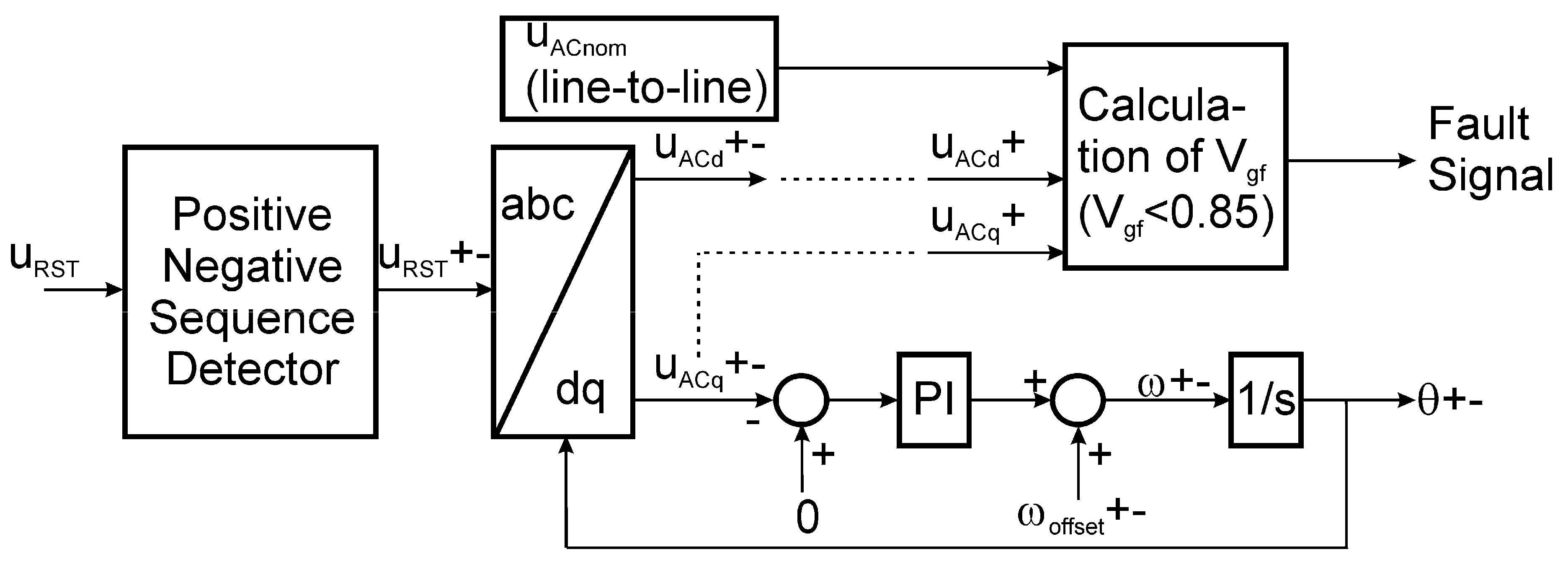
2.3. Synchronization Algorithm
2.4. Control of P and Q
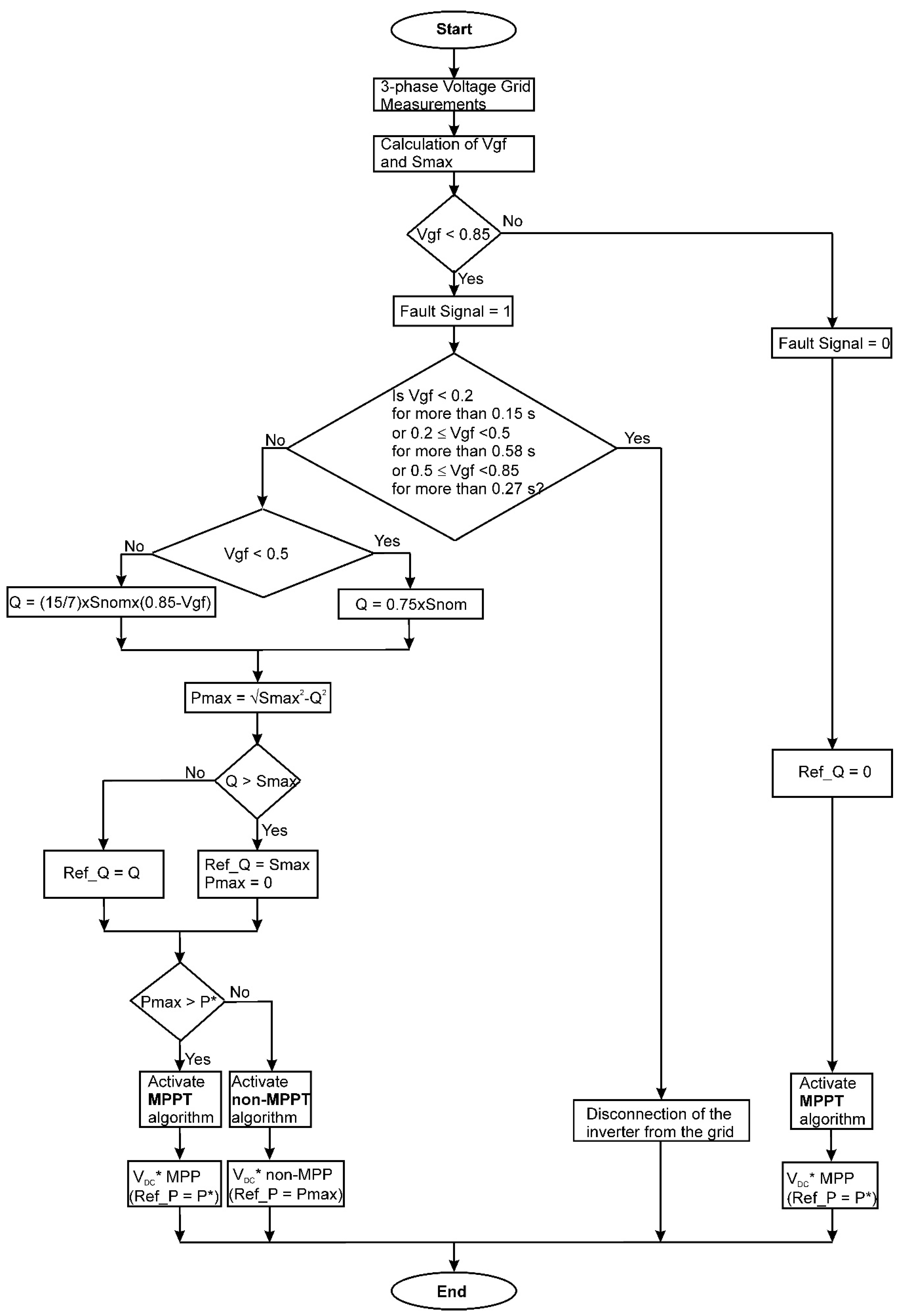
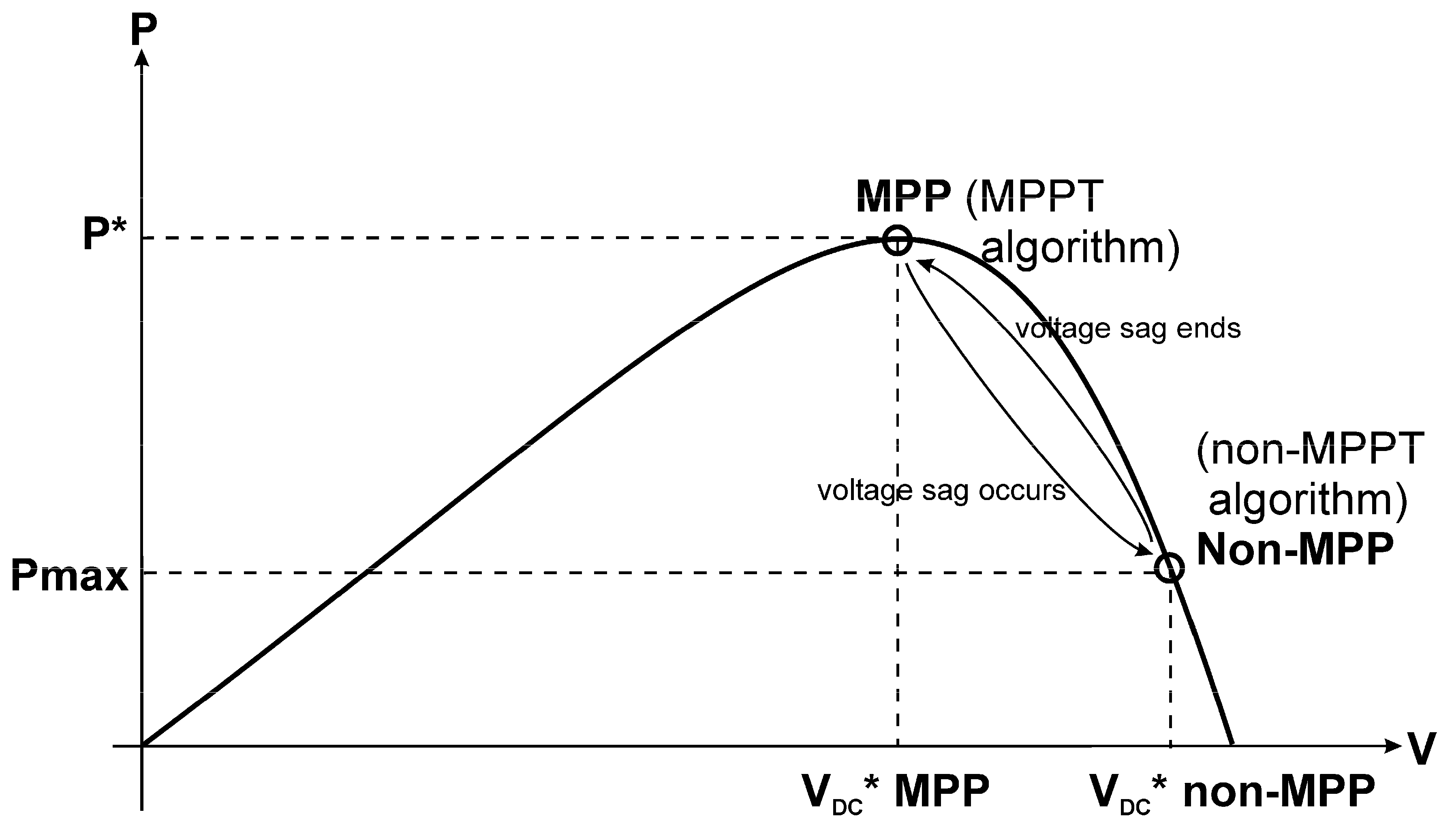
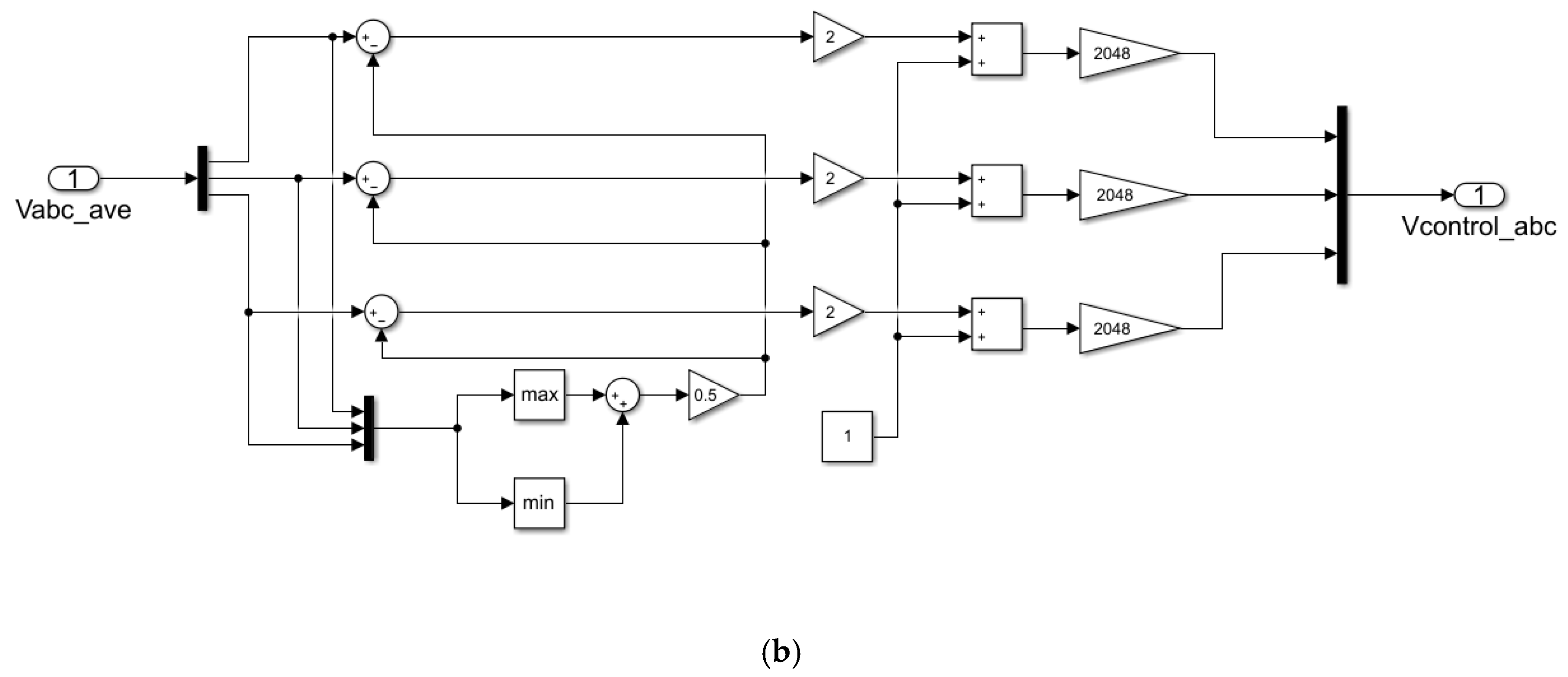
2.5. Limitation of the Output Currents of the Inverter during Voltage Sags
- If Vgf < 0.2 for more than 0.15 s or 0.2 ≤ Vgf < 0.5 for more than 0.58 s or 0.5 ≤ Vgf < 0.85 for more than 0.27 s, the inverter must be disconnected from the utility grid.
- If the fault has a duration less than the previous situation, a certain amount of reactive (Q) according to Equation (8) and active (P) powers are delivered to the utility grid according to the value of Vgf and Smax.
- For depth sags, Q might be greater than Smax and a limitation to the delivered reactive and active powers are imposed (Ref_Q = Smax, Pmax = 0).
- If Pmax > P*, the MPPT algorithm is activated, the maximum power is delivered by the PV generator to the grid (Ref_P = P*) and the DC link voltage reference command is VDC* MPP.
- If Pmax < P*, the non-MPPT algorithm is activated instead, and the power delivered to the grid is Pmax (Ref_P = Pmax) with the VDC* non-MPP as the DC link voltage reference command
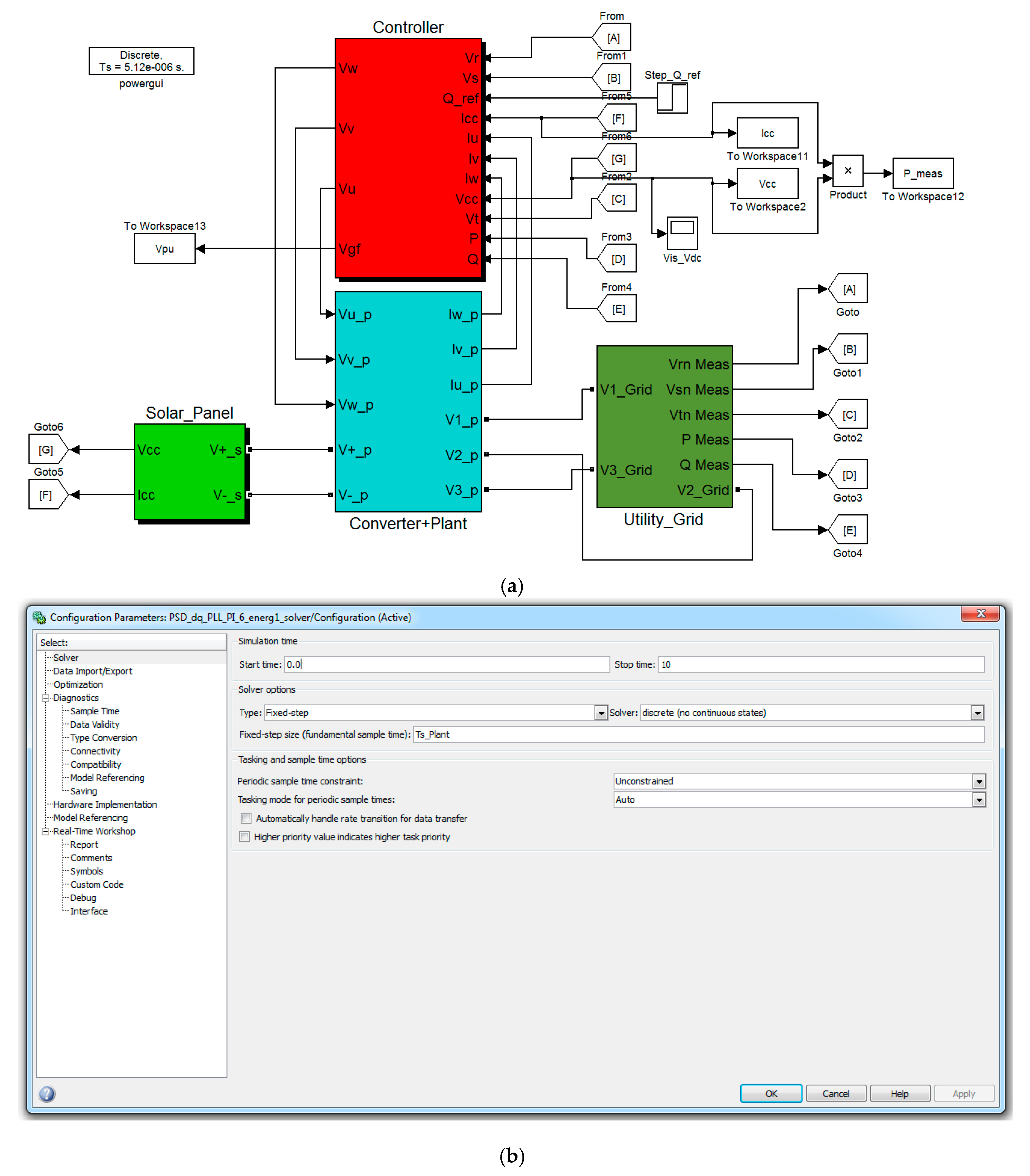
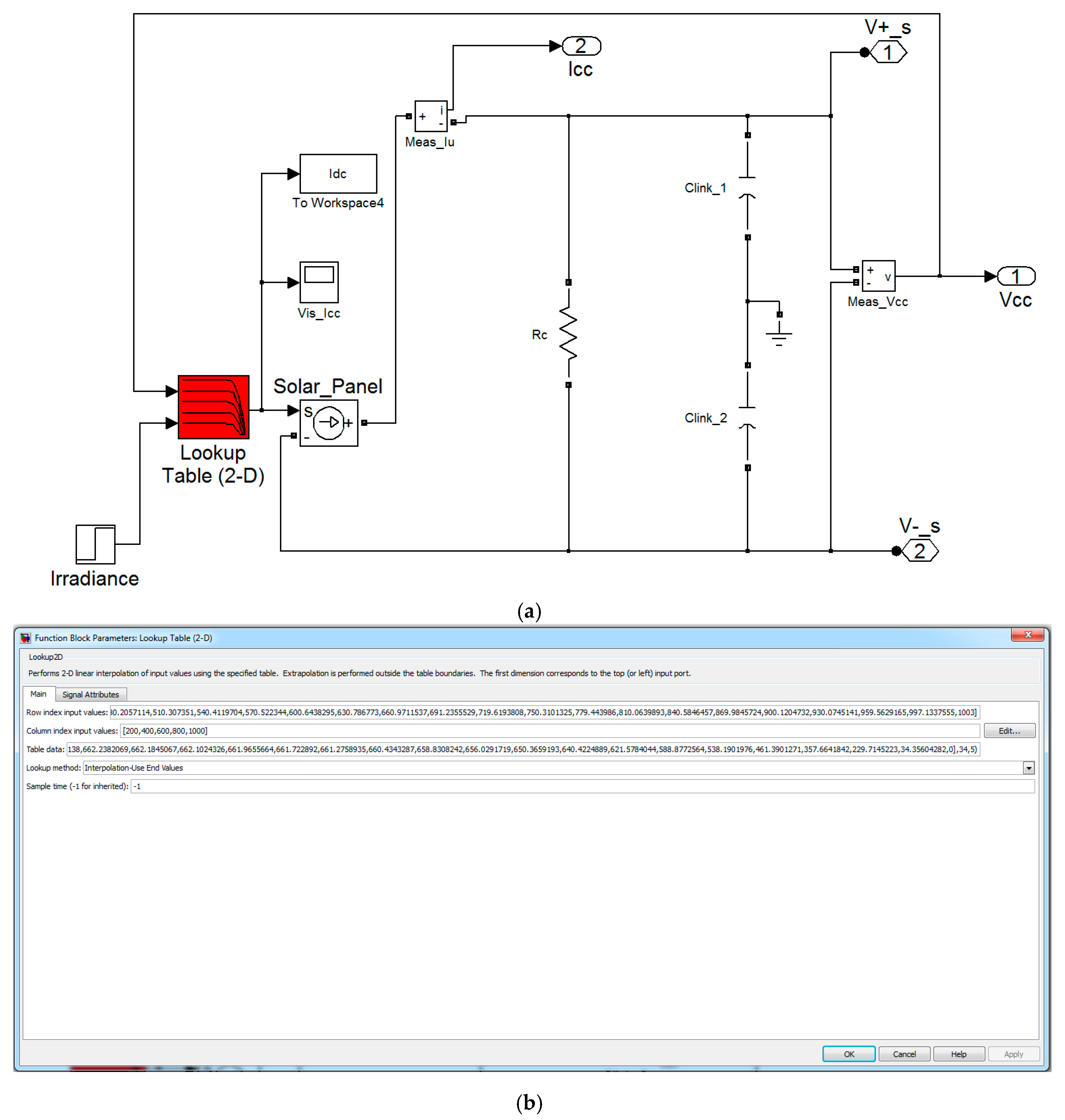
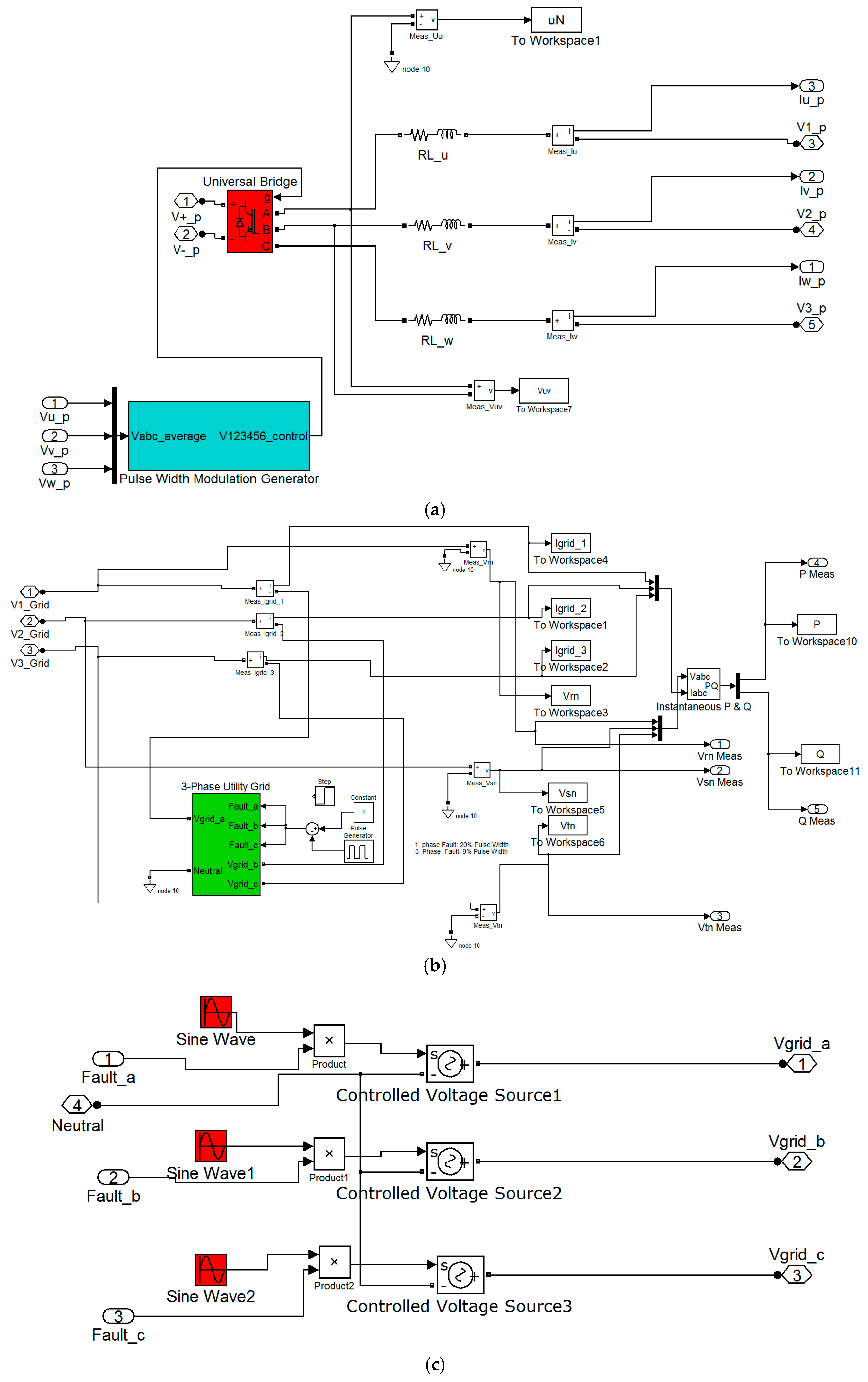
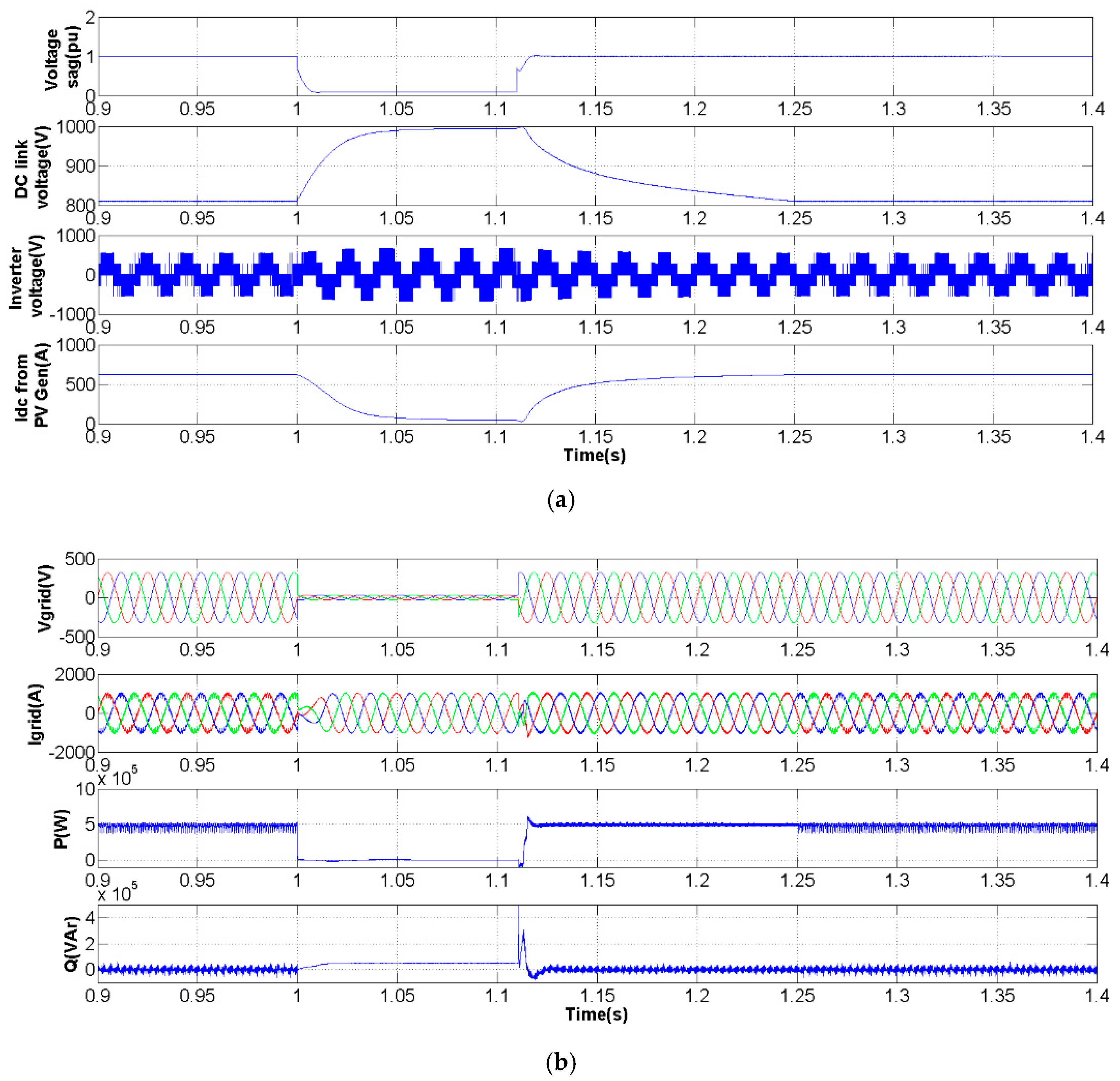
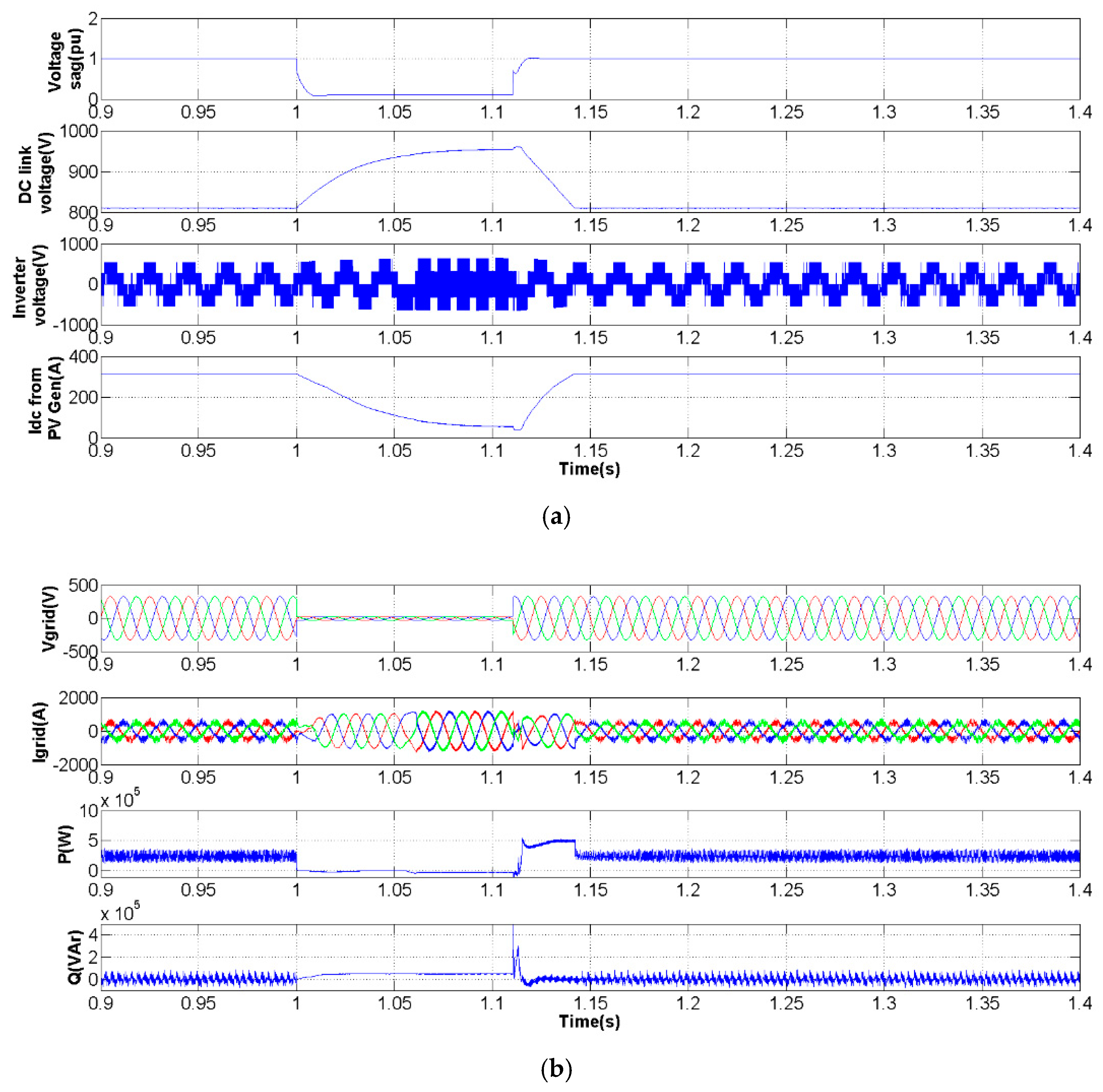
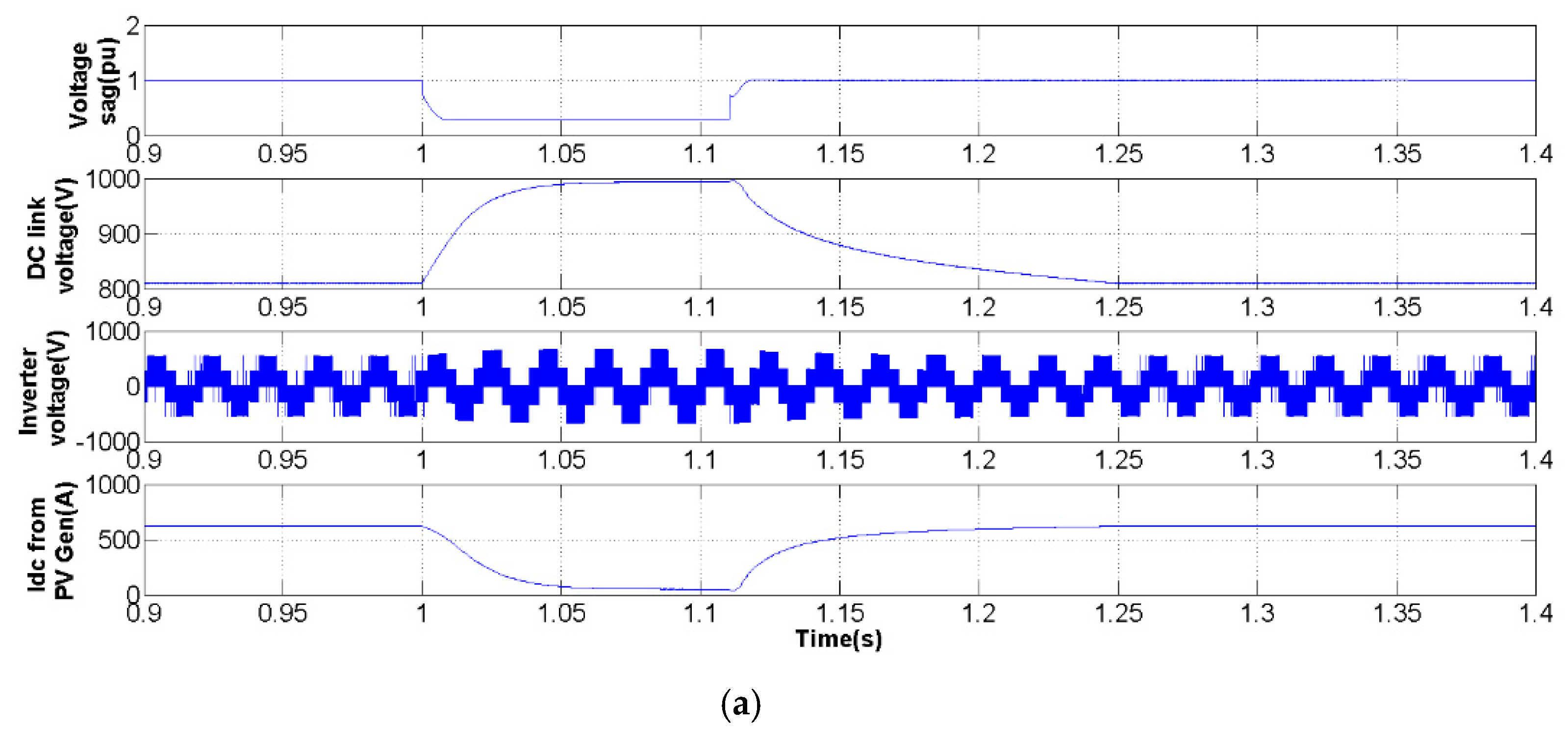
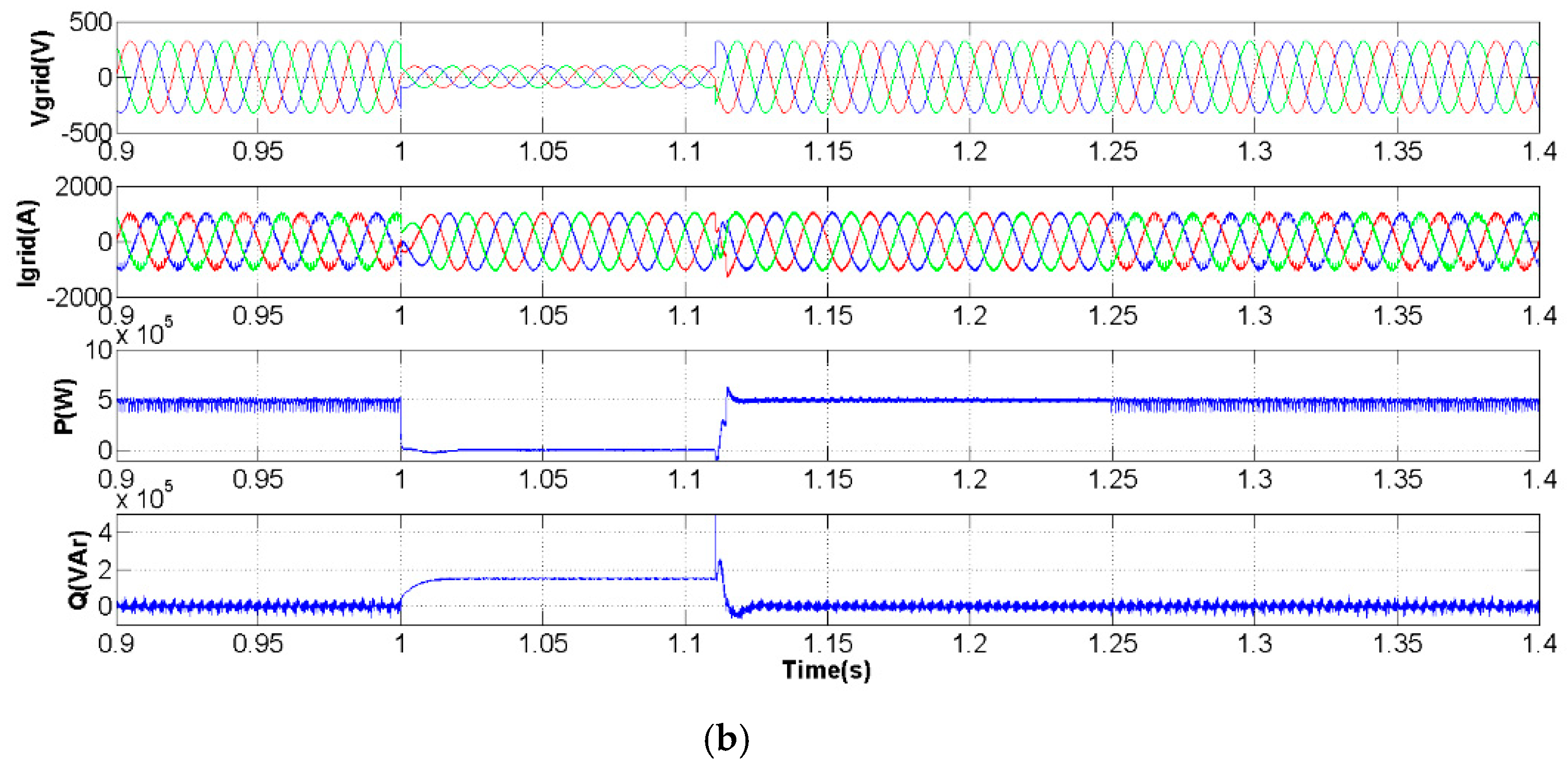
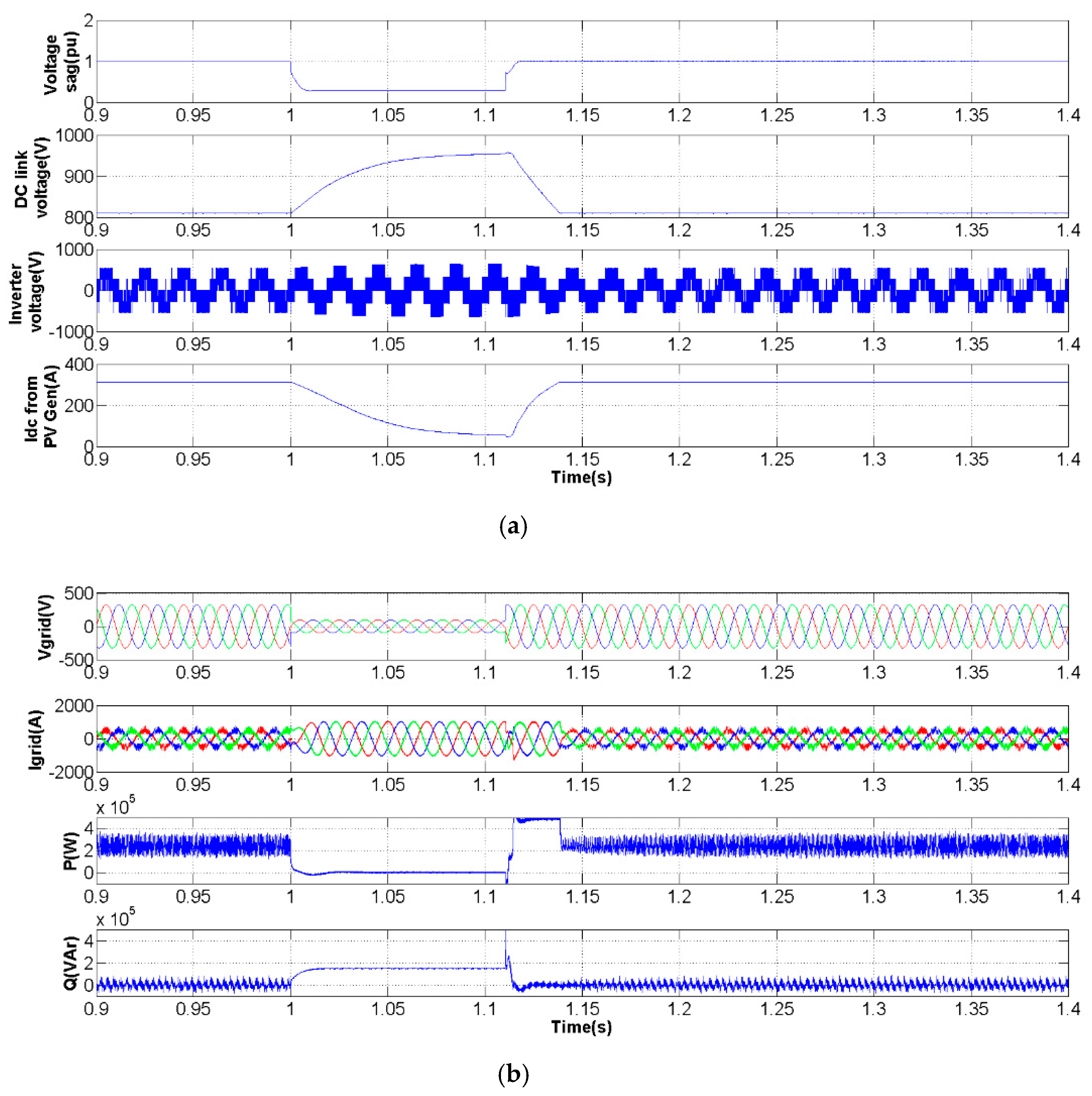
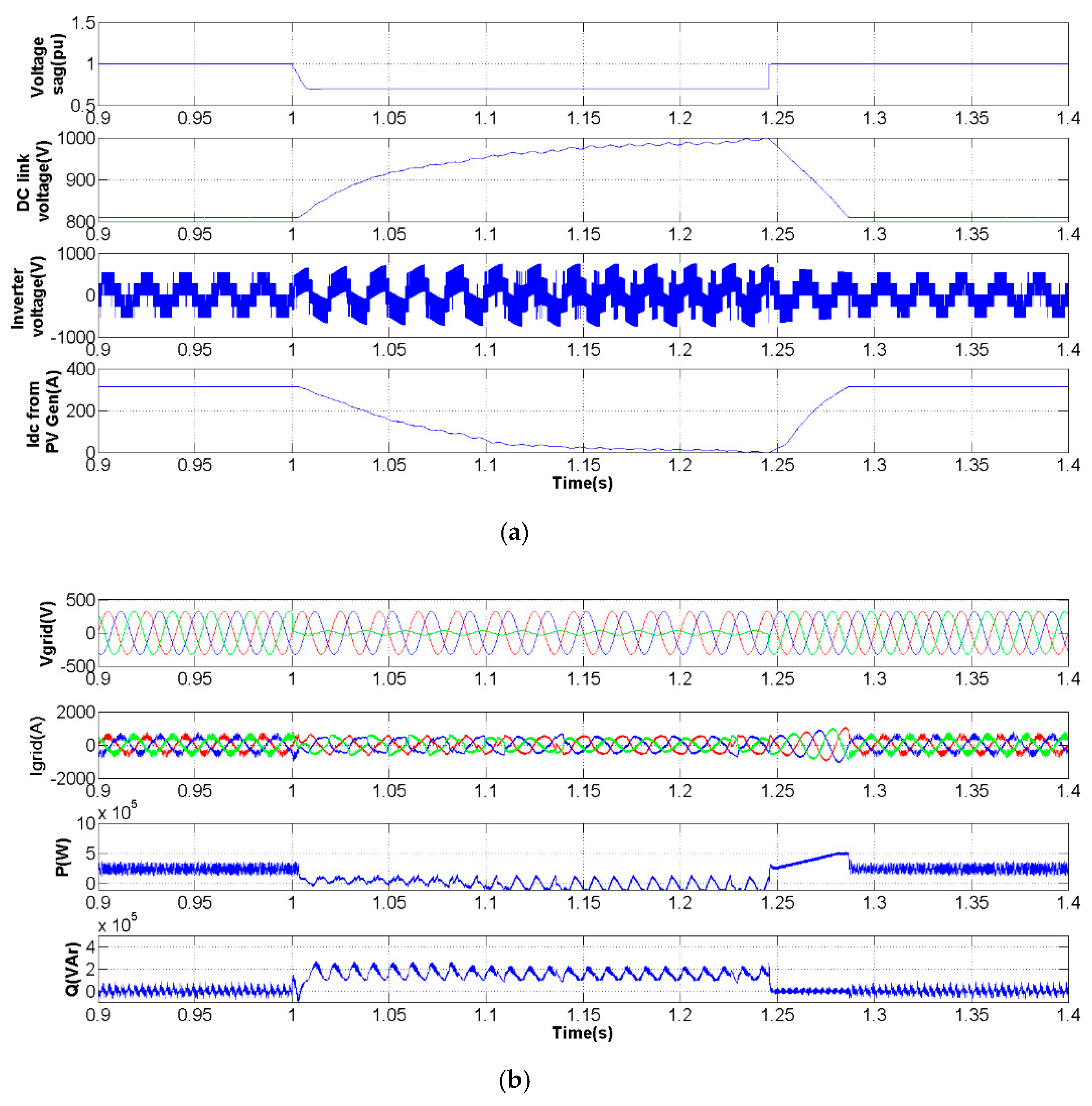
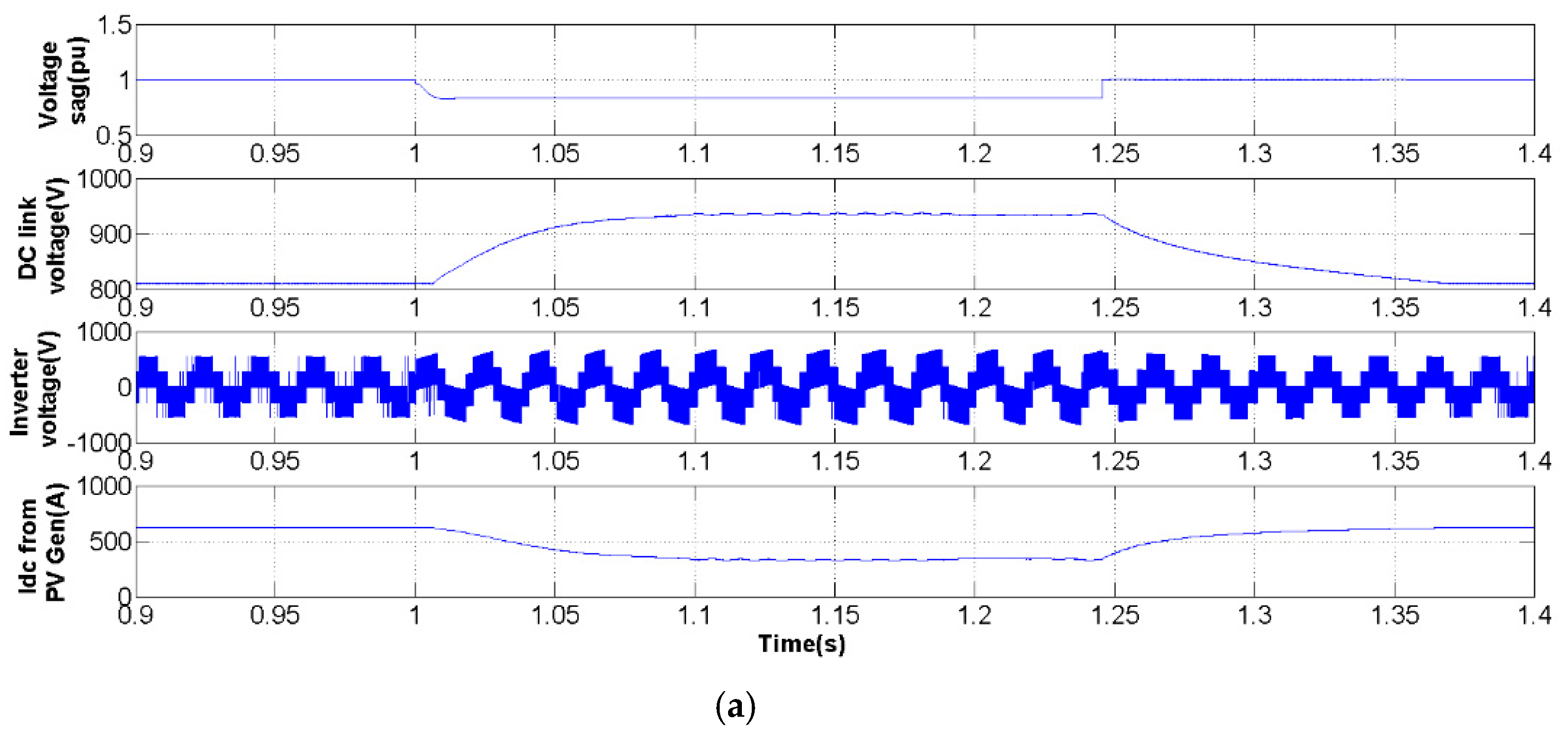
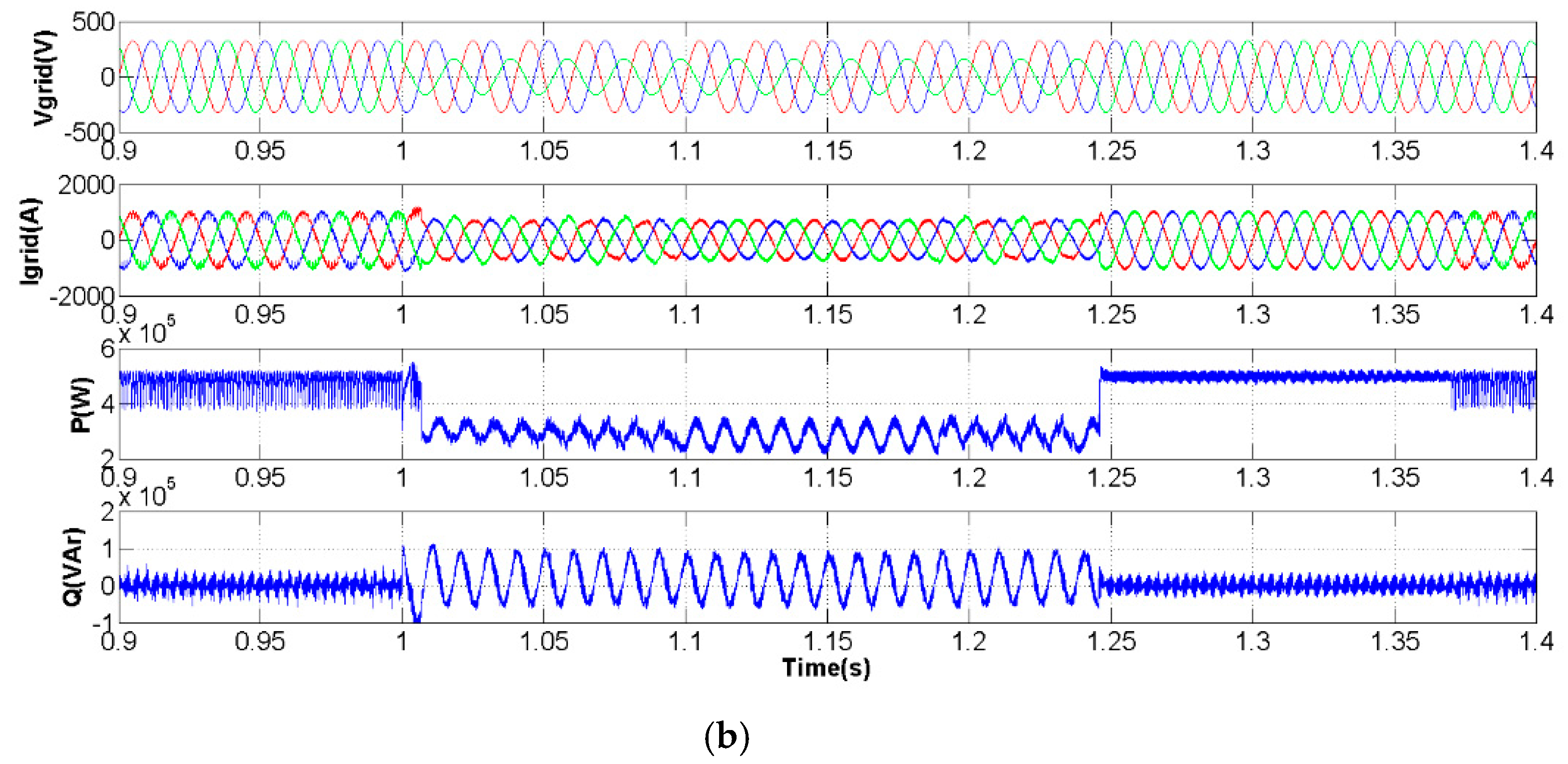
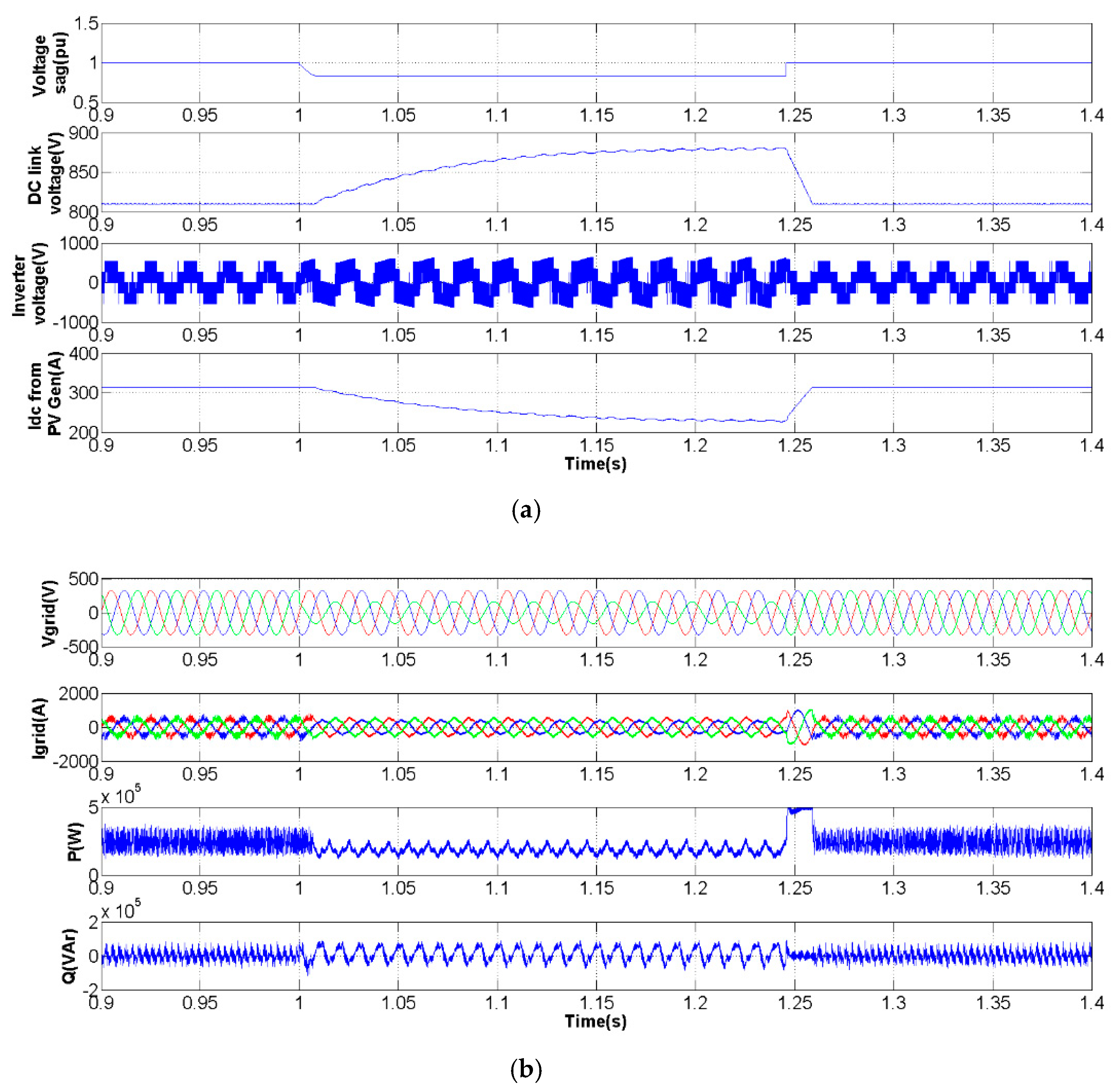
3. Simulation Studies
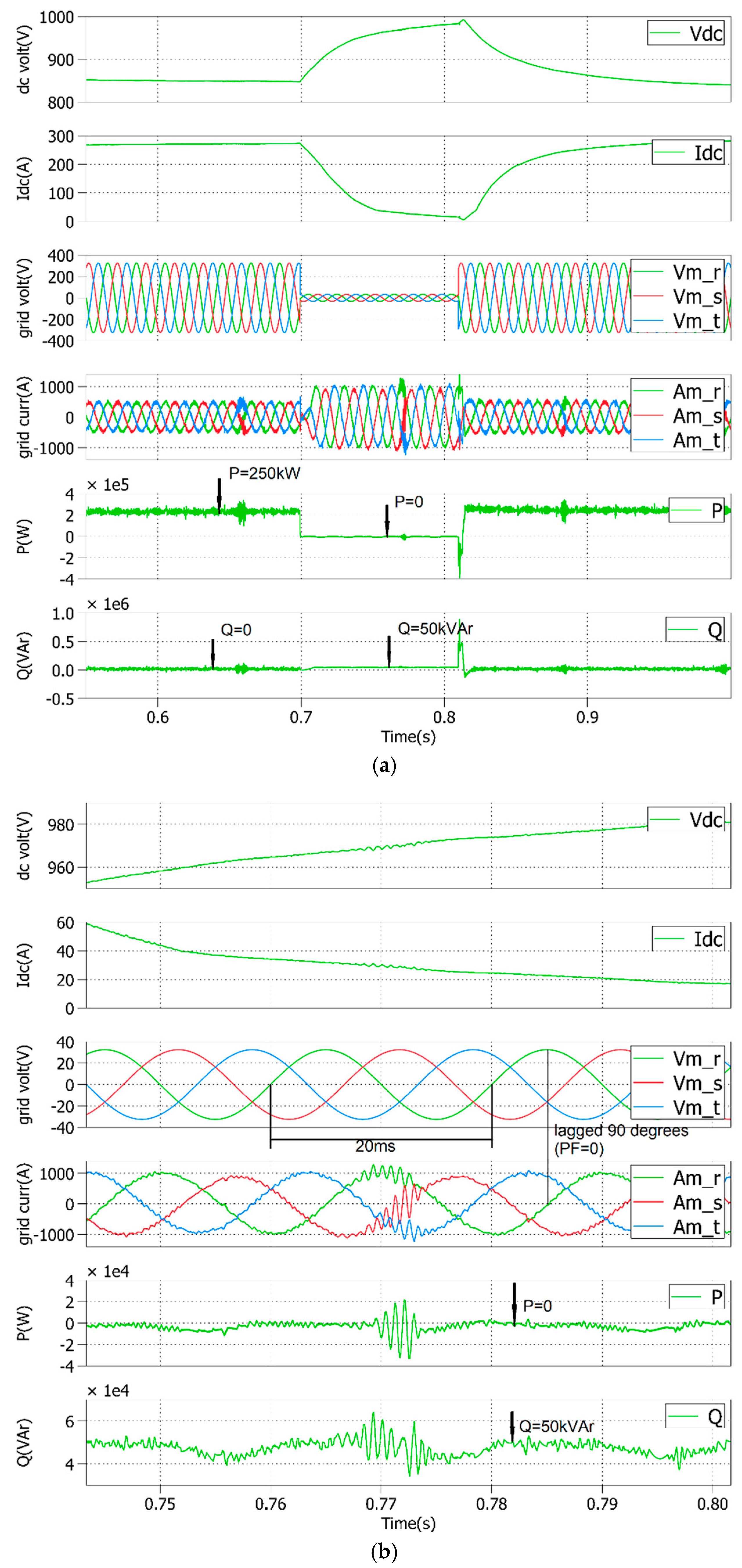
3.1. Three-Phase Voltage Sag
3.2. Voltage Sag in Phase 3
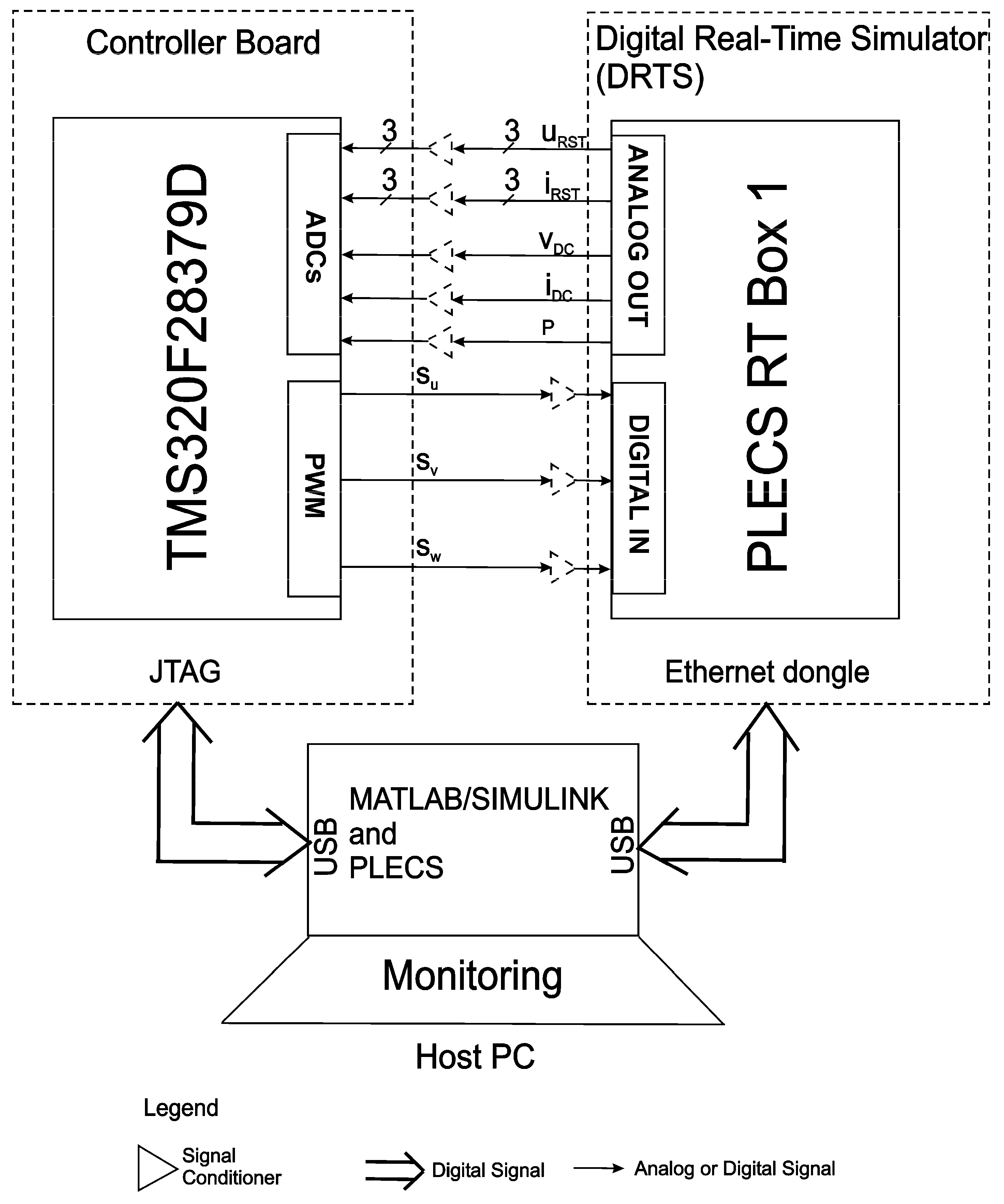
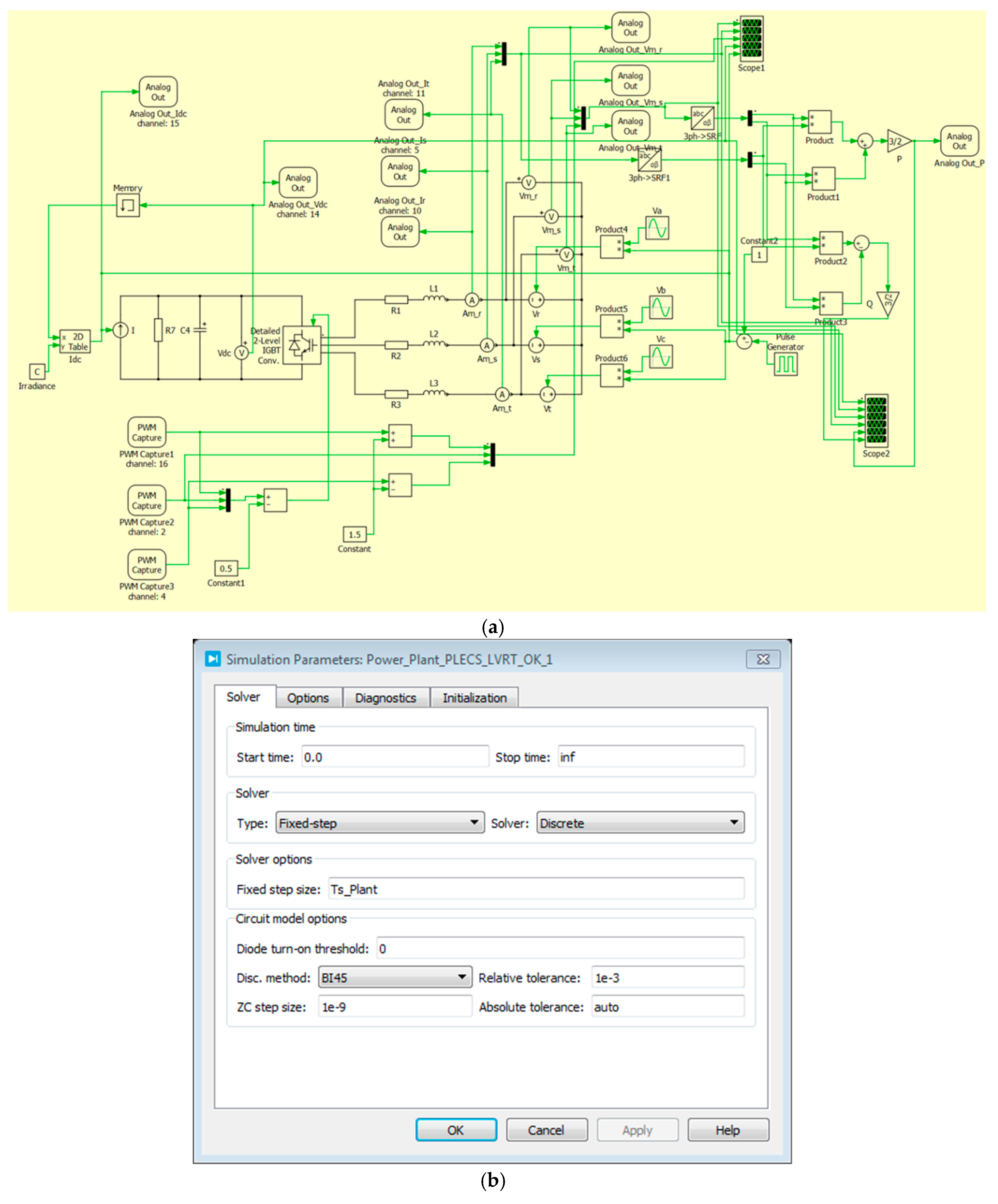
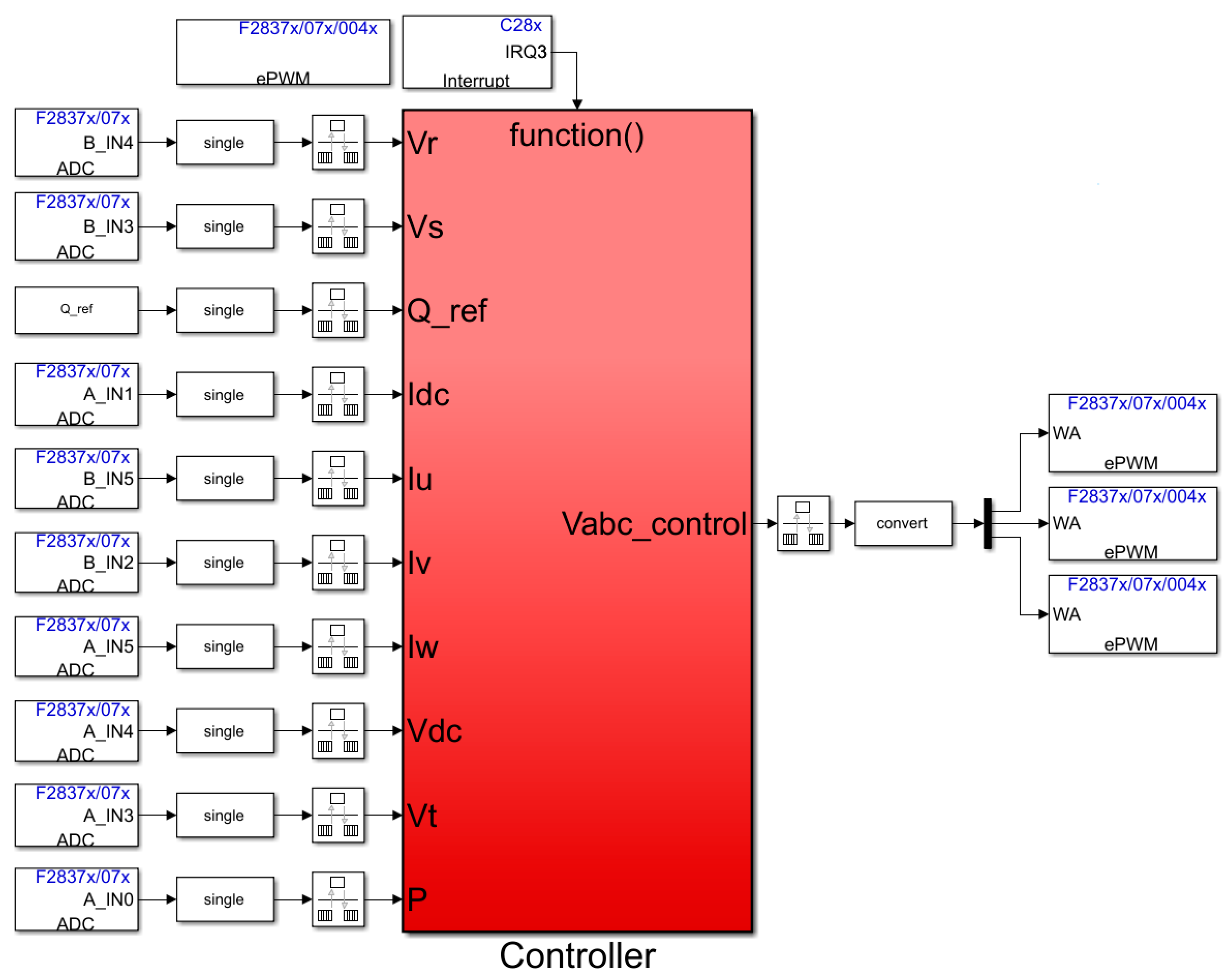
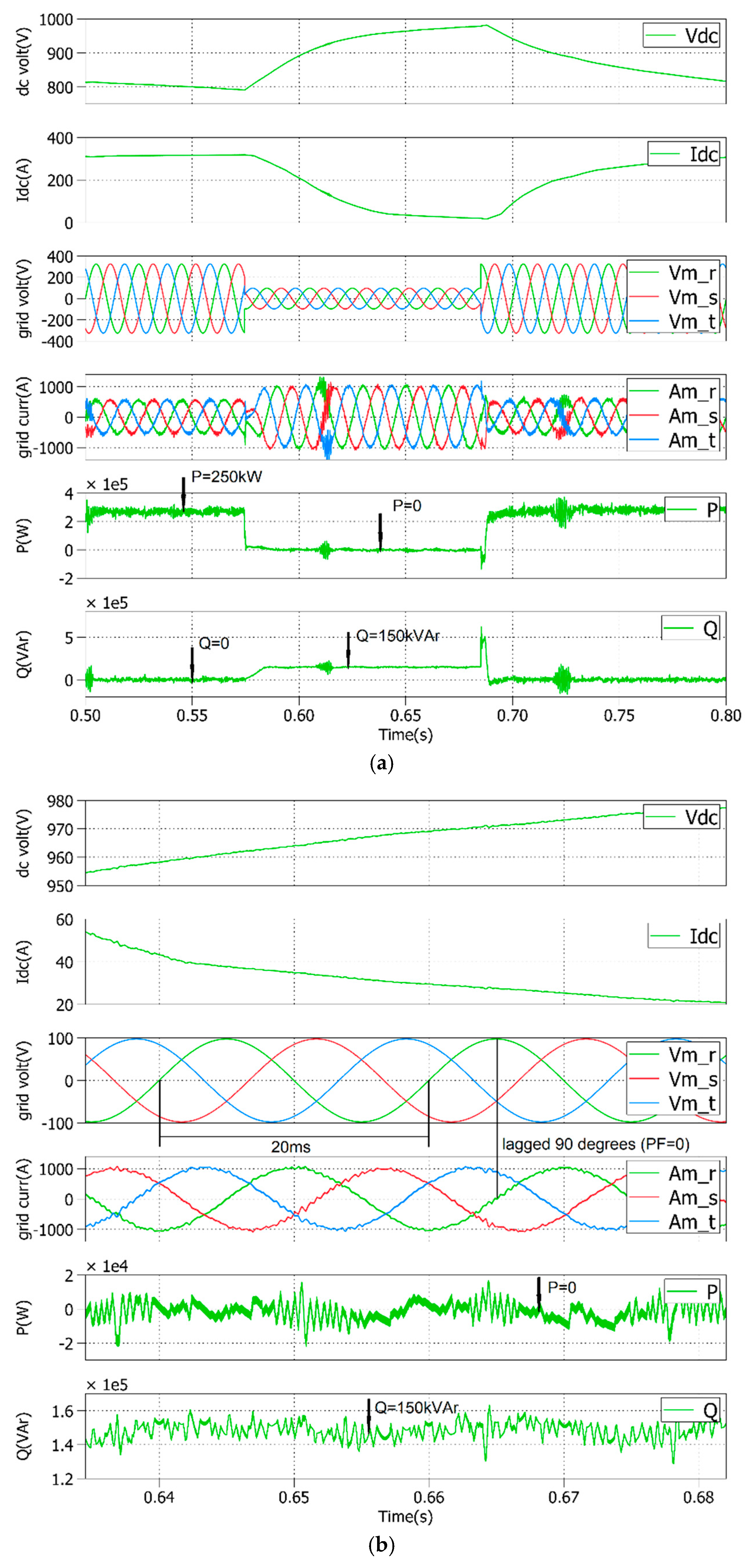
4. Experiments
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Habib, A.; Sou, C.; Hafeez, H.M.; Arshad, A. Evaluation of the effect of high penetration of renewable energy sources (RES) on system frequency regulation using stochastic risk assessment technique (an approach based on improved cumulant). Renew. Energy 2018, 127, 204–212. [Google Scholar] [CrossRef]
- Al-Shetwi, A.Q.; Sujod, M.Z. Modeling and Control of Grid-Connected Photovoltaic Power Plant With Fault Ride-Through Capability. J. Sol. Energy Eng. 2017, 140, 021001. [Google Scholar] [CrossRef]
- Etxegarai, A.; Eguia, P.; Torres, E.; Buigues, G.; Iturregi, A. Current procedures and practices on grid code compliance verification of renewable power generation. Renew. Sustain. Energy Rev. 2017, 71, 191–202. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Wojcik, J.D.; Wang, J.; Li, D.; Draganescu, M.; Li, Y.; Miao, S. Review of voltage and frequency grid code specifications for electrical energy storage applications. Energies 2018, 11, 1070. [Google Scholar] [CrossRef]
- Robles, E.; Haro-Larrode, M.; Santos-Mugica, M.; Etxegarai, A.; Tedeschi, E. Comparative analysis of European grid codes relevant to offshore renewable energy installations. Renew. Sustain. Energy Rev. 2019, 102, 171–185. [Google Scholar] [CrossRef]
- Dehghani, T.H.; Maswood, A.I.; Konstantinou, G.; Pou, J.; Kandasamy, K.; Lim, Z.; Ooi, G.H.P. Low-voltage ride-thorough capability of photovoltaic grid-connected neutral-point-clamped inverters with active/reactive power injection. IET Renew. Power Gener. 2017, 11, 1182–1190. [Google Scholar] [CrossRef]
- Oon, K.H.; Tan, C.K.; Bakar, A.H.A.; Che, H.S.; Mokhlis, H.; Illias, H.A. Establishment of fault current characteristics for solar photovoltaic generator considering low voltage ride through and reactive current injection requirement. Renew. Sustain. Energy Rev. 2018, 92, 478–488. [Google Scholar] [CrossRef]
- Rey-Boué, A.B.; Martinez-Rodrigo, F.; Guerrero-Rodríguez, N.F.; Lucas, H.L.C.; Pablo, S. Enhanced controller for grid-connected modular multilevel converters in distorted utility grids. Electr. Power Syst. Res. 2018, 163, 310–327. [Google Scholar] [CrossRef]
- Afshari, E.; Moradi, G.R.; Rahimi, R.; Farhangi, B.; Yang, Y.; Blaabjerg, F.; Farhangi, S. Control Strategy for Three-Phase Grid-Connected PV Inverters Enabling Current Limitation under Unbalanced Faults. IEEE Trans. Ind. Electron. 2017, 64, 8908–8918. [Google Scholar] [CrossRef]
- Marinopoulos, A.; Papandrea, F.; Reza, M.; Norrga, S.; Spertino, F.; Napoli, R. Grid integration aspects of large solar PV installations: LVRT capability and reactive power/voltage support requirements. In Proceedings of the 2011 IEEE PES Trondheim PowerTech Power Technol, Trondheim, Norway, 19–23 June 2011. [Google Scholar]
- Rodriguez, P.; Luna, A.; Ciobotaru, M.; Teodorescu, R.; Blaabjerg, F. Advanced Grid Synchronization System for Power Converters under Unbalanced and Distorted Operating Conditions. In Proceedings of the IECON 2006 32nd Annu, Paris, France, 6–10 November 2006. [Google Scholar]
- Jaalam, N.; Rahim, N.A.; Bakar, A.H.A.; Eid, B.M. Strategy to enhance the low-voltage ride-through in photovoltaic system during multi-mode transition. Sol. Energy 2017, 153, 744–754. [Google Scholar] [CrossRef]
- IEC 61400-21:2008 | IEC Webstore | rural electrification, wind power, (n.d.). Available online: https://webstore.iec.ch/publication/5434 (accessed on 14 January 2019).
- MathWorks Makers of MATLAB and Simulink MATLAB amp; Simulink, (n.d.). Available online: https://uk.mathworks.com/ (accessed on 14 January 2019).
- Kumar, R.; Bansal, H.O. Hardware in the loop implementation of wavelet based strategy in shunt active power filter to mitigate power quality issues. Electr. Power Syst. Res. 2019, 169, 92–104. [Google Scholar] [CrossRef]
- Lemaire, M.; Sicard, P.; Belanger, J. Prototyping and Testing Power Electronics Systems Using Controller Hardware-In-the-Loop (HIL) and Power Hardware-In-the-Loop (PHIL) Simulations. In Proceedings of the 2015 IEEE Veh, Montreal, QC, Canada, 19–22 October 2015. [Google Scholar]
- Mo, R.; Steurer, M.; Li, H. Controller hardware-in-the-loop (CHIL) simulation of a multi-functional energy storage system based on modular multilevel DC/DC converter (M2DC) for MVDC grid. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference, Hefei, China, 22–26 May 2016. [Google Scholar]
- PARK, R.H. Two-Reaction Theory of Synchronous Machines: Generalized Method of Analysis-Part I. Trans. Am. Inst. Electr. Eng. 1929, 48, 716–727. [Google Scholar] [CrossRef]
- Liang, J.; Gomis-Bellmunt, O.; Ekanayake, J.; Jenkins, N.; An, W. A multi-terminal HVDC transmission system for offshore wind farms with induction generators. Int. J. Electr. Power Energy Syst. 2012, 43, 54–62. [Google Scholar] [CrossRef]
- Arruda, L.N.; Silva, S.M.; Filho, B.J.C. PLL structures for utility connected systems. In Proceedings of the IECON 2006 32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006. [Google Scholar]
- Rodriguez, P.; Timbus, A.V.; Teodorescu, R.; Liserre, M.; Blaabjerg, F. Flexible active power control of distributed power generation systems during grid faults. IEEE Trans. Ind. Electron. 2007, 54, 2583–2592. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, P.; Yin, X.; Ma, Y. Evaluation of low-voltage ride-through capability of a two-stage grid-connected three-level photovoltaic inverter. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems, Hangzhou, China, 22–25 Octumeber 2014. [Google Scholar]
- Ishaque, K.; Salam, Z. A review of maximum power point tracking techniques of PV system for uniform insolation and partial shading condition. Renew. Sustain. Energy Rev. 2013, 19, 475–488. [Google Scholar] [CrossRef]
- Sybille, G. IREQ’s innovations in power system simulation. Eur. J. Electr. Eng. 2011. [Google Scholar] [CrossRef]
- EMTP Transients, Stability Load-flow in the same software, (n.d.). Available online: https://www.emtp-software.com/ (accessed on 17 July 2019).
- Hydro-Québec. SimPowerSystem, Mathworks User´s Guide; MathWorks Inc.: Natick, MA, USA, 2012. [Google Scholar]
- Chiacchio, F.; Famoso, F.; D´Urso, D. Dynamic performance evaluation of photovoltaic power plant by stochastic hybrid fault tree automaton model. Energies 2018. [Google Scholar] [CrossRef]
- Madeti, S.R.; Singh, S.N. Modeling of PV system based on experimental data for fault detection using kNN method. Sol. Energy 2018, 173, 139–151. [Google Scholar] [CrossRef]
- Al-Shetwi, A.Q.; Sujod, M.Z.; Blaabjerg, F. Low voltage ride-through capability control for single-stage inverter-based grid-connected photovoltaic power plant. Sol. Energy 2018, 159, 665–681. [Google Scholar] [CrossRef]
- Roberts, J.J.; Zevallos, M.A.A.; Cassula, A.M. Assessment of photovoltaic performance models for system simulation. Renew. Sustain. Energy Rev. 2017, 72, 1104–1123. [Google Scholar] [CrossRef]
- Al-Shetwi, A.Q. International journal of renewable energy research IJRER. Technol. Dep. Electr. Electron. Eng. 2016. Available online: http://www.ijrer.org/ijrer/index.php/ijrer/article/view/3212 (accessed on 14 January 2019).
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive approach to modeling and simulation of photovoltaic arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Suntech, (n.d.). Available online: http://www.suntech-power.com/ (accessed on 14 January 2019).
- Rey-Boué, A.B.; García-Valverde, R.; Ruz-Vila, F.A.; Torrelo-Ponce, J.M. An integrative approach to the design methodology for 3-phase power conditioners in Photovoltaic Grid-Connected systems. Energy Convers. Manag. 2012, 56, 80–95. [Google Scholar] [CrossRef]
- Buso, S.; Mattavelli, P. Digital Control in Power Electronics; Morgan Claypool Publishers: San Rafael, CA, USA, 2006. [Google Scholar]
- Freijedo, F.D.; Doval-Gandoy, J.; Lopez, O.; Acha, E. Tuning of Phase-Locked Loops for Power Converters Under Distorted Utility Conditions. IEEE Trans. Ind. Appl. 2009, 45, 2039–2047. [Google Scholar] [CrossRef]
- Timbus, A.; Liserre, M.; Teodorescu, R.; Blaabjerg, F. Synchronization Methods for Three Phase Distributed Power Generation Systems. An Overview and Evaluation. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 16 June 2005. [Google Scholar]
- Faruque, M.D.; Strasser, T.; Lauss, G.; Jalili-Marandi, V.; Forsyth, P.; Dufour, C.; Dinavahi, V.; Monti, A.; Kotsampopoulos, P.; Martinez, J.A.; et al. Real-Time Simulation Technologies for Power Systems Design, Testing, and Analysis. IEEE Power Energy Technol. Syst. J. 2015, 2, 63–73. [Google Scholar] [CrossRef]
- Jonke, P.; Stockl, J.; Miletic, Z.; Brundlinger, R.; Seitl, C.; Andren, F.; Lauss, G.; Strasser, T. Integrated rapid prototyping of distributed energy resources in a real-time validation environment. In Proceedings of the 2016 IEEE 25th International Symposium on Industrial Electronics (ISIE), Santa Clara, CA, USA, 8–10 June 2016. [Google Scholar]
- Electrical Engineering Software | Plexim, (n.d.). Available online: https://www.plexim.com/ (accessed on 14 January 2019).
- Analog, Embedded Processing, Semiconductor Company, Texas Instruments - TI.com, (n.d.). Available online: http://www.ti.com/ (accessed on 14 January 2019).
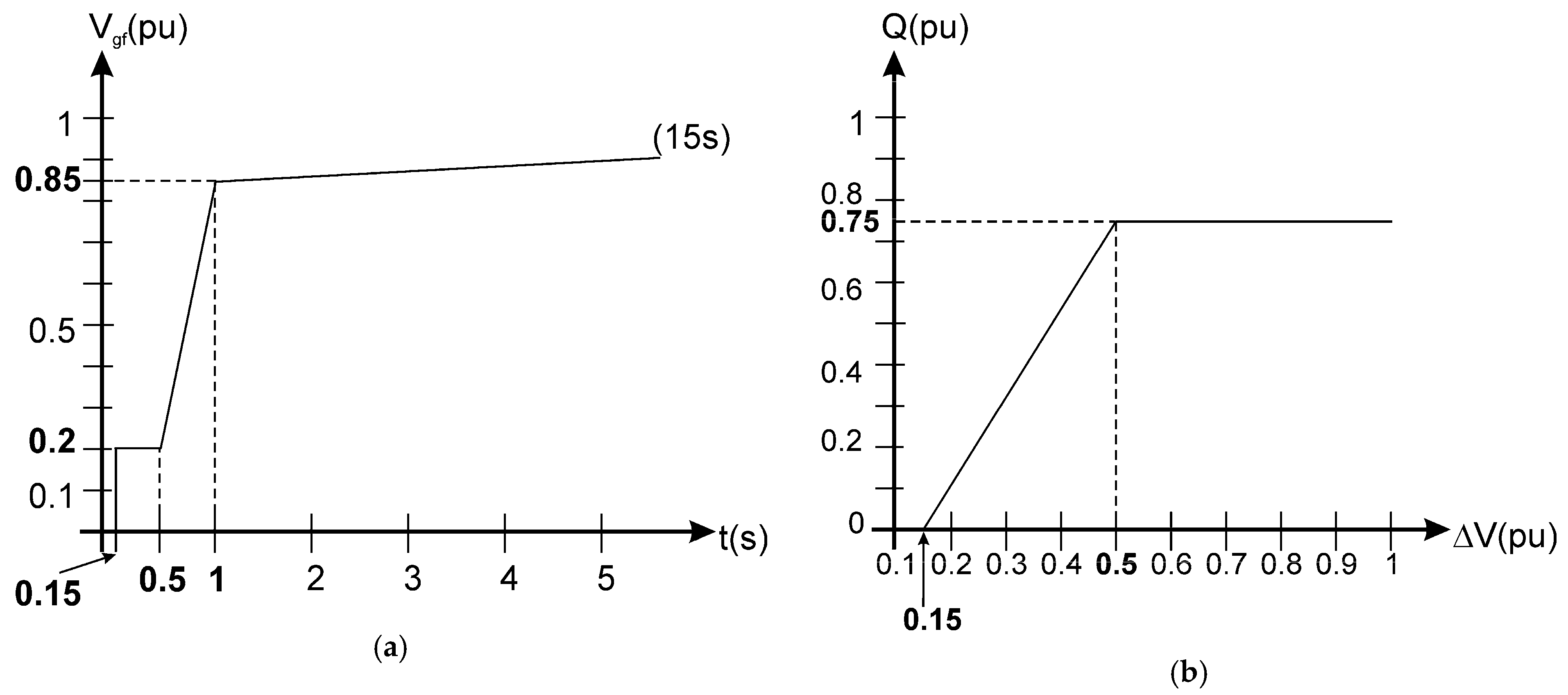


| Parameters | Value |
|---|---|
| Maximum power | Pmp = 320.024 W |
| Maximum power voltage | Vmp = 36.7 V |
| Maximum power current | Imp = 8.72 A |
| Open circuit voltage | Voc = 45.6 V |
| Short circuit current | Isc = 9.07 A |
| Cell number per module | Ncell = 72 |
| Temperature coefficient of Isc | αi = 0.0867%/°C |
| Temperature coefficient of Voc | αv = −0.4278%/°C |
| Parallel resistance | Rp = 4.24074 Ω |
| Series resistance | Rs = 0.3437 Ω |
| Ideally factor of the diode | m = 1.1238 |
| Parameters | Value |
|---|---|
| Number of the strings | Npvst = 72 |
| Number of the series modules | Npvs = 22 |
| Maximum current | Impv = Npvst × Imp = 627.84 A |
| Maximum voltage | Vmpv = Npvs × Vmp = 807.4 V |
| DC output power | Pdc = Vmpv × Impv = 506.91 kW |
| Open circuit voltage | VPV-oc = Npvs × Voc = 1003.2 V |
| Short circuit current | IPV-sc = Npvst × Isc = 653.04 A |
| Maximum DC link voltage (VDC) | 807.4 V |
| Maximum DC current (IDC) | 627.84 A |
| Link Capacitor (Clink) | 65,000 μF |
| Converter Gain (KPWM) | |
| Switching frequency (FPWM) | 24.416 kHz |
| Line Inductance (L) | 0.15 mH |
| AC system (vRST) | - Voltage amplitude: 230 V(rms) phase-to-neutral |
| - Nominal frequency: 50 Hz |
| Crossover frequency of the open current loop (fcI) | 610.4 Hz |
| Phase Margin of the open current loop (PMI) | 63.5° |
| Proportional constant of the current regulators in dq axes (kp,Idq) | 0.0011 |
| Integral constant of the current regulators in dq axes (ki,Idq) | 0.942 |
| Crossover frequency of the open voltage loop (fcV) | 12.208 Hz |
| Phase Margin of the open voltage loop (PMV) | 63.5° |
| Proportional constant of the PI voltage regulator (kp,VDC) | 3977.5 |
| Integral constant of the PI voltage regulator (ki,VDC) | 152,110 |
| Settling time of the PLL (Tset) | 20 ms |
| Damping factor of the PLL (ζ) | |
| Proportional constant of the PI PLL regulator (kp,PLL) | |
| Integral constant of the PI PLL regulator (ki,PLL) | 325.2691 |
| Sample time of the power subsystem (TS) | 5.1196 μs |
| Sample time of the control subsystem (Treg) | 40.957 μs |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rey-Boué, A.B.; Guerrero-Rodríguez, N.F.; Stöckl, J.; Strasser, T.I. Modeling and Design of the Vector Control for a Three-Phase Single-Stage Grid-Connected PV System with LVRT Capability according to the Spanish Grid Code. Energies 2019, 12, 2899. https://doi.org/10.3390/en12152899
Rey-Boué AB, Guerrero-Rodríguez NF, Stöckl J, Strasser TI. Modeling and Design of the Vector Control for a Three-Phase Single-Stage Grid-Connected PV System with LVRT Capability according to the Spanish Grid Code. Energies. 2019; 12(15):2899. https://doi.org/10.3390/en12152899
Chicago/Turabian StyleRey-Boué, Alexis B., N. F. Guerrero-Rodríguez, Johannes Stöckl, and Thomas I. Strasser. 2019. "Modeling and Design of the Vector Control for a Three-Phase Single-Stage Grid-Connected PV System with LVRT Capability according to the Spanish Grid Code" Energies 12, no. 15: 2899. https://doi.org/10.3390/en12152899
APA StyleRey-Boué, A. B., Guerrero-Rodríguez, N. F., Stöckl, J., & Strasser, T. I. (2019). Modeling and Design of the Vector Control for a Three-Phase Single-Stage Grid-Connected PV System with LVRT Capability according to the Spanish Grid Code. Energies, 12(15), 2899. https://doi.org/10.3390/en12152899








