Maximum Power Point Tracker Based on Fuzzy Adaptive Radial Basis Function Neural Network for PV-System
Abstract
1. Introduction
2. Description of the PV System
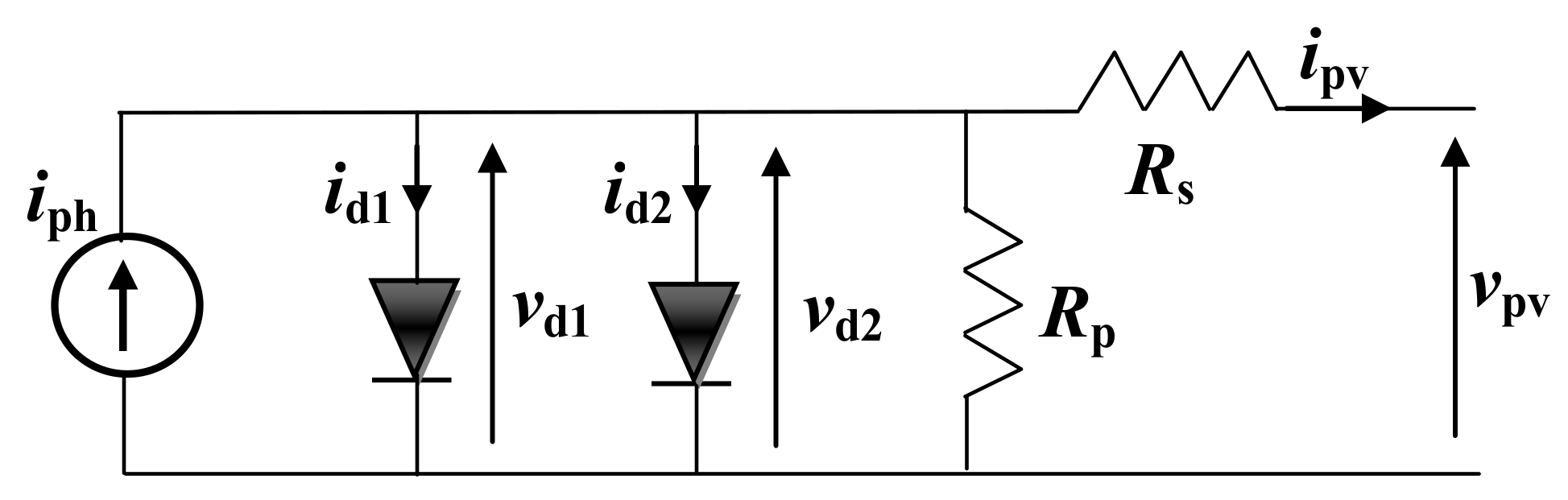
2.1. Modeling of the PV-Module
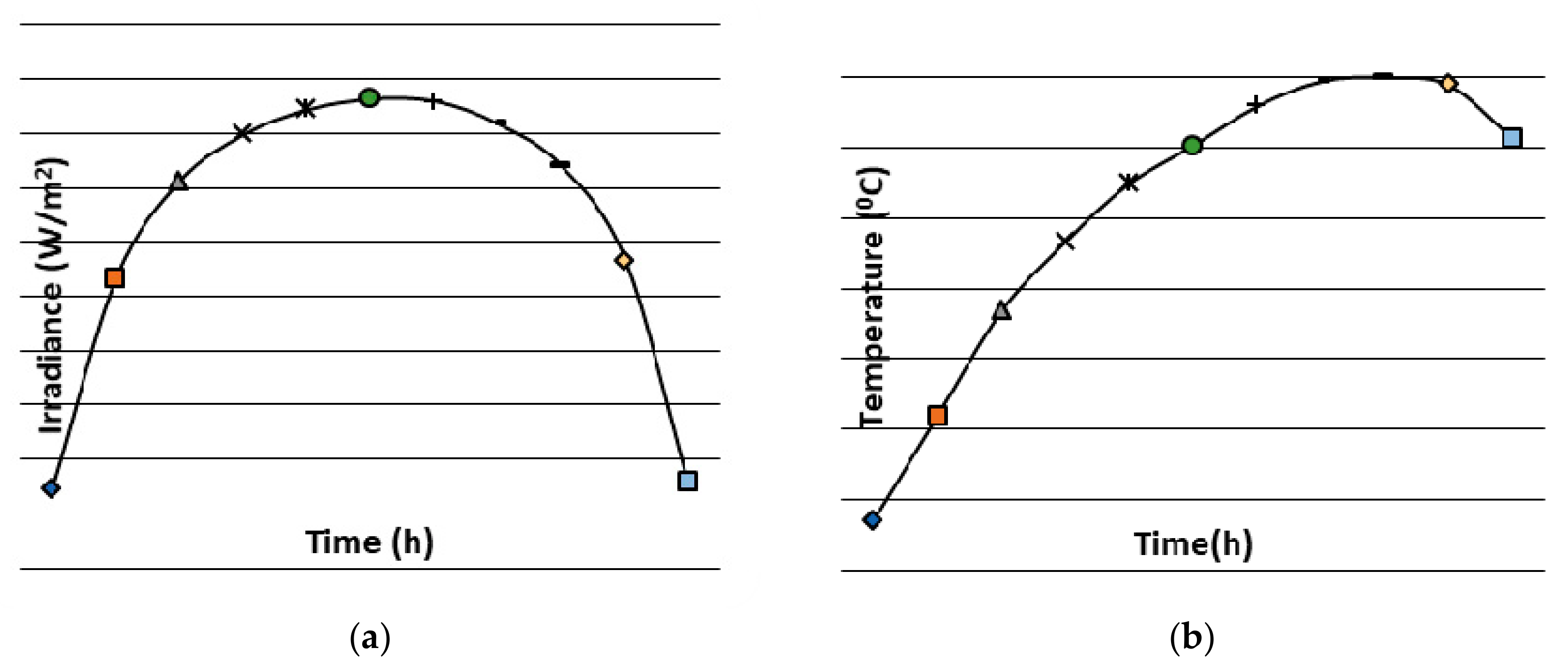
- iph = S·iph-max: Photo-generated current (A) (where S is the irradiance)
- is1, is2: diode saturation currents (A)
- n1, n2: ideality factors of the diodes
- Ns: number of cells connected in series
- k: constant of Boltzmann (1.3806503 × 10−23 J/K)
- T: temperature (K)
- q: charge of electron (1.60217646 ×10−19 C)
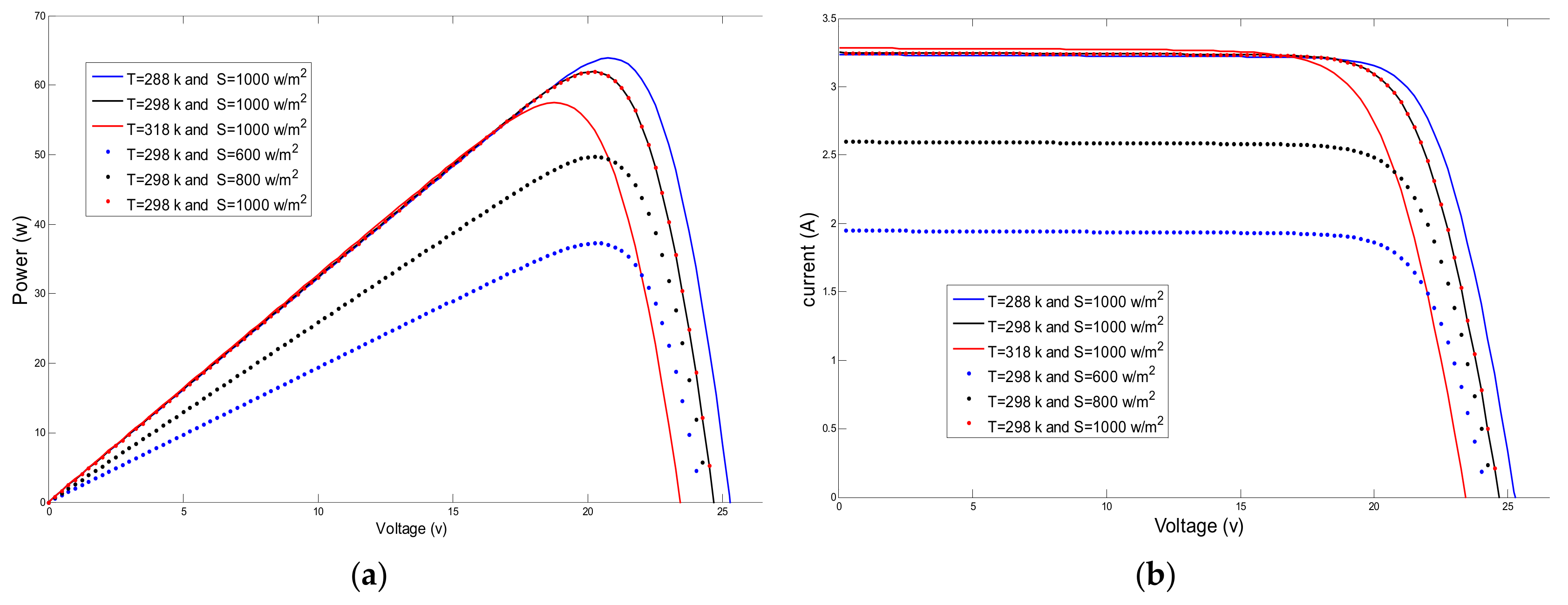
- -
- The maximum power of the PV-module is almost proportional to the irradiance S.
- -
- The maximum power point results from irradiance variation are located in a reduced voltage range.
- -
- Temperature changes produce substantial variations in the maximum voltage while the maximum current remains constant.
2.2. DC-DC Boost Converter
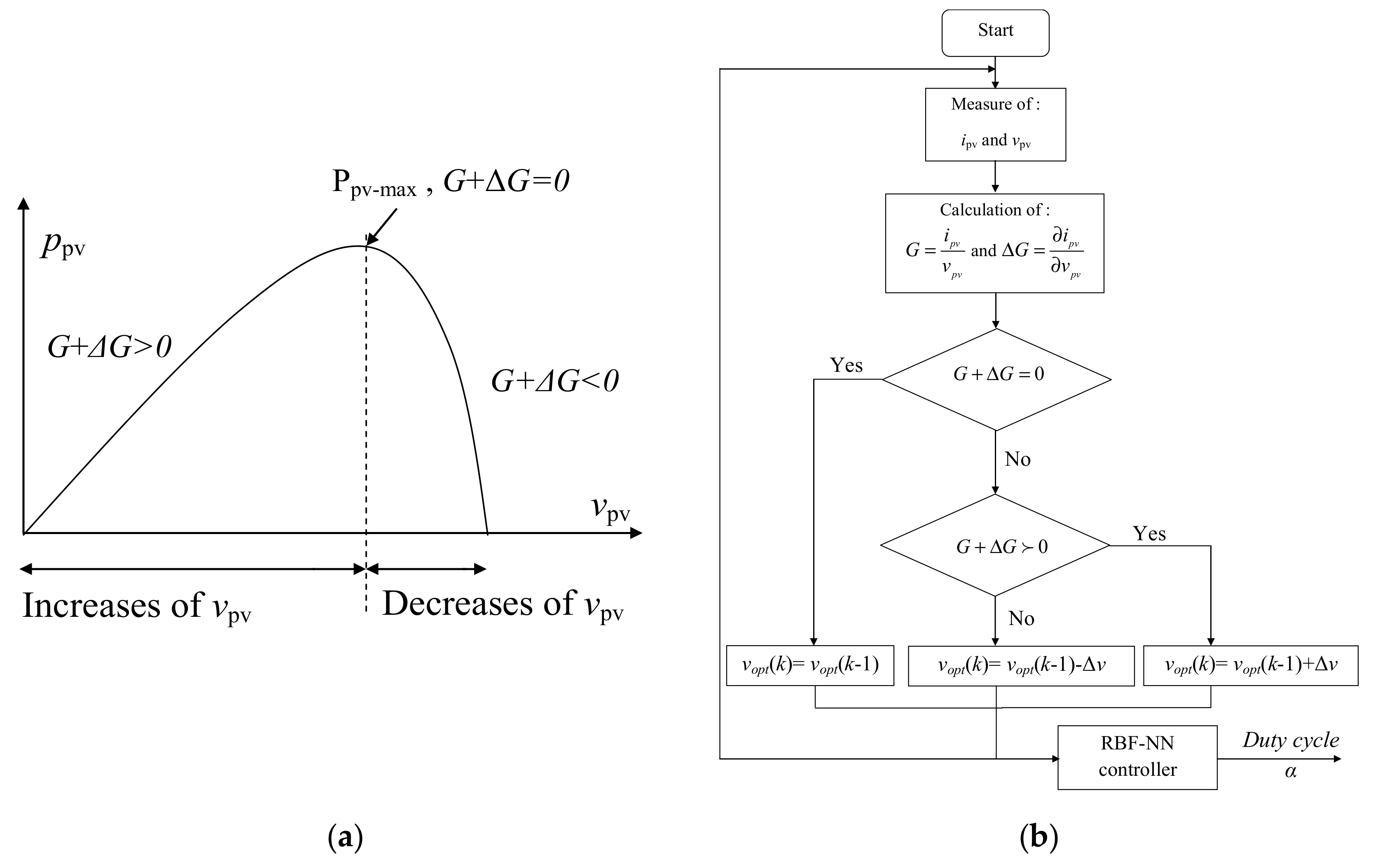
2.3. Principle of the MPP Tracker
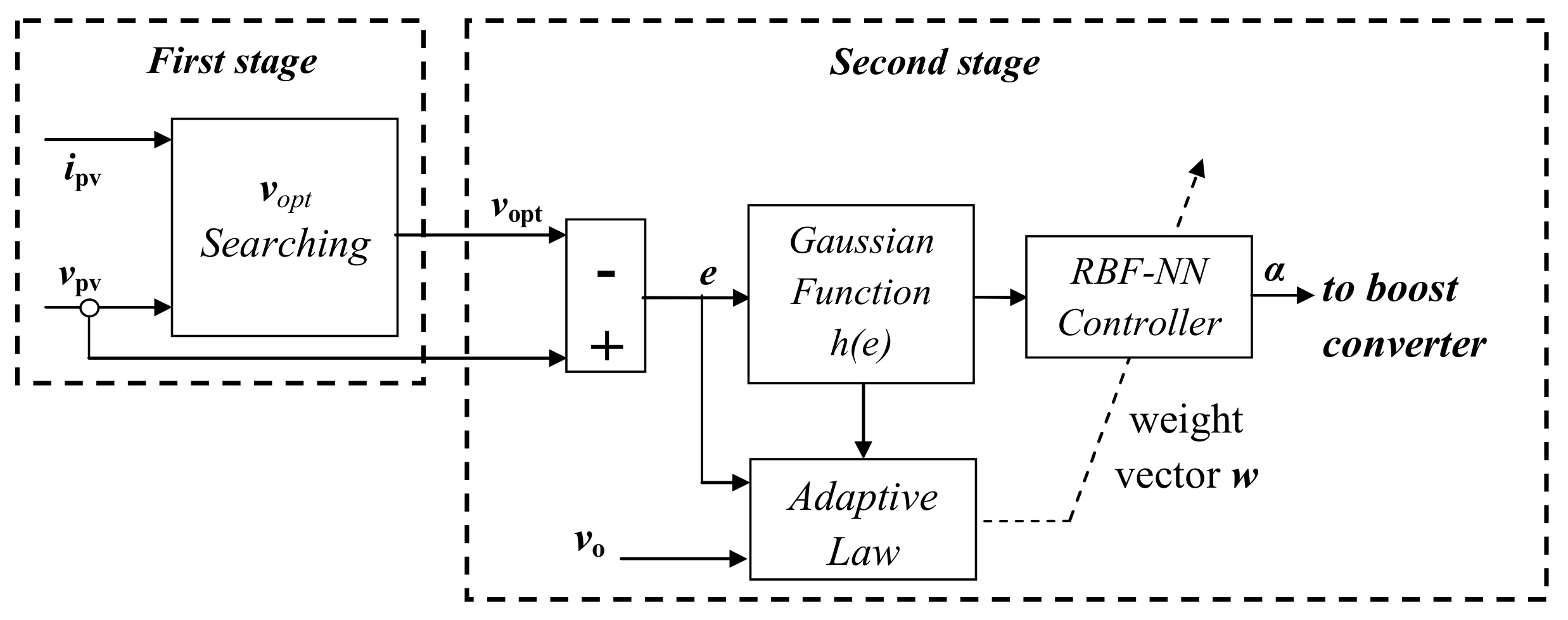
3. MPPT Based INC-Adaptive RBF-NN
3.1. Optimal Voltage Searching (vopt)
3.2. Adaptive RBF-NN Controller
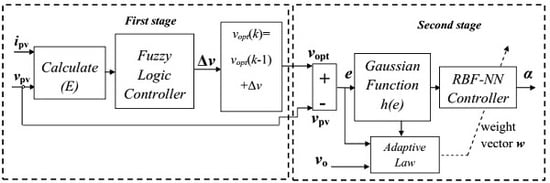
4. Proposed MPPT Based Fuzzy-Adaptive RBF-NN
- -
- The absolute error E less than 0.25, it is considered as “the vopt zone (ZE)”.
- -
- The error E less than 0.5, it is considered as “near to vopt (PS) in the left half-plane”.
- -
- The error E bigger than 0.5, it is considered as “far from vopt in the left half-plane”. In this case, the trapezoidal membership function is used to saturate on (PB).
- -
- The same procedure when E is in the negative part (right half-plane).
- -
- The output Δv is defined in the common normalized range of [−0.3, 0.3]; −0.3 and 0.3 volts are considered as the maximum negative value and maximum positive value that can perturb the PV-module voltage. It is worth noting that increasing the search range helps the fuzzy controller to track the optimal voltage. However, an excessively wide range can cause a loss of power.
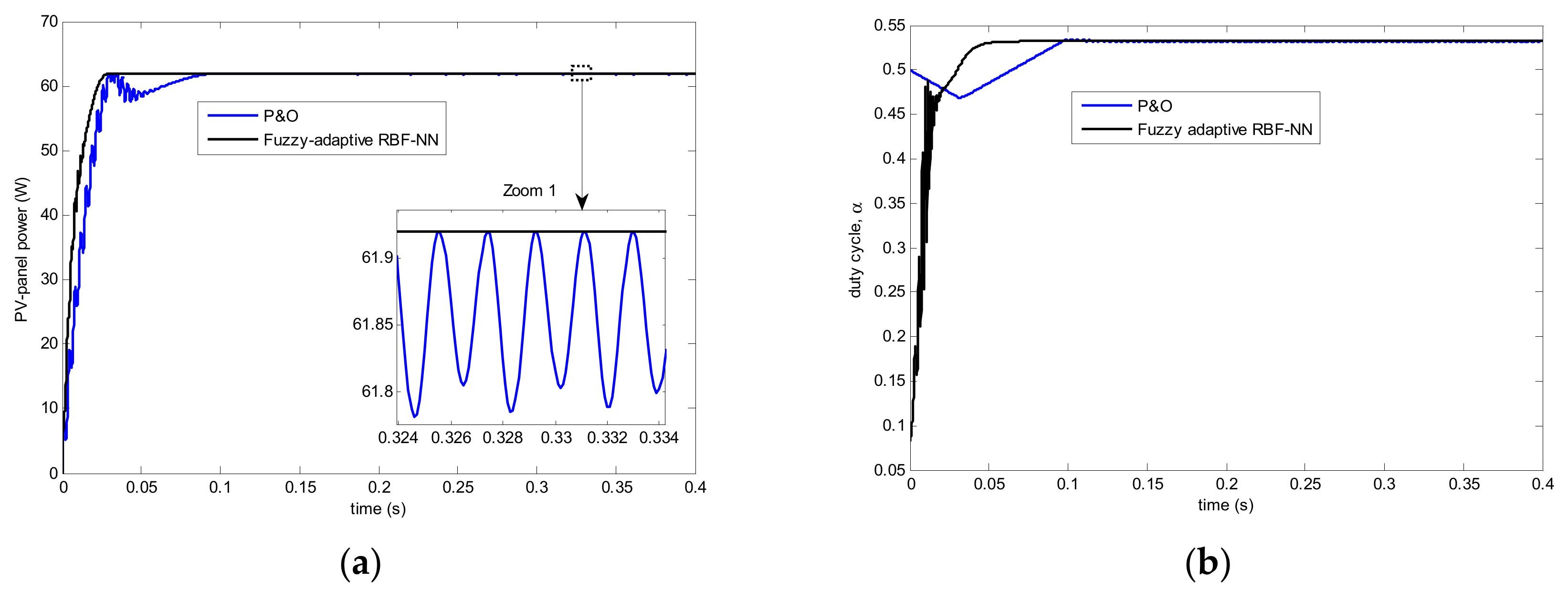
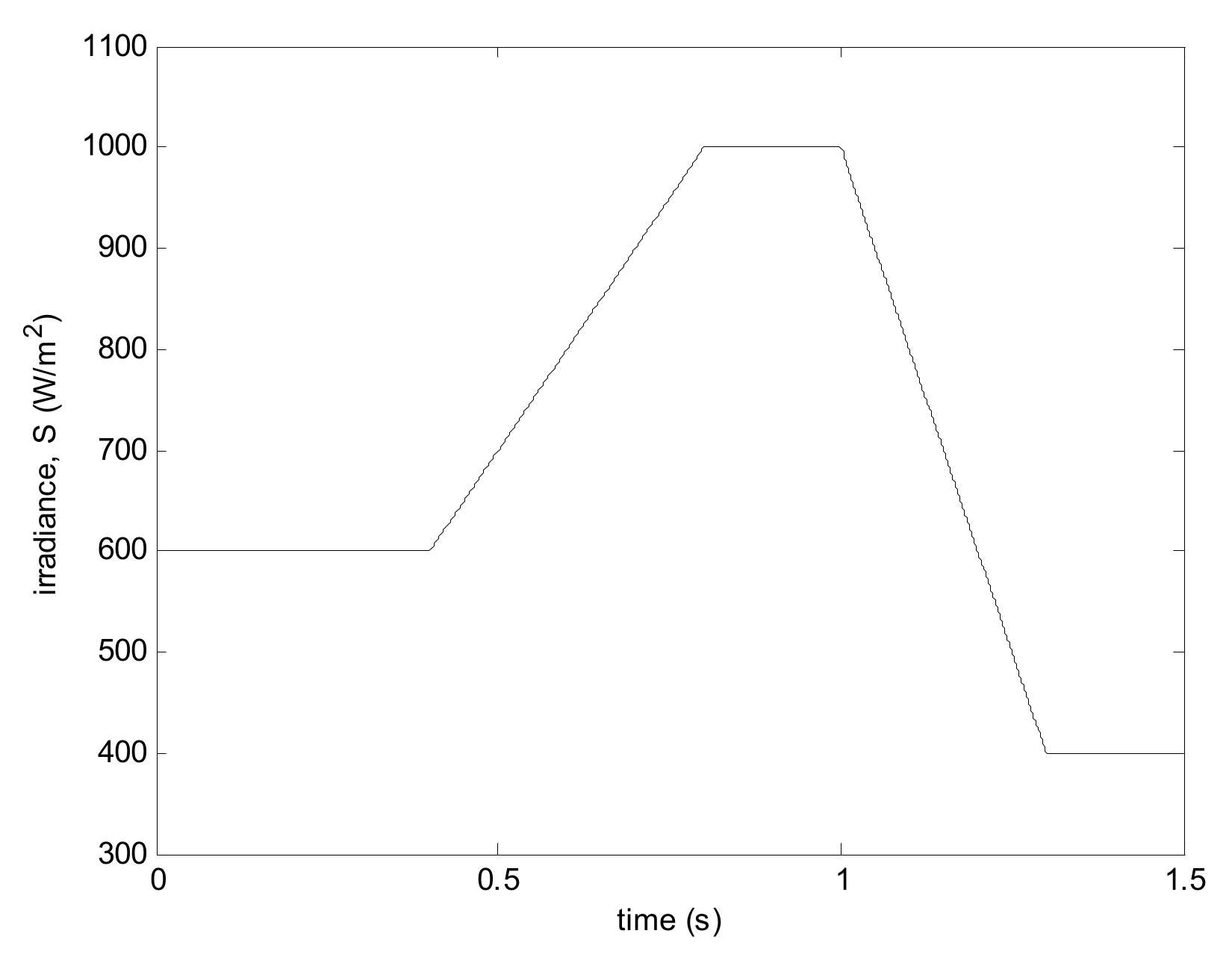
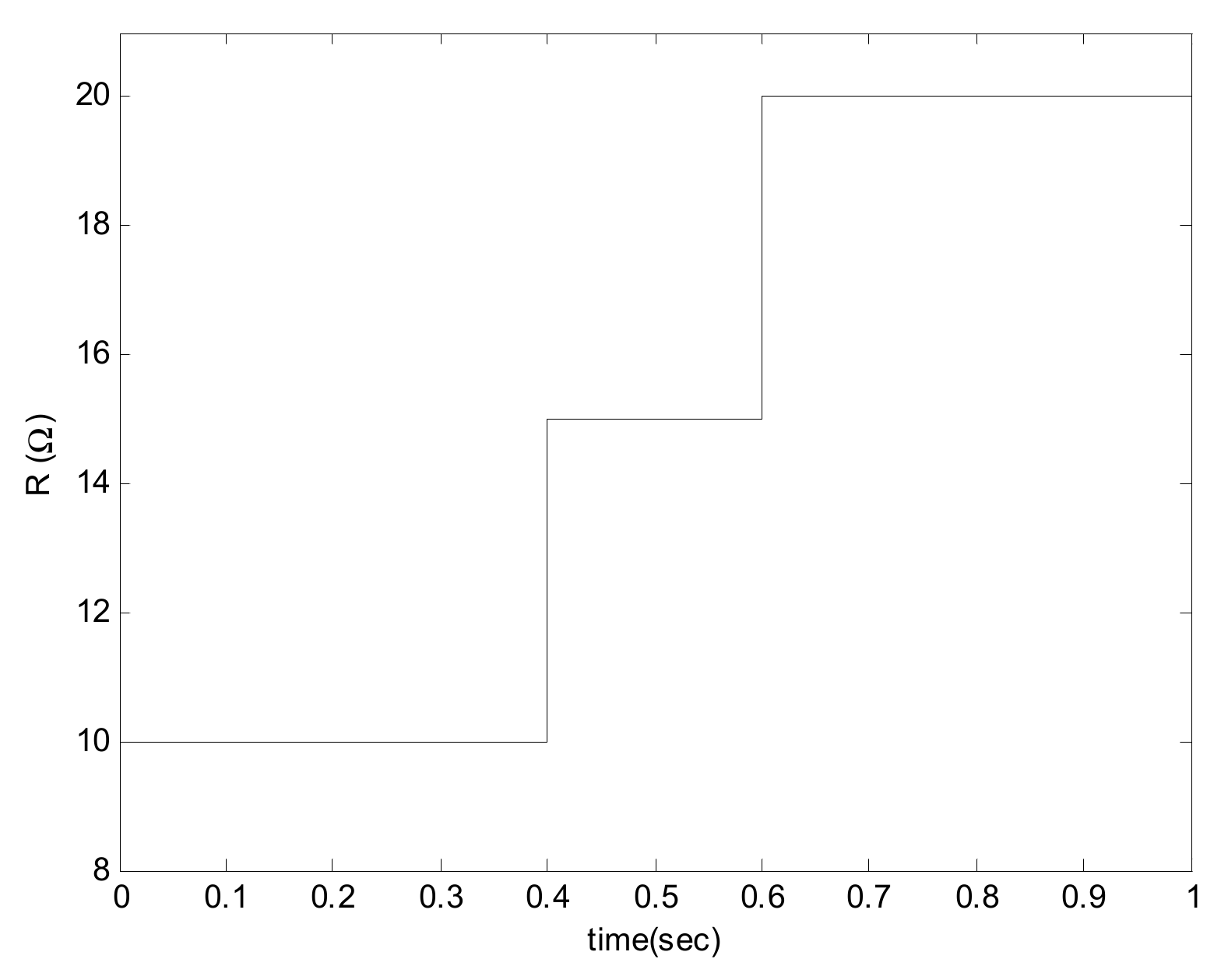
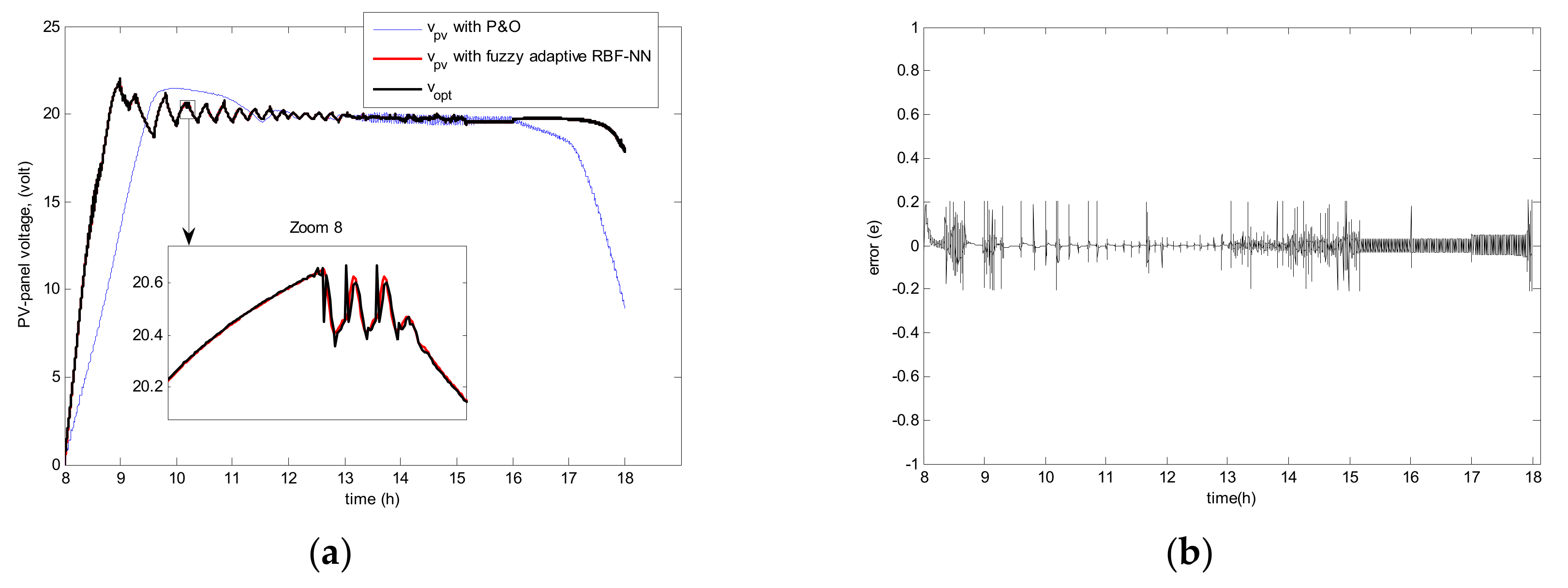
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, F.; Kang, Y.; Zhang, Y.; Duan, S. Comparison of P&O and hill climbing MPPT methods for grid-connected PV converter. In Proceedings of the 2008 3rd IEEE Conference on Industrial Electronics and Applications, Singapore, 3–5 June 2008; pp. 804–807. [Google Scholar]
- Yu, T.-C.; Lin, Y.-C. A study on maximum power point tracking algorithms for photovoltaic systems. Department of Electrical Engineering, Lunghwa University of Science and Technology (LHU) 2010, 30, 27–36. [Google Scholar]
- Hussein, K.; Muta, I.; Hoshino, T.; Osakada, M. Maximum photovoltaic power tracking: an algorithm for rapidly changing atmospheric conditions. IEE Proc.-Gener., Transm. Distrib. 1995, 142, 59–64. [Google Scholar] [CrossRef]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Optimization of perturb and observe maximum power point tracking method. IEEE Trans. Power electron. 2005, 20, 963–973. [Google Scholar] [CrossRef]
- Ilyas, A.; Ayyub, M.; Khan, M.R.; Husain, M.A.; Jain, A. Hardware Implementation of Perturb and Observe Maximum Power Point Tracking Algorithm for Solar Photovoltaic System. Trans. Electr. Electr. Mater. 2018, 19, 222–229. [Google Scholar] [CrossRef]
- Berrera, M.; Dolara, A.; Faranda, R.; Leva, S. Experimental test of seven widely-adopted MPPT algorithms. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–8. [Google Scholar]
- Ahmad, J. A fractional open circuit voltage based maximum power point tracker for photovoltaic arrays. In Proceedings of the 2nd International Conference on Software Technology and Engineering (ICSTE), San Juan, PR, USA, 3–5 October 2010; pp. 1–250. [Google Scholar]
- Noguchi, T.; Togashi, S.; Nakamoto, R. Short-current pulse-based maximum-power-point tracking method for multiple photovoltaic-and-converter module system. IEEE Trans. Ind. Electr. 2002, 49, 217–223. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Lauss, G. The performance of perturb and observe and incremental conductance maximum power point tracking method under dynamic weather conditions. Appl. Energy 2014, 119, 228–236. [Google Scholar] [CrossRef]
- Pandey, A.; Dasgupta, N.; Mukerjee, A.K. Design issues in implementing MPPT for improved tracking and dynamic performance. In Proceedings of the IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 4387–4391. [Google Scholar]
- Liu, F.; Duan, S.; Liu, F.; Liu, B.; Kang, Y. A variable step size INC MPPT method for PV systems. IEEE Trans. Ind. Electr. 2008, 55, 2622–2628. [Google Scholar]
- Ahmed, J.; Salam, Z. An improved perturb and observe (P&O) maximum power point tracking (MPPT) algorithm for higher efficiency. Appl. Energy 2015, 150, 97–108. [Google Scholar]
- Xu, Z.-R.; Yang, P.; Zhou, D.-B.; Li, P.; Lei, J.-Y.; Chen, Y.-R. An improved variable step size MPPT algorithm based on INC. J. Power Electr. 2015, 15, 487–496. [Google Scholar] [CrossRef]
- Mamarelis, E.; Petrone, G.; Spagnuolo, G. A two-steps algorithm improving the P&O steady-state MPPT efficiency. Appl. Energy 2014, 113, 414–421. [Google Scholar]
- Cheikh, M.A.; Larbes, C.; Kebir, G.T.; Zerguerras, A. Maximum power point tracking using a fuzzy logic control scheme. Rev. Des Energies Renouv. 2007, 10, 387–395. [Google Scholar]
- Algazar, M.M.; El-Halim, H.A.; Salem, M.E.E.K. Maximum power point tracking using fuzzy logic control. Int. J. Electr. Power Energy Syst. 2012, 39, 21–28. [Google Scholar] [CrossRef]
- Shiau, J.-K.; Wei, Y.-C.; Chen, B.-C. A study on the fuzzy-logic-based solar power MPPT algorithms using different fuzzy input variables. Algorithms 2015, 8, 100–127. [Google Scholar] [CrossRef]
- Bouarroudj, N.; Boukhetala, D.; Djari, A.; Rais, Y.; Benlahbib, B. FLC based Gaussian membership functions tuned by PSO and GA for MPPT of photovoltaic system: A comparative study. In Proceedings of the 2017 6th International Conference on Systems and Control (ICSC), Batna, Algeria, 7–9 May 2017; pp. 317–322. [Google Scholar]
- Ameur, K.; Ait-Cheikh, M.S.; Essounbouli, N. A PSO-based Optimization of a fuzzy-based MPPT controller for a photovoltaic pumping system used for irrigation of greenhouses. Iran. J. Fuzzy Syst. 2016, 13, 1–18. [Google Scholar]
- Larbes, C.; Cheikh, S.A.; Obeidi, T.; Zerguerras, A. Genetic algorithms optimized fuzzy logic control for the maximum power point tracking in photovoltaic system. Renew. Energy 2009, 34, 2093–2100. [Google Scholar] [CrossRef]
- Guenounou, O.; Dahhou, B.; Chabour, F. Adaptive fuzzy controller based MPPT for photovoltaic systems. Energy Convers. Manag. 2014, 78, 843–850. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Amjad, M.; Mekhilef, S. An improved particle swarm optimization (PSO)–based MPPT for PV with reduced steady-state oscillation. IEEE Trans. Power Electr. 2012, 27, 3627–3638. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Shamsudin, A.; Amjad, M. A direct control based maximum power point tracking method for photovoltaic system under partial shading conditions using particle swarm optimization algorithm. Appl. Energy 2012, 99, 414–422. [Google Scholar] [CrossRef]
- Dolara, A.; Grimaccia, F.; Mussetta, M.; Ogliari, E.; Leva, S. An Evolutionary-Based MPPT Algorithm for Photovoltaic Systems under Dynamic Partial Shading. Appl. Sci. 2018, 8, 558. [Google Scholar] [CrossRef]
- Duan, Q.; Mao, M.; Duan, P.; Hu, B. An intelligent algorithm for maximum power point tracking in photovoltaic system under partial shading conditions. Trans. Inst. Meas. Control 2017, 39, 244–256. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A Maximum Power Point Tracking (MPPT) for PV system using Cuckoo Search with partial shading capability. Appl. Energy 2014, 119, 118–130. [Google Scholar] [CrossRef]
- Mahmoud, A.; Tamer, K.; Mushtaq, N.; Mohd, A.A. An Improved Maximum Power Point Tracking Controller for PV Systems Using Artificial Neural Network. Przegląd Elektrotechniczny (Electr. Rev.) 2012, 88, 116–121. [Google Scholar]
- Sedaghati, F.; Nahavandi, A.; Badamchizadeh, M.A.; Ghaemi, S.; Fallah, M.A. PV maximum power-point tracking by using artificial neural network. Math. Probl. Eng. 2012. [Google Scholar] [CrossRef]
- Farayola, A.M.; Hasan, A.N.; Ali, A. Efficient photovoltaic MPPT system using coarse gaussian support vector machine and artificial neural network techniques. Int. J. Innov. Comput., Inf. Control (IJICIC) 2018, 14, 323–339. [Google Scholar]
- Khanaki, R.; Radzi, M.A.M.; Marhaban, M.H. Artificial neural network based maximum power point tracking controller for photovoltaic standalone system. Int. J. Green Energy 2016, 13, 283–291. [Google Scholar] [CrossRef]
- Kassem, A.M. MPPT control design and performance improvements of a PV generator powered DC motor-pump system based on artificial neural networks. Int. J. Electr. Power&Energy Syst. 2012, 43, 90–98. [Google Scholar]
- Zhang, L.; Bai, Y. On-line neural network training for maximum power point tracking of PV power plant. Trans. Inst. Meas. Control 2008, 30, 77–96. [Google Scholar] [CrossRef]
- Ghedhab, N.; Youcefettoumi, F. Optimized Photovoltaic Power Generator Using Artificial Neural Network Implementation for Maximum Power Point Tracking. Int. J. Environ. Sci. Dev. 2016, 7, 642. [Google Scholar] [CrossRef][Green Version]
- Cheikh, M.A.; Haddadi, M.; Zerguerras, A. Design of a neural network control scheme for the maximum power point tracking (MPPT). Rev. des energies Renouv. 2007, 10, 109–118. [Google Scholar]
- Elobaid, L.; Abdelsalam, A.K.; Zakzouk, E.E. Artificial neural network based maximum power point tracking technique for PV systems. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 937–942. [Google Scholar]
- Punitha, K.; Devaraj, D.; Sakthivel, S. Artificial neural network based modified incremental conductance algorithm for maximum power point tracking in photovoltaic system under partial shading conditions. Energy 2013, 62, 330–340. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Liu, C.-L.; Huang, J.-W.; Chen, J.-H. Neural-network-based maximum power point tracking methods for photovoltaic systems operating under fast changing environments. Sol. Energy 2013, 89, 42–53. [Google Scholar] [CrossRef]
- Ranjani, K.; Raja, M.; Anitha, B. Maximum power point tracking by ANN controller for a standalone photovoltaic system. Int. J. Electr. Comput. Electron. Commun. Eng. 2014, 8, 592–596. [Google Scholar]
- Messalti, S.; Harrag, A.; Loukriz, A. A new variable step size neural networks MPPT controller: Review, simulation and hardware implementation. Renew. Sustain. Energy Rev. 2017, 68, 221–233. [Google Scholar] [CrossRef]
- Kofinas, P.; Dounis, A.I.; Papadakis, G.; Assimakopoulos, M. An Intelligent MPPT controller based on direct neural control for partially shaded PV system. Energy Build. 2015, 90, 51–64. [Google Scholar] [CrossRef]
- Abu-Rub, H.; Iqbal, A.; Ahmed, S.M. Adaptive neuro-fuzzy inference system-based maximum power point tracking of solar PV modules for fast varying solar radiations. Int. J. Sustain. Energy 2012, 31, 383–398. [Google Scholar] [CrossRef]
- Chaouachi, A.; Kamel, R.; Nagasaka, K. MPPT operation for PV grid-connected system using RBFNN and fuzzy classification. World Acad. Sci., Eng. Technol. 2010, 65, 97–105. [Google Scholar]
- Subiyanto, S.; Mohamed, A.; Hannan, M. Intelligent maximum power point tracking for PV system using Hopfield neural network optimized fuzzy logic controller. Energy Build. 2012, 51, 29–38. [Google Scholar] [CrossRef]
- Veerachary, M.; Senjyu, T.; Uezato, K. Neural-network-based maximum-power-point tracking of coupled-inductor interleaved-boost-converter-supplied PV system using fuzzy controller. IEEE Trans. Ind. Electr. 2003, 50, 749–758. [Google Scholar] [CrossRef]
- Belkaid, A.; Gaubert, J.P.; Gherbi, A. An improved sliding mode control for maximum power point tracking in photovoltaic systems. J. Control Eng. Appl. Inform. 2016, 18, 86–94. [Google Scholar]
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Romero, B.; Del Pozo, G.; Arredondo, B. Exact analytical solution of a two diode circuit model for organic solar cells showing S-shape using Lambert W-functions. Sol. Energy 2012, 86, 3026–3029. [Google Scholar] [CrossRef]
- Ahmad, T.; Sobhan, S.; Nayan, M.F. Comparative analysis between single diode and double diode model of PV cell: concentrate different parameters effect on its efficiency. J. Power Energy Eng. 2016, 4, 31. [Google Scholar] [CrossRef]
- Shannan, N.M.A.A.; Yahaya, N.Z.; Singh, B. Single-diode model and two-diode model of PV modules: A comparison. In Proceedings of the 2013 IEEE International Conference on Control System, Computing and Engineering, Mindeb, Malaysia, 29 November–1 December 2013; pp. 210–214. [Google Scholar]
- Duong, M.Q.; Nguyen, H.; Leva, S.; Mussetta, M.; Sava, G.N.; Costinas, S. Performance analysis of a 310Wp photovoltaic module based on single and double diode model. In Proceedings of the 2016 International Symposium on Fundamentals of Electrical Engineering (ISFEE), Bucharest, Romania, 30 June–2 July 2016; pp. 1–6. [Google Scholar]
- AlRashidi, M.; El-Naggar, K.; AlHajri, M. Parameters estimation of double diode solar cell model. Int. J. Electr. Comput. Energ. Electr. Commun. Eng. 2013, 7, 118–121. [Google Scholar]
- Ait-Cheikh, M.S. Etude, Investigation et conception d’algorithmes de commande appliqués aux systèmes photovoltaïques. Ph.D. Thesis, Ecole Nationale Polytechnique, Algiers, Algeria, December 2007. [Google Scholar]
- Yordanov, G.; Midtgård, O.; Saetre, T. Two-diode model revisited: Parameters extraction from semi-log plots of I-V data. In Proceedings of the 25th European Photovoltaic Solar Energy Conference and Exhibition/5th World Conference on Photovoltaic Energy Conversion, Valencia, Spain, 6–10 September 2010; pp. 4156–4163. [Google Scholar]
- Franzitta, V.; Orioli, A.; Gangi, A.D. Assessment of the Usability and Accuracy of Two-Diode Models for Photovoltaic Modules. Energies 2017, 10, 564. [Google Scholar] [CrossRef]
- Bechouat, M.; Younsi, A.; Sedraoui, M.; Soufi, Y.; Yousfi, L.; Tabet, I.; Touafek, K. Parameters identification of a photovoltaic module in a thermal system using meta-heuristic optimization methods. Int. J. Energy Environ. Eng. 2017, 8, 331–341. [Google Scholar] [CrossRef]
- Et-torabi, K.; Nassar-eddine, I.; Obbadi, A.; Errami, Y.; Rmaily, R.; Sahnoun, S.; Agunaou, M. Parameters estimation of the single and double diode photovoltaic models using a Gauss–Seidel algorithm and analytical method: A comparative study. Energy Convers. Manag. 2017, 148, 1041–1054. [Google Scholar] [CrossRef]
- Ovaska, S. Maximum power point tracking algorithms for photovoltaic applications. Master’s Thesis, Aalto University, Espoo, Finland, 14 December 2010. [Google Scholar]
- Ogliari, E.; Dolara, A.; Manzolini, G.; Leva, S. Physical and hybrid methods comparison for the day ahead PV output power forecast. Renew. Energy 2017, 113, 11–21. [Google Scholar] [CrossRef]
- Fei, J.; Wang, Z. Adaptive RBF neural network control for three-phase active power filter. Int. J. Adv. Robot. Syst. 2013, 10, 258. [Google Scholar] [CrossRef]
- Widrow, B.; Lehr, M.A. 30 years of adaptive neural networks: perceptron, madaline, and backpropagation. Proc. IEEE 1990, 78, 1415–1442. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning internal representations by error propagation; Institute for Cognitive Science, University of California: Oakland, CA, USA, September 1985. [Google Scholar]
- Pedrycz, W. Why triangular membership functions? Fuzzy sets Syst. 1994, 64, 21–30. [Google Scholar] [CrossRef]
- Al-Gizi, A.G. Comparative study of MPPT algorithms under variable resistive load. In Proceedings of the 2016 International Conference on Applied and Theoretical Electricity (ICATE), Craiova, Romania, 6–8 October 2016; pp. 1–6. [Google Scholar]
- Bechouat, M.; Soufi, Y.; Sedraoui, M.; Kahla, S. Energy storage based on maximum power point tracking in photovoltaic systems: A comparison between GAs and PSO approaches. Int. J. Hydrog. Energy 2015, 40, 13737–13748. [Google Scholar] [CrossRef]









| Parameters | Values |
|---|---|
| Maximum power Pmax | 61.92 W |
| Open Circuit Voltage voc | 25.25 V |
| Short Circuit Current iph-max | 3.25 A |
| Voltage at Maximum Power vopt | 20 V |
| Current at Maximum Power iopt | 3 A |
| Ideality factor n1 | 1 |
| Ideality factor n2 | 2 |
| Number of series cells Ns | 36 |
| Region 1 | Region 2 | Region 3 | |||
|---|---|---|---|---|---|
| Input E | NB | NS | ZE | PS | PB |
| Output Δv | NB | NS | ZE | PS | PB |
| P and O | INC Adaptive RBF-NN | Fuzzy Adaptive RBF-NN | |
|---|---|---|---|
| Scenario 1 | 96.26 | 96.87 | 98.13 |
| Scenario 2 | 97.03 | 98.56 | 99.21 |
| Scenario 3 | 89.50 | 97.38 | 99.14 |
| Scenario 4 | 94.89 | 97.74 | 98.75 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouarroudj, N.; Boukhetala, D.; Feliu-Batlle, V.; Boudjema, F.; Benlahbib, B.; Batoun, B. Maximum Power Point Tracker Based on Fuzzy Adaptive Radial Basis Function Neural Network for PV-System. Energies 2019, 12, 2827. https://doi.org/10.3390/en12142827
Bouarroudj N, Boukhetala D, Feliu-Batlle V, Boudjema F, Benlahbib B, Batoun B. Maximum Power Point Tracker Based on Fuzzy Adaptive Radial Basis Function Neural Network for PV-System. Energies. 2019; 12(14):2827. https://doi.org/10.3390/en12142827
Chicago/Turabian StyleBouarroudj, Noureddine, Djamel Boukhetala, Vicente Feliu-Batlle, Fares Boudjema, Boualam Benlahbib, and Bachir Batoun. 2019. "Maximum Power Point Tracker Based on Fuzzy Adaptive Radial Basis Function Neural Network for PV-System" Energies 12, no. 14: 2827. https://doi.org/10.3390/en12142827
APA StyleBouarroudj, N., Boukhetala, D., Feliu-Batlle, V., Boudjema, F., Benlahbib, B., & Batoun, B. (2019). Maximum Power Point Tracker Based on Fuzzy Adaptive Radial Basis Function Neural Network for PV-System. Energies, 12(14), 2827. https://doi.org/10.3390/en12142827